Abstract
Deep learning has become indispensable for identifying hierarchical spatial features (SFs), which are crucial for linking neurological disorders to brain functionality, from functional Magnetic Resonance Imaging (fMRI). Unfortunately, existing methods are constrained by architectures that are either linear or nonlinear, limiting a comprehensive categorization of spatial features. To overcome this limitation, we introduce the Semi-Nonlinear Deep Efficient Reconstruction (SENDER) framework, a novel hybrid approach designed to simultaneously capture both linear and nonlinear spatial features, providing a holistic understanding of brain functionality. In our approach, linear SFs are formed by directly integrating multiple spatial features at shallow layers, whereas nonlinear SFs emerge from combining partial regions of these features, yielding complex patterns at deeper layers. We validated SENDER through extensive qualitative and quantitative evaluations with four state-of-the-art methods. Results demonstrate its superior performance, identifying five reproducible linear SFs and eight reproducible nonlinear SFs.
1. Introduction
Spatial features (SFs) extracted from functional Magnetic Resonance Imaging (fMRI) showcase a specific brain region affected by neurological disorders, which is more straightforward than analyzing sequential time series in fMRI [1,2,3]. During the COVID-19 pandemic, investigators have reported an impaired spatial feature in a patient’s brain with olfactory loss [4].
With rapid developments in machine learning, the hierarchy of SFs in the human brain has been explored through various deep linear learning techniques, including Deep Independent Component Analysis (DICA) [5], Sparse Deep Dictionary Learning (SDDL) [6], and Deep Non-negative Matrix Factorization (DNMF) [7,8]. These methods have provided valuable insights into brain functionality, yet they are built on linear frameworks, i.e., without activation functions connecting adjacent layers. Meanwhile, the advent of deep learning has propelled the identification of SFs, introducing a suite of deep nonlinear methods capable of uncovering more intricate hierarchical SFs. In particular, techniques such as the Deep Convolutional Autoencoder (DCAE), Restricted Boltzmann Machine (RBM), Deep Belief Network (DBN), and Convolutional Neural Network (CNN) [9,10,11,12,13,14,15,16] have been employed extensively in functional Magnetic Resonance Imaging (fMRI) research. Among these, the RBM has demonstrated exceptional precision in extracting and reconstructing hierarchical temporal and spatial features [13,17,18,19]. Recent studies have also highlighted the effectiveness of deep nonlinear methods like DCAE and DBN in analyzing task-based fMRI time series, revealing task-evoked spatial features and their hierarchical temporal organization [10,17,18,20]. These methods usually leverage activation functions, such as Sigmoid and Rectified Linear Unit (ReLU) [21], positioning them as essential tools for advancing our understanding of the human brain’s functional architecture [14].
In particular, from a computational neuroscience perspective, methodologies for uncovering the hierarchy of spatial features in the brain can be broadly categorized into two main approaches. On one hand, Deep Linear Methods, such as DNMF and SDDL, focus on identifying linear spatial features. These features are typically conceptualized as linear combinations of shallow features, as described by Smith in 2009 [22] and elaborated on by Wylie in 2021 [5]. On the other hand, Deep Nonlinear Methods, such as Deep Neural Networks (DNNs), are designed to investigate nonlinear spatial features. Unlike linear methods, these approaches model nonlinear combinations of shallow features, often integrating multiple regions in a nonlinear fashion [23]. By leveraging nonlinear activation functions, such as ReLU or Sigmoid, nonlinear methods provide deeper insights into more intricate and complex SFs [12,14]. However, these nonlinear features are often located in deeper layers, making them more difficult to interpret and explain [12,14]. Notably, despite the strengths of both approaches, current deep learning methods are typically constrained to being either linear or nonlinear. This limitation poses significant challenges for researchers aiming to concurrently categorize spatial features as both linear and nonlinear, leaving a gap in the comprehensive understanding of brain functionality.
To address the existing challenges, we introduce the Semi-Nonlinear Deep Efficient Reconstruction (SENDER), a novel hybrid deep learning framework that is specifically designed to concurrently uncover both linear and nonlinear spatial features in the brain. Overall, SENDER incorporates the strengths of deep linear and nonlinear methods, leveraging the efficiency of linear models that require smaller training samples while employing the advanced perception capabilities of nonlinear methods through activation functions and efficient non-fully connected architectures.
Specifically, the methodological contributions of SENDER are detailed as follows: (1). Automatic Hyperparameter Tuning. To implement automatic hyperparameter tuning, such as the number of components (i.e., the number of layers and units/neurons) in each layer [24,25], we have developed a rank reduction technique called the Rank Reduction Technique (RRT) for SENDER. RRT employs orthogonal decomposition, specifically QR matrix decomposition, to estimate the rank of input matrices, e.g., feature matrices, which corresponds to the number of units. This estimation is achieved through three techniques: weighted ratio (WR), weighted difference (WD), and weighted correlation (WC). These techniques systematically reduce the size of feature matrices through all layers until the estimated number of features equals one. (2). Accurate Approximation. SENDER achieves approximation accuracy comparable to that of traditional DNNs, demonstrating its capabilities to deliver precise and reliable results. (3). Efficient Hybrid Architecture. Unlike any existing deep linear or nonlinear method, we demonstrated that the non-fully connected architecture of SENDER not only enhances efficiency, e.g., makes it easy to optimize, but also allows for precise spatial feature extraction at an individual level. (4). Reduced Accumulative Error via Matrix Backpropagation (MBP). When a deep learning model is constructed using a wide array of layers, the accumulative error could potentially deteriorate the accuracy. Thus, we utilize the MBP technique [7,8,26] to further improve the accuracy.
In summary, leveraging the capabilities of SENDER, we identified five linear and eight nonlinear SFs from its second linear and nonlinear layers, respectively. The five linear SFs indicate significant linear integration of various shallow SFs, while the eight nonlinear SFs demonstrate the integration by combining multiple partial regions from these shallow SFs. In contrast, even advanced deep learning methods like DBN can only identify five nonlinear SFs, which predominantly exhibit linear integration of shallow SFs. More importantly, all these linear and nonlinear SFs derived via SENDER showcase strong reproducibility. As our understanding of neuroscience advances, nonlinear SFs are expected to deepen our knowledge of brain functionality.
2. Materials and Methods
This section provides an in-depth description of SENDER, covering several critical aspects of the framework. The following Figure 1 illustrates the computational framework of SENDER.
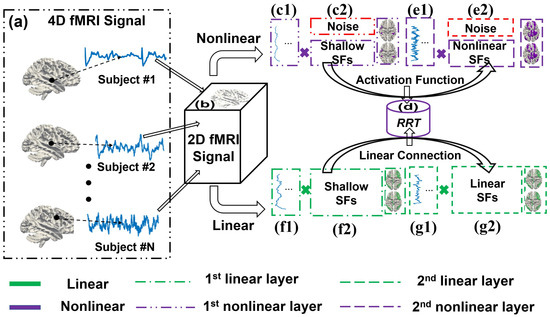
Figure 1.
An illustration of SENDER identifying linear and nonlinear spatial features.
In particular, Figure 1 shows the step-by-step process of SENDER identifying linear and nonlinear SFs. Steps include (a) collecting 4D fMRI raw data and (b) converting all 4D fMRI raw data into 2D matrices. (c1) and (c2): The first nonlinear layer. (d) RRT implements hyperparameter tuning. (e1) and (e2): The second nonlinear layer extracts time series and nonlinear SFs, with a visual example provided. (f1) and (f2): The first linear layer. (g1) and (g2): The second linear layer reveals time series and linear SFs, with a visual example provided.
2.1. Multiband Multi-Echo fMRI Data and Preprocessing
This fMRI data collection was performed using a 3T scanner (Signa Premier, GE Healthcare, Waukesha, WI, USA) equipped with a body transmit coil and a 32-channel NOVA (Nova Medical, Wilmington, MA) receive head coil. Overall, 29 participants’ MB and MBME fMRI data were acquired, and 19 of them returned within two weeks for repeat imaging [27]. Importantly, various works demonstrated that MBME fMRI can improve the spatial resolution and functional sensitivity [27,28,29]. Therefore, the proposed computational framework can benefit from MBME fMRI to present more complex and even never-reported SFs.
Specifically, the maximum gradient strength was 70 mT/m, and the maximum slew rate was 170 mT/m/ms. Each subject underwent two resting-state fMRI (rsfMRI) acquisitions: an MB scan and an MBME scan. The MB scan had the following parameters: TR/TE = 650/30 ms, FOV = 24 cm, matrix size = 80 × 80 with slice thickness = 3 mm (3 × 3 × 3 mm voxel size), 11 slices with a multiband factor of 4 (44 total slices), FA = 60°, and partial Fourier factor = 0.85. The MBME scan had the following parameters: TR/TE = 900/11, 30, 49 ms, FOV = 24 cm, matrix size = 80 × 80 with slice thickness = 3 mm (3 × 3 × 3 mm voxel size), 11 slices with a multiband factor of 4 (44 total slices), FA = 60° and partial Fourier factor = 0.85. Both scans used an EPI readout with in-plane acceleration (R) = 2. The resting-state scans lasted six minutes each, resulting in 400 volumes for the MBME scans. During the resting-state scans, subjects were instructed to close their eyes but remain awake, refrain from any motion, and not think about anything in particular [27,28,29,30,31]. Notably, recent research [32] suggests that having eyes closed tends to correlate with greater integration, while having eyes open correlates with greater specialization. In this work, to advance the identification of linear and nonlinear SFs, an integration of multiple shallow SFs (i.e., SFs identified from the first layer), we recommended that all participants keep their eyes closed.
The MBME fMRI data preprocessing followed the steps in previous works [27,28,31,33,34]. The preprocessing pipelines generally included skull removal, motion correction, slice time correction, spatial smoothing, and BOLD signal filtering. Finally, a brain mask was applied to extract all fMRI signals. Importantly, due to the limitations of ICA demonstrated in previous work [35], we decided to employ the preprocessing pipeline proposed by the works of [33,34] to reduce the influence of ICA by separating SFs at deep layers into independent patterns, which results in missing specific SFs.
Moreover, Figure 2 illustrates a novel hybrid structure for constructing the computational framework of SENDER. In particular, subfigure (a) demonstrates a linear structure without activation functions. In contrast, subfigure (b) showcases nonlinear structure that leverages activation functions (denoted as ) to introduce nonlinearity. This hybrid architecture allows SENDER to identify more complex SFs from fMRI.
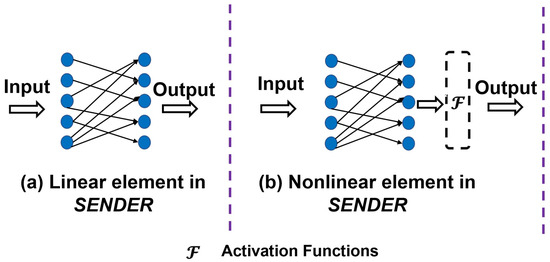
Figure 2.
An illustration of the linear and nonlinear architecture of SENDER. Subfigure (a) illustrates a linear structure without any activation functions. Subfigure (b) showcases a nonlinear structure with activation functions.
2.2. Semi-Estimated Nonlinear Deep Efficient Reconstructor
As previously introduced, SENDER utilizes a hybrid architecture that integrates both linear and nonlinear learning, incorporating an efficient non-fully connected structure [36] along with nonlinear activation functions typically used in DNNs. This section presents the objective function that governs SENDER, outlining how it integrates linear and nonlinear architectures to improve its performance in extracting holistic SFs in the human brain. The specific formulation of the optimization function is presented below:
In the architecture of SENDER shown in Equation (1), denotes the hierarchical weight matrices (i.e., mixing matrices) of the linear SENDER; specifically, denotes the weight matrix at the layer, with k indicating the total layers number. Similarly, refers to the weight matrices for the nonlinear method at each corresponding layer. Additionally, represents deeper spatial features derived via the linear method, where specifically denotes the deep feature matrix at the layer. Concurrently, defines deeper features uncovered through the nonlinear method at each layer. Moreover, represents a series of matrices indicating background noise, calculated using the norm [37] due to their sparsity characteristics. The nonlinear activation function at each layer is denoted by , such as activation functions like Sigmoid or Rectified Linear Unit (ReLU), which are critical for enhancing nonlinearity within the model [12,14]. For instance, suppose the total number of layers is M, and considering the original input data I, the decomposition of data within SENDER can be expressed as follows:
As shown in Equation (1), which is similar to the objective function in previous works [6,8,38], our fundamental assumption is that the previously revealed spatial features, e.g., or , can be further decomposed as a linear product of a deeper weight matrix and spatial features , or as a nonlinear representation involving a deeper weight matrix and spatial features . Additionally, the objective function governing SENDER encompasses more variables than traditional deep linear/nonlinear methods such as DICA, DNMF, and SDDL [5,6,7,8], reflecting its complex aim of extracting a broader spectrum of spatial feature nuances. Therefore, we determine advanced gradient-based optimizer [39] to optimize SENDER. Importantly, we employ an optimizer based on proximal gradient [40] to solve the norm penalty. Each adjacent layer of linear and nonlinear architectures is connected via non-fully connected layers [36].
2.3. Rank Reduction Technique for Automatic Tuning Hyperparameters
To implement automatic hyperparameter tuning and reduce the high dimensionality of the original input dataset, we introduce a novel technique named the Rank Reduction Technique (RRT). This method is designed to calculate and reduce the rank of the current pattern matrices, such as and , until their rank is equivalent to one.
Specifically, inspired by previous works [41,42], RRT incorporates rank-revealing techniques using orthogonal decomposition through QR factorization (e.g., and is a upper triangular matrix) to efficiently estimate and reduce the rank of pattern matrices. Due to the effectiveness of QR factorization in handling sparse and overcomplete matrices, RRT is satisfactory for decomposing these data structures, which are often encountered in deep learning applications for neuroimaging. The application of RRT thus facilitates the handling of complex datasets by simplifying their structure and reducing dimensionality without significant loss of information, which is essential for enhancing the performance of SENDER. The mathematical representation of RRT involves iteratively applying QR factorization to adjust the eigenvalues and eigenvectors of the pattern matrices, effectively minimizing their rank while retaining the essential components within the data. In fact, RRT can reduce the dimensionality of the input data matrix continuously by layers. For instance, RRT can estimate the number of components as 25 at the first layer. Subsequently, RRT continuously estimates the number of components as 6 at the second layer. Finally, RRT reduces the number of components to 1 at the third layer. Lastly, the estimation is completed since it is impossible to decompose a single vector. Thus, RRT can present the number of layers as 3 and the size of components (i.e., the number of artificial neurons) as 25, 6, and 1 across 3 layers, respectively. The RRT can be summarized in the following formula:
where the operator represents the RRT, and is a series of vectors, with each representing an individual vector. When RRT is applied repeatedly to the series of vectors over k iterations, the rank of the matrix formed by these vectors decreases: . Moreover, if k is sufficiently large, there exists a number such that if , the rank of the matrix formed by these vectors satisfies . In this scenario, k corresponds to the total number of layers in the model, as the rank of the pattern matrix at the layer becomes one after repeatedly applying RRT. In detail, at first, the diagonal of matrix R, derived from the pattern matrix using QR decomposition, is non-increasing in magnitude [26,38,43].
Furthermore, along the main diagonal of the matrix R, three techniques named WR, WD, and WC are applied to calculate the maximum rank shown in Equations (3)–(5); then, I is replaced by , , iteratively. It indicates that the rank-reducing technique can yield a reasonable solution using QR factorization [26,38,43]. The following formulas provide details of WR, WD, and WC.
Let and , then WR can be calculated by Equation (3) [38,43]:
where represents a diagonal element of matrix derived by QR decomposition and represents a single value of WR. The value of each WR is calculated by the ratio of the current element of the diagonal and the following element.
Similarly, WD is calculated as
In Equation (4), WD [38,43] is defined as the absolute difference between the current diagonal element and the previous one divided by the cumulative sum of all the previous diagonal elements.
Equation (5), including and representing adjacent columns of matrix R, after QR decomposition, describes the proposed WC as follows:
Since WD, WR, and WC are the cumulative difference, ratio, and correlation of two adjacent components, respectively, the matrix dimension can be reduced by one at least after rank estimation. Thus, the RRT iteratively determines the maximum value position from WD, WR, and WC to conduct the estimated rank.
2.4. Matrix Backpropagation
Another important technical contribution introduced in this work is the implementation of matrix backpropagation (MBP) in SENDER to further reduce potential accumulative error after updating all variables in the model. On the one hand, performing matrix backpropagation on the linear architecture of SENDER focuses on updating feature matrices. First, we group the feature matrix at the last layer and calculate the product of weight and the feature matrix at other layers. Subsequently, we calculate the product of each weight matrix in all layers. Furthermore, we calculate the residual error using the difference between input and nonlinear architecture. Lastly, all positive values within the feature matrix will be updated via integrating the positive and negative values within residual error, the product of all weight matrices, and current feature matrix. For the linear structure in SENDER, the product of the weight matrices , the term , and the residual at the current layer (e.g., the layer) are utilized to perform backpropagation [8,26].
Then, the following formula describes the crucial steps of MBP to update variables of and , representing the hierarchical weight and pattern matrices, respectively. In Equation (8), and represent all positive and negative elements, respectively [7,8].
On the other hand, the derivatives of the activation functions , weight matrices , and feature matrices are adopted to perform backpropagation on the nonlinear architecture of SENDER. In brief, the MBP is similar to the backpropagation utilized in Deep Neural Networks [8]. First, we denote the residual error as the difference between input and linear architecture. Subsequently, we denote an important variable representing the product of weight matrix, its transpose, and the maximum value. Furthermore, we define the derivative of activation function and intermedium variables to update the weight and feature matrices. Lastly, we introduce an iterative framework, using a constant to reduce potential accumulative error in both weight and feature matrices [8,44].
In Equation (9), two important variables are involved: deep weight matrices and pattern matrices in the nonlinear method, where represents the current iteration. These variables are updated using the following backpropagation techniques, as shown in Equation (10) [8,44]:
Finally, the following equations show the process of updating the weight matrix and the pattern matrix in the layer. In addition, is a constant value determined as 0.01 [8].
Notably, we also provide pseudocode of SENDER (Algorithm) and other vital techniques in Appendix B.
2.5. The Accurate Approximation of SENDER
In this section, we theoretically analyze the property of the proposed SENDER. Due to SENDER being organized as a composition of linear and nonlinear architectures, the following theorem demonstrates that SENDER can accurately approximate any real function that is finite almost everywhere [45]. The detailed proof of Theorem 1 can be viewed in Appendix A.
Definition 1.
(SENDER Operator) Denote the initialization operator as , the sparse operator as , the rank reduction operator as , and the STORM operator as . Their norms can be represented as , , , and . SENDER can be treated as a combination of various operators as .
Theorem 1.
(Accurate Approximation of SENDER) Consider a real function and where represents the Lebesgue measure [45]. Given , SENDER includes a linear method and a nonlinear method with multiple activation functions denoted as and . If denotes a series of linear functions and denotes a series of nonlinear functions, then we have .
3. Results
To validate the effectiveness of the proposed SENDER, we utilized publicly available fMRI signals from all healthy individuals in the Multiband Multi-echo fMRI dataset [46]. By augmenting the original 29 test–retest subjects [47], we created a dataset of 100 augmented subjects to validate the proposed SENDER, and the size of an individual fMRI signal matrix is 400 × 902,629. To minimize the heterogeneous effects arising from parameter tuning, all hyperparameters of other peer methods were aligned with the estimation results of SENDER. Specifically, SENDER automatically estimated the number of layers as 3 across all subjects, with the number of SFs per layer being , , and (). Meanwhile, the parameters for other peer methods were tuned according to guidelines from established studies [5,6,8,25] to ensure fairness and consistency in performance evaluation. The activation function for all layers within both SENDER and the DBN was set to ReLU [14]. Importantly, the cross-validation using training and testing is not a suitable evaluation metric for unsupervised learning [12] like SENDER. Thus, in medical research, reproducibility should be one of the most critical gold standards [48] for evaluating the performance of unsupervised methods. Thus, validating the global reproducibility of SENDER and other peer methods across all test–retest subjects is more suitable.
To begin, we validate the robustness, efficiency, and accuracy of SENDER by comparing it with peer methods. The results are quantified in Table 1 and Table 2, and Figure 3, demonstrating the advancements of SENDER over peer approaches.

Table 1.
Estimations (mean ± standard deviation) of layer number across 100 subjects using SENDER and DBN SearchNet.

Table 2.
Time consumption comparison in seconds of SENDER and other peer methods.
In addition, shallow SF templates identified at the shallow layers of computational models [10,19,49] in the first row in Figure 4 and Figure 5 illustrate the fundamental brain functionality, such as auditory (in the fourth column in Figure 4) and primary visualization (in the first column in Figure 4) [10,22]. These have been identified over the past two decades through conventional computational frameworks [22] and continue to play a key role in advancing our understanding of more complex brain functionalities and validating innovative methods for fMRI analysis [2,3,10,19,35,49].
Furthermore, due to the lack of a concrete ground truth for linear and nonlinear SF templates, we employ multiple data-driven pipelines [35,50,51,52] to generate reproducible group-wise linear and nonlinear SFs. In particular, on the one hand, we applied two of the most representative approaches, SDDL [6] and Deep ICA [5] on each real MBME fMRI signal to identify linear SFs, with each real MBME fMRI matrix 400 × 906,629 in size. Importantly, SENDER’s hyperparameters are determined automatically, while those for Deep ICA and Deep SDL were tuned based on prior studies [5,6]. After removing noisy SFs and artifacts [51], we calculated spatial similarity [35] across all SFs identified in the second layer using other peer approaches. We then performed clustering (e.g., k-means) to categorize SFs based on spatial similarity [35,50]. Notably, the number of clusters is not manually designed in this work. In fact, we conduct a series of simulated experiments which are similar to our previous work [35], to present potential linear and nonlinear SFs via SENDER. These simulated experiments pave the way to determine a reasonable number of clusters. Additionally, we create group-wise SFs as templates via Gaussian smoothing [52] based on individual SFs within each dominant cluster, covering at least 90% of subjects [50]. This process yielded five group-wise linear SFs. We employed SENDER and DBN using a similar process. This led to the generation of eight group-wise nonlinear SFs for SENDER and four for DBN, demonstrating SENDER’s superior ability to uncover more complex SFs. These group-wise linear and nonlinear SFs are capable of further mitigating demographic sensitivity and inherent variability in identified SFs.
Finally, in Figure 4, Figure 5, Figure 6 and Figure 7, the values (ranging from red to yellow), e.g., intensities, within each SF reflect the activation intensity of different brain regions, with higher values indicating stronger activation [3]. This information is essential for understanding neural activity levels using fMRI [53,54,55].
3.1. The Robustness, Efficiency, and Accuracy of SENDER
In this section, we evaluate the performance of SENDER using data from 100 augmented subjects, comprising 29 original subjects and 71 augmented subjects derived from MBME fMRI data. The 71 augmented subjects were generated by introducing random noise. The validation process is structured into three key perspectives: (1) Robustness: Assessing the ability of SENDER to reliably estimate vital hyperparameters across all subjects. (2) Efficiency: Comparing the time efficiency of SENDER against other peer methods across all subjects. (3) Accuracy: Measurement of the reconstruction error of SENDER compared to peer methods for all subjects. The details of the computational environment are as follows: Dell PowerEdge R740XD Server with Intel Xeon Gold 6246R (32 Cascade Lake cores) 3.4 G, 35.75 M Cache.
Given the inclusion of noise in the 71 augmented subjects, this evaluation leverages noisy data to ensure rigorous testing of SENDER’s capabilities.
To begin, we incorporated MBME fMRI data from the 100 augmented subjects to estimate the hyperparameters of the data matrix corresponding to each subject. Recognizing the growing prominence of evolutionary search techniques, we employed the Evolutionary Neural Architecture Search (ENAS) [56] and DBN SearchNet [11] frameworks to determine the critical hyperparameters of the DBN. The following Table 1 showcases the robustness comparison of SENDER, ENAS, and DBNSearchNet when estimating critical hyperparameter using 100 augmented subjects.
Furthermore, we evaluate the efficiency of the proposed SENDER in comparison with other peer methods, including DICA [5], DNMF [8], SDDL [6], and DBN [10]. Efficiency is assessed based on the time consumption required by each method to identify spatial features (SFs). Since most methods lack automatic hyperparameter tuning, we standardized the layer number to three and determined the number of components following prior studies [5,6,7,8,10]. Table 2 summarizes the time consumption comparisons. It presents the mean and standard deviation of the time required by each method to extract SFs from 100 augmented subjects. The results reveal that DICA is the fastest method for extracting SFs, while DBN is the slowest, requiring the most time even for a single subject. Notably, SENDER demonstrates faster performance compared to SDDL and shows no significant difference in time consumption compared to DNMF. Meanwhile, a t-test comparing the time consumption of DNMF and SENDER for extracting SFs across 100 augmented subjects yields a p-value of 0.1631 and 0.2146 at the first and second layers, indicating that the efficiency of SENDER is statistically comparable to that of DNMF. These findings highlight SENDER’s efficiency while maintaining robust performance.
Moreover, we validate the accuracy of the proposed SENDER with other peer methods. We utilize the reconstruction loss, which is shown in Equation (12), to represent the accuracy.
In Equation (12), denotes weight or mixing matrices, and represents the identified SFs (i.e., the feature matrix) at the layer. I indicates the input matrix. Within this evaluation, we set the maximum iteration as 5000. For the tuning of other parameters, refer to previous works [5,6,8,10].
In particular, Figure 3a highlights that SENDER achieves the most accurate reconstruction loss among all methods, with most reconstruction losses clustering around 0.00001. To further illustrate the accuracy of SENDER, Figure 3b presents a convergence curve that shows the average reconstruction loss at each iteration. The results demonstrate that SENDER not only converges faster than other peer methods but also achieves more precise reconstruction losses. To substantiate the accuracy of SENDER, we conducted a t-test comparing the reconstruction loss across 100 augmented subjects between SENDER and DBN. The resulting p-value of indicates a statistically significant difference, underscoring SENDER’s superior accuracy.
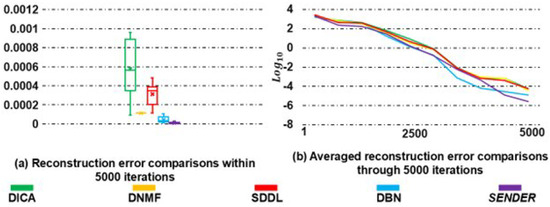
Figure 3.
A quantitative illustration of the identifiability of identified shallow, linear, and nonlinear SFs via SENDER and other peer methods, as well as a comparison of reconstruction accuracy.
Overall, this section demonstrates that SENDER outperforms other peer methods, as evidenced by various statistical measurements and a large sample size. First, leveraging advanced matrix decomposition techniques, SENDER exhibits greater robustness compared to prevalent evolutionary search methods. Notably, SENDER consistently estimates the average number of artificial neurons (i.e., the number of components) as 1, with a standard deviation of 0, across 100 augmented subjects. Second, thanks to its advanced optimizer, SENDER achieves faster decomposition compared to peer methods, with time consumption comparable to DNMF [7,8]. Third, SENDER delivers the most accurate reconstruction loss, excelling in the extraction of both linear and nonlinear spatial features (SFs). Its reconstruction loss is significantly more precise than that of other methods, underscoring its superior accuracy. Finally, given that the fMRI signal matrices of 71 augmented subjects were generated by adding random noise, the results—particularly in hyperparameter estimation and accuracy—highlight the robustness of SENDER. This robustness can be attributed to the integration of the norm, which effectively enhances denoising capabilities.
3.2. Qualitative Comparison of Identified Shallow and Linear SFs via SENDER with Other Peer Methods
In this section, we validate the performance of SENDER to reveal SFs with other peer methods. Briefly, we validate whether SENDER can identify more precise SFs compared with ground-truth and more linear as well as nonlinear SFs with higher reproducibility.
Figure 4 and Figure 5 showcase a comparative identification of shallow SFs [22] using SENDER at the first linear and nonlinear layers, alongside other peer methods, including DICA [5], DNMF [7,8], SDDL [6], and DBN [25]. The results from the linear and nonlinear architectures of SENDER and the other four peer methods are measured against ground-truth SFs [22]. This experimental validation illustrates that the identification of shallow SFs using SENDER aligns closely with established ground-truth SFs [22], demonstrating no significant variance.
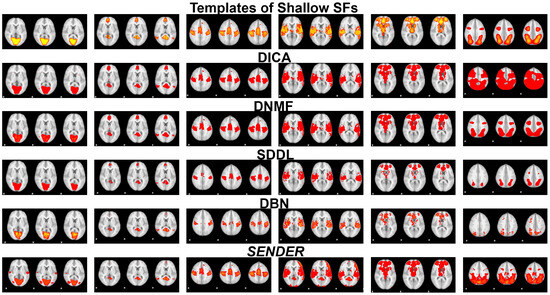
Figure 4.
This figure illustrates three representative slices of six shallow SFs derived via SENDER and four other peer methods at the first linear and nonlinear layer.
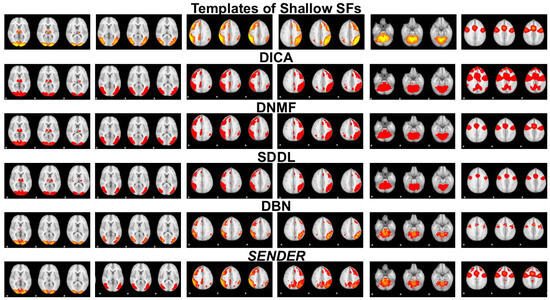
Figure 5.
This figure illustrates three representative slices of another six shallow SFs derived via SENDER and four other peer methods at the first linear and nonlinear layer.
Importantly, the parameters for other peer methods were tuned according to guidelines from established studies [5,6,8,25] to ensure fairness and consistency in performance evaluation. The activation function for all layers within both SENDER and the DBN was set to ReLU. The following figure illustrates qualitative results of identified shallow spatial features via SENDER and other peer methods. Meanwhile, leveraging the previously introduced data-driven pipelines [35,50,51,52], we identify and present twelve group-wise shallow SFs that exhibit the highest spatial similarity with established ground-truth templates [22]. This consistency underscores the robustness of SENDER in detecting reproducible shallow SFs.
Notably, Figure 6 demonstrates that the linear SFs identified from SENDER’s second linear layer, like other methods, capture similar group-wise linear SFs at the second layer. Due to the lack of concrete ground truth for linear SFs, we sourced five representative linear ground-truth SFs from several key studies [5,57]. Overall, in Figure 3, linear SFs derived via SENDER at its second linear layer showcase a significant spatial similarity compared with ground-truth SFs in the first row. In particular, SENDER identifies larger spatial areas than DICA, with linear SFs aligning with SDDL but differing from DNMF; however, SDDL misses some SFs in the fourth column that SENDER can capture.
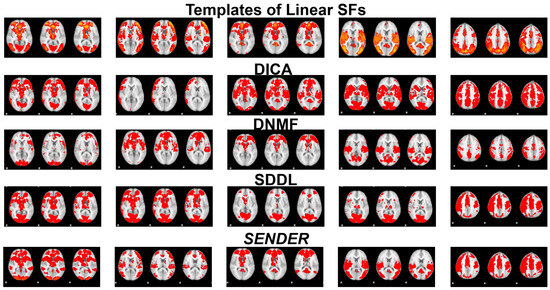
Figure 6.
This figure presents three representative slices of linear SFs revealed via SENDER at the second linear layer and three other peer methods at the second layer.
3.3. Qualitative Comparison of Identified Nonlinear SFs via SENDER and Other Peer Methods
Moreover, we present the qualitative results of nonlinear SFs extracted by SENDER and DBN, as illustrated in Figure 4. Since there is no concrete ground truth for nonlinear SFs, we employ multiple data-driven pipelines [50,51,52] to conduct a ground truth for these networks. Specifically, after removing noisy SFs and artifacts [51], we calculate the spatial similarity [35] for identified SFs at the second layer across all test and retest subjects. We then perform clustering (e.g., k-means) to categorize SFs based on spatial similarity [35]. Finally, we derive group-wise nonlinear SFs using Gaussian smoothing [52] on individual SFs within each dominant cluster, including at least 90% of all subjects [50].
In particular, as shown in Figure 7, SENDER demonstrates a superior capability in revealing eight nonlinear SFs compared to DBN, one of the most widely used nonlinear learning methods [25]. For instance, in the first row and the first and second columns of Figure 7, two nonlinear SFs derived by SENDER highlight left and right partial regions with an SF, combined with major visual and auditory networks [22]. In contrast, all SFs extracted by DBN exhibit approximate linear integration of various shallow SFs. Notably, other linear methods, such as DICA [5], DNMF [8], and SDDL [6], fail to consistently identify these nonlinear SFs, with a low reproducibility.
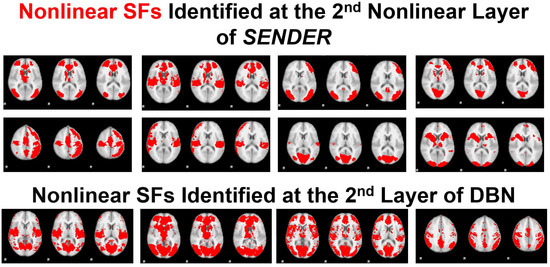
Figure 7.
This figure provides 8 nonlinear SFs identified via SENDER at the second nonlinear layer and 4 SFs extracted by DBN at the second layer.
3.4. Quantitative Comparison of Identified Shallow, Linear, and Nonlinear SFs via SENDER and Four Other Peer Methods
As discussed before, cross-validation and overfitting evaluation are not suitable metrics for unsupervised learning [12,14] like SENDER; thus, in medical research, reproducibility should be one of the most critical gold standards [27,48,58,59,60] for evaluating the performance of unsupervised methods. To validate the global reproducibility of SENDER across all test–retest subjects, we employed identifiability, a measure ranging from 0 to 1, where higher values indicate greater reproducibility [48] across all subjects. Identifiability was calculated based on the similarity of test and retest SFs [48], in particular, after converting each 3D SF into a vector [35,50]. The reproducibility results can be viewed in Figure 5. In addition, we examine the consistency of the hyperparameter estimator on all subjects.
Specifically, in Figure 8a,b, we used identifiability [48] by calculating the spatial similarity [35] of test–retest SFs identified by SENDER and other methods, using ground-truth SFs [22]. For shallow SFs identified in Figure 8a, SENDER achieves an identifiability value of approximately 0.70. Meanwhile, the identifiability of most linear SFs identified by SENDER in Figure 8b exceeds 0.80, demonstrating substantial reproducibility [48]. Notably, the identifiability of nonlinear SFs in Figure 8c reaches nearly 0.90, which is higher than that of SFs extracted by DBN. Lastly, compared with other methods, SENDER achieves the most accurate reconstruction error, below .
In comparison, while other peer methods can identify twelve shallow features and five comparable linear spatial features at their first and second layers, respectively, the reproducibility of these features is notably lower. Specifically, the majority of the shallow and linear spatial features reported by these methods exhibit identifiability values below 0.70. This suggests that the features identified by these traditional methods are less consistent and may be more prone to variations across different datasets. The higher identifiability of features detected by SENDER underscores its superior performance in capturing consistent and reproducible features in the data, which is crucial for both basic neuroscience research and clinical applications. High reproducibility is particularly important in clinical settings, where consistent identification of brain features can lead to more accurate diagnoses and in-depth understanding of neurological conditions.
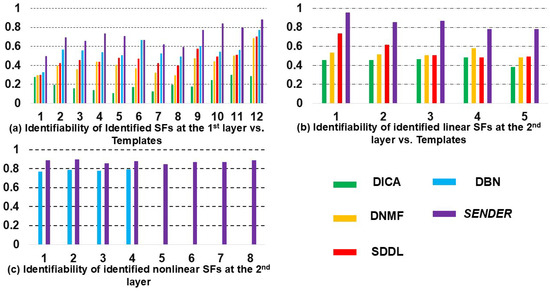
Figure 8.
A quantitative illustration of the identifiability of identified shallow, linear, and nonlinear SFs via SENDER and other peer methods as well as a comparison of reconstruction accuracy.
4. Discussion
We introduced an innovative computational framework, SENDER, designed to concurrently reveal reproducible linear and nonlinear spatial features (SFs) from MBME fMRI data. SENDER bridges the gap between traditional linear methods [5,6,7,8] and newer nonlinear approaches [10,18,19].
Notably, a key strength of SENDER lies in its ability to consistently, efficiently, and accurately reveal hierarchical SFs without requiring extensive fMRI datasets or high-performance computing resources such as GPUs or TPUs. Unlike DCAE [19] and DBN [10], SENDER is more explainable, as demonstrated by theoretical predictions validated through comparisons with peer methods [5,6,8,10]. In particular, SENDER achieves faster convergence and more accurate reconstruction loss by leveraging the advanced STORM optimizer [61], which is particularly well suited for hybrid problems combining linear and nonlinear architectures [61,62]. Additionally, SENDER employs the Rank Reduction Technique (RRT) for data-driven hyperparameter estimation, a significant improvement over peer methods that rely on manual tuning [5,6,7,8]. The integration of the norm penalty enhances denoising capabilities, enabling SENDER to outperform conventional methods, such as hierarchical clustering, in identifying linear and nonlinear SFs.
In addition, SENDER produces reproducible SFs at deeper layers, outperforming peer methods in terms of robustness and precision [5,6,8,10]. For example, hierarchical clustering methods often fail to integrate SFs with low spatial similarity, whereas SENDER effectively consolidates such features into unified SFs through its advanced framework [10,11,35]. Importantly, our research categorizes hierarchical SFs in the human brain into five linear and eight nonlinear SFs. Notably, these SFs align with established neurophysiological representations for resting-state fMRI [22,33,35]. For instance, the Salience Network (SN) modulates anticorrelated connectivity between the Default Mode Network (DMN) and the Executive Control Network (ECN) [63]. Similarly, functional coupling between vision and auditory networks, as observed in our results, reflects known neurophysiological dynamics [64]. By evaluating linear SFs identified by peer methods, SENDER demonstrates superior accuracy, attributable to its integration of advanced sparsity and RRT with the STORM optimizer. Additionally, SENDER reveals nonlinear SFs that exhibit asymmetrical organization, further showcasing its capability to uncover complex brain dynamics.
Furthermore, SENDER produces relatively reproducible SFs at the deeper layers compared with other peer methods [5,6,8,10]. This can be attributed to DICA’s relatively fast convergence rate and independence constraint [35]. The mathematical evaluation framework and the fMRI validation procedure provided in this work should enable further development of deep matrix decomposition optimized for different types of real-world applications in biomedical imaging, with SENDER as the current prevalent computational framework for fMRI analytics. Importantly, we also provided theoretical analyses as Theorem 1 to explain why SENDER has more accurate reconstruction loss, which is comparable to deep neural networks.
Moreover, in this research, we not only validate the proposed computational framework named SENDER but also successfully categorize hierarchical SFs within the human brain into five linear and eight nonlinear SFs. Meanwhile, both the linear and nonlinear SFs also showcase the superiority of MBME fMRI, attributable to the former’s better specificity for an in-depth understanding of neural activities. In this initial exploratory work on linear and nonlinear SFs using MBME fMRI, multiple derived linear and nonlinear SFs are consistent with neurophysiological representations between shallow SFs from previous studies [22,33,35] on resting-state fMRI. For instance, the Salience Network, one of the most important SFs, is known to modulate the anticorrelated connectivity of other SFs, such as the Default Mode Network (DMN) and the Executive Control Network (ECN) [63], hence the linkage of their nodes into a single linear SF (in Figure 3, in the third column). The functional coupling of vision networks with an auditory network, shown in Figure 3 in the fourth column, is also well known, given the role that the abnormal auditory stimulus plays in visual attention [64]. Future neuroscientific studies will be required to empirically validate these linear SFs using demographic, clinical, cognitive, behavioral, and/or electrophysiological data. By evaluating most linear SFs identified among peer methods, we notice that SENDER can accurately reveal linear SFs using MBME fMRI, whereas the identifications of other peer methods are not as accurate as SENDER. These results could be attributed to its joint use of advanced sparsity and RRT in conjunction with the STORM optimizer.
Specifically, in Figure 7, we discovered more nonlinear SFs than DBN. Notably, some nonlinear SFs showcase an asymmetrical organization. For example, in the first row and first and second columns, identified SFs only include partial regions of a linear SF, shown in the first row and column in Figure 7. Since the identification of these linear and nonlinear SFs does not require extensive training datasets nor specialized computing infrastructure, they can be easily applied to clinical research with the potential to generate novel SFs to play an important role as a wide array of biomarkers for neurodevelopmental, neurodegenerative, and psychiatric disorders [65], including for diagnosis, prognosis, and treatment monitoring. This is particularly significant given the recent observation that neuropathology and psychopathology often affect shallow SFs differently than linear and nonlinear SFs at deeper layers. For example, various psychiatric disorders have been found to decrease shallow sensory SFs uniformly across patients [66,67] while increasing distinctiveness among patients in either linear or nonlinear SFs at the deeper layers [65]. In fMRI studies of mild traumatic brain injury (TBI), altered brain functionality has been found early after concussion within the patient’s brain, such as the SN, DMN, and ECN [68]. The linear interactions of SFs, such as those between the SN and the DMN, are thought to be especially important for outcomes after TBI and can be used to guide personalized treatment [69,70]. Disordered coupling of the SN with the DMN and ECN has also been shown in mild cognitive impairment [71].
Hence, prevalent neurological disorders such as head trauma and neurodegenerative diseases are thought to affect multiple levels of the functional organization in human brains. Such linear and nonlinear interactions across multiple SFs can be investigated with deeper layers of an advanced deep learning model like SENDER that integrate their spatially distinct gray matter nodes into a linear or nonlinear SF, as shown in Figure 3 (refer to the top row). These examples show how more principled data-driven characterization of this hierarchy, particularly at its higher levels, holds great promise for providing clinically actionable diagnostics of neurological and psychiatric diseases.
Lastly, despite its advantages, SENDER has room for improvement. Enhancements to RRT, integration with Reinforcement Learning, and optimization of its computational efficiency are needed. For example, the current decomposition of a single fMRI signal matrix requires approximately two hours, highlighting the need for faster optimization techniques. Furthermore, SENDER currently lacks insight into the neurological representations of SFs and their associations with specific disorders. Future research will apply SENDER to diverse fMRI datasets, including those for Alzheimer’s and Parkinson’s diseases, to identify disorder-specific linear and nonlinear SFs. Improved fMRI sensitivity and resolution, such as SLIDER-SMS fMRI [72], will enable SENDER to uncover even more complex SFs, advancing our understanding of brain functionality.
To summarize, the benefits of SENDER gain importance as the spatial and temporal resolution and sensitivity of fMRI continue to increase with improved MR imaging hardware and pulse sequences. Briefly, SENDER delivers several advantages in detecting the hierarchical and overlapping organization of SFs compared to previously described methods in a data-driven manner, such as DICA [5], DNMF [8], SDDL [6], and DBN [10]. Notably, SENDER does not have the constraints of spatial independence that DICA has [35]. Since SENDER can reveal extensively overlapped SFs [10,11,35] and estimates the vital hyperparameters automatically, it is easy to leverage the number and size of each layer, i.e., the number of artificial neurons. Other peer methods, such as DICA [5], SDDL [6], DNMF [8], and DBN [10], require manual hyperparameter tuning. Moreover, compared to Deep Neural Networks, SENDER has several advantages: (a) fewer training samples, i.e., the capability to reconstruct a single individual’s scan; (b) fewer extensive computational resources; (c) guaranteed convergence to a unique fixed point; and (d) automatic hyperparameter estimation. In this research, our results showcase the benefits of SENDER for MBME imaging [27,28,29]. Additionally, we aim to push further beyond SENDER, advancing our understanding of brain functionality through innovative computational frameworks that further deepen and expand our insights in a comprehensive understanding of brain functionality. Moreover, SENDER is capable of incorporating Electroencephalogram (EEG) to explore physiological representation and potential association of linear and nonlinear SFs with neurological disorders. Meanwhile, by leveraging advanced norm penalty, SENDER can enable the detection of abnormal answering of students, such as rapid guessing.
5. Conclusions
The SENDER framework represents a groundbreaking hybrid learning approach, seamlessly integrating linear and nonlinear architectures with a data-driven Rank Reduction Technique (RRT) for automatic hyperparameter tuning.
In particular, leveraging its hybrid and efficient non-fully connected architectures, SENDER excels at uncovering comprehensive spatial features, including both linear and nonlinear components, with superior identifiability compared to other state-of-the-art methods. The RRT facilitates automatic determination of all hyperparameters in a data-driven manner, streamlining the model configuration process. Furthermore, qualitative analyses underscore SENDER’s ability to extract a greater number of nonlinear features than peer methods. Simultaneously, quantitative evaluations reveal that SENDER identifies highly reproducible features with exceptional identifiability. Notably, the framework achieves precise approximations of input data and demonstrates a rapid convergence rate, often outperforming algorithms such as Deep Neural Networks (DNNs). Moreover, the capacity of SENDER to concurrently extract reproducible linear and nonlinear spatial features opens avenues for synergistic advancements in research on neurodevelopmental, neurodegenerative, and psychiatric disorders. These features, characterized by high reconstruction accuracy, hold promise as clinical biomarkers, enabling personalized diagnostics, prognostics, and treatment monitoring [73,74]. In summary, SENDER emerges as a transformative deep hybrid learning method, with the potential to make significant contributions to deep learning, computational neuroscience, and clinical translational research. By bridging these fields, SENDER paves the way for pioneering advancements in machine learning and neuroscience applications.
Author Contributions
In this research project, W.Z., the corresponding author, led the development of the hybrid deep learning concept and the design of the computational pipeline. A.H.Z. focused on fMRI data preprocessing, manuscript drafting, and generating visual representations. A.J. took charge of conducting empirical experiments and performing validations, while Y.B. contributed by designing experiments and assisting the corresponding author with theoretical analyses and proofs. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the AU-GSU Seed Award Program for Collaborative Clinical and Translational Research (AUGSU00016).
Data Availability Statement
All test–retest Multiband Multi-echo (MBME) fMRI datasets are available for download from OpenfMRI at https://openfmri.org/dataset/ds000216/. The data has been accessible since 26 January 2017. Additional imaging data, including T1- and T2-weighted images, can be requested directly from Professor Alexander D. Cohen at the Medical College of Wisconsin via email at acohen@mcw.edu.
Acknowledgments
We sincerely acknowledge the support of Yang Wang and Alexander Cohen for providing access to the Multiband Multi-echo (MBME) fMRI datasets utilized in this research. We also extend our gratitude to the AU-GSU Seed Award Program for Collaborative Clinical and Translational Research (AUGSU00016) for supporting this study.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SFs | spatial features |
| fMRI | functional Magnetic Resonance Imaging |
| SENDER | Semi-Nonlinear Deep Efficient Reconstruction |
| DNNs | Deep Neural Networks |
Appendix A
Theorem A1.
(Accurate Approximation of SENDER) Consider a real function and where represents the Lebesgue measure [45]. Given , SENDER includes a linear method and a nonlinear method with multiple activation functions denoted as and . If denotes a series of linear functions and denotes a series of nonlinear functions, then we have .
Proof.
According to Luzin Theorem [45], we have a close set:
The real function f is continuous in each .
Then, we have another real function g, which is continuous within , and obviously, we have
Since for any continuous real function, we have
In Equation (A3), is a series of polynomials with the highest power k, such as . Let , according to Equation (A1), and obviously, we have
According to Equations (A2)–(A4), if a real function denoted on F, we can derive
Meanwhile, if is a nonlinear function with isolated discontinuous points, we also have
Therefore, according to Equations (A5) and (A6), we have
Compared with the proposed SENDER, represents the linear component and denotes the nonlinear component, which demonstrates that integration of linear and nonlinear function can approximate any real function , e.g., an original input dataset. □
Appendix B

Table A1.
All abbreviations of ground truth SFs in methodological validation.
Table A1.
All abbreviations of ground truth SFs in methodological validation.
| Name | Number/Abbreviation |
|---|---|
| Primary Visual Network | 1/VIS-1 |
| Perception Visual Shape Network | 2/VIS-2 |
| Perception Visual Motion Network | 3/VIS-3 |
| Default Mode Network | 4/DMN |
| Brainstem and Cerebellum Network | 5/BC |
| Sensorimotor Network | 6/SM |
| Auditory Network | 7/AUD |
| Executive Control Network | 8/ECN |
| Left Frontoparietal Network | 9/FP-L |
| Right Frontoparietal Network | 10/FP-R |
| Dorsal Attention Network | 11/DAN |
| Salience Network | 12/SN |
| Algorithm A1 (Core algorithm): Semi-Nonlinear Deep Efficient Reconstruction (SENDER). |
|
| Algorithm A2 Rank Reduction Technique (RRT). |
|
| Algorithm A3 Weighted difference (WD). |
|
| Algorithm A4 Weighted ratio (WR). |
|
| Algorithm A5 Weighted correlation (WC). |
|
References
- Peng, L.; Luo, Z.; Zeng, L.L.; Hou, C.; Shen, H.; Zhou, Z.; Hu, D. Parcellating the human brain using resting-state dynamic functional connectivity. Cereb. Cortex 2023, 33, 3575–3590. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, N.; Schrader, P. A study of brain networks for autism spectrum disorder classification using resting-state functional connectivity. Mach. Learn. Appl. 2022, 8, 100290. [Google Scholar] [CrossRef]
- Agarwal, S.; Al Khalifah, H.; Zaca, D.; Pillai, J.J. fMRI and DTI: Review of Complementary Techniques. In Functional Neuroradiology: Principles and Clinical Applications; Springer: Cham, Switzerland, 2023; pp. 1025–1060. [Google Scholar]
- Wingrove, J.; Makaronidis, J.; Prados, F.; Kanber, B.; Yiannakas, M.C.; Magee, C.; Castellazzi, G.; Grandjean, L.; Golay, X.; Tur, C.; et al. Aberrant olfactory network functional connectivity in people with olfactory dysfunction following COVID-19 infection: An exploratory, observational study. eClinicalMedicine 2023, 58, 101883. [Google Scholar] [CrossRef]
- Wylie, K.P.; Kronberg, E.; Legget, K.T.; Sutton, B.; Tregellas, J.R. Stable Meta-Networks, Noise, and Artifacts in the Human Connectome: Low-to High-Dimensional Independent Components Analysis as a Hierarchy of Intrinsic Connectivity Networks. Front. Neurosci. 2021, 15, 625737. [Google Scholar] [CrossRef]
- Qiao, C.; Yang, L.; Calhoun, V.D.; Xu, Z.B.; Wang, Y.P. Sparse deep dictionary learning identifies differences of time-varying functional connectivity in brain neuro-developmental study. Neural Netw. 2021, 135, 91–104. [Google Scholar] [CrossRef]
- Trigeorgis, G.; Bousmalis, K.; Zafeiriou, S.; Schuller, B. A deep semi-nmf model for learning hidden representations. In Proceedings of the International Conference on Machine Learning, PMLR, Beijing, China, 21–26 June 2014; pp. 1692–1700. [Google Scholar]
- Trigeorgis, G.; Bousmalis, K.; Zafeiriou, S.; Schuller, B.W. A deep matrix factorization method for learning attribute representations. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 417–429. [Google Scholar] [CrossRef]
- Iraji, A.; Fu, Z.; Damaraju, E.; DeRamus, T.P.; Lewis, N.; Bustillo, J.R.; Lenroot, R.K.; Belger, A.; Ford, J.M.; McEwen, S.; et al. Spatial dynamics within and between brain functional domains: A hierarchical approach to study time-varying brain function. Hum. Brain Mapp. 2019, 40, 1969–1986. [Google Scholar] [CrossRef]
- Zhang, W.; Zhao, S.; Hu, X.; Dong, Q.; Huang, H.; Zhang, S.; Zhao, Y.; Dai, H.; Ge, F.; Guo, L.; et al. Hierarchical organization of functional brain networks revealed by hybrid spatiotemporal deep learning. Brain Connect. 2020, 10, 72–82. [Google Scholar] [CrossRef]
- Zhang, W.; Zhao, L.; Li, Q.; Zhao, S.; Dong, Q.; Jiang, X.; Zhang, T.; Liu, T. Identify hierarchical structures from task-based fMRI data via hybrid spatiotemporal neural architecture search net. In Proceedings of the Medical Image Computing and Computer Assisted Intervention–MICCAI 2019: 22nd International Conference, Shenzhen, China, 13–17 October 2019; Proceedings, Part III 22. Springer: Berlin/Heidelberg, Germany, 2019; pp. 745–753. [Google Scholar]
- Bengio, Y.; Courville, A.C.; Vincent, P. Unsupervised feature learning and deep learning: A review and new perspectives. CoRR 2012, 1, 2012. [Google Scholar]
- Hannun, A.Y.; Rajpurkar, P.; Haghpanahi, M.; Tison, G.H.; Bourn, C.; Turakhia, M.P.; Ng, A.Y. Cardiologist-level arrhythmia detection and classification in ambulatory electrocardiograms using a deep neural network. Nat. Med. 2019, 25, 65–69. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Esteva, A.; Robicquet, A.; Ramsundar, B.; Kuleshov, V.; DePristo, M.; Chou, K.; Cui, C.; Corrado, G.; Thrun, S.; Dean, J. A guide to deep learning in healthcare. Nat. Med. 2019, 25, 24–29. [Google Scholar] [CrossRef] [PubMed]
- Plis, S.M.; Hjelm, D.R.; Salakhutdinov, R.; Allen, E.A.; Bockholt, H.J.; Long, J.D.; Johnson, H.J.; Paulsen, J.S.; Turner, J.A.; Calhoun, V.D. Deep learning for neuroimaging: A validation study. Front. Neurosci. 2014, 8, 92071. [Google Scholar] [CrossRef] [PubMed]
- Gurovich, Y.; Hanani, Y.; Bar, O.; Nadav, G.; Fleischer, N.; Gelbman, D.; Basel-Salmon, L.; Krawitz, P.M.; Kamphausen, S.B.; Zenker, M.; et al. Identifying facial phenotypes of genetic disorders using deep learning. Nat. Med. 2019, 25, 60–64. [Google Scholar] [CrossRef]
- Hu, X.; Huang, H.; Peng, B.; Han, J.; Liu, N.; Lv, J.; Guo, L.; Guo, C.; Liu, T. Latent source mining in FMRI via restricted Boltzmann machine. Hum. Brain Mapp. 2018, 39, 2368–2380. [Google Scholar] [CrossRef]
- Huang, H.; Hu, X.; Zhao, Y.; Makkie, M.; Dong, Q.; Zhao, S.; Guo, L.; Liu, T. Modeling task fMRI data via deep convolutional autoencoder. IEEE Trans. Med. Imaging 2017, 37, 1551–1561. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [PubMed]
- Dubey, S.R.; Singh, S.K.; Chaudhuri, B.B. Activation functions in deep learning: A comprehensive survey and benchmark. Neurocomputing 2022, 503, 92–108. [Google Scholar] [CrossRef]
- Smith, S.M.; Fox, P.T.; Miller, K.L.; Glahn, D.C.; Fox, P.M.; Mackay, C.E.; Filippini, N.; Watkins, K.E.; Toro, R.; Laird, A.R.; et al. Correspondence of the brain’s functional architecture during activation and rest. Proc. Natl. Acad. Sci. USA 2009, 106, 13040–13045. [Google Scholar] [CrossRef]
- Motlaghian, S.M.; Belger, A.; Bustillo, J.R.; Ford, J.M.; Iraji, A.; Lim, K.; Mathalon, D.H.; Mueller, B.A.; O’Leary, D.; Pearlson, G.; et al. Nonlinear functional network connectivity in resting functional magnetic resonance imaging data. Hum. Brain Mapp. 2022, 43, 4556–4566. [Google Scholar] [CrossRef]
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed]
- Hinton, G.; Deng, L.; Yu, D.; Dahl, G.E.; Mohamed, A.r.; Jaitly, N.; Senior, A.; Vanhoucke, V.; Nguyen, P.; Sainath, T.N.; et al. Deep neural networks for acoustic modeling in speech recognition: The shared views of four research groups. IEEE Signal Process. Mag. 2012, 29, 82–97. [Google Scholar] [CrossRef]
- Ding, C.H.; Li, T.; Jordan, M.I. Convex and semi-nonnegative matrix factorizations. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 32, 45–55. [Google Scholar] [CrossRef] [PubMed]
- Cohen, A.D.; Yang, B.; Fernandez, B.; Banerjee, S.; Wang, Y. Improved resting state functional connectivity sensitivity and reproducibility using a multiband multi-echo acquisition. Neuroimage 2021, 225, 117461. [Google Scholar] [CrossRef]
- Cohen, A.D.; Jagra, A.S.; Yang, B.; Fernandez, B.; Banerjee, S.; Wang, Y. Detecting task functional MRI activation using the multiband multiecho (MBME) echo-planar imaging (EPI) sequence. J. Magn. Reson. Imaging 2021, 53, 1366–1374. [Google Scholar] [CrossRef] [PubMed]
- Cohen, A.D.; Chang, C.; Wang, Y. Using multiband multi-echo imaging to improve the robustness and repeatability of co-activation pattern analysis for dynamic functional connectivity. Neuroimage 2021, 243, 118555. [Google Scholar] [CrossRef]
- Glasser, M.F.; Sotiropoulos, S.N.; Wilson, J.A.; Coalson, T.S.; Fischl, B.; Andersson, J.L.; Xu, J.; Jbabdi, S.; Webster, M.; Polimeni, J.R.; et al. The minimal preprocessing pipelines for the Human Connectome Project. Neuroimage 2013, 80, 105–124. [Google Scholar] [CrossRef]
- Kundu, P.; Santin, M.D.; Bandettini, P.A.; Bullmore, E.T.; Petiet, A. Differentiating BOLD and non-BOLD signals in fMRI time series from anesthetized rats using multi-echo EPI at 11.7 T. NeuroImage 2014, 102, 861–874. [Google Scholar] [CrossRef]
- Han, J.; Zhou, L.; Wu, H.; Huang, Y.; Qiu, M.; Huang, L.; Lee, C.; Lane, T.J.; Qin, P. Eyes-open and eyes-closed resting state network connectivity differences. Brain Sci. 2023, 13, 122. [Google Scholar] [CrossRef]
- Lv, J.; Jiang, X.; Li, X.; Zhu, D.; Chen, H.; Zhang, T.; Zhang, S.; Hu, X.; Han, J.; Huang, H.; et al. Sparse representation of whole-brain fMRI signals for identification of functional networks. Med. Image Anal. 2015, 20, 112–134. [Google Scholar] [CrossRef]
- Smith, S.M.; Beckmann, C.F.; Andersson, J.; Auerbach, E.J.; Bijsterbosch, J.; Douaud, G.; Duff, E.; Feinberg, D.A.; Griffanti, L.; Harms, M.P.; et al. Resting-state fMRI in the human connectome project. Neuroimage 2013, 80, 144–168. [Google Scholar] [CrossRef]
- Zhang, W.; Lv, J.; Li, X.; Zhu, D.; Jiang, X.; Zhang, S.; Zhao, Y.; Guo, L.; Ye, J.; Hu, D.; et al. Experimental comparisons of sparse dictionary learning and independent component analysis for brain network inference from fMRI data. IEEE Trans. Biomed. Eng. 2018, 66, 289–299. [Google Scholar] [CrossRef] [PubMed]
- Sboev, A.; Rybka, R.; Serenko, A.; Vlasov, D. A Non-fully-Connected Spiking Neural Network with STDP for Solving a Classification Task. In Advanced Technologies in Robotics and Intelligent Systems; Proceedings of ITR 2019; Springer: Cham, Switzerland, 2020; pp. 223–229. [Google Scholar]
- Xu, M.; Hu, D.; Luo, F.; Liu, F.; Wang, S.; Wu, W. Limited-angle X-ray CT reconstruction using image gradient l0-norm with dictionary learning. IEEE Trans. Radiat. Plasma Med. Sci. 2020, 5, 78–87. [Google Scholar] [CrossRef]
- Wen, Z.; Yin, W.; Zhang, Y. Solving a low-rank factorization model for matrix completion by a nonlinear successive over-relaxation algorithm. Math. Program. Comput. 2012, 4, 333–361. [Google Scholar] [CrossRef]
- Levy, K.Y.; Kavis, A.; Cevher, V. STORM+: Fully Adaptive SGD with Momentum for Nonconvex Optimization. arXiv 2021, arXiv:2111.01040. [Google Scholar]
- Zhang, J.; Yang, X.; Li, G.; Zhang, K. A smoothing proximal gradient algorithm with extrapolation for the relaxation of l0 regularization problem. Comput. Optim. Appl. 2023, 84, 737–760. [Google Scholar] [CrossRef]
- Zhang, Y.K.; Huang, T.J.; Ding, Y.X.; Zhan, D.C.; Ye, H.J. Model spider: Learning to rank pre-trained models efficiently. Adv. Neural Inf. Process. Syst. 2024, 36, 13692–13719. [Google Scholar]
- Yuan, Z.; Yuan, H.; Tan, C.; Wang, W.; Huang, S.; Huang, F. Rrhf: Rank responses to align language models with human feedback without tears. arXiv 2023, arXiv:2304.05302. [Google Scholar]
- Shen, Y.; Wen, Z.; Zhang, Y. Augmented Lagrangian alternating direction method for matrix separation based on low-rank factorization. Optim. Methods Softw. 2014, 29, 239–263. [Google Scholar] [CrossRef]
- Nikdan, M.; Pegolotti, T.; Iofinova, E.; Kurtic, E.; Alistarh, D. SparseProp: Efficient sparse backpropagation for faster training of neural networks at the edge. In Proceedings of the International Conference on Machine Learning, PMLR, Honolulu, HI, USA, 23–29 July 2023; pp. 26215–26227. [Google Scholar]
- Royden, H.L.; Fitzpatrick, P. Real Analysis; Macmillan: New York, NY, USA, 1988; Volume 32. [Google Scholar]
- Cohen, A.D.; Wang, Y. Multiband Multi-Echo BOLD fMRI. 2018. Available online: https://openneuro.org/datasets/ds000216/versions/00001 (accessed on 17 July 2018).
- Pei, S.; Wang, C.; Cao, S.; Lv, Z. Data augmentation for fMRI-based functional connectivity and its application to cross-site ADHD classification. IEEE Trans. Instrum. Meas. 2022, 72, 2501015. [Google Scholar] [CrossRef]
- Van De Ville, D.; Farouj, Y.; Preti, M.G.; Liégeois, R.; Amico, E. When makes you unique: Temporality of the human brain fingerprint. Sci. Adv. 2021, 7, eabj0751. [Google Scholar] [CrossRef] [PubMed]
- Stam, C.J. Modern network science of neurological disorders. Nat. Rev. Neurosci. 2014, 15, 683–695. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Chen, H.; Li, Y.; Lv, J.; Jiang, X.; Ge, F.; Zhang, T.; Zhang, S.; Ge, B.; Lyu, C.; et al. Connectome-scale group-wise consistent resting-state network analysis in autism spectrum disorder. Neuroimage Clin. 2016, 12, 23–33. [Google Scholar] [CrossRef]
- Satterthwaite, T.D.; Ciric, R.; Roalf, D.R.; Davatzikos, C.; Bassett, D.S.; Wolf, D.H. Motion artifact in studies of functional connectivity: Characteristics and mitigation strategies. Hum. Brain Mapp. 2019, 40, 2033–2051. [Google Scholar] [CrossRef]
- Gao, K.; Sener, O. Generalizing gaussian smoothing for random search. In Proceedings of the International Conference on Machine Learning, PMLR, Baltimore, MD, USA, 17–23 July 2022; pp. 7077–7101. [Google Scholar]
- Dimova, V.; Welte-Jzyk, C.; Kronfeld, A.; Korczynski, O.; Baier, B.; Koirala, N.; Steenken, L.; Kollmann, B.; Tüscher, O.; Brockmann, M.A.; et al. Brain connectivity networks underlying resting heart rate variability in acute ischemic stroke. Neuroimage Clin. 2024, 41, 103558. [Google Scholar] [CrossRef]
- Oathes, D.J.; Zimmerman, J.P.; Duprat, R.; Japp, S.S.; Scully, M.; Rosenberg, B.M.; Flounders, M.W.; Long, H.; Deluisi, J.A.; Elliott, M.; et al. Resting fMRI-guided TMS results in subcortical and brain network modulation indexed by interleaved TMS/fMRI. Exp. Brain Res. 2021, 239, 1165–1178. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Huang, J.; Liu, M.; Zhang, D. Modeling dynamic characteristics of brain functional connectivity networks using resting-state functional MRI. Med. Image Anal. 2021, 71, 102063. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Zhang, W.; Zhao, L.; Wu, X.; Liu, T. Evolutional neural architecture search for optimization of spatiotemporal brain network decomposition. IEEE Trans. Biomed. Eng. 2021, 69, 624–634. [Google Scholar] [CrossRef]
- Zhang, S.; Yang, W.; Li, M.; Wen, X.; Shao, Z.; Li, J.; Liu, J.; Zhang, J.; Yu, D.; Liu, J.; et al. Reconfigurations of dynamic functional network connectivity in large-scale brain network after prolonged abstinence in heroin users. Curr. Neuropharmacol. 2024, 22, 1144–1153. [Google Scholar] [CrossRef]
- Botvinik-Nezer, R.; Wager, T.D. Reproducibility in neuroimaging analysis: Challenges and solutions. Biol. Psychiatry Cogn. Neurosci. Neuroimaging 2023, 8, 780–788. [Google Scholar] [CrossRef] [PubMed]
- Niso, G.; Botvinik-Nezer, R.; Appelhoff, S.; De La Vega, A.; Esteban, O.; Etzel, J.A.; Finc, K.; Ganz, M.; Gau, R.; Halchenko, Y.O.; et al. Open and reproducible neuroimaging: From study inception to publication. NeuroImage 2022, 263, 119623. [Google Scholar] [PubMed]
- Poldrack, R.A. The costs of reproducibility. Neuron 2019, 101, 11–14. [Google Scholar] [CrossRef] [PubMed]
- Cutkosky, A.; Orabona, F. Momentum-based variance reduction in non-convex sgd. Adv. Neural Inf. Process. Syst. 2019, 32, 15236–15245. [Google Scholar]
- D’Amour, A.; Heller, K.; Moldovan, D.; Adlam, B.; Alipanahi, B.; Beutel, A.; Chen, C.; Deaton, J.; Eisenstein, J.; Hoffman, M.D.; et al. Underspecification presents challenges for credibility in modern machine learning. J. Mach. Learn. Res. 2022, 23, 10237–10297. [Google Scholar]
- Schimmelpfennig, J.; Topczewski, J.; Zajkowski, W.; Jankowiak-Siuda, K. The role of the salience network in cognitive and affective deficits. Front. Hum. Neurosci. 2023, 17, 1133367. [Google Scholar] [CrossRef] [PubMed]
- Besso, L.; Larivière, S.; Roes, M.; Sanford, N.; Percival, C.; Damascelli, M.; Momeni, A.; Lavigne, K.; Menon, M.; Aleman, A.; et al. Hypoactivation of the language network during auditory imagery contributes to hallucinations in Schizophrenia. Psychiatry Res. Neuroimaging 2024, 341, 111824. [Google Scholar] [CrossRef]
- Parkes, L.; Satterthwaite, T.D.; Bassett, D.S. Towards precise resting-state fMRI biomarkers in psychiatry: Synthesizing developments in transdiagnostic research, dimensional models of psychopathology, and normative neurodevelopment. Curr. Opin. Neurobiol. 2020, 65, 120–128. [Google Scholar] [CrossRef]
- Elliott, M.L.; Romer, A.; Knodt, A.R.; Hariri, A.R. A connectome-wide functional signature of transdiagnostic risk for mental illness. Biol. Psychiatry 2018, 84, 452–459. [Google Scholar] [CrossRef] [PubMed]
- Kebets, V.; Holmes, A.J.; Orban, C.; Tang, S.; Li, J.; Sun, N.; Kong, R.; Poldrack, R.A.; Yeo, B.T. Somatosensory-motor dysconnectivity spans multiple transdiagnostic dimensions of psychopathology. Biol. Psychiatry 2019, 86, 779–791. [Google Scholar] [CrossRef] [PubMed]
- Palacios, E.M.; Yuh, E.L.; Chang, Y.S.; Yue, J.K.; Schnyer, D.M.; Okonkwo, D.O.; Valadka, A.B.; Gordon, W.A.; Maas, A.I.; Vassar, M.; et al. Resting-state functional connectivity alterations associated with six-month outcomes in mild traumatic brain injury. J. Neurotrauma 2017, 34, 1546–1557. [Google Scholar] [CrossRef] [PubMed]
- Jilka, S.R.; Scott, G.; Ham, T.; Pickering, A.; Bonnelle, V.; Braga, R.M.; Leech, R.; Sharp, D.J. Damage to the salience network and interactions with the default mode network. J. Neurosci. 2014, 34, 10798–10807. [Google Scholar] [CrossRef]
- Li, X.; Jia, X.; Liu, Y.; Bai, G.; Pan, Y.; Ji, Q.; Mo, Z.; Zhao, W.; Wei, Y.; Wang, S.; et al. Brain dynamics in triple-network interactions and its relation to multiple cognitive impairments in mild traumatic brain injury. Cereb. Cortex 2023, 33, 6620–6632. [Google Scholar] [CrossRef] [PubMed]
- Chand, G.B.; Wu, J.; Hajjar, I.; Qiu, D. Interactions of the salience network and its subsystems with the default-mode and the central-executive networks in normal aging and mild cognitive impairment. Brain Connect. 2017, 7, 401–412. [Google Scholar] [CrossRef] [PubMed]
- Shou, Q.; Shao, X.; Wang, D.J. Super-resolution arterial spin labeling using slice-dithered enhanced resolution and simultaneous multi-slice acquisition. Front. Neurosci. 2021, 15, 737525. [Google Scholar] [CrossRef]
- Lee, J.; Chi, S.; Lee, M.S. Personalized diagnosis and treatment for neuroimaging in depressive disorders. J. Pers. Med. 2022, 12, 1403. [Google Scholar] [CrossRef] [PubMed]
- Zhao, K.; Xie, H.; Fonzo, G.A.; Tong, X.; Carlisle, N.; Chidharom, M.; Etkin, A.; Zhang, Y. Individualized fMRI connectivity defines signatures of antidepressant and placebo responses in major depression. Mol. Psychiatry 2023, 28, 2490–2499. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).