Abstract
With the rapid development of cloud technology, a growing volume of encrypted data is being stored on cloud servers. Public key searchable encryption (PEKS) has emerged as a solution to the challenge of retrieving encrypted data. However, most PEKS schemes are vulnerable to frequency analysis attacks (FAA), which can potentially expose sensitive information. To address this issue, we propose a pairing-free public key searchable encryption scheme that is specifically designed to resist such attacks. Our scheme is built upon the decisional Diffie–Hellman (DDH) assumption, and effectively mitigates the risk of malicious adversaries extracting keyword information through trapdoor search frequencies. The pairing-free nature of our approach not only enhances the security against FAA but also improves the retrieval efficiency compared to traditional PEKS schemes. We formally prove that our scheme satisfies both chosen keyword attack (CKA) security and keyword guessing attack (KGA) security. Additionally, we perform comprehensive theoretical and experimental evaluations to assess the scheme’s efficiency, showcasing its practical applicability in real-world scenarios.
1. Introduction
With the rapid advancement of computer network technology, more and more data are being stored in cloud servers, making cloud storage an essential tool for both individuals and businesses. The appeal of cloud storage lies in its flexibility, accessibility, security, and collaborative features, which make it an ideal solution for managing digital information in today’s interconnected world. However, to ensure data security, cloud servers often store encrypted data. This in turn creates a challenge in that encrypted data cannot be directly retrieved by users. One possible approach is for users to download all encrypted files and decrypt them locally; however, this method is inefficient, requiring significant network bandwidth and storage capacity.
Boneh et al. proposed the concept of public key encryption with keyword search (PEKS) [1] to tackle this problem. First, the data owner creates an encrypted keyword index for the keyword W linked to a file and uploads it to the cloud server together with the encrypted file. Second, the user generates a search trapdoor for the desired keyword and forwards it to the cloud server. Third, the cloud server compares the trapdoor with the encrypted index and returns the results if there is a match. The PEKS framework laid the foundation for further development of searchable encryption schemes. Subsequent advancements in public key searchable encryption include several specialized schemes. For instance, attribute-based encryption schemes [2,3,4,5] integrate access control with searchable encryption, allowing for fine-grained management of who can search and access specific encrypted data. Multiple-keyword searchable encryption schemes [6,7,8,9,10] enable efficient searching across multiple keywords within encrypted files, improving search flexibility and performance. Additionally, fuzzy keyword search schemes [11,12,13,14] enhance search capabilities by allowing for approximate keyword matching, thereby accommodating spelling errors or variations in search terms.
Other notable contributions include Cheng et al.’s proposal of the first PEKS scheme resistant to frequency analysis attacks [15]. Bai et al. introduced a pairing-free public key searchable encryption solution [16], thereby avoiding the overhead associated with pairings. Li et al. developed a scheme that integrates identity-based authentication for designated servers in the context of public key searchable encryption [17]. Furthermore, Cheng et al. introduced a certificate-free public key authenticated searchable encryption (CLPASE) scheme, which addresses the frequency analysis vulnerability in earlier models. Their comparative analysis demonstrated that this new scheme provides enhanced protection for user privacy while maintaining efficiency comparable to other existing CLPASE solutions [18]. Verma et al. proposed an attribute-based encryption scheme for blockchain applications that enables searchable encryption. It addresses key challenges in privacy-preserving data retrieval within decentralized blockchain environments [19]. Sun et al. proposed a non-interactive searchable encryption scheme with both forward and backward security [20]. Liu et al. proposed a cloud platform-based multiple-keyword searchable encryption scheme that implements fine-grained access control through attribute-based encryption [21]. Wu et al. proposed a scheme leveraging cryptographic reverse firewall technology. This scheme removes the requirement for gateways to store random numbers, greatly minimizing both management and storage overhead. In addition, it enables multi-keyword searches, enhancing its practicality for real-world use [22].
1.1. Contributions of This Article
We introduce the concept of pairing-free public key searchable encryption designed to resist frequency analysis attacks. Compared to other schemes, our scheme can effectively resist frequency analysis attack and is more efficient. Specifically, our main contributions can be summarized by the following points:
- We formally define the concept of a pairing-free public key searchable encryption that is resistant to frequency analysis attacks, and provide its security model.
- We introduce the frequency analysis attack in detail. By analyzing existing PEKS schemes, we explain why public key searchable encryption schemes are susceptible to frequency analysis attacks.
- We construct a specific pairing-free searchable encryption scheme that resists frequency analysis attacks based on the DDH hypothesis. We utilize the cloud server’s public key during the construction of the search trapdoor, which enables the scheme to withstand frequency analysis attacks while maintaining the retrieval functionality. Additionally, we demonstrate that our scheme achieves both CKA security and KGA security.
- Because there is no bilinear pairing operation in our scheme, the time overhead is smaller than in the scheme of Cheng et al. We conducted both theoretical analysis and experimental testing to assess the performance of the scheme. The results indicate that our scheme is practical and well-suited for real-world applications.
1.2. Related Work
In 2000, Song et al. pioneered the idea of searchable encryption, illustrating that encrypted data can be transformed into a searchable form, thereby enabling search operations without decryption [23]. Seven years later, Boneh et al. proposed an asymmetric searchable encryption scheme [24], the first to employ public-key cryptography for keyword search on encrypted data, eliminating the need for decryption. In 2014, Cash et al. [25] introduced an attribute-based searchable encryption scheme, allowing queries based on data attributes. Two years later, Rhee et al. [26] presented a variant that supports keyword updates, in which the server can modify the ciphertext of a given keyword W (denoted ) to a new ciphertext corresponding to a different keyword (denoted ). Yin et al. proposed an attribute-based multiparty searchable encryption model which implements access control through attribute settings and supports the participation of multiple users [27]. Senouci et al. proposed a secure certificate-free public-key searchable encryption scheme that is effective in resisting keyword guessing attacks [28]. Li et al. designed a PEKS scheme that improves keyword search efficiency through the use of an inverted index [29]. In 2021, Zhang et al. proposed a verifiable bidirectional public key searchable encryption scheme which features the ability to support retrieval by both the email sender and receiver simultaneously [30]. Huang et al. introduced an innovative public key searchable encryption scheme that integrates ciphertext deduplication to minimize storage requirements. Additionally, their scheme employs inverted indexing to enhance retrieval efficiency [31].
Despite these advancements, PEKS schemes remain susceptible to keyword guessing attacks (KGA). To mitigate this risk, Rhee et al. defined the concept of trapdoor indistinguishability [32] and introduced a secure dPEKS (designated tester searchable public-key encryption) scheme, ensuring trapdoor safety. In 2013, Xu et al. [33] developed a fuzzy keyword searchable encryption scheme that reduces KGA vulnerability by restricting the server to perform only fuzzy searches while handling exact matches locally, preventing the leakage of precise trapdoor information. In 2016, Chen et al. [34] proposed the dual-server public key encryption with keyword search (DS-PEKS) scheme, leveraging two independent servers to collaboratively test the trapdoor in order to enhance resistance to attacks from malicious servers.
Frequency analysis attacks, which are common in cryptography, can expose trapdoor information in searchable encryption schemes. To address this, Cheng et al. [15] introduced a new PEKS scheme in 2023 that is resistant to frequency analysis. Their approach incorporates two random values in the construction of search trapdoors, preventing the leakage of search frequency patterns and bolstering the overall security of the system.
1.3. Organization
Section 2 of this paper presents the preliminary knowledge utilized in our scheme. Section 3 introduces the concept of frequency analysis attacks and analyzes why PEKS schemes are vulnerable to this attack. Section 4 introduces the specific structure of our scheme in detail and proves that it satisfies both CKA security and KGA security under the random oracle model. Section 5 analyzes the operating efficiency of our scheme through theory and experiment. Finally, Section 6 summarizes our work in this paper.
2. Preliminaries
In this chapter, we introduce the prerequisite knowledge used in our scheme, including the DDH assumption and system model. Table 1 provides the meanings of some of the symbols used in this paper.

Table 1.
Related notation.
2.1. Decisional Diffie–Hellman Assumption
The Decisional Diffie–Hellman (DDH) assumption is a fundamental hypothesis in cryptography, where it is primarily used to establish the security of cryptographic protocols. One of its key advantages is its simplicity and efficiency, which makes protocols based on it more straightforward to design and analyze. Additionally, the DDH assumption is applicable to a wide range of cryptographic protocols, including public key encryption, digital signatures, and identity-based encryption, demonstrating broad utility. Compared to more complex security assumptions, DDH offers similar security guarantees while incurring lower computational costs. Most notably, protocols relying on the DDH assumption are resistant to various types of attacks, such as chosen ciphertext and chosen plaintext attacks, providing robust security for cryptographic systems. As a result, the DDH assumption not only simplifies security analysis but also offers strong protection in practical applications, making it a widely adopted and foundational assumption in modern cryptography. This is the primary reason we have selected this hard problem in our scheme [35].
The Decisional Diffie–Hellman (DDH) assumption is based on the difficulty of distinguishing between two specific 4-tuples in a cyclic group G of prime order q, where g is a generator of G. Given random elements and from , we can form two tuples and , where Q is a random element of G that is independent of and .
The DDH assumption asserts that it is computationally hard for any efficient algorithm to distinguish between these two tuples. Specifically, an adversary cannot determine whether the fourth element is or a random Q. The ability of an adversary to distinguish between these tuples is measured by the following advantage:
For any PPT adversary this advantage is negligible, meaning that distinguishing the two tuples is computationally infeasible. The DDH assumption underpins the security of cryptographic protocols such as the Diffie–Hellman protocol by ensuring that values generated during key exchange remain unpredictable and indistinguishable to attackers.
2.2. Scheme Model
This section introduces the system model of the proposed scheme and details the entities involved. The proposed system consists of three main entities: the cloud server, data owner, and data user. The data owner is responsible for generating encrypted keywords that correspond to the encrypted file; on the other hand, the data receiver generates search trapdoors for the specific keywords that the user intends to search for. The cloud server, acting as an intermediary, is tasked with matching the generated search trapdoor to the encrypted keywords stored in the cloud. Our scheme is constructed using seven distinct algorithms: , and . Each of these algorithms plays a pivotal role in ensuring the system’s security, efficiency, and overall functionality.
- : Given a security parameter , the algorithm initializes by generating a global parameter , which serves as the fundamental setup for the system. This parameter is derived from and ensures that all subsequent cryptographic operations adhere to the required security standards. The global parameter is then distributed to all entities within the system, enabling them to securely perform operations while preserving confidentiality and integrity.
- : The data sender initiates the process. Based on this parameter, the algorithm generates a key pair for the sender; may be shared with other entities, while the private key remains confidential and is used exclusively by the sender for secure operations such as encryption. This key pair is essential for enabling secure interactions between the sender and the system, ensuring the integrity and confidentiality of the transmitted data.
- : The data receiver executes the algorithm to generate a public–private key pair for itself. The public key can be distributed to other entities, while the private key remains confidential and is used exclusively by the receiver for decryption or other secure operations. This key pair is essential for the receiver to securely interact with the system and ensure the confidentiality of the data it receives.
- : This algorithm is responsible for generating a key pair for the cloud server; can be distributed to other entities to enable secure communication, while the private key remains secret and is used solely by the cloud server for tasks such as decryption or validating queries. This key pair is crucial for maintaining secure communication and interactions between the cloud server and other system components.
- : The data sender inputs , , and a keyword W extracted from the file into this algorithm. The algorithm subsequently produces an encrypted keyword index, , associated with the keyword W. This encrypted index enables the cloud server to perform secure keyword-based operations on the encrypted data. Once the index is generated, the data sender transmits it to the cloud server for further processing.
- : The data receiver executes the algorithm to generate a search trapdoor for the keyword that the user wishes to search. Using , , , and , the algorithm produces the trapdoor . This search trapdoor is then sent to the cloud server. The trapdoor enables the cloud server to securely match the search query with the encrypted keyword without disclosing any information about itself.
- 0/1 ←(): Upon receiving the search trapdoor and encrypted keyword index , the cloud server executes the matching algorithm. Using its private key , the server performs the matching operation between and . If the keyword that the user wishes to search for matches the keyword W associated with the encrypted index , the match is successful and the algorithm outputs 1, indicating a successful search. If the keywords and W do not match, the match fails and the algorithm outputs 0, indicating that no match was found.
2.3. Security Model
Our scheme can provide users with a safe keyword retrieval function. Figure 1 specifically shows the security model of our scheme. For any PPT adversary, our scheme has both CKA security and KGA security. Thus, the adversary is unable to infer any information about a keyword from its ciphertext or search trapdoor based on the knowledge they possess.
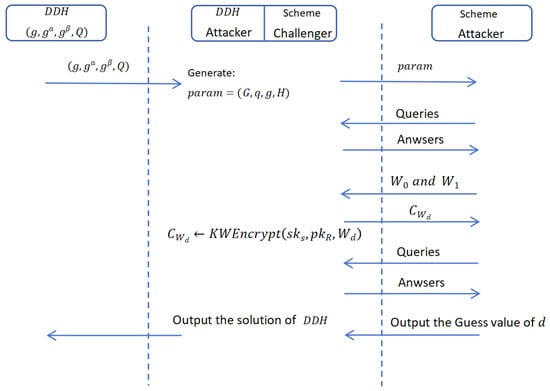
Figure 1.
Security model.
We formally define the CKA security of our scheme through the interaction between and in the following game.
- 1.
- Setup. The challenger runs the algorithm to generate the system parameters , which are then made publicly available. Using these system parameters, the challenger generates key pairs for the sender, receiver, and cloud server, denoted as , , and , respectively. Finally, the challenger sends the system parameters along with the public keys to the adversary .
- 2.
- Phase 1. In this phase, a polynomial number of adaptive queries to the challenger’s ciphertext oracle and trapdoor oracle is allowed for the adversary . The challenger is required to provide responses to these queries based on the system’s setup and the information available to them.
Ciphertext oracle: The adversary picks a keyword W at random and presents it to the ciphertext oracle. In response, the challenger runs the algorithm to encrypt the keyword W using and , generating the corresponding keyword ciphertext . This ciphertext is then returned to the adversary .
Trapdoor oracle: The adversary randomly chooses a keyword and submits it to the trapdoor oracle for a query. Upon receiving this request, the challenger uses the algorithm to generate a corresponding search trapdoor . The trapdoor generation process involves utilizing , and to create the trapdoor. After the trapdoor has been generated, it is returned to the adversary for further use in attack or analysis.
- 3.
- Challenge. After performing the polynomial number of queries, the adversary randomly selects two distinct keywords and and submits them to the challenger. The only condition for these keywords is that they must not have been queried in previous phases. Upon receiving these two keywords, the challenger randomly chooses a value and computes the corresponding keyword ciphertext for the selected keyword. The challenger then sends to .
- 4.
- Phase 2. During this phase, may query the two previously mentioned random oracles, but is restricted from obtaining information about and .
- 5.
- Guess. Finally, outputs a guess value . If , then wins the game.
In the above interaction process, the probability of the adversary winning is . As shown in Equation (1), the adversary’s ability to compromise the ciphertext indistinguishability of our scheme can be expressed as follows:
If is negligible, then the scheme is secure against PPT adversaries.
The security model of the trapdoor indistinguishability of our scheme is the same as above.
3. Frequency Analysis Attack
In traditional cryptography, frequency analysis attacks exploit the fact that different text units such as letters or words appear with varying frequencies in natural languages. By analyzing these frequencies in ciphertext, an attacker may decrypt the message. Similarly, in searchable encryption, frequency analysis targets the search trapdoors generated for keywords. In real-world applications, keyword spaces often have low entropy, meaning that certain keywords are searched more frequently than others. An attacker can gather information about these frequencies through methods such as big data analytics or access to public datasets. If the attacker knows the frequency of each keyword in the search space, they can analyze the search trapdoor for a given keyword and compare it with the known frequency distribution. This allows the attacker to deduce the plaintext keyword associated with the trapdoor, undermining the security of the searchable encryption scheme. To evaluate the robustness of searchable encryption schemes, we assume that the adversary has knowledge of the search frequencies for all possible keywords. In this case, the attacker can use frequency analysis on the trapdoor to recover the keyword, potentially breaking the encryption and revealing the plaintext.
In searchable encryption schemes, the trapdoors generated by a deterministic trapdoor generation algorithm are invariant for each keyword. This inherent property leads to potential vulnerabilities, as an adversary can exploit the consistency of trapdoor generation to perform frequency analysis attacks. In such attacks, the adversary gains insights into the distribution of keywords in the encrypted dataset based on the repeated appearance of the same trapdoor for identical keywords. For instance, consider the scheme proposed by Bai et al. [16], where the trapdoor generation algorithm is deterministic. In this scheme, the trapdoor for a given keyword is computed using the function , where H is a cryptographic hash function, K is a fixed key, and W represents the keyword being searched. Thus, for two distinct keywords and , the corresponding trapdoors are calculated as and . The deterministic nature of the algorithm means that if , then , leading to identical trapdoors for the same keyword. This predictability poses a significant vulnerability, as an attacker who intercepts these trapdoors can infer the search frequency of a keyword based on the repeated occurrence of the same trapdoor. By examining the frequency of these keywords, the attacker could potentially infer the plaintext information associated with them. To mitigate this weakness, our encryption scheme eliminates the deterministic trapdoor generation approach and introduces randomness into the trapdoor creation process, strengthening its resistance against frequency analysis attacks.
In probabilistic searchable encryption schemes, random values are introduced during trapdoor generation to ensure that each search trapdoor is unique, making it more challenging for attackers to correlate trapdoors with specific keywords. However, this method is not fully resistant to frequency analysis attacks. In traditional searchable encryption schemes, when a probabilistic trapdoor generation algorithm is used, the random values must be included in the search trapdoor and sent to the server to allow for the proper matching operation. Although these random values are designed to obscure the link between the trapdoor and its corresponding keyword, an attacker can still exploit this randomness to perform frequency analysis and extract meaningful information. For example, consider the trapdoor generation scheme from Li et al. [17], which uses probabilistic trapdoors. Given two keywords and , the corresponding search trapdoors are generated as follows: and . Here, r and are random values, K is a fixed parameter, and g and h are generators of the group G, while H is a cryptographic hash function that combines K with the keyword or to generate a unique value associated with the keyword. To match a search trapdoor to a keyword, an adversary can compute the following ratio of bilinear pairings between the two trapdoors:
where equation e represents the bilinear pairing operation. This operation satisfies the property that for any . The key observation here is that the bilinear pairing operation allows the attacker to isolate the influence of the random values r and . After performing this operation, the effect of these random values is eliminated, and the result depends only on the keywords and . If , then the ratio will simplify to 1; otherwise, it will be different.
By performing this operation across multiple trapdoors, an attacker can determine whether two different trapdoors correspond to the same keyword. By calculating the proportion of trapdoors generated with a given keyword, the attacker can estimate the search frequency for that keyword. Thus, while the use of random values in probabilistic trapdoor generation makes each trapdoor unique, the approach remains vulnerable to frequency analysis. The random components can be neutralized through bilinear pairings, allowing the attacker to correlate trapdoors with keywords and determine their search frequencies. This means that the randomness introduced by the trapdoor generation algorithm does not fully protect against the threat of frequency analysis.
Our searchable encryption scheme leverages a cloud server’s key pair to generate search trapdoors while employing a hash function to obfuscate the components containing random values. Because the adversary does not have access to the server’s private key, they cannot extract meaningful information from the trapdoor to distinguish the obfuscated parts. Furthermore, as the random value components are masked by the hash function, the adversary is unable to mitigate their effect through computation, ensuring that our scheme provides robust protection against frequency analysis attacks.
4. A Pairing-Free Searchable Encryption Scheme
4.1. Construction of Our Scheme
We introduce a searchable encryption scheme that is free from pairings and resilient against frequency analysis attacks. The sender encrypts data and generates search trapdoors, which the receiver uses to search the encrypted data. The cloud server stores the encrypted data and performs the search. By eliminating pairing operations and separating the roles of the entities, our scheme achieves improved efficiency and security, preventing attackers from inferring data from search patterns.
- : The algorithm takes a security parameter as input to generate global parameters , where G is a multiplicative cyclic group with order q, q is a prime number, g is a generator of the group (meaning that all elements of G can be obtained by applying the group operation to powers of g), and H is a cryptographic hash function that maps arbitrary inputs to fixed-size outputs in order to ensure secure mapping of messages (such as keywords) to group elements:
- : The data sender randomly selects an element from the set , which serves as their private key . Using this private key, the sender computes the corresponding public key , where g serves as the generator of the group G. The public key is then published for use in subsequent operations.
- : The data receiver randomly selects an element from the set to serve as their private key . Using this private key, the receiver computes the corresponding public key , where g is the generator of the group G. The receiver then publishes the public key for use in subsequent operations.
- : This algorithm takes the global parameters as input and outputs the public and private keys for the cloud server. The cloud server randomly selects an element from the set to serve as its private key . Using this private key, the cloud server computes the corresponding public key , where g is the generator of the group G. The cloud server then publishes the public key for use in subsequent operations.
- : The data sender uses their private key and the data receiver’s public key to encrypt the keyword W extracted from the file. The encryption is accomplished by computing the keyword ciphertext , where . In the end, the data sender forwards to the cloud server, where it is stored for later retrieval.
- : The data receiver generates a search trapdoor for the keyword that the user wishes to search. The trapdoor is computed as , where S is a randomly selected element from and is the public key of the cloud server. Additionally, is computed as . After the trapdoor is generated, the data receiver sends it to the cloud server to perform the search.
- 0/1 ←(): After receiving and , the cloud server determines whether is true. If the equation is satisfied, then the match is considered successful; otherwise, it is deemed a failure.
4.2. Correctness Statement
Equation (4) provides a brief explanation of the scheme’s correctness. Upon receiving the search trapdoor derived from the user’s keyword , the cloud server proceeds to compare it against the encrypted keyword index generated by the data sender. If the keyword that the user is searching for matches the keyword extracted from the data file (i.e., ), then
The above formula indicates that the cloud server can determine whether W and are the same keyword based on comparison of and .
4.3. Security Proof
DDH is a mathematically hard problem; therefore, any PPT adversary cannot distinguish the keyword ciphertext constructed by our scheme.
Proof.
Assuming that there is a PPT adversary that can break the ciphertext indistinguishability of our scheme with a non-negligible advantage, then we can construct a polynomial algorithm to solve the DDH assumption. First, has an instance , , g is a generator of G, and Q is a random element on group G. □
Setup. sets a system parameter and makes it public. Then, takes in the DDH tuple as the public keys of the data sender and receiver; that is, , which implicitly means .
Phase 1. The adversary can adaptively query two random oracles in polynomial time:
Ciphertext oracle: When the adversary arbitrarily selects a keyword W, the challenger uses the algorithm to generate the corresponding keyword ciphertext .
Trapdoor oracle: When the adversary arbitrarily selects a keyword , generates the corresponding trapdoor , where S is a random element from .
Challenge. At this point, the adversary picks two distinct keywords and , then submits them to the challenger . These keywords must not have been queried by the adversary in Phase 1. The challenger then randomly chooses a bit and selects the corresponding keyword . Using this keyword, the challenger computes the associated ciphertext for . Finally, the challenger sends the ciphertext to the adversary as the challenge ciphertext.
Phase 2. In this phase, after receiving the challenge ciphertext from the challenger, may query the two previously mentioned random oracles. The query keyword is required to be different from both and .
Guess. After the adversary queries the polynomial degree, the value of the challenge keyword is guessed. The adversary randomly selects as the guess value. If , then the challenger will determine .
If the adversary is able to correctly determine the value of d, the challenger would be able to verify whether Q equals . By employing a proof by contradiction, we can conclude that if an adversary can solve a Decisional Diffie–Hellman (DDH) assumption with probability , then the adversary can distinguish whether Q equals . In turn, this implies that the adversary can predict the value of d with the same probability. Thus, the adversary’s ability to break the ciphertext indistinguishability of our scheme can be quantified as follows:
Because the DDH assumption is a hard problem, the challenger cannot efficiently determine whether Q is equal to . Consequently, the adversary cannot reliably distinguish the value of d (i.e., cannot distinguish between ciphertexts). Therefore, we conclude that the attacker cannot break the ciphertext indistinguishability of our scheme. Q.E.D.
DDH is a mathematically hard problem; therefore, any PPT adversary cannot distinguish the trapdoor constructed by our scheme.
Proof.
Assuming that there is a PPT adversary that can break the trapdoor indistinguishability of our scheme with a non-negligible advantage, then we can construct a polynomial algorithm to solve the DDH problem. First, the challenger has an instance , , with Q being a random element on group G. □
Setup. sets a system parameter and makes it public. Then, takes in the DDH tuple as the public keys of the cloud server, that is (which implicitly means ). The challenger randomly selects two elements on group as the private keys of the data sender and receiver, then calculates their public keys .
Phase 1. The adversary can adaptively query two random oracles in polynomial time:
Ciphertext oracle: When the adversary arbitrarily selects a keyword W, the challenger uses the algorithm to generate the corresponding keyword ciphertext .
Trapdoor oracle: When the adversary arbitrarily selects a keyword , generates the corresponding trapdoor , where S is a random element from .
Challenge. At this stage, the adversary picks two keywords and and sends them to , ensuring that these keywords have not been previously queried during Phase 1; then randomly picks a bit and chooses the keyword . Based on this chosen keyword, the challenger computes the corresponding trapdoor and sends it to the adversary as the challenge trapdoor.
Phase 2. In this phase, after receiving the challenge trapdoor from the challenger , may query the two previously mentioned random oracles. The query keyword is required to be different from both and .
Guess. After the adversary queries the polynomial degree, the value of the challenge keyword is guessed. The adversary randomly selects as the guess value. If , then the challenger will determine .
We observe that if the adversary successfully predicts the value of d, then the challenger would be able to determine whether Q is equal to . If the DDH assumption is solvable with probability , implying that the adversary can distinguish whether Q equals , it follows that the adversary can also guess d with the same probability. Therefore, the adversary’s ability to break the trapdoor indistinguishability in our scheme can be quantified by its advantage:
Due to the hardness of the DDH assumption, the challenger has no advantage in determining whether Q is equal to . As a result, the adversary cannot correctly determine the value of d (i.e., cannot accurately distinguish the trapdoor). Therefore, we conclude that the attacker cannot break the trapdoor indistinguishability of our scheme. Q.E.D.
5. Efficiency Analysis
5.1. Computational Complexity
Table 2 compares the computational complexity of several schemes. In the table, P denotes a bilinear pairing operation, E represents an exponentiation operation in group G, and H is a hash operation.

Table 2.
Computational complexity.
First, in the comparison of encryption keyword algorithms, our scheme exhibits the lowest computational complexity. This indicates that our scheme incurs less time overhead to encrypt the same number of keywords. Regarding the trapdoor generation and matching algorithms, the computational complexity of these two algorithms is relatively moderate due to the use of a pairing-free approach. In subsequent practical evaluations, we also collect the actual execution times of each algorithm to further validate the computational complexity.
5.2. Algorithm Running Time
In addition to the theoretical explanation of computational complexity, we conducted a specific experimental analysis of the algorithm running time of each scheme. We used the JPBC library in JAVA to implement the algorithms of several schemes and collected the running time of each algorithm. The curve used in the experiment was a Type-A elliptic curve of the form , where q is a 512-bit prime number. The experimental equipment was a laptop configured as i7-12700H 2.30 GHz CPU with 16 GB of RAM.
Figure 2, Figure 3 and Figure 4 illustrates the running times of the different scheme algorithms, offering an intuitive comparison of the retrieval efficiency of searchable encryption schemes. The horizontal axis represents the number of keywords in the various datasets, while the vertical axis shows the time required for each algorithm to process all of the keywords. As can be seen in the figure, the running time of our proposed algorithm grows linearly, which indicates that the efficiency of our scheme remains stable across datasets containing different numbers of keywords.
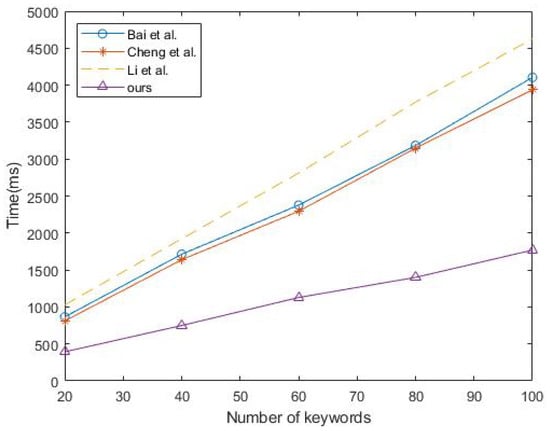
Figure 2.
KWEncrypt [15,16,17] algorithm.
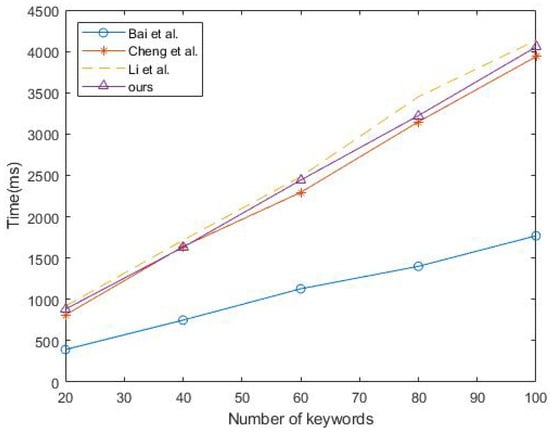
Figure 3.
Trapdoor [15,16,17] algorithm.
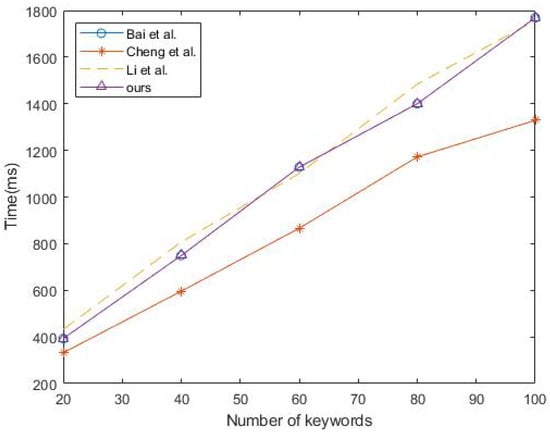
Figure 4.
Test [15,16,17] algorithm.
Figure 5 presents the execution times for each algorithm in the different schemes for a single retrieval operation. The bar chart clearly demonstrates that our scheme incurs significantly lower time overhead when performing a complete search operation compared to the other schemes. Based on the data in the figures, it can be concluded that our pairing-free searchable encryption scheme offers a distinct efficiency advantage. This efficiency makes it particularly beneficial in practical applications, as it helps to reduce the time cost associated with retrieval operations, thereby enhancing overall system performance.
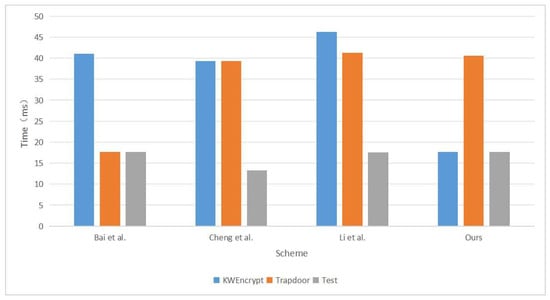
Figure 5.
Schemes [15,16,17].
5.3. Theoretical Comparison
Our scheme is based on the hardness of the Decisional Diffie–Hellman (DDH) assumption, which guarantees its security against any PPT adversary. In particular, it ensures both CKA security and KGA security, providing robust protection against various types of attacks. Table 3 illustrates the functional differences between our scheme and other schemes.

Table 3.
Selected performance metrics.
Many existing searchable encryption schemes are vulnerable to frequency analysis attacks, which represents a significant security concern. For example, the schemes presented by Bai et al. [16] and Zhang [30] et al. both rely on a deterministic trapdoor generation algorithm, which does not effectively guard against frequency analysis attacks. On the other hand, the probabilistic trapdoor generation approach in the schemes presented by Li et al. [17] and Huang [31] et al. remains susceptible to these attacks due to its inability to fully obscure the frequency patterns in the encrypted data.
In contrast, our proposed scheme incorporates mechanisms to protect against frequency analysis attacks, ensuring its security against this specific vulnerability, which we refer to as Frequency Analysis Attack (FAA) security. While Cheng et al.’s scheme [15] also provides resistance to frequency analysis attacks, it relies on relatively complex pairing operations which can introduce additional computational overhead. In comparison, our scheme is pairing-free, offering a more efficient solution by enhancing the performance of searching encrypted keywords without compromising security. By eliminating pairing operations, the efficiency is substantially improved, making it an ideal choice for real-world scenarios that demand a balance between high performance and robust security.
6. Conclusions and Future Work
This article introduces a pairing-free public key searchable encryption (PKSE) scheme designed to address vulnerabilities from frequency analysis attacks which exploit keyword usage patterns to infer sensitive information from encrypted data. To counter this, our scheme employs a novel method for generating search trapdoors by combining the server’s public key with a random value, effectively concealing keyword search frequencies and thwarting adversarial pattern analysis.
We formally define the scheme’s concepts and propose a tailored security model to resist frequency analysis attacks. Our scheme’s security relies on the Decisional Diffie–Hellman (DDH) assumption, with rigorous proofs demonstrating strong protection against polynomial-time (PPT) adversaries. Comprehensive experiments were performed on datasets containing different numbers of keywords to evaluate the scalability, efficiency, and security of the proposed scheme under real-world conditions. Results show that the scheme achieves an effective balance, offering robust security with minimal computational overhead. Its linear scalability with keyword numbers further underscores its suitability for large datasets. This pairing-free PKSE scheme provides a secure and efficient solution for applications requiring strong confidentiality, particularly in environments that are vulnerable to frequency analysis attacks.
One of the key limitations of our scheme is that it currently supports only a one-to-one application model, which means that it is designed to handle scenarios with a single data owner and a single data user. While this structure ensures strong security and is efficient for certain use cases, it may not be suitable for more complex environments such as those involving multiple users or collaborative data sharing. To address this limitation, future research could focus on extending the proposed scheme to support one-to-many or many-to-many models. This would allow it to be applied to a broader range of real-world scenarios, such as cloud storage systems with multiple users or multi-party data sharing environments, while continuing to maintain the same level of security and efficiency. Enhancing the scalability and flexibility of our scheme to accommodate these more complex settings would be an important next step in the development of searchable encryption technology.
Author Contributions
Conceptualization, W.W.; methodology, W.W. and H.S.; software, H.S.; validation, H.S.; formal analysis, H.S.; writing—original draft preparation, H.S.; writing—review and editing, W.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Science and technology research project of Hebei higher education: ZD2021011.
Data Availability Statement
The data that support the findings of this study are available in the Java Pairing-Based Cryptography (JPBC) library at https://github.com/Clindbergh/jpbc (accessed on 15 February 2024). These data were derived from the following resources available in the public domain: JPBC Fork Repository: https://github.com/Clindbergh/jpbc (accessed on 15 February 2024); documentation and example code for JPBC: https://github.com/Clindbergh/jpbc/tree/master/examples (accessed on 15 February 2024). These resources were utilized to implement and evaluate the cryptographic schemes discussed in this study.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Boneh, D.; Di Crescenzo, G.; Ostrovsky, R.; Persiano, G. Public key encryption with keyword search. In Proceedings of the Advances in Cryptology-EUROCRYPT 2004: International Conference on the Theory and Applications of Cryptographic Techniques, Interlaken, Switzerland, 2–6 May 2004; Proceedings 23. Springer: Berlin/Heidelberg, Germany, 2004; pp. 506–522. [Google Scholar]
- Cui, H.; Deng, R.H.; Liu, J.K.; Li, Y. Attribute-based encryption with expressive and authorized keyword search. In Proceedings of the Information Security and Privacy: 22nd Australasian Conference, ACISP 2017, Auckland, New Zealand, 3–5 July 2017; Proceedings, Part I 22. Springer International Publishing: Cham, Switzerland, 2017; pp. 106–126. [Google Scholar]
- Hayata, J.; Ishizaka, M.; Sakai, Y.; Hanaoka, G.; Matsuura, K. Generic construction of adaptively secure anonymous key-policy attribute-based encryption from public-key searchable encryption. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2020, 103, 107–113. [Google Scholar] [CrossRef]
- Li, J.; Ma, M.; Zhang, J.; Fan, S.; Li, S. Attribute-based keyword search from lattices. In Proceedings od the International Conference on Information Security and Cryptology, Nanjing, China, 6–8 December 2019; Springer International Publishing: Cham, Switzerland, 2019; pp. 66–85. [Google Scholar]
- Miao, Y.; Deng, R.H.; Liu, X.; Choo, K.-K.R.; Wu, H.; Li, H. Multi-authority attribute-based keyword search over encrypted cloud data. IEEE Trans. Dependable Secur. Comput. 2019, 18, 1667–1680. [Google Scholar] [CrossRef]
- Wang, B.; Song, W.; Lou, W.; Hou, Y.T. Inverted index based multi-keyword public-key searchable encryption with strong privacy guarantee. In Proceedings of the 2015 IEEE Conference on Computer Communications (INFOCOM), Hong Kong, China, 26 April–1 May 2015; pp. 2092–2100. [Google Scholar]
- Yang, X.; Chen, G.; Wang, M.; Li, T.; Wang, C. Multi-keyword certificateless searchable public key authenticated encryption scheme based on blockchain. IEEE Access 2020, 8, 158765–158777. [Google Scholar] [CrossRef]
- Liu, X.; Yang, G.; Susilo, W.; Tonien, J.; Liu, X.; Shen, J. Privacy-preserving multi-keyword searchable encryption for distributed systems. IEEE Trans. Parallel Distrib. Syst. 2020, 32, 561–574. [Google Scholar] [CrossRef]
- Zarezadeh, M.; Mala, H.; Ashouri-Talouki, M. Multi-keyword ranked searchable encryption scheme with access control for cloud storage. Peer-to-Peer Netw. Appl. 2020, 13, 207–218. [Google Scholar] [CrossRef]
- Huang, H.; Du, J.; Wang, H.; Wang, R. A multi-keyword multi-user searchable encryption scheme based on cloud storage. In Proceedings of the 2016 IEEE Trustcom/BigDataSE/ISPA, Tianjin, China, 23–26 August 2016; pp. 1937–1943. [Google Scholar]
- Ge, X.; Yu, J.; Hu, C.; Zhang, H.; Hao, R. Enabling efficient verifiable fuzzy keyword search over encrypted data in cloud computing. IEEE Access 2018, 6, 45725–45739. [Google Scholar] [CrossRef]
- Dong, Q.; Guan, Z.; Wu, L.; Chen, Z. Fuzzy keyword search over encrypted data in the public key setting. In Proceedings od the Web-Age Information Management: 14th International Conference, WAIM 2013, Beidaihe, China, 14–16 June 2013; Proceedings 14; Springer: Berlin/Heidelberg, Germany, 2013; pp. 729–740. [Google Scholar]
- Liu, Q.; Peng, Y.; Wu, J.; Wang, T.; Wang, G. Secure multi-keyword fuzzy searches with enhanced service quality in cloud computing. IEEE Trans. Netw. Serv. Manag. 2020, 18, 2046–2062. [Google Scholar] [CrossRef]
- Chen, J.; He, K.; Deng, L.; Yuan, Q.; Du, R.; Xiang, Y.; Wu, J. EliMFS: Achieving efficient, leakage-resilient, and multi-keyword fuzzy search on encrypted cloud data. IEEE Trans. Serv. Comput. 2017, 13, 1072–1085. [Google Scholar] [CrossRef]
- Cheng, L.; Meng, F. Public key authenticated searchable encryption against frequency analysis attacks. Inf. Sci. 2023, 640, 119060. [Google Scholar] [CrossRef]
- Bai, L.; Yong, L.; Chen, Z.; Shao, J. Pairing-free public-key authenticated encryption with keyword search. Comput. Stand. Interfaces 2024, 88, 103793. [Google Scholar] [CrossRef]
- Li, H.; Huang, Q.; Shen, J.; Yang, G.; Susilo, W. Designated-server identity-based authenticated encryption with keyword search for encrypted emails. Inf. Sci. 2019, 481, 330–343. [Google Scholar] [CrossRef]
- Cheng, L.; Qin, J.; Meng, F. Privacy leakage of certificateless public key authenticated searchable encryption via frequency analysis: Attacks and revises. Comput. Stand. Interfaces 2024, 87, 103762. [Google Scholar] [CrossRef]
- Verma, G.; Kanrar, S. Secure document sharing model based on blockchain technology and attribute-based encryption. Multimed. Tools Appl. 2024, 83, 16377–16394. [Google Scholar] [CrossRef]
- Sun, S.F.; Steinfeld, R.; Lai, S.; Yuan, X.; Sakzad, A.; Liu, J.K.; Nepal, S.; Gu, D. Practical non-interactive searchable encryption with forward and backward privacy. In Proceedings of the Usenix Network and Distributed System Security Symposium, Online, 21–25 February 2021; The Internet Society: Reston, VA, USA, 2021. [Google Scholar]
- Liu, J.; Li, Y.; Sun, R.; Pei, Q.; Zhang, N.; Dong, M.; Leung, V.C.M. EMK-ABSE: Efficient multikeyword attribute-based searchable encryption scheme through cloud-edge coordination. IEEE Internet Things J. 2022, 9, 18650–18662. [Google Scholar] [CrossRef]
- Wu, A.; Li, F.; Xin, X.; Zhang, Y.; Zhu, J. Efficient public-key searchable encryption against inside keyword guessing attacks for cloud storage. J. Syst. Archit. 2024, 149, 103104. [Google Scholar] [CrossRef]
- Song, D.X.; Wagner, D.; Perrig, A. Practical techniques for searches on encrypted data. In Proceedings of the 2000 IEEE Symposium on Security and Privacy, S&P 2000, Berkeley, CA, USA, 14–17 May 2000; pp. 44–55. [Google Scholar]
- Boneh, D.; Waters, B. Conjunctive, subset, and range queries on encrypted data. In Proceedings od the Theory of Cryptography: 4th Theory of Cryptography Conference, TCC 2007, Amsterdam, The Netherlands, 21–24 February 2007; Proceedings 4; Springer: Berlin/Heidelberg, Germany, 2007; pp. 535–554. [Google Scholar]
- Cash, D.; Grubbs, P.; Perry, J.; Ristenpart, T. Leakage-abuse attacks against searchable encryption. In Proceedings of the 22nd ACM SIGSAC Conference on Computer and Communications Security, Denver, CO, USA, 12–16 October 2015; pp. 668–679. [Google Scholar]
- Rhee, H.S.; Lee, D.H. Keyword updatable PEKS. In Proceedings od the Information Security Applications: 16th International Workshop, WISA 2015, Jeju Island, Republic of Korea, 20–22 August 2015; Revised Selected Papers 16; Springer International Publishing: Cham, Switzerland, 2016; pp. 96–109. [Google Scholar]
- Yin, S.; Li, H.; Teng, L.; Laghari, A.A.; Estrela, V.V. Attribute-based multiparty searchable encryption model for privacy protection of text data. Multimed. Tools Appl. 2024, 83, 45881–45902. [Google Scholar] [CrossRef]
- Senouci, M.R.; Benkhaddra, I.; Senouci, A.; Li, F. An efficient and secure certificateless searchable encryption scheme against keyword guessing attacks. J. Syst. Archit. 2021, 119, 102271. [Google Scholar] [CrossRef]
- Li, H.; Huang, Q.; Huang, J.; Susilo, W. Public-key authenticated encryption with keyword search supporting constant trapdoor generation and fast search. IEEE Trans. Inf. Forensics Secur. 2022, 18, 396–410. [Google Scholar] [CrossRef]
- Zhang, W.; Qin, B.; Dong, X.; Tian, A. Public-key encryption with bidirectional keyword search and its application to encrypted emails. Comput. Stand. Interfaces 2021, 78, 103542. [Google Scholar] [CrossRef]
- Huang, Q.; Huang, P.; Li, H.; Huang, J.; Lin, H. A more efficient public-key authenticated encryption scheme with keyword search. J. Syst. Archit. 2023, 137, 102839. [Google Scholar] [CrossRef]
- Rhee, H.S.; Park, J.H.; Susilo, W.; Lee, D.H. Trapdoor security in a searchable public-key encryption scheme with a designated tester. J. Syst. Softw. 2010, 83, 763–771. [Google Scholar] [CrossRef]
- Xu, P.; Jin, H.; Wu, Q.; Wang, W. Public-key encryption with fuzzy keyword search: A provably secure scheme under keyword guessing attack. IEEE Trans. Comput. 2012, 62, 2266–2277. [Google Scholar] [CrossRef]
- Chen, R.; Mu, Y.; Yang, G.; Guo, F.; Wang, X. Dual-server public-key encryption with keyword search for secure cloud storage. IEEE Trans. Inf. Forensics Secur. 2015, 11, 789–798. [Google Scholar] [CrossRef]
- Diffie, W.; Hellman, M.E. New directions in cryptography. In Democratizing Cryptography: The Work of Whitfield Diffie and Martin Hellman; Association for Computing Machinery: New York, NY, USA, 2022; pp. 365–390. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).