Bidirectional Pattern Recognition and Prediction of Bending-Active Thin Sheets via Artificial Neural Networks
Abstract
1. Introduction
- It helps to overcome the constraints of traditional physical parameter measurement by avoiding the requirement to directly measure complex physical parameters;
- It improves the simulation accuracy of complex structures and provides a more flexible method for structural design and analysis.
2. Related Works
2.1. Research on Active-Bending Simulation and Analysis
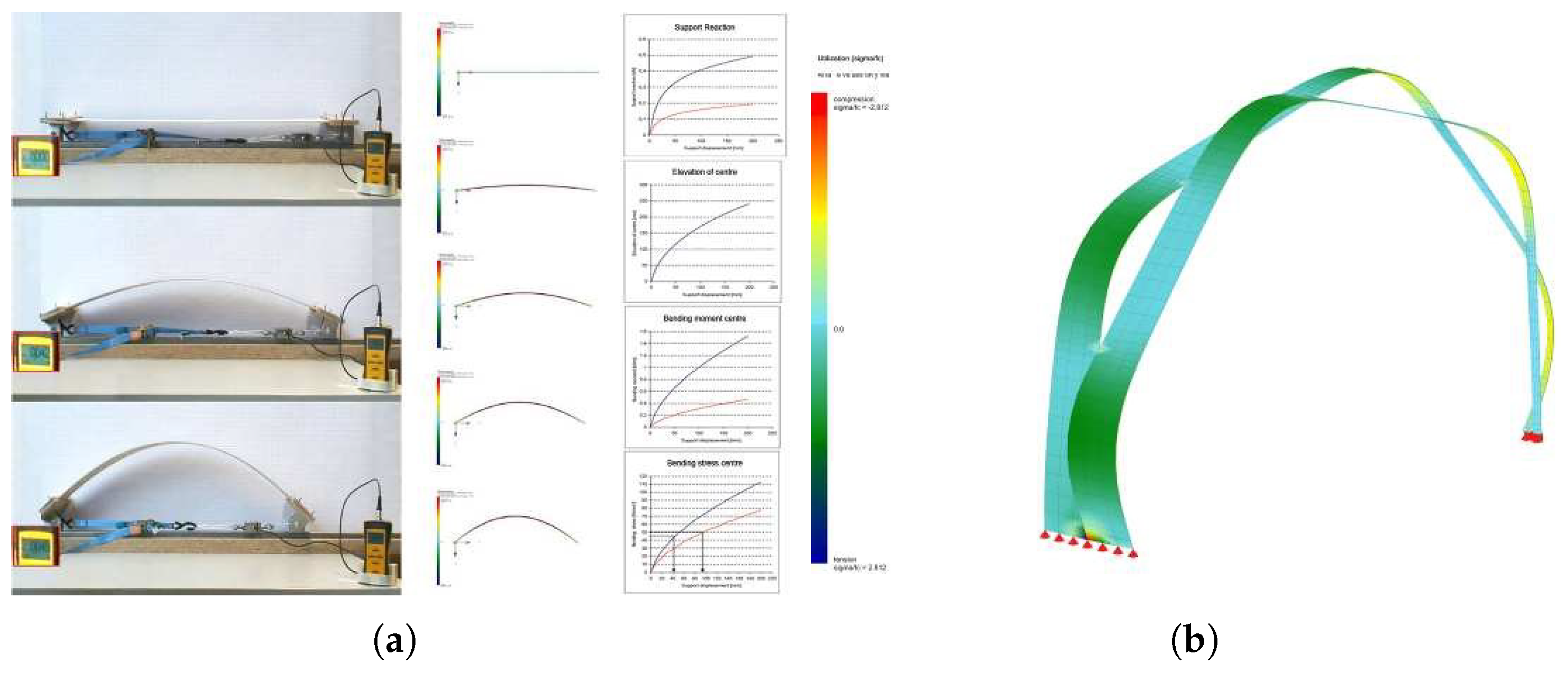
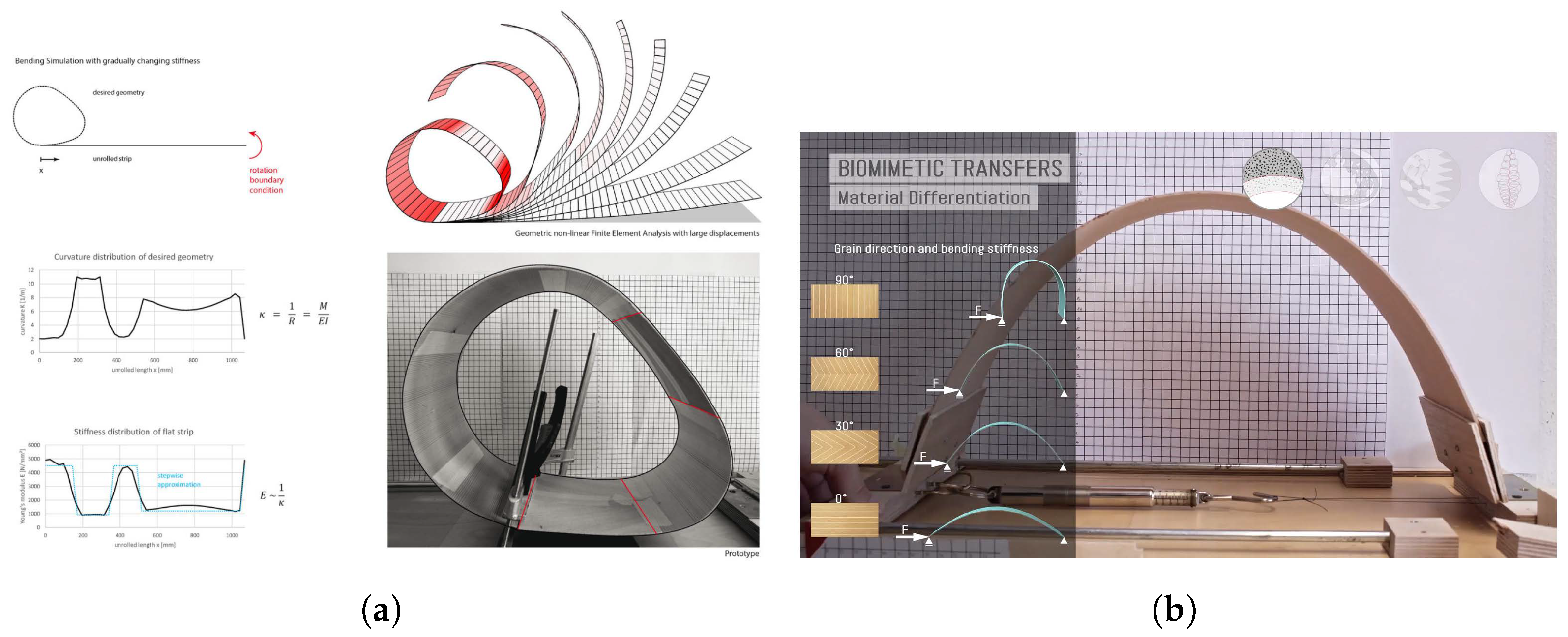
2.1.1. Previews Analysis Methods
2.1.2. Problems in Existing Analysis Methods of Bending-Active Geometry
2.2. Artificial Intelligence and Its Application
3. Research Method
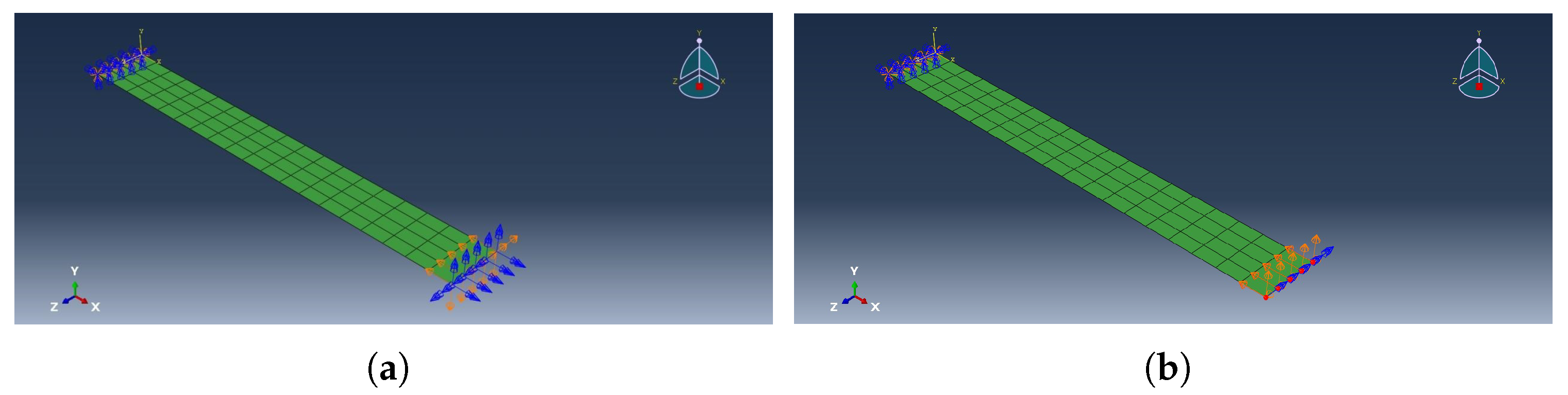
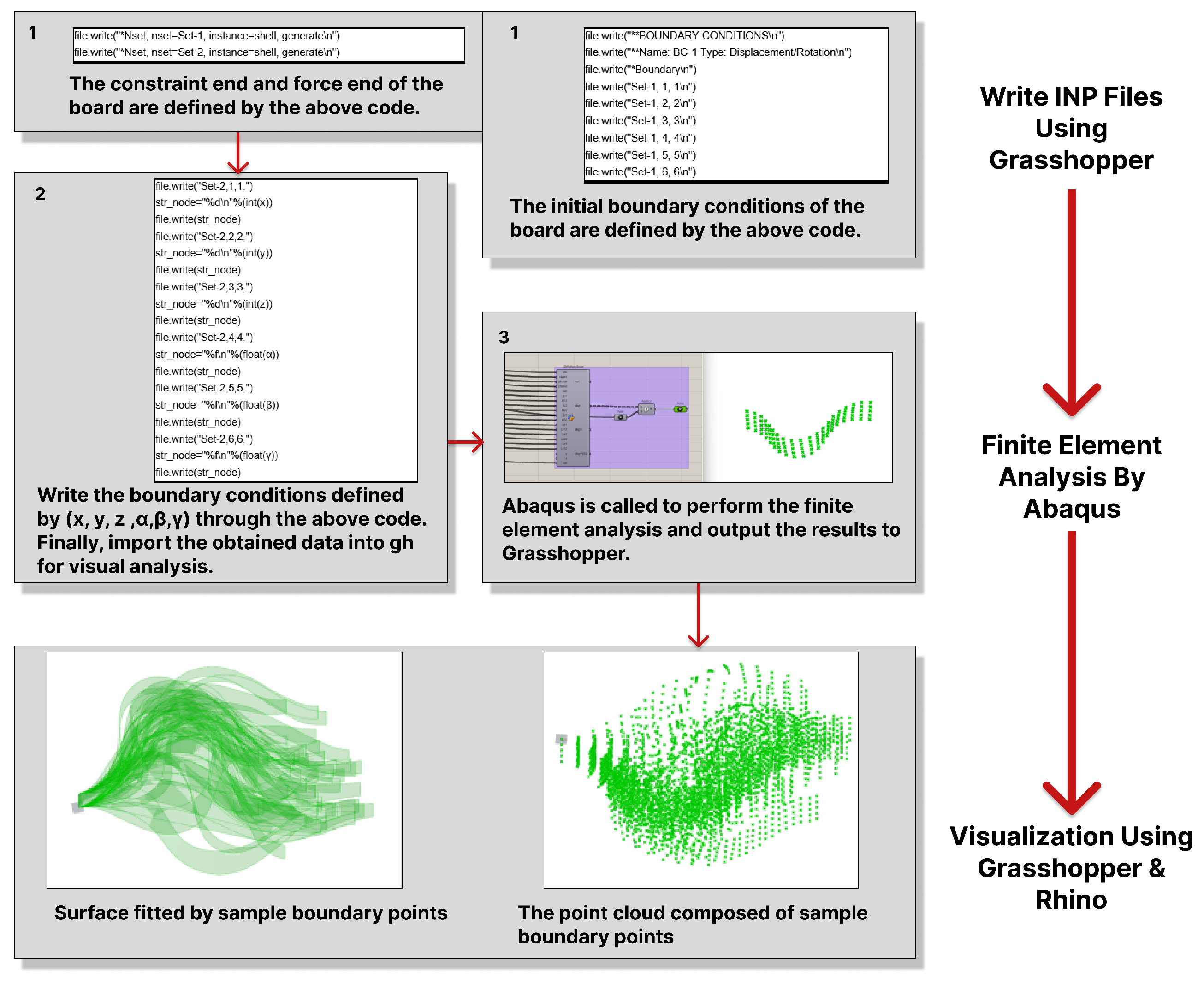
3.1. Data Collection
- The displacement components (x, y, z) of the points on the two corresponding boundary lines.
- The bending of the plate, represented by the displacement component along the z-axis of the points at the boundary line.
- The twist angle, represented by the twist angle of the cross-sectional line that forms a curved surface through two boundary lines.
3.2. The Neural Network
3.2.1. Dataset
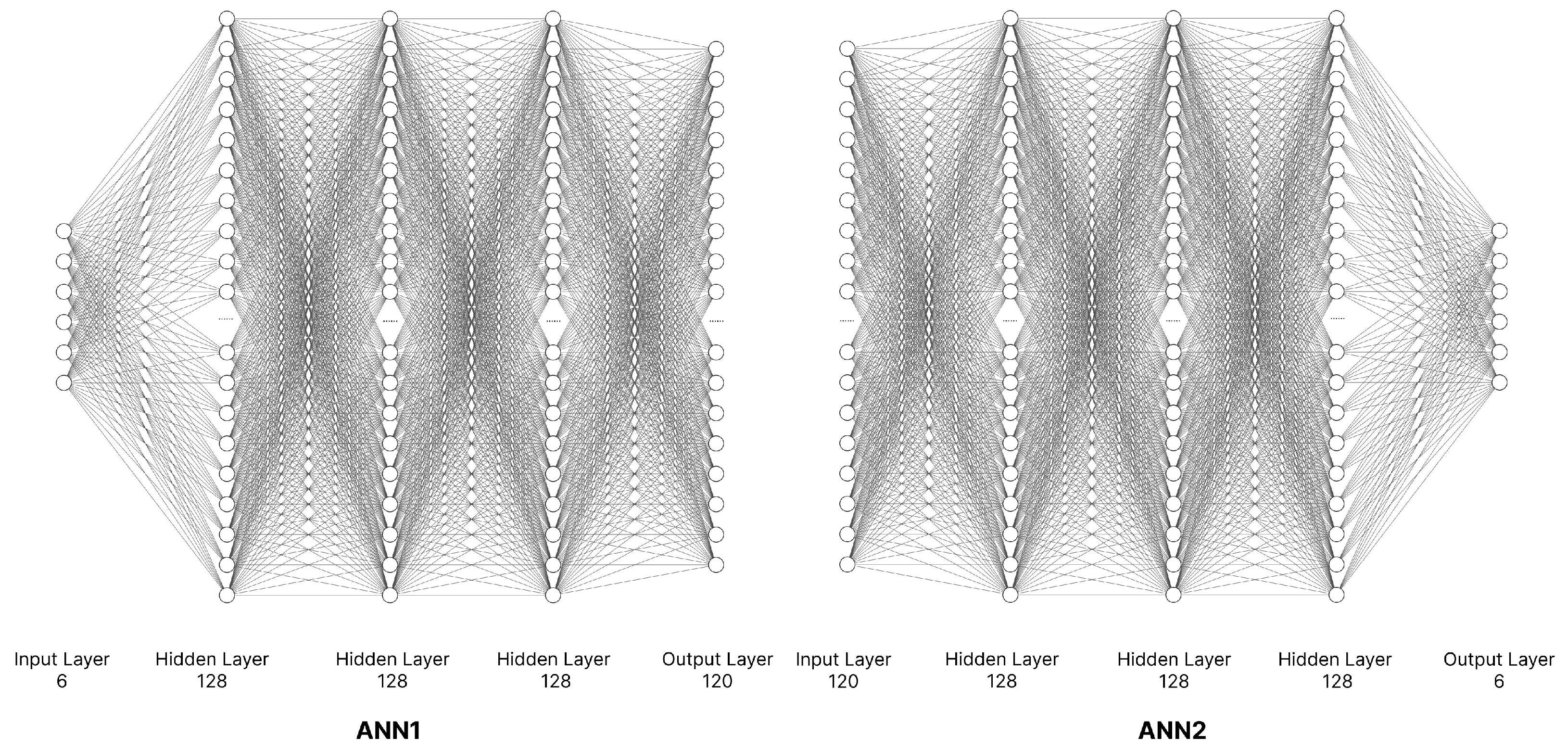
3.2.2. Basic Neural Network Architecture
3.2.3. Model Training
4. Results
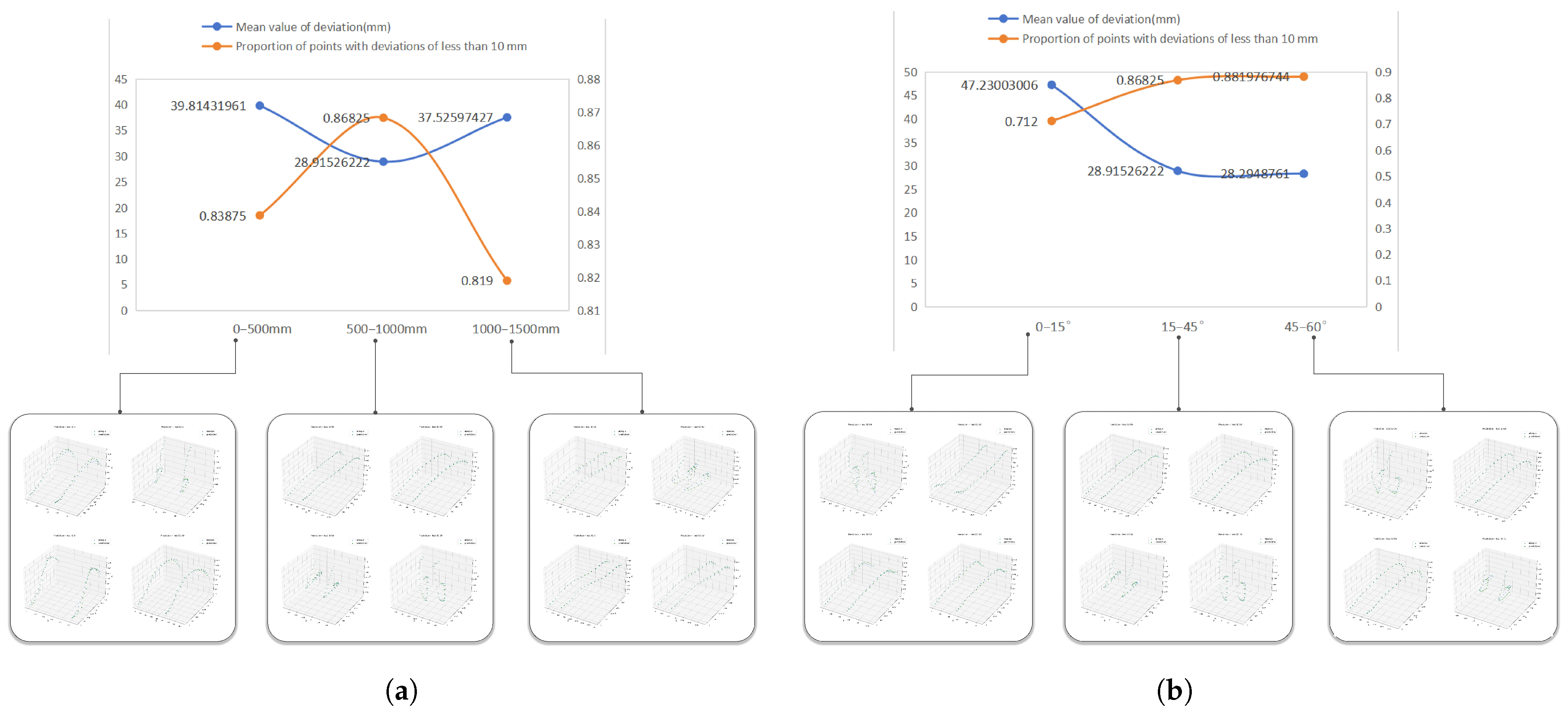
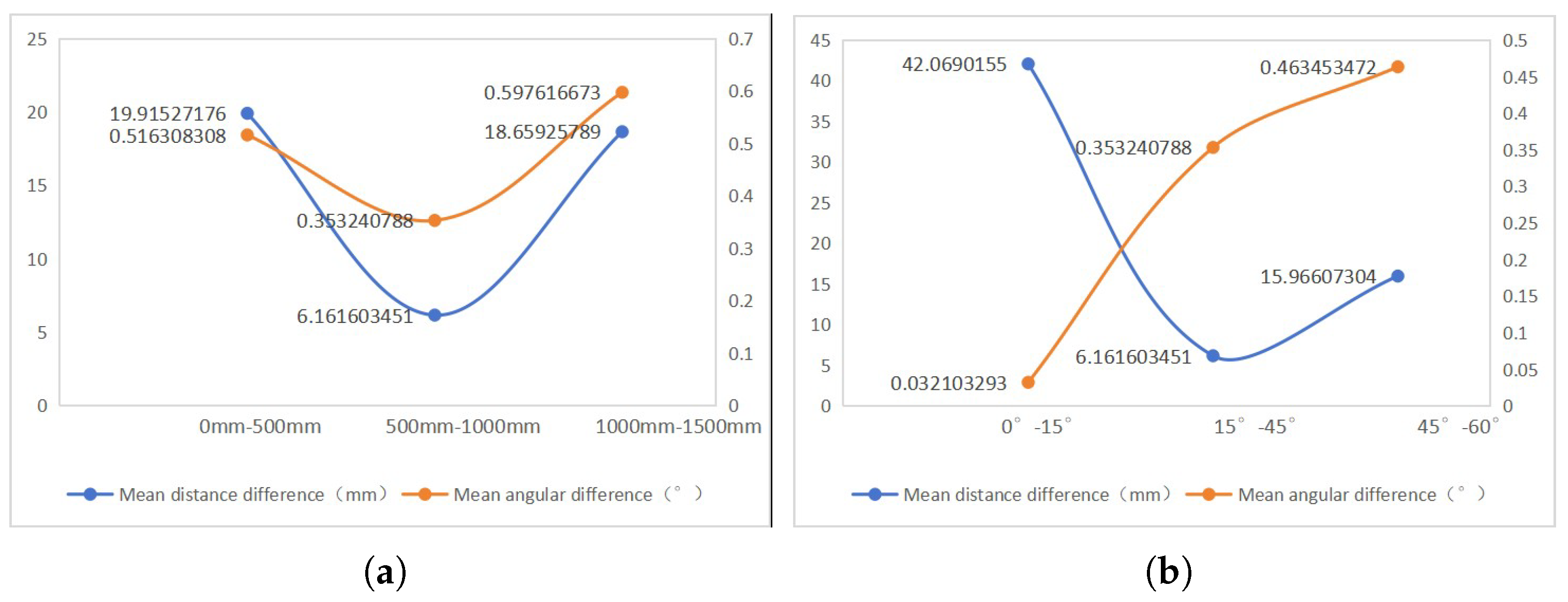
4.1. Forward Bending Shape Prediction
4.2. Reverse Boundary Condition Prediction
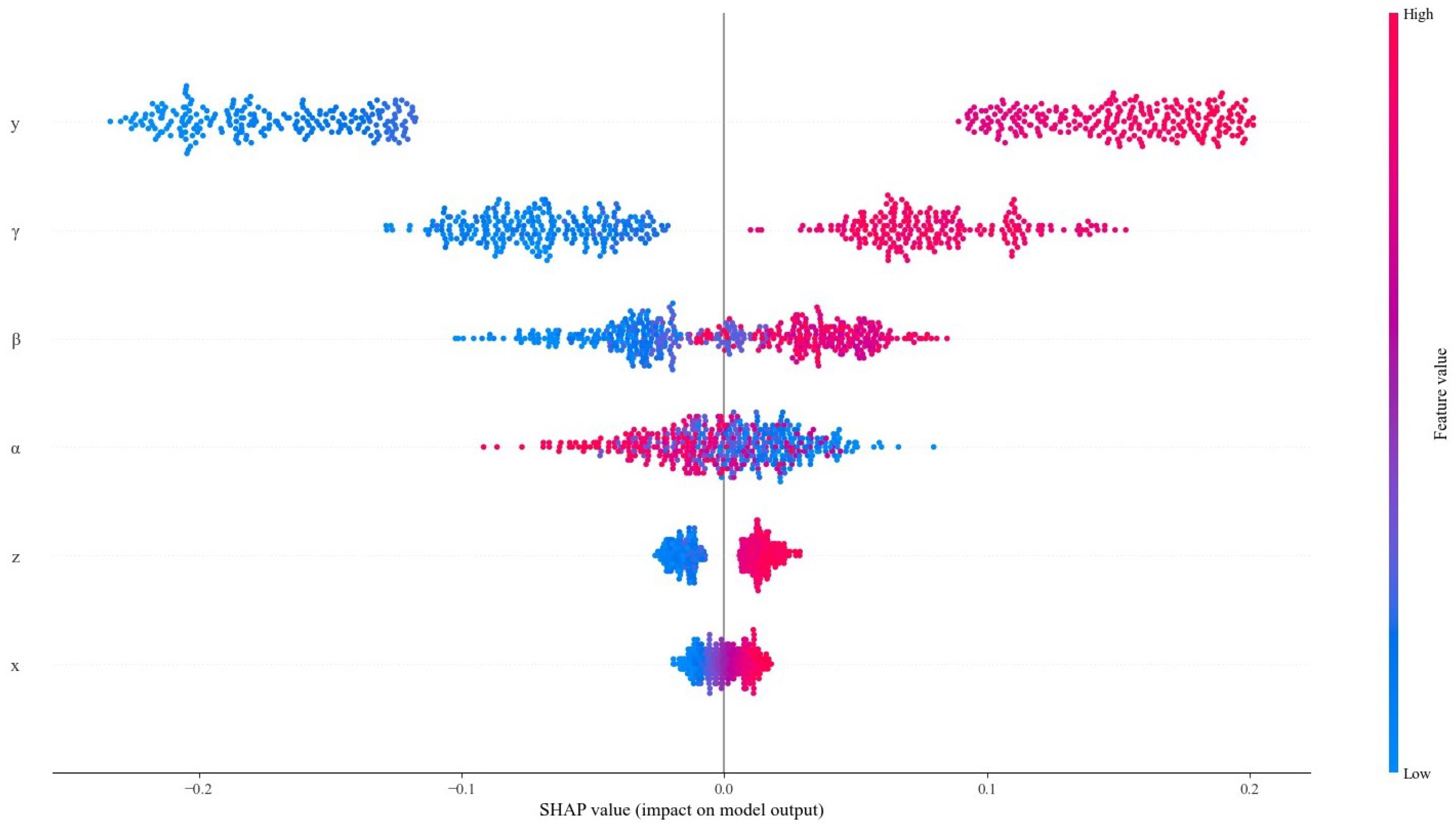
4.3. SHAP Analysis
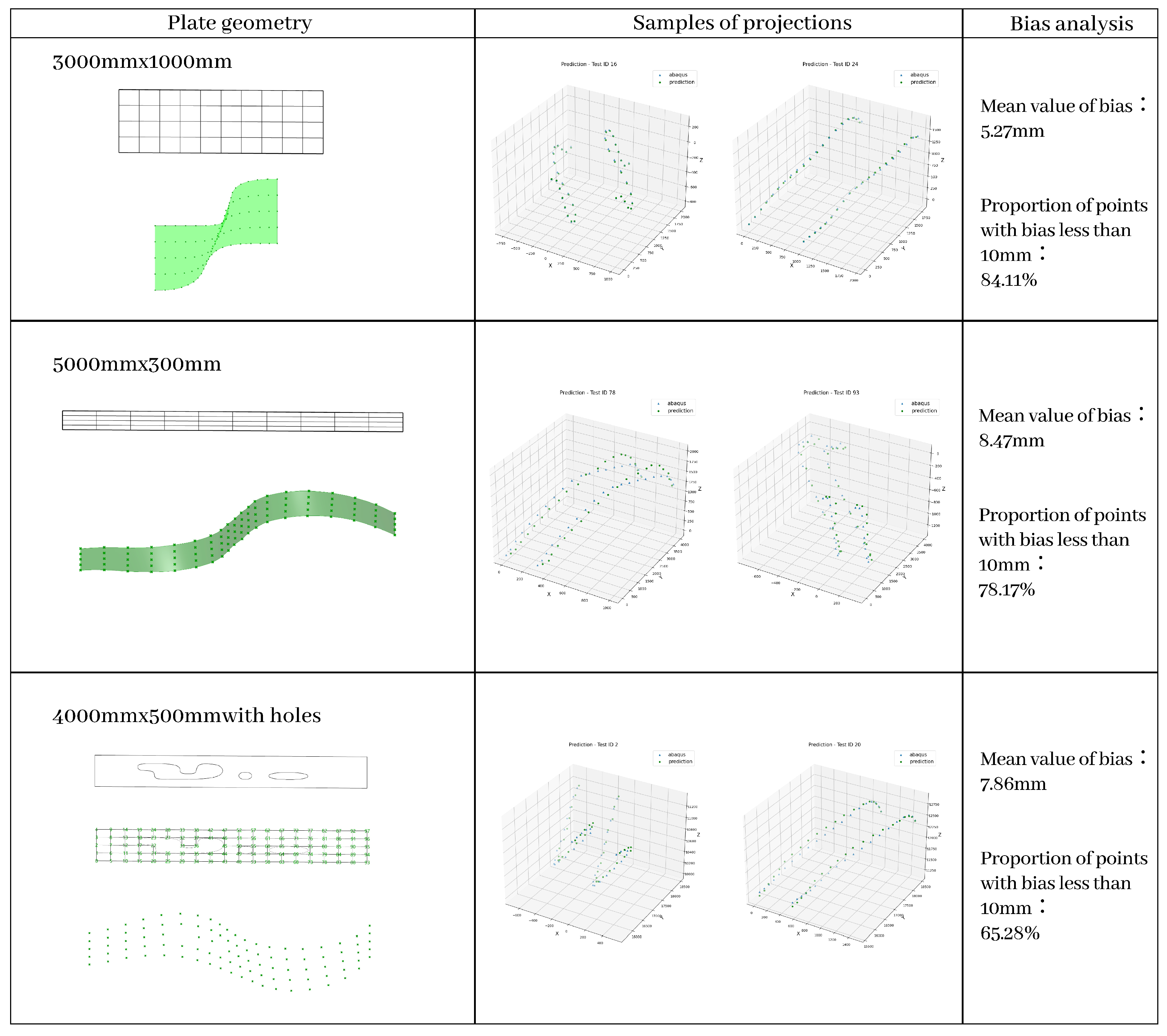
4.4. Test with Different Geometries
4.5. Transfer Learning
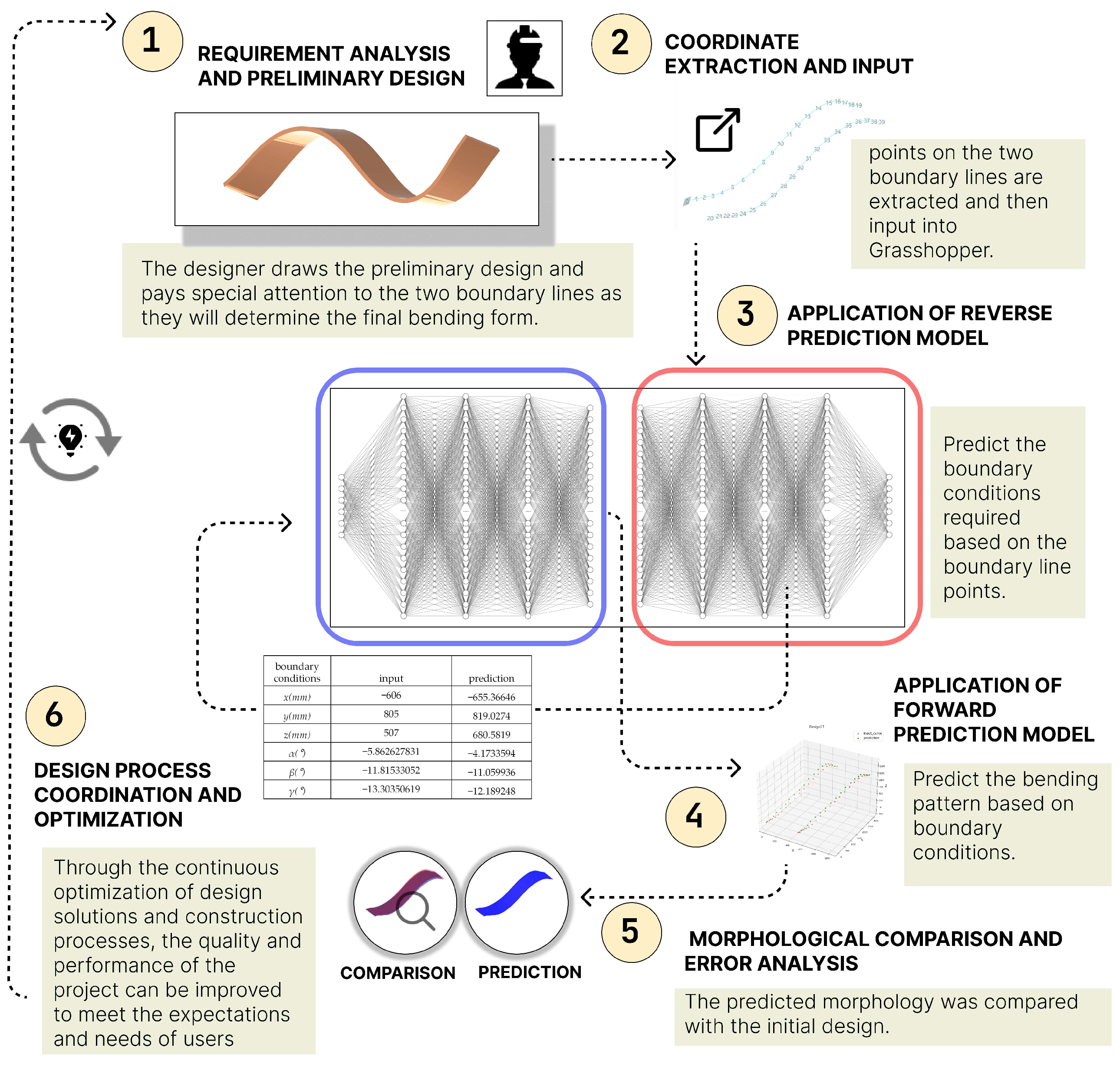
4.6. Application of Neural Networks to the Design Process
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gengnagel, C.; Alpermann, H.; Lafuente, E. Active Bending in Hybrid Structures. In FORM-RULE| RULE-FORM; Innsbruck University Press: Innsbruck, Austria, 2013; pp. 12–27. [Google Scholar]
- Lienhard, J.; Alpermann, H.; Gengnagel, C.; Knippers, J. Active bending, a review on structures where bending is used as a self-formation process. Int. J. Space Struct. 2013, 28, 187–196. [Google Scholar] [CrossRef]
- Lienhard, J.; Gengnagel, C. Recent developments in bending-active structures. In Proceedings of the IASS Annual Symposia, International Association for Shell and Spatial Structures (IASS), Boston, MA, USA, 16 July 2018; Volume 2018, pp. 1–8. [Google Scholar]
- Nicholas, P.; Tamke, M. Computational strategies for the architectural design of bending active structures. Int. J. Space Struct. 2013, 28, 215–228. [Google Scholar] [CrossRef]
- Schleicher, S.; Rastetter, A.; La Magna, R.; Schönbrunner, A.; Haberbosch, N.; Knippers, J. Form-finding and design potentials of bending-active plate structures. In Modelling Behaviour: Design Modelling Symposium, 2015; Springer: Cham, Switzerland, 2015; pp. 53–63. [Google Scholar]
- Lienhard, J. Bending-Active Structures: Form-Finding Strategies Using Elastic Deformation in Static and Kinetic Systems and the Structural Potentials Therein. 2014. Available online: https://elib.uni-stuttgart.de/handle/11682/124 (accessed on 1 January 2020).
- Designboom, n. Uni. of Calgary Team Designs, Builds, & Installs Experimental Pavilion. Available online: https://www.designboom.com/architecture/university-of-calgary-evds-experimental-pavilion-block-week-11-07-2015/ (accessed on 1 January 2020).
- Alpermann, H.; Lafuente Hernández, E.; Gengnagel, C. Case-studies of arched structures using actively-bent elements. In Proceedings of the IASS-APCS Symposium: From Spatial Structures to Space Structures, Seoul, Republic of Korea, 21–24 May 2012. [Google Scholar]
- Laccone, F.; Malomo, L.; Pietroni, N.; Cignoni, P.; Schork, T. Integrated computational framework for the design and fabrication of bending-active structures made from flat sheet material. In Structures; Elsevier: Amsterdam, The Netherlands, 2021; Volume 34, pp. 979–994. [Google Scholar]
- Puystiens, S.; Van Craenenbroeck, M.; Van Hemelrijck, D.; Van Paepegem, W.; Mollaert, M.; De Laet, L. Implementation of bending-active elements in kinematic form-active structures-Part I: Design of a representative case study. Compos. Struct. 2019, 216, 436–448. [Google Scholar] [CrossRef]
- Brancart, S.; De Laet, L.; Vergauwen, A.; De Temmerman, N. Transformable active bending: A kinematical concept. Mob. Rapidly Assem. Struct. IV 2014, 136, 171–182. [Google Scholar]
- De Laet, L.; Veenendaal, D.; Van Mele, T.; Mollaert, M.; Block, P. Bending incorporated: Designing tension structures by integrating bendingactive elements. In Proceedings of the TensiNet 2013 Symposium [RE] THINKING Lightweight Structures, Istanbul, Turkey, 8–10 May 2013; pp. 251–256. [Google Scholar]
- Vorstermans, R.L.; van Wijk, J.; Teuffel, P.; Habraken, A.P.; Houtman, R. Integration of form-finding, analysis process and production of a bending-active textile hybrid into one model. In Proceedings of the 6th Tensinet Symposia, Milan, Italy, 3–5 June 2019; pp. 123–134. [Google Scholar]
- Alpermann, H.; Gengnagel, C. Restraining actively-bent structures by membranes. In Proceedings of the Textiles Composites and Inflatable Structures VI: Proceedings of the VI International Conference on Textile Composites and Inflatable Structures, Barcelona, Spain, 9–11 October 2013; CIMNE: Barcelona, Spain, 2013; pp. 62–70. [Google Scholar]
- Lienhard, J.; La Magna, R.; Knippers, J. Form-finding bending-active structures with temporary ultra-elastic contraction elements. Mob. Rapidly Assem. Struct. IV 2014, 107, 115. [Google Scholar]
- D’Amico, B.; Zhang, H.; Kermani, A. A finite-difference formulation of elastic rod for the design of actively bent structures. Eng. Struct. 2016, 117, 518–527. [Google Scholar] [CrossRef]
- Liuti, A.; Mazzola, C.; Zanelli, A. Where design meets construction: A review of bending active structures. In Proceedings of the IASS Annual Symposia, International Association for Shell and Spatial Structures (IASS), Boston, MA, USA, 16 July 2018; Volume 2018, pp. 1–8. [Google Scholar]
- Fleischmann, M.; Menges, A. ICD/ITKE Research Pavilion: A case study of multi-disciplinary collaborative computational design. In Computational Design Modelling: Proceedings of the Design Modelling Symposium Berlin, 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 239–248. [Google Scholar]
- Menges, A. Integrative design computation for advancing wood architecture. In Advancing Wood Architecture; Routledge: London, UK, 2016; pp. 97–109. [Google Scholar]
- Menges, A.; Knippers, J. Architecture Research Building: ICD/ITKE 2010–2020; Birkhäuser: Basel, Switzerland, 2020. [Google Scholar]
- archDaily. ICD-ITKE Research Pavilion 2015-16/ICD-ITKE University of Stuttgart, Germany. Available online: https://www.archdaily.cn/cn/787034/icd-itke-yan-jiu-zhan-ting-2015-16-icd-itke-de-guo-si-tu-jia-te-da-xue (accessed on 1 January 2020).
- Brew, J.; Brotton, D. Non-linear structural analysis by dynamic relaxation. Int. J. Numer. Methods Eng. 1971, 3, 463–483. [Google Scholar] [CrossRef]
- Cuvilliers, P.; Yang, J.R.; Coar, L.; Mueller, C. A comparison of two algorithms for the simulation of bending-active structures. Int. J. Space Struct. 2018, 33, 73–85. [Google Scholar] [CrossRef]
- Pone, S. Digital tools and experimentations for structures realised with the active bending. Techne-J. Technol. Archit. Environ. 2017, 306–312. [Google Scholar] [CrossRef]
- Senatore, G.; Piker, D. Interactive real-time physics: An intuitive approach to form-finding and structural analysis for design and education. Comput.-Aided Des. 2015, 61, 32–41. [Google Scholar] [CrossRef]
- Hairer, E.; Hochbruck, M.; Iserles, A.; Lubich, C. Geometric numerical integration. Oberwolfach Rep. 2006, 3, 805–882. [Google Scholar] [CrossRef]
- La Magna, R.; Schleicher, S.; Knippers, J. Bending-active plates. Adv. Archit. Geom. 2016, 2016, 170–187. [Google Scholar]
- Bauer, A.M.; Längst, P.; La Magna, R.; Lienhard, J.; Piker, D.; Quinn, G.; Gengnagel, C.; Bletzinger, K.U. Exploring software approaches for the design and simulation of bending active systems. In Proceedings of the IASS Annual Symposia, International Association for Shell and Spatial Structures (IASS), Boston, MA, USA, 16 July 2018; Volume 2018, pp. 1–8. [Google Scholar]
- Larson, M.G.; Bengzon, F. The Finite Element Method: Theory, Implementation, and Applications; Springer Science & Business Media: Boston, NY, USA, 2013; Volume 10. [Google Scholar]
- Norrie, D.H.; De Vries, G. The Finite Element Method: Fundamentals and Applications; Academic Press: New York, NY, USA, 2014. [Google Scholar]
- Singh, K.; Kapania, R.K. Accelerated optimization of curvilinearly stiffened panels using deep learning. Thin-Walled Struct. 2021, 161, 107418. [Google Scholar] [CrossRef]
- Veeramachaneni, K.; Peram, T.; Mohan, C.; Osadciw, L.A. Optimization using particle swarms with near neighbor interactions. In Proceedings of the Genetic and Evolutionary Computation—GECCO 2003: Genetic and Evolutionary Computation Conference, Chicago, IL, USA, 12–16 July 2003; Proceedings, Part I. Springer: Berlin/Heidelberg, Germany, 2003; pp. 110–121. [Google Scholar]
- Zadeh, L.A. Fuzzy logic, neural networks, and soft computing. In Fuzzy Sets, Fuzzy Logic, and Fuzzy Systems: Selected Papers by Lotfi A Zadeh; World Scientific: London, UK, 1996; pp. 775–782. [Google Scholar]
- Maier, H.R.; Dandy, G.C. Neural networks for the prediction and forecasting of water resources variables: A review of modelling issues and applications. Environ. Model. Softw. 2000, 15, 101–124. [Google Scholar] [CrossRef]
- Fateh, A.; Hejazi, F. Experimental testing of variable stiffness bracing system for reinforced concrete structure under dynamic load. J. Earthq. Eng. 2022, 26, 1416–1437. [Google Scholar] [CrossRef]
- Bouman, K.L.; Xiao, B.; Battaglia, P.; Freeman, W.T. Estimating the material properties of fabric from video. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013; pp. 1984–1991. [Google Scholar]
- Davis, A.; Bouman, K.L.; Chen, J.G.; Rubinstein, M.; Durand, F.; Freeman, W.T. Visual vibrometry: Estimating material properties from small motion in video. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 5335–5343. [Google Scholar]
- Wang, H.; Yang, Y. Descent methods for elastic body simulation on the GPU. ACM Trans. Graph. (TOG) 2016, 35, 1–10. [Google Scholar] [CrossRef]
- Rodriguez-Pardo, C.; Prieto-Martin, M.; Casas, D.; Garces, E. How will it drape like? Capturing fabric mechanics from depth images. In Computer Graphics Forum; Wiley Online Library: Hoboken, NJ, USA, 2023; Volume 42, pp. 149–160. [Google Scholar]
- Gavriil, K.; Guseinov, R.; Pérez, J.; Pellis, D.; Henderson, P.; Rist, F.; Pottmann, H.; Bickel, B. Computational design of cold bent glass façades. ACM Trans. Graph. (TOG) 2020, 39, 1–16. [Google Scholar] [CrossRef]
- Mojtabaei, S.M.; Becque, J.; Hajirasouliha, I.; Khandan, R. Predicting the buckling behaviour of thin-walled structural elements using machine learning methods. Thin-Walled Struct. 2023, 184, 110518. [Google Scholar] [CrossRef]
- Kingma, D.P. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]








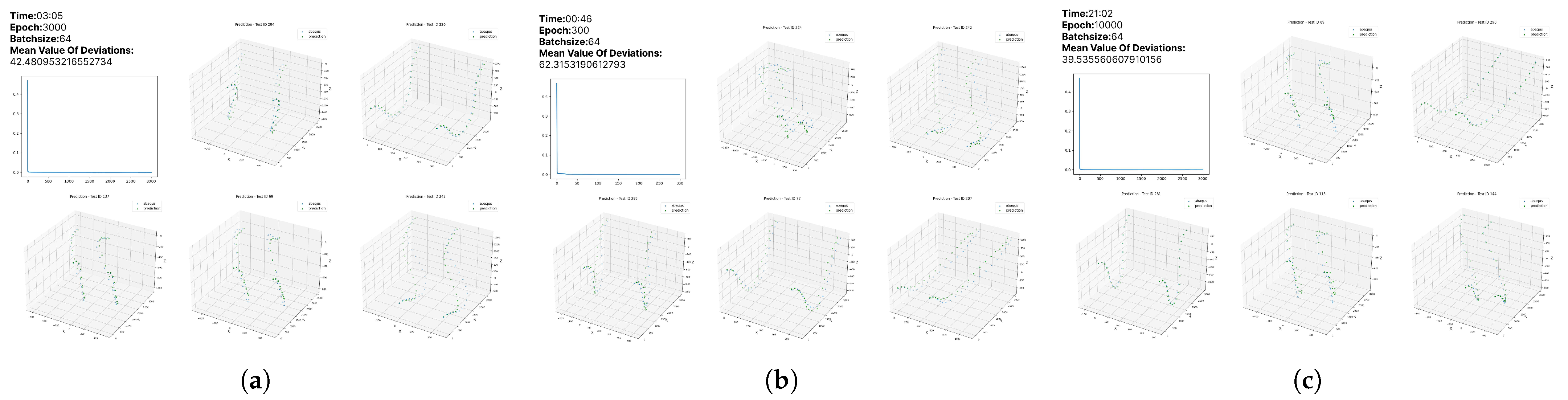







| Hyperparameter | Value |
|---|---|
| Learning Rate | 1.00 |
| Epochs | 3000 |
| Loss Function | Mean squared error (MSE) |
| Activation Function | ReLU |
| Optimizer | Adam optimizer |
| Batch Size | 64 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Y.; Wang, X.; Zhou, X.; Zhou, Q. Bidirectional Pattern Recognition and Prediction of Bending-Active Thin Sheets via Artificial Neural Networks. Electronics 2025, 14, 503. https://doi.org/10.3390/electronics14030503
Xie Y, Wang X, Zhou X, Zhou Q. Bidirectional Pattern Recognition and Prediction of Bending-Active Thin Sheets via Artificial Neural Networks. Electronics. 2025; 14(3):503. https://doi.org/10.3390/electronics14030503
Chicago/Turabian StyleXie, Yuxin, Xiang Wang, Xinjie Zhou, and Qiang Zhou. 2025. "Bidirectional Pattern Recognition and Prediction of Bending-Active Thin Sheets via Artificial Neural Networks" Electronics 14, no. 3: 503. https://doi.org/10.3390/electronics14030503
APA StyleXie, Y., Wang, X., Zhou, X., & Zhou, Q. (2025). Bidirectional Pattern Recognition and Prediction of Bending-Active Thin Sheets via Artificial Neural Networks. Electronics, 14(3), 503. https://doi.org/10.3390/electronics14030503





