ResShift-4E: Improved Diffusion Model for Super-Resolution with Microscopy Images
Abstract
1. Introduction
2. Related Works
2.1. Super-Resolution Image Datasets
2.2. Super-Resolution Methods Based on Diffusion Models
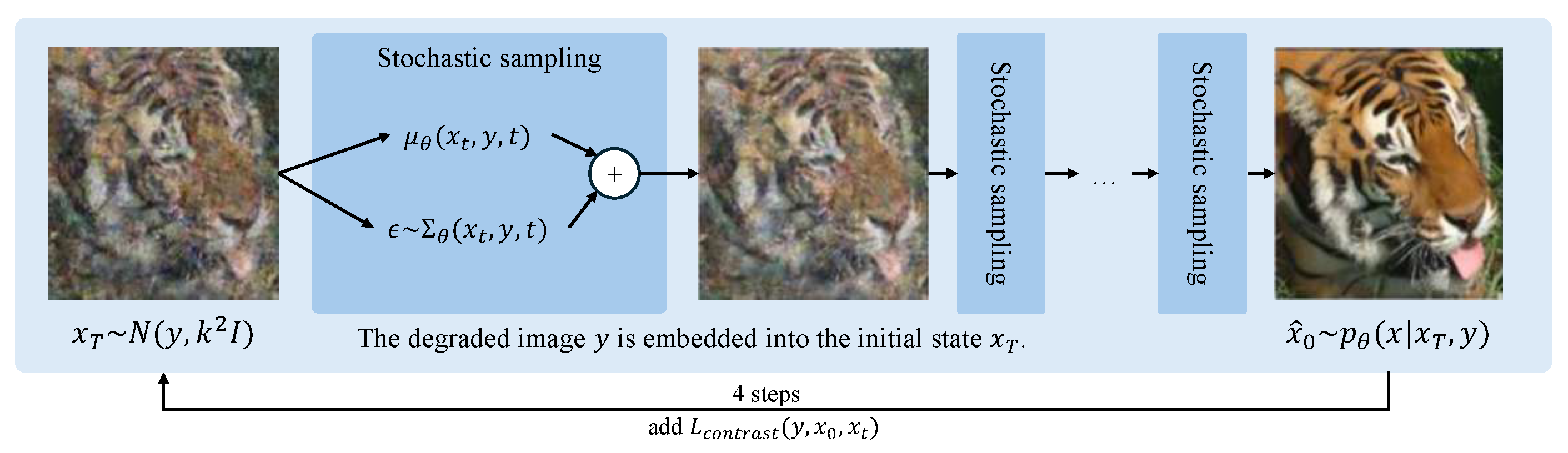
3. The Proposed Method
4. Experiments
4.1. The MHMI Dataset
4.2. Experiment Settings
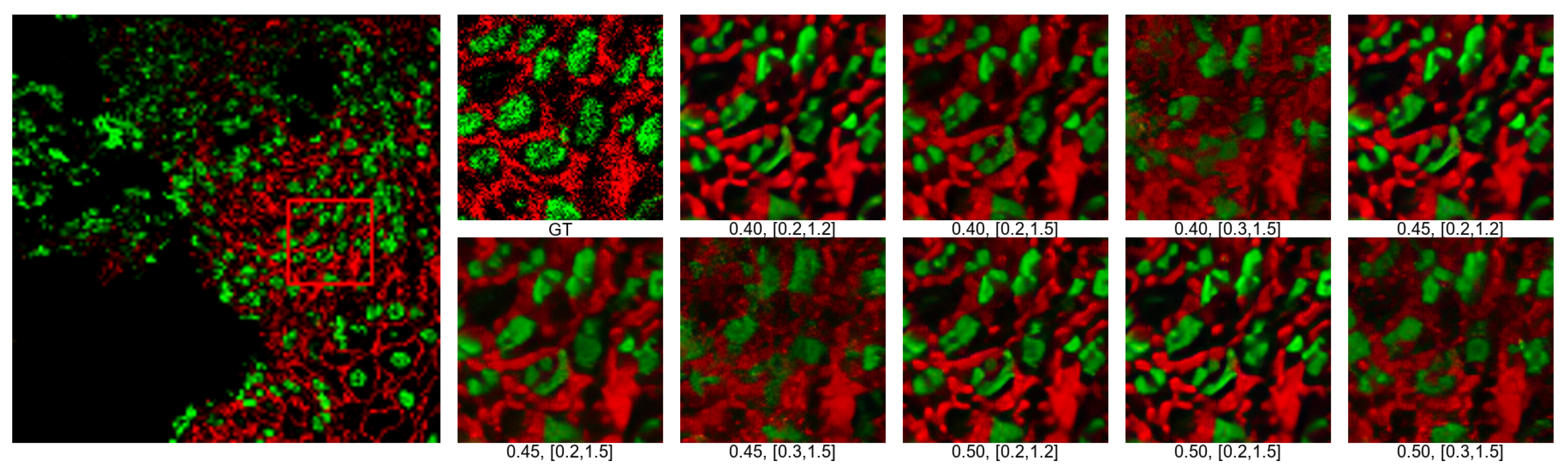
4.3. Effect of Different Noise and Blur on Training Results
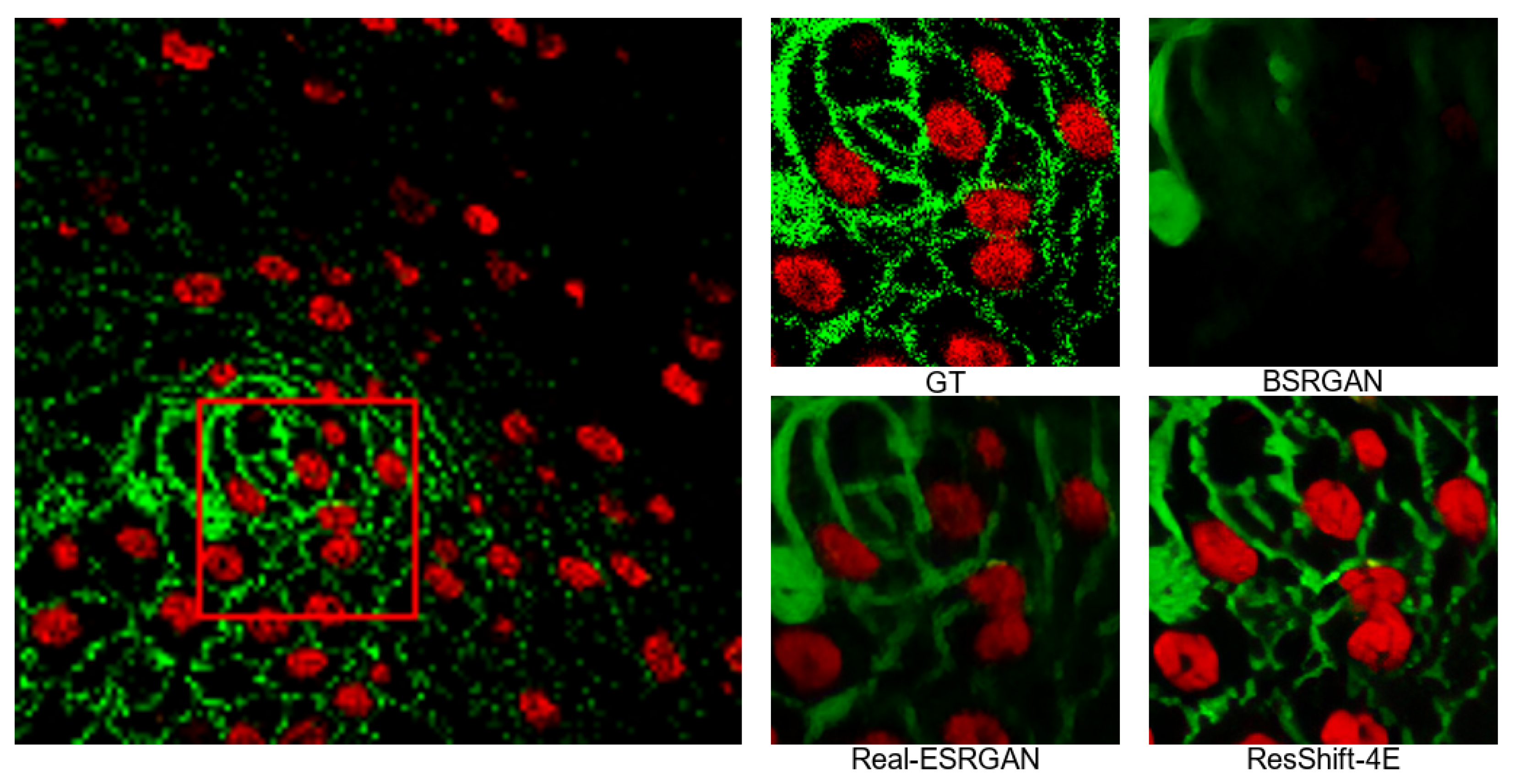
4.4. Visual Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xie, W.; Kuang, Z.; Wang, M. SCIFI: 3D face reconstruction via smartphone screen lighting. Opt. Express 2021, 29, 43938–43952. [Google Scholar] [CrossRef]
- Gao, J.; Tang, N.; Zhang, D. A Multi-Scale Deep Back-Projection Backbone for Face Super-Resolution with Diffusion Models. Appl. Sci. 2023, 13, 8110. [Google Scholar] [CrossRef]
- Zhang, X.; Cheng, B.; Yang, X.; Xiao, Z.; Zhang, J.; You, L. Improving Single-Image Super-Resolution with Dilated Attention. Electronics 2024, 13, 2281. [Google Scholar] [CrossRef]
- Shan, G.; Fan, X.; Hongjia, L.; Fudong, X.; Mingshu, Z.; Pingyong, X.; Fa, Z. DETECTOR: Structural information guided artifact detection for super-resolution fluorescence microscopy image. Biomed. Opt. Express 2021, 12, 5751–5769. [Google Scholar]
- Ci, X.; Yajun, C.; Cahoyue, S.; Longxiang, Y.; Rongzhen, L. AM-ESRGAN: Super-Resolution Reconstruction of Ancient Murals Based on Attention Mechanism and Multi-Level Residual Network. Electronics 2024, 13, 3142. [Google Scholar] [CrossRef]
- Feng, X.; Pan, Z. Detail enhancement for infrared images based on Relativity of Gaussian-Adaptive Bilateral Filter. OSA Contin. 2021, 4, 2671–2686. [Google Scholar] [CrossRef]
- Bing, H.; Xuebing, M.; Bo, K.; Bingchao, W.; Xiaoxue, W. DDMAFN: A Progressive Dual-Domain Super-Resolution Network for Digital Elevation Model Based on Multi-Scale Feature Fusion. Electronics 2024, 13, 4078. [Google Scholar] [CrossRef]
- Qi, J.; Ma, H. A Combined Model of Diffusion Model and Enhanced Residual Network for Super-Resolution Reconstruction of Turbulent Flows. Mathematics 2024, 12, 1028. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, F.; Lu, L.; Su, Z.; Pan, W.; Dai, X. Reconstruction of transparent objects using phase shifting profilometry based on diffusion models. Opt. Express 2024, 32, 13342–13356. [Google Scholar] [CrossRef]
- AlHalawani, S.; Benjdira, B.; Ammar, A.; Koubaa, A.; Ali, A.M. DiffPlate: A Diffusion Model for Super-Resolution of License Plate Images. Electronics 2024, 13, 2670. [Google Scholar] [CrossRef]
- Lai, X.; Li, Q.; Chen, Z.; Shao, X.; Pu, J. Reconstructing images of two adjacent objects passing through scattering medium via deep learning. Opt. Express 2021, 29, 43280–43291. [Google Scholar] [CrossRef]
- Long, Y.; Ruan, H.; Zhao, H.; Liu, Y.; Zhu, L.; Zhang, C.; Zhu, X. Adaptive Dynamic Shuffle Convolutional Parallel Network for Image Super-Resolution. Electronics 2024, 13, 4613. [Google Scholar] [CrossRef]
- Park, S.; Min, C.H.; Han, S.; Choi, E.; Cho, K.O.; Jang, H.J.; Kim, M. Super-resolution Microscopy with Adaptive Optics for Volumetric Imaging. Curr. Opt. Photon. 2022, 6, 550–564. [Google Scholar]
- Dehez, H.; Piché, M.; De Koninck, Y. Resolution and contrast enhancement in laser scanning microscopy using dark beam imaging. Opt. Express 2013, 21, 15912–15925. [Google Scholar] [CrossRef]
- Agustsson, E.; Timofte, R. Ntire 2017 challenge on single image super-resolution: Dataset and study. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 126–135. [Google Scholar]
- Timofte, R.; Agustsson, E.; Van, G.L.; Yang, M.H.; Zhang, L. Ntire 2017 challenge on single image super-resolution: Methods and results. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 114–125. [Google Scholar]
- Xintao, W.; Ke, Y.; Kelvin, C.K.C. Basicsr. 2020. Available online: https://github.com/xinntao/BasicSR (accessed on 10 December 2024).
- Lugmayr, A.; Danelljan, M.; Timofte, R. Ntire 2020 challenge on real-world image super-resolution: Methods and results. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Seattle, WA, USA, 14–19 June 2020; pp. 494–495. [Google Scholar]
- Cai, J.; Zeng, H.; Yong, H.; Cao, Z.; Zhang, L. Toward real-world single image super-resolution: A new benchmark and a new model. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 3086–3095. [Google Scholar]
- Wei, P.; Xie, Z.; Lu, H.; Zhan, Z.; Ye, Q.; Zuo, W.; Lin, L. Component divide-and-conquer for real-world image super-resolution. In Proceedings of the 16th European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 101–117. [Google Scholar]
- Bevilacqua, M.; Roumy, A.; Guillemot, C.; Alberi, M.; Marie, L. Low-complexity single-image super-resolution based on nonnegative neighbor embedding. In Proceedings of the British Machine Vision Conference, Surrey, UK, 3–7 September 2012. [Google Scholar]
- Zeyde, R.; Elad, M.; Protter, M. On single image scale-up using sparse-representations. In Proceedings of the 7th International Conference on Curves and Surfaces, Avignon, France, 24–30 June 2012; pp. 711–730. [Google Scholar]
- Martin, D.; Fowlkes, C.; Tal, D.; Malik, J. A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics. In Proceedings of the 8th IEEE International Conference on Computer Vision, Vancouver, BC, Canada, 7–14 July 2001; pp. 416–423. [Google Scholar]
- Huang, J.B.; Singh, A.; Ahuja, N. Single image super-resolution from transformed self-exemplars. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 5197–5206. [Google Scholar]
- Matsui, Y.; Ito, K.; Aramaki, Y.; Fujimoto, A.; Ogawa, T.; Yamasaki, T.; Aizawa, K. Sketch-based manga retrieval using manga109 dataset. Multimed. Tools Appl. 2017, 76, 21811–21838. [Google Scholar] [CrossRef]
- Wang, X.; Yu, K.; Dong, C.; Loy, C.C. Recovering realistic texture in image super-resolution by deep spatial feature transform. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 606–615. [Google Scholar]
- Ignatov, A.; Kobyshev, N.; Timofte, R.; Vanhoey, K.; Van, G.L. Dslr-quality photos on mobile devices with deep convolutional networks. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 3277–3285. [Google Scholar]
- Zhou, B.; Zhao, H.; Puig, X.; Xiao, T.; Fidler, S.; Barriuso, A.; Torralba, A. Semantic understanding of scenes through the ade20k dataset. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; Volume 127, pp. 302–321. [Google Scholar]
- Ho, J.; Jain, A.; Abbeel, P. Denoising diffusion probabilistic models. Adv. Neural Inf. Process. Syst. 2020, 33, 6840–6851. [Google Scholar]
- Ramesh, A.; Dhariwal, P.; Nichol, A.; Chu, C.; Chen, M. Hierarchical text-conditional image generation with clip latents. arXiv 2022, arXiv:2204.06125. [Google Scholar]
- Rombach, R.; Blattmann, A.; Lorenz, D.; Esser, P.; Ommer, B. High-resolution image synthesis with latent diffusion models. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 10684–10695. [Google Scholar]
- Sahak, H.; Watson, D.; Saharia, C.; Fleet, D. Denoising diffusion probabilistic models for robust image super-resolution in the wild. arXiv 2023, arXiv:2302.07864. [Google Scholar]
- Yue, Z.; Wang, J.; Loy, C.C. Resshift: Efficient diffusion model for image super-resolution by residual shifting. Adv. Neural Inf. Process. Syst. 2024, 36. [Google Scholar]
- Gu, J.; Zhai, S.; Zhang, Y.; Susskind, J.; Jaitly, N. Matryoshka diffusion models. In Proceedings of the 12th International Conference on Learning Representations, Kigali, Rwanda, 1–5 May 2023. [Google Scholar]
- Li, H.; Yang, Y.; Chang, M.; Chen, S.; Feng, H.; Xu, Z.; Li, Q.; Chen, Y. Srdiff: Single image super-resolution with diffusion probabilistic models. Neurocomputing 2022, 479, 47–59. [Google Scholar] [CrossRef]
- Song, J.; Meng, C.; Ermon, S. Denoising diffusion implicit models. arXiv 2020, arXiv:2010.02502. [Google Scholar]
- Liu, J.; Wang, Q.; Fan, H.; Wang, Y.; Tang, Y.; Qu, L. Residual denoising diffusion models. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 2773–2783. [Google Scholar]
- Li, M.; Cai, T.; Cao, J.; Zhang, Q.; Cai, H.; Bai, J.; Jia, Y.; Li, K.; Han, S. Distrifusion: Distributed parallel inference for high-resolution diffusion models. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–22 June 2024; pp. 7183–7193. [Google Scholar]
- Sohl, J.; Weiss, E.; Maheswaranathan, N.; Ganguli, S. Deep unsupervised learning using nonequilibrium thermodynamics. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 2256–2265. [Google Scholar]
- Zhang, K.; Liang, J.; Van, G.L.; Timofte, R. Designing a practical degradation model for deep blind image super-resolution. In Proceedings of the IEEE International Conference on Computer Vision, Montreal, BC, Canada, 10–17 October 2021; pp. 4791–4800. [Google Scholar]
- Wang, X.; Xie, L.; Dong, C.; Shan, Y. Realesrgan: Training real-world blind super-resolution with pure synthetic data supplementary material. Comput. Vis. Found. Open Access 2022, 1, 2. [Google Scholar]
- Zhang, Y.; Zhu, Y.; Nichols, E.; Wang, Q.; Zhang, S.; Smith, C.; Howard, S. A poisson-gaussian denoising dataset with real fluorescence microscopy images. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 11710–11718. [Google Scholar]
- Ma, J.; Xie, R.; Ayyadhury, S.; Ge, C.; Gupta, A.; Gupta, R.; Gu, S.; Zhang, Y.; Lee, G.; Kim, J.; et al. The multimodality cell segmentation challenge: Toward universal solutions. Nat. Methods 2019, 21, 1103–1113. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Zhang, R.; Isola, P.; Efros, A.A.; Shechtman, E.; Wang, O. The unreasonable effectiveness of deep features as a perceptual metric. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 586–595. [Google Scholar]





| PSNR↑ | LPIPS↓ | ||||||
|---|---|---|---|---|---|---|---|
| Noise | Blur | Noise | Blur | ||||
| [0.3,1.5] | [0.2,1.5] | [0.1,1.2] | [0.3,1.5] | [0.2,1.5] | [0.1,1.2] | ||
| 0.50 | 29.74 | 29.95 | 29.83 | 0.50 | 0.4414 | 0.4249 | 0.4300 |
| 0.45 | 29.70 | 30.00 | 29.79 | 0.45 | 0.4338 | 0.4217 | 0.4246 |
| 0.40 | 29.66 | 29.96 | 29.69 | 0.40 | 0.4338 | 0.4241 | 0.4251 |
| NIQE↓ | |||||||
| Noise | Blur | ||||||
| [0.3,1.5] | [0.2,1.5] | [0.1,1.2] | |||||
| 0.50 | 10.2901 | 10.2517 | 10.8768 | ||||
| 0.45 | 9.8009 | 10.0176 | 10.7537 | ||||
| 0.40 | 9.6013 | 9.8927 | 10.2258 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, D.; Gong, Y.; Cao, J.; Wang, B.; Zhang, H.; Dong, J.; Qiu, J. ResShift-4E: Improved Diffusion Model for Super-Resolution with Microscopy Images. Electronics 2025, 14, 479. https://doi.org/10.3390/electronics14030479
Gao D, Gong Y, Cao J, Wang B, Zhang H, Dong J, Qiu J. ResShift-4E: Improved Diffusion Model for Super-Resolution with Microscopy Images. Electronics. 2025; 14(3):479. https://doi.org/10.3390/electronics14030479
Chicago/Turabian StyleGao, Depeng, Ying Gong, Jingzhuo Cao, Bingshu Wang, Han Zhang, Jiangkai Dong, and Jianlin Qiu. 2025. "ResShift-4E: Improved Diffusion Model for Super-Resolution with Microscopy Images" Electronics 14, no. 3: 479. https://doi.org/10.3390/electronics14030479
APA StyleGao, D., Gong, Y., Cao, J., Wang, B., Zhang, H., Dong, J., & Qiu, J. (2025). ResShift-4E: Improved Diffusion Model for Super-Resolution with Microscopy Images. Electronics, 14(3), 479. https://doi.org/10.3390/electronics14030479







