Efficient Quantization and Data Access for Accelerating Homomorphic Encrypted CNNs

Abstract

Due to the ability to perform computations directly on encrypted data, homomorphic encryption (HE) has recently become an important branch of privacy-preserving machine learning (PPML) implementation. Nevertheless, existing implementations of HE-based convolutional neural network (HCNN) applications are not satisfactory in inference latency and area efficiency compared to the unencrypted version. In this work, we first improve the additive powers-of-two (APoT) quantization method for HCNN to achieve a better tradeoff between the complexity of modular multiplication and the network accuracy. An efficient multiplicationless modular multiplier–accumulator (M-MAC) unit is accordingly designed. Furthermore, a batch-processing HCNN accelerator with M-MACs is implemented, in which we propose an advanced data partition scheme to avoid multiple moves of the large-size ciphertext polynomials. Compared to the latest FPGA design, our accelerator can achieve $11\times$ resource reduction of an M-MAC and $2.36\times$ speedup in inference latency for a widely used CNN-11 network to process 8K images. The speedup of our design is also significant compared to the latest CPU and GPU implementations of the batch-processing HCNN models.

1. Introduction

Fully homomorphic encryption (FHE) [1] is a promising solution for privacy-preserving machine learning (PPML) [2] because of the characteristic of performing computation on encrypted data without decryption. After encryption, the inputs are converted to high-degree polynomials, and the HE evaluation is executed over the polynomial ring with a large modulus. Therefore, inference on large machine learning models such as the widely used convolutional neural networks (CNNs) suffers from large computational complexity and memory usage compared to the unencrypted version [3].

As the first framework enabling HE-based CNN (HCNN) inference, CryptoNets [4] adopted Chinese remainder theorem (CRT) to pack the pixels at the same position in a batch of images into a ciphertext polynomial. This packing approach is friendly for batch-processing scenarios and has been adopted in GPU implementation [5] and FPGA implementation [6]. Different packing methods [7,8,9] have been proposed recently to reduce the inference latency of a single image, but introduced expensive homomorphic rotation operations [10]. Several pruning schemes have been introduced to further reduce the computation effort, including powers-of-two weight quantization [11], standard pruning [6,11] and packing-aware pruning [12]. Faster CryptoNets [11] showed a significant reduction in operations, while the integer encoder employed was much less efficient than the batch encoder. The FPGA accelerator [6] first introduced weight sparsity and focused on the dataflow optimization of 8K images simultaneously, but the inference latency could not be reduced when processing small batches of images. The packing-aware pruning method in [12] was based on the packing method of GAZELLE [7], so the rotation operation is inevitable.

To improve the inference efficiency, we propose an efficient modular multiplicationless convolution architecture. The specific contributions are summarized as follows:

• An HE-friendly additive powers-of-two (APoT) quantization method is adopted and improved to reduce the multiplication operation of HCNN inference, which can achieve negligible accuracy loss compared with the floating-point CNNs.
• A corresponding multiplicationless modular multiplier–accumulator (M-MAC) unit is proposed to achieve $11\times$ area reduction compared to the standard M-MAC unit adopted by the latest FPGA accelerators [6].
• An HCNN accelerator with an M-MAC array is designed to implement the widely used CNNs with a moderate batch size. Repeated transmission of input and output polynomials is avoided based on our proposed data access strategy. When processing 8K images in the CIFAR-10 dataset, our FPGA design is $2.36\times$ and $3.95\times$ faster than recent batch-processing FPGA and GPU implementations, respectively.

2. Preliminaries

2.1. Homomorphic Encryption

Most of the modern HE instantiations rely on the hardness of the Ring-LWE (RLWE) problem and operate over the polynomial ring. In this paper, we adopt the BFV scheme [10] to implement, but the proposed techniques are also applicable to other RLWE-based schemes such as CKKS [13]. The HE scheme can be described as follows. The plaintext ($pt$) message is first encoded to the polynomial representation and then encrypted as ciphertext ($ct$) polynomials. The $ct$ polynomials support the following homomorphic computations: $ct$-$pt$ addition, $ct$-$ct$ addition, $ct$-$pt$ multiplication, $ct$-$ct$ multiplication and $ct$ rotation. The noise will grow as homomorphic computations are performed, and the decryption function will return the correct result only when the noise does not exceed the bound. There are three essential parameters in the BFV scheme: the polynomial degree n, the plaintext ($pt$) modulus t and the ciphertext ($ct$) modulus q. The coefficients of the $ct$ and $pt$ polynomials can be viewed as elements over ${\mathbb{Z}}_q$ and ${\mathbb{Z}}_t$, respectively.

2.2. Encrypted CNN Linear Layers

Given the characteristic of FHE, linear layers of CNN such as convolution, fully connected and average-pooling layers can be directly implemented using homomorphic computation. Nevertheless, nonlinear layers such as activation functions and max-pooling operations need to be modified to accommodate homomorphic evaluation [4] or achieved by multi-party computation (MPC) [7]. Here, we focus on the acceleration of the linear layers with encrypted inputs and unencrypted weights as in [4,5,6,7,8,9]. There are many different data representations of input features and weights, and this paper supports three of them in LoLa [8]:

• Sparse representation: Each element $v_i$ in $\mathbf{v}$ is represented by a message in which every coordinate is equal to ${\mathbf{v}}_i$.
• SIMD representation: The i-th item of multiple vectors $\{{\mathbf{v}}_{\mathbf{0}},\dots ,{\mathbf{v}}_{\mathbf{j}-\mathbf{1}}\}$$(j\le n)$ is sequentially mapped to each item of a message.
• Convolution representation: The img2col technique [14] is introduced to flatten the input images. Each column after flattening is mapped to a message, which is multiplied by the same weight.

For a convolution layer, the input $X_{in}$ and output $X_{out}$ are 3D tensors with size $I_c\times I_h\times I_w$ and $O_c\times O_h\times O_w$, where ${(·)}_w$, ${(·)}_h$ and ${(·)}_c$ denote width, height and channel number, respectively. The corresponding weight matrix W is a 4D tensor with size $O_c\times I_c\times d\times d$ where d denotes the kernel size and the stride is set to S. Generally, the input features are represented by SIMD or convolution representation, and the weights are converted into sparse representation since only element-wise modular multiplication and addition operations are needed. The representation of a fully connected layer with I inputs and O outputs is similar, except that the input features can only be represented by SIMD representation. Average-pooling layers can be regarded as convolution layers with all-one weights.

3. Efficient Modular Processing Element Based on APoT Quantization Method

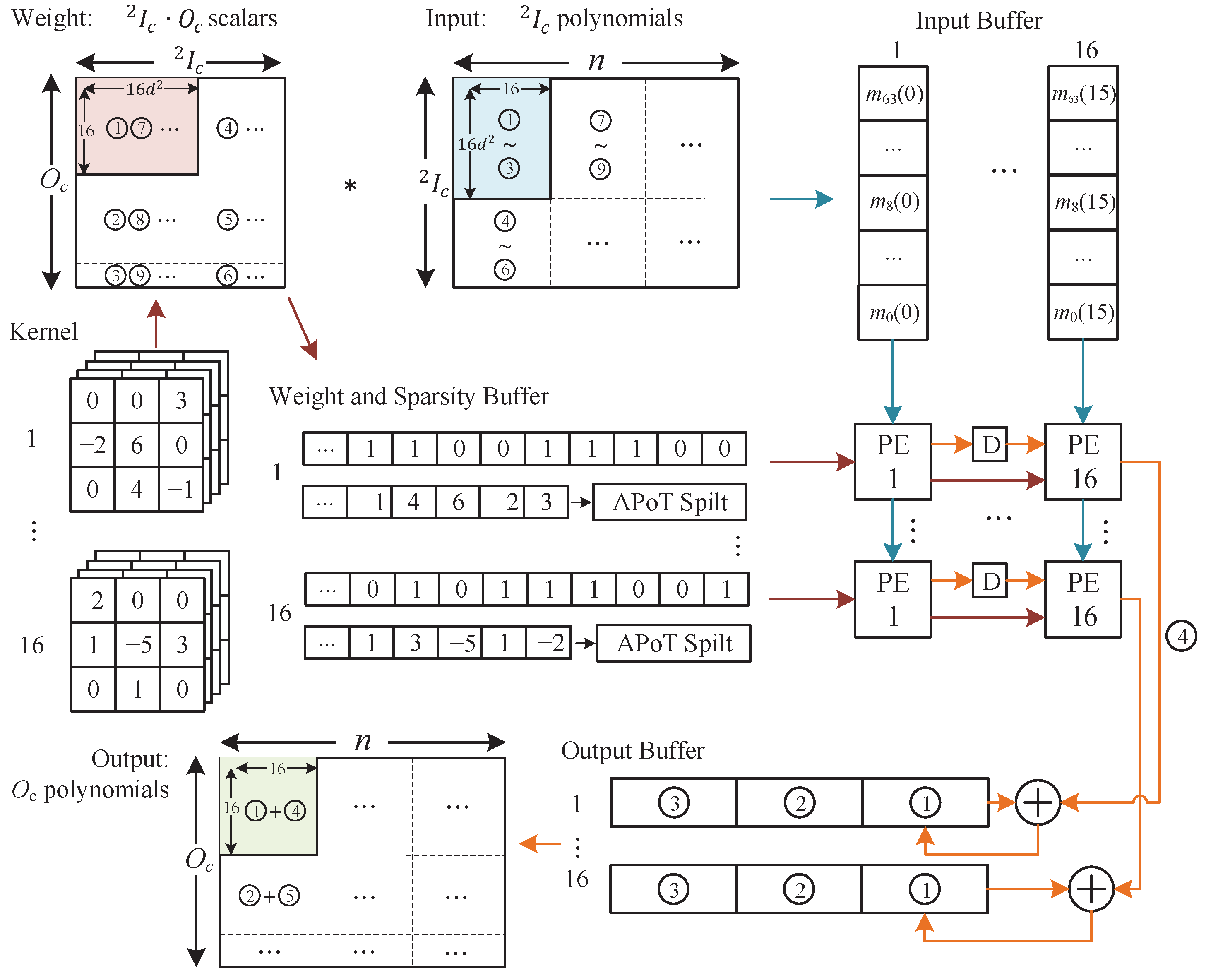
3.1. Optimized APoT Quantization Method

Since the BFV scheme only supports integer computation, the floating-point inputs and weights need to be quantized to fixed-point integers. CryptoNets [4] and HCNN [5] adopted the uniform quantization method. Faster CryptoNets [11] adopted powers-of-two weight quantization to reduce the complexity of modular multiplication. Nevertheless, the powers-of-two quantization method represents a lower resolution compared to the uniform quantization method under the same bit width, which causes obvious accuracy loss.

To achieve a better tradeoff between inference accuracy and complexity of modular multiplication, we first introduce the additive powers-of-two (APoT) quantization method [15] to HCNN training and inference. For a $\delta$-bit weight x, the quantized value $\widehat{x}$ is denoted by the sum of two powers-of-two numbers:

$$\widehat{x}=sign\left(x\right)·({\varphi }_1<<k_1+{\varphi }_2<<k_2),$$

(1)

where $sign\left(x\right)=x\ge 0$? 1:−1; $0\le k_1,k_2<\delta -1$; ${\varphi }_1,{\varphi }_2\in \{0,1\}$. Note that, when ${\varphi }_1=0$, the APoT scheme will devolve into the PoT scheme. We count the weight distribution of the third convolutional layer in CNN-11; the histogram is shown in Figure 1. Compared with the original APoT scheme which uses $\delta$ to denote the bit width required to store $k_1,k_2$, i.e., $k_1,k_2<2^{\delta -1}-1$, our scheme adopts a tighter shift range and allows the quantized weights to be distributed in a range closer to zero. To enable backpropagation during training, the straight-through estimator (STE) [16] is adopted. The proposed APoT quantization strategy is advantageous for HCNN inference since it can slow down the growth in bit width during computing. Limited by the fact that the BFV scheme cannot support division operations, the bit width of results will keep growing during HCNN inference. A tighter shift range not only reduces the bit width of the shifted addition but also significantly reduces the parameter size of the BFV scheme [5]. To ensure the correctness of the final decryption, the value of the final results must not exceed t. However, a larger value of t will result in a larger ciphertext size and more computational effort.

3.2. Multiplicationless Modular Multiplier–Accumulator

Since the computation of linear layers can be expressed as a series of $ct$ polynomials multiplied by the corresponding weight scalar values and added together over ${\mathbb{Z}}_q$, the main subject of the processing element (PE) of an HCNN accelerator is the modular multiplier–accumulator (M-MAC). The modular multiplication between the coefficients of the $ct$ polynomial and the quantized weight can be simplified by adopting the APoT quantization method. The modular multiplier is implemented by a multiplier and a modular reduction unit. We replace the multiplier with shift and addition, and adopt the improved Barrett reduction method [17] to reduce the resource consumption. The modular adder is implemented in the same way as [18]. A six-stage pipelined architecture is designed to implement the low bit-width M-MAC; the architecture is shown in Figure 2.

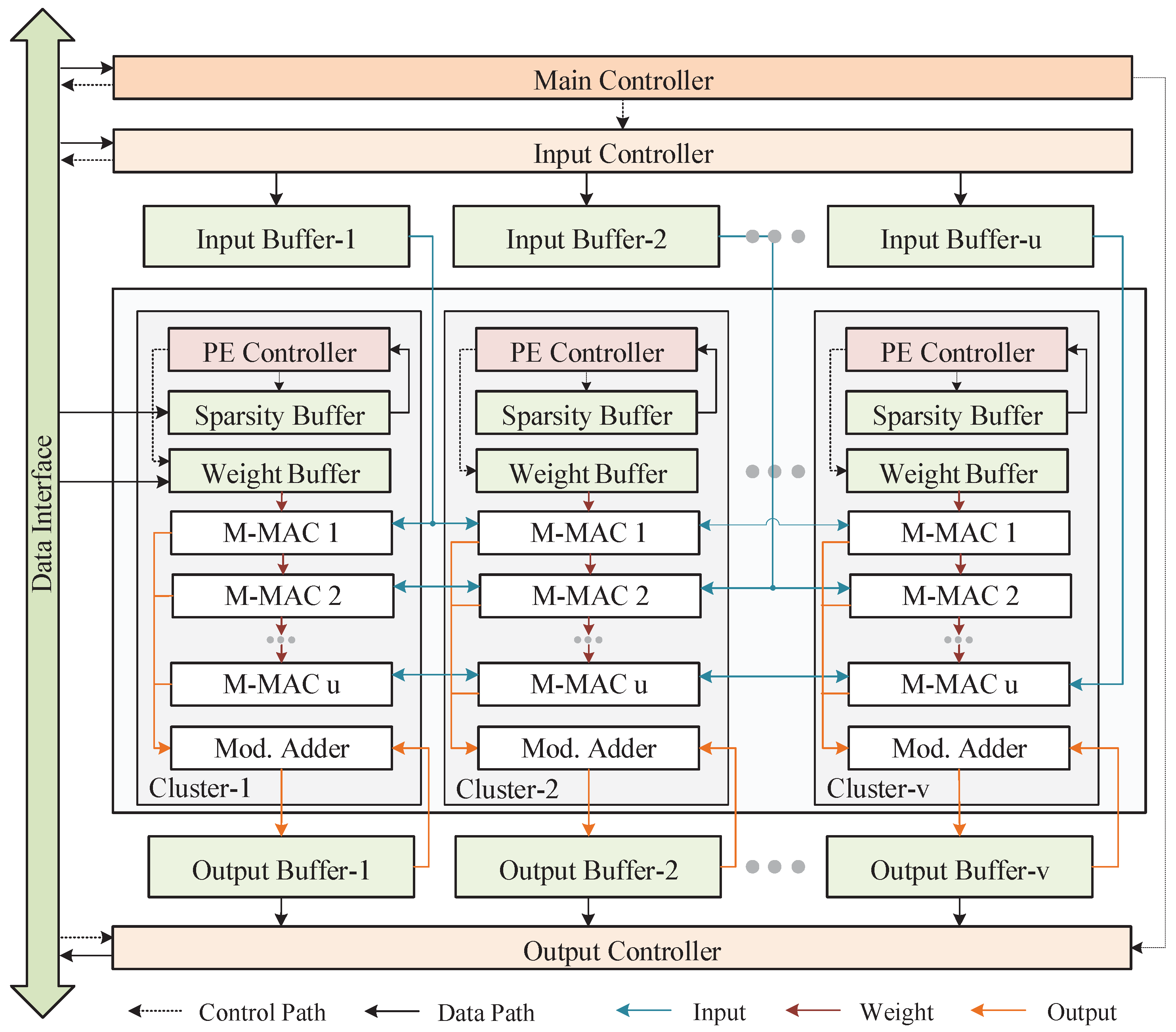
4. Transmission-Efficient Homomorphic CNN Accelerator with M-MACs

4.1. Overall Architecture

The implementation of homomorphic CNNs has the following properties different from those of the unencrypted CNNs: First, the required data size grows by more than four orders of magnitude, because the inputs and outputs are all based on a set of $ct$ polynomials represented by Chinese remainder theorem (CRT), each containing $2·r$ polynomials, where r denotes the number of moduli after splitting. Second, since all operations in the linear layer after encryption are over ${\mathbb{Z}}_q$, the resulting frequently modular operations will significantly increase the hardware resource overhead. In this section, we aim to implement a homomorphic CNN accelerator to demonstrate the efficiency of the proposed M-MAC. Furthermore, an advanced data partition and transfer strategy is proposed to reduce the on-chip data transfer time. The accelerator supports the sparse representation weight and convolution representation input which facilitates the processing of small batches of images. Therefore, the computation of linear layers is transformed into the matrix multiplication operation.

The overall architecture is shown in Figure 3. The input and output controllers are responsible for distributing data to the buffer and aggregating data from the buffer to the data interface, respectively. The computing array consists of v clusters. Within each cluster, there are u M-MACs, a modular adder, a PE controller, a weight buffer, and a sparse weight index buffer. After weighing the computation time and data transmission time, we finally choose to implement an array of moderate size with $u=v=16$. By introducing the ping-pong strategy, the majority of data transmission time can be hidden by computing time.

4.2. Implementation Details

In this subsection, we present the details of the data transfer and computing process. In this paper, the computation of the linear layers is converted to matrix multiplication for fast execution. Here, we use a convolutional layer as an example, which can also be applied to the fully connected layer and the average-pooling layer. We use $poly$ to denote the size of a ciphertext input, which is equal to $2·r·n·\lceil {log}_2{q}_i\rceil$ bits ($q={\sum }_{i=1}^r{q}_i$). Assuming that $O_h\times O_w$ is less than n, then the memory usage required for $\lfloor {\displaystyle \frac{n}{O_h\times O_w}}\rfloor$ batches of inputs and outputs is $d^2{I}_c\times poly$ and $O_c\times poly$, respectively. After introducing the weight-pruning technique, the memory usage required for weights is $d^2\times I_c\times O_c\times (1-sparsity)\times \delta$ bits. No bias is used in linear layers as in [5].

The data size of weights is relatively small, so the weights of each layer can be directly stored on-chip before computing. To reduce the storage area, only the non-zero weights and an index buffer characterizing whether the weight at each position is non-zero are stored. Nevertheless, it is impractical to store all the encrypted input data (∼GB) on the chip. The entire input data will be first stored in the off-chip DDR and transferred to the on-chip memory segmentally as required. Since the polynomials over different ${\mathbb{Z}}_{q_i}$ in a ciphertext are independent, only one polynomial of each ciphertext is operated firstly, and the rest of the polynomials are operated after this set of operations is finished. The data of the convolution layer are partitioned as shown in Figure 4, where the numbers in the circles indicate the order of access. Here, $16d^2\times 16$ inputs and corresponding weights at a unit of 16 output channels are loaded for one calculation. Since the quantity of weights is much smaller than that of inputs, repeated reading of weights rather than inputs is adopted. Each input polynomial tile loaded from the DRAM will be discarded after all the computations involved have been completed. The non-zero weights are decomposed by a lookup table (LUT) into the input format required by the M-MACs, i.e., s, $k_1$, $k_2$, ${\varphi }_1$, ${\varphi }_2$. The 16-way parallel inputs and weights are broadcasted to corresponding M-MACs, and the obtained output results are pipelined to the modular adders. The results are added with the intermediate results of the previous round to achieve the accumulation of the $I_c$ dimension. The M-MAC will be gated (stop toggling) when receiving the zero-value weights, but the latency is not reduced for simplifying the control logic. The advantage of our proposed strategy is that, regardless of the amount of data to be computed, both the input and the output polynomials only need to be transmitted once, without any overhead of repeated transmission.

5. Experimental Results

5.1. Experimental Setup

For a fair comparison, we target the two most commonly studied homomorphic CNNs, CNN-6 (for MNIST) and CNN-11 (for CIFAR-10) [4,5,6,7,8], for deployment. The architectures of the two CNNs are shown in

Table 1. Network architectures.

CNN-6	Input Size	Description
Conv-1	$1\times 28\times 28$	filter: $5\times 1\times 5\times 5$, stride: 2, activ
Conv-2	$5\times 13\times 13$	filter: $50\times 5\times 5\times 5$, stride: 2, activ
Fc-1	$50\times 4\times 4$	filter: $100\times 1250$
Fc-2	$1\times 100$	filter: $10\times 100$
CNN-11	Input Size	Description
Conv-1	$3\times 32\times 32$	filter: $32\times 3\times 3\times 3$, stride: 1
Pool-1	$32\times 32\times 32$	average, $2\times 2$, stride: 2, activ
Conv-2	$32\times 16\times 16$	filter: $64\times 32\times 3\times 3$, stride: 1
Pool-2	$64\times 16\times 16$	average, $2\times 2$, stride: 2, activ
Conv-3	$64\times 8\times 8$	filter: $128\times 64\times 3\times 3$, stride: 1
Pool-3	$128\times 8\times 8$	average, $2\times 2$, stride: 2, activ
Fc-1	$128\times 4\times 4$	filter: $128\times 2048$
Fc-2	$1\times 128$	filter: $10\times 128$

. The pooling operation is executed before the activation function to reduce the inputs of the activation function. Networks are trained, quantized and pruned using the PyTorch v1.7 framework, and then implemented on SEAL library [19] to verify the accuracy.

The HE parameters are chosen as in [6], i.e., $n=8192$; the bit width of q is 218-bit and 304-bit for CNN-6 and CNN-11, respectively. Note that both n and q can be smaller because the required multiplication depth is very shallow under MPC. The modulus q consists of several small moduli selected in SEAL [19] with the maximum bit width of 60-bit.

5.2. Network Accuracy

We train two networks and test the inference results of the proposed APoT quantization method, and compare the results with the floating version and uniform quantization version. The results of two activation functions, ReLU and polynomial approximation, are given in

Table 2. Accuracy results.

Model	Quant. Method	δ+	Accuracy
			ReLU	Poly
CNN-6	Float	32	98.94%	98.99%
	Uniform	4	98.83%	98.8%
	Ours (APoT)	4	98.93%	98.85%
CNN-11	Float	32	82.74%	78.49%
	Uniform	8	82.37%	$77.1{\% }^{★}$
	Ours (APoT)	8	82.15%	78.36%

⁺ δ denotes the actual bit width of the weights${. }^{★}$ The accuracy is obtained from [6].

. CNN-6 and CNN-11 adopt $x^2$ and $a{x}^2+bx+c$ as activation functions, respectively. The input images are both scaled by 255. It can be found that the proposed APoT quantization method is also applicable to the HCNN model that applies polynomial approximation as the activation function. Although the use of polynomial approximation leads to a decrease in the accuracy of CNN-11, the quantization-aware training method can avoid significant accuracy degradation and outperform the post-training uniform quantized method.

To further compress the model size, we evaluate several pruning strategies. Among them, structured pruning not only compresses the weights, but also reduces the size of the input and output polynomials, which can efficiently reduce the computational effort of the hardware accelerator. Therefore, we adopt the structured pruning supported by Pytorch and achieve $50.4\%$ and $57.3\%$ weight sparsity for CNN-6 and CNN-11, respectively.

5.3. Implementation Results of Modular Multiplication

The HCNN accelerator is implemented and evaluated on a Xilinx Virtex-UltraScale XCVU440-FLGA2892 FPGA board (Xilinx, San Jose, CA, USA). The FPGA is connected to the CPU via the PCIe Gen3 x8 interface to transmit data. The measured transmission bandwidth of 8 GB DRAM attached to FPGA is about 12 GB/s. When evaluating the effects of the end-to-end implementation, we find that the communication overhead of the MPC implementation between the client and the server is quite high. Therefore, we finally choose the server-only multi-batch HCNN implementation as described in [4,5,6] for evaluation. By adopting SIMD encoding, 8192 images can be inferred simultaneously. The activation function based on polynomial multiplication is performed on an Intel Xeon Gold 6154 CPU (36 threads) running at $3.0$ GHz.

The performance of our accelerator and the most similar end-to-end HCNN accelerator [6] is listed in

Table 3. Performance comparison between the two FPGA accelerators.

Design	Accel-L [6]	Our Design
FPGA Device	Xilinx U200	Xilinx XCVU440
Frequency (MHz)	175	$166.7$
LUT/FF/DSP	360K/424K/2320	194K/158K/768
BRAM/URAM	$698/264$	$103.5/0$
Inference Latency (s) of CNN-6 (8K images)
CPU to FPGA	$0.140$	0.462 ⋄
Linear ${\mathrm{Layers} }^{★}$	$0.639$	$0.314$
Activ. Layers	2.706 ≀	$2.175$
Total	$3.485$	$2.951$
Inference Latency (s) of CNN-11 (8K images)
CPU to FPGA	$2.771$	15.323 ⋄
Linear ${\mathrm{Layers} }^{★}$	$98.384$	$24.846$
Activ. Layers	80.131 ≀	$36.729$
Total	$181.286$	$76.898$

^⋄ The latency of converting the encrypted data to convolutional representation and rearranging the result polynomials is included${. }^{★}$ The latency of DRAM to accelerator is included. ^≀ The latency is obtained on the same CPU platform as our design.

. After employing the simplified M-MAC architecture, our proposed M-MAC consumes only three DSPs, which is $11\times$ fewer compared to [6]. Because there is no need to transfer a complete polynomial to the on-chip memory, the memory size of our design is also smaller. Other reduction in resource consumption mainly comes from the reduction in datapath width. The end-to-end inference latency is the sum of the off-chip data transfer latency, the latency of the on-chip linear layer operations and the latency of the CPU-side activation function operations. The off-chip data transfer latency is limited by two points: the bandwidth of PCIe and DRAM in this design is lower than that in [6] and the convolution representation naturally requires more data to be transferred than the SIMD representation. The linear layer operations are the focus of this design. When executing CNN-6, the latency reduction is insignificant because [6] achieves $90\%$ sparsity. When executing CNN-11, the execution time of the linear layer can be reduced by $3.96\times$, and the execution time of the activation function can be halved because pooling is executed before the activation function. In total, our design can achieve $1.18\times$ and $2.36\times$ speedup compared with [6] during the end-to-end implementation. The speedup of our design is also significant compared to the latest CPU and GPU implementations of multi-batch HCNN models. CryptoNet [4] takes $10.251$ s to process 8K images using CNN-6 on the same CPU platform, while the inference latency of the latest GPU implementation HCNN [5] is $5.1$ s and 304 s when processing 8K images using CNN-6 and CNN-11, respectively.

6. Conclusions

An HCNN accelerator with improved M-MACs by adopting the APoT quantization method is proposed in this paper. An efficient data tiling strategy is designed to minimize the data movement. To the best knowledge of the authors, the proposed FPGA accelerator is the fastest end-to-end implementation of the batch-processing HCNN models.