A Quasi-Uniform Magnetic Coupling Array for a Multiload Wireless Power Transfer System with Flexible Configuration Strategies

Abstract

The coupling problem between the transmitter coils (Tx) and receiving coils (Rx) is influenced by the transmission power and efficiency for a multiload wireless power transfer (WPT) system. In order to solve this problem, a novel array WPT system with quasi-uniform coupling (QC) is proposed in this paper. Owing to the comprehensive design of the Tx and its mutual positional relationship, the proposed system supports simultaneous activation of multiple and even adjacent Tx while maintaining QC. In addition, the structure of Tx is simple and can be obtained with a low-cost optimization procedure, and the compact Rx coil provides sufficient misalignment transmission tolerance for one or two Rx within the Tx and overlapping areas. Furthermore, a parity-time (PT) symmetry-based Rx position detection method is adopted to support flexible unit operation strategies without additional communication procedures. Each Tx unit is equipped with an ingenious dynamic compensation circuit to solve the frequency detuning problem caused by adjacent Tx cross-coupling. Finally, the effectiveness of the design is proved by the prototype; the Tx can provide a QC area that is 1.44 times or 4.44 times the Rx coil area for each receiver in independent and composite modes, and it can match the operation strategy to achieve optimal configuration of the charging area.

1. Introduction

Wireless power transfer (WPT) eliminates the need for physical wiring [1] in electrical equipment, offering significant advantages in terms of flexibility and practicality. WPT technology has been used in industrial production, medical treatment, consumer electronics [2,3,4,5], and other fields, and it is a research hotspot.

To enhance the robustness of transmission efficiency in WPT systems across varying coil coupling distances, Reference [6] introduced a WPT system in 2017 based on parity-time symmetry (PT) theory. A negative resistor circuit was designed using an operational amplifier to replace the traditional excitation source, ensuring stable transmission efficiency regardless of the coupling coefficient between coils in the PT strong coupling region. While the system’s power output was limited to the milliwatt range, its simplicity—requiring no complex control loops—sparked significant interest in PT symmetry-based WPT systems (PT-WPT) [7]. Building on this, Reference [8] incorporated a self-oscillating inverter to create negative resistance, increasing the output power to levels suitable for electronic devices. Reference [9] applied PT symmetry theory to multiple decoupled receiver unit coils (Rx), enabling high-power transmission with a reduced current across each Rx. In Reference [10], further steady-state analysis of PT systems used a mutual inductance model to inform primary-side power control schemes, revealing a clearer relationship between transmission performance and circuit parameters than previous coupled-mode theory models. Although the transmission efficiency of a PT system is robust with respect to transmission distance, it is only valid in the strong coupling region [11]. When the system’s coupling coefficient falls below a critical value, the system loses its robustness to coupling distance, as it operates in the weak coupling region [12]. Reference [13] proposed a frequency-locked system that satisfies higher-order PT symmetry, achieving nearly constant transmission power and efficiency. References [14,15] proposed a higher-order PT system, realizing efficient transmission in a three-coil WPT system. The results indicated that the third-order system exhibits lower sensitivity to the coupling coefficient compared to the second-order system.

A great deal of innovative work has been conducted on coil structures and operation modes to increase the flexibility of the coupler application. Some research is omnidirectional charging with a 3D structure, such as splicing multiple irregular windings into a bowl shape [16,17] so that an omnidirectional uniform magnetic field is formed in the hemisphere. Meanwhile, some studies [18,19] configured circular coils to form spherical transmitters through orthogonalization and matched them with inverters that could independently control the phase, thus realizing WPT in any direction in space. Similarly, there are various structures and transmission methods such as mechanical rotary, cube [20,21], cross [22], three-sector coil coupling [23], etc. These omnidirectional systems greatly improve the flexibility and operability of charging. However, the 3D structure typically requires the receiving coil to be continuously positioned around or inside the transmitter. While this design enhances the receiver’s posture degrees of freedom, it also somewhat increases the constraints on the misalignment transmission range of the WPT system. Meanwhile, Rx has a high degree of flexibility, and the coupler cannot be guaranteed to be in a good alignment state all the time. In this case, misalignment tolerance is an important indicator to ensure system performance.

Coil magnetic field synthesis [24], multi-coil combination [25,26], high-order resonant topology [27], etc. have been investigated in misaligned transmission research. It has been shown that previous ordinary circular and D-type structures have weak misalignment transmission capabilities and cannot guarantee the uniformity of internal mutual inductance. Once the misalignment exceeds a certain range, the system transmission performance will decline sharply [28]. A dual-frequency operation-based WPT system was proposed to simultaneously detect the presence of metal objects and coil misalignment [29]. By analyzing output voltage variations, the proposed approach effectively differentiates efficiency losses caused by metallic objects from those resulting from coil misalignment. However, the experimental validation was primarily conducted under static conditions, leaving dynamic and complex scenarios unexplored.

The combined design of coils is considered an effective method to improve the misalignment performance of the WPT system [30], and multiple transmitter coils (Tx) can be formed into a large-sized array to provide a sufficient charging area. Similar studies included this [31,32]. However, these studies lacked an in-depth discussion of the array’s synthetic magnetic field and its coupling characteristics, and the mutual inductance at each position has a negative impact on the system’s efficiency and stability. Especially for moving receivers, the discontinuous mutual inductance can reduce the transient performance of the system control block [31]. Reference [33] discussed the mutual inductance characteristics of rectangular coils under positional misalignment conditions in a double-sided electromagnetically shielded environment, and although the error is reduced, the accuracy is not sufficient. Few studies have investigated the comprehensive design of element winding and array configuration to achieve near-constant coupling performance at any position, which helps to reduce the influence caused by Rx movement. The quasi-uniform coupling (QC) of the array by adding auxiliary windings in the winding is improved by Reference [32], but the prototype only supports a fixed number of Tx activations, making it so the QC area cannot be configured diversely according to the number and position of Rx.

Furthermore, the system’s stability is also impacted by the introduction of the novel capacitor. The compensation capacitor was optimized by Reference [34], which solved the dynamic load and mutual inductance changes that occurred during the use of the three-coil WPT system. A multi-coil secondary-side inductive linked with an independent DD structure and orthogonal coils was proposed to reduce the influence of coupling fluctuations on the power imbalance during reception [35]. Other studies [36,37,38,39] applied high-order resonance compensation networks, such as LCC/S, LCC/LCC, and LCCC/S. They are matched with ingenious parameter setting methods for energy storage components so that the system has constant voltage and constant current output, thus reducing the influence of mutual inductance fluctuations caused by misalignment. Although the above-mentioned studies have brought great improvements, the problem of misaligned transmission has not been completely solved, and high-order networks suffer from high design and fabrication complexity.

In summary, there is no research on achieving constant transmission characteristics and excellent anti-offset effects for dual-load systems. To this end, this paper proposes a WPT system with QC. One notable feature of the proposed WPT system is that a large-scale array composed of several Tx units can be flexibly configured and expanded based on Rx, which helps to realize a flexible power supply to 1 or 2 Rx. The main contributions of this work are as follows:

• WPT system modeling with dual-load coils is conducted, and the one to two transmission characteristics of the PT system are explored. The results are exploited to support the subsequent Rx position detection method and the flexible configuration scheme of the effective coupling area.
• A Tx coil with extended capability and an Rx coil with a multilayer compact structure are proposed. Meanwhile, an efficient and low-cost coil design algorithm is established by acquiring prior knowledge of the coupling performance of the coupler. Based on this, Tx maintains QC in both independent activation and composited activation of adjacent coils, which enables the transmitter array (TA) to dynamically configure the charging area and misalignment tolerance.
• Based on the Rx position detection method, the system performs an operation strategy for TA, which ensures the balance of the stray magnetic field and charging area. Meanwhile, a modular resonant compensation topology is proposed to solve the cross-coupling problem within the array and achieve independent control of each Tx coil.

The rest of the paper is organized as follows: Section 2 presents the principle and characteristics of the dual-load PT system. Section 3 outlines the overall structure and configuration method of the prototype. Section 4 introduces the structure of Tx and Rx coils and the design method of their parameters. Section 5 explains the effective configuration strategy of the array and proposes a modular resonant compensation circuit. Section 6 presents the verification and comparison of the results. Finally, the conclusions are given in Section 7.

2. Principle Analysis of the PT-WPT System

2.1. Modeling of the PT-WPT System

Unlike the adjustable phase of the output voltage and current in magnetic coupling resonance (MCR) technology, the controller in a PT-WPT system automatically switches the conduction direction of the inverter’s MOSFET when the resonant cavity current crosses zero [4,40]. Consequently, the output of the inverter can be effectively modeled as a nonlinear resistive element with a negative value [7], denoted as −R_n, which supplies energy to the subsequent circuitry. The equivalent circuit of a dual-load PT-WPT system is shown in Figure 1.

The two Rx structures are the same, so the equivalent resistance is r₂. Since the two Rx are small in size and far away from each other, the coupling between Rx can be ignored, i.e., M_S1S2 = 0. Under this condition, the equivalent circuit can be simplified as

$$\left[\begin{array}{ccc}{\displaystyle \frac{{\mathsf{\omega }}_1}{\mathsf{\omega }}}-{\displaystyle \frac{\mathsf{\omega }}{{\mathsf{\omega }}_1}}-\mathit{j}{\mathit{Q}}_1^{-1}& {\displaystyle \frac{\mathsf{\omega }}{{\mathsf{\omega }}_1}}{\mathit{k}}_{\mathit{PS}1}\sqrt{{\displaystyle \frac{{\mathit{L}}_{\mathit{S}1}}{{\mathit{L}}_{\mathit{P}}}}}& {\displaystyle \frac{\mathsf{\omega }}{{\mathsf{\omega }}_1}}{\mathit{k}}_{\mathit{PS}2}\sqrt{{\displaystyle \frac{{\mathit{L}}_{\mathit{S}2}}{{\mathit{L}}_{\mathit{P}}}}}\\ {\displaystyle \frac{\mathsf{\omega }}{{\mathsf{\omega }}_2}}{\mathit{k}}_{\mathit{PS}1}\sqrt{{\displaystyle \frac{{\mathit{L}}_{\mathit{P}}}{{\mathit{L}}_{\mathit{S}1}}}}& {\displaystyle \frac{{\mathsf{\omega }}_2}{\mathsf{\omega }}}-{\displaystyle \frac{\mathsf{\omega }}{{\mathsf{\omega }}_2}}+\mathit{j}{\mathit{Q}}_2^{-1}& 0\\ {\displaystyle \frac{\mathsf{\omega }}{{\mathsf{\omega }}_3}}{\mathit{k}}_{\mathit{PS}2}\sqrt{{\displaystyle \frac{{\mathit{L}}_{\mathit{P}}}{{\mathit{L}}_{\mathit{S}2}}}}& 0& {\displaystyle \frac{{\mathsf{\omega }}_3}{\mathsf{\omega }}}-{\displaystyle \frac{\mathsf{\omega }}{{\mathsf{\omega }}_3}}+\mathit{j}{\mathit{Q}}_3^{-1}\end{array}\right]\left[\begin{array}{c}\dot{I_{\mathit{P}}}\\ \dot{I_{\mathit{S}1}}\\ \dot{I_{\mathit{S}2}}\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right],$$

(1)

where k_PS1 and k_PS2 are the coupling coefficients between the two Rx coils and TA; ω₁, ω₂, ω₃, Q₁, Q₂, and Q₃ are the natural resonant angular velocity and the quality factor of the coils, with ${\mathsf{\omega }}_1={\displaystyle \frac{1}{\sqrt{{\mathit{L}}_{\mathit{P}}{\mathit{C}}_{\mathit{P}}}}}$, ${\mathsf{\omega }}_2={\displaystyle \frac{1}{\sqrt{{\mathit{L}}_{\mathit{S}1}{\mathit{C}}_{\mathit{S}1}}}}$, ${\mathsf{\omega }}_3={\displaystyle \frac{1}{\sqrt{{\mathit{L}}_{\mathit{S}2}{\mathit{C}}_{\mathit{S}2}}}}$, ${\mathit{Q}}_1={\displaystyle \frac{{\mathsf{\omega }}_1{\mathit{L}}_{\mathit{P}}}{{-\mathit{R}}_{\mathit{n}}+{\mathit{r}}_1}}$, ${\mathit{Q}}_2={\displaystyle \frac{{\mathsf{\omega }}_2{\mathit{L}}_{\mathit{S}1}}{{\mathit{R}}_{\mathit{L}1}+{\mathit{r}}_2}}$, and ${\mathit{Q}}_3={\displaystyle \frac{{\mathsf{\omega }}_3{\mathit{L}}_{\mathit{S}2}}{{\mathit{R}}_{\mathit{L}2}+{\mathit{r}}_2}}$. The PT system [41] satisfies ω₁ = ω₂ = ω₃ = ω₀ and Q₁ = Q₂ = Q₃ = Q₀. If there is a non-zero solution to the bivariate homogeneous linear equations in (1), the value of its coefficient determinant must be zero. Therefore, the imaginary and real parts of the determinant can be expressed as

$$\left\{\begin{array}{c}\mathit{R}\mathit{e}:({\mathit{k}}_{\mathit{PS}1}^2+{\mathit{k}}_{\mathit{PS}2}^2){\mathsf{\omega }}^4-({\mathsf{\omega }}^2-{\mathsf{\omega }}_0^2{)}^2-{\displaystyle \frac{{\mathsf{\omega }}^2{\mathsf{\omega }}_0^2}{{\mathit{Q}}_0^2}}=0\\ I\mathit{m}:({\mathsf{\omega }}^2-{\mathsf{\omega }}_0^2)[({\mathit{k}}_{\mathit{PS}1}^2+{\mathit{k}}_{\mathit{PS}2}^2){\mathsf{\omega }}^4-({\mathsf{\omega }}^2-{\mathsf{\omega }}_0^2{)}^2-{\displaystyle \frac{{\mathsf{\omega }}^2{\mathsf{\omega }}_0^2}{{\mathit{Q}}_0^2}}]=0\end{array}\right.,$$

(2)

The system operates at an angular frequency of $\omega \ne {\mathsf{\omega }}_0$, and $({\mathsf{\omega }}^2-{\mathsf{\omega }}_0^2)$ of the imaginary part of the equation is not equal to zero, so the second factor of the imaginary part of the equation must be zero for the equation to hold. Therefore, according to (2), the calculation yields the solution for ω under condition $\omega \ne {\mathsf{\omega }}_0$:

$$\left\{\begin{array}{c}\begin{array}{c}{\mathsf{\omega }}_{+}={\displaystyle \frac{{\mathsf{\omega }}_0}{\sqrt{2\left[1-\left({\mathit{k}}_{\mathit{PS}1}^2+{\mathit{k}}_{\mathit{PS}2}^2\right)\right]}}}\end{array}\sqrt{2-{\mathit{Q}}_0^{-2}+\sqrt{4({\mathit{k}}_{\mathit{PS}1}^2+{\mathit{k}}_{\mathit{PS}2}^2-1)+(2-{\mathit{Q}}_0^{-2}{)}^2}}\\ \begin{array}{c}{\mathsf{\omega }}_{-}={\displaystyle \frac{{\mathsf{\omega }}_0}{\sqrt{2\left[1-\left({\mathit{k}}_{\mathit{PS}1}^2+{\mathit{k}}_{\mathit{PS}2}^2\right)\right]}}}\end{array}\sqrt{2-{\mathit{Q}}_0^{-2}-\sqrt{4({\mathit{k}}_{\mathit{PS}1}^2+{\mathit{k}}_{\mathit{PS}2}^2-1)+(2-{\mathit{Q}}_0^{-2}{)}^2}}\end{array}\right.,$$

(3)

To ensure that the operating angular frequency of the system has real physical significance, ω should be a positive real solution of the equation, and thus, the system satisfies the following constraints:

$$\left\{\begin{array}{c}{\mathit{k}}_{\mathit{C}}=\sqrt{1-{\displaystyle \frac{1}{4}}(2-{\mathit{Q}}_0^{-2}{)}^2}\le \sqrt{{\mathit{k}}_{\mathit{PS}1}^2+{\mathit{k}}_{\mathit{PS}2}^2}<1\\ {\mathit{Q}}_0>{\displaystyle \frac{\sqrt{2}}{2}}\end{array}\right.,$$

(4)

where k_C is referred to as the critical coupling coefficient of the system, and the region of ${\mathit{k}}_{\mathit{C}}\le \sqrt{{\mathit{k}}_{\mathit{PS}1}^2+{\mathit{k}}_{\mathit{PS}2}^2}<1$ corresponding to the coupling coefficient is referred to as the strong coupling region, which is consistent with the previous coupled mode analysis method. From Equation (3), it is easy to find that, when the coil quality factor and the transceiver coupling coefficient satisfy the critical coupling condition, the PT system operating frequency will appear as a bifurcation phenomenon, with two branches of high-frequency angular frequency ω₊ and low-frequency angular frequency ω₋. This also indicates that the PT system is significantly different from the traditional MCR-WPT technology that operates at the intrinsic resonance frequency, and its operating frequency f ($\mathit{f}={\displaystyle \frac{\mathsf{\omega }}{2\mathsf{\pi }}}$) is not fixed but depends on the dual-load coil coupling coefficients k_PS1 and k_PS2 and the Q₀, and the system automatically adjusts the operating frequency f according to the different parameters to the frequency trajectories during the operation.

The system operates at an angular frequency of $\omega ={\mathsf{\omega }}_0$, and the coupling coefficients do not satisfy the constraint equations. The $0<\sqrt{{\mathit{k}}_{\mathit{PS}1}^2+{\mathit{k}}_{\mathit{PS}2}^2}<{\mathit{k}}_{\mathit{C}}$ is called the weak coupling region, in which the actual oscillation speed of the system will always be equal to the intrinsic resonant frequency of the resonant cavity f₀.

Based on the above analysis, the operating angular velocity of the system under different constraints can be calculated as

$$\left\{\begin{array}{c}\begin{array}{c}{\mathsf{\omega }}_{\text{±}}={\displaystyle \frac{{\mathsf{\omega }}_0}{\sqrt{2\left[1-\left({\mathit{k}}_{\mathit{PS}1}^2+{\mathit{k}}_{\mathit{PS}2}^2\right)\right]}}}\end{array}\sqrt{2-{\mathit{Q}}_0^{-2}\text{±}\sqrt{4({\mathit{k}}_{\mathit{PS}1}^2+{\mathit{k}}_{\mathit{PS}2}^2-1)+(2-{\mathit{Q}}_0^{-2}{)}^2}},\\ {\mathit{k}}_{\mathit{C}}\le \sqrt{{\mathit{k}}_{\mathit{PS}1}^2+{\mathit{k}}_{\mathit{PS}2}^2}<1\\ {\mathsf{\omega }}_0,0<\sqrt{{\mathit{k}}_{\mathit{PS}1}^2+{\mathit{k}}_{\mathit{PS}2}^2}<{\mathit{k}}_{\mathit{C}}\end{array}\right.,$$

(5)

2.2. Frequency Characteristics of a Dual-Rx PT System

Based on Equation (5), the operating frequency characteristics of the dual-load WPT system are calculated and illustrated in Figure 2. Specifically, Figure 2a depicts the operating frequency characteristics of the system with the dual-load k_PS1 and k_PS2 treated as independent variables. In contrast, Figure 2b combines k_PS1 and k_PS2 into a single variable, $\sqrt{{\mathit{k}}_{\mathit{PS}1}^2+{\mathit{k}}_{\mathit{PS}2}^2},$ and examines the effects of increasing Q₀, presenting the resulting variation curve.

The system parameters set in the calculations are resonant cavity intrinsic resonant frequency${\mathit{f}}_0=400\mathrm{kHz}$, receiving coil self-inductance ${\mathit{L}}_{\mathit{S}1}={\mathit{L}}_{\mathit{S}2}=72.26\mathrm{u}\mathrm{H},$ load resistance ${\mathit{R}}_{\mathit{L}1}={\mathit{R}}_{\mathit{L}2}=10\mathsf{\Omega }$, and coil internal resistance ${\mathit{R}}_2=0.25\mathsf{\Omega }$. Observing Figure 2a, it is easy to find that the dual-load PT-WPT system has a high-frequency branching surface f ₊ and a low-frequency branching surface f₋ in the strong coupling region of the operating frequency, and as the coupling coefficients of the two loaded coils move closer to the weak coupling region, the two branching surfaces are merged together at the trajectory of the k_C. In the weak coupling region, the system f will always be equal to the f₀. In addition, the offsets of the high- and low-frequency branches from the f₀ are asymmetric, and the frequency offset of the f₋ is smaller than that of f₊. Figure 2b shows that the k_C of the system increases as the Q₀ decreases, and the load resistance is negatively correlated with the width of the strongly coupled region. Under the condition that Equation (4) is satisfied, this characteristic requires that the Q₀ of the dual-load PT-WPT system should not be too low; otherwise, it will reduce the size of the load resistance R_L that can be driven by the system or affect the width of the strong coupling region and thus reduce the transmittable distance of the system. Therefore, this also places requirements on the coupler design.

2.3. Transfer Characteristics of the System

Since Rx and TA placed horizontally on the same plane naturally have an equal transmission distance, Rx can be considered to satisfy ${\mathit{k}}_{\mathit{PS}1}={\mathit{k}}_{\mathit{PS}2}{=\mathit{k}}_{\mathit{PS}}$. When the two Rx have the same design, condition ${\mathit{L}}_{\mathit{S}1}={\mathit{L}}_{\mathit{S}2}={\mathit{L}}_{\mathit{S}}$ is satisfied. According to Equation (1), by analyzing the current and voltage, combining the characteristics of the strong coupling regions and weak coupling regions, it can be concluded that the current gains G_I and voltage gains G_V expressions for driving a PT-WPT system with a quasi-uniformly coupled TA are obtained as

$${\mathrm{G}}_I={\displaystyle \frac{I_{\mathit{S}}}{I_{\mathit{P}}}}=\left\{\begin{array}{c}\begin{array}{cc}{\displaystyle \frac{\sqrt{2}}{2}}\sqrt{{\displaystyle \frac{{\mathit{L}}_{\mathit{P}}}{{\mathit{L}}_{\mathit{S}}}}},& {\mathit{k}}_{\mathit{C}}\le \sqrt{2}{\mathit{k}}_{\mathit{PS}}<1\end{array}\\ \begin{array}{cc}\mathit{k}{\mathit{Q}}_0\sqrt{{\displaystyle \frac{{\mathit{L}}_{\mathit{P}}}{{\mathit{L}}_{\mathit{S}}}}},& \sqrt{2}{\mathit{k}}_{\mathit{PS}}<{\mathit{k}}_{\mathit{C}}\end{array}\end{array}\right.,$$

(6)

$${\mathrm{G}}_{\mathit{V}}={\displaystyle \frac{{\mathit{V}}_{\mathit{S}}}{{\mathit{V}}_{\mathit{P}}}}=\left\{\begin{array}{c}\begin{array}{cc}{\displaystyle \frac{\sqrt{2}}{2}}\sqrt{{\displaystyle \frac{{\mathit{L}}_{\mathit{S}}}{{\mathit{L}}_{\mathit{P}}}}},& {\mathit{k}}_{\mathit{C}}\le \sqrt{2}{\mathit{k}}_{\mathit{PS}}<1\end{array}\\ \begin{array}{cc}\mathit{k}{\mathit{Q}}_0\sqrt{{\displaystyle \frac{{\mathit{L}}_{\mathit{S}}}{{\mathit{L}}_{\mathit{P}}}}},& \sqrt{2}{\mathit{k}}_{\mathit{PS}}<{\mathit{k}}_{\mathit{C}}\end{array}\end{array}\right.,$$

(7)

According to Equations (6) and (7), when the system operates in the strong coupling regions, both the G_I and G_V are solely dependent on the system’s intrinsic parameters and are independent of the coupling coefficient and the quality factor. This demonstrates that the application of PT symmetry theory to the system results in constant transmission characteristics.

Ignoring that the internal resistances r₁ and r₂ are much smaller than the load, and combined with the formula for calculating the voltage ${\mathit{U}}_{\mathit{P}}=I_{\mathit{P}}{\mathit{R}}_{\mathit{n}}$, across the negative resistor, the output power of two Rx can be obtained:

$$\left\{\begin{array}{c}{\mathit{P}}_{\mathit{L}1}={\displaystyle \frac{{\mathit{U}}_{\mathit{P}}^2\frac{{\mathit{k}}_{\mathit{PS}1}^2}{{\mathit{k}}_{\mathit{PS}1}^2+{\mathit{k}}_{\mathit{PS}2}^2}}{{\mathit{R}}_{\mathit{L}1}\frac{{\mathit{L}}_{\mathit{P}}}{{\mathit{L}}_{\mathit{S}1}}}}\\ {\mathit{P}}_{\mathit{L}2}={\displaystyle \frac{{\mathit{U}}_{\mathit{P}}^2\frac{{\mathit{k}}_{\mathit{PS}2}^2}{{\mathit{k}}_{\mathit{PS}1}^2+{\mathit{k}}_{\mathit{PS}2}^2}}{{\mathit{R}}_{\mathit{L}2}\frac{{\mathit{L}}_{\mathit{P}}}{{\mathit{L}}_{\mathit{S}2}}}}\end{array}\right.,$$

(8)

According to Equation (8), it is observed that, when operating in the strong coupling region, the output power of the two Rx coils depends only on the load resistances R_L1 and R_L2, the coupling coefficients k_PS1 and k_PS2, and the inductance ratio between the transmitting and receiving coils but is independent of the system’s operating frequency f. Moreover, for the QC transmitting array proposed in this study, it ensures that the two Rx coils have approximately identical coupling coefficients, denoted as ${\mathit{k}}_{\mathit{P}\mathit{S}1}={\mathit{k}}_{\mathit{P}\mathit{S}2}$, at the same transmission distance. Under these conditions, the output of the PT-WPT system becomes independent of k_PS1 and k_PS2, resulting in a constant power output characteristic, as long as the load remains unchanged.

If the loads of the two Rx are the same, i.e., ${\mathit{R}}_{\mathit{L}1}={\mathit{R}}_{\mathit{L}2}={\mathit{R}}_{\mathit{L}}$, the total output power P_total and efficiency η_total can be simplified into Equation (9). The PT system maintains a constant total power output.

$$\left\{\begin{array}{c}{\mathit{P}}_{\mathit{total}}=I_{\mathit{S}1}^2{\mathit{R}}_{\mathit{L}1}+I_{\mathit{S}2}^2{\mathit{R}}_{\mathit{L}2}={\displaystyle \frac{{\mathit{U}}_{\mathit{P}}^2{\mathit{R}}_{\mathit{L}}}{({\mathit{R}}_2+{\mathit{R}}_{\mathit{L}}{)}^2\frac{{\mathit{L}}_{\mathit{P}}}{{\mathit{L}}_{\mathit{S}}}+2({\mathit{R}}_2+{\mathit{R}}_{\mathit{L}}){\mathit{R}}_1+\frac{{\mathit{L}}_{\mathit{S}}}{{\mathit{L}}_{\mathit{P}}}{\mathit{R}}_1^2}}\\ {\mathsf{\eta }}_{\mathit{total}}={\displaystyle \frac{{\mathit{P}}_{\mathit{total}}}{{\mathit{P}}_{\mathit{in}}}}={\displaystyle \frac{{\mathit{R}}_{\mathit{L}}{\mathit{L}}_{\mathit{P}}}{{\mathit{R}}_1{\mathit{L}}_{\mathit{S}}+{\mathit{L}}_{\mathit{P}}({\mathit{R}}_{\mathit{L}}+{\mathit{R}}_2)}}\end{array}\right.,$$

(9)

3. Overview of the Proposed Array Prototype

Previous studies on anti-offset WPT systems have extensively utilized MCR technology. However, its output characteristics exhibit high sensitivity to variations in the coupling state, posing challenges in fully meeting the transmission requirements of anti-offset systems. For this reason, this paper actively explores new wireless energy transmission technology and carries out a study on the working mechanism based on PT-WPT. From the current state of research on couplers for WPT systems, it is not difficult to find that distributed coil designs generally have better offset transmission performance due to their larger transmitter sizes compared to monolithic coils [30].

Therefore, in this paper, the basic configuration of the coupler is firstly identified as a distributed coil, and an attempt is made to improve the system’s offset resistance by configuring multiple Tx into an array. However, most of the existing distributed coil systems are activated by a fixed number of units and suffer from the problems of complex unit structure and unit placement topology. This not only results in the system not being able to flexibly adjust the charging area according to the position of the Rx efficiently, but also, the distributed system is not easy to expand the configuration, which limits the flexibility of the application. For this reason, a TA structure consisting of planar coils is proposed in this paper, as shown in Figure 3. Several identical Tx units are arranged to form a neatly shaped TA, and each neighboring Tx unit is placed parallel to each other with an equal overlap width of the units l_o. Moreover, the Tx is a square spiral winding, which has the advantages of simple structure and easy fabrication. In addition, the square shape has symmetry in the X and Y directions, which simplifies the difficulty of analyzing the offset transmission performance of the coupler under different misalignment conditions.

Secondly, in this paper, a coil structure parameter optimization algorithm is proposed to design Tx units with QC characteristics. This approach enables the generation of an approximately uniform magnetic field along the Z-axis within the Rx coil’s motion plane, ensuring nearly constant coupling coefficients during the Rx’s horizontal movement. In addition, when multiple Tx units in the array operate simultaneously, adjusting the overlap width of the units l_o achieves the adjustment of the total magnetic field distribution of the array. Based on this, in this paper, the structural parameters of Tx itself and l_o will be comprehensively optimized in the coupler design part, so that not only the expansion of charging area is achieved when adjacent Tx units work together but also the approximate stable magnetic field uniformity can still be maintained in the area. This feature can effectively increase the offset transmission range and offset resistance of the array WPT system.

Finally, in terms of the flexible configuration of the array configuration, the distributed coil structure in previous studies enhanced the charging area and enhanced the flexibility of use, but the fixed number of units operated in such a way that many non-essential Tx units were activated. This not only increases the magnetic leakage of the system and reduces the efficiency but also poses a safety hazard of electrically heating the metal objects in the array. For this reason, the proposed TA will follow the principle of minimizing electromagnetic radiation, i.e., the Tx units operating at the same time will be controlled independently of each other depending on the Rx conditions. This feature not only allows the proposed coupler to independently configure the position and size of the charging area for one or two Rx coils but also balances the offset transmission range and coupler leakage, improving the practicality and safety of the system.

The circuit structure of a WPT system with four Tx coils and two Rx coils is shown in Figure 4. The meanings of the symbols in the figure are listed in

Table 1. The symbols and their meanings in the equivalent circuit.

Symbol	Meaning
Udc	Input voltage of DC power supply
iP and iS	Current in Tx and Rx coils loops
CP, CS1, and CS2	Compensation capacitors for Tx and Rx coils
LPN	Inductance of Tx coil
LP	The equivalent inductance of TA
LS1 and LS2	The inductance of the two Rx coils
r1 and r2	The equivalent resistance of Tx and Rx coils
RL1 and RL2	The equivalent resistance of the load
SN	Switch of Tx Coil #N
MNN	Cross mutual inductance between adjacent Tx
MPNS1 and MPNS2	Mutual inductance between Tx and two Rx

. Due to space constraints, the mutual inductance of Rx2 and the array is not represented separately. The TA consists of a number of Tx units connected in a series, with the homonymous ends of each unit connected sequentially to avoid magnetic field cancellation due to reverse coil operation. A switch S_N is connected in parallel with each Tx coil, and the Tx units are controlled by changing the open or closed state of each S_N. This design provides the system with the ability to switch each Tx unit independently. In this paper, S_N can be constructed by relay contacts, which provides high expansion convenience and reliability of coil control. In addition, as shown on the left side of Figure 4, the proposed TA can be driven by only one AC power supply, which greatly reduces the manufacturing cost.

For 1 or 2 Rx, several possible operation strategies of the TA are listed in

Table 2. The operational strategy of the TA.

TA’s Operation Strategy	Schematic Diagram	The Number of Supported Rx	Description
#1		1	Activate one Tx coil
#2 × 1	or	1 or 2	Activate a composite coil
#2 × 2 × 1		2	Activate two composite coils
#1 + 1		2	Activate two non-adjacent Tx coils
#1 + 2 × 1		2	Activates a composite coil and an extra Tx coil

. In this table, the gray area indicates the TA area provided by a single Tx or 2 × 1 composite coils, and the red circle indicates the position and quantity of Rx, and Rx can move freely within the corresponding gray range. For one Rx, the system has the option to activate one Tx or one composite coil. For two Rx, the operation strategies of the TA include #2 × 2 × 1, #1 + 1, and #1 + 2 × 1. To accommodate changes in the Rx position, the controller adjusts the strategy by configuring the switch settings based on Table 2. Additionally, different from the previous MCR-WPT system, the TA is driven by an inverter designed based on the PT theory, so it has a wide high-efficiency region and mutual inductance tolerance, which ensures the effectiveness of the TA’s operation strategy when dealing with two Rx. Moreover, the detuning problem caused by the cross-coupling of adjacent Tx coils will be solved by a modular compensation circuit.

The PT-WPT system not only has a wider high-efficiency region and stronger tolerance to mutual inductance fluctuations but also avoids the more complicated frequency control, phase detection, and resonance compensation topology with multiple energy storage elements in the MCR-WPT system. Therefore, it is more suitable for the anti-offset WPT system with complex coupler structure proposed in this paper. In the following, the modeling and theoretical analysis of the dual-load PT-WPT system will be carried out to ensure the effectiveness of the proposed anti-offset system from the perspective of the transmission principle.

4. Parameter Design of T_X and R_X

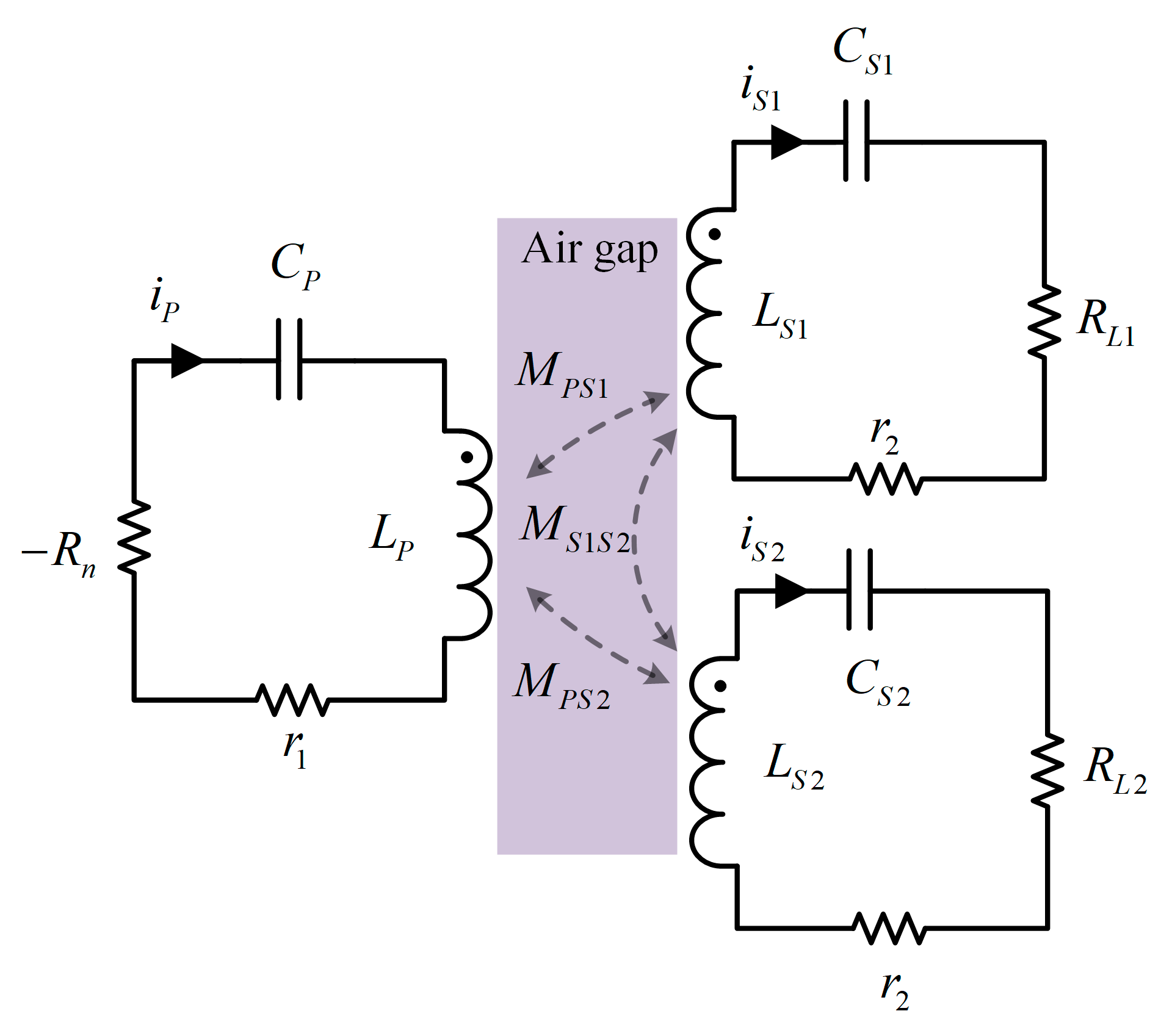
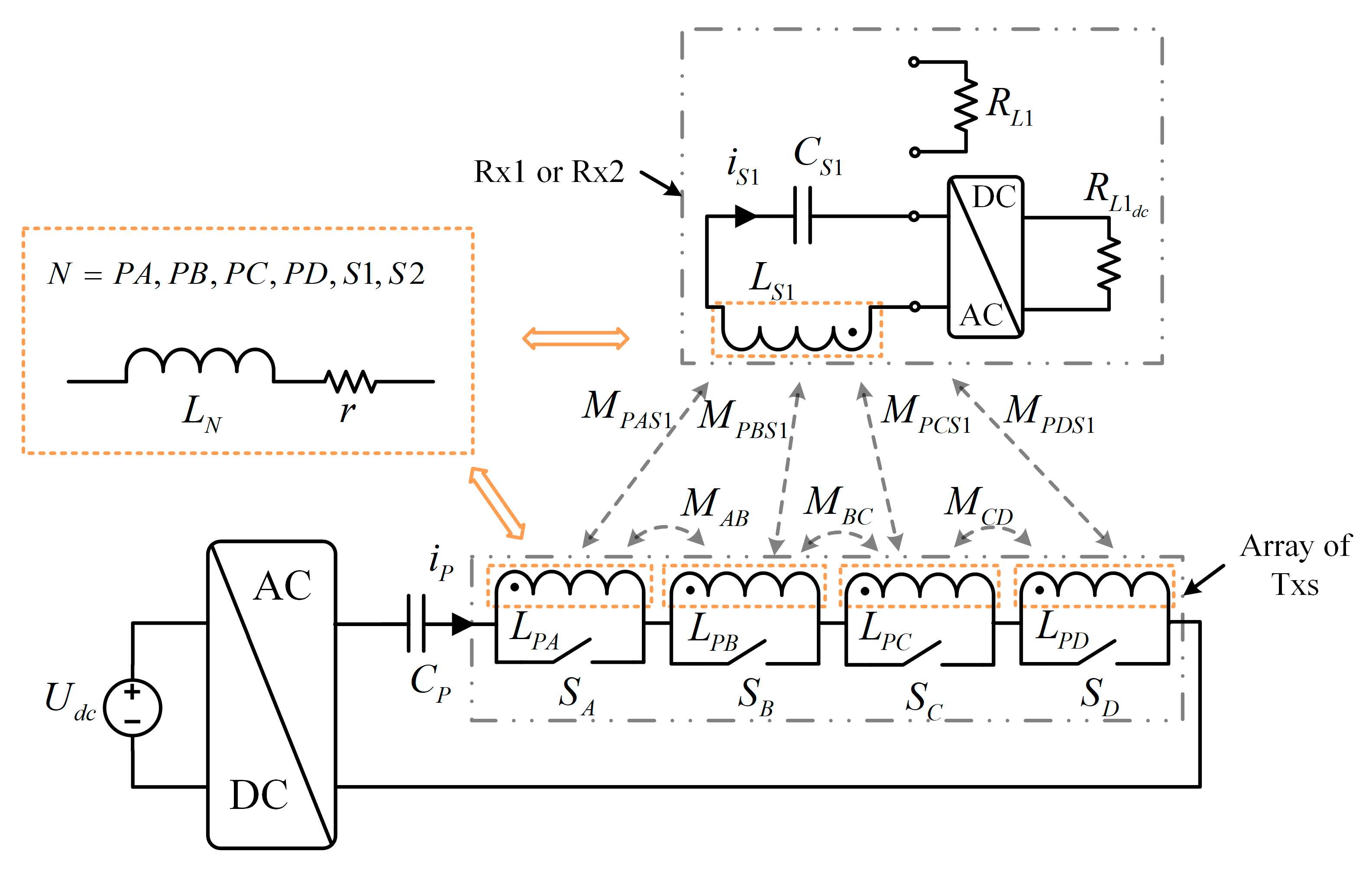
4.1. Structure of the Coils in the Array

The near-field WPT essentially utilizes a Tx to direct the flow of the current through the wire structure to achieve the excitation of the electromagnetic field. Afterwards, the receiving device with closed windings interlinks with the magnetic inductance and inducts to obtain the current, thus realizing the conversion of electrical energy–magnetic energy–electrical in the WPT system. Therefore, the design of the coupler used for the conversion of electrical and magnetic energy directly determines the system’s offset resistance.

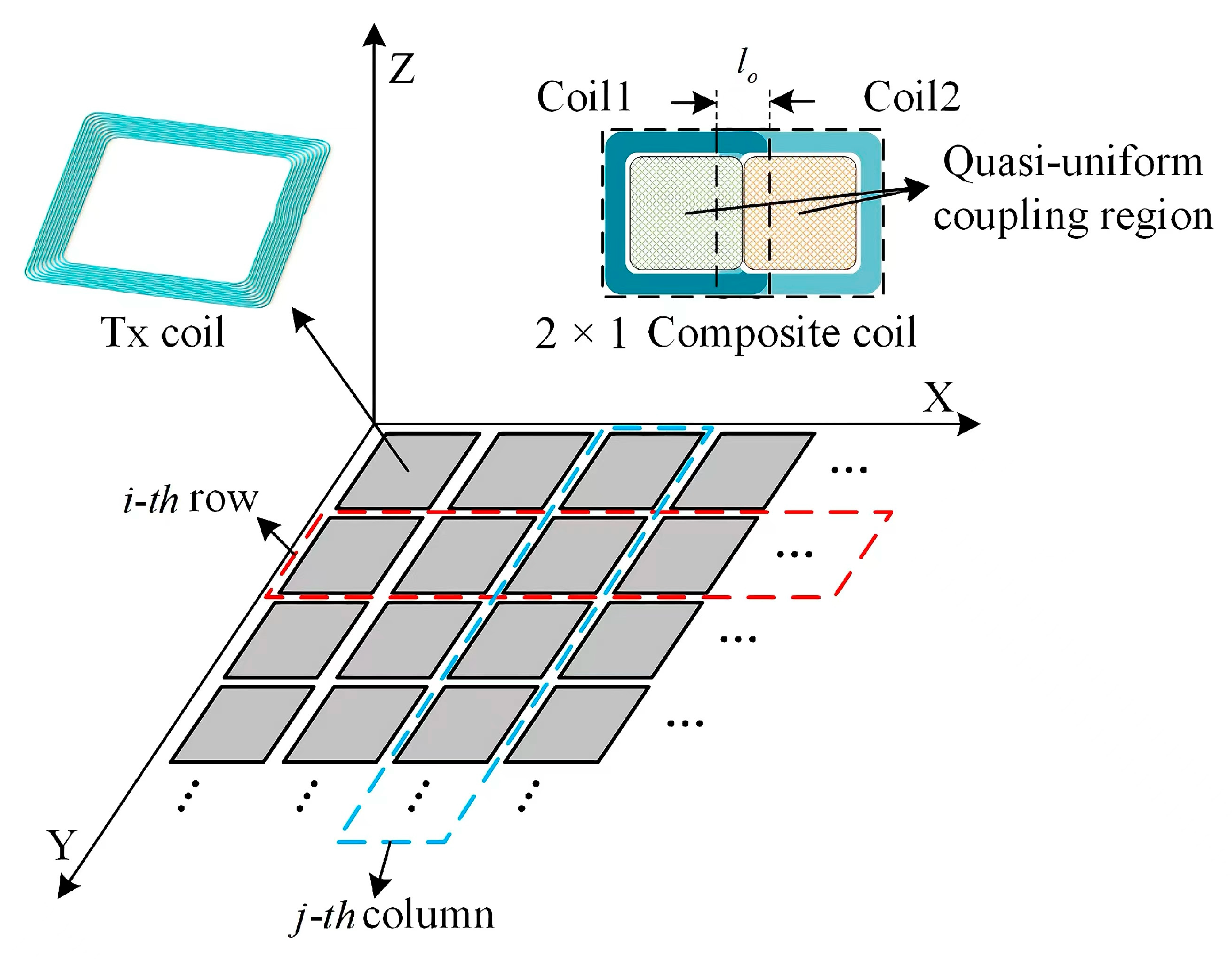
To ensure that Rx can receive sufficient power at any position, it is necessary for TA to have QC. The mutual inductance and coupling coefficient in this region are approximately constant, which can significantly reduce the interference caused by coil movement to the system. A few studies have investigated QC to improve the misalignment tolerance of the array, but the additional winding brings a complex structure, and it only supports independent Tx activation, which indicates that the size of the charging area cannot be flexibly configured. To this end, this study designs the Tx and Rx coils based on the PT system and follows some necessary design principles to ensure effectiveness and operability:

• The coils should balance performance and cost. Excessive material consumption and design complexity are not conducive to the expansion of the array and the embedding of application objects.
• The 2 × 1 composite coils should still maintain QC to ensure stable power transfer for Rx in different configurations.
• The cross-coupling between Tx should be estimated to achieve precise resonance compensation.
• There should be a sufficient coupling coefficient between the compact Rx coil and Tx to meet the strong coupling requirements of the PT system.

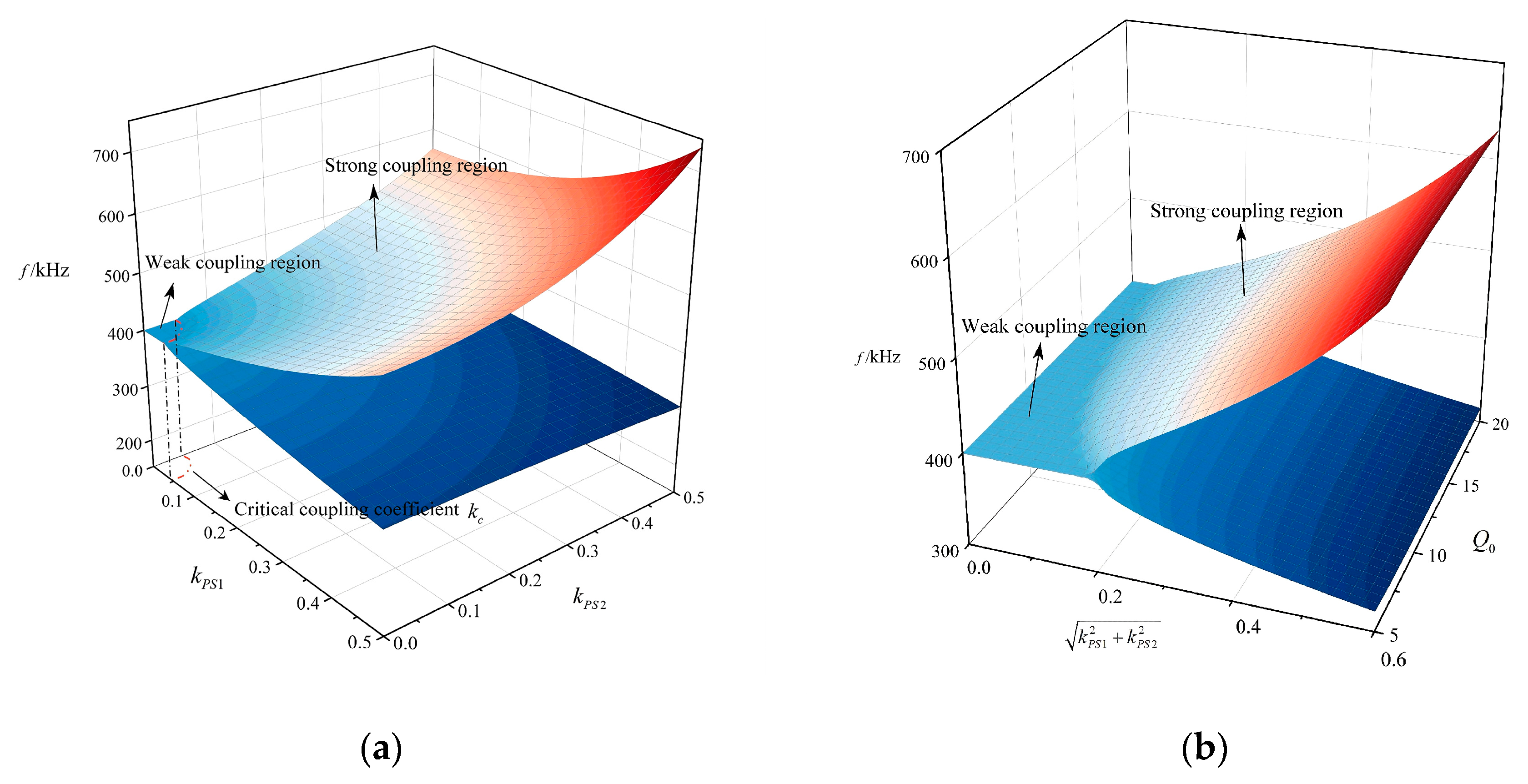
The previous mechanism study of the dual-load PT system shows that, for the system to work in the strong coupling region to achieve constant characteristic transmission, the coupling coefficients of the two Rx coils cannot be too low and must satisfy ${\mathit{k}}_{\mathit{C}}\le \sqrt{{\mathit{k}}_{\mathit{PS}1}^2+{\mathit{k}}_{\mathit{PS}2}^2}$, which essentially implicitly requires that the homogeneity of the magnetic field in the airgap should be high or else there exists a possibility for the flexibly moving Rx to move into the weak coupling region, which results in the destabilization of the system. For this reason, an array unit Tx with QC characteristics is proposed in this study. 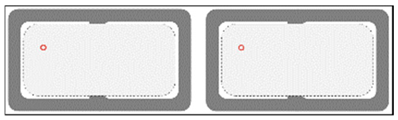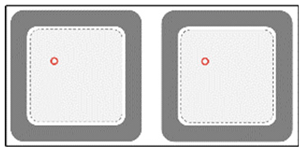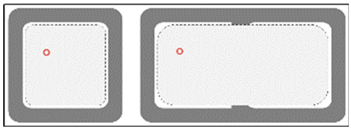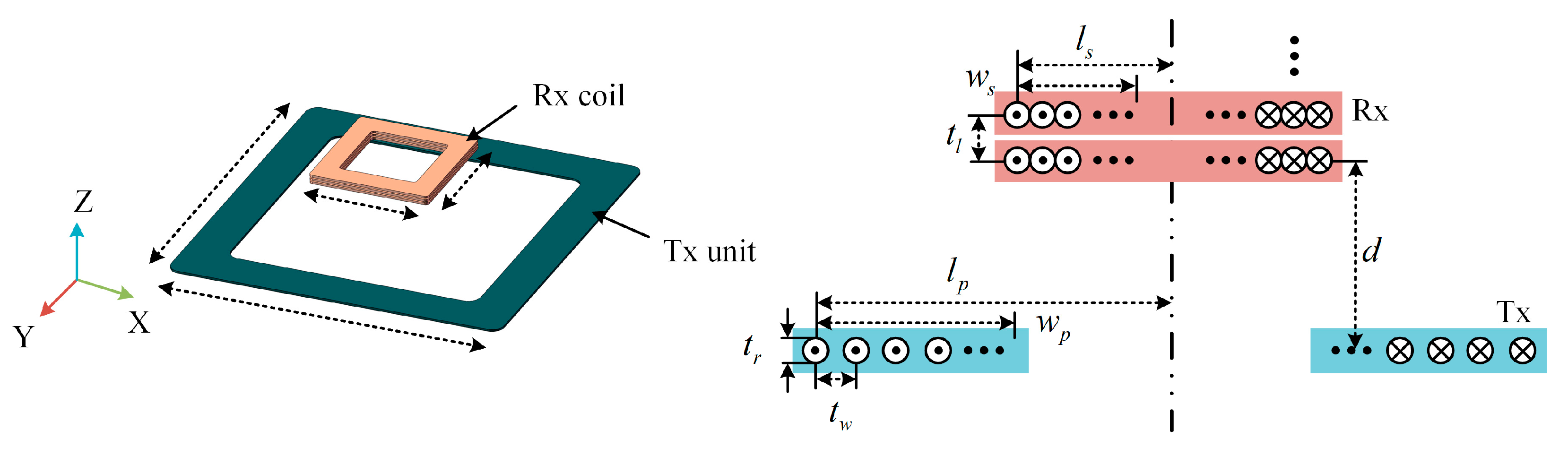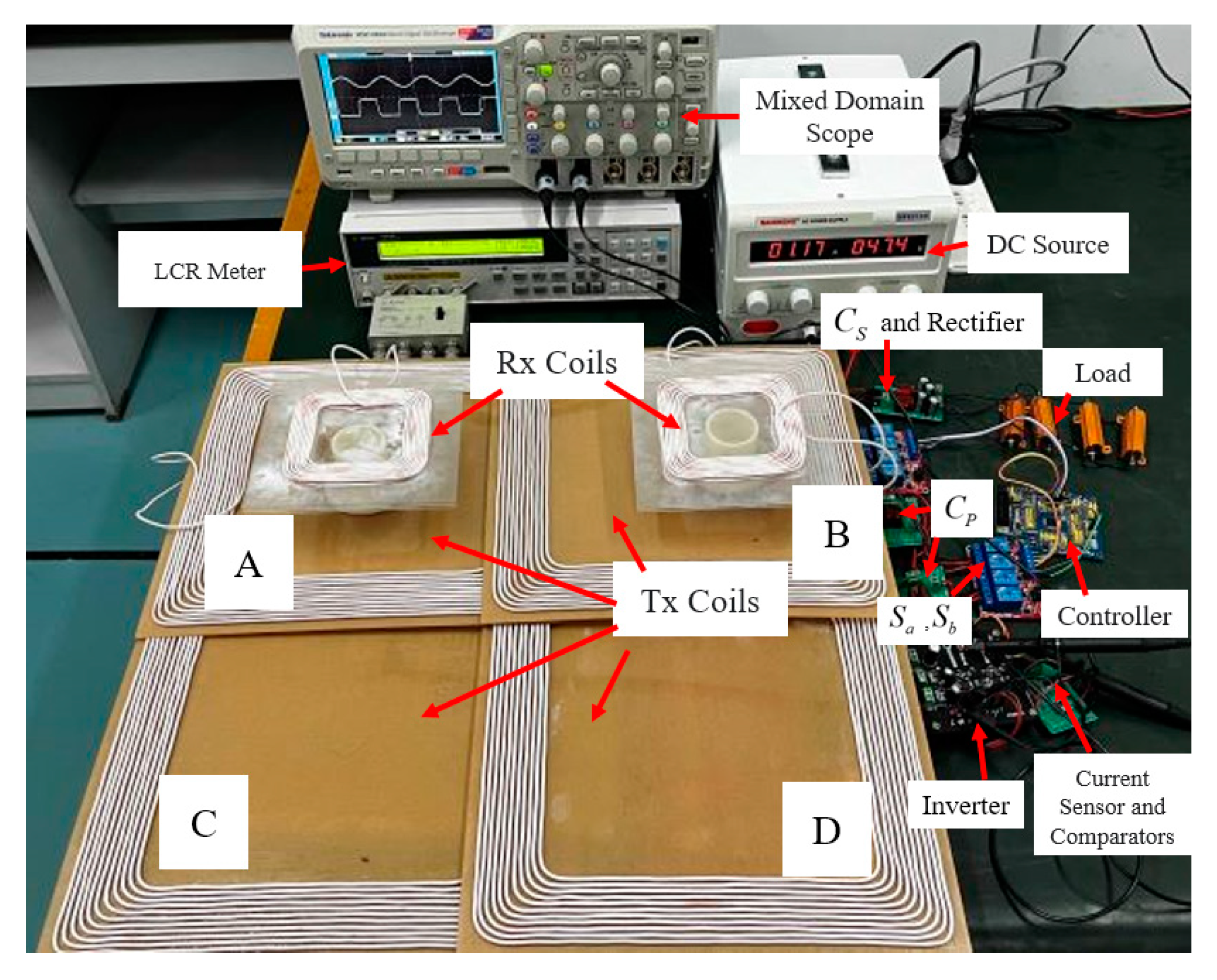Figure 5 illustrates the structure of the Tx and the Rx, whereas the parameters are defined in

Table 3. The symbols and their definitions.

Symbol	Meaning	Symbol	Meaning
d	The transmission distance between Tx and Rx	Nl	The number of layers of the Rx coil
lP and lS	Half the length of the Tx and Rx coils	tl	Layer spacing of the Rx coil
wP and wS	Winding width of Tx and Rx coils	NP	The number of turns of the Tx coil
tw	Winding spacing of Tx	NS	The number of turns of each layer of the Rx coil
tr	Wire diameter	rd(=wP/lP)	Tx winding width ratio
lQ	Mutual inductance QC area width

.

4.2. Tx Coil Design

The Tx unit is formed by multi-turns of square windings, which is simple and easy to fabricate, and the symmetry of the structure ensures that the Tx has consistent coupling performances in the X and Y directions, while the Rx coils are formed by multilayers of square windings, which are compact and easy to be installed in various electronic products. In this study, the Tx and Rx coils are placed horizontally to simulate the common application scenarios of the WPT system. The transmission distance d of the system is set at 5 cm, which is used to ensure that the device has enough air gap height for mounting the housing, fixing the fixture, and necessary redundancy.

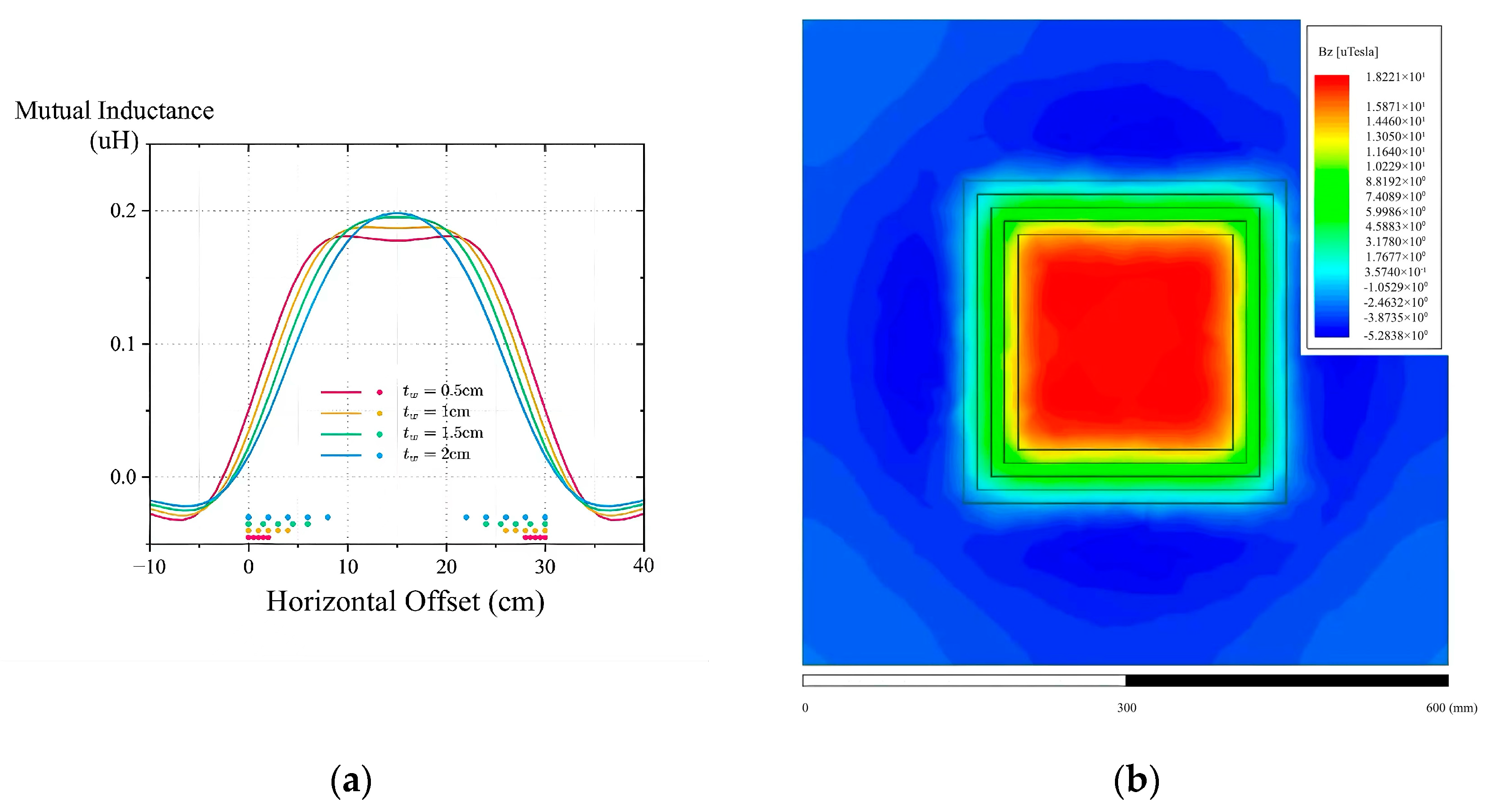
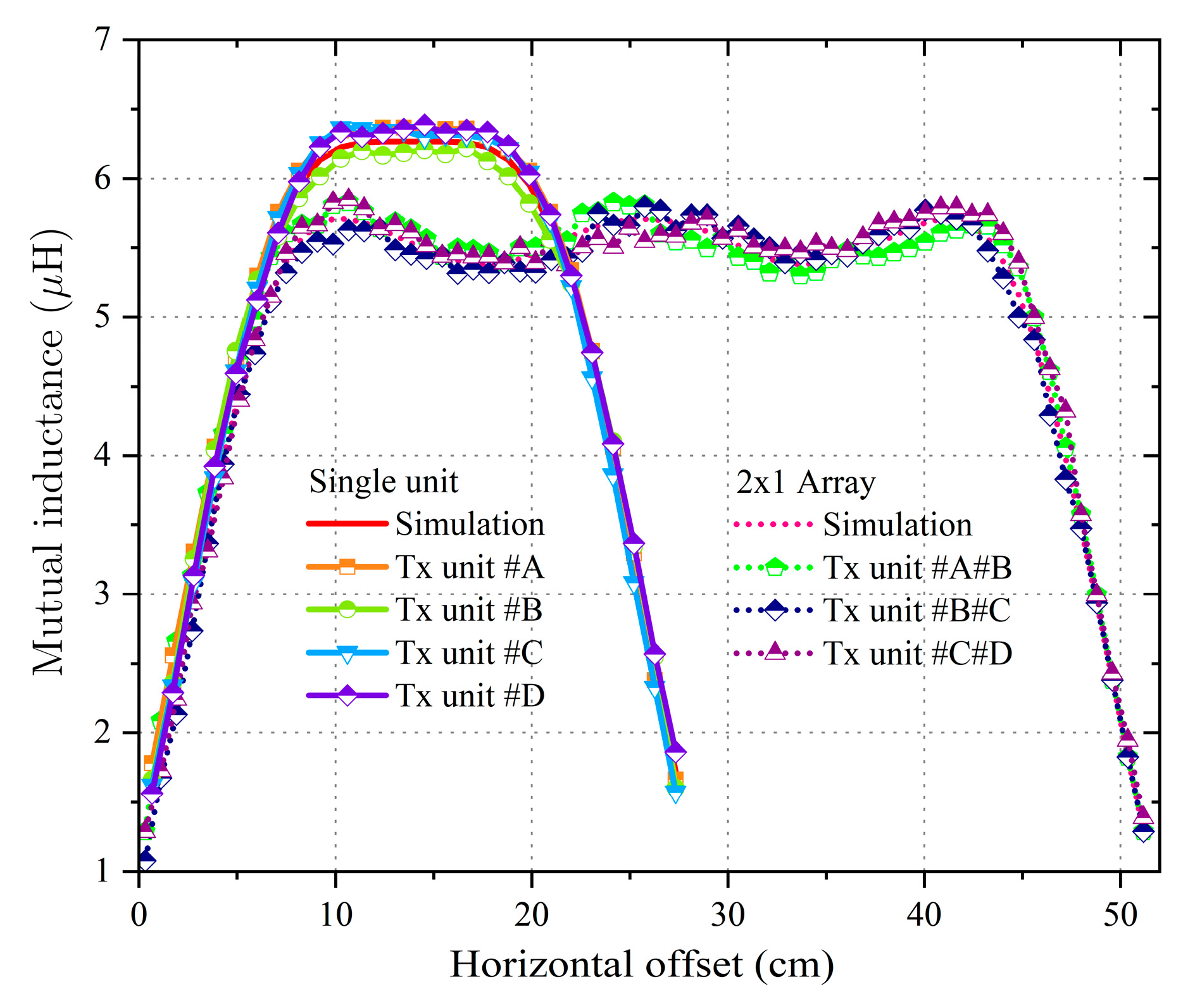
The structural parameters of the Tx coil will directly affect the magnitude and vector direction of the magnetic field in the air gap, and the parameters of the square coil that can have a significant effect on the magnetic field include the coil half-length l_P, the winding spacing t_w, and the number of turns of the winding N_P. Figure 6a demonstrates the mutual inductance distribution curves with different X-axis offsets for fixed ${\mathit{L}}_{\mathit{P}}=15\mathrm{cm}$, ${\mathit{n}}_{\mathit{P}}=15\mathrm{cm},$ and ${\mathit{t}}_{\mathit{w}}=15\mathrm{cm}$ when adjusting t_w. As the Tx coil exhibits uniform coupling characteristics in both the X and Y directions, scanning along the X-axis alone is adequate when the Rx is concentrically aligned with the Tx along the Y-axis. It can be observed that the mutual inductance distribution curve shrinks from wide to narrow when t_w varies from small to large. The width of the QC area at the center of Tx is the maximum when ${\mathit{t}}_{\mathit{w}}=1\mathrm{cm}$. According to the flux calculation formula $\mathit{d}\mathsf{\Phi }=\mathit{BdS}\mathit{cos}\mathsf{\theta }$, it can be seen that, for Rx and Tx placed in parallel, the effective flux receivable by Rx is the component perpendicular to the plane around which the coil is placed. Based on this, Figure 6b shows the Z-axis component B_Z of the magnetic induction B in the plane where Rx is located obtained using the Ansys analysis platform, and the simulation results are used to verify the uniformity of the magnetic field generated by the Tx unit. In the simulation, the loading current $I=1\mathrm{A}$ is set, and from the results, it is easy to find that the Tx unit generates a B_Z approximate uniform region in the plane of Rx, i.e., the QC area, which is located in the inner part of the Tx winding. The Rx has approximately the same mutual inductance and k_PS at any position in this region, and this property effectively ensures that the two Rx coils satisfy the ${\mathit{k}}_{\mathit{PS}1}={\mathit{k}}_{\mathit{PS}2}$, which ensures that the dual-loaded coils of the offset-resistant transmission system proposed in this paper have equal output power.

4.3. Array Expansion Method

Two adjacent coils, A and B, in the composite coils are placed with an overlapping width of l_o, shown in Figure 7. When two Tx provide magnetic fields at the same time, the total mutual inductance M_AB is a function of the horizontal offset of Rx, and M_AB can be represented as

$${\mathit{M}}_{\mathit{AB}}={\mathit{M}}_{\mathit{A}}(\mathrm{x})+{\mathit{M}}_{\mathit{B}}(\mathrm{x}),$$

(10)

where M_A and M_B are the mutual inductances generated by coils A and B, respectively. The results when M_AB varies with l_o are shown in Figure 8. The results indicate that the adjustment of l_o has a significant impact on the mutual inductance distribution in the overlapping area because the outer side of the Tx winding will provide a negative mutual inductance area and interact with the adjacent coil. With an appropriately set l_o, such as ${\mathit{L}}_{\mathrm{o}}=4\mathrm{cm}$, the mutual inductance in the overlapping area remains relatively stable. To ensure optimal performance, an optimization process is implemented to adjust the Tx parameters and placement distances.

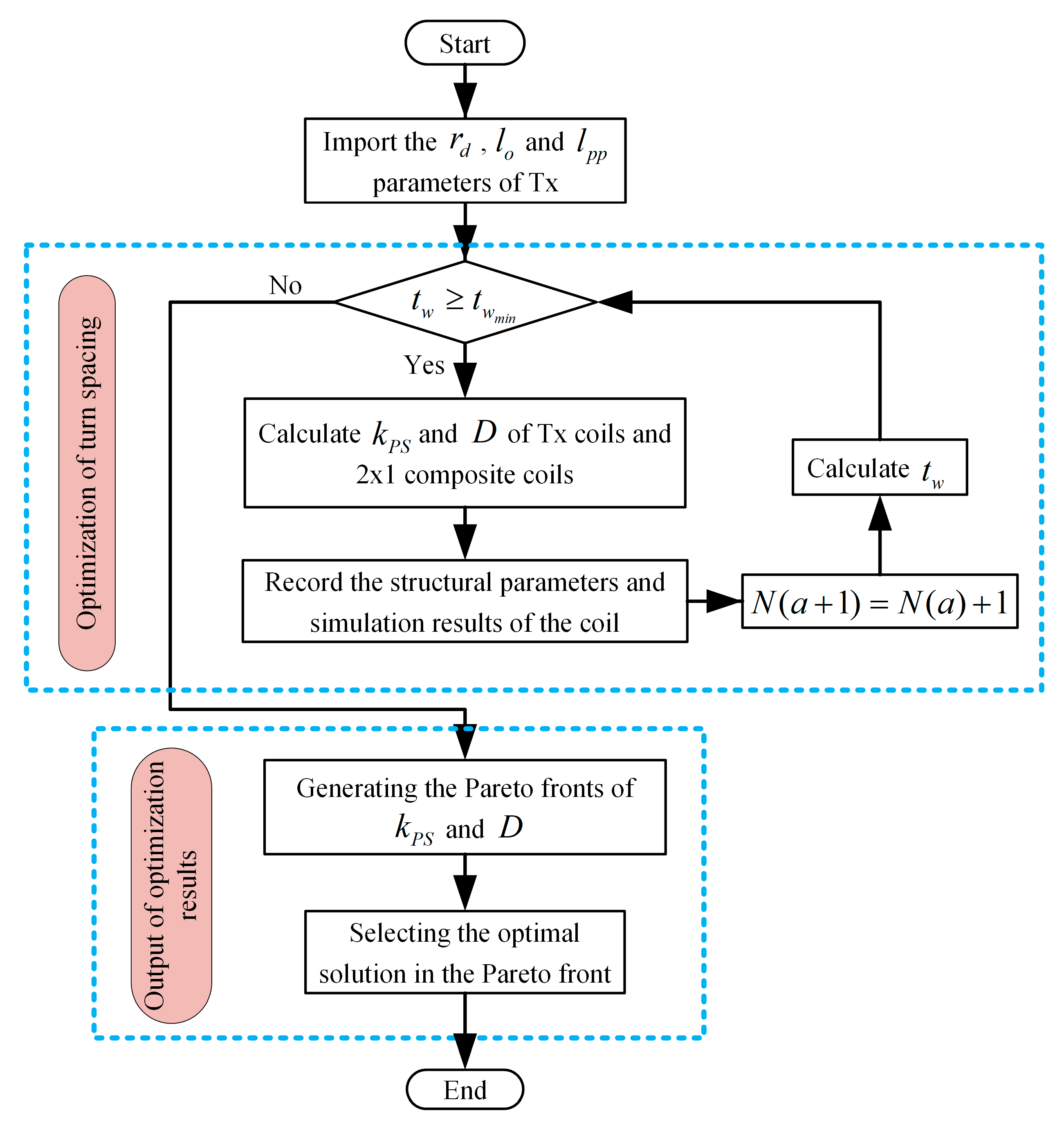
4.4. Multi-Objective Optimization of Array Structural Parameters

In order to ensure good QC of the TA for both a single Tx unit and neighboring Tx cooperating to form a 2 × 1 combined coil, multiple independent parameters contained in the coil structure need to be finely captured.

Some studies [42,43] adopted a general multi-objective optimization algorithm for coil design. However, Tx contains many parameters, and taking too many parameters as independent variables will result in a huge calculation cost. To address this problem principle, an analysis of the influence effect of the coil parameters is first conducted to gain prior knowledge. Based on this, the precise parameters of Tx can be determined by a simple and low-cost calculation procedure. The adjustable parameters of Tx include the maximum half-length l_pp (the optimized value of l_P), winding spacing t_w, winding width ratio r_d, and Tx overlap width l_o; the optimization goals include the QC area width l_Q, average mutual inductance in the QC area M_Q, coupling coefficient k_PS, and coil material consumption D (defined as the total winding length). In addition, the ratio of l_Q to Tx width, i.e.,${\mathit{\alpha }}_{\mathit{Q}}={\mathit{L}}_{\mathit{Q}}/(2\text{×}{\mathit{L}}_{\mathit{pp}}),$ is self-defined as a measure of the size of the QC area provided by Tx. The effect of adjusting t_w and r_d on ${\mathit{\alpha }}_{\mathit{Q}}$, M_Q, and k_PS is shown in Figure 9. Specifically, Figure 9a shows that there is a significant correlation between r_d and ${\mathit{\alpha }}_{\mathit{Q}}$, and a too large r_d will shrink the QC area; also, changing t_w has little effect on ${\mathit{\alpha }}_{\mathit{Q}}$. Figure 9b shows that adjusting t_w and r_d can affect M_Q, but the effect on r_d is more obvious. The PT system is sensitive to the k_C, and the coil needs to meet the condition ${\mathit{k}}_{\mathit{C}}\le \sqrt{2}{\mathit{k}}_{\mathit{PS}}$ to ensure efficient power output. Figure 9c demonstrates that increasing r_d can effectively improve the coupling coefficient k_PS, but the effect of t_w is not significant. This is because, when r_d is fixed, reducing t_w will increase the number of winding turns, and the mutual inductance will greatly increase the self-inductance of Tx, resulting in only a slight increase in k_PS. For example, at ${\mathit{R}}_{\mathit{d}}=0.4$, when t_w is reduced from 0.5cm to 0.25 cm, k_PS only slightly increases by 0.02, but this leads to about a doubling of the material consumption.

Table 4. The effect of Tx parameters on the coupling performance.

The Influence on Coupling Performance	${\mathit{\alpha }}_{\mathbf{Q}}$	MQ	D	kPS
Increase rd	Significantly reduced	Moderately increase	Slightly increase	Significantly increase
Decrease tw	Approximately constant	Moderately increase	Significantly increase	Significantly reduced
The relationship between the two variables	Unrelated	No conflict	No conflict	No conflict

summarizes the correlation between Tx parameters and performance indicators.

Table 4 shows that adjusting r_d and t_w has unrelated or non-conflicting effects on the coupling performance. However, there are optimization conflicts among multiple evaluation indicators, i.e., the optimization of one indicator will degrade other indicators. For example, increasing r_d can improve k_PS but reduce α_Q. According to this characteristic, this study proposes a segmented optimization method for Tx and placement distance, which reduces the computational complexity by reducing the number of variables for one-time optimization. The first step is to adjust r_d to ensure that Tx and composite coils have sufficient QC areas. Then, the second step is to optimize t_w to achieve the best correction between D and k_PS. The model is specifically described as:

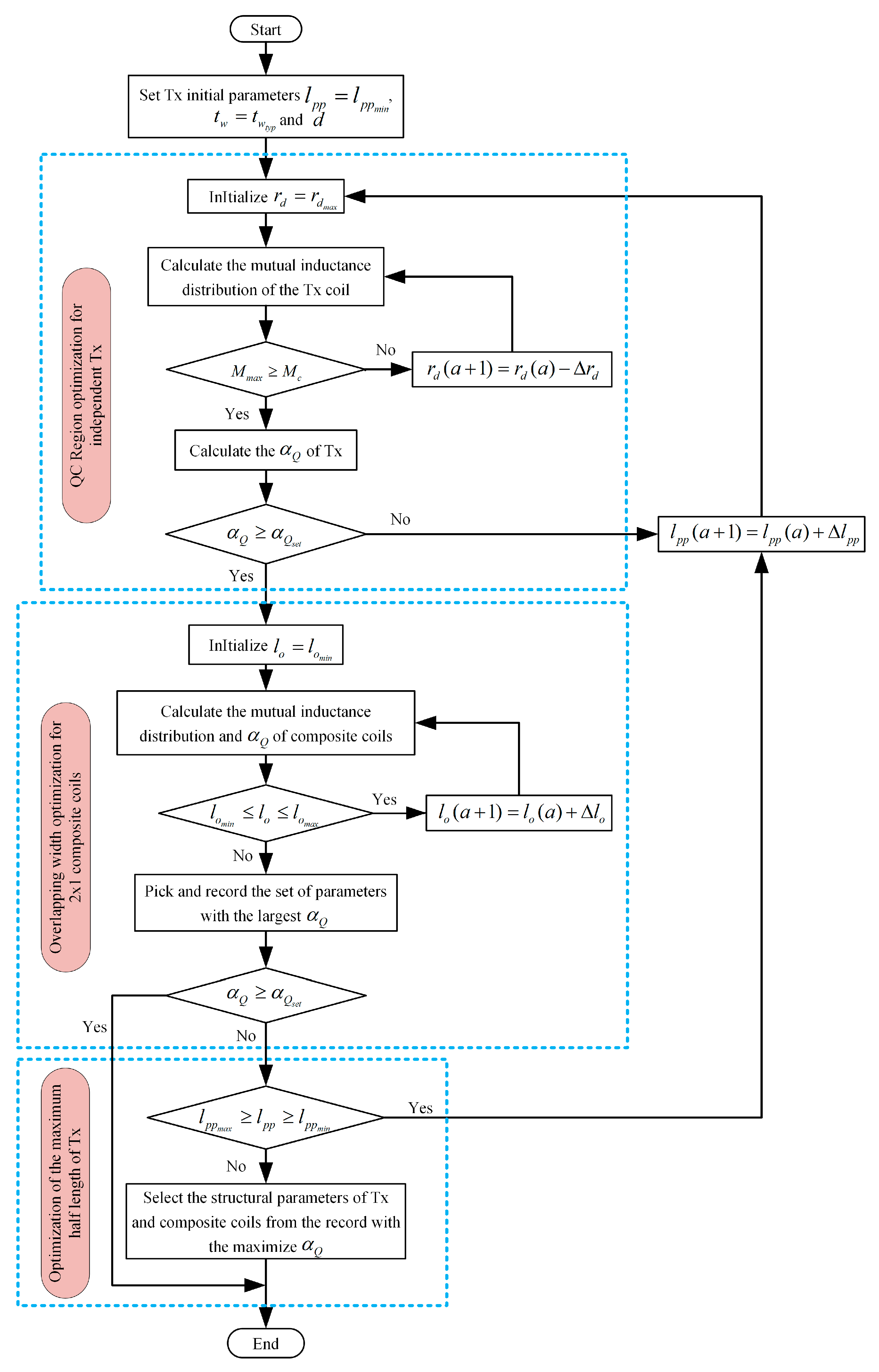
Step 1: l_o, r_d, and l_pp are adjusted to maximize l_Q. Figure 10 shows the optimization scheme of Step 1.

Since the influence of t_w on α_Q is negligible, t_w is first initialized to a typical value, i.e., t_wyp = 5 mm. Step 1 consists of three parts: the first part is to adjust r_d to optimize the l_Q of Tx.

First, r_d is set to the maximum limit value of 0.9, and combined with finite element analysis (FEA), the distribution curve of the Rx offset and mutual inductance is obtained. If the maximum mutual inductance M_max in the curve satisfies ${\mathit{M}}_{\mathit{max}}>{\mathit{M}}_{\mathit{C}}$, then the α_Q of Tx is calculated; otherwise, the above procedure is repeated after a small amount of ∆r_d is subtracted from r_d. 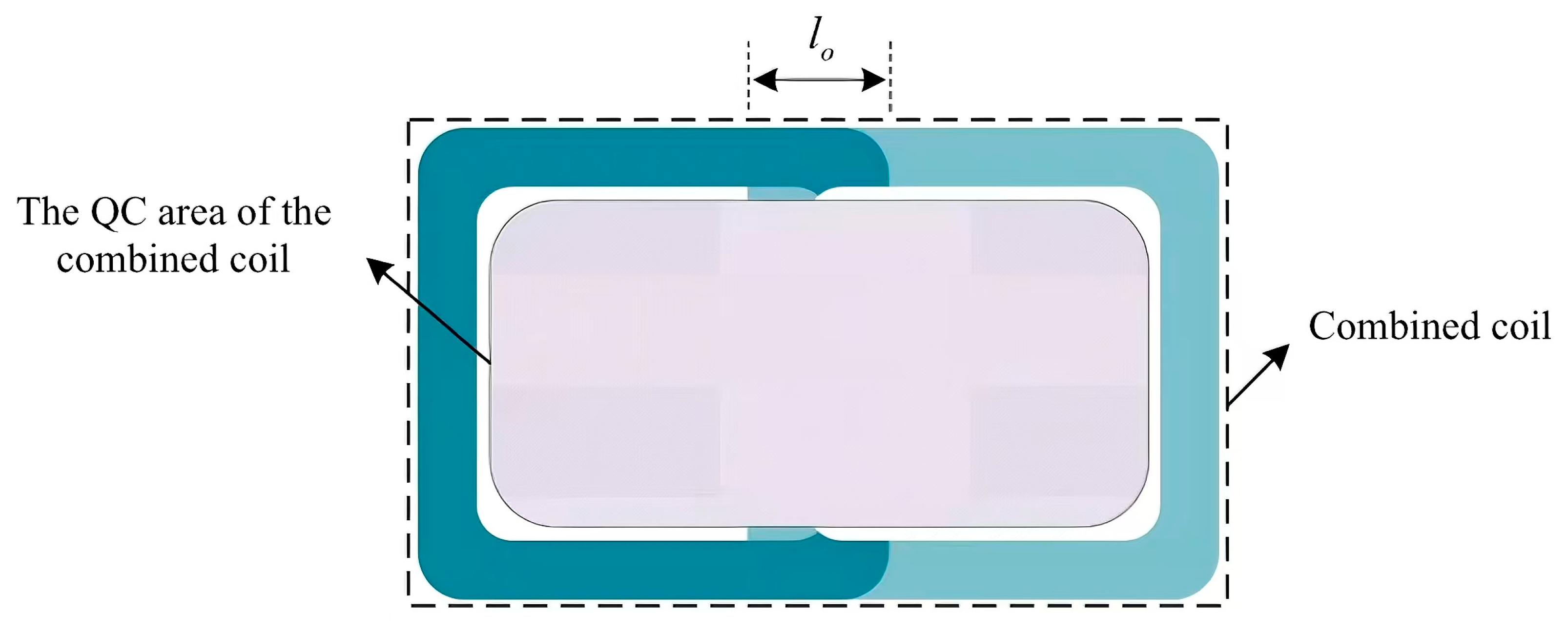Afterward, it is determined whether α_Q is greater than the minimum limit ${\mathit{\alpha }}_{\mathit{Qset}}=0.5$; if this condition is not satisfied, l_pp increases with ∆l_pp as the step size, and this part is re-executed; if this condition is satisfied, the second part is executed. The second part optimizes the overlapping width of the 2 × 1 composite coils to ensure stable QC after the adjacent Tx is activated simultaneously. 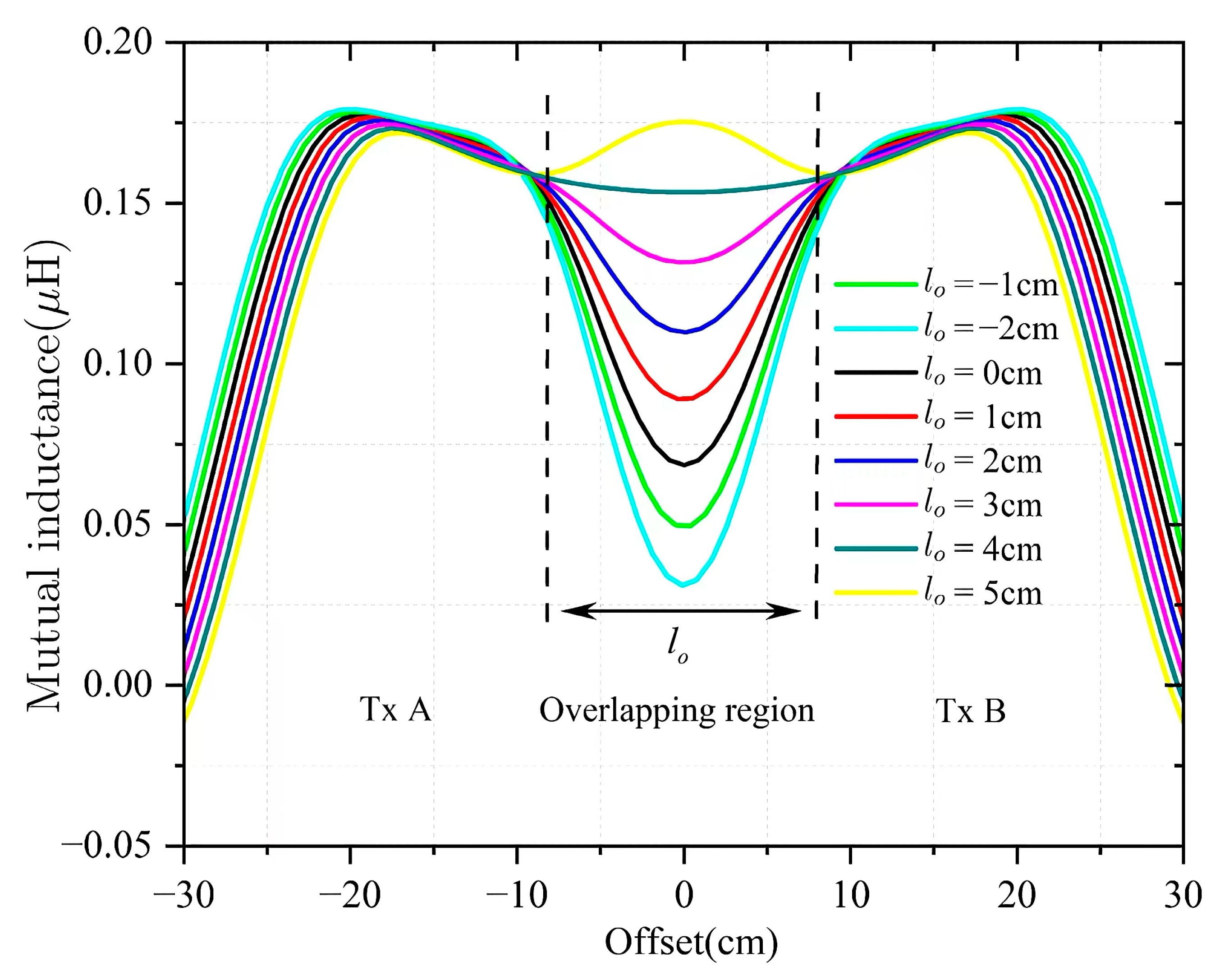Figure 8 shows that l_o has a potential effective optimization range, and setting l_o too large or too small will lead to unstable mutual inductance in overlapping areas. According to the mutual inductance characteristic of Tx, the optimal range of l_o is limited to half of l_pp, i.e., ${\mathit{l}}_{\mathit{omin}}=0$ and ${\mathit{l}}_{\mathit{omax}}={\displaystyle \frac{{\mathit{L}}_{\mathit{pp}}}{2}}$. Then, l_o is increased iteratively with a step size of ∆ l_o, and the α_Q of the composite coils obtained by each calculation is recorded. Upon completion of the program execution, the parameter settings corresponding to the maximum α_Q are identified as optimal for the current l_pp. Afterward, it is judged whether the program satisfies the exit condition ${\alpha }_{\mathit{Qset}}<{\alpha }_{\mathit{Q}}$, and if so, the program is terminated in advance; otherwise, the third part is executed. After correcting l_pp in an increment of ∆l_pp, the program goes back to the beginning of the first part and runs again with the new parameter of l_pp.

If there is no qualified parameter after the running, the third part will select the result with the largest α_Q under different values of l_pp as the output of Step 1 according to the records. Considering the practicability and installation limitations of Tx, the maximum l_pp of Tx is set in the range of 10 cm to 15 cm, i.e., l_ppmin = 10 cm and l_ppmax = 15 cm.

Step 2: The winding spacing t_w of Tx will be optimized under the balance of the coupling coefficient k_PS and material consumption D to ensure that the coil has a balanced coupling coefficient and an acceptable cost. The optimization scheme of Step 2 is demonstrated in Figure 11.

Step 2 first imports the output parameters of Step 1, including l_pp, l_o, and r_d of Tx. Since the composite coils have a larger self-inductance than the single Tx, its k_PS with Rx is lower, which is difficult to meet the strong coupling condition. Therefore, Step 2 will take the composite coils as the calculation object to simulate the limit condition. When the number of windings turns, N_P is initialized to 2, the program will calculate k_PS and D cyclically when N_P changes, and these results and the current coil parameters after each calculation are recorded. This process is continued after adding one turn until the winding cannot ensure that t_w satisfies the current and power constraints ${\mathit{t}}_{\mathit{wmin}}>2.5\mathrm{mm}$ and the cycle ends. Subsequently, the program will generate a two-dimensional Pareto front [43] according to the records, and based on this, the Pareto optimal solution is selected as the final output.

Based on the proposed optimization method, the final Tx coil parameters are listed in

Table 5. The design parameters of the Rx and Tx coils.

Coil	Parameter	Value	Coil	Parameter	Value
Tx	rd	0.25	Rx	ls	5 cm
	lP	14 cm		ws	2 cm
	lo	4.5 cm		Nl	3
	tw	0.378 cm		tl	0.15 mm
	NP	11		Ns	8
	D	21.56 cm
	wp	3.78 cm

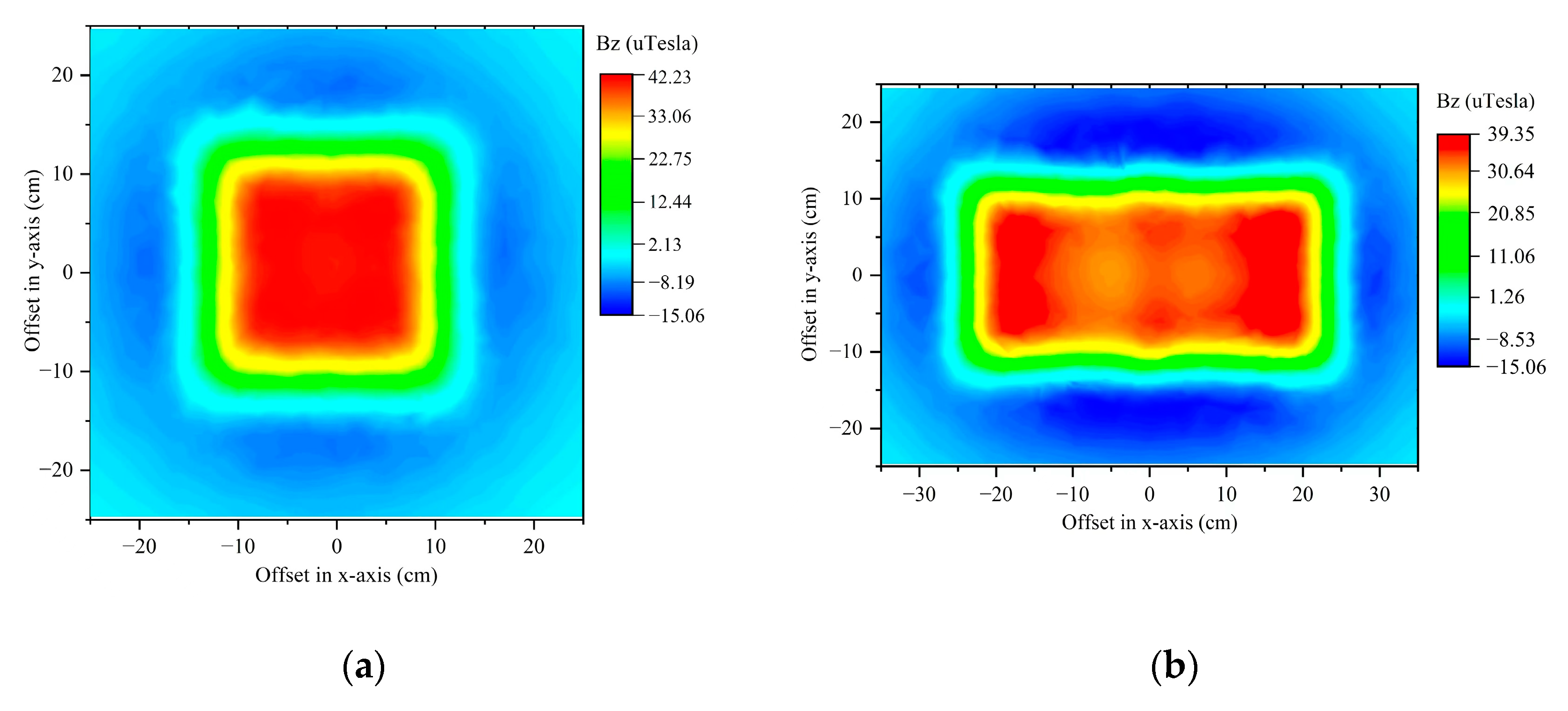
. Figure 12 shows the magnetic field generated by the Tx and composite coils on the Rx plane obtained by FEA, which is employed to verify the effectiveness of the Tx design. As the effective magnetic flux received by the Rx is a component of the vertical winding, Figure 12 illustrates the Z-axis component of the magnetic field strength. The loading current is set to 1A.

The results indicate that the Tx can provide a square QC area at the center of the winding and the composite coils can expand the QC area width to 41.6 cm, which leads to greater misalignment tolerance and a larger usable area. An Rx placed horizontally within this region has approximately constant magnetic flux reception.

The comparison with the distributed coil design in the previous literature is as follows: (i) The Tx in References [32,44] is internally configured with additional forward or reverse coupling windings, which results in a more complex structure and optimization process. The proposed Tx adopts a simple square structure that can be obtained by a low-cost procedure based on prior knowledge. (ii) Unlike the designs in [26,45] that only support a fixed number of Tx activations, considering the mutual inductance effect, in our design, adjacent Tx are allowed to be activated simultaneously to obtain a more flexible QC configuration, which allows TA to handle two random Rx. (iii) Different from the complex pitch layout adopted by the distributed coils in [25,46], the proposed planar array has concise expansion with bidirectional alignment, which contributes to high cost-effectiveness.

4.5. Rx Coil Design

The principal analysis indicates that the PT system can provide stable power transmission and high efficiency for two Rx coils in the strong coupling region. Therefore, the Rx should be designed to match the Tx to meet the necessary transmission conditions. The Rx should follow two design principles: (1) a high coil quality factor, which ensures a sufficiently low k_C and a larger movement tolerance, and (2) a compact size, although the large-sized Rx design has a larger surrounding area to capture more magnetic flux, and the excessive volume will affect its embedding into the application object. As the R_L and r₂ are fixed, increasing Q₀ will make the Rx coil have a greater self-inductance L_S, which has a negative effect on ${\mathit{k}}_{\mathit{PS}}={\mathit{M}}_{\mathit{PS}}/\sqrt{{\mathit{L}}_{\mathit{P}}{\mathit{L}}_{\mathit{S}}}$. A decrease in k_C results in a corresponding decrease in k_PS. In an ideal magnetic field with a uniform Z-axis component, each turn placed horizontally coaxially around an N-turn coil with an area of S satisfies

$${\mathit{R}}_{\mathit{m}}={\displaystyle \frac{{\mathit{M}}_{\mathit{PS}}}{\sqrt{{\mathit{L}}_{\mathit{S}}}}}\text{∝}{\mathit{C}}_1\sqrt{\mathit{S}}={\mathit{C}}_2,$$

(11)

where ${\mathit{R}}_{\mathit{m}}$ is the ratio of the mutual inductance to the root self-inductance, and${\mathit{C}}_1$, ${\mathit{C}}_2$, and ${\mathit{R}}_{\mathit{m}}$ are constants. Equation (11) can be simplified to ${\mathit{k}}_{\mathit{PS}}={\mathit{C}}_2/\sqrt{{\mathit{L}}_{\mathit{P}}}$, and L_S is not related to the value of ${\mathit{k}}_{\mathit{PS}}$. This indicates that, in the Z-axis quasi-uniform magnetic field provided by TA, the Rx should adopt a design with approximately the same surrounding area of each turn winding to improve ${\mathit{k}}_{\mathit{PS}}$ redundancy. To this end, an Rx coil with a multilayer winding structure is proposed in this study, as shown in Figure 5. Multilayer windings can arrange more windings in a limited space to increase mutual inductance. Also, this helps to reduce the width of the windings to make the situation close to the ideal one that the diameter of each turn is the same.

The values of r_m for different combinations of Rx layers and turns under unit vertical magnetic induction (B = 1 web/m²) are shown in

Table 6. $r_m(\sqrt{uH})$ Corresponding to different Rx design parameters under unit magnetic field strength.

Layers\Turns	6	7	8	9	10
2	0.408	0.469	0.441	0.463	0.460
3	0.471	0.449	0.489	0.457	0.476
4	0.469	0.434	0.459	0.465	0.444

. Considering the limited installation space of Rx, the number of stacked layers is set to no more than 4, the number of turns of each layer ranges from 5 to 10, and the maximum radius of Rx l_S is fixed at 5 cm. Obviously, according to Equation (11) and Table 6, a winding configured with three layers and eight turns per layer has maximized r_m, so it is chosen as the parameter setting of Rx. This design ensures that the winding width is less than 2 cm, and the overall height of the coil is less than 0.5 cm. The compact size makes it easy to install the R_X coil in various WPT applications.

5. Efficient Configuration of a WPT System with Multiple Tx

Although an appropriate Tx parameter setting ensures that sufficient and stable QC is provided to Rx, realizing automatic configuration of the charging area following the position of Rx is still the key to the efficient operation of the array WPT system. To this end, the following content introduces an Rx position detection method and a flexible operation strategy for TA. In addition, a modular resonant compensation circuit is applied to solve the detuning problem caused by the widely existing cross-inductance in the array.

5.1. Rx’s Position Detection Method and TA’s Operation Strategy

Equation (5) and Figure 2 show that, as the R_L is fixed in the PT system, i.e., as the Q₀ is constant, the operating frequency f is determined by k_PS. The larger the k_PS, the larger the offset ${\mathsf{\omega }}_{\mathit{d}}=|\mathsf{\omega }-{\mathsf{\omega }}_1|$ between f and the natural frequency of the system. Therefore, the degree of coupling between TA and Rx can be judged by measuring ω_d, which can be used to indicate the positional relationship between Rx and Tx. A larger ω_d indicates a smaller distance between the Rx and the activated Tx. This feature reveals the status of the system. An Rx position detection method and a TA operation scheme are shown in Figure 13, and

Table 7. The Rx position judgment table and the corresponding TA operation.

Label	Sn	Ss	Sd	The Position of Rx	The TA Operation Adopted
1	1	0	1	Overlapping area	#2 × 1
2	1	1	Not need	In Tx	#1 or #2 × 1
3	2	0	1	The Same overlapping area	#2 × 1
4	2	0	2	Not the same overlapping area	#2 × 2 × 1
5	2	1	0 + (4)	In Tx and its adjacent overlapping area	#2 × 1
6	2	1	1 + (4)	In Tx and non-adjacent overlapping areas	#1 + 2 × 1
7	2	2	Not need	Different Tx	#1 + 1 or #2 × 2 × 1

is a judgment table in the scheme, where S_n is the number of Rx, S_s is the result of independent scanning, and S_d is the result of combined scanning. This method can locate the position of Rx and activate the correct Tx by making a simple logical judgment on the value of ω_d.

In Figure 13, independent scanning indicates that the controller activates each Tx in turn and measures the steady-state frequency to calculate ω_d, respectively; composite scanning indicates that the controller activates each composite coil in turn, which is used to estimate the Rx at a particular position. Specifically, for the Rx in the center of the Tx overlapping area, i.e., at the winding edge of two adjacent Tx, there is a lower k_PS. In this case, it is easy to obtain wrong detection results by performing an independent scan. Therefore, an additional composite scan is applied in this study, and a larger measurement area ensures that all Rx can be identified. The counts of ${\mathsf{\omega }}_{\mathit{d}}=0$ in the independent scan and the composite scan are taken as scan results S_s and S_d, respectively. For the Rx inside the Tx, ${\mathit{S}}_{\mathit{S}}=1$ and ${\mathit{S}}_{\mathit{d}}=1$. For the Rx located in the Tx overlapping area, ${\mathit{S}}_{\mathit{S}}=0$ and ${\mathit{S}}_{\mathit{d}}=1$.

An independent scanning process is performed first. When ${\mathit{S}}_{\mathit{S}}={\mathit{S}}_{\mathit{n}}$, Rx is directly determined to be in the QC area provided by a single Tx, the system controls TA to activate the corresponding 1 Tx or 2 Tx, and the Tx can be non-adjacent. When ${\mathit{S}}_{\mathit{S}}={\mathit{S}}_{\mathit{n}}$, it indicates that there is an Rx in the overlapping area of adjacent Tx, then a composite scan is performed to cooperate with S_s to judge the position of the Rx, and all possible situations are listed in Table 7. Note that the additional parentheses in No. 5 and 6 indicate that the known Rx coils detected by the independent scan are repeated four times in the composite scan. Based on this strategy, TA can provide an effective power supply for at least one unit to an Rx at any position; also, it can selectively activate the composite coils to expand the misalignment tolerance and charging area and deal with the Rx coils located in the overlapping area. For two Rx, the execution of the strategy is based on the relative position of the Rx: one composite coil when closer or two non-adjacent composite coils (#1 + 1 or #1 + 2 × 1) when farther away.

5.2. Modular Compensation Circuit Configuration

The overlapping configuration of Tx results in cross-coupling inside the TA, which causes the self-inductance of the composite coil to be less than twice the Tx self-inductance. Therefore, L_P cannot be guaranteed to be an integral multiple of the self-inductance of Tx, which makes the simple compensation method of the series capacitor fail to obtain satisfactory results. To this end, a resonant compensation topology and switching method are proposed in this study, applied to each Tx coil to ensure a stable resonant frequency of the system during flexible unit operations. The equivalent circuits of the discrete compensation method are presented in Figure 14. The natural resonant angular velocity of the WPT system can be represented as

$${\mathsf{\omega }}_0={\displaystyle \frac{1}{\sqrt{{\mathit{L}}_{\mathit{P}}{\mathit{C}}_{\mathit{P}}}}}={\displaystyle \frac{1}{\sqrt{{\mathit{nL}}_{\mathit{A}}\frac{1}{\mathit{n}}{\mathit{C}}_{\mathit{A}}}}},$$

(12)

where L_A and C_A denote the self-inductance and compensation capacitance of each Tx, respectively. Equation (12) shows that, when n identical Tx are activated simultaneously, the capacitance of the discrete compensation is n times that of the total compensation, which can improve the margin of component selection for the resonant capacitor with a usually small capacity. Meanwhile, the independently connected capacitors bring the advantage of reduced current stress. When the activated Tx is cut off, the switch will short-circuit the Tx winding, which causes a large current in the loop, but the additional series capacitor will eliminate the potential overcurrent to avoid burning the winding.

Considering the cross-coupling between Tx, the equivalent self-inductance L_2×1 of the composite coil can be expressed as

$${\mathit{L}}_{2\text{×}1}={\mathit{L}}_{\mathit{A}}+{\mathit{L}}_{\mathit{B}}+{2\mathit{M}}_{\mathit{AB}},$$

(13)

where ${\mathit{M}}_{\mathit{AB}}$ is the cross-mutual inductance between Tx A and Tx B, and the value of ${\mathit{M}}_{\mathit{AB}}$ depends on l_o, according to Equation (10); L_A and L_B are the self-inductance of the two Tx windings, respectively. Self-define L_2×1 = aL_A, and since each Tx winding maintains the same direction in a series relationship, the cross-coefficient $1<\mathit{a}<2$. Based on this, a modular discrete compensation topology is proposed in this study, as shown in Figure 15. Here, Tx is connected in parallel with normally open contacts S_a and S_b, which have the capability of capacitive switching and coil activation. When the relay is powered off, the normally closed S_b ensures that Tx is always in a short-circuit state. Only when S_b is disconnected by the controller can Tx be activated normally, which helps to avoid safety hazards caused by accidents. When S_a is powered off, $({\displaystyle \frac{2}{\mathit{a}}}-1){\mathit{C}}_{\mathit{A}}$ and C_A are connected in parallel to form ${\displaystyle \frac{2}{\mathit{a}}}{\mathit{C}}_{\mathit{A}}$. As the S_a is disconnected, the Tx winding connects C_A in a series. It is worth mentioning that, in the proposed topology, only two switches are connected to each Tx, which significantly increases the manufacturing cost and control difficulty.

As more Tx are expanded and configured into a large array, the controller can still perform Rx position judgment and capacitor configuration. Its contribution is that the modular topology allows the expansion process to solve the frequency mismatch problem caused by cross-coupling without involving any complicated system changes, thus realizing flexible independent control of Tx.

6. Experiment

6.1. Experiment Setup

To verify the effectiveness of the design, an array WPT prototype with two Rx coils is built, as shown in Figure 16. The TA consists of four Tx experimental coils (#A, #B, #C, and #D). A full-bridge inverter is connected to TA for the power supply, and a current transformer-based detection circuit is configured to measure the input current and system operating frequency. Meanwhile, relays with normally open and normally closed contacts are used to make the module circuits for each Tx winding. Additionally, the logical judgment process of Rx position detection and the configuration strategy of Tx introduced in Section 5 are programmed in the STM32 controller. The prototype is powered by a 48 V DC power supply, which is compatible with batteries, wind energy, solar energy, and other clean energy sources, as well as DC microgrids in buildings.

6.2. Experiment Result

The l_o directly affects the cross-coupling of Tx, which is related to the parameters of the experimental coils and the accurate correction of capacitance. Considering this, verification of the composite coils is first conducted. The obtained results of the self-inductance ratio ${\mathit{L}}_{2\text{×}1}/{\mathit{L}}_{\mathit{A}}$ and the cross-inductance ratio ${\mathit{M}}_{\mathit{AB}}/{\mathit{L}}_{\mathit{A}}$ of the two overlapping Tx are shown in Figure 17. The derivation of the equivalent self-inductance ${\mathit{L}}_{2\text{×}1}$ of the composite coil, as given in Equation (13), is presented. The results indicate that, as l_o decreases, there is a reverse coupling ${\mathit{M}}_{\mathit{AB}}<0$ between the windings, which leads to ${\mathit{L}}_{2\text{×}1}/2{\mathit{L}}_{\mathit{A}}$. An excessively large l_o will produce forward coupling so that the equivalent self-inductance of the composite coil is greater than the sum of the self-inductances of the two Tx, i.e., ${\mathit{L}}_{2\text{×}1}/2{\mathit{L}}_{\mathit{A}}$. In this figure, the green symbol marks the position of the proposed Rx coil and ${\mathit{L}}_{2\text{×}1}/1.77{\mathit{L}}_{\mathit{A}}$, so the crossover coefficient is $\mathit{a}=1.77$. Note that, when $\mathit{a}<2$ of the prototypes, compared to #1 + 1 of the non-adjacent activated Tx, the activation of the adjacent Tx has a larger k_PS. This result indicates that the proposed nonfixed number Tx configuration is successful, which not only enlarges the effective charging area and QC size but also has a positive cross-coupling effect. Based on this, the Rx and Tx experimental coils are fabricated using the above-mentioned parameters, and the parameters of the coils, resonant compensation capacitors, and prototype are determined, as shown in

Table 8. The parameters and their values.

Parameter	Value	Parameter	Value
${\mathit{U}}_{\mathit{dc}}$	48 V	${\mathit{L}}_{\mathit{P}\mathit{D}}$	59.71 μH
${\mathit{L}}_{\mathit{PA}}$	59.52 μH	${\mathit{C}}_{\mathit{PD}1}$	3.01 nF
${\mathit{C}}_{\mathit{PA}1}$	2.99 nF	${\mathit{C}}_{\mathit{PD}2}$	0.39 nF
${\mathit{C}}_{\mathit{PA}2}$	0.39 nF	${\mathit{R}}_{\mathit{P}\mathit{D}}$	0.268 Ω
${\mathit{R}}_{\mathit{PA}}$	0.233 Ω	${\mathit{L}}_{\mathit{S}\mathit{A}}$	72.26 μH
${\mathit{L}}_{\mathit{P}\mathit{B}}$	59.33 μH	${\mathit{C}}_{\mathit{SA}1}$	2.49 nF
${\mathit{C}}_{\mathit{PB}1}$	3.02 nF	${\mathit{R}}_{\mathit{S}\mathit{A}}$	0.534 Ω
${\mathit{C}}_{\mathit{PB}2}$	0.39 nF	${\mathit{L}}_{\mathit{SB}}$	73.19 μH
${\mathit{R}}_{\mathit{P}\mathit{B}}$	0.264 Ω	${\mathit{C}}_{\mathit{SB}1}$	2.47 nF
${\mathit{L}}_{\mathit{P}\mathit{C}}$	57.65 μH	${\mathit{R}}_{\mathit{SB}}$	0.621 Ω
${\mathit{C}}_{\mathit{PC}1}$	3.01 nF	${\mathit{L}}_{2\text{×}1}$	105.41 μH
${\mathit{C}}_{\mathit{PC}2}$	0.38 nF	$\mathit{\alpha }$	1.77
${\mathit{R}}_{\mathit{P}\mathit{C}}$	0.257 Ω	${\mathit{f}}_0$	377 kHz

.

The X-axis offset results of the mutual inductance between each Tx, compound coil, and Rx are obtained by using the LCR instrument, as shown in Figure 18. It can be seen that the mutual inductance characteristics of the four experimental Tx coils are consistent with the simulation results. For an Rx with a diameter of 10 cm, the Tx and composite coils can provide 12 cm and 37 cm of misalignment tolerance with QC, respectively, and the misalignment tolerance ratio reaches 1.2 and 3.7, which is higher than that in the literature [32]. In addition, the system has a generalized power transfer region, which indicates that k_PS still satisfies strong coupling, and stable power transfer is still provided to Rx despite the decrease in the uniformity and the mutual inductance at the edges of the windings. For one Rx, the generalized allowable offsets for the Tx and compound coils are 19 cm and 41 cm, respectively. For two Rx, this area expands to 23 cm and 45 cm, respectively.

In this region, as the experimental load of the two Rx connections is ${\mathit{R}}_{\mathit{L}1}={\mathit{R}}_{\mathit{L}2}=6.67\mathsf{\Omega }$, the receiving coil can provide a maximum total output power of 163.58 W and maintain an efficiency of 84.26%.

The four Tx experimental coils are arranged according to Figure 19, and typical test points are set to verify the Rx position detection method. The results of the measured points and the estimated position of Rx are presented in

Table 9. The experimental results of the Rx position detection scheme.

Detection Scheme	Test Point	${\mathsf{\omega }}_{\mathit{d}}$ Corresponding to Different Tx Coils Value				Detected Rx Position	TA Operation
		A	B	C	D
Independent measurement	P1	19.7 kHz	0	0	0	A	#1
	P2	1.1 kHz, approximate to 0	0	0	0	None, continue composite measurements	to be determined
	P3	0	0	0	0	None, continue composite measurements	to be determined
		AB	CD	AC	BD
Composite measurement	P1	9.4 kHz	0	9.3 kHz	0	A	#1 or #2 × 1
	P2	10.8 kHz	0	0	0	The overlapping area between #A and #B	#2 × 1
	P3	0	0	0	0	Rx does not exist in TA	Close all Tx

. It can be observed that the prototype can accurately identify the Rx of different test points, and the corresponding TA operation type is selected. Note that, when the system works in the weakly coupled region, TA is always driven by a power supply equal to its natural frequency, and the output power is greatly increased, which will cause the system to be current-limited. Based on this phenomenon, the overcurrent condition is marked as ${\mathsf{\omega }}_{\mathit{d}}=0$ to maintain consistency with the logic judgment process in the proposed Rx detection method. Moreover, the individual test points located at P2 have slight measurement errors when they are measured independently, which leads to ${\mathsf{\omega }}_{\mathit{d}}\ne 0$. However, these weakly coupled Rx have very low ${\mathsf{\omega }}_{\mathit{d}}$ measurements, which can be filtered by simply setting the threshold so that the accuracy of the measurement scheme is not affected.

Table 9 shows the L_P corresponding to different TA operation types. The calculated coupling coefficient of the remaining TA structures based on the coupling coefficient ${\mathit{k}\text{’}}_{\mathit{PS}}$ of a single Tx is shown in

Table 10. The TA self-inductance ${\mathit{L}}_{\mathit{P}}$ and coupling coefficient ${\mathit{k}}_{\mathit{PS}}$ corresponding to different types of operations.

The Number of Rx	TA Operation	$\mathbf{Self}-\mathbf{Inductance}\mathbf{of}\mathbf{Composite}\mathbf{Coils}{\mathit{L}}_{\mathit{P}}$	Coupling Coefficient	The Number of Rx	TA Operation	$\mathbf{Self}-\mathbf{Inductance}\mathbf{of}\mathbf{Composite}\mathbf{Coils}{\mathit{L}}_{\mathit{P}}$	Coupling Coefficient
1	#1	${\mathit{L}}_{\mathit{A}}$	${\mathit{k}\text{’}}_{\mathit{PS}}={\displaystyle \frac{{\mathit{M}}_{\mathit{PS}}}{\sqrt{{\mathit{L}}_{\mathit{P}}{\mathit{L}}_{\mathit{S}}}}}$	2	#2 × 1	$1.77{\mathit{L}}_{\mathit{A}}$	$1.06{\mathit{k}\text{’}}_{\mathit{PS}}$
2	#1 + 1	$2{\mathit{L}}_{\mathit{A}}$	${\mathit{k}\text{’}}_{\mathit{PS}}$	2	#1 + 2 × 1	$2.77{\mathit{L}}_{\mathit{A}}$	$0.85{\mathit{k}\text{’}}_{\mathit{PS}}$
1	#2 × 1	$1.77{\mathit{L}}_{\mathit{A}}$	$0.75{\mathit{k}\text{’}}_{\mathit{PS}}$	2	#2 + 2 × 1	$3.54{\mathit{L}}_{\mathit{A}}$	$0.75{\mathit{k}\text{’}}_{\mathit{PS}}$

. It can be seen that activating more Tx will increase the self-inductance of TA and reduce k_PS such as operation types #1 and #2 × 1 for one Rx. Under the current Rx design, the operation type #2 × 1 driving one Rx and the operation type #2 × 2 × 1 driving two Rx have the lowest coupling coefficients. However, even with up to four Tx experimental coils activated, the k_PS remained at 0.75 times the baseline. The coupling coefficient characteristics and load characteristics corresponding to different operation types are calculated and tested, as shown in Figure 20. In this figure, the vertical bars mark the location of the proposed Rx design. The results indicate that k_PS of the prototype is greater than k_C no matter if charging one or two Rx at the same time. This result satisfies the strong coupling working condition of the PT system and ensures the validity of the Tx and Rx design. Additionally, all TA operation types have the same k_C curve, so k_C is independent of the number of activated Tx, which is consistent with the principal analysis result.

The above characteristics are meaningful for array WPT charging, i.e., the k_PS will not change with TA’s switching strategies and Tx design. Therefore, prototyping can focus on Rx to maintain a high level of k_PS and meet the expected maximum drive load or obtain the optimal Tx coil size under the Rx installation space constraints. This enables the array WPT and flexible configuration strategies to be applied to a wide range of charging scenarios at a low cost.

6.3. Comparison with Other WPT Systems

Enhancing the anti-offset ability of WPT systems offers significant advantages, including an expanded range of misalignment transmission and improved device flexibility, making it a key research focus in the current WPT field. To this end, this paper investigates the design of distributed coupler structures and multi-configuration activation methods. For the first time in the field of distributed coils, a novel PT-WPT technology is introduced, and a dual-load WPT system with high misalignment tolerance and constant output characteristics is proposed.

Table 11. Comparison between the proposed system and others.

Reference	Coil Structure	Number of Loads	Frequency	Output Power and Efficiency	Anti-Offset Ability
[47]	3D cylinder	2	20 kHz	Unstable	None
[41]	Planar coil	2	130 kHz, 200 kHz	Constant	None
[48]	Planar coil	1	1.293 MHz	Constant	None
[35]	Planar coil	1	85 kHz	Constant	General
[49]	Planar coil	2	6.78 MHz	Unstable	High
This work	Planar coil	2	400 kHz	Constant	High

contrasts the results in this paper with those in other published papers. Compared to existing research, this paper offers several advantages: based on PT symmetry theory, the transmission characteristics of the dual-load system are analyzed. Simulations and experiments validate the effectiveness of the proposed distributed misalignment-tolerant coupler design method, demonstrating the practicality of PT technology in addressing output disturbances caused by uneven coupling coefficients in misalignment transmission systems.

6.4. Error Analysis

The discrepancies between the experimental and theoretical data can be attributed to several factors: (1) The asymmetric coupling coil design in this study led to deviations in the coupling coefficients, though the system maintained PT symmetry. (2) The internal resistance of the proposed multilayer coil can only be minimized in practice, not entirely eliminated. (3) Tolerances in the coupling coil and compensation capacitor may cause shifts in the resonant frequency, while the use of multiple parallel capacitors can help mitigate this, potentially introducing capacitor errors. (4) The experimental measurement equipment also contributed to some degree of error.

Since this paper primarily explores the QC array of the dual-load WPT system under PT symmetry theory, the simulations were focused solely on the internal magnetic field of the proposed system. A limitation of the experiment is that it did not investigate the influence of external magnetic field environments on the system’s anti-offset ability. In this study, both the transmitting and receiving experimental coils were hand-wound, making it difficult to ensure consistent coupling performance. This resulted in considerable effort spent on fine-tuning the coil self-inductance and resonance capacitor matching. This aspect will be addressed in subsequent experiments.

6.5. Future Prospects

In terms of application scenarios, the system’s constant transmission characteristics serve as a fundamental consideration and starting point for optimizing QC performance in array coupling designs. For common misalignment-tolerant WPT applications, such as desktop office scenarios, logistics robots, and industrial scenarios like drone hovering charging, the Rx can be easily arranged in parallel at an equal distance from the transmitter array. The QC array further ensures that both maintain nearly identical coupling coefficients at any position, greatly enhancing the stability of the array charging system.

Experimental measurements revealed that adjustments to the overlap width between units are highly sensitive to the uniformity of the coupling performance. Therefore, future work may explore the use of custom coils along with a fixed-slot design to ensure secure installation and accurate array expansion. In addition, future work could consider incorporating ferromagnetic materials into the coil design to further enhance the coupling efficiency.

Additional solar charging panels [1] and renewable energy sources can be added to power the system in order to minimize the impact on the environment and achieve environmental sustainability. In terms of algorithms, WPT systems can also be improved by combining the particle swarm optimization (PSO) algorithm [50], genetic algorithm [51], pulse density modulation [52], etc. In the study of adaptive control of coils, coil optimization and improvement can also be carried out by machine learning [53], resulting in a system with stable transmission characteristics.

7. Conclusions

An array WPT system configured with multiple identical Tx extensions to power one or two Rx in the horizontal direction is presented in this paper. Compared with the existing work, the Tx not only has the ability of QC but also forms a composite coil with adjacent units to enhance the coverage of QC in the overlapping area. Meanwhile, the Tx can provide a QC area that is 1.44 times and 4.44 times the area of Rx for each Rx in independent and composite modes and a generalized transmission range of 3.61 times and 7.79 times, respectively. This indicates that the Rx can achieve a balance between the number of Tx activations and misalignment tolerance according to demand, and the flexibility of the charging area size and location is improved. Moreover, the potential of PT-WPT systems combined with array couplers is investigated in this paper. Analysis and verification are conducted under different types of TA operations and array configurations to ensure that the array design meets the strongly coupled transmission conditions of the PT system. The results confirm that the PT system for dual loads is successful. This is because the simpler system structure achieved by the Rx position detection method does not involve complex communication, and the special working critical conditions of the PT system simplify the design ideas and processes of the array.