Open-Set Automatic Modulation Recognition Based on Circular Prototype Learning and Denoising Diffusion Model
Abstract
1. Introduction
- Known Known Classes (KKCs): Classes for which we know that labeled samples exist during the training phase.
- Unknown Unknown Classes (UUCs): Classes for which no information is available during the training phase.
- How to fully utilize the KKC samples during training remains the key challenge of OSAMR, as only these samples are accessible. UUC samples that appear in testing are invisible during the training phase. According to the information bottleneck theory [20], any supervised learning is to extract minimal but sufficient statistics with respect to the objective function. Therefore, methods that adopt metric learning may suffer significant information loss. Meanwhile, methods attempting to simulate UUC samples offer limited and uncertain benefits as the number of UUCs is unknown and could be extremely large. The key to achieving OSAMR lies in fully extracting the information from the training samples.
- How to enhance the detection capability for UUCs while maintaining the recognition accuracy of KKCs. In open-set recognition tasks, improving the UUC detection performance is often achieved at the cost of the recognition accuracy of KKCs. In other words, an improvement in one of performance typically results in a decline in the other. The ideal open-set recognition technology would achieve a higher detection rate for UUCs at the expense of only a slight reduction in the KKC recognition accuracy.
- We enhance prototype learning by optimizing and fixing each prototype and encouraging samples to surround their corresponding prototype in a circular manner. This approach is termed circular prototype learning (CPL).
- We propose a diffusion model-based OSAMR strategy, where a certain amount of noise is randomly added to the samples. The probability of a sample belonging to the KKCs is proportional to the amount of noise removed by the diffusion model.
- We extend circle prototype learning with the diffusion model to more fully exploit the information in the training samples and jointly utilize both methods for the combined prediction of the samples.
2. Related Works
2.1. Traditional Automatic Modulation Recognition
2.2. Deep Learning-Based Automatic Modulation Recognition
2.3. Open-Set Recognition
3. Materials and Methods
3.1. Problem Definition
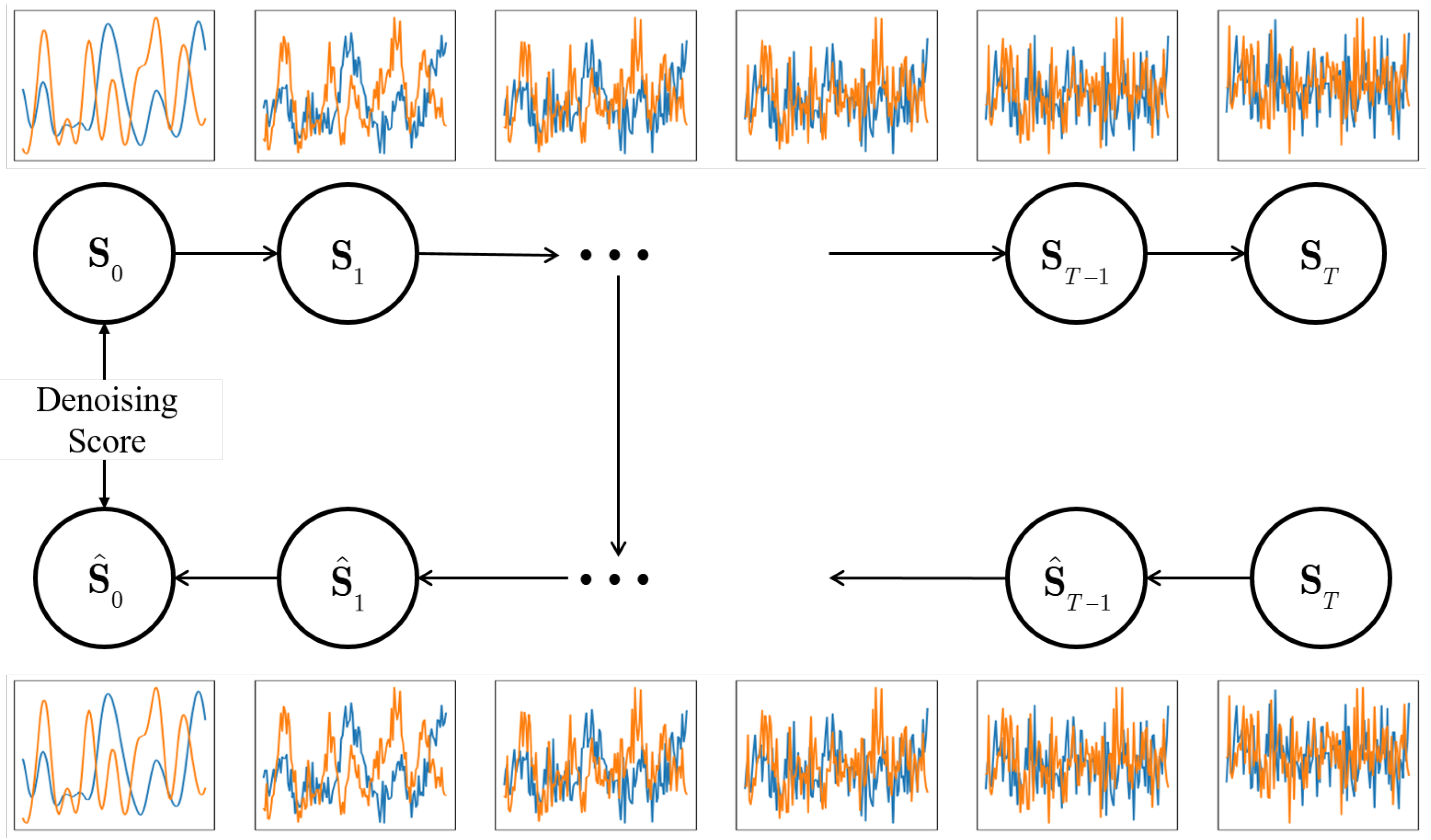
3.2. Overview
- Circular prototype learning for the close-set prediction and similarity score.
- Denoising diffusion model for denoising the score.
- Score integration and prediction calibration.
3.3. Circular Prototype Learning
3.3.1. Data Process and Encoding
3.3.2. Prototype Pre-Optimization
3.3.3. Circular Constraints
3.4. Denoising Score on Denoising Diffusion Model
3.4.1. -Objective Training
3.4.2. DDIM-Based Denoising Score
- Input and into to produce an estimate of the velocity as
- Calculate an estimation for at time step as
3.5. Class-Wise Threshold Co-Calibration
4. Results
4.1. Datasets
4.2. Experimental Setup
4.2.1. Environment
4.2.2. Parameters and Models
4.2.3. Evaluation Metrics
- AUROC. The receiver operating characteristic (ROC) curve is used to evaluate the prediction performance of a binary classification model. This is achieved by plotting the model’s True Positive Rate (TPR) against the False Positive Rate (FPR) at various threshold settings, resulting in a curve that describes the classification model’s performance. The AUROC refers to the area under the ROC curve, which is commonly used to quantify the overall performance of a binary classification model. Its value ranges from 0 to 1, with larger values indicating better classification performance.
- OSCR. This metric improves the AUROC by replacing the TPR value with the Correct Classification Rate (CCR) while keeping the same FPR. In this manner, the OSCR takes into accounts the classification performance of the OSR algorithm. The value of the OSCR also ranges from 0 to 1 and is commonly lower than the value of the AUROC for declines in classification accuracy.
- TNR. This metric indicates the detection rate for UUC samples. As the goal of the OSR is to detect UUC samples while remaining high in KKC recognition accuracy, the TNR is generally obtained under the condition that the TPR equals 95%.
4.3. Experimental Results
4.3.1. OSAMR Performance
4.3.2. Recognition on KKC and Detection on UUC
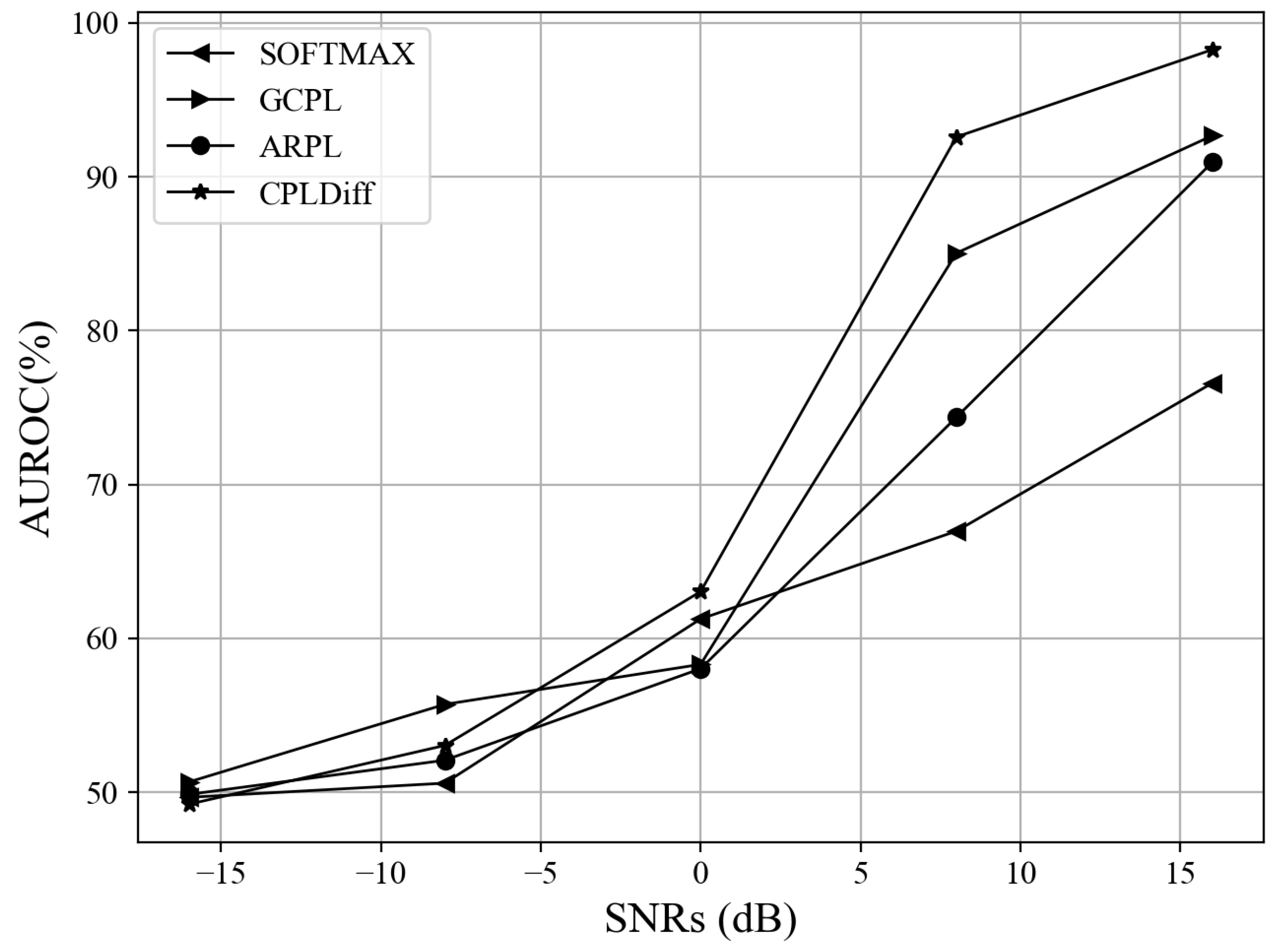
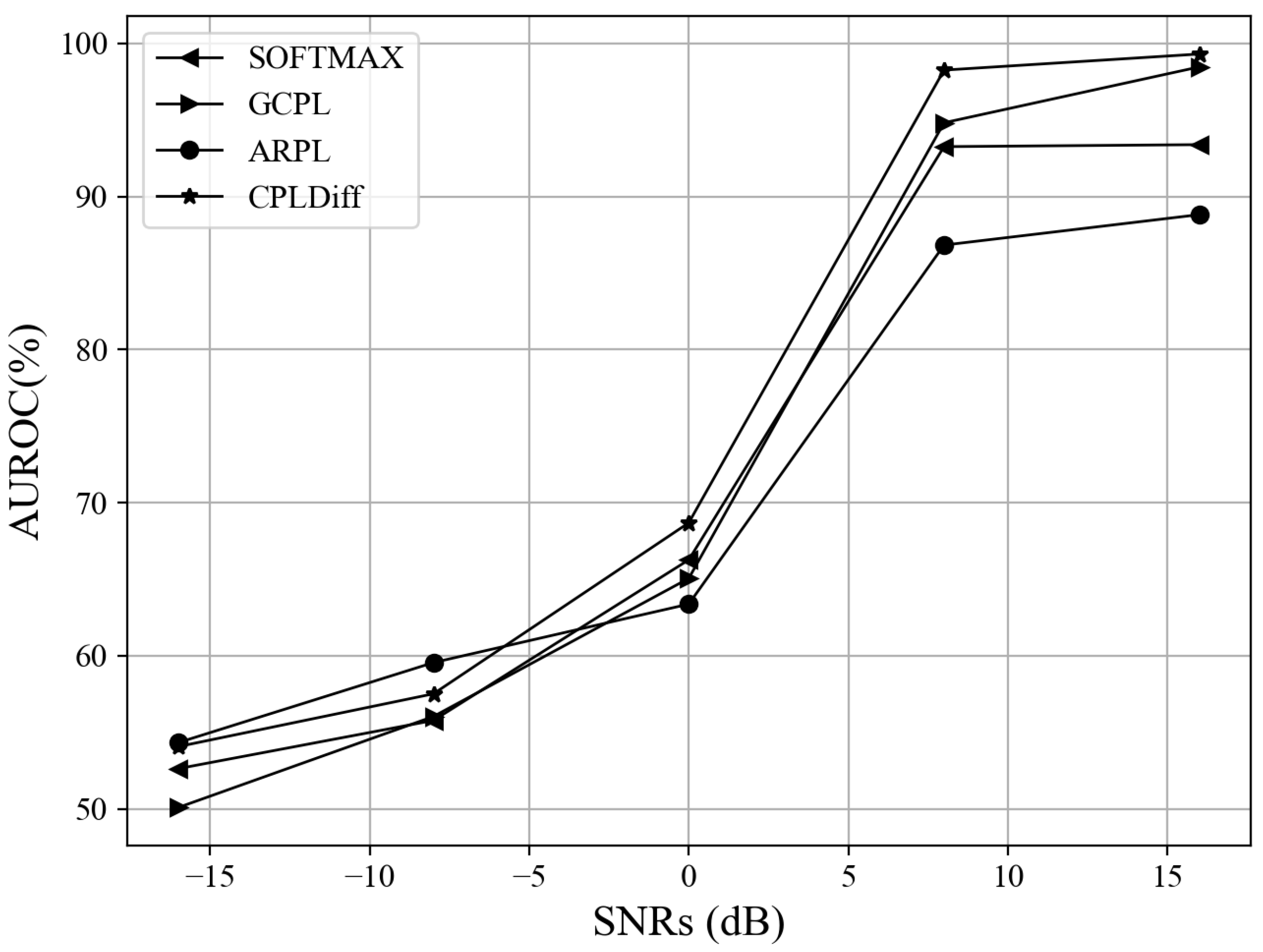
4.3.3. OSAMR Results at Different SNRs
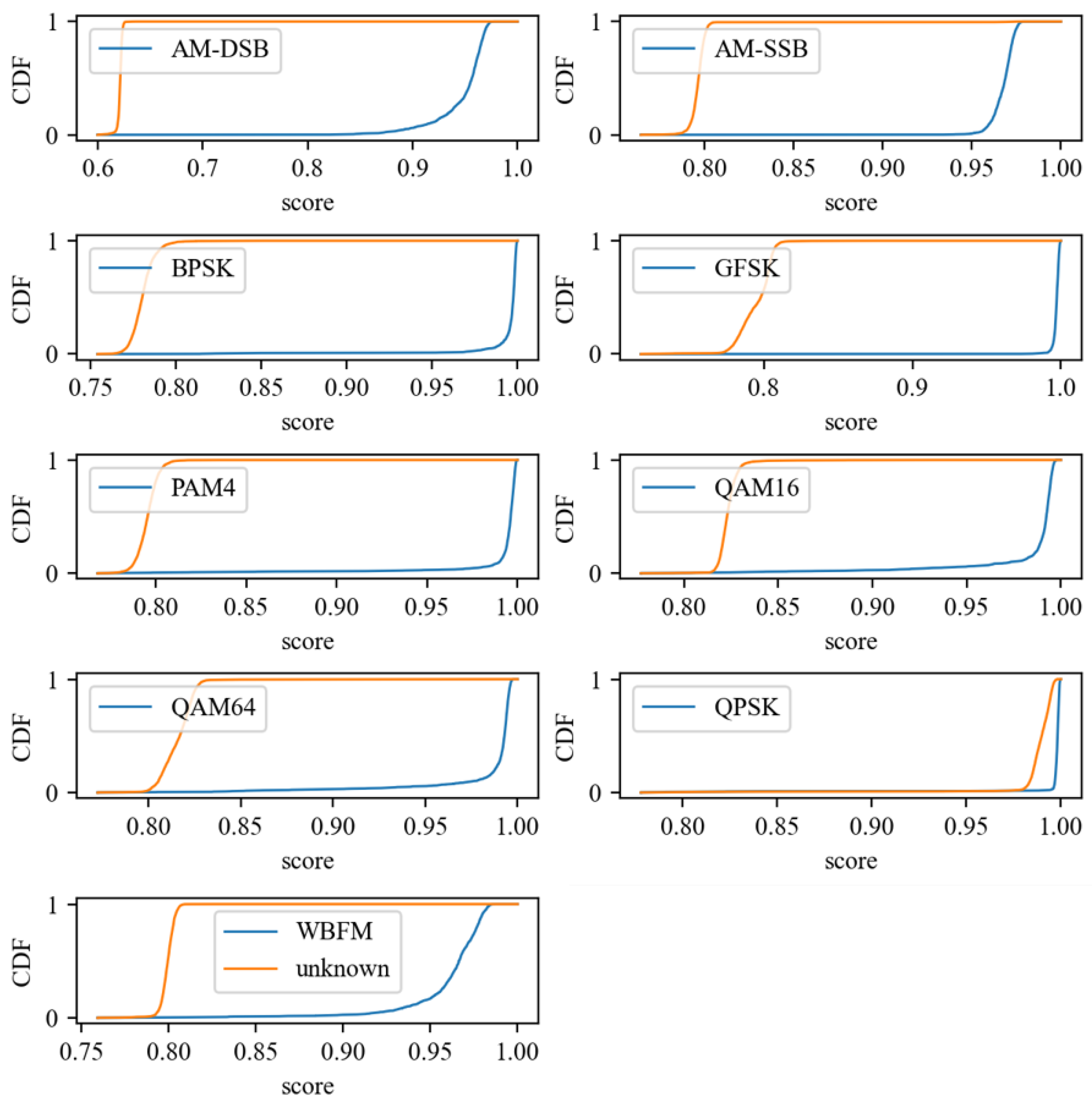
4.3.4. Visualization
4.4. Further Experiments
4.4.1. Effectiveness of DDM
4.4.2. Few-Shot Performance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Peng, S.; Sun, S.; Yao, Y.D. A survey of modulation classification using deep learning: Signal representation and data preprocessing. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 7020–7038. [Google Scholar] [CrossRef] [PubMed]
- Kulin, M.; Kazaz, T.; Moerman, I.; De Poorter, E. End-to-End Learning From Spectrum Data: A Deep Learning Approach for Wireless Signal Identification in Spectrum Monitoring Applications. IEEE Access 2018, 6, 18484–18501. [Google Scholar] [CrossRef]
- Di, C.; Ji, J.; Sun, C.; Liang, L. SOAMC: A Semi-Supervised Open-Set Recognition Algorithm for Automatic Modulation Classification. Electronics 2024, 13, 4196. [Google Scholar] [CrossRef]
- Zheng, S.; Chen, S.; Yang, L.; Zhu, J.; Luo, Z.; Hu, J.; Yang, X. Big data processing architecture for radio signals empowered by deep learning: Concept, experiment, applications and challenges. IEEE Access 2018, 6, 55907–55922. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Z.; Wang, X.; Meng, X.; Wu, Y.; Han, Z. Model-Based Data-Efficient Reinforcement Learning for Active Pantograph Control in High-Speed Railways. IEEE Trans. Transp. Electrif. 2024, 10, 2701–2712. [Google Scholar] [CrossRef]
- Meng, X.; Hu, G.; Liu, Z.; Wang, H.; Zhang, G.; Lin, H.; Sadabadi, M.S. Neural Network-Based Impedance Identification and Stability Analysis for Double-Sided Feeding Railway Systems. IEEE Trans. Transp. Electrif. 2024; early access. [Google Scholar] [CrossRef]
- Scheirer, W.J.; de Rezende Rocha, A.; Sapkota, A.; Boult, T.E. Toward open set recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 35, 1757–1772. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Wen, Z.; Long, Y.; Hong, Z.; Zheng, S.; Yu, L.; Chen, B.; Yang, X.; Shao, L. The importance of expert knowledge for automatic modulation open set recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 13730–13748. [Google Scholar] [CrossRef] [PubMed]
- Hu, G.; Meng, X.; Wang, X.; Liu, Z. A Novel Explainable Impedance Identification Method Based on Deep Learning for the Vehicle-grid System of High-speed Railways. IEEE Trans. Transp. Electrif. 2024; early access. [Google Scholar] [CrossRef]
- Meng, X.; Zhang, Q.; Liu, Z.; Hu, G.; Liu, F.; Zhang, G. Multiple Vehicles and Traction Network Interaction System Stability Analysis and Oscillation Responsibility Identification. IEEE Trans. Power Electron. 2024, 39, 6148–6162. [Google Scholar] [CrossRef]
- Pimentel, M.A.; Clifton, D.A.; Clifton, L.; Tarassenko, L. A review of novelty detection. Signal Process. 2014, 99, 215–249. [Google Scholar] [CrossRef]
- Zhou, H.; Bai, J.; Niu, L.; Xu, J.; Xiao, Z.; Zheng, S.; Jiao, L.; Yang, X. Electromagnetic signal classification based on class exemplar selection and multi-objective linear programming. Remote Sens. 2022, 14, 1177. [Google Scholar] [CrossRef]
- Masana, M.; Liu, X.; Twardowski, B.; Menta, M.; Bagdanov, A.D.; Van De Weijer, J. Class-incremental learning: Survey and performance evaluation on image classification. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 5513–5533. [Google Scholar] [CrossRef]
- Salehi, M.; Mirzaei, H.; Hendrycks, D.; Li, Y.; Rohban, M.H.; Sabokrou, M. A unified survey on anomaly, novelty, open-set, and out-of-distribution detection: Solutions and future challenges. arXiv 2021, arXiv:2110.14051. [Google Scholar]
- Chen, G.; Peng, P.; Wang, X.; Tian, Y. Adversarial reciprocal points learning for open set recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 8065–8081. [Google Scholar] [CrossRef]
- Yang, H.M.; Zhang, X.Y.; Yin, F.; Liu, C.L. Robust classification with convolutional prototype learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 19–21 June 2018; pp. 3474–3482. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. Adv. Neural Inf. Process. Syst. 2014, 27. [Google Scholar] [CrossRef]
- Oza, P.; Patel, V.M. C2ae: Class conditioned auto-encoder for open-set recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 18–20 June 2019; pp. 2307–2316. [Google Scholar]
- Yoshihashi, R.; Shao, W.; Kawakami, R.; You, S.; Iida, M.; Naemura, T. Classification-reconstruction learning for open-set recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 18–20 June 2019; pp. 4016–4025. [Google Scholar]
- Tishby, N.; Zaslavsky, N. Deep learning and the information bottleneck principle. In Proceedings of the 2015 IEEE Information Theory Workshop (ITW), Jerusalem, Israel, 26 April–1 May 2015; pp. 1–5. [Google Scholar]
- Huan, C.Y.; Polydoros, A. Likelihood methods for MPSK modulation classification. IEEE Trans. Commun. 1995, 43, 1493–1504. [Google Scholar] [CrossRef]
- Wang, L.X.; Ren, Y.J. Recognition of digital modulation signals based on high order cumulants and support vector machines. In Proceedings of the 2009 ISECS International Colloquium on Computing, Communication, Control, and Management, Sanya, China, 8–9 August 2009; Volume 4, pp. 271–274. [Google Scholar]
- Das, D.; Bora, P.K.; Bhattacharjee, R. Cumulant based automatic modulation classification of QPSK, OQPSK, 8-PSK and 16-PSK. In Proceedings of the 2016 8th International Conference on Communication Systems and Networks (COMSNETS), Bangalore, India, 5–10 January 2016; pp. 1–5. [Google Scholar]
- Xie, L.; Wan, Q. Cyclic feature-based modulation recognition using compressive sensing. IEEE Wirel. Commun. Lett. 2017, 6, 402–405. [Google Scholar] [CrossRef]
- O’Shea, T.J.; Roy, T.; Clancy, T.C. Over-the-air deep learning based radio signal classification. IEEE J. Sel. Top. Signal Process. 2018, 12, 168–179. [Google Scholar] [CrossRef]
- Chen, Z.; Cui, H.; Xiang, J.; Qiu, K.; Huang, L.; Zheng, S.; Chen, S.; Xuan, Q.; Yang, X. SigNet: A Novel Deep Learning Framework for Radio Signal Classification. IEEE Trans. Cogn. Commun. Netw. 2022, 8, 529–541. [Google Scholar] [CrossRef]
- Liu, X.; Yang, D.; El Gamal, A. Deep neural network architectures for modulation classification. In Proceedings of the 2017 51st Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 29 October–1 November 2017; pp. 915–919. [Google Scholar]
- Zhu, H.; Ma, Y.; Zhang, X.; Hao, C. Adaptive Denoising With Efficient Channel Attention for Automatic Modulation Recognition. In Proceedings of the ICC 2024-IEEE International Conference on Communications, Denver, CO, USA, 9–13 June 2024; pp. 2113–2118. [Google Scholar]
- Chen, J.; Teo, T.H.; Kok, C.L.; Koh, Y.Y. A Novel Single-Word Speech Recognition on Embedded Systems Using a Convolution Neuron Network with Improved Out-of-Distribution Detection. Electronics 2024, 13, 530. [Google Scholar] [CrossRef]
- Wang, Y.; Bai, J.; Xiao, Z.; Zhou, H.; Jiao, L. MsmcNet: A Modular Few-Shot Learning Framework for Signal Modulation Classification. IEEE Trans. Signal Process. 2022, 70, 3789–3801. [Google Scholar] [CrossRef]
- Chen, Y.; Shao, W.; Liu, J.; Yu, L.; Qian, Z. Automatic modulation classification scheme based on LSTM with random erasing and attention mechanism. IEEE Access 2020, 8, 154290–154300. [Google Scholar] [CrossRef]
- Hamidi-Rad, S.; Jain, S. Mcformer: A transformer based deep neural network for automatic modulation classification. In Proceedings of the 2021 IEEE Global Communications Conference (GLOBECOM), Madrid, Spain, 7–11 December 2021; pp. 1–6. [Google Scholar]
- Lei, J.; Li, Y.; Yung, L.Y.; Leng, Y.; Lin, Q.; Wu, Y.C. Understanding Complex-Valued Transformer for Modulation Recognition. IEEE Wirel. Commun. Lett. 2024, 13, 3523–3527. [Google Scholar] [CrossRef]
- Xu, J.; Luo, C.; Parr, G.; Luo, Y. A Spatiotemporal Multi-Channel Learning Framework for Automatic Modulation Recognition. IEEE Wirel. Commun. Lett. 2020, 9, 1629–1632. [Google Scholar] [CrossRef]
- Zhang, Z.; Luo, H.; Wang, C.; Gan, C.; Xiang, Y. Automatic modulation classification using CNN-LSTM based dual-stream structure. IEEE Trans. Veh. Technol. 2020, 69, 13521–13531. [Google Scholar] [CrossRef]
- Ruikar, J.D.; Park, D.H.; Kwon, S.Y.; Kim, H.N. HCTC: Hybrid Convolutional Transformer Classifier for Automatic Modulation Recognition. Electronics 2024, 13, 3969. [Google Scholar] [CrossRef]
- Deng, W.; Wang, X.; Huang, Z.; Xu, Q. Modulation Classifier: A Few-Shot Learning Semi-Supervised Method Based on Multimodal Information and Domain Adversarial Network. IEEE Commun. Lett. 2023, 27, 576–580. [Google Scholar] [CrossRef]
- Bai, J.; Wang, X.; Xiao, Z.; Zhou, H.; Ali, T.A.A.; Li, Y.; Jiao, L. Achieving efficient feature representation for modulation signal: A cooperative contrast learning approach. IEEE Internet Things J. 2024, 11, 16196–16211. [Google Scholar] [CrossRef]
- Bai, J.; Liu, X.; Wang, Y.; Xiao, Z.; Chen, F.; Zhou, H.; Jiao, L. Integrating Prior Knowledge and Contrast Feature for Signal Modulation Classification. IEEE Internet Things J. 2024, 11, 21461–21473. [Google Scholar] [CrossRef]
- Rajendran, S.; Meert, W.; Giustiniano, D.; Lenders, V.; Pollin, S. Deep learning models for wireless signal classification with distributed low-cost spectrum sensors. IEEE Trans. Cogn. Commun. Netw. 2018, 4, 433–445. [Google Scholar] [CrossRef]
- Geng, C.; Huang, S.j.; Chen, S. Recent advances in open set recognition: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 43, 3614–3631. [Google Scholar] [CrossRef] [PubMed]
- Hendrycks, D.; Gimpel, K. A baseline for detecting misclassified and out-of-distribution examples in neural networks. arXiv 2016, arXiv:1610.02136. [Google Scholar]
- Bendale, A.; Boult, T.E. Towards open set deep networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016; pp. 1563–1572. [Google Scholar]
- Zhou, D.W.; Ye, H.J.; Zhan, D.C. Learning placeholders for open-set recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Virtual, 21–25 June 2021; pp. 4401–4410. [Google Scholar]
- Chen, G.; Qiao, L.; Shi, Y.; Peng, P.; Li, J.; Huang, T.; Pu, S.; Tian, Y. Learning open set network with discriminative reciprocal points. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part III 16. Springer: Berlin/Heidelberg, Germany, 2020; pp. 507–522. [Google Scholar]
- Ge, Z.; Demyanov, S.; Chen, Z.; Garnavi, R. Generative openmax for multi-class open set classification. arXiv 2017, arXiv:1707.07418. [Google Scholar]
- Neal, L.; Olson, M.; Fern, X.; Wong, W.K.; Li, F. Open set learning with counterfactual images. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 613–628. [Google Scholar]
- Shah, S.A.W.; Abed-Meraim, K.; Al-Naffouri, T.Y. Multi-modulus algorithms using hyperbolic and Givens rotations for blind deconvolution of MIMO systems. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), South Brisbane, Australia, 19–24 April 2015; pp. 2155–2159. [Google Scholar]
- Ho, J.; Jain, A.; Abbeel, P. Denoising diffusion probabilistic models. Adv. Neural Inf. Process. Syst. 2020, 33, 6840–6851. [Google Scholar]
- Song, J.; Meng, C.; Ermon, S. Denoising diffusion implicit models. arXiv 2020, arXiv:2010.02502. [Google Scholar]
- Qiao, T.; Zhang, J.; Xu, D.; Tao, D. Mirrorgan: Learning text-to-image generation by redescription. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 18–20 June 2019; pp. 1505–1514. [Google Scholar]
- Ho, J.; Chan, W.; Saharia, C.; Whang, J.; Gao, R.; Gritsenko, A.; Kingma, D.P.; Poole, B.; Norouzi, M.; Fleet, D.J.; et al. Imagen video: High definition video generation with diffusion models. arXiv 2022, arXiv:2210.02303. [Google Scholar]
- Zhang, C.; Zhang, C.; Zheng, S.; Zhang, M.; Qamar, M.; Bae, S.H.; Kweon, I.S. A survey on audio diffusion models: Text to speech synthesis and enhancement in generative ai. arXiv 2023, arXiv:2303.13336. [Google Scholar]
- Schneider, F.; Kamal, O.; Jin, Z.; Schölkopf, B. Moûsai: Efficient text-to-music diffusion models. In Proceedings of the 62nd Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), Bangkok, Thailand, 11–16 August 2024; pp. 8050–8068. [Google Scholar]
- Huang, H.; Wang, Y.; Hu, Q.; Cheng, M.M. Class-specific semantic reconstruction for open set recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 4214–4228. [Google Scholar] [CrossRef]
- O’Shea, T.J.; Corgan, J.; Clancy, T.C. Convolutional radio modulation recognition networks. In Proceedings of the Engineering Applications of Neural Networks: 17th International Conference, EANN 2016, Aberdeen, UK, 2–5 September 2016; Proceedings 17. Springer: Berlin/Heidelberg, Germany, 2016; pp. 213–226. [Google Scholar]
- Loshchilov, I. Decoupled weight decay regularization. arXiv 2017, arXiv:1711.05101. [Google Scholar]
- Chen, J.; Zhao, C.; Huang, X.; Wu, Z. Data Augmentation Aided Automatic Modulation Recognition Using Diffusion Model. In Proceedings of the 2024 IEEE Wireless Communications and Networking Conference (WCNC), Dubai, United Arab Emirates, 21–24 April 2024; pp. 1–6. [Google Scholar]




| Task | Training | Testing | Goal |
|---|---|---|---|
| Close-set AMR | KKCs | KKCs | classifying KKCs |
| Open-set AMR | KKCs | KKCs and UUCs | identifying KKCs and rejecting UUCs |
| Items | RadioML2016.10a | RadioML2016.04c |
|---|---|---|
| Max carrier frequency offset | 50 Hz | 100 Hz |
| Max sampling rate offset | 500 Hz | 1000 Hz |
| Energy normalization | Yes | No |
| Number of modulation schemes | 11 | 11 |
| Signal shape | ||
| SNR range (dB) | −20∼18, with an interval of 2 | −20∼18, with an interval of 2 |
| Number of signals per SNR | 11,000 | 8103 |
| Number of sinusoids used in frequency selective fading | 8 | 8 |
| Channel environment | Additive Gaussian white noise, selective fading (Rician + Rayleigh), Center Frequency Offset (CFO), Sample Rate Offset (SRO) | Additive Gaussian white noise, selective fading (Rician + Rayleigh), Center Frequency Offset (CFO), Sample Rate Offset (SRO) |
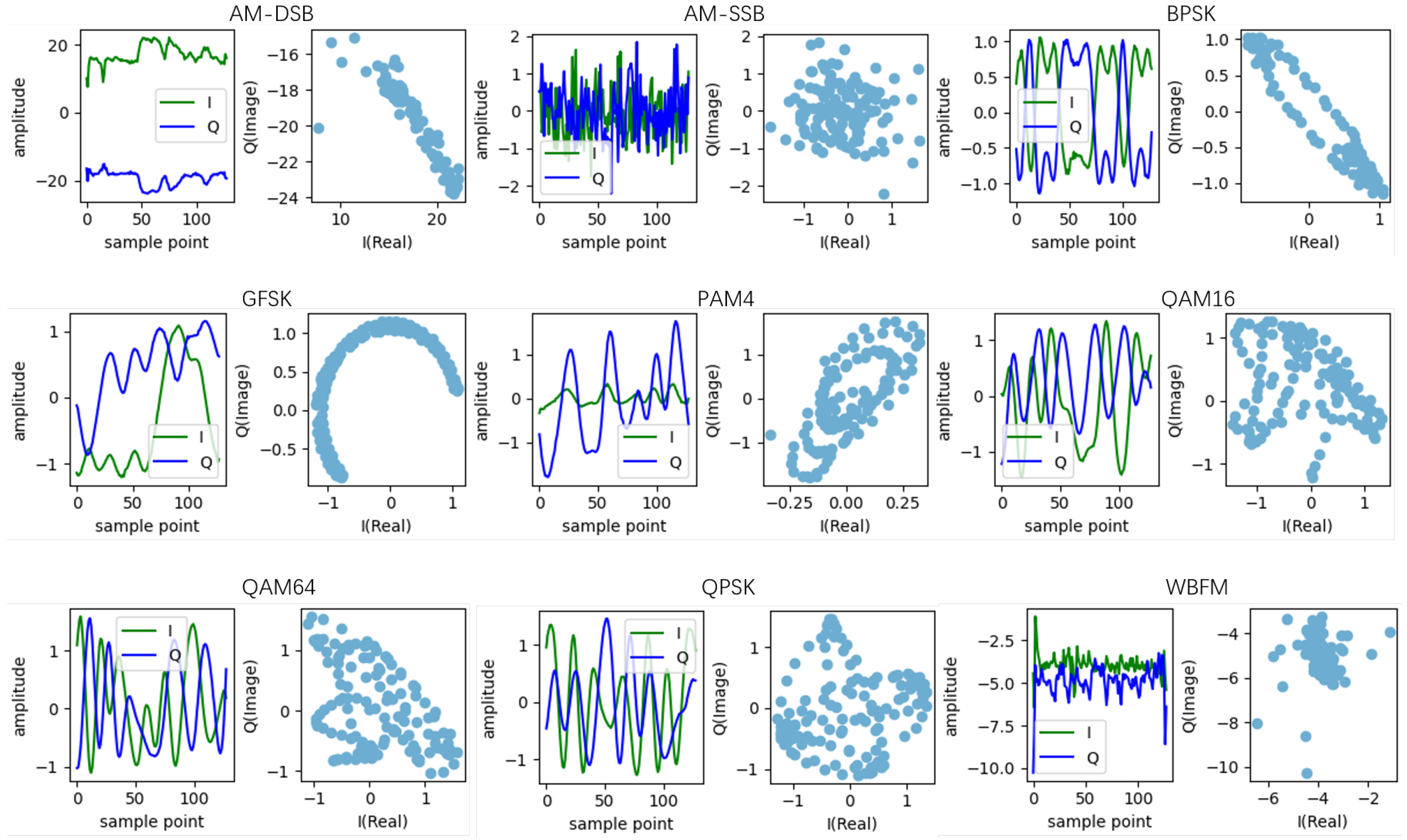
| KKCs | AM-DSB, AM-SSB, BPSK, GFSK, PAM4, QAM16, QAM64, QPSK, WBFM | AM-DSB, AM-SSB, BPSK, GFSK, PAM4, QAM16, QAM64, QPSK, WBFM |
| UUCs | 8PSK, CPFSK | 8PSK, CPFSK |
| Training size–testing size | 7:3 class-wise | 7:3 class-wise |
| Class | SoftMax | GCPL | ARPL | ARPL+CS | CPLDIff |
|---|---|---|---|---|---|
| AM-DSB 1 | 100.0 | 100.0 | 100.0 | 97.87 | 100.0 |
| AM-SSB | 99.74 | 99.72 | 99.77 | 98.53 | 99.96 |
| BPSK | 99.91 | 99.97 | 99.99 | 99.93 | 99.99 |
| GFSK | 99.99 | 100.0 | 99.97 | 99.99 | 100.0 |
| PAM4 | 99.52 | 99.94 | 99.92 | 99.40 | 99.57 |
| QAM16 | 72.27 | 99.65 | 99.35 | 67.59 | 99.30 |
| QAM64 | 99.48 | 99.92 | 99.88 | 99.72 | 99.56 |
| QPSK | 97.94 | 90.44 | 89.67 | 91.84 | 97.74 |
| WBFM | 99.99 | 100.0 | 100.0 | 96.62 | 99.74 |
| AUROC 2 | 76.59 | 92.67 | 90.94 | 63.96 | 98.26 |
| OSCR | 71.68 | 81.86 | 83.49 | 59.89 | 90.85 |
| TNR 3 | 31.41 | 75.12 | 65.04 | 31.62 | 96.95 |
| Class | SoftMax | GCPL | ARPL | ARPL+CS | CPLDIff |
|---|---|---|---|---|---|
| AM-DSB | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 |
| AM-SSB | 99.90 | 99.90 | 99.94 | 99.91 | 99.94 |
| BPSK | 99.99 | 99.93 | 99.99 | 99.99 | 99.99 |
| GFSK | 97.83 | 100.0 | 99.69 | 99.97 | 100.0 |
| PAM4 | 99.89 | 99.62 | 99.97 | 99.94 | 99.86 |
| QAM16 | 93.20 | 98.70 | 98.48 | 98.25 | 98.39 |
| QAM64 | 98.66 | 98.77 | 98.69 | 98.11 | 97.09 |
| QPSK | 99.27 | 98.40 | 89.09 | 92.55 | 99.26 |
| WBFM | 100.0 | 99.99 | 100.0 | 99.99 | 99.97 |
| AUROC | 93.39 | 98.47 | 88.82 | 91.21 | 99.31 |
| OSCR | 92.13 | 96.12 | 87.10 | 89.96 | 97.83 |
| TNR | 72.89 | 94.98 | 75.60 | 76.00 | 98.59 |
| Metrics | RML2016.10a | RML2016.04c | ||
|---|---|---|---|---|
| CPL | CPLDiff | CPL | CPLDiff | |
| AUROC | 86.17 | 98.26 | 89.08 | 99.31 |
| OSCR | 79.48 | 90.85 | 87.79 | 97.83 |
| TNR | 67.66 | 96.93 | 76.15 | 98.59 |
| Method | RML2016.10a | RML2016.04c | ||||
|---|---|---|---|---|---|---|
| Precision | Recall | F1 Score | Precision | Recall | F1 Score | |
| SoftMax | 81.02 | 81.31 | 81.13 | 93.96 | 94.23 | 93.76 |
| GCPL | 80.27 | 80.41 | 78.85 | 91.41 | 91.84 | 91.21 |
| ARPL | 80.95 | 79.33 | 77.95 | 90.44 | 90.17 | 90.77 |
| ARPL+CS | 75.48 | 75.59 | 75.30 | 92.62 | 92.64 | 92.42 |
| CPL | 81.98 | 81.69 | 81.24 | 93.36 | 93.92 | 93.32 |
| CPL+ | 82.29 | 81.89 | 81.33 | 93.77 | 94.12 | 93.32 |
| Method | RML2016.10a | RML2016.04c | ||||
|---|---|---|---|---|---|---|
| AUROC | OSCR | TNR | AUROC | OSCR | TNR | |
| Softmax | 48.17 | 38.68 | 11.67 | 80.53 | 76.43 | 44.16 |
| GCPL | 69.02 | 55.94 | 19.69 | 87.52 | 82.73 | 30.33 |
| ARPL | 36.81 | 29.19 | 2.000 | 51.96 | 47.49 | 2.534 |
| ARPL+CS | 32.58 | 23.96 | 0.986 | 60.90 | 57.14 | 8.380 |
| CPLDiff | 90.45 | 73.44 | 51.96 | 92.69 | 87.11 | 74.65 |
| CPLDiff+ | 94.69 | 77.49 | 66.63 | 95.85 | 90.43 | 80.98 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, H.; Xie, X.; Cheng, X.; Bai, J. Open-Set Automatic Modulation Recognition Based on Circular Prototype Learning and Denoising Diffusion Model. Electronics 2025, 14, 430. https://doi.org/10.3390/electronics14030430
Niu H, Xie X, Cheng X, Bai J. Open-Set Automatic Modulation Recognition Based on Circular Prototype Learning and Denoising Diffusion Model. Electronics. 2025; 14(3):430. https://doi.org/10.3390/electronics14030430
Chicago/Turabian StyleNiu, Huiying, Xun Xie, Xiaojing Cheng, and Jing Bai. 2025. "Open-Set Automatic Modulation Recognition Based on Circular Prototype Learning and Denoising Diffusion Model" Electronics 14, no. 3: 430. https://doi.org/10.3390/electronics14030430
APA StyleNiu, H., Xie, X., Cheng, X., & Bai, J. (2025). Open-Set Automatic Modulation Recognition Based on Circular Prototype Learning and Denoising Diffusion Model. Electronics, 14(3), 430. https://doi.org/10.3390/electronics14030430






