Accurate Joint Estimation of Position and Orientation Based on Angle of Arrival and Two-Way Ranging of Ultra-Wideband Technology
Abstract
1. Introduction
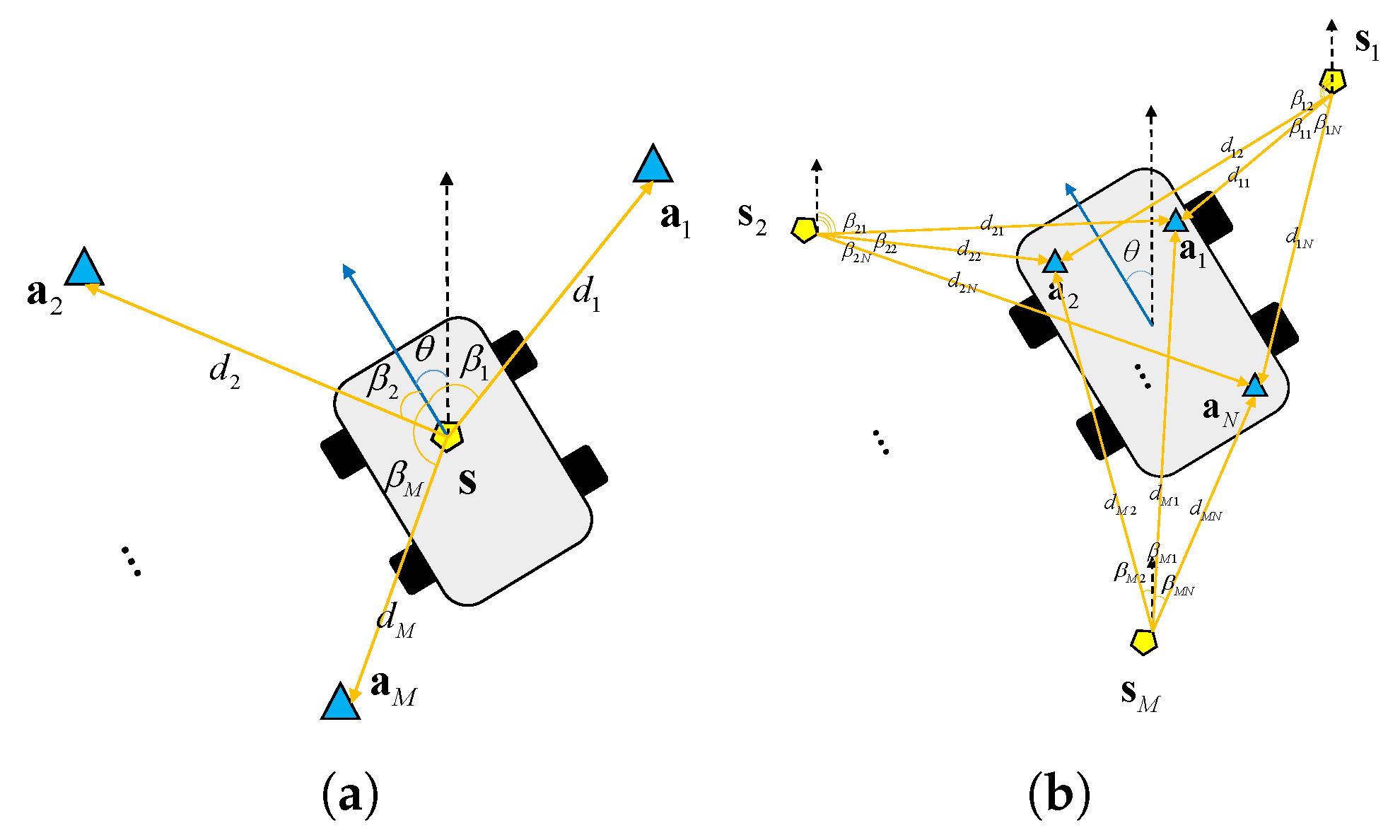
2. Signal Model and Problem Formulation
3. SL Algorithm Based on Constrained Weighted Least Squares
| Algorithm 1 SL-CWLS. |
Input: Measured AOAs , DS-TWRs , noise variance . Output: Estimation of , including location and rotation . Initialization from (15). for do Construct the Lagrange function of (31) Construct Karush–Kuhn–Tucker condition. ,,,,. Newton direction solution with Karush–Kuhn–Tucker condition. Update variables. , stop condition. or . end for |
4. Constrained Cramér–Rao Lower Bound
5. Computational Complexity Analysis
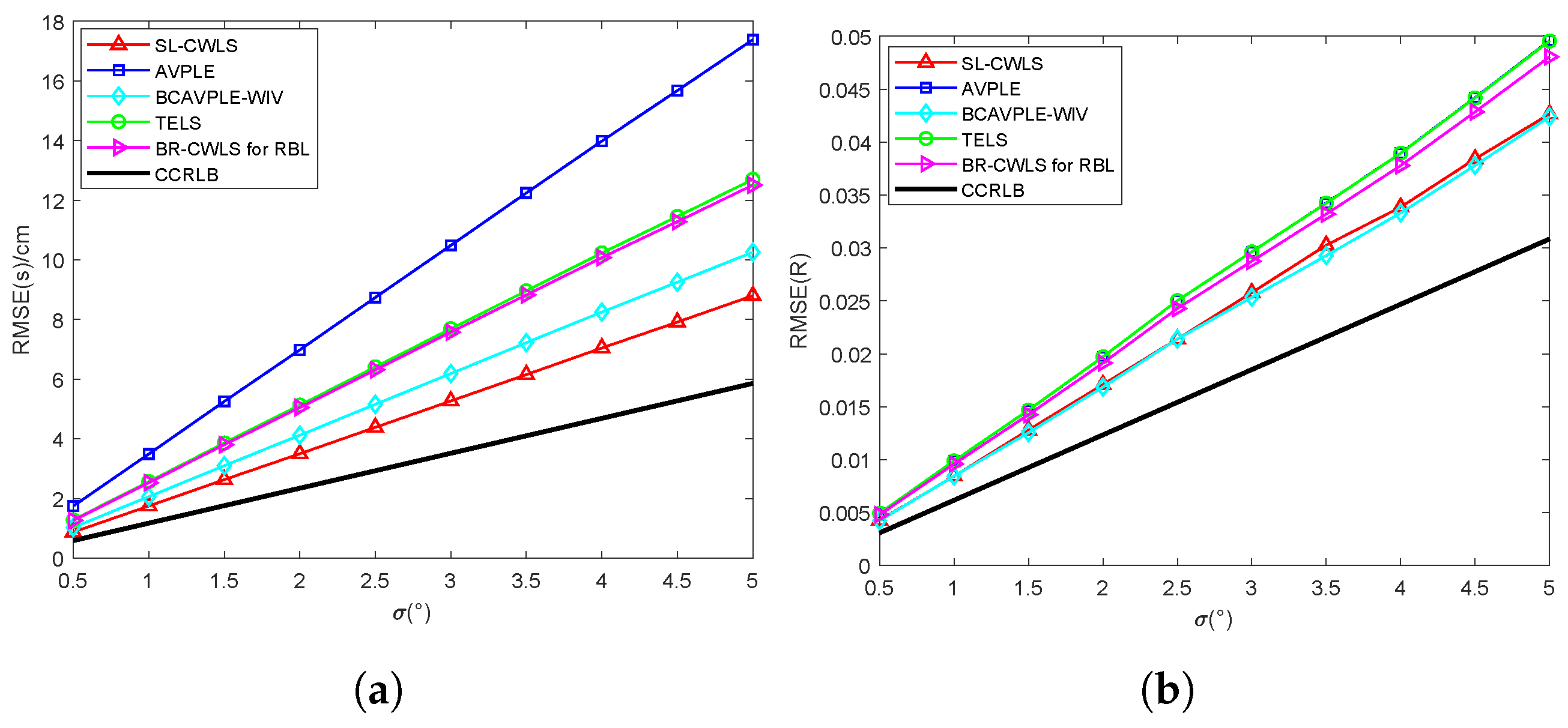
6. Simulation Evaluation
6.1. Static Points Tests
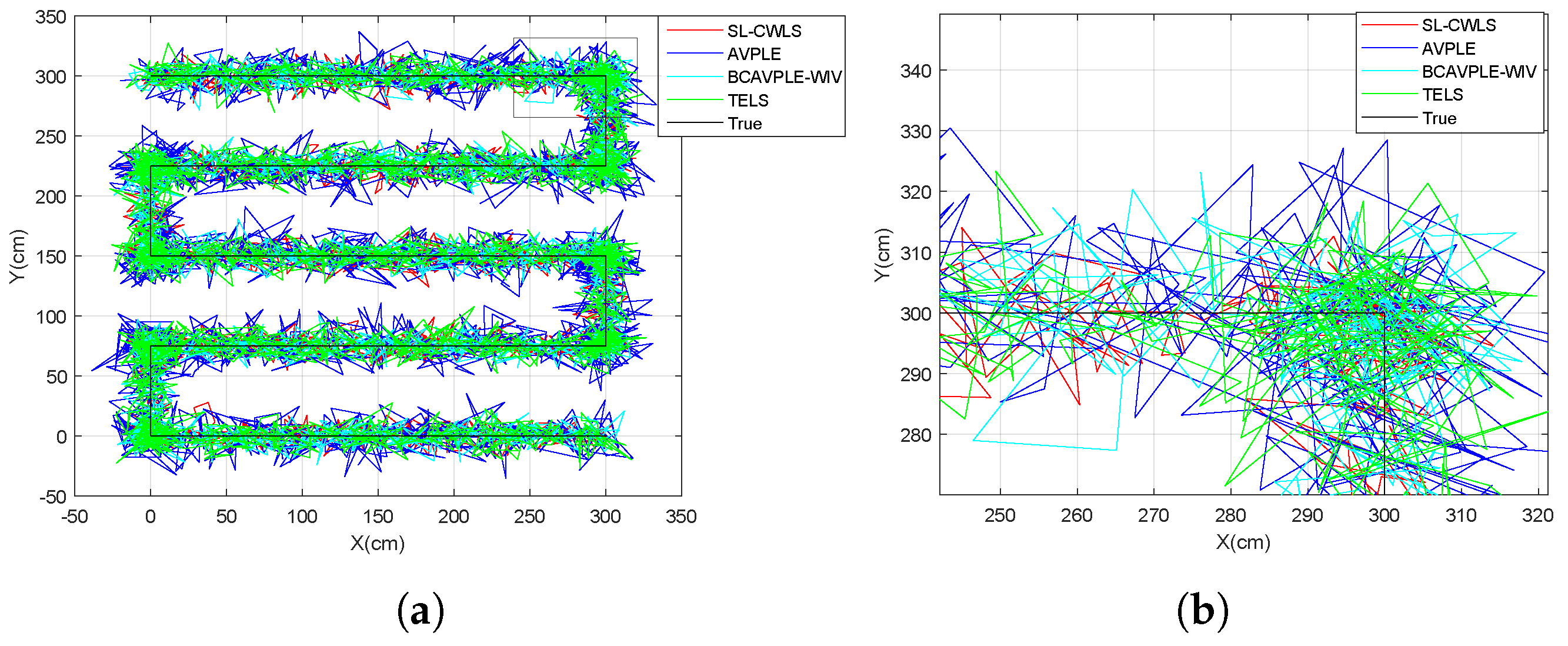
6.2. Dynamic Trajectory Test
7. Real-World Experiment
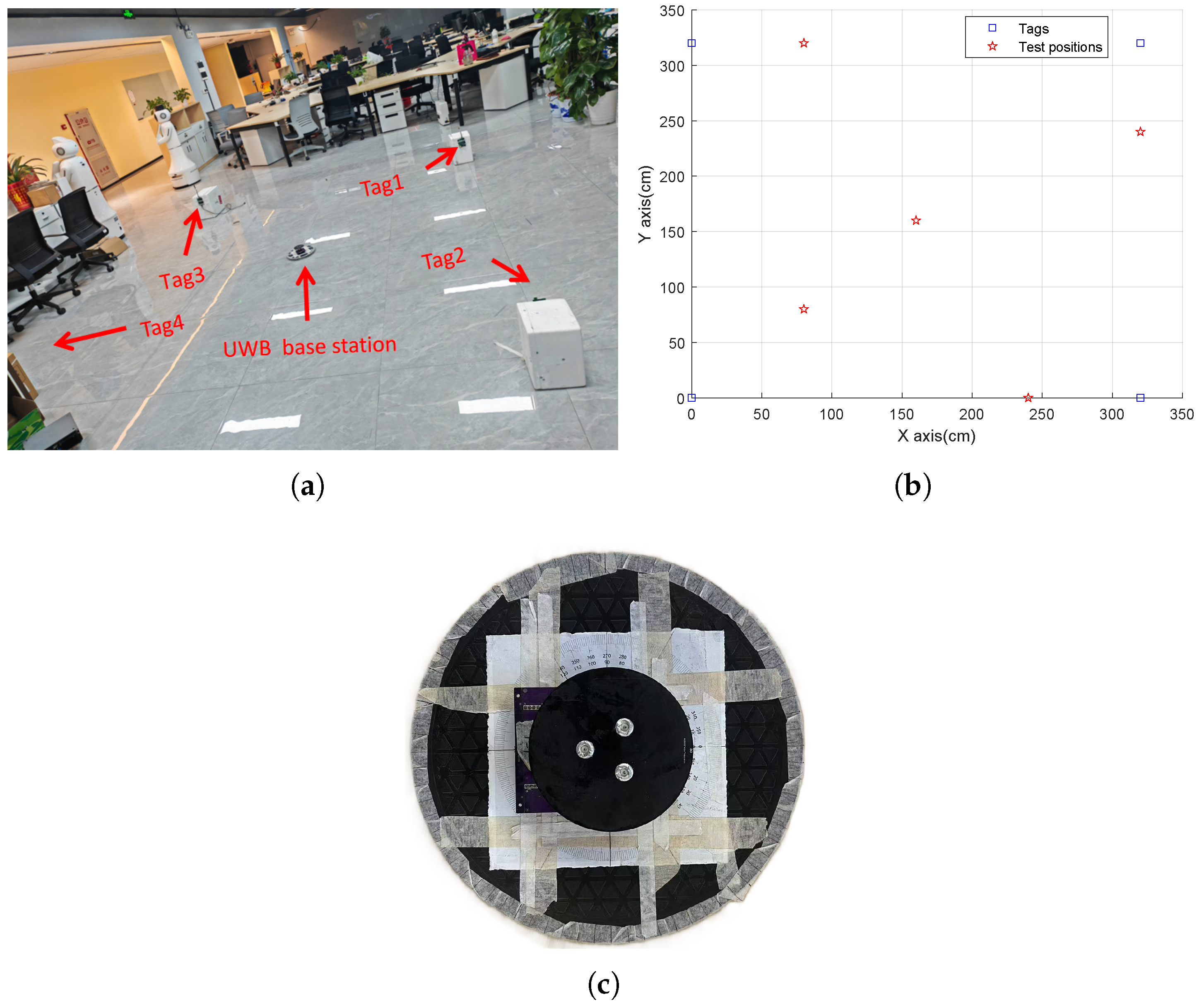
7.1. Experiment Settings
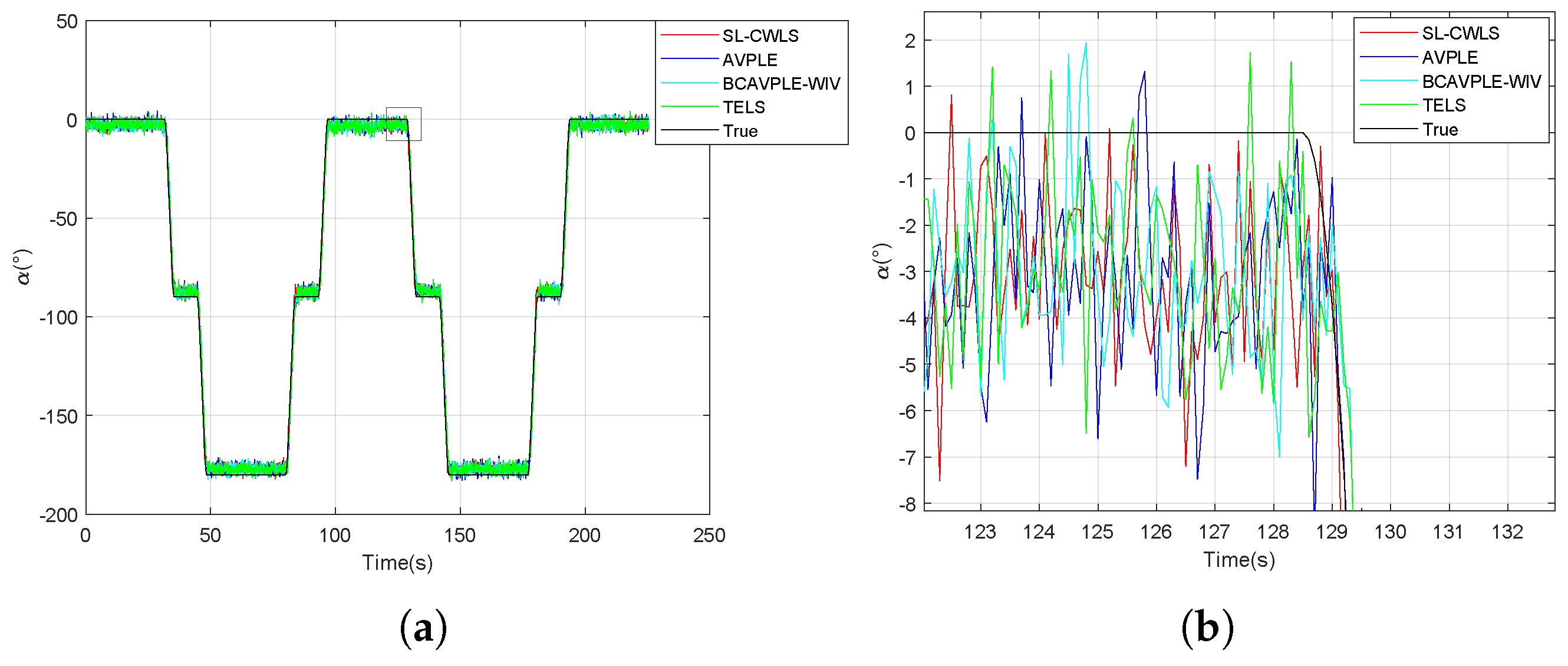
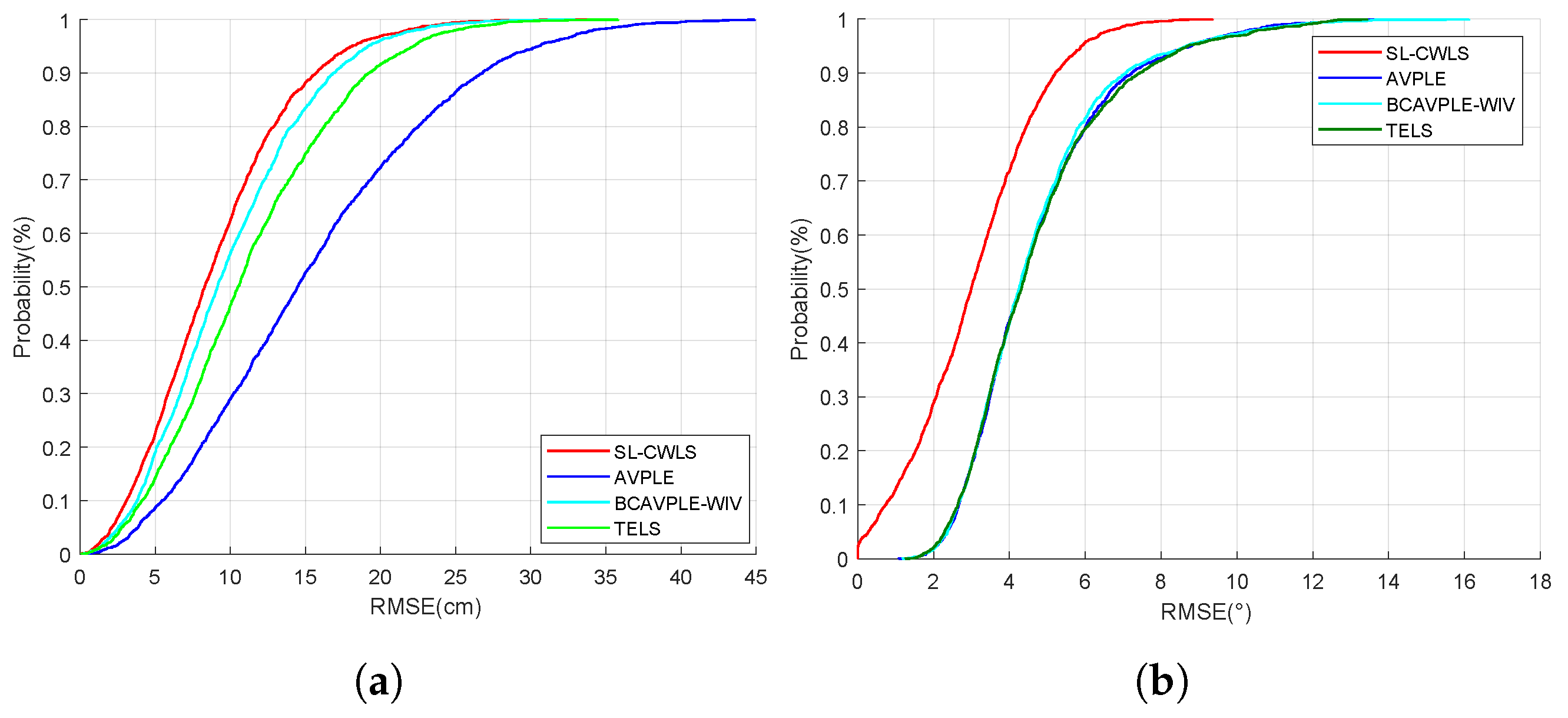
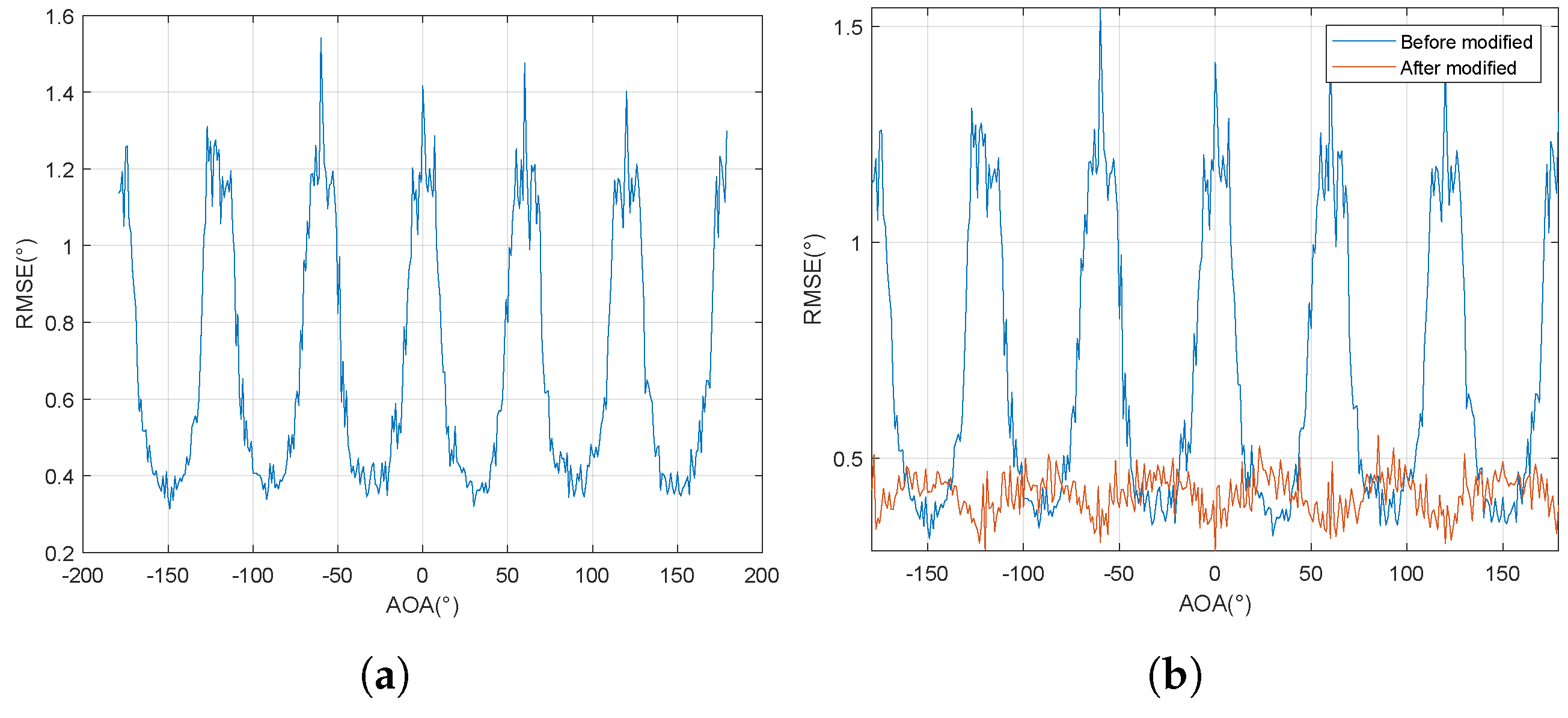
7.2. Analysis of Experimental Results
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| WSNs | Wireless sensor networks |
| UWB | Ultra-wideband |
| RSSI | Received signal strength indicator |
| TOA | Time of arrival |
| TDOA | Time difference of arrival |
| AOA | Angle of arrival |
| DS-TWR | Double-sided two-way ranging |
| IMU | Inertial measurements |
| RBL | Rigid body localization |
| SDP | Semi-definite program |
| SL | Self-localization |
| CWLS | Constrained weighted least squares |
| CCRLB | Constrained Cramér–Rao lower bound |
| CRLB | Cramér–Rao lower bound |
| FIM | Fisher information matrix |
| RMSE | Root mean square error |
| CDF | Cumulative distribution function |
| NLOS | Non-line-of-sight |
References
- Liu, A.; Wang, J.; Lin, S.; Kong, X. A dynamic UKF-based UWB/wheel odometry tightly coupled approach for indoor positioning. Electronics 2024, 13, 1518. [Google Scholar] [CrossRef]
- Win, M.Z.; Scholtz, R.A. Ultra-wide bandwidth time-hopping spread-spectrum impulse radio for wireless multiple-access communications. IEEE Trans. Wireless Commun. 2000, 48, 679–689. [Google Scholar] [CrossRef]
- Zafari, F.; Gkelias, A.; Leung, K.K. A Survey of Indoor Localization Systems and Technologies. IEEE Commun. Surveys Tutorials 2019, 21, 2568–2599. [Google Scholar] [CrossRef]
- Davide, S.; Stefano, M.; Vineeth, T.; Upadhyay, P.K.; Magarini, M. Experimental comparison of UAV-Based RSSI and AOA localization. IEEE Sens. Lett. 2024, 8, 1–4. [Google Scholar]
- Chehri, A.; Fortier, P.; Tardif, P.M. On the TOA estimation for UWB ranging in complex confined area. In Proceedings of the 2007 International Symposium on Signals, Systems and Electronics, Montreal, QC, Canada, 30 July–2 August 2007; pp. 533–536. [Google Scholar]
- Ma, T.; Zhang, D.; Zhuang, J.; You, C.; Yin, G.; Tang, S. TDOA-based UWB indoor 1D localization via weighted sliding window filtering. Digital Signal Process. 2024, 151, 104544. [Google Scholar] [CrossRef]
- Smaoui, N.; Heydariaan, M.; Gnawail, O. Single-antenna AOA estimation with UWB radios. In Proceedings of the 2021 IEEE Wireless Communications and Networking Conference (WCNC), Nanjing, China, 29 March 2021–1 April 2021; pp. 1–7. [Google Scholar]
- Igor, D.; Andrew, C.; Ma, H.; Jeff, C.; Michael, M. Angle of arrival estimation using decawave DW1000 integrated circuits. In Proceedings of the 2017 14th Workshop on Positioning, Navigation and Communications (WPNC), Bremen, Germany, 26 October 2017; pp. 1–6. [Google Scholar]
- Wang, T.; Zhao, H.; Shen, Y. An efficient single-anchor localization method using ultra-wide bandwidth systems. Appl. Sci. 2020, 10, 57. [Google Scholar] [CrossRef]
- Sun, Y.; Ho, K.C.; Wan, Q. Eigenspace solution for AOA localization in modified polar representation. IEEE Trans. Signal Process. 2020, 68, 2256–2271. [Google Scholar] [CrossRef]
- Zheng, Y.; Sheng, M.; Liu, J.; Li, J. Exploiting AOA Estimation Accuracy for Indoor Localization: A Weighted AOA-Based Approach. IEEE Wireless Commun. Lett. 2019, 8, 65–68. [Google Scholar] [CrossRef]
- Zou, Y.; Wu, W.; Zhang, Z. Source Localization Based on Hybrid AOA, TDOA, and RSS Measurements. IEEE Sens. J. 2023, 23, 16293–16302. [Google Scholar] [CrossRef]
- Zou, Y.; Wu, W.; Fan, J.; Liu, H. Constrained Weighted Least-Squares Algorithms for 3-D AOA-Based Hybrid Localization. IEEE Open J. Signal Process. 2024, 5, 436–448. [Google Scholar] [CrossRef]
- Alonge, F.; D’Ippolito, F.; Garraffa, G.; Sferlazza, A. Hybrid Observer for Indoor Localization with Random Time-of-Arrival Measurments. In Proceedings of the 2018 IEEE 4th International Forum on Research and Technology for Society and Industry (RTSI), Palermo, Italy, 10–13 September 2018; pp. 1–6. [Google Scholar]
- Zhou, B.; Fang, H.; Xu, J. UWB-IMU-Odometer Fusion Localization Scheme: Observability Analysis and Experiments. IEEE Sens. J. 2023, 23, 2550–2564. [Google Scholar] [CrossRef]
- Zhou, B.; Ai, L.; Dong, X.; Yang, L. DoA-based rigid body localization adopting single base station. IEEE Commun. Lett. 2019, 23, 494–497. [Google Scholar] [CrossRef]
- Wang, G.; Ho, K.C.; Chen, X. Bias reduced semidefinite relaxation method for 3-D rigid body localization using AOA. IEEE Trans. Signal Process. 2021, 69, 3415–3430. [Google Scholar] [CrossRef]
- Chepuri, S.P.; Leus, G.; van der Veen, A.-J. Rigid Body Localization Using Sensor Networks. IEEE Trans. Signal Process. 2014, 62, 4911–4924. [Google Scholar] [CrossRef]
- Jiang, H.; Wang, W.; Shen, Y.; Li, X.; Ren, X.; Mu, B. Efficient Planar Pose Estimation via UWB Measurements. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023; pp. 1954–1960. [Google Scholar]
- Abouzar, P.; Michelson, D.G.; Hamdi, M. RSSI-Based Distributed SL for Wireless Sensor Networks Used in Precision Agriculture. IEEE Trans. Wireless Commun. 2016, 15, 6638–6650. [Google Scholar] [CrossRef]
- Shao, H.; Zhang, X.; Wang, Z. Efficient closed-form algorithms for AOA based SL of sensor nodes using auxiliary variables. IEEE Trans. Signal Process. 2014, 62, 2580–2594. [Google Scholar] [CrossRef]
- Taponecco, L.; D’Amico, A.A.; Mengali, U. Joint TOA and AOA Estimation for UWB Localization Applications. IEEE Trans. Wireless Commun. 2011, 10, 2207–2217. [Google Scholar] [CrossRef]
- Wang, G.; Ho, K.C. Accurate semidefinite relaxation method for rigid body localization using AOA. In Proceedings of the 2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 4955–4959. [Google Scholar]
- Watanabe, F. Wireless Sensor Network Localization Using AoA Measurements With Two-Step Error Variance-Weighted Least Squares. IEEE Access 2021, 9, 10820–10828. [Google Scholar] [CrossRef]
- IEEE Std 802.15.4-2011 (Revision of IEEE Std 802.15.4-2006); IEEE Standard for Local and metropolitan area networks–Part 15.4: Low-Rate Wireless Personal Area Networks (LR-WPANs). IEEE: New York, NY, USA, 2011; pp. 1–314.



| Method | Description | Complexity |
|---|---|---|
| AVPLE | PLE method in [21] based on AOA | |
| BCAVPLE-WIV | Two-step method in [21] based on AOA and TWR | |
| TELS | Two-step method in [24] based on AOA | |
| BC-CWLS | RBL method in [17] based on AOA | |
| SL-CWLS | Proposed method based on AOA and TWR |
| Positions | Mean of AOA errors (°) | Standard deviation of AOA errors (°) | ||||||
| 30° | −30° | 60° | −60° | 30° | −30° | 60° | −60° | |
| (80,320) | 0.0340 | 0.0480 | −0.0463 | 0.0515 | 5.0723 | 5.1210 | 5.0559 | 5.0933 |
| (160,160) | 0.0453 | 0.0380 | 0.0258 | −0.0373 | 5.0935 | 5.1267 | 5.0807 | 5.1010 |
| (80,80) | −0.0418 | 0.0640 | 0.0103 | 0.0473 | 5.1112 | 5.0832 | 5.1210 | 5.0318 |
| (240,0) | 0.0405 | 0.0175 | 0.0193 | −0.1900 | 5.0895 | 5.0687 | 5.0909 | 5.0810 |
| (320,240) | 0.0475 | 0.0293 | −0.0488 | −0.0498 | 5.1186 | 5.0357 | 5.0563 | 5.0672 |
| Mean of DS-TWR errors (cm) | Standard deviation of DS-TWR errors (cm) | |||||||
| 30° | −30° | 60° | −60° | 30° | −30° | 60° | −60° | |
| (80,320) | 0.4760 | −0.4863 | 0.5005 | 0.5110 | 5.0361 | 5.0628 | 4.9380 | 5.0356 |
| (160,160) | −0.5415 | 0.4058 | 0.4768 | 0.4878 | 4.9482 | 5.0749 | 4.9644 | 5.0428 |
| (80,80) | 0.4923 | −0.5203 | 0.5098 | −0.5658 | 5.0476 | 4.0733 | 5.0616 | 5.0496 |
| (240,0) | 0.4440 | 0.4708 | −0.5430 | 0.4785 | 4.9528 | 5.0515 | 5.0426 | 5.0354 |
| (320,240) | −0.5198 | 0.5175 | −0.5110 | 0.4883 | 5.0397 | 4.9682 | 5.0569 | 5.0419 |
| Positions | RMSE (cm) | |||
|---|---|---|---|---|
| AVPLE | BCAVPLE-WIV | TELS | SL-CWLS | |
| (80,320) | 27.9279 | 16.4774 | 20.2654 | 13.7289 |
| (160,160) | 28.4858 | 16.8066 | 20.2518 | 12.6901 |
| (80,80) | 29.2753 | 17.2724 | 20.8831 | 10.5079 |
| (240,0) | 31.1556 | 18.3818 | 22.4452 | 8.1818 |
| (320,240) | 30.4628 | 18.0705 | 22.0644 | 9.2941 |
| Positions | RMSE | |||
|---|---|---|---|---|
| AVPLE | BCAVPLE-WIV | TELS | SL-CWLS | |
| (80,320) | 0.04763 | 0.04239 | 0.04760 | 0.04330 |
| (160,160) | 0.04841 | 0.04309 | 0.04818 | 0.04272 |
| (80,80) | 0.04887 | 0.04350 | 0.04806 | 0.04443 |
| (240,0) | 0.05410 | 0.04815 | 0.05104 | 0.04806 |
| (320,240) | 0.05254 | 0.04346 | 0.04964 | 0.04335 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, D.; Xu, H.; Zhan, L.; Li, Y.; Yin, G.; Wang, X. Accurate Joint Estimation of Position and Orientation Based on Angle of Arrival and Two-Way Ranging of Ultra-Wideband Technology. Electronics 2025, 14, 429. https://doi.org/10.3390/electronics14030429
Zhang D, Xu H, Zhan L, Li Y, Yin G, Wang X. Accurate Joint Estimation of Position and Orientation Based on Angle of Arrival and Two-Way Ranging of Ultra-Wideband Technology. Electronics. 2025; 14(3):429. https://doi.org/10.3390/electronics14030429
Chicago/Turabian StyleZhang, Di, Hongbiao Xu, Li Zhan, Ye Li, Guangqiang Yin, and Xinzhong Wang. 2025. "Accurate Joint Estimation of Position and Orientation Based on Angle of Arrival and Two-Way Ranging of Ultra-Wideband Technology" Electronics 14, no. 3: 429. https://doi.org/10.3390/electronics14030429
APA StyleZhang, D., Xu, H., Zhan, L., Li, Y., Yin, G., & Wang, X. (2025). Accurate Joint Estimation of Position and Orientation Based on Angle of Arrival and Two-Way Ranging of Ultra-Wideband Technology. Electronics, 14(3), 429. https://doi.org/10.3390/electronics14030429





