Control Strategy for Asymmetric Faults on the Low-Frequency Side of a Sparse Modular Multilevel Converter

Abstract

Sparse modular multilevel converters (SMMCs) are a new type of lightweight high-voltage large-power AC/AC converter that significantly reduces the number of components compared to modular multilevel matrix converters (M3Cs). This study proposes a fault ride through a control strategy for SMMC to address the issues of arm energy imbalances and valve-side overvoltage, which occur during asymmetric faults on the low-frequency side. First, we establish models of the energy deviation of the arms under asymmetric short-circuit faults on the low-frequency side of SMMC. We also study the influence mechanism of the control strategies on the arm energy imbalance during faults. On this basis, an arm energy balancing strategy based on zero-sequence voltage injections combined with AC voltage control is proposed; this can achieve arm energy balance and suppress the negative sequence current and overvoltage of the SMMC. Finally, we construct a simulation model of an offshore wind power low-frequency transmission system based on the SMMC. The simulation results show that the proposed energy balance strategy can realize the stable operation of the low-frequency transmission system (LFTS) under asymmetric faults on the low-frequency side, that the maximum capacitor voltage deviation during the fault does not exceed 10% and that capacitor voltage returns to normal 0.25 s after the fault occurs.

1. Introduction

Low-frequency transmission systems (LFTSs) reduce the operational frequency of AC transmission lines from the standard 50 Hz to low frequencies such as 50/3 Hz or 20 Hz in order to shorten the electrical distance of AC transmission lines, thereby increasing their power transmission capacity. There are some potential application scenarios such as offshore wind power integration, large-scale renewable energy collection and transmission in weak grids [1,2,3,4].

High-voltage high-power AC/AC converters are the core components of low-frequency transmission technology [5]. As the current main AC/AC converter topology [6,7,8], modular multilevel matrix converters (M3Cs) have been trialed in flexible low-frequency transmission projects in Hangzhou and Taizhou, Zhejiang Province, China [4]. However, M3C stations still encounter footprint challenges due to the presence of a large number of sub-modules.

To address the lightweight issue of M3Cs, a series of topologies with different structures have been proposed, such as Y-type modular multilevel converters (Y-type MMCs) [9] and the hexagonal converter (Hexconverter) [10]. However, these converters still have a relatively large number of sub-modules. In contrast to these approaches, the sparse modular multilevel converter (SMMC) is a novel AC/AC converter based on sinusoidal half-wave frequency conversion, whereby the total number of components can be reduced to the same capacity. Notably, SMMC has 75% and 67% fewer capacitors and inductors respectively, resulting in lower costs compared to back-to-back modular multilevel converters (MMCs) and M3Cs. Moreover, SMMCs offer ZVS for more than half of their semiconductors, which are used for the voltage sharing of series-connected semiconductors [11].

In recent years, research on SMMCs has mainly focused on the basic principles, conventional power control, and arm energy balancing control [12,13,14]; meanwhile, the transient characteristics and fault ride-through (FRT) methods of SMMCs under LFTS faults have not been addressed. Most studies on the FRT control strategies of LFTS are based on the operational principles of M3C. Unlike the FRT control strategies for M3C-based LFTS [15,16], the arm energy balancing mechanism of SMMCs is more complex due to their half-wave multilevel modulation.

For generalized MMCs, voltage imbalance is a significant challenge. Over the past few years, many control methods have been proposed to achieve balance in the arm or submodule voltage, such as online vector calculation and constraint techniques [17] and simplified linear cluster voltage balancing controls based on zero-sequence voltage (ZSV) injections [18], etc. Regarding arm energy balancing, one study [19] presents a three-layer closed-loop control method based on conduction angles, ZVS, and nearest-level modulation (NLM), which achieves voltage balance across all submodules even under unbalanced conditions. The authors of [20] performed a comprehensive analysis of MMC, focusing on the voltage components applied to different arms to achieve internal energy balance by considering the degrees of freedom. Another study [21] proposes an independent energy balancing control method for each sub-converter of M3Cs, which balances the energy among the three arms by injecting only output-frequency circulating currents.

When an asymmetric fault occurs in the grid, there is usually a three-phase power imbalance in the converter. To effectively manage the interphase power distribution in converters, standard instantaneous power theory (IPT) is typically used to determine the reference values of active and reactive power, which, in turn, are used to calculate the required current and voltage references. The authors of [22] derived the analytical expression of the instantaneous ZSV and employed this theory to address interphase power imbalance issues in a small-scale Cascaded H-Bridge (CHB) system. Meanwhile, [23] introduces a ZSV injection method that can provide instantaneous ZSV references using steady-state ABC frame variables without the need for numerical iteration or phase-locked loops.

Under the conditions of asymmetric faults, SMMCs not only suffer from interphase power imbalances but also need to deal with the internal arm energy balance of the single phase. When an asymmetric fault occurs on the low-frequency side, the low-frequency terminal voltage introduces asymmetric characteristics if the conventional constant AC voltage control is adopted. The magnitude ratio of AC terminal voltages on both sides of the SMMC deviate from the arm energy balance constraint, and the degrees of deviation among the three phases are different, which poses a challenge to the stable operation of the LFTS. Moreover, during the faults, the overvoltage issue is also coupled with the arm energy unbalancing of the SMMC. Conventional instantaneous power theory cannot by itself address the energy balance issue. Based on the arm energy balance mechanism, a comprehensive consideration of overvoltage suppression, fault current suppression, and energy balance control strategies is needed.

This study investigates the transient characteristics and FRT strategies of the SMMC under the conditions of asymmetric faults on the low-frequency side for a windfarm-connected LFTS. The main contributions of this study are as follows:

• The mathematical models of SMMC arm energy under the conditions of low-frequency-side asymmetric faults are established to analyze the arm energy imbalance phenomenon in the converter using an existing energy balancing control strategy.
• The constraint conditions of the arm energy balance with a zero-sequence voltage injection are derived under the condition of asymmetric faults, and an energy balance control method based on the zero-sequence voltage injection is proposed.
• Combining zero-sequence voltage injections and constant power factor angle AC voltage control, a FRT strategy for the SMMC-based LFTS is proposed, which effectively maintains the arm energy balance in the converter while suppressing the negative sequence current and overvoltage.

At the end of this study, based on the proposed control strategy, we perform a simulation for low-frequency transmission systems that connect offshore windfarms and the grid, in order to verify the effectiveness of the proposed control strategy.

2. SMMC Model and Control Strategy

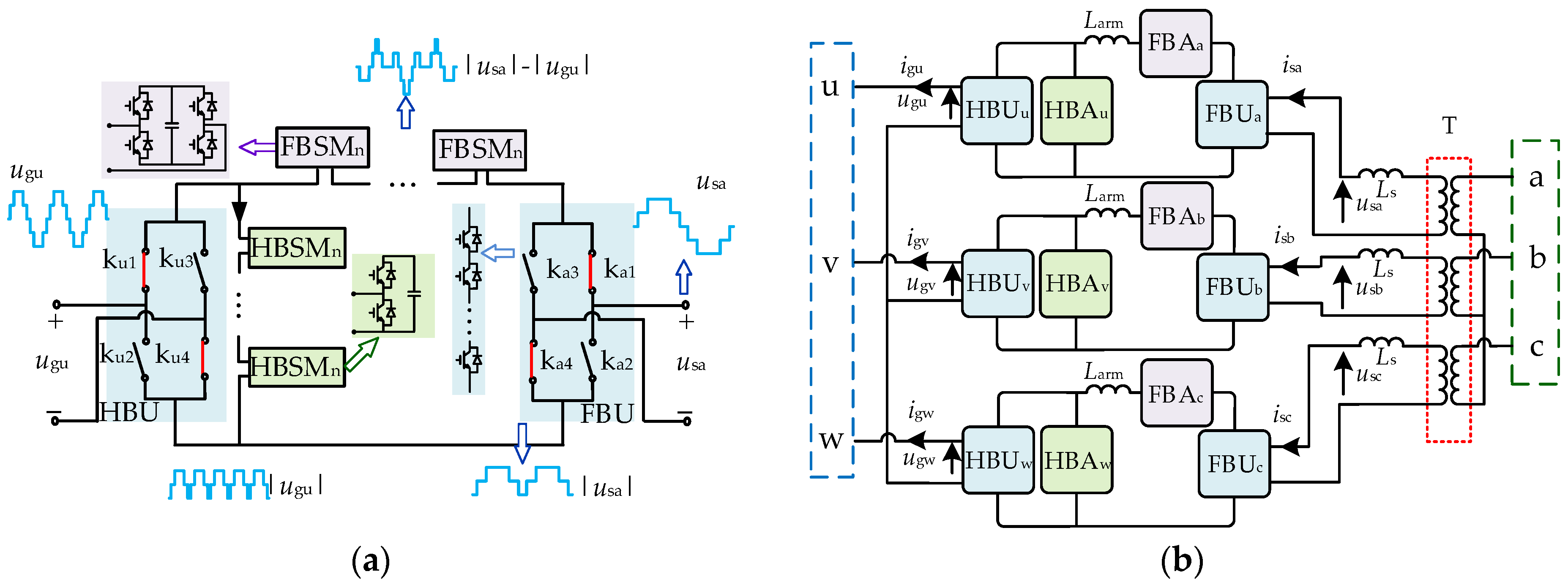
2.1. SMMC Topology and Operating Principles

The SMMC topology is shown in Figure 1; it connects two AC systems with different frequencies and magnitudes. The low-frequency terminal voltage is denoted as u_sa, u_sb, and u_sc and the current as i_sa, i_sb, and i_sc. The line-frequency (grid-side) terminal voltage is denoted as u_gu, u_gv, and u_gw and the current as i_gu, i_gv, and i_gw. L_arm represents the arm inductance, and L_s is the equivalent inductance on the low-frequency side. For SMMC, three single-phase two-winding transformers are needed to achieve interphase isolation.

Each single-phase SMMC consists of two low-frequency unfolders (HBU and FBU), a cascaded half-bridge submodule arm (HBA), and a cascaded full-bridge submodule arm (FBA). In Figure 1a, k_u1~k_u4 and k_a1~k_a4 are the switches for the unfolders on both sides, which are four strings of series-connected semiconductor devices.

The voltages and currents on both sides can be expressed as:

$$\begin{array}{l}\left\{\begin{array}{l}{u}_{\mathrm{gu}}=U_{\mathrm{gm}}\sin ({\omega }_{\mathrm{g}}t)\\ i_{\mathrm{gu}}=I_{\mathrm{gm}}\sin ({\omega }_{\mathrm{g}}t-{\phi }_{\mathrm{g}})\end{array}\right.\\ \left\{\begin{array}{l}{u}_{\mathrm{sa}}=U_{\mathrm{sm}}\sin ({\omega }_{\mathrm{s}}t+{\theta }_{\mathrm{f}})\\ i_{\mathrm{sa}}=I_{\mathrm{sm}}\sin ({\omega }_{\mathrm{s}}t+{\theta }_{\mathrm{f}}-{\phi }_{\mathrm{s}})\end{array}\right.\end{array}$$

(1)

where U_gm and I_gm and U_sm and I_sm are the magnitudes of the voltage and current on the corresponding side, respectively; φ_g and φ_s are the power factor angles; ω_g and ω_s are the angular frequencies; and θ_f is the initial phase difference between the voltages of both sides.

In Figure 1a, the typical waveforms are also given before and after each conversion. The HBA generates the line-frequency half-wave multilevel voltage |u_gu|, and the FBA modulates the difference voltage |u_sa|−|u_gu|, which produces the low-frequency half-wave multilevel voltage |u_sa|. The half-wave multilevel voltages |u_gu| and |u_sa| on both sides are unfolded by HBU and FBU to obtain the line-frequency and low-frequency sinusoidal multilevel voltages u_gu and u_sa. The switching functions of the unfolders can be defined as follows:

$$S_{\mathrm{u}}=\left\{\begin{array}{l} 1,u_{\mathrm{gu}}\ge 0\\ -1,u_{\mathrm{gu}}<0\end{array}\right., S_{\mathrm{a}}=\left\{\begin{array}{l} 1,u_{\mathrm{sa}}\ge 0\\ -1,u_{\mathrm{sa}}<0\end{array}\right.$$

(2)

According to Figure 1 and Equations (1) and (2), the voltages of HBA and FBA, u_Hu and u_Fa, and the arm currents i_Hu and i_Fa can be expressed as follows:

$$\begin{array}{l}\left\{\begin{array}{l}{u}_{\mathrm{Hu}}=S_{\mathrm{u}}{u}_{\mathrm{gu}}\\ i_{\mathrm{Hu}}=S_{\mathrm{a}}{i}_{\mathrm{sa}}-S_{\mathrm{u}}{i}_{\mathrm{gu}}\end{array}\right.\\ \left\{\begin{array}{l}{u}_{\mathrm{Fa}}=S_{\mathrm{a}}{u}_{\mathrm{sa}}-S_{\mathrm{u}}{u}_{\mathrm{gu}}\\ i_{\mathrm{Fa}}=S_{\mathrm{a}}{i}_{\mathrm{sa}}\end{array}\right.\end{array}$$

(3)

As shown in Figure 2, the input power p_a of phase a is transmitted to the intermediate power p_m through FBA_a, and then, p_m provides the power of HBA_u, p_Hu, and the output power of phase u, p_u. All the above power can be expressed as follows:

$$\left\{\begin{array}{l}{p}_{\mathrm{m}}=u_{\mathrm{Hu}}{i}_{\mathrm{Fa}}=S_{\mathrm{u}}{S}_{\mathrm{a}}{u}_{\mathrm{gu}}{i}_{\mathrm{sa}}\\ p_{\mathrm{u}}=u_{\mathrm{gu}}{i}_{\mathrm{gu}}\\ p_{\mathrm{a}}=u_{\mathrm{sa}}{i}_{\mathrm{sa}}\end{array}\right.$$

(4)

Based on Equations (2)–(4), p_Hu and the power of FBA_a, p_Fa are obtained as follows:

$$\left\{\begin{array}{l}{p}_{\mathrm{Hu}}=p_{\mathrm{m}}-p_{\mathrm{u}}\\ p_{\mathrm{Fa}}=p_{\mathrm{a}}-p_{\mathrm{m}}\end{array}\right.$$

(5)

According to Equation (5), to achieve arm energy balance, it is necessary to ensure that the arm average P_Hu and P_Fa values are zero over the fluctuation period T of the submodule capacitor energy within the arms. Therefore, the energy balance constraint can be written as follows:

$$P_{\mathrm{a}}=P_{\mathrm{u}}=P_{\mathrm{m}}$$

(6)

where P_a, P_u, and P_m represent the average values of p_a, p_u, and p_m, respectively. P_a and P_u can be expressed as:

$$\left\{\begin{array}{l}{P}_{\mathrm{a}}={\displaystyle \frac{1}{2}}{U}_{\mathrm{sm}}{I}_{\mathrm{sm}}\cos {\phi }_{\mathrm{s}}\\ P_{\mathrm{u}}={\displaystyle \frac{1}{2}}{U}_{\mathrm{gm}}{I}_{\mathrm{gm}}\cos {\phi }_{\mathrm{g}}\end{array}\right.$$

(7)

Based on Equations (4), (6), and (7), the energy balance constraint can be further derived as follows:

$${\displaystyle \frac{U_{\mathrm{sm}}}{U_{\mathrm{gm}}}}={\displaystyle \frac{2{\displaystyle {\int }_T{S}_{\mathrm{a}}\sin ({\omega }_{\mathrm{s}}t-{\phi }_{\mathrm{s}}+{\theta }_{\mathrm{f}})\left|\sin ({\omega }_{\mathrm{g}}t)\right|dt}}{T\cos {\phi }_{\mathrm{s}}}}$$

(8)

Under the arm energy balance constraint, Equation (8) shows that the amplitude ratio of the SMMC AC voltage is related to the frequencies of the AC systems on both sides, the power factor, and the initial phase difference. There is no analytical solution for the voltage amplitude ratio, but numerical analysis shows that, for LFTS with a line frequency of 50 Hz and a low frequency of 20 Hz, U_sm/U_gm is approximately a fixed value of 0.81 [12] when arm energy balance is achieved. When U_sm/U_gm deviates from 0.81, conventional controls cannot maintain the arm energy balance, and energy balance controls must be employed.

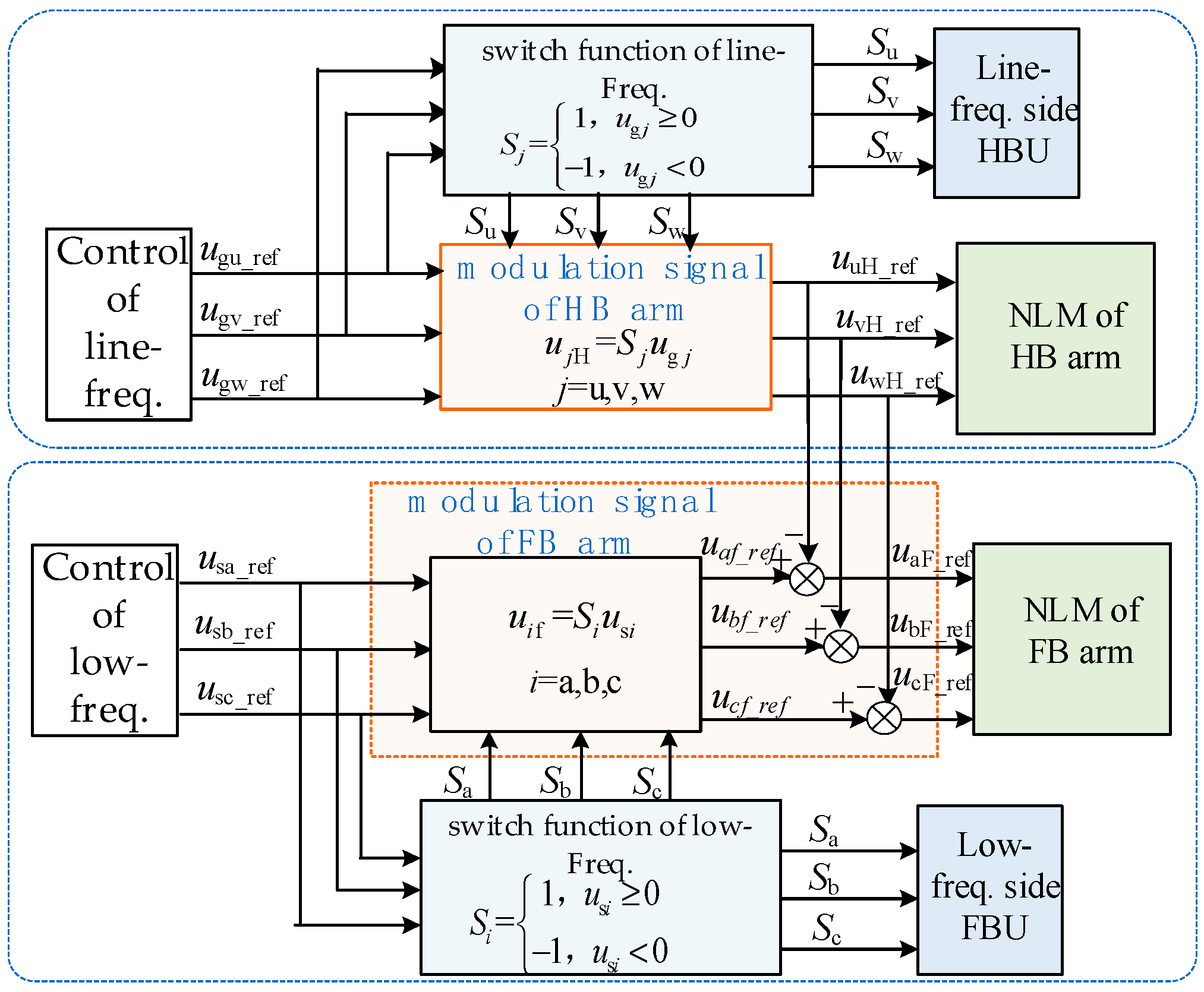
2.2. Basic Control of SMMC Normal Operations

The topology of the offshore wind power low-frequency transmission system is shown in Figure 3. U_L represents the equivalent inductance voltage on the low-frequency side, and u_st indicates the low-frequency-transformer converter-side voltage. U_ss and i_ss are the transformer low-frequency line-side voltage and current, respectively. U_sw and V_wg represent the low-frequency cable-side voltage of the windfarm and the wind power collection-side voltage, respectively. L_w is the equivalent inductance of the windfarm. To simplify the analysis, the windfarm is equated with a current-controlled voltage source converter (VSC). The windfarm output is 20 Hz AC power, which is transmitted through the submarine cable to the low-frequency side of the frequency conversion station; then, it is transformed into line-frequency AC power using an SMMC and integrated into the onshore grid.

To support the voltage of the offshore windfarm, an AC voltage control is applied on the low-frequency side of SMMC. The authors of [12] introduce a third harmonic voltage injection on the low-frequency side of SMMC as an additional control to achieve arm energy balance when the converter operates over a wide voltage range.

The third harmonic voltage can be expressed as:

$$u_3=k_3{U}_{\mathrm{sm}}\sin (3{\omega }_{\mathrm{s}}t+{\beta }_3)$$

(9)

The value of k₃ is determined by the control of the total submodule capacitor voltage of the three-phase full-bridge arm:

$$k_3=(u_{\mathrm{CN}}-u_{\mathrm{CF}}\left)\right(k_{\mathrm{p}1}+{\displaystyle \frac{k_{\mathrm{i}1}}{s}})$$

(10)

where u_CN is the rated value of the sub-module capacitor voltage, u_CF is the average value of the full-bridge arm sub-module capacitor voltage, and k_p1 and k_i1 are the proportional and integral coefficients of the full-bridge arm energy balance PI controller.

Additionally, to achieve balance in the capacitor voltages of the sub-modules within the arm, both the half-bridge and full-bridge arms use a nearest-level modulation strategy based on a capacitor voltage-sorting algorithm. The basic control strategy based on a third harmonic injection for SMMCs under normal operational conditions is shown in Figure 4. In the figure, L_g represents the equivalent grid-connected inductor on the line frequency side. U_gd, u_gq, i_gd, and i_gq represent the d and q axis components of u_g and i_g, respectively. I_ssd and i_ssq represent the d and q axis components of i_ss, respectively.

3. Analysis of the Energy Imbalance Mechanism in SMMC Arms

Single-phase grounding faults are the most common type of fault in the grid [24]. Two phase-to-phase short circuit faults constitute another common type of fault, usually occurring between two phases. Although not as common as single-phase grounding faults, they also have a high probability of occurrence. These two kinds of fault are considered in this section.

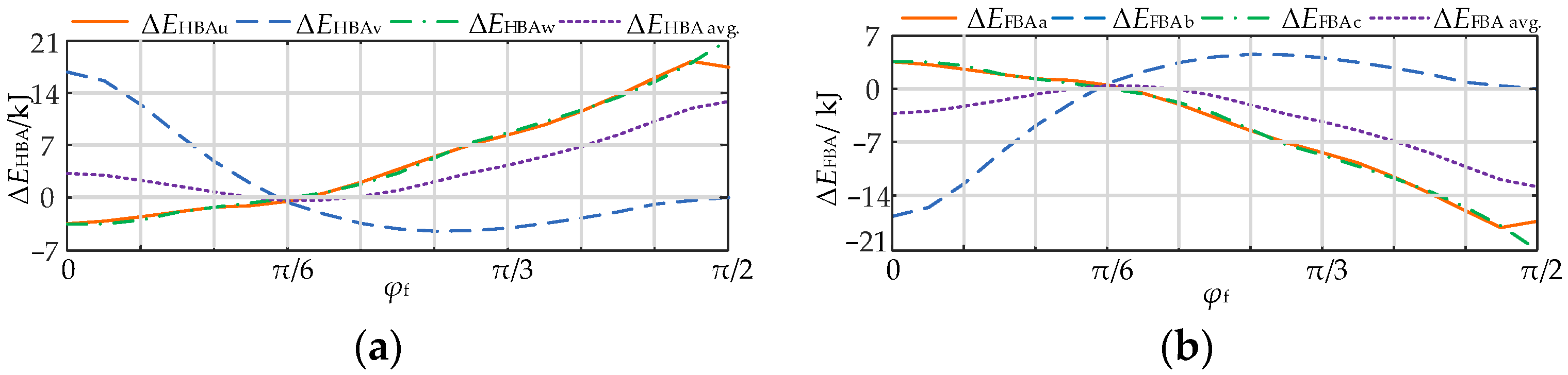
3.1. Analysis of the Arm Energy Imbalance Mechanism Under a Single-Phase Short-Circuit Fault

Considering that submarine cable faults are mostly permanent faults and FRT cannot be achieved, in the following analysis, it is assumed that temporary faults occur on the low-frequency side of the SMMC. During a single-phase ground short-circuit fault, the onshore converter station generally adopts a negative sequence current suppression strategy to reduce the negative sequence current to zero. Considering the zero-sequence current at the fault location is very small, we can assume that the zero-sequence voltage at the fault location is also zero. Taking phase a as an example, the voltage sequence components on the cable side of the transformer have the following relationships [25]:

$$\left\{\begin{array}{l}{u}_{\mathrm{ssa}+}+u_{\mathrm{ssa}-}=0\\ u_{\mathrm{ssa}0}=0\end{array}\right.$$

(11)

where u_ssa+, u_ssa−, and u_ssa0 represent the positive sequence, negative sequence, and zero-sequence components of u_ssa, respectively.

The positive and negative sequence components of u_ss can be expressed as:

$$\left[\begin{array}{l}{u}_{\mathrm{ssa}+} u_{\mathrm{ssa}-}\\ u_{\mathrm{ssb}+} u_{\mathrm{ssb}-}\\ u_{\mathrm{ssc}+} u_{\mathrm{ssc}-}\end{array}\right]=U_{\mathrm{fm}}\left[\begin{array}{l}\sin ({\omega }_{\mathrm{s}}t)\hspace{1em}\hspace{1em}\hspace{1em}-\sin ({\omega }_{\mathrm{s}}t)\\ \sin ({\omega }_{\mathrm{s}}t-{\displaystyle \frac{2\mathsf{\pi }}{3}}) \sin ({\omega }_{\mathrm{s}}t-{\displaystyle \frac{\mathsf{\pi }}{3}})\\ \sin ({\omega }_{\mathrm{s}}t+{\displaystyle \frac{2\mathsf{\pi }}{3}}) \sin ({\omega }_{\mathrm{s}}t+{\displaystyle \frac{\mathsf{\pi }}{3}})\end{array}\right]$$

(12)

Since the transformer adopts a Y₀/Δ connection, the positive sequence voltage of u_st leads u_ss+ by π/6, and the negative sequence voltage of u_st lags u_ss− by π/6. Therefore, the phase voltage of u_st can be further expressed as:

$$\left[\begin{array}{l}{u}_{\mathrm{sta}}\\ u_{\mathrm{stb}}\\ u_{\mathrm{stc}}\end{array}\right]=U_{\mathrm{fm}}\left[\begin{array}{c}\sin ({\omega }_{\mathrm{s}}t+{\displaystyle \frac{\mathsf{\pi }}{6}})+\sin ({\omega }_{\mathrm{s}}t+{\displaystyle \frac{5\mathsf{\pi }}{6}})\\ \sin ({\omega }_{\mathrm{s}}t-{\displaystyle \frac{\mathsf{\pi }}{2}})+\sin ({\omega }_{\mathrm{s}}t-{\displaystyle \frac{\mathsf{\pi }}{2}})\\ \sin ({\omega }_{\mathrm{s}}t+{\displaystyle \frac{5\mathsf{\pi }}{6}})+\sin ({\omega }_{\mathrm{s}}t+{\displaystyle \frac{\mathsf{\pi }}{6}})\end{array}\right]$$

(13)

The phase current i_s without negative and zero-sequence components can be expressed as:

$$\left[\begin{array}{l}{i}_{\mathrm{sa}}\\ i_{\mathrm{sb}}\\ i_{\mathrm{sc}}\end{array}\right]=I_{\mathrm{fm}}\left[\begin{array}{c}\sin ({\omega }_{\mathrm{s}}t-{\phi }_{\mathrm{f}}+{\displaystyle \frac{\mathsf{\pi }}{6}})\\ \sin ({\omega }_{\mathrm{s}}t-{\phi }_{\mathrm{f}}-{\displaystyle \frac{2\mathsf{\pi }}{3}}+{\displaystyle \frac{\mathsf{\pi }}{6}})\\ \sin ({\omega }_{\mathrm{s}}t-{\phi }_{\mathrm{f}}+{\displaystyle \frac{2\mathsf{\pi }}{3}}+{\displaystyle \frac{\mathsf{\pi }}{6}})\end{array}\right]$$

(14)

where I_fm is the amplitude of the fault current and φ_f is the power factor angle on the low-frequency side after the fault.

Ignoring the influence of the equivalent inductance L_s, based on Equation (13), there exists both positive sequence and negative sequence components in the voltage on the low-frequency-transformer converter-side voltage u_st, while the current only has positive sequence components. The power generated by the positive sequence voltage and negative sequence voltage are defined, respectively, as positive sequence power P_fsa+, P_fsb+, P_fsc+ and negative sequence power P_fsa−, P_fsb−, P_fsc−. According to Equations (13) and (14), within the fluctuation period T of the sub-module capacitor energy, the average value of the single-phase input power on the low-frequency side of SMMC, P_fsa, P_fsb, P_fsc, is:

$$\left[\begin{array}{l}{P}_{\mathrm{fsa}}\\ P_{\mathrm{fsb}}\\ P_{\mathrm{fsc}}\end{array}\right]=\left[\begin{array}{l}{P}_{\mathrm{fsa}+}\\ P_{\mathrm{fsb}+}\\ P_{\mathrm{fsc}+}\end{array}\right]+\left[\begin{array}{l}{P}_{\mathrm{fsa}-}\\ P_{\mathrm{fsb}-}\\ P_{\mathrm{fsc}-}\end{array}\right]={\displaystyle \frac{1}{2}}{U}_{\mathrm{fm}}{I}_{\mathrm{fm}}\left[\begin{array}{c}\cos {\phi }_{\mathrm{f}}+\cos ({\phi }_{\mathrm{f}}+{\displaystyle \frac{2\mathsf{\pi }}{3}})\\ \cos {\phi }_{\mathrm{f}}+\cos {\phi }_{\mathrm{f}}\\ \cos {\phi }_{\mathrm{f}}+\cos ({\phi }_{\mathrm{f}}-{\displaystyle \frac{2\mathsf{\pi }}{3}})\end{array}\right]$$

(15)

Due to the three-phase symmetry of u_g and i_g, the average output power values of the three phases are equal. Additionally, with the control of total sub-module capacitor voltage in the three-phase arm, the average input and output power of the converter are also equal. It can be determined that the average output power of the single phase on the grid side of the SMMC is:

$$P_{\mathrm{fgu}}=P_{\mathrm{fgv}}=P_{\mathrm{fgw}}={\displaystyle \frac{1}{2}}{U}_{\mathrm{fm}}{I}_{\mathrm{fm}}\cos {\phi }_{\mathrm{f}}$$

(16)

The average intermediate power for each phase P_fmi (i = u, v, w) can be expressed as:

$$P_{\mathrm{fm}}={\displaystyle \frac{{\displaystyle {\int }_T\left|u_{\mathrm{g}}\right|i_{\mathrm{s}}{S}_{3}dt}}{T}}$$

(17)

where S₃ is the switching function of the unfolders on the low-frequency side with third harmonic injection.

The energy deviation of the HBAs and the FBAs that cause the capacitor voltage to be unstable are, respectively:

$$\left\{\begin{array}{l}\mathrm{\Delta }{E}_{\mathrm{HBA}}=(P_{\mathrm{fm}}-P_{\mathrm{fg}})T\\ \mathrm{\Delta }{E}_{\mathrm{FBA}}=(P_{\mathrm{fs}}-P_{\mathrm{fm}})T\end{array}\right.$$

(18)

According to Equation (18), the energy deviations ∆E_HBA and ∆E_FBA of each HBA and FBA with different power factor angles can be drawn, as shown in Figure 5. As seen from the figure, after a single-phase-to-ground fault, the energy deviation of each arm cannot be zero simultaneously under different power factor angles, whatever the third harmonic amplitude is. Moreover, the changing trends of energy deviation exhibit significant differences in different phases. Therefore, the energy balance control strategy using third harmonic injections is no longer valid during the fault period.

3.2. Arm Energy Balance Under a Single-Phase Short Circuit Fault with Zero-Sequence Injections

The negative sequence power generated by the negative sequence voltage causes asymmetry in the input power on the low-frequency side of the SMMC. To achieve an energy balance among the three-phase arms, the three-phase average input power of the SMMC must be equal. We propose injecting zero-sequence voltage on the low-frequency side to generate zero-sequence power to balance the impact of the negative sequence power. The injected zero-sequence voltage is:

$$u_0=k_0\sin ({\omega }_{\mathrm{s}}t+{\beta }_0)$$

(19)

where k₀ is the zero-sequence voltage amplitude and β₀ is the initial phase angle of the zero-sequence voltage.

With the zero-sequence injection, the average values of the three-phase zero-sequence powers P_fsa0, P_fsb0, and P_fsc0 can be expressed as:

$$\left[\begin{array}{c}{P}_{\mathrm{fsa}0}\\ P_{\mathrm{fsb}0}\\ P_{\mathrm{fsc}0}\end{array}\right]={\displaystyle \frac{1}{2}}{k}_0{I}_{\mathrm{fm}}\left[\begin{array}{c}\cos ({\phi }_{\mathrm{f}}+{\beta }_0)\\ \cos ({\phi }_{\mathrm{f}}+{\beta }_0+{\displaystyle \frac{2\mathsf{\pi }}{3}})\\ \cos ({\phi }_{\mathrm{f}}+{\beta }_0-{\displaystyle \frac{2\mathsf{\pi }}{3}})\end{array}\right]$$

(20)

To ensure that P_fsa, P_fsb, and P_fsc are symmetrical, the following equations are required:

$$P_{\mathrm{fsa}-}+P_{\mathrm{fsa}0}=P_{\mathrm{fsb}-}+P_{\mathrm{fsb}0}=P_{\mathrm{fsc}-}+P_{\mathrm{fsc}0}$$

(21)

According to Equations (15), (20), and (21), the amplitude and initial phase angle of the zero-sequence voltage to be injected under a single-phase fault are obtained:

$$\left\{\begin{array}{l}{k}_0=U_{\mathrm{fm}}\\ {\beta }_0={\displaystyle \frac{\mathsf{\pi }}{2}}-2{\phi }_{\mathrm{f}}\end{array}\right.$$

(22)

With a zero-sequence injection, the energy deviations ∆E_HBA and ∆E_FBA of each HBA and FBA under a single-phase ground short-circuit fault are shown in Figure 6. The energy imbalance between the HBAs and FBAs is symmetrical at different power factor angles. More importantly, the energy deviation of the HBAs and FBAs of the different phases are simultaneously zero when the power factor angle is π/6, which gives an arm energy steady-state equilibrium point. As shown in Figure 7, when the power factor angle is π/6 and the zero-sequence injection voltage satisfies Equations (19) and (22), the energy deviation of the arm within one energy fluctuation period T is 0. For a 20 Hz/50 Hz AC/AC conversion system, the value of one energy fluctuation cycle T should be 0.05.

3.3. Arm Energy Balance Under a Two-Phase Short-Circuit Fault with a Zero-Sequence Injection

Two-phase short-circuit faults include inter-phase faults and two-phase ground faults; the mechanism of the arm energy imbalance is similar to that of single-phase ground faults and will not be detailed here. Similarly, the amplitude and initial phase angle of the zero-sequence voltage that should be injected during inter-phase faults are obtained as follows:

$$\left\{\begin{array}{l}{k}_0=-U_{\mathrm{fm}}\\ {\beta }_0={\displaystyle \frac{\mathsf{\pi }}{2}}-2{\phi }_{\mathrm{f}}\end{array}\right.$$

(23)

With a zero-sequence injection, the energy deviations ∆E_HBA and ∆E_FBA of each HBA and FBA under two-phase faults are shown in Figure 8. Near the power factor angle of π/2, the energy deviations of the three-phase HBAs and FBAs are simultaneously zero.

After a two-phase ground fault, unlike the M3C-based LFTS, the zero-sequence current is entirely provided by the offshore windfarm due to the isolation effect of the low-frequency-side single-phase transformer group. The fault point voltage is influenced by both the fault ground resistance and the line current limit. When the fault is relatively minor, the current on both sides of the fault point does not reach the limit, and the sequence component characteristics of the voltage are similar to those of an inter-phase short-circuit fault. In this situation, the mechanism of the arm energy imbalance and zero-sequence voltage injection analysis are the same as those for inter-phase short-circuit faults. As the fault severity increases, the line current on both sides gradually reaches the limit, and the fault-point sequence voltage amplitude is proportional to the ground fault resistance. In the case of a heavy ground fault, it is difficult to maintain the voltage of the offshore windfarm and there is a risk of system collapse.

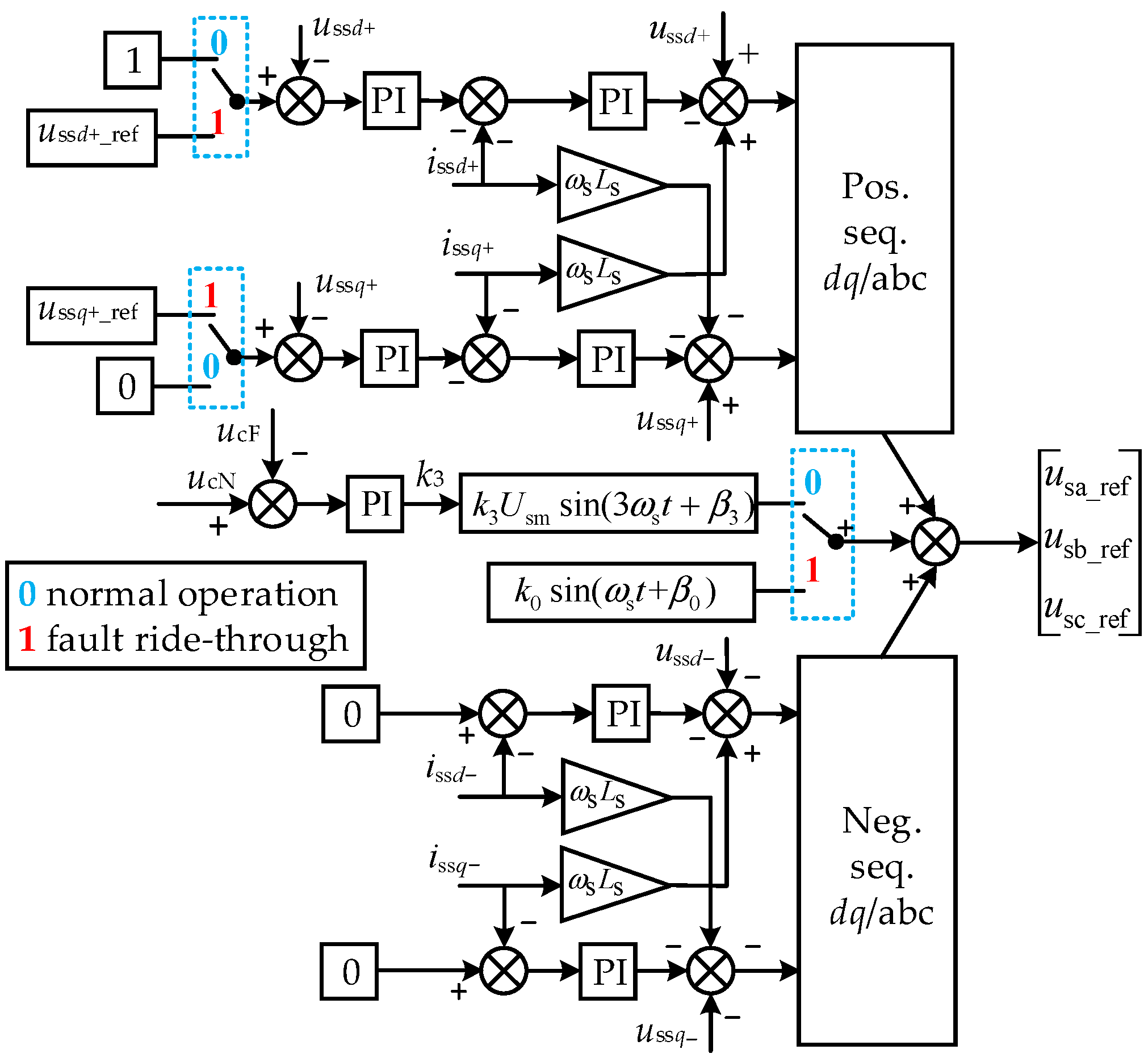
4. Low-Frequency Side Fault Ride-Through Strategy for SMMC-Based LFTS

4.1. Control of Equivalent Converters for Wind Farms

During normal operations, the windfarm equivalent converter adopts a constant power control. Under asymmetric faults, it injects positive sequence dynamic reactive currents to support the recovery of positive sequence voltage and employs a control strategy for negative sequence current suppression to limit fault currents. In addition, according to the requirements of the Chinese National Standard, the dynamic positive sequence reactive current ratio coefficient of the windfarm is set to 0.9 [26]:

$$\left\{\begin{array}{l}{i}_{\mathrm{w}q+}=K_{+}(0.9-\left|V_{\mathrm{wg}+}\right|)I_{\mathrm{fn}}\\ i_{\mathrm{w}d+}=\sqrt{i_{\max }^2-i_{\mathrm{w}q+}^2}\\ i_{\mathrm{w}q-}=0\\ i_{\mathrm{w}d-}=0\end{array}\right.$$

(24)

where i_wq+ and i_wq− are the reference values of the positive and negative sequence reactive currents of the windfarm, respectively, while i_wd+ and i_wd− are the reference values of the positive and negative sequence active currents of the windfarm, respectively. K₊ is the proportional coefficient, and V_wg+ is the positive sequence component of the voltage at the windfarm grid connection point. i_max and I_fn are the maximum value and rated value of the phase current amplitude, respectively.

The switching logic of the overall control strategy of the windfarm is shown in Figure 9, where ω_w is the angular frequency of the windfarm system. V_wd+, V_wq+, V_wd−, and V_wq− are the positive and negative sequence d-q axis components of the voltage at the grid connection point, and V_wa, V_wb, and V_wc are the three-phase voltage modulation signals of the converter.

4.2. Asymmetric Fault Control on the Low-Frequency Side of the SMMC

During the fault, the positive sequence control strategy on the grid side of the SMMC remains unchanged, as shown in Figure 4. The reference value of the negative sequence current control loop is set to 0. On the low-frequency side, zero-sequence voltage should be injected during faults according to the energy balance constraints, and the reference value of the AC voltage control should be regulated to meet the specific power factor angle and prevent over-voltage in the non-faulted phases.

Because the zero-sequence voltage injection and the required power factor angle are different between single-phase to-ground faults and two-phase short-circuit faults, it is necessary to identify the fault type and to apply different voltage control commands. For single-phase to-ground short-circuits, the positive sequence and negative sequence voltages at the fault point are in opposite phases, and, for two-phase short-circuit faults, the positive sequence and negative sequence voltages at the fault point are in phase. The sign k_f of the radio of the positive sequence voltage d-axis component u_ssd+ to the negative sequence voltage d-axis component u_ssd− is used as feedback to determine the fault type:

$$k_{\mathrm{f}}=\mathrm{sgn}({\displaystyle \frac{u_{\mathrm{s}\mathrm{s}d+}}{u_{\mathrm{s}\mathrm{s}d-}}})=\left\{\begin{array}{l} 1,\hspace{1em} \mathrm{single}\text{-}\mathrm{phase} \mathrm{fault}\\ -1,\hspace{1em}\mathrm{two}\text{-}\mathrm{phase} \mathrm{fault}\end{array}\right.$$

(25)

Afterwards, Equations (22) and (23) can be merged as follows:

$$\left\{\begin{array}{l}{k}_0=k_{\mathrm{f}}{U}_{\mathrm{fm}}\\ {\beta }_0={\displaystyle \frac{\mathsf{\pi }}{2}}-2{\phi }_{\mathrm{f}}\end{array}\right.$$

(26)

We can assume that, after the fault, the phase angle of the positive sequence current i_s+ on the low-frequency side of SMMC is θ_I, and the voltage amplitude of the equivalent inductance L_m is U_Lm, which can be expressed as:

$$\left\{\begin{array}{l}{\theta }_I=\arctan ({\displaystyle \frac{i_{s\mathrm{s}q+}}{i_{s\mathrm{s}d+}}})\\ U_{\mathrm{Lm}}={\omega }_{\mathrm{s}}{L}_{\mathrm{s}}\sqrt{i_{s\mathrm{s}d+}^2+i_{s\mathrm{s}q+}^2}\end{array}\right.$$

(27)

where i_ssd+ and i_ssq+ represent the d-q axis components of the positive sequence current on the cable side of the transformer, respectively.

To simplify the analysis, the positive sequence voltage u_s+, the voltage u_L, and the positive sequence voltage u_st+ all refer to the transformer cable side. To suppress the non-fault-phase over-voltage, the reference value for the amplitude of u_s+, denoted as U_fm, is set to a fixed value of 0.58 pu [26]. To achieve arm energy balance, based on the analysis presented in Section 3.2 and Section 3.3, the phase angle θ_s of u_s+ should be:

$${\theta }_{\mathrm{s}}=\left\{\begin{array}{l}{\displaystyle \frac{\mathsf{\pi }}{6}}+{\theta }_{\mathrm{I}}, k_{\mathrm{f}}=1\\ {\displaystyle \frac{\mathsf{\pi }}{2}}+{\theta }_{\mathrm{I}}, k_{\mathrm{f}}=-1\end{array}\right.$$

(28)

The vector diagram of u_s+, u_L, and u_st+ is shown in Figure 10, where u_sd+ and u_sq+ represent the d-q axis components of u_s+, respectively, and u_std+ and u_stq+ represent the d-q axis components of u_st+, respectively.

The reference values for the transformer cable-side voltage u_{ssd+_ref} and u_{ssq+_ref} should be equal to the transformer converter side voltage referring to the cable side, u_std+ and u_stq+. According to Figure 10, under a single-phase fault, the reference values can be obtained as:

$$\left\{\begin{array}{l}{u}_{\mathrm{s}\mathrm{s}d+\_\mathrm{ref}}={\displaystyle \frac{-U_{\mathrm{Lm}}+\sqrt{4U_{\mathrm{fm}}^2-3U_{\mathrm{Lm}}^2}}{2}}\cos {\theta }_{\mathrm{s}}-U_{\mathrm{Lm}}\sin {\theta }_I\\ u_{\mathrm{s}\mathrm{s}q+\_\mathrm{ref}}={\displaystyle \frac{-U_{\mathrm{Lm}}+\sqrt{4U_{\mathrm{fm}}^2-3U_{\mathrm{Lm}}^2}}{2}}\sin {\theta }_{\mathrm{s}}+U_{\mathrm{Lm}}\cos {\theta }_I\end{array}\right.$$

(29)

Under a two-phase fault, the reference values can be obtained as:

$$\left\{\begin{array}{l}{u}_{\mathrm{s}\mathrm{s}d+\_\mathrm{ref}}={\displaystyle \frac{\sqrt{4(U_{\mathrm{fm}}^2-U_{\mathrm{Lm}}^2)}}{2}}\cos {\theta }_{\mathrm{s}}-U_{\mathrm{Lm}}\sin {\theta }_I\\ u_{\mathrm{s}\mathrm{s}q+\_\mathrm{ref}}={\displaystyle \frac{\sqrt{4(U_{\mathrm{fm}}^2-U_{\mathrm{Lm}}^2)}}{2}}\sin {\theta }_{\mathrm{s}}+U_{\mathrm{Lm}}\cos {\theta }_I\end{array}\right.$$

(30)

Accordingly, the injected zero-sequence voltage component during a fault can be expressed as:

$$u_0=k_{\mathrm{f}}{U}_{\mathrm{fm}}\sin ({\omega }_{\mathrm{s}}t+{\theta }_{\mathrm{s}}-2{\phi }_{\mathrm{f}}+{\displaystyle \frac{\mathsf{\pi }}{2}})$$

(31)

In summary, the reference voltage commands for the positive sequence, negative sequence, and zero-sequence control components are superimposed to generate the low-frequency-side voltage modulation signals u_a, u_b, and u_c. The low-frequency transformer can be eliminated, which has a certain impact on the control strategy. After removing the transformer, the phase of the voltage u_st on the low-frequency transformer-converter side will change, and the control strategy only needs to swap the single-phase and two-phase components. The overall control block diagram for the low-frequency side is shown in Figure 11.

Voltage modulation signals u_{gu_ref}, u_{gv_ref}, and u_{gw_ref} generate the switch functions S_u, S_v, and S_w of HBU, which are used to modulate the half-bridge multi-level modulation signals u_{uH_ref}, u_{vH_ref}, and u_{wH_ref}. The low-frequency side voltage modulation signals u_{sa_ref}, u_{sb_ref}, and u_{sc_ref}, derived from Figure 11, participate in determining the switch functions of FBU and are used to modulate the low-frequency half-wave signals u_{ah_ref}, u_{bh_ref}, and u_{ch_ref}. These signals are then further modulated together with the line-frequency half-wave signals u_{uH_ref}, u_{vH_ref}, and u_{wH_ref} to produce the full-bridge multi-level modulation signals u_{aF_ref}, u_{bF_ref}, and u_{cF_ref}. The control block diagram for generating the switch signals and the arm multi-level modulation signals is shown in Figure 12. Specifically, modulation methods of the converter level such as pulse width modulation (PWM) [27] and NLM can be employed, and the latter is adopted in this paper.

5. Simulation Results

The offshore wind power low-frequency transmission system, as shown in Figure 3, was built in Matlab 2021a/Simulink, with the specific parameters listed in

Table 1. Simulation parameters of the SMMC.

Parameters	Value	Parameters	Value
Power rating Sn/MW	2.5	Sub-module capacitor voltage uCN/kV	1.5
Number of SMs/N	15	Low-frequency-side rated voltage Usm/kV	10
Internal arm inductance Larm/mH	1	Grid-side rated voltage Ugm/kV	10
Low-frequency-side equivalent inductance Ls/mH	5	Low-frequency-side frequency f1/Hz	20
SM capacitor C/mF	10	Grid-side frequency f2/Hz	50

. Given that the focus of this study is the fault control of the SMMC, the offshore wind power farm is equivalently represented by a single VSC with an equivalent capacity of 2.5 MW, and the fault duration is set to 625 ms.

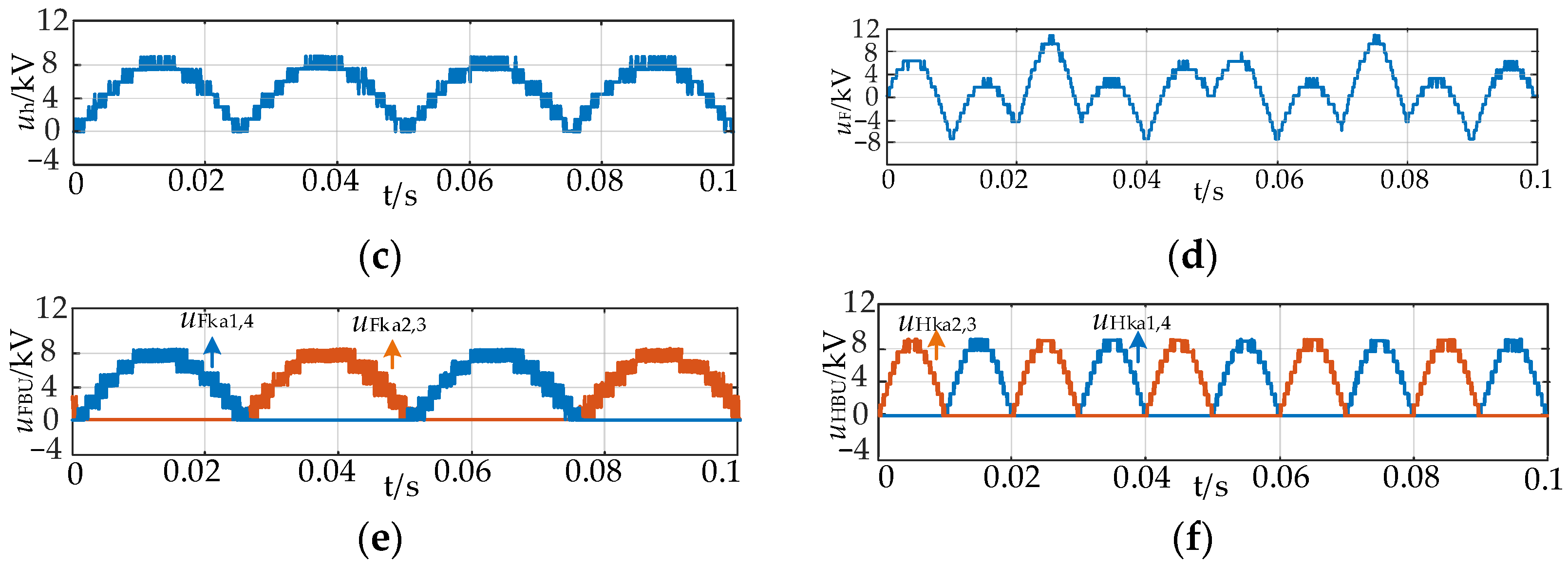
5.1. SMMC Normal Operations

Figure 13 shows the key waveforms of the SMMC during normal operations from 0 s to 0.1 s. As shown in Figure 13a,b, the grid-side full-wave multi-level voltage values u_gu and u_ga are converted into a half-wave multi-level voltage u_Hu by the HBU switch. As shown in Figure 13c, the low-frequency full-wave multi-level voltage u_s is converted into a low-frequency half-wave multi-level voltage u_ha by the FBU switch. As shown in Figure 13d, the FBA voltage u_Fa is the difference between u_ha and u_Hu. The voltages u_Fka1,4 and u_Fka2,3 of k_a1,4 and k_a2,3 in the FBU are shown in Figure 13e, and the voltages u_Hka1,4 and u_Hka2,3 of k_a1,4 and k_a2,3 in the HBU are shown in Figure 13f.

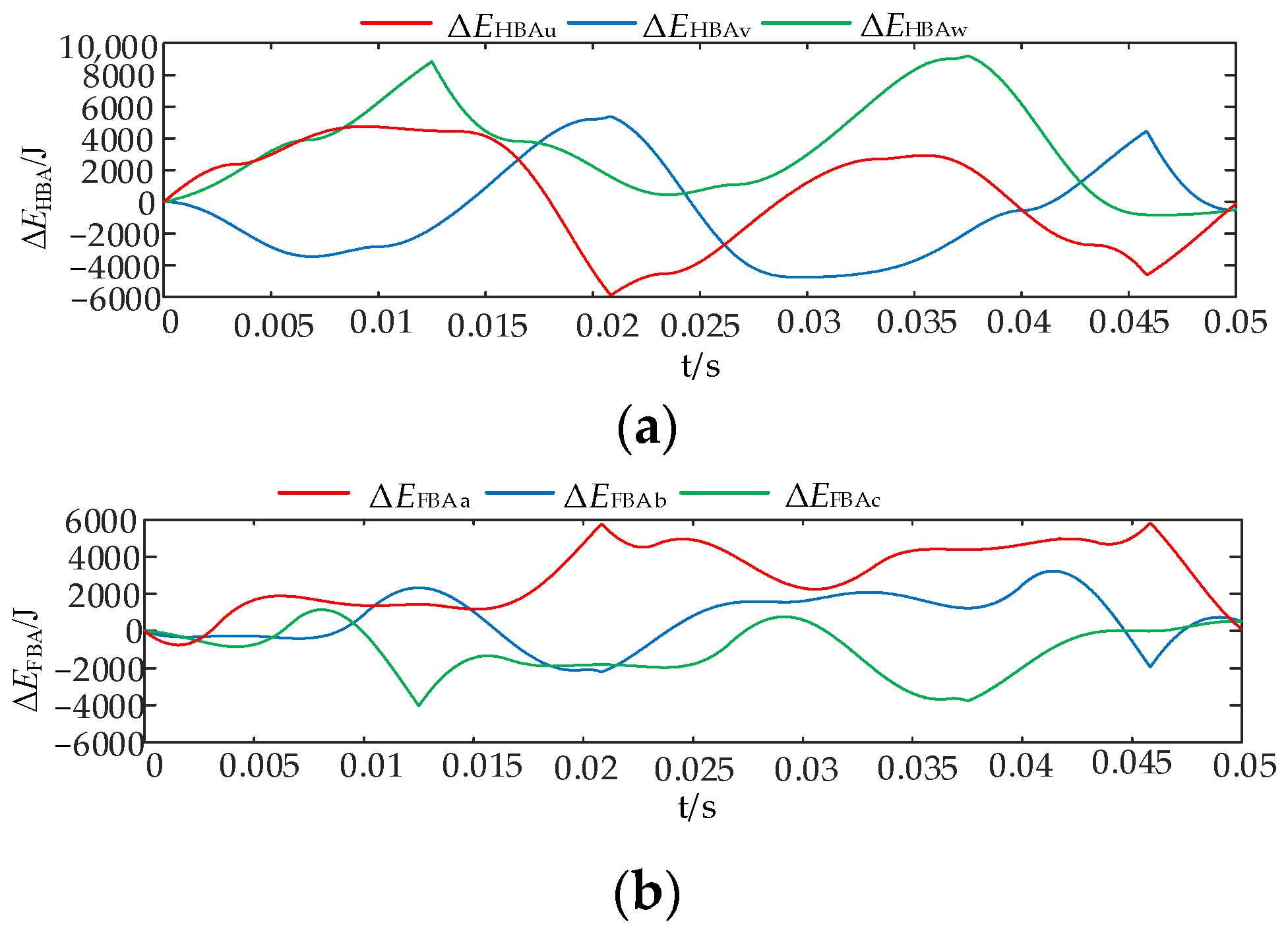
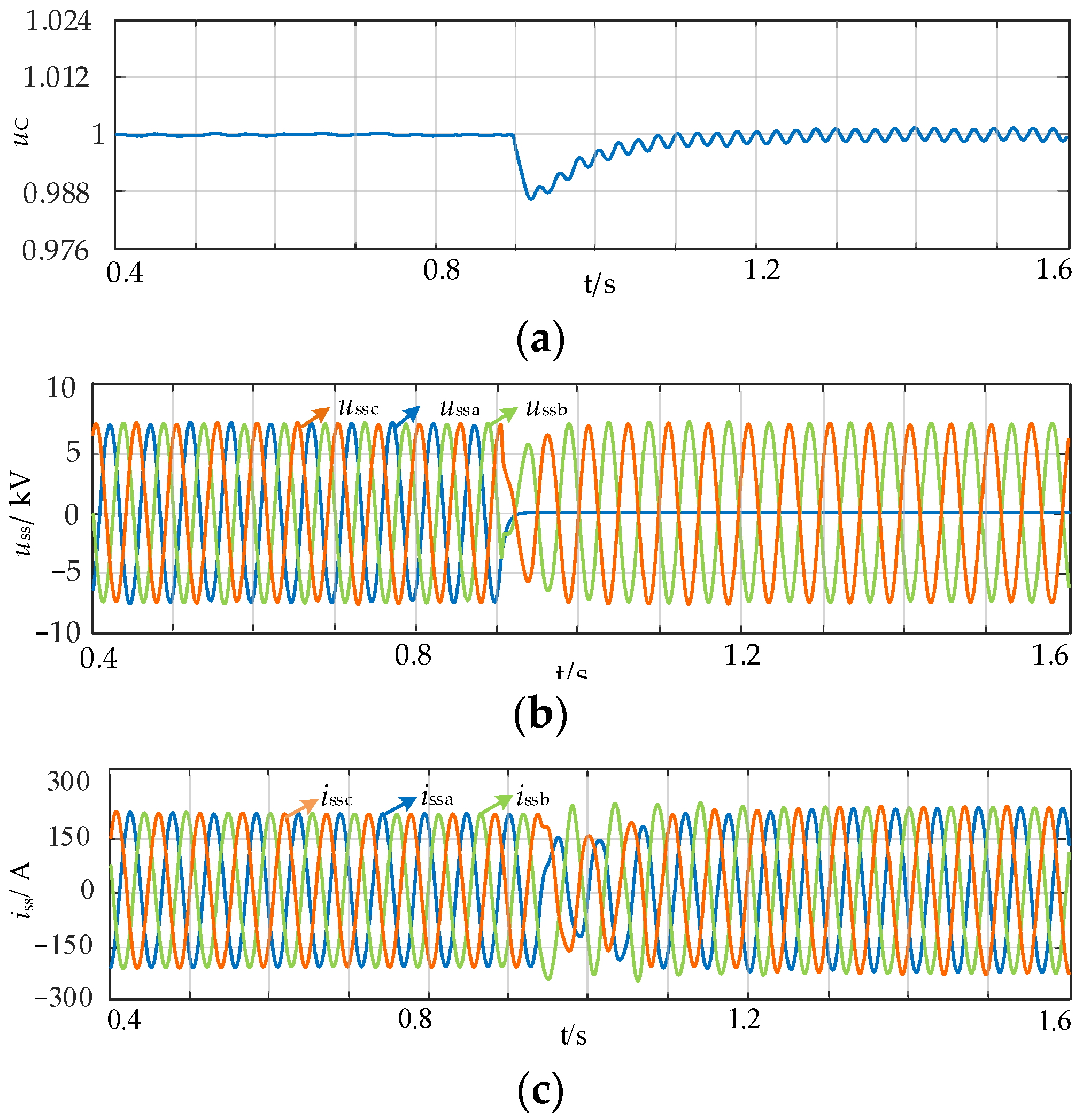
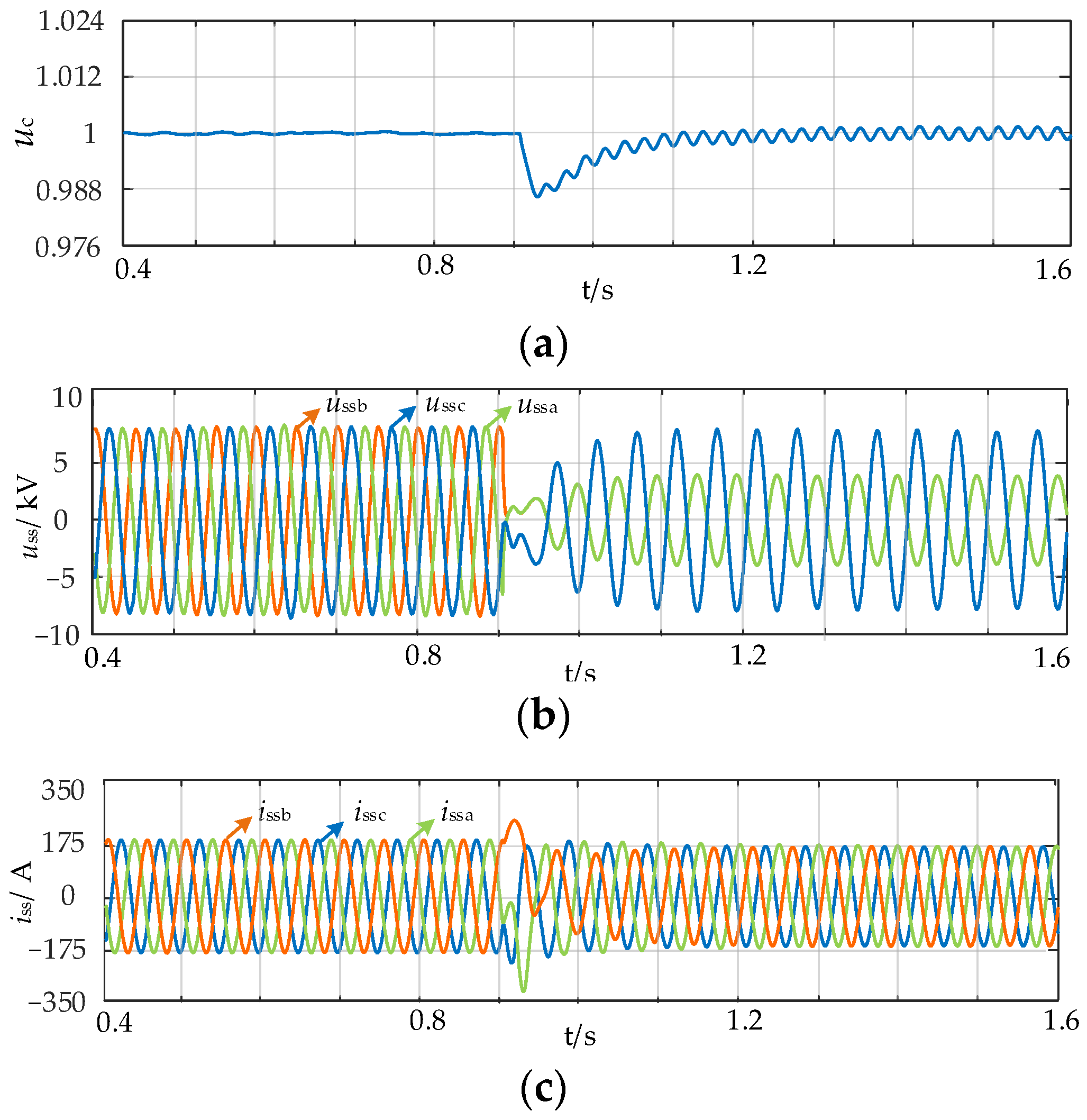
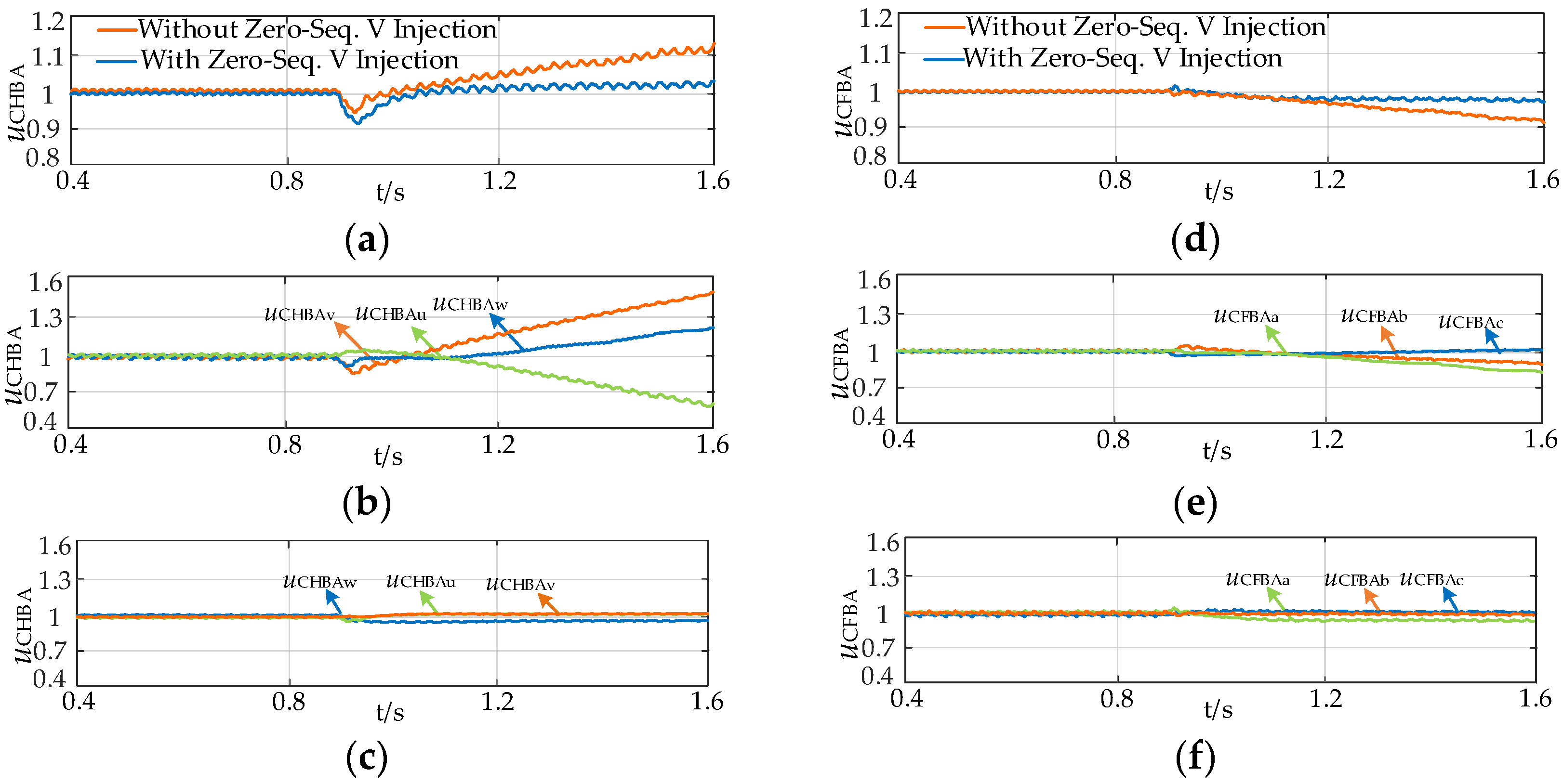
5.2. Single-Phase Ground Fault

To verify the control strategy proposed in this study, a single-phase ground fault is set at the low-frequency cable side of the SMMC station at 0.9 s. Upon detection of the negative sequence voltage and the fault type, zero-sequence voltage is injected into the low-frequency side of the SMMC. Simultaneously, the reference value of the low-frequency-side AC voltage is switched to achieve the specified power factor angle on the low-frequency side. The simulation results of the single-phase fault under the proposed control are shown in Figure 14. As shown in Figure 14a, the total average voltage of all the capacitors of the three-phase submodules, u_C, remains at the rated value before and during the fault. Figure 14b shows that, under the conditions of overvoltage suppression control, the voltage of the non-fault-phase on the low-frequency cable side is regulated to the rated value, and the overvoltage is suppressed. As shown in Figure 14c, during the fault, the three-phase currents on the low-frequency side of the SMMC are symmetrical, and the negative sequence current is suppressed to zero.

Figure 15 shows the average value curves of the three-phase input power of the SMMC with and without the zero-sequence injection energy balance strategy. With a zero-sequence voltage injection, the zero-sequence power offsets the unbalanced impact of the negative sequence voltage on the three-phase input power, achieving symmetrical three-phase active power.

Figure 16 shows the sub-module capacitor voltage waveforms of the SMMC half-bridge and full-bridge arms under a single-phase fault, where u_CHBAu, u_CHBAv, and u_CHBAw represent the average capacitor voltages of phase u, phase v, and phase w, respectively, and u_CFBAa, u_CFBAb, and u_CFBAc represent the average capacitor voltages of phase a, phase b, and phase c, respectively. As shown in Figure 16, without the energy balance strategy, after the fault persists for 625 ms, the average value of the capacitor voltage of all sub-modules in the three-phase half-bridge arms deviates by about 15% from the rated value, and the degree of deviation varies among the three phases (approximately 30% for u_CHBAu and 35% for u_CHBAv and u_CHBAw). This indicates a severe energy imbalance, which fails to meet the fault ride-through requirements. When the energy balance control strategy proposed in this study is adopted, the average capacitor voltage of all sub-modules in the three-phase half-bridge arms remains near the rated value. The average value of the sub-module capacitor voltages of each phase half-bridge briefly deviates from the rated value after the fault but essentially recovers to a balanced and stable state within about 0.1 s. At 625 ms after the fault occurring, the maximum voltage deviation does not exceed 5% of the rated value, which is beneficial to fault ride-through and fault recovery. The variations in the sub-module capacitor voltage of the full-bridge arms are similar to those of HBAs. Using the energy balance control strategy, the average capacitor voltage of all sub-modules in the three-phase full-bridge arms remains close to the rated value.

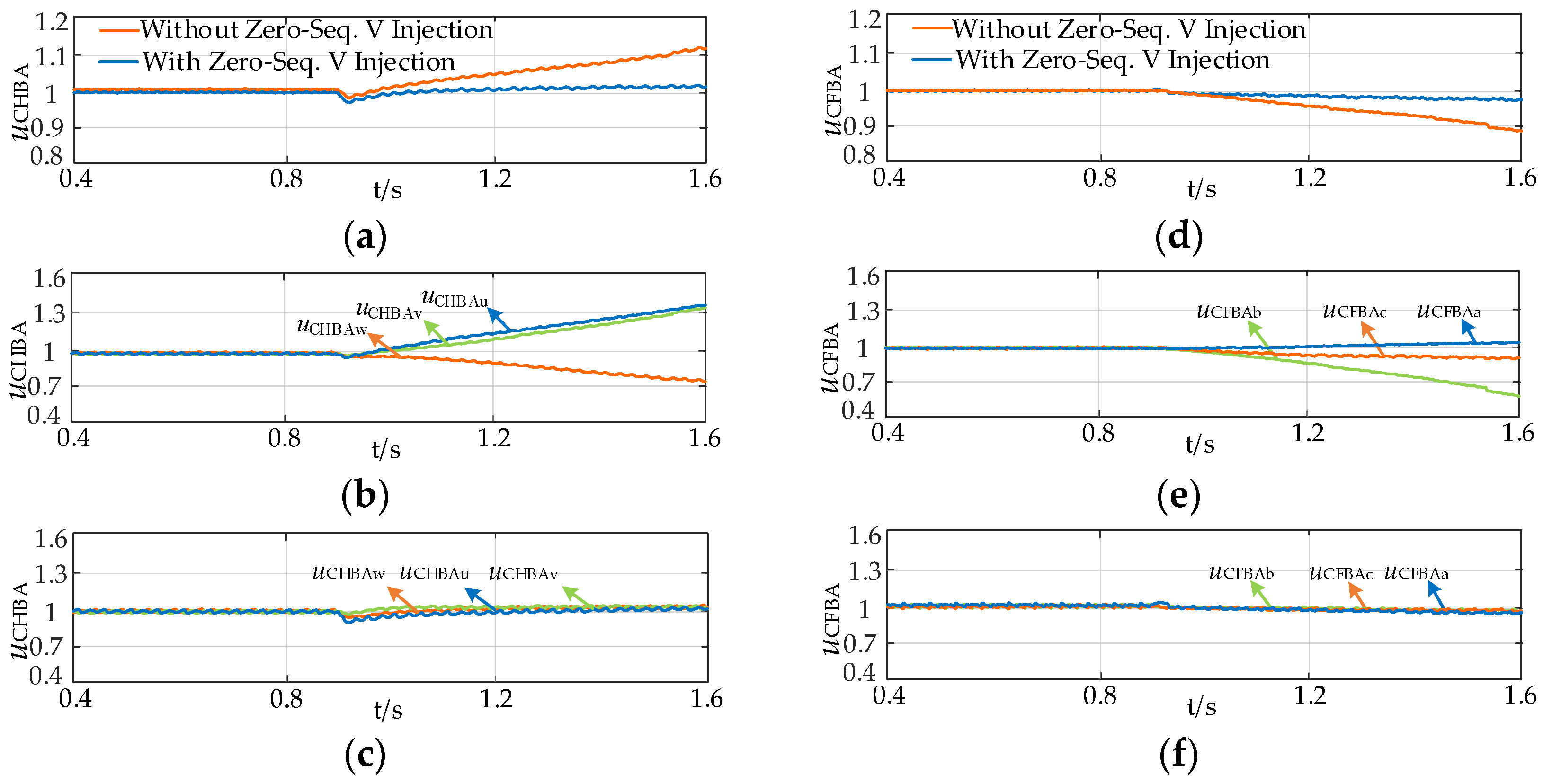
5.3. Two-Phase Interphase Short-Circuit Fault

Figure 17 shows the SMMC simulation results for a situation in which a two-phase short-circuit fault occurs between phase b and phase c in the low-frequency line. The average values of the capacitor voltage of the three-phase sub-modules and the low-frequency cable-side AC voltage and current are shown in Figure 17. The negative sequence current and overvoltage are suppressed after the fault, the average capacitor voltage of all sub-modules in the three-phase arms remains stable, and the total energy of the converter remains balanced.

Based on Figure 18, when using the zero-sequence injection energy balance strategy, the three-phase input power reaches equilibrium in 0.3 s after the fault.

The average capacitor voltages of the sub-modules in the three-phase and single-phase half-bridge and full-bridge arms are shown in Figure 19. Without the energy balance strategy, the average capacitor voltages of each phase in the half-bridge and full-bridge arms deviate significantly from the rated value and diverge over time, indicating a severe energy imbalance that fails to meet fault ride-through requirements. In contrast, when using the energy balance control strategy proposed in this study, the average capacitor voltages of the sub-modules in the half-bridge and full-bridge arms enter a stable state approximately 0.1 s after the fault, not diverging over time. At 625 ms after the fault, the voltage deviation is within 10% of the rated value, which is beneficial for fault ride-through and fault recovery.

6. Conclusions

Targeting the SMMC low-frequency transmission system, this study proposes an arm energy balance method and a fault ride-through control strategy under asymmetric faults, with the aim of achieving the safe and stable operation of the system. Based on a theoretical analysis and simulations, the following conclusions can be drawn:

• When an asymmetric fault occurs on the low-frequency side of the SMMC transformer, the asymmetric phase voltage causes different balancing targets for the three-phase arms of the SMMC. Using the traditional control strategy in this situation will result in an imbalanced distribution of energy among phases and within phases, threatening the stable operation of the system.
• Based on the analysis of the energy imbalance mechanism, under asymmetric faults on the low-frequency side, the amplitude and phase of the zero-sequence voltage injection in the SMMC must meet specific conditions to achieve energy balance in all arms, ensuring the capacitor voltage in the half-bridge and full-bridge arm modules does not exceed 10%, which is beneficial for fault ride-through and fault recovery.
• The proposed fault ride-through strategy for the low-frequency transmission system, based on a zero-sequence voltage injection and constant power factor angle AC voltage control, can maintain energy balance in the half-bridge and full-bridge arms of the SMMC while suppressing negative sequence current and overvoltage. This ensures the ride-through of asymmetric faults on the low-frequency side.