Automatic Modulation Classification of Mixed Signals Based on Phase Noise-Insensitive High-Order Cumulant and Distribution Characteristics in Radio-over-Fiber System

Abstract

To overcome the limitations of existing automatic modulation classification (AMC) methods that mainly target single-signal scenarios in radio-over-fiber (RoF) system, a mixed-signal AMC scheme based on phase noise-insensitive high-order cumulants (PNI-HOC) and distribution characteristics is proposed. The approach enables accurate classification of mixed signals in RoF system. Specifically, a PNI-HOC algorithm is first introduced to mitigate the influence of laser linewidth-induced phase noise. Then, distribution characteristics derived from the signal amplitude histogram are extracted to construct a two-dimensional characteristics space. These characteristics are subsequently fed into decision tree and support vector machine (SVM) classifiers for signal identification. To validate the effectiveness of the scheme, a 10 GBaud RoF system with a 70 km fiber link is implemented. The simulation results show that, compared with the conventional high-order cumulant method, the approach solely based on amplitude histogram distribution characteristics and the scheme based on deep neural networks (DNN) classifier using histogram characteristics, the proposed scheme achieves significantly higher classification accuracy at low optical signal–noise ratios (OSNRs). In particular, when the fiber length is 70 km and the OSNR is ≥16 dB, the classification accuracy of mixed signals is consistently maintained at 100%. Furthermore, the robustness of the proposed method is verified under various system impairments, including laser phase noise, chromatic dispersion and nonlinear effects, amplified spontaneous emission noise, multipath fading, etc., confirming its superior and stable performance.

1. Introduction

With the rapid advancement of emerging technologies, the demand for high-capacity and high-speed transmission continues to grow [1,2,3]. However, the spectrum below 6 GHz is becoming increasingly congested, while the millimeter-wave (mmWave) band from 30 to 300 GHz, despite its vast potential, remains underutilized. Owing to its short wavelength, high propagation loss, and severe multipath effects, mmWave communication suffers from a limited transmission range in wireless channels, posing challenges to achieving large scale and reliable connectivity. Radio-over-fiber (RoF) technology provides a promising solution by integrating the flexible access of wireless communication with the high bandwidth and low attenuation of optical fiber links. This combination not only extends the transmission distance of mmWave signals and reduces system cost but also enables Gbps-level high-speed data transmission. Consequently, RoF offers a feasible pathway for constructing next generation wireless networks with high capacity and broad coverage.

On the basis of efficient transmission of the RoF system, accurate identification of signal modulation formats in complex environments has become a key challenge for further improving communication performance. Automatic modulation classification (AMC) is a promising technology with wide ranging applications, playing a critical role in both modern military communications and civilian electromagnetic monitoring. Typical applications include intercepted signal demodulation and recovery, spectrum surveillance, and related tasks [4,5,6]. In recent years, AMC has been the focus of extensive researches, giving rise to a variety of methods that can generally be classified into two categories: likelihood-based (LB) decision theoretic approaches, which rely on likelihood ratio tests, and feature-based (FB) statistical pattern recognition approaches, which rely on feature extraction. Compared with LB methods, FB approaches have attracted more attention in recent years due to their advantages of lower computational complexity and more stable performance [7]. For instance, a novel feature derived from fourth-order and sixth-order cumulants was proposed in [8], where a neural network classifier was employed to distinguish nine modulation formats, including ASK, PSK, and MSK. Similarly, nonlinear power transformation techniques have been applied for the classification of M-ary PSK and QAM signals [9]. More recently, deep learning-based AMC methods have gained significant traction, leveraging models such as deep neural networks (DNNs) [10,11], residual neural networks (ResNets) [12,13], convolutional neural networks (CNNs) [14,15], and long short-term memory networks (LSTMs) [16,17].

In RoF systems, complex optical impairments such as phase noise, chromatic dispersion, and fiber nonlinearities significantly challenge the performance of traditional AMC algorithms originally designed for wireless communication environments, highlighting the urgent need for targeted improvements and optimization. To address this issue, an autoencoder neural network was proposed for automatic feature extraction and classification in RoF systems [18]. Meanwhile, with the widespread deployment of diverse devices such as radar, communication, navigation, and broadcasting, multiple signals from different sources are often received simultaneously, leading to increasingly severe time–frequency aliasing. In such environments, conventional AMC methods designed for single-signal scenarios are no longer sufficient for practical applications. Consequently, recent research has shifted toward AMC algorithms for mixed signals. For example, a mixed-signal recognition method based on cyclic spectral projection and deep neural network is proposed, using gray projection on the two-dimensional cyclic spectrum for feature enhancement, achieving effective recognition of mixed signals [19]. A multi-signal modulation classification method based on sliding window detection and a frequency-domain complex CNN is proposed. The overlapping time-domain signals are transformed via FFT, segmented by energy detection, and classified accurately using the CNN [20]. However, these methods still do not consider the influence of complex optical impairment effects such as laser phase noise, dispersion, and nonlinear effects on the performance of mixed-signal AMC. Therefore, the development of a high-efficiency mixed-signal AMC technique for RoF system is both necessary and highly anticipated.

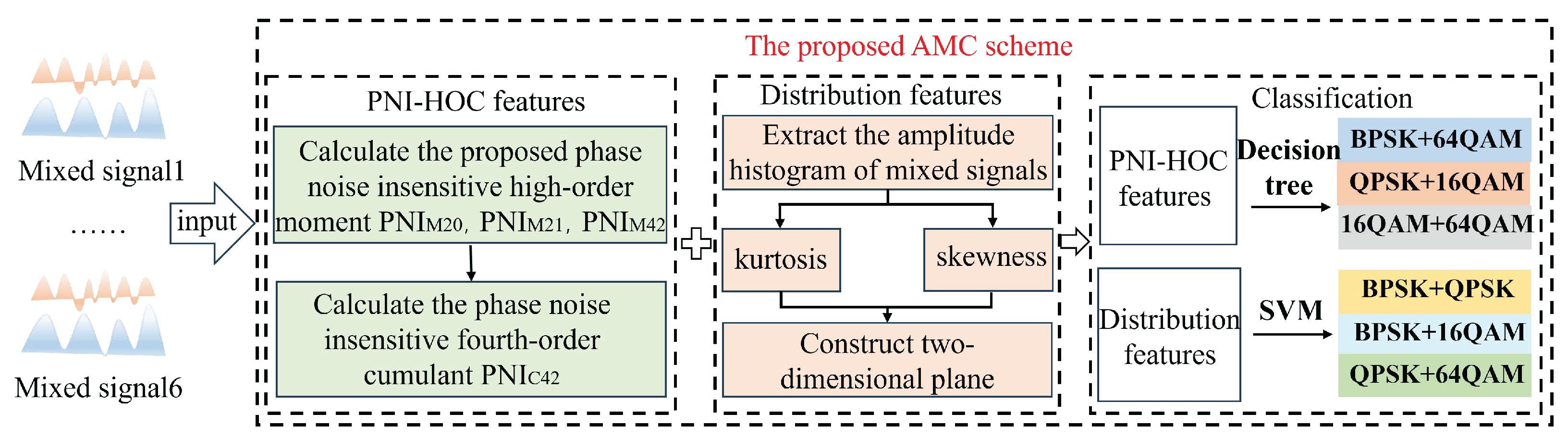
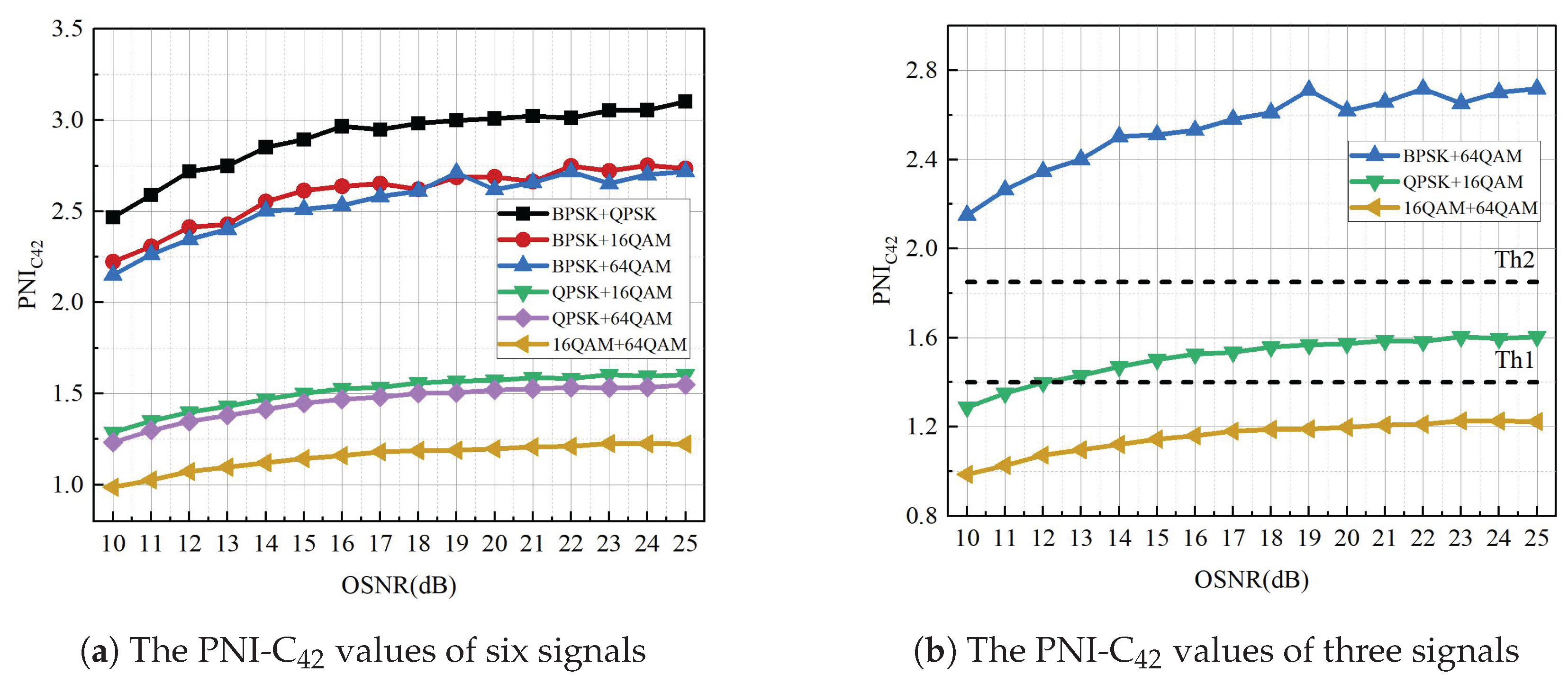
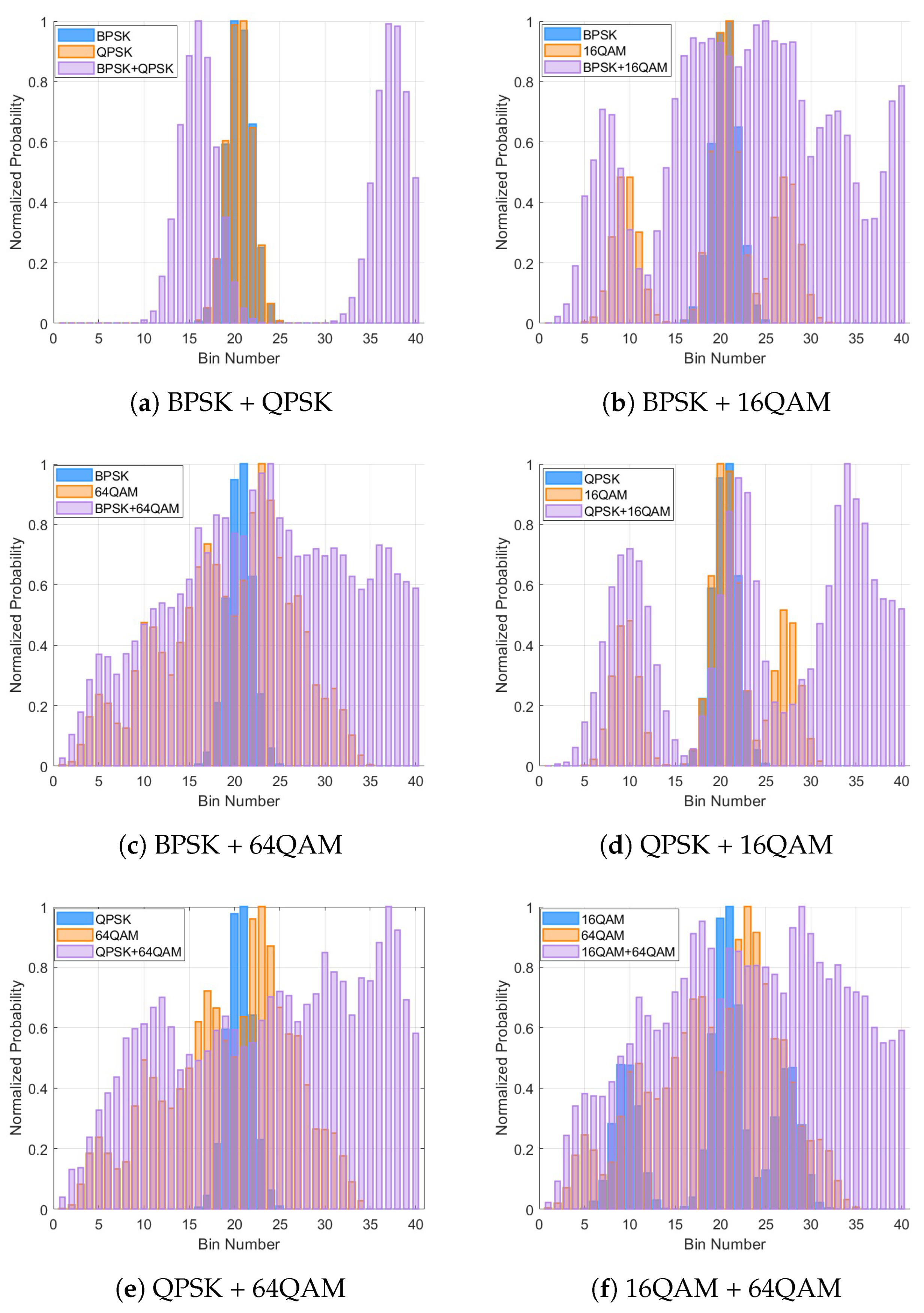
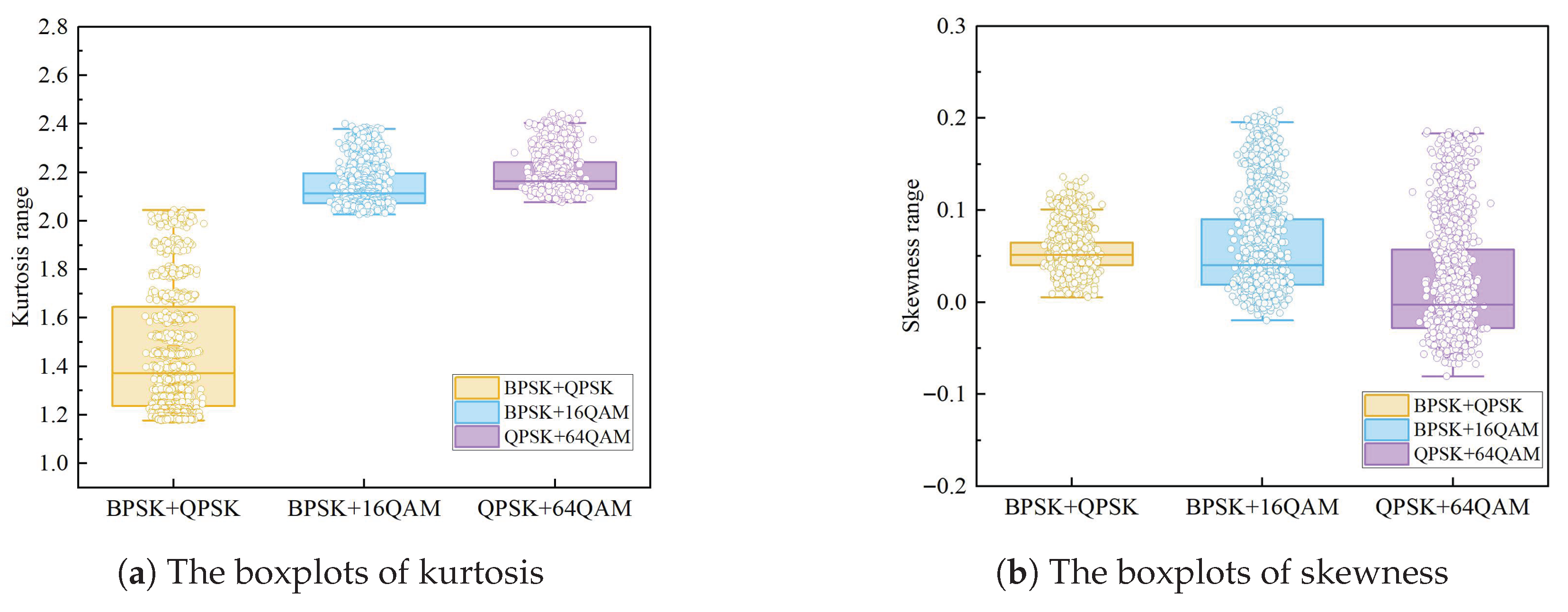
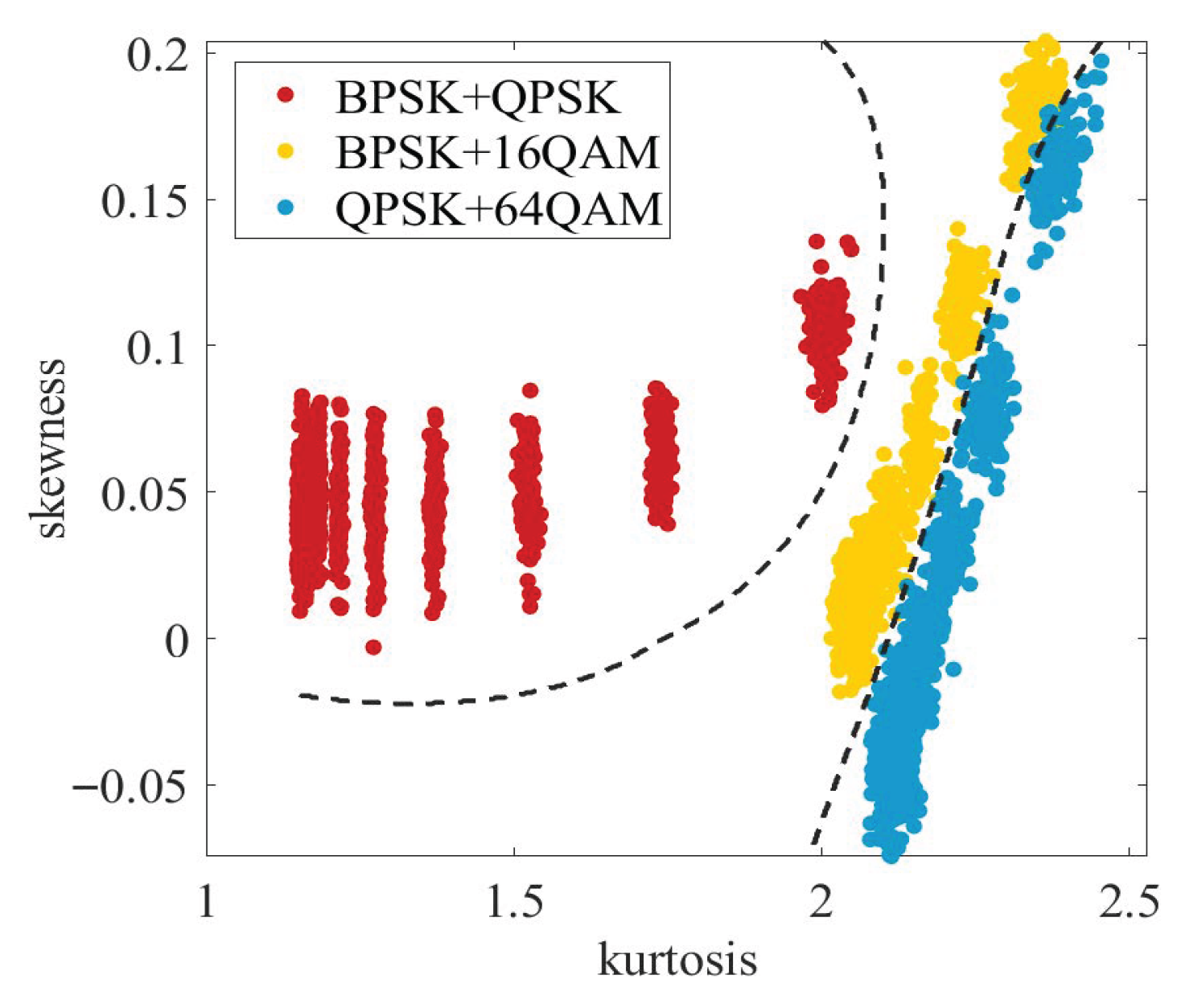
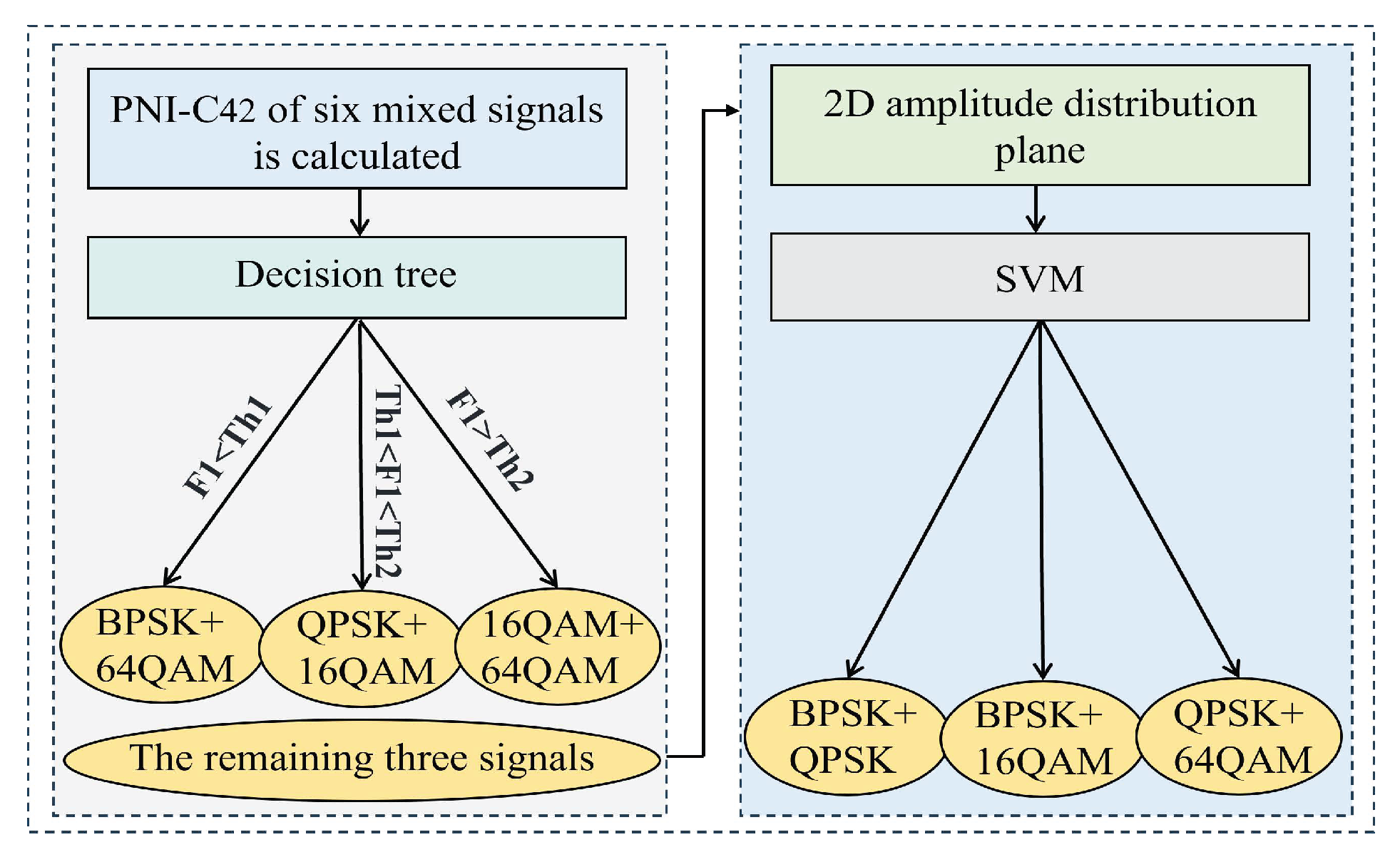
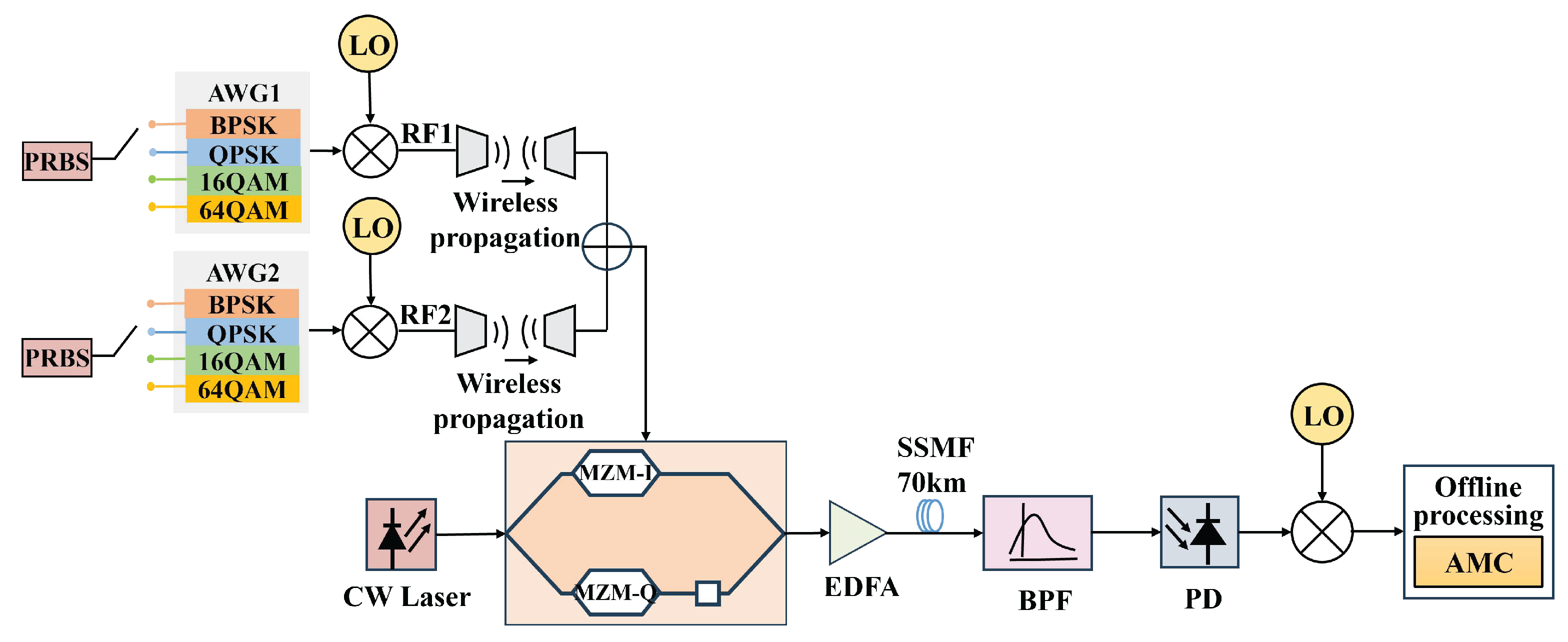
In this paper, a mixed-signal AMC method based on PNI-HOC and distribution characteristics in ROF system is proposed, which can accurately identify the mixed modulation formats. Firstly, a PNI-HOC algorithm is proposed and its value for the mixed signal is calculated. Then, the distribution characteristics kurtosis and skewness of the signal histogram are extracted to construct a two-dimensional plane. These characteristics are subsequently input into decision tree and support vector machine (SVM) classifiers for modulation classification. The proposed method effectively compensates for the influence of laser phase noise on high-order cumulants and achieves reliable identification of mixed modulation formats. To validate its effectiveness, a 10 GBaud RoF system with a 70 km fiber link is simulated, with the OSNR varied from 10 dB to 25 dB in 1 dB increments. The AMC scheme determines the six mixed signals composed of PSK signals and QAM signal, namely BPSK + QPSK, BPSK + 16QAM, BPSK + 64QAM, QPSK + 16QAM, QPSK + 64QAM, and 16QAM + 64QAM. To demonstrate the feasibility and superiority of this scheme, simulation results show that, compared with the conventional high-order cumulant method, the approach solely based on amplitude histogram distribution characteristics and the scheme based on the deep neural network (DNN) classifier using histogram characteristics, the proposed scheme achieves superior classification performance at low OSNR. In particular, when the fiber length is 70 km and the OSNR is ≥16 dB, the recognition accuracy of the six mixed signals remains consistently at 100%.

2. Theory and Principle

The system principle of the proposed mixed-signal AMC method for the RoF system based on PNI-HOC and distribution characteristics is illustrated in Figure 1. First, to mitigate the effect of laser phase noise on high-order cumulants, the PNI-HOC algorithm is applied, and the $PN{I}_{C_{42}}$ values of the mixed signals are computed. The characteristics are then input into a decision tree classifier, enabling accurate identification of three out of the six mixed-signal types. Subsequently, kurtosis and skewness are extracted from the signal amplitude histogram to construct a two-dimensional characteristics space. Within this space, the remaining three mixed signals are effectively classified using an SVM classifier.

2.1. The Received Signal Model

Assume that the expression of the received signal is

$$s\left(t\right)=A\left(t\right)e^{j(\omega t+\varnothing (t)+\theta (t\left)\right)}+n\left(t\right),$$

(1)

where $A\left(t\right)$ denotes the amplitude, $\omega t$ is the ideal phase, $\varnothing \left(t\right)$ is the useful phase information, $\theta \left(t\right)$ resprents the phase noise component, and $n\left(t\right)$ is the noise component. Assume that the amplitude term and the phase component are statistically independent.

The laser phase noise $\theta \left(t\right)$ is modeled as a Wiener process [21]:

$$\begin{array}{c}\hfill \theta \left(t\right)=\sum _{i=-\infty }^k{v}_i.\end{array}$$

(2)

$\theta \left(t\right)$ is an independent uniformly distributed Gaussian random variable with zero mean and variance ${\sigma }^2$ [22]. ${\sigma }^2$ can be expressed as

$$\begin{array}{c}\hfill {\sigma }^2=2\pi \Delta vT,\end{array}$$

(3)

$$\begin{array}{c}\hfill T=N\ast T_s,\end{array}$$

(4)

where $\Delta v$ is the laser linewidth, $T_s$ is the symbol period, and N is a multiple of the number of signal symbols.

Assume that in the receiver, K independent narrowband signals fall within the bandwidth of the receiver and these signals are statistically independent of each other. Each signal can be fully received for a period of time with the presence of noise interference. Then the mathematical model of the mixed signal is expressed as

$$\begin{array}{c}\hfill S\left(t\right)=\sum _{i=1}^K{s}_i\left(t\right)+n\left(t\right)=\sum _{i=1}^K{A}_i\left(t\right)e^{j\left({\omega }_{i}t+{\phi }_i\left(t\right)+{\theta }_i\left(t\right)\right)}+n\left(t\right),\end{array}$$

(5)

where $s_i\left(t\right)$ is i-th the received signal, and $n\left(t\right)$ is the noise component.

The received signal and noise are statistically independent of each other. This study investigates modulation identification for mixed signals, so the signal model in this paper is expressed as

$$\begin{array}{cc}\hfill S\left(t\right)& =s_1\left(t\right)+s_2\left(t\right)+n\left(t\right),\hfill \end{array}$$

(6)

where $s_1\left(t\right)$ and $s_2\left(t\right)$ denote any two power-normalized baseband signals selected from BPSK, QPSK, 16QAM, and 64QAM, such that the power ratio is 1:1.

2.2. The Theory of Algorithm Based on PNI-HOC

2.2.1. High-Order Cumulant Algorithm

High-order cumulants are widely used in the field of modulation identification, which can reflect the high-order statistical properties of signals. High-order cumulants not only have good anti-fading properties, but also can effectively suppress Gaussian noise and are robust to the rotation and offset of constellation diagrams [23]. Assuming that $s_i\left(t\right)$ is the original signal restored by demodulation in ROF system, the p-order mixing moment is [24]

$$\begin{array}{c}\hfill M_{pq}=E\left\{{s_i\left(t\right)}^{p-q}{\left[s_i^{*}\left(t\right)\right]}^q\right\},\end{array}$$

(7)

where $E\left\{\right\}$ represents taking the expectation, * represents taking the conjugate, and q represents the number of conjugate sequences taken. Then, when $q=0$, $M_{p0}$ can be expressed as

$$\begin{array}{c}\hfill M_{p0}=E\left[{s_i\left(t\right)}^p\right]=E\left[{A_i^p\left(t\right)\ast e}^{pj\left({\omega }_{i}t+{\varnothing }_i\left(t\right)+{\theta }_i\left(t\right)\right)}\right].\end{array}$$

(8)

When $q\ne 0$, $M_{pq}$ can be expressed as

$$\begin{array}{c}\hfill M_{pq}=E\left\{{s_i\left(t\right)}^{p-q}{\left[s_i^{*}\left(t\right)\right]}^q\right\}=E\left[A_i^{p-q}\left(t\right)\right].\end{array}$$

(9)

2.2.2. Phase Noise-Insensitive High-Order Cumulant Algorithm

In ROF systems, the signal phase is affected by the laser linewidth. A broader linewidth results in larger phase noise, which in turn degrades signal quality. As shown in Equation (8), when $q=0$, the phase noise component $\theta \left(t\right)$ is enlarged, thereby amplifying the impact of phase noise on $M_{p0}$. Since assuming that the phase noise $\theta \left(t\right)$ follows a Wiener process with zero mean and variance ${\sigma }^2$, then $M_{p0}$ can also be expressed as

$$\begin{array}{c}\hfill M_{p0}=E\left[A_i^p\left(t\right)e^{jp({\omega }_{i}t+{\varphi }_i\left(t\right))}\right]·E\left[e^{jp{\theta }_i\left(t\right)}\right]=E\left[A_i^p\left(t\right)e^{jp({\omega }_{i}t+{\varphi }_i\left(t\right))}\right]·e^{-{\displaystyle \frac{1}{2}}{p}^2{\sigma }^2}.\end{array}$$

(10)

As the laser linewidth broadens, the associated phase noise intensifies, leading to greater deviations of $M_{p0}$ from its theoretical values. To mitigate this error, when $q=0$, the expression of the proposed PNI-HOC algorithm is

$$\begin{array}{c}\hfill PN{I}_{M_{p0}}=M_{p0}·e^{{\displaystyle \frac{1}{2}}{p}^2{\sigma }^2}.\end{array}$$

(11)

Even under increased laser phase noise, the proposed algorithm yields smaller deviations of $M_{p0}$ from its theoretical values.

From Equation (9), when $q\ne 0$, the signal is multiplied by its complex conjugate, thereby eliminating the phase noise component $\theta \left(t\right)$. This operation effectively mitigates the influence of phase noise, such that even with increasing laser linewidth, its impact on the values of $M_{pq}$ remains minimal. Accordingly, the proposed algorithm for the case of $q\ne 0$ is

$$\begin{array}{c}\hfill PN{I}_{M_{pq}}=M_{pq}.\end{array}$$

(12)

Then, the PNI-HOC of the signal $s\left(t\right)$ can be calculated using mixed moments, and the expression between the forth-order PNI-HOC and PNI-HOMs is

$$\begin{array}{cc}\hfill PN{I}_{C_{42}}=& PN{I}_{M_{42}}-{\left|PN{I}_{M_{20}}\right|}^2-2{\left(PN{I}_{M_{21}}\right)}^2.\hfill \end{array}$$

(13)

From Equation (12), the values of the $PN{I}_{C_{42}}$ of the four modulation formats can be calculated. Due to the “semi-invariance” property of high-order cumulants, if two random processes X_i and Y_i are independent, then

$$\begin{array}{c}\hfill Cum\left(X_1+Y_1,\dots ,X_k+Y_k\right)=Cum\left(X_1,\dots ,X_k\right)+Cum\left(Y_1,\dots ,Y_k\right).\end{array}$$

(14)

Then, the PNI-HOC of the mixed signal S(t) affected by Gaussian white noise can be expressed as

$$\begin{array}{c}\hfill Cum\left(S\left(t\right)\right)=Cum\left(s_1\left(t\right)\right)+Cum\left(s_2\left(t\right)\right).\end{array}$$

(15)

From Equation (14), the $PN{I}_{C_{42}}$ of mixed signals formed by any two of the four modulation formats can be derived. In this paper, $PN{I}_{C_{42}}$ is employed as the primary feature parameter to distinguish six types of mixed signals. The theoretical values of $PN{I}_{C_{42}}$ for these six mixed signals are summarized in

Table 1. Theoretical characteristic parameter $PN{I}_{C_{42}}$.

Signal Type	${\mathit{PNI}}_{{\mathit{C}}_{42}}$
BPSK + QPSK	3
BPSK + 16QAM	2.68
BPSK + 64QAM	2.619
QPSK + 16QAM	1.68
QPSK + 64QAM	1.619
16QAM + 64QAM	1.299

. As observed from Table 1, the characteristic values exhibit clear differences across the mixed signals, demonstrating that $PN{I}_{C_{42}}$ can serve as an effective discriminating feature.

Figure 2 illustrates the relationship between $PN{I}_{C_{42}}$ and the OSNR for the six mixed modulation formats, where each $PN{I}_{C_{42}}$ value is obtained by averaging over 100 signal realizations. As shown in Figure 2a, the $PN{I}_{C_{42}}$ values of the six mixed signals are stable and close to the theoretical values in the OSNR range of 10 to 25 dB even in the presence of significant phase noise. However, since the $PN{I}_{C_{42}}$ characteristic curves of several mixed signals are closely spaced, complete discrimination among all six signals cannot be achieved. To address this, as shown in Figure 2b, $PN{I}_{C_{42}}$ is first employed to distinguish three of the six mixed signals, namely BPSK + 64QAM, QPSK + 16QAM, and 16QAM + 64QAM, while the remaining three mixed signals require further classification.

2.3. Constructing the Two-Dimensional Plane of Intensity Distribution

As illustrated in Figure 3, the amplitude histograms of different mixed signals exhibit distinct distribution characteristics, which are exploited as distinguishing characteristics in the proposed scheme. In particular, the kurtosis and skewness of the signal amplitude histogram are utilized to differentiate the remaining three mixed signals.

Kurtosis, also referred to as the kurtosis coefficient, is a statistical measure that characterizes the tailedness of the probability distribution of a real-valued random variable, providing a descriptor of the distribution’s shape. Intuitively, it reflects the sharpness of the distribution peak. In the proposed scheme, kurtosis is employed as one of the distribution characteristics extracted from the signal amplitude histogram and is defined as [25]

$$K_{s\left(t\right)}=\mathrm{Kurtosis}\left(D\left(n\right)\right),$$

(16)

where $D\left(n\right)$ is the intensity information of the mixed signal. The amplitude histograms of different mixed signals exhibit varying degrees of peakedness, which are reflected in their distinct kurtosis values.

In addition, skewness is employed as another intensity distribution feature. In probability theory and statistics, skewness quantifies the asymmetry of a probability distribution relative to its mean, serving as a complementary descriptor of the distribution’s shape. The skewness value may be positive, negative, or in some cases undefined. In the proposed scheme, kurtosis and skewness are jointly extracted from the signal amplitude histograms as distribution characteristics, with kurtosis defined as [25]

$$S_{s\left(t\right)}=\mathrm{Skewness}\left(D\right(n\left)\right).$$

(17)

The amplitude histograms of different mixed signals exhibit distinct skewness values, which facilitate the recognition of mixed signals. The boxplots of kurtosis and skewness for the three mixed signals types at a symbol count of 16,384 are shown in Figure 4. The distributions exhibit substantial overlap, indicating that neither feature alone can reliably distinguish the mixed signals. To address this, Figure 5 introduces a two-dimensional feature plane combining kurtosis and skewness, which clearly separates the three regions corresponding to BPSK + QPSK, BPSK + 16QAM, and QPSK + 64QAM. Accordingly, a two-dimensional feature plane-assisted support vector machine (SVM) can be employed to effectively separate these three mixed signals [26].

To evaluate the robustness of kurtosis and skewness against noise, we computed 95% confidence intervals and variances of kurtosis and skewness for each signal type. For BPSK + QPSK, the 95% confidence interval of kurtosis ranges from 1.4463 to 1.4716, with a variance of 0.0664, while the 95% confidence interval of skewness ranges from 0.0536 to 0.0557, with a variance of 0.0005. For BPSK + 16QAM, the kurtosis confidence interval extends from 2.1402 to 2.1489, with a variance of 0.0078, and the skewness confidence interval ranges from 0.0576 to 0.0629, with a variance of 0.0029. For QPSK + 64QAM, the kurtosis confidence interval spans from 2.1901 to 2.1981, with a variance of 0.0068, and the skewness confidence interval ranges from 0.0164 to 0.0225, with a variance of 0.0038. These narrow confidence intervals and small variances show that both characteristics remain statistically stable under noisy conditions. Moreover, the boxplots further indicate that the distribution ranges remain narrow across the OSNR range, confirming robustness against noise.

Additionally, we analyzed the effect of symbol counts on the variance of kurtosis and skewness. As shown in Figure 6, it can be observed that as the number of symbols increases, the kurtosis variance for the three mixed signals changes by only 0.0003, 0.0007, and 0.0011, while skewness variance changes by 0.0006, 0.0004, and 0.0005, respectively. These small variations indicate that the characteristics remain highly stable with respect to symbol count, further confirming their robustness in practical signal classification scenarios. Overall, the robustness of kurtosis and skewness to noise and symbol counts further demonstrates that these characteristics are well-suited for effective separation of mixed signals.

2.4. MFI Classifier Based on Decision Tree and SVM

In this paper, decision tree and SVM classifiers are employed to recognize six types of mixed signals. The classification flowchart based on decision tree and SVM scheme is illustrated in Figure 7. Initially, the characteristic feature $PN{I}_{C_{42}}$ values of the mixed signals are extracted. Since the $PN{I}_{C_{42}}$ values of certain mixed signals are relatively close, the six mixed signals cannot be completely distinguished using this feature alone. By leveraging the decision tree, $PN{I}_{C_{42}}$ can first separate three of the six mixed signals, namely BPSK + 64QAM, QPSK + 16QAM, and 16QAM + 64QAM. Subsequently, the kurtosis and skewness of the signal amplitude histograms are employed to construct a two-dimensional characteristic plane, where the remaining three mixed signals, namely BPSK + QPSK, BPSK + 16QAM and QPSK + 64QAM can be effectively distinguished using an SVM classifier.

As shown in Figure 7, the proposed scheme integrates the two classifiers to achieve accurate recognition of all six mixed signals. For the decision tree, three mixed signals are separated by applying thresholds based on the observed distribution of $PN{I}_{C_{42}}$ values. The thresholds Th1 and Th2 are set to 1.4 and 1.85, respectively, which are determined from the midpoints of the theoretical $PN{I}_{C_{42}}$ values for the mixed signals. A fine-tuned sweep around these midpoint values guided by the observed distribution of $PN{I}_{C_{42}}$ ensures accurate classification of the mixed signals, namely BPSK + 64QAM, QPSK + 16QAM, and 16QAM + 64QAM. Specifically, if F1 < Th1, the signal is identified as BPSK+64QAM; if Th1 < F1 < Th2, it is QPSK + 16QAM; and if F1 > Th2, it is 16QAM + 64QAM. For the SVM classifier, a Radial Basis Function (RBF) kernel is used due to its strong nonlinear mapping capability, which is essential for separating the three remaining mixed signal types. As shown in the 2D characteristics plane, the distributions exhibit nonlinear and curved decision boundaries. Compared with linear and polynomial kernels, the RBF kernel provides smooth boundaries, stable convergence, and the best generalization performance. Hyperparameters C and $\gamma$ were optimized via grid search with five-fold cross-validation, yielding optimal penalty parameter C = 100 and $\gamma$ = 10. In the simulation, 80% of samples were used for training and 20% for testing.

3. Simulation Setup

The configuration of the simulation system adopted in this paper is shown in Figure 8. First, pseudo-random bit sequence (PRBS) are fed into two arbitrary waveform generators (AWGs) to generate any two of the four 10 GBaud baseband signals, including BPSK, QPSK, 16QAM, and 64QAM. Then, the baseband signal is up-converted to a 50 GHz RF signal through mixing with the local oscillator (LO) signal, and after wireless propagation, the RF signals of different modulation formats are linearly superimposed to generate an RF mixed signal. The RF mixed signal is then applied to a Mach–Zehnder modulator (MZM) biased at 8 V, ensuring proper operation for single-sideband (SSB) modulation, with an RF drive power of approximately 4 dBm. The operating point of the MZM is adjusted so that the 1550 nm continuous wave (CW) laser carries a signle-sideband (SSB) signal, and the center frequency of the CW laser is 193.1 THz and the linewidth is 100 KHz. After the RF mixed signal is modulated into the optical signal, it is amplified by an erbium-doped fiber amplifier (EDFA) with the noise factor of 4.5 dB and transmitted into a 70 km standard single-mode fiber (SSMF). Set the attenuation, dispersion, and nonlinear refractive index coefficients of SSMF to 0.2 dB/km, 17 ps/nm/km and $26\times {10}^{-21} {\mathrm{m}}^2/\mathrm{W}$ respectively. At the receiver, the RF mixed signal passes through a band-pass filter (BPF) with a 20 GHz bandwidth to suppress out of band components, and then enters the photodector (PD) for beat frequency conversion to recover the electrical signal. Then, an offline processing module is applied to mitigate impairments and ensure the accuracy of subsequent classification. In the AMC module, the proposed AMC method based on PNI-HOC and distribution characteristics is employed to identify the modulation formats contained in the mixed signal. In all simulations, each OSNR value is obtained through 100 independent simulations with an OSNR interval of 1 dB and a range of 10 dB to 25 dB.

4. Simulation Results and Discussions

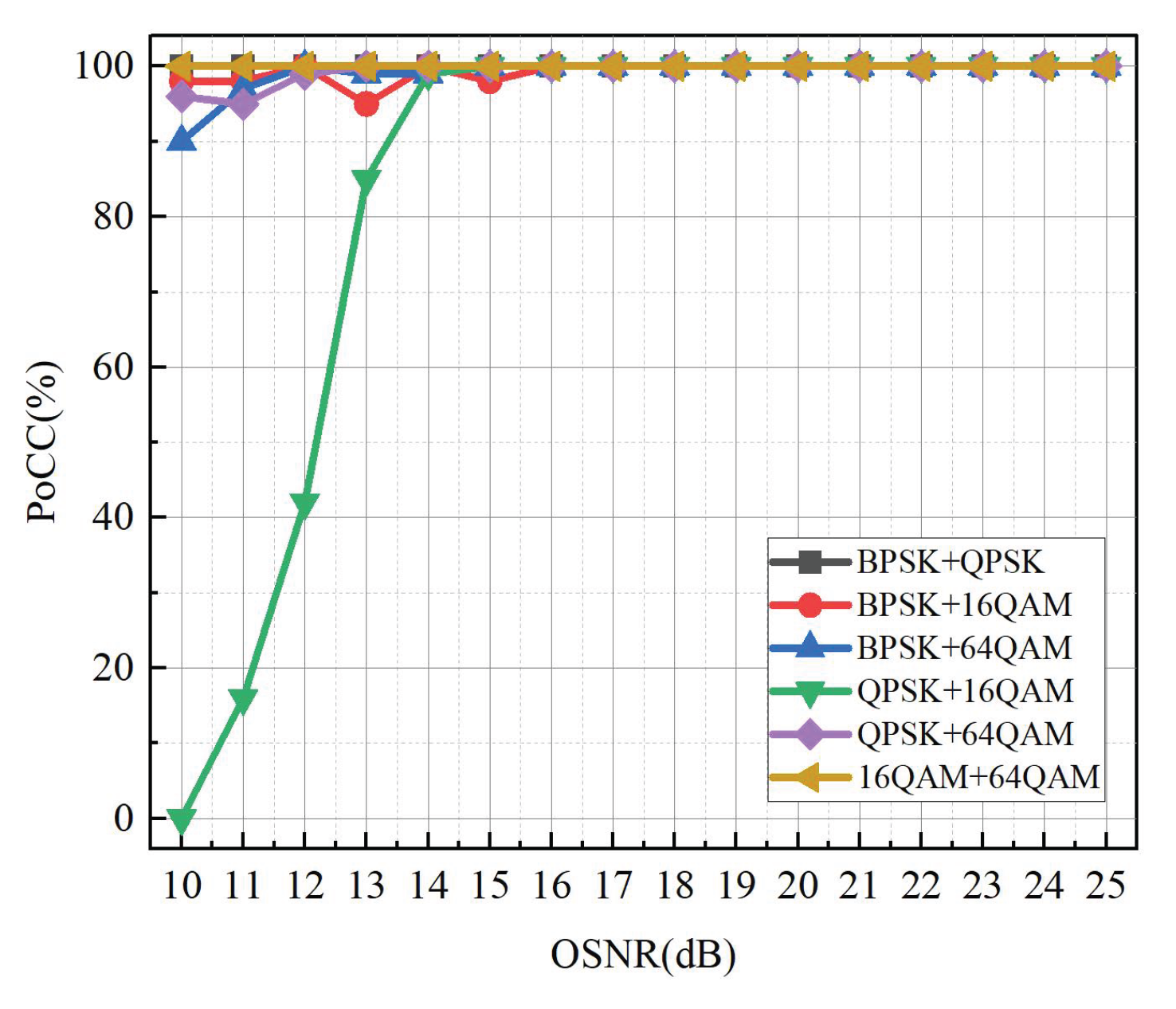
To validate the superiority and feasibility of the proposed scheme, simulations are conducted over a 70 km transmission link using the optimal configuration of training samples and symbols. Specifically, each modulation format sample contained 16,384 symbols, with 80% of the total samples allocated for training and the remaining 20% reserved for testing. Figure 9 presents the probability of correct classification (PoCC) for the six mixed signals under OSNR conditions ranging from 10 to 25 dB. The OSNR values at which the PoCC of BPSK + QPSK, BPSK + 16QAM, BPSK + 64QAM, QPSK + 16QAM, QPSK + 64QAM, and 16QAM + 64QAM reaches 100% and remains stable are 10 dB, 16 dB, 15 dB, 15 dB, 13 dB, and 10 dB, respectively. When the OSNR is relatively low, the received signal quality deteriorates due to increased noise, which can cause partial overlap of constellation points and lead to classification errors. However, even under lower OSNR conditions (<16 dB), the proposed scheme can still maintain a relatively high PoCC, with most mixed signals achieving accuracy above 90%. These results confirm that the proposed AMC method maintains high classification accuracy and demonstrates strong robustness, even under low OSNR conditions.

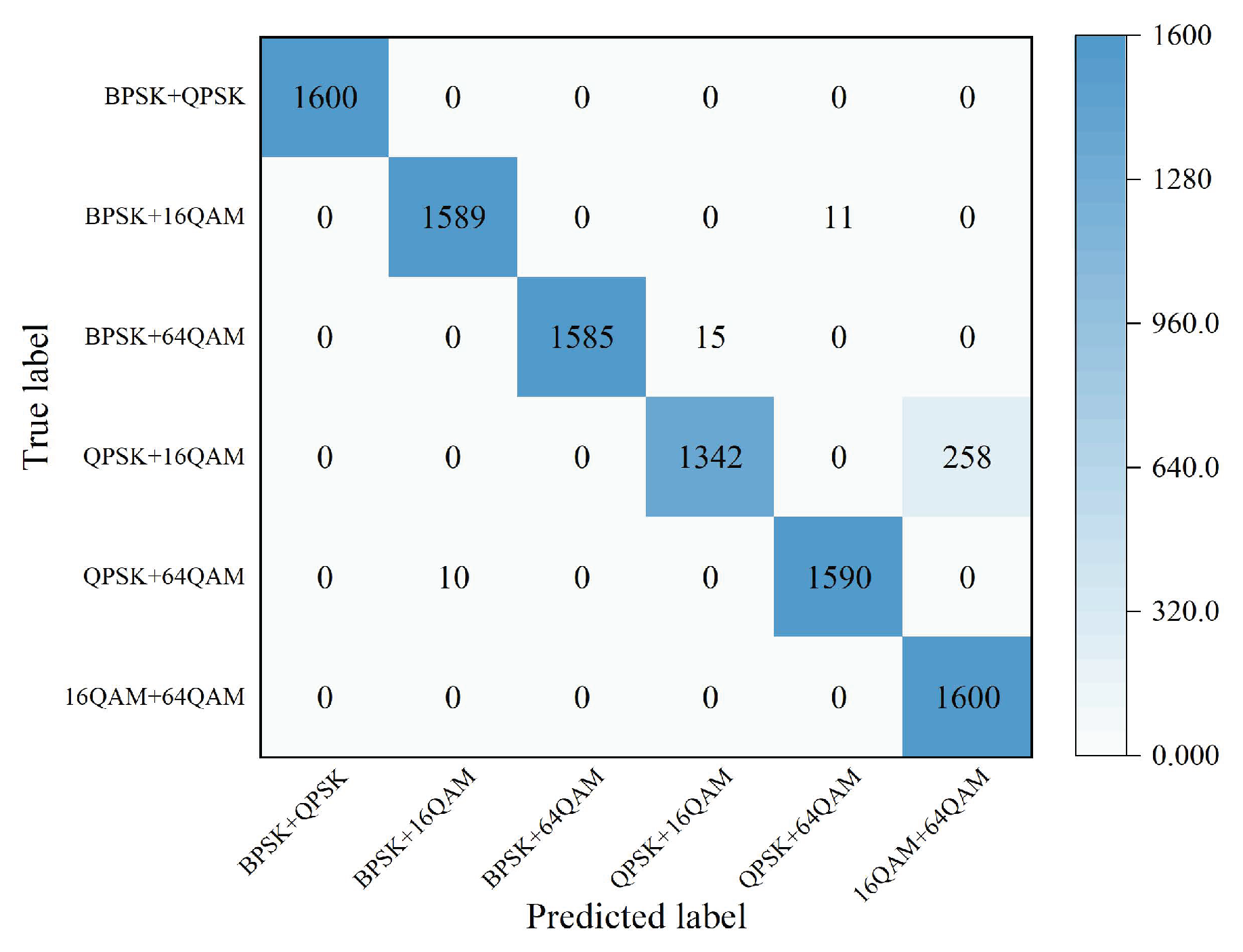
Figure 10 shows the confusion matrix for six mixed signals under the proposed scheme. In the matrix, the horizontal axis denotes the predicted class and the vertical axis denotes the true class. The diagonal entries indicate the numbers of correctly classified samples. Across the examined OSNR range, the average PoCC for BPSK + QPSK, BPSK + 16QAM, BPSK + 64QAM, QPSK + 16QAM, QPSK + 64QAM, and 16QAM + 64QAM are 100.0%, 99.3%, 99.1%, 83.9%, 99.4%, and 100.0%, respectively. Overall, the confusion matrix demonstrates that the proposed method achieves excellent performance in distinguishing the six mixed signals, validating the effectiveness of the proposed approach.

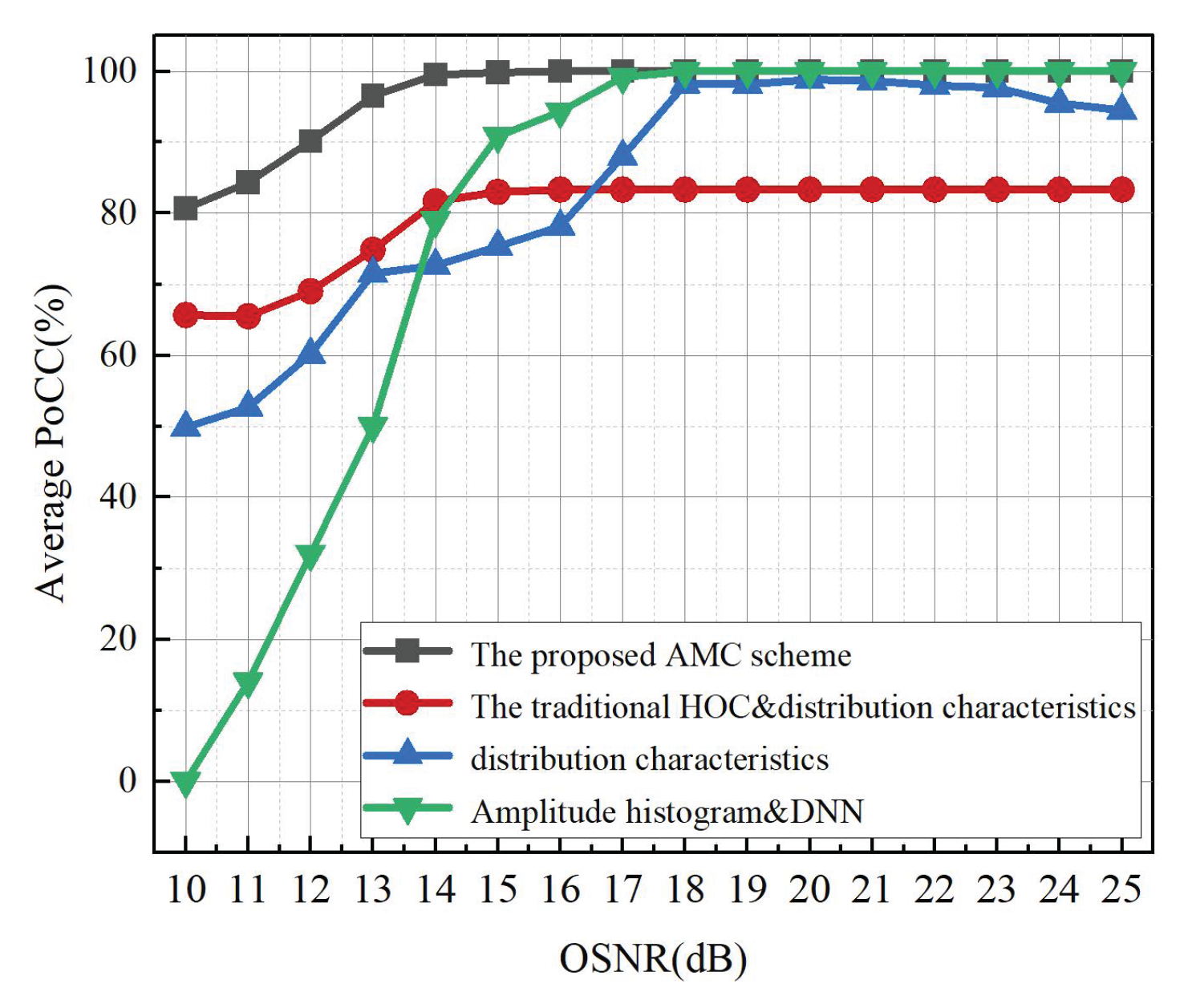
To further demonstrate the superiority of the proposed AMC scheme, its performance is compared with several alternative approaches under a 100 kHz laser linewidth. As shown in Figure 11, the proposed scheme maintains 100% average PoCC for OSNR ≥ 16 dB. In contrast, the DNN-based histogram method reaches 94.3% at 16 dB and achieves 100% only when the OSNR is ≥18 dB. The traditional HOC combined with amplitude distribution characteristics attains 83.3% at 16 dB with no improvement at higher OSNRs, while the method based solely on amplitude distributions yields 78.1% at 16 dB and peaks at 98.8% at 20 dB. Overall, these results demonstrate that the proposed AMC scheme provides significantly higher accuracy and stronger robustness across a broad OSNR range.

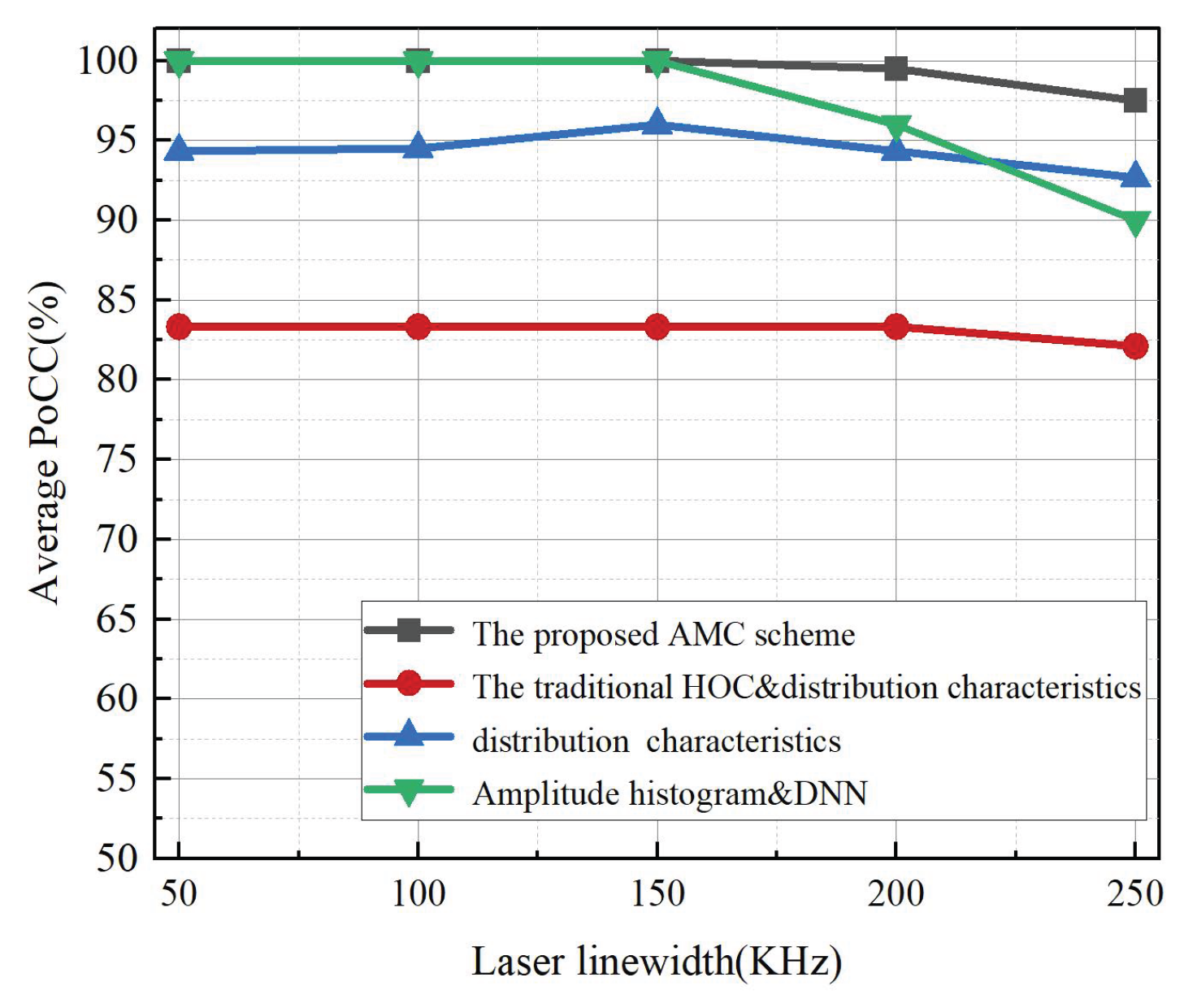
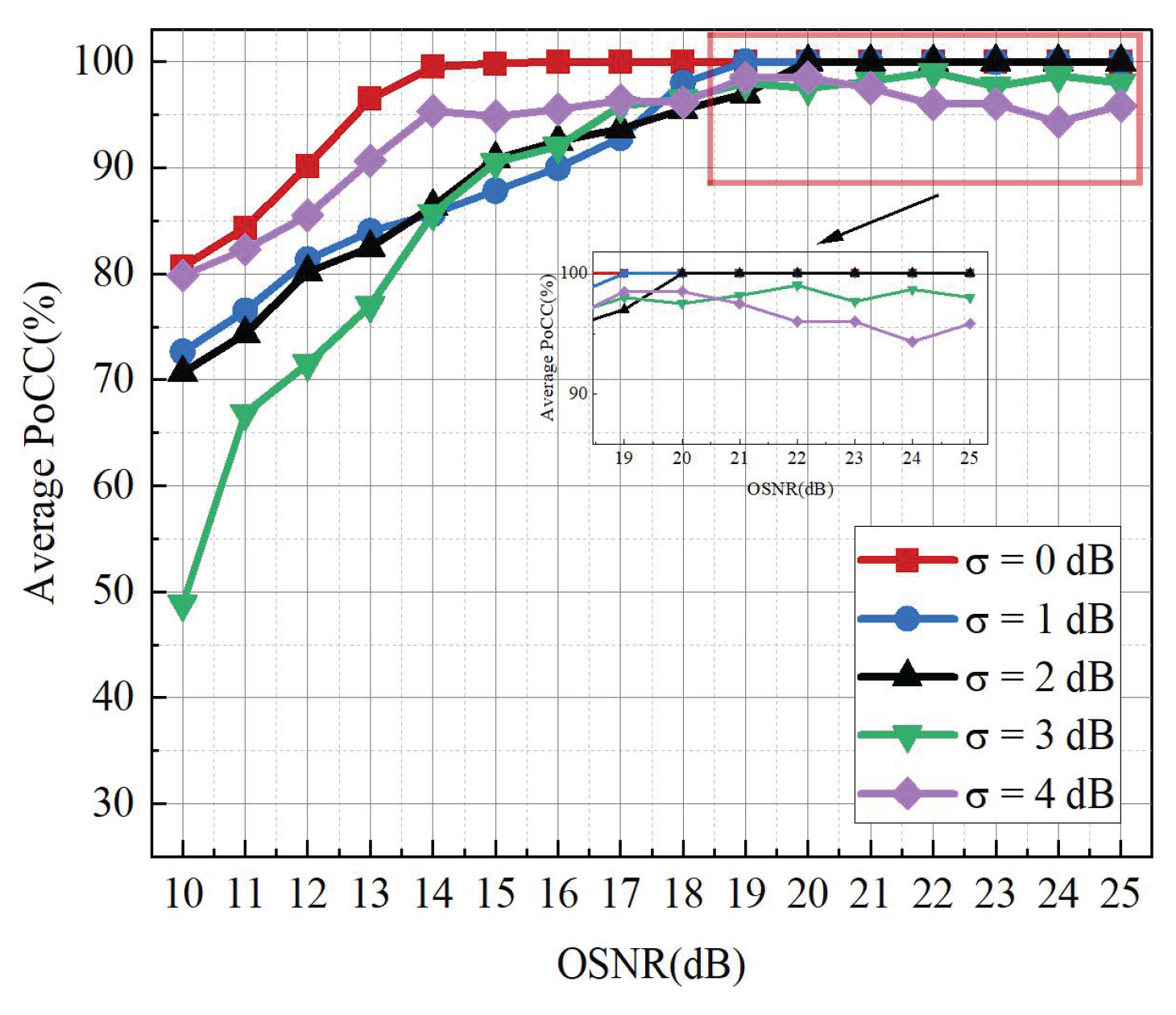
To further assess the tolerance of different AMC schemes to laser phase noise, Figure 12 shows their performance at an OSNR of 25 dB under linewidths of 50 kHz, 100 kHz, 150 kHz, 200 kHz, and 250 kHz. When the linewidth is 50 kHz, 100 kHz, or 150 kHz, both the proposed scheme and the DNN-based scheme maintain a stable 100% average PoCC. In contrast, the traditional HOC combined with distribution characteristics remains at 83.3%, while the scheme using only distribution characteristics peaks at 96%. As the linewidth increases to 200 kHz, the proposed method shows only a slight decrease to 99.5%, whereas the other three schemes drop to 83.3%, 94.3%, and 96%. At 250 kHz, the proposed scheme still achieves 97.5%, while the alternatives fall to 82.1%, 92.6%, and 90%. These results indicate that although laser phase noise degrades AMC performance, the proposed method maintains strong robustness and high accuracy across practical linewidth conditions.

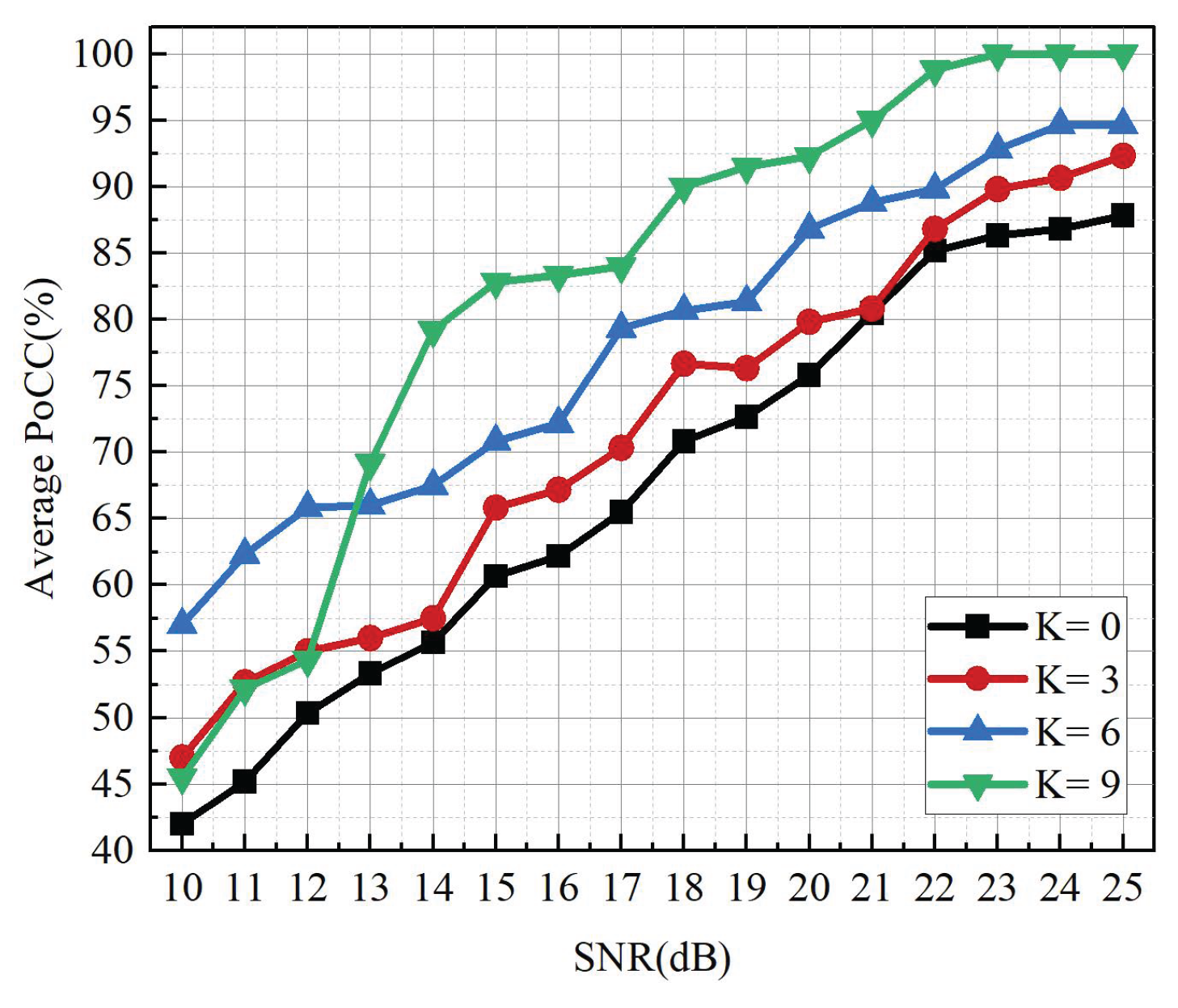
To further assess the robustness of the proposed AMC scheme under multipath fading, we extend the analysis to Rician fading channels. Figure 13 shows the average PoCC of the six mixed signals under a four-path Rician channel with different K factors, K = 0, 3, 6, and 9. The K factor represents the power ratio between the LOS component and scattered multipath components, where a larger K indicates weaker fading. The results show that the proposed AMC scheme maintains 100% average PoCC for SNR ≥ 23 dB when K = 9. For K = 6 and K = 3, the maximum average PoCC reaches 94.7% and 92.3%, respectively. Under the most severe fading, K = 0, the average PoCC is about 85% at high SNR, with a peak of 87.8%. These results indicate that the proposed AMC algorithm maintains stronger robustness even in the presence of pronounced multipath fading.

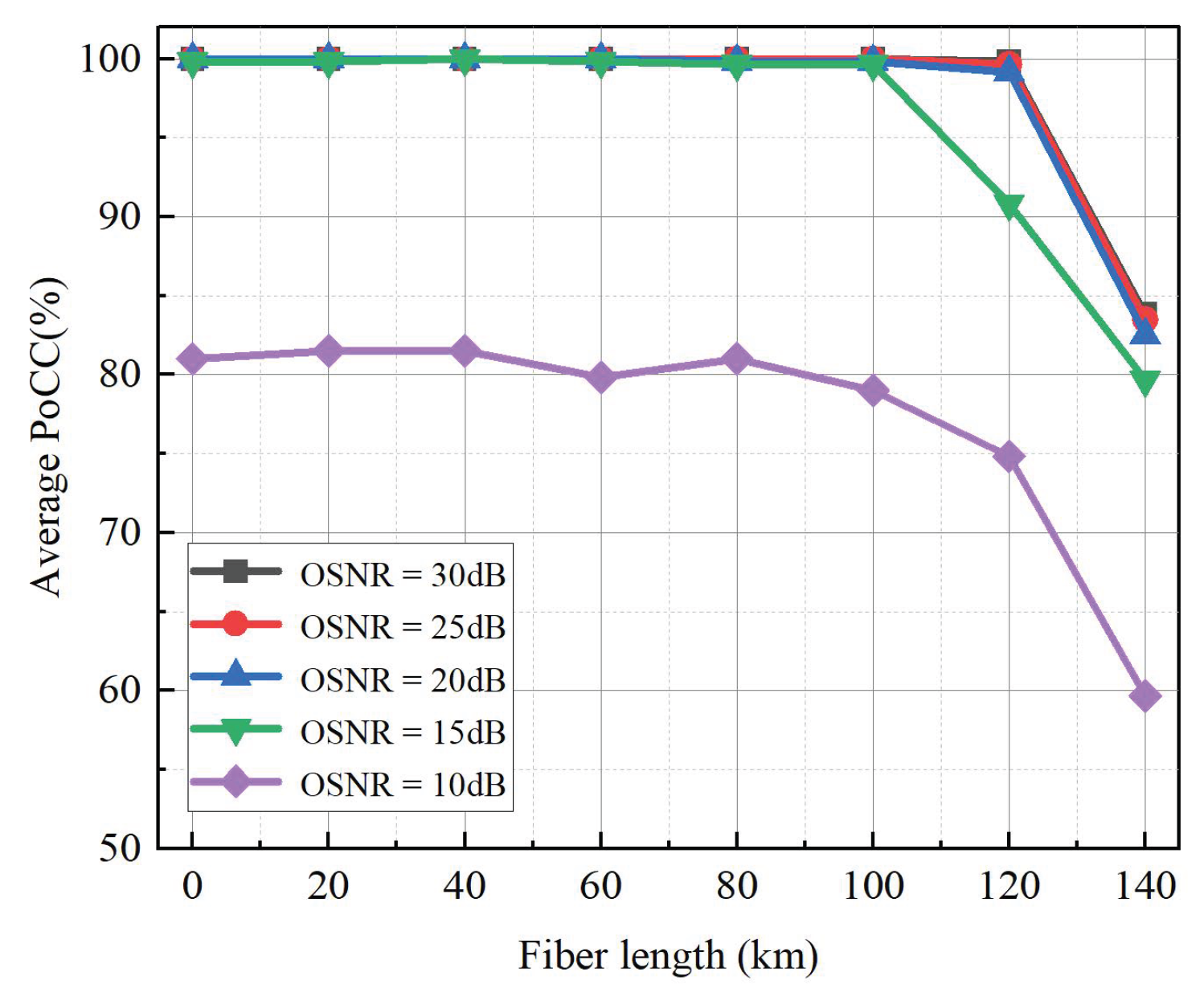
Figure 14 illustrates the relationship between the performance of the proposed scheme and fiber lengths under OSNR values of 10 dB, 15 dB, 20 dB, 25 dB, and 30 dB. The fiber length ranges from 0 to 140 km in steps of 20 km, and each OSNR condition is simulated using 100 sets of 16,384 symbols. The results show that at OSNR values of 25 dB and 30 dB, the average PoCC reaches 100% in the fiber length range of 0 to 100 km, and when the fiber length is 140 km, the average PoCC is 83.8% and 83.5%. When the OSNR is 15dB, the average PoCC reaches 100% in the fiber length range of 0 to 60 km, and 82.5% when the fiber length is 140 km. However, at 10 dB OSNR, the performance degrades more rapidly, with the PoCC dropping to 79% at 100 km.

The observed performance degradation beyond approximately 120 km can be attributed to three impairments: CD accumulation, nonlinear phase shift, and OSNR degradation. In standard single-mode fiber (SSMF), CD accumulates with distance and introduces pulse broadening, which distorts the received signal constellation. Nonlinear phase shift gradually accumulates as the length of the optical fiber increases and introduces additional phase perturbations to the modulated signal. In addition, OSNR gradually decreases because fiber attenuation and the EDFA introduces amplified spontaneous emission (ASE) noise, ultimately affecting the signal quality.

It is worth noting that the proposed system employs optical single-sideband (OSSB) modulation, which effectively mitigates CD fading compared with optical double-sideband (ODSB) modulation. By suppressing one optical sideband, OSSB avoids the strong frequency-selective fading caused by the interference between upper and lower sidebands in ODSB systems. As a result, it better preserves the amplitude and phase of the received RF signal over longer distances, improving robustness against CD-induced distortions and enabling more reliable classification.

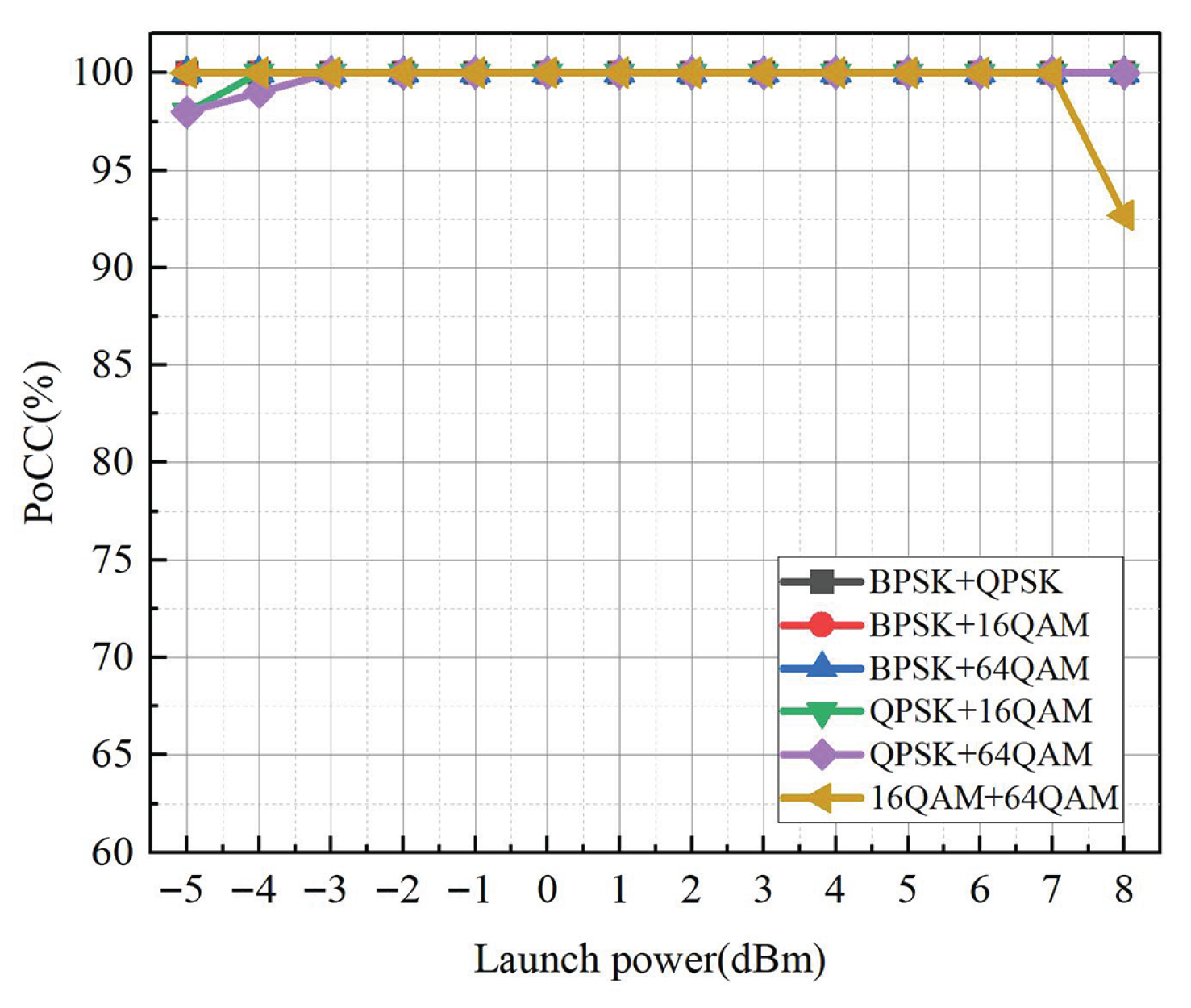
To further demonstrate the robustness of the proposed scheme towards nonlinear effects, the relationship between the PoCC and launch powers ranging from −5 dBm to 8 dBm of the mixed signals is shown in Figure 15. The results indicate that the PoCC remains 100% for all mixed signals between −3 dBm and 7 dBm. However, at 8 dBm launch power, the PoCC for the 16QAM + 64QAM signal decreased to 92.7%, while the remaining five mixed signals maintained 100%. This outcome is anticipated, as higher-order modulation formats exhibit denser constellations that are more susceptible to nonlinear effects. The results demonstrate that the proposed method achieves excellent recognition over a wide range of launch power, exhibiting favorable robustness to nonlinearities.

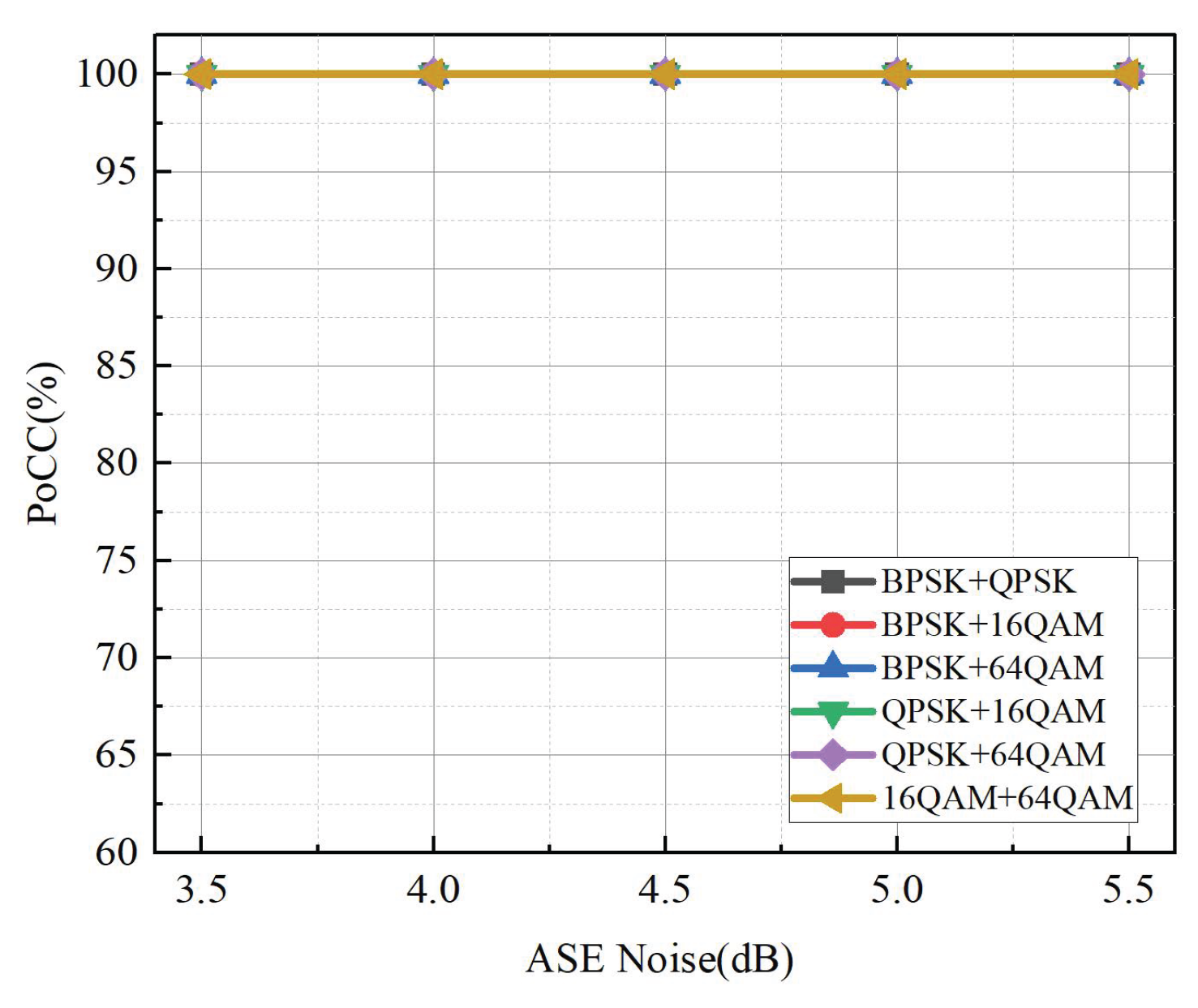
To further evaluate the robustness of the proposed AMC scheme against ASE noise, the relationship between the PoCC and ASE noise variations for the six mixed signals is illustrated in Figure 16. The ASE noise level is varied from 3.5 dB to 5.5 dB. The results indicate that the PoCC of all six mixed signals remains at 100% across the entire ASE noise range, demonstrating the strong robustness of the proposed method against ASE noise fluctuations.

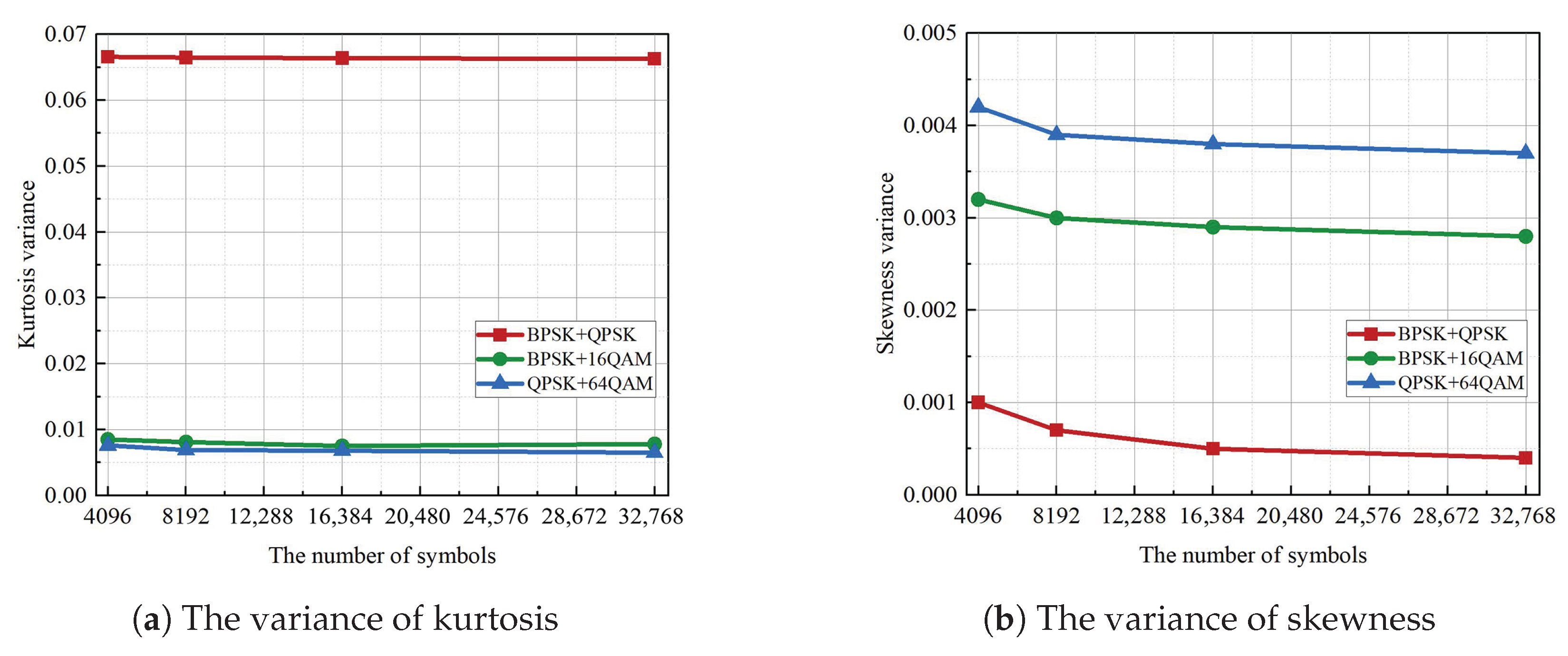
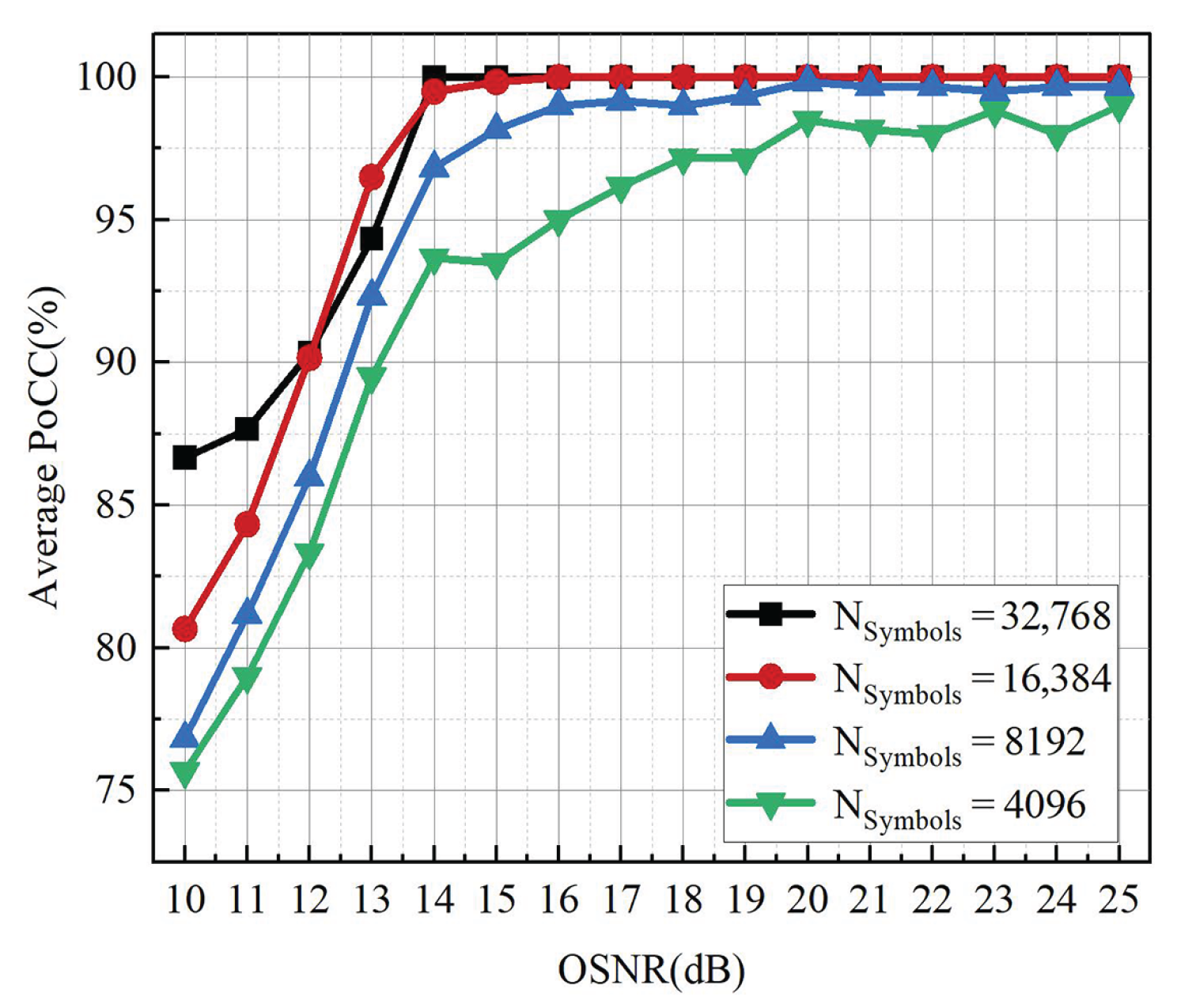
Figure 17 illustrates the impact of symbol numbers on the average PoCC of six mixed signals over a 70 km fiber link. Specifically, when the symbol numbers are 32,768 and the OSNR is ≥14 dB, the average PoCC of the six mixed signals reaches and stabilizes at 100%. With 16,384 symbols, the PoCC also achieves 100% when the OSNR is ≥16 dB. For 819 symbols, the PoCC reaches 99% at 16 dB and fluctuates around 99.5% for OSNR values above 20 dB. When the symbol numbers are further reduced to 4096, the PoCC decreases to 95% at 16 dB and only approaches a maximum of about 99% at 30 dB. These results clearly demonstrate that the numbers of symbols have a significant effect on recognition performance, with differences being particularly evident at lower OSNR levels.

The improvement in the PoCC with increasing symbol numbers can be attributed to two main factors. First, a larger sample size effectively mitigates the influence of random noise and inter-signal interference, thereby reducing the variance of the PNI-HOC statistics. Second, when more symbols are used to estimate the amplitude distribution characteristics, these characteristics become more stable and distinct, which enhances the accuracy and robustness of feature extraction and ultimately improves the PoCC. Although employing 32,768 symbols provides slightly better performance than 16,384 symbols at certain OSNR values, the computational complexity of feature extraction increases approximately linearly with the number of symbols. To balance recognition accuracy and computational efficiency, 16,384 symbols are used in this work, which already ensures a stable PoCC of 100% when the OSNR exceeds 16 dB.

Figure 18 shows the average PoCC of mixed signals as a function of OSNR when the powers of $s_1\left(t\right)$ and $s_2\left(t\right)$ are unequal. The power difference, denoted as $\sigma$, is set to 0 dB, 1 dB, 2 dB, 3 dB, and 4 dB. The results show that classification is optimal when the signals have equal power, with average PoCC remaining at 100% for OSNR ≥ 16 dB. For small power differences of 1 dB and 2 dB, the deviation in the $PN{I}_{C_{42}}$ distribution is minor, and average PoCC maintains 100% for OSNR ≥ 19 dB and 20 dB, respectively. As the power difference increases to 3 dB and 4 dB, the higher-power signal dominates the statistical characteristics, which significantly weakens the amplitude information of the lower-power signal, causing larger deviation in the $PN{I}_{C_{42}}$ distribution. In this case, average PoCC reaches approximately 95% at high OSNR, with maximum PoCC across the OSNR range of 98.7% and 98.5%. These results demonstrate that even under significant power imbalances, the proposed AMC method maintains reliable classification performance.

Although the proposed AMC scheme are evaluated through numerical simulations, the system architecture and parameter settings employed in this work are closely aligned with those used in practical experimental system. The simulation framework incorporates realistic device characteristics and fiber link impairments, thereby ensuring that the modeled system behavior is representative of an actual experimental environment. This alignment supports the practical feasibility of implementing the proposed scheme beyond simulation. In our future work, we plan to further validate the proposed scheme under actual transmission conditions.

5. Complexity Analysis

To assess the feasibility of the proposed AMC algorithm in practical systems, its computational complexity is analyzed. The overall complexity consists of two stages: feature extraction and classification. In the feature extraction stage, the complexity of the traditional high-order cumulant algorithm is O(N), where N is the number of signal samples. The introduced phase noise correction term has a complexity of O(1). Therefore, the overall complexity of the proposed PNI-HOC algorithm is O(N). The subsequent extraction of amplitude histogram characteristics, specifically kurtosis and skewness, also has a complexity of O($2N$). In the classification stage, the decision operation simply compares the PNI-HOC values to corresponding thresholds, resulting in a complexity of O(1). For the SVM classifier using the RBF kernel, the theoretical time complexity of the training process is approximately O(m³), where m is the number of training samples. However, the training process is an offline stage and does not affect the online recognition in practical applications. The dimension of the testing process is approximately O(s*d), since O(s*d) is at the constant level (d = 2, s is the number of finite support vectors), it can be ignored. Therefore, the overall online complexity of the proposed scheme remains O($3N$).

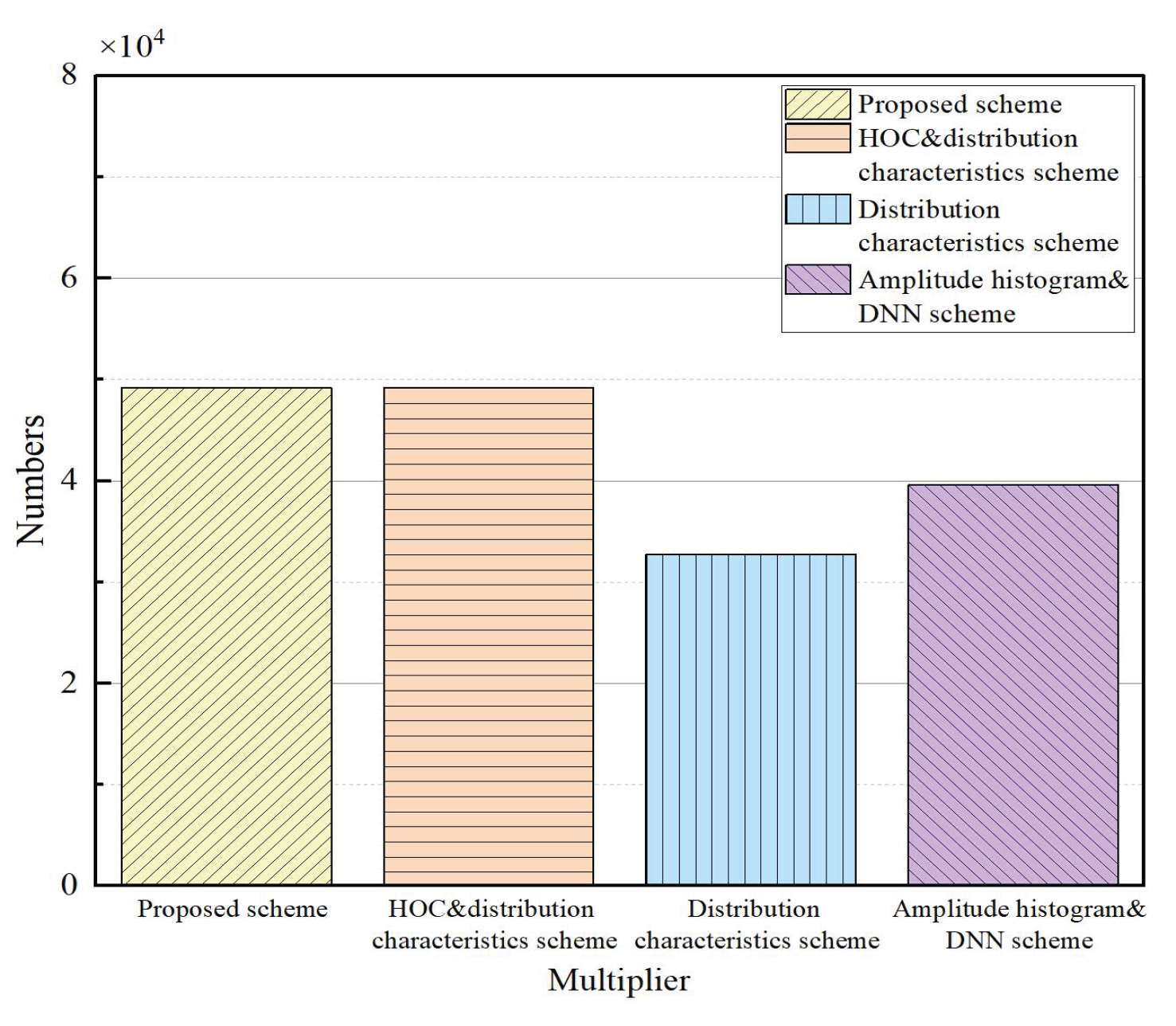
To further evaluate the practical applicability of the proposed algorithm, a comparative analysis of computational complexity among several schemes is conducted under the same sample length N = 16,384. The complexity comparison chart is shown in Figure 19. The traditional HOC combined with distribution characteristics and the proposed PNI-HOC combined with distribution characteristics require $3N$ = 49,152 multiplications, since the phase noise correction in PNI-HOC adds only constant-order operations. When only distribution characteristics are used, the multiplication complexity is reduced to $2N$, i.e., 32,768 multiplications. For the scheme combining amplitude histograms with DNN classification, the complexity includes histogram generation and the forward computation of DNN. With the network configuration $N_1$ = 128, $N_2$ = 64, $N_3$ = 32, and C = 6, the DNN requires $N_1$ = 128, $N_2$ = 64, $N_3$ = 32, and C = 6, where B is the number of histogram bins, while $N_1$, $N_2$, $N_3$ and C represent the number of neurons in the first hidden layer, the second hidden layer, the third hidden layer, and the output layer, respectively. Thus, the total multiplication count becomes N + (100 × 128 + 128 × 64 + 64 × 32 + 32 × 6), which equals 39,616.

These results show that the proposed PNI-HOC scheme maintains the same online computational order as the traditional HOC algorithm while substantially improving robustness under severe phase noise. Compared with both the scheme based on distribution characteristics and the DNN-based approach, it achieves higher recognition accuracy with only minimal additional computational cost. In future work, we will continue to explore strategies that further reduce implementation complexity.

6. Conclusinons

To overcome the constraints of current AMC techniques that predominantly focus on single-signal conditions in RoF systems, an AMC method for mixed signals in ROF system based on statistics and distribution characteristics is presented. Firstly, to mitigate the impact of laser phase noise, the PNI-HOC method is introduced and the distribution characteristics of signal amplitude histogram are extracted to construct a two-dimensional feature space. Six types of mixed signals are then classified using decision tree and SVM classifiers. The simulation results show that compared with other three schemes, the proposed scheme achieves significantly higher classification accuracy at low OSNR. In particular, when the fiber length is 70 km and the OSNR is ≥16 dB, the classification accuracy of mixed signals is consistently maintained at 100%. Furthermore, the method exhibits robust performance under different channel impairments, including laser phase noise, chromatic dispersion and nonlinear effects, amplified spontaneous emission noise, multipath fading, etc., confirming its stability and effectiveness.