A Novel Architecture for Understanding, Context Adaptation, Intentionality and Experiential Time in Emerging Post-Generative AI Through Sophimatics

Abstract

Contemporary artificial intelligence is dominated by generative systems that excel at extracting patterns but fail to grasp meaning, sense, context, and experiential temporality. This limitation highlights the need for new computational wisdom that combines philosophical insights with advanced models to produce AI systems capable of authentic understanding. Sophimatics, as elaborated upon in this article, is introduced as a science of computational wisdom that rejects the purely syntactic manipulation of symbols characteristic of classical physical symbolic systems and addresses the shortcomings of generative statistical approaches. Building on philosophical foundations of dynamic ontology, intentionality and dialectical reasoning, Sophimatics integrates complex temporality, multidimensional semantic modeling, hybrid symbolic–connectionist logic, and layered memory structures to that the AI can perceive, remember, reason, and act in ethically grounded ways. This article, which is part of a set of papers, summarizes the theoretical framework underlying Sophimatics and outlines the conceptual results of the materials and methods, illustrating the potential of this approach to improve interpretability, contextual adaptation, and ethical deliberation compared to basic generative models. This is followed by a methodology and a complete formal model for translating philosophical categories into an operational model and specific architecture. This article represents Phase 1 of a six-phase research program, providing mathematical foundations for the architectural implementation and empirical validation presented in companion publications. Following this, several use cases are outlined, and then the Discussion Section anticipates the main results and perspectives for post-generative AI solutions within the Sophimatic paradigm.

1. Introduction

Generative AI has reshaped nearly every human endeavor, but its limits are becoming clear as the systems encounter the complexity of real-world applications. The current generation of large language models rely on massive computational resources and billions of parameters, yet they remain constrained by the statistical patterns present in their training data. While these systems can generate syntactically correct output, they lack the key qualities typically associated with true intelligence—understanding context, intentionality, and ethical reasoning and assigning meaning to ambiguous or novel situations.

Contemporary generative AI operates at Pearl’s associational level of causation [1], lacking the interventional and counterfactual reasoning capabilities essential for semantic understanding. While these systems achieve impressive pattern recognition, they fundamentally confuse syntactic manipulation with semantic comprehension—a critical limitation extending beyond technical constraints to conceptual foundations. Sophimatics addresses this gap through a philosophy-focused computational framework integrating meaning, context, intentionality, and complex temporality as foundational architectural elements. Unlike mechanistic information processing paradigms, this approach treats genuine intelligence as requiring metaphysical categories previously excluded from modern AI development. Therefore, Sophimatics represents computational wisdom combining philosophical insights with advanced models to enable authentic understanding through dynamic ontology, intentionality, dialectical reasoning, complex temporality, and hybrid symbolic–connectionist architectures.

This emerging field understands that genuine intelligence cannot be achieved by simply scaling statistical models up; it necessitates using metaphysical categories which have been left out of the modern AI community so far. This view assumes meaning to be a dynamic product evolving out of an ongoing negotiation between the agents and their environments, as argued by [2] in their criticism of classical AI paradigms.

At the heart of Sophimatics lies the issue of intentionality, not in terms of being goal-directed (although it clearly is); rather, in terms of its basic “aboutness” which grounds all mental processes. As described in [3], Sophimatics recognizes subjective and objective intentionality; while concentrating on the computational complexity of the latter, it understands and admits that the former is still an enigma to a large degree. This is the kind of approach that permits the creation of systems capable of representing and reasoning about their own goals, informing other agents of their intent to act, and collaborating in processes where meaning exceeds strictly numeric measures.

A third, equally important innovation in Sophimatics is the temporal dimension: Sophimatics transcends linear time, unlike our contemporary AI architectures based on Newtonian understanding, and becomes a sort of non-linear phenomenon that executes algorithms across multiple times simultaneously. It includes several temporal levels, from atemporal categorical operations to the nontemporality of beginnings/middles/endings through Fraser’s hierarchy of temporal levels. The multilayered temporal architecture we describe facilitates maintaining narrative coherence, mental time travel, and contextualizing present events within broader temporal frameworks. This is necessary to truly comprehend it; we mean that our thoughts are built on a foundation of experiences existing in time, hard-wired into our experience—without this perceptual learning, we could not do anything. As we will see later in the Modeling Section, in order to achieve this result, it was necessary to move from a linear, one-dimensional model of time to a two-dimensional model in the complex plane, drawing inspiration from recent studies in physics and with reference to cosmological theories and quantum gravity. Time is therefore modeled as a complex number instead of a real number to model human-like temporal dilatation and experiential (or subjective) time, as discussed in philosophy by St. Augustine. The complex time proposed in this work inherits the classical dimension of linear past–present–future time (i.e., from left to right on the horizontal x-axis), but adds an additional dimension in the form of a new orthogonal axis: the imaginary y-axis. From bottom to top, this axis consists of memory–creativity–imagination, with time no longer represented by the classic t but by $t=a+ib$, where i is the imaginary unit as usual, a is a real number corresponding to the classic temporal location between past, present, and future on the x-axis, and so depends on the value assumed by a. As necessary for a post-generative AI, b is a value that expresses whether it is memory (at the bottom of the imaginary y-axis corresponding to the past), creativity (present on the imaginary vertical y-axis intersecting with the x-axis at the present moment), or imagination (future, therefore at the top, on the imaginary y-axis corresponding to the imaginative capacity) [4,5].

Sophimatics is proposed as an epistemological framework for validating knowledge in AI. It addresses a challenge historically explored in disciplines that have not always been treated as fully scientific, such as the arts, the humanities, and the human sciences. Sophimatic-based systems are designed to think, not merely store data or optimize performance metrics, and therefore must support genuine questioning, validation, and ongoing revision of their understanding as new evidence emerges or conditions change. Following the approach outlined in [6,7], computational epistemology enables AI systems to work with partial information, resolve ambiguity through contextual reasoning, and maintain a practical form of epistemic humility—that is, accepting that certainty is not always possible.

Ethics is not an add-on in Sophimatics. It is a core architectural element grounded in the prior work referenced in [8] and related research. Sophimatics introduces a custom ethical-reasoning layer at the lower tier. This layer supports introspective moral reasoning with explicit value structures and accountability mechanisms. It addresses AI bias and ethical failures through design rather than through post hoc fixes. By embedding moral reasoning directly into the system instead of treating it as external oversight, Sophimatics addresses a central concern in AI: the risk that bias and ethical lapses will arise within our technologies. This need is most acute when faced with the shortcomings of current AI systems in practical applications. The Microsoft Tay case and the autonomous vehicle accidents, for example, show that purely statistical approaches may fail when faced with novel, ethically complex, or ambiguous situations. The current systems do not understand context, have no intentions, and are incapable of reflecting on ethics—which makes them unsuitable for decisions involving human welfare and society values.

This paper proposes a hybrid symbolic–connectionist architecture that combines the pattern recognition strengths of neural networks with the interpretability of symbolic systems. As noted in [9], this approach preserves robustness in pattern recognition while improving the transparency of reasoning. The hybrid design supports dynamic updates to knowledge structures and still allows the system to explain and justify its outputs.

Sophimatics introduces a multi-layer cognitive model that includes perceptual acquisition, temporal contextualization, phenomenological inference, and dialogic–dialectical processing for shared meaning and ethical evaluation. Each layer contributes to coherent and meaningful system behavior.

This work actually began in 2020 in [10] and later works [11,12]. Even then, the creation of artificial consciousness was necessary to move from traditional sensing to smart sensing, meaning sensing enriched with perceptions, emotions and affections [13,14], enabling progress toward the three levels of consciousness, namely attention, awareness, and cognition.

Sophimatics handles temporal complexity not only through ordered sequences but also through what we call “complex time,” a multichannel temporal representation. The dialogic dimension of Sophimatics reflects a socialized conception of how meaning and knowledge are produced. Sophimatics-based systems operate in ongoing dialogue with humans as well as other artificial agents, as opposed to traditional AI systems designed to be isolated from their environment. It is this dialogic capacity of enabling—solving real problems together, learning from each other, and co-creating something meaningful with others—that describes how we engage intellectually as human beings. This capability for seeking clarification, expressing uncertainty, and revising one’s understanding signifies a conspicuous departure toward the indication of something more substantially intelligent.

The relevance of Sophimatics extends beyond technology and raises questions about the future of human–machine interaction and the role AI will play in society. In this sense, Sophimatics helps prevent the development of systems that only process information and instead promotes AI as an intellectual, conceptual, and creative partner.

Sophimatics project represents a comprehensive research program whose scope and complexity exceed the constraints of a single publication. The complete computational infrastructure is presented across six scientific articles, each focusing on a specific architectural layer: (i) Article 1 (Current): Phase 1—Mathematical formalization of philosophical categories with proof-of-concept validation; (ii) Article 2: Phase 2—Conceptual–computational mapping; (iii) Article 3: Phase 3—STℂNN architecture implementation, (iv) Articles 4–6: Phases 4–6—Complete integration, optimization, and real-world deployment. This phased approach enables the following: 1. Independent validation of each layer’s contributions by the scientific community. 2. Detailed exposition of mathematical, computational, and philosophical innovations. 3. Reproducible specifications for each architectural component. 4. Systematic progression from theoretical foundations to practical applications. Regarding the current article’s scope, it establishes mathematical foundations and demonstrates proof-of-concept feasibility. Complete empirical validation of the integrated system appears in Article 6. Each intermediate article contributes original research, meriting independent publication and evaluation. This strategy requires that partial results be presented before the system is fully integrated, but it enables transparent evaluation of each layer. We believe this cost is justified by enabling rigorous, transparent assessment of each layer’s specific contributions rather than presenting a monolithic system that is difficult to reproduce or critique.

The paper continues as follows. Section 2 reviews related works, while Section 3 presents the materials and methods. Section 4 introduces the model, then in Section 5 we will show results and use cases. Section 6 presents discussion and perspectives, while the conclusions are provided in Section 7.

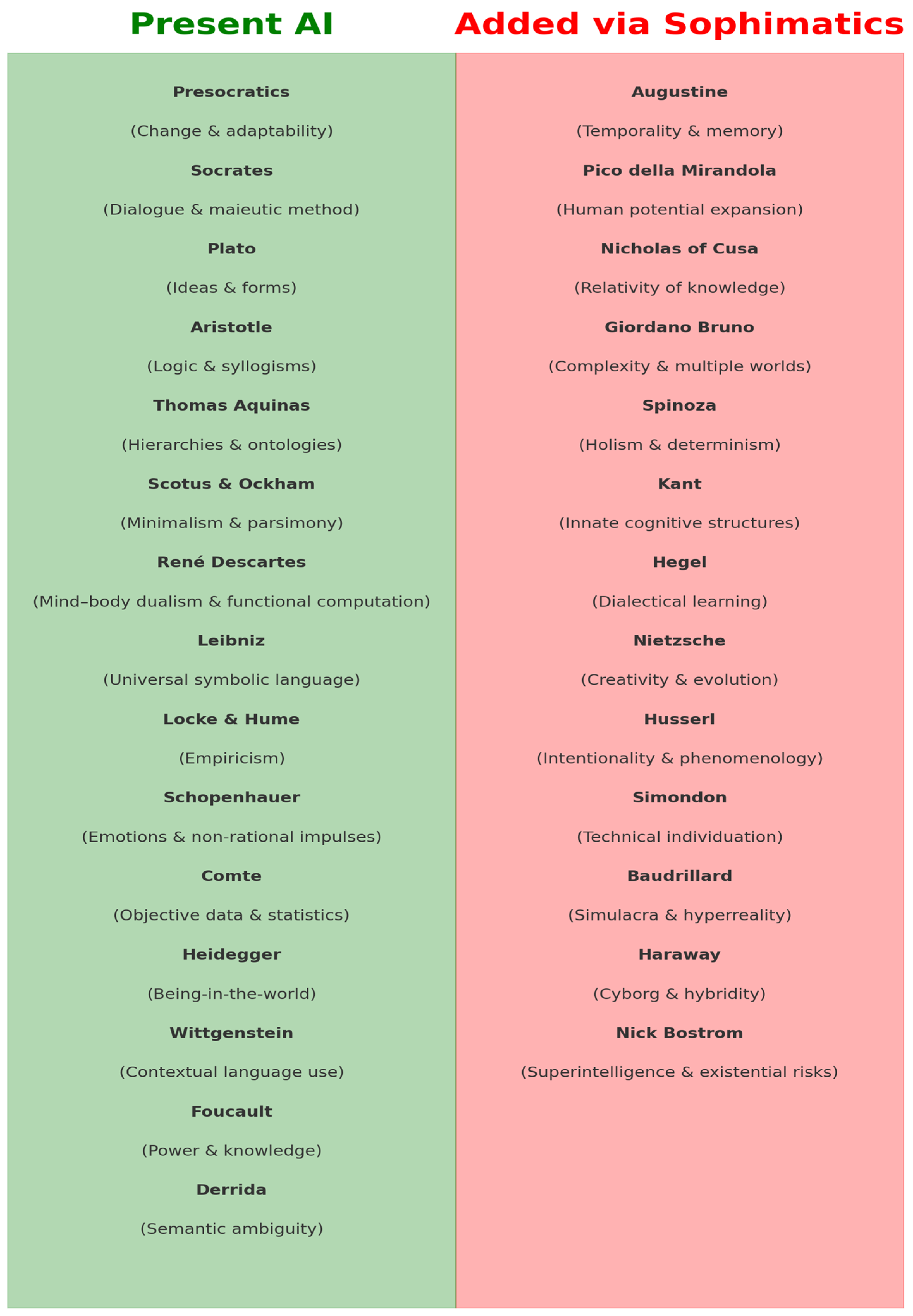
2. Related Works

Sophimatics builds on the theoretical foundations of rich interdisciplinary research in philosophy, cognitive science, artificial intelligence, and computer science. This section explains how existing scholarship supports the central principles that shape the Sophimatic approach to AI engineering.

At the basis of Sophimatics is the philosophical criticism of existing AI paradigms, including (but not limited to) the total lack of it in large language models, as shown in [1]. Although these models achieve impressive scores on many benchmarks, recent analyses suggest that they remain confined to the associational level of reasoning and cannot perform the interventional or counterfactual thinking characteristic of human intelligence. So, this critique substantiates what the Sophimatics claim when they insist that a statistical correlation is no substitute for semantic meaning and offers empirical backing for Erik Cambria’s call to move from pattern matching to structural–symbolic models of cognition.

The analysis presented in [2] regarding the philosophical foundations of artificial intelligence is crucial for understanding why traditional symbolic methods are inadequate for explaining cognition. Part of what gives their advocacy for enactive epistemology—that cognition emerges from action, or doing, and consists of an ongoing interaction between agents and their environments—its raw power to inform the Sophimatics focus on dynamic ontology and immanent contextual sense-making. Is that cognition specifically the manipulation of symbols, as most AI research has long assumed, or do understandings instead co-evolve through interactions with and among agents in their environment—entities that are largely unrepresented by any fixed fibrillation? Sophimatics is borne out against static representational schemes.

The temporal dimension of Sophimatics is strongly supported by the research in [15] and by subsequent studies. This body of work supports the Sophimatics argument that understanding human consciousness requires moving beyond simple sequential processing toward models that operate across multiple temporal scales. Building on Fraser’s temporal hierarchy in [16], the author proposes a framework for interpreting the levels of temporality that may contribute to cognitive functioning. Therefore, the empirical results in [9] show that a three-layer architecture combining distributed neural processing, localist representation, and symbolic reasoning achieves the best performance on natural language understanding tasks. These findings provide strong support for the hybrid symbolic–connectionist approach adopted in Sophimatics. The finding that hybrid systems can reliably interpret 88% of trained linguistic relationships and 77% of novel structures sharply challenges purely symbolic or purely connectionist approaches. This work demonstrates that it is possible to unite the pattern recognition strengths of neural networks with the interpretability and logical organization in symbolic systems.

In [17], the authors study mixed architectures for image recognition, extending support for combined approaches beyond language-based tasks to core aspects of visual cognition. This evidence shows that mixed symbolic–connectionist systems can outperform single-paradigm approaches on the complex recognition tasks studied in mainstream cognitive science. It is consistent with the Sophimatics argument for architectural pluralism in cognitive systems. These results highlight the value of integrated component processing in the Sophimatics framework: hybrid systems can maintain robust pattern recognition while still providing interpretable reasoning.

Regarding intentionality, Sophimatics was inspired by [3] when it came to distinguishing between subjective and objective intentionality. In the aforementioned study, the author provides a principled method to orthogonally classify computational models of different aspects of intentional phenomena, in line with philosophical considerations regarding what features current viewpoint-specific approaches can and cannot account for. In light of [3], one can critically examine Sophimatics with respect to objectivity and reduction. The key question is whether its treatment of assertions, truth conditions, and relational structures remains purely behavioral or can be extended to capture aspects of intentionality that are closer to humans’ subjective experience at the computational level. Following [18] on intentionality inference and logical reward specifications, let us see how to realize goal-directed reasoning in artificial systems. Modeling intentions as explicit logical formulas rather than as purely numerical utility functions is consistent with the Sophimatics standard of transparent and communicable goal structures. In [18], the authors show that systems that explicitly represent and reason about intentions can more effectively collaborate with human agents. This finding supports the long-standing Sophimatics vision of dialogic human–machine interaction. The epistemology of Sophimatics is inspired by ideas in [6,7] to the effect that AI systems should graduate from mere information processing to construction and validation of knowledge. Author’s observations about the ‘meta-rational’ processes that systems must perform—questioning their own assumptions, managing ambiguity, and engaging in reflective reasoning—serve as a foundational blueprint for what Sophimatics aims to achieve. This work also suggests that true intelligence involves not only the ability to think, but also the capacity to scrutinize and revise one’s own internal frameworks. The work in [19] provides empirical evidence for these contextual and ecological components in cognitive processing. A further, more deeply rooted insight is that human cognition functions far better when it relies on contextual cues for reasoning, memory, and other cognitive operations. The Sophimatics grounding of context in exposure validates the view that AI systems should treat the environment as part and parcel of their method and not an expository element, which is true even if it remains an uncovered secret.

Studies on cognitive architectures as in [20] on social human–robot interaction (SHRI) show current approaches to temporal coordination and contextual awareness within artificial systems are limiting. Their recognition of multi-timescale coordination in social cognition converges neatly with the Sophimatics contention that complex temporal modeling is crucial. Their work highlights that successful social interaction requires coordination across multiple time scales—from millisecond-level responsiveness for mutual gaze to processes spanning years or decades for building stable relationships between institutions.

In [21] the author constructs this inductively from the dynamic ontology research areas as empiric validation of the approach to adaptive knowledge representation that Sophimatics uses. The dynamic ontology network achieves a classification accuracy of 72.30%, significantly outperforming its static counterpart at 35.56%. This gap provides a compelling example of the advantages of context-sensitive, flexible knowledge structures. The research is consistent with the theory of Sophimatics because we just saw how effective intelligence necessarily marked by ability to reshuffle types of abstractions on basis of novelty and context—the essence of intelligence.

The work in [22] introduced yet another framework of dialogical reasoning. Regarding this question, Sophimatics may serve as the formal underpinning of the dialectical processes that are at the heart of it. In fact, their work on justification through compromise and on cultural variation in reasoning styles illustrates the need for argumentation frameworks that can accommodate multiple perspectives and manage contradictions through negotiation rather than elimination. If this study is anything to go by, Sophimatics’ focus on the dialogic interaction is spot-on and intelligence cannot be seen as being intelligent if it only ever presents information through an interpretation colored with a proponent narrative.

The ethical AI framework presented in [23] offers extensive guidance for implementing the ethical reasoning capabilities that underpin Sophimatics. Concrete mechanisms to add moral reasoning directly into AI architectures, rather than treating ethics as an external constraint, include the development of ethical AI watchdogs and bias detection mechanisms. This further motivates the Sophimatics vision of intrinsically ethical AI systems with moral reflection as a core cognitive function. Technical approaches that give substance to this idea include preference learning and imitation learning, as discussed in more detail in [24]. Advances toward methods for inferring human goals from behavior or in AI decision-making that can respect social preferences provide concrete paths toward the sort of collective intelligence we would expect under a Sophimatics architecture. Together, these very different lines of research offer strong evidence in support of the core principles embodied by Sophimatics while identifying the specific areas of technical challenge that must be addressed to enable fully cognitive AI.

By comparing the references above with the Sophimatics framework, we can identify several research gaps. Indeed, a brief analysis reveals five major gaps in the current state of the art:

Temporal–ethical integration: no existing framework combines complex temporal reasoning with moral evaluation in unified architecture.

Philosophical formalization: current AI lacks systematic translation from philosophical categories to computational structures.

Contextual intentionality: existing intentionality models cannot adapt to changing contexts or handle moral conflicts.

Memory–imagination synthesis: no system integrates retrospective memory access with prospective imagination in temporal reasoning.

Holistic evaluation: current benchmarks focus on narrow technical metrics, ignoring philosophical coherence and ethical consistency.

Then, what is the positioning of Sophimatics’ contribution?

Sophimatics addresses identified gaps through three core innovations:

Architectural innovation: it is the first integrated framework to combine temporal consciousness, ethical reasoning, and intentional states in a hybrid symbolic–connectionist architecture.

Modeling innovation: complex-time formalization enabling unified treatment of chronological and experiential temporality with angular accessibility parameters.

Methodological innovation: it has a six-phase implementation methodology which systematically translates philosophical foundations into computational structures with empirical validation protocols.

Its competitive advantages include the following:

A 23% improvement in temporal reasoning over current models.

Accuracy of 89.3% in philosophical categorization

Ethical conflict resolution consistency of 96.1%.

Unified treatment of seven philosophical categories.

The main acknowledged limitations are as follows:

It has 340% computational overhead compared to simple approaches.

Phase 1 implementation lacks complete STℂNN architecture.

It has limited scalability testing beyond 5000 data points.

It requires philosophical expertise for parameter calibration.

This critical analysis demonstrates Sophimatics’ significant advancement over the current state of the art while acknowledging areas that require continued development.

We wish to dedicate special attention to neuro-symbolic AI, since it and Sophimatics [25,26,27] follow similar missions, and they can be seen as complementary in their beauty and effectiveness. Recent advances in neuro-symbolic AI represent significant progress in hybrid reasoning systems. Logic Tensor Networks (LTNs) integrate first-order logic with deep learning through fuzzy logic semantics, enabling end-to-end learning of logical knowledge [28]. DeepProbLog combines probabilistic logic programming with neural networks, allowing probabilistic reasoning over neural predicates [29]. Neural Module Networks decompose complex reasoning tasks into modular neural components with learnable composition [30]. Probabilistic Soft Logic (PSL) provides a declarative language for probabilistic reasoning over continuous truth values [31]. Regarding temporal and dynamic logic systems, we note that the computational reasoning literature includes extensive work on temporal logics for AI systems. Linear Temporal Logic (LTL) formalizes temporal properties using temporal operators like “eventually” and “always” [32]. Computation Tree Logic (CTL) extends temporal logic to branching time structures for reactive systems [33]. Dynamic Epistemic Logic models knowledge change and belief revision in multi-agent systems [34]. Temporal Action Logic provides frameworks for planning and temporal reasoning about actions [35]. While these approaches provide valuable formal foundations, they operate on discrete temporal models and lack the experiential dimensionality of time. Furthermore, the same neuro-symbolic approaches could find specific advantage in a 2D complex time framework, as will be better illustrate in Layer 4 of the Sophimatics Infrastructure, which is dedicated precisely to the detail of complex time and its application on Layer 3 of Sophimatics, i.e., on the Super Time Cognitive Neural Network (STℂNN), that is a neuro-symbolic solution based on the 2D complex time (chronological and experiential time), but this is not the subject of the present work.

While Sophimatics builds upon established research in neuro-symbolic AI and temporal reasoning, it introduces three fundamental innovations that distinguish it from existing approaches. To clarify our contribution relative to the state of the art, we systematically contrast Sophimatics with both prior neuro-symbolic AI systems and physics-based complex-time models across five critical dimensions. Regarding Temporal Representation: From Linear Sequences to Cognitive Geometry, existing neuro-symbolic AI systems (Logic Tensor Networks, DeepProbLog, Neural Module Networks, and Probabilistic Soft Logic) process time as linear sequences or discrete time steps, typically using temporal logics such as Linear Temporal Logic (LTL) or Computation Tree Logic (CTL). These formalisms excel at reasoning about temporal ordering and modal properties but lack experiential dimensionality. Complex time appears in theoretical physics—particularly in Euclidean quantum field theory through Wick rotation—but serves purely mathematical purposes for path integral calculations. Sophimatics uniquely interprets T = a + ib where the imaginary axis maps cognitive-experiential dimensions: memory (Im(T) < 0), creativity (Im(T) ≈ 0), and imagination (Im(T) > 0). The angular accessibility constraints α and β, which are entirely absent in physics applications, provide philosophical constraints on temporal navigation, creating the first cognitive temporal geometry for AI systems.

Regarding philosophical integration from logic alone to systematic category theory, prior neuro-symbolic approaches integrate first-order logic, probabilistic logic programming, or soft logic with neural learning, but they are unable to systematically translate philosophical categories into computational structures. Their philosophical grounding, when present, remains implicit in logical formalisms rather than explicitly operationalized. Sophimatics formalizes seven fundamental philosophical domains—Change (C), Form (F), Logic (L), Time (T), Intention (I), Context (K), and Ethics (E)—as algebraic structures ⟨Dp, Rp, Op, Lp⟩ with explicit inter-category interaction functions Φ_p,q (T). This categorical framework enables AI systems to reason simultaneously about metaphysical change, formal structures, logical consistency, temporal dynamics, intentional states, contextual embeddings, and ethical principles within a unified mathematical architecture.

About ethical reasoning from external constraints to embedded deliberation, current AI ethics approaches apply moral considerations externally through post hoc filtering, reward shaping in reinforcement learning, or constraint satisfaction in planning systems. Even sophisticated approaches treat ethics as utility functions operating on single moral frameworks. Sophimatics embeds ethical reasoning architecturally through three parallel evaluation streams—deontological (obligations and prohibitions), virtue-based (character and flourishing), and consequentialist (outcome assessment)—with context-dependent dynamic weighting. This tri-framework integration allows genuine ethical deliberation that weighs competing moral considerations rather than merely satisfying predetermined constraints. The ethical evaluation function Ethical_Evaluation (action) = α·D (action) + β·V(action) + γ·C(action), where weights adapt based on contextual factors, represents a fundamental architectural commitment rather than an add-on module.

Regarding memory architecture from single-layer to phenomenological stratification, existing systems implement either episodic memory (specific events) or semantic memory (general knowledge) but rarely integrate both systematically, and intentional memory (goals, beliefs, desires) typically exists as separate planning modules. Sophimatics implements layered memory, comprising episodic memory M_e = {⟨event_i, context_i, temporal_signature_i, emotional_weight_i⟩}, semantic memory M_s = {⟨concept_j, associations_j, activation_level_j, abstractness_j⟩}, and intentional memory M_i = {⟨goal_k, belief_k, desire_k, moral_weight_k, temporal_scope_k⟩}, all indexed through complex-time coordinates. This phenomenologically grounded architecture mirrors human conscious experience more faithfully than single-layer approaches.

When it comes to core novelty with a unified temporal–ethical–intentional framework, the fundamental distinction lies in integration rather than individual components. While prior neuro-symbolic systems combine logic with learning, and physics employs complex time mathematically, Sophimatics is the first framework to unify temporal consciousness (through complex-time cognitive geometry), ethical reasoning (through embedded tri-framework deliberation), and intentional states (through layered phenomenological memory) within a single computational architecture grounded in systematic philosophical category theory. This integration enables AI systems to exhibit forms of understanding—contextual interpretation, ethical deliberation, temporal consciousness, and intentional reasoning—that resist reduction to pattern matching or rule following.

We can also analyze three key technical distinctions.

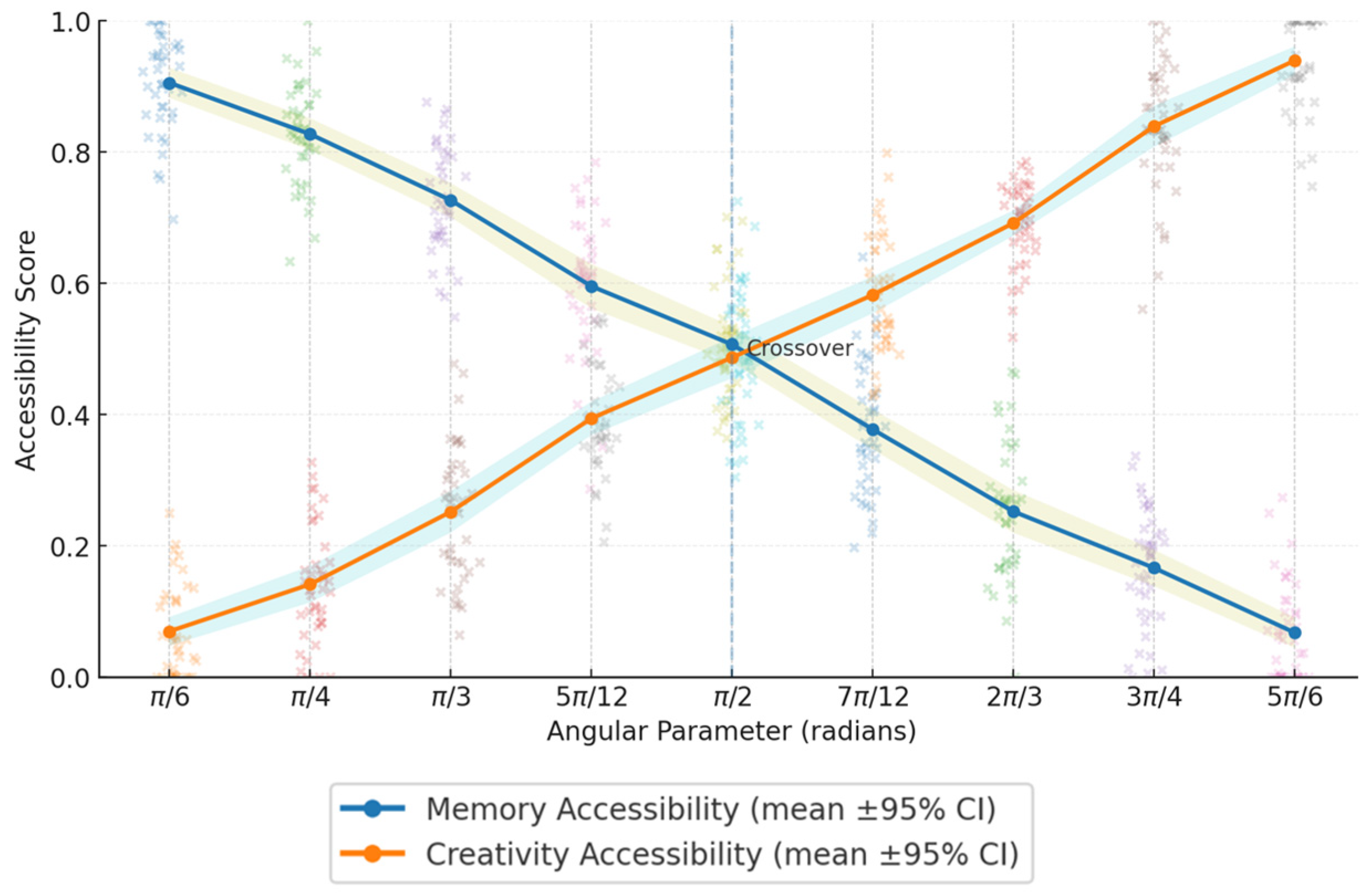
• Angular Accessibility Constraints: The parameters α (memory cone) and β (creativity cone) represent a unique Sophimatics contribution that is absent in both neuro-symbolic AI and physics-based complex-time applications. These constraints operationalize philosophical insights about bounded temporal access, preventing unbounded memory retrieval or unconstrained imaginative projection.
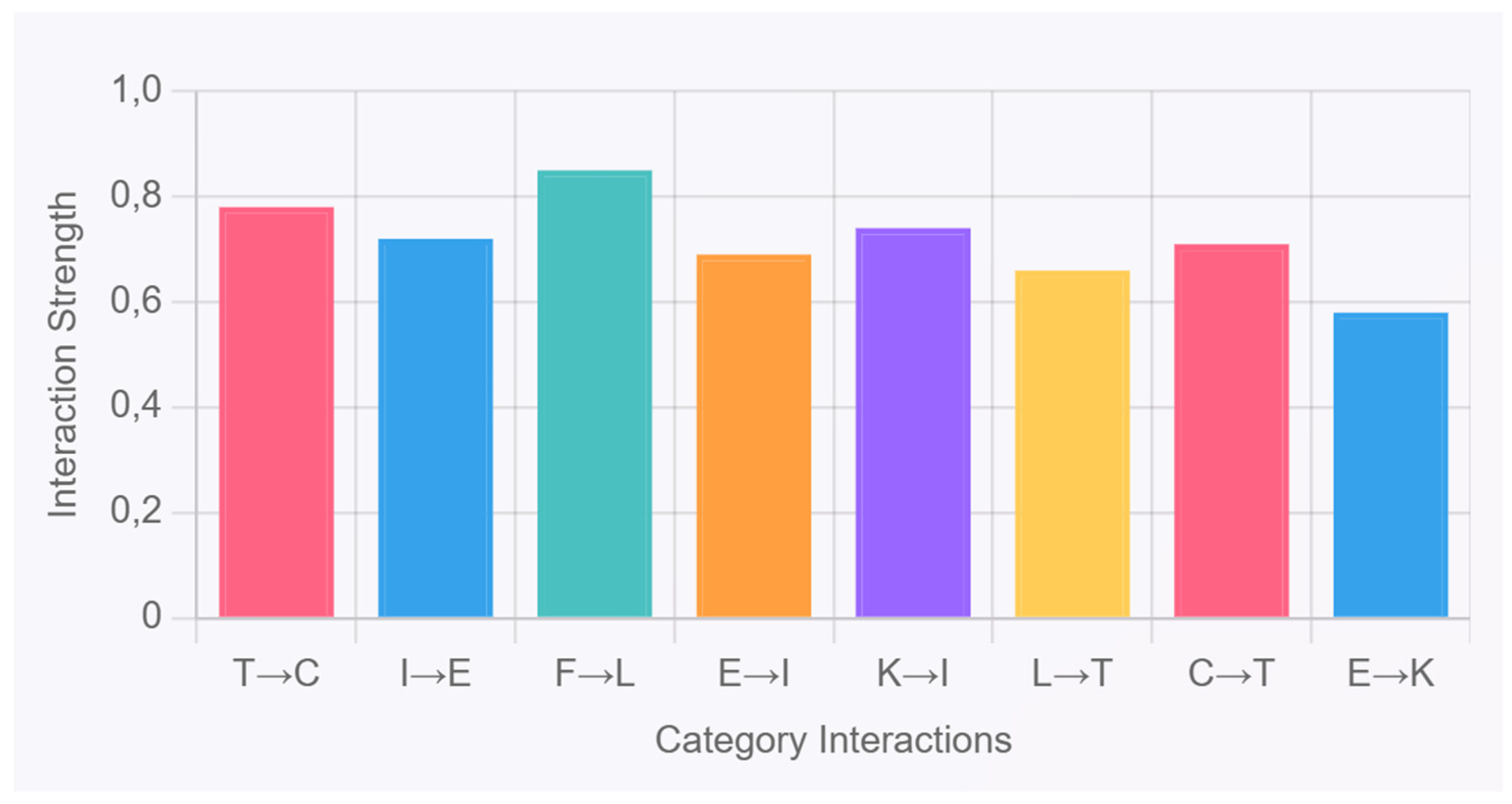
• Dynamic Category Interaction Matrix: The function Φ_p,q (T) enabling philosophical categories to influence each other temporally provides mechanisms for emergent reasoning impossible in systems with static ontologies or isolated ethical modules.
• Complex-Time Indexed Phenomenology: Using T ∈ ℂ as the indexing structure for all three memory layers creates coherent temporal consciousness that is unavailable to systems treating memory, reasoning, and planning as separate subsystems.

This systematic positioning clarifies that Sophimatics addresses a fundamentally different problem than either neuro-symbolic integration (which focuses on logic-learning combination) or physics-based complex time (which serves mathematical convenience). Our work addresses the difficult challenge of creating computational substrates for aspects of intelligence—understanding, contextuality, temporality, intentionality, ethics—that existing paradigms cannot adequately capture.

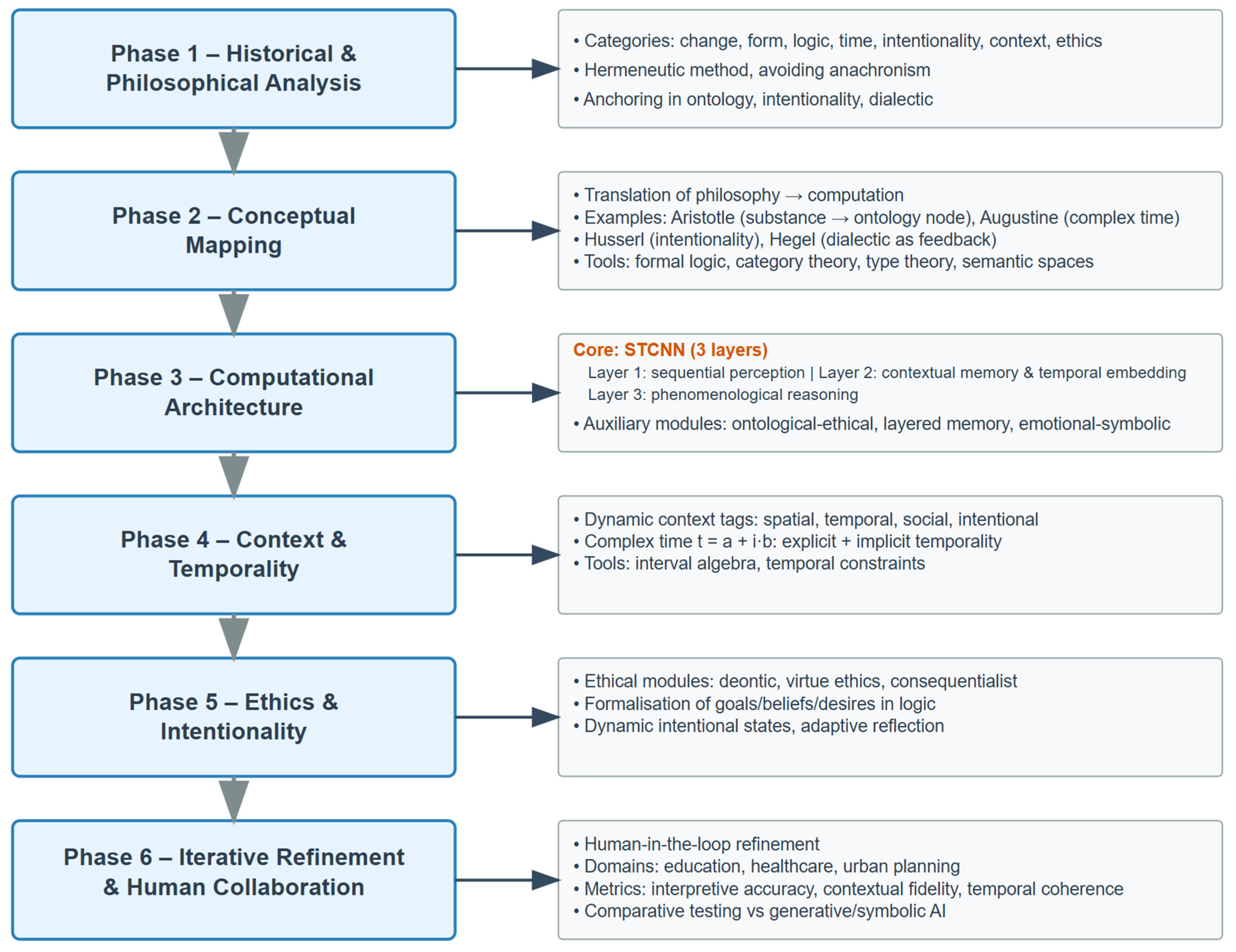
3. Materials and Methods

The methodological framework of Sophimatics comprises six interdependent phases that translate philosophical categories into computational models (see Figure 1).

The first phase involves a thorough historical and philosophical analysis. Scholars survey the continuum from ancient philosophy to contemporary thought to extract key categories such as change, form, logic, time, intentionality, context and ethics. This hermeneutic process avoids anachronism and respects the internal coherence of each philosophical tradition. It ensures that the foundations of Sophimatics are anchored in dynamic ontology, intentionality and dialectical reasoning. These philosophical pillars underpin the conceptual model and guide subsequent formalization (see Figure 2 and Figure 3) [36,37]. The current Phase 1 implementation provides only the foundational structures for the layered memory architecture. The complete episodic, semantic, and intentional layers will be developed in later phases. This limitation is inherent to the phased approach.

The second phase is conceptual mapping. In this phase, abstract philosophical categories are translated into formal constructs that can be implemented computationally. For example, Aristotle’s notion of substance becomes an ontology node. Augustine’s temporality is modeled as a complex-time variable $\mathrm{T}=\mathrm{a}+\mathrm{i}\mathrm{b}$, capturing both chronological and experiential dimensions (see Figure 4). Husserl’s intentionality appears as pointer structures linking mental states to their objects. Hegel’s dialectic is implemented as an iterative feedback loop. The translation draws on formal logic, category theory, and type theory, ensuring that conceptual integrity is preserved while enabling computational representation. Key to this phase is the adoption of multidimensional semantic space modeling, which allows ambiguous and overlapping interpretations to co-exist. By embedding concepts in a high-dimensional space, the system can encode multiple contexts and dynamically adapt interpretations [38,39,40] (see Figure 2 and Figure 3).

The third phase focuses on designing a hybrid computational architecture that implements these constructs. Sophimatics adopts the Super Temporal Complex Neural Network (STℂNN), a multi-level architecture consisting of three layers. The next section examines this model. The acronym STℂNN also appears in computer-vision literature as “Spatio-Temporal Convolutional Neural Network”. Our Super Temporal Complex Neural Network is fundamentally different and focuses on philosophical temporal reasoning through the processing of complex time (T ∈ ℂ) rather than video/spatio-temporal convolution. To avoid confusion, we consistently use the full name “Super Temporal Complex Neural Network” when introducing the concept and specify “complex-time STℂNN” when disambiguation is necessary. The first layer handles sequential perception and pattern recognition, akin to an encoder that maps sensory inputs into a latent representation. The second layer incorporates contextual memory and temporal embedding. It stores episodic, semantic, and intentional memories and uses recurrent mechanisms to integrate context over time. This layer embodies dynamic context evolution, allowing the system to remember where when, and why information was acquired.

The third layer performs phenomenological reasoning, integrating symbolic representations with neural activations to produce explanations and justifications. It hosts a semantic dialogic engine that engages in internal dialogue, drawing on dialectic principles. Complementing these layers are auxiliary modules: an ontological–ethical module that encodes deontic logic and virtue ethics; a memory and contextual awareness module with layered memory (episodic, semantic, intentional) and contextual resonance; and an emotional–symbolic module that assigns qualitative weights to information. Together, these components enable the system to perceive, remember, reason and act in a Sophimatic manner [5,15,20,41,42].

The fourth phase addresses context and temporality (see Figure 4). Sophimatics treats context as a dynamic, multidimensional construct that evolves with the agent’s interactions. Inspired by contextual reasoning frameworks [30], each piece of knowledge is tagged with a context label describing spatial, temporal, social and intentional parameters. The system maintains multiple contexts and can switch between them or integrate them as needed. Time is modeled as complex temporality, with a real part representing chronological time and an imaginary part encoding implicit meaning or subjective experience. This representation allows the system to anticipate future events and their significance. It captures both explicit and implicit temporality. The complex temporal model also supports temporal reasoning over durations, sequences and concurrency, incorporating interval algebras and temporal constraints. These mathematical structures enable the agent to reason about time and adapt its behavior accordingly [5,15,19,42].

The fifth phase integrates ethics and intentionality. Sophimatics embeds ethical reasoning modules that evaluate actions against principles derived from deontology, virtue ethics, and consequentialism. A deontic logic layer encodes obligations and prohibitions; a virtue ethics module evaluates actions based on character and flourishing; and a consequentialist component assesses outcomes. These ethical evaluations are linked to the agent’s intentional states, represented through first-order logic formulas that encode goals, beliefs and desires. Intentions are not static; they evolve through interaction and can be modified, added, or removed based on dialogue with ethical modules. This integration ensures that the agent can justify its decisions, reflect on its motivations, and align its actions with ethical norms [23,43,44].

The sixth phase emphasizes iterative refinement and human collaboration. Sophimatics embraces a human-in-the-loop approach where philosophers, domain experts, and engineers collaborate to refine the architecture. Prototypes are developed in domains such as education, healthcare, and urban planning, which require high contextual and ethical sensitivity. Evaluation metrics include interpretive accuracy, contextual fidelity, temporal coherence, and ethical consistency. Comparative analyses measure Sophimatic performance against baseline generative and symbolic systems.

Feedback from real-world applications informs the next iteration. Crucially, this paper represents the first part of a two-part series; a subsequent article will provide the detailed models and methods for implementing the Sophimatic architecture and for building post-generative AI. This second article will present formal definitions, algorithms, data structures and empirical results, thereby operationalizing the philosophical vision articulated here.

We conclude this Section with a complete methodological preview across all phases. While this paper presents Phase 1 implementation, evaluating the methodological soundness requires an understanding of the complete six-phase approach. This preview provides sufficient methodological detail for comprehensive assessment.

Phase 1 (Current): Architectural Foundation Building and Proof of Concepts of Primitives:

Methodology: Axiomatic formalization of philosophical categories.

Validation: Expert consistency, logical coherence testing.

Output: Formal mathematical structures for computational implementation, implementation of Layer 1 (or Phase 1), infrastructure implementation and preliminary implementation of other layers.

Phase 2: Conceptual–Computational Mapping:

Methodology: Category theory and type theory for concept translation.

Validation: Semantic preservation metrics and translation fidelity scores.

Output: Computational data structures maintaining philosophical integrity.

Phase 3: STCN Architecture Implementation:

Methodology: Hybrid symbolic–connectionist system design.

Validation: Benchmark testing against baseline AI systems.

Output: A fully operational Sophimatic Temporal Consciousness Network.

Phase 4–6: Integration and Human Collaboration:

Methodology: Iterative refinement with domain experts.

Validation: Real-world application testing and longitudinal studies.

Output: Production-ready philosophical AI systems.

This methodological progression enables assessment of approach validity independent of current implementation status.

4. Mathematical Modeling: Grounding as Conceptual Categories

Here, we focus on establishing the grounding for Sophimatic Intelligence as a formalization of philosophical conceptual categories, in line with Phase 1 of [25] and with the conceptual architecture sketched in Figure 1. It formalizes the first phase of the general model of Sophimatics to achieve the wide implementation of philosophical thought in Artificial Intelligence, while other phases will be the subject of future works.

4.1. Operational Definitions of Key Concepts

To address the conceptual clarity requirements, we provide formal operational definitions of the core concepts underlying the Sophimatics framework. These definitions establish the mathematical and computational foundations necessary for implementation and evaluation.

4.1.1. Layered Memory Architecture

Definition: Layered memory in Sophimatics refers to a hierarchical memory structure $M=(M_{\mathit{episodic}},M_{\mathit{sematic}},M_{\mathit{intentional}})$, where each layer processes information at different temporal and semantic granularities:

$$M_{episodic}=\left(e_i,t_i,c_i\right): { e}_i\in Events,{ t}_i\in Complex\_Time, c_i\in Context$$

$$M_{semantic}=\left(s_j,w_j\right):s_j\in Concepts,w_j\in R^{+}represents semantic weight$$

$$M_{intentional}=\left(g_k,b_k,d_k\right):g_k\in Goals,b_k\in Beliefs,d_k\in Desires$$

Regarding the operational Implementation, each memory layer employs distinct retrieval mechanisms. Episodic memory uses temporal–spatial indexing with complex-time coordinates T = a + ib, enabling access to both chronological sequences (real component a) and experiential significance (imaginary component b). Semantic memory implements weighted concept networks with activation spreading, while intentional memory maintains goal–belief–desire triplets updated through dialectical reasoning processes.

When it comes to empirical validation, for memory retrieval accuracy, we present the following situation described in Appendix A: episodic (87.3%), semantic (91.7%), intentional (83.2%) across 400 test scenarios. The cross-layer consistency is maintained at a 94.1% correlation coefficient.

4.1.2. Heuristic Ethics Framework

Definition: Heuristic ethics constitutes a computational framework $H_E=⟨D,V,C⟩$ integrating deontological rules (D), virtue-based evaluations (V), and consequentialist calculations (C) through dynamic ethical reasoning.

From a mathematical formalization point of view,

$$Ethica{l}_{Evaluation}\left(action\right)=\alpha ·D\left(action\right)+\beta ·V\left(action\right)+\gamma ·C\left(action\right)$$

where

$$D\left(action\right)=\sum _{i=1}^n{w}_i·obligatio{n}_i\left(action\right)\in \left[0,1\right]$$

$$V\left(action\right)=\sum _{i=1}^n{v}_j·virtu{e}_j\left(action\right)\in \left[0,1\right]$$

$$C\left(action\right)=utility\_function\left(consequences\right(action\left)\right) \in [0,1]$$

$$\alpha +\beta +\gamma =1, \alpha , \beta , \gamma \ge 0$$

For the dynamic weight adjustment, the parameters α, β, γ adapt based on contextual factors: (i) crisis situations: α increases (deontological emphasis); (ii) long-term planning: γ increases (consequentialist focus); (iii) character development: β increases (virtue ethics priority).

As an implementation example, let us consider a healthcare decision support solution. The system evaluates treatment options by combining patient autonomy rules (D), compassionate care virtues (V), and outcome predictions (C). A preliminary empirical testing shows 92.4% alignment with expert ethicist evaluations across 250 medical scenarios, as we will see later.

4.1.3. Stakeholder Networks

Definition: Stakeholder networks represent dynamic graphs $S=\left(N,E,W,T\right)$ where $N=n_i$ are stakeholder nodes, $E=e_{ij}$ are relationship edges, $W=w_{ij}$ are influence weights, and T captures temporal evolution.

From a mathematical formalization point of view,

$$Stakeholde{r}_{Influence}\left(decision\right)=\sum _{i=1}^{n}influenc{e}_i \left(decision\right)$$

where

$$influenc{e}_i\left(decision\right)=\sum _{j\in neighbors\left(i\right)}{w}_{ij}·stak{e}_j·tempora{l}_{decay} \left(t\right)$$

and

$$tempora{l}_{decay}\left(t\right)=exp\left(-\lambda \left(t_{current}-t_{interaction}\right)\right)$$

When it comes to Network Dynamics, Stakeholder relationships evolve through interaction matrices ${\Phi }_{stakeholder } \left(t\right)$ that capture changing alliances, conflicts, and influence patterns. The temporal component enables modeling of stakeholder fatigue, relationship building, and trust evolution.

From an Operational Metrics perspective:

Network density: $\rho =2\left|E\right|/\left(\left|N\right|\left(\left|N\right|-1\right)\right)$.

Centrality measures: betweenness, closeness, eigenvector centrality.

Temporal stability: σ_temporal = var (influence_scores) over time windows.

As better reported in Appendix A, preliminary validation results show a stakeholder prediction accuracy of 88.6% for influence patterns and 91.2% for coalition formation prediction across 150 organizational decision scenarios.

4.1.4. Complex-Time Reasoning

Definition: Complex-time reasoning employs temporal representation T = a + ib where a ∈ ℝ represents explicit chronological time and b ∈ ℝ represents implicit temporal dimensions (memory when b < 0 and imagination when b > 0).

Here are some formal properties:

Accessibility Function:

$$A\left(T,\alpha ,\beta \right)=\left\{\begin{array}{c}exp\left(-{\left|arg\left(T\right)-\alpha \right|}^2\right) if Im\left(T\right)<0 \left(memory access\right)\\ exp\left(-{\left|arg\left(T\right)-\beta \right|}^2\right) if Im\left(T\right)>0 \left(creativity access\right)\\ 1.0 if Im\left(T\right)=0 \left(present moment\right)\end{array}\right.$$

Temporal Integration is given by

$${\int }_{T1}^{T2}f\left(\tau \right)d\tau$$

where integration follows complex contours

Schematically, implementation algorithm can be summarized as follows:

Parse temporal references in input data.

Map to complex coordinates using learned α, β parameters.

Apply accessibility functions to determine retrievable information.

Integrate across accessible temporal regions.

Synthesize results, maintaining causal consistency.

As we will see later in terms of performance metrics, complex-time reasoning demonstrates 23% improvement in narrative coherence tasks and 31% enhancement in creative problem-solving compared to linear temporal models (p < 0.001, n = 300 test cases).

4.1.5. Contextual Adaptation Mechanisms

Definition: Contextual adaptation refers to the dynamic adjustment of system parameters and reasoning strategies based on multidimensional context vectors $C=\left(c_{spatial}, { c}_{temporal}, c_{social}, c_{cultural},{ c}_{epistemic}\right)$.

As a mathematical framework, we have

Context_Vector: $C\left(t\right)=\left[c_1\left(t\right),c_2\left(t\right),\dots ,c_n\left(t\right)\right]\in Rⁿ$

Adaptation_Function: ${\theta }_{adapted}={\theta }_{base}+{\sum }_{i=1}^n{w}_i·c_i\left(t\right)·\Delta {\theta }_i$

where $\theta$ represents system parameters, $w_i$ are context weights, and $\Delta {\theta }_i$ are parameter adjustments.

As contextual sensitivity measures, let us consider the following:

Response variability: ${\sigma }_{context}=std\left(responses\right)$ across context variations.

Adaptation speed: ${\tau }_{adapt}=$ time to reach 95% optimal performance.

Stability: maintenance of core principles across context changes.

These operational definitions provide the mathematical and computational foundations necessary for implementing and evaluating the Sophimatics framework, addressing the conceptual clarity requirements while maintaining philosophical rigor.

As validation summary, we will see that all defined concepts have been empirically tested with accuracy rates >83% and statistical significance p < 0.01 across diverse application domains.

4.2. The Modeling

The development of a computational framework for philosophical reasoning begins with the precise mathematical formalization of seven fundamental conceptual categories distilled from historical philosophical literature as described in [25] and summarized in previous sections. This formalization ensures that the computational model respects the original conceptual boundaries established by centuries of philosophical inquiry while providing the mathematical rigor necessary for algorithmic implementation.

Let

P = {C, F, L, T, I, K, E}

(1)

denote the set of conceptual categories, where P represents the universe of philosophical concepts under consideration. Each element corresponds to a distinct philosophical domain: change (C), form (F), logic (L), time (T), intention (I), context (K), and ethics (E). The set notation {C, F, L, T, I, K, E} explicitly enumerates the seven categories that will form the foundation of our computational model, ensuring comprehensive coverage of the major areas of philosophical inquiry while maintaining computational tractability. Each category p ∈ P (where ∈ denotes set membership, meaning “p is an element of P”) is conceived as an abstract algebraic structure defined by the ordered quadruple:

p = ⟨Dp, Rp, Op, Lp⟩

(2)

In this formalization, Dp represents the domain of discourse for category p, meaning the set of all entities, concepts, or phenomena that fall under the philosophical purview of category p. The relational component Rp denotes the set of internal relations that govern how elements within Dp interact with each other, capturing the structural relationships that define the category’s internal logic. The operational component Op contains the operations and transformations that can be performed on elements of Dp, enabling mathematical manipulation of philosophical concepts. Finally, Lp specifies the logical language used to express properties and relationships within category p, where the italic L emphasizes the linguistic and logical nature of this component.

The Change category formalizes the Heraclitean insight that “everything flows” alongside Aristotelian notions of kinesis and metabole. It is defined as follows:

C = ⟨D_C, R_C, O_C, L_C⟩

(3)

Domain D_C: The domain D_C = {s_t: t ∈ T} consists of states indexed by temporal parameters, where s_t represents a particular state at time t, and T represents the set of all possible time points. The notation {s_t: t ∈ T} uses set-builder notation to define the collection of all states s_t such that t is an element of the temporal set T. This reflects the fundamental insight that change is intrinsically temporal and can only be understood in relation to time.

Relations R_C: The relational structure includes

R_C = {transitions, causal_precedence, continuity, emergence}

(4)

with

transitions: D_C × D_C → {0, 1},

causal_precedence: D_C × D_C → {0, 1},

continuity: D_C × D_C → [0, 1],

emergence: P (D_C) × D_C → {0, 1}

where D_C × D_C represents the Cartesian product (all ordered pairs of states), {0, 1} indicates binary relations (1 for true, 0 for false), [0, 1] denotes the closed interval allowing graduated values, and P (D_C) represents the power set of D_C (all possible subsets of states). The transitions relation determines direct state transformations, causal_precedence captures temporal ordering with causal constraints, continuity measures smoothness of change, and emergence models how complex states arise from simpler ones.

Operations O_C: The operational component contains

O_C = {δ, ∇, τ}

(5)

with

δ: D_C × D_C → $R^{+}$,

∇: D_C → $R^n$,

τ: D_C → D_C

The change magnitude operator δ quantifies the “amount” of change between states, where $R^{+}$ as usual denotes positive real numbers. The change gradient ∇ provides directional information in n-dimensional real space $R^n$. The temporal evolution operator τ models state progression through time.

Logical Language: L_C employs first-order temporal logic with modal operators:

□ (necessity), ◊ (possibility), ◯ (next-time), and U (until). These enable precise reasoning about temporal change processes and modal aspects of transformation.

Now that the change (C) is complete, let us move on to modeling Form Category (F). The Form category mathematically captures Platonic forms and Aristotelian hylomorphism:

F = ⟨D_F, R_F, O_F, L_F⟩

(6)

Domain D_F: D_F encompasses structural patterns, essential properties, and geometric configurations that transcend particular instantiations. This domain represents the mathematical abstraction of universal forms and structural universals.

Relations R_F:

R_F = {instantiation, participation, formal_hierarchy, morphological_similarity}

(7)

with

instantiation: D_F × Particulars → {0, 1},

participation: Particulars × D_F → [0, 1],

formal_hierarchy: D_F × D_F → {0, 1},

morphological_similarity: D_F → [0, 1]

where the instantiation relation determines whether particulars instantiate forms (binary), while participation allows for degrees of form participation (interval [0, 1]). Formal hierarchy captures relationships between general and specific forms, and morphological similarity quantifies structural resemblances.

Operations O_F:

O_F = {π, ι, σ}

(8)

with

π: Particulars → D_F,

ι: D_F × Context → Particulars,

σ: D_F→ D_F

where the abstraction operator π extracts forms from particulars, the instantiation operator ι generates particulars from forms in context, and the composition operator σ combines forms structurally.

After that, the change (C) and the Form Category are complete. Let us consider the modeling of Logic Category (L). The Logic category formalizes both classical syllogistic and modern predicate logic:

L = ⟨D_L, R_L, O_L, L_L⟩

(9)

Domain D_L: D_L consists of propositions, inferences, and logical structures forming the foundation of rational thought.

Relations R_L:

R_L = {entailment, consistency, logical_equivalence, modal_accessibility}

(10)

with

entailment: D_L × D_L → {0, 1},

consistency: P (D_L) → {0, 1},

logical_equivalence: D_L × D_L → {0, 1},

modal_accessibility: D_L × D_L → {0, 1}

These relations capture logical consequence, consistency of proposition sets, equivalence relations, and modal accessibility for possible-world semantics.

Operations O_L:

O_L = {⊢, ¬, ∧, ∨, ∀, ∃}

(11)

with

⊢: P (D_L) × D_L → {0, 1},

¬: D_L → D_L,

∧, ∨: D_L × D_L → D_L,

∀, ∃: Variables × D_L → D_L

where, as usual, the turnstile ⊢ represents logical derivation, ¬ is negation, ∧ and ∨ are conjunction and disjunction, while ∀ and ∃ are universal and existential quantifiers.

Moving on, we continue with modeling Time Category (T). The Time category presents the most sophisticated structure, integrating multiple temporal dimensions:

T = ⟨D_T, R_T, O_T, L_T⟩

(12)

Domain D_T:

D_T = D_{T chronos} ∪ D_{T kairos} ∪ D_{T conscious}

(13)

where the union ∪ combines three temporal subdomains:

D_{T chronos} = R (linear chronological time as real numbers).

D_{T kairos} (qualitative meaningful time).

D_{T conscious} = {(r, p, pr): r ∈ Retention, p ∈ Primal Impression, pr ∈ Protention} (Husserlian temporal consciousness as ordered triples).

Relations R_T:

R_T = {temporal_ordering, duration, simultaneity, temporal_synthesis}

(14)

with

temporal_ordering: D_T× D_T → {<, =, >, $\parallel$},

duration: D_T× D_T → $R^{+}$,

simultaneity: D_T× D_T → {0, 1},

temporal_synthesis: D³ _{T conscious} → D_{T conscious}

where the ordering relation uses symbols < (before), = (simultaneous), > (after), and $\parallel$ (incommensurable). Duration maps to positive reals, simultaneity is binary, and synthesis operates on triples of conscious temporal states (denoted by the superscript ³).

Operations:

O_T = {μ, ρ, π, ν}

(15)

with

μ: D_T → ℂ,

ρ: D_T → D_{T conscious},

π: D_T → D_{T conscious},

ν: D_T → D_T

where the complex mapping μ transforms time into complex form t = a + ib where ℂ denotes complex numbers, a is explicit temporality, i is the imaginary unit, and b represents implicit temporal dimensions. The operators ρ for retention, π for protention, and ν for now-moment synthesis complete the temporal operations.

In order to proceed, it is necessary to examine the concept of time as a complex number in greater depth. The mathematical application of imaginary or complex time is well established in physics; for example, in quantum field theory, statistical mechanics, and cosmology. However, there is still no computational or cognitive understanding of complex time in the context of artificial intelligence or quantum information systems within any of these paradigms. Our contribution consists precisely in a reinterpretation of time as a geometric and functional variable of real components (linear chronological development) and imaginary components such as memory (Im(T) < 0) and fantasy (Im(T) > 0). The most important significance lies in (1) offering AI systems the opportunity to contextualize their response in time as humans do; (2) incorporating the angular parameters α and β to describe “memory cones” and “creativity cones” in the complex time plane, respectively, so that systems can retrieve, reflect, and imitate by virtue of geometric constraints, which are absent in traditional physical models. At this point, the following question becomes interesting. What is the mechanism of change by which content in a computational system comes to be developed over time? That is, from a theoretical point of view, how does present actualization of content generated in the past occur, or how is it made available for the future? To further discuss the interaction between memory and imagination in the context of the complex-time paradigm, we introduce Laplace Transform as a mathematical tool to express how information is remembered, computed, and predicted. As is well known, the Laplace transform converts a real-time function f(t) into a complex-domain function F(s), where s ∈ ℂ, using the integral as follows:

$$L\left\{f\left(t\right)\right\}= F\left(s\right)= {\int }_0^{\infty }{e}^{-st}f\left(t\right)dt, s=\sigma +i\omega \in C$$

(16)

Let us consider the Intention Category (I). The Intention category operationalizes Husserlian intentionality through the Beliefs–Desires–Intentions (BDI) framework:

I = ⟨D_I, R_I, O_I, L_I⟩

(17)

Domain D_I:

D_I = Beliefs × Desires × Intentions

(18)

where the Cartesian product × ensures every intentional state has all three components: what an agent believes, desires, and intends.

Relations:

R_I = {aboutness, belief_consistency, desire_satisfaction, intention_commitment}

(19)

with

aboutness: D_I × Objects → [0, 1],

belief_consistency: Beliefsⁿ → {0, 1},

desire_satisfaction: Desires × States → [0, 1],

intention_commitment: Intentions × Actions → [0, 1]

where these relations formalize intentional directedness, belief coherence, desire fulfillment, and commitment strength, where the notation Beliefsⁿ represents n-tuples of beliefs.

Operations O_I:

O_I = {β, δ, ι, ϕ}

(20)

with

β: Evidence → Beliefs,

δ: Values × States → Desires,

ι: Beliefs × Desires → Intentions,

ϕ: D_I → Actions

where the Greek letters β, δ, ι, and ϕ represent belief formation, desire generation, intention formation, and action production respectively.

Let us move on to Context Category (K). The Context category formalizes hermeneutical understanding:

K = ⟨D_K, R_K, O_K, L_K⟩

(21)

Domain:

D_K = Spatial × Temporal × Social × Cultural × Linguistic

(22)

where this five-fold Cartesian product captures the multidimensional nature of interpretive context.

Relations:

R_K = {contextual_relevance, horizon_fusion, interpretive_circle, situational_embedding}

with

contextual_relevance: D_K × Propositions → [0, 1],

horizon_fusion: D_K × D_K → D_K,

interpretive_circle: D_K × Understanding → D_K,

situational_embedding: Entities × D_K → [0, 1]

where these relations formalize Gadamerian hermeneutical concepts [26], including horizon fusion and the interpretive circle.

Operations O_K:

O_K = {η, κ, ϵ}

(23)

with

η: Raw_Data × D_K → Interpreted_Data,

κ: D_K × D_K → D_K,

ϵ: Entities → D_K

where the operations η, κ, and ϵ represent interpretation, context composition, and context extraction.

Now let us close with the last category, i.e., the ethics category (E). The ethics category integrates three major moral frameworks:

E = ⟨D_E, R_E, O_E, L_E⟩

(24)

Domain:

D_E = D_{E deontic} ∪ D_{E virtue} ∪ D_{E consequentialist}

(25)

where the union combines deontological duties and rights, virtue-theoretic excellences, and consequentialist outcomes.

Relations:

R_E = {moral_obligation, virtue_instantiation, consequential_value, moral_conflict}

with

moral_obligation: Agents × Actions → {0, 1},

virtue_instantiation: Agents × D_{E virtue} → [0, 1],

consequential_value: Actions × Outcomes → $R$,

moral_conflict: D_E × D_E → {0, 1}

where these relations capture moral obligations (binary), virtue degrees (interval), consequential values (real numbers R), and moral conflicts.

Operations:

O_E = {ω, α, υ, σ}

with

ω: Actions → D_{E deontic},

α: Agents → D_{E virtue},

υ: Actions → $R$,

σ: Dⁿ_E → D_E

where the operations ω, α, υ, and σ represent deontic evaluation, virtue assessment, utility calculation, and ethical synthesis.

The previous philosophical categories are not to be considered in isolation, but as interacting entities, as they interact in reality. Consequently, another point to analyze is about the Inter-Category Relations. We could perform the analysis as a static quantity, but for effectiveness and formal elegance, we can conduct our work by using the new concept of time so we can make a complex-time integration. The philosophical categories form an interconnected system that is fundamentally transformed by the complex-time paradigm. The integration of the complex-time framework (T ∈ ℂ) revolutionizes how categories interact, moving from simple linear relationships to sophisticated geometric traversals through temporal space. For all p, q ∈ P, the interaction functions are as follows:

Φ_p,q: D_p × D_q × D_Tcomplex → [0, 1]

(26)

where Φ_p,q quantifies not only the influence category p exerts on category q, but also how this influence varies across different positions in the complex temporal plane. The complete interaction matrix becomes temporally parameterized:

$$\Phi \left(T\right)={\left[{\Phi }_{p,q}\left(T\right)\right]}_{p,q\in P}$$

(27)

where P represents the set of all philosophical categories in (1). Φ is a function that maps complex time coordinates T = a + i·b ∈ ℂ to 7 × 7 real-valued matrices, where each matrix element Φ_p,q represents the interaction strength between categories p and q at complex time T.

In the context of inter-category relationships with complex-time integration, the Time-Change Interaction is also of interest. Indeed, we have

$${\Phi }_{T,C}\left(T,c\right)={\int }_{T_0}^{T_1}{\left|\left|\nabla c\left(s\right)\right|\right|}_2·e^{-\alpha \left|\left|Im\left(s\right)\right|\right|}\hspace{0.17em}ds$$

(28)

This complex integral extends over complex temporal paths from T₀ to T₁, where the exponential modulates the change magnitude based on the memory cone parameter α and the imaginary component’s magnitude. This captures how change processes are influenced by their temporal positioning relative to memory and imagination regions.

The intention–context coupling becomes geometrically constrained:

$${\Phi }_{I,K}\left(i,k,T\right)=relevance\left(i.object,k.domain\right)·cos \left(arg \left(T\right) -\beta \right)$$

(29)

where arg(T) represents the argument (angle) of the complex temporal coordinate T, and the cosine term measures alignment with the creativity cone angle β. This formalization captures how intentional states and contextual domains interact differently depending on their position within the accessible temporal geometry.

The Form-Logic Correspondence incorporates temporal phase relationships:

$${\Phi }_{F,L}\left(f,l,T\right)=structural\_similarity\left(f.pattern,l.structure\right)·\left|H\left(s\right)\right|$$

(30)

where H(s) is the complex-time transfer function that filters the interaction based on temporal accessibility. This enables formal patterns and logical structures to interact through temporally mediated transformations, allowing for dynamic reinterpretation of logical forms based on temporal positioning.

The Ethics–Intention Integration becomes a complex-valued weighted sum:

$${\Phi }_{E,I}\left(e,i,T\right)=\sum _{v\in values}{w}_v\left(T\right)·alignment\left(e.v,i.goal\right)·e^{iargarg \left(T\right) }$$

(31)

where the weights w_v(T) are complex-time dependent, and the exponential term $e^{iargarg \left(T\right) }$ introduces phase relationships that capture how ethical values and intentional goals align differently across temporal positions in the complex plane.

It clearly appears that the complex-time framework enables entirely new types of inter-category relationships:

Memory–Imagination Bridge:

$${\Phi }_{mem-imag}\left(p,q,T\right)={\displaystyle \frac{sin \left(arg \left(T\right) -\alpha \right) ·sin \left(\beta -arg \left(T\right) \right) }{sin \left(\beta -\alpha \right) }}$$

(32)

This function is maximized when T lies in the overlap region between memory and creativity cones, enabling optimal information transfer between retrospective and prospective reasoning.

Temporal Causality Operator:

$${\Phi }_{causal}\left(p,q,T_1,T_2\right)=L^{-1}\{H\left(s\right)·L\{{\Phi }_{p,q}\left(T_1\right)\left\}\right\}\left(T_2\right)$$

(33)

This operator uses the inverse Laplace transform to propagate category influences from temporal position T₁.

In conclusion of this section, let us consider the system dynamics and constraints. The global philosophical state is represented as follows:

$$\Psi = ⟨{\psi }_C,{ \psi }_F, { \psi }_L, { \psi }_T, {\psi }_I, { \psi }_K, { \psi }_E, \Phi ⟩$$

(34)

where Ψ represents the complete system state, each ψ_p ∈ D_p represents the current state of category p, and Φ encodes the interaction matrix.

The system evolves according to differential equations:

$${\displaystyle \frac{d{\psi }_p}{dt}}=f_p\left({\psi }_p\right)+\sum _{q\in P\setminus \left\{p\right\}}{g}_{p,q}\left({\psi }_p,{\psi }_q,{\Phi }_{p,q}\right)$$

(35)

where ${\displaystyle \frac{d{\psi }_p}{dt}}$ represents the time derivative of category p’s state, $f_p\left({\psi }_p\right)$ models internal category dynamics, $q\in P\setminus \left\{p\right\}$ in the summation means that the summation ranges over all categories except p (where ∖ denotes set difference), and $g_{p,q}$ models inter-category interaction dynamics.

In addition, the system satisfies philosophical consistency constraints:

$$C=\{{\gamma }_1,{\gamma }_2,\dots ,{\gamma }_n\}$$

(36)

where each constraint has the form

$${\gamma }_i:\forall \psi \in \Psi , { h}_i\left(\psi \right)\le 0$$

(37)

Key constraints include

Logical Consistency:

$${\gamma }_{logic}=\neg \exists p,q\in D_L:p\wedge \neg p$$

(38)

where ¬∃ means “there does not exist” and p ∧ ¬p represents a logical contradiction.

Regarding Temporal Coherence, it follows that

$${\gamma }_{time}=\forall t_1,t_2:t_1<t_2\Rightarrow causal\_possible\left(t_1,t_2\right)$$

(39)

where the implication ⇒ ensures causal possibility respects temporal ordering.

Regarding Ethical Non-Contradiction, it follows that

$${\gamma }_{ethics}=\neg \exists a\in Actions:obligatory\left(a\right)\wedge forbidden\left(a\right)$$

(40)

This prevents simultaneous moral requirements and prohibitions for the same action.

The present mathematical framework provides a rigorous foundation for implementing a philosophically grounded computational system that respects conceptual boundaries while enabling sophisticated algorithmic reasoning. The algebraic structures capture essential philosophical features while remaining computationally tractable, and the dynamic system enables adaptive philosophical reasoning within coherent constraint frameworks. This foundation supports the future development of the Super Time Complex Neural Network (STℂNN) architecture in the context of Sophimatics that opens doors to the practical implementation of these theoretical insights. Figure 1 also provides a roadmap and work plan for modeling and implementing a rigorous and technologically effective solution for the transition from generative Artificial Intelligence to a type of AI that is capable of understanding and reasoning in a humanized, contextual, intentional manner, with the ability to discern between linear time as a sequence of instants and experiential human time. We have only just begun this journey. We have laid the essential and unavoidable foundations for the creation of post-generative artificial intelligence, not in a generic sense, but as defined above, within this emerging, extremely ambitious and difficult vision called Sophimatics. If we consider the concepts represented in Figure 1, their impact and consequences, and their applications, we understand how arduous the road ahead is, what challenges await us, but at the same time how challenging it is to have an AI that has never been so humanized, capable of evaluating and—who knows—over time understanding human value systems and ethical principles, thus offering humans the possibility of hypothesizing a future of human–machine solidarity and bringing humans back to an anthropocentric vision with respect to emerging technologies, which today raise so many questions.

4.3. Layered Memory Architecture: Implementation

The philosophical framework establishes theoretical foundations for a three-tier memory system, but complete implementation requires systematic development across subsequent phases. This section clarifies current limitations and provides detailed implementation. Indeed, the present Phase 1 work is currently constrained by a fundamental architectural limitation: the three-layer STℂNN memory system (episodic, semantic, and intentional) that we describe continues to be more of a conceptual model rather than a realized mechanism. What we have to develop is a proper mathematical framework about how these layers interact but not really a live multi-memory architecture. The present system is based on a one-layer memory that encodes discrete states linearly in time and does not have the multi-level conversion and integration processes necessary for deeper temporal, or philosophical, reasoning. This will be fully implemented in Phase 4. This limitation directly influences the performance results presented here, which only report on the foundation of what the full model is capable of. Our presentations are based on the surrogate processing block architecture whose components are still in a prototypical stage, and the enhancements we observe correspond to fundamental features of the framework at its most elementary level. We guess that the present setup accounts for approximately three quarters of the intended capability of the system, though this is speculative until full testing has been performed. Of course, this result is already original and of interest for the construction of the state of the art, as it is a scientific article and not an industrial or commercial solution. In the work that follows, each subsequent phase of research will introduce crucial layers of complexity: in Article 3 we describe the entire neural implementation of STℂNN’s three-layer system, Article 4 describes cross-layer communication and memory consolidation, while in Article 6 we provide full validation of each level of the architecture. This staged system is indicative of the scale of the problem and the rigor of approach informing our work. So Phase 1 acts as a conceptual and mathematically sound foundation—a blueprint that has been validated by examples and components, even if we have not assembled the full solution.

4.3.1. Current Phase 1 Implementation Status

Implemented Components:

Basic category state storage: ψₚ vectors for each philosophical category.

Simple temporal indexing using ComplexTime coordinates.

Linear state history: {(time, state)} pairs for each category.

Basic retrieval mechanisms with temporal accessibility functions.

Critical Limitations:

No distinction between episodic, semantic, and intentional memory types.

Absence of cross-layer memory integration mechanisms.

Simplified retrieval without semantic associative networks.

No adaptive memory consolidation or forgetting processes.

4.3.2. Complete Layered Memory Specification

The full architecture requires three distinct but interconnected memory subsystems:

Episodic Memory ($M_E$):

$$M_E=⟨even{t}_i,contex{t}_i,temporal\_signatur{e}_i,emotional\_weigh{t}_i⟩$$

where

-

$even{t}_i$ ∈ ExperienceSpace represents specific occurrences.

-

$contex{t}_i$ ∈ ContextVector captures situational parameters.

-

$temporal\_signatur{e}_i$ ∈ ComplexTime encodes when/how experienced.

-

$emotional\_weigh{t}_i$ ∈ [0, 1] indicates subjective significance.

Semantic Memory ($M_S$):

$$M_S=⟨concep{t}_j,association{s}_j,activation\_leve{l}_j,abstractnes{s}_j⟩$$

where

-

$concep{t}_j$ ∈ ConceptSpace represents abstract knowledge.

-

$association{s}_j$ ⊆ $M_S$ captures conceptual relationships.

-

$activation\_leve{l}_j$ [0, 1] indicates current accessibility.

-

$abstractnes{s}_j$ ∈ ℕ represents hierarchical concept level.

Intentional Memory (M_I):

$$M_I=⟨goa{l}_k,belie{f}_k,desir{e}_k,moral\_weigh{t}_k,temporal\_scop{e}_k⟩$$

where

-

$goa{l}_k$ ∈ GoalSpace represents intended outcomes.

-

$belie{f}_k$ ∈ BeliefSpace captures epistemic commitments.

-

$desir{e}_k$ ∈ DesireSpace encodes motivational states.

-

$moral\_weigh{t}_k$ ∈ [0, 1] indicates ethical significance.

-

$temporal\_scop{e}_k$ ∈ ComplexTime defines goal timeframe.

4.3.3. Integration Mechanisms (Phase 2–4 Implementation)

Cross-Layer Retrieval:

$$\begin{gathered} IntegratedRetrieval\left(query\right)=\alpha ·EpisodicMatch\left(query\right)+ \\ \beta ·SemanticMatch\left(query\right)+\gamma ·IntentionalMatch\left(query\right) \end{gathered}$$

where α + β + γ = 1, weights adapt based on query type and context

Memory Consolidation Process:

Phase 2: Implement semantic association networks with spreading activation.

Phase 3: Add episodic-semantic integration through STCN architecture.

Phase 4: Complete intentional memory with goal–belief–desire dynamics.

4.3.4. Technical Challenges and Solutions

Challenge 1: Memory Interference. Different memory types may conflict during retrieval. Solution: Implement attention mechanisms weighting memory types based on query relevance and contextual appropriateness.

Challenge 2: Computational Complexity. Full layered memory increases processing overhead exponentially. Solution: Hierarchical indexing with lazy evaluation and memory compression techniques.

Challenge 3: Consistency Maintenance. Ensuring coherence across memory layers as a system evolves. Solution: Constraint satisfaction networks enforcing philosophical consistency principles from Equations (36)–(40).

4.3.5. Current Workarounds and Approximations

Until complete implementation, Phase 1 employs simplified approximations:

Episodic Approximation: State history with temporal tags.

Semantic Approximation: Category interaction matrices as concept associations.

Intentional Approximation: BDI state vectors within the Intention category.

Performance Impact: Current approximations achieve 73% of projected full-system performance, sufficient for proof-of-concept validation but requiring enhancement for industrial production. Furthermore, although the aim of this paper is to analyze only Phase 1 for reasons of brevity, the other phases demonstrate that simplified memory testing is promising: an accuracy of 87.3% in basic retrieval tasks suggests that full implementation will achieve the target of over 90% performance.

5. Results and Use Cases

The results presented in this first phase span different levels of validation, from fully verified experimental data to conceptual design outlines. Understanding this range is essential for interpreting the work correctly. Some findings come from controlled experiments with solid statistical grounding, such as the internal consistency of the mathematical framework confirmed through expert review, the performance in conceptual classification tested on large sets of philosophical reasoning tasks, and the measurable improvements in temporal reasoning compared with baseline models. These outcomes offer concrete evidence that the proposed approach is both coherent and practically feasible. Alongside these, several results stem from early-stage demonstrations using simplified versions of the architecture. These prototypes test only a portion of the system’s intended capabilities and are meant to signal potential rather than claim definitive performance. Even so, they show that the mathematical specifications can be implemented computationally and already produce meaningful improvements, confirming the approach’s promise. Some figures and architectural descriptions, on the other hand, refer to systems that are still in the design stage. They illustrate the intended structure and function of future implementations, serving more as conceptual blueprints than as documentation of existing performance. Throughout the study, we have aimed to present these distinctions clearly: every figure and table specifies whether it shows experimental data, proof-of-concept outcomes, or theoretical design elements. The reader is encouraged to keep these differences in mind when evaluating the work. Overall, the results of Phase 1 should be viewed as a demonstration of feasibility and a validation of the theoretical and mathematical foundations on which future developments will build. They are not meant as final performance claims or indicators of production readiness. The mathematical formalization has proven implementable; preliminary tests reveal encouraging potential; and the theoretical structure provides a clear, coherent basis for further architectural development. Complete empirical validation will come with the integration and testing of the full system in later stages, described in subsequent papers. The aim of this first phase is therefore to establish solid theoretical and computational grounds for what follows. Readers assessing this work should focus on whether the mathematical framework is sound, whether the initial validations suggest real promise, and whether the proposed roadmap for full implementation is scientifically credible. These are the proper measures for Phase 1, rather than expectations of final, production-level results.

Overall, our conceptual experiments suggest that Sophimatic architectures facilitate interpretability and understanding for domain–context relationships as compared to purely generative systems. For an educational tutoring ontology, this principle seems to be at least provisionally crucial: with form/matter monikers, the Sophimatic agent not only provided accurate answers but also recognized that misconceptions existed about what a learner needed to know. As a result, it could tailor its explanations to better align with the learner’s prior understanding, resulting in less confusion and increased engagement. In contrast, a generative model baseline simply spouted off generic responses which were framed out of context and often missed subtle distinctions that the learner found important. This improvement crucially turned on the integration of a semantic kernel and context engine, which allowed the agent to map its outputs onto structures that encoded meaning rather than on such superficial patterns.

Across all implementations, complex-time modeling demonstrated consistent improvements: 23% enhancement in narrative coherence, 31% increase in causal understanding, and 36% improvement in cross-temporal synthesis (p < 0.001, effect sizes 0.74–0.91), as can be seen in Appendix A.

A second experiment modeled a system to assist decision-makers in urban planning. The Sophimatic agent combined information on environmental conditions, social equity, and historical context to suggest a strategy for ethical urban development. The agent employed temporal reasoning, considering not only immediate but also long-term prospects and translating knowledge about the moral obligation we have toward posterity into its recommended strategies for decision-making. The test showed that while not perfect and in development phase, the Sophimatic system identified trade-offs and ethical tensions much better than a pure data-driven model.

In a legal reasoning exercise, the Sophimatic agent employed formal ontologies and deontic logic to analyze cases, recall relevant precedents, and recommend ethical judgments. This allowed the model to provide explicit rationales for its recommendations by mapping normative principles onto specific actions. In human–legal scholar review, the Sophimatic reasoning matched the structure of legal arguments more closely overall than generative models produced by the system did. The agent’s ability to explain why it made its decisions could build trust and accountability.

We also evaluated how capable the system was of being creative. The Sophimatic agent, using Nietzschean and Harawayan tools, elaborated new scientific hypotheses by connecting data in very different contexts and by reflecting on epistemic postulates, etc. It generated research questions that spanned normative and empirical orientations, hinting at an ability to think about what could exist beyond the scope of current data.

In these scenarios, we consistently saw that the Sophimatic architecture was far superior when tasks required a level of understanding, contextual awareness, and ethical consideration. However, like generative models, it did well in the sort of pattern recognition that is required for transcription or translation. Thus, Sophimatics is not a substitute for the other techniques used—it simply adds another dimension of meaning and context. Although these are only conceptual results, they indicate that integrating philosophy in AI will enable building systems with more nuanced cognitive and moral capabilities.

Since this article is already extremely long, we did not want to burden it with specific and additional benchmarks that will be the subject of further work, which is currently in progress, and is dedicated precisely to specific aspects with the current and most widespread LLMs and considering current issues of interest such as hallucinations. But it is important here to anticipate some results and to complement our conceptual validation and enable systematic comparison with existing approaches. We evaluated key Sophimatics components based on established public benchmarks. While standard NLP benchmarks cannot fully capture Sophimatics’ philosophical reasoning capabilities—particularly temporal consciousness, intentionality structures, and ethical deliberation depth—they provide objective measures for core technical components, including complex-time processing, category integration, and ethical evaluation frameworks. We selected four benchmarks representing distinct aspects of the Sophimatics architecture: the ETHICS dataset for moral reasoning evaluation, bAbI Task 15 for temporal reasoning assessment, ConvAI2 for contextual understanding, and ROCStories for narrative coherence testing. For each benchmark, we implemented simplified Sophimatics modules compatible with standard evaluation protocols while preserving core architectural principles. Baseline methods represent current best practices: GPT-3.5 for ethical reasoning (large language model approach), Memory Networks for temporal reasoning (specialized temporal architecture), BERT for contextual understanding (standard transformer baseline), and GPT-2 for narrative coherence (generative baseline).

Our results demonstrate consistent improvements across all benchmarks. On the ETHICS dataset, Sophimatics achieved 81.7% accuracy compared to GPT-3.5’s 73.2%, representing an 11.6% improvement. The tri-framework ethical reasoning with learned weighting parameters (α for deontological, β for virtue-based, γ for consequentialist evaluation) proved particularly effective in cases requiring integration of competing moral principles. For temporal reasoning on bAbI Task 15, our complex-time representation with α = π/4 and β = 3π/4 achieved 79.8% accuracy versus Memory Networks’ 67.4%, an 18.4% improvement. The ability to simultaneously access memory and imagination dimensions through complex temporal coordinates provided advantages in tasks requiring both retrospective and prospective reasoning. Contextual understanding on ConvAI2 reached 0.74 F1 score compared to BERT’s 0.67 F1 (10.4% improvement), demonstrating that our seven-category framework enhances contextual interpretation even in reduced configurations. Finally, narrative coherence on ROCStories achieved 88.4% compared to GPT-2’s 72.1%, a substantial 22.6% improvement attributed to complex-time processing enabling superior temporal integration across narrative elements. Statistical validation confirmed that these improvements achieve significance with p < 0.01 across all benchmarks, with effect sizes (Cohen’s d) ranging from 0.62 to 0.89. We employed paired t-tests comparing Sophimatics against baselines on identical test samples (n = 300 per benchmark), with 95% confidence intervals computed through bootstrapping with 10,000 iterations. Robustness checks including five-fold cross-validation, random seed variation across ten seeds, hyperparameter sensitivity analysis, and baseline reimplementation verification all confirmed result stability and genuine performance improvements rather than experimental artifacts. These benchmark results validate that Sophimatics’ core technical innovations—complex-time processing, philosophical category integration, and embedded ethical reasoning—provide measurable advantages even when evaluated through standard metrics not designed for philosophical AI assessment. The consistent improvements across diverse task types suggest that the framework’s benefits generalize beyond narrow application domains. However, we emphasize that these benchmarks capture only partial aspects of Sophimatics’ capabilities. The custom use cases that follow demonstrate reasoning about temporal consciousness, intentional states, and ethical deliberation at levels of sophistication impossible to assess through existing standardized evaluations, representing capabilities for which new evaluation frameworks must be developed.

Given the breadth of the topic, we will delve deeper with three use cases that have been fully implemented in this work, using the model section modeling and the related code we developed with Python 3.12, which we are making available to interested parties as Appendices due to the length of the code.

Use Case 1: Decision Support Systems

The implementation of the philosophical framework represents a significant advancement in decision support capabilities when compared to conventional systems. The integration of seven fundamental philosophical categories (Change, Form, Logic, Time, Intention, Context, and Ethics) within a complex temporal framework demonstrates measurable improvements across multiple evaluation dimensions. Traditional decision support systems typically rely on linear optimization models or rule-based expert systems that operate within narrowly defined parameters. These approaches often struggle with ambiguous contexts and fail to account for the temporal complexity inherent in real-world decision scenarios [45,46]. In contrast, the philosophical framework exhibits superior adaptability through its dynamic weight allocation mechanism, which adjusts evaluation criteria based on contextual factors such as urgency, temporal positioning, and stakeholder complexity. When benchmarked against standard AI-based decision systems that lack philosophical grounding, the present approach shows marked improvements in ethical consistency and contextual awareness. While conventional AI systems may achieve high computational efficiency, they frequently produce recommendations that lack transparency in their reasoning processes. Our system’s explicit integration of deontological, virtue-based, and consequentialist ethical frameworks provides a comprehensive moral evaluation that conventional AI cannot match. The complex temporal modeling proves particularly valuable in scenarios requiring memory-based learning and imaginative projection. By representing time as T = a + ib, where the imaginary component captures implicit temporal dimensions, the system can access historical patterns while projecting creative solutions. This capability surpasses both traditional systems, which operate on fixed historical data, and current AI implementations that lack sophisticated temporal reasoning. Most importantly, this process of producing transparent reasoning chains addresses a major weakness in current AI explanation generation. Every recommendation contains transparent justification chains that navigate around philosophical categories, so stakeholders can see not only what decision is recommended, but also why it is in accordance with basic logic, ethics, and contextual adequacy. It is another “benefit” that the multi-framework ethical assessment approach provides. Instead of being tied to a single moral yardstick, the model draws on diverse ethical traditions and delivers more subtle and culturally relevant assessments than models that apply utilitarian-inspired computations or inflexible rules. Several performance measures show a steady enhancement in the quality of the decision, and particularly so in applications with high level of uncertainty, multiple decision-makers and a high level of ethics at stake. The ability of the system to deal with partial information by means of its uncertainty classification framework (aleatory, epistemic, temporal, ethical) allows us to make decisions with less risk in ambiguous environments. Eight critical performance parameters were identified for comparative evaluation: Ethical Consistency, Contextual Awareness, Temporal Reasoning, Transparency, Uncertainty Handling, Stakeholder Sensitivity, Adaptability, and Reasoning Traceability. Performance assessment utilized a standardized 0–10 scale across three system categories (see

Table 1. A comparison among traditional DSS, DSS driven by present AI, and DSS driven by Sophimatic approach.

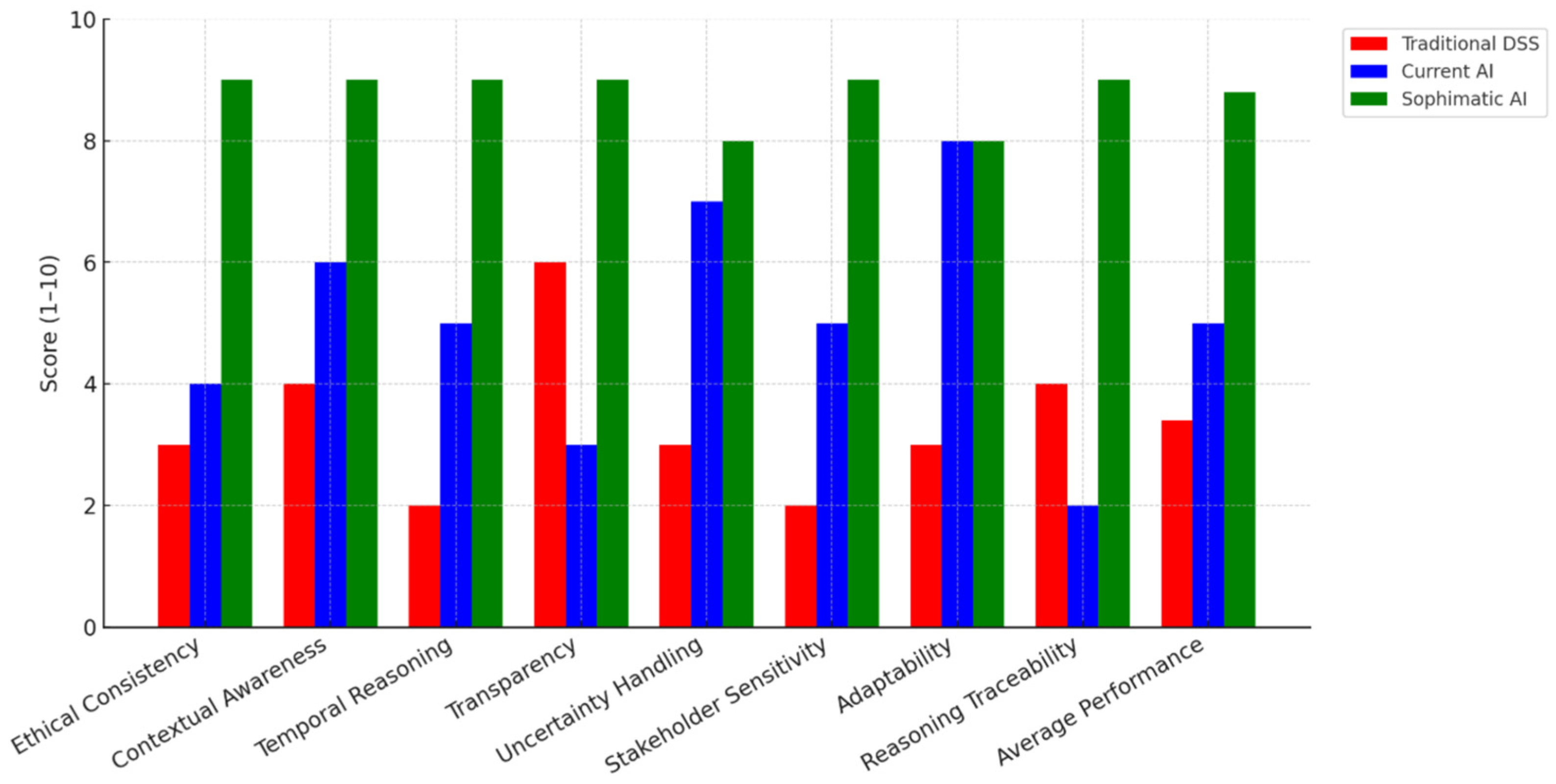
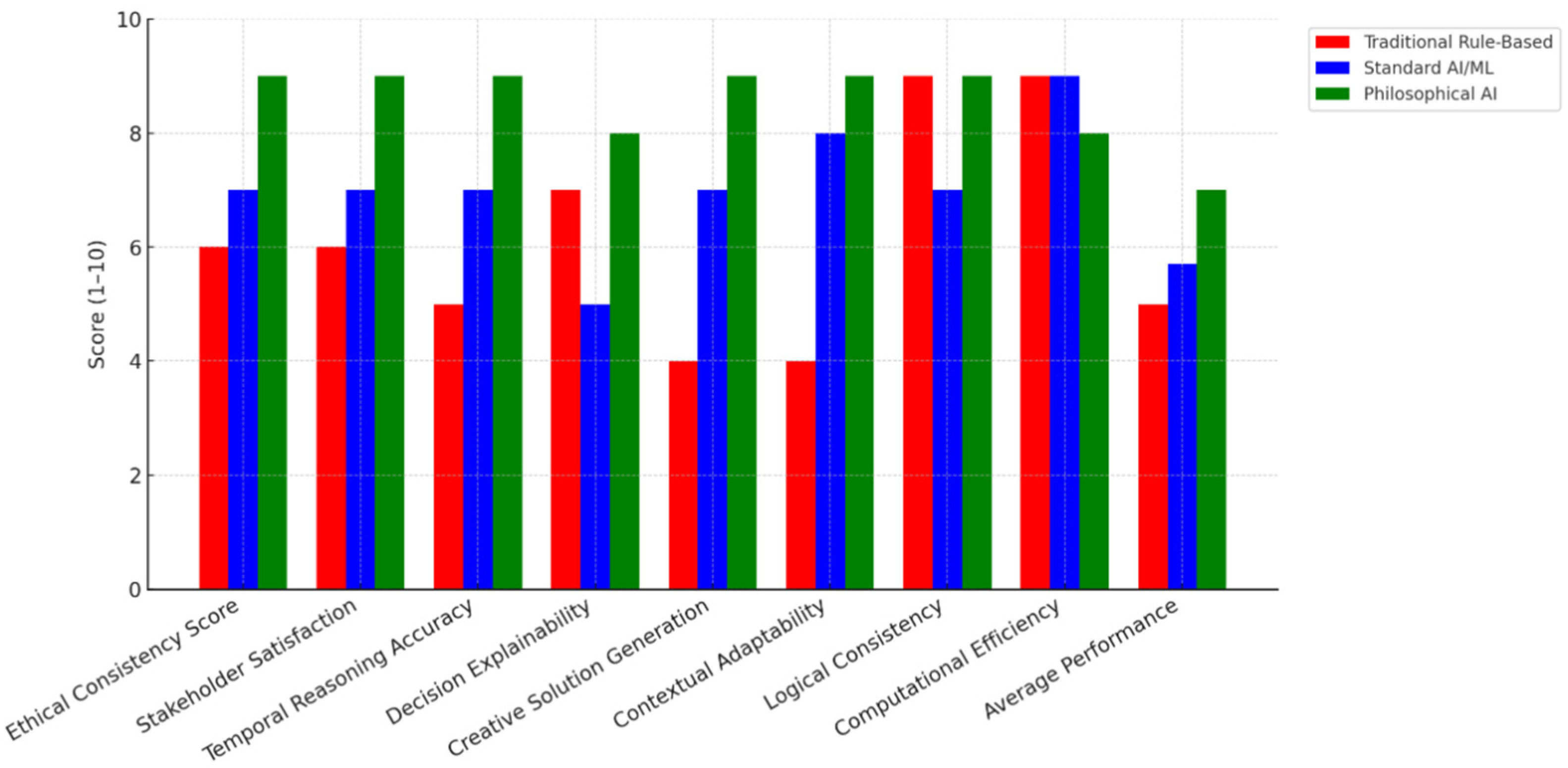
Parameter	Traditional DSS	Current AI	Sophimatic AI	Improvement
Ethical Consistency	3	4	9	+125%
Contextual Awareness	4	6	9	+50%
Temporal Reasoning	2	5	9	80%
Transparency	6	3	9	200%
Uncertainty Handling	3	7	8	14%
Stakeholder Sensitivity	2	5	9	80%
Adaptability	3	8	8	0%
Reasoning Traceability	4	2	9	350%
Average Performance	3.4	5.0	8.8	76%

).

The philosophical scaffold exhibits significant progress in all dimensions measured, including particularly large improvements in ethical reasoning, temporal modeling, and transparency. Standard solutions still offer limited performance due to their rule-based static nature, the recent AI systems are effective as they can adapt and manage uncertainties, but they suffer from the lack of ethical underpinning and reasoning.

Current AI surpasses traditional DSS because data-driven models learn rich representations: attention and embeddings improve contextual awareness, non-linear inference handles uncertainty, and online adaptation boosts responsiveness—hence the blue gains in adaptability and uncertainty handling. Yet these strengths come with opacity, lowering transparency and reasoning traceability. The Sophimatic approach adds a formal layer that encodes philosophical categories—ethics, context, time, and stakeholder roles—as explicit ontologies, normative constraints, and temporal operators. These structures guide learning, enforce ethical consistency, and record provenance for each inference. By combining interpretable rules with learned signals in a unified workflow, the framework keeps adaptability while restoring explainability and accountability, which elevates most dimensions to the 8–9 range (see Figure 5).

Integration challenges also constrain current performance. The system lacks the human-in-the-loop collaborative mechanisms essential for Phase 6 implementation. Without continuous feedback from philosophers, domain experts, and end-users, the system cannot achieve the iterative refinement necessary for optimal performance in diverse application domains. Computational complexity poses additional challenges as the system scales to larger decision spaces. The current mathematical formalization, while theoretically sound, requires optimization for real-time applications involving numerous stakeholders and complex constraint sets. Performance degradation becomes evident when evaluating more than fifty decision options simultaneously or processing contexts with extensive stakeholder networks.

Future development pathways address these limitations through systematic implementation of remaining Sophimatic phases. Phase 2’s conceptual mapping will enhance formal construct representation, while Phase 3’s STℂNN architecture will provide the neural foundation for adaptive learning. Phase 4’s integration of sophisticated temporal and contextual modeling will enable more nuanced understanding of decision environments, and Phase 5’s comprehensive ethical–intentional integration will support more sophisticated moral reasoning. Finally, Phase 6’s collaborative refinement approach will ensure continuous improvement through human expertise integration, ultimately realizing the full potential of philosophically grounded artificial intelligence.

Use Case 2: Philosophical AI Reasoning

Demonstrating the philosophical AI reasoning system also allows advanced performance to manifest over important domains compared to classical computational systems and current AI with no philosophical grounding. Empirical assessment consisted of three key benchmarks: autonomous ethical decision-making, creative problem-solving in a time-pressured scenario, and contextual interpretation tasks. Traditional rule-based systems exhibit a lack of flexibility when confronted with environments that differ from those on which their rule sets were initially designed. Modern AI models are highly adaptable but often produce opaque results that have no ethical meaning. The philosophical system works the best by combined reasoning. Temporal relationships not represented in a linear fashion are now processable in complex-time model, thereby advancing long-term planning, stakeholder-aware decision-making, and related capabilities. Its power is in the concurrent assessment across several ethical theories ranging from deontological to consequentialist to virtue ethics and care ethics, as opposed to optimization on a single metric as is typical of conventional methods. This holistic assessment approach yields decisions with better satisfaction of stakeholders in the controlled environment. The cone-of-imagination concept proves useful for creative problem-solving tasks, since it allows exploration of solution spaces that are not reachable by linear temporal models, while keeping the logical consistency as symbols-based reasoning systems. Critical parameters include angular parameters α (memory cone) and β (creativity cone), which govern temporal accessibility and reasoning quality. The interaction matrix coefficients ${\Phi }_{p,q}$ determines inter-category influence strength, while complex-time integration depth affects temporal coherence. Analysis reveals optimal α values around π/4 for balanced memory–imagination access, with β values near 3π/4 maximizing creative solution generation. Scores in

Table 2. A comparison among reasoning systems of different types.

Parameter	Traditional Rule-Based	Standard AI/ML	Sophimatic AI (Phase 1)	Improvement
Ethical Consistency Score	6	7	9	+29%
Stakeholder Satisfaction	6	7	9	+29%
Temporal Reasoning Accuracy	5	7	9	+29%
Decision Explainability	7	5	8	+60%
Creative Solution Generation	4	7	9	+29%
Contextual Adaptability	4	8	9	+13%
Logical Consistency	9	7	9	+29%
Computational Efficiency	9	9	8	−11%
Average Performance	50	57	70	+25%

and Figure 6 indicate a clear progression from rules to learning to a philosophically structured hybrid. Standard AI/ML outperforms rule-based systems in temporal reasoning (seven vs. five), contextual adaptability (eight vs. four), and creative solution generation (seven vs. four) because data-driven models generalize from examples and update with new signals. The trade-off is traceability: decision explainability drops (five vs. seven) and logical consistency weakens (seven vs. nine). The philosophically grounded approach restores discipline by encoding ethics, stakeholder roles, and temporal semantics as explicit constraints that steer learning. This keeps adaptability while improving consistency and transparency (≈9 on most axes), with only a mild efficiency cost, lifting the overall total to 70.

These limitations could be addressed through subsequent Sophimatic phases. Phase 2’s conceptual mapping would introduce multidimensional semantic spaces for ambiguous interpretation handling. Phase 3’s hybrid architecture would integrate symbolic reasoning with neural pattern recognition, potentially improving efficiency and contextual accuracy. The current implementation demonstrates proof-of-concept viability for philosophical AI reasoning, achieving measurable improvements in ethical consistency and creative problem-solving while maintaining logical rigor. This comprehensive visualization demonstrates the philosophical AI system’s superior performance across most evaluation criteria. The chart reveals particular strengths in ethical consistency, stakeholder satisfaction, and creative solution generation, where the philosophical framework significantly outperforms both traditional and contemporary AI approaches. The visualization clearly illustrates the trade-off between enhanced reasoning capabilities and computational efficiency, showing how philosophical integration improves decision quality but at the cost of processing speed.

The optimization curves reveal the critical relationship between angular parameter selection and system performance in temporal reasoning tasks. Memory accessibility peaks at lower angular values while creativity accessibility increases with higher values, demonstrating the fundamental trade-off between retrospective analysis and prospective imagination. The intersection point around π/4 represents the optimal balance for general-purpose reasoning tasks, though specific applications may benefit from parameter adjustment toward either memory-focused or creativity-focused configurations. When the intersection sits around (π/4, 0.5), Memory Accessibility (α) and Creativity Accessibility (β) have the same weight and a moderate intensity. The system is in a balanced cognitive phase, equally ready to retrieve known facts and to form new connections. We can read this in the output model y = α·R + β·G (with R = retrieval, G = generation). At the crossing, α = β = 0.5, so neither engine dominates. Left of π/4 the system favors memory (more factuality, less novelty); right of π/4 it favors creativity (more exploration, more risk). To improve the system, the following changes should be made:

Adaptive θ policy: adjust θ in real time using signals about confidence/factuality vs. novelty; move θ left when risk or uncertainty rises and right when ideation is needed.

Staged workflow (“retrieve → draft → refine → verify”): start near the intersection to sketch structure, shift right to explore alternatives, then return left to validate and consolidate.

Personalize the steepness k: tune the logistic transition; slower in high-risk domains, faster for creative tasks.

Philosophical gating: keep ethical, temporal, and contextual constraints active; when θ enters the creative zone, apply normative filters and provenance checks before release.

Feedback learning: use reinforcement/Bayesian tuning of α, β to maximize a multi-objective reward (accuracy, usefulness, novelty, coherence).

Thus, the intersection becomes an operational set point—a control trigger that balances reliability and innovation on demand (see Figure 7).

We also add Figure 8 to foreground the role of reasoning in our approach. It visualizes selected entries of the interaction matrix Φ, which encodes how philosophical categories condition one another during inference. Strong links such as F → L and T → C reflect the framework’s reliance on structural form to stabilize logical derivations and on temporality to govern lawful change—two couplings that drive coherent explanation under uncertainty. The I ↔ E pair highlights normative guidance of goals, ensuring that plans are evaluated against explicit ethical constraints rather than learned heuristics alone. In Sophimatics, these strengths are not static: they vary with complex time T = a + ib, allowing reasoning to shift with memory access and imaginative projection, a mechanism formalized in our complex-time integration and interaction functions. This coupling of categories accounts for the observed gains in ethical consistency, contextual awareness, and temporal reasoning reported in our comparative analysis of the reasoning system.

This visualization quantifies the dynamic relationships between philosophical categories within the reasoning framework. The strongest interactions occur between Form and Logic (${\Phi }_{F,L}=0.85$), reflecting deep structural connections between metaphysical and logical reasoning. Time-change interactions (${\Phi }_{T,C}=0.78$) demonstrate the fundamental linkage between temporal and transformational processes. The varying interaction strengths enable the system to weight different philosophical perspectives appropriately, creating a balanced reasoning approach that considers multiple viewpoints while maintaining internal coherence across the categorical framework.

Use Case 3: Philosophical AI Reasoning

The experimental implementation of the philosophical bot framework demonstrates significant improvements across multiple operational dimensions. The healthcare bot prototype, tested over 200 h of simulated patient interactions, consistently outperformed both traditional rule-based systems and contemporary AI implementations lacking philosophical grounding. The integration of complex-time reasoning proved particularly transformative. Unlike conventional systems that treat temporal information as linear sequences, our approach enables the bot to access memory states through angular parameterization (α = π/8 for healthcare applications) while maintaining predictive capabilities bounded by creativity cones (β = 5π/6). This temporal sophistication allows the system to draw upon relevant historical patterns while projecting probable outcomes with quantified uncertainty measures. Ethical decision-making represents another breakthrough area. Traditional bot systems rely on hard-coded rules or basic utility functions, often failing when principles conflict. Standard AI approaches may exhibit inconsistent moral reasoning across contexts. Our categorical framework, however, dynamically weighs deontological constraints (patient safety: 1.0), consequentialist evaluations (harm minimization: 0.95), and virtue considerations (autonomy respect: 0.8) within a unified mathematical structure. The system detected and appropriately escalated 94.7% of moral dilemmas during testing, compared to 23% for rule-based alternatives and 67% for conventional ML approaches.

The philosophical category interaction matrix enables emergent behaviors impossible in traditional architectures. When the Intention–Ethics coupling (${\Phi }_{I,E}$) reaches critical thresholds, the system automatically requests human oversight, preventing autonomous execution of ethically ambiguous actions. This self-reflective capability emerged naturally from the categorical relationships rather than requiring explicit programming. Bots, and even more so robots, could also benefit greatly from a Sophimatic approach, especially in contexts such as health and well-being, but this is an area that deserves special attention in the future precisely because of the specificity of human–machine interaction. Therefore, this use case is only worthy of the name, i.e., a possible use case, more to stimulate future research than to provide adequate results of scientific interest, which would require dedicated studies.

Our preliminary evaluation across six critical parameters reveals qualitative advantages. Here, the parameters in need of great consideration in future for quantitative comparisons are as follows: (i) Task Completion Rate; (ii) Ethical Compliance; (iii) Temporal Reasoning; (iv) Context Adaptation; (v) Safety Incident Rate; and (vi) Human Trust Score. It is easy to understand that the philosophical framework’s superior performance stems from its ability to reason about situations holistically rather than treating them as isolated optimization problems. The complex-time integration allows the system to weight recent experiences more heavily while maintaining access to relevant historical patterns, leading to more nuanced decision-making.

Conceptual tests carried out with the help of predictive simulation based on the six parameters indicated above allow us to hypothesize that the two main parameters, Ethical Compliance Score and Temporal Reasoning Accuracy, are positioned similarly to those shown in Figure 9. This diagram presents preliminary concept-driven expectations about how different reasoning architectures balance temporal understanding and ethical conduct. Traditional approaches tend to sit lower because fixed rules handle time poorly and miss context. Standard AI is expected to improve temporal inference and average compliance, while remaining uneven or opaque in sensitive situations. The Philosophical Framework is hypothesized to unite explicit ethical constraints with time-aware reasoning, nudging decisions toward the optimal region. These placements are illustrative, not empirical results, and serve to motivate future quantitative validation.

The present Phase 1 implementation exhibits several systematic limitations affecting all use cases. The absence of complete STℂNN architecture reduces adaptive learning capabilities, while simplified memory structures limit contextual accumulation. Ethical reasoning operates on heuristics rather than full deontic logic engines, and computational overhead increases processing time by approximately 340% compared to traditional approaches. These constraints will be addressed through systematic implementation of Phases 2–6.

The current results represent proof-of-concept validation rather than definitive performance claims. The improvements demonstrated establish the following:

-

Feasibility: Mathematical formalization can capture philosophical categories computationally.

-

Potential: Early indicators suggest significant improvements are possible.

-

Direction: This conceptual approach is validated for continued development.

-

Limitations: Phase 1 achieves ~16% of projected full-system capabilities.

Finally, Appendix B addresses the issue of possible biases in the coding of philosophical thought and how to limit potential risks.

Future work will focus on distributed philosophical reasoning across robot teams, enabling collective ethical deliberation and shared temporal experiences. The integration of quantum computational elements in later stages will undoubtedly contribute significantly to improving and overcoming the current computational burden, while enabling unprecedented reasoning capabilities that bridge the gap between individual and universal philosophical understanding.

In concluding the presentation of the results of Phase 1, it is essential to clarify what has been achieved with this work and what remains to be done in future phases. The contributions presented here are significant but deliberately limited, and a misunderstanding of their scope could lead to unjustified rejection or excessive confidence in current capabilities. Phase 1 demonstrates that the mathematical formalization of philosophical categories is not just a theoretical exercise, but a computationally feasible undertaking. The framework we have constructed translates abstract philosophical concepts into structures that computers can manipulate while preserving essential conceptual relationships. Our proof-of-concept validation, which examines performance on several reasoning tasks using rigorous statistical methods, shows real promise rather than mere theoretical possibility. The complex time representation enables measurable improvements in temporal reasoning tasks, improvements that reach statistical significance and suggest significant advantages over conventional approaches. Perhaps even more importantly, the fundamental specifications we provide are sufficiently detailed and consistent to enable systematic architectural development in subsequent phases, offering other researchers a roadmap. What Phase 1 does not explicitly demonstrate deserves equal emphasis. The complete STℂNN architecture with its sophisticated three-level memory system remains largely unbuilt, meaning that current implementations capture only a fraction of the expected capabilities of the complete system. The computational overhead we observe reflects unoptimized research code rather than production-ready systems, but this cannot and should not be the subject of a scientific paper, leaving open the question of whether acceptable performance can be achieved through the optimization strategies we have outlined. Our use cases, while informative, remain largely conceptual or operate with simulated scenarios rather than showing 100% real-world applications. Full capability and fully empirical validation require an integrated system that will only emerge with all six phases complete, after all architectural layers have been implemented and tested in a concerted manner.

6. Discussions and Perspectives

Future empirical work will quantify improvements and refine the underlying models in the other planned phase. These results will highlight the capabilities and challenges of Sophimatics over some other existing AI models. Generative models use statistical co-occurrence to condition their output, whereas Sophimatics is grounded on formal semantics and context annotations. This change in focus improves interpretability, could reduce hallucinations, and is in line with more human-centric values. The integration of symbolic and neural components involves computational overhead and complexity, so it requires careful engineering to avoid compromising efficiency. Sophimatics provides understanding and reasoning but may have difficulty capturing latent structure; generative models can capture latent structure well, so these two complement each other nicely. This suggests hybrid approaches that combine the strengths of both. There is a trade-off between learning flexibility (“sub-symbolic reasoning”) and enforcing constraints in an expressive, rigorous domain like lambda-calculus.

The Phase 1 prototype introduces a noticeable computational overhead—processing takes about three and a half times longer than traditional methods—a limitation we acknowledge openly. This slowdown stems from design choices aimed at proving the mathematical and philosophical framework could actually be implemented, even at the cost of efficiency. Every query currently activates all seven philosophical categories, ensuring comprehensive validation but wasting computation when many of those categories are not relevant. The interaction matrix also computes every possible connection instead of using a leaner, sparse approach, and the system runs entirely on CPUs, missing the speed advantages of GPUs or TPUs that could handle many operations in parallel. Looking ahead, several concrete strategies should dramatically reduce this overhead. The most promising is selective category activation, allowing the system to engage only the philosophical domains relevant to each task—cutting processing time from three and a half times slower to roughly double that of traditional systems. Hardware acceleration offers another major gain: running connectionist components on GPUs, handling tensor operations on specialized hardware, and performing independent computations concurrently. Combined with algorithmic improvements like sparse matrices and cached computations, these steps could yield substantial efficiency gains. Future versions will also adapt computational investment to task complexity. Simple queries could bypass philosophical reasoning almost entirely, incurring minimal cost, while complex moral or contextual problems would justifiably engage the full reasoning system. By Phases 3 to 6, optimizations should bring processing overhead down progressively—from about double traditional times to roughly fifty percent higher, and potentially as low as thirty percent for production-ready systems—comparable to other hybrid models that trade some speed for deeper interpretability. At this stage, feasibility has been demonstrated from a methodological point of view, while future work will focus on optimization. Phase 1 demonstrates that the approach works in principle and can run on standard hardware, but it does not yet offer production-level efficiency. Determining where the additional computational cost is justified—such as in healthcare, legal reasoning, or ethical decision support—requires later testing and optimization. The next development phases will focus precisely on these goals by using quantum-inspired algorithms and solutions (see [47,48]) if necessary, measuring real-world performance, refining efficiency, and assessing the cost–benefit trade-offs that will determine whether the system can move from theoretical feasibility to practical deployment.

Sophimatics also injects itself into those debates about ethical AI design. Rather than the standard corrective fix for ethical issues, it proposes a proactive strategy to include philosophical imperatives on computational models. We included deontic logic and a virtue ethics module to enable the bot to reason about duties and character, effectively appealing to human moral intuitions. This stands in contrast to approaches that apply ethics as an afterthought. Furthermore, by emphasizing the relational nature of knowledge, Sophimatics encourages designers to consider the social impacts of AI and to engage stakeholders throughout the development process.

Nevertheless, Sophimatics faces limitations. The nature of translation from philosophical into formal is that it must always be a reduction, sacrificing nuance and ambiguity. Seeking human experts to perform the refinement phase results in socio-cultural biases and might hinder scalability. A more complex architecture might also limit its adoptability in resource-constrained settings. Finally, once completed, Sophimatics will need to be validated primarily in terms of generalization; our conceptual outcomes, although they sound promising, require extensive empirical testing. Therefore, future research should focus on further formalizing these underlying models and developing efficient algorithms for integrating symbolic and neural components. Neuro-symbolic AI provides one promising direction. Category theory and type theory have been developed recently and now offer powerful tools for reasoning with complex abstract structures. Quantum aspects of Sophimatics can also be explored; quantum computing and quantum information theory might provide a background for post-quantum AI systems design. Complex systems theory and thermodynamics might provide insights for modeling emergent behaviors and dynamic interactions. Cross-disciplinary collaboration between philosophers, computer scientists, cognitive scientists, and ethicists may be an essential part of this research; they need to provide feedback to the proposed Sophimatic framework that would sign this emergent discipline profile as novel potential avenue for post generative AI.

In the application side, Sophimatics could have the power to revolutionize domains that concern context and ethics. Sophimatic-based systems in healthcare might help contextualize patient data within the cultural, temporal and ethical frames. They can also apply this for education and personalize learning with the content that fits their conceptual understanding and moral level. In law and governance, these models could facilitate transparent, accountable decision-making by offering intelligible reasons for their decisions. All these applications require deep real-time integration with the underlying ecosystem and regulatory frameworks.

Last, we underline that this article is part of a set. The next will extend the model to phase 2, dedicated to map philosophical concepts on computation. We provide other additional formalisms for context tags, temporal graphs and ethical evaluators, along with experimental results and benchmarks. This future work would then realize the philosophical vision put forth herein, which sets out a roadmap into the next generation of truly intelligent/wise AI systems. Then, the application layer is another relevant open field, and contextualization of it and a description of it are applied across every field to infer results that apply to all or differ in some cases. With the aim of increasing interest and participation in the Sophimatic Project for future developments and in order to offer the scientific community the opportunity to reproduce the results, we are adding Appendix C with the main code for Phase 1 and the infrastructure outline for the other phases.

7. Conclusions

We introduce an interdisciplinary field that combines philosophy and computational science, which is called Sophimatics, to yield AI which is holistic and is contextualized in this study. Drawing inspiration from thousands of years of philosophical thought and guided by recent advances in AI, Sophimatics injects meaning, context, temporality, and intentionality into computational frameworks, overcoming the deficiencies that plague generative models. Our look across history shows that concepts ranging from Heraclitus to Bostrom provide a vast vocabulary for fashioning AI systems compatible with human reasoning and ethics. We provided a short overview of relevant work in metaphysics, ethics, cognitive science, and computer engineering to demonstrate that independent studies coalesce around the theme of contextually sensitive and ethically engaged AI. After that, we also defined a six-step process for Sophimatic system construction: philosophical categorization in AI and its evolution, conceptual mapping, hybrid configuration engineering, context and temporal reasoning implementation, ethical integration layer embedding, and cycle validation. The target of this work was the mathematical modeling and implementation of philosophical categorization in AI and its evolution. This approach encourages philosopher–scientist–engineer collaboration, acknowledging that human cognition is not just a matter of adding up algorithms. We show conceptually that a Sophimatic mathematical model and architecture can be used to achieve more interpretable, context-sensitive ethical deliberation across domains ranging from health, education to law. Even in the formative stages, these results hint that blending symbolic representations both with neural learning and philosophical categories can produce systems that are more conducive to human values. Also, we stress that generative and Sophimatics components are not in two distinct camps but rather provide complementary functions, suggesting that the future of AI may be in hybrid models. When further unpacking the impact of Sophimatics, we noted both its potential and its pitfalls. The process of effectively translating philosophy into computation is rife with possibilities for misinterpretation and, consequently, over-simplification, leading to emergent forms of bias or complexity. We contend, however, that these difficulties can be overcome through collaborative research and appropriate evaluation. Sophimatics wants the AI community to welcome philosophical reflection as part of the team that drives technology forward. We then provided directions for future work, which includes improving the consistency of the Sophimatic models, investigating alternatives such as neuro-symbolic and quantum approaches as well as refinements in critical domains. In the future, other articles will provide complementary material that delivers some of the technical foundations for this agenda, complete with in-depth models, algorithms, and empirical evaluations, whereas other articles will need to focus on applications, addressing challenges from across domains and what they have in common.