A Methodology for Designing High-Efficiency Power Amplifiers Using Simple Microstrip Harmonic Tuning Circuits

Abstract

This paper presents a simple effective methodology for designing high-efficiency power amplifiers (PAs) utilizing a compact microstrip harmonic-tuned load network. The proposed approach employs a combination of a two-section transformer and three shunt-connected stubs, reducing component count relative to conventional harmonic-tuned circuits. The novel load network achieves optimized load impedances at the fundamental, second, and third harmonics while accounting for parasitic effects of packaged transistors. For experimental validation, an inverse Class-F (Class-F⁻¹) PA is designed and fabricated using a Cree GaN HEMT (model CGH40010F) operating at 2.5 GHz. The measured results demonstrate a peak power-added efficiency (PAE) of 79.8% with a saturated output power (P_sat) of 40.2 dBm.

1. Introduction

In modern wireless communication systems, high-efficiency power amplifiers (PAs) are critical for reducing DC power consumption and minimizing heat sink dimensions [1,2,3,4,5,6]. Consequently, a variety of efficiency enhancement techniques have been extensively developed and investigated within the microwave frequency band. Among these approaches, harmonic tuning has emerged as a particularly promising method for improving power-added efficiency (PAE), with representative examples including Class-F PAs and inverse Class-F (Class-F⁻¹) PAs, among others [7,8,9,10,11,12].

Traditional harmonic tuning schemes typically involve inserting a harmonic control circuit (HCC) between the transistor output terminal and the fundamental impedance matching network. Reference [13] employed L-C resonators to design Class-F and Class-F⁻¹ power amplifiers, demonstrating favorable performance in the 300 MHz band. However, due to significant parasitic effects and the self-resonant limitations of lumped components, this topology is inherently constrained to low-frequency applications. Consequently, distributed topologies are predominantly employed in high-frequency implementations.

The HCC comprises two series transmission lines and four shunt stubs for enhanced harmonic control, plus a tuning line to compensate for detuning caused by the device’s parasitic components at the second and third harmonics. However, realizing an HCC in a harmonic-tuned PA demands at least seven transmission lines—resulting in a structurally complex design. Furthermore, a single microstrip tuning line fails to simultaneously and accurately mitigate the frequency-dependent parasitic effects of the packaged transistor at both the second and third harmonics. To address this limitation, several parasitic-compensation techniques have been proposed in prior work [8], significantly boosting PA performance. Unfortunately, these additional parasitic compensation circuits are designed separately to counteract the device’s parasitic effects, further escalating circuit complexity.

This article proposes a novel method for designing high-efficiency power amplifiers using a compact microstrip harmonic-tuned circuit. In theory, this structure requires only a two-section impedance transformer and three connected shunt stubs. The resultant harmonic-tuned network functions as both a fundamental frequency matching stage and a harmonic control element, inherently accounting for the parasitic of the packaged transistor while eliminating the need for extra parasitic compensation circuits or tuning lines—unlike conventional designs. For experimental validation, a Class-F⁻¹ PA was designed and implemented with a Cree GaN HEMT (model CGH40010F) operating at 2.5 GHz. Measurements of the fabricated PA reveal a peak PAE of 79.8% at an output power of 40.2 dBm.

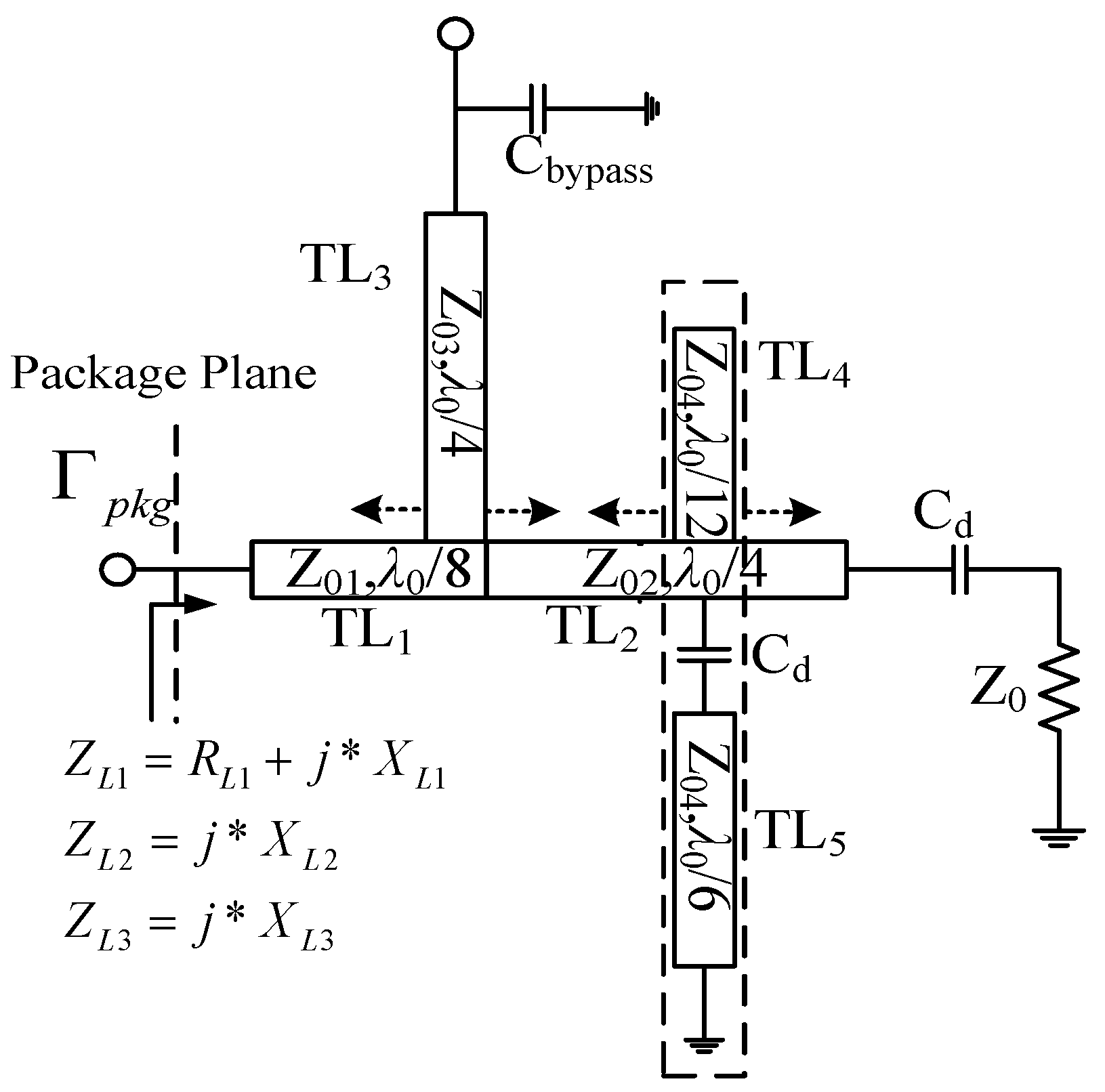
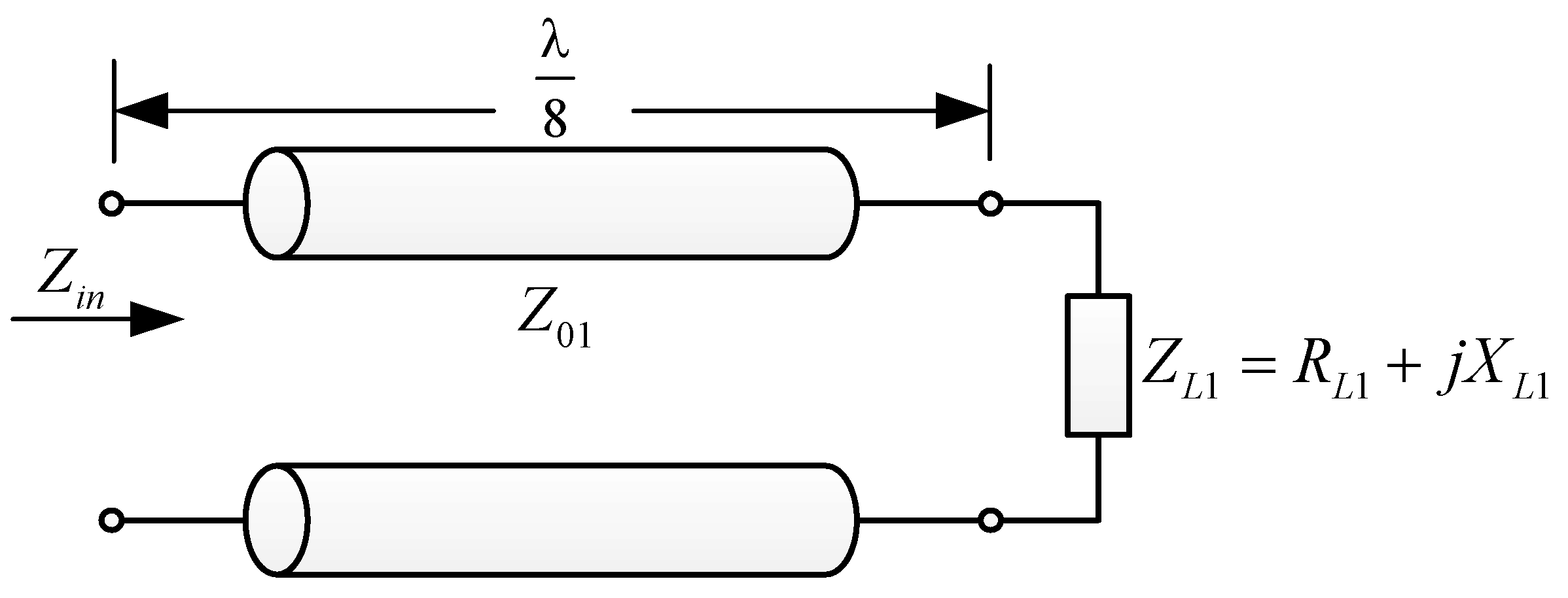
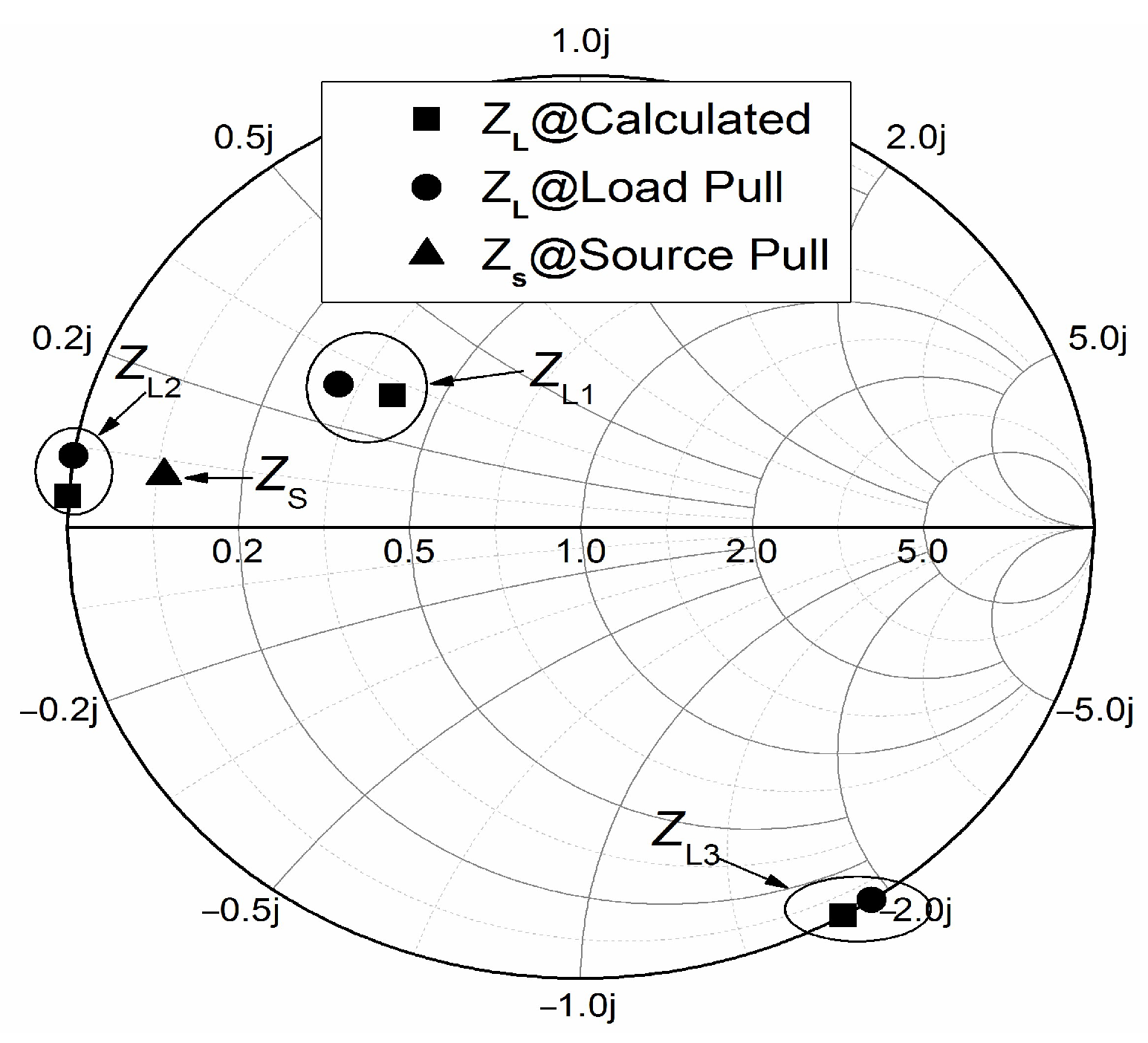
2. Design Methodology

From the design theory of high-efficiency power amplifiers (PAs), ideal harmonic impedances—including those for Class-F and Class-F⁻¹ PAs—share common characteristics: for harmonic orders n > 1, these impedances should theoretically reside on the unit circle (|Γ| = 1) of the Smith Chart to minimize power dissipation. However, it is critical to clarify that these values are derived from the transistor’s intrinsic drain plane (I-generation plane) as ideal benchmarks, neglecting the impact of parasitic elements.

As operating frequency increases, transistor parasitic effects severely impair the realization of target harmonic impedance conditions, leading to a substantial degradation in PAE [14]. To account for these parasitic effects, the S-parameters (SP) of a parasitic parameter model are employed to convert the ideal harmonic impedances from the transistor’s intrinsic drain plane to the package plane via Equation (1).

$${\mathsf{\Gamma }}_{pkg}={{\displaystyle \frac{{\mathsf{\Gamma }}_s-S_{11}^P}{S_{21}^P{S}_{12}^P-S_{11}^P{S}_{22}^P+S_{22}^P\mathsf{\Gamma }}}}_s$$

(1)

where Γ_s is the reflection coefficient at the intrinsic drain plane of the transistor chosen; and Γ_pkg is the reflection coefficient obtained by the package plane, as illustrated in Figure 1.

Since the parasitic of the packaged transistor can be equivalently modeled as a passive, lossless two-port network comprising inductors and capacitors, the optimal harmonic impedances at the package plane can be uniformly derived via Equation (2).

$$Z_L=Z_0{\displaystyle \frac{1+{\mathsf{\Gamma }}_{pkg}}{1-{\mathsf{\Gamma }}_{pkg}}}$$

(2)

Z_L denotes the impedance realized at the package plane; and Z₀ is the standard 50 Ω reference impedance. In practice, harmonic impedances are typically controlled up to the third harmonic, as incorporating higher-order harmonics introduces substantially greater circuit complexity while yielding negligible efficiency improvements.

Based on the characteristics of fundamental and harmonic impedances, a method for controlling the first three harmonic impedances is proposed. Figure 2 presents the proposed topology.

A two-section impedance transformer—comprising two series-connected microstrips (TL₁ and TL₂)—matches the optimal fundamental impedance Z_L1 at the package plane to a 50-Ω load. Three parallel microstrip stubs, integrated with the fundamental impedance matching circuit, realize the second- and third-order harmonic impedances. One stub also serves as the DC bias line. Consequently, the proposed harmonic-tuned network simultaneously and accurately compensates for the packaged transistor’s parasitic at both the second and third harmonics. The method’s implementation is structured into three key steps, detailed below.

The first step matches the optimal fundamental impedance Z_L1 at the package plane to a 50-Ω load. Transmission line TL₁ is designed to convert the impedance from the package plane (Z_L1 at f₀) into a real resistance R₁. Next, a quarter-wavelength (λ₀/4, where λ₀ is the wavelength at f₀) transformer TL₂ performs the transformation between R₁ and the 50-Ω load Z₀. This sets TL₁’s electrical length to λ₀/8. From [15], we can find R₁ = |Z_L1| × R_L1/(|Z_L1| − X_L1). The schematic of the transformation of a λ/8 transmission line is depicted in Figure 3.

From Figure 3, we can obtain

$$Z_{in}=Z_{01}{\displaystyle \frac{Z_{L1}+j{Z}_{01}\tan \frac{\mathsf{\lambda }}{8}\mathsf{\beta }}{Z_{01}+j{Z}_{L1}\tan \frac{\mathsf{\lambda }}{8}\mathsf{\beta }}},$$

(3)

where

$$Z_{L1}=R_{L1}+j{X}_{L1}.$$

(4)

Then we can obtain

$$Z_{in}=Z_{01}{\displaystyle \frac{(R_{L1}+j{X}_{L1})+j{Z}_{01}}{Z_{01}+j(R_{L1}+j{X}_{L1})}},$$

(5)

and then

$$Z_{in}=Z_{01}{\displaystyle \frac{R_{L1}+j(X_{L1}+Z_{01})}{(Z_{01}-X_{L1})+j{R}_{L1}}};$$

(6)

$$Z_{in}={\displaystyle \frac{Z_{01}{R}_{L1}(Z_{01}-X_{L1})+Z_{01}{R}_{L1}(X_{L1}+Z_{01})}{{(Z_{01}-X_{L1})}^2+{R_{L1}}^2}}+j{\displaystyle \frac{Z_{01}(Z_{01}+X_{L1})(Z_{01}-X_{L1})-{R_{L1}}^2{Z}_{01}}{{(Z_{01}-X_{L1})}^2+{R_{L1}}^2}}.$$

(7)

The imaginary part is

$$j{\displaystyle \frac{Z_{01}(Z_{01}+X_{L1})(Z_{01}-X_{L1})-{R_{L1}}^2{Z}_{01}}{{(Z_{01}-X_{L1})}^2+{R_{L1}}^2}}=0,$$

(8)

So,

$$Z_{in}=R_1={\displaystyle \frac{Z_{01}{R}_{L1}(Z_{01}-X_{L1})+Z_{01}{R}_{L1}(X_{L1}+Z_{01})}{{(Z_{01}-X_{L1})}^2+{R_{L1}}^2}}={\displaystyle \frac{Z_{01}{R}_{L1}}{Z_{01}-X_{L1}}}.$$

(9)

That means

$$R_1=={\displaystyle \frac{\left|Z_{L1}\right|R_{L1}}{\left|Z_{L1}\right|-X_{L1}}}.$$

(10)

$$Z_{01}=\left|Z_{L1}\right|=\sqrt{R_{L1}^2+X_{L1}^2}.$$

(11)

$$Z_{02}=\sqrt{R_1{Z}_0}.$$

(12)

The second step involves determining the required second-harmonic impedance Z_L2 at the package plane. Z_L2 can be approximated as a pure imaginary value, as its real component is negligible. The electrical length of the DC biasing line TL₃ is intentionally set to λ₀/4 to present a short circuit for the second harmonic and an open circuit for the first and third harmonics at the junction with the main signal path. This short circuits’ condition at the second harmonic nullifies the circuit’s influence beyond the junction. Consequently, Z_L2 is determined by adjusting the position of TL₃, as illustrated in Figure 2.

The third step determines the required third-harmonic impedance Z_L3 at the package plane. Like Z_L2, Z_L3 is similarly approximated as a pure imaginary value. An λ₀/12 open stub (TL₄) is connected in parallel to present a short circuit for the third harmonic at its junction with the main signal path. However, at the fundamental frequency, this shunt open stub introduces a residual reactance that compromises the fundamental frequency impedance matching established in Step 1. To mitigate this, a λ₀/6 shunt short-circuited stub (TL₅)—with the same characteristic impedance as TL₄—is employed to compensate for the residual reactance at the fundamental frequency. A DC-blocking capacitor C_d is inserted between TL₅ and the main path. Consequently, Z_L3 is achieved by adjusting the position of the TL₄–TL₅ combination, as illustrated in Figure 2. Based on the above content, we can derive the specific values of Z_L1, Z_L2, and Z_L3:

$${\mathrm{Z}}_{\mathrm{L}1}={\displaystyle \frac{{\mathrm{Z}}_{01}+j{Z}_{01}^2(\frac{Z_0\times j{Z}_{04}\frac{3\sqrt{3}}{2+6\sqrt{3}}}{Z_{02}^2(Z_0+j{Z}_{04}\frac{3\sqrt{3}}{2+6\sqrt{3}})})}{1+Z_{01}\frac{Z_0\times j{Z}_{04}\frac{3\sqrt{3}}{2+6\sqrt{3}}}{Z_{02}^2(Z_0+j{Z}_{04}\frac{3\sqrt{3}}{2+6\sqrt{3}})}}}$$

(13)

$${\mathrm{Z}}_{\mathrm{L}2}={\displaystyle \frac{Z_{01}^2}{0}}=+\infty$$

(14)

$${\mathrm{Z}}_{L3}=-j{Z}_{01}\cos {\displaystyle \frac{3}{4}}\pi =-j{Z}_{01}$$

(15)

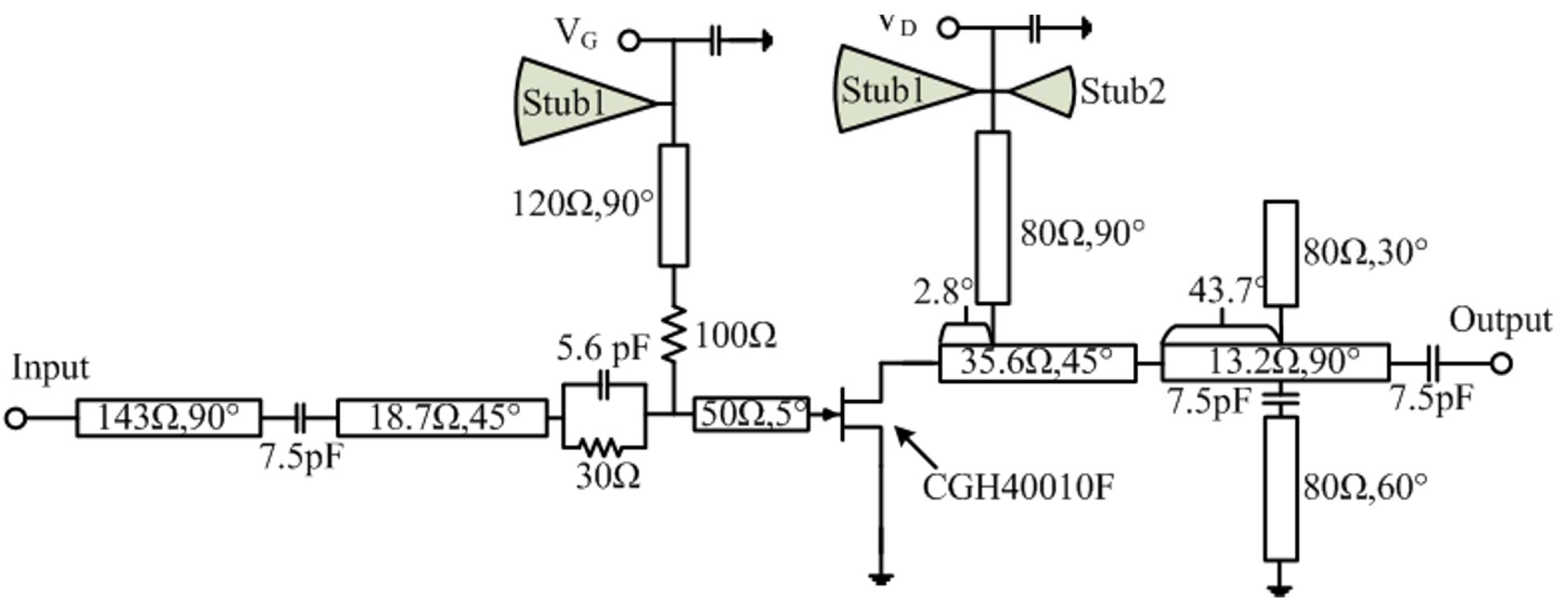
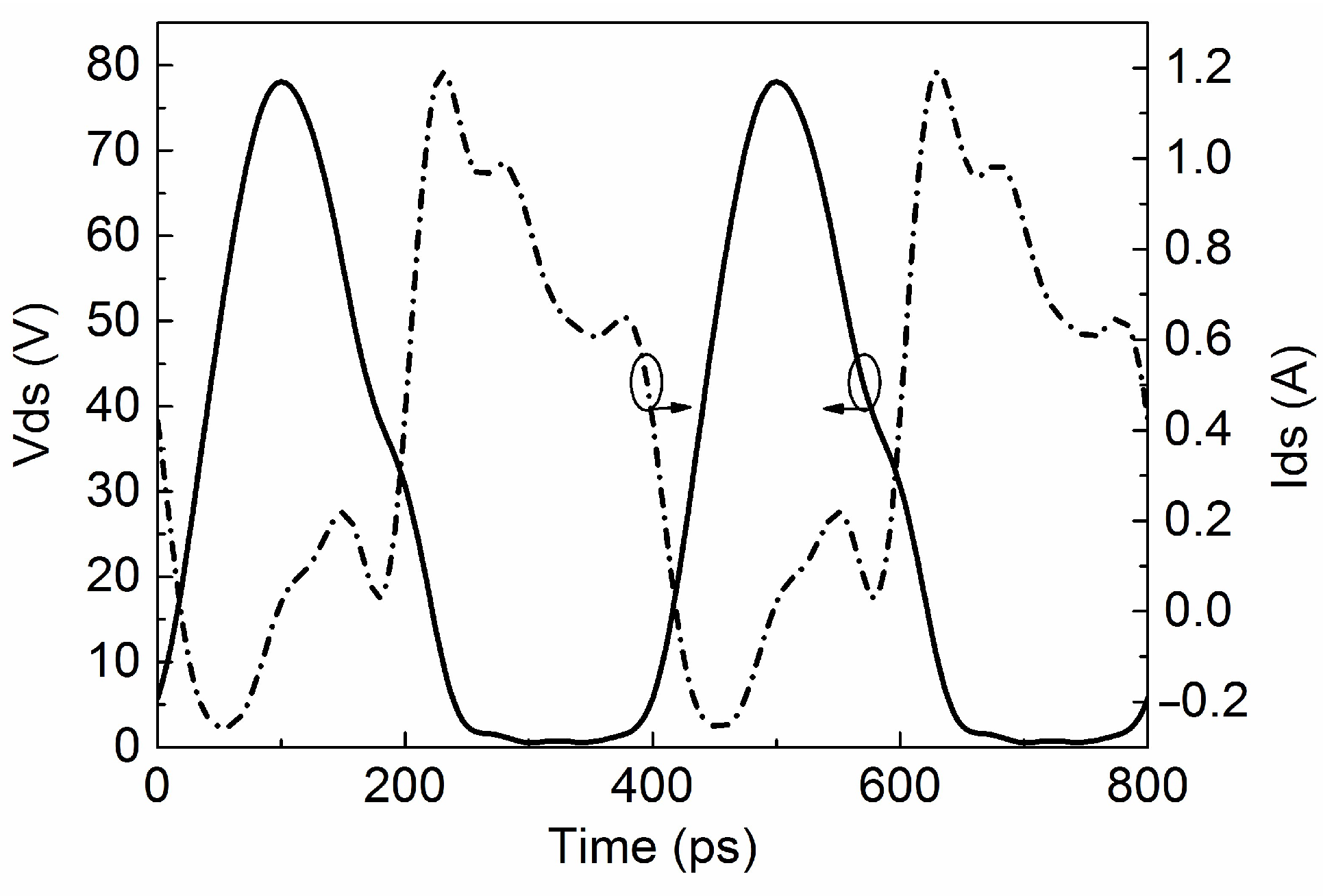
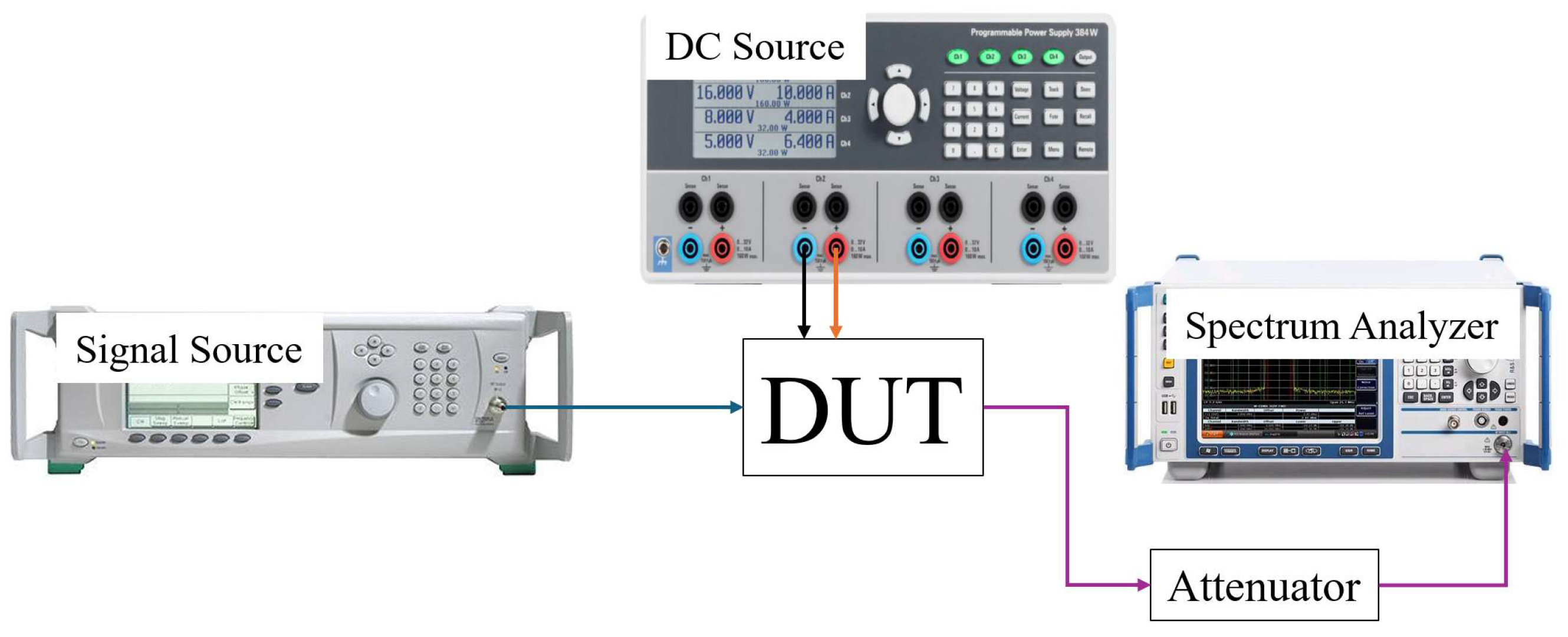
3. Design and Verification

To validate the advantages of the proposed design methodology, a Cree GaN HEMT (model CGH40010F) (Newark, CA, USA)—comprising a bare CGH60015DE die and a Cree 440166 package—is employed to implement a Class-F⁻¹ power amplifier. The package model is provided by the manufacturer, and the approximated equivalent circuit model of the device’s output parasitic network is detailed in [12]. The optimal first three harmonic impedances at the package plane (Z_L1, Z_L2, Z_L3) are initially calculated using Equations (1) and (2).

Notably, device intrinsic parasitic effects are typically nonlinear (voltage-dependent), which degrades the accuracy of the theoretical model under high-power operation. To address this, the manufacturer’s nonlinear device model is incorporated to refine the calculation of the optimal first three harmonic impedances.

Load-pull simulations are then performed on the HEMT using the Keysight Advanced Design System (ADS) (Santa Clara, CA, USA), with the results from Equations (1) and (2) serving as initial guesses. Additionally, optimal source impedance (Z_S) is extracted via source-pull simulations. The impedance distributions for these cases are plotted on the Smith Chart, as presented in Figure 4.

Figure 5 presents the complete schematic of the Class-F⁻¹ power amplifier. An input matching network—implemented with a two-section impedance transformer—achieves complex–conjugate matching at the 2.5 GHz operating frequency to minimize insertion loss. The stability circuit comprises a series R-C network and a 100 Ω resistor in series with the gate bias line.

The output harmonic-tuned network follows the proposed methodology: a two-section impedance transformer converts the standard 50 Ω impedance to the optimal fundamental output impedance, while the positions of the λ₀/4 biasing line and the TL₄–TL₅ combination are optimized along this transformer to achieve the target second- and third-order harmonic impedances.

Open radial stubs (Stub1 and Stub2), functioning as bypass capacitors in the biasing lines, provide short circuits for the fundamental and second harmonics. A capacitor of appropriate size is connected in parallel with Stub1/Stub2 to form a third-harmonic short circuit, simultaneously serving dual functions: DC power supply decoupling capacitor and third-harmonic bypass capacitor. It is particularly important to emphasize that in actual design, the resonance risk and engineering feasibility of this capacitor within the operating frequency band must be evaluated in advance. This supplementary design detail aims to provide a more comprehensive reference basis for subsequent engineering implementation. Finally, the designed Class-F⁻¹ PA schematic is simulated and optimized in Keysight ADS.

Figure 6 presents the simulated time-domain waveforms of the transistor’s drain current and voltage at the de-embedded intrinsic drain plane under Class-F⁻¹ operation (2.5 GHz, 10 W output power). The drain voltage exhibits a near-half-sinusoidal shape, while the drain current approximates a square wave—consistent with ideal Class-F⁻¹ behavior. Future work will expand the testing platform to include frequency domain characterization, thereby deepening our understanding of the underlying mechanisms.

The design and simulation of the passive network in this paper were both completed on the ADS platform, covering the entire process from schematic construction to parameter optimization and performance verification.

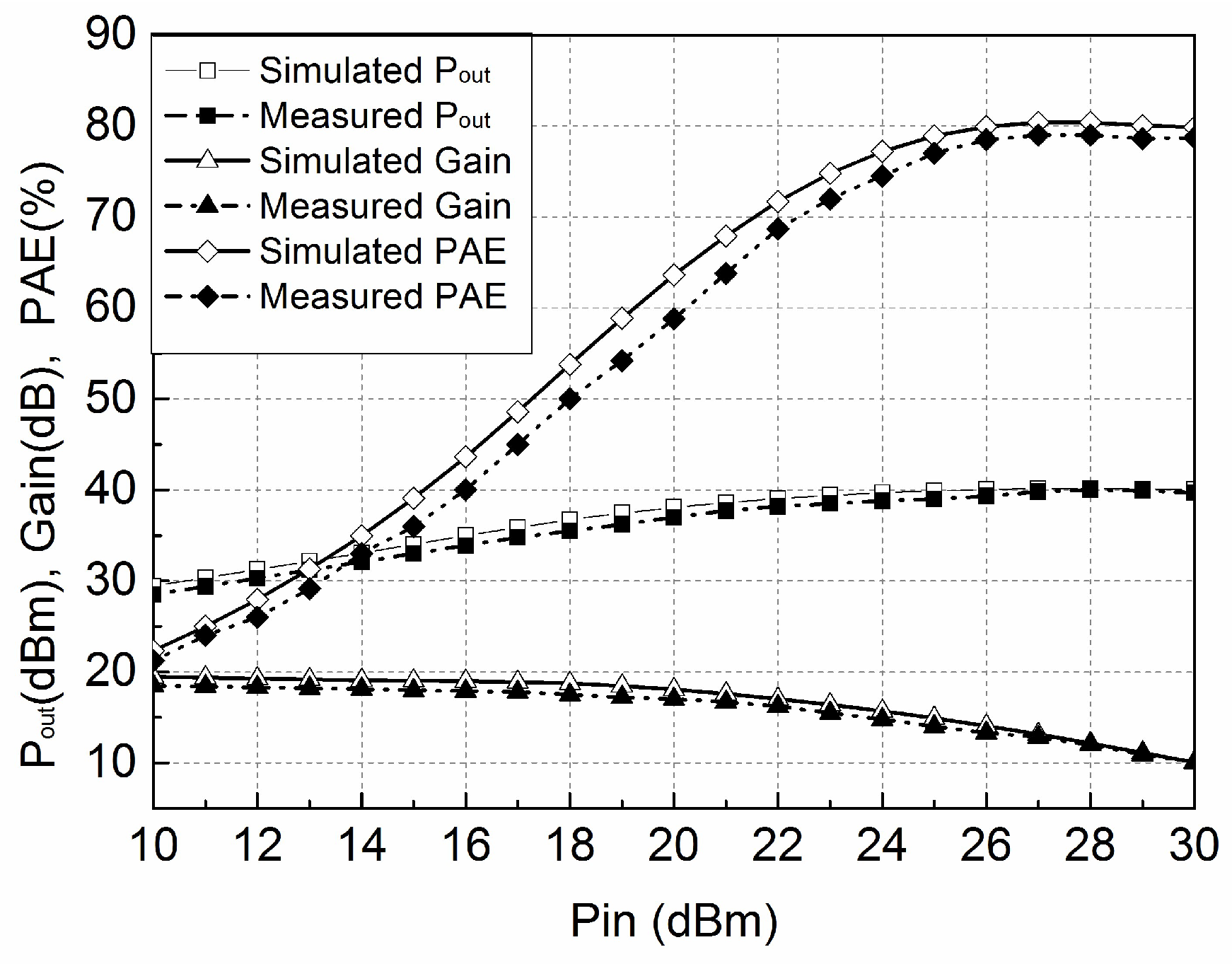
4. Results and Discussion

The Class-F⁻¹ PA is fabricated on a Rogers 5880 (Chandler, AZ, USA) substrate (dielectric constant: ε_r = 2.2; thickness: 31 mils). Figure 7 presents a photograph of the fabricated PA mounted on a heat sink. The packaged transistor is subsequently placed into a metalized slot machined into the substrate, and the final assembly is mounted on a copper test fixture. Two SMA connectors interface with the PA, while two capacitors inserted in the DC path filter out low-frequency noise and DC offsets. The module measures 9 cm × 6.5 cm in total.

The device is biased at a drain voltage (V_d) of 28 V and a gate voltage (V_g) of −3 V. Note that the gate bias must be adjusted slightly to maintain consistent DC drain current between simulation and measurement—this accounts for variations in the 10-W HEMT’s threshold voltage and electron mobility.

As shown in Figure 8, the test setup utilized a signal source, DC voltage source, spectrum analyzer, and attenuator. The attenuator was positioned at the front end of the spectrum analyzer to prevent excessive input power from damaging the analyzer. To enhance measurement accuracy, both the input and output ends were calibrated prior to testing, accounting for losses in cables and the attenuator.

Figure 9 presents comparisons between simulated and measured output power (P_out), gain, and PAE of the Class-F⁻¹ PA as the RF input power is swept from 10 to 30 dBm at 2.5 GHz. The amplifier achieves a peak drain efficiency of 81.6% and a maximum PAE of 79.8%, corresponding to a saturated output power of 40.2 dBm and a gain of 12.2 dB.

Minor discrepancies between simulated and measured results are observed across certain input power levels, attributed to limitations in the HEMT’s large-signal model accuracy, passive component fabrication tolerances, and substrate permittivity variations. Nevertheless, careful post-fabrication tuning of the matching transmission lines (TLs) can mitigate these discrepancies.

Table 1. Performance comparison of various high-efficiency PAs.

Reference	Mode	Frequency (GHz)	Pout (dBm)	PAE (%)	Gain (dB)
[9]-2018	Class-F	2.14	40.2	70.9	12.2
[12]-2017	Class-F	1.8	23.4	73.5	17.5
[13]-2014	Class-F−1	0.3	42.37	79 *	11.37
[16]-2016	Class-E	2.9	40.2	72.2	12.2
[1]-2024	Class-F−1	0.7–1.1	42.6–43.3	66.0 *–74.6 *	13.5–16
[17]-2024	Class-F−1	2.3–2.55	36.76	72.7	13.4
[18]-2023	Class-F−1	1.4–2.0	40	70	13
[19]-2023	Class-F−1	3.0	38.4	64.5	10.3
[20]-2023	Class-F−1	1.5–2.0	40–40.1	70.4	16
[21]-2024	Class-F−1	2.3/3.35	40.34/41.9	72.6/59.5	12.9/8.8
[22]-2023	Class-F−1	3.37–3.52	40–41.2	65–76.2	8.8–11.2
[6]-2025	Class-GF−1	0.6–2.8	39.8–42.5	65 *–74 *	9.8–13.28
This work	Class-F−1	2.5	40.2	79.8	12.2

* Drain efficiency.

compares the performance of the designed Class-F⁻¹ PA to those of recently reported high-efficiency PAs designed using packaged devices. The proposed Class-F⁻¹ PA products have excellent performance at the S-band. It is known that if the operating frequencies increase, the PAE will decrease. The proposed PA achieves a similar PAE as [13] at eight times the frequency [13], demonstrating that our approach is much more efficient. Moreover, our harmonic-tuned circuit achieves a more straightforward structure than those proposed in [9,12,16], respectively. Thus, a lower insertion loss has been introduced into the output of the PA, which results in a higher PAE.

5. Conclusions

This work proposes a simple microstrip harmonic-tuned load network for high-efficiency power amplifier (PA) design. Its efficacy is validated via a Class-F⁻¹ PA implemented with a packaged GaN HEMT, achieving optimal harmonic loading (fundamental, second, and third) at the package plane. Experimental results demonstrate a peak PAE of 79.8% and saturated output power of 40.2 dBm at 2.5 GHz. Notably, this method offers a streamlined solution for harmonic tuning—surpassing traditional multi-line topologies in simplicity—while maintaining high performance. It is further applicable to other harmonic-tuned PA classes (e.g., Class-E/F, Class-FE), underscoring its broad design versatility.