Adaptive Electromagnetic Working Mode Decision-Making Algorithm for Miniaturized Radar Systems in Complex Electromagnetic Environments: An Improved Soft Actor–Critic Algorithm

Abstract

With the advancement of multi-function radar (MFR) technology, miniaturized radar systems (MRSs) inevitably operate in complex electromagnetic environments (CEEs) dominated by MFRs as single-function radars are gradually being replaced by MFRs. MFRs can not only flexibly switch working states and generate diverse radar signal characteristics, but they can also acquire the MRSs’ position information, which has a significant impact on the execution of the MRSs’ close-range remote sensing missions. For resource-constrained MRS, selecting the optimal electromagnetic working mode in such environments becomes a critical challenge. This paper addresses the adaptive electromagnetic working mode decision-making (EWMDM) problem for MRS in CEE by establishing an EWMDM model and proposing a reinforcement learning (RL) method based on an improved soft actor–critic algorithm with prioritized experience replay (SAC-PER). First, we simulate the process of MRS receiving pulse description words (PDWs) from MFR waveforms and introduce noise into the PDWs to emulate real electromagnetic environments. Then we use a threshold to filter out uncertain recognition results to reduce the impact of noise on the MFR’s working state recognition. Subsequently, we analyze the limitations of the SAC-PER algorithm in noisy environments and propose an improved algorithm—SAC with alpha decay prioritized experience replay (SAC-ADPER)—to address the influence of environmental noise and stochasticity. Experimental results show that SAC-ADPER significantly accelerates the convergence speed of EWMDM in noisy environments and validate the effectiveness of the proposed method.

1. Introduction

Over the past few years, significant advancements in radar miniaturization have facilitated the deployment of radar systems on mobile platforms like unmanned aerial vehicles (UAVs) and unmanned ground vehicles (UGVs) [1], thereby opening up novel opportunities for close-range remote sensing applications [2]. These miniaturized radar systems (MRSs) have revolutionized various fields, including infrastructure monitoring [3], 3D urban modeling [4], security screening, and agricultural surveillance [5] by providing higher revisit frequency, operational flexibility, and enhanced spatial resolution compared to traditional airborne and spaceborne platforms [6]. However, advances in radar technology have rendered single-function radars insufficient in modern complex electromagnetic environments (CEE). This leads to the development of multi-function radars (MFR) that are flexible, feature diverse modes, and possess strong anti-interference capabilities [7]. Unlike traditional single-function radars, MFRs can flexibly switch between various operating modes, including search, tracking, and identification [8]. Notably, advancements in beam-scanning radar technologies have further enhanced the flexibility of MFRs in complex electromagnetic environments [9,10]. This flexibility enables MFRs to produce diverse radar signal characteristics, creating an electromagnetic landscape filled with heterogeneous signals [11,12]. And many other studies demonstrate that MFRs have been widely deployed and are now a dominant presence in modern electromagnetic environments [13,14,15]. This inevitably leads to the MRS being detected and tracked by the MFR’s radar during close-range remote sensing missions. In most scenarios, the MRS does not wish to be exposed within the MFR’s field of view. This means these MRSs have to flexibly adjust their electromagnetic working modes to avoid being detected and tracked by MFRs [16]. Therefore, designing a robust MRSs electromagnetic working mode decision-making (EWMDM) algorithm is essential.

Since EWMDM methods must contend with the flexibility of the working states of MFRs in CEE, RL algorithms [17] can be introduced as an effective decision-making tool. The strong generalization capabilities and autonomous learning characteristics of RL algorithms align well with the challenges faced by MRSs in CEE [18]. Currently, RL algorithms have achieved remarkable results in various domains such as gaming, virtual environments, robotics control, autonomous driving, and financial trading [19,20,21]. Similarly, RL algorithms have already been applied to EWMDM methods. Li et al. proposed an EWMDM method based on improved Q-learning, which employs simulated annealing to enhance the exploration strategy, thus improving the efficiency of electromagnetic working mode decisions [22]. Experimental results show that the proposed Q-learning algorithm can fully explore and converge the results to a better solution at a faster speed. Xu et al. introduced an improved Wolpertinger architecture based on the soft actor–critic (SAC) algorithm, significantly accelerated convergence for EWMDM methods in real electromagnetic environments [23]. Due to the use of advanced RL algorithms, their algorithm obtained excellent performance in a variety of scenarios. Zhang et al. applied the improved sparrow search algorithm–support vector machine (ISSA-SVM) for EWMDM effect evaluation and designed a comprehensive interactive CEE using a heuristic accelerated Q-learning algorithm [24]. They realized the modeling of the complete EWMDM process. To further enhance the efficiency and adaptability of electromagnetic working mode decisions, Zhang et al. proposed a hybrid algorithm combining ant colony optimization and Q-learning [25]. Experimental results show that the Q-learning algorithm and the ant colony algorithm fuse well in the cooperative EWMDM scenario. Zhang et al. also simulated a multi-MRS party cooperating scenario against MFR and analyzed the performance of an EWMDM model based on a double deep Q network based on priority experience replay (PER-DDQN) [26]. Moreover, Zhang et al. established the cooperative EWMDM in the frequency domain model and introduced the design idea of hierarchical reinforcement learning (HRL) [27]. Their proposed method effectively realizes the design of intelligent EWMDM in the frequency domain.

However, the EWMDM models established in the above studies do not consider the impact of CEE noise on decision-making algorithms and idealistically assume that the MRS can accurately identify the MFR working state. Such assumptions differ significantly from CEE. Therefore, RL-based EWMDM methods still require improvements in the following areas: (1) The MRS cannot accurately identify the MFR working state, which is a process that needs to be shown in the modeling; (2) Noise in CEE cannot be ignored, and designing specific reward functions that account for environmental noise is essential; (3) Given the environmental noise and stochasticity, more suitable EWMDM methods should be designed to address the scenario.

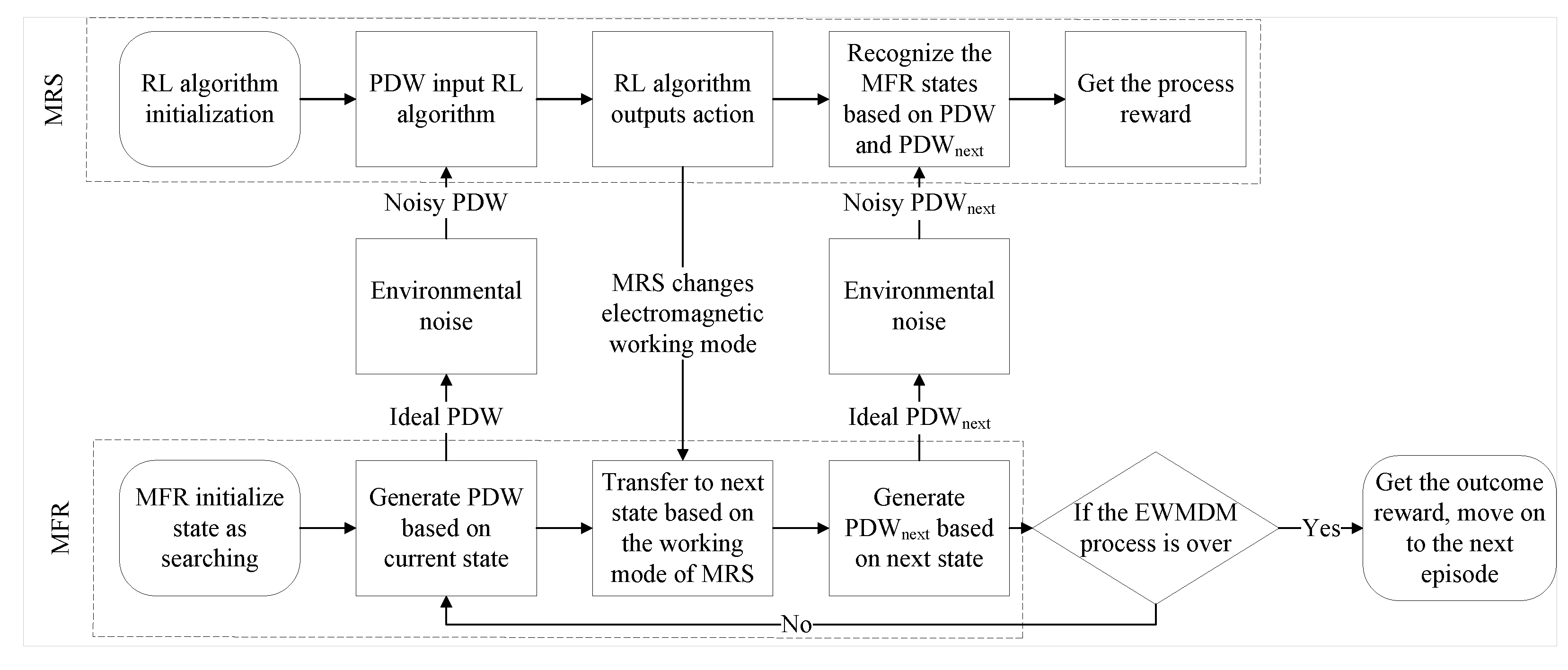
To address the limitations, we develop an EWMDM model for MFR in noisy CEE and propose an improved RL algorithm matched to the characteristics of the noisy environment. Our model simulates the process from the MRS receiving pulse description words (PDWs) to making electromagnetic working mode decisions and introduces enhancements to the reward function to minimize the impact of noise. Furthermore, we deployed the SAC algorithm and the SAC with prioritized experience replay (SAC-PER) algorithm on the proposed model, then analyzed the shortcomings of the existing SAC-PER algorithm in CEE and proposed corresponding improvements, resulting in the SAC with alpha decay prioritized experience replay (SAC-ADPER) algorithm suited for such applications. Finally, multiple simulation experiments were conducted to validate the effectiveness of the model and algorithm. The main contributions of this paper can be summarized as follows:

• To approximate real-world conditions, we assumed that the MRS extracts PDWs of the transmitted waveform from the MFR to identify the MFR’s working state, which inherently contains a certain level of environmental noise. By incorporating this noise uncertainty, the EWMDM model better reflects practical application scenarios.
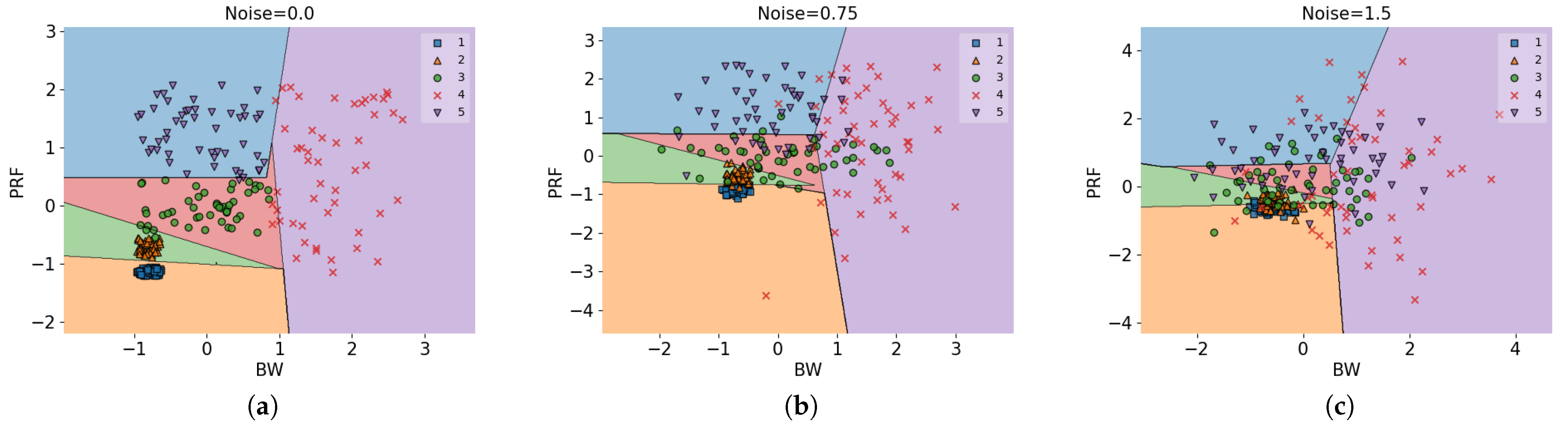
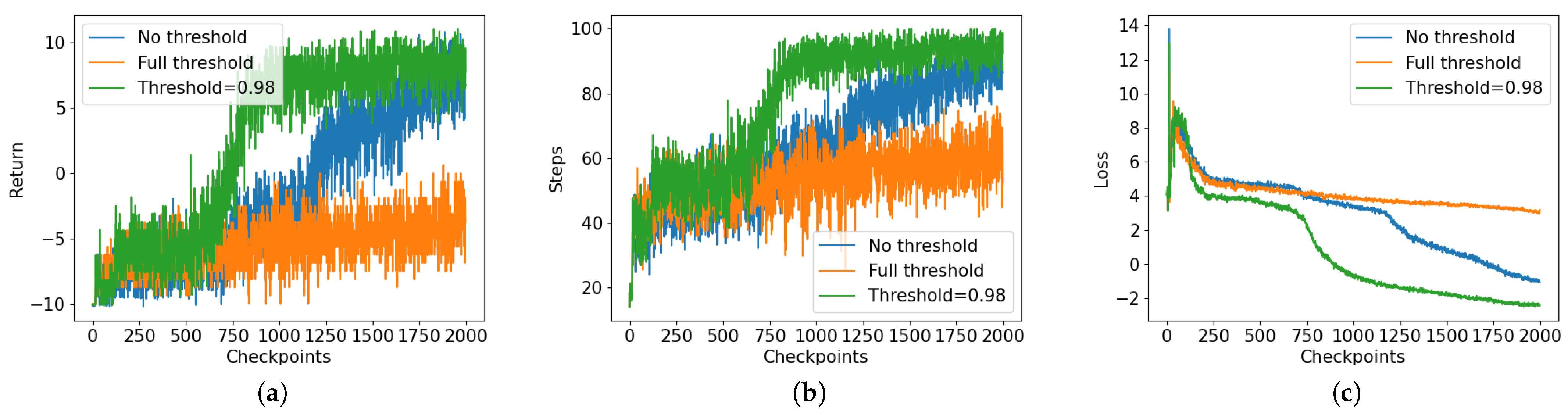
• To alleviate the impact of noise on EWMDM, we designed a probability threshold mechanism to filter out uncertain MFR states. While this approach introduces some sparsity into the MRS’s reward function, it significantly reduces the degree of incorrect guidance in the reward function, thereby enhancing the model’s robustness.
• The stochasticity of the EWMDM model and the noise in CEE introduce sparsity into the reward function. Initially, we employed the SAC-PER algorithm to handle this challenge. However, through analysis, we identified limitations of SAC-PER in noisy environments. To address these limitations, we introduced an alpha decay mechanism to adjust the PER, resulting in the SAC-ADPER algorithm. The alpha decay mechanism effectively reduces the sampling of unlearnable samples by PER.

The rest of this paper is organized as follows: Section 2 describes the framework of EWMDM and reiterates the main content of this paper. Section 3 describes the EWMDM effect evaluation method and the Gaussian noise model. Section 4 explains how to model the EWMDM process as a Markov decision process (MDP) for RL. Section 5 discusses the principles of the RL-based EWMDM methods and the improvements introduced in the SAC-ADPER algorithm. Section 6 details the simulation experiments and analyzes the results. Finally, Section 7 concludes the paper.

2. Electromagnetic Working Mode Decision-Making

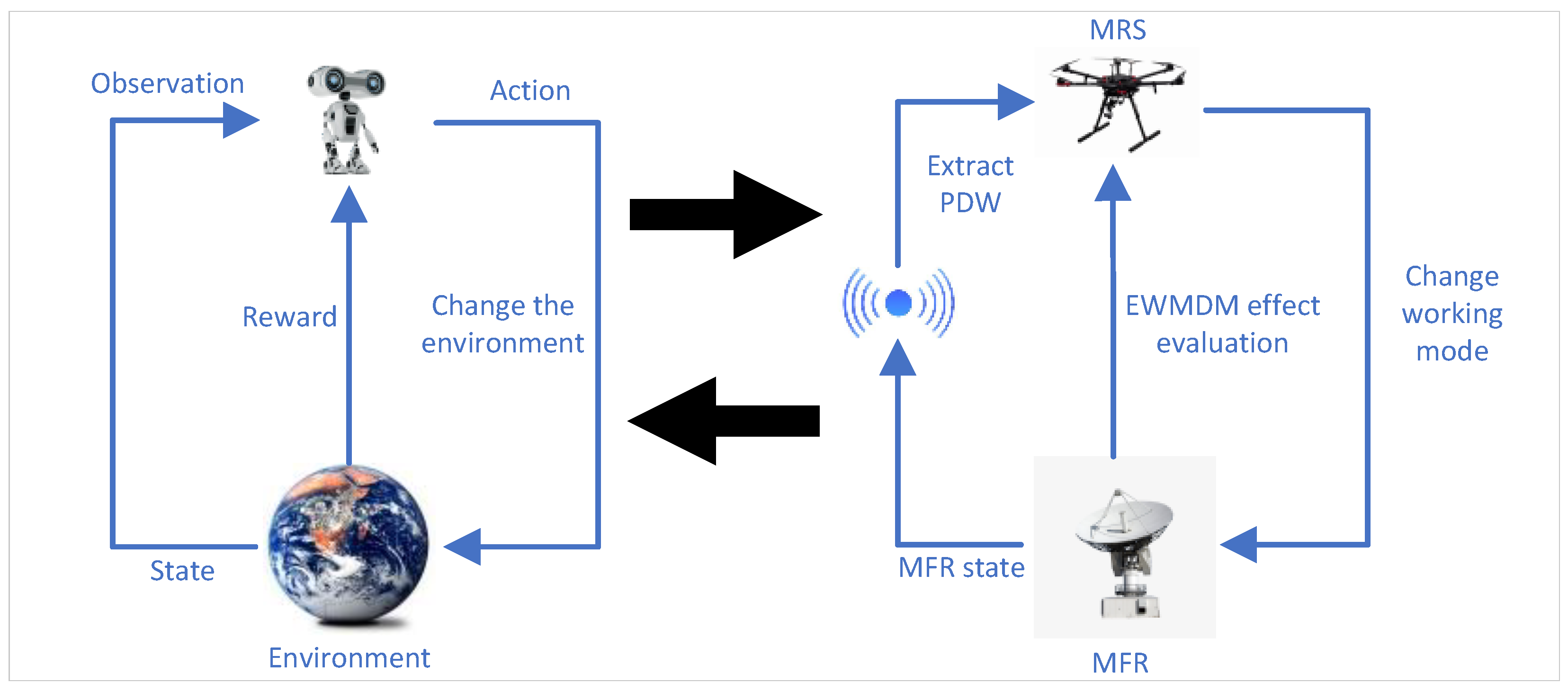
With the rapid development of MFRs, the traditional single electromagnetic working mode for MRS struggles to adapt to CEE dominated by MFR radar signals. In response, researchers have advocated for the integration of cognitive intelligence into the EWMDM process for MRS. As depicted in Figure 1, EWMDM is a sequential decision-making framework where MRS, functioning as the agent, interacts with the MFR-dominated CEE. MFR and MRS maintain an adversarial relationship: once MFR detects the current electromagnetic working mode of MRS, it adjusts its own working state to conduct detecting and tracking of MRS, thereby acquiring position information about it. The objective of MRS is to ensure the completion of its close-range remote sensing missions by continuously altering its electromagnetic working mode to avoid being tracked down by MFR. MRS observes the environment through the PDWs of the MFR signals, assesses performance via reward derived from EWMDM effectiveness, and adapts its electromagnetic working modes accordingly.

This aligns well with reinforcement learning (RL) principles, where an agent interacts with an environment, learns from feedback, and continuously refines its strategy to maximize long-term performance. In RL environment, after the environment updates its state, the agent obtains an observation of the current state. Then, the agent uses an RL algorithm to make a decision and outputs the action to be taken in the current state. Upon receiving the agent’s action, the environment also undergoes corresponding changes. It can be seen that the MRS corresponds to the agent, the MFR corresponds to the environment, the EWMDM effect evaluation corresponds to the reward, the MFR radar signals intercepted by MRS correspond to the observation, the MFR working state corresponds to the state, and the decision of the MRS electromagnetic working mode corresponding action.

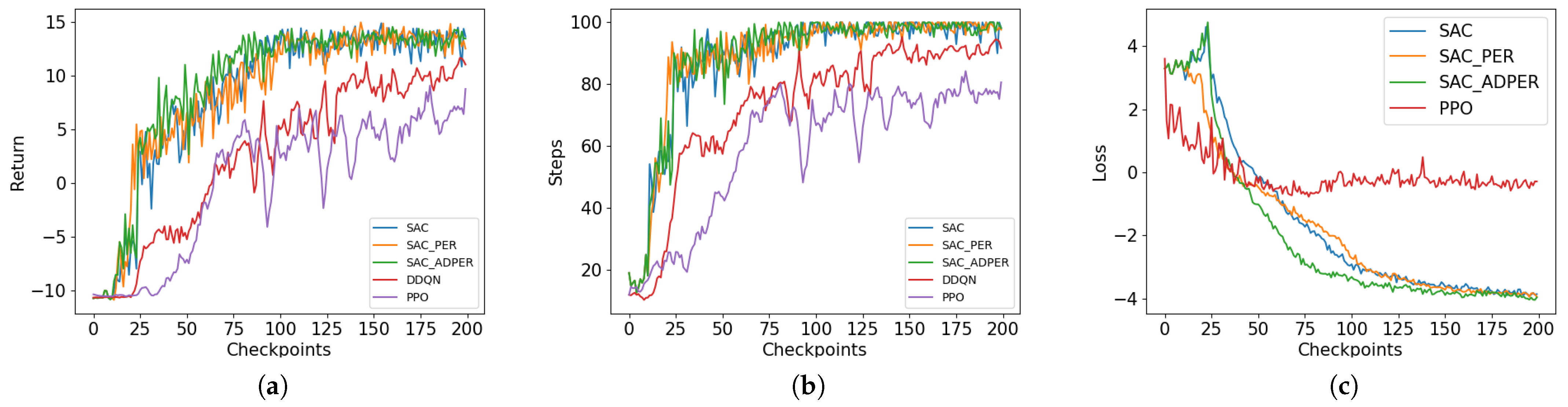
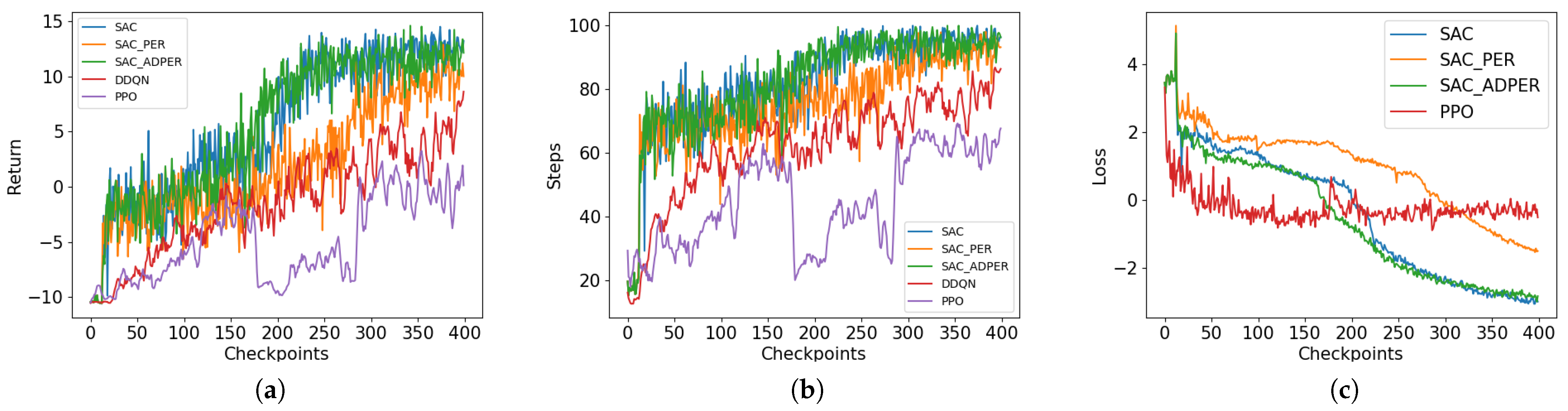
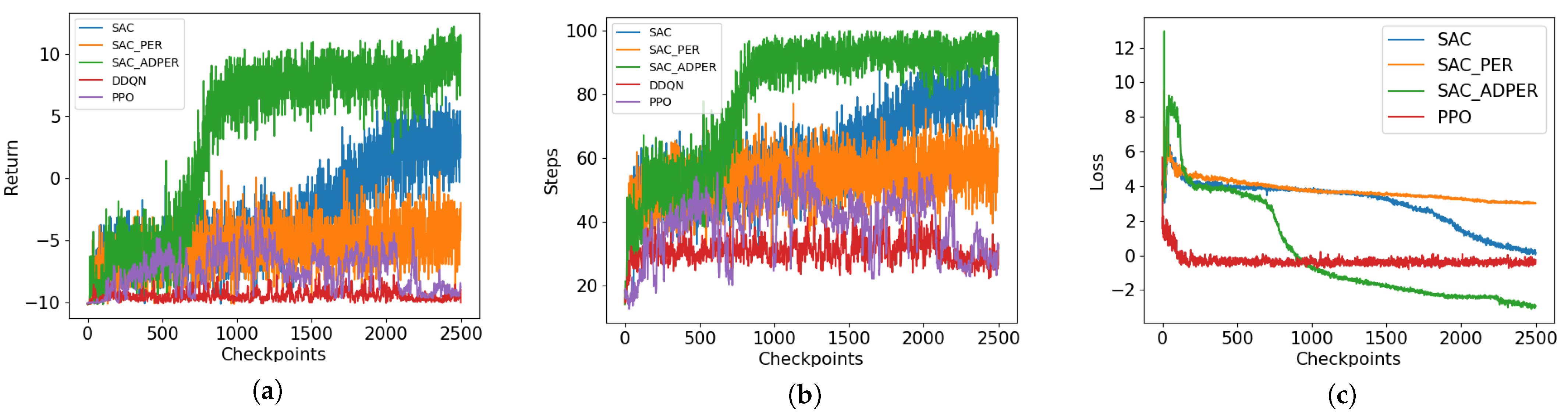
The main content of this paper includes constructing an EWMDM model for noisy CEE by simulating the process where the MRS receives PDWs from the MFR to identify its working state and incorporating environmental noise to better reflect real-world conditions. Then we propose an MFR state recognition probability threshold mechanism to filter out uncertain MFR states. This mechanism helps reduce incorrect guidance in the reward function and enhance model robustness. At last, we improve the SAC-PER algorithm by introducing an alpha decay mechanism to adjust the PER strategy, resulting in the SAC-ADPER algorithm. The fundamental difference between SAC-PER and SAC-ADPER lies in the gradual decay of the alpha parameter in SAC-ADPER to 0 as the number of training steps increases, thereby reducing the frequency of sampling unlearnable experiences by PER in the later stages of training. Multiple experiments conducted in noisy environments demonstrated that the SAC-ADPER algorithm significantly outperforms the traditional SAC-PER algorithm and SAC algorithm. Additionally, we conducted separate experiments for the probability threshold mechanism and the alpha decay mechanism to verify their effectiveness.

3. EWMDM Effect Evaluation

EWMDM effect evaluation is an important component of EWMDM. Since MFRs emit radar signals with different characteristics under various working states, the MRS can intercept these radar signals and analyze these features to effectively identify the MFR’s working state and select the corresponding EWMDM strategy. Pulse Descriptor Word (PDW) is a key parameter that reflects the characteristics of radar signals [28], and the MRS extracts PDWs for EWMDM effect evaluation [24]. Therefore, understanding the specific meaning of PDWs and their roles in radar operation is crucial for making effective electromagnetic working mode decisions. In the following section, we will explain the role of these PDW parameters in the EWMDM process, how we use support vector machine (SVM) to recognize the MFR’s working state, and the impact of noise in the electromagnetic environment on these parameters.

3.1. Pulse Description Word

3.1.1. Pulse Repetition Frequency

Pulse Repetition Frequency (PRF) represents the number of pulses transmitted by the radar per second [29]. The effectiveness of an electromagnetic working mode decision can be evaluated by observing changes in PRF. For example, When a MFR is performing a wide-area searching task, the PRF is usually set in a low range. Once a target is detected, the PRF needs to be increased to achieve higher resolution, narrowing the search range and focusing on the target area. When the MFR switches its working state from searching to tracking, the PRF should also be kept high to ensure that the position of the target is acquired in real time.

3.1.2. Pulse Width

Pulse width (PW) represents the time that the high level of pulse signal is maintained in the time domain [30]. In searching mode, PW is typically longer to boost signal energy, enabling detection of weaker target echoes over greater distances. Conversely, in tracking modes, the PW is shortened to enhance time resolution for more precise target localization.

3.1.3. Carrier Frequency

Frequency agility and frequency diversity techniques are widely used in the field of radar anti-interference. The radar carrier frequency (CF) can be changed quickly by adjusting the agile frequency synthesizer, making it difficult for MRSs to target [31]. In search mode, the MFR operates at a lower CF to facilitate long-distance signal propagation. During tracking mode, CF is increased to enhance resolution and precision. Additionally, these modes often utilize frequency hopping and diversity to resist interference, resulting in a wider range of CF variations to meet the demand for precise target information.

3.1.4. Peak Power

Peak Power (PP) is the maximum power value reached by a radar signal during each pulse cycle. In searching mode, PP is kept low to extend the radar’s range and conserve energy while covering large areas. During tracking mode, PP is increased to strengthen the target return signal for more accurate tracking. In range resolution mode, PP is maximized for precise targeting, maintaining a stable and strong signal even in challenging environments.

3.1.5. Bandwidth

Bandwidth (BW) is the width of the spectral range of a radar signal, usually defined as the difference between the highest and lowest frequencies of the signal frequency. A wider BW can improve the time resolution of the signal, allowing the MFR to measure the target’s distance and velocity more accurately [32]. Wide BW signals enhance the MFR’s ability to detect targets and resist interference by providing more frequency components. As detection accuracy increases, BW gradually expands, reaching its highest in tracking tasks demanding high velocity and range precision.

3.2. MFR Working State Recognition

It is not enough for the MRS to simply know how each PDW parameter changes across different MFR working states. The MRS must also qualitatively recognize the MFR’s working state and evaluate the EWMDM effectiveness based on changes in the threat level posed by the MFR. If the MFR’s threat level decreases, it indicates the probability of MRS being detected and tracked by MFR while operating in its current electromagnetic mode has decreased, which is an effective EWMDM strategy; otherwise, adjustments to the current electromagnetic working mode are required. The formula of threat level variation can be expressed as Equation (1).

$$\Delta TL=TL\left(t+1\right)-TL\left(t\right)$$

(1)

where t represents the time at which the MRS identify the MFR’s working state, and  $TL$ represents the MFR’s threat level. The EWMDM effectiveness is evaluated by analyzing the change in threat level between time t and $t+1$.

In this paper, we use SVM [33] to identify the MFR’s working state to evaluate the EWMDM effectiveness. Since the focus of this study is on improving the EWMDM algorithm and the innovation of the model, we provide a brief introduction to how SVM identifies the MFR’s working state.

Support vector machine (SVM) is a supervised learning algorithm widely used for classification tasks. The core idea of SVM is to find an optimal hyperplane that maximally separates different classes, thereby improving the generalization ability of the classifier. During training, SVM selects support vectors as key data points and optimizes the margin boundaries to enhance classification robustness. In this paper, we use an SVM with a linear kernel for MFR working state recognition. The linear kernel is computationally simple and suitable for cases where the data is approximately linearly separable in the original feature space. Compared to nonlinear kernels (such as the RBF kernel), the linear kernel has lower computational complexity, provides more interpretable decision boundaries, and performs well in high-dimensional feature spaces.

In the task of MFR working state recognition, using an SVM with a linear kernel is a practical and efficient choice. The primary reason is that the PDW features corresponding to different MFR working states often exhibit approximately linear separability in the feature space [24,34]. Unlike highly complex image or speech data, PDW parameters (such as PRF, PW, CF, PP, and BW) typically follow distinct patterns across different MFR working states, making it possible to separate them using a simple linear decision boundary. Moreover, a linear kernel has lower computational complexity compared to nonlinear kernels such as the RBF kernel. This is particularly beneficial when dealing with large-scale PDW data, as it allows for faster training and inference while maintaining good classification performance. Therefore, we use SVM with a linear kernel to identify the MFR working states.

3.3. Noise Model

To better simulate the impact of noise in real electromagnetic environments, we introduce zero-mean Gaussian white noise into the PDW data. In practical scenarios, radar signals received by the MRS are inevitably affected by various noise sources, including thermal noise, external interference, and system imperfections [35]. Although the types of noise in the electromagnetic environment are diverse, for simplicity, this paper uses Gaussian white noise to simulate the complexity of the electromagnetic environment. Many other studies have also adopted similar approaches [36].

Due to the significant differences in the ranges of different PDW parameters, for example, CF typically ranges from 1 to 4 GHz, while PP is usually in the tens or even hundreds of watts; feeding unnormalized PDW data directly into deep RL algorithms may lead to gradient explosion and difficulty in convergence [37,38]. Therefore, we choose to add Gaussian white noise to the PDW and then normalize the PDW to the range of $[-1,1]$. This ensures that all parameters are affected by noise to the same extent and effectively simulates the noise in real electromagnetic environments. The specific procedure is as follows: First, we add Gaussian white noise to the PDW using Equation (2).

$$PD{W}_{noisy}={\displaystyle \frac{PDW+N\left(0,{\sigma }^2\right)+1}{2}}d+PD{W}_{low}$$

(2)

where $PD{W}_{noisy}$ is the PDW after adding noise. $d=\left(PD{W}_{high}-PD{W}_{low}\right)$ represents the length of the PDW range. $PD{W}_{high}$ and $PD{W}_{low}$ represent the upper bound and lower bound of the PDW parameter, respectively. After adding Gaussian white noise, we normalize $PD{W}_{noisy}$ to $[-1,1]$ and use it as the noisy PDW input for the EWMDM algorithm, as shown in Equation (3). It should be noted that we still use $PD{W}_{noisy}$ as the input for the EWMDM effect evaluation algorithm.

$$PD{W}_{normalized}={\displaystyle \frac{2\left(PD{W}_{noisy}-PD{W}_{low}\right)}{d}}-PD{W}_{low}$$

(3)

4. EWMDM Modeling

4.1. RL Background

The EWMDM process is usually described as a Markov decision process (MDP) [39]. An MDP refers to a stochastic process with the Markov property, also known as a Markov chain, where the key characteristic is that the current state depends only on the previous state and is independent of all earlier states [40]. However, since our EWMDM model incorporates PDW and the MRS cannot directly observe the MFR states, we model the problem using a partially observable Markov decision process (POMDP) [41]. POMDP extends the Markov process by incorporating the agent’s actions, the observation space, and a reward function. It is represented by the tuple $\left\{S,A,O,P,r\right\}$ [42], where the following apply:

• S represents the set of states;
• A represents the set of actions;
• O represents the observation space. In our EWMDM model, the PDWs emitted by the MFR constitute the observation space.
• $P\left(s^{\prime }\right|s,a)$ is the state transition probability matrix, representing the probability of transitioning from the radar’s current state s to the radar’s next state $s^{\prime }$ after the EWMDM agent performs action a in the EWMDM environment;
• $r(s,s^{\prime })$ is the reward function. In the EWMDM environment, the reward function differs from typical RL settings, as the reward function depends on the radar’s current state and the subsequent state.

4.2. Environment Setup

The EWMDM environment we constructed simulates a continuous confrontation between the MRS and the MFR at a fixed distance. The MRS needs to continuously counter MFR detection and adapt its EWMDM strategy as the MFR changes working states, aiming to prevent the MFR from entering range resolution mode to obtain accurate MRS position information.

4.2.1. States Setup

The modes of MFR can be broadly categorized into search, tracking, and range resolution; these three modes are progressively more threatening to the MRS. However, MFR has derived track while search (TWS) and track and search (TAS) modes to cope with different mission requirements in order to balance the mission of searching the whole airspace and tracking the detected targets [7]. The threat level of these two modes is between search and tracking. TWS has a larger share of search than TAS; therefore, TWS is less threatening to MRS compared with TAS.

Thus, we set up five states in our environment, each corresponding to one of the MFR’s five radar modes. These radar modes are arranged in order of increasing threat to the MRS as follows: search, TWS, TAS, tracking and range resolution. According to the characteristics of MFR [43], transitions between radar modes can only occur to the previous mode, the next mode, or remain in the current mode, without skipping. For example, if the current mode of the MFR is TWS, the next mode can only be searching, TAS, or TWS. The specific state transition process is illustrated in Figure 2.

4.2.2. EWMDM Process Termination Conditions

Based on the MFR’s radar modes, we set two conditions to terminate the EWMDM process: one is if the MFR enters the range resolution mode twice consecutively, at which point the position information of the MRS is fully acquired by the MFR, leading to an EWMDM failure; the other is if the MRS successfully counters the MFR for 100 steps without entering the range resolution mode, which means that the MRS did not have its location information acquired by the MFR while performing the task, resulting in na EWMDM success.

4.2.3. Actions Setup

Next, we define the action set A for the agent, consisting of five actions that correspond to the MRS’s five working modes: radio frequency (RF) noise interfering mode, noise modulation interfering mode, comb spectrum interfering mode, deceptive interfering mode, and intelligent noise interfering mode. Each working mode has varying effects on different MFR working states. The EWMDM agent’s objective is to identify, through continuous trial and error, which EWMDM strategy is most effective against the MFR in each state.

4.2.4. Transition Probability Setup

In most EWMDM environments, even when the MRS selects an effective electromagnetic working mode, it may not fully suppress the MFR’s detection and tracking capabilities. However, there is a high probability that the MFR will be forced to transfer to a state with a lower threat level. Therefore, the state transition probability matrix $P\left(s^{\prime }\right|s,a)$ is designed based on the EWMDM effectiveness of different electromagnetic working modes on various MFR states. This matrix is three-dimensional, with each dimension representing the current MFR state s, the next MFR state $s^{\prime }$, and the EWMDM action a taken by the MRS. Different models of MFR have different state transition probability matrices. This paper investigates the Mercury MFR, which dynamically switches between multiple working states based on predefined rules [44]. Mercury MFR is a modern MFR characterized by highly flexible waveform parameters and dynamic beam scheduling, which makes its working modes difficult to distinguish using traditional recognition methods. The radar operates in several main working modes—such as search, acquisition, nonadaptive track, range resolution, and track maintenance—each exhibiting distinct patterns in PDW distributions and scheduling. The specific radar state transfer probability matrix for each electromagnetic working mode is shown in

Table 1. RF noise interfering transfer probability setup.

	Next State	Search	TWS	TAS	Tracking	Range Resolution
Current State
Search		0.9	0.1	0.0	0.0	0.0
TWS		0.2	0.4	0.4	0.0	0.0
TAS		0.0	0.25	0.35	0.4	0.0
Tracking		0.0	0.0	0.1	0.1	0.8
Range Resolution		0.0	0.0	0.0	0.2	0.8

,

Table 2. Noise modulation interfering transfer probability setup.

	Next State	Search	TWS	TAS	Tracking	Range Resolution
Current State
Search		0.5	0.5	0.0	0.0	0.0
TWS		0.6	0.3	0.1	0.0	0.0
TAS		0.0	0.25	0.35	0.4	0.0
Tracking		0.0	0.0	0.1	0.1	0.8
Range Resolution		0.0	0.0	0.0	0.2	0.8

,

Table 3. Comb spectrum interfering transfer probability setup.

	Next State	Search	TWS	TAS	Tracking	Range Resolution
Current State
Search		0.5	0.5	0.0	0.0	0.0
TWS		0.4	0.4	0.2	0.0	0.0
TAS		0.0	0.8	0.1	0.1	0.0
Tracking		0.0	0.0	0.1	0.1	0.8
Range Resolution		0.0	0.0	0.0	0.2	0.8

,

Table 4. Deceptive interfering transfer probability setup.

	Next State	Search	TWS	TAS	Tracking	Range Resolution
Current State
Search		0.1	0.9	0.0	0.0	0.0
TWS		0.2	0.2	0.6	0.0	0.0
TAS		0.0	0.1	0.2	0.7	0.0
Tracking		0.0	0.0	0.8	0.1	0.1
Range Resolution		0.0	0.0	0.0	0.5	0.5

and

Table 5. Intelligent noise interfering transfer probability setup.

	Next State	Search	TWS	TAS	Tracking	Range Resolution
Current State
Search		0.1	0.9	0.0	0.0	0.0
TWS		0.2	0.2	0.6	0.0	0.0
TAS		0.0	0.1	0.2	0.7	0.0
Tracking		0.0	0.0	0.2	0.2	0.6
Range Resolution		0.0	0.0	0.0	0.9	0.1

. The design of this transition probability matrix follows the real-world impact of electromagnetic working modes on MFR performance. For instance, RF noise interference is effective against search mode, while deceptive interference tends to induce MFR to transition from search mode to tracking mode.

4.3. Reward Function Setup

4.3.1. Ideal Environment

Unlike most RL scenarios, the reward function in the EWMDM environment does not include the MRS’s action a as an independent variable. This is because different MFRs have different transfer probability settings; there is no prior knowledge available for the MRS to use when designing the reward function. Therefore, the MRS’s reward is determined solely by the current MFR state s and the next state $s^{\prime }$.

In most RL scenarios, the sparse reward problem often arises, where agents struggle to receive effective feedback, thereby delaying policy optimization and the learning process [45]. To avoid the issue of sparse rewards, we design the reward function to be non-sparse [46]. First, we assign rewards at the end of the EWMDM process, where we set a reward of -10 for EWMDM failure and +10 for EWMDM success; this is referred to as the outcome reward, as shown in Equation (4). Additionally, we assign rewards for transitions between different MFR states during the EWMDM process to further avoid sparsity, which is referred to as the process reward, as shown in Equations (5). In Equation (5), the threat level is defined as an integer ranging from 1 to 5, corresponding to increasing threat levels from search to range resolution. This setup is designed to encourage the MRS to alter its electromagnetic working mode to influence MFR, keeping it in the lowest threat state. By combining Equations (4) and (5), the total reward for an episode can be expressed as in Equation (6).

$$r_{result}\left(s^{\prime }|s\right)=\left\{\begin{array}{c}10ifEWMDMsucceed\hfill \\ -10ifEWMDMfailed\hfill \\ 0else\hfill \end{array}\right.$$

(4)

$$r_{process}\left(s^{\prime }|s\right)=\left\{\begin{array}{c}0.1ifthreatleveldecreased\hfill \\ -0.15ifthreatlevelincreased\hfill \\ \left(5-threatlevel\right)/40else\hfill \end{array}\right.$$

(5)

$$r=r_{result}+n{r}_{process}$$

(6)

4.3.2. Noisy Environment

Since the accuracy of MFR state identification decreases after introducing noise, the MRS may fail to obtain valid process rewards. Numerous studies have shown that RL algorithms are highly vulnerable when operating with noisy reward functions, leading agents to learn incorrectly due to the distorted rewards they receive [47,48,49]. To address this problem, we propose using a probability threshold for MFR state identification. First, we calculate the probability of each state identified by the clustering algorithm, and then the clustering algorithm selects the state with the highest identification probability as the result. However, in the presence of noise, we need to ensure that the identification result has a high level of confidence before using it as the basis for the reward function. Therefore, we propose setting a probability threshold: if the identification probabilities for all states identified by the SVM are below this threshold, the identification result is discarded, and the identification is deemed unsuccessful. The reward value for discarded identification results is set to zero, and the process reward function in noisy states, denoted as $r_{process}^{\prime }$, is rewritten as shown in Equation (7). The outcome reward function remains unchanged, as expressed in Equation (4). The total reward is rewritten as Equation (8).

$$r_{process}^{\prime }\left(s^{\prime }|s\right)=\left\{\begin{array}{c}{r}_{process}\left(s^{\prime }|s\right)ifidentificationsucceed\hfill \\ 0else\hfill \end{array}\right.$$

(7)

$$r^{\prime }=r_{result}+n{r}_{process}^{\prime }$$

(8)

4.3.3. EWMDM Process

Based on the MFR state identification and reward function settings under noisy environments, we have established the following EWMDM process as illustrated in Figure 3.

5. RL-Based EWMDM Methods

5.1. Soft Actor–Critic

The SAC algorithm is an off-policy deep RL method designed within the maximum entropy framework. Its primary objective is to optimize both reward maximization and policy entropy, striking a balance between efficient exploitation of learned policies and continuous exploration of the environment [50]. By incorporating an entropy regularization term into the objective function, SAC encourages the agent to maintain stochasticity in its action selection, preventing premature convergence to suboptimal policies [51].

Compared to traditional actor–critic approaches, SAC explicitly enhances the diversity of actions by maximizing the expected entropy of the policy. This results in improved robustness and adaptability, particularly in high-dimensional and complex decision-making tasks. The introduction of entropy regularization ensures that the agent explores a broader range of possible actions, which mitigates overfitting to specific experiences and helps avoid local optima. Additionally, SAC leverages an off-policy learning mechanism, enabling more efficient sample reuse through experience replay, thereby improving training stability and sample efficiency.

5.1.1. Maximum Entropy RL

Entropy denotes the degree of stochasticity of a random variable, and in RL, since the agent learns a stochastic strategy, the entropy $H\left(\pi \right(·\left|s\right))$ can be used to denote the degree of stochasticity of the strategy $\pi$ in state s.

The idea of maximum entropy RL is that the agent not only maximizes the cumulative reward but also explores new state-action pairs [52]. Therefore, an entropy regularity term is added to the objective of maximum entropy RL, defined as in Equation (9), where ${\alpha }^{\prime }$ is a regularization factor to control the importance of entropy.

$${\pi }^{*}=arg\underset{\pi }{max}{\mathbb{E}}_{\pi }\left[\sum _{t}r\left(s_t,a_t\right)+{\alpha }^{\prime }H\left(\pi \left(·\mid s_t\right)\right)\right]$$

(9)

5.1.2. Soft Policy Iteration

Soft policy iteration incorporates the principle of maximum entropy RL into the policy iteration process, resulting in a more stable and efficient RL algorithm [53]. In the maximum entropy RL framework, the objective function is modified, leading to a transformation of the Bellman equation into the Soft Bellman Equation (10). And the state value function is expressed as Equation (11).

$$Q\left(s_t,a_t\right)=r\left(s_t,a_t\right)+\gamma {\mathbb{E}}_{s_{t+1}}\left[V\left(s_{t+1}\right)\right]$$

(10)

$$\begin{array}{c}\hfill V\left(s_t\right)={\mathbb{E}}_{a_t\sim \pi }\left[Q\left(s_t,a_t\right)-{\alpha }^{\prime }log\pi \left(a_t\mid s_t\right)\right]\\ \hfill ={\mathbb{E}}_{a_t\sim \pi }\left[Q\left(s_t,a_t\right)\right]+H\left(\pi \left(·\mid s_t\right)\right)\end{array}$$

(11)

5.1.3. Network Loss Function

For the critic network, the SAC algorithm adopts the idea of double DQN by utilizing two Q-networks. When selecting the Q-value, the smaller of the two is chosen to mitigate the issue of overestimation in Q-values. The loss function for any given Q-network is expressed as Equations (12) and (13).

$$L_Q\left(\omega \right)=\mathbb{E}\left[{\displaystyle \frac{1}{2}}{\left(Q_{\omega }\left(s_t,a_t\right)-\left(r_t+\gamma V_{{\omega }^{-}}\left(s_{t+1}\right)\right)\right)}^2\right]$$

(12)

$$V_{{\omega }^{-}}\left(s_{t+1}\right)=\underset{j=1,2}{min}{Q}_{{\omega }_j^{-}}\left(s_{t+1},a_{t+1}\right)-{\alpha }^{\prime }log\pi \left(a_{t+1}|s_{t+1}\right)$$

(13)

For the actor network, the loss function of the policy $\pi$ is derived from the Kullback–Leibler (KL) divergence, and after simplification, it is expressed as

$$L_{\pi }\left(\theta \right)={\mathbb{E}}_{s_t\sim R_t{a}_t\sim {\pi }_{\theta }}\left[{\alpha }^{\prime }log\left({\pi }_{\theta }\left(a_t\mid s_t\right)\right)-Q_{\omega }\left(s_t,a_t\right)\right]$$

(14)

5.1.4. Automatic Adjustment of Entropy Regularization Terms

In the SAC algorithm, the choice of the entropy regularization coefficient ${\alpha }^{\prime }$ is crucial, as different states require varying levels of policy entropy. To automatically adjust the entropy regularization term, SAC reformulates the RL objective into a constrained optimization problem as Equation (15),

$$\begin{array}{cc}\hfill & \underset{\pi }{max}{\mathbb{E}}_{\pi }\left[\sum _{t}r\left(s_t,a_t\right)\right]\hfill \\ \hfill & \mathrm{s}.\mathrm{t}.{\mathbb{E}}_{\left(s_t,a_t\right)\sim {\rho }_{\pi }}\left[-log\left({\pi }_t\left(a_t\mid s_t\right)\right)\right]\ge H_0\hfill \end{array}$$

(15)

The expected return is maximized while constraining the mean entropy to be greater than $H_0$. After applying mathematical simplifications, the loss function for ${\alpha }^{\prime }$ is derived as

$$L\left({\alpha }^{\prime }\right)={\mathbb{E}}_{s_t\sim R,a_t\sim \pi \left(·\mid s_t\right)}\left[-{\alpha }^{\prime }log\pi \left(a_t\mid s_t\right)-{\alpha }^{\prime }{H}_0\right]$$

(16)

In other words, when the entropy of the policy falls below the target entropy $H_0$, $L\left({\alpha }^{\prime }\right)$ increases the value of ${\alpha }^{\prime }$, thereby enhancing policy stochasticity. Conversely, when the policy entropy exceeds the target entropy, $L\left({\alpha }^{\prime }\right)$ decreases the value of ${\alpha }^{\prime }$, encouraging the agent to focus more on improving the value function.

5.1.5. Algorithm Flow

In conjunction with the previously discussed concepts of maximum entropy RL and soft policy iteration, the pseudocode of the SAC algorithm can be written as shown in Algorithm 1.

Algorithm 1: SAC

1: Use randomized network parameters ${\omega }_1$, ${\omega }_2$ and $\theta$ to initialize Critic network $Q_{{\omega }_1}(s,a)$, $Q_{{\omega }_1}(s,a)$ and Actor network ${\pi }_{\theta }\left(s\right)$; 2: Copy the same parameters ${\omega }_1^{-}\leftarrow {\omega }_1$ and ${\omega }_2^{-}\leftarrow {\omega }_2$ to initialize target network $Q_{{\omega }_1^{-}}$ and $Q_{{\omega }_2^{-}}$; 3: Initialize target entropy $H_0$; 4: Initialize experience replay buffer R; 5: for Episode $e=1\to E$ do 6:  Getting the initial state $s_1$; 7:  for Time step $t=1\to T$ do 8:    Select action $a={\pi }_{\theta }\left(s_t\right)$; 9:    Execute action $a_t$, get the reward $r_t$, state transfer to $s_{t+1}$; 10:   for Training step $k=1\to K$ do 11:    Uniformly sample N tuple from R; 12:    For each tuple, use the target network to compute: $$\begin{array}{cc}& y_i=r_i+\gamma \underset{j=1,2}{min}{Q}_{{\omega }_j^{-}}\left(s_{i+1},a_{i+1}\right)-\hfill \\ \hfill & {\alpha }^{\prime }log{\pi }_{\theta }\left(a_{i+1}\mid s_{i+1}\right)\hfill \end{array}$$ 13:    where $a_{i+1}\sim {\pi }_{\theta }\left(·\mid s_{i+1}\right)$; 14:    Compute two Critic network loss functions and update the Critic network; $$\begin{array}{cc}& L_Q\left({\omega }_j\right)={\displaystyle \frac{1}{N}}\sum _{i=1}^N{\left(y_i-Q_{{\omega }_j}\left(s_i,a_i\right)\right)}^2\hfill \end{array}$$ 15:    Sample the action $\widetilde{a_i}$ with the reparameterization trick, compute the loss function of the Actor network, and update the Actor network; $$\begin{array}{cc}& L_{\pi }\left(\theta \right)=\hfill \\ \hfill & {\displaystyle \frac{1}{N}}\sum _{i=1}^N\left({\alpha }^{\prime }log{\pi }_{\theta }\left({\tilde{a}}_i\mid s_i\right)-\underset{j=1,2}{min}{Q}_{{\omega }_j}\left(s_i,{\tilde{a}}_i\right)\right)\hfill \end{array}$$ 16:    Compute the loss function for ${\alpha }^{\prime }$ and update ${\alpha }^{\prime }$; $$\begin{array}{cc}& L\left({\alpha }^{\prime }\right)={\displaystyle \frac{1}{N}}\sum _{i=1}^N\left(-{\alpha }^{\prime }log\pi \left(a_t\mid s_t\right)-{\alpha }^{\prime }{\mathcal{H}}_0\right)\hfill \end{array}$$ 17:    Soft update two Critic networks; $$\begin{array}{cc}& {\omega }_1^{-}\leftarrow \tau {\omega }_1+(1-\tau ){\omega }_1^{-}\hfill \\ \hfill & {\omega }_2^{-}\leftarrow \tau {\omega }_2+(1-\tau ){\omega }_2^{-}\hfill \end{array}$$ 18:    where $\tau$ is the soft update parameter; 19:   end for 20:  end for 21: end for

Although the SAC algorithm demonstrates robust performance, allowing the agent to rapidly learn reward values while maintaining a certain level of exploration, its uniform sampling strategy in the experience replay structure leads to relatively low sample efficiency. Therefore, improvements are needed to enhance the experience replay structure.

5.2. Prioritized Experience Replay

In standard experience replay, the agent stores its experiences in a replay buffer and uniformly samples from this buffer during training. However, this uniform sampling approach does not ensure the agent learns from the most critical or valuable experiences during each training step.

Prioritized experience replay (PER) is an enhanced experience replay technique in RL designed to accelerate the learning process [54]. This technique is particularly effective in environments with sparse rewards. In sparse reward environments, the agent receives valuable feedback infrequently, but PER prioritizes replaying experiences with more value, thereby speeding up the learning process in such environments.

5.2.1. Priority

The core of PER is the use of a metric to assess whether an experience is worth learning from, referred to as the priority $p_i$ of experience i. A commonly used priority metric is the absolute value of the TD-error $\left|TD\right|$, where higher $\left|TD\right|$ values indicate that the experience is more valuable for replay.

PER does not employ a purely greedy strategy for prioritized experience replay, meaning it does not always replay the experience with the highest priority. Instead, to maintain the exploration capabilities of the agent, PER uses a prioritized replay strategy that balances between purely greedy and uniform sampling. The probability of sampling experience $P\left(i\right)$ is defined as follows:

$$P\left(i\right)={\displaystyle \frac{p_i^{\alpha }}{{\sum }_k{p}_k^{\alpha }}}$$

(17)

Here, $p_i$ represents the priority of experience i, and $\alpha$ determines the ratio between prioritized sampling and uniform sampling. Specifically, when $\alpha =0$, the sampling process is purely uniform.

The priority $p_i$ is typically indicated in a direct form as $p_i=\mid TD\mid +ϵ$, where $ϵ$ is a small positive constant added to prevent the situation where $\left|TD\right|$ equals zero, thus ensuring that the experience remains accessible.

5.2.2. Annealing the Bias

PER alters the sampling probability distribution of experiences, thereby introducing a bias. This bias can be mitigated by using importance sampling weights.

$$w_i={\left({\displaystyle \frac{1}{N}}·{\displaystyle \frac{1}{P\left(i\right)}}\right)}^{\beta }$$

(18)

where N represents the size of the experience replay buffer, and $\beta$ denotes the degree of bias correction. Specifically, when $\beta =1$, all experience update weights are equal, and thus no bias correction is applied.

It is important to note that this parameter, in conjunction with the $\alpha$ parameter, affects the priority of the experience. If an experience has a high $\left|TD\right|$, then during the algorithm’s update phase, a higher importance sampling weight will be used. Consequently, the $\left|TD\right|$ for that experience will decrease in the next time step to ensure that the experience is not always sampled.

To ensure the stability of the RL algorithm, PER also normalizes the importance sampling weights using $1/{max}_i{\omega }_i$. Additionally, in practical applications, $\beta$ is typically annealed linearly to 1 over the course of training steps. This approach ensures strong bias correction in the early stages of training, while in the later stages, as the algorithm converges and most experiences have similar $\left|TD\right|$, the need for bias correction diminishes.

5.2.3. Algorithm Flow

Combining SAC with PER, the following pseudo-code for the SAC-PER algorithm can be written as Algorithm 2:

Algorithm 2: SAC-PER

1: Use randomized network parameters ${\omega }_1$, ${\omega }_2$ and $\theta$ to initialize Critic network $Q_{{\omega }_1}(s,a)$, $Q_{{\omega }_1}(s,a)$ and Actor network ${\pi }_{\theta }\left(s\right)$; 2: Copy the same parameters ${\omega }_1^{-}\leftarrow {\omega }_1$ and ${\omega }_2^{-}\leftarrow {\omega }_2$ to initialize target network $Q_{{\omega }_1^{-}}$ and $Q_{{\omega }_2^{-}}$; 3: Initialize target entropy $H_0$; 4: Initialize the prioritized experience replay buffer R and the parameters $\alpha$ and $\beta$; 5: Store $(s_t,a_t,r_t,s_{t+1})$ in the replay buffer R, assigning the maximum priority $p_t={\max }_{\mathrm{i}\le \mathrm{t}}{!}_{\mathrm{i}}$ to each experience; 6: for Episode $e=1\to E$ do 7:  Getting the initial state $s_1$; 8:  for Time step $t=1\to T$ do 9:    Select action $a={\pi }_{\theta }\left(s_t\right)$; 10:   Execute action $a_t$, get the reward $r_t$, state transfer to $s_{t+1}$; 11:   Store $(s_t,a_t,r_t,s_{t+1})$ in the replay buffer R; 12:    for Training step $k=1\to K$ do 13:    Compute the sampling probability $P\left(i\right)$ for each experience according to (17), and sample N experiences ${(s_i,a_i,r_i,s_{i+1})}_{i=1,\dots ,N}$ based on these probabilities; 14:    Compute the importance sampling weights for each experience according to (18); 15:    Linearly anneal the parameter $\beta$ until it reaches 1; 16:    Compute two Critic network loss functions and update the Critic network; 17:    Sample the action $\widetilde{a_i}$ with the reparameterization trick, compute the loss function of the Actor network, and update the Actor network; 18:    Compute the loss function for ${\alpha }^{\prime }$ and update ${\alpha }^{\prime }$; 19:    Soft update two Critic networks; 20:   end for 21:  end for 22: end for

The algorithm combines SAC with PER, modifying the sampling probability distribution of experience replay to prioritize the retrieval of valuable experiences. While it shows significant improvement over SAC in relatively ideal environments, the presence of stochasticity in EWMDM environments introduces instability to the PER improvement. Therefore, we innovatively propose a noise-robust PER improvement based on $\alpha$ parameter decay, termed Alpha Decay PER (ADPER).

5.3. Alpha Decay Prioritized Experience Replay

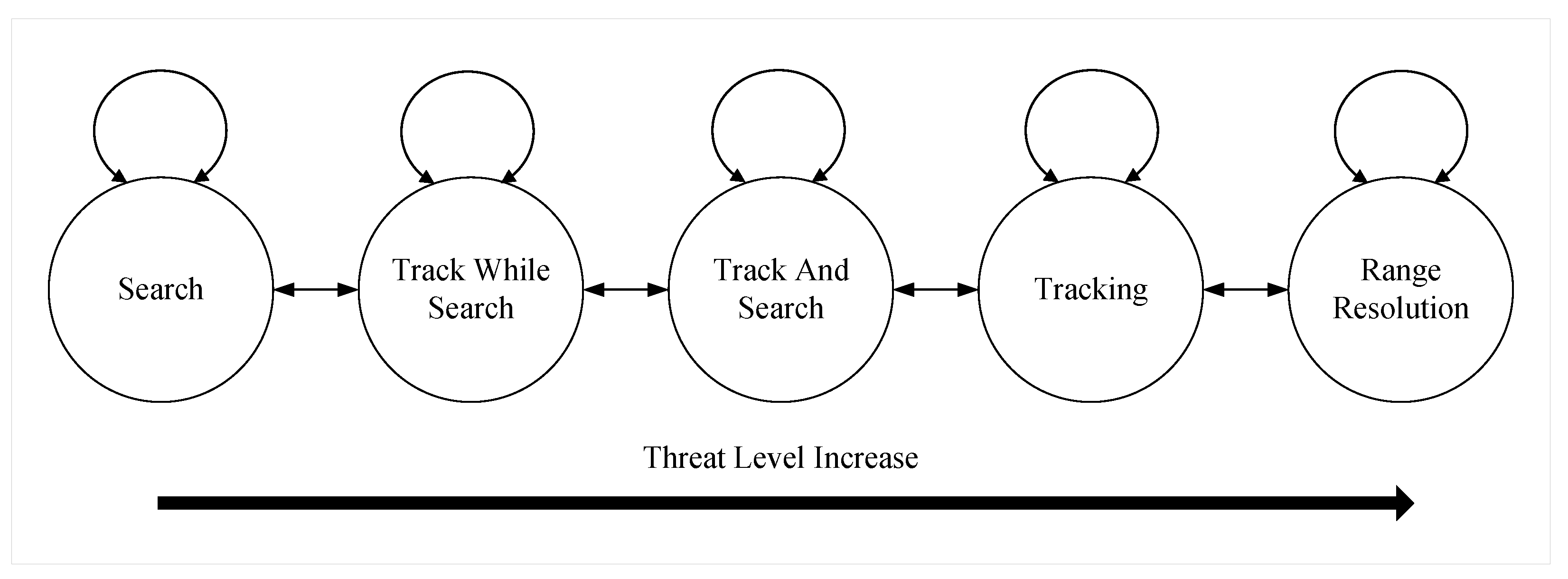
In EWMDM environments, environmental noise is an essential factor that cannot be ignored. As the electromagnetic environment becomes more complex, the accuracy of the MRS’s identification of MFR states decreases, causing the MRS to receive the incorrect reward. In addition, environmental stochasticity in EWMDM environments also affects RL algorithms. In Section 4, we model the MFR state transition process as a probabilistic transition matrix. This matrix introduces stochasticity into the EWMDM environment, meaning that regardless of the EWMDM method employed, the MFR state has a probability of transitioning in one of three directions: increasing, maintaining, or decreasing in threat level. Merely, for the most effective EWMDM method in the current MFR state, the probability of transitioning to a lower threat state is the highest. During the mid-to-late stages of agent training, the agent may have already learned certain correct strategies, meaning it can make optimal decisions in some MFR states. 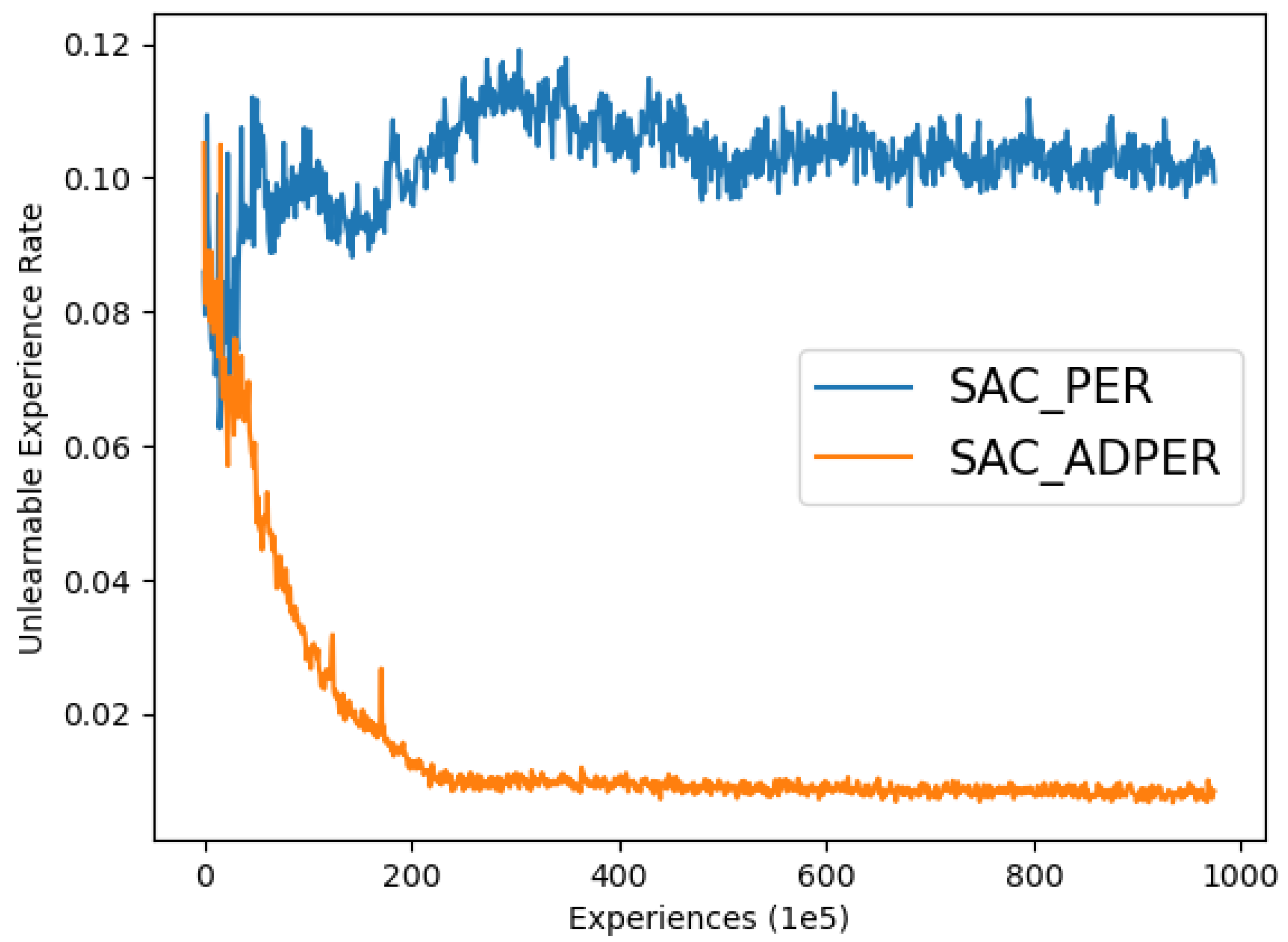So in the mid-to-late stages of agent training, if the agent employs the most effective method in a given MFR state, but the MFR state transitions towards a higher threat level, the $\left|TD\right|$ in this experience will be high, which will increase the sampling probability of the experience in PER improvement and sample the experience more frequently. This experience offers little left for the intelligent agent to learn, and in fact runs counter to the original intent of PER. In reality, we do not want the agent to learn from such unlearnable experiences, which will cause the agent to learn in the wrong direction.

Based on the aforementioned characteristics of the EWMDM environment, we propose the ADPER improvement, where the $\alpha$ parameter is linearly annealed from its initial value to zero. Compared to the PER improvement, it can be anticipated that although this approach may reduce the agent’s sampling frequency from experiences with high $\left|TD\right|$ to some extent, it will also decrease the frequency with which the agent is guided by unlearnable experiences. In the early stages of training, most experiences exhibit high $\left|TD\right|$ due to the imperfection of the agent’s policy, rather than being caused by environmental noise or unexpected results. Therefore, sampling experiences based on priority during the early stages of training can effectively accelerate the algorithm’s convergence speed. However, in the mid to late stages of training, as the agent’s policy becomes more refined, most experiences will have low $\left|TD\right|$. At this point, if PER continues to prioritize sampling experiences with high $\left|TD\right|$, there is a high probability of sampling unlearnable experiences caused by environmental stochasticity, which will slow down the algorithm’s convergence. Consequently, due to the noise and stochasticity inherent in EWMDM environments, adopting ADPER improvement is necessary.

Algorithm 3 presents the pseudocode for the SAC combined with the ADPER improvement.

Algorithm 3: SAC-ADPER

1: Use randomized network parameters ${\omega }_1$, ${\omega }_2$ and $\theta$ to initialize Critic network $Q_{{\omega }_1}(s,a)$, $Q_{{\omega }_1}(s,a)$ and Actor network ${\pi }_{\theta }\left(s\right)$; 2: Copy the same parameters ${\omega }_1^{-}\leftarrow {\omega }_1$ and ${\omega }_2^{-}\leftarrow {\omega }_2$ to initialize target network $Q_{{\omega }_1^{-}}$ and $Q_{{\omega }_2^{-}}$; 3: Initialize target entropy $H_0$; 4: Initialize the prioritized experience replay buffer R and the parameters $\alpha$ and $\beta$; 5: Store $(s_t,a_t,r_t,s_{t+1})$ in the replay buffer R, assigning the maximum priority $p_t={\max }_{\mathrm{i}\le \mathrm{t}}{!}_{\mathrm{i}}$ to each sample; 6: for Episode $e=1\to E$ do 7:  Getting the initial state $s_1$; 8:  for Time step $t=1\to T$ do 9:    Select action $a={\pi }_{\theta }\left(s_t\right)$; 10:   Execute action $a_t$, get the reward $r_t$, state transfer to $s_{t+1}$; 11:   Store $(s_t,a_t,r_t,s_{t+1})$ in the replay buffer R; 12:   for Training step $k=1\to K$ do 13:    Compute the sampling probability $P\left(i\right)$ for each experience according to (17), and sample N experiences ${(s_i,a_i,r_i,s_{i+1})}_{i=1,\dots ,N}$ based on these probabilities; 14:    Compute the importance sampling weights for each experience according to (18); 15:    Linearly anneal the parameter $\beta$ until it reaches 1; 16:    Linearly anneal the parameter $\alpha$ until it reaches 0; 17:    Compute two Critic network loss functions and update the Critic network; 18:    Sample the action $\widetilde{a_i}$ with the reparameterization trick, compute the loss function of the Actor network, and update the Actor network; 19:    Compute the loss function for ${\alpha }^{\prime }$ and update ${\alpha }^{\prime }$; 20:    Soft update two Critic networks; 21:   end for 22:  end for 23: end for

6. Experimental Results and Analysis

6.1. Experimental Setup

In the simulation experiments, our PDW dataset is referenced from the paper [24], which refers to the waveform PDW settings of the “Mercury” MFR [35]. The Mercury MFR dataset is a simulated radar signal dataset designed to reflect the complex, multi-level behavior of a real MFR system. It covers five key PDWs: RF, PW, BW, PRF and PP. The dataset simulates various working states and incorporates realistic disturbance factors. This dataset effectively simulates the environment faced by MRS [55]. Referencing the characteristic of Mercury MFR’s PDW being randomly generated within a certain range as described in other literature, this paper also generates the dataset with intervals shown in

Table 6. PDW Parameter Setup.

CF/GHz	PW/µs	BW/MHz	PRF/KHz	PP/W	MFR States
[1, 4]	[0.5, 20]	[1, 10]	[0.5, 5]	[50, 100]	Search
[1, 4]	[0.5, 20]	[1, 10]	[10, 20]	[100, 300]	TWS
[1, 4]	[10, 30]	[1, 50]	[20, 50]	[100, 300]	TAS
[2, 8]	[30, 50]	[50, 100]	[0.5, 100]	[200, 500]	Tracking
[2, 8]	[10, 30]	[1, 50]	[50, 100]	[300, 800]	Range Resolution

.

6.2. MFR State Recognition Experiment

Within the parameter ranges, we generated 1000 samples for each MFR state to train the SVM, splitting the dataset into training and testing sets at a 7:3 ratio. It should be noted that, similar to many MFR state recognition studies [35], we use noise-free simulated data for SVM training. To demonstrate the impact of the Gaussian noise model introduced in Section 3 on EWMDM effect evaluation, we conduct MFR working state recognition experiments under different conditions: the ideal case (noise-free) and noise variance ${\sigma }^2$ of 0.75, and 1.5. Since the PDW consists of five parameters, we select BW and PRF as the horizontal and vertical axes, respectively, to visualize the decision boundaries fitted by SVM under different noise conditions.

The experimental results are shown in Figure 4. The icons labeled 1–5 in the upper right corner represent, in order: Search, TWS, TAS, Tracking and Range Resolution. It can be clearly observed that as the noise variance increases, more data points cross the SVM decision boundary. These data points, which are misclassified due to the interference of noise, lead to incorrect recognition of the MFR working state. Therefore, it can be concluded that the larger the noise variance, the lower the accuracy of MFR state recognition. The identification accuracy is detailed in

Table 7. MFR states recognition in noisy environments.

Noise Coefficient	Recognition Accuracy
0	0.998
0.75	0.895
1.5	0.721

. At ${\sigma }^2=0$, the recognition accuracy is 99.8%. At ${\sigma }^2=0.75$, it drops to 89.5%. And at ${\sigma }^2=1.5$, it further declines to 72.1%. These results further illustrate that as the noise coefficient increases, the MFR state identification accuracy decreases, and the SVM shows greater uncertainty in recognizing more MFR states.

6.3. Parameter Setup

To explore the impact of different noise levels on the performance of RL algorithms, we conducted three groups of experiments with noise variances of 0, 0.75 and 1.5. We observe that when the noise variance exceeds 1.5, the accuracy of MFR state identification drops sharply, making convergence difficult for all algorithms. Thus, we set 1.5 as our noise boundary. Given that the impact of noise on the accuracy of SVM recognition of MFR states differs within Section 6.2, we established different recognition thresholds tailored to different noise conditions. To mitigate the impact of erroneous MFR state recognition results on the MRS’s reward function, we adjusted the thresholds to increase proportionally with rising noise levels. This approach aims to filter out a greater number of incorrect MFR state recognition results.

For SAC, SAC-PER and SAC-ADPER, we maintained consistent common parameters across all algorithms. Additionally, we employed different PER and ADPER parameters under varying noise conditions to validate the effectiveness of SAC-ADPER. In addition to SAC, SAC-PER, and SAC-ADPER, we have also selected two classical RL algorithms, DDQN and PPO, for comparison. These two algorithms are not only commonly used as benchmarks in numerous studies but also demonstrate commendable performance in noisy environments and sparse reward settings [16,26,27].

We set the common parameters for all five algorithms to the same values. The parameter settings for the common parameters of the five algorithms are shown in

Table 8. Common parameter setup of the five algorithms.

Name	Description	Size
$r_{Actor}$	Actor learning rate	$3\times {10}^{-5}$
$r_{Critic}$	Critic learning rate	$3\times {10}^{-4}$
$r_{Alpha}$	Alpha learning rate	$1\times {10}^{-2}$
$di{m}_1$	Hidden dim 1 size	128
$di{m}_2$	Hidden dim 2 size	128
$\tau$	Soft update factor	$0.05$
$\gamma$	Discount factor	$0.98$
N	Batch size	256
$H_{target}$	Target entropy	$-0.5$
$N_{min}$	Minimal update size	2000

. The unique parameters specific to DDQN are shown in

Table 9. DDQN parameter setup.

Name	Description	Size
$r_{DDQN}$	DDQN learning rate	$3\times {10}^{-5}$
$f_{upd}$	DDQN update frequency	50
${ϵ}_{DDQN}$	DDQN epsilon	$0.01$

. And the unique parameters specific to PPO are shown in

Table 10. PPO parameter setup.

Name	Description	Size
${\lambda }_{PPO}$	PPO GAE parameter	$0.9$
${ϵ}_{PPO}$	PPO clipping parameter	$0.1$
$n_{PPO}$	Number of gradient descent iterations	10

. To demonstrate the effectiveness of the ADPER improvement, we conducted simulations by keeping $\beta$, and ${\beta }_{\mathrm{step}}$ consistent between the PER and ADPER improvements, only altering the $\alpha$ and ${\alpha }_{\mathrm{step}}$ in the ADPER improvement under different noise conditions. As noise and probability thresholds are introduced, the SVM filters out uncertain MFR states, causing the reward function to become more sparse. Therefore, in terms of the parameter settings for the PER and ADPER improvements, we adopted a more aggressive priority strategy for a higher noise variance environment. Compared to the ideal environment experiment, we increased the initial value of $\alpha$ to 0.8, while keeping $\beta$ constant at 0.4. Additionally, since the convergence speed varies under different noise coefficient environments, the annealing steps for the $\alpha$ and $\beta$ parameters need to be synchronized with the convergence speed. The specific parameter settings are shown in

Table 11. PER, ADPER and threshold parameter setup.

Name	${\mathit{\sigma }}^2=0$	${\mathit{\sigma }}^2=0.75$	${\mathit{\sigma }}^2=1.5$
$\alpha$	0.6	0.7	0.8
$\beta$	0.4	0.4	0.4
${\alpha }_{\mathrm{step}}$	$2\times {10}^3$	$7\times {10}^3$	$1\times {10}^5$
${\beta }_{\mathrm{step}}$	$2\times {10}^3$	$7\times {10}^3$	$1\times {10}^5$
threshold	None	0.75	0.98

, where ${\sigma }^2$ represents noise variance.

Additionally, to reduce the randomness of the experimental results, we employed a checkpoint setting method to depict the experimental metrics. We set a checkpoint every 10 training steps, where all network parameters are frozen, and 1024 Monte Carlo experiments are conducted to obtain the agent’s metrics under the current training state.

6.4. Performance Analysis

6.4.1. Impact of Noise Variance

We conducted simulations in the environments under noise variance ${\sigma }^2$ of 0, 0.75 and 1.5 based on the parameter settings mentioned above. The comparison results of the five algorithms are shown in Figure 5, Figure 6 and Figure 7. In the experiments, we recorded the following three metrics for the SAC and its improved algorithms: return value, confrontation steps, and actor network loss, with the horizontal axis representing the number of checkpoints. In the experimental result figures, the X-axis represents the checkpoints, and the Y-axis represents the various metrics evaluated at each checkpoint. Here, an agent evaluation is conducted every 10 training steps, which we refer to as a checkpoint. As DDQN is an improved method based on the DQN architecture rather than the actor–critic architecture, there is no actor loss evaluation standard in it. Therefore, we cannot show the actor network loss curve of DDQN in the third subfigure of all results.

It can be observed that when ${\sigma }^2=0$, the return values of SAC, SAC-PER and SAC-ADPER converged around 100 checkpoints, with SAC-ADPER converging the fastest, followed by SAC and SAC-PER. DDQN converges at around 125 checkpoints and PPO converges at 50 checkpoints. The reward values for SAC, SAC-PER and SAC-ADPER converged around 15. However, DDQN converges around 10 and PPO converges around 5. Concurrently, the confrontation steps in SAC, SAC-PER and SAC-ADPER stabilized around 100. However, the confrontation steps for DDQN and PPO converge at 80 and 70, respectively. This result indicates that SAC, SAC-PER and SAC-ADPER have converged to the global optimum, but DDQN and PPO only converge to a local optimum. We can observe that DDQN lacks the exploratory nature of maximum entropy RL, which makes it difficult to converge to the global optimum in the EWMDM environment. Also, PPO has a bad performance in the EWMDM environment due to its on-policy nature, which can limit exploration and make it susceptible to converging prematurely to a local optimum in noisy settings. Due to the exploration-encouraging nature of the maximum entropy RL algorithm, significant fluctuations in the return values persisted even after convergence. Therefore, it was challenging to discern which algorithm converged the fastest by observing the return values alone, given their similar convergence speeds. However, by examining the actor losses as shown in Figure 5c, it is evident that SAC-ADPER converged at 75 checkpoints, SAC at 90 checkpoints, SAC-PER at 100 checkpoints and PPO at 50 checkpoints. Although PPO converges faster than the SAC series of algorithms, the SAC series of algorithms ultimately converges to the global optimum, whereas PPO tends to converge to a local optimum.

For the results with ${\sigma }^2=0.75$, we observe that SAC and SAC-ADPER maintain better convergence speed and convergence values even under moderate noise conditions. Both algorithms converge to a return value of approximately 13. Specifically, SAC-ADPER converges at 160 checkpoints (as seen in Figure 6c), while SAC converges at 250 checkpoints. In contrast, SAC-PER is more noticeably affected by noise, converging to a return value of around 10 at the 300 checkpoints. Both DDQN and PPO show a more significant decline in performance compared to the ${\sigma }^2=0$ scenario and fail to converge. With ${\sigma }^2=1.5$, a clear performance gap emerges between SAC-ADPER and SAC. SAC-ADPER converges to a return value of about 7 at 1000 checkpoints, whereas SAC converges to approximately 3 at the 2200 checkpoints. However, SAC-PER, DDQN, and PPO are unable to converge under these conditions. A statistical summary of the convergence training steps for all four algorithms is presented in

Table 12. Convergence training steps in different environments.

${\mathit{\sigma }}^2$	PPO	DDQN	SAC	SAC-PER	SAC-ADPER
0	500	1250	900	1000	750
0.75	–	–	2500	–	1600
1.5	–	–	22,000	–	10,000

.

It is shown that under environments with noise variances ${\sigma }^2$ of 0, 0.75 and 1.5, the convergence speed of SAC-ADPER relative to SAC increased by 16.6%, 36% and 54.5%, respectively. We observe that the performance of DDQN and PPO declines most significantly with the increase in noise variance, which proves that DDQN and PPO are not suitable for the EWMDM environment with strong stochasticity. As the noise variance increases, the probability threshold set in the environment filters out more uncertain MFR state recognition results, leading to sparser rewards. Consequently, the agent receives less feedback during the confrontation process, causing a decline in the overall convergence speed of all five algorithms. Furthermore, the PER improvement was originally inspired by the sparse reward problem and shows significant improvement in environments with sparse rewards [54]. Thus, adopting the PER improvement in the early stages of training can have a noticeable impact. However, in the mid-to-late stages of training, high $\left|TD\right|$ experiences are primarily caused by the stochasticity of the environment, and such experiences can guide the agent to learn in the wrong direction. Therefore, prioritized experience replay should degrade to uniform sampling in the mid-to-late stages of training. This explains why the SAC-ADPER algorithm exhibits significantly faster convergence than the other two algorithms in noisy environments. SAC-ADPER also uses PER in the early stages of training, sampling experiences with high $\left|TD\right|$. In contrast, SAC can more evenly leverage different reward values, which explains why SAC converges faster than SAC-ADPER under non-sparse rewards.

6.4.2. Impact of Probability Threshold

To assess the impact of the probability threshold mechanism on algorithm performance, we conducted three sets of experiments with SAC-ADPER under an environment with a noise variance of ${\sigma }^2=1.5$. The probability thresholds for the MRS were configured as follows: no probability threshold, full probability threshold, and a probability threshold of 0.98. Notably, no probability threshold implies that the MRS’s reward is based on MFR state recognition results regardless of their correctness. Conversely, the full probability threshold filters out all MFR state recognition results, preventing the MRS from receiving any process rewards. The results are shown in Figure 8.

The experimental results show that SAC-ADPER achieves the best convergence performance with a threshold of 0.98, followed by the no-threshold setting, and lastly the full-threshold setting. It showns that SAC-ADPER with a threshold set to 0.98 has the best convergence performance, converging to a return value of approximately 7 at 1000 checkpoints. Following closely is SAC-ADPER without a threshold, which converges to a return value of around 5 at 1300 checkpoints. The worst convergence performance is observed in SAC-ADPER with a full threshold, as the experimental results indicate that it fails to converge. In the no-threshold setup, the incorporation of numerous incorrect MFR state recognition results into the MRS’s reward function leads to incorrect process rewards, thereby misguiding the RL agent’s learning process. However, some incorrect MFR state recognition results may occasionally yield correct rewards. For instance, if the current MFR state is searching and the next state is actually TWS but misidentified as TAS by the MRS, the process reward remains positive, promoting the RL agent to learn the corresponding strategy. This occurrence ensures algorithm convergence without a threshold with a notably slower convergence rate. In the full-threshold scenario, all MFR state recognition results are masked, preventing the MRS from receiving any process rewards during confrontation until the end of an episode, resulting in a completely sparse reward environment. This hinders the RL agent’s ability to evaluate each action, ultimately leading to non-convergence. This outcome validates the effectiveness of the environmental reward function design.

6.4.3. The Effectiveness of the ADPER Mechanism

To validate the effectiveness of the ADPER mechanism, we conducted a comparative analysis of $\left|TD\right|$ and learnability of experiences collected by SAC-PER and SAC-ADPER during both early and mid-to-late stages in scenarios with a noise variance of ${\sigma }^2=1.5$. Learnability is defined as follows: Using the converged policy of SAC-ADPER as a reference, a sample was deemed learnable if it effectively helped the agent’s convergence towards this policy. Those that do not meet this condition are referred to as unlearnable experiences. Specifically, this occurred when the agent either selected the correct action and received a negative reward or chose an incorrect action and received a positive reward. Such experiences are then labeled as unlearnable. We counted the experiences collected within 20,000 iterations that were not filtered out by the threshold, then calculated the rate of unlearnable experiences with $\left|TD\right|\ge 2$ among these experiences. The results are shown in Figure 9.

The results show that SAC-PER maintains a persistently high rate of unlearnable experiences, about 10%, throughout training, reflecting its vulnerability to the stochasticity in CEE. In SAC-PER, we can conclude that high $\left|TD\right|$ unlearnable experiences are over-sampled causing the agent to learn a less optimal policy. In contrast, the SAC-ADPER curve begins to decline gradually around $2\times {10}^6$ experiences and converges to 1% by approximately $2\times {10}^7$ experiences, which means the ADPER mechanism effectively reduced sampling of unlearnable experiences by 90% in the mid-to-late stages of training. This improvement is attributed to ADPER’s adaptive prioritization mechanism, which is to maintain frequent sampling of high $\left|TD\right|$ experiences in the early stages, then transition to uniform sampling in the mid-to-late stages. The suppression of unlearnable experiences directly explains SAC-ADPER’s 54.5% faster convergence: by filtering out noise-dominated experiences, ADPER minimizes wasted parameter updates and focuses on learnable experiences that genuinely improve policy alignment. In conclusion, the ADPER mechanism enhances both convergence speed and the robustness of the learned policy in noisy environments.

7. Conclusions

With the rapid advancement of MFR and the growing complexity of noise in CEE, there is an urgent need for a noise-robust EWMDM algorithm. This paper systematically models the EWMDM problem in both ideal and noisy environments and proposes an improved RL algorithm. Initially, we construct an EWMDM model that simulates real-world electromagnetic noise by introducing noise into the PDWs, which interferes with the MRS’s ability to identify MFR states. To mitigate the impact of noise on the reward function, we innovatively introduce a probability threshold filtering mechanism that assigns zero rewards to uncertain MFR states, thereby preventing the agent from being misguided by incorrect rewards. Then we integrate PER into the SAC algorithm and propose the ADPER improvement. During training, the $\alpha$ parameter is linearly annealed to zero, significantly reducing the agent’s sampling frequency of unlearnable experiences. Experimental results demonstrate that SAC-ADPER is highly effective for EWMDM in noisy environments, with the probability threshold being essential for effective decision-making. This adaptive prioritization approach, which dynamically adjusts the sampling strategy to focus on learnable experiences while minimizing the impact of noise, highlights the innovative advantages of the ADPER mechanism in enhancing learning efficiency and decision-making performance in challenging CEE.

Beyond theoretical contributions, the practical implications of this research are substantial, particularly in fields such as electronic warfare and stealth technology for UAVs. In electronic warfare, the ability to make accurate and timely decisions in noisy environments is critical for effective countermeasures against advanced radar systems. Similarly, in UAV radar stealth, optimizing decision-making under noisy conditions can significantly enhance the survivability and mission success rates of UAVs operating in contested airspaces. By providing a robust and adaptive algorithmic solution, this research not only advances the theoretical understanding of EWMDM but also offers tangible benefits for real-world applications, making the study both convincing and highly relevant. Looking forward, future research could focus on integrating advanced RL techniques and real-time data fusion to enhance algorithm adaptability and situational awareness. Collaborations with industry could lead to real-world prototypes, paving the way for smart MRS that make intelligent decisions in complex environments.