High-Frequency Guided Dual-Branch Attention Multi-Scale Hierarchical Dehazing Network for Transmission Line Inspection Images

Abstract

To address the edge blurring issue of drone inspection images of mountainous transmission lines caused by non-uniform haze interference, as well as the low operational efficiency of traditional dehazing algorithms due to increased network complexity, this paper proposes a high-frequency guided dual-branch attention multi-scale hierarchical dehazing network for transmission line scenarios. The network adopts a core architecture of multi-block hierarchical processing combined with a multi-scale integration scheme, with each layer based on an asymmetric encoder–decoder with residual channels as the basic framework. A Mix structure module is embedded in the encoder to construct a dual-branch attention mechanism: the low-frequency global perception branch cascades channel attention and pixel attention to model global features; the high-frequency local enhancement branch adopts a multi-directional edge feature extraction method to capture edge information, which is well-adapted to the structural characteristics of transmission line conductors and towers. Additionally, a fog density estimation branch based on the dark channel mean is added to dynamically adjust the weights of the dual branches according to haze concentration, solving the problem of attention failure caused by attenuation of high-frequency signals in dense haze regions. At the decoder end, depthwise separable convolution is used to construct lightweight residual modules, which reduce running time while maintaining feature expression capability. At the output stage, an inter-block feature fusion module is introduced to eliminate cross-block artifacts caused by multi-block processing through multi-strategy collaborative optimization. Experimental results on the public datasets NH-HAZE20, NH-HAZE21, O-HAZE, and the self-built foggy transmission line dataset show that, compared with classic and cutting-edge algorithms, the proposed algorithm significantly outperforms others in terms of Peak Signal-to-Noise Ratio (PSNR) and Structural Similarity Index (SSIM); its running time is 19% shorter than that of DMPHN. Subjectively, the restored images have continuous and complete edges and high color fidelity, which can meet the practical needs of subsequent fault detection in transmission line inspection.

1. Introduction

The employment of Unmanned Aerial Vehicles (UAVs) for transmission line inspection, fault detection, and timely mitigation of potential risks has evolved into an essential auxiliary approach in the operation and maintenance of modern power systems [1,2]. However, images acquired by UAVs are susceptible to degradation in quality due to factors such as haze, consequently impairing the accuracy of subsequent visual tasks.

Currently, numerous methods exist in the field of image dehazing, which can generally be categorized into three major types: image enhancement, physics model-based methods, and deep learning-based approaches. The objective of image dehazing is to restore haze-free images from hazy inputs. Traditional image enhancement techniques improve visual quality by accentuating image details or enhancing contrast. Specific algorithms include the Retinex algorithm, histogram equalization, and partial differential equation-based methods [3,4,5]. Although these approaches amplify image detail features through certain statistical and transformational means, they often result in incomplete haze removal to a significant extent.

The Atmospheric Scattering Model (ASM) [6] is commonly employed to explain the process of image dehazing, as represented by Equation (1):

$$\begin{array}{l}I(x)=J(x)t(x)+A(1-t(x))\\ t(x)=e^{-bd(x)},0\le d(x)\le 1\end{array}$$

(1)

where $I(x)$ represents the hazy image; $J(x)$ denotes the restored image; $t(x)$ signifies the transmission map; $d(x)$ indicates the scene depth; $A$ stands for the global atmospheric light.

The principle of image dehazing based on physical models simulates the scattering and absorption processes of light in the atmosphere to estimate the scene depth, subsequently derive the transmission map, and ultimately restore a clear image. The Dark Channel Prior (DCP) [7] is a representative algorithm. While it improves dehazing performance in the atmospheric scattering model by providing more accurate scene depth estimation and atmospheric light estimation, it tends to over-enhance sky regions and is susceptible to image noise. For instance, in reference [8], the gradient features of directly transmitted light intensity estimated by the DCP algorithm were used as guidance to solve and optimize the target degree of polarization for image dehazing. Although the resulting images are relatively clear to some extent, the high dependency on parameter accuracy leads to noise and color artifacts in the images. In reference [9], bilateral filtering was employed as the transfer function for homomorphic filtering to estimate atmospheric light and scene reflectance. This approach maintains edge clarity from the perspective of color components, but the independent dehazing operations on each color channel result in inconsistent dehazing effects across channels, thereby weakening edge and texture information. To preserve edge information in clearly dehazed images, edge-preserving filters have been introduced. For example, reference [10] proposed a weighted guided image filter. The method decomposes multiple underexposed images generated with different gamma values, refines the weights of each decomposed image block using this filter, and finally performs image fusion. However, due to the decomposition and fusion processes, the algorithm requires longer computational time, making it unsuitable for real-time image processing.

In addition to visual sensors such as cameras, other sensing technologies, including LiDAR, have also been applied in image dehazing. For instance, in reference [11], single-photon counting was utilized to enhance the GM-APD LiDAR system. By performing maximum likelihood estimation on echo photons, the backscattering distribution was obtained, and target echo positions were extracted to achieve image dehazing. However, this method exhibits limited echo signal extraction capability under dense fog conditions. In reference [12], a fusion strategy combining images and LiDAR data was adopted for dehazing. Nevertheless, relying solely on the mean pixel value to estimate the dark channel mean deviates from the scattering coefficient estimation model, leading to suboptimal dehazing performance. Moreover, LiDAR noise points increase significantly in heavy fog. Reference [13] proposed a fusion approach integrating radar and LiDAR data through a bird’s-eye view representation to enhance edge clarity. However, this method requires substantial computational resources for dense bird’s-eye view queries and assigns uniform attention to all features, lacking adaptive emphasis. Although the aforementioned dehazing methods can produce relatively clear images to some extent, they struggle to achieve satisfactory performance in complex scenarios such as non-uniform fog.

Deep learning methods are capable of learning haze patterns and image priors from large-scale data, without imposing stringent requirements on the accuracy of model parameters, and demonstrate strong adaptability to non-uniform haze or complex scenes. Consequently, convolutional neural network (CNN)-based image dehazing algorithms have been extensively studied in recent years. In reference [14], an edge extraction branch was incorporated as an additional edge prior, supplemented by an edge loss to impose secondary constraints on the network. Reference [15] introduced a depth-refinement branch to recover structural information in the form of a depth map, which guided a dehazing branch to enhance contour restoration. However, this method performs poorly at depth discontinuities and tends to lose information in low-light regions. In reference [16], multi-scale parallel large convolutional kernels and an enhanced parallel attention module were employed for feature extraction and reconstruction. Reference [17] proposed a dynamic convolution mechanism that adaptively adjusts the weights of output channels and spatial dimensions based on input characteristics. This was combined with depthwise separable convolution to leverage multi-dimensional features for haze-free image recovery. Although these approaches improve dehazing performance by expanding multi-scale receptive fields to capture both global and local features, they often increase model complexity, making it difficult to meet practical requirements for real-time inspection. In reference [18], a lightweight encoder–decoder dehazing architecture was used as a teacher network, while a student network constructed via channel multipliers distilled knowledge encoded from hazy images; the teacher-student collaboration aimed to reduce computational complexity. Reference [19] adopted a parallel combination of standard and dilated convolutions to enlarge the receptive field, along with downsampling operations prior to haze extraction and removal modules to reduce computational load in subsequent layers. Nevertheless, this approach inherently increases the number of convolutional layers and kernels. Reference [20] employed atrous convolutions to construct a multi-scale adaptive module for balancing dehazing performance and computational cost. It introduced a lightweight channel attention-guided fusion module to improve feature extraction. However, the conventional serial attention structure fails to adequately account for the non-uniform distribution of haze, leading to insufficient dehazing in dense haze regions.

Generative Adversarial Networks (GANs) have also been introduced into dehazing algorithms. Reference [21] proposed an enhanced cycle-consistent GAN model that employs local-global discriminators to address non-uniformly distributed haze, thereby reducing residual haze in the restored images. Nevertheless, due to the lack of paired training data in image dehazing tasks, GAN-based methods often struggle to generate high-quality dehazed images with satisfactory perceptual and quantitative performance. Furthermore, With the remarkable performance of Transformer models in image-related tasks, numerous studies have begun to employ Transformer architectures for image dehazing. In reference [22], a dual-branch collaborative dehazing network integrating both Transformer and CNN components was proposed. This network utilizes residual modules to extract features and incorporates a non-autoregressive mechanism with lateral connections in the Transformer blocks to preserve features at different depths. However, Transformer-based models generally involve a large number of parameters and high computational latency, making them difficult to deploy in practical scenarios.

In the field of engineering inspection, machine learning technologies have demonstrated the value of scenario-specific model optimization, which can significantly enhance their detection performance in complex engineering environments. For instance, in Reference [23], researchers leveraged Bayesian optimization to automatically tune the hyperparameters of the LSTM model, addressing the inherent parameter tuning challenges of traditional machine learning methods and achieving high classification accuracy for Concrete-Filled Steel Tube (CFST) debonding defects of different levels.

Therefore, to address the core requirement of balancing dehazing performance and computational efficiency in the scenario of UAV-based transmission line inspection, this paper proposes a fast multi-patch hierarchical algorithm based on machine learning. This approach enhances defogging effects in drone inspection photos of power transmission lines by incorporating high-frequency guidance to improve the attention mechanism and utilizing an asymmetric encoder–decoder architecture. A Mix structure module is embedded in the encoder to establish a dual-branch attention coordination mechanism. Multi-source high-frequency features guide attention allocation, integrating Laplace, Sobel-X/Y, and Prewitt operators to extract multi-directional edge features. This enhances edge capture capabilities for critical targets such as horizontal conductors and vertical towers. Simultaneously, a new fog density estimation branch based on the dark channel mean is introduced. This dynamically adjusts the weights of the dual branches according to fog concentration, resolving attention failure caused by high-frequency signal attenuation in dense fog areas. At the decoder stage, depthwise separable convolutions (DSCs) are employed to build lightweight residual modules, significantly reducing computational load while preserving feature combination capabilities. An inter-block feature fusion module is introduced at the decoder output, utilizing a multi-scale weighted fusion strategy to eliminate edge artifacts accumulated through multi-level segmentation. This further enhances edge continuity and overall image quality in the defogged output.

2. Dehazing Treatment in Non-Uniform Haze Areas

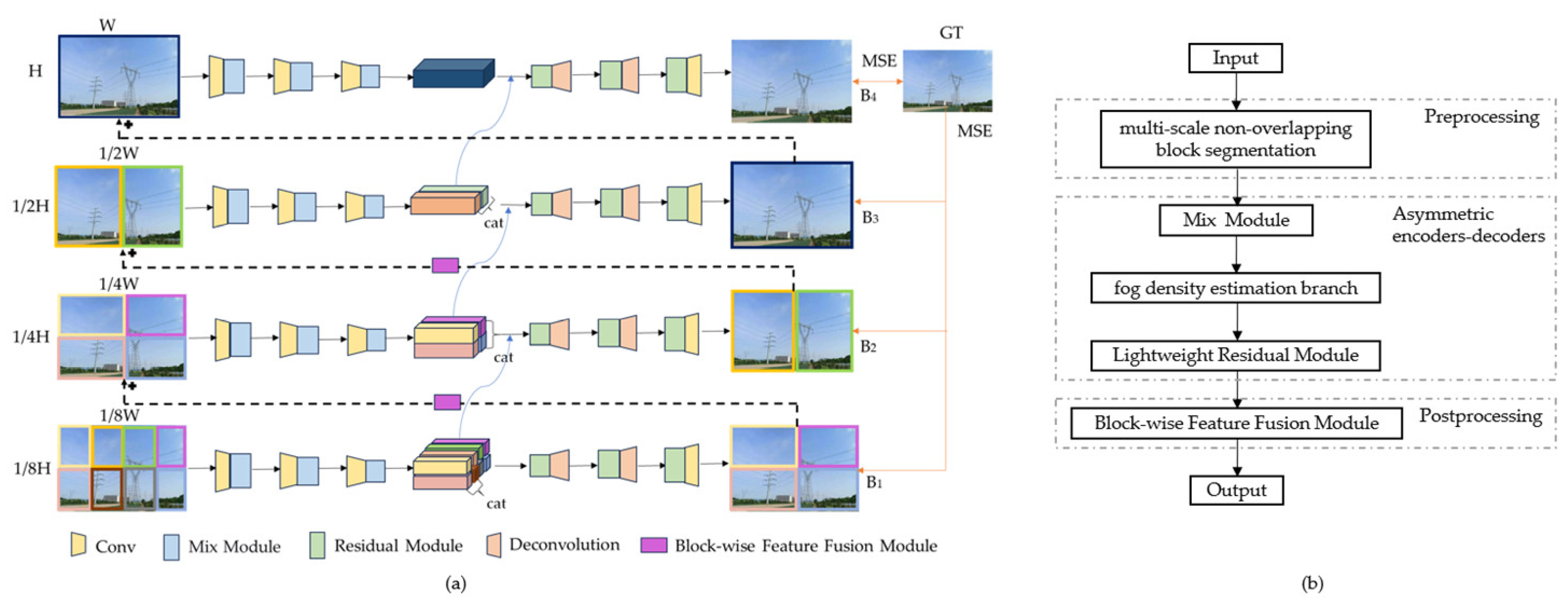
Multi-scale segmentation is a common strategy in fog removal, but existing methods suffer from issues such as fragmented inter-block features or poor scale adaptability. The algorithm proposed in this paper adopts a multi-layer architecture that progresses from coarse to fine, fully integrating features from different levels, as shown in Figure 1a. Each layer employs an asymmetric encoder–decoder structure, with asymmetry primarily manifested in the distinct modules they comprise. For each pair of encoder–decoder modules at different levels, the algorithm processes image blocks at distinct scales, reconstructing corresponding clear images at each scale. Processing at multiple scales enables richer spatial feature information and defogged downsampled images. The input raw image is segmented into multiple non-overlapping blocks as inputs for each scale. This approach alters the receptive field by varying the image size, thereby capturing more feature information and enhancing image clarity.

This structure comprises four distinct scales ($B_i$, $i=1,2,3,4$), each of which segments the input image into $2^{4-i}$ number of non-overlapping image blocks. Let $I$ denote the input image, $I_{i,j}$ represent the $i-th$ scale, and the $j-th$ block. Here, $j=8,4,2,1$ indicates the number of image blocks at each scale, and $I_{4,1}$ denotes the final defogged output image. Through the aforementioned multi-scale process, richer spatial guided features $F_i^n$ can be obtained, which can be expressed as Equation (2):

$$F_{i,j}^n=Ne{t}^n(I_{i,j}^n,F_{i,j}^{n-1};{\theta }^{Pn})$$

(2)

where $Ne{t}^n$ denotes the non-uniform dehazing algorithm proposed in this paper, and ${\theta }^{Pn}$ represents the training parameters. Since the algorithm is recurrent, $F_{i,j}^n$ serves as the intermediate state features to enable cross-scale flow from $n-1$ to $n$. Each encoder branch consists of 3 convolutions, with a Mix structure module following each convolutional layer. Furthermore, in each decoder branch, a residual module is placed prior to each deconvolutional layer. The blue arrow denotes the intermediate feature map $F_{i,j}^n$, which is obtained by performing dual upsampling on $F_{i,j}^{n-1}$ and the input original image.

The workflow of the algorithm proposed in this paper is illustrated in Figure 1b. First, the input hazy image is divided into non-overlapping blocks according to the aforementioned 4 scales, and then each block under different scales is separately fed into the asymmetric encoder–decoder at the corresponding level. Blocks and scales interact through cross-scale feature flow—after bilinear upsampling, the block features of the previous scale serve as the initialization features of the corresponding block in the next scale, ensuring the coherence of block features across different scales. Specifically, the encoder embeds a Mix structure module to construct the dual-branch attention mechanism, and at the same time, the fog density estimation branch calculates the haze concentration based on the dark channel mean to dynamically adjust the weight allocation between the low-frequency global perception branch and the high-frequency local enhancement branch in the Mix module; the decoder adopts DSC to construct lightweight residual modules for feature reconstruction. Then, the inter-block feature fusion module performs weighted fusion processing on the reconstructed features of each block at layers B₁ (1/2) and B₂ (1/4), eliminating inter-block artifacts caused by multi-block division. Finally, the fused features are output as haze-free images.

2.1. Asymmetric Encoders-Decoders

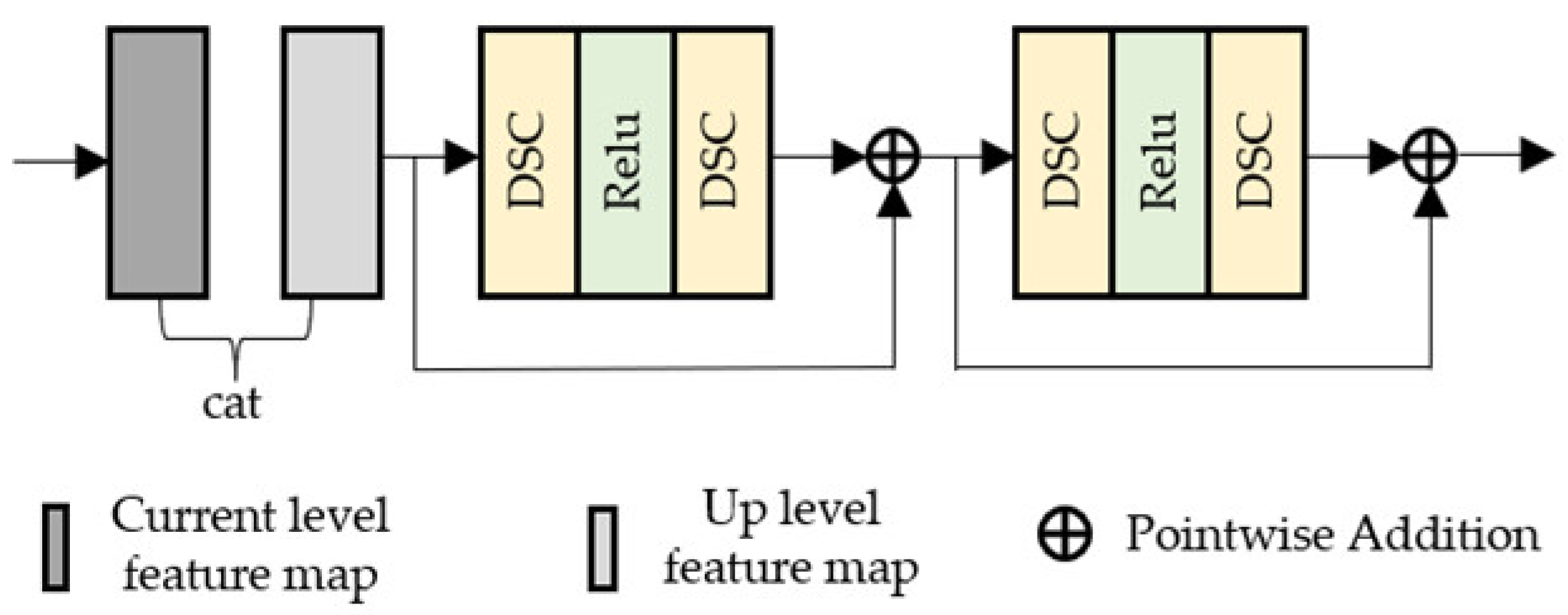
Current mainstream lightweight networks, such as MobileNet and EfficientNet, are designed to optimize end-to-end computational efficiency. They adopt strategies like depthwise separable convolution to reduce the parameter count and computational complexity; however, they focus on balanced efficiency improvement across all modules, leading to inadequate performance in complex scenarios. To address the problems of increased computational complexity and blurred edge feature regions in dehazing algorithms, this paper employs an asymmetric encoder–decoder structure.

Within the architecture proposed in this paper, asymmetry is primarily achieved through the differentiation of modules in the encoder and decoder branches. The decoder module is composed of 2 deconvolutional layers, 3 lightweight residual modules, and 1 convolutional layer. Each of these 3 lightweight residual modules contains two DSC, with a ReLU activation function placed in the middle, as illustrated in Figure 2. The encoder module consists of 3 convolutional layers and 3 hybrid modules. Specifically, each module within the residual modules comprises two standard convolutions, with a ReLU activation function inserted in between, as illustrated in Figure 3.

In contrast, standard convolutions are employed in the hybrid structure modules of the encoder branches to avoid the inter-channel information disconnection caused by DSC. Additionally, an attention mechanism guided by high-frequency feature maps is introduced into these branches to ensure the complete extraction of density differences and edge details in non-uniform hazy regions. Meanwhile, the decoder adopts DSC to reconstruct the features extracted by the encoder into haze-free images, which can reduce computational complexity while maintaining the feature combination capability.

To eliminate the inter-block edge artifacts accumulated across multiple levels, such as the inter-block discontinuity of transmission lines, an inter-block feature fusion module is introduced at the output of the decoder. Input images of different scales are processed through a pair of encoders-decoders, denoted as $E_i$ and $D_i$ ($i=1,2,3,4$), yielding the global feature $F_i$, as formulated in Equation (3):

$$F_i=D_i(E_i(I_{i,j}),F_{i-1})$$

(3)

where $F_{i-1}$ denotes the intermediate feature of the previous level, which enables cross-scale feature flow and avoids inter-block discontinuity. The inter-block weights are calculated via cosine similarity to achieve smooth fusion, as shown in Equation (4):

$$\begin{array}{l}{F}_i={\displaystyle \sum _{j=1}^{N_i}{\alpha }_{i,j}\cdot D_i(E_i(I_{i,j}))}\\ {\alpha }_{i,j}={\displaystyle \frac{\exp (Sim(D_i(E_i(I_{i,j})),D_i(E_i(I_{i,k}))))}{{\displaystyle {\sum }_{k=1}^{N_i}\exp (Sim(D_i(E_i(I_{i,j})),D_i(E_i(I_{i,k}))))}}}\end{array}$$

(4)

Scale $B_4$ requires no fusion and directly outputs the global feature map for generating the final haze-free image $J_{4,1}$, as shown in Equation (5):

$$J_{4,1}=F_4=D_4(E_4(I_{4,1}),F_3)$$

(5)

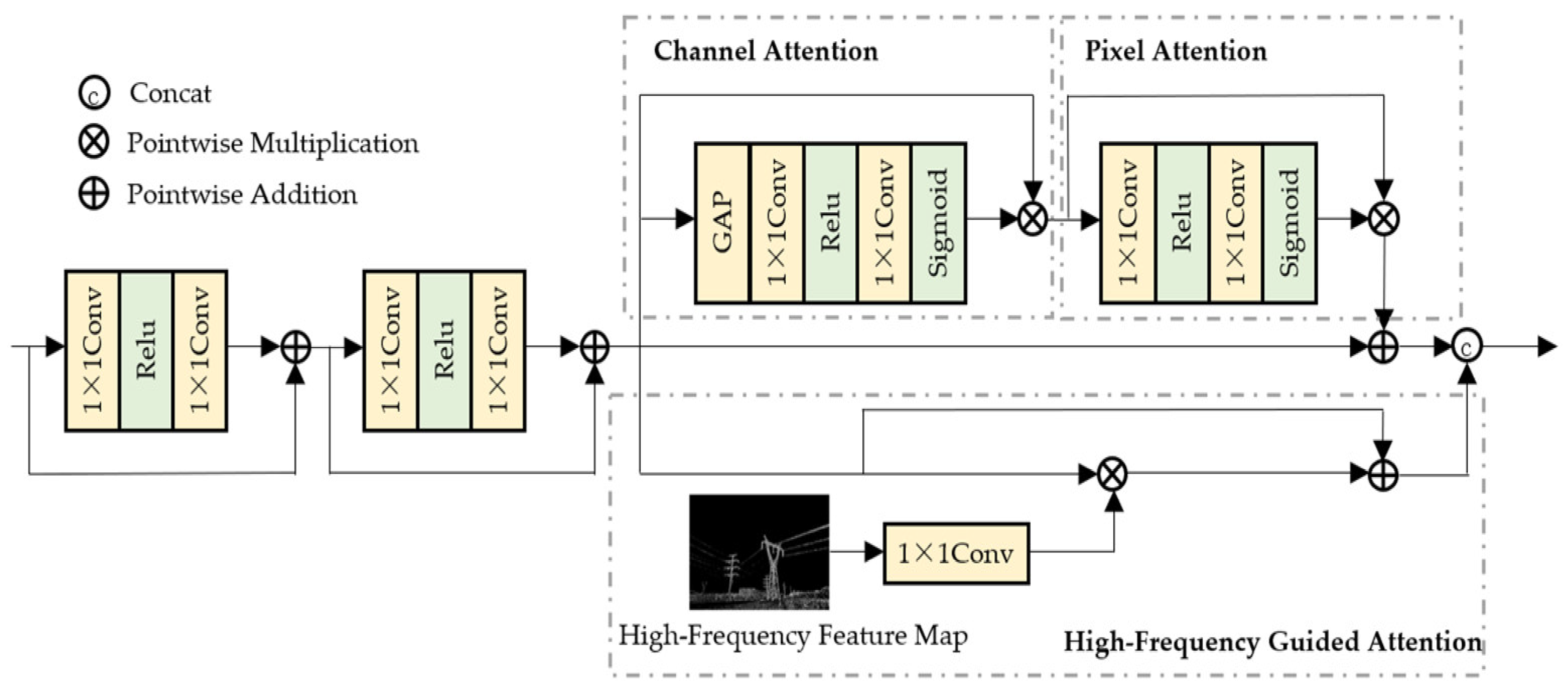
2.2. Mix Structure Module

The Mix structure module is embedded in the encoder and comprises a residual module and an attention module guided by high-frequency feature maps. The overall structure of the module is illustrated in Figure 3.

Existing high-frequency guided methods mostly suffer from problems such as a single branch, poor noise resistance, or low adaptability. To address these issues, this paper achieves differentiated advantages through a dual-branch collaboration and noise-resistant optimization approach. The core structure of the dual-branch attention collaboration module consists of two complementary branches: a low-frequency global perception branch and a high-frequency local enhancement branch. A frequency domain decomposition strategy is adopted to realize the collaborative optimization of global context modeling and local detail preservation, thereby improving the network’s adaptability to the non-uniform distribution of haze. This hierarchical attention mechanism can dynamically adjust the feature weights of different channels and spatial positions, effectively overcoming the limitations of traditional methods.

The low-frequency global perception branch cascades Channel Attention (CA) and Pixel Attention (PA) to model cross-channel dependencies and spatial local features, respectively. Feature extraction is performed on the input image via a residual module to obtain a shallow feature map, which is then fed into the attention module guided by high-frequency features.

CA primarily focuses on the importance of different channels in the feature map, enabling effective extraction of global information and adjustment of the channel dimension of features. It aggregates spatial information through a global average pooling operation and then employs convolutional layers to learn the weight of each channel, assisting the model in enhancing the feature channels most useful for the current task. Assuming the feature map is $y$, CA can be expressed as Equation (6):

$$y_{ca}=y\otimes Sigmoid(PWConv(Relu(PWConv(Gap(y)))))$$

(6)

where $PWConv$ denotes pointwise convolution; $Sigmoid$ represents the assignment of different weights to each channel; and $GAP$ stands for global average pooling.

PA, by contrast, focuses more on the importance of each pixel in the feature map, enhancing the representational capability of the feature map and the detailed features of the image. The pixel attention module enables the model to better focus on high-frequency regions in the image, assigning higher weights to regions with significant variations in fog density, thereby improving the dehazing effect. Pixel attention can be expressed as Equation (7):

$$y_{pa}=y_{ca}\otimes Sigmoid(PWConv(Relu(PWConv(y_{ca}))))$$

(7)

where $y_{pa}$ denotes the feature map after pixel attention.

In the high-frequency local enhancement branch, the given hazy image is denoised using a Gaussian function to pre-smooth the image. Subsequently, the Laplacian operator is employed to separate the texture edge information in the image, and information interaction is performed through convolution operations to obtain high-frequency features of the image. To compensate for the directional limitation of a single operator, multi-directional edge features—including Sobel-X (horizontal), Sobel-Y (vertical), and Prewitt (diagonal)—are fused to fully capture the edges of horizontal conductors and vertical towers of transmission lines. Finally, the two types of high-frequency edge features are fused and used as weight information to guide the model in learning the edge information of the image from the image features. Detailed explanations of each operator are provided in Appendix A.

To address the issue of attention mechanism failure caused by high-frequency signal attenuation in dense haze regions, an additional fog density estimation branch is introduced, which adjusts the weights of the dual branches based on an adaptive fog density-guided mechanism. Firstly, the fog density $D$ is estimated via the dark channel mean value, as shown in Equation (8):

$$D={\min }_{c\in \{R,G,B\}}{\min }_{x,y\in \mathsf{\Omega }}{\displaystyle \frac{1}{\left|\mathsf{\Omega }\right|}}{\displaystyle {\sum }_{(x,y)\in \mathsf{\Omega }}{I}_c(x,y)}$$

(8)

where $c$ denotes the RGB channels; $\mathsf{\Omega }$ represents the local window of the image; $I_c(x,y)$ stands for the pixel value of channel $c$ at coordinates $(x,y)$.

Subsequently, the weights of the dual branches are adjusted according to $D$: global guidance is enhanced in dense haze, while local guidance is strengthened in light haze, as shown in Equation (9):

$$Y=D(y\oplus y_{pa})+(1-D)(y\oplus (y_{HF}\otimes y))$$

(9)

where $Y$ denotes the finally output feature map; $y_{HF}$ is the fused multi-directional high-frequency edge feature map.

This feature attention mechanism adopts a differentiated weight allocation strategy to dynamically adjust inter-channel dependencies and spatial features, assigning adaptive attention weights to different channels and pixels. Furthermore, high-frequency features, which provide abundant multi-scale edge prior information, are introduced as attention modulation factors to guide the network in strengthening edge regions during feature learning. This mechanism allocates more weights to image edge regions, thereby improving the dehazing effect in dense haze regions.

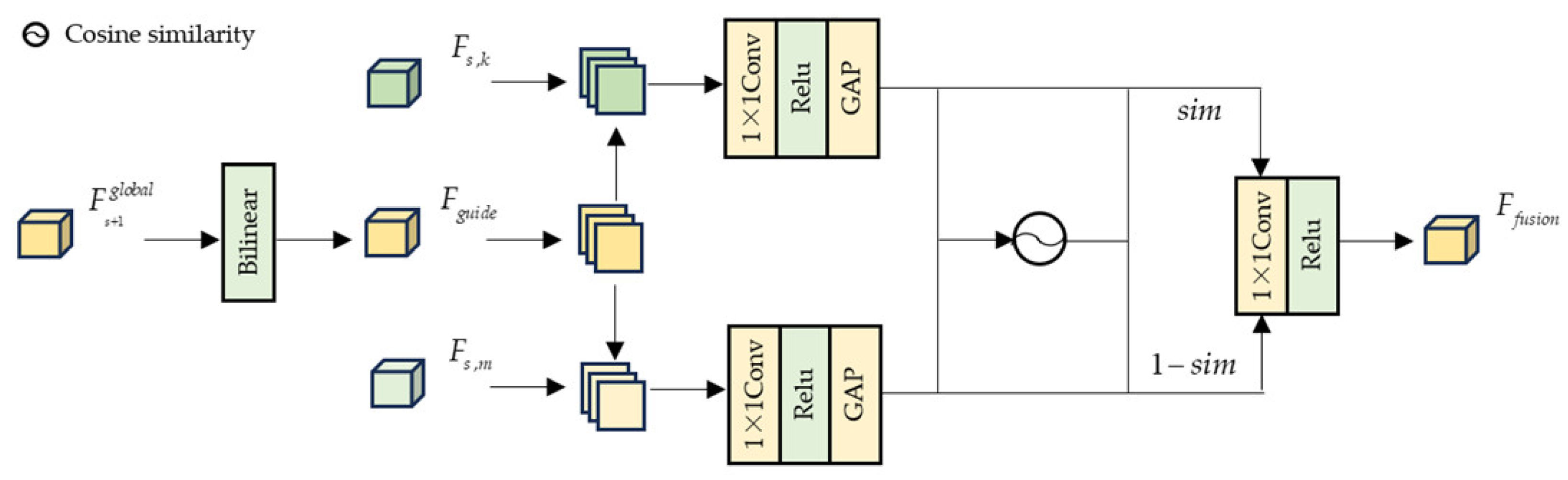
2.3. Block-Wise Feature Fusion Module

Although the block-wise features output by the decoder can effectively preserve local image details, the non-overlapping block processing method is prone to causing the problem of inter-block edge discontinuity. To address this issue, this paper proposes an inter-block attention fusion module at the output end of the decoder, as illustrated in Figure 4. Through the core strategies of cross-scale feature alignment, cosine similarity-based edge continuity quantification, and region-wise weighted fusion, this module effectively resolves the inter-block edge discontinuity problem.

Feature alignment is guided by the global feature $F_{s+1}^{global}$ after fusion at the previous scale, which calibrates the spatial deviation of adjacent blocks at the current scale and avoids edge misalignment caused by block cropping. $F_{s+1}^{global}$ is enlarged to the resolution of the current scale via bilinear upsampling to obtain the guiding feature map $F_{guide}$, as shown in Equation (10):

$$F_{guide}=Upsample(F_{s+1},2)$$

(10)

For adjacent blocks at the current scale, with $F_{guide}$ as the reference, extract the right pixel region of the edge region $F_{s,k}$ of one adjacent block and the left pixel region of the edge region $F_{s,m}$ of the other adjacent block. Then, find the regions with the maximum grayscale correlation to them in $F_{guide}$, respectively, and calculate the spatial offsets $\Delta x$ and $\Delta y$. We define the edge offset threshold $\theta$. If condition $\Delta x>\theta$ or $\Delta y>\theta$ is satisfied, spatial translation calibration is performed on $F_{s,m}$ to ensure edge alignment.

Perform global average pooling only on the calibrated edge regions to compress the spatial dimensions and obtain edge feature vectors, as shown in Equation (11):

$$v_{s,k}(c)={\displaystyle \frac{1}{H\times W}}{\displaystyle \sum _x{\displaystyle \sum _y{F}_{s,k}(x,y,c)}}$$

(11)

Calculate the cosine similarity of the feature vectors of adjacent blocks to quantify edge continuity. If the edges of the two blocks are continuous, sim approaches 1; if the edges are discontinuous, sim approaches below 0.3, as shown in Equation (12):

$$sim(F_{s,k},F_{s,m})={\displaystyle \frac{v_{s,k}\cdot v_{s,m}}{‖v_{s,k}‖\cdot ‖v_{s,m}‖}}$$

(12)

Weighted fusion only weights the edge connection region $R$, while retaining the original features in non-overlapping regions to avoid distortion in non-edge regions. For each pixel $(x,y)$ in the connection region, weighting is performed according to similarity to highlight continuous edge features; original features are retained in non-connection regions, as shown in Equation (13):

$$F_i(x,y)=\left\{\begin{array}{l}sim\cdot F_{s,k}(x,y)+(1-sim)\cdot F_{s,m}(x,y),(x,y)\in R\\ F_{s,k}(x,y),(x,y)\notin R\end{array}\right.$$

(13)

2.4. Loss Function

The loss function serves as a performance evaluation metric that dynamically quantifies the prediction deviation of the model during training. Through gradient-based optimization strategies, it continuously drives parameter updates, guiding the model toward convergence to an optimal or sub-optimal solution. This process enhances the model’s representational learning capability and task-specific adaptability.

This paper adopts a multi-scale progressive optimization approach, where, within a coarse-to-fine hierarchical structure, the output images at each scale are constrained to restore the true haze-free scene. Accordingly, the training loss is defined as the Mean Square Error (MSE) between the dehazed result at each scale and the corresponding ground-truth image. This ensures consistent dehazing performance and detail fidelity across different resolution levels, as formalized in Equation (14):

$$L_{MSE}={\displaystyle \sum _{n=1}^3\frac{{\beta }_n}{C_n{H}_n{W}_n}}{‖J_n-G_n‖}_2^2$$

(14)

where ${‖\cdot ‖}_2$ denotes the $L_2-norm$, $J_n$ and $G_n$ represent the dehazed image and the ground-truth image at the $n-th$ scale, respectively, ${\beta }_n$ indicates the weight assigned to each scale, and $C_n$, $H_n$, $W_n$ specify the dimensions of the multi-scale images.

Furthermore, to mitigate stripe artifacts in the dehazed images, a Laplacian loss is introduced, as defined in Equation (15):

$$L_{Laplacian}={\displaystyle \frac{1}{H_n{W}_n}}{\displaystyle \sum _{x,y}{‖{\nabla }^2{J}_n\left(x,y\right)-{\nabla }^2{G}_n\left(x,y\right)‖}_2^2}$$

(15)

where $(x,y)$ denotes the pixel coordinates in the image, and ${\nabla }^2$ represents the Laplacian operator.

Furthermore, to constrain the edge consistency after inter-block fusion, an additional edge consistency loss is introduced to ensure the matching degree between the edges of the dehazed image and the real edges, as defined in Equation (16):

$$L_{edge}={\displaystyle \frac{1}{H_n{W}_n}}{\displaystyle \sum _{x,y}{\left|J_n(x,y)-G_n(x,y)\right|}^2}$$

(16)

Therefore, the total loss is defined as follows in Equation (17):

$$L={\lambda }_1{L}_{MSE}+{\lambda }_2{L}_{Laplacian}+{\lambda }_3{L}_{edge}$$

(17)

where ${\lambda }_1=1,{\lambda }_2=0.3,{\lambda }_3=0.2$ is used to control the influence of the Laplacian loss and the gradient consistency loss.

3. Analyze the Performance and Runtime Consumption of the Algorithm

3.1. Processing of Detection Algorithm Datasets

The experimental validation was conducted on multiple datasets: the NH-HAZE20 [24] and NH-HAZE21 [25] datasets for non-uniform haze removal, the O-HAZE [26] dataset for homogeneous haze removal, the NTIRE2021 test set with NH-Haze20 as additional evaluation data, and a self-built transmission line haze dataset. The NH-HAZE20 dataset contains 55 hazy-clear image pairs with a resolution of 1600 × 1200, featuring diverse outdoor scenes with non-uniform haze distribution. The NH-HAZE21 dataset includes 25 hazy-clear image pairs. The O-HAZE dataset, originally proposed for the NTIRE-2018 dehazing challenge, consists of 45 hazy-clear image pairs. The self-built transmission line haze dataset comprises 54 hazy-clear image pairs captured in real-world transmission line scenarios. To address the issue of limited data volume in the dataset, this experiment implements sample expansion through data augmentation strategies to ensure the model training effect. The specific experimental training settings of the proposed algorithm are shown in

Table 1. Training Details of the Proposed Algorithm.

Training Parameter	Specification
Hardware	GPU: NVIDIA TITAN Xp CPU: Intel(R) Xeon(R) CPU E5-2680 v4 @ 2.40 GHz
Framework	PyTorch 1.11.0
Number of Epochs	200
Optimizer	Adam (β1 = 0.9, β2 = 0.999, weight decay = 1 × 10−5)
Initial Learning Rate	0.0001
Batch Size	4
Data Augmentation	1. Random horizontal/vertical flipping 2. Random cropping 3. Brightness adjustment 4. Contrast adjustment
Loss Weights	λ1 (MSE loss weight) = 1.0; λ2 (Laplacian loss weight) = 0.3; λ3 (edge consistency loss weight) = 0.2

.

In accordance with the evaluation standards of the NTIRE Non-Homogeneous Image Dehazing Challenge, this experiment adopted three metrics to comprehensively evaluate the algorithm’s performance. The peak signal-to-noise ratio (PSNR) was used to quantify the reconstruction quality of images affected by lossy compression, while the structural similarity index (SSIM) assessed the structural similarity between image pairs. Additionally, runtime was measured to evaluate the computational efficiency of the algorithm.

3.2. Performance and Time Consumption Analysis

To evaluate the performance of the proposed algorithm, this study selected four representative and advanced dehazing algorithms for comparison: DCP [27], AOD-Net [28], GridDehaze [29], DMPHN [30], MSBDN [31] and Dehamer [32]. To ensure the reliability of the comparative results, all compared methods were trained and tested under a unified experimental environment, including consistent hardware configurations, training data, and test sets, thereby eliminating the influence of environmental factors on the performance evaluation.

For the objective analysis of the detection algorithm’s performance and time consumption, the results are shown in

Table 2. Quantitative comparison with different algorithms across multiple datasets.

Method	NH-HAZE20			NH-HAZE21
	PSNR	SSIM	Runtime	PSNR	SSIM	Runtime
DCP	11.63	0.5786	0.518	11.60	0.6159	0.518
AOD-Net	15.12	0.6481	0.725	16.74	0.6971	0.763
GridDehze	17.87	0.6947	1.837	19.27	0.7456	1.560
DMPHN	19.74	0.7684	0.031	21.95	0.8183	0.030
MSBDN	20.13	0.7886	1.201	22.72	0.8255	1.255
Dehamer	18.62	0.7056	0.978	21.18	0.7999	0.944
The proposed method	20.93	0.8048	0.025	23.80	0.8478	0.024
Method	O-HAZE			Self-Built Transmission Line Haze Dataset
	PSNR	SSIM	Runtime	PSNR	SSIM	Runtime
DCP	15.37	0.6569	0.518	18.94	0.7511	0.518
AOD-Net	17.86	0.6945	0.765	20.41	0.7890	0.770
GridDehze	19.96	0.7441	1.357	21.83	0.8094	1.360
DMPHN	19.85	0.7657	0.030	21.06	0.7972	0.031
MSBDN	19.40	0.7698	1.403	20.68	0.7740	1.350
Dehamer	20.87	0.7174	1.179	22.90	0.8100	1.036
The proposed method	21.63	0.7856	0.023	25.30	0.9039	0.023

. The experimental results on NH-HAZE20, NH-HAZE21, O-HAZE, and the self-built foggy transmission line inspection dataset indicate that the proposed algorithm significantly outperforms the comparative algorithms in terms of image quality evaluation metrics, namely PSNR and SSIM. Meanwhile, to verify the computational efficiency of the proposed algorithm, the average processing time per image was calculated. Experiments show that the proposed algorithm reduces the processing time by approximately 19% compared with the DMPHN algorithm. The advantages exhibited by the proposed algorithm stem from its in-depth optimized design tailored to the particularities of dense haze regions and the comprehensiveness of its feature modeling for complex foggy scenarios. Specifically, in the dual-branch attention mechanism guided by high-frequency information, an additional fog density estimation branch is introduced. This branch quantifies the haze concentration of each pixel via a formula, dynamically adjusts the weights of the dual branches, and thereby avoids the high-frequency feature failure problem that is prone to occur in dense haze regions. Furthermore, through the cross-scale feature flow mechanism combined with the inter-block feature fusion module at the output end, the problems of long-distance feature separation and color inconsistency caused by local processing are effectively avoided.

For the subjective performance analysis of the detection algorithms, Figure 5, Figure 6, Figure 7 and Figure 8 present the visual comparisons of different algorithms on various datasets, respectively. Experimental analysis indicates that the traditional DCP algorithm has obvious limitations in dehazing performance, exhibiting insufficient brightness, severe color distortion, and detail loss across different datasets. Mainstream deep learning-based image dehazing methods, namely AOD-Net and GridDehaze, suffer from more severe haze residue issues on non-uniform haze datasets, as shown in Figure 5 and Figure 6. On the uniform haze dataset in Figure 7, they have less haze residue but generate dehazed images with an overall dark color. Moreover, while improving the dehazing effect, GridDehaze distorts the original colors of the scene, leading to significant color deviation in the dehazed images—for instance, the unnatural colors in the sky area in Figure 7 and the grass area in Figure 6. The DMPHN algorithm achieves remarkable improvements in color recovery and dense haze area restoration through multi-scale feature fusion based on a multi-block hierarchical architecture. However, it has more prominent problems of local artifacts in Figure 8 and color irregularities in the sky area in Figure 7. MSBDN realizes effective cross-scale feature fusion via dense connections and feature feedback, which considerably enhances dehazing performance, with results close to real images. Nevertheless, it exhibits color distortion in large sky areas in Figure 7 and Figure 8, as well as black artifacts in dense haze regions on the ground in Figure 6. Dehamer dynamically fuses the global features of Transformer and the local features of CNN, also improving dehazing performance, but it still produces a large number of black artifacts in the sky area in Figure 7 and obvious edge blurring in Figure 5.

In contrast, the proposed algorithm demonstrates excellent color restoration capability and edge preservation performance on dehazing datasets. Leveraging the high-frequency guided dual-branch attention mechanism in the encoder, the low-frequency branch models the global color distribution, while the high-frequency branch captures image edge textures, effectively avoiding color distortion issues—for example, preserving the natural color transition in sky areas. Meanwhile, the decoder adopts a lightweight residual module constructed with depthwise separable convolution, which reduces computational redundancy while ensuring feature expression capability. Coordinated with the inter-block feature fusion module at the output end, it avoids artifacts caused by multi-block processing and further enhances edge information. However, when handling certain extreme dense haze scenarios—such as the dense haze area around the wooden stake in Figure 5—the algorithm still has the shortcoming of a small amount of residual haze, limited by the objective condition of severe attenuation of high-frequency signals. Overall, its dehazing performance in most practical scenarios, such as non-uniform haze and uniform haze, significantly outperforms that of comparative methods. It better enables the complete restoration of target contour boundaries, providing image data support for subsequent downstream tasks such as fault detection.

3.3. Ablation Experiments of Algorithms

To validate the necessity of each module in the proposed algorithm, ablation studies were conducted with the following four experimental configurations:

• Model 1: A model using standard residual modules in both the encoder and decoder;
• Model 2: Based on Model 1, an attention module is incorporated into the encoder;
• Model 3: Based on Model 2, an inter-block feature fusion module is incorporated into the decoder part;
• Model 4: To further improve Model 3, an asymmetric network model is proposed, where the decoder is replaced with lightweight residual modules.

The same NH-HAZE20/21 and O-HAZE training datasets are used in this paper to train each algorithm, and performance evaluation is conducted, with the experimental results shown in

Table 3. Quantitative Comparison of Ablation Studies Across Different Datasets.

Method	NH-HAZE20			NH-HAZE21			O-HAZE			OVERHEAD
	PSNR	SSIM	Runtime	PSNR	SSIM	Runtime	PSNR	SSIM	Runtime	Params(M)	Flops(G)
Model 1	19.52	0.7591	0.032	21.73	0.8076	0.030	19.68	0.7582	0.030	12.8	1.85
Model 2	20.85	0.8026	0.035	22.18	0.8260	0.036	21.03	0.7854	0.034	13.5	1.92
Model 3	21.05	0.8102	0.039	23.69	0.8521	0.041	21.50	0.7871	0.038	14.2	2.01
Model 4	20.93	0.8048	0.025	23.80	0.8478	0.024	21.63	0.7856	0.023	11.5	1.70

. The results indicate that Model 1 has poor dehazing performance. With the assistance of the multi-directional edge feature-guided attention mechanism, Model 2 provides more natural results in dense haze regions. However, due to the block-wise strategy of the overall structure, the dehazed images suffer from inter-block artifacts. Model 3’s inter-block fusion effectively restores the overall texture of the image and avoids inter-block artifacts; nevertheless, its processing speed slows down due to improved performance and increased parameters. In contrast, the complete model proposed by us—Model 4—achieves a better balance among performance, complexity, and speed. This verifies that the proposed lightweight design effectively reduces redundant parameters and computational costs while shortening the algorithm’s running time.

4. Conclusions

To address the problem of edge blurring in mountainous transmission line inspection images caused by non-uniform haze, as well as the drawback of low operational efficiency in traditional dehazing algorithms due to high network complexity, this paper proposes a multi-block hierarchical dehazing network based on high-frequency guided feature fusion. The network adopts an asymmetric encoder–decoder with residual channels as its core framework: at the encoder end, a Mix structure module is embedded to construct a dual-branch attention mechanism—the low-frequency branch cascades channel attention and pixel attention to model global features, while the high-frequency branch fuses Laplacian, Sobel-X/Y, and Prewitt operators to extract multi-directional edge features, adapting to the structural characteristics of transmission lines; an additional fog density estimation branch based on the dark channel mean dynamically adjusts the weights of the dual branches, solving the problem of attention failure in dense haze regions. At the decoder end, lightweight residual modules constructed with depthwise separable convolution reduce computational overhead while maintaining feature expression capability; the inter-block feature fusion module at the output stage eliminates cross-block artifacts through cross-scale feature alignment, cosine similarity-based edge continuity quantification, and region-wise weighted fusion. Experimental results demonstrate that the proposed algorithm outperforms other comparative algorithms on various datasets.

Despite these advantages, the algorithm still has limitations in extremely dense haze scenarios: when the haze concentration is excessively high (e.g., the area around the wooden stake in Figure 5), the restored images will have a small amount of residual haze and slightly blurred edges. This is because high-frequency signals are severely attenuated in extremely dense haze environments, leading to insufficient feature extraction by the high-frequency branch in the Mix module. Two improvement directions will be adopted in the future: (1) Fuse infrared and visible images to supplement high-frequency information. (2) Design an adaptive weight adjustment strategy based on fog density and add a residual connection to the high-frequency branch.

In addition, the proposed algorithm can be migrated to other vision tasks requiring visibility enhancement. In the field of autonomous driving, by adjusting edge extraction operators to focus on road markings, vehicles, and pedestrians, the framework can be adapted to visibility enhancement tasks under adverse weather conditions; in the field of infrared image restoration, the high-frequency branch can be modified to extract thermal edge features, improving the clarity of thermal imaging targets under low-visibility conditions. This generalization potential is not limited to the scenario of transmission line inspection but also provides insights into visibility enhancement in various complex environments.