Coprime Distributed Array for Super-Resolution DOA Estimation
Abstract
1. Introduction
- Array Geometry: We introduce a systematic geometry for distributing prime subarrays to form a large and sparse aperture. This structure is designed to maximize the array aperture, thereby simultaneously improving achievable depth of field and resolution. This new distributed structure, which elevates the concept of coprime arrays from the sensor level to the subarray level, represents a paradigm shift in array design.
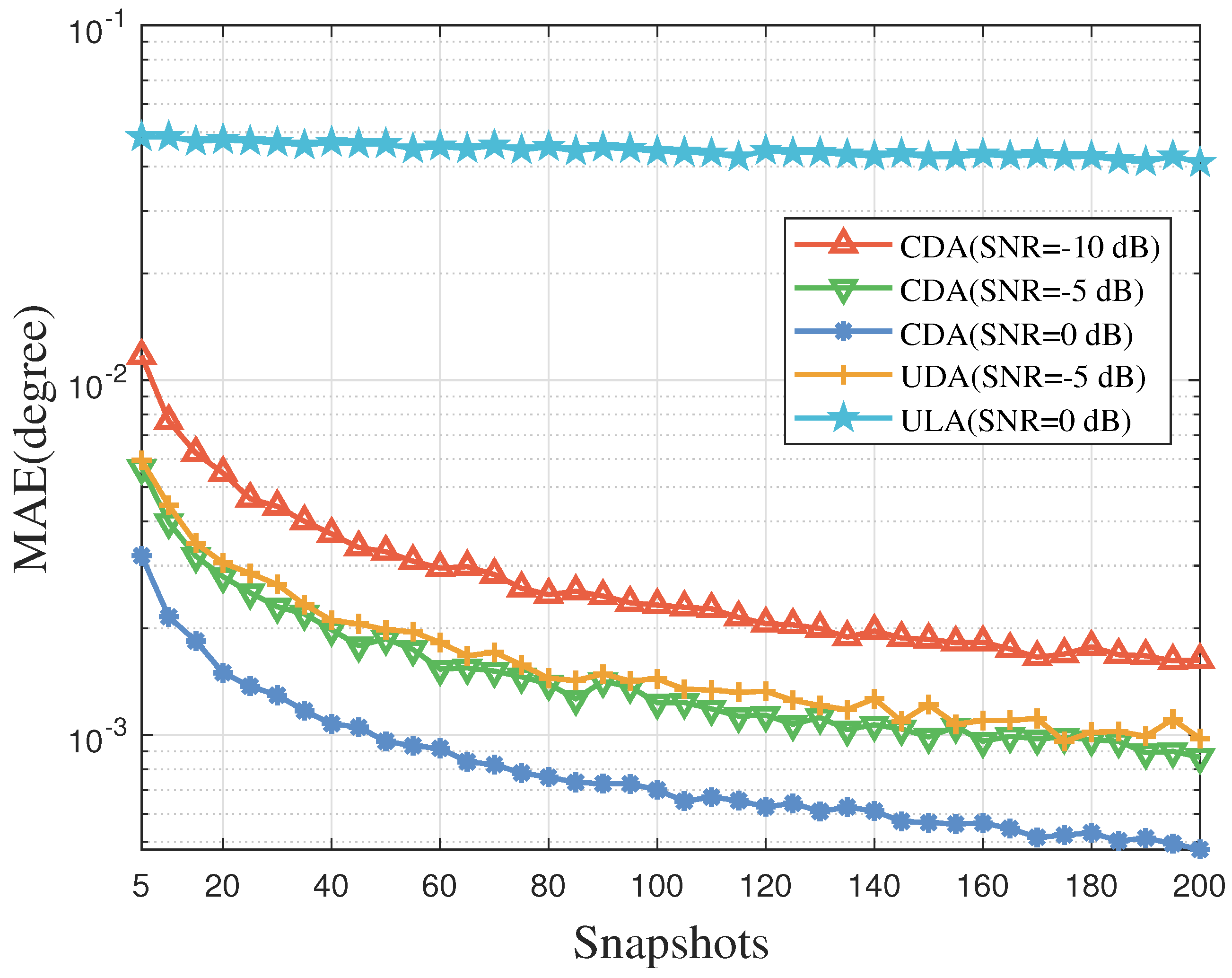
- Theoretical and Numerical Analysis: Comprehensive simulations quantify the significant advantages of the proposed structure in estimation accuracy and resolution. We designed systematic experiments comparing the CDA with benchmark structures, such as the traditional ULA and uniformly distributed array (UDA). The results clearly demonstrate that, at the same hardware cost, the proposed structure achieves significant improvements in key metrics including estimation error and angular resolution.
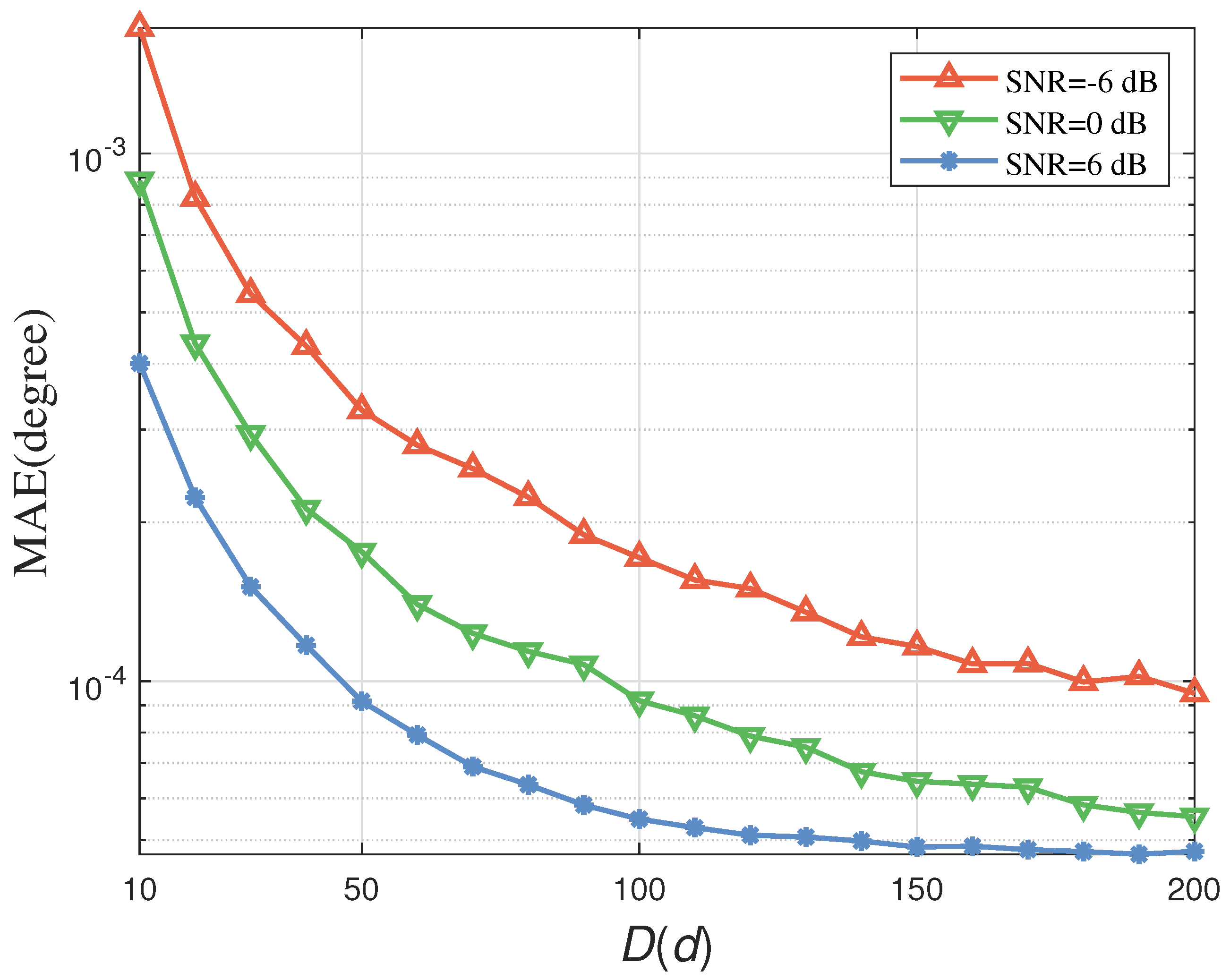
- Performance–Parameter Relationship: We clearly delineate the relationship between performance and key parameters (e.g., baseline length and number of snapshots), providing valuable design guidelines for practical engineering applications.
2. Signal Model
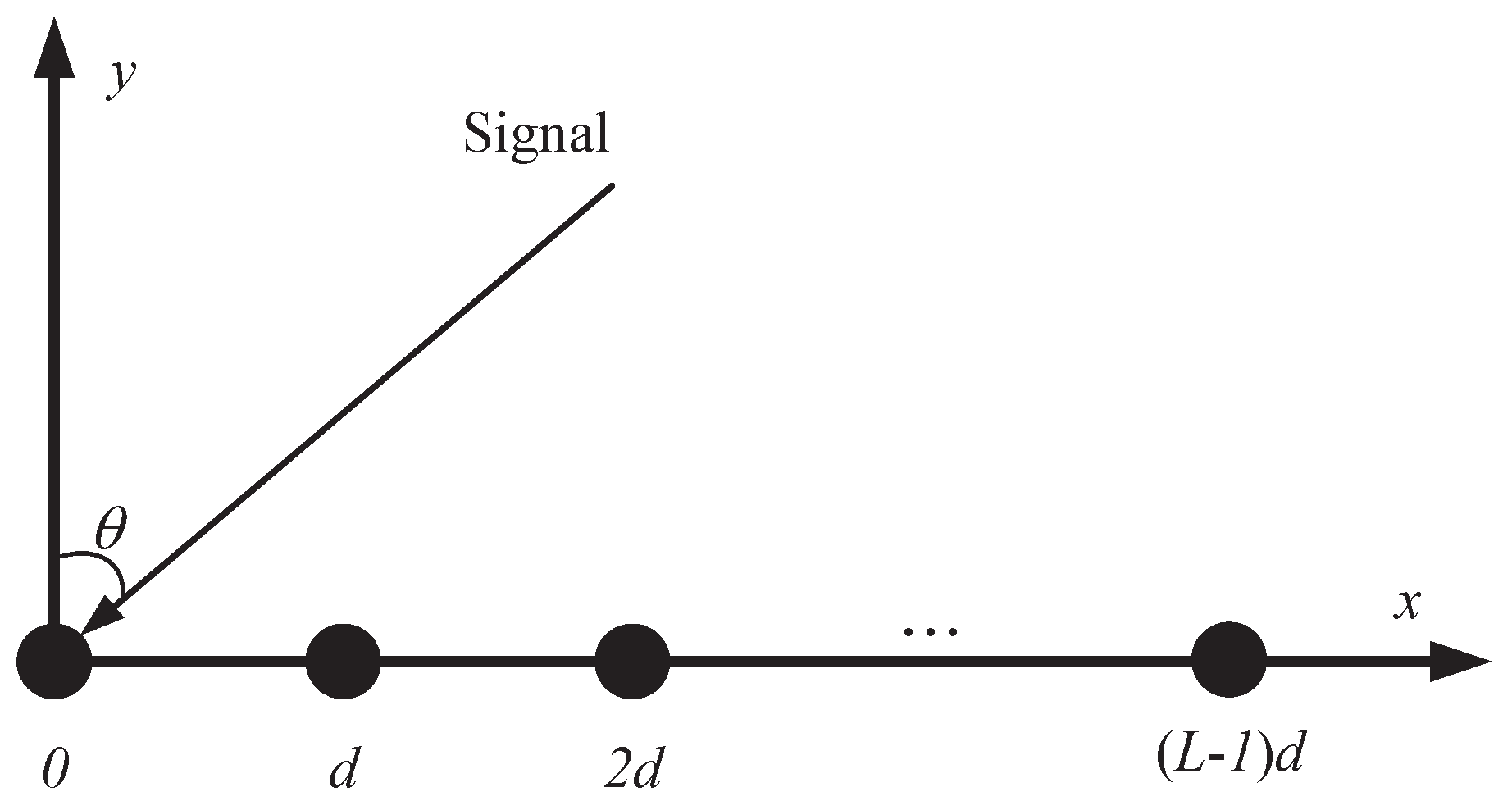
2.1. ULA Model
- (1)
- The signal received by the antenna receiving array is a far-field plane wave signal.
- (2)
- The various signal sources are uncorrelated, and the incident signal is a narrowband signal; that is, the carrier frequency of the signal is greater than the bandwidth of the signal.
- (3)
- The number of signal sources of the incident signal is known.
- (4)
- The array elements in the antenna array are isotropic; that is, the antenna gain does not change with the direction of the incident wave. The noise received by each array element is Gaussian white noise, and the noise is uncorrelated with the signal.
2.2. DOA Estimation Algorithm
3. The Distributed Array and the Proposed Architecture
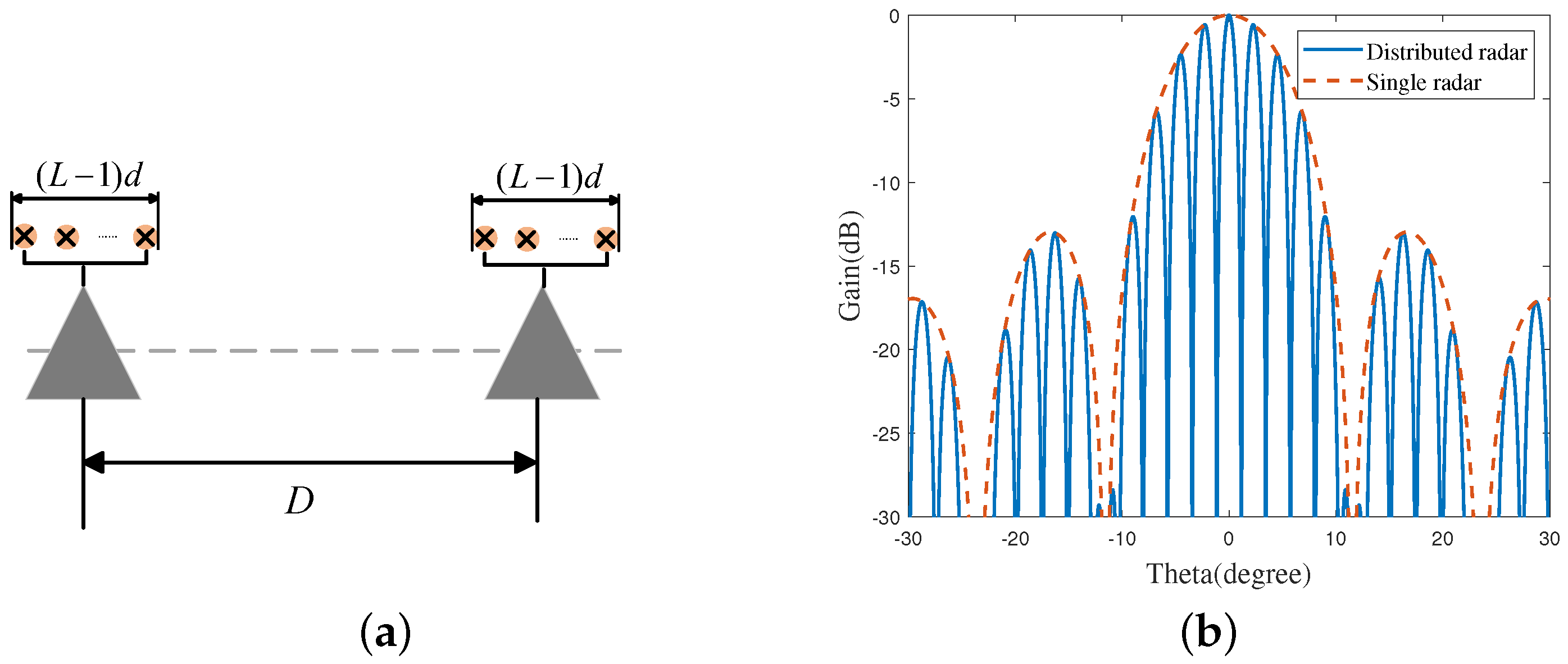
3.1. Principles of Distributed Arrays
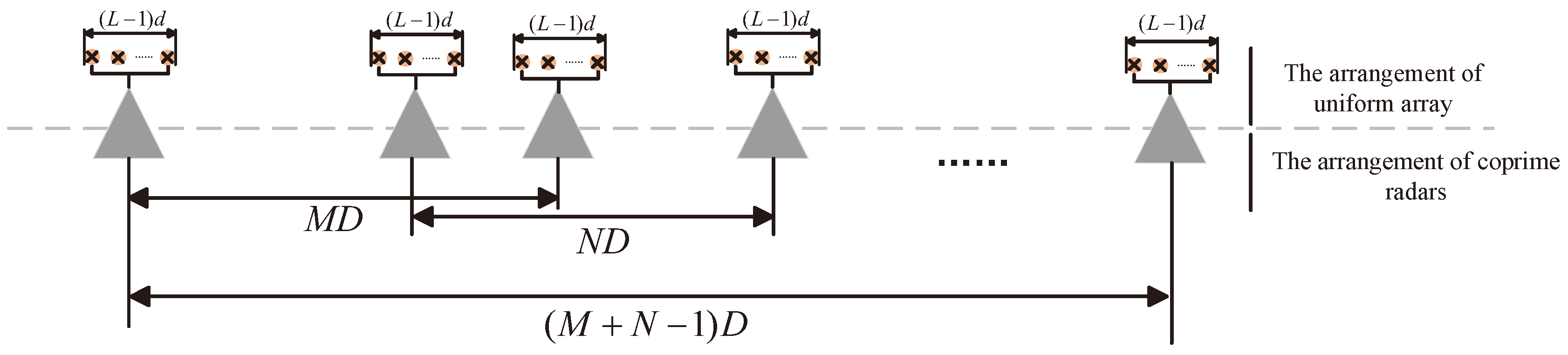
3.2. The Proposed Architecture
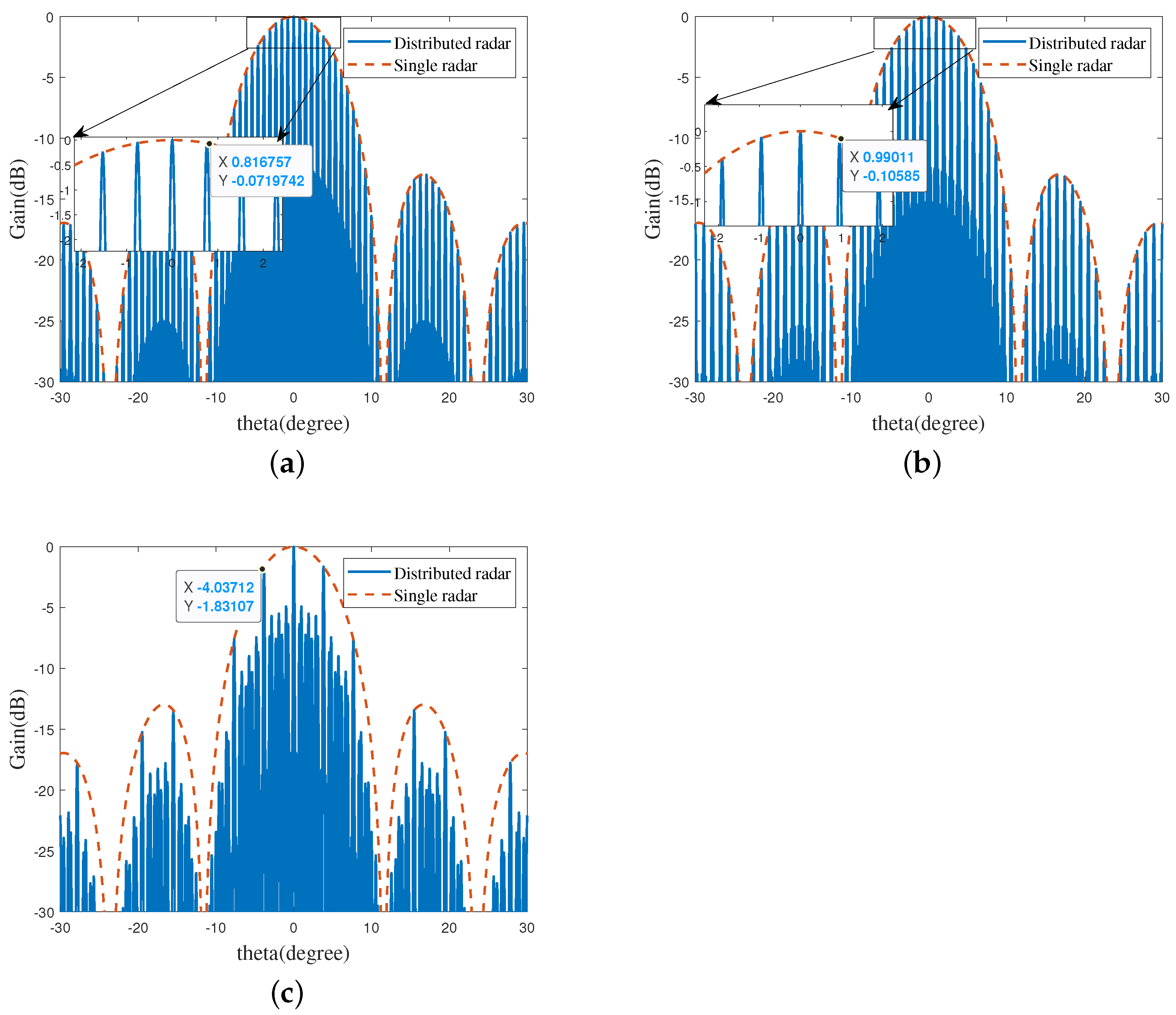
3.3. Discussion on Ambiguity and Grating Lobes
4. Simulations
4.1. Estimation Results of the Proposed Structure
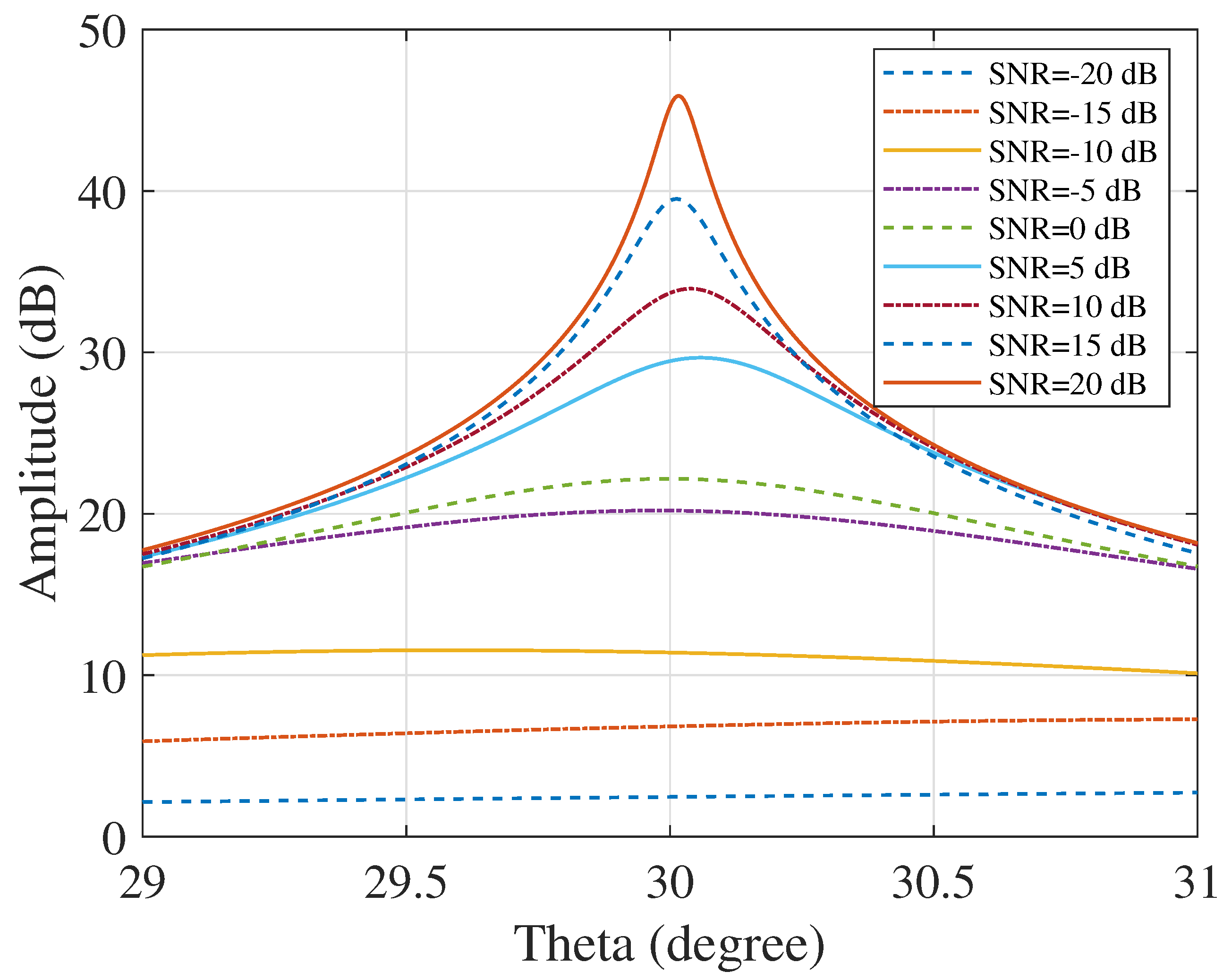
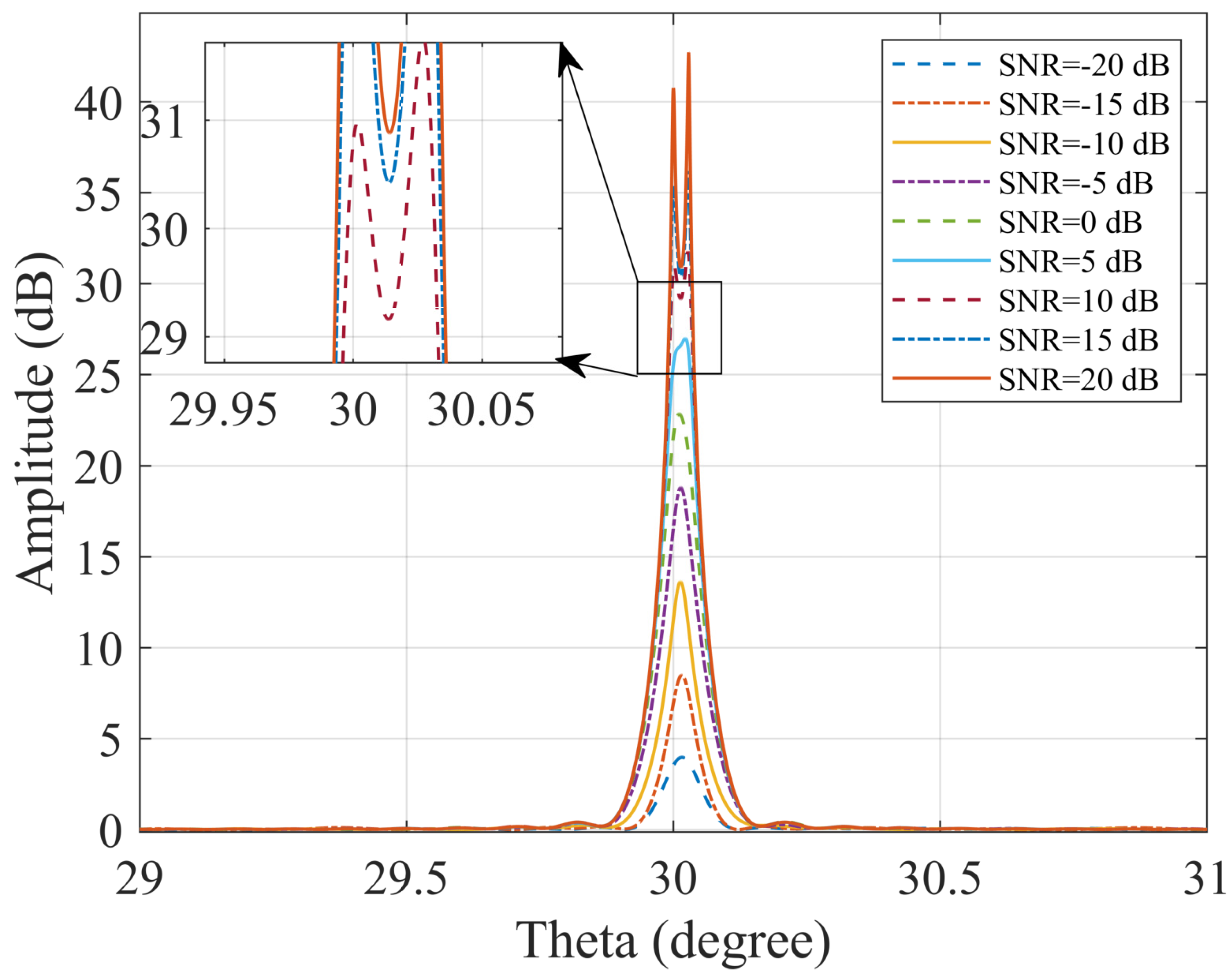
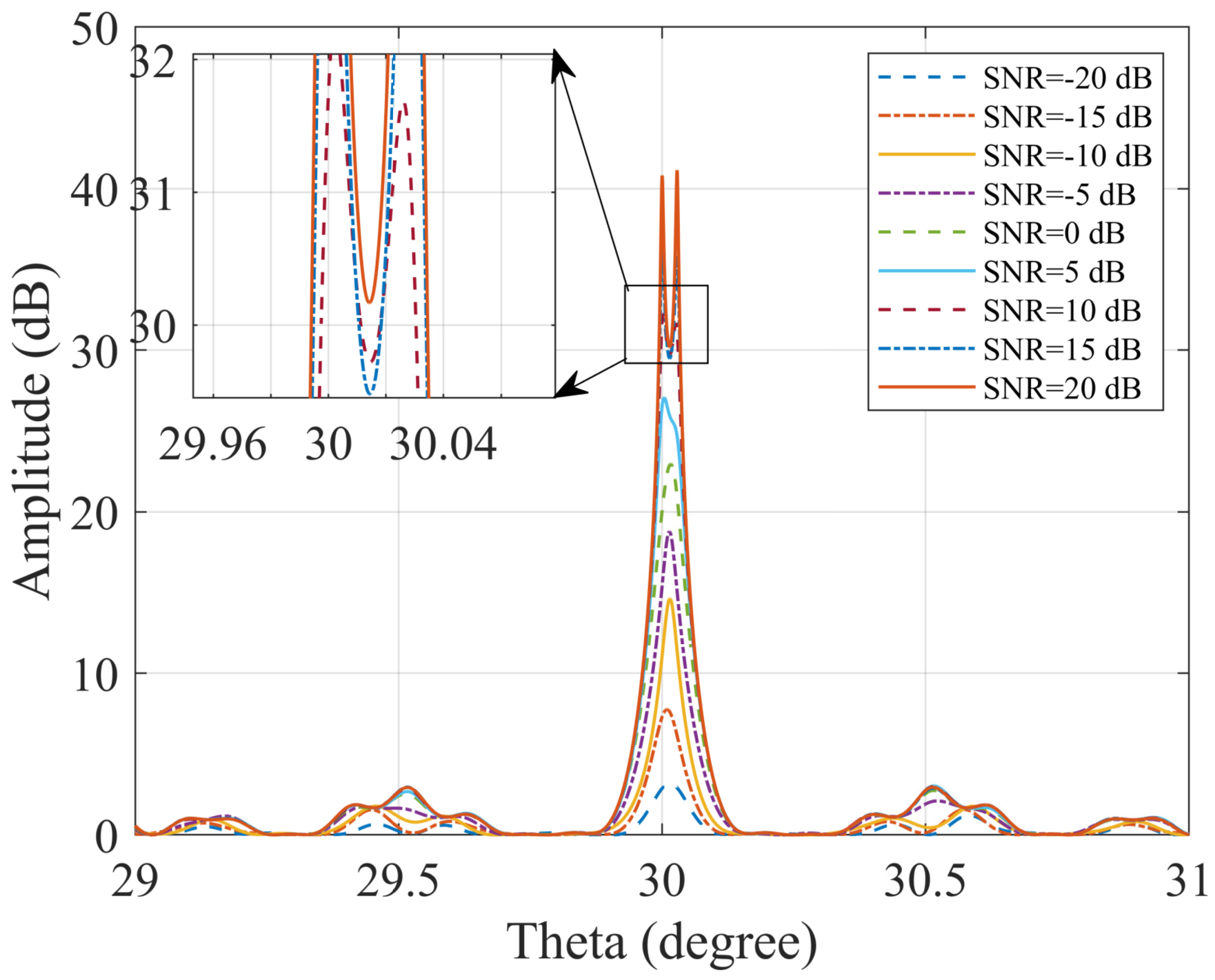
4.2. Simulation of Estimated Performance
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, W.; Haardt, M.; Greco, M.S.; Mecklenbräuker, C.F.; Willett, P. Twenty-Five Years of Sensor Array and Multichannel Signal Processing: A review of progress to date and potential research directions. IEEE Signal Process. Mag. 2023, 40, 80–91. [Google Scholar] [CrossRef]
- Tsui, J.; Stephens, J. Digital microwave receiver technology. IEEE Trans. Microw. Theory Tech. 2002, 50, 699–705. [Google Scholar] [CrossRef]
- Dang, X.; Liu, H.; Yan, J. Robust Elliptic Positioning via Sparse Regularization and ADMM for a Distributed MIMO Radar in the Presence of Outliers. IEEE Signal Process. Lett. 2024, 31, 2110–2114. [Google Scholar] [CrossRef]
- Shi, J.; Wen, F.; Liu, T. Nested MIMO Radar: Coarrays, Tensor Modeling, and Angle Estimation. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 573–585. [Google Scholar] [CrossRef]
- Tong, X.; Hu, Y.; Deng, Z.; Hu, E. Accelerating Broadband DOA Estimation: A Real-Valued and Coherent Sparse Bayesian Approach for 5G Sensing. Electronics 2025, 14, 3174. [Google Scholar] [CrossRef]
- Tong, X.; Chen, Y.; Deng, Z.; Hu, E. An Off-Grid DOA Estimation Method via Fast Variational Sparse Bayesian Learning. Electronics 2025, 14, 2781. [Google Scholar] [CrossRef]
- Zheng, H.; Zheng, G.; Song, Y.; Xiao, L.; Qin, C. Direction-of-Arrival Estimation with Discrete Fourier Transform and Deep Feature Fusion. Electronics 2025, 14, 2449. [Google Scholar] [CrossRef]
- Schmidt, R. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Roy, R.; Kailath, T. ESPRIT-estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 984–995. [Google Scholar] [CrossRef]
- Florio, A.; Coviello, G.; Talarico, C.; Avitabile, G. Adaptive DDS-PLL Beamsteering Architecture based on Real-Time Angle-of-Arrival Estimation. In Proceedings of the 2024 IEEE 67th International Midwest Symposium on Circuits and Systems (MWSCAS), Springfield, MA, USA, 11–14 August 2024; pp. 628–631. [Google Scholar] [CrossRef]
- Avitabile, G.; Man, K.L.; Talarico, C. DDS-PLL Architecture for Adaptive Beam Steering. In Proceedings of the 2024 21st International SoC Design Conference (ISOCC), Sapporo, Japan, 19–22 August 2024; pp. 205–206. [Google Scholar] [CrossRef]
- Florio, A.; Coviello, G.; Talarico, C.; Avitabile, G. Adaptive Beamsteering Architecture Based on AoA Estimation with Phase Shift on LO-Path for 5G NR. In Proceedings of the 2024 9th International Conference on Smart and Sustainable Technologies (SpliTech), Bol and Split, Croatia, 25–28 June 2024; pp. 1–5. [Google Scholar] [CrossRef]
- Florio, A.; Avitabile, G. Characterization of a Multisource Angle of Arrival Estimation Technique based on Phase Interferometry. In Proceedings of the 2022 18th International Conference on Synthesis, Modeling, Analysis and Simulation Methods and Applications to Circuit Design (SMACD), Villasimius, Italy, 12–15 June 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Florio, A.; Avitabile, G.; Coviello, G. Multiple Source Angle of Arrival Estimation Through Phase Interferometry. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 674–678. [Google Scholar] [CrossRef]
- Florio, A.; Avitabile, G.; Talarico, C.; Coviello, G. A Reconfigurable Full-Digital Architecture for Angle of Arrival Estimation. IEEE Trans. Circuits Syst. I Regul. Pap. 2024, 71, 1443–1455. [Google Scholar] [CrossRef]
- Zhang, S.; Xue, C.; Luo, J.; Wen, B.; Han, Y.; Sheng, W. Sparse Array Wideband Beamforming Based on Covariance Matrix Reconstruction and Neural Network. IEEE Trans. Veh. Technol. 2025, 1–13. [Google Scholar] [CrossRef]
- Zhang, S.; Gu, Q.; Ma, X.; Sheng, W.; Kirubarajan, T. A data alternating extraction general structure and its algorithms for adaptive space–time wideband beamforming. Digit. Signal Process. 2022, 126, 103478. [Google Scholar] [CrossRef]
- Wang, X.; Zhai, W.; Wang, X.; Amin, M.; Zoubir, A. Wideband Near-Field Integrated Sensing and Communications: A hybrid precoding perspective. IEEE Signal Process. Mag. 2025, 42, 88–105. [Google Scholar] [CrossRef]
- Wang, X.; Huang, J.; Wang, X.; Huang, T.; Amin, M. Optimal Sparse Array Design for Airborne Weather Radar with Integrated Communications. IEEE Trans. Aerosp. Electron. Syst. 2025, 61, 4238–4254. [Google Scholar] [CrossRef]
- Chen, H.; Wang, W.; Liu, W.; Tian, Y.; Wang, G. An Exact Near-Field Model Based Localization for Bistatic MIMO Radar with COLD Arrays. IEEE Trans. Veh. Technol. 2023, 72, 16021–16030. [Google Scholar] [CrossRef]
- Wang, X.; Guo, Y.; Wen, F.; He, J.; Truong, T.K. EMVS-MIMO Radar with Sparse Rx Geometry: Tensor Modeling and 2-D Direction Finding. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 8062–8075. [Google Scholar] [CrossRef]
- Dong, X.; Zhao, J.; Sun, M.; Zhang, X.; Wang, Y. A Modified Generalized Labeled Multi-Bernoulli Filtering for Multi-Source DOA Tracking with Coprime Array. IEEE Trans. Wirel. Commun. 2023, 22, 9424–9437. [Google Scholar] [CrossRef]
- Luo, J.; Zhu, H.; Zhang, S.; Han, Y.; Sheng, W. Low Complexity Neural Network Guided Robust Space-time Adaptive Wideband Beamforming. IEEE Trans. Aerosp. Electron. Syst. 2025, 1–15. [Google Scholar] [CrossRef]
- Chen, H.; Guo, H.; Liu, W.; Shen, Q.; Wang, G.; So, H.C. Fourth-Order Sparse Array Design From a Sum-Difference Co-Array Perspective. IEEE Trans. Signal Process. 2025, 73, 2243–2254. [Google Scholar] [CrossRef]
- Moffet, A. Minimum-redundancy linear arrays. IEEE Trans. Antennas Propag. 1968, 16, 172–175. [Google Scholar] [CrossRef]
- Vaidyanathan, P.P.; Pal, P. Sparse sensing with coprime arrays. In Proceedings of the 2010 Conference Record of the Forty Fourth Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 7–10 November 2010; pp. 1405–1409. [Google Scholar] [CrossRef]
- Wang, Q.; Xue, C.; Zhang, S.; Zhang, R.; Sheng, W. Design of Extensible Structured Interferometric Array Utilizing the “Coarray” Concept. Remote Sens. 2023, 15, 1934. [Google Scholar] [CrossRef]
- Pal, P.; Vaidyanathan, P.P. Nested Arrays: A Novel Approach to Array Processing with Enhanced Degrees of Freedom. IEEE Trans. Signal Process. 2010, 58, 4167–4181. [Google Scholar] [CrossRef]
- Malioutov, D.; Cetin, M.; Willsky, A. A sparse signal reconstruction perspective for source localization with sensor arrays. IEEE Trans. Signal Process. 2005, 53, 3010–3022. [Google Scholar] [CrossRef]
- Chi, Y.; Scharf, L.L.; Pezeshki, A.; Calderbank, A.R. Sensitivity to Basis Mismatch in Compressed Sensing. IEEE Trans. Signal Process. 2011, 59, 2182–2195. [Google Scholar] [CrossRef]
- Wong, K.; Zoltowski, M. Direction-finding with sparse rectangular dual-size spatial invariance array. IEEE Trans. Aerosp. Electron. Syst. 1998, 34, 1320–1336. [Google Scholar] [CrossRef]
- Liao, Y.; Zhao, R.; Liu, H. DOA Estimation Method with the Distributed Nested Array. In Proceedings of the 2018 10th International Conference on Wireless Communications and Signal Processing (WCSP), Hangzhou, China, 18–20 October 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Liao, Y.; Lin, Y.; Zhao, R. 2D-DOA Estimation Using L-shaped Distributed Augmented Nested Array. In Proceedings of the 2021 13th International Conference on Wireless Communications and Signal Processing (WCSP), Changsha, China, 20–22 October 2021; pp. 1–7. [Google Scholar] [CrossRef]
- Vasylyshyn, V. Closed-form DOA estimation with multiscale unitary ESPRIT algorithm. In Proceedings of the First European Radar Conference (EURAD 2004), Amsterdam, The Netherlands, 11–15 October 2004; pp. 317–320. [Google Scholar]
- Yu, W.; He, P.; Cui, A.; Wang, H.; Zhou, H.; Xu, Z. DOA Estimation Ambiguity Resolution Method for Near Field Distributed Array. In Proceedings of the 2021 6th International Conference on Intelligent Computing and Signal Processing (ICSP), Xi’an, China, 9–11 April 2021; pp. 870–875. [Google Scholar] [CrossRef]
- Chowdhury, M.W.T.S.; Zhang, Y.D. Direction-of-Arrival Estimation Exploiting Distributed Sparse Arrays. In Proceedings of the 2021 55th Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 31 October–3 November 2021; pp. 231–235. [Google Scholar] [CrossRef]
- Xie, Q.; Wang, Z.; Wen, F.; He, J.; Truong, T.K. Coarray Tensor Train Decomposition for Bistatic MIMO Radar with Uniform Planar Array. IEEE Trans. Antennas Propag. 2025, 73, 5310–5323. [Google Scholar] [CrossRef]
- Xie, Q.; Shi, J.; Wen, F.; Zheng, Z. Higher-order tensor decomposition for 2D-DOD and 2D-DOA estimation in bistatic MIMO radar. Signal Process. 2026, 238, 110196. [Google Scholar] [CrossRef]
- Pavel, S.R.; Chowdhury, M.W.T.S.; Zhang, Y.D.; Shen, D.; Chen, G. Machine Learning-Based Direction-of-Arrival Estimation Exploiting Distributed Sparse Arrays. In Proceedings of the 2021 55th Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 31 October–3 November 2021; pp. 241–245. [Google Scholar] [CrossRef]
- Zhang, S.; Thiyagalingam, J.; Sheng, W.; Kirubarajan, T.; Ma, X. Low-complexity adaptive broadband beamforming based on the non-uniform decomposition method. Signal Process. 2018, 151, 66–75. [Google Scholar] [CrossRef]
| ULA | UDA | CDA | |
|---|---|---|---|
| Element spacing (d) | |||
| Number of arrays | 1 | 21 | 9 |
| Number of elements per subarray (L) | 10 | 10 | 10 |
| Subarray spacing (D) | – | m | m |
| Array aperture | m | 9 m | 9 m |
| Frequency of the incident signal (f) | 10 GHz | 10 GHz | 10 GHz |
| Target angle interval | ° | ° | ° |
| SNR | −20∼20 dB | −20∼20 dB | −20∼20 dB |
| Spatial spectrum grid | ° | ° | ° |
| Number of snapshots | 256 | 256 | 256 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, M.; Ma, T.; Shen, Z.; Liu, Z.; Zhou, Y.; Li, S.; Wang, J. Coprime Distributed Array for Super-Resolution DOA Estimation. Electronics 2025, 14, 4562. https://doi.org/10.3390/electronics14234562
Guo M, Ma T, Shen Z, Liu Z, Zhou Y, Li S, Wang J. Coprime Distributed Array for Super-Resolution DOA Estimation. Electronics. 2025; 14(23):4562. https://doi.org/10.3390/electronics14234562
Chicago/Turabian StyleGuo, Ming, Tingting Ma, Zixuan Shen, Zewei Liu, Yuee Zhou, Shenghui Li, and Jian Wang. 2025. "Coprime Distributed Array for Super-Resolution DOA Estimation" Electronics 14, no. 23: 4562. https://doi.org/10.3390/electronics14234562
APA StyleGuo, M., Ma, T., Shen, Z., Liu, Z., Zhou, Y., Li, S., & Wang, J. (2025). Coprime Distributed Array for Super-Resolution DOA Estimation. Electronics, 14(23), 4562. https://doi.org/10.3390/electronics14234562






