A Personalized Trajectory Planning Approach for Exoskeleton Robots Using GPR and Fourier Series

Abstract

To address the unique gait characteristics of individuals, this paper proposes a personalized trajectory planning method for exoskeleton robots. Gait trajectory data is collected using an inertial motion capture system, and personalized musculoskeletal models are built via OpenSim 4.5 to calculate joint angle data. The Trainable Time Warping (TTW) algorithm is used to align data from different time series, followed by Gaussian Mixture Model and Gaussian Mixture Regression (GMM-GMR) to fit multiple data sequences. The fitted joint angle curves are expanded using Fourier series to obtain Fourier coefficients. A Gaussian Process Regression (GPR) model is then established to map anthropometric parameters (thigh length, calf length, weight) to Fourier coefficients, which are used to plan gait trajectories. Experiments conducted with a lower limb exoskeleton robot demonstrate that this trajectory planning method achieves accurate trajectory tracking, with a root mean square error (RMSE) of 1.82° for the hip joint and 1.89° for the knee joint. The method also yielded a high user satisfaction rate of 90%, confirming its effectiveness in generating personalized and comfortable gait patterns.

1. Introduction

Lower limb exoskeletons are increasingly used for gait rehabilitation of stroke patients [1,2], and have proven to be effective intervention tools for improving motor function in this population [3]. These devices help restore gait symmetry, improve the range of motion, increase walking speed, and enhance overall mobility and function [3,4,5,6]. The main technical points include motion intention recognition, gait pattern generation, and stable gait control [7,8,9,10,11].

1.1. Related Works

Previous research on exoskeleton control has primarily focused on improving trajectory tracking by imposing predefined gait patterns on patients [12,13,14]. However, while this has led to some improvements in post-stroke recovery, it may also reduce patient engagement and motor learning, resulting in less significant improvements [12,15,16]. In contrast, personalized gait training has been shown to be more effective in promoting gait recovery [13,17,18,19,20]. Nonetheless, personalized gait planning poses significant challenges. The existing research results show that each person’s gait pattern is unique [12]. The uniqueness of human gait is influenced by factors such as age, gender, height, body type, and mood [21,22,23,24]. Therefore, the exoskeleton robot for rehabilitation must be adjustable to accommodate different body parameters of users, and finding a generalized method for personalized gait planning is a crucial area of research.

Planning an appropriate gait trajectory for each patient has become an active research topic in the field of lower-limb exoskeleton robots [25,26]. The methods of gait trajectory generation have been utilized on exoskeleton robot. For instance, Vallery et al. [27] proposed an online trajectory generation method called Complementary Limb Motion Estimation, which is particularly suitable for hemiplegic subjects. This approach has the advantage of allowing subjects to walk with less assistance from the robot; however, it requires unimpaired limbs to generate reference movements. Kagawa et al. [28] developed a motion planning method in joint space for a wearable robot with a variable stride length and walking speed. This method considers factors such as motion range, maximum speed, step size, and balance, effectively producing high-speed and efficient gait patterns. Despite their merits, these methods primarily account for leg symmetry or length when predicting gait patterns. Addressing this limitation, Wu et al. [29] introduced an Individualized Gait Pattern Generation (IGPG) method for Shared Lower Limb Exoskeleton (SLEX) robots. This approach employs GPR with automatic relevance determination to map body parameters, walking speed, and gait features, resulting in gait trajectories tailored to individual users. However, challenges were observed during data collection, as subjects struggled to maintain a consistent walking speed and natural gait.

1.2. Contributions

This paper proposes a personalized trajectory planning method. In order to better adapt to the gait of subjects of different body types, trajectories are planned in joint space rather than workspace to avoid ill posed problems without solutions in inverse kinematics. Firstly, the physical parameters of the subjects were measured, and the walking data were collected using the Xsens MVN [30], which is an inertial motion capture system. A personalized musculoskeletal model was established using OpenSim [31] to obtain the hip joint flexion and extension angles and knee joint angles. The TTW [32] algorithm and GMM-GMR [33] were used to fit multiple experimental results into a specific gait trajectory, which was then expanded into a Fourier series to obtain Fourier coefficients. Establish the mapping relationship between human body parameters and Fourier coefficients through GPR method, and obtain gait pattern trajectories that are suitable for different people. Recruit participants to validate the feasibility of the experimental method and conduct a satisfaction survey on comfort.

The main contributions of this article are as follows.

(1) A method for generating subject-specific joint angle trajectories by applying the TTW algorithm and GMM-GMR to raw walking data, effectively capturing individual walking styles.

(2) A data-driven mapping between anthropometric parameters (thigh length, calf length, weight) and the Fourier coefficients of joint motion, built using GPR, which allows for the generation of personalized gait patterns for diverse anthropometrics.

(3) The design and experimental validation of a lower-limb exoskeleton, confirming the efficacy of our approach through rigorous trajectory tracking tests and positive subjective feedback on comfort and satisfaction.

To the best of our knowledge, this is the first study to establish a direct mapping from static anthropometric parameters to the dynamic Fourier coefficients of joint angles using GPR, enabling a “zero-shot” personalization of gait trajectories for new users based solely on their body measurements. Furthermore, the integrated framework that synergistically combines the TTW algorithm, GMM-GMR, and GPR for end-to-end personalized gait generation presents a novel methodology in the field of lower-limb exoskeleton control.

The rest of this paper is organized as follows. Section 2 presents the method for personalized trajectory planning. Section 3 details the design of the exoskeleton. Section 4 describes the design and result analysis of data acquisition experiments and gait experiments.

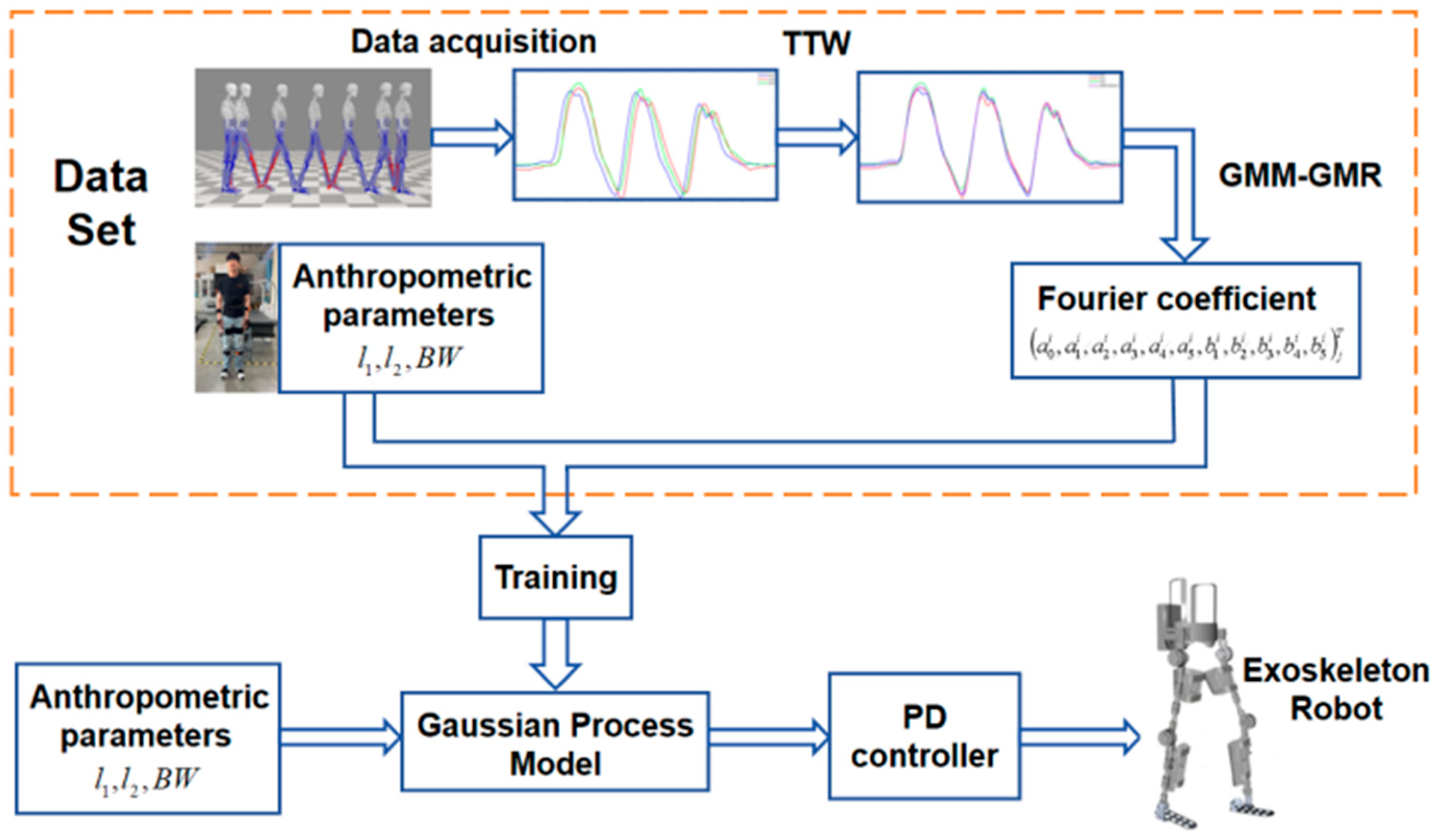
2. Method

This section details the integrated framework for personalized gait planning, as illustrated in Figure 1. The process initiates with the acquisition of human demonstration data. The TTW algorithm and GMM-GMR are then applied to these trajectories to extract a smooth, generalized motion profile. A key step involves transforming this continuous trajectory into a low-dimensional parameter set via a 5th-order Fourier series expansion. Since the bandwidth of the signal is limited, it does not need to extend to infinity. The maximum walking frequency for a normal person does not exceed 6 Hz [34]. Therefore, when expanding the hip and knee joint angles using Fourier series, a 5th order expansion is sufficient. The innovative element of this workflow is the use of Gaussian Process Regression (GPR), which learns a mapping from an individual’s anthropometric features to their specific Fourier coefficients. This allows for the synthesis of customized gait trajectories for novel subjects based on simple body measurements, completing the personalization loop.

2.1. Gaussian Mixture Model (GMM) and Gaussian Mixture Regression (GMR)

GMM consists of multiple single Gaussian models and can smoothly approximate density distributions of any shape. GMR represents the data in the input and output spaces as Gaussian distributions, training the model using the standard Expectation-Maximization (EM) algorithm, and predicting the output given a specific input. GMR has important applications in trajectory planning and control for robots.

A mixture model with K components is defined through the probability density function [35] as follows:

$$p\left({\xi }_j\right)={\displaystyle {\sum }_{k=1}^{K}p\left(k\right)p\left({\xi }_j\left|k\right.\right)}$$

(1)

The number of Gaussian components K in the GMM is a critical hyperparameter. To determine the optimal K, we fitted models with K ranging from 1 to 10 and selected the model that minimized the Bayesian Information Criterion (BIC), which penalizes model complexity to prevent overfitting. The BIC curve indicated an optimum at K = 4 components, which was subsequently used for all GMM-GMR analyses in this study.

There is a dataset of sampled joint angles ${\xi }_j={\left\{{\xi }_j^t,{\xi }_j^s\right\}}_{j=1}^N\in {ℝ}^D$. It consists of N data points in D dimensions. N is the number of demonstrations, and D is the duration of each demonstration. t is the sampling time of the data. s represents the joint angles. The dataset is modeled by a K GMM in D dimensions. The parameters in Equation (1) become

$$p\left(k\right)={\pi }_k$$

(2)

$$\begin{array}{ll}p\left({\xi }_j\left|k\right.\right)& =N\left({\xi }_j|{\mu }_k,{\Sigma }_k\right)\\ & ={\displaystyle \frac{1}{\sqrt{{\left(2\pi \right)}^D\left|{\Sigma }_k\right|}}}{e}^{-\frac{1}{2}\left({\left({\xi }_j-{\mu }_k\right)}^T{\Sigma }_k^{-1}\left({\xi }_j-{\mu }_k\right)\right)}\end{array}$$

(3)

where $\left\{{\pi }_k,{\mu }_k,{\Sigma }_k\right\}$ are the parameters of the kth Gaussian defining the prior, mean and covariance matrix, respectively. The EM algorithm is used to iteratively perform maximum likelihood estimation of the mixture parameters [35]. EM is a local iterative algorithm used in statistics to find probability models that rely on unobservable hidden variables using to solve the GMM.

For GMR [33], our goal is to predict the corresponding joint angles ${\widehat{\xi }}^s$ based on the continuous temporal values ${\xi }^t$. The mean and covariance matrix of the Gaussian component k are defined as:

$${\mu }_k=\left\{{\mu }_k^t,{\mu }_k^s\right\}, {\Sigma }_k=\left(\begin{array}{cc}{\sum }_k^{tt}& {\sum }_k^{ts}\\ {\sum }_k^{st}& {\sum }_k^{ss}\end{array}\right)$$

(4)

The joint angles ${\widehat{\xi }}^s$ can be represented as a conditional probability distribution:

$$p\left({\xi }^s\left|{\xi }^t\right.\right)={\displaystyle {\sum }_{k=1}^K{h}_k\left({\xi }^t\right)}N\left({\xi }^s\left|{\mu }_k^{s\left|t\right.},{\Sigma }_k^{s\left|t\right.}\right.\right)$$

(5)

where

$$h_k\left({\xi }^t\right)={\displaystyle \frac{{\pi }_{k}N\left({\xi }^t|{\mu }_k^t,{\Sigma }_k^{tt}\right)}{{\Sigma }_{j=1}^K{\pi }_{j}N\left({\xi }^t|{\mu }_j^t,{\Sigma }_j^{tt}\right)}}, {\mu }_k^{s\left|t\right.}={\mu }_k^s+{\Sigma }_k^{st}{\left({\Sigma }_k^{tt}\right)}^{-1}\left(t^{\ast }-{\mu }_k^t\right), {\Sigma }_k^{s\left|t\right.}={\Sigma }_k^{ss}-{\Sigma }_k^{st}{\left({\Sigma }_k^{tt}\right)}^{-1}{\Sigma }_k^{ts}$$

(6)

where $h_k$ is the weight of the kth single Gaussian model.

2.2. Trajectory Representation and Personalization Mode

This paper employs GPR for prediction, complemented by Fourier series for expressing personalized gait trajectory planning. First, a number of subjects with varying heights and weights are recruited to perform walking experiments, recording their physical data and measuring the changes in hip and knee joint angles during the experiment. To simplify the representation of the joint angle function, we expand it into the form of a Fourier series. According to Fourier theory, any periodic signal can be represented by a Fourier series. A continuous signal x(t) with a period of L can be expanded in the form of Equation (7).

$$f\left(t\right)={\displaystyle \frac{1}{2}}{a}_0+{\displaystyle \sum _{n=1}^{\infty }\left(a_n\cos n\omega t+b_n\sin n\omega t\right)}$$

(7)

$$a_0={\displaystyle \frac{1}{T}}{\displaystyle {\int }_{t_0}^{t_0+T}f\left(t\right)dt}$$

(8)

where $a_0$ is the DC component of the signal, $a_n$ and $b_n$ are the harmonic coefficients of the signal. $f(t)$ is sampled at uniform time intervals, with the data expanded according to the discrete 5th order Fourier series as shown in Equation (9):

$$f\left(t\right)={\displaystyle \frac{a_0}{2}}+{\displaystyle \sum _{n=1}^5\left(a_n\cos \frac{2\pi nk}{K}+b_n\sin \frac{2\pi nk}{K}\right)}, k=0, 1, \cdots , \left(K-1\right)$$

(9)

where $a_n$ and $b_n$ are the Fourier coefficients; $K$ is the number of samples per period.

The harmonic coefficient formulas are obtained from Equations (10) and (11):

$$a_n={\displaystyle \frac{2}{K}}{\displaystyle \sum _{k=1}^{K}f\left(t\right)}\cos {\displaystyle \frac{2\pi nk}{K}}, n=1,2,\cdots {\displaystyle \frac{K}{2}}$$

(10)

$$b_n={\displaystyle \frac{2}{K}}{\displaystyle \sum _{k=1}^{K}f\left(t\right)\sin \frac{2\pi nk}{K}}, n=1,2,\cdots {\displaystyle \frac{K}{2}}$$

(11)

Obtain gait feature vectors $u_j^i$ as Equation (12):

$$u_j^i={\left(a_0^i,a_1^i,a_2^i,a_3^i,a_4^i,a_5^i,b_1^i,b_2^i,b_3^i,b_4^i,b_5^i\right)}_j^T$$

(12)

Using classic GPR (single-output-GPR), a multiple-input single-output model is employed. This results in n training input sample parameters X and n training output samples y. The definition is as follows in Equation (13):

$$X=\left[\begin{array}{c}{x}_i\\ ⋮\\ x_n\end{array}\right],y=\left[\begin{array}{c}{a}_0^1\\ ⋮\\ a_0^n\end{array}\right]$$

(13)

where $x_i={\left[\begin{array}{ccc}{l}_1^i& l_2^i& B{W}^i\end{array}\right]}^T$, $l_1^i$ is the thigh length of the ith sample; $l_2^i$ is the calf length of the ith sample; $B{W}^i$ is the body weight of the ith sample; and $a_0^i$ is the Fourier harmonic coefficient $a_0$ of the ith sample. The remaining 10 Fourier harmonic coefficients are defined similarly.

The anthropometric parameters—thigh length, calf length, and weight—were selected as inputs for the GPR model due to their direct biomechanical relevance to gait kinematics. Thigh and calf lengths directly determine the kinematic chain and inertia of the leg, fundamentally influencing swing leg dynamics and step length. Body weight is a primary factor governing the joint torques required for locomotion, which influences the posture and range of motion adopted by individuals. While other parameters like total leg length, gender, or age are also influential, our chosen set provides a parsimonious yet physically meaningful representation for personalization. Total leg length was excluded because the explicit segmentation into thigh and calf lengths offers a more detailed model of the limb’s dynamics. Gender and age were not included in this initial study to maintain a focused model and because their effects are often correlated with and can be partially captured by the included physical parameters; however, we explicitly identify their inclusion for future work.

A Gaussian process is determined by its mean function and covariance function [36]. Its defining model is given in Equation (14):

$$f\left(x\right)=GP\left(m\left(x\right),k\left(x,x^{\prime }\right)\right)$$

(14)

where $m\left(x\right)$ is the mean function and $k\left(x,x^{\prime }\right)$ is the covariance function.

For the prediction model, we assume that the mean function and covariance function are defined as Equations (15) and (16):

$$m\left(x\right)=0$$

(15)

$$k\left(x,x^{\prime }\right)={\sigma }_f^2\exp \left(-{\displaystyle \frac{1}{2{\lambda }^2}}{\left|x-x^{\prime }\right|}^2\right)$$

(16)

where the parameters $\lambda$ and ${\sigma }_f^2$ are hyperparameters $\theta$, and the values of these hyperparameters determine the characteristics of the GPR model.

Based on the selection of the above parameters, we can derive the probability distribution of the predicted values, defined as Equation (17):

$$\begin{array}{l}{\widehat{f}}^{\ast }\left|x,y,{\widehat{x}}^{\ast }\right|\sim N\left(K\left(x^{\ast },x\right){\left[K\left(x,x\right)\right]}^{-1}y,\right.\\ k\left(x^{\ast },x^{\ast }\right)-K\left(x^{\ast },X\right)\times {\left[K\left(X,X\right)\right]}^{-1}K\left(X,x^{\ast }\right)\end{array}$$

(17)

where $f^{\ast }$ is the predicted value at the prediction point $x^{\ast }$; $cov\left(f^{\ast }\right)$ is the variance at the prediction point $x^{\ast }$; $K\left(X,X\right)$ is a positive definite covariance matrix, with elements are given by $k_{ij}=k\left(x_i,x_j\right)$.

The hyperparameters $\theta$ are obtained using the maximum likelihood method. The negative log-likelihood function for the training samples is established as shown in Equation (18):

$$\log p\left(y\left|X,\theta \right.\right)=-{\displaystyle \frac{y^{{\rm T}}{K}^{-1}y+\log \left|K\right|+\log 2\pi NT}{2}}$$

(18)

By taking the derivative of this function and using the conjugate gradient method, the optimal solution for the hyperparameters is derived.

The Fourier harmonic coefficients obtained from the Gaussian process model can be used to calculate the joint angles of the joints for control purposes, as expressed in Equation (19):

$${\theta }_{\mathrm{angle}}={\displaystyle \frac{a_0^1}{2}}+{\displaystyle {\sum }_{p=1}^5\left(a_p^1\cos \frac{2\pi pn}{N}+b_p^1\sin \frac{2\pi pn}{N}\right)}$$

(19)

where n = 1, 2, 3, …, N, N is the total number of samples per cycle.

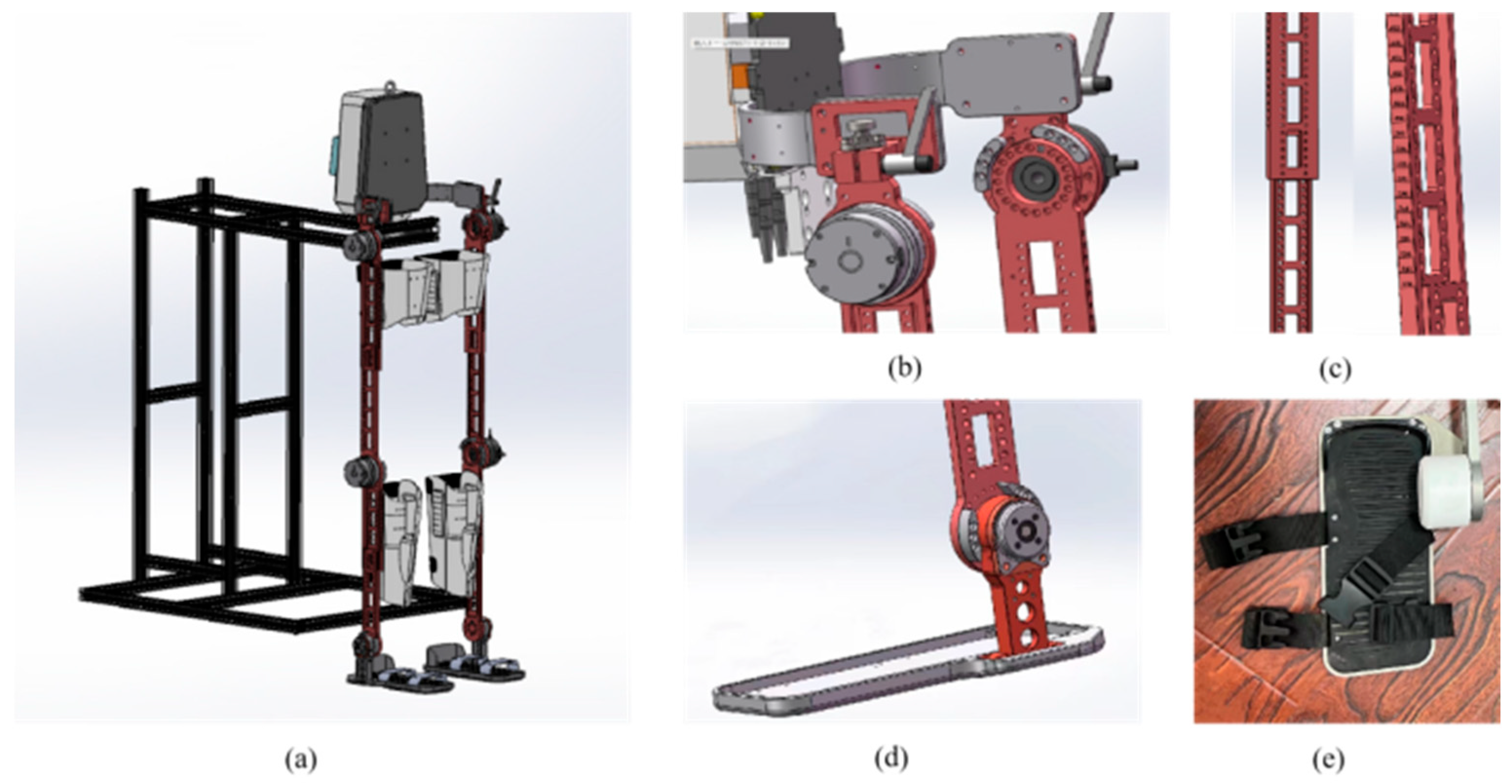
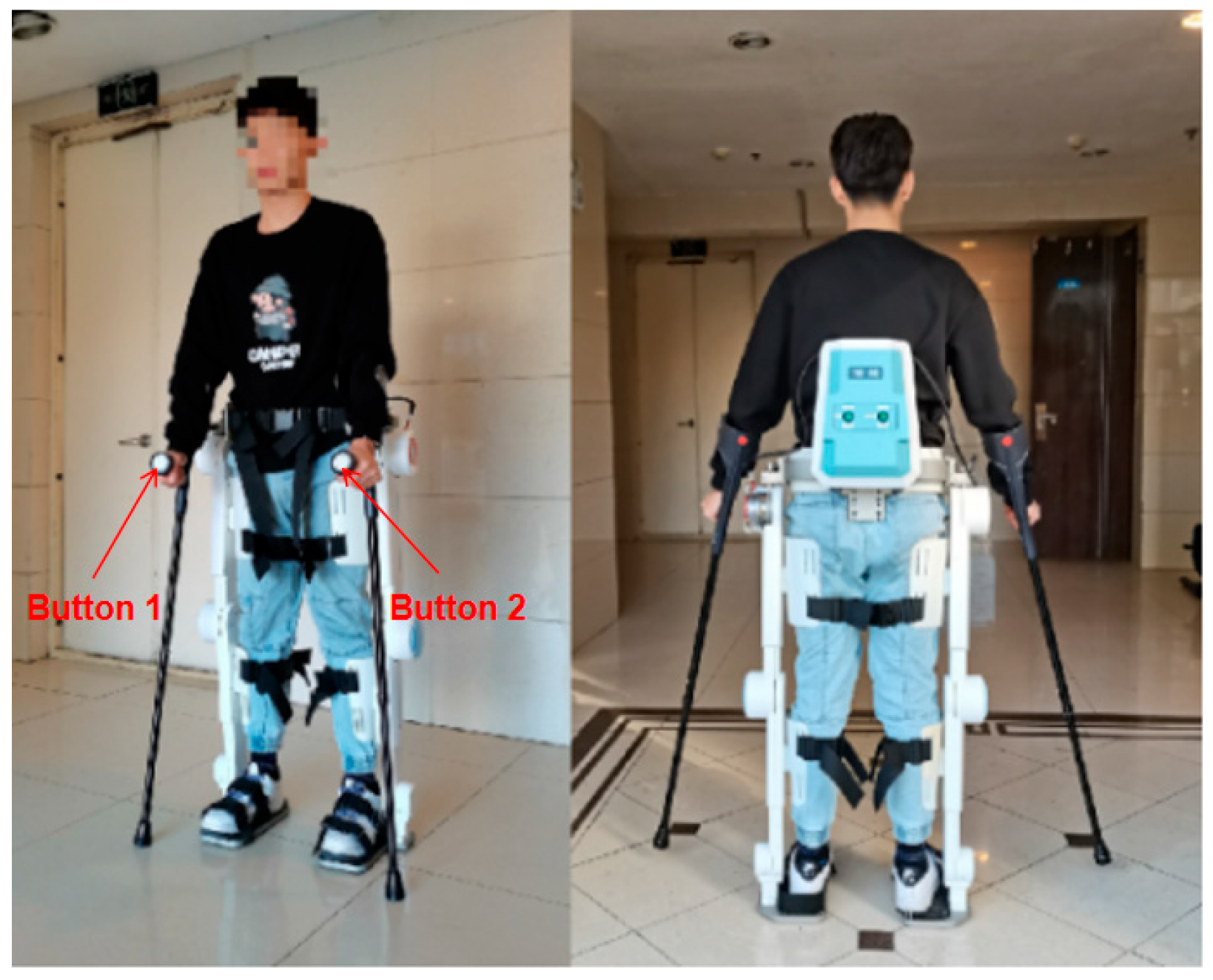
3. Design of the Lower Limb Exoskeleton

To validate the proposed personalized trajectory planning method, a lower-limb exoskeleton robot was designed and developed. This section details the mechanical, sensory, and control architecture of the system, which serves as the experimental platform for this study. The exoskeleton is primarily intended for sagittal-plane gait assistance at the hip and knee joints, featuring four active DoFs (DoFs) and two passive DoFs.

3.1. Structural Composition

The exoskeleton system was designed to be ergonomic, durable, and lightweight, targeting applications in human performance augmentation. As shown in Figure 2a, the lower limb exoskeleton system in this design has a total of six DoFs. It features four active joints at the hip and knee that provide driving torque, powered by DC servomotors as illustrated in Figure 2b. The DC motors have the same power of 400 W and can provide 90 Nm torque. Additionally, there are two dampers at the ankle joint, as shown in Figure 2d, which generate damping force to prevent the wearer from falling due to insufficient ankle strength. Both the motors and dampers are equipped with limiters, as depicted in Figure 2b, to prevent joint rotation beyond angles that the human body can safely tolerate. To accommodate individuals of different heights, two rigid linkages are designed as extendable components with adjustable lengths, marked with measurement scales on the sides for convenience (Figure 2c). In addition to the joints and rigid linkages, adjustable straps with buckles are provided around the waist, thigh, calf, and foot, as shown in Figure 2e, to connect the exoskeleton system to the wearer, allowing for a more flexible attachment. A pair of crutches equipped with buttons is designed to help maintain balance, prevent falls, and issue motion commands. As shown in Figure 2a, a rack is designed to suspend and store the exoskeleton robot when not in use.

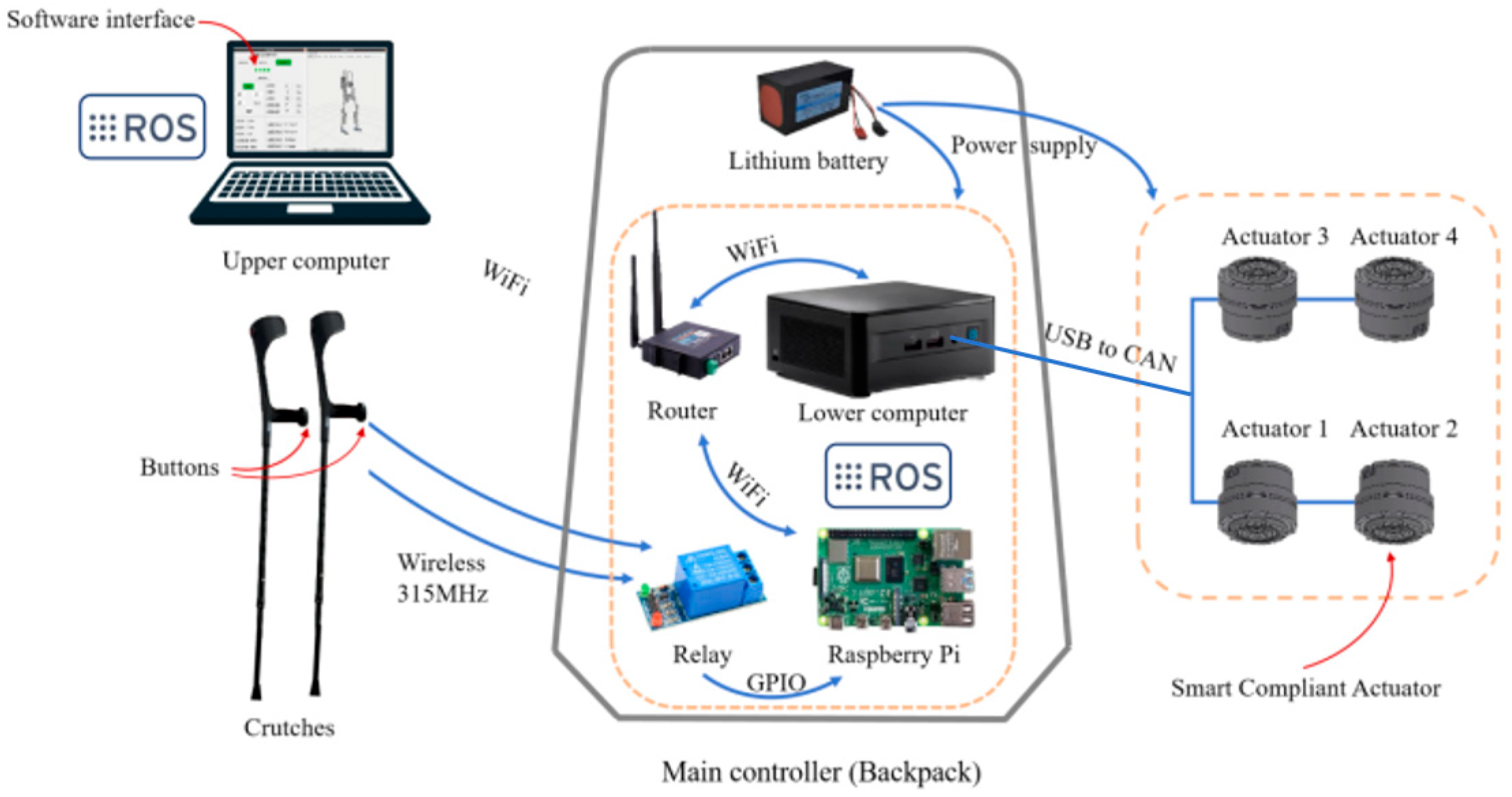
3.2. Electrical Structure

The system consists of a main controller and four node controllers, as shown in Figure 3. The main controller composed of a lower computer and a Raspberry Pi is housed in a backpack and runs control interface and control algorithms. Four joint actuators, which integrate brushless motor, planetary gearbox, and driver board, are communicated with the lower computer via CAN bus. A upper computer runs human interface for state monitoring and human–computer interaction. The upper computer, lower computer and the Raspberry Pi are connected in a local network via the router compacted in the backpack. A lithium battery with 24 V is used to supply power for the whole system.

Both the upper computer and the lower computer are equipped with ROS systems and communicate with a Raspberry Pi via WiFi. The lower limb exoskeleton robot monitors its current state through a combination of encoders, a Raspberry Pi, and the upper computer. The encoders are integrated into the joint actuators to measure the current status of each joint. The Raspberry Pi monitors the switches of two crutch buttons to determine whether commands are executed: the right crutch button issues walking commands (taking one step for each press), while the left crutch button issues stop commands to return to a standing position.

4. Experiment Results

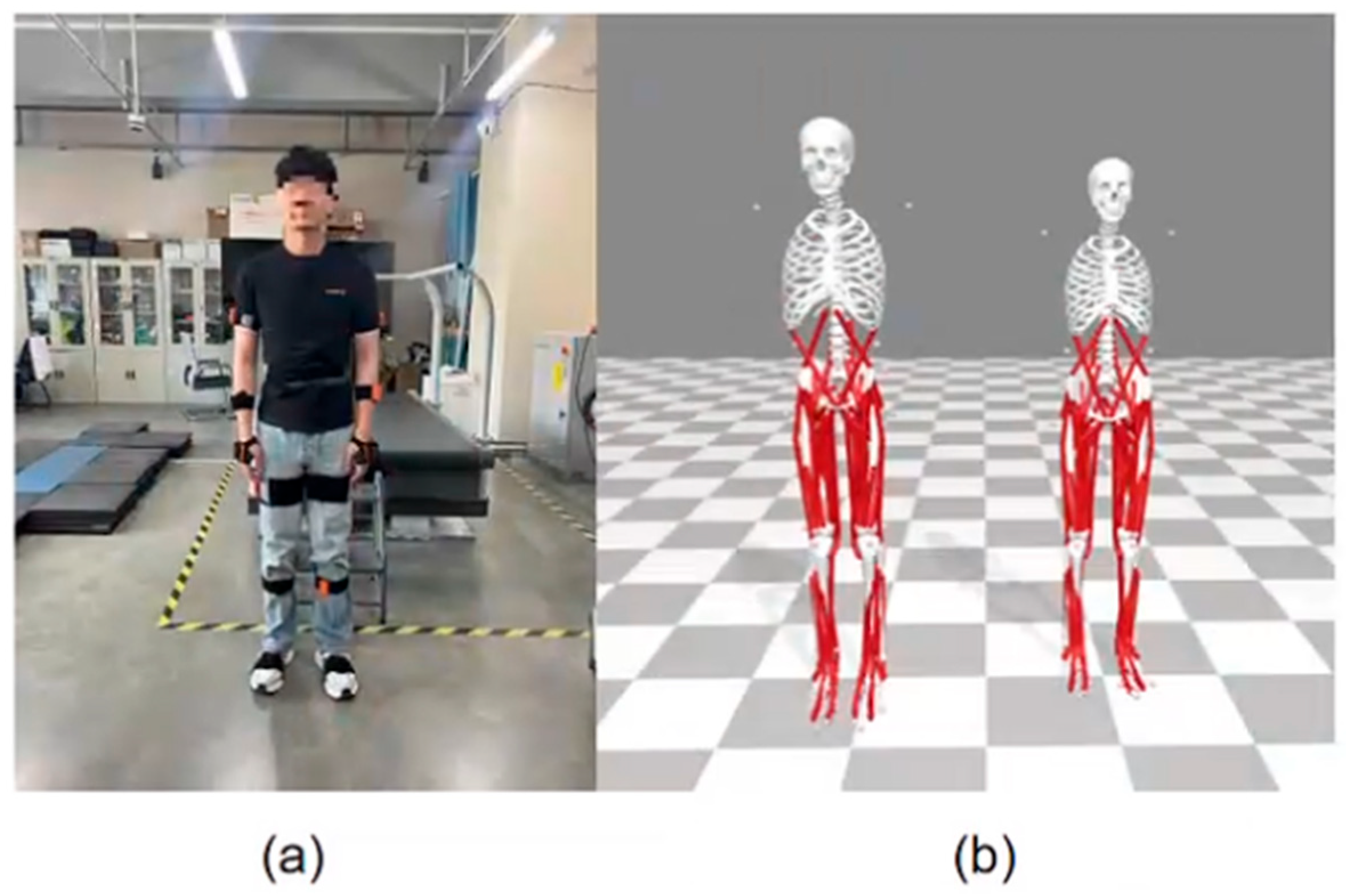
4.1. Experimental Procedure

This experiment is designed as a five-step walking task, requiring participants to stand at attention, take a step with the left foot, and return to a standing position after the fifth step. Figure 4 illustrates a schematic of each step for the participants. Each participant repeats the experiment three times. 60 participants were recruited, aged between 20 and 30 years, with heights ranging from 160 to 188 cm, and a gender ratio of 1:1. Data from 40 training samples were used to obtain the GPR model. First, users input their thigh length, calf length, and weight into the upper computer software interface to generate personalized joint angle trajectory curves for gait.

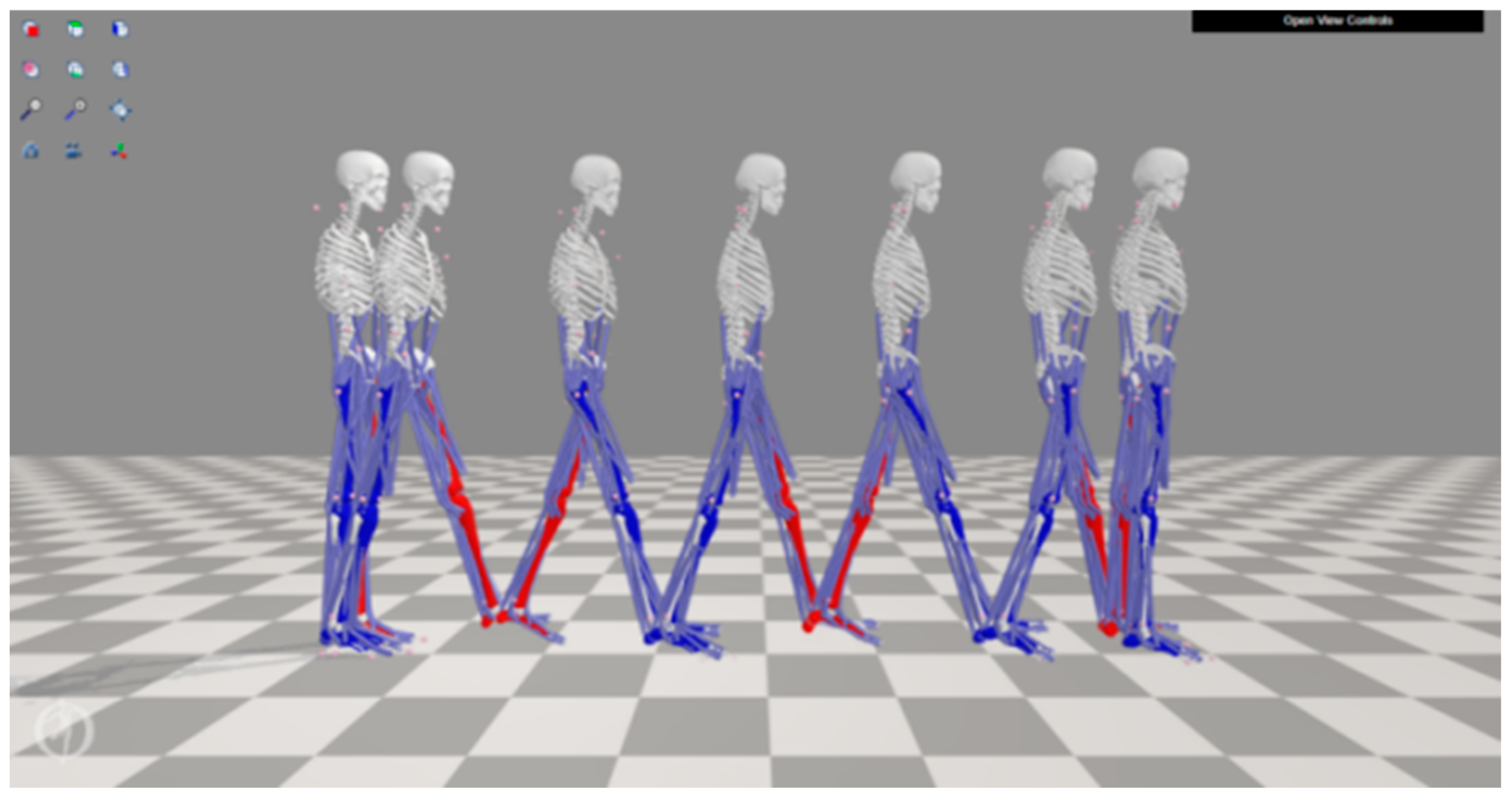
4.2. Data Collection

The Xsens MVN, an inertial motion capture system, was used to collect gait trajectory data while walking, as shown in Figure 5a. A total of 64 marker points were exported; however, 43 were selected for subsequent processing to simplify calculations. Since it is challenging for a person to walk in a straight line and the hip joint has three DoFs, allowing for flexion, extension, abduction, adduction, and rotational movements along three mutually perpendicular axes, this study only considers the extension direction of the hip joint and the variations in knee joint movement. Using the Gait2392 musculoskeletal model from the OpenSim model library, personalized musculoskeletal models were generated by scaling according to the participants’ weight and dimensions. Figure 5b shows two musculoskeletal models: the one on the right is the standard 2392 model (180 cm, 75.1646 kg), while the left model is the scaled version (184 cm, 71.35 kg). Inverse kinematics were employed to determine the desired angles for the hip and knee joints.

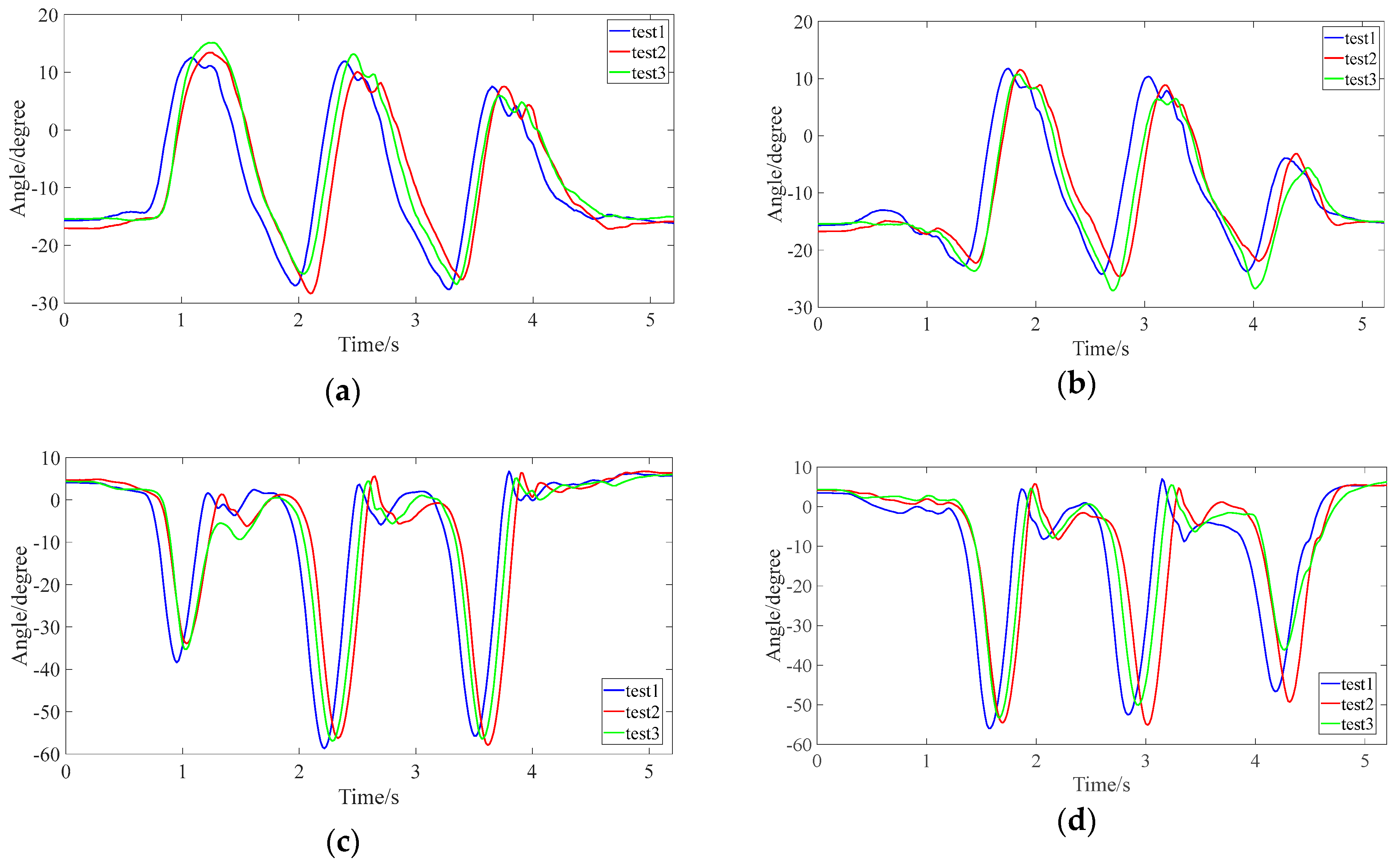
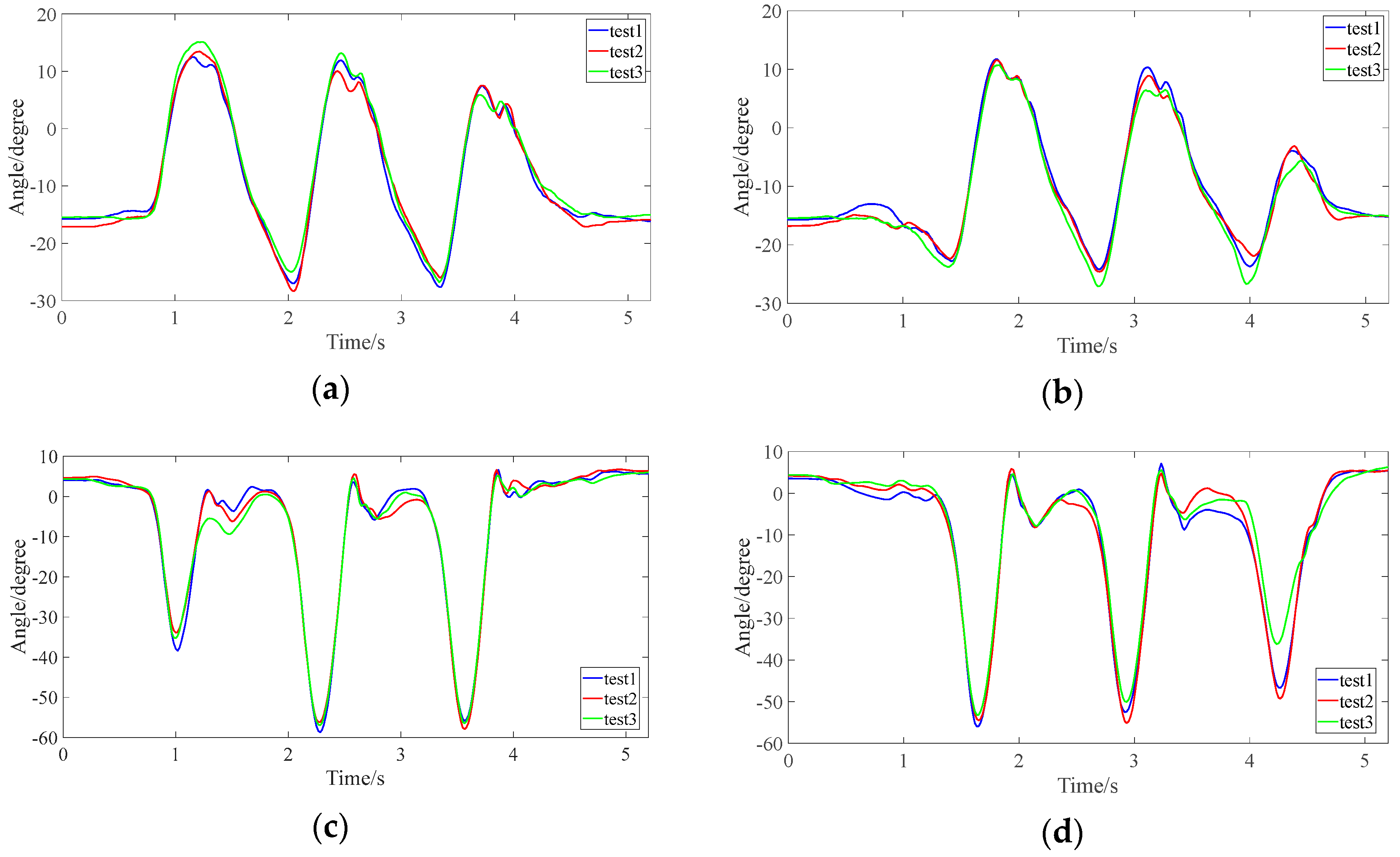
4.3. Data Processing

Due to the difficulty in controlling the speed consistently across multiple trials, the lengths of the time series and walking positions vary for each experiment, as shown in Figure 6. Time series alignment is a critical issue in various applications, including bioinformatics, computer vision, speech recognition, speech synthesis, and human motion recognition [32]. The most commonly used method for performing this alignment is Dynamic Time Warping (DTW), which can be employed to discover similar walking patterns, even if one participant walks faster than the other or if one is decelerating or accelerating. However, the traditional DTW algorithm can only align two sets of sequences; therefore, we chose to use TTW. TTW first aligns the input sequences and then averages the synchronized sequences to compute the centroid signal. TTW utilizes a sinc convolution kernel along with gradient-based optimization techniques to synchronize multiple time series [37]. TTW first aligns the input sequences and then averages the synchronized sequences to compute the centroid signal [37]. This process of synchronizing all trials to a common centroid is particularly beneficial for the subsequent GMM-GMR step. It ensures that all demonstrations are aligned to a unified temporal baseline, effectively eliminating phase shifts and temporal warping as sources of variance. This results in a cleaner, more stable dataset for the GMM to learn the underlying probability distribution of the gait trajectory. Consequently, the GMR can generate a smoother and more representative generalized trajectory that accurately captures the consistent spatial–temporal patterns across all trials.

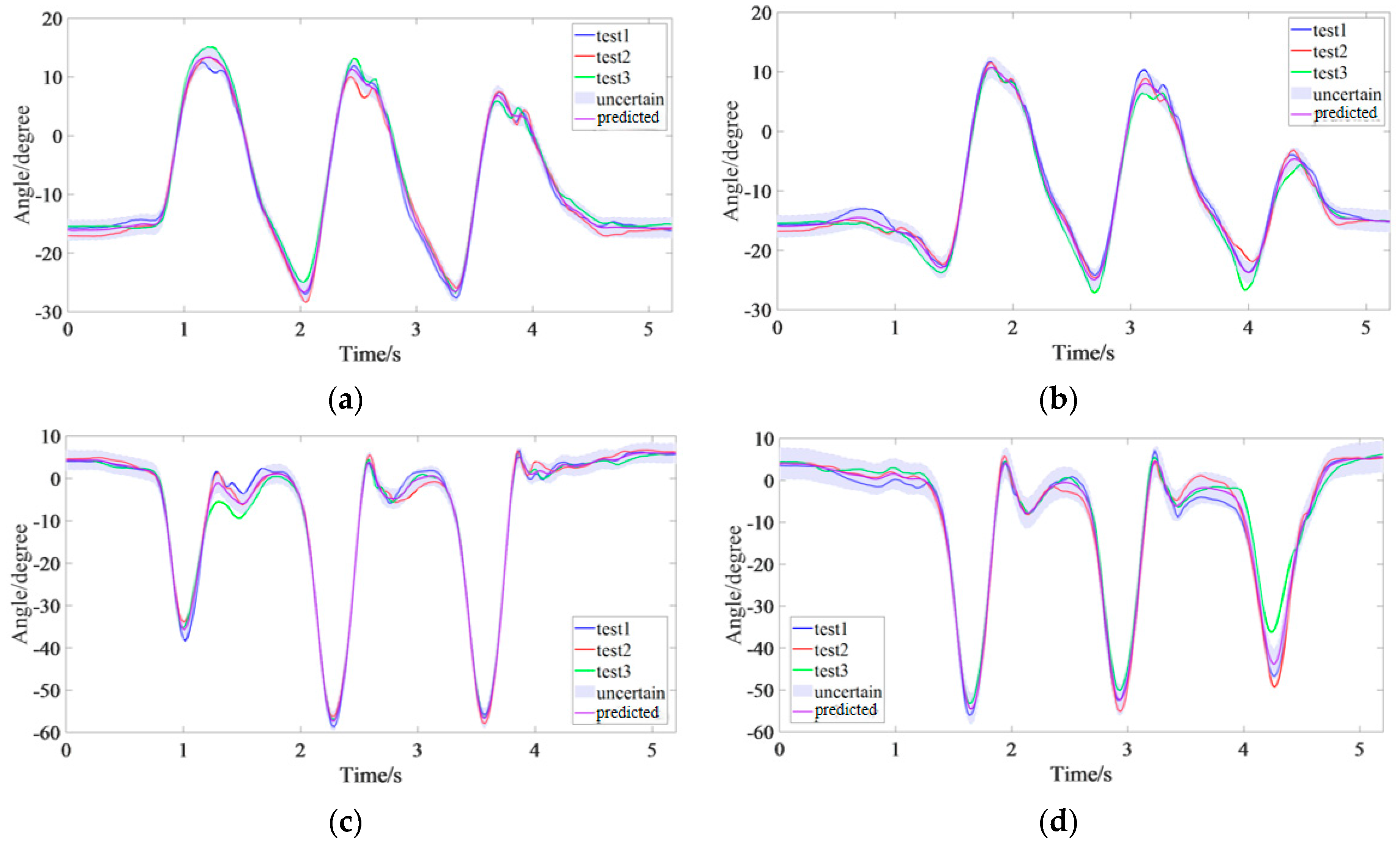
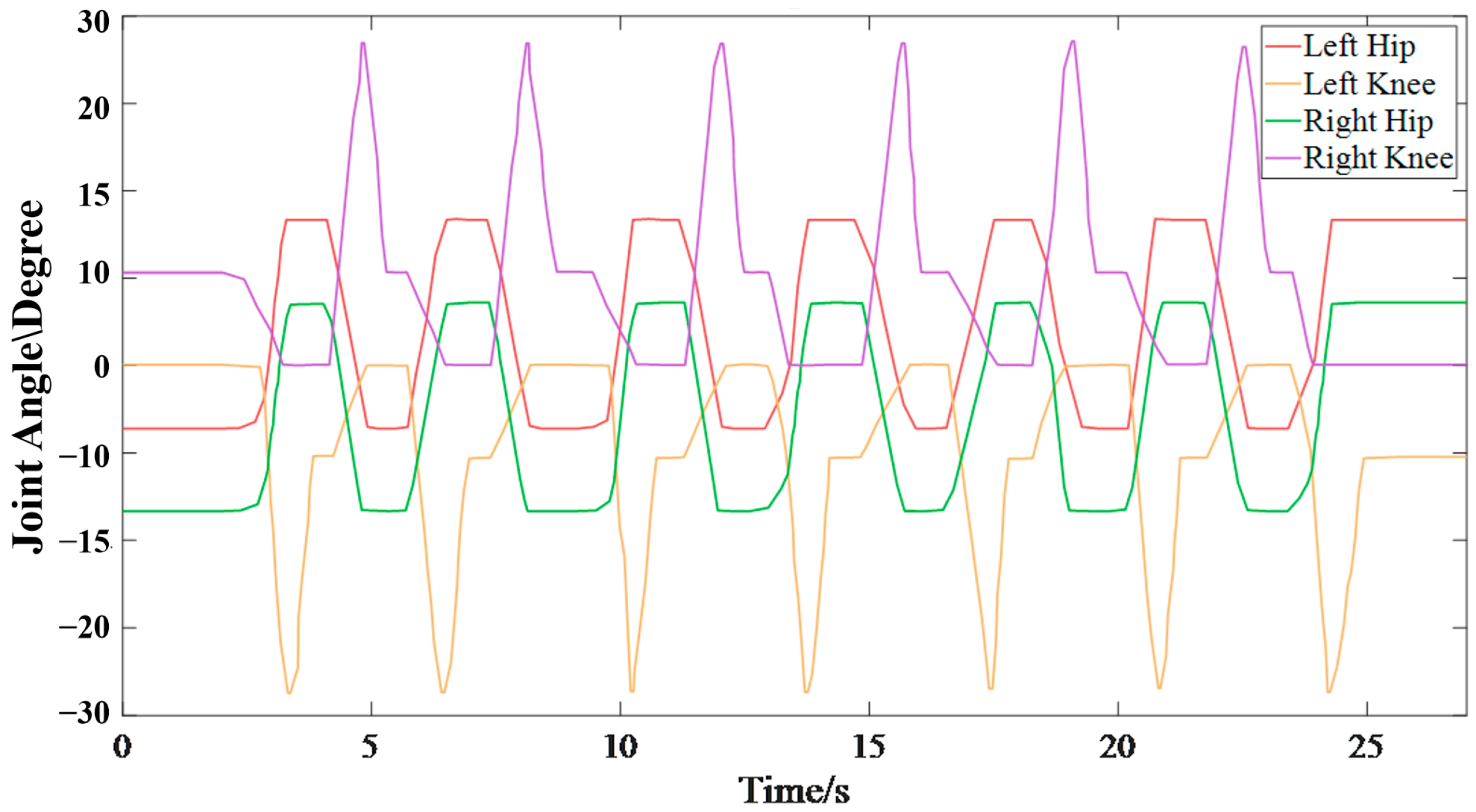
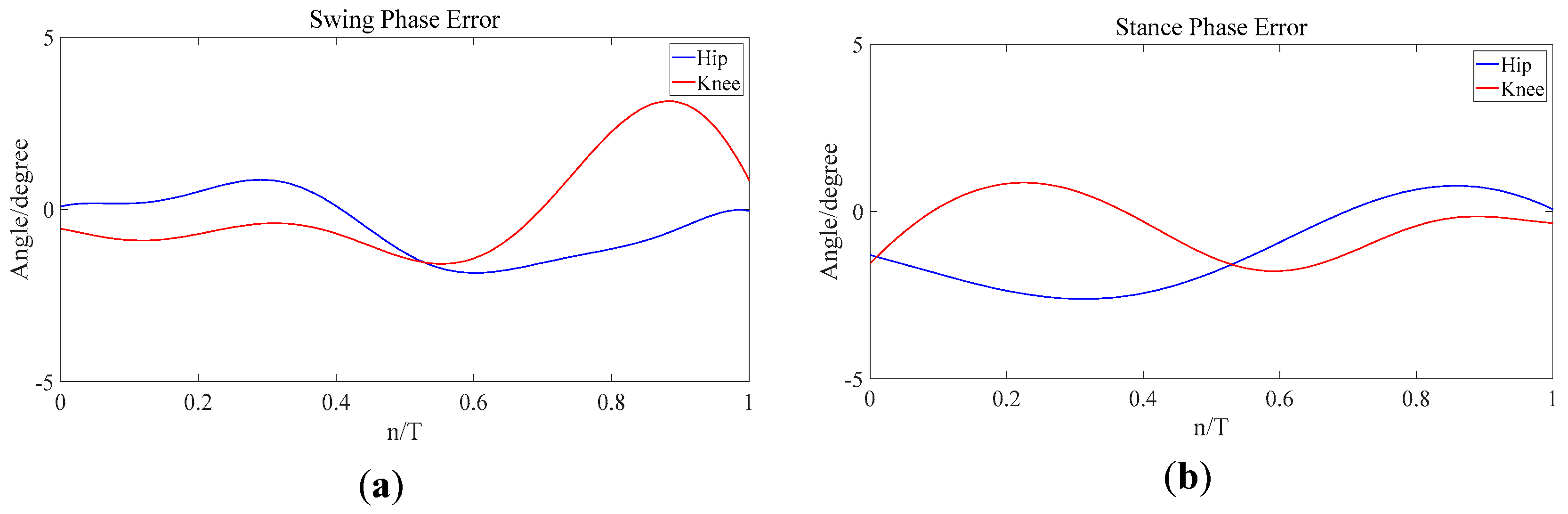
4.4. Experimental Results and Discussion

First, body parameters were measured for 40 participants. They were instructed to walk in a relaxed gait while performing the five-step walking task. Using OpenSim, inverse kinematics were utilized to calculate the angle data for the hip and knee joints. A random participant’s joint angle data during the experiment is displayed in Figure 6.

The TTW algorithm was used to perform time alignment on the data from the three trials, with the results shown in Figure 7.

After GMM-GMR processing, the participants’ joint angle data were utilized to obtain the mean and variance features of the joint angle probability trajectories based on EM. The results of the joint angle data are shown in Figure 8.

Gait is the process of posture change during human movement. It is periodic and regular; the typical gait cycle includes heel strike (HS), toe strike (TS), heel off (HO), toe off (TO), and swing midpoint [11]. Since the exoskeleton robot can only walk step by step and is controlled either via a host computer or buttons, this experiment partitions the walking process based on the minimum hip joint angle. The walking process is divided into the swing phase and support phase for the left and right legs, with the left leg entering the swing phase while the right leg enters the support phase, allowing the legs to alternate between swinging and supporting. The joint angle curves for the swing and support phases are then expanded using a fifth-order Fourier series, resulting in 11 Fourier harmonic coefficients. A gait planning model is trained using GPR to predict personalized gait trajectories for different participants. Verification experiments were conducted on the remaining 20 participants, as shown in Figure 9. The leg length and weight parameters were input into the host computer software interface. After predicting using the offline gait planning model, the required 11 Fourier harmonic coefficients for the hip and knee joints were generated. The Fourier function reconstructed using these coefficients was used as the joint angle trajectory curve for experimentation.

Figure 10 presents the recorded trajectory data for a participant, providing a qualitative validation of the proposed personalized planning method. The generated trajectories demonstrate a physiologically coherent gait pattern. For instance, the hip joint angles (red and green lines) exhibit a smooth, sinusoidal-like pattern, while the knee joint angles (yellow and purple lines) show the characteristic ‘double-peak’ pattern during the swing phase for foot clearance. The anti-phase relationship between the left and right limb trajectories is clearly visible, which is a fundamental feature of stable, bipedal walking.

The walking process was divided into the support phase and swing phase, and the joint angle errors were calculated for the left and right legs when acting as the supporting leg and swinging leg, respectively. As shown in Figure 11, the errors remained within 3°, with an average error of 1.0025°, demonstrating high consistency and control performance.

An investigation was conducted to assess the satisfaction of participants in the prediction experiment regarding gait comfort, with a satisfaction rate reaching 90%. The gait trajectory planning method presented in this study is suitable for users with individual differences.

4.5. Comparative Analysis with Baseline Methods

To quantitatively validate the superiority of the proposed personalized GPR model, its performance was compared against two baseline methods on the same validation set of 20 participants:

Baseline 1 (Population-Average): A generic gait trajectory was constructed by averaging the GMM-GMR fitted trajectories from all 20 participants in the training set. This represents a ‘one-size-fits-all’ approach.

Baseline 2 (Linear Model): A linear regression model was trained to map the anthropometric parameters (thigh length, calf length, weight) to the Fourier coefficients, replacing the non-linear GPR model.

As shown in

Table 1. Mean (Std) Tracking Errors for Different Methods.

Method	Hip Joint RMSE (°)	Knee Joint RMSE (°)	Overall MAE (°)
Proposed (GPR)	1.82 (0.38)	1.89 (0.45)	1.85 (0.41)
Baseline 1 (Average)	3.75 (0.91)	4.10 (0.85)	3.92 (0.88)
Baseline 2 (Linear)	2.95 (0.62)	3.20 (0.70)	3.07 (0.66)

, our proposed GPR method significantly outperforms both baselines. The population-average trajectory (Baseline 1) resulted in the highest error, as it fails to account for individual anthropometric differences. The linear model (Baseline 2) performed better than the average trajectory but was still substantially worse than our method. This performance gap underscores the necessity of a non-linear model like GPR to capture the complex relationship between body parameters and gait kinematics. A paired t-test confirmed that the reduction in Overall MAE achieved by our method over both baselines was statistically significant.

The significantly lower tracking error achieved by the personalized trajectories, under the identical PD control law that produced higher errors for the baseline trajectories, provides compelling evidence that our method generates motions which are not only kinematically appropriate but also dynamically better suited for the exoskeleton system and the individual user. This demonstrates that the personalization occurs effectively at the planning level, producing trajectories that are inherently easier to execute precisely.

These results provide quantitative evidence that our GPR-based personalization is not merely feasible but is critically necessary for achieving low tracking error and, by extension, the high comfort ratings reported by users, who were walking with trajectories tailored specifically to their body shape.

5. Conclusions

This paper has presented a novel, data-driven framework for personalized gait trajectory planning in lower-limb exoskeleton robots. The core of our method lies in establishing a direct mapping from static anthropometric parameters (thigh length, calf length, and weight) to the dynamic characteristics of gait, represented by the Fourier coefficients of hip and knee joint angles. This was achieved through an integrated pipeline that synergistically combines the TTW algorithm for data alignment, GMM-GMR for robust trajectory extraction, and GPR for learning the personalized mapping. Experimental validation on a custom lower-limb exoskeleton demonstrated that the generated trajectories achieve accurate tracking performance with an average joint angle error of 1.0025° and overall RMSE of 1.85°, significantly outperforming population-average and linear regression baselines. The method also received a high user satisfaction rate of 90% regarding comfort. These quantitative results confirm the feasibility and effectiveness of our approach for generating personalized, physiologically appropriate, and user-accepted gait patterns for individuals with different body characteristics.

The main limitations of the current study include the participant demographic, which was limited to a young age group, and the exoskeleton’s mechanical design, which focused on sagittal-plane motion. Future work will prioritize expanding the gait dataset to include older and clinical populations, incorporating age as a model input to enhance generalizability. Furthermore, we plan to design exoskeletons with additional degrees of freedom at the hip and ankle to improve natural balance and eliminate the reliance on crutches, moving closer to fully autonomous gait assistance.