Offline Metrics vs. Online Performance in SDN: A Performance Reversal Study of MLP and GraphSAGE

Abstract

Software-Defined Networking (SDN) provides centralized control over routing paths through a logically centralized controller. Although Graph Neural Networks (GNNs) such as GraphSAGE have shown strong potential for network topology analysis, their superiority over simpler models like the Multi-Layer Perceptron (MLP) in dynamic SDN control remains unclear. In this study, we compare MLP and GraphSAGE using three training data volumes (70, 100, and 140) and spatio-temporal features that integrate spatial and temporal characteristics of each node. Experimental results reveal a distinct discrepancy between offline classification metrics and online SDN performance. Offline evaluation showed that MLP achieved a slightly higher F1-score (0.62) than GraphSAGE (0.59). However, when deployed in a SDN controller, GraphSAGE reduced latency by 17%, increased throughput by 8%, and improved jitter by 31%. These results demonstrate that higher offline accuracy does not necessarily translate into better real-time control performance, since offline metrics fail to capture topology-aware routing, congestion recovery, and dynamic adaptation effects. The findings provide a practical guideline for SDN-oriented AI model evaluation, emphasizing end-to-end system performance over isolated offline metrics.

1. Introduction

1.1. Background and Motivation

Software-Defined Networking (SDN) is an architecture that separates the control plane from the data plane, enabling centralized network management through a controller [1]. This architectural flexibility has led to extensive studies on intelligent traffic engineering and dynamic path control [2,3]. Recently, Graph Neural Networks (GNNs) [4] have been incorporated into SDN environments to model network topologies as graph structures, which allows traffic to be predicted and controlled more effectively, thereby significantly enhancing overall network performance [5].

Among various GNN models, GraphSAGE [6] has demonstrated superior performance in dynamic network environments by learning node representations that exploit the spatial information of network topologies. Several recent studies have applied GNNs to SDN environments for tasks such as traffic prediction [7], routing optimization [8], and anomaly detection [9,10], generally reporting that GNN-based approaches outperform traditional machine learning methods.

However, recent studies have pointed out that the superiority of GNNs is not guaranteed under all circumstances [11]. In particular, they have empirically shown that when the amount of training data is limited, simpler models can outperform GNNs. This issue is especially critical in SDN environments, where collecting diverse network states—normal, congested, and failed—is practically difficult due to constraints in cost, time, and experimental conditions. Despite these practical limitations, there is still a lack of systematic research comparing simple models (e.g., Multi-Layer Perceptron, MLP) and complex graph-based models (e.g., GraphSAGE) with respect to data volume.

Moreover, most existing studies have focused solely on evaluating model classification accuracy, with limited attention given to how such models affect actual network performance indicators such as throughput, latency, and jitter [12]. As network environments change in real time, AI-based network control requires models that ensure both stability and adaptability. Recent studies have emphasized that improving model performance adaptability under real-time constraints is a key factor in enhancing SDN control efficiency and resilience [13,14]. This study aims to strengthen the methodological linkage between AI-based network control and real-time constraint-based model performance. Additionally, we evaluate model performance in online network environments to verify the practical applicability of existing research.

To address these limitations, we systematically compare the MLP and GraphSAGE models in SDN path control scenarios, focusing on the discrepancy between offline classification metrics and online control performance. In particular, this study investigates whether offline accuracy (e.g., F1-score) correlates with improved network-level indicators such as throughput, latency, and jitter. In addition to classification metrics, we also evaluate improvements in actual network performance, providing a practical guideline for model selection in resource-constrained SDN environments.

1.2. Related Work

1.2.1. SDN-Based Intelligent Path Control

In SDN environments, numerous studies have explored intelligent path control by leveraging machine learning and deep learning techniques. In [3], a method utilizing Deep Reinforcement Learning (DRL) was proposed to optimize Virtual Network Function (VNF) placement in SDN/NFV environments. This approach reduced end-to-end latency by up to 28% and improved the service acceptance rate by up to 22% compared with traditional heuristic algorithms and conventional Q-learning-based methods. However, this study assumed that sufficient training data were available, and it had limitations in collecting and dynamically reflecting unpredictable real-time state data occurring in actual network environments.

In [5], a Graph Transformer-based DRL approach was introduced to consider long-range dependencies in SDN routing. Although it achieved superior performance in complex topologies, the issue of increased data requirements resulting from higher model complexity was not addressed. In particular, it overlooked the possibility of overfitting in small-scale networks or data-limited environments. In [15,16], a hybrid GNN–DRL framework was proposed to optimize network paths, whereas [15] discussed the risk of overfitting and poor generalization inherent to such models. Furthermore, [14] emphasized only the reduction in average end-to-end delay, which may potentially degrade other key metrics such as bandwidth utilization, packet loss, and jitter.

1.2.2. GNN Applications in Network Management

GNNs are well-suited for representing node information by modeling the structure of network topologies, making them useful for routing research in SDN environments. In [7], a comprehensive review of end-to-end networking solutions combining GNNs and DRL was presented, demonstrating that GNNs are capable of learning the spatial dependencies of network topologies. However, this study did not sufficiently consider the limitations of data collection in real deployment environments.

In [17], L-GraphSAGE was proposed to classify encrypted traffic in Internet of Vehicles (IoV) environments, achieving over 95% accuracy. In [11], it was reported that when GCNs are applied to graphs with low homophily, the aggregation of neighboring nodes (often from different classes) can contaminate the unique features of nodes, thereby degrading class separability. Consequently, it was argued that a simple MLP—which ignores the graph structure and focuses solely on individual node features—can sometimes outperform GNNs. Nevertheless, models such as GraphSAGE, which aggregate information through neighboring features, can alleviate this feature contamination and maintain effective node distinction.

1.2.3. Performance Comparison Studies

In the networking field, various studies have compared the performance of different machine learning models. In [17], a GNN-based rate-limiting framework was proposed to mitigate DDoS attacks in SDN environments. The framework learned traffic relationships between hosts as a graph and penalized abnormal hosts to restrict their traffic. However, this study did not address the potential real-time processing overhead or the trade-off between accuracy and model complexity that may arise from using a GNN. Furthermore, research that links the amount of training data to actual network performance metrics remains limited.

In [18], it was explained that due to the aggregation mechanism of the GraphSAGE model, it can be challenging to effectively learn minority-class neighbor information and structural diversity. To mitigate this, the study incorporated additional subgraph structures of specific nodes, which improved the performance of imbalanced node classification. Nevertheless, the improvement achieved by adding subgraph information was marginal, and it remained unclear to what extent the generated subgraphs effectively reflected the true structural characteristics of the network.

1.3. Research Gap and Contribution

While numerous studies have evaluated GNN-based models using offline metrics such as F1-score or accuracy, few have examined how these evaluation results translate into actual SDN control performance. Moreover, the relationship between model-level metrics and system-level outcomes (e.g., throughput, latency and jitter) remains largely unexplored. This study bridges this gap by analyzing the discrepancy between offline evaluation metrics and online performance in SDN path control.

Specifically, this paper aims to:

• Compare the offline evaluation results of MLP and GraphSAGE models with their online SDN controller performance
• Analyze the discrepancy between offline metrics (e.g., F1-score) and online indicators (throughput, latency, jitter)
• Provide a practical guideline for model selection emphasizing end-to-end performance rather than standalone accuracy

To achieve this, we train MLP and GraphSAGE models using data collected from the SDN environment to classify network states (NORMAL, ABNORMAL, and FAIL). The trained models are then deployed in the SDN controller to perform intelligent path control in real time, verifying whether the network condition improves after applying the proposed models.

2. Methods

2.1. Overall Architecture

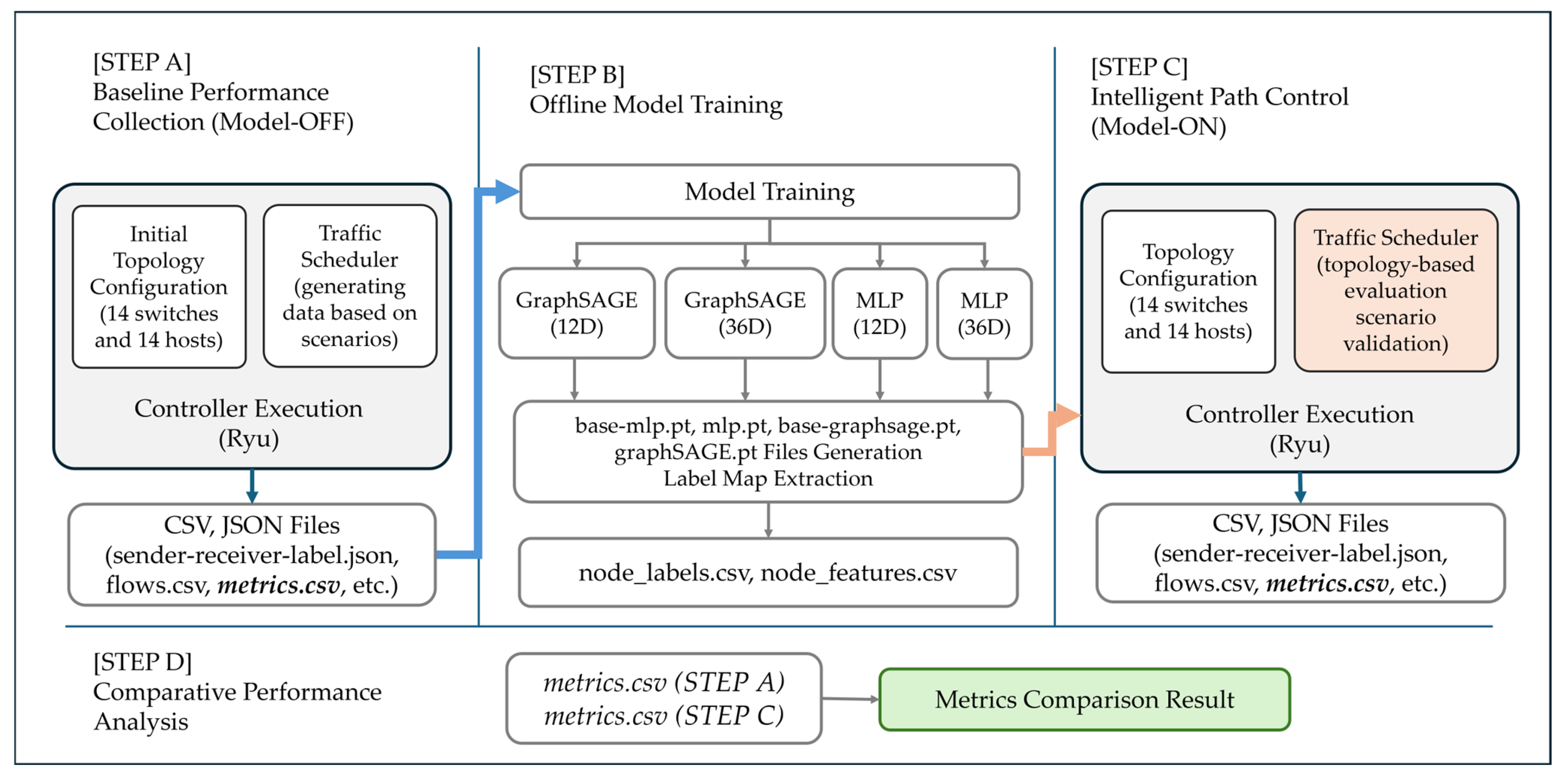
This section details a four-step experimental pipeline designed to compare offline model metrics with online SDN performance, as illustrated below.

• [STEP A] Baseline Performance Collection (Model-OFF): This stage collects (or generates) the data required for training the GNN model. Network states are deliberately configured to represent NORMAL, ABNORMAL, and FAIL conditions, and the corresponding network logs are recorded.
• [STEP B] Offline Model Training: In this stage, the GraphSAGE/MLP model is trained offline using the log files collected in Step A.
• [STEP C] Intelligent Path Control (Model-ON): The trained model from Step B is loaded into the SDN controller to verify its ability to recognize real-time network conditions and perform intelligent path control.
• [STEP D] Comparative Performance Analysis: The metrics and logs obtained from Steps A and C are compared to derive the final performance evaluation results.

An overview of the proposed algorithm is presented in Figure 1.

2.2. [STEP A]: Baseline Performance Collection (Model-OFF)

[STEP A] serves two primary purposes: (1) baseline performance measurement and (2) collection of training data for model learning. Accordingly, the simulation environment was designed to operate three core components simultaneously, enabling them to interact organically. In [STEP A], four categories of information were collected to establish a baseline performance measurement and construct a dataset for model training:

(1)

Traffic-level statistics—Packet transmission and reception rates (bps, pps) per second for each port, collected from flow.csv and ports.csv.

(2)

Event and link state information—Link status, connection, and disconnection events recorded in events.csv.

(3)

Performance indicators—Throughput, latency, and jitter of end-to-end paths, extracted from metrics.csv.

(4)

Topology and flow mapping—Source–destination pairs, routing paths, and node labels stored from sender-receiver-label.json and NSFNet-topology.py

These four categories include both spatial (topology-based) and temporal (change-based) information required to construct the spatio-temporal feature vector in [STEP B].

In [STEP A], first, the SDN controller is executed to establish the basic SDN environment. Next, the NSFNet-topology.py script is used to construct a topology consisting of 14 switches and 14 hosts, after which connectivity between hosts is verified through successful ping tests.

Simultaneously, the controller operates in data collection mode (Model-OFF) without a trained model, meaning that it does not actively control paths but only logs the traffic occurring within the topology.

As shown in

Table 1. Data Collection Scenarios.

Class	Traffic Bandwidth Range (Mbps)	Scenario Ratio (%)
NORMAL	1–3	20
ABNORMAL	4–8	20
FAIL	3	60

, the NORMAL, ABNORMAL, and FAIL scenarios were intentionally generated in a ratio of 2:2:6, with particular emphasis on collecting a larger amount of FAIL traffic, which is more difficult to detect.

Through this process, several data files are generated, including CSV files (ports.csv, events.csv, flows.csv, metrics.csv) and JSON files (e.g., h12-h24-normal.json). These datasets are used for both model training and comparative evaluation. Specifically, in [STEP B], the files ports.csv, events.csv, flows.csv, and sender-receiver-label.json are utilized to extract 12-D and 36-D feature vectors and to generate corresponding ground-truth labels for training. In contrast, [STEP D] employs metrics.csv to compare pre- and post-model performance in terms of throughput, latency, and jitter.

2.3. [STEP B]: Offline Model Training

In [STEP B], four offline model training processes are conducted based on the log files (CSV and JSON) collected in [STEP A]. In this study, two models—MLP and GraphSAGE—were evaluated for path control in the SDN environment. The MLP model controls paths using only the information from an individual node, while the GraphSAGE model incorporates neighboring node information through a graph-structured aggregation mechanism, allowing a comparative analysis between simple and graph-based approaches.

Both models are trained using two types of feature representations: a 12-dimensional feature vector (derived from 12 traffic-related log attributes; see Section 2.3.1) and a 36-dimensional feature vector (12 features × 3 time steps: t-2, t-1, t₀) that includes temporal information. Thus, a total of four models were trained.

Table 2. Four Learning Models (Offline Training).

Model	Graph Structure	Spatial	Temporal Window	Input Dim	Description
Base MLP	✗	✓	✗	12	Independently classifies each node (single-time-step)
Full MLP	✗	✓	✓	36	Applies the temporal information of each node
Base GraphSAGE	✓	✓	✗	12	Utilizes only the graph structure (single-time-step)
Full GraphSAGE	✓	✓	✓	36	Utilizes both the graph structure and temporal information

summarizes these four learning models.

For MLP, which classifies nodes independently without considering the graph structure, two versions are used depending on whether temporal features are applied: 12D (Base MLP) and 36D (Full MLP). Similarly, for GraphSAGE, two configurations are employed: 12D (Base GraphSAGE) and 36D (Full GraphSAGE). In particular, for the GraphSAGE model, experiments are conducted using three aggregation functions—mean, max, and min—to analyze the effect of different aggregation mechanisms.

Through [STEP B], four models were trained, and their performance was compared using evaluation metrics such as F1-score, AUC, and Accuracy. The generated model files (gsage.pt and mlp.pt) were subsequently utilized in [STEP C], where they were deployed in the SDN controller to control the routing of newly generated traffic.

2.3.1. Spatio-Temporal Feature Vector (12D and 36D)

In this study, a 36-dimensional spatio-temporal feature set was derived based on the log information generated at each switch. To this end, key features were selected with reference to previous studies on network monitoring and anomaly detection [19,20], which primarily utilized traffic volume per link as a core metric. In the present work, this approach was extended by employing aggregated statistical measures—sum, mean, and maximum—to more comprehensively capture traffic characteristics.

The extracted features encompass traffic volume, distribution, temporal variation, and QoS, and are used to distinguish between the NORMAL, ABNORMAL, and FAIL classes. Among the proposed 36-dimensional feature vectors, the 12-dimensional feature subset is classified into five major categories.

• Traffic Volume and Load Features: Indicators that quantify the overall traffic throughput and load level of each switch. The traffic volume serves as a fundamental metric for assessing network congestion.
• Traffic Distribution and Imbalance Features: Metrics designed to evaluate whether the traffic is evenly distributed among switch ports. Detecting traffic imbalance helps identify routing inefficiencies or anomalies along specific paths.
• Temporal Dynamic Features: Features that capture the trend of traffic variation by comparing the current network state with previous states.
• QoS Features: Indicators that represent network quality. Increased delay or packet loss implies potential congestion or failure conditions.
• Traffic Profiling Features: Features used to detect deviations from normal traffic behavior and to identify abnormal traffic patterns.

Table 3. Descriptions of 12-Dimensional Feature Vector Elements.

Feature Category	Feature Vector	Description
Traffic Volume and Load	sum_bps	The total transmitted and received traffic (BPS) across all active ports; an indicator representing the overall traffic volume.
	mean_bps	The average BPS of active ports, used to assess the average load per port.
	max_bps	The maximum BPS among active ports, detecting traffic concentration on specific ports.
	util_bps	The average link utilization; used to determine congestion based on the load-to-capacity ratio.
Traffic Distribution	std_bps	Measures traffic imbalance (variance) among ports.
	port_util_variance	Measures variance in port utilization, indicating uneven traffic distribution.
Temporal Dynamic	delta_mean	The rate of change in average BPS compared with the previous window, capturing sudden traffic fluctuations.
	bps_growth_rate	The overall BPS growth rate, specialized for detecting abnormal traffic.
QoS	rtt_mean	The mean response time, a key indicator of network congestion.
	rtt_jitter	The jitter of response time, assessing the consistency of latency.
Traffic Profiling	avg_packet_size	The average packet size, used for detecting abnormal traffic patterns.
	burstiness	Measures traffic burstiness.

provides a detailed explanation of the elements that compose the 12-dimensional feature vector. Each of the twelve features is derived from the statistical information of active ports and serves as an input component of the feature vector to characterize network properties such as link congestion status and link utilization.

The 12 features in Table 3 are calculated based on packet logs collected for each flow and represent the statistical characteristics of the traffic within a time window. The ‘Traffic Volume and Load’ category assesses the link’s load status using traffic statistical information such as sum, mean, and max. For example, sum_bps uses cumulative values such as total transmission volume (byte_sum), total packet count (pkt_sum), and total error count (err_sum). mean_bps determines the average load through average transmission speed (mean_bps), average delay (mean_delay), and average jitter (mean_jitter). Furthermore, max_bps identifies traffic concentration by measuring the maximum throughput within a specific interval using values such as max_throughput and max_delay.

To incorporate time-series characteristics into the 12-dimensional (Table 3) feature vector, values from t-1 and t-2 were derived relative to a specific time window, t₀. This forms a 36-dimensional spatio-temporal feature vector: 12 features (spatial) times 3 time steps (temporal) = 36 dimensions.

In this study, the same aggregation process was applied to both the [STEP A] data collection and the [STEP C] performance verification methods.

2.3.2. Comparison of Model Architecture

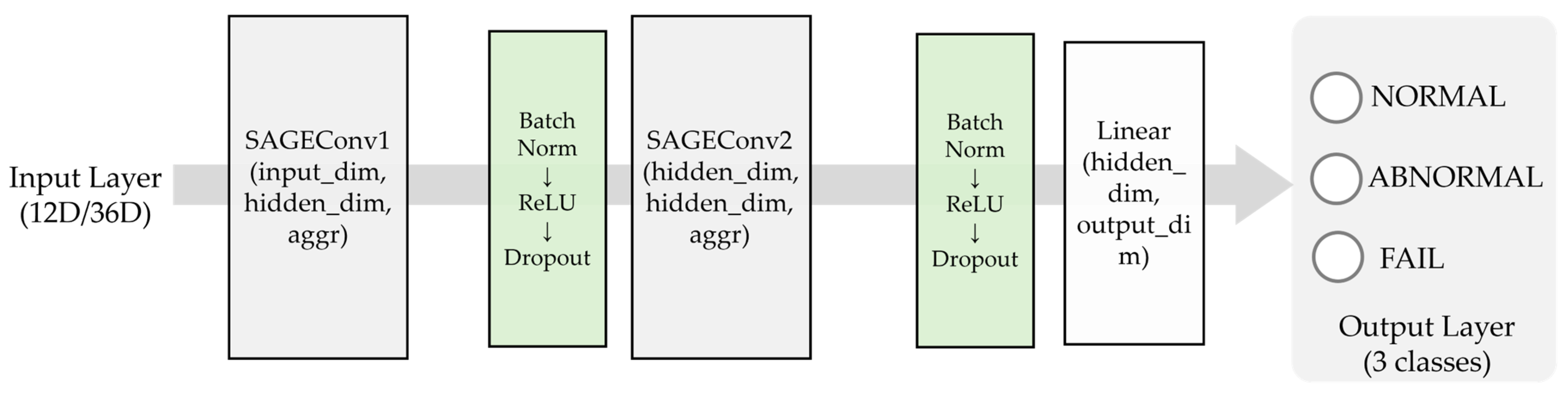
GraphSAGE Model

In this study, the existing GraphSAGE model was employed as a node state classification model incorporating spatio-temporal feature information. GraphSAGE generates node embeddings by sampling and aggregating the features of neighboring nodes. This approach enables flexible management of frequent link delays and disconnections in SDN environments.

The GraphSAGE model designed in this study adopts a two-layer architecture (see Figure 2). The input dimension is set to 12 (Base GraphSAGE) or 36 (Full GraphSAGE), the hidden dimension to 96, and the output dimension to 3, corresponding to the three classes: NORMAL, ABNORMAL, and FAIL. The model architecture comprises two SAGEConv layers followed by a Linear layer for classification. To prevent overfitting, a dropout rate of 20% (p = 0.2) is applied between layers.

In particular, to analyze the performance variation according to aggregation methods, three aggregation functions—mean, max, and min—were applied and evaluated experimentally. As a result of experimenting with each of the three aggregation functions, the max-based aggregation method demonstrated the most stable and highest F1-score overall. Accordingly, max aggregation was used as the default configuration in the online performance evaluation stage of this study.

MLP Model

To compare the performance with GraphSAGE, MLP was adopted as the baseline model in this study. The MLP does not exploit graph structural information and classifies each node independently, thereby enabling verification of the effectiveness of incorporating graph structure through comparison with GraphSAGE.

The MLP model designed for this study follows a simple three-layer architecture. The input layer receives a feature vector of 12 dimensions (Base MLP) or 36 dimensions (Full MLP). The hidden layer consists of 32 neurons, with the ReLU activation function applied to introduce nonlinearity. The output layer comprises three neurons corresponding to the three classes: NORMAL, ABNORMAL, and FAIL.

Since the MLP model classifies nodes independently without considering graph topology, it provides a clear contrast to GraphSAGE. Owing to its simplicity, it serves as an appropriate baseline for evaluating the contribution of graph structural information.

Model Architecture and Training Parameters

To ensure reproducibility in our proposed study, the detailed architectures and training parameters for the MLP and GraphSAGE models are summarized in

Table 4. Detailed architectures and training hyperparameters used for the MLP and GraphSAGE models.

Model	Layers	Hidden Dimension	Activation Function	Dropout	Optimation	Training Rate	Batch Size	Epoch	Loss Functions	Aggregator
MLP	3 (Input–Hidden–Output)	32	ReLU	0.2	Adam	0.001	64	150	$\mathrm{Focal} \mathrm{Loss} (\gamma =2.5$)	-
GraphSAGE	2 SAGEConv + Linear	96	ReLU	0.2	AdamW	0.001	64	150	$\mathrm{Focal} \mathrm{Loss} (\gamma = 2.5$)	Mean/Max/Min

.

The MLP model has a 3-layer architecture using ReLU activation, with the hidden layer set to 32 dimensions. The GraphSAGE model consists of two SAGEConv layers and one Linear layer (hidden dimension 96), and dropout (p = 0.2) was applied between layers to prevent overfitting.

Both models utilized the softmax activation function in the output layer for classification into the three classes (NORMAL, ABNORMAL, and FAIL). For optimization, Adam (learning rate 0.001, weight decay $1\times {10}^{-4}$) was used, and the batch size was set to 64. Training was conducted for a maximum of 150 epochs, but early stopping was applied if the validation loss did not improve for 40 consecutive epochs.

To mitigate class imbalance, Focal Loss with $\gamma =2.5$ was used. Furthermore, AdamW was employed to separate the weight decay term from the momentum update, thereby aiming to enhance training stability. Additionally, the aggregation functions (mean, max, and min) were applied independently to compare performance differences.

2.3.3. Model Training Process

In this study, the same training pipeline was applied to both the MLP and GraphSAGE models to ensure a fair comparison.

First, stratified sampling was employed to divide the dataset into training and testing sets at a ratio of 7:3. Because the ABNORMAL and FAIL classes exhibited severe class imbalance, the dataset was organized such that at least one sample from each of these classes was included in the test set. If only one sample existed for a given class, it was assigned exclusively to the training set. All feature vectors were standardized using the StandardScaler, normalizing each feature to have a mean of 0 and a standard deviation of 1 to account for differences in feature scales.

Second, since the experimental data used in this study were collected from a network environment dominated by NORMAL traffic, the proportions of ABNORMAL and FAIL classes were intentionally increased. Data were collected in a ratio of NORMAL (2): ABNORMAL (2): FAIL (6). Although the proportion of NORMAL samples was reduced, significant class imbalance remained. To address this, data augmentation was performed by oversampling the ABNORMAL class by a factor of three and the FAIL class by a factor of two. New samples were generated by adding Gaussian noise (5%) to the original feature vectors. Furthermore, the Focal Loss [21] function was applied to focus the training process more on hard-to-classify samples.

$$FL\left(p_t\right)=-{\alpha (1-p_t)}^{\gamma }log\left(p_t\right)$$

(1)

In Equation (1), the parameter $\gamma$ was set to 2.5 to emphasize the loss for misclassified samples. In addition, class-specific weighting factors $\alpha$ were configured to increase the importance of minority classes. Depending on the aggregation method, the following weight settings were applied: mean [1.0, 3.5, 2.0], max [1.0, 4.0, 2.0], and min [1.0, 3.5, 2.5].

The Adam optimizer was employed with a learning rate of 0.001 and a weight decay of 1 × 10⁻⁴ to prevent overfitting. For GraphSAGE, AdamW [22,23] was additionally used in combination with a Cosine Annealing with Warm Restarts [24] scheduler to enhance training stability. The maximum number of epochs was set to 150, but early stopping was applied so that training was terminated if the validation loss did not improve for 40 consecutive epochs.

2.4. [STEP C]: Intelligent Path Control (Model-ON)

In [STEP C], the model.pt files trained in [STEP B] were deployed to the SDN controller to enable real-time path control. For this purpose, four model files—base-mlp.pt, mlp.pt, base-graphsage.pt, and graphsage.pt—were individually applied and evaluated.

In this study, Equal-Cost Multi-Path (ECMP) routing, one of the simplest multipath control methods, was employed. In the proposed approach, routing paths are determined based on node states and their assigned weights, and the paths are selected according to the classification results (see Algorithm 1). The ECMP mechanism was implemented following the method specified in RFC 2992.

Algorithm 1: Intelligent Path Control using Model Prediction and Weighted ECMP.
Input	Loaded_Model: The .pt file trained in [STEP B] (MLP or GraphSAGE model). Current_Features: Real-time collected 12-D or 36-D feature vectors. Network_Graph: The current network topology graph. Link_to_Port_MAP: Information mapping the inter-switch port connections.
Output	Updated OpenFlow Group Tables and Flow Rules in switches for dynamic path control.
	Predict Node Status: Use the Model(*.pt) and Features to predict the status                 (‘NORMAL’, ‘ABNORMAL’, ‘FAIL’) Calculate Weighted ECMP:  FOR EACH source switch s:   FOR EACH destination switch d:    Find shortest paths and identify potential next_hops s -> d    Assign Weights (NORMAL = 3, ABNORMAL = 1, FAIL = 0)    Update/Create OpenFlow Group Table on switch s for destination d:     Define buckets pointing to next_hops     Replicate buckets according to their assigned weights      (more weight = more buckets = more traffic)     Send OFPGroupMod <- switch s.   Ensure OFPFlowMod directs traffic for d’s IPs to this Group Table.

The controller identifies potential next-hop switches by considering up to $k=3$ shortest paths for each source–destination switch pair. Subsequently, each switch is classified as NORMAL, ABNORMAL, or FAIL according to the prediction results obtained from the model.pt file. Based on the classified node states, differential weights (priorities) are assigned to the next-hop candidates.

Using these weights, the controller dynamically updates the OpenFlow Group Table to perform real-time path control according to the current link states.

2.5. [STEP D]: Comparative Performance Analysis

[STEP D] represents the final analysis stage, which quantitatively verifies the differences in path control effectiveness among models according to the data volume. For this purpose, the baseline performance collected in [STEP A] was compared with the performance measured in [STEP C] under each model type and data volume condition (70, 100, and 140 training iterations).

For the analysis, the throughput, latency, and jitter values recorded in each condition’s metrics.csv file were utilized. These metrics serve as essential indicators for evaluating the effectiveness of dynamic path control in SDN environments.

• Throughput (throughput_bps): Indicates the degree of network capacity utilization; higher values represent more efficient utilization.
• Latency (latency_ms): Represents how quickly traffic rerouting occurs during congestion or failure events; lower values indicate faster responsiveness to network disruptions.
• Jitter (jitter_ms): Reflects the stability of the network after path control; lower jitter values indicate better quality for real-time services.

For each metric, descriptive statistics such as the mean, median, and standard deviation before and after model application were compared, and distributional changes were visually analyzed using boxplots. The comparative analysis results are presented in Section 3 (Results) to illustrate how data volume influences the actual path control performance of the MLP and GraphSAGE models.

2.6. Experimental Setup

2.6.1. Simulation Environments

All experiments in this study were conducted on an Ubuntu 20.04.6 LTS Server equipped with a 12th-generation Intel Core i9-12900 processor (16 cores, 24 threads), 62 GB RAM, and an NVIDIA GeForce RTX 3080 GPU with 12 GB VRAM. The GPU driver version was NVIDIA-SMI 570.133.07.

To evaluate the proposed approach, the experiments were performed following a four-step process (see Figure 1), which enabled the SDN controller to train and evaluate both the MLP and GraphSAGE models. The SDN environment was implemented using Mininet 2.3 for network topology emulation (as described in Section 2.6.2), and the SDN controller was developed on the open-source Ryu 4.34 framework. Communication between the controller and switches was managed via the OpenFlow 1.3 protocol implemented by Open vSwitch 3.6.0.

Both the MLP and GraphSAGE models were implemented and trained in Python 3.8, utilizing PyTorch 2.2.2 and PyTorch Geometric 2.5.3, respectively. Graph-based operations and path computations within the controller were performed using NetworkX 3.1, and all training procedures were executed on the CPU.

Table 5. Key Software Configurations for the SDN Simulation Environment.

System Configure	Version
Operating System	Ubuntu 20.04.6 LTS
Language	Python 3.8
Library	Torch_geometric 2.5.3 Pandas 2.0.3 Scikit-learn 1.3.2 Numpy 1.24.4
Components	Mininet 2.3 Ryu 3.4 NetworkX 3.1 Pytorch 2.2.2

summarizes the configuration of the SDN simulation environment.

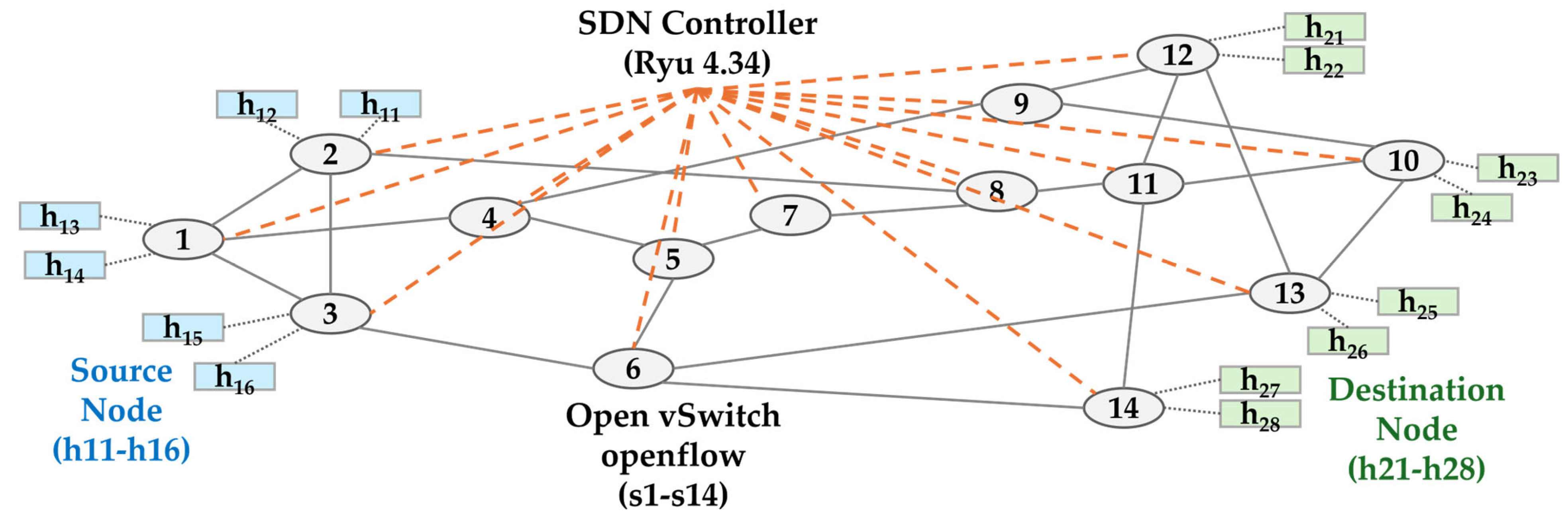
2.6.2. Experimental Topology

This section describes the structure of the virtual network environment used for the simulation (Figure 3). In this study, the network topology was constructed based on NSFNet, which is one of the most widely adopted benchmark topologies in graph-based model research and features the smallest number of nodes among them.

The topology consists of 14 OpenvSwitch (s1–s14) and 14 hosts (h11–h28), which were created in the Mininet environment. All switches (s1–s14) in the topology are managed by the SDN controller (Ryu 4.34) through the OpenFlow 1.3 protocol. The hosts are divided into source nodes (h11–h16), which generate traffic, and destination nodes (h21–h28), which receive traffic. Each host is connected to a specific switch, as shown in Figure 3 (e.g., h11 and h12 are connected to s2).

The NSFNet-topology.py script, used for topology initialization and traffic generation, has been made available in a GitHub repository (https://github.com/my2jo/NSFNet-topology) (accessed on 17 November 2025) for reproducibility.

2.6.3. Data Collection and Evaluation Scenarios

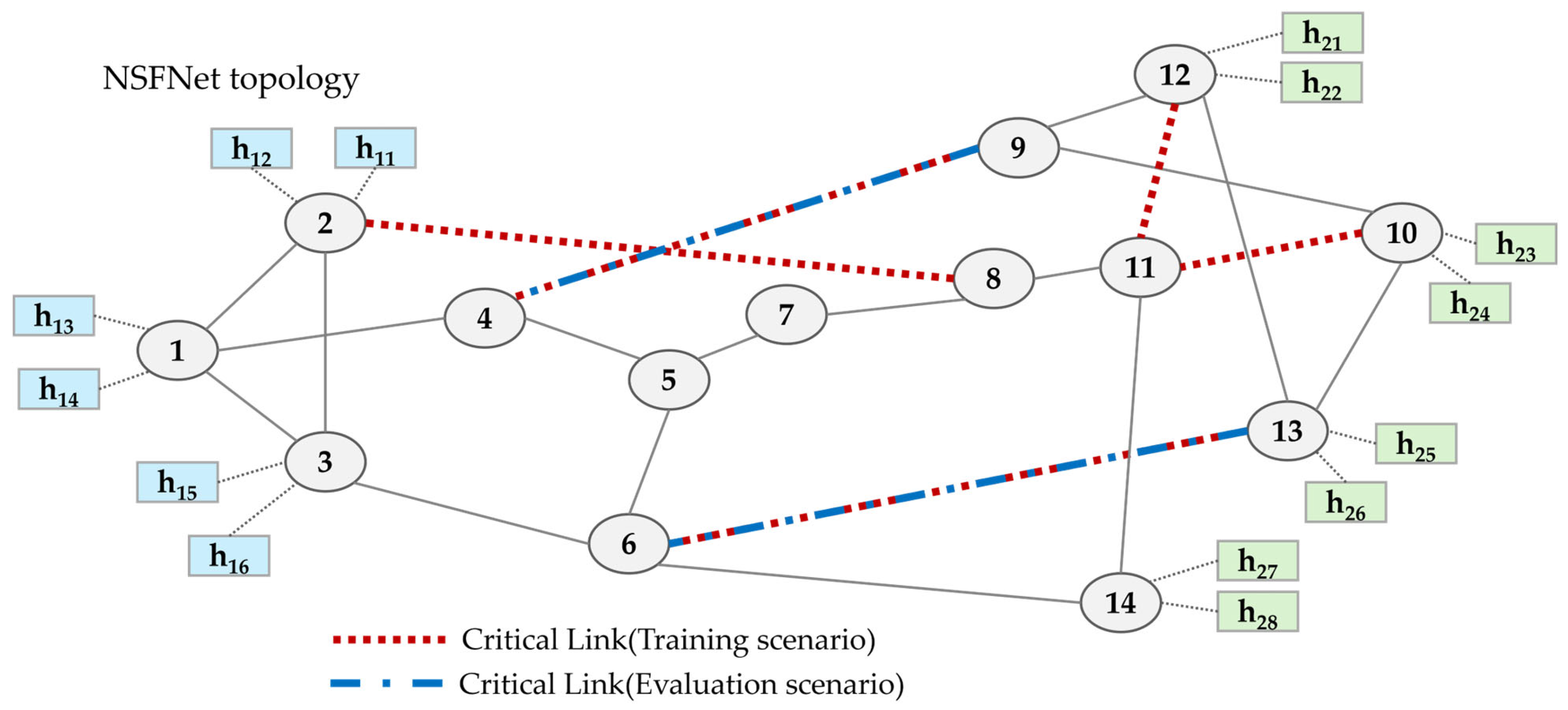
In [STEP A], the topology shown in Figure 3 is used as the experimental environment for baseline performance measurement and training data collection. In [STEP C], the topology illustrated in Figure 4 serves as a testbed to verify the real-time path control performance of the trained models.

The simulation was conducted by configuring different routing paths for each scenario, based on the topology illustrated in Figure 4.

[STEP A] Data Collection Scenario:

• To ensure the diversity of training data, traffic flows were generated between the host pairs specified in Table 5.
• To simulate the FAIL scenario, Critical Links (represented as dashed connections in Table 5) were defined. A Critical Link refers to a link for which an alternative route is available even if a failure occurs on that link. For example, the shortest path for the h13–h21 traffic includes the s4–s9 link; even if this link fails, the traffic can still be rerouted through another path (h13 → s1 → s4 → s9 → s12 → h21).

In this study, a single data collection cycle refers to one emulation run that initializes the NSFNet topology (14 switches and 14 hosts) and then simultaneously generates UDP traffic between 12 host pairs for 60 s. During each cycle, flow-level and switch-level statistical data (port.csv, flows.csv, metrics.csv, events.csv) are collected at 1 s intervals. Therefore, approximately $12 \times 60 = 720$ flow-level samples are generated in a single cycle. By performing a total of 70, 100, and 140 data collection cycles, approximately 50,400, 72,000, and 100,800 samples were generated, respectively.

A 12-dimensional feature vector was constructed from the data collected at each time point. This vector was configured by integrating key parameters of switches and flows (Rx/Tx bytes, Rx/Tx packets, throughput, latency, jitter, and degree within the topology). Furthermore, to reflect temporal changes, the features from time points t-2, t-1, and t₀ were concatenated to create a 36-dimensional spatio-temporal feature vector.

[STEP C] Performance Evaluation Scenario:

• To verify the generalization capability and real-time control performance of the trained models, a different set of host pairs—distinct from those used in [STEP A]—was employed (see

  Table 6. Scenarios for Data Collection [STEP A] and Performance Analysis [STEP C].

  Phase	Scenario Path	Critical Link
  [STEP A] Scenario for Data collection (12 host pairs)	h11–h25, h11–h23, h12–h24, h12–h28, h13–h21, h13–h23, h14–h22, h14–h28, h15–h25, h15–h27, h16–h21, h16–24	s2–s8, s4–s9, s6–s13 s10–s11, s11–s12
  [STEP C] Scenario for Performance Analysis	h11–h28, h12–h23, h13–h24, h13-h26 h14–h26, h15–h23, h16–h25, h16–h26,	s4–s9, s6–s13

  ).
• The Critical Links for failure recovery testing were also configured to include partially different links compared to those in [STEP A] (see Table 6).

2.7. Performance Evaluation Methods

To evaluate the performance of the proposed intelligent path control approach in the SDN environment, the simulation scenarios, network performance indicators, and model classification metrics were defined and employed.

2.7.1. Simulation Scenario

The main focus of the simulation was on the model performance and the amount of training data. To this end, three types of datasets were constructed, as summarized below, and the simulations were performed accordingly. Each scenario represents the number of executions for training data collection ([STEP A]) and performance evaluation ([STEP C]).

• Scenario-Small: 70 training + 30 evaluation runs
• Scenario-Medium: 100 training + 40 evaluation runs
• Scenario-Large: 140 training + 60 evaluation runs

As presented in the simulation scenarios, experiments were conducted with varying data volumes to evaluate the data dependency and scalability of each model. This approach also aimed to observe whether a performance reversal phenomenon occurs depending on the amount of available data.

2.7.2. Network Performance Evaluation Metrics

In [STEP D], the network performance was evaluated by comparing the overall network metrics before and after model deployment, in order to measure the effectiveness of dynamic path control.

• Throughput: Refers to the total amount of data successfully transmitted through the network. A higher throughput indicates a more efficient utilization of network capacity.
• Latency: Represents the average time taken for a packet to travel from the source to the destination. It is used to measure delays caused by congestion or link failures.
• Jitter: Indicates the variation in packet arrival intervals, which reflects the quality and stability of the network service.

2.7.3. Model Performance Evaluation Metrics

In [STEP B], the classification performance of the offline-trained MLP and GraphSAGE models was evaluated using the metrics described below. Since the dataset used in this study is highly imbalanced, with a ratio of NORMAL:ABNORMAL:FAIL = 2:2:6, the use of accuracy alone may distort the actual model performance. Therefore, the following metrics [25,26,27,28]—which are robust to class imbalance—were employed. Here, $N$ denotes the total number of classes, and $i$ represents the index of each class in the classification task.

• F1-Score (Macro): The harmonic mean of Precision and Recall, computed for each class and then averaged using the macro-average method. This was used as the primary metric for comparing offline classification performance.

$${F1}_{macro}={\displaystyle \frac{1}{N}} \sum _{i=1}^N{\displaystyle \frac{2\times {Precision}_i\times {Recall}_i}{{Recision}_i+{Recall}_i}}$$

• Balanced Accuracy (BA): The mean of Recall values across all classes, assigning equal weight to each class regardless of its size. This metric served as a complementary indicator to support the F1-Score comparison.

$$BA={\displaystyle \frac{1}{N}}\sum _{i=1}^N{Recall}_i$$

• G-Mean (Geometric Mean): The geometric mean of Recall for all classes. Because a low Recall in any class decreases the overall score, this metric was used for secondary validation of balanced performance across minority and majority classes.

$$G-Mean={\left(\prod _{i=1}^N{Recall}_i\right)}^{1/N}$$

The evaluation therefore focused on F1-Score, Balanced Accuracy, and G-Mean, which provide a consistent basis for analyzing the relationship between offline model accuracy and online SDN performance.

3. Results

3.1. Classification Performance Comparison

In this study, the results of a comprehensive performance comparison between the MLP and GraphSAGE models under different training data volumes and feature vectors are presented. Distinct trends were observed across model performance metrics, data volume, and network performance indicators.

3.1.1. Effect of Training Data Volume

Table 7. Model Performance Metrics According to Data Volume and Feature Vector.

Training Dataset	Model Type	Features	F1-Score	AUC
70	GraphSAGE MLP GraphSAGE MLP	12D 12D 36D 36D	0.6197 0.5892 0.5909 0.6236	0.8858 0.8770 0.8697 0.8981
100	GraphSAGE MLP GraphSAGE MLP	12D 12D 36D 36D	0.5156 0.5463 0.4031 0.5009	0.7837 0.8622 0.7754 0.8635
140	GraphSAGE MLP GraphSAGE MLP	12D 12D 36D 36D	0.4094 0.4425 0.4530 0.5100	0.7065 0.8064 0.7655 0.8663

presents the classification performance of the MLP and GraphSAGE models under different training data volumes (70, 100, and 140 training iterations) and feature dimensions (12D and 36D). As shown in Table 7, the classification performance of both models exhibits a clear dependence on the training data volume. At 70 training iterations, both models achieved their highest F1-score and AUC values. Specifically, the GraphSAGE model using the 12-dimensional feature vector achieved an F1-score of 0.6197 and an AUC of 0.8858, while the MLP model using the 36-dimensional feature vector recorded an F1-score of 0.6236 and an AUC of 0.8981.

However, as the amount of training data increased to 100 and 140 training iterations, the performance of both models declined.

In particular, for the dataset collected from 140 training iterations, the GraphSAGE (12D) model dropped to an F1-score of 0.4094 and an AUC of 0.7065, while the MLP model yielded an F1-score of 0.4425 and an AUC of 0.8064. This degradation is attributed to the severe class imbalance observed in the dataset, as illustrated in Figure 5.

3.1.2. Effect of Class Imbalance

Figure 5 illustrates the class distribution of NORMAL, ABNORMAL, and FAIL across datasets of different sizes. Although minority classes (ABNORMAL and FAIL) were intentionally oversampled during data collection with a target ratio of 2:2:6 (NORMAL: ABNORMAL: FAIL), the NORMAL class still accounted for more than 70% of the total samples, and this imbalance became even more pronounced as the dataset size increased. This trend indicates that expanding the dataset inadvertently amplified the dominance of the majority class, further aggravating the imbalance problem.

This phenomenon explains that models trained on large datasets with severe class imbalance do not necessarily achieve better performance. As the dataset grows, the model becomes increasingly biased toward the majority class (NORMAL), leading to degraded classification capability for minority classes such as ABNORMAL and FAIL.

3.1.3. Minority-Class Recall Performance Comparison

Figure 6 presents the minority-class recall performance of each model according to data volume. At 70 training iterations, the GraphSAGE model exhibited higher recall than the MLP model. This improvement originates from the graph-based aggregation mechanism, which leverages topological relationships among neighboring nodes. By incorporating structural context, GraphSAGE can better distinguish minority-class samples that otherwise resemble majority-class patterns.

However, as the training iterations increased to 100 and 140, both models experienced a notable decline in recall performance. This observation confirms that when severe class imbalance exists, simply increasing the number of training iterations or collected data does not guarantee improved minority-class detection. Instead, it emphasizes the necessity of addressing data imbalance—such as through targeted augmentation or resampling—to maintain detection robustness in SDN environments.

3.1.4. Performance Tradeoff Analysis

Figure 7 illustrates the trade-off between minority-class detection capability (minority-class recall) and overall classification accuracy (F1-score). In the experiment with 70 training iterations, MLP (36D) achieved the highest overall F1-score (0.6236) but exhibited a relatively lower minority-class recall compared to GraphSAGE (12D, F1 = 0.6197). This trade-off is a critical aspect of SDN path control. While achieving high overall classification accuracy is important, maintaining reliable detection of rare yet critical network states (e.g., FAIL class) is essential for ensuring operational stability. Accurate identification of these minority events enables the controller to perform timely rerouting and congestion mitigation, thereby sustaining network reliability and efficiency in dynamic SDN environments.

3.1.5. Effect of Spatial and Spatio-Temporal Feature Vectors (12D and 36D)

The introduction of spatio-temporal feature vectors did not consistently enhance model performance. In the dataset with 70 training iterations, the MLP model showed an improvement in F1-score from 0.5892 to 0.6236 with the inclusion of temporal features, whereas the GraphSAGE model exhibited a performance decline from 0.6197 to 0.5909. This result suggests that the addition of temporal features can, in some cases, degrade performance rather than enhance it—particularly when class imbalance remains unresolved. The findings further imply that without appropriate data augmentation or feature balancing, incorporating temporal dimensions may increase model complexity without yielding proportional performance gains.

3.2. Network Performance Metrics

Figure 8 compares the throughput, latency, and jitter before and after model deployment to evaluate network performance improvements.

Specifically, it illustrates how the deployment of MLP- and GraphSAGE-based models—each utilizing either 12-dimensional (spatial) or 36-dimensional (spatio-temporal) features—affects the overall SDN network performance.

3.2.1. Throughput Performance

In the baseline configuration (Model-OFF), the median throughput was 35.2 Mbps.

After deploying the models, the overall throughput improved; however, noticeable performance differences emerged between the models.

• MLP 12D: median 64.6 Mbps—an improvement of approximately 83.5% over the baseline
• MLP 36D: median 58.1 Mbps—an improvement of approximately 65.1%
• GraphSAGE 12D: median 62.3 Mbps—an improvement of approximately 77.0%
• GraphSAGE 36D: median 63.0 Mbps—an improvement of approximately 78.9%

From a throughput perspective, MLP 12D achieved the highest median value.

However, inspection of the boxplot in Figure 8a reveals that the MLP models exhibit a high degree of variance and numerous outliers, indicating unstable performance. By contrast, the GraphSAGE models demonstrate relatively lower variance and a more compact distribution, signifying consistent and reliable throughput.

Although the MLP occasionally achieved higher instantaneous throughput, its results lacked stability. GraphSAGE, while yielding a slightly lower median value, provided more predictable and steady performance overall. The effect of the spatio-temporal features (36D) also varied by model: for MLP, performance decreased with the inclusion of temporal features (64.6 → 58.1 Mbps), whereas for GraphSAGE, a slight improvement was observed (62.3 → 63.0 Mbps). These findings indicate that GraphSAGE maintains both competitive throughput and higher stability, particularly when temporal dynamics are incorporated.

3.2.2. Latency Performance

Table 8. Network Performance Metrics Comparison Across Different Dataset Sizes.

Dataset (Training Iterations)	Model	Throughput (Mbps)	Latency (ms)	Jitter (ms)	Improvement
70	Baseline	35.2	77.6	169.7	-
	MLP 12D	64.6 (+83.5%)	44.1 (−43.2%)	133.7 (−21.2%)	Moderate
	MLP 36D	58.1 (+65.1%)	43.1 (−44.5%)	94.3 (−44.4%)	Good
	GraphSAGE 12D	62.3 (+77.0%)	50.8 (−34.5%)	150.0 (−11.6%)	Stable
	GraphSAGE 36D	63.0 (+78.9%)	35.8 (−53.9%)	117.2 (−30.95)	Best
100	Baseline	35.2	76.9	184.4	-
	MLP 12D	60.4 (+71.6%)	36.2 (−53.4%)	107.7 (−36.5%)	Best
	MLP 36D	58.8 (+67.0%)	56.0 (−27.8%)	131.4 (−22.6%)	Moderate
	GraphSAGE 12D	62.3 (+76.9%)	50.8 (−34.5%)	150.0 (−11.6%)	Stable
	GraphSAGE 36D	58.3 (+65.6%)	39.0 (−49.7%)	120.5 (−29.05)	Good
140	Baseline	35.2	56.5	139	-
	MLP 12D	61.2 (+73.9%)	42 (−25.7%)	132.2 (−4.9%)	Good
	MLP 36D	59.7 (+69.6%)	49.3 (−12.7%)	138.2 (−0.6%)	Moderate
	GraphSAGE 12D	62.6 (+77.8%)	37.2 (−34.2%)	111.6 (−19.7%)	Stable
	GraphSAGE 36D	62.0 (+76.1%)	42.5 (−24.8%)	123.8 (−10.9%)	Best

presents the network performance results corresponding to the datasets with 70, 100, and 140 training iterations shown in Figure 8. As indicated in the table, latency was significantly reduced in all configurations after model deployment, and GraphSAGE consistently outperformed MLP. In the baseline configuration (Model-OFF), the median latency was 77.6 ms. Among all tested models, GraphSAGE 36D achieved the lowest median latency of 35.8 ms, representing an approximate 54% reduction relative to the baseline. This finding suggests that the best latency performance can be achieved when both spatio-temporal features and graph-structural information are utilized simultaneously.

Furthermore, an examination of the boxplot distributions reveals that the GraphSAGE models exhibit lower variance compared with MLP, indicating more stable network behavior. In particular, GraphSAGE 36D shows a highly compact distribution with minimal spread, confirming that it delivers consistently low-latency performance in the SDN environment.

3.2.3. Jitter Performance

Figure 8c presents the variation in packet arrival intervals, expressed as jitter (ms).

Lower jitter values indicate stable packet delivery and higher network quality, which are especially critical for real-time services such as VoIP and video streaming. In the baseline configuration (Model-OFF), the median jitter reached 169.7 ms, indicating a highly unstable transmission state. After model deployment, an outstanding improvement in jitter reduction was observed with GraphSAGE.

In particular, MLP 36D achieved the lowest median jitter (94.3 ms), corresponding to an approximately 44% reduction relative to the baseline. However, a closer examination of the boxplot reveals that MLP 36D includes numerous outliers, suggesting unstable performance. By contrast, GraphSAGE 36D achieved a slightly higher median jitter (117.2 ms) but exhibited a much narrower distribution and fewer outlers, thereby providing a more stable and predictable network quality.

Notably, GraphSAGE 12D achieved only a modest jitter reduction rate (11.6%), whereas incorporating spatio-temporal features (36D) substantially enhanced its jitter performance (11.6% → 30.9%). These findings highlight that the integration of temporal information enables GraphSAGE to deliver not only lower latency but also more consistent end-to-end transmission quality in SDN environments.

4. Discussion

4.1. Performance Reversal Analysis

In this study, we confirmed a discrepancy between offline classification metrics and online network performance results in the SDN environment. Although MLP achieved a higher F1-score in the offline evaluation, GraphSAGE demonstrated superior network performance when deployed in the SDN controller. This performance reversal phenomenon provides critical insights for model selection in practical SDN deployment environments.

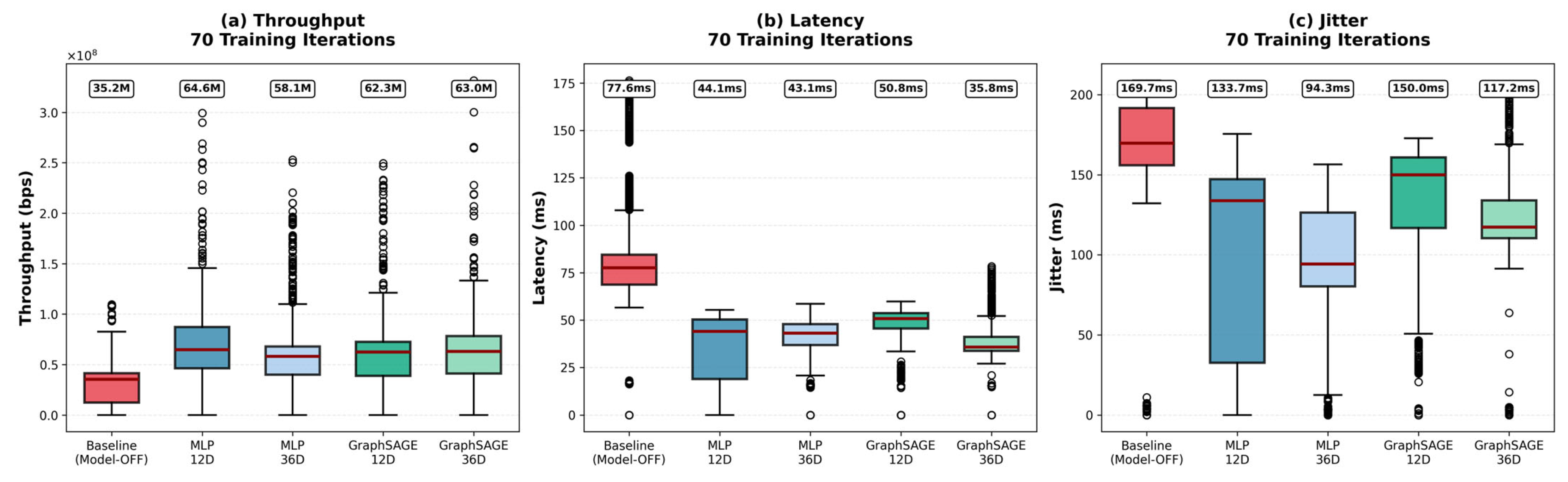
This study confirmed that high offline classification accuracy does not necessarily guarantee the performance of path control. In the dataset from 70 training iterations, MLP 36D exhibited a higher F1-score (0.6236) than GraphSAGE 36D (0.5909). However, after these models were deployed in the SDN controller, GraphSAGE 36D surpassed MLP’s performance by reducing latency by 53.9% and improving jitter by 30.9%. This reversal phenomenon occurs because offline model metrics, such as the F1-score, only measure how accurately switches are classified.

GraphSAGE, which leverages graph structural information to comprehensively consider the states of neighboring nodes, enables a holistic understanding of the entire network rather than representing only the current node’s state. In particular, by aggregating the traffic status of neighboring nodes, the model can detect congestion and select alternative paths, thereby reducing latency. When a link state is classified as FAIL, a routing weight of 0 is assigned, triggering high-priority rerouting that ensures lower latency and jitter. Consequently, dynamic path reconfiguration based on the topology structure and state enhances network stability, which in turn contributes to jitter reduction.

Additionally, although the MLP’s average throughput was somewhat high, its control performance was inconsistent due to large variance and numerous outliers. However, GraphSAGE showed slightly lower average throughput but demonstrated overall stable and predictable control performance with small fluctuations in latency and jitter and fewer outliers, confirming the performance stability of the GraphSAGE model.

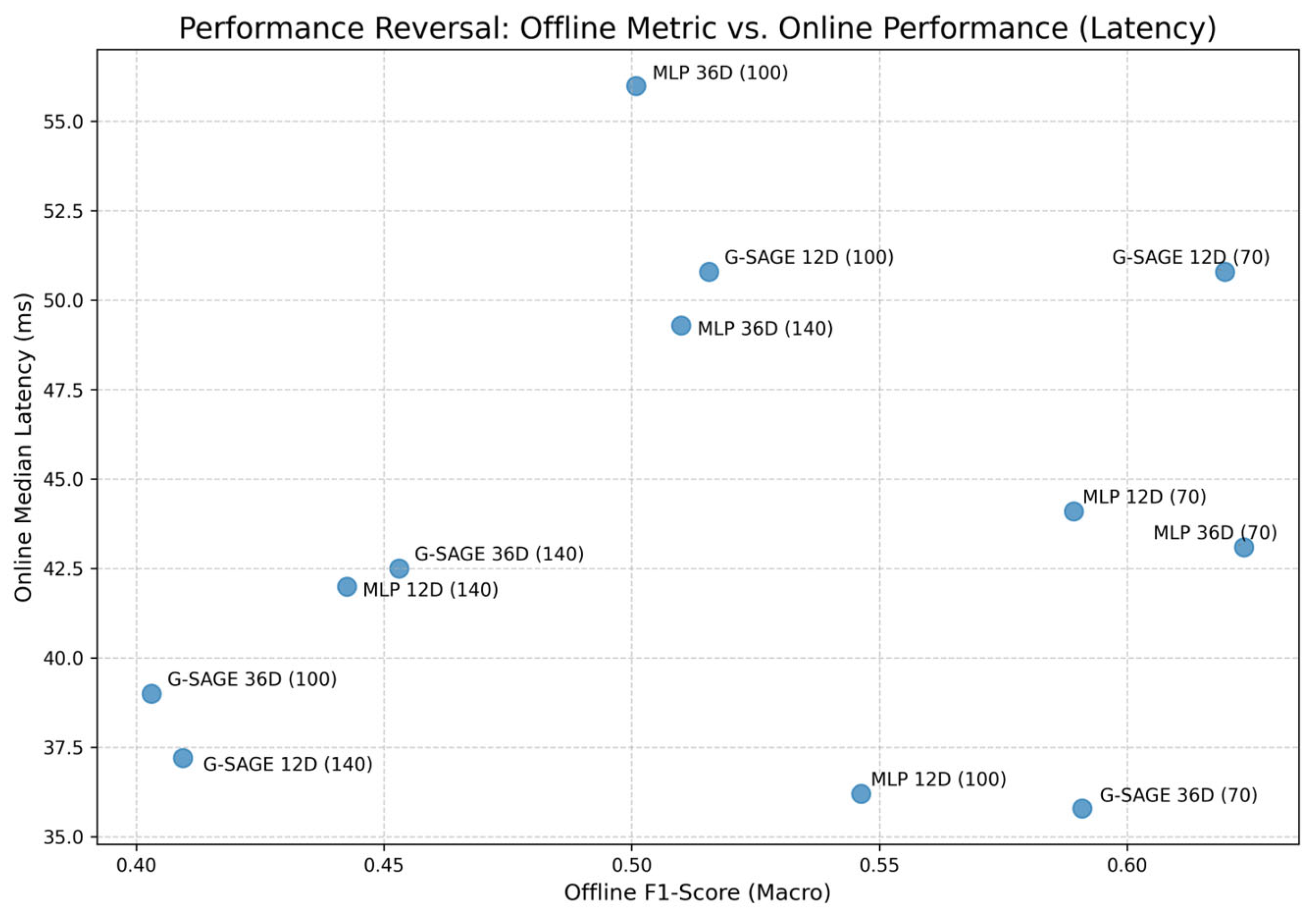
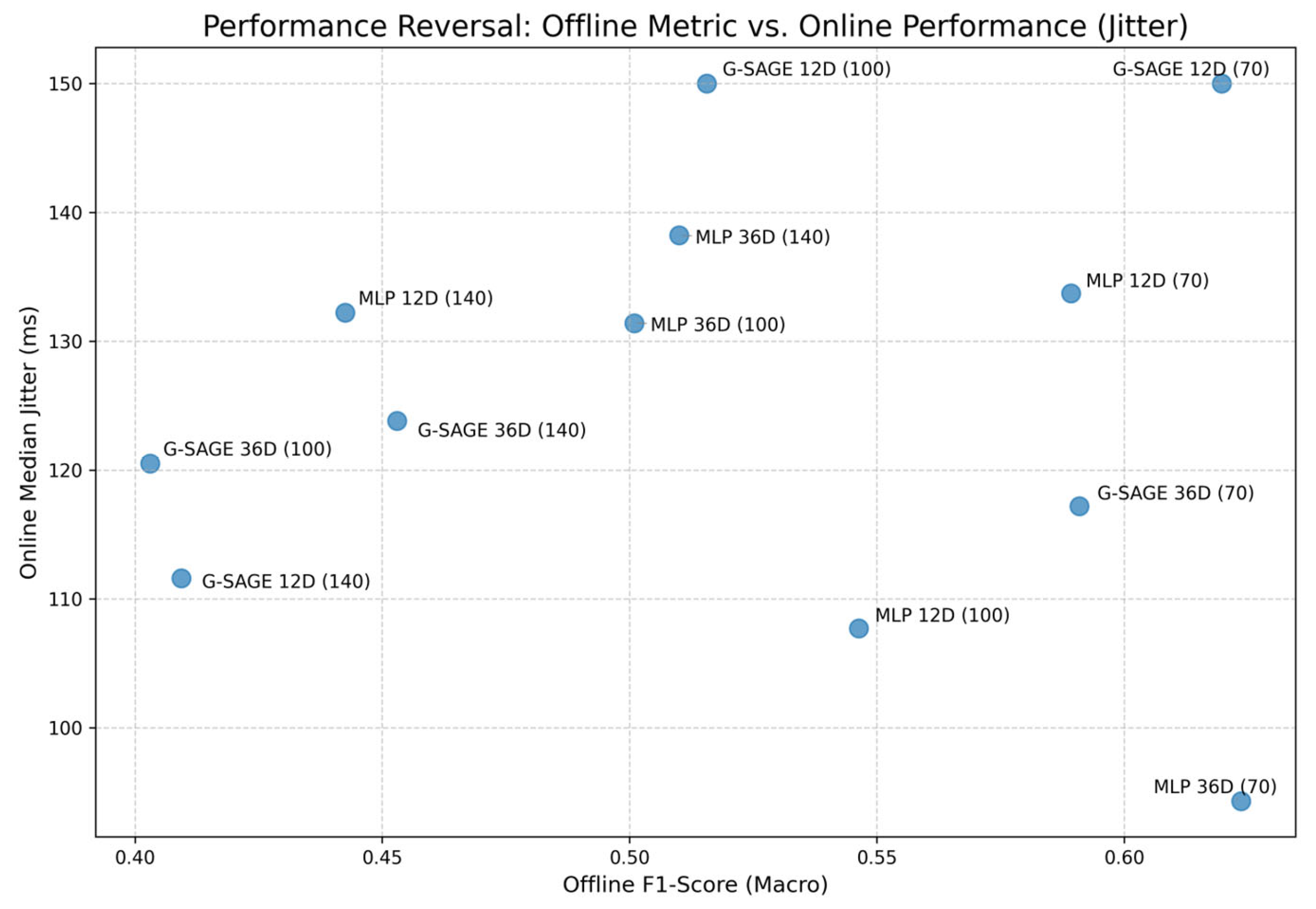
To quantitatively verify the performance-reversal phenomenon observed in this study, a Pearson correlation analysis was conducted between the offline F1-score and the online performance indicators. The results showed that the correlations between the offline F1-score and the online metrics were not statistically significant—latency (r = 0.1912, p = 0.5517) and jitter (r = 0.0072, p = 0.9824).

As illustrated in Figure 9 and Figure 10, no clear linear trend was observed, and the data points were widely scattered. This lack of correlation demonstrates that offline classification metrics do not adequately predict actual online control performance.

Consequently, the confirmed performance-reversal phenomenon indicates that SDN-based control performance is determined not only by classification accuracy but also by topological adaptability and spatio-temporal situational awareness. Unlike conventional GNN-based SDN studies, this work quantitatively verifies that a model’s offline classification accuracy does not directly translate into real network control efficiency. These findings provide a practical implication for model selection in SDN controllers and offer a new perspective for evaluating the adaptability of AI models in real-time network environments.

Consequently, the observed performance reversal phenomenon suggests that SDN-based control performance is determined not only by simple classification accuracy but also by topological adaptability and spatio-temporal situational awareness. In particular, unlike existing GNN-based SDN research, this study quantitatively verified that the offline classification performance of a model does not directly translate into actual network control efficiency. These results provide a critical practical basis for the model selection process in SDN controllers and present a new perspective for evaluating AI model adaptability.

4.2. Factors Influencing Model Performance

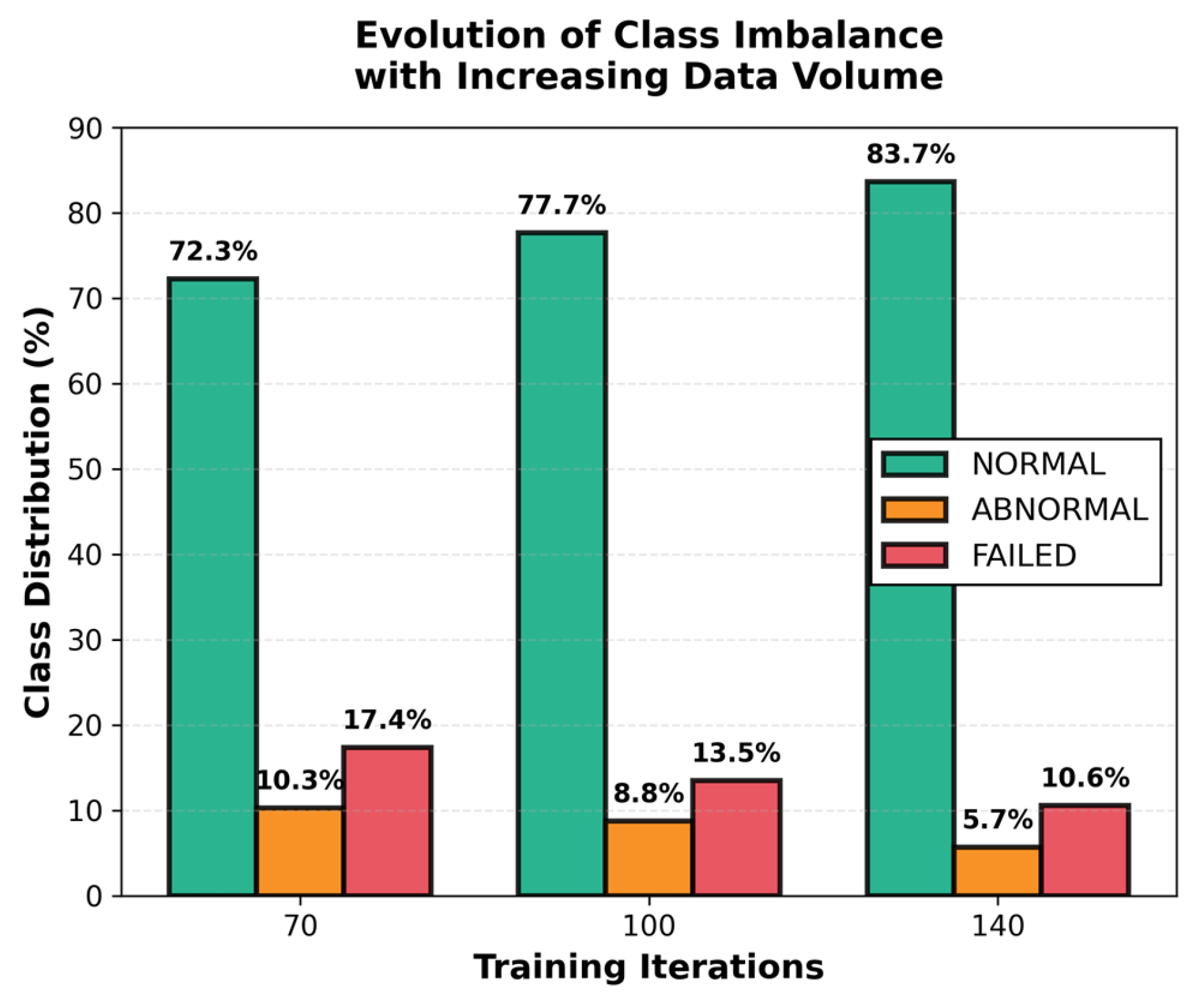
It is generally known that a large amount of training data leads to improved model performance. However, the results of this study (Table 8) show that this assumption does not hold in an environment with severe class imbalance. It was confirmed that the F1-score decreased as the amount of collected data increased. This performance degradation is explained by the class distribution (Figure 5).

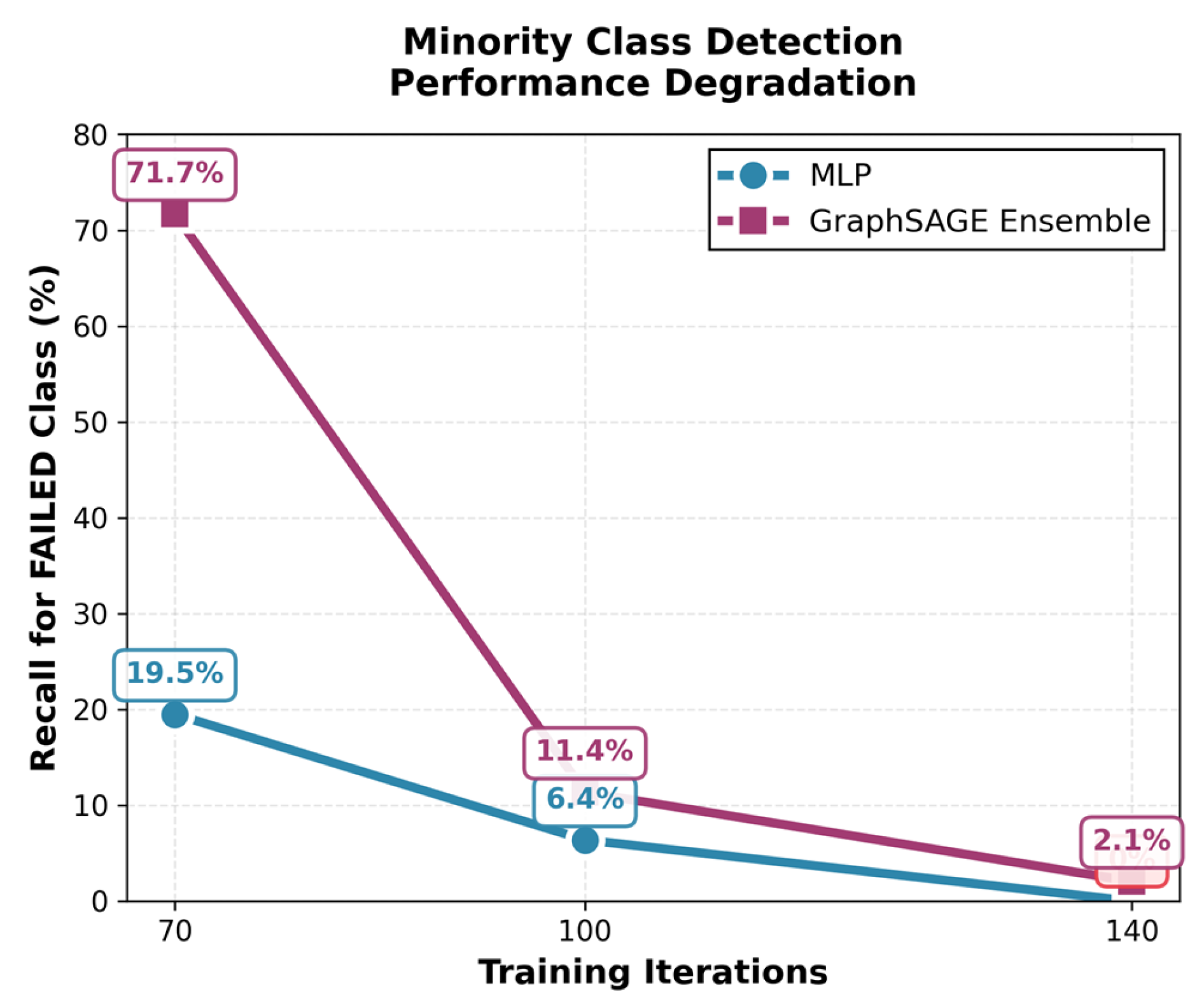
In this study, although we intended to collect NORMAL, ABNORMAL, and FAIL scenarios at a ratio of 2:2:6, the actually collected samples were overwhelmingly dominated by the NORMAL class. As the number of data collection iterations increased, the absolute number of NORMAL samples grew faster than other classes, further exacerbating the class imbalance. This caused the model to be biased toward the NORMAL class during training, resulting in a degradation of minority class detection capability.

When collecting training data in an SDN environment, balancing the classes is more important than increasing the overall volume of data8. In particular, sufficient samples for minority classes, such as failure situations, must be secured through intentional simulations.

In this study, the Gaussian noise oversampling technique was applied to mitigate the class imbalance of the training data. This was intended to reflect the variability of actual network traffic while enhancing the model’s generalization ability. However, the Gaussian noise method does not consider the proximity relationships between data, so it has limitations in generating samples near the class boundaries.

Future research plans to resolve the minority class imbalance by applying oversampling techniques such as SMOTE [29] or ADASYN [30], or by referencing graph-based SMOTE application methods proposed in recent studies [31,32,33,34,35]. Furthermore, methods combining an Autoencoder-based hybrid structure or metaheuristic optimization (e.g., Honey Badger Algorithm) are planned for consideration to improve minority class detection.

The network performance indicators, such as latency, jitter, and throughput, presented in this study were calculated as the average values from 70/100/140 repeated iterations for each scenario, and the standard deviation was also measured to consider the variability of the repeated runs.

Finally, in the case of the spatio-temporal feature vector, results were not consistently derived depending on the model or the amount of data. It was confirmed that if these spatio-temporal features are not properly reflected, it may only manifest as learning difficulties due to the increased feature dimensions. The spatio-temporal feature vector used in this study was designed with a structure that integrates and learns the traffic states of consecutive time points (t-2, t-1, t₀). However, in the SDN environment, there are cases where traffic patterns at a specific time point change rapidly, or the spatio-temporal correlation between neighboring nodes is not constant. In such abnormal patterns, simply combining temporal information may act as noise and interfere with the model’s representation learning. Especially for neighbor-node aggregation-based models like GraphSAGE, there is a possibility that learning stability may be degraded as features of nodes with large inter-temporal changes propagate to adjacent nodes. Future research plans to quantitatively evaluate the relative contribution of each time point through time point-weighted aggregation models or time-series sensitivity analysis.

4.3. Limitations and Future Work

This study analyzed the offline-online performance discrepancy of MLP and GraphSAGE models in an SDN environment; however, it has a limitation in that the simulation topology was confined to a single NSFNet structure (14 switches and 14 hosts).

First, the experiments were conducted on a single NSFNet topology consisting of 14 switches and 14 hosts. Therefore, it could not address heterogeneous topological structures such as large-scale backbone networks (e.g., GEANT2) or edge environments, where network connection density, the number of paths, and traffic distribution characteristics may differ. Due to this limitation, it is difficult to fully verify the scalability and generalization performance of the models.

Second, this study used only two models, MLP and GraphSAGE, as comparison targets and did not include other representative graph neural networks (e.g., GCN, GAT). Furthermore, it did not compare with traditional routing algorithms such as OSPF.

Future work plans to comprehensively evaluate the performance of the proposed approach by applying various evaluation models and routing algorithms, such as GCN, GAT, and OSPF, and including large-scale topologies such as GEANT2.

5. Conclusions

In this study, the offline classification performance and online network control behavior of the MLP and GraphSAGE models were comparatively analyzed in an SDN environment. Experiments conducted with three training data volumes and two feature dimensions revealed a clear discrepancy between offline evaluation metrics and network-level performance.

The main findings are as follows:

First, although MLP achieved a higher offline F1-score (0.62), a performance reversal was observed when the models were deployed in the SDN controller—GraphSAGE reduced latency by 17% and improved jitter by 31%.

Second, under class-imbalanced conditions, increasing the data volume degraded model performance due to the disproportionate expansion of majority-class samples, which intensified the imbalance.

Third, while the inclusion of spatio-temporal features did not consistently enhance offline classification accuracy, it effectively reduced network latency during real-time operation.

The contributions of this work are twofold.

This study empirically demonstrates that offline evaluation metrics alone are insufficient to predict actual control performance in SDN environments, highlighting the importance of directly assessing end-to-end network performance when selecting models. Furthermore, the study quantitatively verifies that GraphSAGE, by leveraging graph structural information, provides more stable and topology-aware routing behavior than non-graph-based models.

Future work will extend the validation to larger-scale network topologies (e.g., GEANT2) and diverse traffic datasets such as UNSW-NB15 and Bot-IoT. In addition, further comparative studies on various GNN architectures and investigations into real-time inference optimization are planned.