A Robust and Adaptive Service Recommendation Framework for Distinct Behavioral Services in Dynamic Multi-Cloud Environments

Abstract

Effective service recommendation is essential in multi-cloud environments, directly influencing system performance, resource utilization, and service composition quality. However, existing methods often overlook key issues: (i) the inability to identify distinct behavioral services (DBS), leading to inaccurate or inefficient recommendations; (ii) the neglect of temporal dynamics in service behaviors, which results in unstable or outdated decisions; and (iii) the lack of effective strategies for handling cold-start and data sparsity, causing incomplete or biased scoring. To address these challenges, this study proposes a behavior-aware recommendation framework that explicitly integrates DBS characteristics. First, three types of DBS are defined and identified through a two-phase topology-based detection algorithm. Second, a sliding window with role-stability judgment is introduced to capture behavioral evolution and ensure consistent role labeling. Third, a Markov-based scoring model is designed to propagate compatibility scores across the invocation topology, enabling infrequently invoked services to obtain nonzero scores during early iterations. Extensive simulations demonstrate notable gains in accuracy and robustness, showing a 22.85% improvement in precision and a 41.69% improvement in F1-score, effectively mitigating cold-start and sparsity challenges.

1. Introduction

Cloud services offer scalable, flexible, and on-demand resources that enable enterprises and individuals to deploy applications, store data, and apply artificial intelligence without dedicated infrastructure. As cloud computing evolves, organizations increasingly adopt multi-cloud environments, utilizing services from multiple providers to enhance reliability and performance. The diversity of service providers and offerings introduces significant complexity in service discovery and selection [1]. To address this, cloud service recommendation has become a vital mechanism for assisting users in identifying appropriate services efficiently and accurately.

Existing cloud service recommendation approaches [2] can be broadly categorized into the following three paradigms: (i) Collaborative Filtering (CF) methods [3] analyze user-service interaction patterns to infer preference but suffer from cold-start and data sparsity problems; (ii) Context-aware methods [4] incorporate external information such as time, location, or device context to enhance personalization, yet often ignore structural characteristics of services [5]; and (iii) QoS-aware methods [6] focus on predicting non-functional service attributes such as response time and availability but typically treat services as static entities without modeling their invocation behavior [7]. While these approaches significantly improve recommendation accuracy from different angles, they generally neglect the behavioral characteristics of services, which can directly affect both the relevance and efficiency of recommendations.

Motivations. Despite the prevalence of service recommendation systems, these methodologies often overlook an important aspect: the behavioral patterns of services within invocation workflows, which significantly impact their practical effectiveness, especially in complex, dynamic environments such as multi-cloud service ecosystems [8]. In such environments, services are often distributed across different cloud providers, leading to heterogeneous deployment standards, isolated logging mechanisms, and fragmented service invocation paths. These characteristics make it more likely for services to exhibit behaviorally irregular patterns—such as never being invoked together with others, only appearing at the end of workflows, or lacking historical records altogether. We define such anomalies as DBS. Unlike traditional single-cloud or centralized systems, multi-cloud settings amplify the occurrence and impact of DBS, making it imperative to design recommendation mechanisms that are explicitly aware of such behavioral irregularities.

Several key reasons contribute to this oversight: (i) Ignoring service behavior patterns reduces recommendation efficiency. Some services, such as Isolated Services, rarely interact and may introduce noise, while Ending Services frequently appear as workflow endpoints and should be prioritized. New Member Services, despite lacking historical records, may be crucial in specific contexts. Failing to differentiate these Distinct Behavioral Services (DBS) results in inefficient recommendations and redundant computations. (ii) Ignoring the dynamic nature of service behavior leads to misclassification and reduced recommendation accuracy. Services transition [9] between behavioral states due to workload shifts [10], cloud migration [11], or user demand changes [12]. Static models  [13] fail to capture these shifts, making it difficult to distinguish evolving patterns. For example, an Isolated Service may become highly interactive, or an Ending Service may transition to an intermediate role in cross-domain workflows. (iii) Neglecting DBS cold start and data sparsity issues hinders their effective utilization in recommendation. Many DBSs have low or no historical invocation frequency, making conventional approaches ineffective. However, some DBSs, despite their sparse historical records, should still be prioritized over structurally similar services due to their contextual significance in workflows. In a word, DBSs exhibit fragmented, unstable, or irregular invocation behaviors in multi-cloud service environments, making them difficult to model using conventional scoring techniques. DBSs often suffer from inaccurate or missing recommendation scores due to their structural uniqueness which not only reduces the overall recommendation quality, but also aggravates common issues such as cold-start and data sparsity. To address this, we propose a DBS identification and scoring framework that explicitly models such behavioral structures, offering both improved recommendation fairness and enhanced robustness against sparsity-related challenges. Our approach integrates dynamic monitoring mechanisms to track behavioral shifts over time, ensuring DBS classification remains adaptive to multi-cloud environments.

Challenges. The proposed framework addresses the following challenges (i): Differentiating DBS with similar static invocation patterns. DBS categories can have similar invocation records, making them hard to distinguish. Ending and Isolated Services may both exhibit low frequency, yet serve different roles. New Member Services may resemble inactive services. Effective identification must go beyond static similarity and incorporate topological and temporal features. (ii): Ensuring dynamic adaptability of DBS classification. Service behaviors change over time, requiring adaptive classification. A service may transition from Isolated to Interactive or Ending to Mid-Workflow based on evolving workflows. The challenge is designing an identification mechanism that updates DBS classification in response to real-time behavioral shifts. (iii): Addressing cold start and data sparsity issues. DBS often have limited historical data, making classification difficult. Traditional collaborative filtering and graph-based methods rely on sufficient invocation records, rendering them ineffective for DBS. A robust method should leverage contextual and topological intelligence to infer relevance even in sparse environments.

Contributions. To address these challenges, we make the following contributions:

• A Novel DBS Identification Framework. We define Distinct Behavioral Services (DBS) and introduce an invocation topology-based approach to classify services into Isolated, Ending, and New Member Services. Our method captures both topological and temporal features to improve classification accuracy beyond conventional invocation-based methods.
• A Dynamic Monitoring and Adaptative Detection of Behavioral Role Shifts based on Sliding Windows. We implement a sliding window mechanism to track behavioral shifts, ensuring DBS classification adapts to evolving interactions. A Markov-based transition model predicts state changes in DBS, preventing misclassification due to short-term fluctuations.
• A Markov-Based Scoring Strategy against Cold-Start and Sparse Issues. We design a topology-aware scoring model that leverages the homogeneous and irreducible properties of Markov Chains. This enables complete and stable score propagation for DBS services even when invocation data is sparse or unavailable, effectively addressing cold-start limitations.
• Comprehensive Validation Supporting the Proposed Framework. To validate the effectiveness of our framework, we design five dedicated simulations that assess its accuracy, stability, and robustness under cold-start and sparsity scenarios. These evaluations demonstrate the practical viability of our behavior-aware strategies in dynamic service environments.

The remainder of this paper is structured as follows. Section 2 reviews the literature on collaborative filtering, context-aware, QoS-aware, behavior-aware service recommendation together with cold-start and data sparsity issues. Section 3 presents the overall architecture of the proposed DBS-aware framework. Section 4 details the system design, including DBS definitions, invocation topology construction, the DBS-based filtering algorithm, and the sliding time window mechanism. Section 5 describes the simulation settings, dataset preprocessing, evaluation metrics, and baseline methods. Section 6 reports and analyzes the experimental results across dynamic environments, temporal stability, data sparsity, and cold-start scenarios. Section 7 concludes the paper and discusses limitations and future research directions.

2. Literature Review

2.1. Collaborative Filtering-Based Service Recommendation

Collaborative Filtering (CF) relies on user-service interaction patterns to infer preferences. Traditional CF methods, including user-based and item-based techniques, estimate similarity by comparing co-usage behaviors. To overcome data sparsity and cold-start problems, matrix factorization and deep learning variants have been proposed to enhance representation learning. For example, Pan et al. [14] proposed a hybrid recommendation system for university libraries that combines user-based CF, content-based filtering, and K-means clustering to alleviate data sparsity. Zhao et al. [15] further enhanced CF by integrating knowledge graph (KG) embeddings to capture richer semantic relationships between users and items. However, these approaches treat services uniformly and overlook their behavioral roles within service invocation networks, which limits their ability to filter or prioritize structurally significant services.

2.2. Context-Aware Service Recommendation

Context-aware recommendation methods enhance accuracy by integrating factors such as user location, time, and environment. These approaches often use embedding models or deep collaborative filtering to incorporate contextual information into the recommendation process. For instance, Wang et al. [16] introduced DFORM, a deep learning-based model that fuses contextual signals with collaborative features for IoT service recommendation. Fan et al. [4] proposed CASR-TSE, which models spatial relevance and temporal decay to improve QoS prediction in web service recommendation. However, these methods mainly emphasize external context and still treat services as static entities, failing to capture or utilize their internal behavioral dynamics and structural roles in workflows.

2.3. QoS-Aware Service Recommendation

QoS-aware approaches aim to improve service selection by predicting non-functional attributes such as latency, throughput, and reliability. These methods often employ machine learning or probabilistic models to estimate QoS values under varying user conditions. Wang et al. [17] proposed WAMTL, a multi-task learning framework that jointly predicts multiple QoS attributes by leveraging their interdependencies. Zhang et al. [18] combined trust propagation and QoS modeling in SIoT environments to improve reliability and satisfaction. Despite these innovations, existing QoS-aware models generally ignore service behavior patterns and offer no pre-filtering mechanism based on structural or temporal analysis. While QoS modeling is critical in traditional service composition or SLA optimization, it is less effective when service invocation behaviors exhibit instability, fragmentation, or sparsity—characteristics often observed in multi-cloud environments. Moreover, most QoS-aware approaches lack structural analysis capabilities and do not consider behavioral roles of services in invocation workflows, which limits their applicability in scenarios involving DBSs.

2.4. Behavior-Aware Service Recommendation

Behavior-aware service recommendation refers to approaches that explicitly model and leverage the behavioral patterns of services or users (such as interaction sequences, role changes, or multi-type behaviors) to improve recommendation accuracy and relevance. For instance, Kim et al. [19] proposed a graph convolutional network (GCN) framework for multi-behavior sequence-aware recommendation, capturing dependencies among different user behaviors such as viewing, adding to cart, and purchasing. While effective in modeling behavioral correlations, this approach relies on black-box embeddings and does not provide mathematically defined behavior roles, leaving the interpretation of behavior categories implicit. Similarly, Su et al. [20] introduced a personalized behavior-aware Transformer (PBAT) that employs attention mechanisms to distinguish between multiple behavior types and personalize recommendations. Despite its advanced modeling capabilities, PBAT also remains largely opaque and does not integrate service invocation topology or role-based classification into its framework. However, most existing behavior-aware methods still rely on black-box feature learning and lack mathematically defined service roles or explicit integration with service invocation topology.

2.5. Cold Start in Service Recommendation

2.5.1. Root Causes

Cold start arises when newly deployed or rarely invoked services lack behavioral traces in the invocation graph. Without such traces, collaborative or graph-based models cannot estimate their relevance with confidence. In multi-cloud settings, fragmented logs and domain boundaries intensify the problem, so new services may appear as isolated nodes with no exploitable connectivity.

2.5.2. Mainstream Solutions

Content-based methods [21] infer initial relevance from textual descriptions, metadata, or side QoS; they can operate without history, but quality hinges on the richness of side information and its cross-domain consistency. Initialization-based approaches [22] assign non-zero priors or meta-learned warm starts; this ensures early visibility in ranking, yet the priors may be arbitrary and unstable under domain shift. Context-aware models [23] leverage exogenous signals (e.g., time, location, social ties) to compensate for missing interactions; these signals are often noisy or misaligned across providers. Cross-domain/transfer-learning techniques [24] reuse knowledge from data-rich domains to the sparse target; they help when feature spaces align, but can suffer negative transfer when domain gaps are large.

Current practices lack a clear, topology-grounded rule for identifying newly joined services and for tracing their early role transitions. Most approaches provide no guarantee of nonzero scoring for cold-start or isolated services when the invocation graph is fragmented across domains. A unified mechanism that integrates role-aware filtering with a provably convergent propagation process remains largely absent.

2.6. Data Sparsity in Service Recommendation

2.6.1. Root Causes

Sparse interactions between users and services, often amplified by long-tail usage and multi-cloud fragmentation, lead to weak connectivity and even disconnected subgraphs; this undermines both similarity estimation and path-based propagation. Over time, sparsity not only reduces accuracy but also narrows system coverage, hiding potentially useful yet less popular services.

2.6.2. Mainstream Solutions

Matrix factorization [25] compresses the interaction matrix into low-rank factors to fill missing values; it works at moderate sparsity but degrades when observations are extremely scarce. Clustering-based methods [26] densifies interactions within groups and improves coverage; however, coarse clusters may blur individual differences. Graph-based propagation [27] exploits indirect paths to collect multi-hop evidence; this helps with few links but remains sensitive to graph disconnection and restart bias. Deep models (e.g., GNNs, autoencoders) [28] capture higher-order patterns beyond co-occurrence and can be robust in some sparse regimes; they nevertheless require large-scale training and still depend on sufficient structural signals.

Under extreme sparsity and cross-domain fragmentation, similarity estimation and path-based propagation become unreliable, leading to brittle recommendations. Existing solutions seldom combine role-aware filtering with formal coverage guarantees when the graph is disconnected. Practical assurances of nonzero scoring and stability in severely sparse regimes are still limited.

2.7. Summary and Research Gap

Existing research in CF, context-aware, QoS-aware and behavior-aware service recommendation has led to significant advances by leveraging interaction history [29], contextual signals [30], performance metrics [31] and behavioral patterns. However, these approaches commonly lack mechanisms to model or monitor service behavior in dynamic invocation environments. Specifically, few methods attempt to identify services with distinct behavioral roles, such as isolated, ending, or newly introduced services or consider how these roles evolve over time.In contrast, our work introduces a behavior-aware and structure-sensitive filtering mechanism based on the notion of DBS, explicitly modeling service roles within the invocation topology and enabling dynamic behavior tracking. This framework complements existing recommendation strategies by improving recommendation fairness, robustness against sparsity, and interpretability in multi-cloud environments.

In order to provide a clearer comparison of existing solutions,

Table 1. Comparative analysis of related methods and capabilities. Note: ✓ indicates support, while ✗ indicates the feature is not supported.

Method	Approach Category	Role Modeling	Pre-Filtering	Dynamic Adaptation	Cold Start Handling	Topology-Aware
DFORM [16]	Context-aware	✗	✗	✗	✓	✗
CASR-TSE [4]	Context-aware	✗	✗	✗	✓	✗
Hybrid [14]	CF	✗	✓	✗	✗	✗
CA-WebAPI [32]	CF + KG	✗	✗	✗	✗	✓
WAMTL [17]	QoS-aware	✓	✗	✗	✓	✗
TrustQoS-SIoT [18]	QoS-aware	✓	✗	✗	✓	✗
Ours	DBS-aware	✓	✓	✓	✓	✓

summarizes the representative methods discussed in this section along five key capability dimensions, including role modeling, pre-filtering, dynamic adaptation, cold-start handling, and topology-awareness. As shown in the table, most methods focus on a single aspect of the problem, such as service semantic modeling or QoS-aware selection, while none of them simultaneously address the temporal dynamics, behavioral distinctions, and topology-aware adaptation in multi-cloud environments. In particular, existing works rarely incorporate topology-based behavioral similarity or dual-sided dynamic evolution (i.e., dynamic user behaviors and dynamic service pools), which leaves a methodological gap for robust and adaptive service recommendation under highly dynamic settings. This gap motivates the design of our DBS-aware framework, which integrates DBS identification, temporal sliding-window adaptation, and Markov-based compatibility scoring to provide a more holistic and adaptive solution.

3. Framework Overview

This section presents the overall architecture of our DBS-aware service recommendation system in multi-cloud environments. As illustrated in Figure 1, the architecture can be conceptually divided into two major components: the core backbone architecture and the behavioral parameter system derived from DBS strategies.

3.1. Backbone Architecture

The backbone of the system handles the full lifecycle of a user request, from input ingestion to recommendation output. It is composed of the following coordinated modules:

• User Interface and API Gateway: The process begins when a user initiates a service request via the user interface. The request is routed through the API Gateway, which standardizes access and forwards requests to the backend logic.
• Unified Data Management Module: This module serves as a bridge between user interaction and cloud resources. It is responsible for gathering invocation data from multiple cloud providers, synchronizing service descriptions, and triggering the construction of invocation topologies.
• Data Integration and Standardization: Based on collected logs, the system incrementally constructs a time-aware service invocation graph $G_t=(V_t,E_t)$ within a sliding window, and performs initial domain assignment for each service node.
• DBS-Recognition Module: Once the topology is established, the system identifies behaviorally significant services, referred to as Distinct Behavioral Services (DBS), by analyzing their connectivity and invocation roles.
• DBS-Aware Filtering: A sliding time window strategy is applied to monitor role transitions over time. Services whose behavioral roles remain consistent over k consecutive windows are marked as stable and exempt from repeated updates. This dynamic judgment reduces noise and accelerates recommendation updates.
• Recommendation Engine: Finally, the refined and behavior-aware service pool is passed to the recommendation engine, which generates personalized ranking results and returns them to the user.

3.2. Behavioral Parameter System via DBS

The yellow block in Figure 1 represents the DBS-aware parameter system, which encodes the behavioral semantics extracted during the filtering process. The system maintains a sliding time window of invocation topologies $T\left[b_{ij}\right]$ to sketch multi-cloud interactions, computes the Markov-based base score of each service, and extracts behavioral sets such as $S_n$, $S_{ue}$, $S_{ne}$, and $S_{is}$. These symbols together support the identification and role maintenance of each service node, where the evolving role ${\mathrm{Role}}_t\left(s\right)$ serves as the key indicator for filtering control. This lightweight symbolic system enables precise behavioral representation and supports strategy triggering without full recomputation, forming a compact yet expressive interface between topology dynamics and recommendation logic.

4. System Design

4.1. Distinct Behavioral Services: Definition and Mathematical Formulation

To capture the structural and behavioral characteristics of services within a dynamic multi-cloud environment, we define a special class of services, referred to as Distinct Behavioral Services (DBS). These services deviate from typical invocation patterns and are categorized into three types: Isolated Services, Ending Services, and New Member Services. Their classification is based on the topological features observed within a service invocation graph constructed over a sliding time window. The key mathematical symbols are summarized in

Table 2. Key Mathematical Notations.

Symbol	Description
R	Set of invocation records within the time window. Each record is a tuple $(u_i,s_j,t_k)$ indicating user $u_i$ invoked service $s_j$ at time $t_k$.
$[t-\Delta ,t]$	Time window ranging from $t-\Delta$ to t, used to construct the invocation graph.
$G_t=(V_t,E_t)$	Invocation graph for time window t, where $V_t$ is the set of services and $E_t$ is the set of invocation edges.
$w_{ij}$	Transition frequency from service $s_i$ to service $s_j$ within $E_t$.
$M_{ij}$	Transition probability from service $s_i$ to $s_j$, computed as $M_{ij}={\displaystyle \frac{w_{ij}}{{\sum }_k{w}_{ik}}}$.
$M^T$	Transpose of the transition matrix M (used for Markov iteration with column vectors).
$v_t$	Column vector representing service scores at iteration t.
$ϵ$	Small initialization constant for unreachable services, ensuring irreducibility of the Markov chain.
$base\text{\_}score\left(s_j\right)$	Base importance score for service $s_j$ after convergence.

.

The time window $[t-\Delta ,t]$ defines the temporal scope for constructing the invocation graph. Here, $\Delta$ represents the window size, and t is the current evaluation time. All service invocation records falling within this interval are considered valid when building $G_t$. This design enables the system to capture short-term behavioral trends while adapting to the dynamic nature of service environments. The value of $\Delta$ can be tuned according to service invocation density or domain-specific time granularity.

Let the service invocation graph at time t be denoted as:

$$G_t=(V_t,E_t),$$

(1)

where:

• $V_t$ is the set of services active in the time window $[t-\Delta ,t]$;
• $E_t\subseteq V_t\times V_t$ is the set of directed edges representing invocation relationships.

We define the following DBS categories:

4.1.1. Isolated Service

A service $s\in V_t$ is classified as Isolated if it has no interaction with other services in the time window:

$${deg}_t^{in}\left(s\right)+{deg}_t^{out}\left(s\right)=0.$$

(2)

Optionally, s may only invoke itself: $(s,s)\in E_t$. Isolated Services are completely disconnected from the service invocation graph in the current time window, either due to inactivity or self-invocation only.

4.1.2. Ending Service

A service $s\in V_t$ is an Ending Service if it only appears at the terminal position of invocation workflows:

$${deg}_t^{out}\left(s\right)=0\mathrm{and}\exists u\in V_t,(u,s)\in E_t.$$

(3)

Ending Services act as leaf nodes in invocation workflows, frequently terminating invocation chains, and are categorized based on whether the final invocation comes from the same or a different domain. We further distinguish:

• Cross-domain Ending: the last invocation to s originates from a different domain;
• Intra-domain Ending: the last invocation to s originates from the same domain.

4.1.3. New Member Service

A service s is considered a New Member if it has not appeared in any invocation record within the time window:

$$s\notin V_t\mathrm{and}\nexists (u,s)\in E_t\wedge \nexists (s,u)\in E_t.$$

(4)

New Member Services are newly appeared services with no prior records, representing cold-start entities. Each service s is assigned a behavioral role based on these definitions:

$$\mathrm{Role}\left(s\right)\in \{\mathrm{Normal},\mathrm{Isolated},\mathrm{Ending},\mathrm{New}\mathrm{Member}\}.$$

(5)

These definitions provide deterministic and reproducible DBS classification based on strict graph-theoretic conditions and forms the basis for downstream service filtering and behavior-aware scoring.

4.1.4. Impact of DBSs on Recommendation Accuracy

The three types of DBS introduce distinct disruptions to recommendation accuracy by interfering with the structural integrity and information flow within invocation topologies. Isolated Services, having no outward or inward connections, receive little to no propagation of collaborative information, resulting in severe score underestimation or exclusion. Ending Services, which often situated at the tail of invocation sequences and act as dead ends in the graph, preventing score propagation to earlier nodes and causing an asymmetry in score distribution. New Member Services, lacking any prior interactions, face absolute cold-start conditions, where traditional history-based models cannot even assign initial values. These conditions lead to information asymmetry in the recommendation system, where certain services are disproportionately undervalued, and introduce scoring imbalance across the pool. Without explicit recognition and compensation of these behavioral anomalies, the system risks biased rankings, missed high-quality candidates, and overall degradation in recommendation robustness. To mitigate these effects, we introduce a DBS identification and structure-aware scoring mechanism that explicitly models the behavioral roles of atypical services. By leveraging the invocation topology and its propagation paths, the mechanism compensates for data deficiencies and behavioral irregularities, ensuring that structurally significant services are assigned more reasonable and reliable scores.

4.2. Service Pool Topology Construction and Initial Scoring

To support behavior-aware analysis and recommendation, we first construct a directed invocation topology from service logs within a given sliding time window. Each invocation record is denoted as:

$$\mathrm{Record}(u,s,t),$$

(6)

where user u invokes service s at time t.

From the filtered records, we build a directed service invocation graph:

$$G_t=(V_t,E_t),$$

(7)

where:

• $V_t$ represents the set of services active during the sliding time window $[t-\Delta ,t]$;
• $E_t\subseteq V_t\times V_t$ represents the directed edges that denote invocation transitions. If service $s_i$ is followed by $s_j$ in a user session, then an edge $(s_i,s_j)$ is added to $E_t$.

To compute the preliminary importance or activation level of each service, we define a transition probability matrix M derived from $G_t$:

$$M_{i,j}={\displaystyle \frac{w_{i,j}}{{\sum }_k{w}_{i,k}}},$$

(8)

where $w_{i,j}$ is the frequency of invocation from $s_i$ to $s_j$. This matrix captures the probability that a service call transitions from one service to another.

Let ${\pi }_t^{\left(0\right)}$ denote the initial invocation probability vector at time t. A standard Markov Chain iteration computes the steady-state distribution as:

$${\pi }_t^{(k+1)}={\pi }_t^{\left(k\right)}M.$$

(9)

Once the sequence $\left\{{\pi }_t^{\left(k\right)}\right\}$ converges, the resulting vector represents the base importance score for each service:

$${\pi }_t^{\ast }=\underset{k\to \infty }{lim}{\pi }_t^{\left(k\right)}.$$

(10)

Each score ${\pi }_t^{\ast }\left(s\right)$ reflects the centrality and activation likelihood of service s in the current topology. These scores are subsequently adjusted based on DBS classification in the filtering and recommendation stages.

Algorithm 1 is designed to compute the base importance scores for all services within a sliding time window, serving as the initialization for downstream recommendation and filtering tasks. The algorithm transforms raw invocation records into a directed service invocation graph, constructs a transition probability matrix based on invocation frequencies, and propagates service influence scores using Markov Chain dynamics until convergence. The core steps of the algorithm can be interpreted as follows:

Algorithm 1 Initial Service Scoring via Markov-Based Topology Analysis

1: Input: Invocation records R, time window $[t-\Delta ,t]$   2: Output: Base importance score $\mathit{base}\text{\_}\mathit{score}\left(s\right)$ for each service s   3: Filter R to obtain records in $[t-\Delta ,t]$   4: Construct invocation graph $G_t=(V_t,E_t)$   5: Count transition frequencies $w_{ij}$ from $E_t$   6: Compute transition matrix $M_{ij}={\displaystyle \frac{w_{ij}}{{\sum }_k{w}_{ik}}}$   7: Initialize vector $v_0$   8: for all $s_j\in V_t$ do   9:       $v_0\left[j\right]\leftarrow 1$ 10: end for 11: for all $s_j\notin V_t$ do 12:       $v_0\left[j\right]\leftarrow \epsilon$                              ▹$\epsilon >0$ to avoid zero-score propagation 13: end for 14: while not converged do 15:       $v_{t+1}\leftarrow M^{\mathsf{T}}·v_t$ 16:       $t\leftarrow t+1$ 17: end while 18: for all $s_j\in V_t\cup \left\{\mathrm{unreachable}\mathrm{nodes}\right\}$ do 19:       $\mathit{base}\text{\_}\mathit{score}\left(s_j\right)\leftarrow v_t\left[j\right]$ 20: end for

4.2.1. Initial Scoring via Markov Propagation

The Markov-based scoring mechanism operates on the invocation records within a sliding time window. The scoring procedure, as detailed in Algorithm 1, can be interpreted as follows:

• Lines 1–4: Filter the raw invocation records R within the window $[t-\Delta ,t]$, and construct a directed invocation graph $G_t=(V_t,E_t)$.
• Lines 5–6: Count transition frequencies $w_{ij}$ and normalize them into a row-stochastic transition matrix M, where $M_{ij}$ represents the probability of invoking service $s_j$ after $s_i$.
• Line 7: Declare and initialize the score vector $v_0$.
• Lines 8–13: For each service, assign $v_0\left[j\right]=1$ if $s_j\in V_t$; otherwise assign a small constant $\epsilon >0$ to avoid zero-score contamination.
• Lines 14–17: Perform iterative matrix-vector multiplication $v_{t+1}\leftarrow M^T·v_t$ until convergence.
• Lines 18–19: Assign the converged scores $v_t\left[j\right]$ as the base scores $base\text{\_}score\left(s_j\right)$ for each service.
• Line 20: End of loop.

4.2.2. Time and Space Complexity

Let $n=|V_t|$ be the number of services, $m=|E_t|$ the number of edges, $\left|R\right|$ the number of raw invocation records, and K the number of iterations until convergence. The time complexity of each component is:

• Lines 1–2: Filtering and graph construction takes $\mathcal{O}\left(\right|R\left|\right)$.
• Line 3: Transition frequency counting takes $\mathcal{O}\left(m\right)$.
• Lines 4–5: Score vector initialization takes $\mathcal{O}\left(n\right)$.
• Line 6: Transition matrix normalization takes theoretically $\mathcal{O}\left(m^2\right)$ in the worst case, but $\mathcal{O}\left(\right|R|+K·m)$ in the proposed mechanism.
• Lines 7–9: Score value assignment for reachable and unreachable nodes takes $\mathcal{O}\left(n\right)$.
• Lines 10–13: Markov propagation iterations takes $\mathcal{O}(K·m)$.
• Lines 14–18: Final score assignment takes $\mathcal{O}\left(n\right)$.

Hence, the total time complexity is:

$$\mathcal{O}\left(\right|R|+m^2+K·m)$$

The space complexity, dominated by the storage of the sparse transition matrix and the score vector, is:

$$\mathcal{O}(n+m)$$

4.2.3. Practical Complexity with Fixed-Invocation Windows

Although the theoretical worst-case complexity may reach $\mathcal{O}\left(m^2\right)$ during the construction of the transition matrix M in Line 6, this situation only arises when the invocation graph becomes densely connected, leading to a large number of non-zero entries in each row. However, in our design, the sliding window mechanism is based on a fixed number of invocation operations (i.e., $\Delta =100$), rather than a fixed time span. This design ensures that the number of recorded invocations per window is controlled, effectively limiting the number of edges and keeping the resulting graph sparse.

As a result, the actual complexity of Markov scoring is $\mathcal{O}\left(\right|R|+K·m)$, where $\left|R\right|$ denotes the number of invocations in the window, K is the number of Markov iterations, and m is the number of active services. Since $\left|R\right|$ is fixed and the graph remains sparse across all windows, the matrix M is efficiently computable and the overall scoring process maintains near-linear complexity in practical scenarios.

4.3. DBS-Based Service Filtering Algorithm

After assigning behavioral roles to services based on the topology structure, we apply a DBS-based filtering algorithm to refine the candidate service pool prior to recommendation. This step improves both computational efficiency and semantic relevance by eliminating low-value services and prioritizing behaviorally significant ones.

The filtering process is executed in two phases.

4.3.1. Phase I: Behavioral Role Sorting

In the first phase, each service is examined within its current time-slot topology matrix. The row and column activity vectors are computed to detect null interactions. Services are classified as Isolated, Ending, or New Member based on their invocation activity and, in cases beyond the first time-slot, whether they appeared in previous topologies. This classification is formalized in Algorithm 2.

Algorithm 2 DBS Sorting Algorithm

1: Input: $T_k\left[a_{ij}\right]$: Topology matrix at time slot k   2: Output: $S_{is}$, $S_e$, $S_n$: Sets of Isolated, Ending, and New Member Services   3: for $i=1$ to n do   4:     $row\left[i\right]\leftarrow \mathrm{any}(T_k\left[a_{ij}\right],1)$   5:     $col\left[i\right]\leftarrow \mathrm{any}(T_k\left[a_{ij}\right],2)$   6: end for   7: for $i=1$ to n do   8:     if $row\left[i\right]=0$ then   9:         if $col\left[i\right]=0$ then 10:            if $k=1$ or $i\notin T_{k-1}$ then 11:                $S_n\left[i\right]\leftarrow i$ 12:            else 13:                $S_{is}\left[i\right]\leftarrow i$ 14:            end if 15:         else 16:            $S_e\left[i\right]\leftarrow i$ 17:         end if 18:     end if 19: end for

Algorithm Explanation

• Lines 3–6: Filter invocation relationships using the topology matrix $T_k$, and traverse all service nodes to prepare for behavioral classification.
• Lines 7–14: For services with neither incoming nor outgoing edges, determine if they are newly appeared or belong to the first time slot; classify them as New Members or Isolated Services accordingly.
• Lines 15–17: For services that are only invoked by others but never invoke any service, classify them as Ending Services.

Complexity Analysis

Let n be the number of services and m be the number of time slots.

• Computing the row and column activity vectors takes $\mathcal{O}\left(n\right)$ for each time slot.
• The unified iteration over n services involves only constant-time checks and conditional assignments.
• Overall time complexity per time slot: $\mathcal{O}\left(n\right)$.
• Total complexity over m time slots:

  $$\mathcal{O}(m·n).$$

4.3.2. Phase II: Ending Role Refinement

In the second phase, the previously detected Ending Services are further divided into Cross-Domain Ending, -, or Universal Ending types by analyzing domain boundaries and inter-domain invocation patterns. This additional semantic distinction is detailed in Algorithm 3.

Algorithm 3 Ending Services Sorting Algorithm

1: Input: $T_k\left[a_{ij}\right]$: Topology matrix at time k; $S_e\left[i\right]$: Ending Services set; $D_i$: Domain of i   2: Output: $S_{ce}$: Cross-Domain Endings; $S_{ue}$: Universal Endings; $S_{we}$: Within-Domain Endings   3: for $i=1$ to n and $i\notin D_i$ do   4:     if $col\left[i\right]=0$ then   5:         $S_{ce}\left[i\right]\leftarrow i$   6:     else   7:         $S_{ue}\left[i\right]\leftarrow i$   8:     end if   9: end for 10: for each $i\in D_i$ do 11:     if $col\left[i\right]=0$ then 12:         $S_{we}\left[i\right]\leftarrow i$ 13:     else 14:         $S_{ue}\left[i\right]\leftarrow i$ 15:     end if 16: end for

Algorithm Explanation

• Lines 3–9: For each ending service, examine cross-domain interactions. If it receives calls from services outside its domain, it is labeled as Cross-Domain Ending; otherwise, it is initially assigned to Universal Ending.
• Lines 10–15: Within the same domain, further classification determines whether the service is Within-Domain Ending or remains Universal.

Complexity Analysis

The domain-based classification requires a single comparison per service. Assuming domain membership lookup is $\mathcal{O}\left(1\right)$, the overall complexity remains:

$$\mathcal{O}(m·n).$$

4.3.3. Impact of Filtering

The results from both phases determine the behavioral status of each service, which is then used to control its inclusion and impact in the recommendation engine. Isolated Services are typically filtered out due to their lack of structural engagement. Ending Services receive score amplification due to their contextual significance, and New Member Services are conditionally retained with neutral or default weights.

This filtering step serves as a lightweight, rule-based pre-processing module that enhances the interpretability and effectiveness of the final recommendation phase without adding substantial computational overhead.

4.4. Sliding Time Window Strategy and Role Judgment

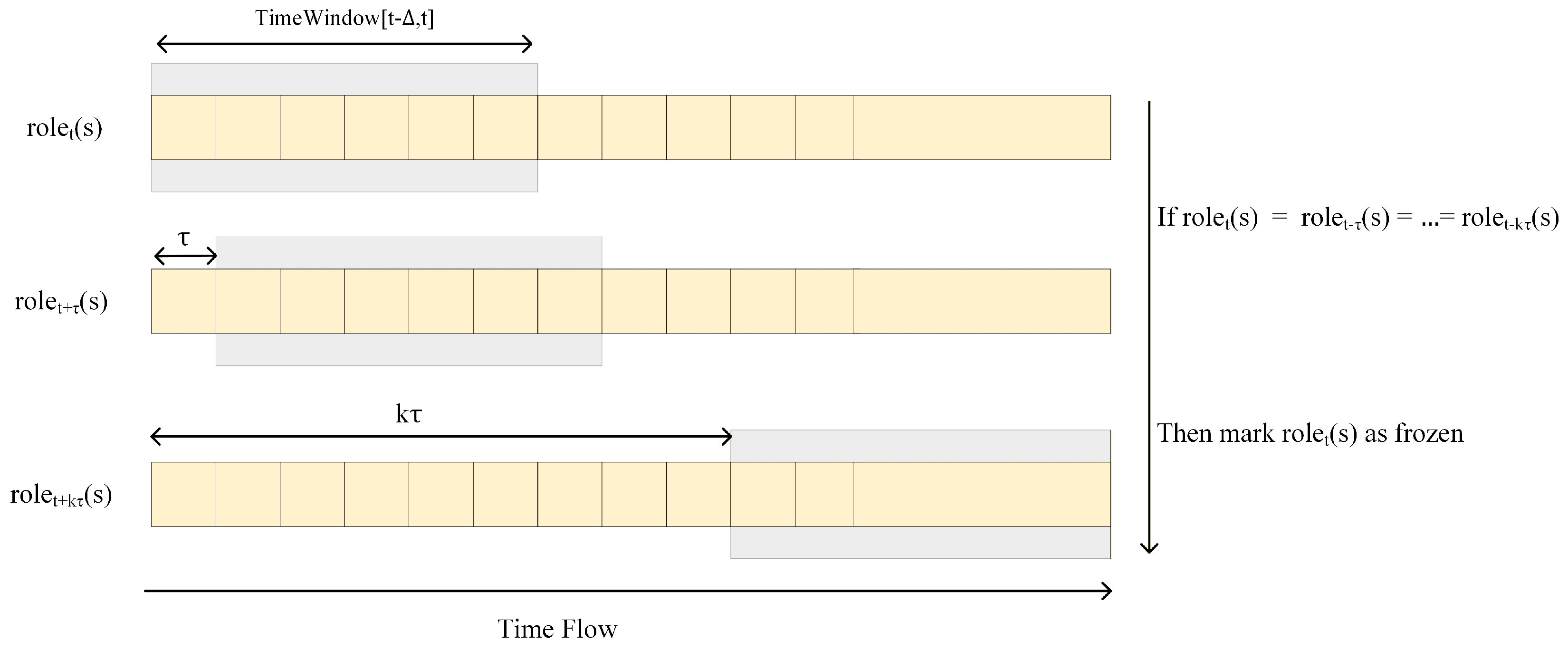
To support dynamic adaptation in service behavior analysis, we implement a sliding time window strategy that incrementally updates the invocation topology and behavioral roles of services over time, shown in Figure 2, this mechanism enables the system to reflect temporal patterns and evolving invocation contexts without requiring full historical recomputation.

Let $\Delta$ denote the window size and $\tau$ the sliding step. At each evaluation timestamp t, the system constructs the service invocation graph $G_t=(V_t,E_t)$ using records within the time interval $[t-\Delta ,t]$. After computing the behavioral roles ${\mathrm{role}}_t\left(s\right)$ for all $s\in V_t$, the system waits for $\tau$ time units before updating the window to $[t+\tau -\Delta ,t+\tau ]$, and recomputes $G_{t+\tau }$ and ${\mathrm{role}}_{t+\tau }\left(s\right)$ accordingly.

To capture role evolution and reduce noise due to temporary fluctuations, we define a stability condition that monitors whether a service maintains the same role across multiple consecutive windows. Formally, for a service s, its role is considered temporally stable if:

$${\mathrm{role}}_t\left(s\right)={\mathrm{role}}_{t-\tau }\left(s\right)=\dots ={\mathrm{role}}_{t-k\tau }\left(s\right),$$

where k is a predefined stability threshold. Once a service satisfies this condition, its role label can be frozen, avoiding unnecessary recomputation or misclassification due to transient invocation patterns.

This sliding mechanism enables the DBS filtering module to dynamically respond to real-time behavior while preserving consistency for structurally stable services. It also allows for efficient incremental updates to recommendation scores when combined with streaming-friendly architectures.

• Algorithm Explanation

Algorithm 4 maintains the temporal evolution of service behavioral roles using a sliding time window approach. At each update step, it extracts recent invocation records to reconstruct the topology, recomputes behavioral roles using the DBS filtering logic (Algorithms 2 and 3), and checks the stability of each service’s role across previous windows.

• Lines 3–5: Initialize the current timestamp and construct the current invocation graph $G_t$ from logs in $[t-\Delta ,t]$.
• Line 6: Behavioral roles for all active services are recomputed based on current topology and domain-aware DBS rules.
• Lines 7–11: For each service, check whether its current role matches the previous k roles over $\tau$-spaced windows. If so, the role is marked as frozen to avoid redundant updates in future steps.
• Line 12–13: Move the time window forward by $\tau$ and repeat the process.

Algorithm 4 Sliding Window Update Procedure for DBS Role Maintenance

1: Input: Service logs $R=\langle u_i,s_j,t_k\rangle$; window size $\Delta$; step size $\tau$; stability threshold K   2: Output: Updated role labels ${\mathrm{role}}_t\left(s\right)$ for each service s   3: Initialize $t\leftarrow \Delta$   4: while new data arrives do   5:     Filter R within window $[t-\Delta ,t]$ to construct $G_t=(V_t,E_t)$   6:     Compute ${\mathrm{role}}_t\left(s\right)$ for all $s\in V_t$ using Algorithms 2 and 3   7:     for all $s\in V_t$ do   8:         if ${\mathrm{role}}_t\left(s\right)={\mathrm{role}}_{t-\tau }\left(s\right)=\dots ={\mathrm{role}}_{t-K\tau }\left(s\right)$ then   9:            Mark ${\mathrm{role}}_t\left(s\right)$ as frozen 10:         end if 11:     end for 12:     $t\leftarrow t+\tau$ 13: end while

• Time Complexity

Let n be the number of services, m the number of invocation edges within the window, and T the number of total time units (i.e., number of windows processed). The complexity per update step includes:

• Filtering records and constructing $G_t$: $\mathcal{O}\left(\right|R_t\left|\right)$, where $|R_t|$ is the number of logs in window $[t-\Delta ,t]$.
• Computing roles via Algorithms 2 and 3: $\mathcal{O}\left(n\right)$ (assuming per-slot DBS filtering is linear).
• Checking stability for all n services across k prior windows: $\mathcal{O}(k·n)$.

Hence, the time complexity per iteration is:

$$\mathcal{O}\left(\right|R_t|+k·n),$$

and the total complexity over T updates is:

$$\mathcal{O}\left(T·\left(\right|R_t|+k·n)\right).$$

• Space Complexity

The algorithm maintains:

• The current invocation graph $G_t$: $\mathcal{O}(n+m)$;
• A short history of previous k roles per service: $\mathcal{O}(k·n)$;

Thus, the total space complexity is:

$$\mathcal{O}(n+m+k·n).$$

• Stability Efficiency

The use of role freezing significantly reduces redundant recomputation for behaviorally stable services. Once a service is frozen, its role does not need to be re-evaluated in subsequent iterations unless its topology context changes, thus enhancing performance in dynamic but stable environments.

5. Simulations

5.1. Dataset

5.1.1. Brief Introduction

All simulations are conducted on the Santander Smart City dataset [33] from the SmartSantander EU Project, which records fine-grained service invocations across multiple urban domains. Although the dataset originates from IoT-based city services, its multi-domain invocation structure resembles heterogeneous service deployments commonly observed in multi-cloud environments, where domain-specific services may be operated by different departments or vendors [34]. This characteristic enables us to reasonably extend the dataset to simulate multi-cloud scenarios.

To adapt Santander for our evaluation, we apply a randomized but balanced allocation strategy to distribute services across several logical clouds, ensuring that each cloud hosts a comparable number of services while preserving the dataset’s inherent invocation topology. This design allows us to simulate both inter-cloud and intra-cloud interactions in a controlled manner without introducing artificial structural bias. Furthermore, Santander provides large-scale, dynamic, and diverse invocation traces, which makes it particularly suitable for evaluating behavior-aware recommendation frameworks like ours, especially under settings involving temporal evolution and cross-domain behavioral dynamics.

5.1.2. Preprocessing

Each invocation record is structured as a tuple $\langle u_i,s_j,t_k\rangle$, indicating that user $u_i$ invoked service $s_j$ at time $t_k$. To adapt the dataset for our framework, we preprocess the original fields and semantically map them to cloud service concepts. The mapping is summarized in

Table 3. Mapping from Santander City Entities to Cloud Service Concepts.

Original Entity	Mapped Entity	Mapped Entity Description
id_device	id_service	Identifier of cloud service instances
device_type	service_type	Service category/type
id_req_application	id_req_service	Requested cloud service from the user’s perspective
id_off_application	id_off_service	Offered cloud service from the provider side

. We adopted a randomized yet balanced allocation strategy: services are randomly assigned to clouds while ensuring each cloud hosts a comparable number of services and retains a diverse mix of service types. This design avoids the creation of ‘single-function clouds’, which could distort compatibility evaluation, and instead mimics real-world multi-cloud ecosystems where services are deployed heterogeneously across providers.

To simulate a multi-cloud deployment, we partition the full service pool into two logical clouds, ${\mathcal{C}}_1$ with 8115 services and ${\mathcal{C}}_2$ with 8101 services, based on service ID ranges or domain attributes. This separation enables the modeling of inter-cloud invocations while maintaining controllable experimental scope.

For dynamic analysis, we adopt a sliding window mechanism with window size $\Delta$ and step size $\tau$ to segment the data temporally. Within each window, we extract sequential invocation paths and construct a directed graph $G_t=(V_t,E_t)$, where nodes represent services and edges represent temporal invocations. This evolving topology forms the basis for DBS identification, scoring, filtering, and recommendation evaluation in our simulations.

5.2. Simulation Design

To comprehensively evaluate the effectiveness of our DBS-aware framework, we design five targeted groups of simulations. Each group focuses on a specific aspect of system performance, ranging from recommendation accuracy to behavioral stability and robustness under real-world constraints. The design intentionally aligns with the role semantics and structural innovations proposed in this paper.

• Group I: Ablation Study on DBS-Aware Recommendation. To validate the effect of DBS-aware mechanisms, we performed an ablation study using synthetic invocation data. The dataset simulated a service pool with 100 services and 1000 invocation records, where a configurable proportion (10%, 20%, 30%) of services were artificially marked as DBS. These included Isolated Services, Ending Services, and New Member Services, all exhibiting behavioral anomalies such as lack of invocations or unbalanced connectivity.
  We compared two system variants:

  –

  NoDBS: The baseline system without any DBS identification or filtering.

  –

  FullDBS: The enhanced system that integrates full DBS detection and filtering workflows.

  For each setting, a fixed user group was used to simulate invocation-based recommendation, and Precision, Recall, and F1-score were calculated based on the overlap between recommended and relevant services. The simulation was repeated under three different DBS ratios to assess the robustness and contribution of the DBS module under varying degrees of service pool contamination.
• Group II: Recommendation Performance. This group evaluates how the DBS-enhanced service filtering affects the final recommendation quality. Specifically, we assess the ranking performance using Precision, Recall, and F1-score under varying Top-N recommendation thresholds. These metrics jointly reflect the accuracy, completeness, and overall reliability of the recommendation results. Comparisons are made against both classical and state-of-the-art baselines.
• Group III (a): Window Size Sensitivity Simulation. This group evaluate the stability of behavior role classification under sliding window mechanisms and pick the most suitable length of the window size, we designed a window size sensitivity simulation based on synthetic data. Instead of using fixed time intervals, this simulation adopts a fixed number of service invocations as the segmentation unit, thereby eliminating biases introduced by uneven invocation densities.
• Group III (b): Temporal Role Stability. This group measures the stability of recommendation results under the sliding time window. It investigates whether the role judgment and filtering mechanisms introduce volatility or maintain consistent service outputs across adjacent windows. Top-N list overlap and Jaccard Similarity are used as core indicators.
• Group IV: Coverage under Data Sparsity. This group validates whether the Markov-based scoring process, combined with DBS filtering, can sustain service recommendation coverage when invocation records become sparse. It simulates controlled data sparsity ratios and measures the impact on overall service recommendation coverage.
• Group V: Cold-Start Scoring Capability. This group specifically targets cold-start services—particularly those identified as New Member and Isolated by the DBS mechanism. It measures whether these behaviorally low-frequency services can still be scored and ranked effectively, using our irreducible Markov process. The evaluation metric is cold-start scoring rate (CSR).

These four simulation groups together provide a well-rounded evaluation of our framework from the perspectives of performance, consistency, robustness, and adaptability.

Finally, to ensure that the performance improvements of the proposed framework over baseline methods are not only empirical but also statistically validated, we planned a paired t-test as part of the simulation design. This statistical test compares the proposed approach with all baselines (GNN, TCF, TREP, and MCTSE) under both experimental scenarios, providing a formal significance assessment to support the reliability of the conclusions.

All simulations were implemented in Matlab 2024b and conducted on a workstation equipped with an Intel i7 CPU and 32 GB RAM.

5.3. Evaluation Metrics

To enable targeted evaluation, we adopt four types of metrics across the four simulation groups, as summarized in

Table 4. Summary of Evaluation Metrics Used in Validations and Simulations.

Metric	Purpose	Definition/Formula	Used in
Precision	Measures correctness of Top-N recommendation	$\mathrm{Precision}@N={\displaystyle \frac{|\mathrm{Recommended}\cap \mathrm{Relevant}|}{\left|\mathrm{Recommended}\right|}}$	Group I
Recall	Measures completeness of Top-N recommendation	$\mathrm{Recall}@N={\displaystyle \frac{|\mathrm{Recommended}\cap \mathrm{Relevant}|}{\left|\mathrm{Relevant}\right|}}$	Group I
F1-score	Harmonic mean of Precision and Recall	$\mathrm{F}1@N=2·{\displaystyle \frac{\mathrm{Precision}@N·\mathrm{Recall}@N}{\mathrm{Precision}@N+\mathrm{Recall}@N}}$	Group I
Jaccard Similarity	Measures Top-N list stability over time	$\mathrm{Jaccard}@N={\displaystyle \frac{|L_t\cap L_{t-\tau }|}{|L_t\cup L_{t-\tau }|}}$	Group II
Coverage Ratio	Measures scoring reach under sparse data	$\mathrm{Coverage}={\displaystyle \frac{\left|\mathrm{Scored}\mathrm{Services}\right|}{\left|\mathrm{All}\mathrm{Services}\right|}}$	Group III
Cold-Start Scoring Rate (CSR)	Measures scoring success on cold-start services	$\mathrm{CSR}={\displaystyle \frac{\left|\mathrm{Cold}\text{-}\mathrm{start}\mathrm{services}\mathrm{with}\mathrm{scores}\right|}{\left|\mathrm{All}\mathrm{cold}\text{-}\mathrm{start}\mathrm{services}\right|}}$	Group IV

. Each metric is designed to evaluate a specific aspect of the framework, such as recommendation quality, temporal stability, scoring coverage, and cold-start support.

5.4. Baseline

To prove the effectiveness of our proposed framework, we choose four state-of-the-art research works to be the baseline of our simulations.

Trust-Based Approach (TCF) [35]: Trust-Based Approach: A service recommendation that relies on a distributed collaborative filtering rating system using friendship and social relationships as the filtering criteria.

Interface Matching Graph Neural Network (GNN): [36] This GNN-based service recommendation method combines an interface-matching graph construction process with a two-layer GCN scoring module. In our study, we adapted IM GNN by using invocation graphs as input to fairly compare its GNN-based scoring with our DBS framework.

Trust and Reputation Approach (TREP) [37]: This approach to service recommendation which integrates trust and reputation within the recommendation process.

Mutual Context-Aware Trustworthy Service Evaluation (MCTSE) [38]: This framework is another trust-based recommendation system that leverages the time and location of services to establish trust among them.

A comparative evaluation with representative state-of-the-art methods—TCF, TREP, MCTSE and GNN—is conducted using precision, recall, and F1-score metrics, as summarized in Section 6.

6. Results and Analysis

6.1. Ablation Study on DBS-Aware Recommendation

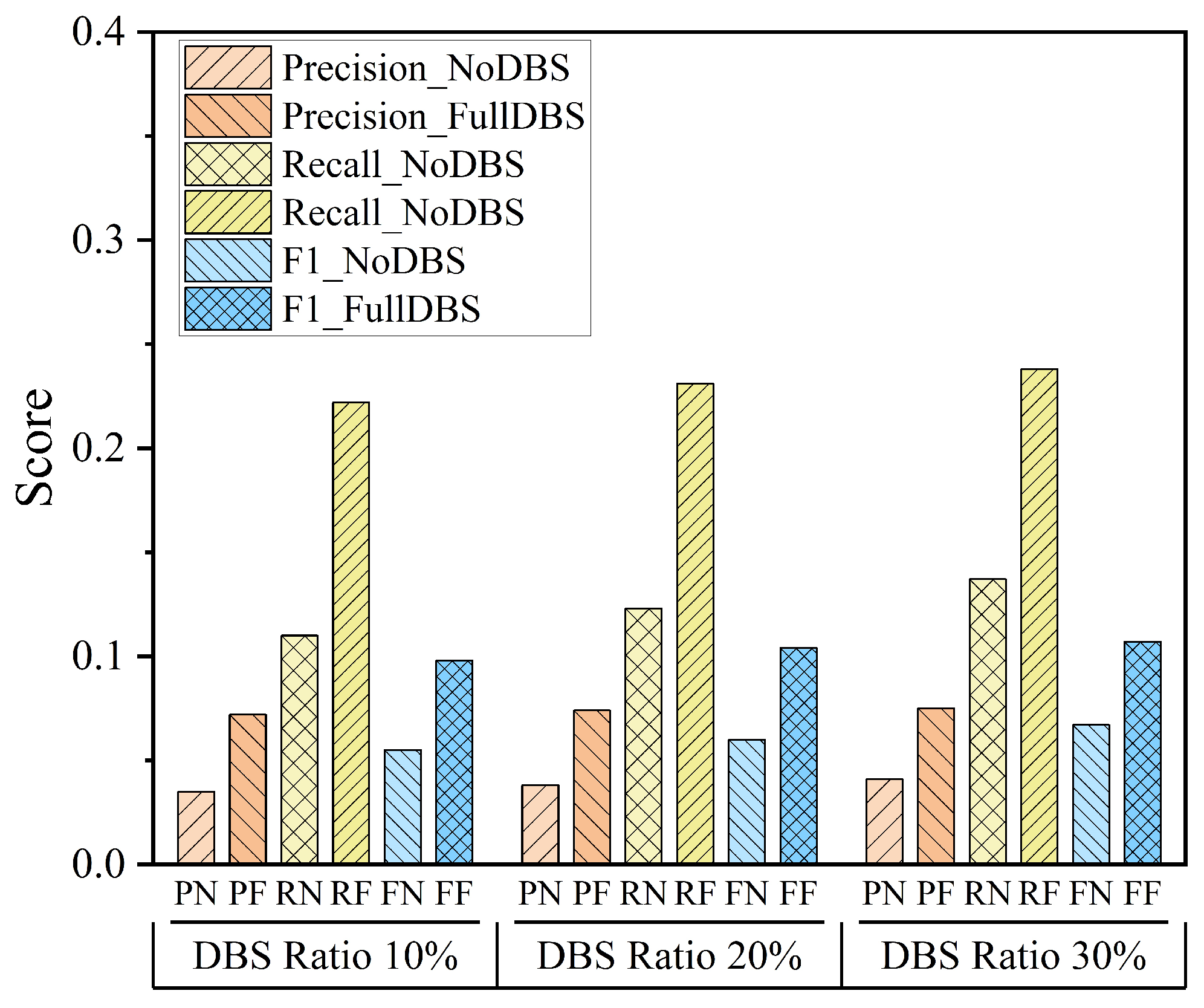
To evaluate the contribution of DBS-aware mechanisms to recommendation performance, we conducted an ablation study comparing two variants: the baseline without DBS filtering (NoDBS), and the full version integrating DBS identification and filtering (FullDBS). The proportion of DBS in the service pool was set to 10%, 20%, and 30%, and evaluation was performed based on Precision, Recall, and F1-score.

As shown in Figure 3, FullDBS consistently outperforms NoDBS across all metrics and DBS ratios. In particular, the F1-score exhibits the most significant improvement, with relative gains exceeding 130% on average. Precision and Recall also show substantial improvements, generally ranging between 85% and 135%. These results clearly demonstrate that DBS-aware filtering helps eliminate low-quality services and enhance the relevance of recommended items.

Notably, as the DBS ratio increases, the performance gap between FullDBS and NoDBS becomes more pronounced, confirming that proper detection and handling of behavioral outliers (e.g., isolated or newly joined services) is essential for maintaining recommendation accuracy and stability.

6.2. Recommendation Accuracy Under Dynamic Environments

To evaluate the robustness and adaptability of the proposed DBS-based model in such scenarios, we design two complementary simulations:

• Dynamic Service Pool: Simulates a gradually expanding set of services, increasing from 1000 to 10,000. This setting tests the model’s ability to score and recommend effectively in the presence of newly added, low-visibility services.
• Dynamic User Crowd: Simulates a growing population of service requesters, ranging from 1000 to 10,000. This scenario evaluates how the model responds to shifts in user behavior and the emergence of sparse interaction patterns.

In both simulations, we evaluate five methods: TCF, TREP, MCTSE, GNN, and the proposed method. Precision, Recall, and F1-score are used as performance metrics. All methods share a unified recommendation pipeline to ensure fair comparison, with DBS detection performed uniformly before scoring and ranking.

6.2.1. Performance Under Dynamic Service Pool

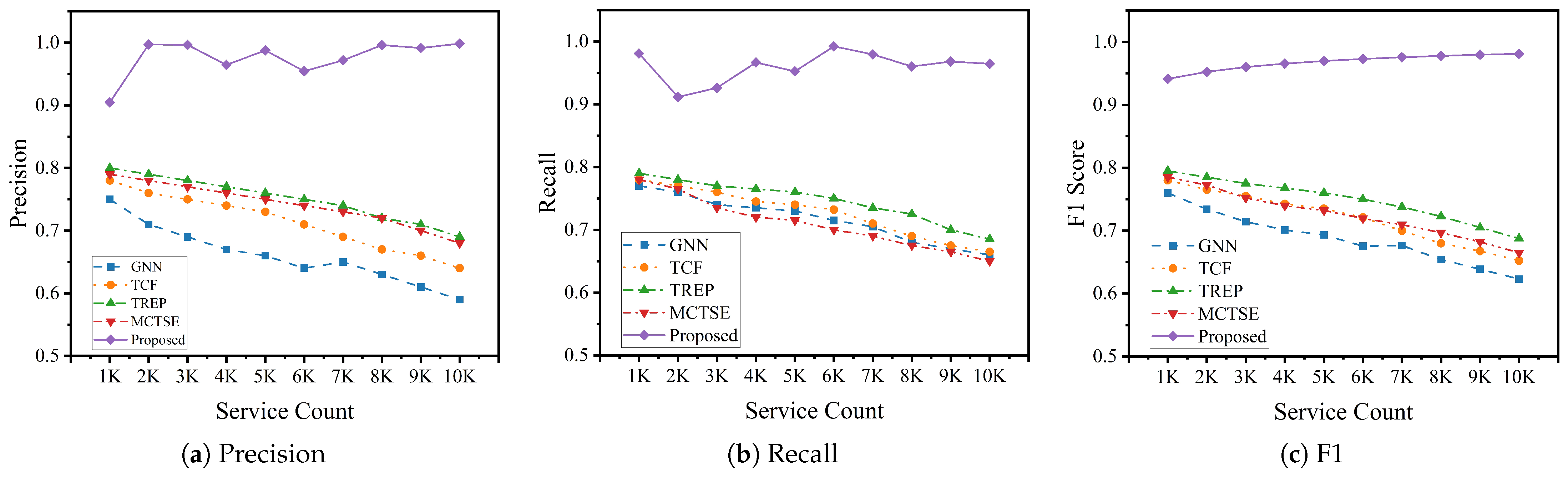
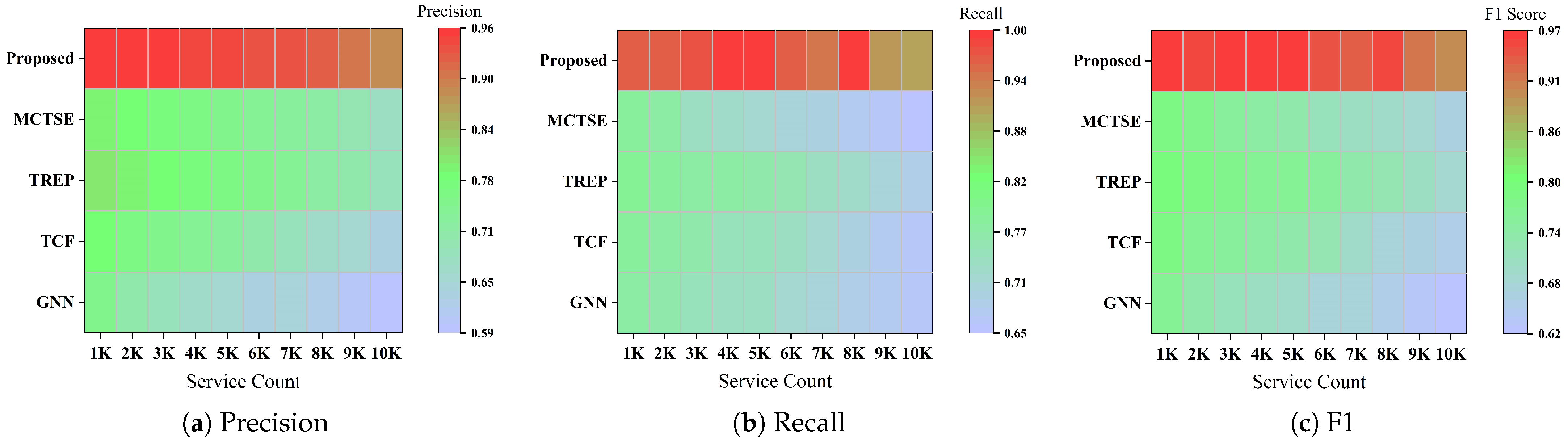
Shown in Figure 4, as the number of available services increases, most baseline methods experience a clear decline across all three metrics. TREP and GNN show the most severe degradation, with precision and recall dropping by more than 20%, highlighting their inability to cope with newly added, sparsely connected services. TCF and MCTSE maintain relatively better performance but still exhibit instability. Notably, MCTSE suffers from a gradual decline in precision, likely due to its bias toward highly connected nodes, which becomes problematic when the pool expands and the average connectivity drops.

In contrast, the proposed method demonstrates outstanding robustness. Precision remains above 0.9 even as the pool size increases tenfold, while recall and F1-score show minimal variance. Compared with the best-performing baseline, our model achieves a 46.7% improvement in precision, 42.79% in recall, and 43.76% in F1-score under this setting. This is largely due to the DBS filtering mechanism, which removes unstable or uninvoked services—such as Isolated or Ending types—thereby improving the overall quality of the candidate set and mitigating cold-start effects.

6.2.2. Performance Under Dynamic User Crowd

Figure 5 visualizes the performance trends under user-side dynamics. As user count increases from 1000 to 10,000, most baseline methods show a notable drop in recall. GNN, in particular, falls below 0.65 in high-volume settings, revealing its limited ability to generalize to unseen user behaviors. MCTSE maintains competitive performance in smaller-scale settings but shows increasing volatility in recall and F1-score as the user base grows. This suggests that while it handles structural noise reasonably well, it does not adapt effectively to behavioral variation introduced by dynamic users.

In contrast, the proposed method maintains high and stable performance, with all three metrics remaining above 0.9 across the entire user range. Notably, the model delivers a 40.5% increase in precision, 41.2% in recall, and 39.62% in F1-score compared to the best-performing baseline in this setting. This robustness is attributed to two key factors: (i) DBS filtering helps stabilize the service graph regardless of user fluctuation, and (ii) the Markov scoring ensures smooth and fair score propagation even when user-service interactions are sparse or newly formed.

6.3. Temporal Role Stability Under Sliding Window

6.3.1. Window Size Sensitivity

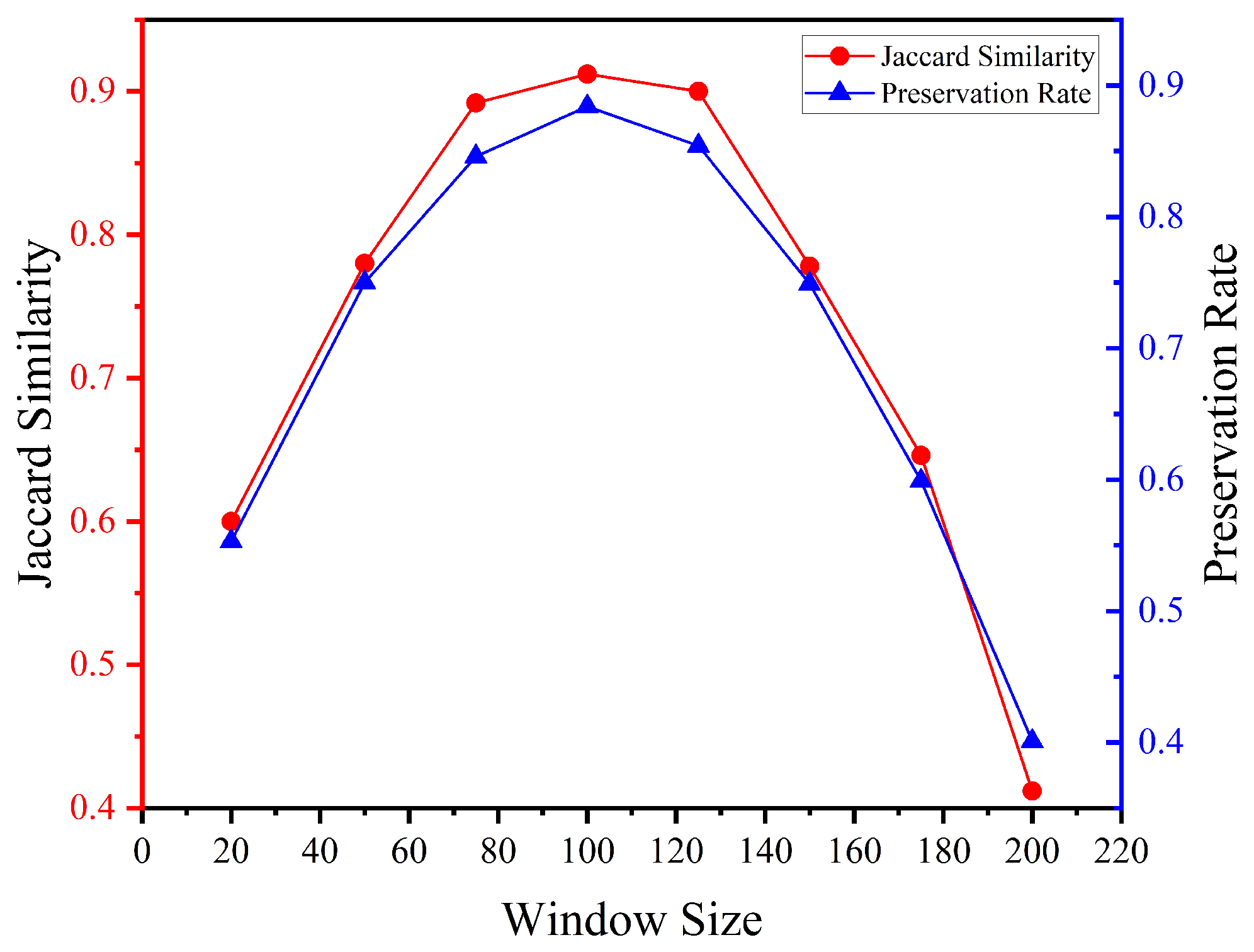
To further evaluate the stability of service behavior identification under different sliding window configurations, we conducted a sensitivity analysis based on window size. Instead of using fixed time intervals, we adopted the number of invocation operations as the unit of segmentation to mitigate density imbalance caused by usage fluctuations. Specifically, we simulated a service pool with 100 services and 1000 total invocations, and divided the timeline into windows of varying sizes: 25, 50, 75, 100, 125, 150, 175, and 200 operations per window. Within each window, the system identified behavioral roles for services (i.e., Isolated, Ending, and New Member), and we computed the role consistency across adjacent windows. Two metrics were used for evaluation:

• Jaccard Similarity: measures the overlap of role-specific service sets between adjacent windows.
• Preservation Rate: reflects how consistently a service maintains its assigned role across windows.

As shown in the Figure 6, both metrics peak at a window size of 100, reaching 0.91 and 0.88 respectively. These results indicate that a window size of 100 offers optimal stability for role classification, and it is thus adopted as the default configuration in subsequent simulations.

6.3.2. Temporal Role Stability

This simulation evaluates the temporal stability of recommendation results when applying the proposed sliding time window strategy and behavioral role freezing. We aim to test whether filtering services based on stable DBS roles reduces noise and prevents recommendation list volatility over time.

We segment the service invocation data using a sliding window strategy based on operation counts rather than time intervals, aligning with the findings of our window size sensitivity analysis. Specifically, we set the window size to 100 service invocations and a sliding step size of 25 invocations. For each window, the system constructs an invocation graph $G_t=(V_t,E_t)$ and generates Top-N recommendations for active users ($N=10$). We compare two variants of the system across 20 consecutive windows and evaluate the consistency of recommendation outputs.

Two variants of the system are compared:

• Ours (Sliding Windows(SW) + freeze): we refer to a common strategy in temporal smoothing and behavioral stability analysis, where consistency observed across three or more consecutive observations is typically considered a strong indicator of stable behavior. Services whose roles remain unchanged for $k=3$ consecutive windows are frozen, and their roles are reused in future filtering.
• Ours (Slinding Windows (SW)): Role judgment is recomputed independently in every window, without considering temporal consistency.

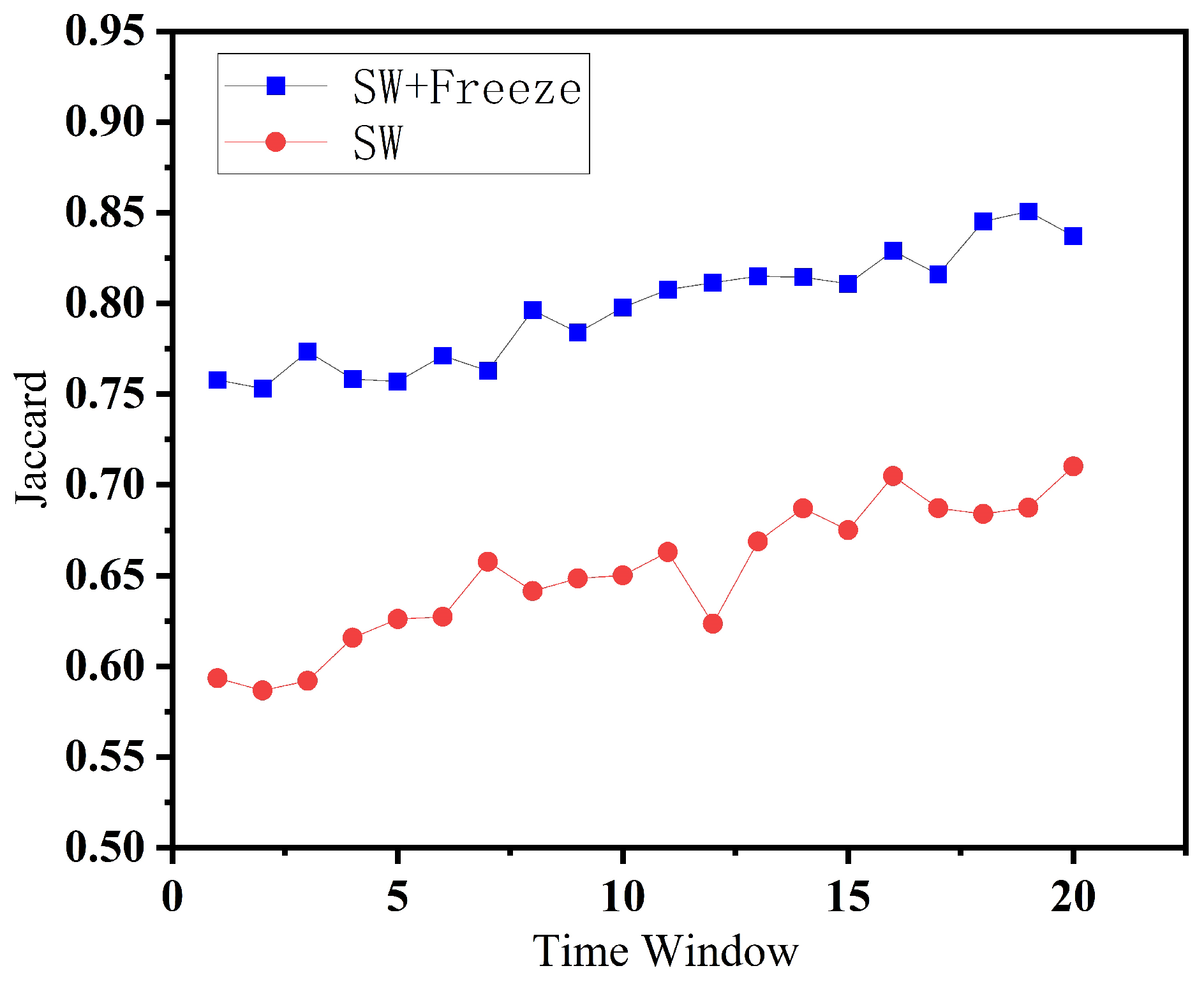
Figure 7 shows the Jaccard@10 scores over 20 sliding windows. The method with role freezing consistently achieves higher overlap (typically above 0.75), while the version without freezing fluctuates at lower values (around 0.62). This indicates that the freezing strategy stabilizes the recommendation list across time.

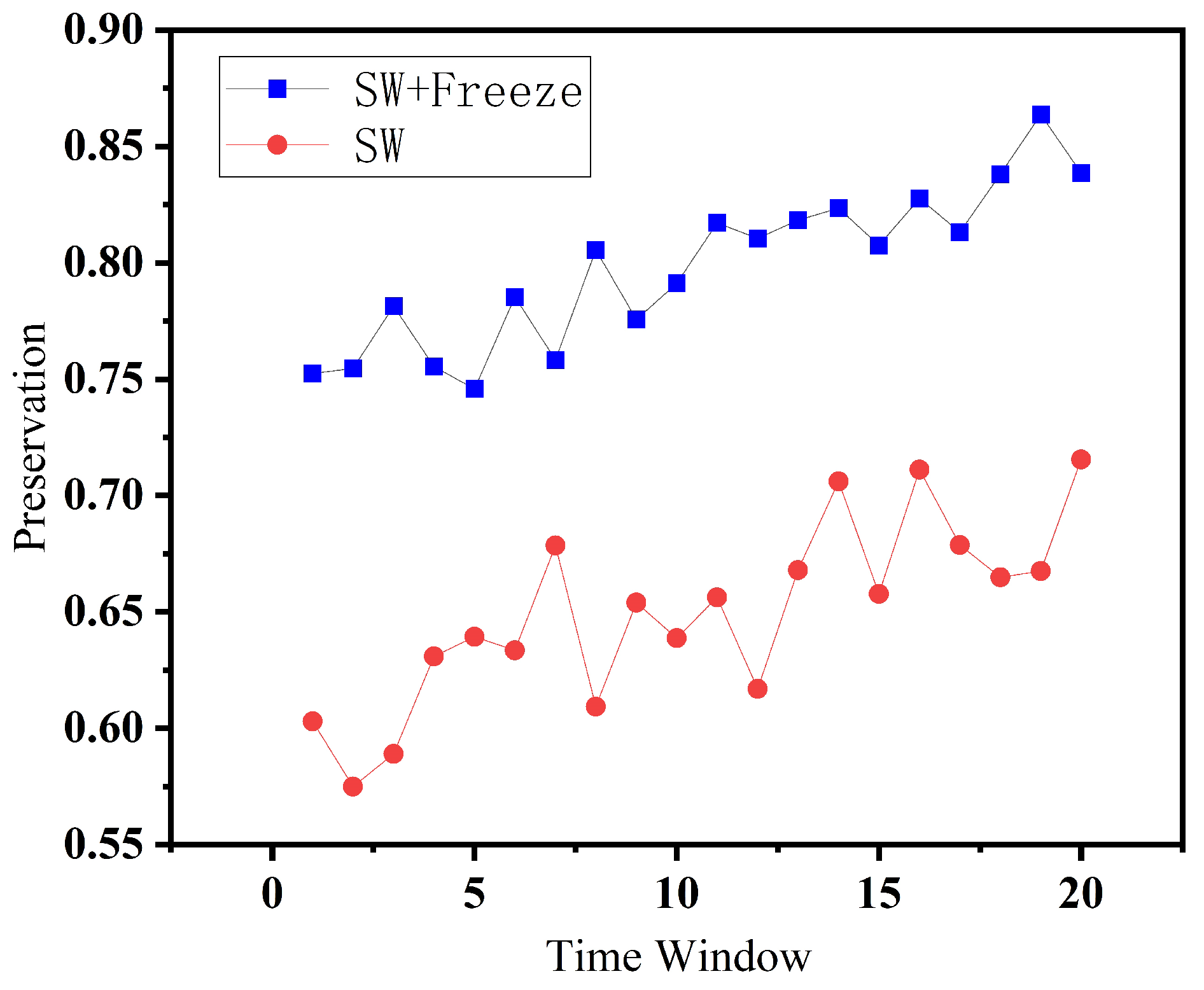
In Figure 8, we visualize the Preservation@10 metric. Similar to Jaccard, the method with role freezing shows higher preservation rates, indicating that previously recommended services are more likely to persist in subsequent windows. This reinforces the idea that the role stability mechanism prevents premature removal of useful services due to transient behavior shifts. Both metrics confirm that our sliding window strategy with behavioral role freezing improves the temporal stability of recommendations. Compared to the setting without freezing, our proposed strategy achieves a 22.85% improvement across sliding windows, demonstrating its effectiveness in maintaining recommendation stability over time. It helps retain high-confidence services and avoids fluctuations caused by unstable DBS classifications, resulting in more consistent and reliable recommendation behavior over time.

6.4. Coverage Under Data Sparsity

We evaluate scoring coverage under five predefined sparsity levels: {10%, 30%, 50%, 70%, 90%}, representing increasingly severe data sparsity in the service invocation records. For each sparsity level, a corresponding proportion of invocation data is randomly removed from the original dataset to simulate incomplete service histories. Based on the resulting topology, we apply the scoring process and calculate the Scoring Coverage Rate (SCR), which measures the proportion of services receiving non-zero scores. A higher SCR indicates better robustness to sparse data conditions.

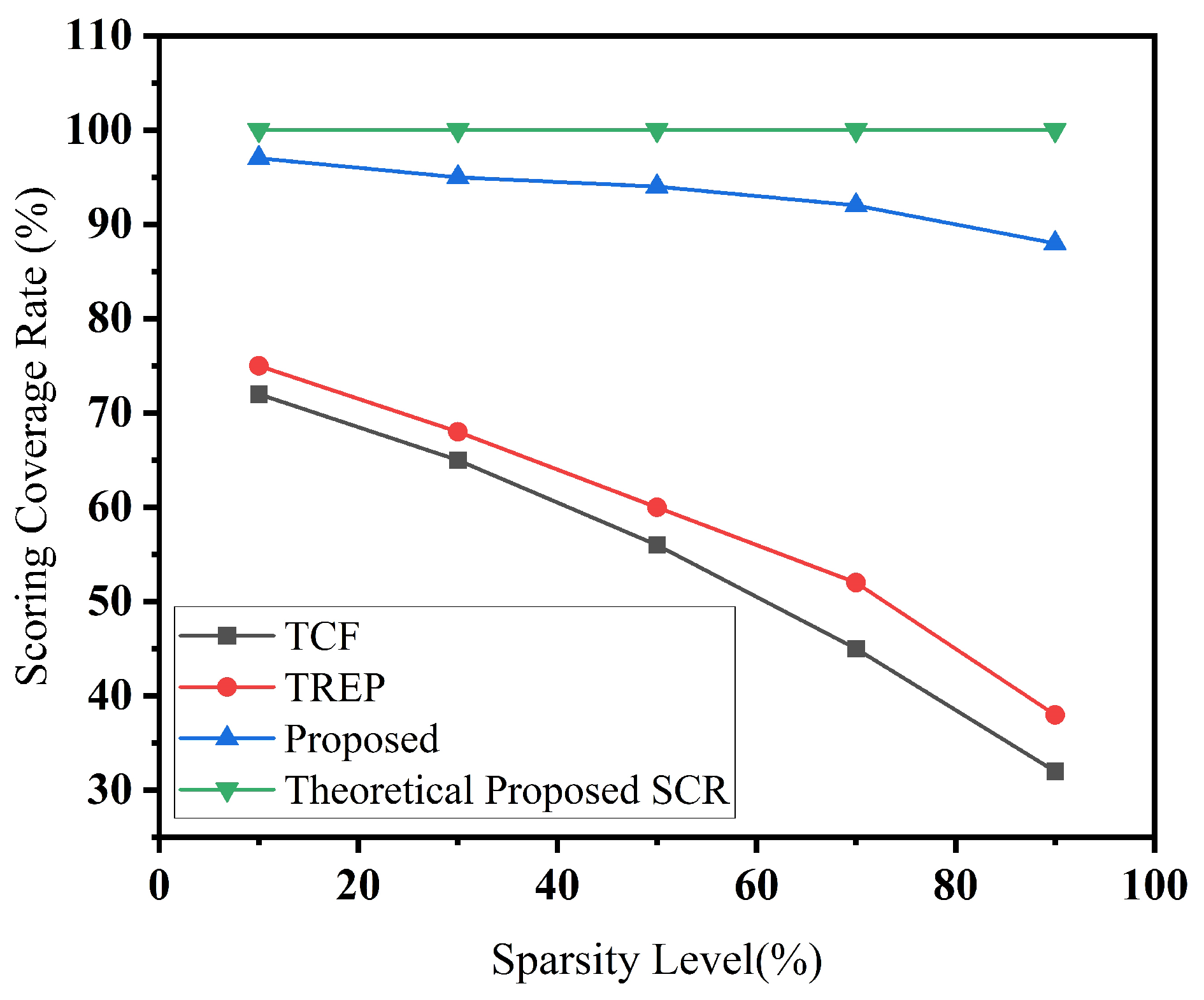
The results are shown in Figure 9. As the sparsity level increases, both TCF and TREP exhibit consistent drops in scoring coverage. For example, at 90% sparsity, their SCRs decrease to 32% and 38%, respectively, indicating that a large portion of services fail to receive valid scores due to insufficient invocation data or limited connectivity.

In contrast, our proposed Markov Chain-based method demonstrates significantly stronger resilience. Even under the most extreme sparsity condition (90%), it achieves an SCR of 88%, and steadily improves as more data is available—reaching 97% when sparsity drops to 10%. This consistent high coverage is aligned with the theoretical guarantee of our method, which ensures complete score propagation as long as the service topology remains connected and irreducible.

To highlight this point, we include a horizontal reference line representing the theoretical upper bound of 100% SCR, derived from the homogeneous irreducibility of our Markov Chain model. The minor gap between the actual and ideal coverage stems primarily from occasional topological fragmentation during random edge removal. Nevertheless, our approach consistently outperforms TCF and TREP, showing clear superiority in handling sparse service environments.

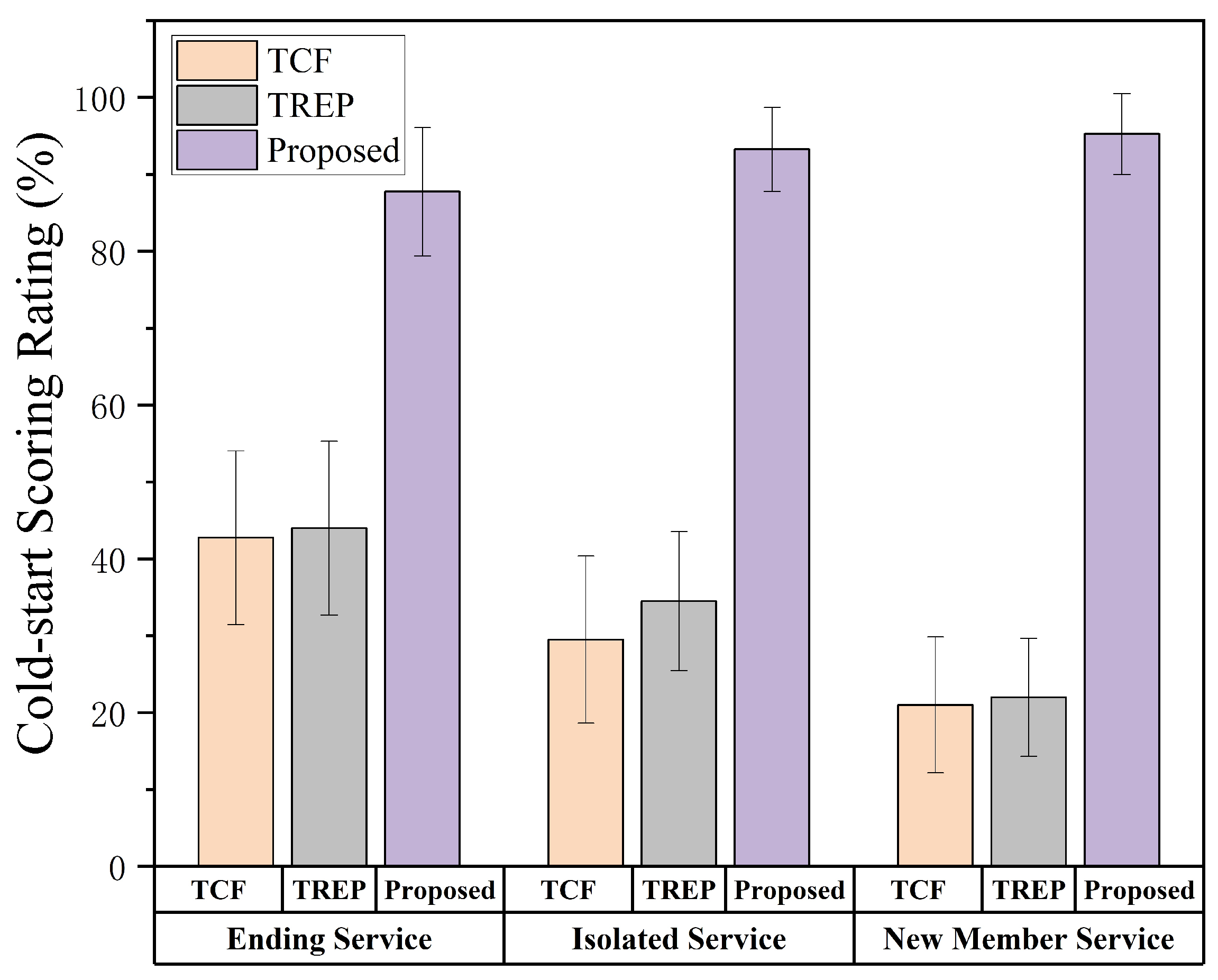
6.5. Cold-Start Scoring Rate on DBS Services

DBS exhibit strong cold-start characteristics due to their limited or nonexistent invocation histories. Traditional recommendation methods, such as Collaborative Filtering (TCF) and trust-based approaches (TREP), often fail to assign scores to these services, resulting in poor coverage and ineffective recommendations. To assess the cold-start handling capability of our model, we define the Cold-Start Scoring Rate (CSR) as the proportion of DBS services receiving non-zero scores. All three types of DBS services are considered, and the CSR is evaluated across 20 randomized simulations to ensure statistical stability. The compared methods include: (i) TCF, (ii) TREP, and (iii) our proposed Markov Chain-based scoring method.

The average CSR results and standard deviations over 20 experimental runs are summarized in Figure 10. Our proposed model significantly outperforms baseline methods across all DBS categories. In particular, it achieves a CSR of 95% on New Member services, whereas TCF and TREP score only 22% and 23%, respectively. Similarly, for Isolated and Ending services, our method maintains CSR above 88%, while the baselines drop below 45%.

These results validate the model’s strong cold-start robustness, which stems from its reliance on the topological structure of the service invocation graph rather than historical co-occurrence. Furthermore, the low standard deviation across all runs demonstrates the consistency of the scoring mechanism. Although the theoretical CSR of our model is expected to reach 100% due to its homogeneous and irreducible Markov Chain properties, slight deviations may still occur. These are primarily caused by fully disconnected nodes in the DBS set or by numerical thresholds that treat extremely low scores as zero. Nevertheless, the achieved performance remains superior in both coverage and stability.

6.6. Statistical Significance Test

To further validate the reliability of our experimental results, we conducted a paired t-test to examine whether the performance improvements of the proposed method over baseline approaches are statistically significant. The test was performed on the F1-scores obtained across all device count settings under both experimental scenarios: Dynamic User Crowd and Dynamic Pool.

Specifically, we compared the Proposed framework against four representative baselines (GNN, TCF, TREP, and MCTSE) using paired samples from identical experimental configurations. Shown in

Table 5. Paired t-test p-values comparing proposed with baselines.

Baseline	Dynamic User Crowd	Dynamic Pool
GNN	$1.88\times {10}^{-10}$	$3.89\times {10}^{-11}$
TCF	$5.04\times {10}^{-10}$	$5.04\times {10}^{-9}$
TREP	$2.26\times {10}^{-12}$	$3.97\times {10}^{-9}$
MCTSE	$6.15\times {10}^{-11}$	$2.53\times {10}^{-12}$

, the resulting p-values are consistently far below the commonly accepted threshold of 0.05 (in the order of ${10}^{-9}$ to ${10}^{-12}$), confirming that the observed improvements are not due to random variation but are statistically significant.

This statistical validation reinforces the conclusion that the proposed method consistently and significantly outperforms existing baselines across diverse experimental settings, providing stronger evidence for the robustness and generalizability of our framework.

7. Conclusions

7.1. Summary of Contributions

In this paper, we introduced the concept of Distinct Behavioral Services (DBS) and proposed a structural classification framework that identifies special service types such as New Member, Isolated, and Ending services based on invocation topology. These services typically suffer from extreme sparsity or lack of co-invocation records, posing serious challenges for conventional recommendation systems. To address this, we designed a unified scoring model that integrates DBS detection with a Markov Chain-based scoring mechanism. This approach ensures that even under cold-start or sparse conditions, services can receive consistent and topology-aware scores. The proposed framework is scalable and domain-agnostic, making it suitable for complex multi-cloud service environments.

Extensive simulations were conducted under four perspectives: recommendation accuracy, stability under sliding time windows, scoring coverage under data sparsity, and cold-start performance on DBS services. Results confirm the superiority of our approach over existing collaborative filtering and topology-based methods. In particular, our method consistently achieves higher precision, recall, and F1 score, while maintaining robustness in dynamic user and service environments.

7.2. Limitations and Future Work

Although the proposed DBS-aware recommendation framework demonstrates strong performance and robustness across different dynamic scenarios, several limitations remain.

(1)

Dataset Generalizability.

The Santander Smart City dataset reflects urban IoT-style service interactions, which are not fully equivalent to real-world multi-cloud service invocation ecosystems. While it provides representative dynamic behaviors and invocation patterns, the absence of genuine cross-cloud workflow traces may limit the direct generalizability of the evaluation results.

(2)

Topology Reconstruction Assumptions.

The framework assumes that invocation relations can be accurately extracted from logs to construct topology matrices. In large-scale multi-cloud deployments, log completeness, monitoring granularity, or privacy restrictions may introduce missing or noisy topology information.

(3)

Temporal Window Sensitivity.

The sliding-window mechanism involves selecting a fixed window size. Although experiments demonstrate stable performance across different settings, extreme fluctuations in service pool dynamics may require adaptive or learned window sizes.

Future work will focus on collecting real multi-cloud workflow traces, designing adaptive temporal windows, and exploring learning-based topology extraction to further improve the applicability of DBS-aware recommendation in large-scale cloud environments.