Stochastic Game-Based Anti-Jamming Control Method for Heavy-Haul Train Group Operation

Abstract

With the growing global demand for mineral resources, enhancing the transport capacity of heavy-haul railways (HHR) has emerged as a key area of research. As an emerging train formation technology, the virtual coupling train system (VCTS) has the potential to substantially increase the traffic density of heavy-haul trains (HHT) and thereby improve transport efficiency. However, the stable operation of virtually coupled fleets relies on train-to-train (T2T) communication, which is vulnerable to jamming attacks (JAs) within the complex operational environments of HHR. To address issues such as train decoupling and emergency braking in the VCTS that may be caused by JAs, this study proposes a stochastic game-based anti-jamming control (SGAC) strategy aimed at ensuring the stability and operational safety of the VCTS operating within HHR. The proposed approach models both JAs and defensive actions as a stochastic game and employs an $H^{\infty }$-based cross-layer control method to mitigate their adverse effects. The control performance is analyzed through frequency-domain mapping, and a quantitative evaluation is conducted using the $H^{\infty }$ norm. The simulation results demonstrate that the SGAC scheme significantly enhances the resilience of VCTS cooperative control under JAs, offering a robust solution for ensuring the stable operation of HHR.

1. Introduction

Heavy-haul trains (HHT) serve as the backbone of bulk cargo transportation, offering significant advantages in both scale and cost-effectiveness. They play a crucial role in maintaining stable resource distribution and promoting sustainable economic growth by ensuring the continuous operation of critical energy and mineral supply chains [1]. To meet the increasing global demand for these resources, enhancing the transport capacity and operational efficiency of heavy-haul railways (HHR) has become a major focus of innovation. As an advanced train control technology, the virtual coupling train system (VCTS) employs real-time train-to-train (T2T) communication and high-precision positioning to dynamically shorten inter-train spacing from the absolute braking distance to the relative braking distance. This capability substantially reduces train headways and enhancing overall line capacity [2], addressing the urgent need for higher efficiency in HHR.

However, implementing VCTS in HHR introduces unique challenges absent in conventional rail systems. The enormous mass and length of HHT make them highly sensitive to internal forces, where even minor communication delays or losses may trigger control actions leading to serious safety risks, such as in-train force instability or derailment. Moreover, heavy-haul railways often operate in remote, complex terrains with unreliable wireless channels, rendering the system vulnerable to both natural interference and intentional attacks. Given the high strategic and economic value of transported cargo, ensuring the security and resilience of VCTS operation in HHR is crucial. Consequently, the integrity and availability of T2T communication in VCTS are highly vulnerable to jamming attacks (JAs) and other external disturbances [3]. JAs, as one of the most prevalent forms of communication threats, directly compromise the stability of VCTS by causing transmission delays and degrading T2T communication quality [4], which can lead to unintentional decoupling or emergency braking events [5]. Therefore, mitigating the effects of JAs on the operation of virtually coupled fleets in HHR is of vital importance.

In response to these operational and safety challenges, a substantial body of research has explored cooperative control strategies for VCTS. Early studies use model-based control frameworks such as dynamic programming (DP) and model predictive control (MPC) [5,6] for trajectory optimization and predictive coordination. Subsequent work sought to enhance robustness by integrating adaptive and nonlinear control techniques, including sliding mode control and variable-structure control, to address model uncertainties and disturbances [7,8,9]. At the formation-control level, hybrid and distributed approaches have also been proposed, such as integrating generalized predictive control (GPC) with potential field methods or deploying distributed MPC (DMPC) for multi-train coordination [10,11]. Recently, a paradigm shift toward data-driven and learning-based control has emerged. Reinforcement learning (RL) and other model-free methods are increasingly applied to cope with nonlinear dynamics without requiring precise physical models [12,13,14,15]. Meanwhile, the broader control community has explored imitation learning for approximating stochastic models of systems with complex uncertainties [16].

In HHR, these control paradigms have been extended to address unique operational challenges. Research efforts have focused on cooperative speed tracking, trajectory smoothing, and train formation coordination [17,18,19]. Operational-level studies have also tackled problems such as headway-energy joint optimization, disruption-tolerant timetable rescheduling, and large-scale scheduling optimization [20,21,22]. Furthermore, recent work has emphasized distributed communication-based learning protocols to mitigate the effects of in-train forces and enhance cooperative stability [23,24,25].

From a methodological standpoint, robust control and game theory have independently proven effective in ensuring stability under uncertainty. On one hand, $H^{\infty }$ control has been widely adopted in railway systems to guarantee bounded responses against stochastic faults and disturbances [26]. On the other hand, game-theoretic approaches have been used to capture strategic interactions in networked control systems, with cooperative frameworks such as potential games enabling optimal coordination among agents to achieve a system-wide objective [27].

Nevertheless, most existing VCTS studies implicitly assume an ideal and secure communication environment, overlooking the strategic and adversarial nature of cyber-physical threats. While some efforts have addressed communication resilience through event-triggered control (ETC) or resilient distributed methods for intermittent data transmission under attacks [28,29], these approaches are predominantly reactive. More recently, a proactive defense based on a stochastic game framework has also been proposed for jamming-resistant virtual coupled trains [30]. However, a critical research gap remains in applying such advanced defense mechanisms specifically to the unique operational context of HHR. The stringent stability requirements of HHR, magnified by their immense mass and the severe consequences of control failure, present unique challenges under communication uncertainty that are not fully addressed by general VCTS security frameworks. To bridge this gap, this paper proposes a stochastic game-based anti-jamming control (SGAC) strategy. The SGAC method explicitly couples the adversarial dynamics at the physical communication layer, modeled as a stochastic game, with the robust $H^{\infty }$ control synthesis at the network layer. This cross-layer co-design offers a proactive defense mechanism capable of anticipating and mitigating worst-case jamming attacks, thereby ensuring the stability, safety, and resilience of virtually coupled heavy-haul train systems.

The main contributions of this paper are summarized as follows:

• A novel cross-layer defense method is proposed, specifically tailored to the stringent stability requirements of VCTS in HHR. This method systematically couples the adversarial dynamics at the communication layer, modeled as a stochastic game, with the design of a robust $H^{\infty }$ controller at the physical layer.
• A zero-sum stochastic game is formulated to model the strategic conflict between the jammer and the VCTS. Solving for the saddle-point equilibrium of this game yields an optimal probabilistic defense strategy, enabling a paradigm shift from conventional reactive measures to proactive, anticipatory defense.
• A Game-Theory-Based $H^{\infty }$ controller is developed through a co-design process. The equilibrium outcomes of the stochastic game are systematically embedded into the linear matrix inequality (LMI) constraints of the controller synthesis, ensuring the controller is inherently robust against the worst-case attacks predicted by the game.

Together, these innovations establish a proactive, cross-layer defense mechanism that significantly enhances the resilience of virtual coupling train systems in heavy-haul railways. The remainder of this paper is organized as follows: Section 2 introduces the proposed SGAC methodology, including the stochastic game formulation and $H^{\infty }$-based control synthesis. Section 3 presents numerical simulations and comparative analysis, and Section 4 concludes the paper with future research directions.

2. The Stochastic Game-Based Anti-Jamming Control (SGAC) Strategy

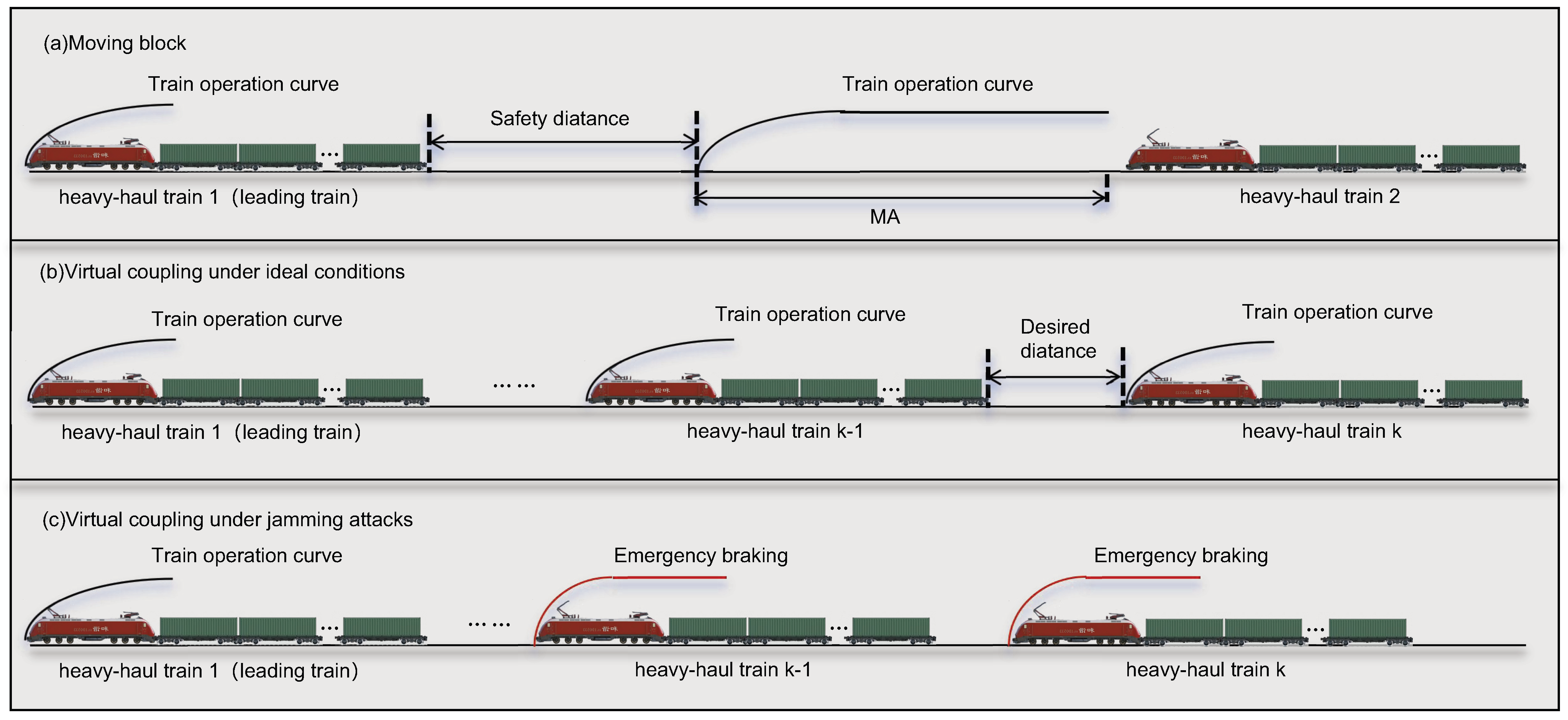
To address the critical security vulnerabilities of VCTS in HHR, this paper proposes a SGAC strategy. The fundamental challenge motivating this work is illustrated in Figure 1. While VCTS enables efficient operation under ideal conditions, its reliance on T2T communication makes it susceptible to jamming attacks. As shown, JAs can degrade communication quality, leading to hazardous events such as emergency braking, which highlights the necessity for a robust defense mechanism.

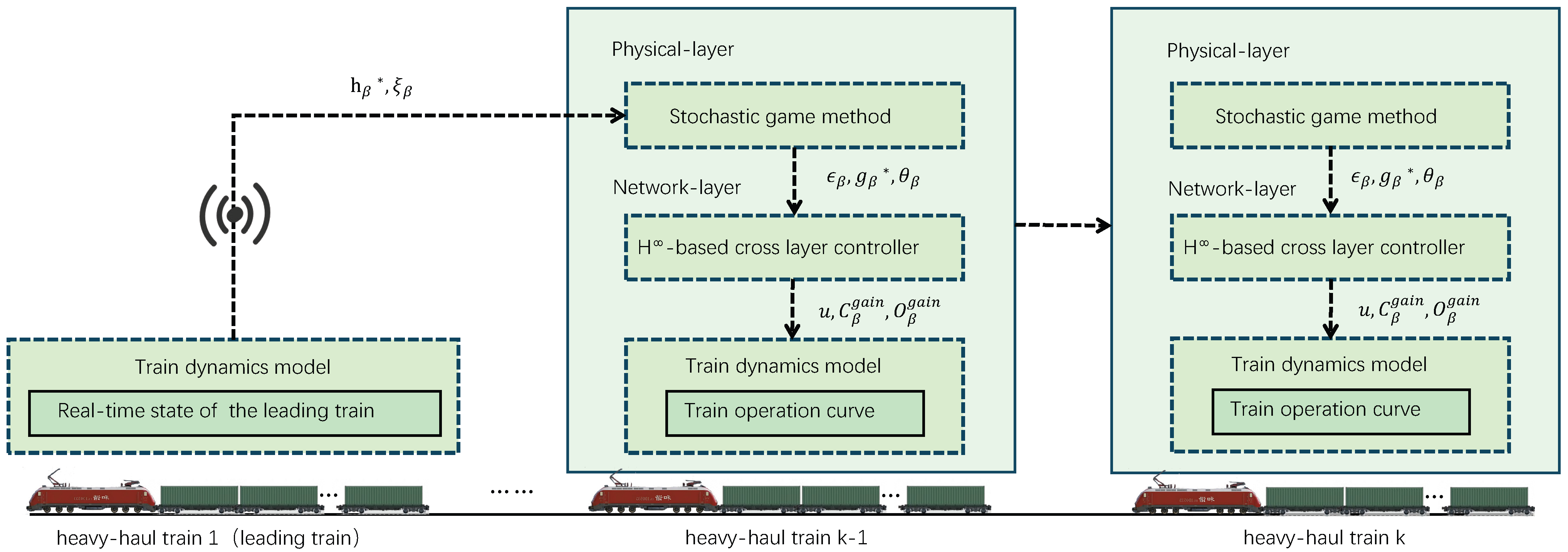
The overall architecture of the proposed SGAC strategy is illustrated in Figure 2. The method adopts a cross-layer co-design that integrates game-theoretic decision-making at the physical layer with robust control synthesis at the network layer. This architecture enables a proactive defense paradigm that anticipates and mitigates adversarial actions, rather than reacting to them.

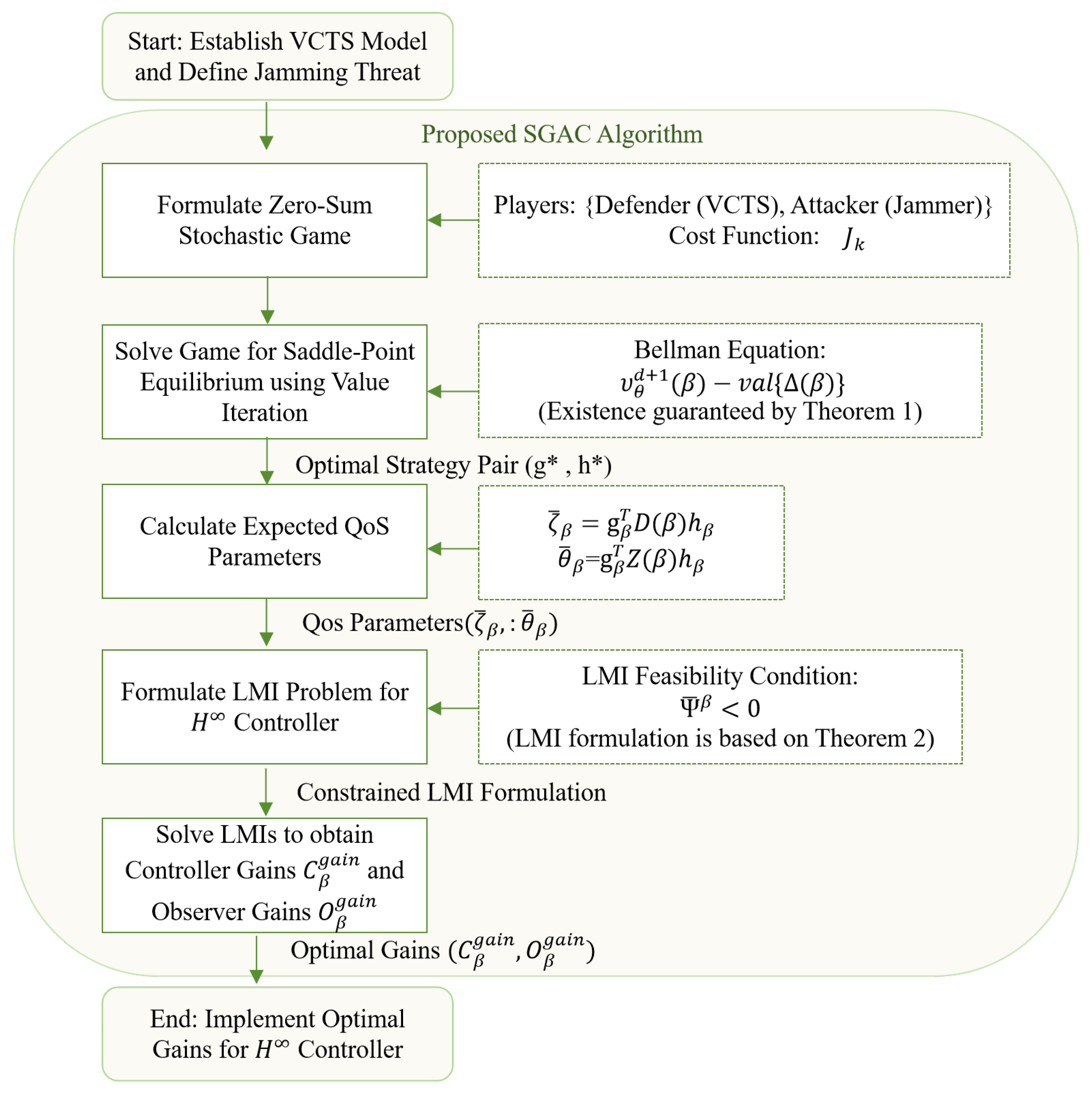
The methodological workflow of SGAC is presented in Figure 3, providing a detailed roadmap from problem formulation to final controller synthesis. At its core, SGAC formulates a zero-sum stochastic game between the attacker and defender, where jamming attacks are modeled as stochastic disturbances causing random packet losses. Solving for the saddle-point equilibrium yields the optimal probabilistic defense strategy, which is subsequently mapped to control actions through an $H^{\infty }$ robust controller to ensure system stability and performance under worst-case attacks.

In summary, the SGAC method provides a unified methodology that translates strategic decisions into robust control actions, ensuring safe and efficient operation under contested communication environments. The following section details its mathematical formulation and algorithmic implementation.

2.1. Train Dynamics Model

The longitudinal dynamics of virtually coupled train fleets in heavy-haul transportation can be expressed as follows:

$$\begin{array}{c}\hfill M_k\dot{v_k}\left(t\right)=-F_k\left(t\right)-B_k^r\left(t\right)-R_k^b\left(t\right)-R_k^l\left(t\right)\end{array}$$

(1)

where the subscript k denotes the k-th train in a virtually coupled fleet. $M_k$ and $v_k$ represent the mass and speed of the k-th train, respectively. $F_k$ is the traction or dynamic braking force generated by the locomotive, and $B_k^r$ denotes the air braking force. $R_k^b$ and $R_k^l$ represent the basic resistance and line resistance, respectively. The variable t denotes the running time.

$$R_k^b=M_k{g}_0{F}_k^{br}\times {10}^{-3}$$

(2)

where $g_0$ is the standard acceleration due to gravity, and $F_k^{br}=c_0+c_1{v}_k\left(t\right)+c_2{v}_k^2\left(t\right)$ is an empirical resistance coefficient. The constants $c_0$, $c_1$, and $c_2$ are positive coefficients determined by the train type and external environment.

The line resistance represents the additional resistance caused by the railway line’s geometric and topographic features, including both gradient and curvature effects. It is defined as

$$R_k^l=M_k{g}_0\left(G_k^{ra}+{\displaystyle \frac{E^{mp}}{C_k^{ur}}}\right)\times {10}^{-3}$$

(3)

where $G_k^{ra}$ is the track gradient, $C_k^{ur}$ is the track curvature radius, and $E^{mp}$ is an empirical coefficient reflecting the influence of curve sharpness and train length.

2.2. The Hybrid Control Model of Heavy-Haul Train-Based Virtual Coupling Train System

Let $s_k\left(t\right)$ and $\beta \left(t\right)$ represent the dynamic characteristics of the k-th train and the state of T2T communication. The hybrid control model of VCTS can be expressed as

$$\begin{array}{c}\hfill \dot{s_k}\left(t\right):=g(t,s_k,u_k,f_k^{dist};\beta (t,Jas,Def)),s_k\left(t_0\right)=s_{k,0}\end{array}$$

(4)

$$\begin{array}{c}\hfill u_k\left(t\right):={\vartheta }_k(t,s_k\left(t\right);\beta \left(t\right)),t\in [t_0,t_i)\end{array}$$

(5)

$$\begin{array}{c}\hfill f_k^{dist}\left(t\right):={\varrho }_k(t,s_k\left(t\right);\beta \left(t\right)),t\in [t_0,t_i)\end{array}$$

(6)

where $s_k$ represent the state of the k-th train, $u_k$ denote the control input, $f_k^{dist}$ is the disturbance and $s_{k,0}$ represent the state of the k-th train at the initial time $t_0$. The time-varing state value $\beta$ depends on the defense action $Def$ and the attack action $Jas$. $\vartheta$ represents the cross-layer control strategy. Besides, attacks are defined as ${\mathcal{A}}_k$, while defense strategies are defined as ${\mathcal{D}}_k$.

2.3. The Stochastic Game Method in SGAC

The proposed SGAC algorithm transforms the robust control problem into a minimax optimization by employing a zero-sum game framework. Within the VCTS, the stochastic game in SGAC represents the interactive decision-making process between two agents: the jammer (attacker) and the train control system (defender). The jammer seeks to maximize communication degradation by inducing packet loss and delay, whereas the defender aims to minimize performance deterioration via adaptive control. Each player’s strategy affects communication quality, thereby influencing the accuracy and timeliness of control information exchange. Thus, the stochastic game method quantitatively describes how cyber-level conflicts translate into variations in the control performance of the VCTS.

To obtain the optimal closed-loop controller ${\vartheta }^{\ast }\in {\mathcal{U}}_k$, the attacker–defender interaction is formulated as a minimax stochastic game, in which the performance cost $\mathcal{L}$ quantifies the influence of closed-loop disturbances and serves as a guaranteed upper bound on system degradation.

$$\begin{array}{c}\hfill \underset{{\varrho }_k\subseteq {\mathcal{P}}_k}{\sup }\mathcal{L}({\vartheta }^{\ast },\varrho )=\underset{{\vartheta }_k\subseteq {\mathcal{U}}_k}{\inf }\underset{{\varrho }_k\subseteq {\mathcal{P}}_k}{\sup }\mathcal{L}(\vartheta ,\varrho )\end{array}$$

(7)

The cost function is composed of two main components:

$${\mathcal{J}}_k(t,s,u,f_k^{dist};\beta )={\mathcal{J}}_{0,k}(t,s,u,f_k^{dist};\beta )-\tilde{\eta }{w}_k(f_k^{dist},\beta )$$

(8)

where ${\mathcal{J}}_{0,k}$ denotes the nominal system performance, and the second term models the degradation caused by jamming, reflecting the trade-off between control effort and robustness.

By treating the stochastic game outcome as an uncertainty source in system dynamics, the optimal attenuation level ${\eta }_{min}$ can be determined, yielding the corresponding $H^{\infty }$ controller ${\vartheta }^{\ast }$ that guarantees robustness against worst-case jammer-induced disturbances, as constrained by

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \underset{f_k^{dist}\in \mathcal{N}}{sup}\left\{{\displaystyle \frac{{\mathbb{E}}_{\beta }\{q_i(s\left(t_i\right);\beta \left(t_i\right))+{\int }_{t_0}^{t_i}{J}_0(t,s_k\left(t\right),u_k\left(t\right),f_k^{dist}\left(t\right);\beta \left(t\right))dt\}}{{\mathbb{E}}_{\beta }\{\parallel f_k^{dist}{\parallel }^2+q_0(s_0;\beta \left(t_0\right))\}}}\right\}\end{array}\end{array}$$

where $\parallel ·\parallel$ denotes the ${\mathcal{L}}_2$-norm.

When the game reaches its saddle-point equilibrium, the optimal strategies $({\vartheta }^g,{\varrho }^g)$ define an upper-bound value function, obtained from the following partial differential equation:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill -V_t^i(t,s_k)& =\underset{f^{dist}\in \mathbb{R}}{sup}\{V_{s_k}^i(t,s_k)g(t,s_k,{\vartheta }^g(t,s_k;i),{\varrho }^g(t,s_k;i);i)\hfill \\ \hfill & +\mathcal{J}(t,s_k,{\vartheta }^g(t,s_k;i),{\varrho }^g(t,s_k;i);i)+\sum _{j=1}^{\mathcal{X}}{\lambda }_{ij}{V}_{t,s_k}^j\}\hfill \end{array}\end{array}$$

where ${\lambda }_{ij}$ denotes the state transition probability of the system.

As both players act simultaneously and independently, neither knows the other’s decision in advance, and each action affects both the instantaneous cost and state transition probability of the VCTS. To quantify this effect, a cost function $\mathcal{J}(t,s_k,{\vartheta }^g,{\varrho }^g)$ is defined, mapping the current system state and player strategies to the corresponding instantaneous performance loss. To evaluate the long-term impact of repeated attacker–defender interactions, a discounted payoff metric is introduced to quantify the expected cumulative performance degradation of the VCTS over time, given an initial communication state $\beta$ and the strategy pair $(g,h)$. The specific calculation is formulated as follows:

$$\begin{array}{c}\hfill {\upsilon }_{\theta }(i,g,h):={\int }_0^{\infty }{e}^{-\theta t_n}{\mathbb{E}}^{g\left(t_n\right),h\left(t_n\right)}{\mathcal{J}}_k(De{f}_i,Ja{s}_j;{\vartheta }^g,{\varrho }^g)d{t}_n,\end{array}$$

where $\theta$ denotes the discounting factor, and ${\mathbb{E}}^{g\left(t_n\right),h\left(t_n\right)}$ represents the expectation operator.

Before deriving the optimal defensive control law, the existence of an equilibrium under the given stochastic dynamics must be ensured, as formalized in the following theorem.

Theorem 1.

Consider a game defined for each state $k\in \mathcal{X}$. If the following conditions hold:

1. 

the state transition rates ${\lambda }_{ij}\left(t_n\right)$ are continuous with respect to the mixed strategy pair $(g_i,h_j)$;

2. 

the cost function $J(t,s_k,u_k,f_k^{dist};i)$ is bounded.

• then, for each state $k\in \mathcal{X}$, there exists at least one static strategy pair $(g^{\ast },h^{\ast })\in {\mathcal{D}}_{\mathcal{X}}\times {\mathcal{A}}_{\mathcal{X}}$ that satisfies the following equilibrium condition:

  $$\begin{array}{cc}\hfill \theta {\upsilon }_{\theta }^{\ast }\left(i\right)& ={\widehat{\mathcal{J}}}_i(g^{\ast },h^{\ast })+\sum _{j\in \mathcal{X}}{\lambda }_{ij}(g^{\ast },h^{\ast })v_{\theta }^{\ast }\left(j\right)\hfill \\ \hfill & =\underset{g\in {\mathcal{D}}_{\mathcal{X}}}{sup}\underset{h\in {\mathcal{A}}_{\mathcal{X}}}{inf}\{{\widehat{\mathcal{J}}}_i(g,h)+\sum _{j\in \mathcal{X}}{\lambda }_{ij}(g,h)v_{\theta }^{\ast }\left(j\right)\}:={\mathcal{T}}_{\theta }\left(i\right)\hfill \\ \hfill & =\underset{h\in {\mathcal{A}}_{\mathcal{X}}}{inf}\underset{g\in {\mathcal{D}}_{\mathcal{X}}}{sup}\{{\widehat{\mathcal{J}}}_i(g,h)+\sum _{j\in \mathcal{X}}{\lambda }_{ij}(g,h)v_{\theta }^{\ast }\left(j\right)\}:={\mathcal{U}}_{\theta }\left(i\right)\hfill \end{array}$$

  where $\widehat{{\mathcal{J}}_i}(g,h)$ is the abbreviation for ${\mathbb{E}}^{g\left(t_n\right),h\left(t_n\right)}$. Additionally, ${\mathcal{T}}_{\theta }\left(i\right)$ and ${\mathcal{U}}_{\theta }\left(i\right)$ denote the lower and upper bounds of the mixed-strategy game, respectively. The pair $(g^{\ast },h^{\ast })$ constitutes a saddle-point equilibrium algorithm, with a unique game value $v_{\theta }^{\ast }\left(i\right)$ satisfying ${\mathcal{T}}_{\theta }\left(i\right)={\mathcal{U}}_{\theta }\left(i\right)$.

Given the existence of equilibrium, the saddle-point is rigorously defined to characterize the relationship between both players’ optimal strategies. This definition serves as the foundation for deriving the optimal defensive algorithm through a cross-layer design approach.

Definition 1

(Saddle-Point Equilibrium). A pair of strategies $(g^{\ast },h^{\ast })$ constitutes a saddle-point equilibrium for a zero-sum stochastic game if the following inequalities hold for any other strategy pair $(g,h)$, and for all initial states i:

$${\widehat{\mathcal{J}}}_i(g^{\ast },h)\le {\widehat{\mathcal{J}}}_i(g^{\ast },h^{\ast })\le {\widehat{\mathcal{J}}}_i(g,h^{\ast })$$

where ${\widehat{\mathcal{J}}}_i$ represents the cumulative discounted return. The unique value ${\upsilon }_{\theta }^{\ast }={\widehat{\mathcal{J}}}_i(g^{\ast },h^{\ast })$ is called the Value of the Game.

The equilibrium strategies can be computed via a value iteration algorithm, which reformulates the stochastic game as a dynamic programming problem and updates the expected cost recursively until convergence according to the Bellman equation:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\upsilon }_{\theta }^{d+1}\left(\beta \right)& =\mathit{val}\{\Delta (\beta \left)\right\},\hfill \\ \hfill {[\Delta \left(\beta \right)]}_{ij}& =\mathcal{J}(\beta ,g,{\mathcal{X}}_{Jas})+\theta \sum _{{\beta }^{\prime }\in B}\mathbb{P}\left({\beta }^{\prime }\right|\beta ,g,{\mathcal{X}}_{Jas})v_{\theta }^d\left({\beta }^{\prime }\right)\hfill \end{array}\end{array}$$

(9)

where the $\mathit{val}$ operator computes the value of the matrix game $\Delta \left(\beta \right)$, which is constructed at each step from the immediate cost $\mathcal{J}(·)$ and the expected future costs.

Once the value iteration process has converged, the saddle-point equilibrium strategies $(g^{\ast },h^{\ast })$ constitute the optimal policies satisfying the following condition:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \{g^{\ast }\left(\beta \right),h^{\ast }\left(\beta \right)\}\in \mathit{arg}\mathit{val}\{\Delta \left(\beta \right)\}\end{array}\end{array}$$

(10)

The SGAC algorithm integrates game-theoretic equilibrium strategies with an $H^{\infty }$ controller to ensure robustness against worst-case JAs. This establishes a cross-layer link from communication-layer defense to physical-layer control, ensuring safe headway and coordinated motion under varying jamming conditions. The next section details the final solution process of the SGAC algorithm.

2.4. The $H^{\infty }$-Based Cross-Layer Controller in SGAC Strategy

The SGAC algorithm is a robust closed-loop state-feedback controller formulated within the $H^{\infty }$ framework to ensure the operational stability of virtual coupling fleets in HHR, even under worst-case conditions. Within the VCTS architecture, the controller continuously regulates traction and braking commands according to real-time communication states, which may be disrupted by jamming attacks manifested as random packet losses.

To formalize this process, the relationship between the ideal controller output and the received measurement at time $t_n$ is expressed as

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{p}_k\left(t_n\right)=\overline{W}{s}_k\left(t_n\right)\hfill \\ p_{k,e}\left(t_n\right)=(1-{\zeta }_{\beta })p_k\left(t_n\right)+{\zeta }_{\beta }{p}_k\left(t_{n-1}\right)\hfill \end{array}\right.\end{array}$$

(11)

At time $t_n$, the controller cannot directly access the ideal output $p_k\left(t_n\right)$ due to potential communication disruptions and instead relies on the received measurement $p_{k,e}\left(t_n\right)$ transmitted through an unreliable channel. This formulation explicitly captures the information mismatch caused by packet loss, distinguishing the intended control signal from the actually received measurement.

The state of the T2T communication link is denoted by $\beta \in {\mathcal{X}}_{com}$, where the discrete state space is defined as ${\mathcal{X}}_{com}:=\left\{{\beta }_1,{\beta }_2,\cdots ,{\beta }_x\right\}$. Packet loss events are modeled as a state-dependent random variable ${\zeta }_{\beta }$. Under the influence of JAs, the random variable ${\zeta }_{\beta }$ follows a Bernoulli distribution:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\overline{\zeta }}_{\beta }:=\mathbb{P}\{{\zeta }_{\beta }=1\}=\mathbb{E}\left\{\zeta \right\},\hfill \\ \mathbb{P}\{{\zeta }_{\beta }=0\}=1-\mathbb{E}\left\{\zeta \right\}=1-{\overline{\zeta }}_{\beta }.\hfill \end{array}\right.\end{array}$$

(12)

where ${\zeta }_{\beta }=0$ signifies a successful data transmission, allowing the controller to use the current information, $p_{k,e}\left(t_n\right)=p_k\left(t_n\right)$. Conversely, ${\zeta }_{\beta }=1$ indicates that a packet has been lost, requiring the controller to utilize the information from the previous time step, $p_{k,e}\left(t_n\right)=p_k\left(t_{n-1}\right)$.

The dynamics of the SGAC observer and state-feedback controller under stochastic packet losses are described by the following state-space equations, which serve as the basis for subsequent $H^{\infty }$ stability and performance analysis:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill \widehat{s}\left(t_{n+1}\right)& =\overline{G}\widehat{s}\left(t_n\right)+\overline{K}(1-{\theta }_{\beta })u_{vo}\left(t_n\right)+O_{\beta }^{gain}\overline{W}(s\left(t_n\right)-\widehat{s}\left(t_n\right))\hfill \\ \hfill u\left(t_n\right)& =C_{\beta }^{gain}\widehat{s}\left(t_n\right)\hfill \\ \hfill u_{vo}\left(t_n\right)& =(1-{\theta }_{\beta })u_{vo}\left(t_n\right)\hfill \end{array}\right.\end{array}$$

(13)

where ${\widehat{s}}_k\left(t_n\right)$ is the estimated state of train k at time $t_n$, $u_{vo}\left(t_n\right)$ denotes the control signal received by the vehicle onboard controller, and $C_{\beta }^{gain},O_{\beta }^{gain}\in \mathbb{R}$ are the control and the observation gains, respectively.

The quality of service (QoS) of the T2T communication link is quantified using two random variables, ${\zeta }_{\beta }$ and ${\theta }_{\beta }$, whose distributions are dynamically governed by the strategic interaction between JAs and the system’s defense mechanisms. Given the communication state $\beta$ and the players’ strategies $(g_{\beta },h_{\beta })$, the expectations of these QoS indicators are calculated as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\overline{\zeta }}_{\beta }& :=D_1(\beta ,g_{\beta },h_{\beta })=g_{\beta }^{T}D\left(\beta \right)h_{\beta }\hfill \end{array}\end{array}$$

(14)

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\overline{\theta }}_{\beta }& :=Z_1(\beta ,g_{\beta },h_{\beta })=g_{\beta }^{T}Z\left(\beta \right)h_{\beta }\hfill \end{array}\end{array}$$

(15)

The preceding equations establish a mathematical linkage between the attacker–defender game strategies and the resulting QoS performance, providing a bridge through which the SGAC algorithm dynamically adjusts each train’s control input according to the real-time communication state. Based on this connection, the next section derives the $H^{\infty }$ performance metrics for the VCTS hybrid system, explicitly accounting for these game-dependent variables.

2.5. The SGAC Model Solution

The central principle of the proposed cross-layer design is the establishment of a direct link that translates the strategic outcomes of the stochastic game into robust control actions. This linkage is achieved by explicitly mapping the expected results of the game-theoretic strategies $(g_{\beta },h_{\beta })$ to the system’s overall $H^{\infty }$ performance index ${ϵ}_{\beta }$ for each network state $\beta$.

For zero initial conditions, the performance objective is achieved if ${ϵ}_{\beta }$ satisfies the following inequality for all possible states $\beta \in B$:

$${\mathbb{E}}^{(g_{\beta },h_{\beta })}\left\{\sum _{t_n=0}^{\infty }\{\parallel z_k\left(t_n\right){\parallel }^2\}<{ϵ}_{\beta }^2\sum _{t_n=0}^{\infty }\{\parallel f_k^{dist}\left(t_n\right){\parallel }^2\right\}\},$$

(16)

A smaller value of ${ϵ}_{\beta }$ signifies better disturbance rejection performance.

Although this inequality defines the control objective, it cannot be directly solved and must therefore be reformulated into a tractable form. To this end, the following section will convert this $H^{\infty }$ control condition into a set of linear matrix inequalities.

Theorem 2.

For a given scalar ${ϵ}_{\beta }>0$ and any state $\beta \in B$, if there exist positive definite matrices $Q_{11}\in {\mathbb{R}}^{j\times j}$, $Q_{22}\in {\mathbb{R}}^{i-j\times i-j}$, $Q_2\in {\mathbb{R}}^{i\times i}$, $X_1\in {\mathbb{R}}^{i\times i}$ and $X_2\in {\mathbb{R}}^{i\times i}$, and real matrices $M_{\beta }\in {\mathbb{R}}^{j\times q}$, $N_{\beta }\in {\mathbb{R}}^{j\times i}$, such that the LMI ${\tilde{\Psi }}^{\beta }<0$ is feasible, then a hybrid algorithm pair $(g_{\beta },h_{\beta })$ exists that guarantees the following properties:

1. 

The VCTS hybrid system is exponentially mean-square stable.

2. 

The prescribed $H^{\infty }$-norm constraint ${ϵ}_{\beta }$ is satisfied for all nonzero disturbances $f_k^{dist}$.

The LMI feasibility condition is given by inequality:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\tilde{\Psi }}^{\beta }=\left[\begin{array}{cc}{\tilde{\Psi }}_{11}^{\beta }& \ast \\ {\tilde{\Psi }}_{21}^{\beta }& {\tilde{\Psi }}_{22}^{\beta }\end{array}\right]<0,\end{array}\end{array}$$

(17)

where the entries of the matrix ${\tilde{\Psi }}^{\beta }$ are given as follows:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill Q_1:=T_1^T{Q}_{11}{T}_2+T_1^T{Q}_{22}{T}_2,\end{array}\end{array}$$

(18)

$$\left[\begin{array}{c}{T}_1\\ T_2\end{array}\right]K_{2}V=\left[\begin{array}{c}\tilde{\Gamma }\\ 0\end{array}\right],\tilde{\Gamma }=\mathbf{diag}\{{\tilde{\gamma }}_1,{\tilde{\gamma }}_2,\cdots ,{\tilde{\gamma }}_j\},$$

(19)

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & {\tilde{\Psi }}_{11}^{\beta }=\left[\begin{array}{ccccc}{Q}_1-Q_2& \ast & \ast & \ast & \ast \\ 0& X_1-X_2& \ast & \ast & \ast \\ 0& 0& -Q_2& \ast & \ast \\ 0& 0& 0& -X_2& \ast \\ 0& 0& 0& 0& -{\widetilde{ϵ}}_{\beta }^{2}I\end{array}\right],\hfill \\ \hfill & {\tilde{\Psi }}_{22}^{\beta }=\left[\begin{array}{ccccc}-Q_1& \ast & \ast & \ast & \ast \\ 0& -X_1& \ast & \ast & \ast \\ 0& 0& -Q_1& \ast & \ast \\ 0& 0& 0& -X_1& \ast \\ 0& 0& 0& 0& -I\end{array}\right],\hfill \\ \hfill & {\tilde{\Psi }}_{21}^{\beta }=\left[\begin{array}{cc}{\tilde{\Psi }}_{21}^{\beta }(1,1)& {\tilde{\Psi }}_{21}^{\beta }(1,2)\\ {\tilde{\Psi }}_{21}^{\beta }(2,1)& {\tilde{\Psi }}_{21}^{\beta }(2,2)\end{array}\right],\hfill \end{array}\end{array}$$

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & {\tilde{\Psi }}_{21}^{\beta }(1,1)=\left[\begin{array}{cc}{Q}_1^{\beta }\overline{G}+(1-{\overline{\theta }}_{\beta })\overline{K}{N}_{\beta }& -(1-{\overline{\theta }}_{\beta })\overline{K}{N}_{\beta }\\ 0& X_1^{\beta }\overline{G}-(1-{\overline{\zeta }}_{\beta })M_{\beta }\mathcal{J}\left(\beta \right)\end{array}\right],\hfill \\ \hfill & {\tilde{\Psi }}_{21}^{\beta }(1,2)=\left[\begin{array}{ccc}\overline{\theta }\overline{K}{N}_{\beta }& -{\overline{\theta }}_{\beta }\overline{K}{N}_{\beta }& Q_1^{\beta }\overline{W}\\ 0& -{\overline{\zeta }}_{\beta }{M}_{\beta }\mathcal{J}\left(\theta \right)& X_1^{\beta }\overline{W}\end{array}\right],\hfill \\ \hfill & {\tilde{\Psi }}_{21}^{\beta }(2,1)=\left[\begin{array}{cc}{\tilde{\mu }}_1^{\beta }\overline{K}{N}_{\beta }& -{\tilde{\mu }}_1^{\beta }\overline{K}{N}_{\beta }\\ {\tilde{\mu }}_2^{\beta }{M}_{\beta }\mathcal{J}\left(\beta \right)& 0\\ H& 0\end{array}\right],\hfill \\ \hfill & {\tilde{\Psi }}_{21}^{\beta }(2,2)=\left[\begin{array}{ccc}-{\tilde{\mu }}_1^{\beta }\overline{K}{N}_{\beta }& {\tilde{\mu }}_1^{\beta }\overline{K}{N}_{\beta }& 0\\ -{\tilde{\mu }}_2^{\beta }{M}_{\beta }\mathcal{J}\left(\beta \right)& 0& 0\\ 0& 0& 0\end{array}\right],\hfill \end{array}\end{array}$$

$$\begin{array}{c}\hfill \begin{array}{ccc}\hfill & {\tilde{\mu }}_1^{\beta }={\left[(1-{\overline{\theta }}_{\beta }){\overline{\theta }}_{\beta }\right]}^{1/2},\hfill & \hfill {\tilde{\mu }}_2^{\beta }={\left[(1-{\overline{\zeta }}_{\beta }){\overline{\zeta }}_{\beta }\right]}^{1/2}.\end{array}\end{array}$$

Furthermore, if the LMI condition is satisfied, the controller gain $C^{gain}\beta$ and observer gain $O^{gain}\beta$ can be derived as follows:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill C_{\beta }^{gain}=V{\Gamma }^{-1}{Q}_{11}\Gamma V^T{N}_{\beta },O_{\beta }^{gain}=X_1{M}_{\beta },\end{array}\end{array}$$

(20)

Building on the feasibility conditions of the previous theorem, Formulas (18) and (19) are reformulated into a convex optimization problem in Theorem 2, which determines the minimum achievable $H^{\infty }$ performance index ${\widetilde{ϵ}}_{\beta }$ and offers quantitative performance guarantees for the controller design:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\widetilde{ϵ}}_{\beta }=& \underset{Q_{11}^{\beta }>0,Q_{22}^{\beta }>0,Q_2^{\beta }>0,X_1^{\beta }>0,X_2^{\beta }>0,N_{\beta },M_{\beta }}{min}{ϵ}_{\beta }\hfill \end{array}\end{array}$$

(21)

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & s.t.subjectedto\left(16\right).\hfill \end{array}\end{array}$$

where ${ϵ}_{\beta }$ denotes the optimal value obtained from the optimization, corresponding to the game value in the underlying zero-sum stochastic method. To formalize this relationship, we define the system’s performance payoff matrix, $\mathcal{J}\left(\beta \right)\in {\mathbb{R}}^{j\times i}$, where each element ${\mathcal{J}}_{mn}\left(\beta \right)$ represents the physical layer $H^{\infty }$ performance under $De{f}_i,Ja{s}_j$. Consequently, the Value of the Game, ${ϵ}_{\beta }$, is the expected outcome of this payoff matrix when both players adopt their saddle-point equilibrium strategies $(g_{\beta },h_{\beta })$. The value ${\widetilde{ϵ}}_{\beta }$ results from the following mapping:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\widetilde{ϵ}}_{\beta }=g_{\beta }^T\mathcal{J}\left(\beta \right)h_{\beta }\end{array}\end{array}$$

(22)

Based on the theoretical analysis and objective control function, the stochastic game defense algorithm employs a coupled co-design to address the $H^{\infty }$ index and the $H^{\infty }$ optimal controller. The solution to the LMI problem presented in Theorem 2 simultaneously provides both the optimal game strategies $(g_{\beta }^{\ast },h_{\beta }^{\ast })$ and the corresponding optimal controller gains. These strategies then determine the expected Qos of the communication link, ensuring that the design satisfies the conditions ${\overline{\zeta }}_{\beta }={g_{\beta }^{\ast }}^{T}D\left(\beta \right)h_{\beta }^{\ast }$ and ${\overline{\theta }}_{\beta }={g_{\beta }^{\ast }}^{T}Z\left(\beta \right)h_{\beta }^{\ast }$. The proof of Theorem 2 can be found in the Appendix A.

The primary control objective for the VCTS system is to maintain a predefined target spacing between consecutive trains. Strict adherence to this spacing is crucial for ensuring platoon stability and guaranteeing both operational efficiency and safety. However, this critical task is compromised by JAs that disrupt the T2T communication necessary for cooperative control.

To address this challenge, this paper has developed the SGAC algorithm, an integrated defense strategy that combines stochastic game theory with robust $H^{\infty }$ control. By jointly optimizing the communication defense strategies and physical control parameters, the SGAC method enables the VCTS to dynamically adjust its feedback control inputs in response to real-time network states, thereby preserving stability and coordination under severe jamming attacks.

3. Numerical and Simulation Results

In this section, a series of simulations are conducted to validate the effectiveness and robustness of the proposed SGAC algorithm. The simulations are implemented in MATLAB R2021a, using the YALMIP toolbox [Available online: https://yalmip.github.io/; accessed on 20 October 2024]; to formulate the convex optimization problem and the SDPT3 solver [Available online: https://www.math.nus.edu.sg/~mattohkc/sdpt3.html; accessed on 20 October 2024].

The simulation is based on a virtual platoon scenario consisting of four heavy-haul trains. The predefined target spacing between consecutive trains in the VCTS is set to 600 m. Each train is configured to include one HXD1 locomotive and fifty C80 carriages, resulting in a total train length of 635 m. The emergency braking deceleration is set to −0.6 m/s².

The primary objective of these experiments is to evaluate the performance of the SGAC strategy under varying probabilities and durations of JAs. To highlight its superiority, the robustness of the proposed SGAC algorithm is compared against two classical control methods: DP and MPC.

The state-space matrices for the train dynamics model are defined as follows: $\overline{G}=[1,1,0.5;0,1,1;0,0,1]$, $\overline{K}=[1;1;1]$; $\overline{H}=[1;1;1]$, Other system parameters are set to $R=6$ and $\epsilon =0.05$. The state transition matrix for the Signal-to-Interference-plus-Noise Ratio (SINR), which is used for the payoff matrices $D\left(\beta \right)$ and $Z\left(\beta \right)$, is given by

$$\begin{array}{c}\hfill \begin{array}{c}\hfill D\left(\beta \right)=Z\left(\beta \right)=\left[\begin{array}{cccc}0.8374& 0.1626& 0& 0\\ 0.0217& 0.7901& 0.1779& 0\\ 0& 0.6035& 0.3930& 0.0246\\ 0& 0& 0.4375& 0.5625\end{array}\right].\end{array}\end{array}$$

Before running the dynamic simulations, the LMI optimization problem presented in Theorem 2 is solved to synthesize the required controller and derive the game-theoretic solution. The results of this offline computation are as follows: the Saddle-point equilibrium strategies are $g_{\beta }^{\ast }={\left[0.7740.1350.0230.067\right]}^T$ and $h_{\beta }^{\ast }={\left[0.2260.4230.1570.194\right]}^T$. The optimized minimum value of $H^{\infty }$ is ${\widetilde{ϵ}}_{\beta }=0.7354$. The controller gain is $C_{\beta }^{gain}=[-0.01026-0.13300.1281]$ and the observer gain is $O_{\beta }^{gain}={[-0.00560.00560.0045]}^T$. These synthesized gains and strategies are then used to implement the SGAC controller in the following simulation tests.

The operational performance of the proposed SGAC strategy was comprehensively evaluated against baseline methods under jamming attacks using quantitative criteria. To facilitate this rigorous assessment, the root mean square error (RMSE) metric is employed. The RMSE quantifies the average magnitude of deviation between the actual and reference values over the simulation horizon, providing a clear measure of tracking performance and stability. A lower RMSE value indicates superior performance. The RMSE is calculated as follows:

$${\mathrm{RMSE}}_v=\sqrt{{\displaystyle \frac{1}{T(N-1)}}{\sum }_{n=1}^T{\sum }_{k=2}^N{\left(v_k\left(t_n\right)-v_{k-1}\left(t_n\right)\right)}^2},$$

(23)

$${\mathrm{RMSE}}_s=\sqrt{{\displaystyle \frac{1}{T(N-1)}}{\sum }_{n=1}^T{\sum }_{k=2}^N{\left(\left[x_k\left(t_n\right)-x_{k-1}\left(t_n\right)\right]-d_{\mathrm{des}}-L\right)}^2},$$

(24)

where $v_k\left(t_n\right)$ and $x_k\left(t_n\right)$ are the speed and position of train k at time $t_n$, $d_{\mathrm{des}}$ is the desired inter-train headway, and L denotes the physical length of train.

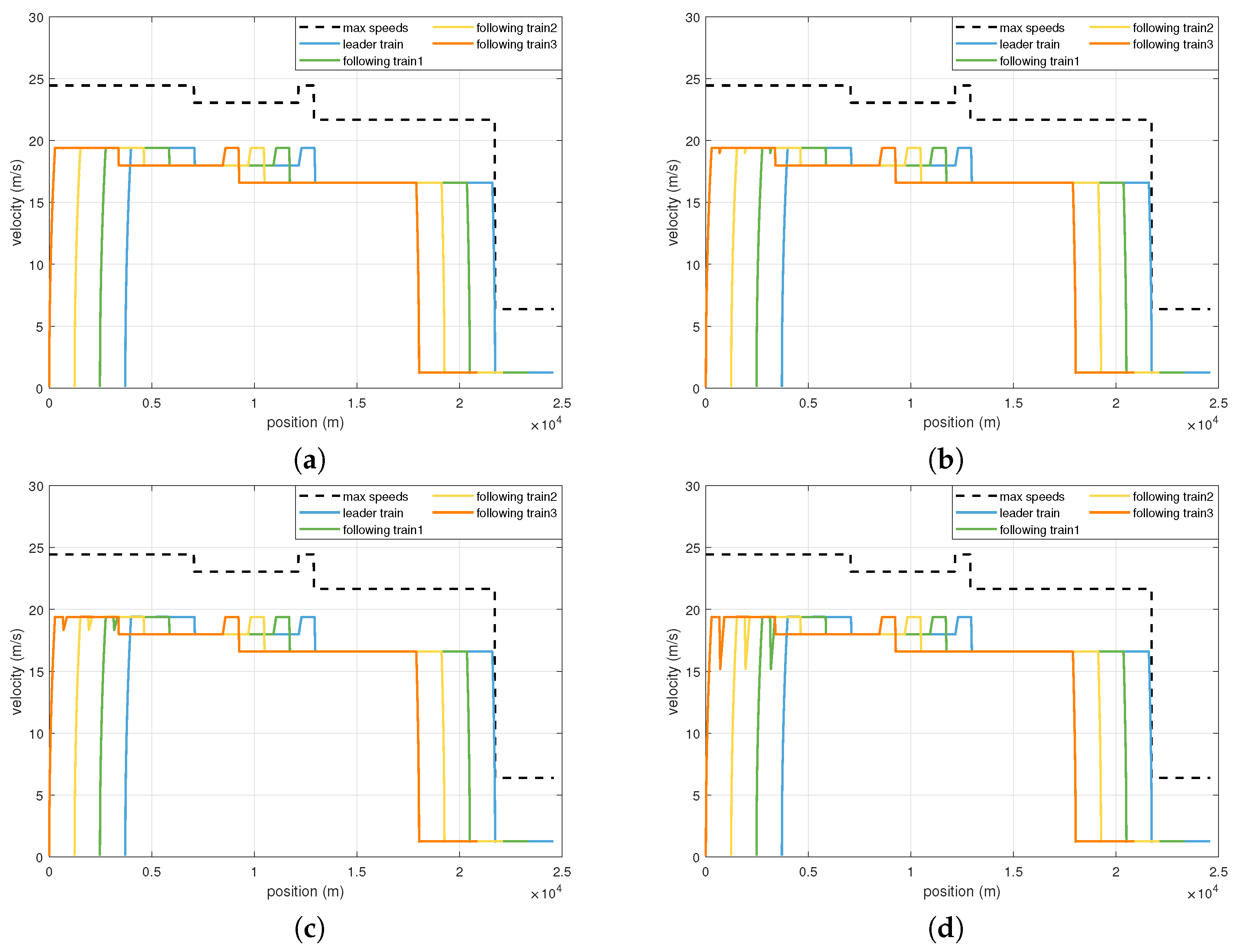
Figure 4 illustrates the trajectory results under a targeted jamming attack, while

Table 1. Root Mean Square Error (RMSE) Performance Comparison of Different Control Strategies.

Control Strategy	Speed RMSE (m/s)	Headway RMSE (m)
Ideal Condition (No Attack)	0.0000	0.0000
Proposed SGAC	0.0001	0.1315
Event-triggered Control [28]	0.0520	2.1031
Model Predictive Control [5]	4.9504	4191.5384
Dynamic Programming [6]	5.3016	3742.0636

summarizes the corresponding quantitative RMSE metrics. In the simulated scenario, a communication loss occurs in the second train. As clearly shown in Figure 4b,c, both the traditional DP and MPC algorithms interpret this data loss as a critical fault, forcing all subsequent trains into emergency braking. This behavior results in catastrophic degradation, reflected in their extremely high headway RMSE values exceeding 3700 m (Table 1). The ETC strategy, depicted in Figure 4d, demonstrates significantly better resilience compared to DP and MPC, managing to avoid complete failure but still exhibiting noticeable deviations, resulting in a headway RMSE of $2.1031$ m. In stark contrast, the proposed SGAC method, shown in Figure 4e, maintains exceptional stability. By leveraging its integrated game-theoretic model and robust $H^{\infty }$ controller, the SGAC algorithm effectively anticipates and compensates for the disruption, achieving a near-ideal headway RMSE of only $0.1315$ m, significantly outperforming all baseline methods.

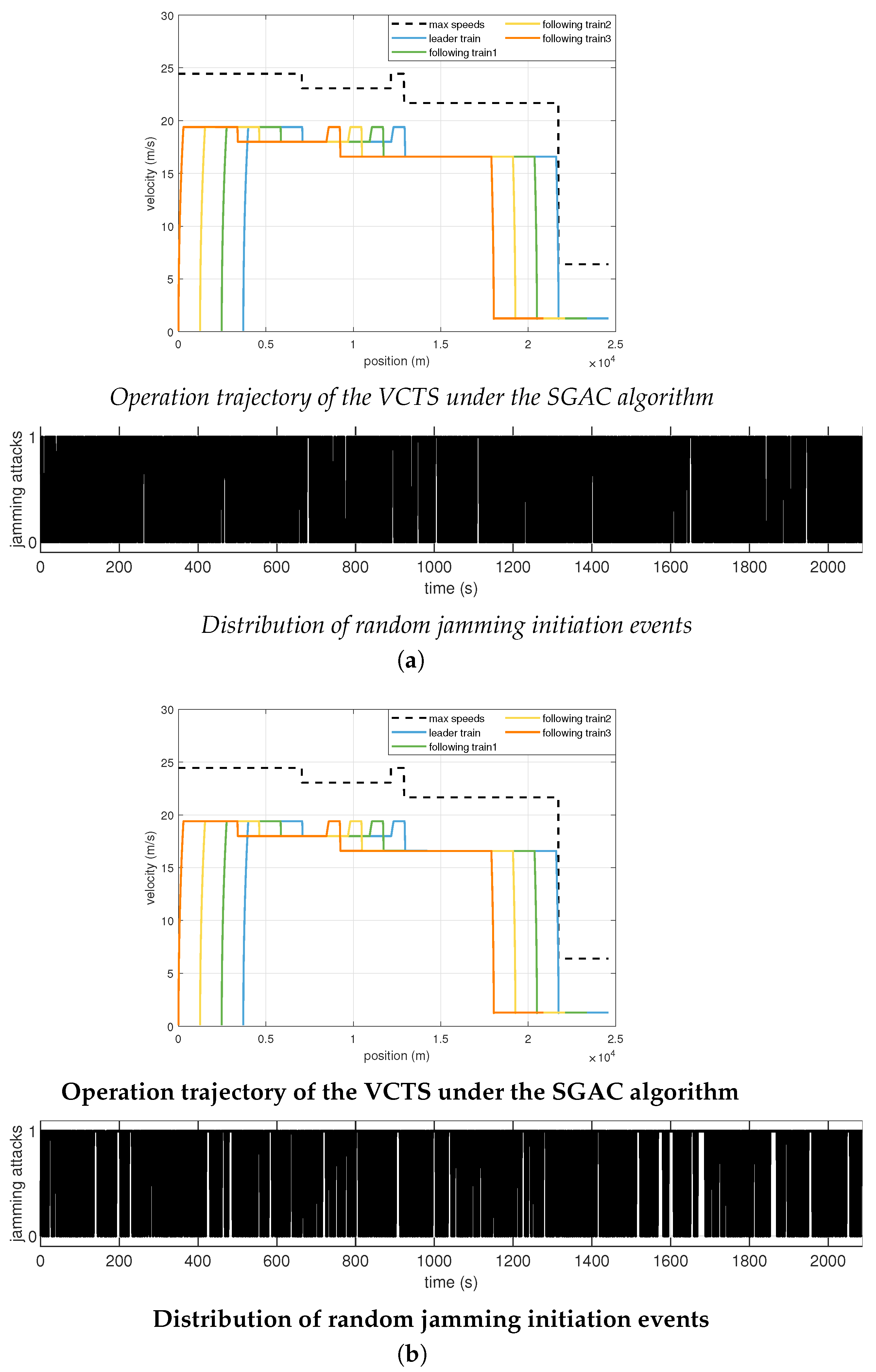
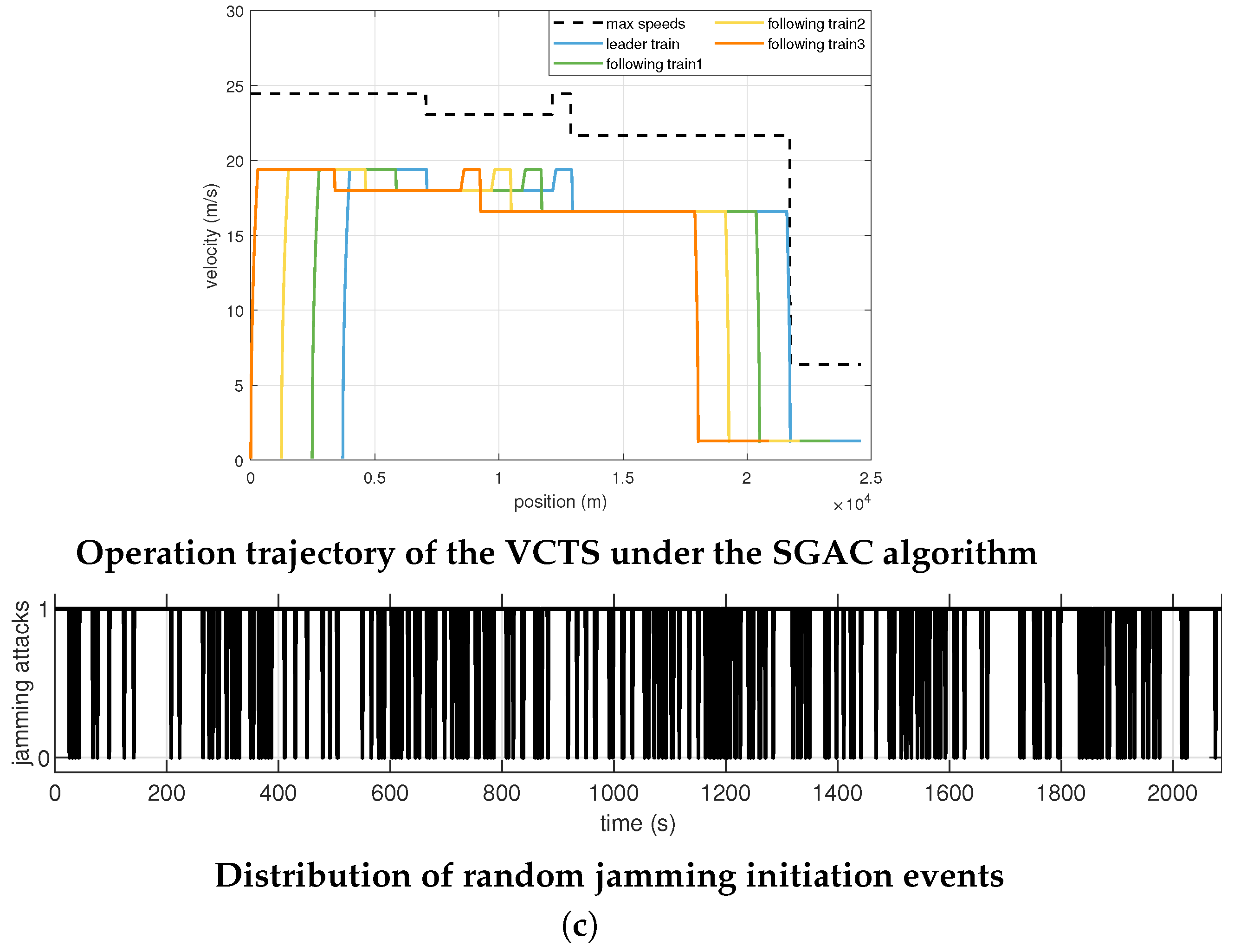
The robustness of the SGAC strategy against varying attack intensities was further assessed, as shown in Figure 5 and quantified in

Table 2. RMSE Performance of the Proposed SGAC Strategy under Varying Attack Conditions.

Attack Condition	Speed RMSE (m/s)	Headway RMSE (m)
Varying Attack Duration
1 Communication Cycle	0.0001	0.1315
2 Communication Cycles	0.0045	0.2208
5 Communication Cycles	0.0200	2.9379
10 Communication Cycles	0.0873	3.9468
Varying Attack Initiation Probability
50% Probability	0.0002	0.1272
70% Probability	0.0003	0.1595
90% Probability	0.0005	0.2782

. The lower plot in each subfigure of Figure 5 visualizes the corresponding random distribution of jamming events. Despite the visually evident increase in attack frequency and randomness, the operational trajectories demonstrate that platoon stability is well preserved across all scenarios. This qualitative observation is strongly corroborated by the quantitative data in Table 2, where the headway RMSE remains negligible even as the jamming probability increases to a high of $90\%$, rising only from $0.1272$ m to $0.2782$ m. These results confirm the high resilience of the SGAC strategy against frequent and intermittent attacks.

The capability of the SGAC system to withstand sustained communication disruptions is illustrated in Figure 6, with quantitative results listed in Table 2. When the communication failure is transient (lasting 1–5 cycles), the operational dynamics remain largely unaffected, as the state observer and predictive game strategy effectively compensate for short-term data loss. As the failure duration increases to 10 cycles, uncertainty in the state estimation grows, resulting in more conservative speed regulation. Nevertheless, the headway RMSE increases only to $3.9468$ m, demonstrating the system’s graceful degradation property. Unlike the abrupt performance collapse observed in the baseline methods, the SGAC method degrades smoothly and predictably as the attack severity intensifies, validating its effectiveness as a proactive and robust game-theoretic defense mechanism for secure train operations.

4. Conclusions and Future Works

This paper proposes an SGAC strategy to ensure stable and efficient train convoy operations in VCTS under uncertain JAs. The SGAC strategy integrates $H^{\infty }$ control optimization with a stochastic game method, balancing the interactions between the attacker and defender through a saddle–point equilibrium. Simulation studies compare convoy dynamics with and without the SGAC strategy under stochastic JAs. The results demonstrate that the SGAC strategy effectively mitigates T2T communication failures caused by JAs with probabilities ranging from $50\%$ to $90\%$ and single-attack durations of 1–5 communication cycles, thereby maintaining stable convoy dynamics. Additionally, the SGAC strategy ensures operational safety under single jamming attacks lasting from 1 to 10 communication cycles. Although the simulation results indicate the effectiveness of the SGAC strategy, its performance has yet to be confirmed in real-world experiments or using actual railway data, which will be addressed in future studies. Future research work will primarily focus on three aspects: First, extending the algorithm to more diverse railway operational scenarios. Second, further enhancing its anti-jamming performance based on the existing method, such as machine learning. Third, validating the algorithm using real-world railway data or experimental tests to ensure its practical effectiveness and reliability.