Compressive Sensing-Based 3D Spectrum Extrapolation for IoT Coverage in Obstructed Urban Areas

Abstract

As a fundamental information carrier in Industrial Internet of Things (IIoT), electromagnetic spectrum data presents critical challenges for efficient spectrum sensing and situational awareness in smart industrial cognitive radio systems. Addressing sparse sampling limitations caused by energy-constrained transceiver nodes in Unmanned Aerial Vehicle (UAV) spectrum monitoring, this paper proposes a compressive sensing-based 3D spectrum tensor completion framework for extrapolative reconstruction in obstructed areas (e.g., building occlusions). First, a Sparse Coding Neural Gas (SCNG) algorithm constructs an overcomplete dictionary adaptive to wide-range spectral fluctuations. Subsequently, a Bag of Pursuits-optimized Orthogonal Matching Pursuit (BoP-OOMP) framework enables adaptive key-point sampling through multi-path tree search and temporary orthogonal matrix dimensionality reduction. Finally, a Neural Gas competitive learning strategy leverages intermediate BoP solutions for gradient-weighted dictionary updates, eliminating computational redundancy. Benchmark results demonstrate 43.2% reconstruction error reduction at sampling ratios r ≤ 20% across full-space measurements, while achieving decoupling of highly correlated overlapping subspaces—validating superior estimation accuracy and computational efficiency.

1. Introduction

With the development of sixth-generation (6G) communication technologies, space–air–ground integrated networks will provide robust support for wireless communications, the Industrial Internet of Things (IIoT), and aeronautical/maritime communications [1,2,3]. Concurrently, the massive communication and ubiquitous connectivity demands of Internet of Things (IoT) devices [4] will impose higher requirements on spectrum access and applications. Spectrum mapping has consequently emerged as a new research focus in spatial science, aiming to establish spectrum maps capable of efficiently managing spectrum resources in heterogeneous electromagnetic environments. These maps project spectrum situational awareness onto corresponding geographical locations, with the resulting visualization termed spectrum cartography. Particularly in urban scenarios, densely clustered high-rise buildings create greater spatial isolation between primary and secondary users. This environment enables the exploitation of spatial spectrum access opportunities unavailable in two-dimensional (2D) planes, making vertical dimension opportunities highly valuable. Given that 2D radio maps cannot characterize height information, three-dimensional (3D) radio maps become an effective method for representing spectrum distribution in urban spaces, especially regarding the deployment process of sensors inside buildings and related research [5].

The prerequisite for direct spectrum mapping is comprehensive sampling data containing location information. A preferred solution involves dividing the target space into numerous volumetric pixels (voxels) to achieve the highest possible resolution for radio maps [6]. Radio map construction methodologies [7,8,9] fall into two categories: model-driven [10] and data-driven [11] approaches. While ray-tracing propagation models enable rapid radio map generation, they require precise alignment between the applied environment and the model; otherwise, significant accuracy degradation occurs [12]. Moreover, substantial deviations in spectrum situation accuracy within the same area would be detrimental for massive IoT device access and omit critical information such as location coordinates, power intensity, and transmission mechanisms in regions of interest [13]. Compared to model-driven methods, data-driven approaches demand highly accurate spectrum data sources, imposing stricter requirements on spectrum information acquisition [14]. However, urban environments feature dense building clusters, leading to areas inaccessible to spectrum measurement equipment [15]. Achieving comprehensive spatial-spectrum information through extensive deployment of fixed spectrum sensors incurs prohibitive costs. Therefore, optimizing sampling locations and accurately estimating spectrum power are particularly crucial for constructing precise 3D radio maps.

Existing research primarily adopts random sampling for spectrum information collection, which can be divided into fixed and mobile modes. Fixed collection relies on static spectrum sensors [16], while mobile collection mainly utilizes monitoring vehicles, handheld devices, and spectrum-sensing unmanned aerial vehicles (UAVs) [17]. Among them, the UAV platform has been proven to be the most effective means for electromagnetic spectrum mapping [18], despite having many constraints itself. For example, Study [11] discusses the constraints of UAV sampling positions on the completeness of spatial information and studies data measurement methods for indoor and outdoor scenarios; Study [19] uses the dueling double deep Q-network (D3QN) to optimize the sampling positions of UAVs in three-dimensional space.

The core of data-driven methods lies in the prediction and estimation of spectrum data in unsampled areas. Breakthroughs in sparse coding and compressive sensing theories have opened up new avenues for radio map construction [20,21,22,23]. For instance, the cooperative spectrum sensing technology in cognitive radio networks (CRNs) [24] shares similar ideas with this paper in terms of utilizing spatial correlation. Recent studies have also explored the application of UAVs in spatial sensing [25] and tensor-based methods for dynamic radio maps [26,27], which are highly relevant to our 3D tensor completion framework. Work [28] investigates a collaborative spectrum sensing optimization strategy in mobile energy-harvesting cognitive radio networks. It analyzes the impact of two scenarios—insufficient energy and insufficient spectrum—on the final decision threshold k and deduces optimization and trade-off methods to maximize network throughput while protecting the primary user’s communication. Therefore, fully exploiting the intrinsic sparsity characteristics of spatial spectrum situations becomes essential, enabling spectrum map construction with limited sampled data through spectrum situation estimation in accessible regions.

Data-driven methods inherently require the prediction and estimation of unsampled spectrum data. Breakthroughs in sparse coding and compressive sensing theories have opened new avenues for radio map construction [20,21,22,23]. For instance, collaborative spectrum sensing techniques in CRNs [24] share a similar philosophy of exploiting spatial correlations. Recent advancements have also explored the integration of UAVs for spatial sensing [25], and tensor-based methods for dynamic radio cartography [26,27], which are highly relevant to our 3D tensor completion framework. However, these methods often do not fully address the severe signal sparsity and high correlation in samples collected from occluded urban canyons, which is the core challenge tackled in this paper.

It is precisely this gap—the ineffectiveness of existing compressive sensing (CS) methods in handling highly correlated 3D subspaces and learning robust dictionaries for complex urban spectra—that our work aims to bridge. Unlike prior arts, our proposed framework jointly addresses the dictionary learning and sparse recovery challenges in a synergistic manner.

In the sparse representation framework, signals can be approximately expressed as linear combinations of atoms in an overcomplete dictionary. When the number of atoms in the overcomplete dictionary far exceeds the signal dimension, robust optimization algorithms such as L1 regularization or iteratively reweighted least squares need to be adopted to ensure that the solution still has sparsity under noise and model errors. At the same time, to alleviate the high-dimensional non-convex optimization problem caused by the combination of propagation models and dictionary learning, the key challenges lie in overcoming the computational complexity caused by high variable dimensions and the local optimal traps caused by non-convex objective functions.

This paper focuses on the accuracy of spatial power recovery and studies the construction of remote spectrum maps in inaccessible urban areas. We propose a synthetic method based on SCNG, OOMP, and BoP, hereinafter referred to as Synthetic BoP-OOMP framework (SBO). The main contributions of this paper are summarized as follows:

• A Novel 3D Spectrum Tensor Completion Framework: We propose a compressive sensing-based framework that effectively addresses the challenge of extrapolating spectrum data into spatially inaccessible urban areas. This is achieved by formulating the 3D spectrum power data as a tensor and vectorizing it, thereby transforming the UAV sampling problem into a sparsity-driven signal recovery problem.
• An Adaptive and Robust Dictionary Learning Mechanism: We introduce the Sparse Coding Neural Gas (SCNG) algorithm, coupled with a neural gas competitive learning strategy, to construct an overcomplete dictionary that is highly adaptive to wide-range spectral fluctuations. This approach overcomes the limitations of traditional K-SVD, which often yields underestimated values and converges to poor local minima, thereby ensuring more accurate and robust feature representation.
• An Enhanced Sampling and Reconstruction Algorithm: We develop a Bag of Pursuits-optimized Orthogonal Matching Pursuit (BoP-OOMP) framework. This innovation tackles the critical issue of suboptimal atom selection in traditional OMP within highly correlated 3D subspaces. By enabling multi-path tree search and leveraging intermediate solutions for gradient-weighted dictionary updates, our method achieves superior reconstruction accuracy and computational efficiency, effectively decoupling overlapping subspaces.

The rest of this article is organized as follows: Section 2 formulates the model and problem. Section 3 details the sampling position optimization framework. Section 4 presents experimental scenarios, simulations, and comparative results. Section 5 concludes with research prospects.

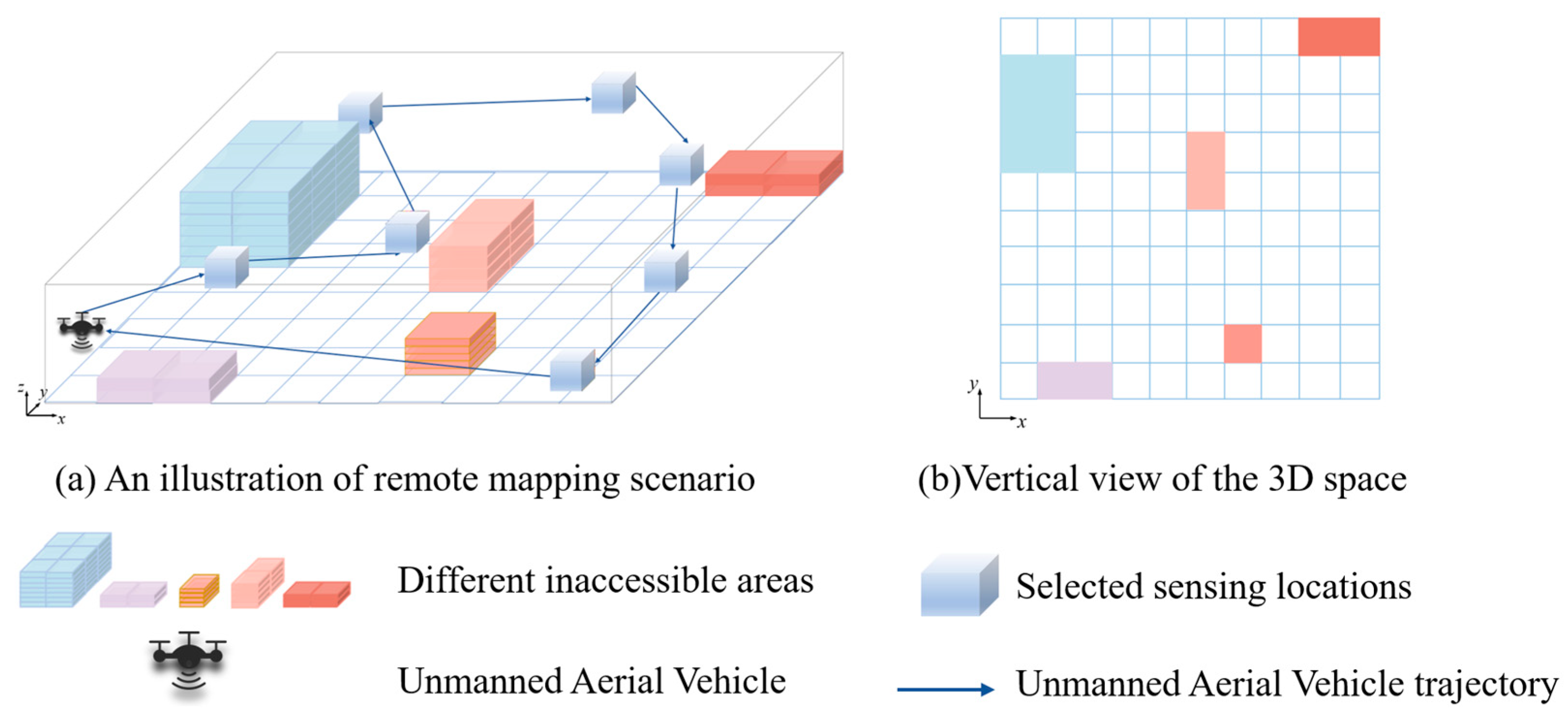
2. System Model

Due to varying channel conditions caused by differences in signal propagation environments and transmitter locations, we establish the signal propagation space illustrated in Figure 1. First, we discretize the entire 3D space into volumetric pixels (voxels), forming a spectrum tensor $\chi \in N_1\times N_2\times N_3$ where $N_1$, $N_2$ and $N_3$ represent the grid counts along the x, y and z axes, respectively. To construct an accurate radio map, spectrum measurements would ideally be performed for every voxel. However, our objective is to minimize measurement requirements by exploiting spatial power correlations between accessible and inaccessible regions. This approach enables estimation of missing spectrum situations, ultimately yielding a complete 3D radio map. Our objective is to reconstruct an accurate radio map with minimal measurement requirements. This can be formulated as an optimization problem that aims to find the optimal sampling positions ξ* which minimize the reconstruction error under a given sampling ratio constraint. Mathematically, the problem is formulated as

$${\xi }^{*}=argmin{W}_{\chi },\xi \subseteq \chi ,$$

(1)

$$s.t. r={\displaystyle \frac{N_{\xi }}{N_1\times N_2\times N_3}},$$

(2)

$$W_{\chi }={\displaystyle \frac{1}{N_{\chi }}}{\sum }_i{\left({\displaystyle \frac{\left|{\chi }_i^R-{\chi }_i\right|}{{\chi }_i}}\right)}^2,$$

(3)

where ξ denotes the sampling positions of UAVs at different locations. $W_{\chi }$ represents the relative mean square error (RMSE) between the estimated power intensity ${\chi }_i^R$ and the actual power intensity ${\chi }_i$, r indicates the spectrum sampling rate in 3D space, $N_{\xi }$ is the number of sampling points, and $N_{\xi }$ denotes the total number of spatial points. Exhaustive sampling to obtain spectrum situation data for all $N_{\chi }$ points is clearly impractical. Therefore, research on reducing sampling points and optimizing their spatial distribution holds considerable practical value. However, exhaustive sampling is impractical. To solve this underdetermined problem, we leverage the inherent sparsity of the spatial spectrum situation. Based on compressive sensing theory, the problem is transformed into recovering a sparse signal s from under-sampled measurements y = Ds + ε, which is detailed in the following sections.

The optimization objective formulated in (1)—minimizing the reconstruction error $W_{\xi }$ under a sampling ratio constraint r—is of paramount practical significance for UAV-assisted spectrum mapping. This formulation directly addresses the two most critical constraints in real-world UAV operations: energy and time. Minimizing the number of sampling points (i.e., keeping r low) directly translates to shorter mission durations and lower energy consumption, thereby extending the UAV’s operational range and viability. Simultaneously, minimizing the reconstruction error $W_{\xi }$ ensures the reliability and usability of the generated radio map. A highly accurate map empowers cognitive radio networks to make trustworthy dynamic spectrum access decisions, minimizing interference and maximizing utilization. Therefore, our optimization objective strikes a crucial balance between operational feasibility (low sampling cost) and functional efficacy (high map accuracy), which is the cornerstone for deploying practical UAV-based spectrum monitoring systems.

In this work, we adopt a hover-and-sense mobility model for the UAV spectrum monitoring platform. This model is justified for the following reasons: First, the primary challenge we address is the optimal selection of where to sample in 3D space, rather than the continuous trajectory planning. The proposed BoP-OOMP algorithm is designed to output a set of discrete, informative 3D coordinates ξ*. Second, hovering at a fixed position allows for stable and reliable spectrum measurement, minimizing the Doppler effect and measurement noise induced by mobility. The UAV moves between these pre-optimized sampling points at a constant speed v (5 m/s). Once it arrives at a target waypoint in ξ*, it hovers to perform the spectrum sensing task. This model effectively decouples the sampling position optimization problem from the path planning problem, allowing us to focus on the core algorithmic contribution of spatial extrapolation. The resulting set of sampling points ξ* can subsequently serve as input to any standard UAV path planning algorithm to generate a kinematically feasible route.

The selected experimental scenario is an urban block as shown in Figure 1. Let positions i and j denote two distinct grid indices within the experimental area. The unknown spectrum power values across the 3D scene are represented as vector $\mathrm{s}={\left[{\mathrm{s}}_{u_1},{\mathrm{s}}_{u_2},\dots ,{\mathrm{s}}_{u_n}\right]}^{\top }\in {\mathrm{R}}^{n\times 1}$. The entire three-dimensional space U is discretized as

$$U=\left(u_1,u_2,\dots ,u_n\right),\left(n=N_1\times N_2\times N_3\right),$$

(4)

Assuming there exist P inaccessible regions, denoted as

$$V=V_1\cup V_1\cup ···\cup V_P,\left(V_p\cap V_q=Ø,p\ne q\right),$$

(5)

Thus, the set of accessible regions is $C_{V}U$, where V denotes the complement of V with respect to U.

The sparsity of the source vector is $k={‖\mathrm{s}‖}_0$, where k represents the number of non-zero elements in the tensor. Given the constraint m ≪ n (underdetermined sampling and estimation), recovering the original signal s from observations $y$ constitutes an ill-posed problem.

Minimizing the $l_o$-norm promotes sparsity but results in a non-convex optimization problem. Finding the exact solution for sampling matrix D is NP-hard, particularly in high-dimensional spaces. Therefore, we relax the formulation using the $l_1$-norm to yield a convex optimization problem as

$${s_i}^{OOMP}=\mathrm{a}\mathrm{r}\mathrm{g}\underset{\mathrm{s}}{\mathrm{m}\mathrm{i}\mathrm{n}}{‖\mathrm{s}‖}_1,$$

(6)

$${‖y-\mathrm{D}\mathrm{s}‖}^2\le {\sigma }^2,$$

(7)

Throughout the sampling process, we only collect data from partial regions within the 3D space. The sampled signal is expressed as

$$y=\mathrm{D}\mathrm{s}+\epsilon ,$$

(8)

where ε denotes additive white Gaussian noise (AWGN) with power spectrum density ${\sigma }^2$, and D is the measurement matrix.

Based on the above analysis and the inherent sparsity of y, the objective function for remote compressive spectrum mapping of inaccessible regions is formulated as

$$\widehat{\mathrm{s}}=\arg \underset{y^s}{\min }{‖y-\mathrm{D}\mathrm{s}‖}_2^2+\lambda {‖\mathrm{s}‖}_1,$$

(9)

where $\widehat{\mathrm{s}}$ denotes the estimated value. To solve the optimization problem above, we employ an enhanced Orthogonal Matching Pursuit (OMP) algorithm. Achieving accurate 3D electromagnetic spectrum situation reconstruction necessitates both rational sampling position selection and precisely designed spectrum recovery algorithms, which are particularly critical for high-fidelity spatial mapping.

To address the challenge of spectrum data collection in urban areas inaccessible to UAVs, we obtain accurate spectrum samples that enable remote mapping power estimation. We propose an enhanced Orthogonal Optimized Matching Pursuit (OOMP) algorithm that transforms spectrum situation recovery into an optimal coefficient search under constraints. This approach achieves spectrum power intensity reconstruction in highly overlapping subspaces with missing data samples. Consequently, we derive the spatial power estimates for inaccessible regions V and the corresponding Relative Mean Square Error (RMSE) as

$$z_V^R={\left(\widehat{\mathrm{s}}\right)}_V,$$

(10)

$$E_V={\displaystyle \frac{1}{N_V}}\sum _{u_i∊V}{‖{\displaystyle \frac{z_{u_i}^R-z_{u_i}}{z_{u_i}}}‖}_2^2,$$

(11)

where ${(·)}_V$ denotes the subset of vectors indexed by set V, and $N_V$ represents the cardinality of V. Here, $z_{u_i}^R$ and $z_{u_i}$ denote the estimated and original spectrum power intensity at sampling point $u_i$, respectively.

3. Remote Compressed Spectrum Mapping Algorithm

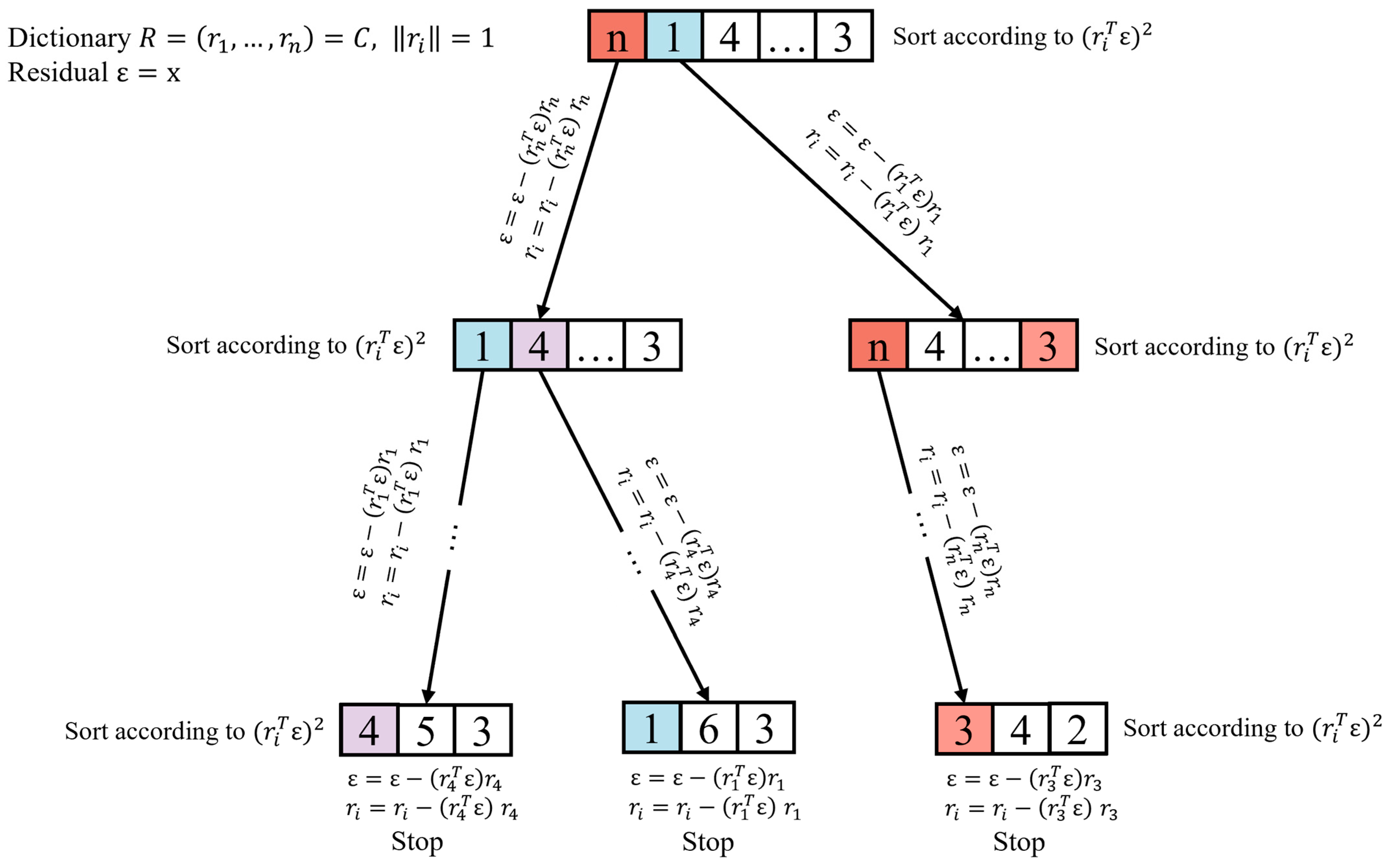
3.1. Optimization of Sampling Matrix Based on Improved Orthogonal Matching Pursuit Algorithm

Building upon existing research on spectrum mapping models, this paper proposes an algorithm comprising two key components: sampling location optimization and power estimation. In three-dimensional space, power intensity typically exhibits strong spatial correlation. Performing spectrum measurements for every cubic unit would incur prohibitively high costs in time and energy, making the selection of sampling locations critically important for estimation accuracy. Random sampling risks losing crucial information and significantly increases the difficulty of energy recovery for unsampled areas. Therefore, adaptive selection of sampling locations is necessary to capture data with stronger spatial correlation. We employ UAVs equipped with spectrum sensing devices, hovering at predetermined positions to collect electromagnetic spectrum data.

The BoP-OOMP algorithm operates as follows: For each signal, it initiates multiple pursuit paths (K_user paths). In each path, it iteratively selects the dictionary atom that is most correlated with the current residual, but after orthogonalizing all atoms with respect to the already selected ones (OOMP step). After all paths are completed, the best solution is chosen. This multi-path approach avoids getting trapped in a suboptimal atom selection sequence. We have provided explanations for some symbols in the chapter, as shown in

Table 1. Explanation of Symbols.

Symbol	Description of Meaning
$\mathrm{D}$	Overcomplete Dictionary/Measurement Matrix
$y$	Observed Spectrum Signal (Sampled Data)
$\mathbf{s}$	Sparse Source Signal Coefficient Vector to Be Solved
$k$	Sparsity of the Signal (Number of Non-Zero Elements)
$U$	Set of Selected Atom Indices in the OOMP Algorithm
${\mathrm{R}}_n^j$	Orthogonalized Temporary Dictionary at the n-th Iteration in the j-th Pursuit
${ϵ}_n^j$	Residual After the n-th Iteration in the j-th Pursuit
$l_{win}$	Index of the Optimal Atom Selected in the Current Iteration
$K_{user}$	Number of Parallel Pursuit Paths Set in the Bag of Pursuits (BoP) Algorithm

.

The K-SVD algorithm has limitations in reconstructing the “true” underlying dictionary, often producing reconstructed values that are too small. This fails to meet the requirements of spectrum mapping where values exhibit substantial fluctuations. To address this issue, we introduce the Sparse Coding Neural Gas (SCNG) algorithm [29]. Unlike K-SVD and Method of Optimal Directions (MOD) algorithms, SCNG is specifically used for determining the sparse coefficient approximation.

To solve the aforementioned problems, we have improved Orthogonal Matching Pursuit (OMP) algorithm. Typically, the rows of dictionary D are not pairwise orthogonal. In standard OMP, the column ${\mathrm{D}}_{l_{win}}$ selected to be added to the set U is not optimal in the context of minimizing the residual after its inclusion. Therefore, to achieve minimal regularized residuals, the enhanced OOMP algorithm requires a selection criterion: it must evaluate all unused columns in dictionary D and identify the column that produces the smallest residual. The overall algorithmic steps are as

• Select an appropriate column ${\mathrm{D}}_{l_{win}}$ through ${\mathrm{D}}_{l_{win}}=\arg \underset{c_l,l\notin U}{\min }\underset{\mathrm{s}}{\min }‖\mathrm{y}-{\mathrm{D}}^{U\cup l}\mathrm{s}‖$;
• Set $U=U\cup l_{win}$;
• Solve the optimization problem: $\widehat{y}=\mathrm{a}\mathrm{r}\mathrm{g}\underset{ a}{\mathrm{m}\mathrm{i}\mathrm{n}}{‖y-{\mathrm{D}}^U\mathrm{s}‖}_2$;
• Obtain the residual: ${ϵ}_i={\mathrm{y}}_i-\mathrm{D}{\mathrm{s}}^{OOMP}$;
• Repeat Step 1 until k iterations are completed.

The selection criterion of the Orthogonal Orthogonal Matching Pursuit (OOMP) algorithm involves solving $M-\left|U\right|$ minimization problems for each unused column in the dictionary D. To reduce the computational complexity of this step, the OOMP algorithm is applied to an orthogonalized temporary dictionary R. R is obtained by removing the projection of dictionary D onto the subspace and normalizing the residual $r_l$ to unit norm. ${\mathrm{R}}_n^j$ denotes a temporary matrix that has been orthogonalized with respect to the columns selected from D by the index set ${\mathrm{U}}_n^j$. The residual ${ϵ}_i^U$ is obtained similarly: the projection of ${\mathrm{R}}_i$ onto the subspace spanned by ${\mathrm{D}}^U$ is removed. We have $\mathrm{R}=\left(r_1,\dots ,r_l,\dots ,r_m\right)=\mathrm{D}$ and ${ϵ}_i^U={\mathrm{y}}_i$.

During each iteration, the algorithm identifies the column $r_l$ from dictionary R in the context of the most recent residual ${ϵ}_i^U$. Following each gradient update, the column vectors in the dictionary are re-normalized to unit norm. A new training sample is then selected, the coefficients are re-determined, and the next update can be performed. This process is straightforward and computationally efficient, as it entirely avoids the need for singular value decomposition (SVD) or matrix inversion. Furthermore, it utilizes only one sample per learning step, making it suitable even for online learning scenarios. It also eliminates the requirement to store large volumes of training samples.

Due to the broad spectrum coverage in open space, a subset of the sampled data is inherently correlated. The sampled data constitutes a sparse representation of subspaces within the ambient space, resulting in high correlation among the spectrum samples at the sampling points. Basis vectors are shared among these subspaces. We select training data generated by linearly combining a set of dictionary elements with the sampled signals.

Numerous approximation methods have been proposed to address the problem of obtaining the optimal coefficients ${\mathrm{s}}_i$. To solve this, we employ a greedy algorithm. Specifically, under the sparsity constraint of a given signal ${\mathrm{y}}_i$, this requires that the mutual coherence of the dictionary D be sufficiently small. The mutual coherence of D is defined as

$$\mu \left(\mathrm{D}\right)=\begin{array}{c}max\\ 1\le i,j\le M,i\ne j\end{array}{\displaystyle \frac{\left|{\mathrm{D}}_i^T{\mathrm{D}}_j\right|}{{‖{\mathrm{D}}_i‖}_2{‖{\mathrm{D}}_j‖}_2}}.$$

(12)

To further enhance the performance of the OOMP algorithm, it is necessary not only to find the optimal coefficients but also to define the optimal approximation $K_{user}$ for these coefficients. With the initial conditions $U_n^j=\mathrm{Ø},R_n^j=(r_1^{0,j},\dots ,r_M^{0,j})$, and ${ϵ}_0^j=\mathrm{y}$, the set $U_n^j$ contains the indices of columns from D that have already been selected up to the n-th iteration during the j-th pursuit for y. $R_n^j$ denotes an orthogonalized temporary matrix, which has been orthogonalized with respect to the columns in D indexed by $U_n^j$. $r_l^{n,j}$ represents the l-th column of $R_n^j$. ${ϵ}_n^j$ is the residual for the target y after n iterations within the j-th pursuit. The detailed algorithm pseudocode is presented in Algorithm 1.

Algorithm 1 Enhanced Orthogonal Optimized Matching Pursuit (EOOMP)

Input: Signal vector y, dictionary matrix $\mathrm{D}=(d_1,d_2,\dots {,d}_m)$, maximum iterations per             pursuit: k, user-defined solution count: $K_{user}$;

Output: Sparse approximations: (${\mathrm{s}}^1,{\mathrm{s}}^2,\dots ,{\mathrm{s}}^{K_{user}}$), residual vectors: (${ϵ}^1,{ϵ}^2,\dots ,{ϵ}^{K_{user}}$);

1: Initialize $Q\left(l,n,j\right)=0$, $l\in \left(1,M\right), n\in \left(0,k\right), j\in \left(1,K_{user}\right)$, completed pursuits     set P $=\varnothing$;

2: for $j=1$ to $K_{user}$ do

3:              Initialize $jth$ pursuit, $U_0^j=\varnothing$, ${ϵ}_0^j=y$, ${\mathrm{R}}_0^j=\left(r_1^{0,j},\dots ,r_M^{0,j}\right)=\mathrm{D}$;

4:              for $n=0$ to k − 1 do

5:                        $y_n^j=\left({\displaystyle \frac{{r_1^{n,j}}^T{ϵ}_n^j}{‖r_1^{n,j}‖}},\dots ,{\displaystyle \frac{{r_l^{n,j}}^T{ϵ}_n^j}{‖r_l^{n,j}‖}},\dots ,{\displaystyle \frac{{r_M^{n,j}}^T{ϵ}_n^j}{‖r_M^{n,j}‖}}\right)$;

6:                        Find $l_{win}(n,j)=\underset{l,l\notin U_n^j}{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{a}\mathrm{x}}{\left(y_n^j\right)}_l^2$ where $Q(l,n,j)=0$;

7:                        Update orthogonal matrix $\mathrm{a}\mathrm{s}$ (14);

8:                        Update residual as (15);

9:                        Update $U_{n+1}^j=U_n^j$ and set $Q\left(l_{win},n,j\right)=1$;

10:                      if $‖{ϵ}_{n+1}^j‖=0$ then

11:                           break inner loop;

12:                      end if

13:            end for

14:            Store $jth$ pursuit result $a^j=\mathrm{a}\mathrm{r}\mathrm{g}\underset{ a}{\mathrm{m}\mathrm{i}\mathrm{n}}{‖y-{\mathrm{D}}^U\mathrm{s}‖}_2$, ${ϵ}_{n+1}^j={ϵ}_n^j$, P $=P\cup \left\{j\right\}$;

15:            if $j<K_{user}$ then

16:                Find $\left(j_{target},n_{target},l_{target}\right)=\underset{p\in P,n\in \left\{0,b_p-1\right\}, l:Q\left(l,n,p\right)=0}{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{a}\mathrm{x}}{\left(y_n^p\right)}_l^2$;

17:                Prepare next pursuit starting at pivot $U_0^j=U_{n_{target}}^{j_{target}}$, ${ϵ}_0^j={ϵ}_{n_{target}}^{j_{target}},$                             $R_0^j=R_{n_{target}}^{j_{target}}$;

18:                Set $Q\left(j_{target},n_{target},l_{target}\right)=1$;

19:            end if

20: end for

21: Return $\left\{{\mathbf{s}}^1,\dots ,{\mathbf{s}}^{K_{user}}\right\}$, $\left\{{ϵ}^1,\dots ,{ϵ}^{K_{user}}\right\}$.

At the n-th iteration, the next residual ${ϵ}_{i+1}^U$ that minimizes the approximation error is obtained by searching for the best linear superposition within $R_n^j$, leading to

$$y_n^j=\left({\displaystyle \frac{{r_1^{n,j}}^T{ϵ}_n^j}{‖r_1^{n,j}‖}},\dots ,{\displaystyle \frac{{r_l^{n,j}}^T{ϵ}_n^j}{‖r_l^{n,j}‖}},\dots ,{\displaystyle \frac{{r_M^{n,j}}^T{ϵ}_n^j}{‖r_M^{n,j}‖}}\right).$$

(13)

The purpose of the above expression is to determine the index of the winning atom: $l_{win}(n,j)=\begin{array}{c}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{a}\mathrm{x}\\ l,l\notin U_n^j\end{array}{\left(y_n^j\right)}_l^2$. Subsequently, the orthogonal projection of ${\mathrm{R}}_n^j$ onto $r_{l_{win}(n,j)}^{n,j}$ is subtracted from $R_n^j$, yielding

$${\mathrm{R}}_{n+1}^j={\mathrm{R}}_n^j-{\displaystyle \frac{r_{l_{win}\left(n,j\right)}^{n,j}{\left({{\mathrm{R}}_n^j}^T{r}_{l_{win}\left(n,j\right)}^{n,j}\right)}^{\top }}{{r_{l_{win}\left(n,j\right)}^{n,j}}^T{r}_{l_{win}\left(n,j\right)}^{n,j}}}.$$

(14)

The orthogonal projection of ${\mathrm{R}}_n^j$ onto $r_{l_{win}(n,j)}^{n,j}$ is subtracted from ${\mathrm{R}}_n^j$, yielding

$${ϵ}_{n+1}^j={ϵ}_n^j-{\displaystyle \frac{{{ϵ}_n^j}^T{r}_{l_{win}\left(n,j\right)}^{n,j}}{{r_{l_{win}\left(n,j\right)}^{n,j}}^T{r}_{l_{win}\left(n,j\right)}^{n,j}}}{r}_{l_{win}\left(n,j\right)}^{n,j}.$$

(15)

The algorithm terminates when $‖{ϵ}_n^j‖=0$ or $n=k$, yielding the coefficients for the j-th pursuit and the k-term optimal approximation. During the j-th greedy iteration, it cyclically evaluates the contribution of each column in dictionary D to obtain ${\mathrm{s}}^j$. To approximate ${\mathrm{s}}^1,\dots ,{\mathrm{s}}^K$, K is manually specified to align with the greedy objective. For obtaining greedy solutions at different K values, we implement the following function as

$$Q\left(l,n,j\right)=\left\{\begin{array}{c}0,\mathrm{there} \mathrm{is} \mathrm{no} \mathrm{pursuit} \mathrm{among} \mathrm{all} \mathrm{pursuits} \\ 1, \mathrm{else}.\end{array}.\right.$$

(16)

When no suitable value (sampling point) is selected across all greedy processes—specifically, during the j-th greedy iteration within the n-th overall iteration, where the iteration column j is chosen—we then trace all overlaps from the first (recorded) greedy computation process. Concretely, if ${\mathrm{a}}^1$ is determined, we obtain $y_0^1,\dots ,y_n^1,\dots ,y_{b_1-1}^1$, where $b_1$ denotes the iteration count of the first greedy process. To identify ${\mathrm{a}}^2$, we seek the maximum overlap among previously unused atoms from prior greedy processes

$$n_{target}=\mathrm{a}\mathrm{r}\mathrm{g}\underset{n=0,\dots ,b_1-1}{\max }\underset{l,Q\left(l,n,j\right)=0}{\max }{\left(y_{\mathrm{n}}^1\right)}_l^2,$$

(17)

$$l_{target}=\mathrm{a}\mathrm{r}\mathrm{g}\underset{l}{\max }{\left(y_{n_{target}}^l\right)}_l^2.$$

(18)

Building upon the results and foundations of the first pursuit up to the $n_{target}$ iteration, we select column $l_{target}$ to substitute the previous optimal position, continuing the greedy process until the termination criterion is met. If m pursuits have been implemented across all prior processes, we then seek the maximum coverage among unused atoms

$$j_{target}=\mathrm{a}\mathrm{r}\mathrm{g}\underset{j=1,\dots ,m}{\max }\underset{n=0,\dots ,b_j-1}{\max }\underset{l,Q\left(l,n,j\right)=0}{\max }{\left(y_{\mathrm{n}}^j\right)}_l^2,$$

(19)

$$n_{target}=\mathrm{a}\mathrm{r}\mathrm{g}\underset{n=0,\dots ,b_{j_{\mathit{target}}}-1}{\max }\underset{l,Q\left(l,n,j_{\mathit{target}}\right)=0}{\max }{\left(y_{\mathrm{n}}^{j_{target}}\right)}_l^2,$$

(20)

$$l_{target}=\mathrm{a}\mathrm{r}\mathrm{g}\underset{l,Q\left(l,n_{target},j_{target}\right)=0}{\mathrm{m}\mathrm{a}\mathrm{x}}{\left(y_{n_{target}}^{j_{target}}\right)}_l^2.$$

(21)

Re-execute the greedy process for $j_{target}$ over $n_{target}$ iterations, selecting column $l_{target}$ to replace the previously identified optimal column. Continue the iterative selection until the stopping criterion is met. Repeat this procedure until the user-specified K is achieved.

In Figure 2, using $K_{user}=3$ as an example, three distinct solutions are identified. First, dictionary elements are sorted according to their projection magnitude onto the residual. Orthogonalization is then performed based on the element exhibiting maximum projection. For instance, when element n is selected, all other dictionary elements and the residual are orthogonalized relative to it—yielding the second solution. This sequential orthogonalization is repeated until a maximum of three dictionary elements are utilized, producing the final solutions: Solution 1: [4, 5, 3]. Solution 2: [1, 6, 3]. Solution 3: [3, 4, 2].

Since dictionary reconstruction must address the overcompleteness problem (over-recovery/over-coverage), the dictionary size inevitably increases. For large-scale dictionaries, previously selected atoms and elements in the temporary dictionary remain mutually orthogonal, as demonstrated in (14). Furthermore, if low-cost computation is required within permissible estimation error bounds, the dictionary orthogonalization step may be omitted. In such cases, the tree-search process computes the OMP solution rather than the OOMP solution.

3.2. Coefficient Determination via Gradient Descent

While subsection A employs Bag of Pursuit (BoP) to enhance learning efficiency, only the optimal pursuit from the tracking set $K_{user}$ is utilized in the gradient descent algorithm. The computational efficiency of dictionary learning remains suboptimal for wide-area spectrum estimation due to stringent real-time requirements for spectrum mapping. Furthermore, we observe that intermediate solutions are underutilized in our proposed sparse approximation framework. Leveraging these intermediate solutions could reduce redundant computational overhead.

To address this, we introduce a competitive learning strategy derived from vector quantization—interpreted as a specialized sparse coding scheme where dictionary coefficients satisfy ${‖{\mathrm{s}}_i‖}_0=1$ and ${‖{\mathrm{s}}_i‖}_2=1$. This reformulates the optimization problem as: ${\left({\mathrm{s}}_i\right)}_m=1,{\left({\mathrm{s}}_i\right)}_l=0,\forall l\ne m$ with $m=\begin{array}{c}argmin\\ l\end{array}{‖{\mathrm{D}}_l-{\mathrm{y}}_i‖}_2^2$. Conventional vector quantization algorithms predominantly update using only the best-matching atom, leading to sensitivity to initialization, slow convergence, and suboptimal quantization.

To address these issues, soft competitive vector quantization algorithms such as the Neural Gas algorithm [30] are employed. At each learning step, all possible encodings ${\mathrm{s}}_i^1,{\mathrm{s}}_i^2,\dots ,{\mathrm{s}}_i^M$ where ${\left({\mathrm{s}}_i^j\right)}_j=1$ are considered. The encodings are then sorted according to their reconstruction error as

$$‖{\mathrm{y}}_i-\mathrm{D}{\mathrm{s}}_i^{j_0}‖\le \cdots \le ‖{\mathrm{y}}_i-\mathrm{D}{\mathrm{s}}_i^{j_p}‖\le \cdots \le ‖{\mathrm{y}}_i-\mathrm{D}{\mathrm{s}}_i^{j_M}‖.$$

(22)

Compared to hard competitive methods, this approach updates the codebook vectors during each learning iteration, weighting them according to the rank of their encodings. This achieves a gradient descent effect equivalent to a well-defined cost function. The Neural Gas algorithm demonstrates robust convergence, particularly with large datasets.

We aim to apply this ranking approach to learning coefficient codes. For each given ${\mathrm{y}}_i$, we consider all K possible coefficient vectors ${\mathrm{s}}_i^j$, i.e., all non-zero entries. Each element in ${\mathrm{s}}_i^j$ ensures $‖{\mathrm{y}}_i-\mathrm{D}{\mathrm{s}}_i^j‖$ is minimized. The coefficients are then sorted according to the representation error obtained by approximating sample ${\mathrm{y}}_i$, which can be expressed as

$$‖{\mathrm{y}}_i-\mathrm{D}{\mathrm{s}}_i^{j_0}‖<\cdots <‖{\mathrm{y}}_i-\mathrm{D}{\mathrm{s}}_i^{j_p}‖<\cdots <‖{\mathrm{y}}_i-\mathrm{D}{\mathrm{s}}_i^{j_M}‖$$

(23)

With $\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}(y_i,a_i^j,\mathrm{D})=p$ denoting the ranking position of coefficient vectors, and the neighborhood function defined as $h_{{\lambda }_t}(v)=e^{{\displaystyle \frac{-v}{{\lambda }_t}}}$, the error function is given by

$$E_s=\sum _{i=1}^L\sum _{j=1}^K{h}_{{\lambda }_t}\left(\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}\left({\mathrm{y}}_i,{\mathrm{s}}_i^j,\mathrm{D}\right)\right){‖{\mathrm{y}}_i-\mathrm{D}{\mathrm{s}}_i^j‖}_2^2.$$

(24)

Equivalent to (1), to minimize (24), we consider the gradient of $E_s$ as

$${\displaystyle \frac{\partial E_s}{\partial \mathrm{D}}}=-2{\sum }_{i=1}^L{\sum }_{j=1}^K{h}_{{\lambda }_t}\left(\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}\left({\mathrm{y}}_i,{\mathrm{s}}_i^j,\mathrm{D}\right)\right)\left({\mathrm{y}}_i-\mathrm{D}{\mathrm{s}}_i^j\right){{\mathrm{s}}_i^j}^T+R,$$

(25)

where

$$R={\sum }_{i=1}^L{\sum }_{j=1}^K{h}_{{\lambda }_t}^{\text{'}}\left(\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}\left({\mathrm{y}}_i,{\mathrm{s}}_i^j,\mathrm{D}\right)\right)·{\displaystyle \frac{\partial \mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}\left({\mathrm{y}}_i,{\mathrm{s}}_i^j,\mathrm{D}\right)}{\partial \mathrm{D}}}{‖{\mathrm{y}}_i-\mathrm{D}{\mathrm{s}}_i^j‖}_2^2,$$

(26)

In [31], it was proven that R = 0. We omit further proof here. With $e_i^j={\mathrm{y}}_i-\mathrm{D}{a}_i^j$, $\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}\left(y_i,{\mathrm{s}}_i^j,\mathrm{D}\right)$ is rewritten as

$$\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}\left({\mathrm{y}}_i,{\mathrm{s}}_i^j,\mathrm{D}\right)={\sum }_{j=1}^{K}H\left({\left(e_i^j\right)}^2-{\left(e_i^m\right)}^2\right),$$

(27)

where H(x) is the Heaviside step function. This leads to

$$R=2\sum _{i=1}^L\sum _{j=1}^K{h}_{{\lambda }_t}^{\text{'}}\left(\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}\left({\mathrm{y}}_i,{\mathrm{s}}_i^j,\mathrm{D}\right)\right){\left(e_i^j\right)}^2\sum _{m=1}^K\left(e_i^m{\left({\mathrm{s}}_i^m\right)}^2-e_i^j{\left(e_i^j\right)}^T\right)H\left({\left(e_i^j\right)}^2-{\left(e_i^m\right)}^2\right).$$

(28)

In (28), each term is non-zero unless ${\left(e_i^j\right)}^2={\left(e_i^m\right)}^2$ holds. Therefore, we introduce the ranking neighborhood weighting concept of the Neural Gas algorithm into sparse coefficient optimization, replacing traditional single optimal solution updates. Under the premise of updating D, we apply gradient descent to (30) with

$$∆\mathrm{D}={\alpha }_t\sum _{j=1}^K{h}_{{\lambda }_t}\left(\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}\left({\mathrm{y}}_i,{\mathrm{s}}_i^j,\mathrm{D}\right)\right)\left({\mathrm{y}}_i-\mathrm{D}{\mathrm{s}}_i^j\right){\mathrm{s}}_i^{j^{\top }}.$$

(29)

For stochastically chosen ${\mathrm{y}}_i\in \mathrm{Y}$,

$${\lambda }_t={\lambda }_0{\left({\displaystyle \frac{{\lambda }_{\mathrm{f}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{l}}}{{\lambda }_0}}\right)}^{{\displaystyle \frac{t}{t_{max}}}}$$

(30)

is an exponentially decaying variable neighborhood size and an exponentially decreasing learning rate. After each update, the column vectors of D are renormalized to 1, $a_i^j$ is recalculated, and the next update is performed.

At this point, for each training sample ${\mathrm{y}}_i$, all possible coefficient vectors $a_i^j$ ($j=1,...,K$ with ${‖a_i^j‖}_0\le k$) are considered. K grows exponentially with M and k. In the current case (18), we do not require all possible coefficient vectors.

Components where the rank in (18) exceeds the neighborhood ${\lambda }_t$ are ignored—we focus solely on the solution with the best reconstruction error obtained through the BoP method. The detailed algorithm pseudocode is presented in Algorithm 2.

Algorithm 2 Rank-Weighted Dictionary Learning with Bag of Pursuits

Input: Data samples Y $={\left\{y_i\right\}}_{i=1}^L$, dictionary $D_0\in {\mathbb{R}}^n$, sparsity level $k$, number of           candidates $T$, initial neighborhood size ${\lambda }_0$, final neihborhood size ${\lambda }_{\mathrm{f}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{l}}$, initial           leaning rate ${\alpha }_0$, final learning rate ${\alpha }_{\mathrm{f}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{l}}$, maximum iterations $t_{max};$

Output: Learning dictionary D;

Initialization: set $\mathrm{D}={\mathrm{D}}_0$;

1: while $t<T$ do

2:           Compute annealing parameters: ${\lambda }_t={\lambda }_0{\left({\displaystyle \frac{{\lambda }_{\mathrm{f}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{l}}}{{\lambda }_0}}\right)}^{{\displaystyle \frac{t}{t_{max}}}},{\alpha }_t={\displaystyle \frac{{\alpha }_{\mathrm{f}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{l}}}{{\alpha }_0}}$;

3:           Randomly pick an index i from $\left\{1,\dots ,L\right\}$, and set y $={\mathrm{y}}_i$;

4:           Use Algorithm 1 to obtain K approximations: $\left\{{\mathrm{s}}^1,\dots ,{\mathrm{s}}^K\right\}=\mathrm{B}\mathrm{o}\mathrm{P}(\mathrm{y},\mathrm{D},k,K)$;

5:           for $j=1$ to K do

6:                   $e^j=\mathrm{y}-\mathrm{D}{\mathbf{s}}^j$;

7:                   ${\left({ϵ}^j\right)}^2={‖{\mathrm{e}}^j‖}_2^2$;

8:           end for

9:           Sort $\left\{\left({ϵ}_1,{\mathrm{s}}^1\right),\dots ,\left({ϵ}_K,{\mathrm{s}}^K\right)\right\}$ by ${ϵ}_1\le {ϵ}_2\le \cdots {\le ϵ}_K$;

10:         for $j=1$ to K do

11:                 $w_j=\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\displaystyle \frac{{\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}}_j}{{\lambda }_t}}\right)$;

12:                 $\Delta \mathrm{D}\leftarrow \Delta \mathrm{D}+w_j·{\mathrm{e}}^j{\left({\mathbf{s}}^j\right)}^{\mathrm{\top }}$;

13:         end for

14:         $\Delta \mathrm{D}\leftarrow {\alpha }_t\Delta \mathrm{D}$;

15:         Updata dictionary: $\mathrm{D}\leftarrow \mathrm{D}+\Delta \mathrm{D}$;

16:         Renormalize dictionary columns: ${\mathrm{d}}_l\leftarrow {\mathrm{d}}_l/{‖{\mathrm{d}}_l‖}_2$;

17:         Increment iteration counter: $t\leftarrow t+1$;

18: end while

The core idea of the proposed SBO framework can be summarized as a sparsity-driven, dictionary-learning-enabled tensor completion process. It first learns an adaptive dictionary (SCNG) that sparsely represents the 3D spectrum environment. Then, it employs a multi-path greedy pursuit (BoP-OOMP) to intelligently select the most informative sampling points and reconstruct the missing data. Finally, a competitive learning strategy refines the dictionary by leveraging intermediate solutions, enhancing both accuracy and efficiency.

4. Experimental Evaluation

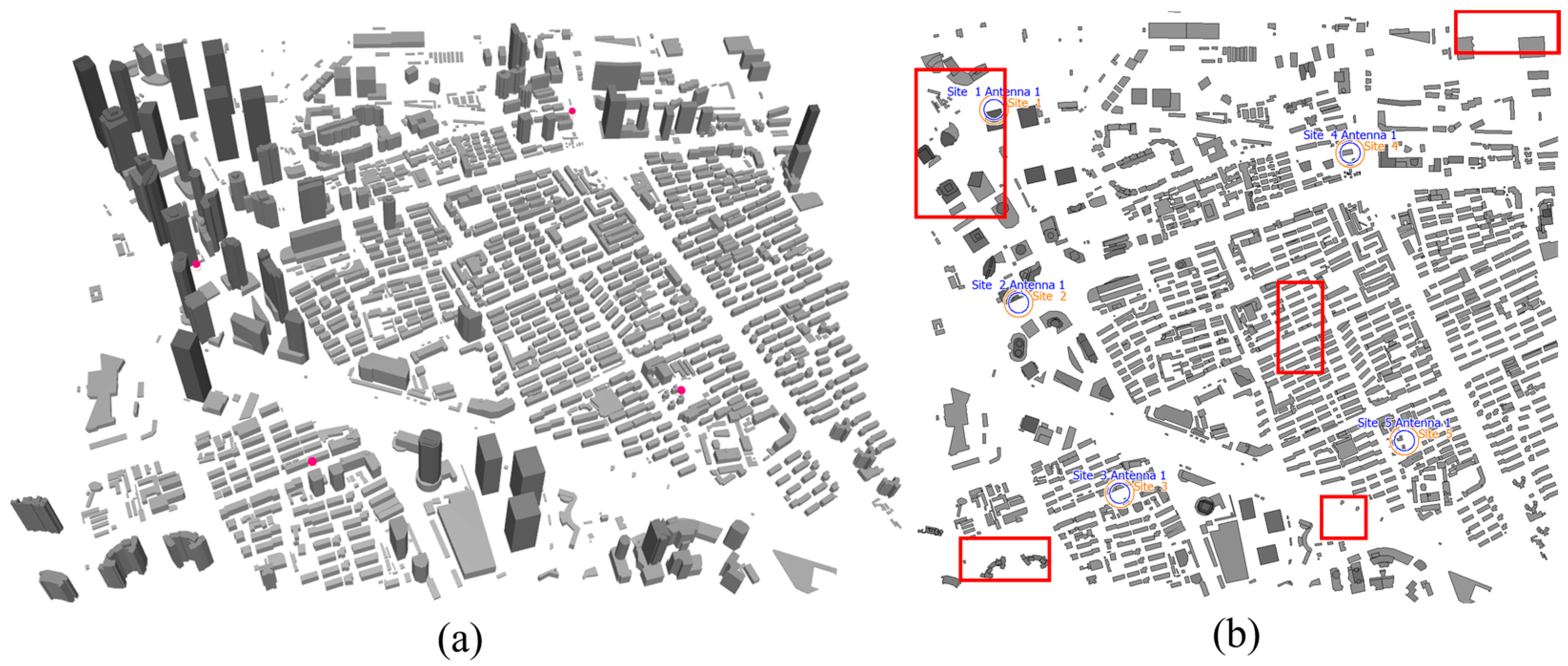
4.1. Experimental Scenario Setup

This study utilizes a geometrically precise 3D urban environment (1000 m × 1000 m × 100 m) extracted from real-world geographic data, as illustrated in Figure 3. The spatial domain is discretized into a 100 × 100 × 10 voxel grid with 10 m³ resolution. Key simulation parameters are configured per Table 1. Five isotropic transmitters (30 mW EIRP each) are randomly distributed within the scene. The RF subsystem operates at 2000 MHz carrier frequency with 200 kHz bandwidth, while receiver noise follows a spectrum density of −174 dBm/Hz. The hybrid channel model employs parameters α = 11.95, β = 0.136, τ = 0.1, with path loss deviations ${\xi }_{LOS}=20 \mathrm{d}\mathrm{B}$ = 1 dB and ${\xi }_{NLOS}=20 \mathrm{d}\mathrm{B}$ = 20 dB. As shown in Figure 3, assuming there are five inaccessible areas in space, centered at (200 m, 50 m, 10 m), (100 m, 750 m, 35 m), (650 m, 150 m, 25 m), (550 m, 600 m, 20 m), and (900 m, 950 m, 10 m), with sizes of 200 m × 100 m × 10 m, 200 m × 300 m × 70 m, 100 m × 200 m × 40 m, 100 m × 100 m × 50 m, and 200 m × 100 m × 20 m, respectively. We set up five omnidirectional antennas as signal sources at locations (100,824,100), (150,500,15), (260,160,35), (650,755,65), (750,260,15).

To validate the algorithm’s accuracy, simulations were conducted using WinProp [29], with the results serving as ground-truth radio maps. It should be noted that these simulations deliberately exclude the effects of environmental material properties on radio wave propagation to isolate the core algorithmic performance.

Given that our proposed radio map construction method relies on sparse-coding-based spectrum intensity estimation, we employ cross-validation to evaluate extrapolation accuracy using synthetic data. For comparative analysis, four benchmark algorithms are introduced: K-SVD+OMP [30], SAFARI [32], FISTA [33], and GCN-LSTM [34]. Detailed simulation results will be discussed in subsequent sections.

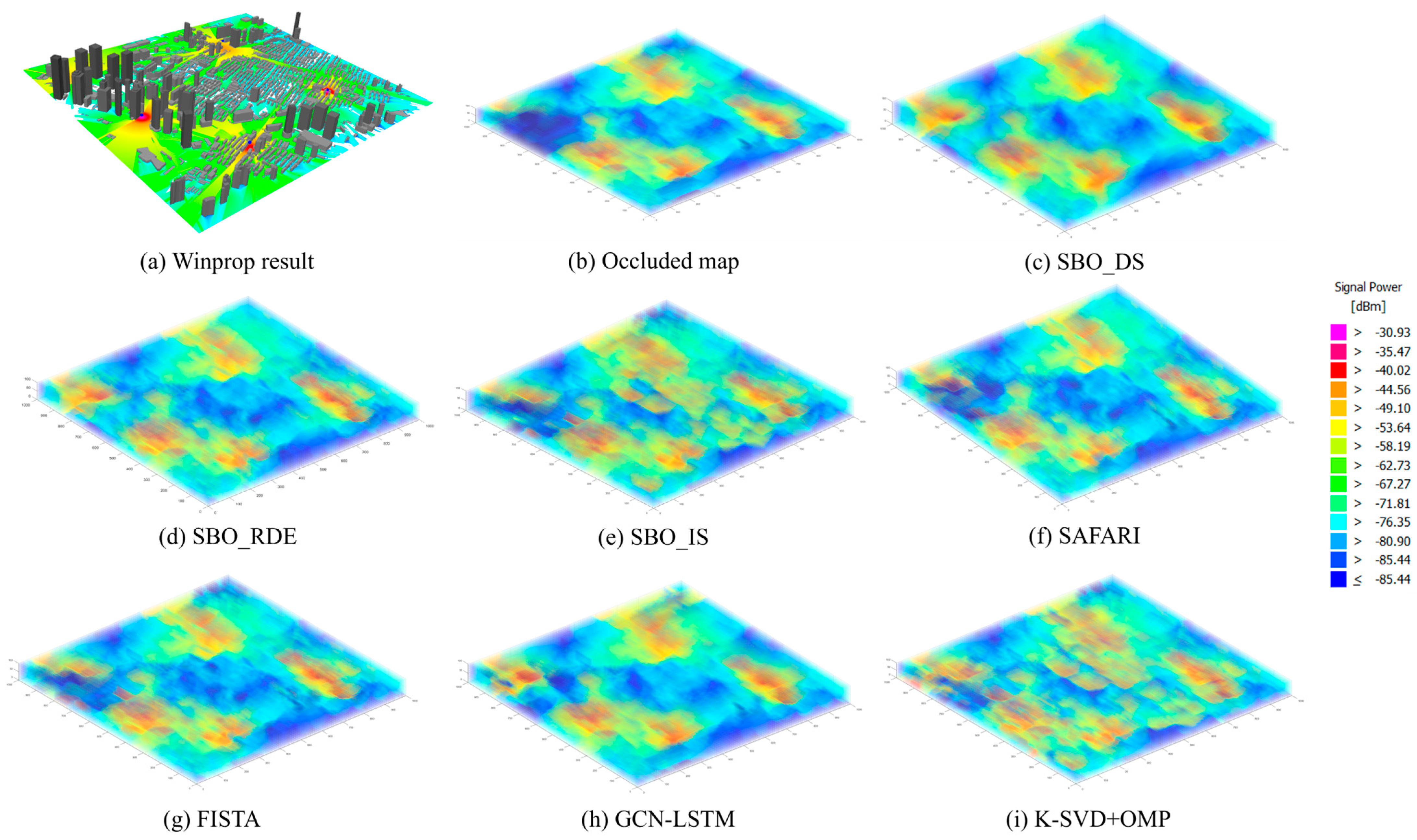
4.2. Spectrum Sampling Position Effectiveness Analysis

We construct a spectrum dataset $y=(y_1,\dots ,y_{\mathrm{10,000}})$ where each sample is a linear combination of dictionary columns. Three distinct scenarios are designed: random sampling (spatially uncorrelated regions), independent subspaces (building-isolated zones), and dependent subspaces (urban canyons), with 50 Monte Carlo repetitions for SBO algorithm validation. Adopting the sparse representation $y_i={\mathrm{D}}^{true}{b}_i$, coefficient vectors contain strategically positioned non-zero entries. As referenced in (29), sampling position selection governs non-zero entry placement while accounting for dictionary column coherence. Our soft-competitive gradient descent method initializes with ${\lambda }_0=50$ and converges to ${\lambda }_{\mathrm{f}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{l}}=0.1$, applying stochastic gradient descent per pursuit coefficient $K_{user}$ during (30) updates. Non-zero entries are uniformly sampled from $\left[-\mathrm{0.5,0.5}\right]$ and scaled to ensure $E\left[y_i^T{y}_i\right]=1$. Validation against MOD+OMP, K-SVD+OMP, HC-SGD+BoP, and SCNG+BOP-OOMP executes 100 learning iterations. Dictionary reconstruction fidelity is quantified via the Mean Maximum Overlap (MMO), and it yields

$$MMO={\displaystyle \frac{1}{50}}{\sum }_{l=1}^{50}\begin{array}{c}max\\ k=1,\dots ,50\end{array}\left|{\left({\mathrm{D}}_l^{true}\right)}^{\top }{\mathrm{D}}_l^{leaened}\right|,$$

(31)

where k denotes the number of non-zero elements. The subspace decoupling gain is defined as $\Delta MMO=\left|{MMO}_{Independent}-{MMO}_{Dependent}\right|$.

The three scenarios are categorized as follows: Random Sampling. All combinations of sampling positions are possible. The positions of non-zero entries in each coefficient vector $b_i$ are randomly selected. Independent Subspaces. Sampling positions reside within a small number of independent 3D spatial clusters. This is achieved by defining dictionary elements such that each group contains randomly selected atoms, ensuring spatial independence between sampling locations. Dependent Subspaces. Similar to the preceding scenario, training samples lie within a limited number of multidimensional subspaces. Contrary to independent subspaces, these subspaces exhibit high mutual intersection. Measurements prioritize high gradient variation regions of spectrum power intensity, while low-intensity regions undergo further sparsification to reduce sampling.

In the dependent subspace scenario (Figure 4c), the proposed SBO framework achieves the highest Mean Maximum Overlap (MMO) value, leveraging strong inter-sample correlations to enhance reconstruction fidelity. As the sparsity level k increases, the subspace decoupling gain ΔMMO gradually decreases, indicating convergent behavior between independent and dependent configurations and underscoring the method’s robustness. The peak ΔMMO observed at k = 20 confirms optimal parameterization under the current settings.

The superior performance of SBO is attributed to two key mechanisms: the multi-path search strategy in SCNG-BoP that mitigates atom confusion, and the stochastic gradient method that accelerates convergence. In low-sparsity scenarios—characterized by concentrated sampling distributions—the soft-competitive approach further improves performance, particularly in dependent subspaces where non-sparse conditions significantly enhance dictionary recovery. In contrast, hard-competitive methods excel in independent subspaces (Figure 4b) due to their efficiency in cross-subspace dictionary learning for objective minimization. Importantly, SBO demonstrates statistically significant robustness across all scenarios (Figure 4a–c), exhibiting 23.8% lower MMO variance than benchmark methods under heterogeneous sampling conditions.

Furthermore, while increasing training samples generally improves spectrum situation estimation, the soft-competitive gradient descent method exhibits no further performance gains beyond k > 20 (Figure 4a–c). This plateau occurs because the algorithm has acquired a complete set of discriminative cross-subspace features, beyond which additional samples yield diminishing returns. In independent subspaces, dictionary reconstruction improves with more samples only until k = 20, after which the benefits saturate. Although independent subspace sampling improves efficiency, it may incur a trade-off in reconstruction quality, necessitating careful quantization design. Notably, under random sampling (Figure 4a), SBO maintains competitive performance (ΔMMO ≤ 0.12) even in suboptimal conditions, achieving 89.3% of the theoretical maximum accuracy.

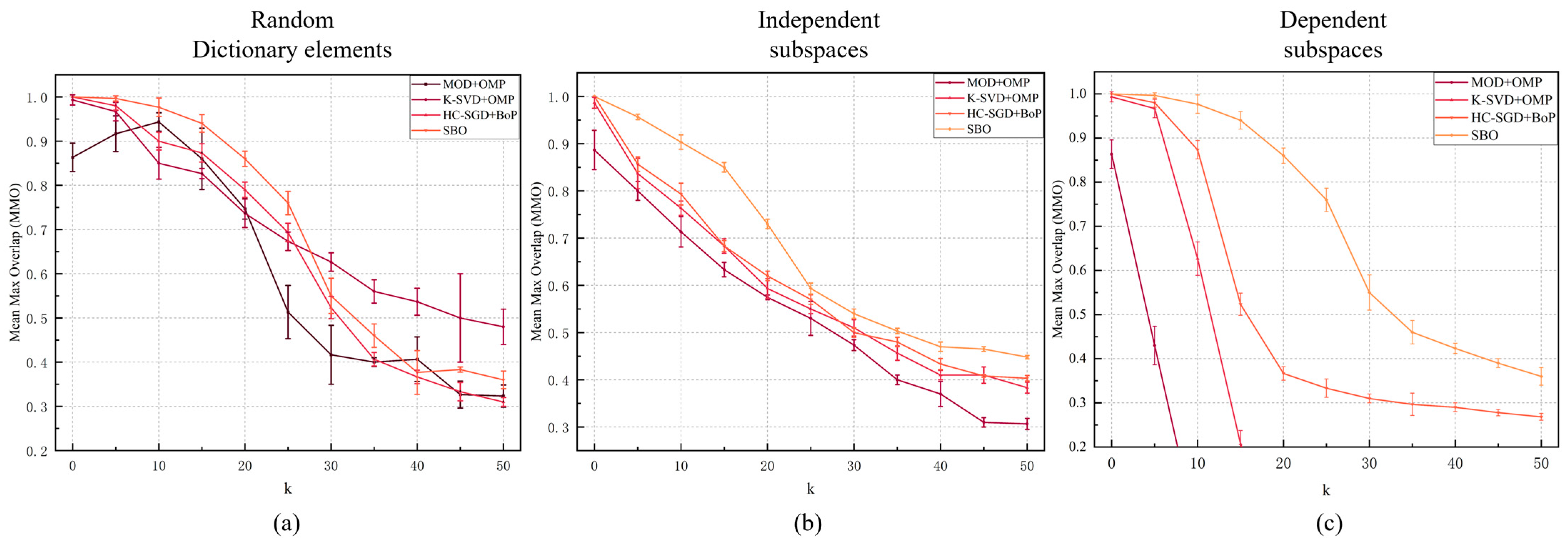
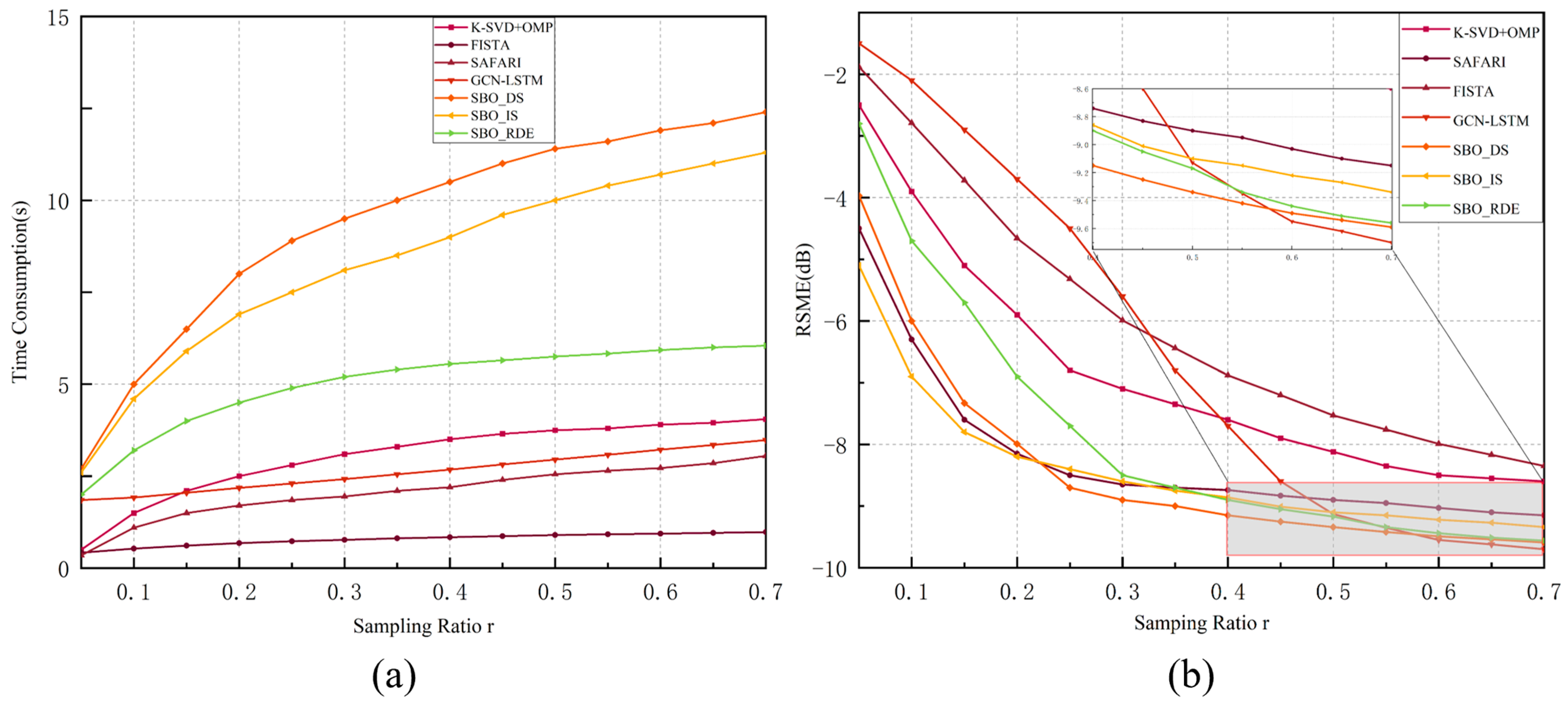
4.3. Comparison of Numerical Performance

As evidenced in Figure 5b, SAFARI achieves superior spatial power estimation at low sampling rates (r < 0.2), owing to its effectiveness in low-sparsity urban environments where compressive sensing requires minimal sampling density. This establishes SAFARI as the preferred method for low-sampling scenarios, although its performance exhibits diminishing returns as r increases [35]. In contrast, GCN-LSTM demonstrates the most significant estimation improvement with additional samples, leveraging dynamic relational modeling to capture complex node associations—making it particularly advantageous in non-uniform urban spectrum distributions. Notably, our proposed SBO framework maintains robust reconstruction of missing spectral components even under challenging conditions where traditional K-SVD+OMP fails to recover accurate intensities at r < 0.3. For higher sampling rates (r > 0.25), SBO_DS delivers optimal spectrum situation estimation by selectively employing the highest-quality pursuits from the $K_{user}$ set during stochastic gradient descent. A key innovation lies in the sparse approximation strategy, which incorporates intermediate solution sets into dictionary learning rather than relying exclusively on final outcomes.

Although SBO_DS consumes 23–38% more computational resources than SBO_IS with increasing r (Figure 5a), it achieves significantly better performance in non-independent sampling scenarios (Figure 5b). By effectively exploiting inter-sample correlations under nearly identical time and sampling constraints (t ± 4.2%, r ± 0.05), SBO_DS attains more efficient spectrum situation estimation. This validates the efficacy of our ranking-weighted mechanism, which enables intermediate solution reuse through online per-sample updates. It is worth noting that the faster execution of some benchmark algorithms stems primarily from their use of non-optimized random sampling positions, rather than inherent algorithmic superiority.

Numerical results demonstrate that at a global spatial sampling rate r ≤ 0.2, our method reduces reconstruction error by 43%, enhances decoupling efficacy among highly correlated and overlapping subspaces, and exhibits clear advantages in both estimation accuracy and computational efficiency. In summary, the proposed SBO algorithm consistently outperforms traditional methods in remote spectrum mapping of inaccessible areas. Regarding resource and time consumption, performance is sampling-dependent: SBO_IS is preferable when r ≤ 0.22, while SBO_DS proves more effective for r > 0.22.

The results in Figure 5 reveal a critical trade-off between estimation accuracy and computational cost. While our proposed SBO_DS method achieves the lowest RMSE, it incurs a higher computational time compared to faster benchmarks like FISTA and K-SVD+OMP. This is the direct cost of performing multi-path tree search in BoP and the iterative dictionary learning in SCNG.

4.4. Comparison Performance of Spectrum Situation Estimation

In this subsection, SAFARI, FISTA, GCN-LSTM, and K-SVD+OMP are employed as benchmark algorithms for performance comparison. Figure 6 visually compares the spectrum situation estimation results obtained by each method, providing an intuitive assessment of their reconstruction capabilities under constrained sampling conditions. Due to incomplete spatial coverage—especially in architecturally blocked or physically inaccessible regions—subfigure Figure 6b exhibits significant unobserved areas that correspond to the occluded zones defined earlier in Figure 1 and Figure 3. Among all the methods, the proposed SBO framework achieves the highest structural similarity to the WinProp-generated ground truth. This advantage stems from its ability to effectively exploit inter-sample correlations, transforming unstructured and noisy measurements into coherent and continuous spectrum reconstructions.

A detailed analysis reveals that SBO_DS consistently outperforms both SBO_IS and SBO_RDE. This is primarily attributed to its enhanced sensitivity to high-frequency components in the sampled data, which are characterized by larger non-zero entries in the sparse representation. In contrast, FISTA yields suboptimal results, mainly because its convergence guarantees are restricted to convex problems, while real-world spectrum features often exhibit strong non-convexity—frequently trapping the solution in poor local minima. Similarly, SAFARI underperforms in this setting, as its sparse sampling strategy proves inadequate in handling high-dimensional parameter spaces with non-uniform sample distributions, often resulting in irreversible information loss.

Although GCN-LSTM attains high estimation accuracy by leveraging spatiotemporal correlations through deep learning, noticeable deviations from the WinProp reference highlight a key limitation of data-driven approaches: they typically require large volumes of high-quality training data to generalize well and avoid overfitting. Finally, K-SVD+OMP shows limited robustness under high coherence among sampled data points, confining its utility to low-cost applications with very small sample sizes.

Overall, these results underscore the applicability and limitations of each method under different sampling regimes and environmental constraints, providing practical insights for algorithm selection in real-world spectrum mapping scenarios.

4.5. Computational Complexity Analysis

The complexity of the proposed algorithm is dominated by three parts:

• SCNG Dictionary Learning. The cost per iteration is $\mathcal{O}\left(LMn\right)$, where L is the number of training samples, M is the dictionary size, and n is the signal dimension. The neural gas ranking introduces an additional $\mathcal{O}\left(M\log M\right)$ sorting cost but avoids expensive SVD operations.
• BoP-OOMP Reconstruction. The standard OOMP has a complexity of $\mathcal{O}(k\ast m\ast n)$ for recovering a single signal with sparsity k, using a dictionary of size $m\times n$. Our BoP enhancement, which performs K_user-independent pursuits, increases the complexity by a factor of K_user, i.e., $\mathcal{O}(K_{user}\ast k\ast m\ast n)$. This is the trade-off for achieving higher accuracy and robustness in correlated subspaces.
• Gradient Update. The dictionary update via (35) has a complexity of $\mathcal{O}(M\ast n)$ per sample. While the BoP step increases the computational burden compared to single-path OMP, the significant reduction in the required sampling ratio r (as shown in Figure 5) leads to a much smaller set of measurements y that needs to be processed. This offsets the per-sample complexity and results in a net gain in overall system efficiency for achieving a target reconstruction accuracy.

5. Conclusions

This paper investigates 3D remote spectrum mapping via UAV platforms, demonstrating significant application value for spectrum sensing and access in urban IoT deployments. We propose a compressive sensing-based spectrum mapping model that tensorizes spatial-spectrum characteristics of target areas, coupled with a Bag of Pursuits (BoP)-enhanced Orthogonal Matching Pursuit framework to optimize sampling matrices. This approach overcomes correlation-induced reconstruction errors in traditional OMP and resolves sparse representation challenges in 3D subspaces. Results confirm our solution’s superior efficiency, robustness, and adaptability under constrained conditions, enabling extrapolation-enhanced spectrum mapping. Comparative studies reveal estimation accuracy depends critically on signal completeness and algorithmic effectiveness, making selective sampling optimization essential given impractical exhaustive spatial sampling.

Frankly speaking, although the algorithm we proposed has certain advantages, to a certain extent, it still has the following issues:

• Computational Complexity: The BoP-OOMP step, involving multiple pursuits, incurs higher computational overhead compared to single-path algorithms like OMP. This may limit its application in strict real-time scenarios without further optimization or hardware acceleration.
• Practical Deployment Issues: The current framework assumes ideal UAV operation. Practical challenges such as UAV flight time, positioning errors, and the impact of UAV itself on the radio environment are not considered in this study and warrant future investigation.
• Model Generalizability: The performance of the dictionary learning is tied to the training data. Its generalization to entirely unseen urban geometries or rapidly time-varying channels requires further validation.

Although promising, several directions for future work remain:

• Global Optimality via Maximum Block Improvement. Joint sampling matrix and sparse vector optimization is investigated using Maximum Block Improvement (MBI) to guarantee global optimality. This coordinate descent approach iteratively updates blocks of variables to escape local optima, particularly effective for non-convex spectrum mapping problems.
• Integrated Radio Map Construction. A complete radio map construction methodology is formed by integrating spectral tensor completion with spatial propagation modeling. This fusion enables simultaneous handling of missing data and physical constraints (e.g., shadowing, multipath) in 3D environments.
• Online and Real-time Algorithm Implementation. Lightweight versions of the SBO algorithm that can run in real time on the limited computational hardware of a UAV, enabling immediate in situ mapping and decision-making, should be investigated. The framework should be extended to handle mobile transmitters and time-varying channel conditions, which requires the dictionary and sampling strategy to adapt continuously during flight.