Methods for Predicting the Repair Stack in an Electronics Module Manufacturing Company

Abstract

This article addresses the problem of predicting the workload of the repair department in a company manufacturing electronic modules. The number of modules needing repair is called a repair stack. A deterministic algorithm and a machine learning-based algorithm are proposed to predict the repair stack for subsequent weeks based on historical data, current yield data, and planned production. These methods allow for estimation of the repair stack and appropriate selection of repair department staff to ensure the ongoing repair of defective products. The proposed algorithms are described and the results of their practical verification based on historical data from a large enterprise are presented. The practical utility of both algorithms is demonstrated and the impact of selected factors on their accuracy is analyzed. It is shown that using the proposed algorithms, it is possible to predict the repair stack for the coming week with a relative error not exceeding a few percentages on the basis of historical data from the previous 8 weeks. These algorithms were successfully implemented in industrial practice.

1. Introduction

During the production of electronic modules, a number of technological operations are performed, such as applying solder paste, placing components on a printed circuit board, soldering, attaching peripherals, etc. [1,2,3,4]. Electronic module assembly may also require the use of mixed-mode assembly, through-hole technology (THT), or surface-mount devices (SMDs), which further complicates the process [5,6]. Each of these operations can be performed unsatisfactorily or with a defective component, which can result in incorrect operation of the completed module. Therefore, after each important stage of the assembly process, tests are conducted to confirm the correct operation of the assembled modules. If the assembled module passes the test, it is moved on to the next stages of the production process. Otherwise, corrective actions are taken [7,8].

During production, many requirements have to be met, e.g., [8,9,10,11,12,13,14]:

• Ensuring the high quality of the production process and control of material flow;
• Meeting a number of quality standards;
• Meeting the constraints of customers, who often place additional requirements and expectations on manufactured products.

Depending on factors such as the complexity of the technological process, the density of component packing on the PCB, and experience in manufacturing a given module, different values of parameters characterizing production efficiency are obtained [15,16,17,18]. Therefore, depending on the production volume, the number of modules requiring repair at individual stages of the production process varies. Because damaged modules are not always repaired promptly, the repair department maintains a number of modules awaiting repair. This number is called the repair stack. Due to the fact that one person can repair a fixed number of modules in one working day, it is important to select an appropriately large and experienced staff in the repair department [7,19].

This issue is not trivial, as in production practice, the range of modules produced often changes, and each module has a different production yield. In industrial practice, not only does the number of products produced change from week to week, but their type does too. Production results are linked to the production plans created based on customer orders. Despite long-term forecasts of demand for specific products, in reality, the data containing the actual production plan is updated weekly. This means that actual production deviates significantly from what was initially assumed. The situation requires flexibility in preparing to store the appropriate amount of material for manufacturing products. The same applies to having human resources ready for production according to initial assumptions. Any changes in the production forecast are significant costs for a company producing electronic modules. The relatively low predictability of production over the long term impacts the repair stack and the resources necessary to reduce it.

It is important to predict the number of modules of each type that will require repair in each week. A proper balance should be maintained to avoid a backlog of modules requiring repair, meaning that the same number of modules should be delivered to the repair department and released after the fault has been rectified. Otherwise, the accumulation of damaged devices will result in them being considered material waste. The same may occur with aging products, which pose a high risk of material waste (TML) [19].

To date, no risk forecast has been defined for electronic modules undergoing repair that do not conform to production process requirements. Forecasts should be prepared in advance to prepare for upcoming products for repair and minimize material losses [20]. Therefore, the goal of the research presented in this paper is to estimate the quantity and value of products delivered for repair in the coming weeks, based on the known forecast, production yield, and the efficiency and effectiveness of repairs.

Many industries use methods to predict the effects of different production processes. For example, ref. [21] describes a method for predicting the effects of a production process in the food industry and the impact of process parameters on its efficiency and product quality using artificial intelligence (AI). The authors of [22] describe the results of research on the use of AI to optimize the fault diagnostics process in semiconductor devices. It is shown that the integration of machine learning, deep learning, and pattern recognition allows for optimization of process parameters and product quality. In [23], an in-depth and machine learning-based photovoltaic power forecasting methodology was proposed, using different machine learning methods. The paper [24] presents the results of research on modeling and simulation of the impact of four economic indicators (industrial production, internal R&D expenditure, sales turnover and volume, and employment) on the evolution of the European Economic Sentiment Index. Artificial intelligence methods were used in this research. In [25], a method for predicting the near-field magnetic shielding effectiveness (NSE) of ferrite sheets was proposed. Eight regression models were extracted using regression analysis in Minitab 20 software, using data from the measurement of NSE and relative permittivity of ferrite sheets.

The aim of this article is to develop and test a mathematical model and its variants for the best possible estimation of the repair stack in the coming weeks of production. This solution will address the need for increased control over the costs of storing out-of-specification products and improve the effectiveness of reducing their number. This will also indirectly enable estimation of the human resources required for this purpose. Two types of models were formulated, hereinafter referred to as the deterministic model and the AI model.

The properties of the models regarding their efficiency and effectiveness in predicting the repair stack for the following weeks were checked using statistical methods based on a set of tools existing for this type of task in the Minitab application described, among others, in [26,27]. Data on repair results will be analyzed based on the results obtained from Six Sigma statistical analyses [28,29,30].

Due to the lack of an existing model to compare the results with, a methodology was used, comprising the phases of identification, design, optimization, and validation (IDOV). This is one of the popular methods for designing products, processes, and services to meet Six Sigma standards [17,31]. Unlike the DMAIC method described in [26], it is used when a new product or process is being created. Both methods are similar. In IDOV, the measurement and analysis phases are included in the design phase. Similarly, the improvement and control phases are part of the optimization and verification of a new design or process being created (optimize, validate).

The rest of this paper is organized as follows: Section 2 describes the deterministic prediction algorithm. Section 3 presents test results for the basic version of this algorithm. Section 4 analyzes the impact of selected modifications to the basic algorithm on the prediction accuracy of the repair stack. Section 5 describes the statistical properties of the deterministic algorithm. Section 6 describes the developed AI algorithm incorporating machine learning (ML) elements and analyzes the results obtained using it.

2. Deterministic Prediction Algorithm

A model for forecasting the number of modules scheduled for repair in the next month was developed, using data from the last four weeks, with a weekly checkpoint. For this model, a data package from the last four weeks of production is created weekly. A preliminary version of this model is described in [32]. The following assumptions were made in the model’s formulation:

• Production completed in the last 4 weeks is taken into account to determine the repair stack expected in the next 4 weeks;
• All indicators required to predict the repair stack are calculated based on 4 weeks of historical data and updated weekly;
• Data characterizing the production quality and the number of modules produced over the last 4 full weeks are taken into account for each test station and for each product produced;
• Repairability is calculated as the reduction in the number of modules requiring repair compared to all modules delivered for repair in the past 4 weeks;
• Repair stack prediction coefficients are calculated only for products whose expected production within 4 weeks will exceed 50 pieces;
• The number of products in the existing repair stack that have not been produced in the last 4 weeks but have been repaired influences the new repair stack in line with the repair progress trend;
• The expected maximum difference between the actual and predicted values of the repair stack should not be greater than 10% for more than 30 pieces in the repair stack or by ±3 pieces when the stack does not exceed 30 pieces.

Before analyzing the number of products in the repair stack, it is necessary to determine the values of parameters describing the boundary conditions and production conditions based on historical data. These parameters include the following:

• FPY (first pass yield)—yield equal to the number of good products divided by the number of all products produced;
• K—a coefficient defining the rate of reduction in the repair stack, most often expressed as the quotient of the number of repaired products to the number of products that were added to the repair stack in the analyzed period of time;
• N_rs (new repair stack)—expected number of products in the repair stack;
• C_rs (current repair stack)—current number of products in the repair stack;
• E_in (estimated in)—expected number of products that will be added to the repair stack;
• E_out (estimated out)—expected number of products that will be repaired;
• Max_v (max value)—the largest number of the same products that were checked at one of the test stations in a given period of time and at the same time indicates the true number of products produced;
• F_cp (factor core predictor)—weight factor for predicting the number of products in the repair stack;
• Test_qty (tested quantity)—number of products tested at a given test station;
• D (demand)—number of products expected to be produced;
• Sum_In—the total number of products delivered for repairs;
• Sum_Out—total number of products that have been repaired.

The main equation describing the deterministic model for estimating the number of products in the repair stack in the upcoming 4 weeks of production is [32]

$$N_{rs}=C_{rs}+e_{in}-e_{out}$$

(1)

One of the most important parameters of the model is the number of products produced each week. For the purposes of the predictive model, the number of products of a given type produced in a given 4-week period is designated as max_v. To determine the value of this parameter, it is necessary to know the number of individual products produced in a given week and their production process. This allows for the establishment of individual testing stations used to validate the quality of manufactured products.

In other words, if all test stations for a given product and the number of products tested at those stations are known, the max_v value can be determined. Knowing the value of this indicator and the total number of products produced, the f_cp weighting factor can also be determined. This factor is necessary for predicting the repair stack and allows us to estimate what proportion of manufactured products will be subject to validation at individual stations. This is because, depending on the production process, all products of the same type are validated at a specific test station, while sometimes only a subset are checked.

In the presented model, the weighting factor f_cp is defined by the formula

$$f_{cp}={\displaystyle \frac{tes{t}_{qty}}{{\max }_V}}$$

(2)

For individual test stations through which finished products pass, the value of the f_cp parameter ranges from 0 to 1.

The product production process is based on the execution of successive production stages, which are predetermined. These are expected to be performed based on the most accurate forecasts and production orders (demand). When such a production order is issued, it is known at which test stations the manufactured product will be checked for production quality and meeting expectations. The only thing that can change is the newly planned quantities of products to be manufactured in the coming weeks. Knowing that newly planned production often takes into account different quantities of ordered products (demand) than the analyzed historical data, and after previously determining the f_cp value along with the current FPY for the analyzed period, the value of the e_in parameter can be estimated using the following formula:

$$e_{in}=D\cdot f_{cp}\cdot \left(1-FPY\right)$$

(3)

Equation (3) combines all the above-mentioned indicators, i.e., the f_cp factor, the demand D, and the FPY yield. With the e_in parameter thus defined, it is possible to predict in advance how many products can be added to the new repair stack N_rs that will be created during the planned production. One of the limitations of the accuracy of determining the e_in value is the narrow production period, the results of which are used to determine the f_cp value.

A special case is e_in = 0, which means that no product was damaged and this state is expected to be maintained in future production. Furthermore, when e_in = 0, changes in the predicted repair stack will depend only on whether a repair stack currently exists for that product and if any successful repairs are being performed. Therefore, if such a stack does not currently exist, it is predicted that a new repair stack will still not appear, since the yield so far is FPY = 1. However, if a repair stack exists and we have several products waiting for repair, two situations can occur depending on whether such products are repaired or not:

• When the product repair stack is not reduced, the value of the current repair stack is transferred to the projected repair stack at an unchanged number.
• When the repair stack for a given product is non-zero and there have been repair results in the historically examined time period, then the repair rate will be determined using the factor k and a value of the parameter marked as e_out will appear, describing how quickly the current repair stack will be reduced.

From the properties of the e_in and e_out parameters described above, it is easy to see that these are parameters of the predictive model that indicate how the predicted repair stack will change. They do not indicate its final value, but rather the range of changes in these values, which will be used to analyze the repair stack trend over the next four weeks.

It can be concluded that the model being developed for predicting the repair stack utilizes the parameters related to production results analyzed so far. These parameters allow us to determine how many subsequent products will appear in the repair stack, which allows us to estimate its final state.

To determine the repair rate, a proportionality factor, k, was introduced, which allows for the assessment of whether the repair stack increased, remained unchanged, or decreased during the analyzed period. During production, defective products are repaired at a specified rate. Each product repair ends with revalidation. This is necessary because its status in the production control system indicates that the product failed the test at a given test station and is non-compliant (Fail status). After repair, the expected change to Pass status is achieved. A production control system containing information about the flow of products through the individual assembly, validation, and repair processes is crucial because the method of monitoring product status allows for the determination of the number of necessary product repairs. This method allows for the identification of the test station from which the test results for individual products after repair originate. Each product that leaves the repair stack after repair can be assigned an Out status. The sum of all Out statuses is the number of repaired products, which reduces the existing repair stack or prevents its expansion.

The coefficient k is defined by the following formula [32]:

$$k=\left\{\begin{array}{ll}{\displaystyle \frac{su{m}_{Out}}{su{m}_{In}}}& if su{m}_{In}>0 i su{m}_{Out}\ge 0\hfill \\ su{m}_{Out}& if su{m}_{In}=0 i su{m}_{Out}>0\hfill \\ 1& if su{m}_{In}=0 i su{m}_{Out}=0\hfill \end{array}\right.$$

(4)

where sum_Out is the number of all repaired products in the last 4 weeks of production, while sum_In is the number of all products that were added to the repair stack in the analyzed period.

The value of the k coefficient translates into the value of the e_out parameter, which is expressed by the formula [32]:

$$e_{out}=\left\{\begin{array}{ll}k\cdot e_{in}& if k\ge 0 i e_{in}>0\hfill \\ 1& if k=1 i e_{in}=1\hfill \\ {\displaystyle \frac{k}{4}}& if k>0 i e_{in}=0\hfill \end{array}\right.$$

(5)

The e_out value calculated from Equation (5) is rounded down to the nearest integer. From Equation (5) it can be concluded that the e_out parameter can take the value 0 in two cases, when the coefficient k = 0 or when the production process is perfect (sum_In = 0, k > 0), i.e., the FPY = 1. Additionally, for a zero repair stack, e_in = 0 is also obtained.

However, it is important to remember that a current shortage of products flowing into the repair department does not affect the repairs currently being performed in the existing repair stack (sum_In = 0 does not mean sum_Out = 0). The number of previously accumulated products in the repair stack can still be reduced even though the module is not currently being produced.

To summarize the information about the k factor, it is determined based on collected historical data on the number of products added to the repair stack and the number of products that were repaired. The value of the N_rs parameter is primarily influenced by the e_in and e_out values associated with parameter k in Equation (5). These predicted changes in the repair stack can lead to a situation in which the predicted e_out value over a 4-week period has a strong upward trend and the rate of reduction in the repair stack is so high that the repair stack is reduced to 0 in the first analyzed week. Therefore, in the following weeks, there will be nothing left to repair, and then N_rs = 0. In this case, despite the prediction of a continuous reduction in the repair stack, the value of the N_rs parameter is 0.

Upcoming production will also include products for which the f_cp parameter cannot be determined. This situation applies to modules that were not produced in the analyzed period (last four weeks) and products that are not in the current repair stack (not on the list on the reporting date) and there is no repair history for these products. Such conditions describe a situation in which there are no values for the appropriate coefficients to determine the f_cp value. Therefore, it is important to specify in the model’s recording rules which components influence the final number of products in the repair stack, which consists of

• Products that are out of date and have been waiting for repair for a long time and products that are currently being repaired;
• At the same time, repairs continue, both for products remaining in the repair stack and those coming in from the production process.

Therefore, the repair stack is in fact constantly changing and it is worth treating it as a picture of the situation on a daily basis, and for the necessary analyses of changes in its trend—on a weekly and monthly basis.

The next step in forecasting results is to check the current production demand, which largely determines which products may appear in the future repair stack. Products to be produced (demand), assigned a value for parameter k according to Equation (4), should be added to the list of modules to be produced. This completes the list of parameters that can be considered the main ones influencing the outcome of the future repair stack. Based on this, we can calculate the portion of the new repair stack that will likely be created in the coming weeks. The considered algorithm was implemented in Excel software. The input data of this algorithm are D, FPY, sum_In, sum_Out, C_rs, test_qty and max_V.

3. Deterministic Model Verification Results

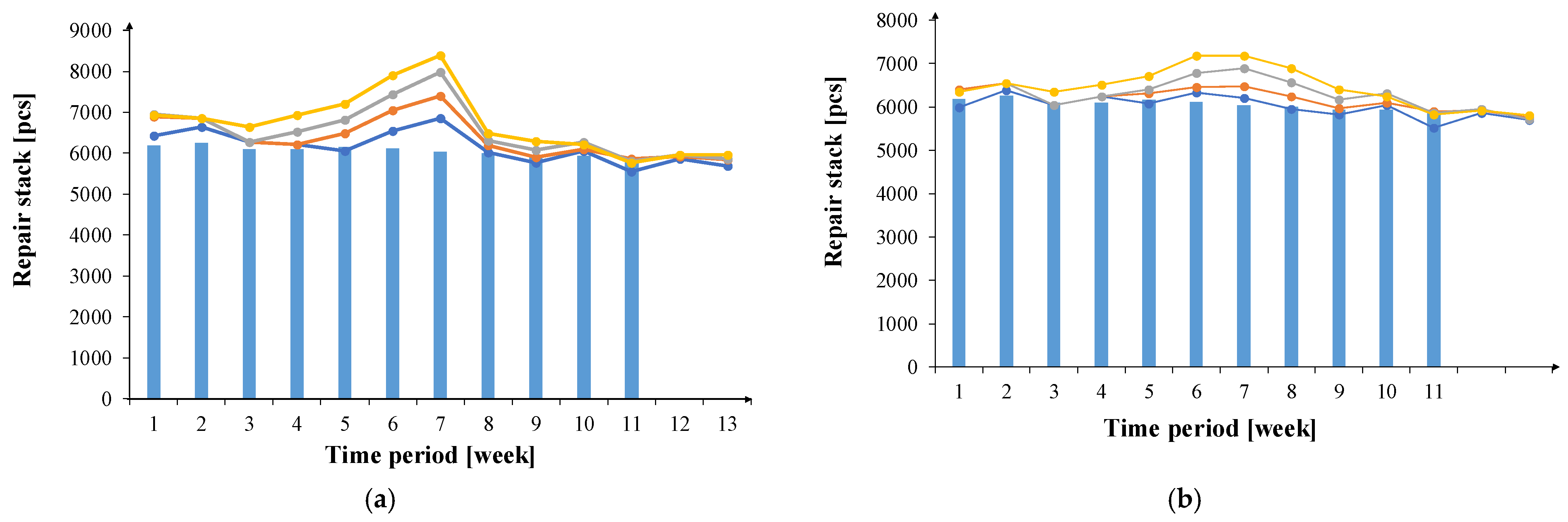
Using the model described in Section 2, the repair stack was predicted based on historical data from 4 and 8 weeks of production. The results are shown in Figure 1. In this figure, the blue bars indicate the actual repair stack values at the beginning of each week, the blue line indicates the forecasted repair stack values 1 week ahead, the orange line indicates 2 weeks ahead, the gray line indicates 3 weeks ahead, and the yellow line indicates 4 weeks ahead.

The quality of the prediction algorithm is characterized by the relative deviation between the predicted and actual values of the repair stack. These deviations are then expressed as a percentage of the actual value of the repair stack.

The prediction results based on a 4-week data set are shown in Figure 1a, and those based on an 8-week set are shown in Figure 1b. It can be observed that the prediction results approach the actual values as the prediction date approaches the date of the actual repair stack reading. In the case of a 4-week prediction, the deviation between the predicted value and the actual value can be as high as 30%, while for a 1-week prediction, this deviation does not exceed 10%.

Figure 1b shows that extending the time period from which historical data is used improves the prediction accuracy. The maximum deviation between the predicted and actual repair stack values does not exceed 20% (for the 4-week prediction), and for the 1-week prediction, the deviation is at most a few percent. This proves the practical usefulness of the presented algorithm.

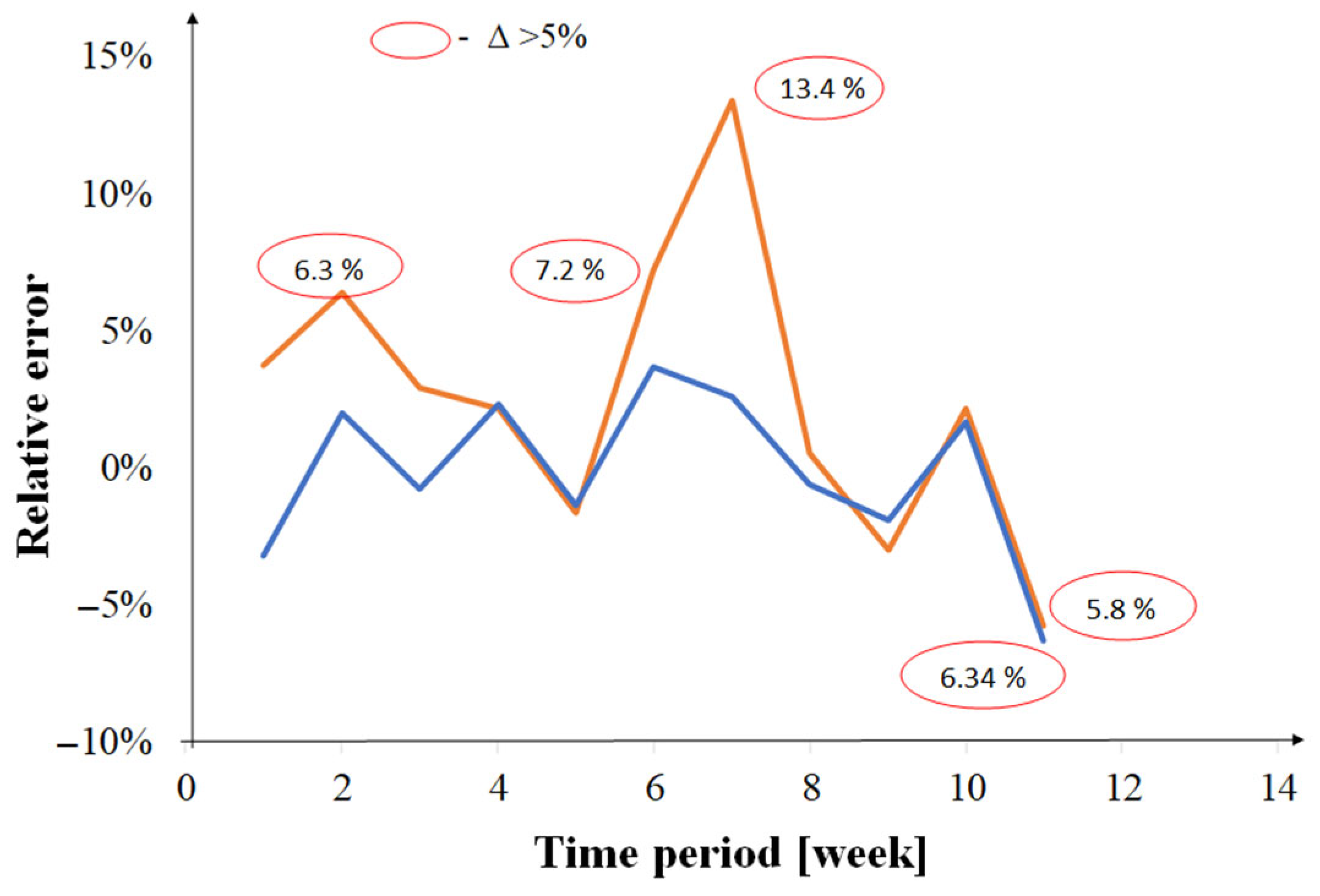
To compare the accuracy of the prediction algorithm using historical data from different periods, Figure 2 compares the relative error of the 1-week repair stack prediction obtained by considering historical data from 8 (blue line) and 4 (orange line) weeks.

As can be seen, in most cases, using a longer time period for predictions allows for a lower prediction error. Using data from the previous four weeks, the error can exceed 13%, while using data from eight weeks, it only reaches 6%. It is worth noting that typical values for the error considered do not exceed 3%. This is a fully acceptable prediction accuracy, allowing for appropriate planning of repair department staffing. Furthermore, the predictive model allows for precise determination of the value of material frozen in the repair stack.

The results of the presented analyses indicate that using data from the last 8 weeks significantly improves the repair stack prediction results compared to predictions using data from the previous 4 weeks. Therefore, an attempt was made to increase the amount of data used to shape the model and use a data package from the last 12 weeks. The performed test showed that increasing the scope of analyzed historical data to the 12 weeks preceding current production did not significantly improve the accuracy of repair stack prediction compared to using data from the 8 weeks preceding the start of production. On the other hand, data relating to the production process changes significantly over the course of 12 weeks. Therefore, they may differ significantly from the parameters from the period immediately preceding the expected production period. Therefore, extending the time range from which the historical data is used does not significantly improve the prediction accuracy. The prediction error using 8 weeks of data is approximately 3%, and using 12 weeks of data, it is approximately 2.9%.

For the results shown in Figure 1, Root Mean Squared Error (RMSE) values were determined and normalized to the mean repair stack value. For the data shown in Figure 1a, the normalized RMSE values obtained were 5.6% for 1-week prediction, 9.7% for 2-week prediction, 13.5% for 3-week prediction, and 17.3% for 4-week prediction. For the data shown in Figure 1b, the normalized RMSE values obtained were 2.8% for 1-week prediction, 3.8% for 2-week prediction, 6.75% for 3-week prediction, and 10.2% for 4-week prediction.

4. The Impact of Modifying the Deterministic Algorithm on the Prediction Accuracy

The repair stack prediction model described by Equations (1)–(5) can be written as a linear regression equation with the general form

$$y=a_1\cdot x_1+a_2\cdot x_2+b$$

(6)

where a₁, a₂, b are the coefficients of the equation. The explanatory data x₁, x₂ were assigned the parameters derived from Equations (1)–(5): x₁ = e_in, x₂ = e_out, and the parameter b is a constant representing the initial value of the repair stack C_rs. The parameter e_in was replaced by Equation (3), and e_out by Equation (5), and the equation was obtained in the following form:

$$y=a_1\cdot D\cdot f_{cp}\cdot \left(1-FPY\right)+a_2\cdot k\cdot D\cdot f_{cp}\cdot \left(1-FPY\right)+b$$

(7)

Data from several months of production were entered into Minitab to calculate the parameters described in Equations (1)–(5), which come from the production system. Equation (7) was then entered into the regression window of the program and the parameter values were determined: a₁ = 0.117, a₂ = −0.118.

The determined values of coefficients a₁ and a₂ have similar absolute values. The number of products flowing into and out of the repair stack does not significantly change the number of products in the repair stack. The initial number of products in this stack has the greatest impact on the prediction result. This is consistent with the real-world situation, where repair process management strives to maintain a balance of products flowing into and out of the repair stack and to ensure that the number of products in this stack is close to 0 [7,19]. Building the repair stack (the surplus e_in over e_out) quickly becomes a source of financial risk and material loss. Therefore, it is important to predict the number of products in the repair stack as accurately as possible to prepare appropriate resources in advance to reduce it. In Equation (7), the demand D and the yield FPY are very important parameters, which strongly influence the number of predicted products for repairs.

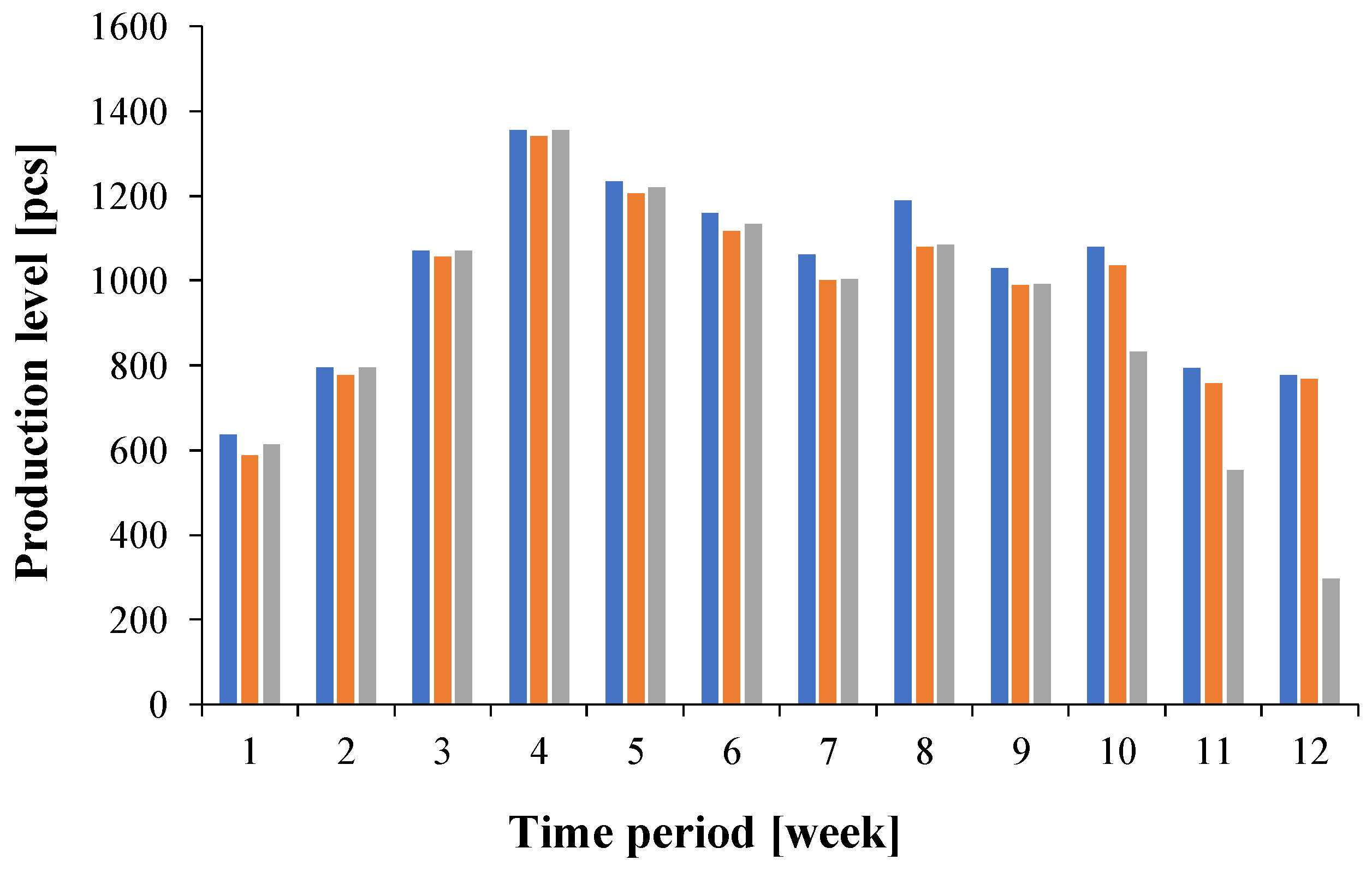
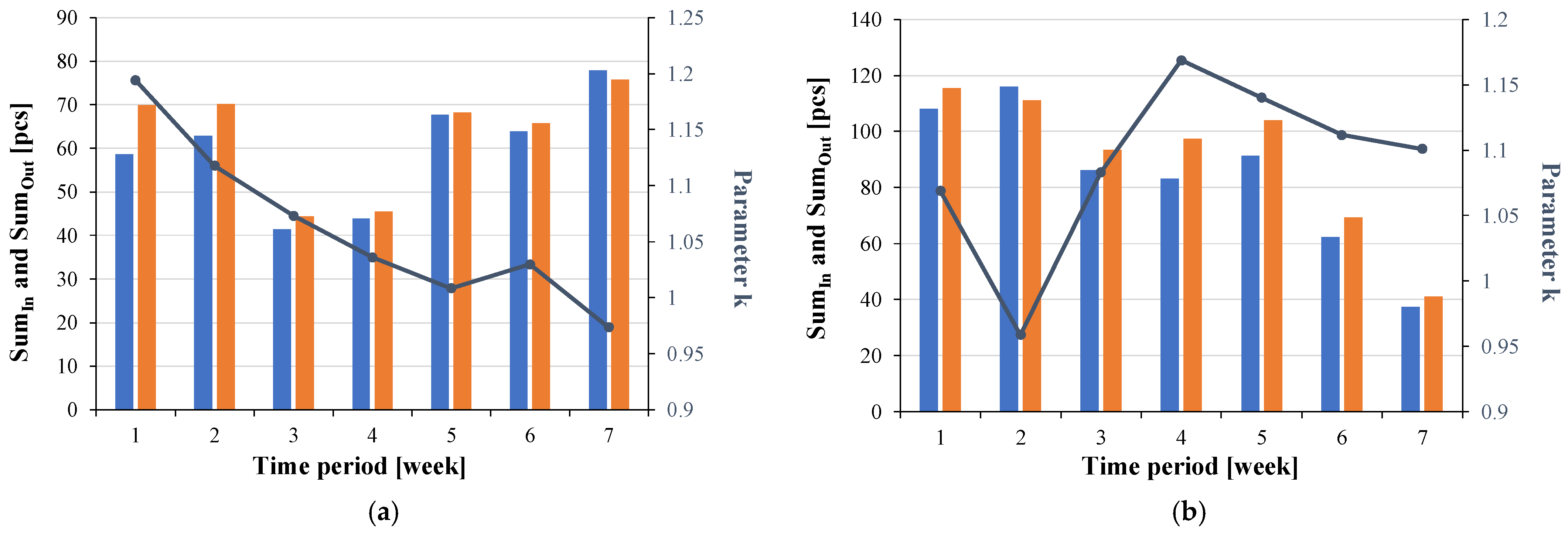
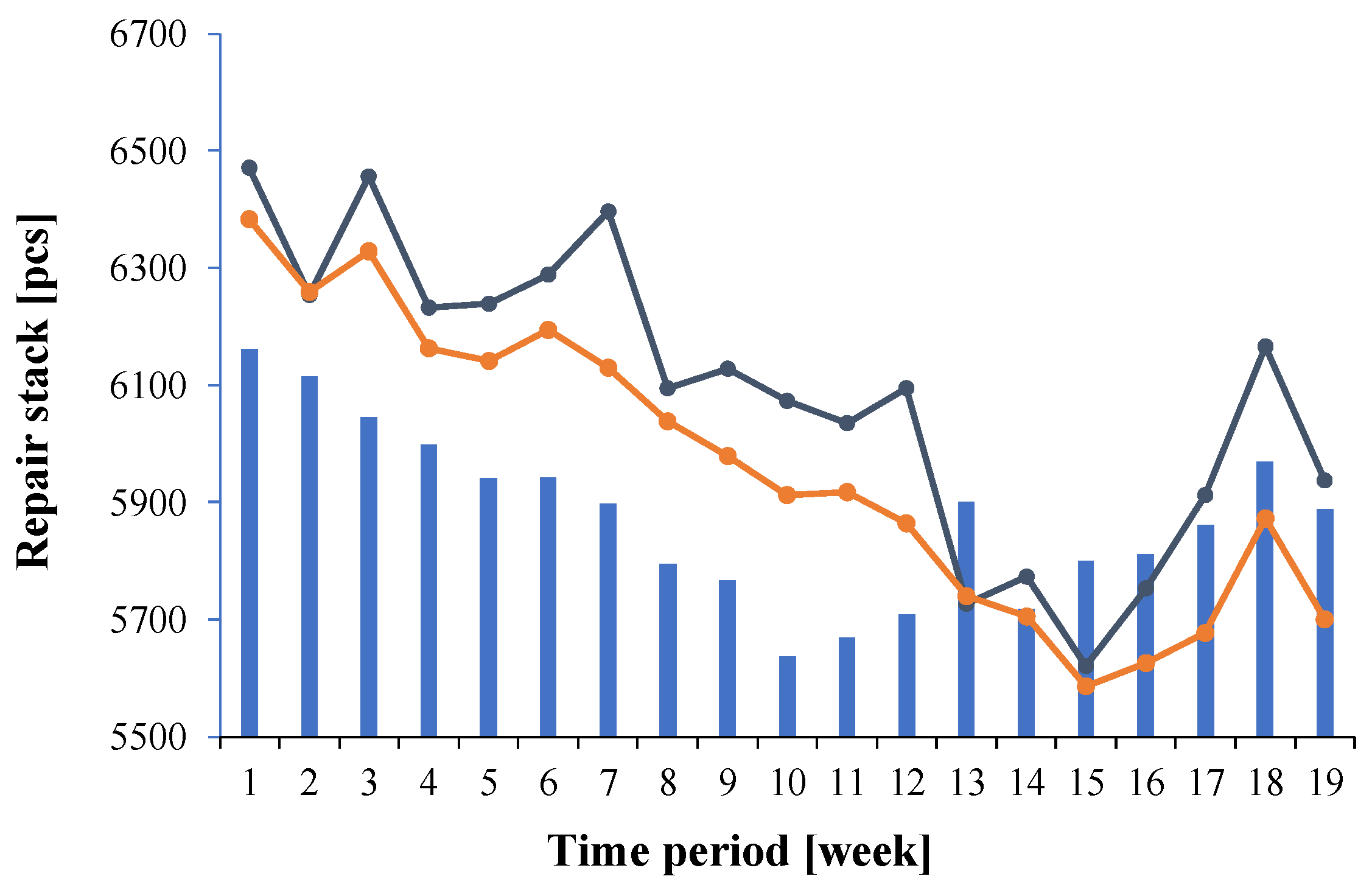
The obtained ANOVA test results, mean value, and standard deviation determined the selection of an 8-week data set for predicting the future repair stack. Using the proposed model (Equations (1)–(5)), sample prediction analyses were performed for the selected product, described by the symbol AA_1. The results are presented in Figure 3. The numbers of products produced in each week that arrived at the warehouse are shown in blue. These results differ slightly from the quantities recorded at individual test stations during the analyzed time period, excluding the last 3 weeks.

You can see that at the opCU_AT station, the number of tested products, represented by the orange bars, is slightly lower than those marked in blue. However, the number of items registered at the oPIM_AT station, represented by the gray bars, has decreased by 20% to 60% over the last three weeks in the period presented compared to those delivered to the warehouse.

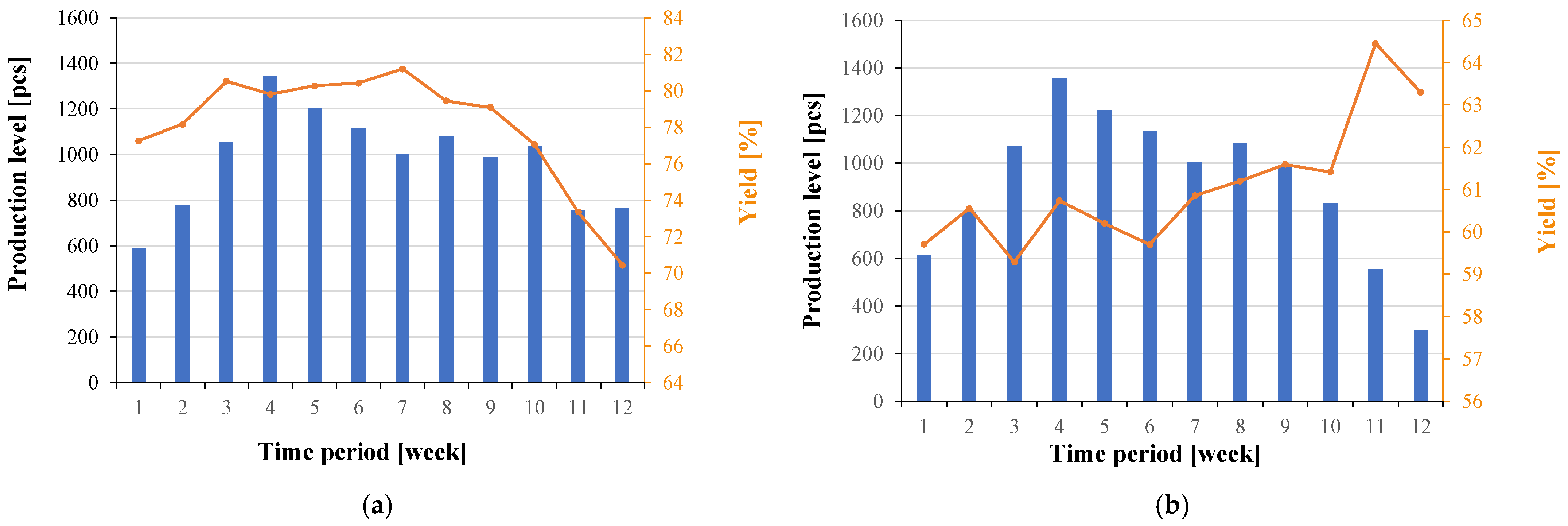
Figure 4 shows the production level and yield of the product AA_1 at individual test stations. Figure 4a shows that from week 7, the yield at the opCU test station decreases. This indicates an increase in the repair stack. However, at the same time, the yield at the oPIM test station began to increase.

Knowing the production level of each product and the yield level for each test station in the production process assigned to the manufactured products, the number of products that reach repair stations (sum_In) can be calculated. At the same time, the number of such products that pass through these stations after repair actions with a positive result (sum_Out) is recorded. These values define the parameter k described above using Equation (4). An example analysis of the number of product entries and exits from the repair stack, along with the resulting trend in parameter k, is shown in Figure 5.

Figure 5 shows that parameter k exceeds 1 for most of the analyzed time. This means that despite the increase in the number of products arriving for repairs from week 7 (Figure 5a), the work efficiency necessary to reduce the repair stack is sufficient. In weeks where k < 1, the number of products arriving for repairs exceeds the repair capacity of the dedicated repair team and causes the repair stack to grow. Comparing the changes in the quantity of the same product for repairs, which originate from different test stations, shows that each week the number of products entering the repair stack and the number of these products repaired vary and can range from several to several dozen items. This situation illustrates the importance of monitoring the efficiency of the repair team to control the state of the repair stack and keep the number of products in the repair stack under control.

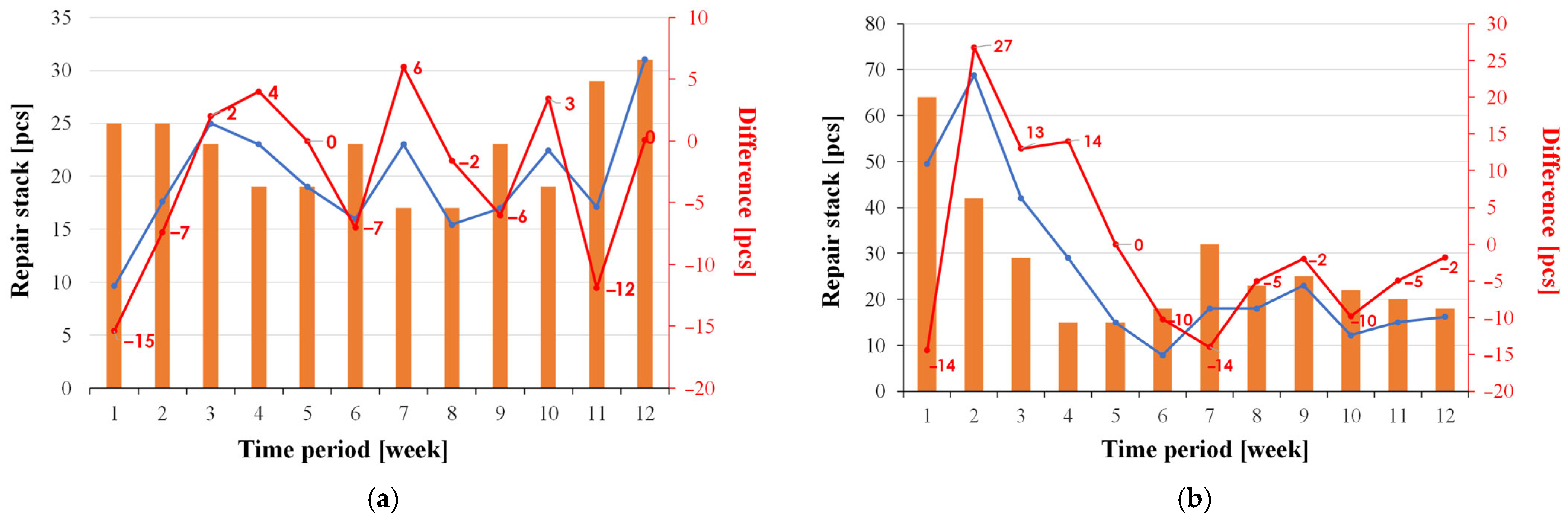
Using the proposed prediction model, the differences between the actual and estimated values were compared using an 8-week data package for the tested product and a specific test station (Figure 6).

As part of the analysis of the prediction results for the repair stack changes associated with a given test station, it was noted that regardless of the weekly changes in this stack and the station being considered, the difference between the actual and predicted values can range from several to as much as 50%, depending on the week under consideration. To improve the prediction results and approach the actual repair stack value, the next step will be to verify possible changes to the model that would lead to meeting the requirements described in Section 2.

Modifications to the predictive model described in Section 2 were proposed. The validity of these modifications was verified by comparing the results obtained with those obtained using the described model and eight weeks of historical production data. The aim of the analyses is to verify the model’s performance not only based on forecasted production data but also to understand how the model would behave if the quantities of products produced were precisely known in advance.

The number of products currently entering the In repair stack is unambiguous and easy to detect in the production system, as each test station always generates a non-compliant (Fail) status for a damaged product. However, it is known that certain exceptions to the repair loop affect sum_Out values. A Pass test result can indicate an Out exit from the repair loop. However, sometimes this result does not directly refer to the In product input entered in the system but may refer to the next step in the repair process. Such an additional step between the repair process and the test result and Pass status is difficult to detect with a dedicated function or procedure in the database of the system controlling the product flow. For such process cases with additional steps in the repair process, it is easier to insert dedicated exceptions, such as the Out_sp (Out special) parameter. This parameter is equal to the number of modules needing more than one attempt in the repair process.

Out_sp was defined by observing changes in the repair stack value in subsequent weeks. It was observed that for a certain group of products, the predicted repair stack for both the next week (1-week prediction) and the fourth week (4-week prediction) can differ significantly, while the actual repair stack remains unchanged or varies only slightly from week to week. In practice, there are products requiring In repairs whose sum is significantly greater than those being repaired (sum_In >> sum_Out). This situation results in the calculation of a low value of the k coefficient, ranging from 0 to 1.

The situation described above indicates that the calculations do not take into account the appropriate number of repaired products, which are used to estimate the future repair stack. The final actual repair stack remains virtually unchanged, meaning the actual number of repairs performed differs only slightly from the number of products that arrive for repair (sum_In ≈ sum_Out).

For such cases, the product flow set up in the production control system, known as routing, was traced, i.e., the subsequent stages in the production of the given products, and exceptions were noted. This situation occurs when there are additional steps in the production process between the non-conforming (Fail) and compliant (Pass) statuses, such as performing a test calibration or repeating a test immediately after obtaining the (Fail) status. This situation means that some repair results resulting in a positive test result may be omitted (too few results related to the detection of the Out status). Additional processes in the repair loop disrupt the standard procedure for the normally described inspection process.

In the cases described above, it was observed that the sum_In − sum_Out difference was significantly larger (over 10 times) than the actual number of products in the repair stack. Therefore, it was assumed that the new model is valid only when the following inequality is satisfied:

$${\displaystyle \frac{su{m}_{In}-su{m}_{Out}}{C_{rs}}}>20$$

(8)

where C_rs is the current number of products in the repair stack.

For this condition, to improve the model’s prediction accuracy, the Out_sp coefficient was introduced. The original version of this equation is given by Formula (1). As a result of the modification and introduction of Out_sp when condition (8) is met, the model described by Equation (1) takes the form:

$$N_{rs}=C_{rs}+e_{in}-\left(e_{out}+Ou{t}_{sp}\right)$$

(9)

Equation (9) in the predictive model ensures that the current repair stack is always consistent with the new repair stack in the following weeks. When inequality (8) is satisfied, the Out_sp coefficient is set to such a value that the repair stack remains balanced and constant according to the equation:

$$Ou{t}_{sp}=C_{rs}+e_{in}-e_{out}$$

(10)

The Out_sp parameter allows you to fill in the missing number of repaired products that were missed due to non-standard routing in the repair loop.

The following two main repair stack prediction models have been defined:

• Model A is the basic model, described by Equations (1)–(5);
• Model B is the model described by Equations (2)–(5) and (8)–(10).

Both models above are tested with future production data based on preliminary customer orders (forecast). The parameter describing the planned number of products to be manufactured in the upcoming production is D (demand) in Equation (3), which has a direct impact on the value of e_in. However, our experience shows that actual production often deviates from its initial plan. The demand value can change over time. Therefore, to compare the repair stack prediction results from models A and B, while eliminating the production forecasting error, the following notations were introduced for these models:

• Model C is described by the same equations as model A, but in Equation (3) the parameter D representing the forecasted demand is replaced by the number of actually produced products;
• Model D is described by the same equations as model B, but in Equation (3) the parameter D is replaced by the actual number of products produced.

Both model variants (C and D) are hypothetical because actual production values are not known in advance. Using historical data on actual production levels, we tested the performance of models A and B without including the production forecast error.

Because the production forecast provided by the customer is subject to error and the production plan is likely to change, model variants A and B, using average production data from the last eight weeks, are worth considering. In this case, it is assumed that the production plan defined in this way will differ less from actual production data than forecasting based on customer data. At the same time, the forecast error for the repair stack is expected to be smaller. For this case, model variants A and B are labeled as follows:

• Model E is described by the same equations as model A, but parameter D in Equation (3) is replaced by the average production value from the last 8 weeks;
• Model F is described by the same equations as model B, but parameter D in Equation (3) is substituted with the average production value for the last 8 weeks.

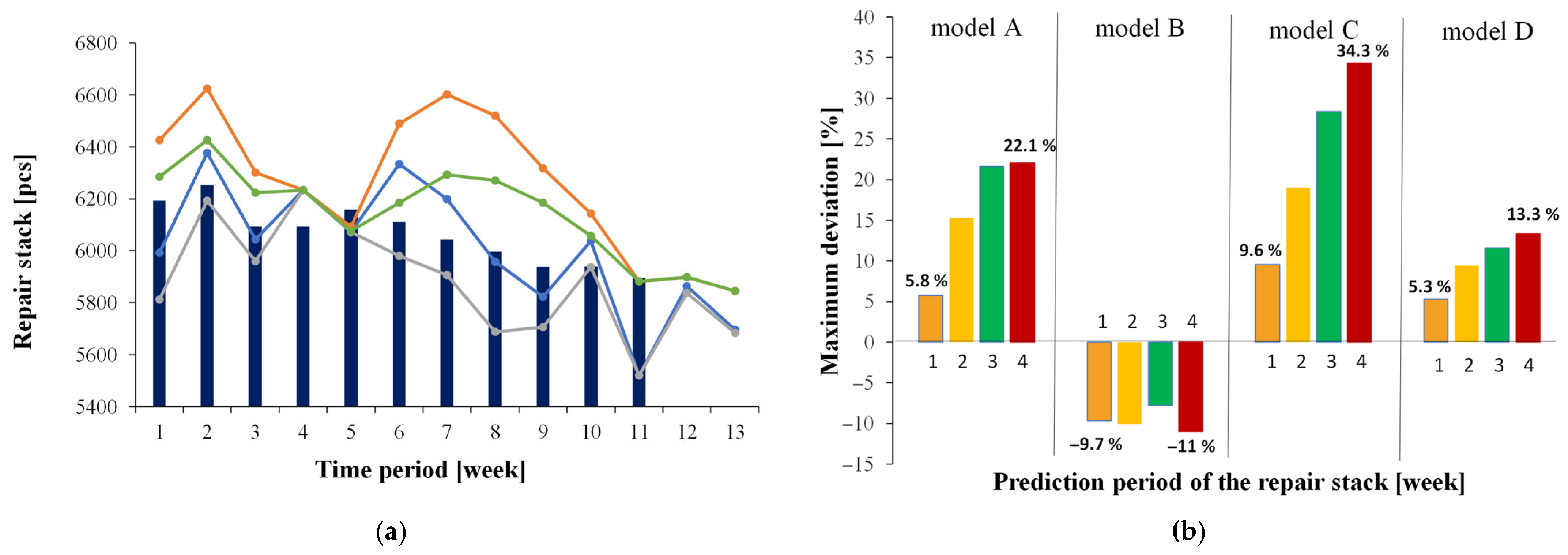
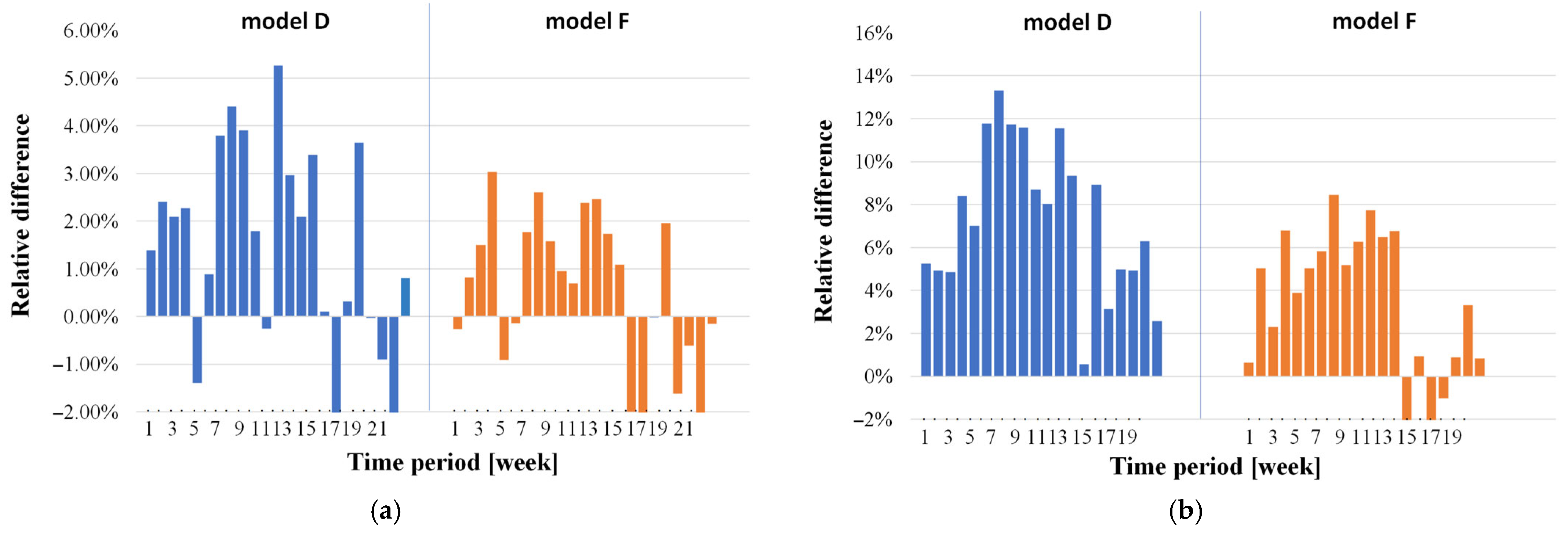
The repair stack prediction results using models A–D are compared in Figure 7. In Figure 7a, the bar chart represents the actual repair stack. The blue line represents the repair stack prediction results using model A. The gray line indicates the results from model B. The topmost orange line represents the results from model C. The green line describes the results from model D. This figure shows that the values calculated using model C are the highest. The position of the prediction graph above the actual repair stack indicates that the predicted number of products with the Fail status is too high. Analyzing the results of model C, the graph shows a jump in the weekly results recorded in week 2, when the deviation from the actual stack value was 6%, and for week 7 it was above 9%.

The above conclusions are confirmed by the data in Figure 7b. It shows the deviation values between the repair stack prediction results from individual models (A–D) and the actual value of this stack in subsequent weeks of prediction. The largest deviations in the repair stack prediction were recorded using model C. The maximum deviation for the nearest prediction week is 9.6%, but for predictions 4 weeks ahead, the deviation can be as much as over 34%.

Observing the trend for model A in Figure 7a, one can see a deviation from the actual value, which is on average about 3.5%. Model A stably reflects the actual repair stack each week. In Figure 7b, with a 1-week prediction of the repair stack, the maximum observed deviation is 5.8%. This is an acceptable value. The model shows greater discrepancies with each subsequent week of prediction, and with a 4-week prediction, this deviation exceeds 22%.

The curve obtained for model B is most often on average 4% below the actual value. The repair stack predictions of model B are very stable in terms of error in each of the predicted weeks, as can be seen in Figure 7b. The maximum deviation, regardless of whether it concerns the prediction for the next week or for 4 weeks ahead, does not exceed 11%.

Also noteworthy is the point in Figure 7a from week 11. In the considered week, the results from models A and B are similar, and the prediction result in both cases is 6.5% below the actual value. Therefore, the results from models C and D accurately reflect the repair stack value, and the deviation for them is below 0.1%.

The results for model D are the most accurate and close to the expected deviation target (maximum 10% for predictions four weeks ahead). For predictions for the following week, the prediction deviation using model D compared to the actual repair stack is only 5.3%, while for predictions four weeks ahead, it is no greater than 13.3%. The result was close to the expected result, but it ignored the production forecasting error because it was based on known actual and historical data. As already mentioned, in practice, data from actual production cannot be used in the model to predict the repair stack, because it is not known until it happens.

Comparing the prediction error obtained for models A/B and C/D, it can be seen that, contrary to expectations, taking into account the actual demand value results in a deterioration of prediction accuracy. As can be seen in Figure 7b, model C is characterized by worse accuracy than model A for each of the considered prediction periods. In turn, model D is characterized by better accuracy than model B for a one- or two-week prediction period. For longer prediction periods, model D shows a larger prediction error than model B.

These considerations were conducted only to observe a situation in which production forecasting was perfectly consistent with actual product production. It is also not possible to use the actual FPY yield level present in Equation (3) of the models discussed. Its underestimation causes an overestimation of the number of products entering the repair stack, thus causing the prediction line to jump relative to the actual trend in the number of products to be repaired. However, the results of this test confirm the need to improve production forecasting to make the repair stack prediction model more accurate.

5. Statistical Analysis of Selected Variants of the Deterministic Algorithm

Variance tests were performed in Minitab to compare the deviations of the repair stack predictions obtained from models A through F with the actual value of this stack. The analysis was performed for the upcoming week and four weeks in advance.

The obtained test result for the prediction for the coming week was P_value = 0.167. A P_value ≥ 0.05 confirms that all variants using the 8-week data package, for predictions one week ahead, produce similar variability. This means that the standard deviation from the mean value of the differences between the model prediction results and the actual value of the repair stack is statistically similar (

Table 1. Standard deviations between the models predicting the repair stack from A to F for the next week and the actual value of this stack.

Repair Stack Prediction Model	Average Value of Differences Between Repair Stack Prediction Models and Its Actual Value [%]	Standard Deviation of the Mean Value of the Differences Between the Prediction Models and the Actual Value of the Repair Stack [%]
A	0.52	2.89
B	3.36	2.79
C	4.12	3.00
D	1.43	2.24
E	2.59	1.76
F	0.45	1.81

). For this case, a comparison can be performed using one-way ANOVA analysis (One-way ANOVA in Minitab).

The result of the ANOVA test was P_value = 0. The obtained P_value < 0.05 confirms that there are statistical differences between the repair stack prediction of models A to F. Table 1 shows that for the 1-week prediction, the smallest mean values of the differences between the model prediction value and the actual value are presented by models A, D, and F, and they are less than 2%.

Similarly, variance tests were conducted for the 4-week prediction. In this case, consistent data were not obtained to confirm that models A through F are similar, as P_value = 0. Therefore, all prediction models were compared with each other in terms of the width of the confidence intervals of the standard deviation results. By comparing the ranges and standard deviation values for each of the presented prediction models, it is possible to assess the differences between them. These differences may be significant enough to require the one-way ANOVA test to discard some model variants in further comparisons. The range of confidence intervals and standard deviations for the differences between the prediction models and the actual repair stack values are provided in

Table 2. Standard deviation of the differences between the actual repair stack and the prediction models for the next 4 weeks.

Repair Stack Prediction Model	Standard Deviation of the Differences Between the Prediction Results and the Actual Value of the Repair Stack) [%]	Confidence Interval of Standard Deviations [%]
A	7.8	od 5.4 do 13.2
B	3.7	od 2.5 do 6.1
C	8.3	od 5.8 do 14.0
D	3.5	od 2.5 do 6.0
E	6.1	od 4.3 do 10.4
F	3.6	0.024–0.059

.

From Table 2, it can be observed that the standard deviation results marked in yellow are closest to 0, and the corresponding confidence intervals are similar. For models B, D, and F, the variance comparison in Minitab resulted in P_value = 0.977. This value confirms that the standard deviation values are similar.

Models B, D, and F were compared using a one-way ANOVA test, which resulted in a P_value of 0. This result confirms that there are statistical differences between the models. The mean values and standard deviations obtained from the ANOVA test are presented in

Table 3. Mean values and standard deviation of the differences in the prediction of the repair stack of models B, D, and F and the actual value of this stack, obtained in the one-way ANOVA test in Minitab.

Repair Stack Prediction Model	Average Value of the Differences Between the Repair Stack Prediction Models and Its Actual Value [%]	Standard Deviation of the Mean Value of the Differences Between the Prediction Models and the Actual Value of the Repair Stack [%]
B	0.86	3.7
D	7.39	3.5
F	3.46	3.5

. Comparing the data presented in this table, models B, D, and F have similar standard deviations, while the mean value closest to 0 was obtained for model B.

The proposed model is intended to be useful in predicting the number of products in the repair stack for the upcoming (+1 week) and the next week (+4 weeks). For the 1-week prediction of this stack, models D and F have lower values of the discussed average values than model B. However, for the 4-week prediction, model D is less accurate relative to the average value than F and B. Therefore, after comparing all the results, it was decided to choose repair stack prediction model F. Another reason for choosing this model is that the predicted values are most often above the actual value. This means that the predicted repair stack will be the same or slightly larger than the actual one, which protects against the risk of underestimating the resources needed to reduce it.

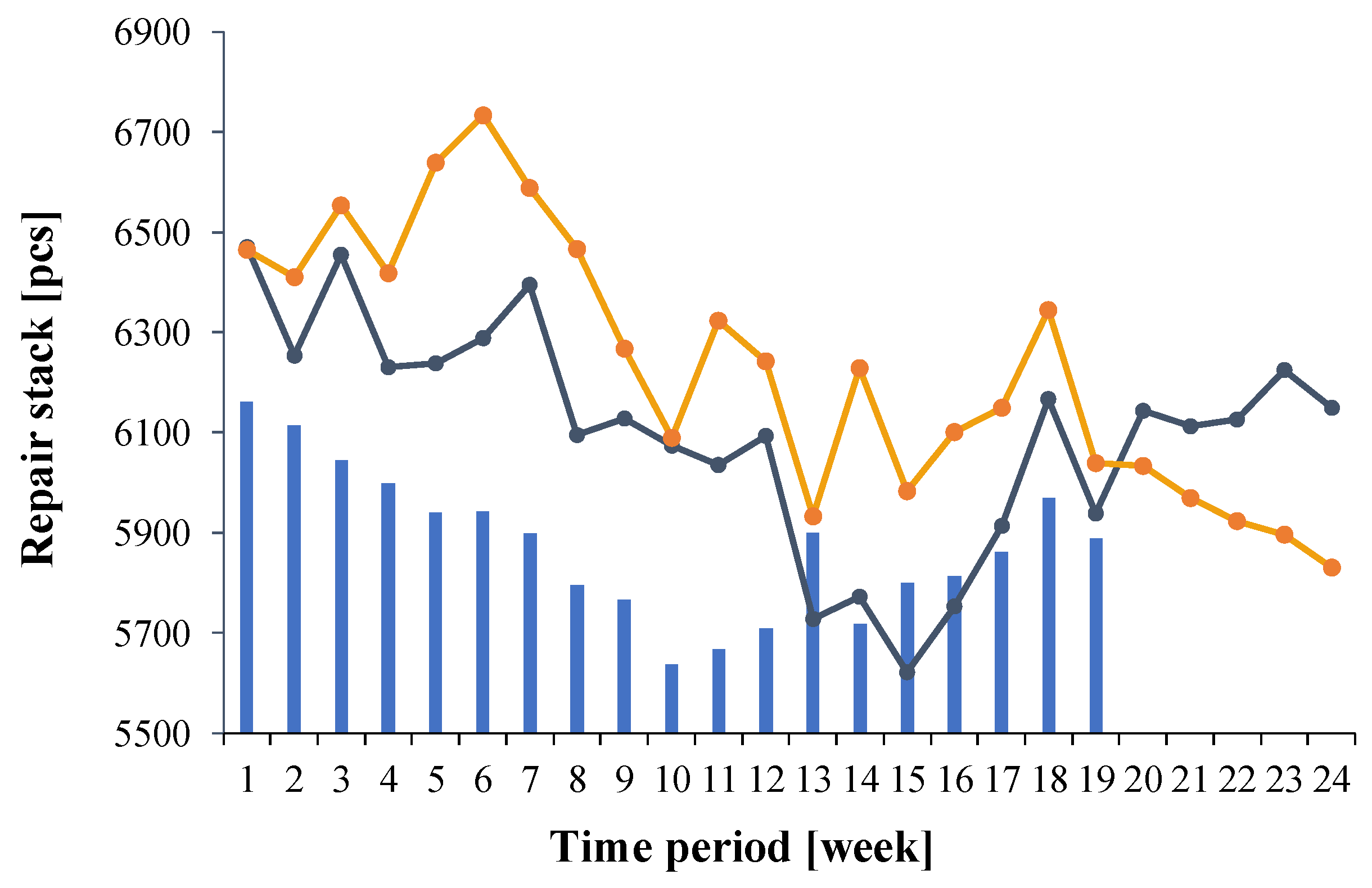
Figure 8 compares the trends in the repair stack prediction results using models D and F. The focus was on verifying the proposed model variants in the perspective of 4-week predictions. Figure 8 shows that the repair stack predicted from model F (blue line) more accurately reflects the actual state compared to model D (orange line).

To illustrate the situation more precisely, Figure 9 presents the deviation values between the predicted values and the actual value.

For predictions one week ahead, the deviations in the repair stack prediction using model D can be as much as 5%, and with model F, a maximum of 3%. For model D, even greater deviations are noted for predictions 4 weeks ahead, where the differences from the actual repair stack value can be up to 14%, and with model F they do not exceed 9%.

The number of products in the actual repair stack is the sum of individual products that are included in the repair stack when a defect is detected at one of the test stations verifying their correct operation. Therefore, it is important to obtain a repair stack value that accurately reflects not only the total number of products in the stack, as closely as possible to the actual number, but also takes into account the distribution of these quantities across the individual test stations from which the defective products originated. To this end, the prediction results obtained from models D and F were subjected to a statistical DOE (Design of Experiments) analysis. Analyses were conducted for the nearest week (+1 week) and the furthest week (+4 weeks). This experiment also examined how the size of the data package, model variant, and their interaction affect the accuracy of the prediction results.

The analyses conducted show that model D allows for estimation of the repair stack, taking into account the distribution of products contained within it among individual test stations, for the next week (+1) with a deviation of up to 22.5%. This value increases to 42.1% for the furthest predicted week (+4). Significantly smaller deviations in these predictions were noted using model F. When we provide averaged data from historical information on the number of completed products, instead of forecasted production data, the resulting deviation for the next predicted week (+1) is only 10.2%. This deviation meets expectations and goals. It increases to 28% when predicting the value of the repair stack for the furthest week (+4), which can be considered a satisfactory result.

6. Repair Stack Prediction Using Machine Learning Algorithm

For several years now, we have been observing the intensive development of artificial intelligence (AI). It is being used in various industries. The mathematical algorithms used in this technology are based on well-known statistical methods. However, some tasks require many complex, time-consuming calculations. AI technology, using specially developed libraries, can perform numerous calculations in a short time.

The main advantage of machine learning methods is the ability to determine coefficient values in equations describing the relationships between input and output quantities without using a complex estimation procedure. Additionally, by using an algorithm tuning procedure, it is possible to obtain a more accurate fit of data from calculations and experiments than with a deterministic approach [33]. The main goal of ML is to automatically detect patterns in data sets and use them to improve the effectiveness of decision-making. It differs from classical programming methods in that ML systems independently adapt their operation based on the provided information [33]. Popular algorithms used in this approach include linear and logistic regression (used for predicting numerical values and binary classification) [34] and decision trees and random forest (used in classification and regression, often used in the analysis of large data sets) [35].

The AI model learns by analyzing collected historical data, for example, on production process settings, and can provide information about their most effective values. This allows for improving the efficiency of these processes and, consequently, company profits [36,37]. Different methods of machine learning are described in the literature [34,35]. These include tree-based prediction and linear regression [34].

Tree-based prediction models can be found in the literature [38,39]. They use a decision tree to represent how different input variables can be used to predict a target value. Machine learning uses tree-based models for both classification and regression problems, such as product type or value. Input variables are repeatedly segmented into subsets to build a decision tree, and each branch is tested for forecast accuracy and evaluated for efficiency and effectiveness. However, they are primarily used in economic analysis for business [38]. The linear regression method is simple to implement and it allows for rapid training of the algorithm [34]. This method was selected for further investigations.

This section proposes an AI model for predicting repair stacks based on linear regression. This is achieved using the sci-kit learn [40] and tensorflow [40] libraries, which are used for machine learning and for selecting one of the built-in statistical models. These libraries can be used in the Python 3.12 programming language to build an AI model. The provided machine learning (ML) data and the chosen statistical model define the model’s accuracy.

Machine learning methods require properly prepared input data. Preparing data for machine learning and verifying the accuracy of the repair stack predictions using the proposed AI model are the main topics discussed later in this section.

Modern production relies heavily on the Internet of Things (IoT). It connects machines, computers, and sensors to obtain a holistic view of the production facility and its resources in order to increase production efficiency and quality [41,42,43]. At the same time, attention should be paid to the diversity of data and its potential for solving various problems. New solutions in the field of machine learning and data analysis are being applied. Recent years have brought the idea of training a single model on multiple clients while maintaining data privacy [41]. However, more important is the ability to use artificial intelligence and machine learning to visualize this data [43,44,45].

In the methods discussed, data on the process parameters for which the devices are configured is collected from machine sensors. Communication between machines takes place via the cloud, a dedicated internet location created to monitor the parameters of the set process. As long as the processes operate stably, according to assumptions, and there are no deviations from the set parameters, statistical methods for analyzing their results do not indicate the need to generate a signal about an emerging problem. However, data is collected continuously. All anomalies and deviations from the set standards in the process are recorded. The data is so large, and usually comes from so many devices, that analyzing it and drawing conclusions is difficult. Various types of statistical analyses can be used with Six Sigma tools and DMA-IC methods, which effectively identify parameters or relationships between them that influence the stability of the studied process. These methods allow for determining the current state of the process and whether it is controllable.

It should be noted that these methods are very labor-intensive. Furthermore, analyses based on historical data may no longer be valid at this point in time. A significant change in the process that may have occurred at a given moment and was not accounted for in the historically analyzed data may result in the statistical results not representing the current state of affairs. In the case of the described repair stack prediction model, there is a risk that such changes in the production process will occur that the proposed model will not provide the required accuracy. Therefore, there is a need to determine the values of the set process parameters over time and continuously, thus ensuring continuous control over them.

Given the above, implementing continuous data analysis methods is the best solution. Machine learning techniques, along with the use of AI, can incorporate continuously collected data into statistical analyses. This allows for immediate feedback on the results of these analyses. These methods take into account any changes in parameter trends in the analyzed process. Therefore, our goal was to formulate a new repair stack prediction model based on machine learning methods using linear regression, as described in one of the Python scikit-learn libraries [40]. During machine learning, the input data used to train the prediction model must be appropriately prepared by scaling and encoding. The next step is to verify the results of the machine learning by running a test. The test result illustrates the level of accuracy of the repair stack prediction based on the data provided so far.

The machine learning method using the scikit-learn library [40] includes the following steps:

• Preparing data for machine learning;
• Coding;
• Separation of input and output data;
• Division of data into training and test data;
• Scaling;
• Training and creating a model;
• Verification of model accuracy.

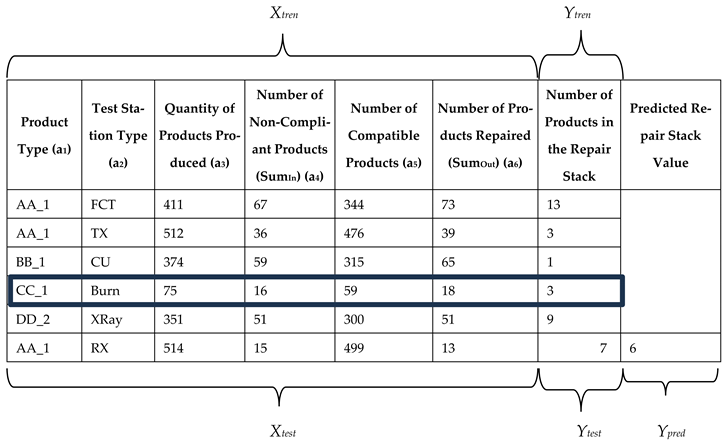
Input data must be clear and understandable for the machine learning process. It should be prepared so that all information related to the parameters to be analyzed has an appropriate range of values. This means that any erroneous data or missing information about the value of a given parameter should be removed to avoid disrupting the learning process. In addition to numerical data, there is attribute data (described with text). The clarity rule also applies to this data. If attribute data is missing any information (e.g., product name), then that attribute should be removed as it introduces an error in the model training process. The data for training the prediction model using linear regression are summarized in

Table 4. An example set of parameters used for machine learning.

In Table 4, the individual parameters are: X_tren—input training data (marked in blue), Y_tren—output training data (marked in green), X_test—input data for the test, Y_test—output data being the expected test result, Y_pred—output data being the result of the prediction model.

.

Table 4 omits information about data collection dates and historical production. These dates do not affect the results of the proposed linear regression. They should be referenced in the final model calculation.

Due to the existence of attribute data, it is necessary to convert them into numerical data that can be recognized by the new model. This requires encoding, which is the next step in preparing the data for machine learning. Using linear regression requires encoding the attribute data into numerical values. In the case under consideration, all product types and test station names must be converted to numerical form. This is achieved using the appropriate tensorflow library for Python, developed by Google [46]. It contains functions for converting text to numerical data. The result of this transformation is a vector matrix containing numbers for each attribute and parameter described in Table 4. This data matrix can be further transformed during the process of building a prediction model.

The next step is to determine which data are used to predict the repair stack and distinguish them from the stack’s values. Separating the data into input and output data creates two data matrices, which must be divided into training and test data. Generally, the training data should contain 80% of the total information, with the remaining 20% used for testing. The model is trained on a large amount of data. The remaining 20% of the information is then used as input to calculate the output. The result is compared with the actual output from this 20% portion of the data set. It is expected that the model output and the actual output used for testing will be reasonably consistent.

In Table 4, the penultimate column contains information about the actual state of the repair stack (Y_tren, expected output). The main data in the table constitutes a separate input to machine learning (X_tren, input data). Both pieces of information will be used in the process of creating a new prediction model for the repair stack. The data in the last row of Table 4 are sample data used to verify the resulting prediction model (X_test and Y_test). This division into input and output data, as well as test and training data, creates four data matrices: X_tren, Y_tren, X_test, and Y_test.

The next step in preparing data for machine learning is scaling. Attribute data are not scaled, as they do not affect the result; they only serve to distinguish individual parameters. Scaling is the process of establishing weights to equalize the influence of indicators derived from numerical input data. No parameters entering the process should dominate the others. There are several options for scaling. One is normalization, when the input data has a normal distribution. There is also a standardization process, which does not require normally distributed data but causes the data to converge towards a normal distribution. This process uses the standard deviation of the analyzed parameters and can be described by the following formula:

$$X_{scaled}={\displaystyle \frac{X_i-X_{mean}}{\sigma }}$$

(11)

where X_i—parameter value, X_mean—average value of the analyzed data, σ—standard deviation.

The scaling results apply to each of the four data matrices mentioned above. Thanks to scaling, the standard deviation for each parameter is equal to 1. After the scaling process, model training can begin. The scikit-learn library was used for this purpose. This library contains methods for implementing a linear regression model (calling the model with the linear regression function). In the Python program, a function is called whose arguments are the X_tren and Y_tren matrices. As a result of analyzing the training data matrix, a linear regression equation is created, which constitutes a newly defined prediction model. This equation has as many coefficients as the parameters specified in the X_train input data (six coefficients from a₁ to a₆, corresponding to the number of parameters described in Table 4). Model training is repeated with each new set of input data provided weekly (X_tren and Y_tren). Therefore, the coefficients of the regression equation take on different values each week. This model was used to predict the number of products in the repair stack, which is described in Table 4 as Y_pred (the output representing the predicted value of the repair stack). The Y_pred values obtained using the model can be compared with the Y_test output. This allows us to assess how well the developed model will reflect actual data.

As a result of previous analyses and the results obtained for deterministic models, the F model, using data from the last 8 weeks of production, has so far best reflected the actual repair stack. The results of predicting the repair stack 4 weeks in advance are interesting. Therefore, Figure 10 compares the values of the actual repair stack with the prediction results of this stack 4 weeks in advance, which were obtained using the F model and a new model derived from machine learning based on a linear regression equation, hereinafter referred to as the AI model. It can be seen that the repair stack prediction results using the AI model (orange line) are, in most cases, closer to the actual value of this stack than the results obtained from the F model (blue line).

Over a period of several months, the maximum deviations from the actual value of this stack were checked for predictions for the next, second, third, and fourth week before production. The values of these deviations from both prediction models are summarized in Figure 11.

From Figure 11, it can be seen that when using the F model, the maximum deviations from the actual repair stack value range from 3%, when the prediction concerns the nearest (+1) week, to 8.5% in the furthest (+4) week. The closer to the production week, the smaller the repair stack estimation error. The largest deviation values are within the assumed model requirements and the goal (error below 10%). However, the results obtained from the AI model do not deviate from the actual value by more than 5%, regardless of the week for which the repair stack prediction was performed.

The AI model demonstrates high accuracy in reflecting the actual repair stack and stable performance regardless of the week for which the future repair stack is being estimated. This indicates that the AI model is the best one proposed so far for estimating the future repair stack. It most accurately predicts the possible number of repair items that may appear in the stack several weeks in advance.

7. Conclusions

This paper proposes original models for predicting the repair stack for a company producing electronic modules. The proposed deterministic algorithm is based on historical data characterizing repair effectiveness, the number of modules of each type produced, the number of modules awaiting repair, and the number of modules planned for production. The proposed mathematical formulas are commented on in detail.

The practical usefulness of the proposed model was initially verified using a three-month period of production data. It was demonstrated that the proposed algorithm achieved good accuracy in predicting the repair stack value using eight weeks of historical data. This means that the initial assumption of using four weeks of historical data for prediction is insufficient. When this period was extended, the algorithm’s accuracy significantly improved, and the differences between the actual and estimated values were reduced by as much as half. The relative error of prediction performed using this algorithm does not exceed a few percentages. Such accuracy is fully satisfied from the point of view of a typical manufacturing company.

In its current version, the proposed deterministic model can accurately predict the repair stack a week in advance. With longer time horizons, the prediction error increases significantly. This is due to the realities of the company’s operations, including fluctuating material availability, the arrival of new orders, and ongoing changes to production plans.

Ultimately, the total predicted repair stack is the sum of the individual module counts from each test station. This type of analysis links the product quantity estimation results to the test stations and provides in-depth validation of the proposed model.

In addition to the deterministic algorithm, an AI model utilizing machine learning concepts was also proposed. The Python program enabled an effective learning procedure, enabling the determination of coefficient values in the linear regression equation, ensuring high accuracy in predicting the repair stack over a 1-, 2-, 3-, and 4-week timeframe. The prediction error for this model did not exceed 5%. Both the deterministic algorithms and the AI algorithm have been implemented in industrial practice and received positive reviews from production managers.