ADEmono-SLAM: Absolute Depth Estimation for Monocular Visual Simultaneous Localization and Mapping in Complex Environments
Abstract
1. Introduction
2. Related Work
2.1. SLAM Based on Traditional Geometric Methods
2.2. SLAM Based on Deep Learning Methods
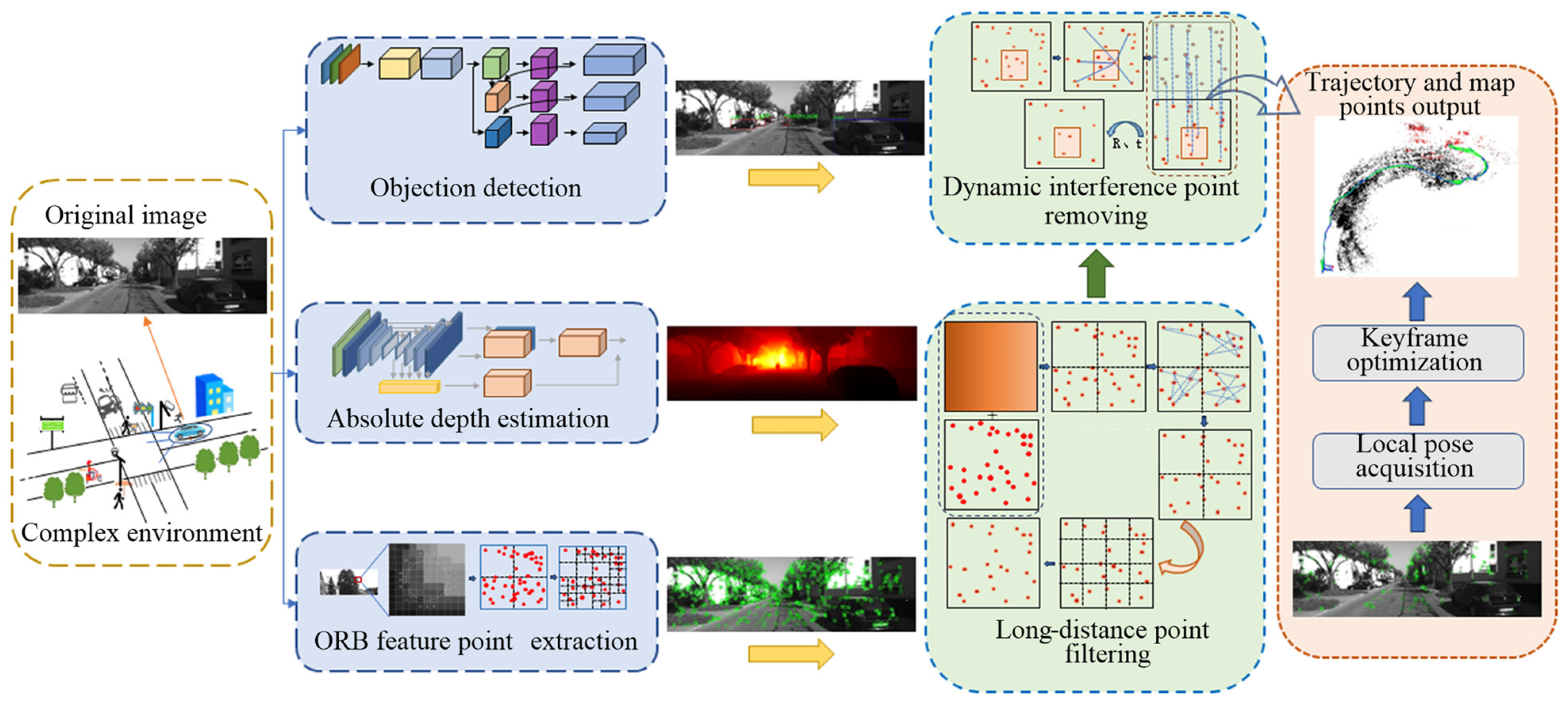
3. The Proposed Method
3.1. Absolute Depth Estimation Network
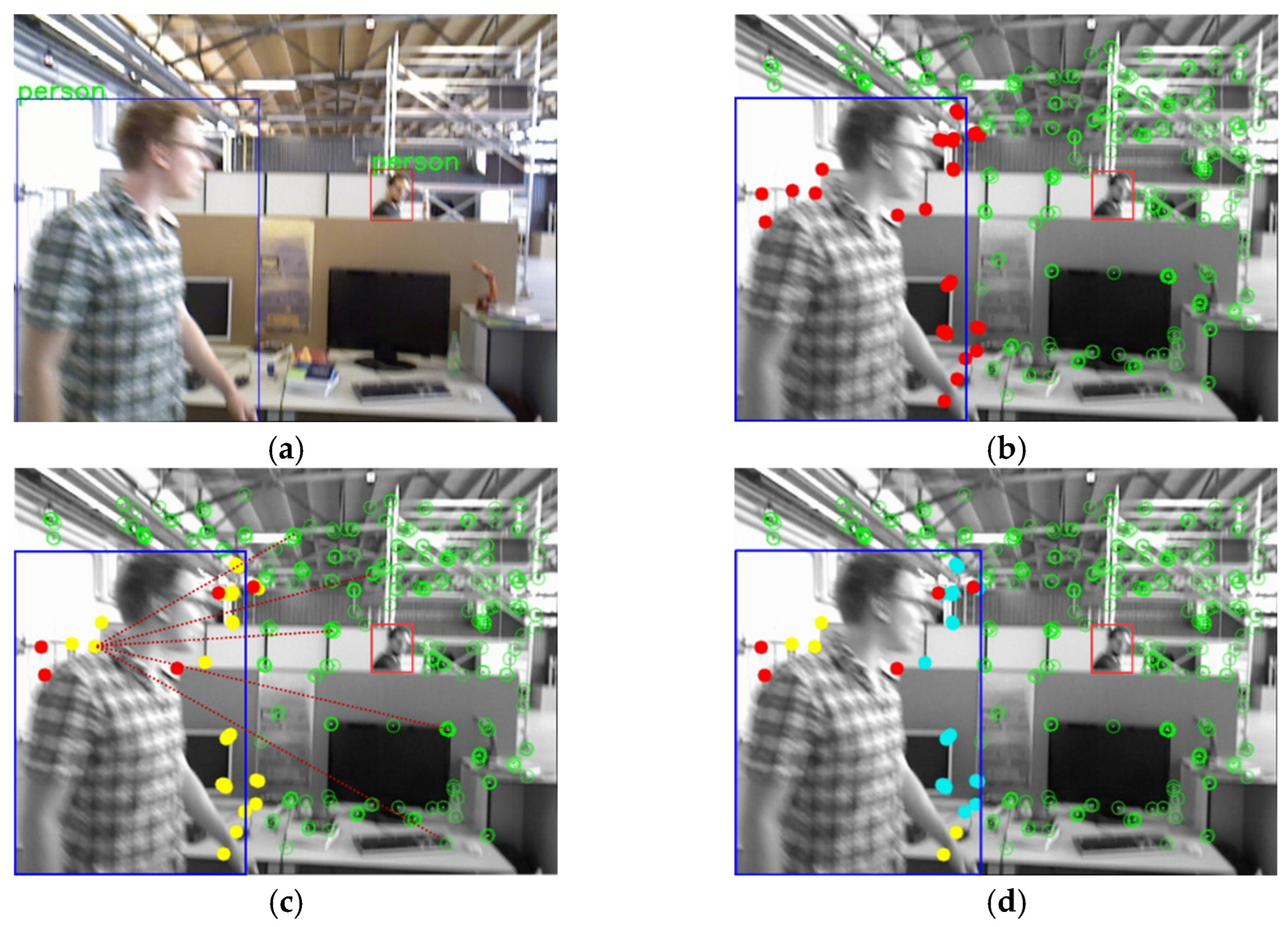
3.2. Dynamic Interference Point Removal
3.3. Long-Distance Point Filtering
| Algorithm 1: Distant point filtering algorithm | ||||
| Input: | Image to be processed | |||
| Set Depth Threshold | ||||
| Output: | Filter to get reliable feature points for feature matching | |||
| 1: | All feature points of the monocular image output in the previous stage | |||
| 2: | predicts each pixel of the current image through the absolute depth estimation network to obtain a depth map | |||
| 3: | Set a random seed with respect to time | |||
| 4: | the feature point: | |||
| 5: | Calculate the corresponding depth value di according to the two-dimensional pixel coordinates of the feature point | |||
| 6: | if(di > fd) | |||
| 7: | Obtain a random number from 0 to 1 | |||
| 8: | ||||
| 9: | Eliminate long-distance feature points with unreliable depth values | |||
| 10: | ||||
| 11: | ||||
| 12: | ||||
4. Experiment and Analysis
4.1. Experiments on KITTI Odometer Image Dataset
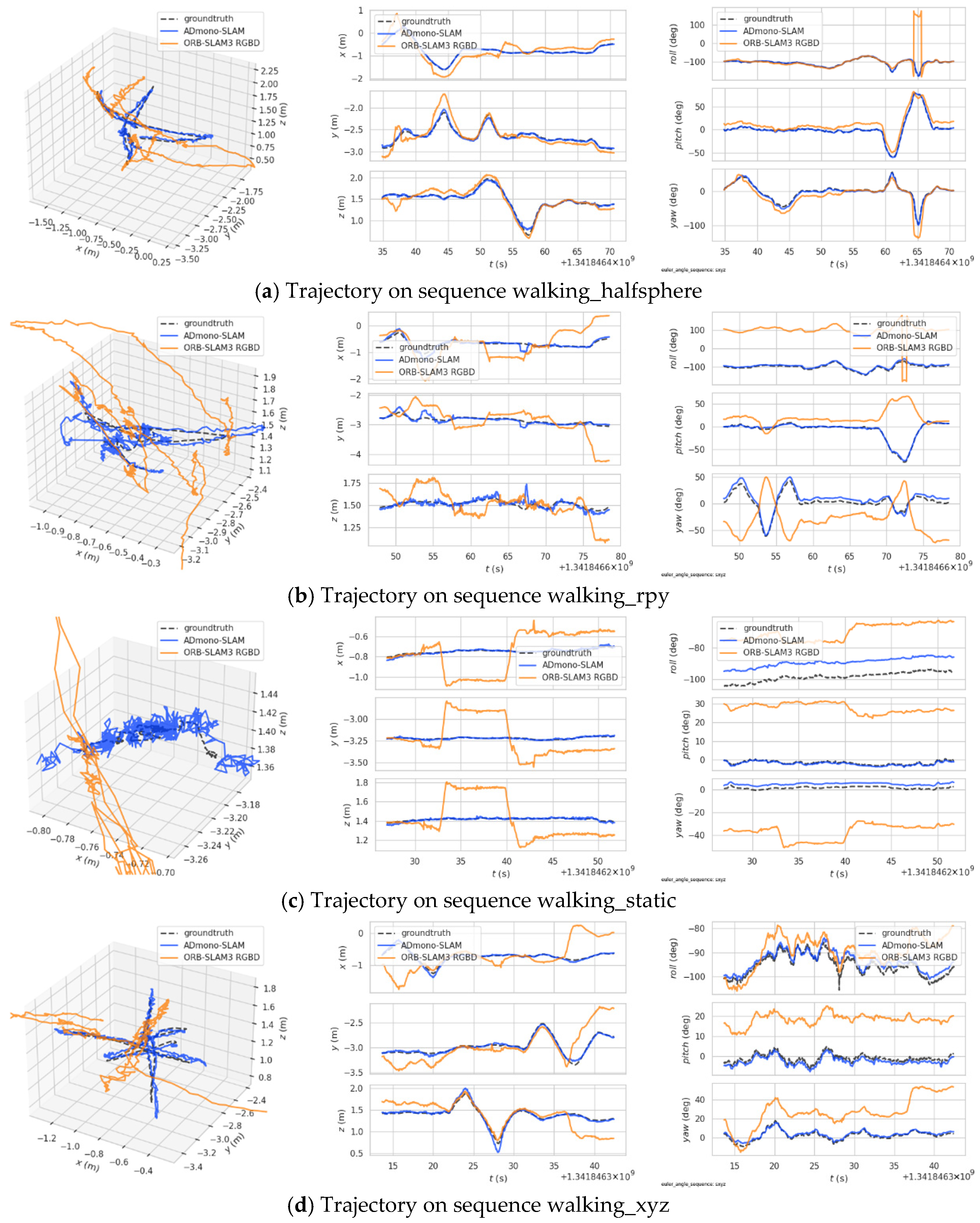
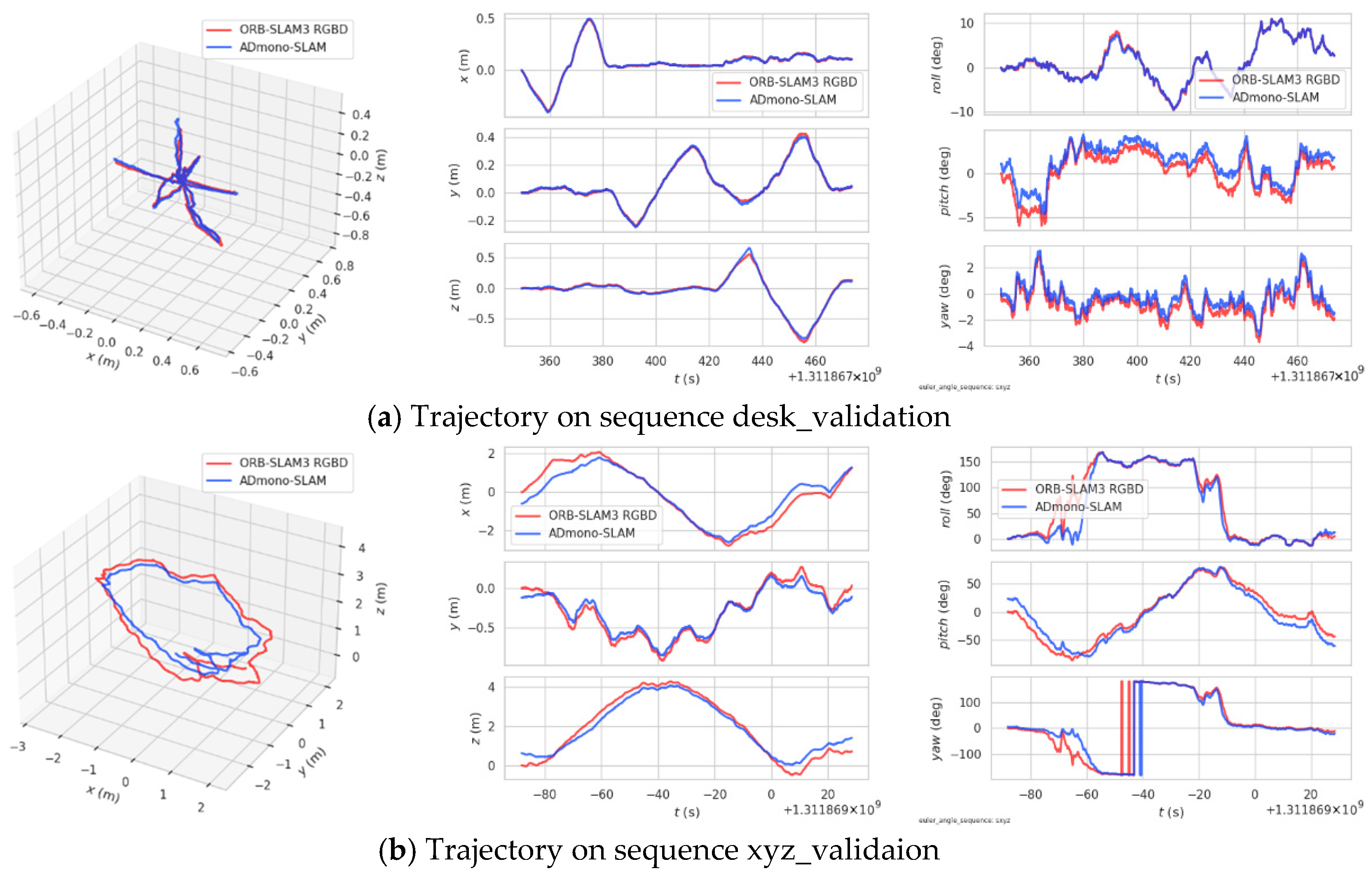
4.2. Experiments on TUM RGBD Dataset
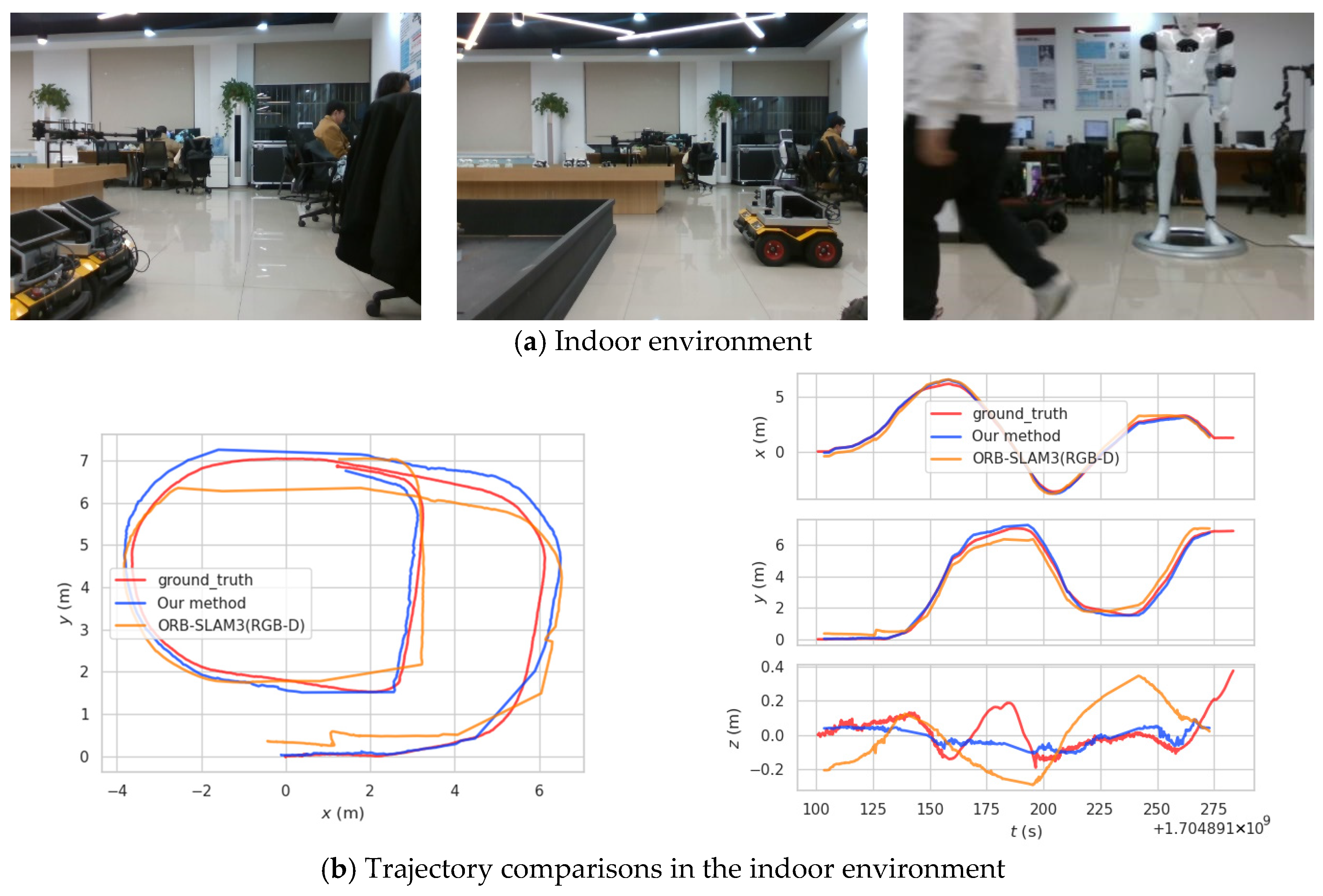
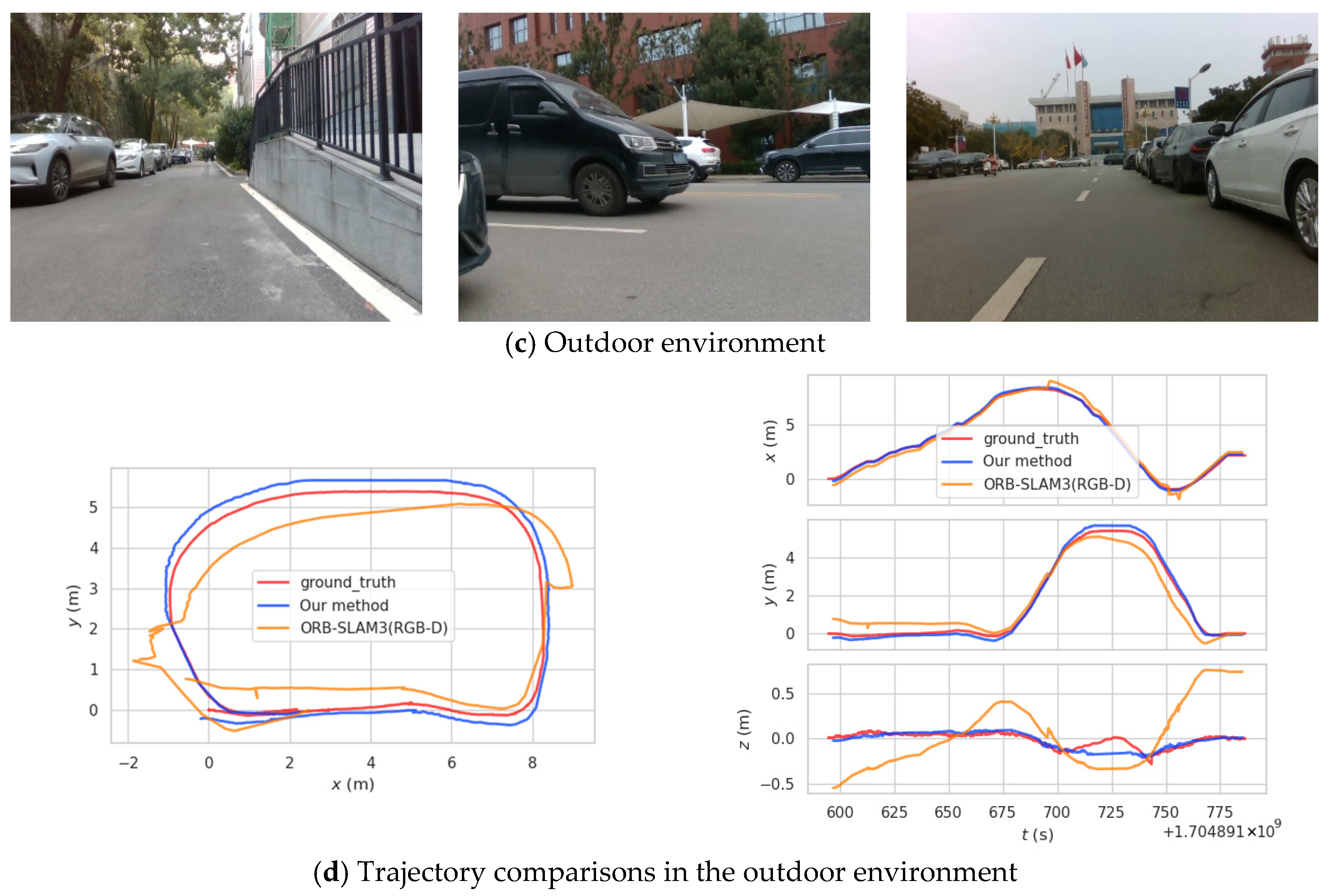
4.3. Experiments on Mobile Robot Platform
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Durrant-Whyte, H.; Bailey, T. Simultaneous localization and mapping: Part I. IEEE Robot. Autom. Mag. 2006, 13, 99–110. [Google Scholar] [CrossRef]
- Bailey, T.; Durrant-Whyte, H. Simultaneous localization and mapping (SLAM): Part II. IEEE Robot. Autom. Mag. 2006, 13, 108–117. [Google Scholar] [CrossRef]
- Fuentes-Pacheco, J.; Ruiz-Ascencio, J.; Rendon-Mancha, J.M. Visual simultaneous localization and mapping: A survey. Artifificial Intell. Rev. 2015, 43, 55–81. [Google Scholar] [CrossRef]
- Chen, Y.; Zhou, Y.; Lv, Q.; Deveerasetty, K.K. A review of V-SLAM. In Proceedings of the 2018 IEEE International Conference on Information and Automation (ICIA), Wuyishan City, China, 11–13 August 2018; IEEE: New York, NY, USA, 2018; pp. 603–608. [Google Scholar]
- Gao, X.; Zhang, T. The Fourteen Lectures on Visual SLAM; Publishing House of Electronics Industry: Beijing, China, 2017; pp. 16–18. [Google Scholar]
- Geiger, A.; Lenz, P.; Urtasun, R. Are we ready for autonomous driving? The KITTI vision benchmark suite. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; IEEE: New York, NY, USA, 2012; pp. 3354–3361. [Google Scholar]
- Sturm, J.; Engelhard, N.; Endres, F.; Burgard, W.; Cremers, D. A benchmark for the evaluation of RGB-D SLAM systems. In Proceedings of the 2012 IEEE International Conference on Intelligent Robots and Systems, Vilamoura-Algarve, Portugal, 7–12 October 2012; pp. 573–580. [Google Scholar]
- Davison, A.J.; Reid, I.D.; Molton, N.D.; Stasse, O. MonoSLAM: Real-Time Single Camera SLAM. IEEE Trans Pattern Anal. Mach. Intell. 2007, 29, 1052–1067. [Google Scholar] [CrossRef]
- Klein, G.; Murray, D. Parallel Tracking and Mapping for Small AR Workspaces. In Proceedings of the IEEE International Symposium on Mixed & Augmented Reality, Cambridge, UK, 15–18 September 2008. [Google Scholar]
- Mur-Artal, R.; Montiel, J.M.M.; Tardos, J.D. ORB-SLAM: A versatile and accurate monocular SLAM system. IEEE Trans. Robot. 2015, 31, 1147–1163. [Google Scholar] [CrossRef]
- Mur-Artal, R.; Tardós, J.D. ORB-SLAM2: An open-source SLAM system for monocular, stereo, and RGB-D cameras. IEEE Trans. Robot. 2017, 33, 1255–1262. [Google Scholar] [CrossRef]
- Campos, C.; Elvira, R.; Rodríguez, J.J.G.; Montiel, J.M.M.; Tardos, J.D. ORB-SLAM 3: An accurate open-source library for visual, visual–inertial, and multimap SLAM. IEEE Trans. Robot. 2021, 37, 1874–1890. [Google Scholar] [CrossRef]
- Engel, J.; Koltun, V.; Cremers, D. Direct sparse odometry. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 611–625. [Google Scholar] [CrossRef]
- Qi, L.; Wang, R.; Hu, C.; Li, S.; Xu, X. Time-Aware Distributed Service Recommendation with Privacy-Preservation. Inf. Sci. 2018, 480, 354–364. [Google Scholar] [CrossRef]
- Lu, Y.W.; Lu, G.Y. An unsupervised approach for simultaneous visual odometry and single image depth estimation. In Proceedings of the 2022 International Joint Conference on Neural Networks (IJCNN), Padua, Italy, 18–23 July 2022. [Google Scholar]
- Wang, S.; Clark, R.; Wen, H.; Trigoni, N. Deepvo: Towards end-to-end visual odometry with deep recurrent convolutional neural networks. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; IEEE: New York, NY, USA, 2017; pp. 2043–2050. [Google Scholar]
- Wang, S.; Clark, R.; Wen, H.; Trigoni, N. End-to-end, sequence-to-sequence probabilistic visual odometry through deep neural networks. Int. J. Robot. Res. 2018, 37, 513–542. [Google Scholar] [CrossRef]
- Li, R.; Wang, S.; Long, Z.; Gu, D. Undeepvo: Monocular visual odometry through unsupervised deep learning. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; IEEE: New York, NY, USA, 2018; pp. 7286–7291. [Google Scholar]
- Zhao, C.Q.; Yen, G.G.; Sun, Q.Y.; Zhang, C.Z.; Tang, Y. Masked GAN for unsupervised depth and pose prediction with scale consistency. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 5392–5403. [Google Scholar] [CrossRef] [PubMed]
- Cimarelli, C.; Bavle, H.; Sanchez-Lopez, J.L.; Voos, H. RAUM-VO: Rotational Adjusted Unsupervised Monocular Visual Odometry. Sensors 2022, 22, 2651. [Google Scholar] [CrossRef] [PubMed]
- Françani, A.O.; Maximo, M.R.O.A. Transformer-based model for monocular visual odometry: A video understanding approach. arXiv 2023, arXiv:2305.06121. [Google Scholar] [CrossRef]
- Zhu, R.; Yang, M.; Liu, W.; Song, R.; Yan, B.; Xiao, Z. DeepAVO: Efficient pose refining with feature distilling for deep visual odometry. Neurocomputing 2022, 467, 22–35. [Google Scholar] [CrossRef]
- Ma, P.; Bai, Y.; Zhu, J.; Wang, C.; Peng, C. DSOD: DSO in dynamic environments. IEEE Access 2019, 7, 178300–178309. [Google Scholar] [CrossRef]
- Bhat, S.F.; Birkl, R.; Wofk, D.; Wonka, P.; Muller, M. Zoedepth: Zero-shot transfer by combining relative and metric depth. arXiv 2023, arXiv:2302.12288. [Google Scholar]
- Liang, W.; Chen, X.H.; Huang, S.; Xiong, G.; Yan, K.; Zhou, X. Federated Learning Edge Network Based Sentiment Analysis Combating Global COVID-19. Comput. Commun. 2023, 204, 33–42. [Google Scholar] [CrossRef]
- Zhou, X.; Zheng, X.; Cui, X.; Shi, J.; Liang, W.; Yan, Z.; Yang, L.T.; Shimizu, S.; Wang, K.I.-K. Digital Twin Enhanced Federated Reinforcement Learning with Lightweight Knowledge Distillation in Mobile Networks. IEEE J. Sel. Areas Commun. 2023, 41, 3191–3211. [Google Scholar] [CrossRef]
- Meng, F.; Chen, X.H. Generalized Archimedean Intuitionistic Fuzzy Averaging Aggregation Operators and Their Application to Multicriteria Decision-Making. Int. J. Inf. Technol. Decis. Mak. 2016, 15, 1437–1463. [Google Scholar] [CrossRef]
- Zhang, P.; Wang, J.; Li, W. A Learning Based Joint Compressive Sensing for Wireless Sensing Networks. Comput. Netw. 2020, 168, 107030. [Google Scholar] [CrossRef]
- Ranftl, R.; Lasinger, K.; Hafner, D.; Schindler, K.; Koltun, V. Towards robust monocular depth estimation: Mixing datasets for zero-shot cross-dataset transfer. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 44, 1623–1637. [Google Scholar] [CrossRef] [PubMed]
- Zou, Y.; Ji, P.; Tran, Q.H.; Huang, J.-B.; Chandraker, M. Learning Monocular Visual Odometry via Self-Supervised Long-Term Modeling; ECCV 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 710–727. [Google Scholar]
- Wang, Q.; Zhang, H.; Liu, Z.; Li, X. Information Theoretic Learning-Enhanced Dual-Generative Adversarial Networks with Causal Representation for Robust OOD Generalization. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 1632–1646. [Google Scholar]
- Wightman, R. Pytorch image models. Available online: https://github.com/liyanhui607/rwightman_pytorch-image-models (accessed on 10 April 2024).
- Bhat, S.F.; Alhashim, I.; Wonka, P. LocalBins: Improving Depth Estimation by Learning Local Distributions. In Proceedings of the ECCV 2022: 17th European Conference, Tel-Aviv, Israel, 23–27 October 2022. [Google Scholar]
- Zhang, L.; Li, H.; Wang, Q. Point-by-point feature extraction of artificial intelligence images based on the internet of things. Comput. Commun. 2020, 155, 1–9. [Google Scholar]
- Qi, L.; Zhang, X.; Dou, W.; Hu, C.; Yang, C.; Chen, J. A Two-Stage Locality-Sensitive Hashing Based Approach for Privacy-Preserving Mobile Service Recommendation in Cross-Platform Edge Environment. Future Gener. Comput. Syst. 2018, 88, 636–643. [Google Scholar] [CrossRef]
- Chen, Z.S.; Chen, J.Y.; Chen, Y.H.; Yang, Y.; Jin, L.; Herrera-Viedma, E.; Pedrycz, W. Large-Group Failure Mode and Effects Analysis for Risk Management of Angle Grinders in the Construction Industry. Inf. Fusion 2023, 97, 101803. [Google Scholar] [CrossRef]
- Rahima, K.; Muhammad, H. What is YOLOv5: A deep look into the internal features of the popular object detector. arXiv 2024, arXiv:2407.20892. [Google Scholar] [CrossRef]
- Zhou, X.; Li, Y.; Liang, W. CNN-RNN Based Intelligent Recommendation for Online Medical Pre-Diagnosis Support. IEEE Trans. Comput. Biol. Bioinform. 2021, 18, 912–921. [Google Scholar] [CrossRef]
- Lv, P.Q.; Wang, J.K.; Zhang, X.Y.; Shi, C.F. Deep supervision and atrous inception-based U-Net combining CRF for automatic liver segmentation from CT. Sci. Rep. 2022, 12, 16995. [Google Scholar] [CrossRef]
- Zhang, J.; Bhuiyan, M.Z.A.; Xu, X.; Hayajneh, T.; Khan, F. Anticoncealer: Reliable Detection of Adversary Concealed Behaviors in EdgeAI-Assisted IoT. IEEE Internet Things J. 2022, 9, 22184–22193. [Google Scholar] [CrossRef]
- Zhou, X.; Liang, W.; Yan, K.; Li, W.; Wang, K.I.-K.; Ma, J.; Jin, Q. Edge-Enabled Two-Stage Scheduling Based on Deep Reinforcement Learning for Internet of Everything. IEEE Internet Things J. 2023, 10, 3295–3304. [Google Scholar] [CrossRef]
- Liu, C.; Kou, G.; Zhou, X.; Peng, Y.; Sheng, H.; Alsaadi, F.E. Time-Dependent Vehicle Routing Problem with Time Windows of City Logistics with a Congestion Avoidance Approach. Knowl. Based Syst. 2020, 188, 104813. [Google Scholar] [CrossRef]
- Shan, T.; Englot, B. Lego-loam: Lightweight and ground-optimized lidar odometry and mapping on variable terrain. In Proceedings of the 2018 IEEE International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; IEEE: New York, NY, USA, 2018; pp. 4758–4765. [Google Scholar]








| Sequence | ADEmono-SLAM | ORB-SLAM3 (Short Version) [12] | ORB-SLAM3 (Full Version) [12] | ORB-SLAM2 [11] |
|---|---|---|---|---|
| 00 | 20.89 | 81.85 | 6.95 | 6.20 |
| 02 | 22.99 | 38.17 | 27.47 | 29.97 |
| 03 | 3.70 | 1.69 | 1.31 | 0.97 |
| 05 | 5.18 | 41.98 | 5.27 | 5.20 |
| 06 | 4.33 | 50.61 | 15.05 | 13.27 |
| 07 | 2.21 | 17.42 | 3.17 | 1.88 |
| 08 | 14.51 | 51.94 | 56.97 | 51.83 |
| 09 | 9.88 | 57.46 | 7.68 | 62.17 |
| 10 | 4.06 | 7.83 | 7.33 | 7.61 |
| Average | 9.75 | 38.77 | 14.58 | 19.90 |
| Method | Sequence | Average Value | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 00 | 02 | 03 | 05 | 06 | 07 | 08 | 09 | 10 | |||
| trel | UndeepVO [18] | 4.14 | 5.58 | - | 3.40 | - | 3.15 | 4.08 | - | - | 4.07 |
| ESP-VO [17] | - | - | 6.72 | 3.35 | 7.24 | 3.52 | - | - | 9.77 | 6.12 | |
| LSTMVO [19] | 11.9 | 6.91 | - | 7.15 | - | 8.75 | 7.65 | - | - | 8.47 | |
| DSOD [23] | - | 15.0 | 16.3 | 14.4 | 14.6 | 15.5 | 15.1 | 13.8 | 13.5 | 14.7 | |
| DeepAVO [22] | - | - | 3.64 | 2.57 | 4.96 | 3.36 | - | - | 5.49 | 4.00 | |
| RAUM-VO [20] | 2.54 | 2.57 | 3.21 | 3.04 | 3.03 | 2.39 | 3.63 | 2.92 | 5.84 | 3.24 | |
| TSformer-VO [21] | 4.64 | 4.73 | 12.8 | 12.5 | 28.9 | 22.9 | 4.32 | 5.45 | 16.0 | 12.47 | |
| ADmono-SLAM | 3.20 | 3.58 | 2.55 | 1.73 | 1.89 | 1.51 | 2.97 | 3.09 | 2.09 | 2.51 | |
| UndeepVO [18] | 1.92 | 2.44 | - | 1.50 | - | 2.48 | 1.79 | - | - | 2.03 | |
| ESP-VO [17] | - | - | 2.76 | 1.21 | 1.50 | 1.71 | - | - | 2.04 | 1.84 | |
| LSTMVO [19] | 4.29 | 1.99 | - | 2.36 | - | 3.54 | 1.97 | - | - | 2.83 | |
| DeepAVO [22] | - | - | 1.89 | 1.16 | 1.34 | 2.15 | - | - | 2.49 | 1.80 | |
| RAUM-VO [20] | 0.77 | 0.58 | 1.33 | 1.15 | 0.83 | 1.03 | 1.07 | 0.31 | 0.68 | 0.86 | |
| TSformer-VO [21] | 1.89 | 1.56 | 5.75 | 5.13 | 8.83 | 11.5 | 1.67 | 2.08 | 5.16 | 4.84 | |
| ADmono-SLAM | 0.93 | 0.47 | 0.27 | 0.33 | 0.60 | 0.31 | 0.44 | 0.35 | 0.44 | 0.46 | |
| RAUM-VO [20] | 16.2 | 16.1 | 2.60 | 17.4 | 9.23 | 2.16 | 16.3 | 8.66 | 12.2 | 11.20 | |
| TSformer-VO [21] | 46.5 | 55.2 | 14.1 | 61.3 | 88.3 | 31.4 | 26.4 | 23.6 | 22.6 | 41.04 | |
| ADmono-SLAM | 20.8 | 22.9 | 3.70 | 5.18 | 4.33 | 2.21 | 14.5 | 9.88 | 4.06 | 9.72 | |
| Sequence | ADEmono-SLAM | ORB-SLAM3 RGBD [19] |
|---|---|---|
| fr3/walking_halfsphere | 0.043 | 0.319 |
| fr3/walking_rpy | 0.109 | 0.671 |
| fr3/walking_static | 0.014 | 0.361 |
| fr3/walking_xyz | 0.066 | 0.622 |
| Method | Indoor Environment | Outdoor Environment |
|---|---|---|
| ADEmono-SLAM | 0.381 | 1.209 |
| ORB-SLAM3 RGBD [19] | 0.419 | 2.165 |
| ADEmono-SLAM without dynamic interference point removal | 0.507 | 1.986 |
| ADEmono-SLAM without long-distance point filtering | 0.466 | 2.372 |
| ADEmono-SLAM without dynamic interference point removal and long-distance point filtering | 1.131 | 4.625 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, K.; Yu, Z.; Zhou, X.; Tan, P.; Yin, Y.; Luo, H. ADEmono-SLAM: Absolute Depth Estimation for Monocular Visual Simultaneous Localization and Mapping in Complex Environments. Electronics 2025, 14, 4126. https://doi.org/10.3390/electronics14204126
Zhou K, Yu Z, Zhou X, Tan P, Yin Y, Luo H. ADEmono-SLAM: Absolute Depth Estimation for Monocular Visual Simultaneous Localization and Mapping in Complex Environments. Electronics. 2025; 14(20):4126. https://doi.org/10.3390/electronics14204126
Chicago/Turabian StyleZhou, Kaijun, Zifei Yu, Xiancheng Zhou, Ping Tan, Yunpeng Yin, and Huanxin Luo. 2025. "ADEmono-SLAM: Absolute Depth Estimation for Monocular Visual Simultaneous Localization and Mapping in Complex Environments" Electronics 14, no. 20: 4126. https://doi.org/10.3390/electronics14204126
APA StyleZhou, K., Yu, Z., Zhou, X., Tan, P., Yin, Y., & Luo, H. (2025). ADEmono-SLAM: Absolute Depth Estimation for Monocular Visual Simultaneous Localization and Mapping in Complex Environments. Electronics, 14(20), 4126. https://doi.org/10.3390/electronics14204126






