Novel Tight Jensen’s Inequality-Based Performance Analysis of RIS-Aided Ambient Backscatter Communication Systems

Abstract

This paper presents a performance analysis of the reconfigurable intelligent surface (RIS)-aided ambient backscatter communication (AmBC) network. The system consists of a base station (BS), a backscatter device (BD), an RIS, and a destination (D). No direct link exists between the BS and RIS and between the BD and D. We propose a novel tight Jensen’s inequality. A new tighter upper bound is derived for the ergodic capacity, and we demonstrate that the proposed upper bound is much tighter than the existing bound. Monte Carlo simulations are performed to validate the analytical results. The tightened upper bound is found to be almost identical to that in the Monte Carlo simulation results, and the ergodic capacity significantly increases with the number of reflecting elements. In addition, the ergodic capacity improves when the RIS is placed close to the BD or D, and when the distance between the BS and BD is small, the ergodic capacity is severely affected.

1. Introduction

The growth of the Internet of Things (IoTs) has paved the way for ambient backscatter communication (AmBC) for spectral and energy efficiency. AmBC employs ambient radio frequency (RF) signals for low-power communication and leverages wireless signal modulation to enable cost-effective communication [1,2,3,4]. We employ a low-power multi-antenna design and a novel coding mechanism that can be decoded on backscatter devices (BDs), and these designs rely solely on energy harvested from television (TV) and solar sources [1]. In [2], a novel communication system that bridges RF-powered devices with the internet, i.e., Wi-Fi backscatter, is proposed. A communication system that enables two devices to communicate using only ambient RF as the source of power is presented in [3]. The performance of RF-powered cognitive radio networks (CRNs) with AmBC is investigated in [4]. Applications of AmBC include radio frequency identification (RFID) and electronic toll collection. Several challenges of AmBC technology include complex RF signals, transmission range, limited data rates, security concerns, and interference [5]. To enable technologies for next-generation mobile systems, reconfigurable intelligent surfaces (RISs) have emerged as promising solutions in both academia and industry [6]. An RIS consists of many passive and low-cost reflecting elements, each of which can independently reflect an electromagnetic wave with phase shifts [7]. Thus, RISs have recently received considerable interest on account of their enhanced energy efficiency and improved spectral efficiency [8,9,10,11,12]. An RIS for downlink multi-user communication from a multi-antenna base station is investigated in [8]. The authors of [9] introduced the emerging research field of RIS-empowered smart radio environments (SREs). A physics-based model and a scalable optimization framework for large IRSs were developed in [10]. The secrecy rate of an IRS-assisted Gaussian multiple-input–multiple-output (MIMO) wiretap channel (WTC) was enhanced in [11]. An IRS-aided multiple-input–single-output (MISO) wireless transmission system was investigated in [12]. The authors optimized the passive phase shift of each element at the IRS to maximize the downlink-received signal-to-noise ratio (SNR).

Therefore, investigating RIS-assisted AmBC systems is essential. RIS-assisted AmBC systems have previously been proposed to improve the capacity of space–air–ground-integrated networks (SAGINs) [13]. In [14], the achievable rate was maximized by optimizing the phase shifts in RIS-assisted AmBC systems. In [15], the average achievable rate was computed under the assumption of a central limit theorem (CLT), and an arbitrary number of RIS-reflecting elements was considered. Moreover, the outage probability (OP) and average symbol error rate (ASER) of the RIS-assisted AmBC system were derived in [16]. The effect of RIS on individual links in AmBC systems was investigated in [17].

In this paper, the effects of the locations of, and distances between, the base station (BS), BD, RIS, and D on the performance of RIS-assisted AmBC systems are examined. The ergodic capacity of RIS-assisted AmBC systems is analyzed. A closed-form expression for the upper bound on the ergodic capacity is derived using a novel tight Jensen’s inequality and a tighter upper bound. Numerical results are presented to investigate whether the derived tightened upper bound is the same as that derived from the Monte Carlo simulation. Moreover, the ergodic capacity increases significantly with the number of reflecting elements. In addition, the ergodic capacity improves when the RIS is placed close to the BD or D. In particular, the effect of the distance between the BS and BD on the capacity performance is significant at a close distance.

The major contributions of this paper are as follows:

(1)

A closed-form expression for the upper bound on the ergodic capacity of RIS-assisted AmBC systems is derived.

(2)

A novel tight Jensen’s inequality is proposed for a tighter upper bound on the ergodic capacity.

(3)

The advantages of utilizing RIS and the impact of BD or RIS placement on the ergodic capacity are presented.

(4)

We demonstrate that including BS, the capacity curve is more flexible and the system can be more freely designed.

The rest of the paper is organized as follows: Section 2 represents the system model for RIS-assisted AmBC systems. A performance analysis of the RIS-assisted AmBC systems is given in Section 3. In Section 4, the numerical results, along with the Monte Carlo simulation results, are presented. Finally, Section 5 concludes the paper.

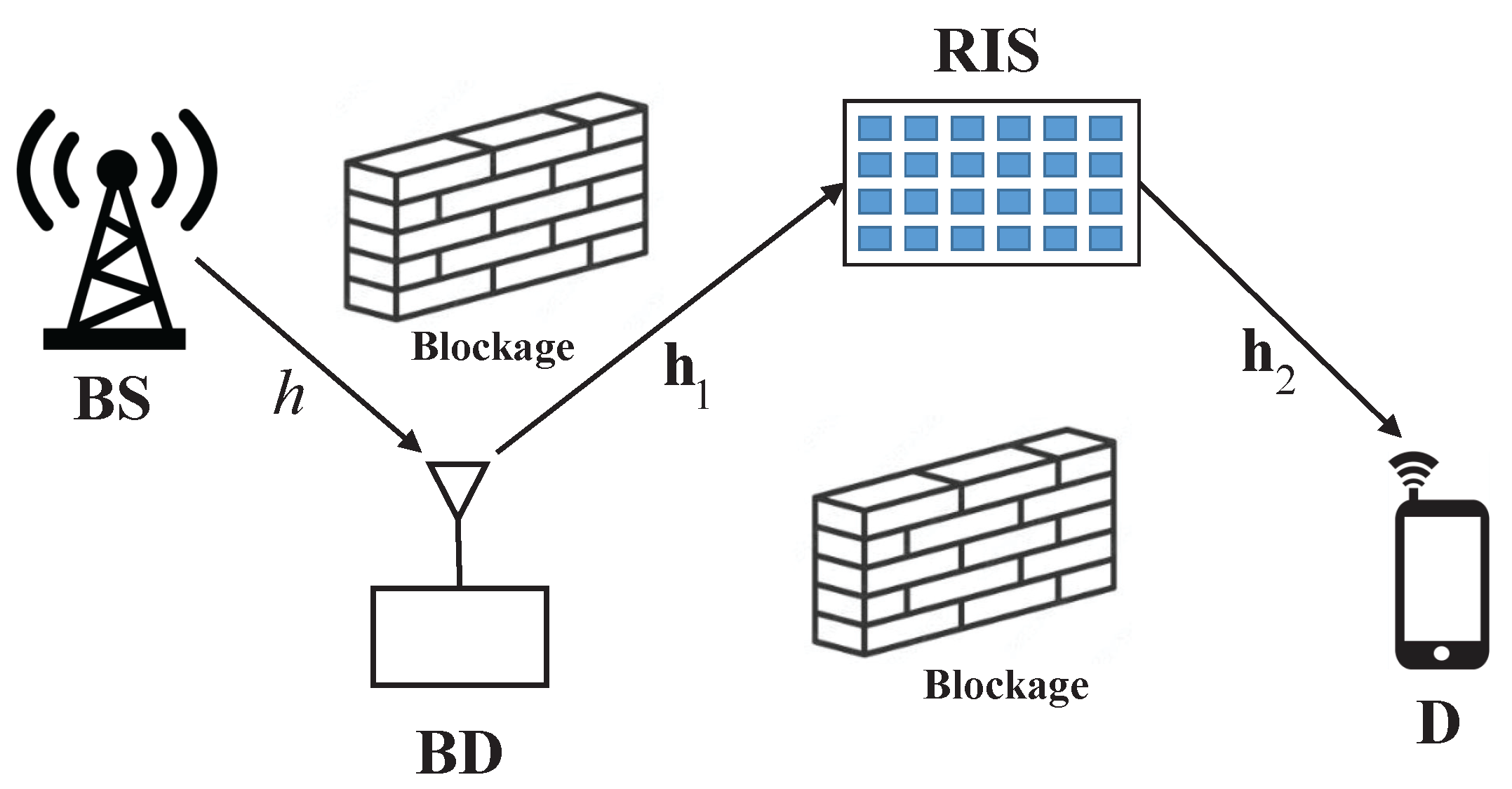
2. System Model

We consider an RIS-aided backscatter communication system consisting of a BS, BD, RIS with N reflecting elements, and D. The BS, BD, and D are equipped with a single antenna, as shown in Figure 1. Owing to severe blockages in urban and deeply shadowed regions, no direct link is assumed to exist between the BS and RIS and between the BD and D. P is the transmit power and x is the normalized transmit signal with the average unit power. The received signal x at D can be expressed as follows:

$$y={\mathbf{h}}_2^{\mathrm{T}}\mathbf{\Phi }{\mathbf{h}}_{1}h\sqrt{P}x+w,$$

(1)

where $w\sim CN(0,N_0)$ is a complex additive white Gaussian noise (AWGN) term; h is the channel coefficient from BS to BD; $\mathbf{\Phi }=\mathrm{diag}\left({\omega }_1{e}^{j{\theta }_1},{\omega }_2{e}^{j{\theta }_2},\dots ;{\omega }_N{e}^{j{\theta }_N}\right)$ denotes a diagonal matrix ${\omega }_n\in \left(0,1\right]$; $n\in \left\{1,\dots ,N\right\}$ is the amplitude reflection coefficient of the n-th reflecting element; ${\theta }_n\in \left[0,2\pi \right)$ is the phase shift of the n-th reflecting element; and the $N\times 1$ vectors ${\mathbf{h}}_1$ and ${\mathbf{h}}_2$ are the channel coefficient vectors from BD to RIS and from RIS to D, respectively. ${\mathbf{h}}_1$ and ${\mathbf{h}}_2$ are modeled using Rician fading, and h is modeled using Rayleigh fading. Therefore, the channel gains can be expressed as follows:

$${\mathbf{h}}_1={\displaystyle \frac{1}{\sqrt{d_1^{{\alpha }_1}}}}\left(\sqrt{{\displaystyle \frac{K_1}{K_1+1}}}{\overline{\mathbf{h}}}_1+\sqrt{{\displaystyle \frac{1}{K_1+1}}}{\tilde{\mathbf{h}}}_1\right),$$

(2)

$${\mathbf{h}}_2={\displaystyle \frac{1}{\sqrt{d_2^{{\alpha }_2}}}}\left(\sqrt{{\displaystyle \frac{K_2}{K_2+1}}}{\overline{\mathbf{h}}}_2+\sqrt{{\displaystyle \frac{1}{K_2+1}}}{\tilde{\mathbf{h}}}_2\right),$$

(3)

and

$$h={\displaystyle \frac{1}{\sqrt{d_3^{{\alpha }_3}}}}\tilde{h},$$

(4)

where $d_1,d_2, \mathrm{and} d_3$ and ${\alpha }_1,{\alpha }_2, \mathrm{and} {\alpha }_3$ denote the distances and path loss exponents, respectively, and $K_1,K_2$ denote the Rician factors. ${\overline{\mathbf{h}}}_1,{\overline{\mathbf{h}}}_2$ denote the normalized LOS components, and ${\tilde{\mathbf{h}}}_1,{\tilde{\mathbf{h}}}_2,$ and $\tilde{h}$ denote the normalized non-LOS components. The channel coefficients from BD to the n-th reflecting element, those from the n-th reflecting element to D, and those from BS to BD can be expressed as follows:

$${\left({\mathrm{h}}_1\right)}_n=\left|{\left({\mathrm{h}}_1\right)}_n\right|e^{j{\phi }_n},$$

(5)

$${\left({\mathrm{h}}_2\right)}_n=\left|{\left({\mathrm{h}}_2\right)}_n\right|e^{j{\varphi }_n},$$

(6)

and

$$h=\left|h\right|e^{j{\vartheta }_n},$$

(7)

where ${\phi }_n,{\varphi }_n,{\vartheta }_n\in \left[0,2\pi \right)$ are the phase shifts and $\left|{\left({\mathrm{h}}_1\right)}_n\right|,\left|{\left({\mathrm{h}}_2\right)}_n\right|,\left|h\right|$ are the magnitudes. The optimal phase shifts and amplitude reflection coefficients are adopted to maximize the channel gain, as

$${\theta }_n=-{\phi }_n-{\varphi }_n-{\vartheta }_n,$$

(8)

and

$${\omega }_n=1,$$

(9)

where for $n\in \left\{1,\dots ,N\right\}$. The maximum channel gain can be expressed as

$${\left|h\right|}_{max}=\left|h\right|\underset{\xi }{\underbrace{\sum _{n=1}^N\left|{\left({\mathrm{h}}_1\right)}_n\right|\left|{\left({\mathrm{h}}_2\right)}_n\right|}}=\left|h\right|\xi ,$$

(10)

where $\xi ={\displaystyle \sum _{n=1}^N}\left|{\left({\mathrm{h}}_1\right)}_n\right|\left|{\left({\mathrm{h}}_2\right)}_n\right|$. The received signal in (1) at D can then be given by

$$y=\left(\left|h\right|\xi \right)\sqrt{P}x+n.$$

(11)

3. Performance Analysis

In this section, we provide a detailed analysis of the ergodic capacity. The ergodic capacity is expressed as follows:

$$C=E_{\left|h\right|,\xi }\left[{log}_2\left(1+{\displaystyle \frac{{\left(\left|h\right|\xi \right)}^{2}P}{N_0}}\right)\right],$$

(12)

where $E[·]$ is the expectation operator. Notably, the probability distribution function (PDF) of ${\left(\left|h\right|\xi \right)}^2$ is intractable. Therefore, Jensen’s inequality is used. However, in our case, the upper bound of the conventional Jensen’s inequality is not tight. Therefore, we propose a tightened Jensen’s inequality, the tightened upper bound of which is almost identical to the Monte Carlo simulation results. First, we prove Theorem 1 regarding the tightened Jensen’s inequality. Second, we determine the upper bound of the conventional Jensen’s inequality. Finally, a tightened upper bound is obtained. We begin with Theorem 1. Before that, we introduce Jensen’s inequality: if X is RV and f is a convex function, then $f\left(\mathrm{E}\left[\mathrm{X}\right]\right)\le \mathrm{E}[f\left[\mathrm{X}\right]].$

Theorem 1.

Given the conventional Jensen’s inequality, by inserting a tightened upper bound, the tightened Jensen’s inequality is given by the following:

$$E_{X,Y}\left[g(X,Y)\right]\le E_Y\left[g(E\left[X\right],Y)\right]\le g(E\left[X\right],E\left[Y\right]),$$

(13)

where X and Y are independent random variables (RVs) and $g(·,·)$ is a concave function of the two variables.

Proof. 

By applying Jensen’s inequality only to the RV X, we obtained the following inequality.

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & E_{X,Y}\left[g(X,Y)\right]={\int }_0^{\infty }{\int }_0^{\infty }g(X,Y)p_X\left(x\right)p_Y\left(y\right)dxdy\hfill \\ \hfill & \le E_Y\left[g(E\left[X\right],Y)\right]={\int }_0^{\infty }g\left({\int }_0^{\infty }X{p}_X\left(x\right)dx,Y\right)p_Y\left(y\right)dy.\hfill \end{array}\end{array}$$

(14)

Similarly, when Jensen’s inequality is applied only to the RV Y, we obtain the right inequality

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & E_Y\left[g(E\left[X\right],Y)\right]={\int }_0^{\infty }g\left({\int }_0^{\infty }X{p}_X\left(x\right)dx,Y\right)p_Y\left(y\right)dy\hfill \\ \hfill & \le g(E\left[X\right],E\left[Y\right])=g\left({\int }_0^{\infty }X{p}_X\left(x\right)dx,{\int }_0^{\infty }Y{p}_Y\left(y\right)dy\right).\hfill \end{array}\end{array}$$

(15)

Q.E.D. □

Notably, Theorem 1 has more applications than a standard application of Jensen’s inequality for concave functions of multiple independent random variables. Second, we provide the upper bound of the conventional Jensen’s inequality

$$\begin{array}{c}\hfill \begin{array}{c}\hfill C_{\mathrm{U}}={log}_2\left(1+{\displaystyle \frac{E\left[{\left(\xi \right)}^2\right]E\left[{\left|h\right|}^2\right]P}{N_0}}\right),\end{array}\end{array}$$

(16)

where

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & E\left[{\left|h\right|}^2\right]={\displaystyle \frac{1}{d_3^{{\alpha }_3}}}E\left[{\left|\tilde{h}\right|}^2\right]\hfill \\ \hfill & ={\displaystyle \frac{1}{d_3^{{\alpha }_3}}},\hfill \end{array}\end{array}$$

(17)

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & E\left[{\left(\xi \right)}^2\right]=E\left[{\left(\sum _{n=1}^N\left|{\left({\mathrm{h}}_1\right)}_n\right|\left|{\left({\mathrm{h}}_2\right)}_n\right|\right)}^2\right]\hfill \\ \hfill & =E\left[\left(\sum _{n=1}^N{\left|{\left({\mathrm{h}}_1\right)}_n\right|}^2{\left|{\left({\mathrm{h}}_2\right)}_n\right|}^2\right)\right]\hfill \\ \hfill & +E\left[\left(\sum _{n=1}^N\sum _{\genfrac{}{}{0pt}{}{m=1\hfill }{m\ne n\hfill }}^N\left|{\left({\mathrm{h}}_1\right)}_n\right|\left|{\left({\mathrm{h}}_2\right)}_n\right|\left|{\left({\mathrm{h}}_1\right)}_m\right|\left|{\left({\mathrm{h}}_2\right)}_m\right|\right)\right]\hfill \\ \hfill & ={\displaystyle \frac{N}{d_1^{{\alpha }_1}{d}_2^{{\alpha }_2}}}+{\displaystyle \frac{N\left(N-1\right){\pi }^2}{16d_1^{{\alpha }_1}{d}_2^{{\alpha }_2}\left(K_1+1\right)\left(K_2+1\right)}}\hfill \\ \hfill & \times {\left({\mathrm{L}}_{\frac{1}{2}}\left(-K_1\right){\mathrm{L}}_{\frac{1}{2}}\left(-K_2\right)\right)}^2,\hfill \end{array}\end{array}$$

(18)

where ${\mathrm{L}}_{\frac{1}{2}}\left(·\right)$ denotes the Laguerre polynomial [18]. Notably, when correlation is considered, the results will be different. However, for the complexity reduction, we remove the correlation.

Third, we derive the tightened upper bound

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & C_{\mathrm{T}}=E\left[{log}_2\left(1+{\displaystyle \frac{E\left[{\left(\xi \right)}^2\right]{\left|h\right|}^{2}P}{N_0}}\right)\right]\hfill \\ \hfill & ={\int }_0^{\infty }{log}_2\left(1+{\displaystyle \frac{E\left[{\left(\xi \right)}^2\right]{\left|h\right|}^{2}P}{N_0}}\right)p_{\left|H\right|}\left(\left|h\right|\right)d\left|h\right|\hfill \\ \hfill & ={\int }_0^{\infty }{log}_2\left(1+{\displaystyle \frac{E\left[{\left(\xi \right)}^2\right]{\left|h\right|}^{2}P}{N_0}}\right)e^{-{\displaystyle \frac{{\left|h\right|}^2}{d_3^{-{\alpha }_3}}}}2{\displaystyle \frac{\left|h\right|}{d_3^{-{\alpha }_3}}}d\left|h\right|\hfill \\ \hfill & ={\int }_0^{\infty }{log}_2\left(1+{\displaystyle \frac{E\left[{\left(\xi \right)}^2\right]d_3^{-{\alpha }_3}{\left|\tilde{h}\right|}^{2}P}{N_0}}\right)e^{-{\left|\tilde{h}\right|}^2}2\left|\tilde{h}\right|d\left|\tilde{h}\right|\hfill \\ \hfill & ={\int }_0^{\infty }{log}_2\left(1+\gamma {\left|\tilde{h}\right|}^2\right)e^{-{\left|\tilde{h}\right|}^2}2\left|\tilde{h}\right|d\left|\tilde{h}\right|,\hfill \end{array}\end{array}$$

(19)

where in the fourth equation, we change the variable $\left|h\right|=\sqrt{d_3^{-{\alpha }_3}}\left|\tilde{h}\right|$, and $\gamma ={\displaystyle \frac{E\left[{\left(\xi \right)}^2\right]d_3^{-{\alpha }_3}P}{N_0}}$. Notably, we can consider $\xi$ averaging. However, this method is more difficult and provides a worse performance.

Now, we further simplify Equation (19) as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & C_{\mathrm{T}}={\displaystyle \frac{1}{ln2}}{\int }_0^{\infty }ln\left(1+\gamma {\left|\tilde{h}\right|}^2\right)e^{-{\left|\tilde{h}\right|}^2}2\left|\tilde{h}\right|d\left|\tilde{h}\right|\hfill \\ \hfill & ={\displaystyle \frac{1}{ln2}}{\left[\left(e^{{\left|\tilde{h}\right|}^2+{\displaystyle \frac{1}{\gamma }}}\mathrm{Ei}\left(-{\left|\tilde{h}\right|}^2-{\displaystyle \frac{1}{\gamma }}\right)-ln\left(1+\gamma {\left|\tilde{h}\right|}^2\right)\right)e^{-{\left|\tilde{h}\right|}^2}\right]}_{\left|\tilde{h}\right|=0}^{\infty }\hfill \\ \hfill & =-{\displaystyle \frac{1}{ln2}}{e}^{{\displaystyle \frac{1}{\gamma }}}\mathrm{Ei}\left(-{\displaystyle \frac{1}{\gamma }}\right),\hfill \end{array}\end{array}$$

(20)

where the exponential integral $\mathrm{Ei}\left(x\right)$ is defined as

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \mathrm{Ei}\left(x\right)=-{\int }_{-x}^{\infty }{\displaystyle \frac{e^{-t}}{t}}dt={\int }_{-\infty }^x{\displaystyle \frac{e^t}{t}}dt.\end{array}\end{array}$$

(21)

Finally, we express Inequality (13) in Theorem 1 in our capacity notation, that is,

$$\begin{array}{c}\hfill \begin{array}{c}\hfill C\le C_{\mathrm{T}}\le C_{\mathrm{U}},\end{array}\end{array}$$

(22)

where the Monte Carlo simulations are less than or equal to the tightened upper bound or the upper bound of conventional Jensen’s inequality.

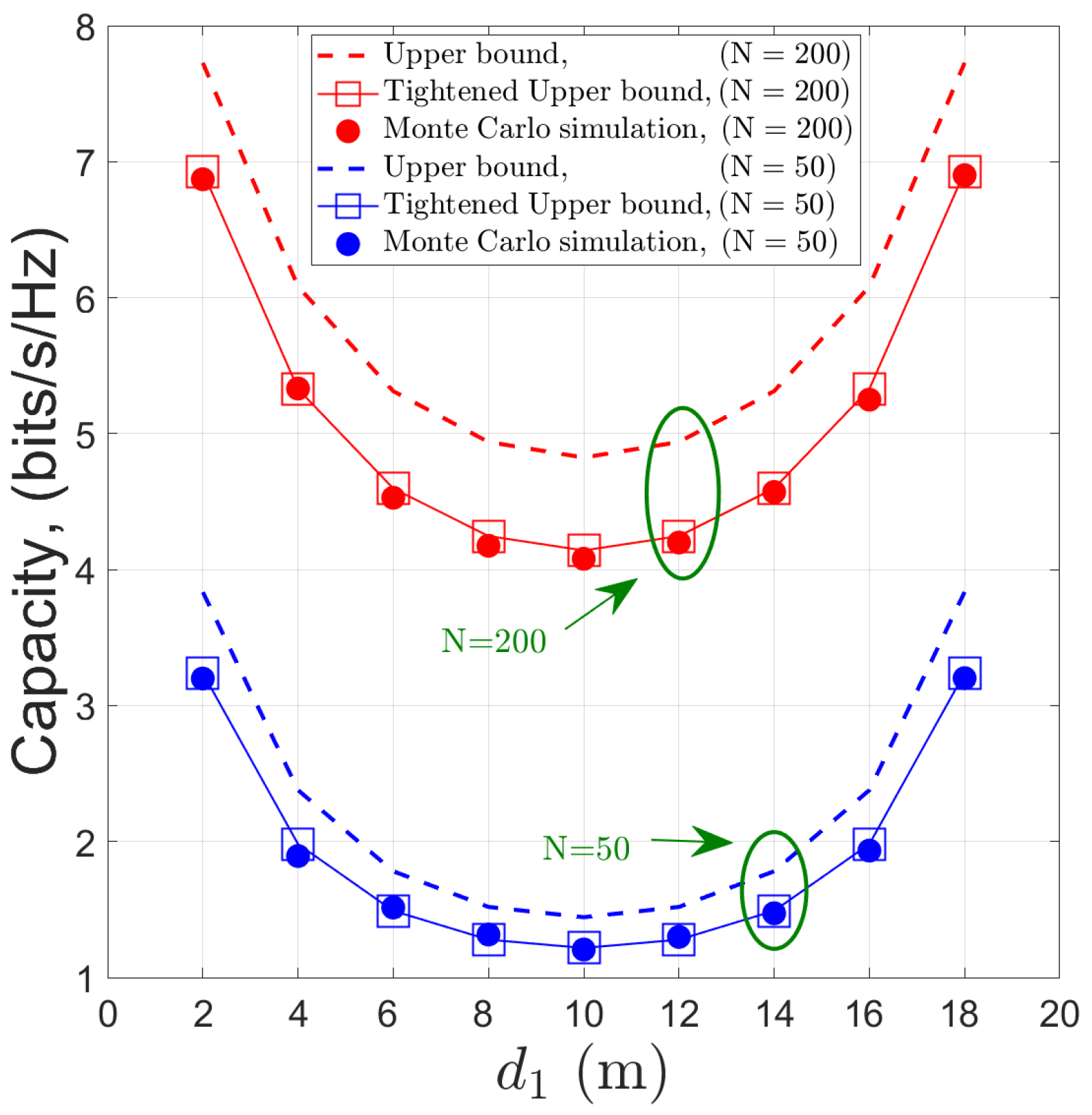
4. Numerical Results and Discussions

In this section, the simulation results are presented, and the analysis in the previous section is validated. A set of parameters is used to obtain the numerical results. In [18], an often-cited paper, N = 32, 64, and 256 is used. Therefore, we use similar numbers: N = 50, 200. The path loss exponents are given by ${\alpha }_1={\alpha }_2={\alpha }_3=2$. We set the Rician factor to $K_1=K_2=1$. Unless otherwise specified, the distances are set to $d_1=d_2=d_3=10$ m.

Figure 2 shows the ergodic capacity versus $P/N_0\left[\mathrm{dB}\right]$ for different values of N. The upper bound $C_{\mathrm{U}}$ of the conventional Jensen’s inequality is not tight for all the different values of N. However, the tightened upper bound $C_{\mathrm{T}}$ is almost the same as the Monte Carlo simulation results for C. Thus, the tightness of $C_{\mathrm{T}}$ in Theorem 1 is verified. In addition, the ergodic capacity intuitively increases with N.

Figure 3 illustrates the impact of $d_1$ or $d_2$ on the ergodic capacity when $d_3=10$ is fixed with $P/N_0=30\left[\mathrm{dB}\right]$. RIS is placed between BD and D using $d_1+d_2=20$ m. Notably, the distance between BS and D is fixed, i.e., $d_1+d_2+d_3=30$ m. The capacity function is observed to be symmetric with respect to $d_1$ and $d_2$, and the minimum capacity is obtained when RIS is at the same distance from BD and D. A higher capacity is obtained when RIS is placed close to BD or D. These observations in the RIS-assisted AmBC system are consistent with those in the conventional RIS-aided system [18].

Figure 4 depicts the effect of distance $d_3$ between BS and BD on capacity performance. In the simulation, $2\le d_3\le 18$, $d_1+d_3=20$, and $d_1+d_2=20$ are employed. Up to $d_3=14$ m, the influence of the distance $d_3$ from the BS to BD is greater than that of the asymmetry between $d_1$ and $d_2$ on the ergodic capacity. For $d_3\ge 14$ m, the impact of the asymmetry between $d_1$ and $d_2$ appears to overcome that of the distance $d_3$ between the BS and BD. In addition, as shown in Figure 3 and Figure 4, the effect of $d_3$ between BS and BD on the capacity performance is significant at a close distance.

5. Conclusions

In this study, we studied the ergodic capacity of the RIS-aided AmBC system under a Rayleigh fading channel from the BS to BD and Rician fading channels from the BD to RIS and from the RIS to D. We proposed a novel tight Jensen’s inequality and derived a new tighter ergodic capacity upper bound, which helped us determine the precise system performance. Monte Carlo simulations were performed to validate the analytical results. The tightened upper bound was almost identical to that derived from the Monte Carlo simulations, and the ergodic capacity increased significantly with the number of reflecting elements. The capacity improved when the RIS was placed close to the BD or D. Notably, the effect of the distance between the BS and BD on the capacity performance was significant at a close distance. Moreover, previous studies [19,20] produced similar results and suggest opportunities for future research. It would be interesting, for example, to consider a more practical path loss model, as in [21]. In addition, many closed-form analyses can be found in [16]. It would be interesting to investigate a multi-antenna scenario. In other words, in order to improve the rank of a RIS-aided multi-antenna system, Theorem 1 might be scalable. Finally, with recent advances in non-orthogonal multiple access (NOMA), in the future, backscattering technologies could have a significant role to play [22].