Edge Computing Task Offloading Algorithm Based on Distributed Multi-Agent Deep Reinforcement Learning

Abstract

As an important supplement to ground computing, edge computing can effectively alleviate the computational burden on ground systems. In the context of integrating edge computing with low-Earth-orbit satellite networks, this paper proposes an edge computing task offloading algorithm based on distributed multi-agent deep reinforcement learning (DMADRL) to address the challenges of task offloading, including low transmission rates, low task completion rates, and high latency. Firstly, a Ground–UAV–LEO (GUL) three-layer architecture is constructed to improve offloading transmission rate. Secondly, the task offloading problem is decomposed into two sub-problems: offloading decisions and resource allocation. The former is addressed using a distributed multi-agent deep Q-network, where the problem is formulated as a Markov decision process. The Q-value estimation is iteratively optimized through the online and target networks, enabling the agent to make autonomous decisions based on ground and satellite load conditions, utilize the experience replay buffer to store samples, and achieve global optimization via global reward feedback. The latter employs the gradient descent method to dynamically update the allocation strategy based on the accumulated task data volume and the remaining resources, while adjusting the allocation through iterative convergence error feedback. Simulation results demonstrate that the proposed algorithm increases the average transmission rate by 21.7%, enhances the average task completion rate by at least 22.63% compared with benchmark algorithms, and reduces the average task processing latency by at least 11.32%, thereby significantly improving overall system performance.

1. Introduction

With the rapid development and widespread adoption of 5G technology, its high-speed and wide-connectivity features have enabled the realization of the Internet of Everything. However, these advantages have simultaneously increased the complexity of ground tasks and accelerated the growth of data volume. Numerous ground-based user devices are constrained by limited CPUs, memory, and other hardware resources, which hinders their ability to process the surge of complex computational tasks. When many computationally intensive tasks arrive simultaneously, user devices often suffer long latency and interruptions, degrading service reliability and user experience. Task offloading can effectively alleviate the computational burden of terminal devices by offloading tasks to edge servers. It is a key technology for achieving optimal resource utilization and enhancing overall system performance. Moreover, it is directly related to latency, energy consumption, and service quality in edge computing, and has therefore become a central research focus in this field [1]. Low-Earth-Orbit (LEO) satellites, owing to their advantages of low latency and high bandwidth, provide efficient and reliable task offloading channels. They can function as edge servers for ground user devices and constitute critical infrastructure to support large-scale task offloading and data transmission [2]. Unmanned Aerial Vehicles (UAVs) can serve as edge relay nodes owing to their flexible deployment and broad coverage capabilities [3]. LEO satellite networks can further leverage UAVs to establish the forwarding layer, thereby enabling the efficient allocation of ground computing tasks to satellites or other edge nodes. This collaboration between UAVs and LEO satellites facilitates task offloading, enhances resource utilization, and improves quality of service (QoS) [4].

In the early stages of task offloading research, heuristic algorithms were extensively employed [5]. However, these algorithms typically rely on artificially defined parameters, exhibit limited adaptability to dynamic network environments, and are prone to being trapped in local optima, thereby making it difficult to optimize offloading decisions and resource allocation on a global scale. Deep Reinforcement Learning (DRL) has become the mainstream approach for addressing task offloading problems, it is particularly well-suited for optimizing strategies under dynamic network conditions and multiple constraints, such as latency and energy consumption [6]. However, single-agent DRL typically treats each node as an independent decision-making entity and lacks an effective coordination mechanism among multiple nodes. Consequently, it is difficult to achieve global optimization in multi-node collaborative environments, and it remains challenging to efficiently balance the joint optimization of discrete and continuous problems [7]. Building on these limitations, a large number of multi-agent deep reinforcement learning (MADRL) algorithms have been developed to address task offloading problems. Reference [8] introduces an MADRL algorithm that integrates an attention mechanism with proximal policy optimization (PPO) to address multi-task offloading and resource allocation problems in satellite Internet of Things (IoT) systems, this approach reduces computational costs and enhances offloading efficiency. Reference [9] proposes an MADRL algorithm designed to optimize the computation offloading strategies of IoT devices in aerial computing, thereby reducing system energy consumption and improving load balancing. Reference [10] proposes a Mixed Multi-Agent Proximal Policy Optimization (Mixed MAPPO) algorithm, in which agents optimize offloading strategies based on local observations without requiring mutual interaction, demonstrating strong performance in metrics such as task latency, load rate, and resource utilization. Reference [11] introduces a task offloading algorithm based on K-D3QN, which enhances the traditional DQN algorithm. The offloading decision process simultaneously considers three optimization objectives—task latency, resource utilization, and load balance—enabling dynamic multi-objective optimization.

However, in satellite edge computing scenarios, these existing methods encounter limitations due to the high dynamism of low-Earth-orbit (LEO) satellite–UAV collaborative networks. Users cannot obtain other users’ task decisions in real time, and the methods require collecting states, actions, and global rewards from all agents, relying on a centralized network optimization strategy. This dependence on global information can lead to excessive communication overhead and high energy consumption. To address these challenges, this paper proposes an edge computing task offloading algorithm based on distributed multi-agent deep reinforcement learning (DMADRL). In DMADRL, agents adapt to dynamic environmental changes through independent learning, make autonomous decisions based on local observations, and indirectly achieve policy coordination via global reward feedback. This distributed approach enables more efficient information sharing, optimizes both task offloading and resource allocation decisions, improves overall resource utilization, and achieves superior dynamic multi-objective optimization compared with centralized or partially distributed methods. In summary, the main contributions of this paper are as follows:

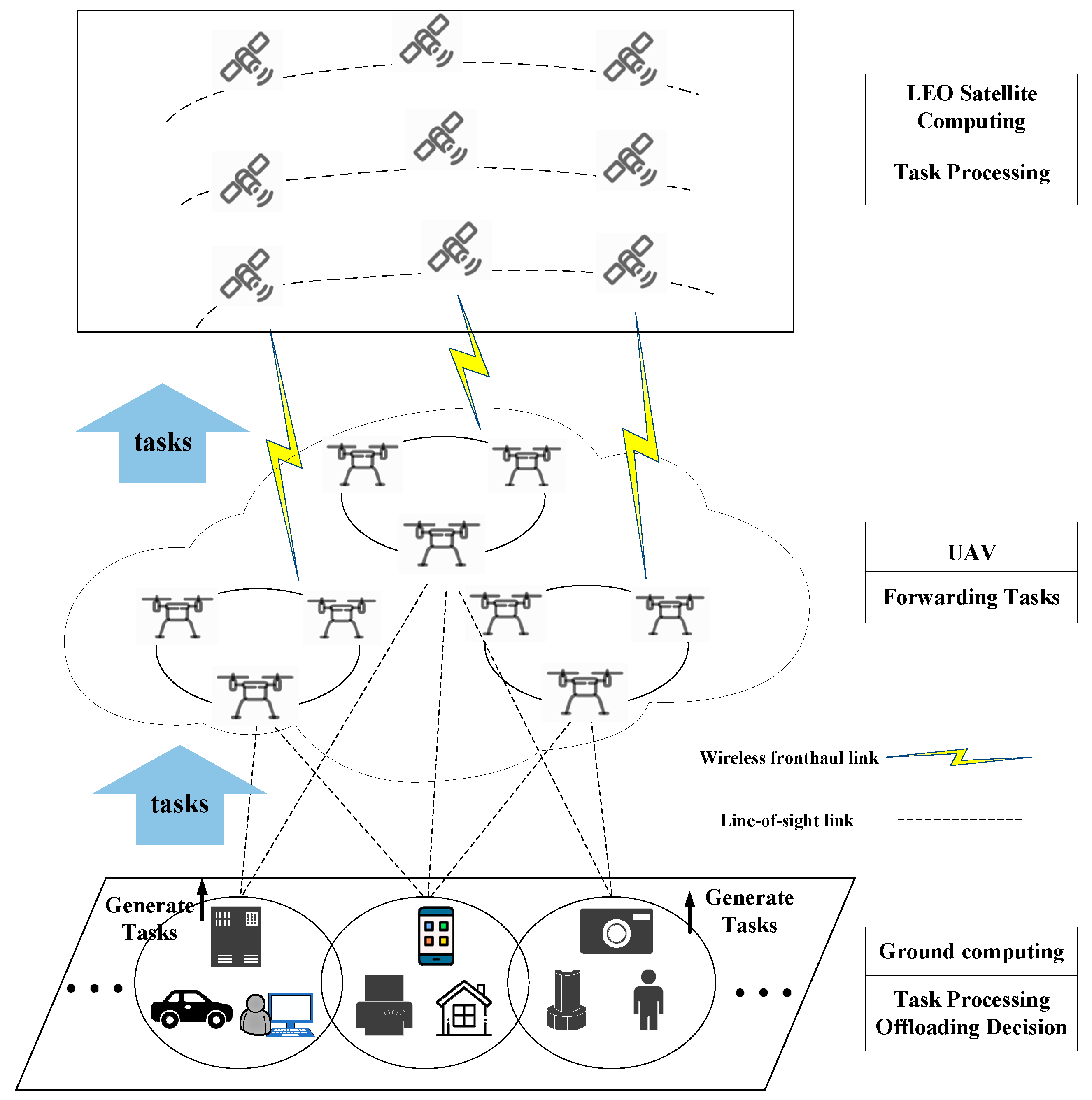
• A three-layer collaborative network architecture, comprising Ground–UAV–LEO satellites, was developed, with UAVs serving as relay layers to forward tasks, thereby enabling high-speed offloading of ground computing tasks to the LEO satellite network. In this architecture, each agent can independently generate offloading decisions without prior knowledge of other agents, ultimately achieving global optimization through global reward feedback.
• The task offloading problem is decomposed into two sub-problems: offloading decisions and resource allocation. The offloading decision sub-problem is formulated as a Markov Decision Process (MDP) and optimized using a distributed multi-agent deep Q-network (DMADQN). Q-value estimation is iteratively optimized via the online and target networks. For the resource allocation sub-problem, the gradient descent method is employed to solve the optimization problem in the continuous action space. This approach enhances the average task completion rate and reduces the average task processing latency.
• The effectiveness of the proposed algorithm was validated through simulation experiments. Compared with existing representative LEO satellite task offloading algorithms, the proposed algorithm increases the average transmission rate by 21.7%, enhances the average task completion rate by at least 22.63%, and reduces the average task processing latency by at least 11.32%, thereby significantly improving system performance and providing an efficient solution for task offloading and resource allocation in LEO satellite–UAV collaborative networks.

The remainder of this paper is organized as follows. Section 2 reviews research on task offloading in satellite edge computing. Section 3 presents the GUL model and its optimization objectives. Section 4 describes the Markov model and the solution procedures for the two sub-problems. Section 5 presents the simulation analysis. Section 6 concludes the paper and provides an outlook.

2. Related Work

In recent years, task offloading in LEO satellite mobile edge computing networks has garnered significant attention from both academia and industry [12]. This section reviews related research on satellite network architectures, deep reinforcement learning (DRL) algorithms, and multi-agent deep reinforcement learning (MADRL) algorithms. Satellite network architectures define the constraints that must be addressed at the architectural level, providing the foundational model for subsequent algorithm design. Next, traditional single-agent deep reinforcement learning algorithms are discussed, which can mitigate latency and reduce system energy consumption to a certain extent. However, their limitations are also noted—specifically the lack of a collaborative mechanism and the challenge of achieving global optimization in multi-node collaborative scenarios. Finally, attention is turned to multi-agent deep reinforcement learning (MADRL) algorithms. The core objective is to overcome the limitations of single-agent approaches and address the global optimization problem in multi-node collaborative scenarios. Nevertheless, challenges remain, including dependence on global information and limited robustness. Collectively, these three aspects encompass the core elements of task offloading research and constitute the primary focus of current studies on task offloading problems.

2.1. LEO Satellite Network Architecture Supporting Edge Computing

Currently, satellite–ground networks have emerged as a key architecture for achieving seamless global communications [13]. Cheng et al. [14] proposed an integrated air–ground–space network featuring an edge/cloud offload architecture, where UAVs provide edge computing capabilities and satellites offer cloud access services. Cui et al. [15] proposed a satellite mobile edge computing architecture that integrates edge computing technology into satellite–ground networks, optimizing latency and energy consumption. Yan et al. [16] proposed a 5G satellite edge computing framework comprising an embedded hardware platform and satellite edge computing microservices. This framework aims to reduce latency, expand network coverage, minimize packet loss and bandwidth consumption, and enhance satellite network performance. Based on the principles of deploying edge computing in satellite–ground networks, Xie et al. [17] proposed a satellite–ground edge computing network architecture, utilizing its components to address challenges such as collaborative task offloading, multi-node task scheduling, mobility management, and fault recovery. Zhou et al. [18] proposed an architecture leveraging LEO satellites in combination with federated learning. The architecture employs federated collaborative training, data privacy protection, and LEO’s extensive wireless access. By using decomposition-based and meta-deep reinforcement learning algorithms, it achieves efficient asynchronous federated learning and enhances communication efficiency. Du et al. [19] proposed a space-ground integrated network architecture combining multi-access mobile edge computing with blockchain. Satellites and UAVs serve as edge nodes to provide computing power, while blockchain ensures trust in task offloading, thereby reducing network energy consumption and enhancing resource utilization efficiency. However, when addressing complex multi-task offloading scenarios, the aforementioned edge computing-supported two-tier or three-tier architectures either suffer from high transmission loss in long-distance links due to the lack of a flexible relay layer or face single-point failure risks due to the adoption of centralized UAV control. In contrast, the Ground-UAV-LEO (GUL) architecture proposed in this paper significantly improves transmission efficiency by introducing UAVs as a distributed relay layer.

2.2. Single-Agent DRL Algorithm for Satellite–Ground Collaborative Networks

Some studies focus on algorithms based on single-agent deep reinforcement learning (DRL). Zhou et al. [20] proposed a deep risk-sensitive DRL algorithm that models computing task scheduling in integrated air–space–ground networks as an energy-constrained Markov Decision Process (MDP). Under UAV energy constraints, the algorithm effectively reduces task processing latency and increases the successful task completion ratio. Lyu et al. [21] introduced a prioritized experience replay mechanism in DRL and optimized the computation offloading strategy in a mobile edge computing system supported by collaborative LEO satellites and IoT devices. Through task offloading and inter-satellite task migration between end users and LEO satellites, the system’s weighted total energy consumption and overall latency were significantly reduced. Lakew et al. [22] proposed a hybrid discrete–continuous control DRL algorithm that transforms joint LEO satellite edge computing server selection, transmission power allocation, and partial task offloading decision-making problems into a DRL problem. The algorithm aims to maximize service satisfaction and mitigate energy consumption under constraints such as available energy. Zhang et al. [23] proposed a computation offloading strategy based on a deep deterministic policy gradient (DDPG) algorithm, effectively adapting to time-varying service demands and addressing the dual challenges of discrete offloading decisions and continuous resource allocation. However, these single-agent DRL algorithms often overlook global load status when making individual decisions in dynamic LEO satellite–UAV collaborative networks, potentially leading to idle satellite resources and overloaded ground devices. As a result, tasks may be dropped due to exceeding device processing capacity, resulting in low resource utilization and reduced task completion rates in offloading scenarios [24].

2.3. MADRL Algorithm for Satellite–Ground Cooperative Network

Multi-agent deep reinforcement learning (MADRL) effectively overcomes the limitations of single-agent approaches in global optimization of satellite–ground networks by introducing inter-agent collaboration, becoming a key algorithm for optimizing multi-dimensional strategies such as task offloading and resource allocation [25]. Kim et al. [26] proposed a MADRL algorithm integrating trajectory planning and task offloading. The algorithm jointly optimizes offloading decisions and resource allocation for multiple UAV nodes, adaptively adjusts plans in dynamic environments, balances UAV load, reduces energy consumption, and enhances task completion rates. Wang et al. [27] proposed an algorithm combining MADRL with convolutional long short-term memory networks and prioritized experience replay, applying it to an aerial layered mobile edge computing system to enhance offloading success rate and significantly reduce task latency and abandonment rate. Zhou et al. [28] proposed a satellite-to-ground task offloading algorithm based on generalized proximal strategy optimization, transforming the offloading problem into a Markov Decision Process (MDP). Under constraints such as connection duration and task deadlines, the algorithm reduces average latency and energy consumption, thereby improving task offloading performance. Jia et al. [29] decoupled a non-convex optimization problem into task offloading and resource allocation subproblems, solved the offloading subproblem using a DRL algorithm, and demonstrated that the resource allocation subproblem is convex, which was then solved using the Lagrange multiplier method. She et al. [30] proposed a 6G edge-cloud task offloading algorithm based on MADRL, optimizing the action and state spaces of the multi-agent deep deterministic policy gradient (MADDPG) algorithm, designing fine-grained resource allocation actions, and incorporating indicators such as task size and communication rate to enable agent collaboration and dynamic adjustment. However, due to the highly dynamic nature of LEO satellite–UAV collaborative networks, intelligent agents cannot access the offloading decisions of other agents in real time and often rely on central nodes to collect status, actions, and rewards for unified network optimization. When agents are physically dispersed, this reliance results in higher transmission latency and energy consumption, and central node failures may cause system crashes, leading to poor robustness. Therefore, MADRL is primarily suitable for small-scale networks with low environmental dynamics and centralized management scenarios.

In summary, the related work primarily revolves around satellite network architectures, single-agent DRL algorithms, and MADRL algorithms. As a key enabler of global seamless communication, the satellite–ground network has been extended with various architectures that integrate edge computing; however, the transmission rate remains low, and the system struggles to adapt to dynamic changes in complex multi-task offloading scenarios. The single-agent DRL algorithm can reduce latency and energy consumption, but it lacks a collaborative mechanism in multi-node scenarios and is unable to achieve global optimization. In contrast, the MADRL algorithm overcomes the limitations of single-agent approaches and enables global optimization in multi-node collaboration; however, it suffers from issues such as reliance on global information and limited robustness. To address these issues, this paper proposes an edge computing task offloading algorithm based on distributed DMADRL. In the DMADRL framework, there is no central controller, and agents are physically distributed across terminals or edge nodes. Each agent relies on local observations and indirectly achieves policy co-ordination through global reward feedback, ultimately leading to global optimization. The failure of a single node does not compromise the overall system, and the framework supports the dynamic addition and removal of nodes. This approach is well suited for large-scale, highly dynamic environments and non-centrally managed scenarios [31].

3. Model Description and Problem Analysis

In this section, we first describe the GUL network model supporting LEO satellite mobile edge computing. Then, we analyze the end-to-end latency and system energy consumption of computing tasks in both ground and LEO satellite modes. Finally, we formulate a task offloading problem aimed at minimizing the total task processing latency.

3.1. Overall Model Description

This work considers a three-layer GUL collaborative architecture consisting of user devices, UAVs, and LEO satellites (Figure 1). Here, $\mathcal{U}=\left\{1,\dots u,\dots ,U\right\}$ represents the set of user devices that can generate ground missions; $\mathcal{M}=\{1,\dots ,m,\dots M\}$ represents a collection of UAV networks, responsible for forwarding user equipment tasks; $\mathcal{N}=\{1,\dots ,n,\dots N\}$ represents a collection of LEO satellites that integrate mobile edge computing servers to provide communication services for users. Due to limited computing power, some user devices can only perform lightweight computing tasks on the ground. Therefore, computing-intensive tasks can be offloaded to LEO satellites for processing. Users can flexibly choose to process tasks on the ground or offload tasks to MEC servers on LEO satellites through UAVs for processing.

The network architecture uses wireless fronthaul links and line-of-sight links for data transmission in a time slot manner, dividing a finite period of time into $T$ time slots, the duration of each time slot is defined as $\partial$, and the time slot set is represented as $\mathcal{T}=\{1,\dots ,t,\dots ,T\}$. In each time slot, the number of tasks follows a Poisson distribution $\lambda$ with an arrival rate of. The computing tasks generated by the user device group are expressed as $Task=\left\{tas{k}_1,\dots ,tas{k}_i,\dots tas{k}_I\right\}$; among them, the i-th computing task of the user device can be represented by the triplet $tas{k}_i(t)=\left\{b_i(t),{\eta }_i(t),T_i^{\max }\right\}$, $b_i(t)$ is the data size of the task (bits), ${\eta }_i(t)$ is the computational density (computational cycles/bit), and $T_i^{\max }$ is the maximum tolerable latency in task completion, if the task is not completed within the time slot $t+T_i^{\max }$, it will be discarded. The remaining energy capacity of the user equipment when processing tasks on the ground are recorded as $C_{ground}$, and the remaining energy capacity when processing tasks on the LEO satellite are recorded as $C_{edge}$.

Table 1. Notation table.

Notation	Description
U/M/N	Number of user devices/UAVs/LEO satellites
T	Total number of time slots
$\partial$	Duration of each time slot
$tas{k}_i(t)$	The computational tasks of the user equipment group in time slot t
$b_i(t)$/${\eta }_i(t)$/$T_i^{\max }$	Data size/computation density/maximum tolerable latency of task $i$
$C_{ground}$/$C_{edge}$	Remaining energy capacity on the ground/LEO satellite when processing tasks
$T_i^{wait}(t)$/$T_i^{fin}(t)$	The time slot in which the task waits for latency/full execution or discard
$T_i^{UAV}(t)$/$T_i^{tran}(t)$	Ground/fronthaul transmission latency
$T_i^{ground-deal}(t)$/$T_i^{edge-deal}(t)$	Ground/LEO satellite computing latency
$f_{ground}$/$f_{edge}$	Ground/LEO satellite computing power
$T_i^{ground}(t)$/$T_i^{edge}(t)$	Ground/LEO satellite mission processing latency
$E_i^{ground}(t)$/$E_i^{edge}(t)$	Ground/LEO satellite processing energy consumption

lists some key notations and their related descriptions.

The user equipment and the UAV communicate via a line-of-sight link, while the UAV and the LEO satellite communicate via a wireless fronthaul link. The UAV is responsible for RF and signal transmission, while the LEO satellite is responsible for signal decoding and mission processing.

In this paper, binary offloading is considered and ${\omega }_{in}\left(t\right)=\left\{\begin{array}{l}0,LEOSatelliteComputing\hfill \\ 1,GroundComputing\hfill \end{array}\right.$ is used to represent the offloading decision of user equipment u at time slot t, that is, whether the task needs to be offloaded to the LEO n.

3.2. Ground Computing Model

For some lightweight computing tasks, ground computing can be implemented in a user device group in a collaborative network architecture, the user device u relies on its own CPU, memory, and other computing resources to process tasks. Since latency and energy consumption, respectively, reflect the “efficiency” and “cost” of task processing, they are key indicators for measuring the pros and cons of task offloading algorithms. The optimization goal of this article is to minimize latency under energy consumption constraints, so the ground computing model mainly analyzes latency and energy consumption.

3.2.1. Ground Latency Analysis

The total latency of ground task processing includes waiting latency and ground computing latency. Let $T_i^{wait}(t)$ be the waiting latency of the task on the ground and $T_i^{fin}(t)$ be the time slot for complete execution or abandonment; if the task arrives at time slot t, then the waiting latency $T_i^{wait}(t)$ can be calculated by Equation (1):

$$T_i^{wait}(t)=\max \{{\max }_{t\in \{0,1,\dots ,t-1\}}{T}_i^{fin}(t)-t,0\}$$

(1)

The computing latency of user equipment u in the ground computing task $i$ in time slot t can be calculated by Equation (2):

$$T_i^{ground-deal}(t)={\displaystyle {\sum }_{n\in N}\left(1-{\omega }_{in}\left(t\right)\right)}{\displaystyle \frac{b_i(t){\eta }_i(t)}{f_{ground}}}$$

(2)

Here, $f_{ground}$ is the ground computing capability, which is determined by the performance of the ground network server.

Then the total latency $T_i^{ground}(t)$ of user equipment u in ground processing task $i$ in time slot t can be calculated by Equation (3):

$$T_i^{ground}(t)=T_i^{wait}(t)+T_i^{ground-deal}(t)$$

(3)

3.2.2. Ground Energy Consumption Analysis

In the ground computing model, the energy consumption of user equipment, u, is mainly composed of the dynamic power consumption of the CPU when executing computing tasks. In order to describe the energy consumption of ground execution tasks, this paper adopts the widely used computing cycle energy consumption model $e=\kappa f^2$ [9]; here, $\kappa$ is the energy consumption coefficient, which reflects the power consumption characteristics under unit frequency, and $f$ is the CPU frequency, the square relationship highlights the significant impact of high-frequency computing on energy consumption. Therefore, the energy consumption of user equipment, u, on the ground for processing tasks can be defined as shown in Equation (4):

$$E_i^{ground}(t)=k{(f_{ground})}^2{b}_i(t)$$

(4)

The main factor affecting ground processing energy consumption is the amount of data. For tasks with large amounts of data, processing on ground equipment may result in excessive latency due to insufficient computing power, and its energy consumption cost will also increase.

3.3. Low-Earth-Orbit Satellite Computing Model

For computing-intensive tasks that exceed the processing capability of user devices, ground execution relying solely on the device’s CPU, memory, and other hardware resources becomes infeasible. In this case, tasks can be offloaded to LEO satellites equipped with more powerful computing capacity and executed collaboratively within a satellite cluster. The LEO satellite computing model, analogous to the ground model, primarily evaluates two critical dimensions: latency and energy consumption.

3.3.1. LEO Satellite Latency Analysis

For the offloaded data from user devices, LEO satellites need to recover data based on the signals of all UAVs in the UAV swarm. Therefore, the UAVs in the UAV swarm need to transmit data to the LEO satellite through the wireless forward link. The rate $r_{mn}(t)$ when UAV m transmits the task to the LEO satellite n is shown in Equation (5):

$$r_{mn}(t)=B{\log }_2(1+{\zeta }_{mn}(t))$$

(5)

where $B$ is the fronthaul bandwidth and ${\zeta }_{mn}(t)$ is the signal-to-noise ratio at the LEO satellite.

When the task needs to be offloaded to a LEO satellite, the end-to-end latency of the LEO satellite offloading includes three parts: the transmission latency from the user equipment u to the UAV m, the UAV fronthaul transmission latency, and the computation latency on the LEO n.

When the user equipment sends an offload request to the LEO satellite, the user equipment first transmits the data signal to the UAVs in the UAV group through the access channel. The ground transmission latency $T_i^{UAV}(t)$ of the task $i$ of the user equipment u to the UAV group can be expressed as:

$$T_i^{UAV}(t)={\omega }_{in}\left(t\right){\displaystyle \frac{b_i(t)}{r_{mn}(t)}}$$

(6)

Then, all UAVs in the UAV group will transmit the data of the user equipment they serve to the LEO satellite through the fronthaul channel. The task transmission latency $T_i^{tran}(t)$ of user equipment u in the fronthaul channel can be expressed as the maximum value of the fronthaul transmission latency of all UAVs in the group, as shown in Equation (7):

$$T_i^{tran}(t)={\displaystyle {\sum }_{n\in N}{\omega }_{in}\left(t\right)\max \left\{\frac{b_i(t)}{r_{mn}(t)}\right\}}$$

(7)

The task computing latency $T_i^{edge-deal}(t)$ of user equipment u on LEO satellite n is shown in Equation (8):

$$T_i^{edge-deal}(t)={\displaystyle {\sum }_{n\in N}{\omega }_{in}\left(t\right)}{\displaystyle \frac{b_i(t){\eta }_i(t)}{f_{edge}}}$$

(8)

Here, $f_{edge}$ is the computing power of LEO satellites, which is determined by the performance of LEO satellite network servers.

Therefore, the total unloading latency $T_i^{edge}(t)$ of the user equipment u on the LEO satellite is as shown in Equation (9):

$$T_i^{edge}(t)=T_i^{wait}(t)+T_i^{UAV}(t)+T_i^{tran}(t)+T_i^{edge-deal}(t)$$

(9)

In summary, the total latency $T_i^{total}(t)$ of task offloading of user device u is shown in Equation (10):

$$T_i^{total}(t)=\max \{T_i^{ground}(t),T_i^{edge}(t)\}$$

(10)

The returned result data is extremely small compared to the input data (including information such as task attributes), so the transmission latency of the task computing result return is ignored.

3.3.2. LEO Energy Consumption Analysis

The processing energy consumption of user equipment u in the LEO satellite includes the transmission energy consumption of offloading task $i$ of user equipment u to the UAV swarm, the transmission energy consumption of the UAV swarm offloading task $i$ to LEO, and the computing energy consumption of LEO satellites.

The transmission energy consumption of task $i$ offload to the UAV swarm is defined as shown in Equation (11):

$$E_i^u(t)={\omega }_{in}\left(t\right){\displaystyle \frac{b_i(t)}{r_{mn}(t)}}{p}_u$$

(11)

Here, $p_u$ is the transmission power of task $i$ offload to the UAV swarm.

The transmission energy consumption of offloading the UAV swarm to LEO is defined as shown in Equation (12):

$$E_i^{u-l}(t)={\omega }_{in}\left(t\right)\max \left\{{\displaystyle \frac{b_i(t)}{r_{mn}(t)}}\right\}{p}_{u-l}$$

(12)

Here, $p_{u-l}$ is the transmission power of the mission from the UAV swarm to the LEO satellite.

Similarly to ground computing, the computing energy consumption $E_i^{edge-deal}(t)$ of user equipment u in LEO satellite is defined as shown in Equation (13):

$$E_i^{edge-deal}(t)=k{(f_{edge})}^2{b}_i(t)$$

(13)

Therefore, the total processing energy consumption $E_i^{edge}(t)$ of user equipment u on the LEO satellite is as shown in Equation (14):

$$E_i^{edge}(t)=E_i^u(t)+E_i^{u-l}(t)+E_i^{edge-deal}(t)$$

(14)

In summary, the total energy consumption $E_i^{total}(t)$ of task offloading of the user equipment u is shown in Equation (15):

$$E_i^{total}(t)=\max \{E_i^{ground}(t),E_i^{edge}(t)\}$$

(15)

3.4. Optimization Objectives

In order to achieve efficient offloading decisions and resource allocation, user devices and LEO satellites need to consider the long-term impact of their own behavior when making decisions. Therefore, the optimization goal of this paper is to minimize the long-term average total latency of all user devices.

Assuming $\Omega =\left\{{\omega }_{in}(t)\right\},i\in I,n\in N,t\in T$ and $C=\max \left\{C_{ground}+C_{edge},0\right\},i\in I,n\in N,t\in T$, we can construct an optimization problem to minimize latency under energy consumption constraints, defined as P1. The definition constraint of P1 is shown in Equation (16):

$$\begin{array}{l}P1\text{:}\underset{\Omega ,C}{\min }{\displaystyle \frac{1}{IT}}{\displaystyle \sum _{t=1}^T{\displaystyle \sum _{i=1}^I{T}_i^{total}(t)}}\hfill \\ s.t.\hfill \\ C1: {\omega }_{in}\left(t\right)\in \left\{0,1\right\},\forall i\in I,\forall n\in N\hfill \\ C2: T_i^{\max }\left(t\right)\le \tau ,\forall i\in I,\forall t\in T\hfill \\ C3: 0<f_{ground},0<f_{edge},\forall i\in I,\forall n\in N\hfill \\ C4: 0\le E_i^{ground}(t)\le C_{ground},\forall i\in I,\forall t\in T\hfill \\ C5: 0\le E_i^{edge}(t)\le C_{edge},\forall i\in I,\forall t\in T\hfill \end{array}$$

(16)

$C1$ means that the task of each user device in each time slot can only be processed on the ground or in LEO satellites.

$C2$ means that all tasks of the user equipment must be completed within the maximum tolerable latency; otherwise, they will be discarded.

$C3$ means that both the ground computing power and the LEO satellite computing power are positive values.

$C4$ defines the range of values for the energy consumption allocation for ground task processing, which must not exceed the energy capacity for the remaining ground computing and processing tasks.

$C5$ defines the range of values for the allocation of energy consumption for LEO satellite mission processing, which must not exceed the energy capacity for the remaining LEO satellite computing and processing tasks.

The optimization problem P1 needs to decide whether to offload the task (discrete action) and determine the amount of resource allocation (continuous action), so it is a mixed action space problem, which has been proven to be an NP-hard problem.

4. Distributed Multi-Agent Offloading Decision and Resource Allocation Solution

In this section, we first decompose the task offloading problem and then discuss the offloading decision and resource allocation process of the GUL three-layer collaborative network when the task arrives.

4.1. Decomposition of the Task Offloading Problem

This paper decomposes the task offloading problem into offloading decision subproblems and resource allocation subproblems, as shown in Figure 2. $o$ is the offloading decision subproblem. A distributed multi-agent deep Q network algorithm is adopted to allow the agents to learn in continuous interaction with the environment. Each agent generates an offloading decision based on its own task attributes and the load of the LEO computing satellite. The agent regularly downloads updated network parameters to optimize its policy network. Using these updated parameters, the agent makes new offloading decisions based on the current state, thereby determining the optimal resource allocation strategy. $a$ is the resource allocation subproblem, the gradient descent method is adopted to accelerate the finding of the global optimal solution and ensure reasonable resource allocation.

4.2. Offloading Decision Process

The offloading decision is central to system performance and must adapt to the dynamic GUL environment. This section will focus on the implementation process of the unloading decision process, model the unloading decision problem as a Markov decision process, and realize dynamic unloading decision optimization through a distribution multi-agent deep Q network.

4.2.1. Markov Model

In this paper, the offloading decision problem can be modeled as a Markov model because the state is observable, the action (binary decision of ground or satellite processing) is clear, the reward value is quantifiable, and the optimization goal is consistent with maximizing the long-term cumulative reward. The Markov decision model is described using the five-tuple $\left\{s_t,a_t,r_t,s_{t+1},\gamma \right\}$, where $s_t$ represents the state space, $a_t$ represents the action space, $r_t$ represents the reward function (used to determine the feedback after taking an action in the current state), $s_{t+1}$ represents the state of the next step, and $\gamma$ represents the discount factor (reflecting the importance of future rewards).

(1)

State space

The state variables mainly include the task attributes of the user device u itself and the load of the ground and LEO computing satellites. Assuming the ground load is $C_{ground-load}$ and the load of the LEO computing satellite is $C_{edge-load}$, the state of the user device u is defined as $s_t=\left\{b_i(t),{\eta }_i(t),T_i^{\max },T_i^{wait}(t),C_{ground-load},C_{edge-load}\right\}$.

(2)

Action Space

After obtaining the observation status, the user device needs to make a task offloading decision for the current time slot t and define the action as a discrete variable: $a_t=\left\{{\omega }_{in}(t),\forall i\in I,\forall n\in N\right\}$, where ${\omega }_{in}\left(t\right)=0$ represents the computing task $tas{k}_i(t)$ of user device u being processed on the ground, and ${\omega }_{in}\left(t\right)=1$ represents the choice of offloading the task to the LEO satellite.

(3)

Reward function

According to the state $s_t$, user device u adopts the offloading strategy $a_t$ to interact with the environment and obtains the reward $r_t$. The reward $r_t$ shared by all user devices in time slot t consists of two parts: the value of the average total latency of all user devices and the penalty item of the task processing latency of all user devices. That is $r_t={\displaystyle \frac{1}{I}}{\displaystyle \sum _{i=1}^I{T}_i^{total}(t)}-k^n{\displaystyle \sum _{i=1}^I\frac{T_i^{total}(t)-\min (T^{total}(t))}{\max (T^{total}(t))-\min (T^{total}(t))}}$, where $k^n$ is the penalty item weight, $\min (T^{total}(t))$ denotes the minimum value of the total latency across all user devices, and $\max (T^{total}(t))$ denotes the maximum value of the total latency across all user devices.

The offloading decision process framework based on DMADQN is shown in Figure 3. The framework consists of five modules: user task module, experience replay buffer pool module, training network module, resource allocation module, and loss function module, which revolve around the offloading decision and resource allocation of user tasks. The above five modules realize effective resource allocation for user tasks, allowing the system to achieve a dynamic balance between task processing and resource allocation.

(1)

User task module. Each task contains status information such as task generation, transmission queue, computing queue, and satellite load. The user task module passes the status information to the training network for training. After training, a complete interactive four-tuple experience group $\left\{s_t,a_t,r_t,s_{t+1}\right\}$ is obtained. On the one hand, this four-tuple is passed to the experience playback buffer module for sampling, and on the other hand, it is passed to the resource allocation module to guide resource allocation.

(2)

Experience replay buffer module. The experience gained during training is stored in the replay buffer, from which the agent can sample to improve learning efficiency, accelerate convergence, and suppress overfitting. Specifically, the agent stores the set $\left\{s_t,a_t,r_t,s_{t+1}\right\}$ in the experience replay buffer R. Then, the agent extracts a small batch of N samples from R and updates the parameters ${\theta }_{\mu }$ and ${\theta }_{\nu }$ of the online network.

(3)

Training network module. The action network and the value evaluation network are approximated by two independent frameworks, namely the Action execution network and the Value evaluation network. The functions are as follows: the Action execution network is responsible for executing decisions, while the Value evaluation network is responsible for evaluating the correctness of the behavior. In the Action execution network or the Value evaluation network, there is an online network and a target network. The four networks have the same structure, the parameters of the online network are ${\theta }_{\mu }$ and ${\theta }_{\nu }$, and the parameters of the target network are ${\theta }_{\mu }^{\prime }$ and ${\theta }_{\nu }^{\prime }$. The weights of the target network are copied from the online network regularly, but the update frequency is much lower than that of the online network. This approach helps to reduce the correlation between the target Q value (the expected return) and the current Q value (the actual return), thereby reducing the volatility in the learning process and solving the instability problem of the training process. After training, the actions are passed to the user task module to guide decision-making.

(4)

Resource allocation module. Resources are allocated based on the complete historical interaction experience transmitted by the task module, and then the reward value of the task training sample that completes the communication is passed to the loss function module to calculate the loss function.

(5)

Loss function module. The error between the predicted value and the target value of the evaluation network is calculated to measure the accuracy of the strategy, and the parameters of the training network are updated in reverse.

4.2.2. Decision Process Design

The action execution network outputs a specific action $a_t$ through the strategy and current state $s_t$. When the action decision is determined, the value evaluation network outputs the Q value at time slot t based on the currently observed state and action to evaluate the quality of the current action. The Q value computing formula is Equation (17):

$$Q_{\pi }\left(s_t,a_t\right)=E\left[r_t(s_t,a_t)\left|s_t,a_t,\right.\pi \right]$$

(17)

Equation (17) represents the expected reward of executing action $a_i(t)$ in the observed state $s_i(t)$ under the strategy $\pi$, and $Q_{\pi }$ is the Q value.

The goal of the algorithm DMADQN is to maximize the expected cumulative discounted reward. The optimization goal is to find the optimal offloading strategy value $Q_{\pi }^{\prime }$ for each user device, u, which can be expressed as:

$$Q_{\pi }^{\prime }\left(s_t,a_t\right)=\begin{array}{cc}\underset{\pi }{{\displaystyle \mathrm{argmaxmize}}}& E\left[{\displaystyle \sum _{t=1}^T\gamma \cdot r_t(s_t,a_t)}\left|\pi \right.\right]\end{array}$$

(18)

Here, $\gamma$ is the future discount factor, $\gamma \in \left[0,1\right]$, and the larger the $\gamma$ is, the more importance is attached to future rewards.

The Q value update computing is shown in Equation (19):

$$Q\left(s_t,a_t\right)=Q\left(s_t,a_t\right)+\alpha \times \left[r_t+\gamma Q\left(s_{t-v},a_{t-v}\right)\right]$$

(19)

Here, $Q\left(s_{t-v},a_{t-v}\right)$ is the Q value calculated by the target network, $Q\left(s_t,a_t\right)$ is the Q value calculated by the online network, and $\alpha$ is the learning rate.

The value evaluation network updates parameters by minimizing the loss function. The loss function $\mathcal{L}$ can be calculated by formula Equation (20):

$$\mathcal{L}=E{\left[r_t(s_t,a_t)+\gamma {\max }_{a_i(t)}{Q}_{\pi }^{\prime }\left(s_t,a_t\right)-Q_{\pi }\left(s_t,a_t\right)\right]}^2$$

(20)

Here, ${\max }_{a_i(t)}{Q}_{\pi }^{\prime }\left(s_t,a_t\right)$ represents the future optimal Q value, and $Q_{\pi }\left(s_t,a_t\right)$ represents the current Q value.

The total system loss function ${\mathcal{L}}_{total}$ can be calculated by formula Equation (21):

$${\mathcal{L}}_{total}={\displaystyle \sum _i{\mathcal{L}}_i}$$

(21)

To prevent the training process from diverging and ensure the stability of the algorithm, this scheme uses a constant $\tau$ close to 0 to soft-update the target network parameters, as shown in Equation (22):

$${\theta }_{target}\leftarrow \tau {\theta }_{\nu }+\left(1-\tau \right){\theta }_{\nu }^{\prime }$$

(22)

Since the unloading decision is a discrete action, this paper adopts the $\epsilon \text{-}$ greedy strategy to select the unloading decision. The change trend of the action selection probability $\epsilon$ is shown in Equation (23):

$$\epsilon \leftarrow \epsilon +\Delta$$

(23)

Here, $\Delta$ is a positive value close to 0. In the early stage, it is increased so that the intelligent agent can fully explore the environment, and in the later stage, it is reduced to tend to choose the optimal action.

4.3. Resource Allocation Process

The resource allocation process uses the gradient descent method, which adapts to the dynamic load in satellite edge computing through iterative updates. The objective function gradient computing is shown in Equation (24):

$$C^{new}(t)=C^{old}(t)-\alpha \cdot {\displaystyle \frac{A(t)}{{\left(C^{old}(t)\right)}^2}}$$

(24)

Here, $C^{old}(t)$ is the pre-iteration computing resource allocated to user equipment u in time slot t, $C^{new}(t)$ is the resource allocation amount after gradient descent update, and $A(t)$ is the cumulative amount of data to be processed by user equipment u. The final allocated resources are shown in Equation (25):

$$C^{proj}(t)=\left\{\begin{array}{ll}ϵ,\hfill & if{C}^{new}(t)<ϵ\hfill \\ {\displaystyle \frac{C^{\max }(t)\cdot C^{new}(t)}{{\displaystyle \sum _i{C}^{new}(t)}}},\hfill & if{\displaystyle \sum _i{C}^{new}(t)}>C^{\max }(t)\hfill \\ C^{new}(t),\hfill & otherwise\hfill \end{array}\right.$$

(25)

Here, $C^{proj}(t)$ is the final resource allocation result, $C^{\max }(t)$ is the maximum available resource in a single time slot, and $ϵ$ is a very small positive number to ensure the non-negativity of resources.

The convergence of the iteration of Equation (24) can be judged by Equation (26):

$$if{\displaystyle \frac{{‖f^{proj}(t)-f^{old}(t)‖}_2}{{‖f^{old}(t)‖}_2}}<{\delta }_{thr},thenstopiteration$$

(26)

where $f^{proj}(t)$ is the final resource allocation vector, $f^{old}(t)$ is the resource allocation vector before iteration, which is used to calculate the relative error, ${\Vert \Vert }_2$ is the Euclidean norm used to measure the vector difference, and ${\delta }_{thr}$ (10⁻³) is the convergence threshold. When the relative error is less than this value, the resource allocation is considered to have converged.

The DMADQN algorithm for the task offloading decision is shown in Algorithm 1. The algorithm first randomly initializes the action network and evaluation network parameters and clears the experience replay buffer. For each episode, reset the environment state and reward. Select actions according to the $\epsilon \text{-}$ greedy method in each training round, observe the reward and new state, and store the transition tuple in the buffer. Then, for each agent, randomly extract small batch samples from the buffer for training, calculate the loss function and soft update, and update the state and value evaluation network parameters. After completing the task processing, reduce the exploration rate according to the formula, repeat until the training is completed, and finally return the task processing result. The algorithm improves the accuracy and robustness of task offloading decisions by distributing the estimated value function.

Algorithm 1: DMADQN algorithm for Offloading decision

Input: t time slot task status Output: Offloading decision 1.  Randomly initialize action execution network parameters and value evaluation network parameters. 2.  Initialize the experience replay buffer R to be empty. 3.  For each episode from 1 to $E_{\max }$ do: 4.    Reset the environment state $s_t$ and set the reward $r_t$ to 0. 5.    For each round of training from 1 to $T$ do: 6.      According to $\epsilon \text{-}$, greedily select action $a_t$ and observe reward $r_t$ and new state $s_{t+1}$. 7.      Store the experience tuple $\left\{s_t,a_t,r_t,s_{t+1}\right\}$ into the experience replay buffer R. 8.      For each agent from 1, 2, …, do: 9.        Randomly extract N small batches of samples $\left\{s_t,a_t,r_t,s_{t+1}\right\}$ from the experience replay buffer for training. 10.       Calculate the loss function through $\mathcal{L}=E{\left[r_t(s_t,a_t)+\gamma {\max }_{a_i(t)}{Q}_{\pi }^{\prime }\left(s_t,a_t\right)-Q_{\pi }\left(s_t,a_t\right)\right]}^2$. 11.       Soft update through ${\theta }_{target}\leftarrow \tau {\theta }_{\nu }+\left(1-\tau \right){\theta }_{\nu }^{\prime }$. 12.       Update Status $s_{t+1}\leftarrow s_t$. 13.     End for. 14.     Update value evaluation network parameters. 15.   End for. 16.   After completing the task processing, the result is returned to the user device. 17.   Reduce exploration rate according to $\epsilon \leftarrow \epsilon +\Delta$. 18. End for.

4.4. Algorithm Complexity Analysis

The computational complexity of the proposed distributed multi-agent deep Q-network (DMADQN)-based task offloading algorithm is analyzed along two core dimensions: time complexity and space complexity, with the overall complexity determined by their combination.

(1)

Time Complexity

The time complexity of the DMADQN algorithm is determined by three primary factors: the number of training iterations, the computational overhead per iteration, and the number of trainable parameters. Let $N_{epi}$ denote the number of training iterations, $C_{epi}$ denote the computational overhead per iteration (including experience replay sampling, Q-value computation, loss optimization, and parameter updates), and $N_{par}$ denote the number of trainable parameters. Accordingly, the time complexity can be expressed as: $O(N_{epi}·C_{epi}·N_{par})$.

(2)

Space Complexity

For the proposed DMADQN algorithm, the space complexity primarily depends on the storage overhead of training data and the number of neurons in the network. Let $S_{data}$ denote the storage required for training data, and ${\displaystyle \sum _i^I{l}_{ai}}$ denote the total number of neurons across all network layers. The space complexity can thus be expressed as: $O(S_{data}+{\displaystyle \sum _i^I{l}_{ai}})$.

In summary, the total computational complexity of the distributed multi-agent deep Q-network (DMADQN) algorithm is obtained by combining its time and space complexities and can be expressed as: total computational complexity = $O=(N_{epi}·C_{epi}·N_{par}+S_{data}+{\displaystyle \sum _i^I{l}_{ai}})$. In practical scenarios, time complexity dominates the overall computational cost, whereas space complexity is relatively negligible. This observation is consistent with the simulation results presented in Section 5.2.1, where the algorithm converges stably within 10,000 training episodes, confirming that the complexity remains manageable under the hardware environment considered in this work.

5. Simulation Analysis

In this section, we conduct a simulation analysis of an edge computing task offloading algorithm based on distributed multi-agent deep reinforcement learning. First, we describe the simulation environment and simulation parameter settings. Then, we perform a convergence analysis of the algorithm. Finally, we evaluate its performance by comparing the optimal strategy trained by the DMADQN algorithm with the baseline algorithm under different parameters.

5.1. Simulation Environment Settings

This paper builds a LEO satellite edge computing simulation environment based on reference [9] and verifies the performance of the proposed algorithm through experiments. The experimental hardware configuration is: 32 GB DDR5 memory, NVIDIA (Santa Clara, CA, USA) GeForce RTX 4060 Ti graphics card, 2.5 GHz Intel Core i5-13490F processor; the software environment uses Python v3.13 and TensorFlow v2.4.0.

Referring to the logical framework of the relevant references [32], Algorithm 1 trains the model by setting the maximum number of rounds $E_{\max }$ = 10,000, the number of time slots $T$ = 100, and the maximum time slot length $\partial$ = 200. Assume that the computing power of the ground user equipment is [1, 3] GHz, the computing resources of a single satellite are [30, 50] GHz, the task data size $b_i(t)$ is Distributed in [100, 150] KB, the maximum tolerable latency $T_i^{\max }$ of the task is 0.1 s, the task computing density is Distributed in [500, 1000] Cycle/Bit, the signal-to-noise ratio at the LEO satellite n is 20 dB, and the transmission power of the user equipment group-UAV group and the UAV group-LEO satellite group is 1 W and 3 W, respectively. In addition, in the simulation experiments of this paper, the task arrival rate $\lambda$ follows a Poisson distribution, with an average of 5 tasks arriving per time slot, this enables us to fully verify the algorithm’s ability to handle moderate workloads. The energy consumption coefficient $\kappa$ is set to 10⁻²⁸ with reference to Reference [9], ensuring that the energy consumption calculation unit matches the actual computing energy consumption. The penalty weight $k^n$ for the reward value is set to 0.1, which not only urges the algorithm to reduce overall latency but also reduces the number of tasks discarded due to exceeding the maximum tolerable latency, thereby improving the task completion rate. The exploration rate $\epsilon$ decreases from 1 to 0.01, allowing the agent to learn the environment and ensuring the algorithm converges within 1000 episodes; to balance sample diversity and memory efficiency, the size of the experience replay buffer R is set to 60,000, and the size of the mini-batch sample is set to 256, which ensures stable parameter updates and fast convergence. During training, the future discount factor $\gamma$ is set to 0.95, which can effectively balance immediate rewards and future rewards; to balance convergence speed and stability, The initial learning rate $\alpha$ of both the action execution network and the value evaluation network is set to 0.01. To maintain training stability, the soft update factor $\tau$ is set to 0.001. The parameter settings used in this simulation are summarized in

Table 2. Simulation parameter settings.

Parameter	Value
Poisson Distribution $\lambda$	5
Energy Consumption Coefficient $\kappa$	10−28
Penalty Weight $k^n$	0.1
Exploration Rate $\epsilon$	From 1 to 0.01
Experience Replay Buffer Size R	60,000
Mini-Batch Sample Size	256
Discount Factor $\gamma$	0.95
Initial Learning Rate $\alpha$	0.01
Soft Update Factor $\tau$	0.001

.

5.2. Simulation Results Analysis

This section analyzes the convergence of the DMADQN algorithm and compares the performance of the algorithm with five benchmark algorithms through simulation experiments.

5.2.1. Algorithm Convergence Analysis

Convergence indicates that the algorithm reaches a stable state within a limited number of iterations, adapting to network changes and yielding consistent offloading decisions.

Figure 4 shows the convergence of the DMADQN algorithm in the simulation experiment of this paper. As training rounds increase, the algorithm’s reward gradually rises and stabilizes around 1000 rounds. During the pre-training period, the average reward was unstable because the $\epsilon \text{-}$ greedy strategy selected actions with a large amplitude. In the later stage, the optimal action was selected by reducing the value of $\epsilon$, and the average reward was relatively stable.

5.2.2. Performance Comparison Analysis

This section compares the DMADQN algorithm with the following five baseline algorithms:

(1)

Local Computing (LC): In each time slot, all arriving tasks are processed by the user equipment on the ground.

(2)

Deep Q Network (DQN) [33]: This strategy implements resource allocation by discretizing the continuous action space. The network architecture of the algorithm is the same as the value evaluation network in this paper, and the ε-greedy strategy is also adopted during the exploration process.

(3)

Dual Deep Q Network (DDQN) [34]: Since the maximization operation in DQN easily leads to large Q value estimation, DDQN was proposed based on the original DQN to reduce this overestimation problem. The algorithm improves the accuracy of algorithm learning by decoupling the action selection and evaluation process of the objective value function.

(4)

Deep Deterministic Policy Gradient (DDPG) [35]: DDPG employs deep reinforcement learning (DRL) to optimize dynamic decision-making for continuous actions in task offloading. It aims to balance multiple objectives, including latency and energy consumption, while adapting to changing environments, but its convergence speed is relatively slow.

(5)

Distributed Multi-Agent Deep Deterministic Policy Gradient (MADDPG) [36]: This algorithm is a multi-agent extension of DDPG, addressing the value estimation bias issue in multi-agent environments. During the execution phase, each agent generates continuous actions based on its own local observations and an independent policy network without relying on global information.

When the number of UAVs is fixed at 30 and the number of LEO satellites is fixed at 10, the comparison of the average transmission rates of the GUL model in this paper and the ground–LEO satellite model is shown in Figure 5. In task offloading scenarios, transmission rates decrease as tasks increase, but our model consistently maintains a higher rate, which is an average increase of 21.7% compared with the ground–LEO satellite model. The reason is that the transmission distance is greatly shortened by UAV relay to reduce path loss and utilize the short-distance and high-bandwidth characteristics of high-frequency bands. At the same time, UAVs can dynamically adjust their positions to avoid terrain and building obstructions and use cognitive radio technology to avoid interference bands. Since the LC algorithm does not involve offloading tasks to LEO satellites, it is not discussed here.

The task completion rates of DMADQN and five baseline algorithms under varying numbers of tasks are presented in Figure 6. As the number of tasks increases, the task completion rates for all algorithms decline. The DMADQN algorithm, discussed in this paper, effectively mines high-value samples, updates strategies efficiently, maintains smaller value estimation deviations, and better captures and distributes value uncertainty, leading to improved decision-making. Consequently, it consistently achieves the highest task completion rate, exceeding the baseline algorithms by at least 22.63%. In contrast, the LC algorithm experiences the most significant drop-in average task completion rate. This decline occurs because all incoming tasks require the user device to rely solely on its limited CPU, memory, and other hardware resources for processing. When faced with a greater number of tasks, the device cannot handle the load. When MADDPG handles continuous actions, it needs to balance resource allocation and offloading decisions, which easily leads to mismatches between decisions and task requirements, thereby increasing the task drop rate. DQN employs uniform sampling for experience replay and does not target high-value sample mining, resulting in limited learning efficiency. As the number of tasks increases, it struggles to update strategies effectively, leading to a notable decline in task completion rates. Although DDQN utilizes dual networks to mitigate DQN’s overestimation issue, it does not entirely eliminate value estimation deviations. Meanwhile, DDPG, unlike DMADQN, is unable to effectively distribute and manage value uncertainty when confronted with a high volume of tasks, which may result in decision-making failures.

Figure 7 illustrates the average task processing latency for DMADQN compared to five baseline algorithms, evaluated at different task quantities. With more tasks, all algorithms show higher average latency. However, DMADQN consistently maintains the lowest average latency, which is at least 11.32% lower than that of the baseline algorithms. The LC algorithm does not utilize external resources, leading to higher latency for computationally intensive tasks compared to the other five algorithms, primarily due to the limited computing power of the device. MADDPG needs to generate continuous actions through a policy network and undergo parameterized conversion, resulting in higher computational complexity and significant single-step decision latency. DDQN addresses the issue of Q-value overestimation by separating action selection from evaluation. However, it is still based on expected value estimation and struggles with distribution uncertainty. In complex dynamic environments, DDQN often has higher latency compared to DMADQN. DDPG is designed for continuous action spaces but requires mapping continuous actions to discrete choices. In contrast, DMADQN can directly select the optimal discrete action through distribution estimation, which reduces the time overhead associated with intermediate conversions.

The average latency comparison of DMADQN, DQN, DDPG, and DDQN algorithms under different numbers of UAVs is shown in Figure 8. Since the LC algorithm only processes tasks on the ground, the impact of the number of UAVs on its latency is not discussed. Under different numbers of UAVs, the DMADQN algorithm can more accurately evaluate the Q-values of different decision-making actions, with relatively lower average latency overall. It demonstrates superior task scheduling and latency optimization capabilities, and through multi-branch Q-value stabilization, it can better adapt to the scenario of UAV-aided task offloading. In contrast, the MADDPG needs to perform parameterized mapping through a policy network when handling continuous actions, and then adapt to discrete offloading requirements, resulting in a long computational chain, high complexity, and significantly increased decision latency. The DQN algorithm has relatively higher average latency, while the DDQN and DDPG algorithms perform between the two, highlighting the differences in latency optimization for UAV task processing among various reinforcement learning algorithms. This validates the effectiveness of DMADQN in this scenario.

The difference in average energy consumption between DMADQN and the baseline algorithm under different training rounds (episodes) is shown in Figure 9. The average energy consumption shows a downward trend as the number of episodes increases. Taking episode 3000 as an example, Compared with MADDPG, DMADQN reduces energy consumption by approximately 8%; compared with DQN, it reduces energy consumption by about 33%; compared with DDPG, the reduction is roughly 25%; and compared with DDQN, it achieves an energy consumption reduction of around 22%. Since LC does not offload ground computing, its energy consumption remains stable at 0.85 J, which highlights its high energy consumption and lack of room for optimization. By implementing multi-branch Q-value stabilization, DMADQN dynamically optimizes task offloading decisions to effectively reduce energy consumption, maintaining the lowest average energy consumption throughout the process. Particularly as the number of episodes increases, its lightweight network structure enables efficient parameter utilization, avoiding the additional overhead associated with DDPG’s dual-network architecture and the target network of DDQN. Additionally, the discrete DMADQN action space design reduces computational complexity, while multi-branch Q-value stabilization mitigates training fluctuations caused by traditional Q-value overestimation. These optimized strategies give DMADQN a more significant advantage in energy consumption control, demonstrating its outstanding effectiveness in improving energy utilization efficiency.

5.3. Ablation Experiment

This section conducts an analysis of ablation experiments. Under the assumed fixed experimental conditions—with the number of UAVs set to 30, the number of LEO satellites to 10, the number of tasks to 70, and the number of training episodes to 5000—the experimental results are presented in

Table 3. Ablation experiment analysis.

	Average Task Completion Rate (%)	Average Transmission Rate (Mbps)	Average Latency (ms)	Average Energy Consumption (J)
(a)	78.196	13.963	65.638	0.769
(b)	85.635	10.446	69.459	0.864
(c)	89.946	10.856	56.566	0.894
Proposed Method in This Paper	95.452	7.563	51.366	0.616

. These results are derived from sequentially replacing three key components of our proposed approach: the Ground-UAV-LEO (GUL) three-tier architecture, the problem decomposition strategy, and the distributed learning method. Through the analysis of these results, we effectively demonstrate the necessity of the specific combination proposed in this paper and explicitly clarify the systemic benefits it brings. To facilitate the presentation of experimental results, we denote the following combinations using abbreviations (a), (b), and (c): (a) represents “Two-Tier Architecture + Problem Decomposition Strategy + Distributed Learning”; (b) represents “Three-Tier Architecture + Integrated Problem Solving + Distributed Learning”; (c) represents “Three-Tier Architecture + Problem Decomposition Strategy + Non-Distributed Learning”.

As shown in Table 3, the proposed solution achieves improvements of at least 6.12% in average task completion rate and 43.54% in average transmission rate. These gains stem from the UAV relay in the proposed architecture, which shortens transmission distance, mitigates occlusion and interference, increases transmission rate, and reduces task drops caused by transmission timeouts. For average latency, the algorithm achieves a minimum improvement of 10.12%, attributed to the problem decomposition strategy. By avoiding the high complexity and decision inconsistency of joint optimization, this strategy accelerates convergence and reduces latency. In terms of average energy consumption, an optimization of at least 24.84% is observed, benefiting from the distributed learning method, which eliminates the need for a central node and thus lowers both data transmission and computational energy costs.

In summary, the synergy of the proposed Ground–UAV–LEO three-tier architecture, problem decomposition strategy, and distributed learning method enables the system to simultaneously deliver higher task completion and transmission rates, lower latency, and reduced energy consumption.

6. Conclusions and Outlook

This paper addresses the challenges of low transmission rates, low task completion rates, and high latency in task offloading within integrated edge computing and LEO satellite networks and proposes a satellite–UAV computing offloading algorithm based on distributed multi-agent reinforcement learning. A three-layer collaborative architecture, comprising ground, UAVs, and LEO satellites, is designed, in which UAVs serve as relays to enhance data transmission efficiency. The overall task offloading problem is decomposed into two subproblems: decision-making and resource allocation. Offloading decisions are formulated as a Markov decision process (MDP) and optimized using a distributed multi-agent deep Q-network (DQN) to improve task completion and minimize latency, whereas resource allocation is addressed via gradient descent to ensure rapid convergence. Simulation results indicate that the proposed method significantly enhances overall system performance compared with existing algorithms.

In future work, we will expand the complexity of the state space to better approximate the real-world satellite edge computing environment and further optimize the structural design of the distributed multi-agent deep reinforcement learning algorithm to improve the speed and stability of computing task offloading.