Abstract
With the advancement of electromagnetic interference and counter-interference technology, complex and unpredictable interference signals greatly reduce radar detection, tracking, and recognition performance. In multi-interference environments, the overlap of interference cross-correlation peaks can mask target signals, weakening radar interference suppression capability. To address this, we propose a joint waveform and filter design method called Multi-Interference Suppression Network (MISNet) for effective interference suppression. First, we develop a design criterion based on suppression coefficients for different interferences, minimizing both cross-correlation energy and interference peak models. Then, for the non-smooth, non-convex optimization problem, we use complex neural networks and gating mechanisms, transforming it into a differentiable problem via end-to-end training to optimize the transmit waveform and receive filter efficiently. Simulation results show that compared to traditional algorithms, MISNet effectively reduces interference cross-correlation peaks and autocorrelation sidelobes in single interference environments; it demonstrates excellent robustness in multi-interference environments, significantly outperforming CNN, PSO, and ANN comparison methods, effectively improving radar interference suppression performance in complex multi-interference scenarios.
1. Introduction
With the advancement of electromagnetic interference and counter-interference technology, complex and unpredictable interference signals greatly reduce radar detection, tracking, and recognition performance [1,2]. The emergence of digital radio frequency memory (DRFM) technology has further improved the interference generation capability of interference sources. Interference sources can capture radar signals, store them, and retransmit them with modulation, confusing radar systems [3,4]. In multi-interference environments, the overlap of interference cross-correlation peaks can mask target signals, weakening radar interference suppression capability [5,6].
Recent years have witnessed the emergence of adaptive electromagnetic interference technology, making interference signals exhibit intelligent and adaptive characteristics [7,8]. Traditional advanced interference mitigation (AIM) techniques such as frequency agility, adaptive sidelobe cancellation, space-time adaptive processing, and monopulse tracking [9,10] show limitations when facing new intelligent interference. Particularly in complex electromagnetic environments, when multiple types of DRFM interference (such as intermittent sampling repeater jamming ISRJ, intermittent sampling repeater jamming with frequency shifting ISRJ-FR, and smeared spectrum jamming SMSP) exist simultaneously [11,12], traditional methods often cannot effectively suppress them.
To suppress interference signals, many researchers have studied this problem. Current research on interference suppression mainly focuses on echo processing techniques and interference suppression waveform design. Multidimensional signal processing transforms signals into higher dimensions, such as the polarization domain, time-frequency domain, or spatial domain, allowing the design of high-dimensional filters to suppress interference [13,14]. However, higher-dimensional transformations significantly increase the computational load, making it hard to meet radar’s real-time requirements.
With the rapid development of deep learning technology, neural networks are increasingly applied in radar signal processing [15,16]. Complex-valued neural networks (CVNNs) show great potential in processing radar complex-domain signals [17]. The introduction of attention mechanisms further enhances neural networks’ ability to learn complex signal patterns [18].
Waveform design, as an emerging technology, reduces the impact of interference on radar systems by designing the phase of intra-pulse waveforms [19,20]. In [10], a method minimizing the peak sidelobe level (PSL) was proposed, effectively reducing the peak sidelobe level in radar pulse compression. In [11], the signal-to-interference-plus-noise ratio (SINR) was maximized under pulse compression sidelobe constraints, effectively handling clutter and false alarms. In [12], an interference cross-correlation energy model was minimized under constant modulus waveform constraints, reducing the cross-correlation gain of interference signals and effectively suppressing interference.
Recent research demonstrates that joint transmit waveform and receive filter design can more fully utilize the degrees of freedom of the system [14,21]. This optimization approach has potential applications in emerging Integrated Sensing and Communication (ISAC) systems [22,23], where similar joint design principles could be beneficial for multi-functional system architectures. However, these traditional iterative optimization methods have high computational complexity and slow convergence speed, making it difficult to meet the real-time requirements of practical applications [24].
These methods effectively suppress single interference. However, when multiple interferences occur simultaneously, targets can still be overwhelmed by interference cross-correlation peaks, reducing radar target detection performance in interference environments. More severely, in moving target environments, the Doppler effect causes spectral spread of target signals, further exacerbating the difficulty of multi-interference suppression [25].
To efficiently suppress multiple interferences, we propose a joint optimization method for transmit waveforms and receive filters, called Multi-Interference Suppression Network (MISNet). This method utilizes interference cross-correlation peak and energy models, combined with adaptive interference suppression coefficients, fully exploiting the degrees of freedom in waveforms and filters to minimize interference effects under constraints. For the non-smooth, non-convex optimization problem involving multiple maximum functions, we employ complex neural networks and gated networks. Through end-to-end training, we transform it into a differentiable problem, efficiently optimizing the transmit waveform and receive filter [26,27].
Experiments show that compared to traditional algorithms, this method effectively reduces interference cross-correlation peaks and autocorrelation sidelobes in single interference environments; it demonstrates excellent robustness in multi-interference environments, significantly outperforming CNN, PSO, and ANN comparison methods, effectively enhancing radar interference suppression performance in complex multi-interference scenarios.
This paper is arranged as follows. Section 2 formulates the problem of multi-interference suppression. Section 3 presents the proposed Multi-Interference Suppression Network (MISNet), detailing the complex attention mechanism and gating structure optimization method. Section 4 evaluates the performance of MISNet through numerical experiments, comparing it with traditional methods under single and multi-interference scenarios. Section 5 concludes the paper, summarizing the key findings and contributions.
2. Problem Formulation
In complex electromagnetic environments, radar systems frequently face complex scenarios where multiple types of interference signals act simultaneously. These interferences include not only traditional noise and deceptive interference but also intelligent interference using DRFM technology [28].
In this paper, we consider a more complex scenario where multiple interference sources interfere with the radar simultaneously. We assume the radar transmits a phase-coded waveform , where N is the waveform length. The received echo signal can be defined as:
where represents Gaussian white noise with zero mean and variance . is the interference signal from the i-th interference source, expressed as:
and is the interference modulation matrix. In a cognitive radar system, we can obtain the interference modulation matrix from feedback of previous radar scans, providing a foundation for adaptive interference suppression [29].
Interference sources set the interference modulation matrix to gain amplification in pulse compression, overwhelming the radar target peak. The pulse compression gain of the interference is:
where is the gain of the i-th interference after pulse compression at the d-th range bin.
Traditional waveform design methods can suppress single interference effectively by reducing its pulse compression gain. However, multiple interferences significantly degrade radar target detection performance. To suppress interference effectively and fully utilize the degrees of freedom in the transmit waveform and receive filter, we introduce the interference cross-correlation peak model and energy model:
where is the peak of the i-th interference cross-correlation function. A higher can overwhelm the radar target peak, misleading the radar system. is the energy of the i-th interference cross-correlation function. A larger raises the pulse compression noise floor, suppressing the radar.
To fully utilize the degrees of freedom in the transmit waveform and receive filter, we define an interference suppression coefficient:
A larger indicates a greater degree of interference overwhelming the target. We minimize to avoid raising the noise floor and overwhelming strong target peaks. When is small, we optimize to improve radar detection performance for strong targets and adjust the interference suppression weights based on different values.
Additionally, the autocorrelation peak of the transmit waveform and receive filter is crucial to prevent weak targets from being overwhelmed by strong clutter. The model is:
where:
Thus, to effectively suppress interference under waveform constant modulus constraints and filter energy constraints [18,19], we propose a joint interference suppression method based on cross-correlation peaks and energy by designing the transmit waveform and receive filter. The objective function is:
where , , and are three fixed weighting parameters.
3. Complex Attention Mechanism and Residual Structure Optimization Method
In multi-jammer environments, radar systems face simultaneous interference from multiple sources, significantly degrading target detection performance. Traditional methods struggle to effectively suppress complex interference and incur high computational complexity, failing to meet real-time requirements. The development of deep learning technology provides new approaches to solve this problem. Complex neural networks have natural advantages in processing radar complex-domain signals, better preserving amplitude and phase information of signals [30].
To address this, we propose a deep learning-based joint optimization approach, termed “MISNet,” which aims to simultaneously optimize the transmit waveform and receive filter to effectively mitigate multiple interferences and enhance radar interference suppression capabilities.
As shown in Figure 1, our approach leverages a complex neural network (ComplexModel) to tackle this challenge. Unlike traditional real-valued neural networks, complex neural networks can directly process complex-domain signals, avoiding information loss caused by separating real and imaginary parts. The network takes initial noisy waveforms as inputs, extracts features via shared layers, dynamically optimizes through gating units, and outputs optimized , satisfying the constraints:
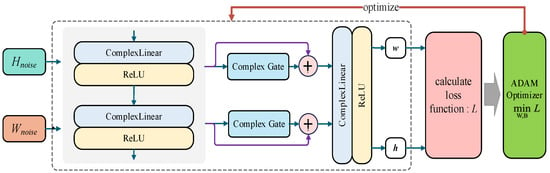
Figure 1.
Overall architecture diagram of MISNet algorithm.
The shared layer applies a linear transformation (where ) to map inputs to a higher-dimensional space, defined as:
where , , , and are shared weights and biases. They reduce model complexity while capturing synergy between and .
As shown in Figure 2, the ComplexGate mechanism is an innovation of MISNet. Defined as , this gating unit takes and as inputs and works in this high-dimensional space. The process is:
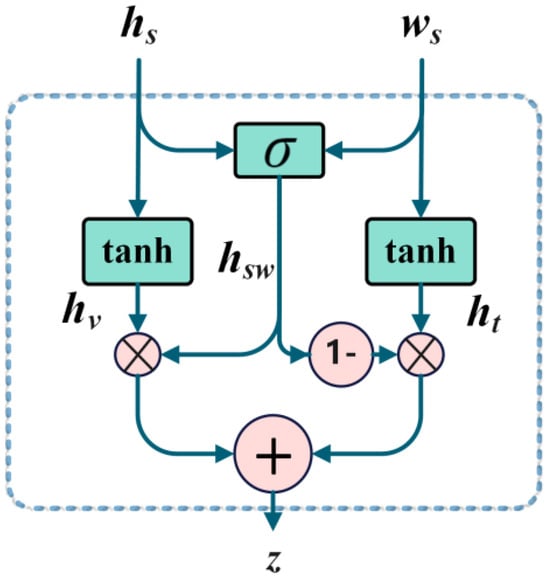
Figure 2.
Structure diagram of ComplexGate gating mechanism.
Then, the gating outputs are:
where and are intermediate vectors from and using . comes from concatenating and (making a -dimensional vector) and applying to get an -dimensional vector. is computed by element-wise multiplication (denoted by ) and addition. Finally, and are the gating unit outputs.
The gating unit adjusts features dynamically using interactions between and , along with , , and . This improves adaptability to different interference patterns.
Next, the independent layer maps features back to the original dimension:
where , , , and are independent parameters. Normalization follows to meet constraints.
The optimization objective is formulated as a loss function to drive network training:
This loss function minimizes sidelobes and interference terms, guiding the network to learn optimal and , with training based on and backpropagation.
4. Numerical Results
4.1. Experimental Setup
This section validates the effectiveness of the proposed MISNet algorithm through numerical simulations. We consider a monostatic radar system equipped with a phase-coded waveform of length N = 256. The maximum number of algorithm iterations is set to 30,000. The weighting parameters are configured as follows: , , , and the pulse compression peak constraint parameter . The MISNet algorithm employs the ASGD optimizer with a learning rate of 0.01, a hidden layer dimension of 512, and training for 30,000 epochs. The algorithm is initialized with random phase sequences. All experiments are conducted on a PC equipped with a 2.80 GHz Intel i9-10900 CPU, 32 GB RAM, and an NVIDIA RTX 3090 GPU.
To comprehensively evaluate the performance of the proposed method, we select comparison algorithms targeting different application scenarios. For single interference suppression scenarios, we compare against the MPSL algorithm [14] and ICEL algorithm [12], where the MPSL algorithm designs waveforms and filters based on minimizing peak sidelobe level criteria, and the ICEL algorithm achieves single interference suppression by minimizing interference cross-correlation energy. For multi-interference suppression scenarios, we select PSO (Particle Swarm Optimization with population size 30, inertia weight 0.7, acceleration factors ), CNN (Convolutional Neural Network with 3-layer 1D convolution structure, channel numbers 32-64-1, ReLU activation function), and ANN (Complex-Valued Artificial Neural Network with 3-layer fully connected structure 256-128-64-256, complex ReLU activation function for complex-domain signal processing) as comparison methods.
This experiment employs two performance metrics for evaluation. The Peak of Interference Cross-correlation Level (PICL) is defined as the maximum peak of the cross-correlation function between the interference signal and the receive filter, expressed as:
where is the interference pulse compression gain at the d-th range bin. Lower PICL values indicate better interference suppression performance.
The Autocorrelation Peak Sidelobe Level (APSL) is defined as the maximum sidelobe peak of the autocorrelation function between the transmit waveform and receive filter, expressed as:
where is the autocorrelation value at the d-th delay. Lower APSL values help prevent weak targets from being masked by strong clutter, improving radar target detection performance.
Following the interference model in reference [14], the experiment employs three typical DRFM interference types, all represented as 256 × 256 real matrices.
The first type is the Intermittent Sampling Repeater Jamming (ISRJ) matrix , expressed as:
where the diagonal vector satisfies:
is the intermittent sampling position set, containing 5 consecutive segments with 8 elements each, totaling 40 non-zero elements, simulating the discontinuous characteristics of intermittent sampling repeater jamming.
The second type is the Intermittent Sampling Radio Frequency Jamming (ISRJ-RF) matrix , expressed as:
where and are the dimensions of the upper and lower blocks, respectively, is the identity matrix, and is the anti-diagonal identity matrix:
This matrix adopts a block anti-diagonal structure, simulating the intermittent sampling repeater characteristics in the radio frequency domain.
The third type is the Smeared Spectrum Jamming (SMSP) matrix , expressed as:
where the i-th row vector satisfies:
This matrix is row-sparse with only one non-zero element per row, distributed with 4-fold periodic intervals, simulating spectrum smearing effects.
4.2. Algorithm Performance Analysis
To verify the convergence performance of the MISNet algorithm in multi-interference environments, we compare the loss function convergence characteristics of different algorithms under the combined action of ISRJ and ISRJ-RF dual interference sources. Figure 3 shows the training convergence curves of four algorithms: PSO, CNN, ANN, and MISNet.
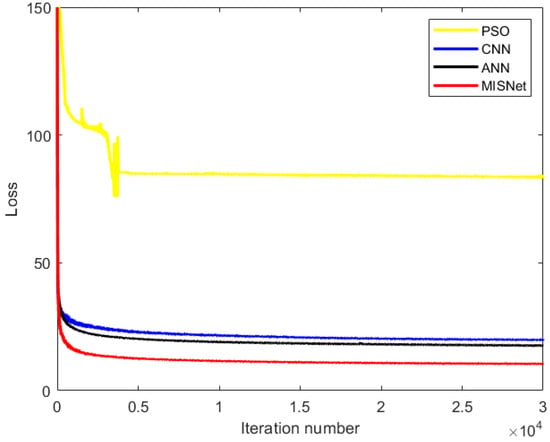
Figure 3.
Comparison of loss function convergence curves for different algorithms.
Figure 3 demonstrates that the PSO algorithm exhibits significant convergence fluctuations during optimization, with final convergence results notably inferior to other algorithms. CNN, ANN, and MISNet show comparable convergence speeds, but MISNet significantly outperforms other algorithms in final convergence results. This result fully validates the effectiveness of complex neural networks combined with gating mechanisms, indicating that MISNet can better perform feature selection and complex domain information processing, achieving superior performance in multi-interference suppression optimization problems.
From the perspective of engineering implementation feasibility, we can pre-analyze all possible interference parameters and generate an offline waveform library covering comprehensive interference mitigation scenarios. During actual deployment, the system does not need to run complex neural network computations in real-time, but only needs to quickly identify current interference characteristics to achieve millisecond-level optimal waveform retrieval from the waveform library, fully meeting radar’s stringent real-time requirements.
4.3. Performance Evaluation in Single Interference Environment
Since traditional methods only optimize interference suppression performance for single interference, to verify the effectiveness of the proposed method in single interference environments, we compare MISNet with traditional algorithms ICEL [12] and MPSL [14], using a single SMSP interference matrix .
Figure 4a shows the waveform autocorrelation function characteristics designed by the three algorithms. It can be observed that the MISNet algorithm achieves the lowest sidelobe level near the main peak, effectively suppressing autocorrelation sidelobes. Figure 4b displays the cross-correlation function between the interference signal and the receive filter. Compared to other algorithms, the MISNet algorithm maintains lower cross-correlation levels across the entire range, demonstrating excellent interference suppression capability.
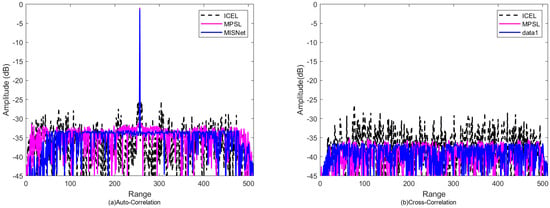
Figure 4.
Correlation function comparison of different algorithms under single interference source. (a) Waveform autocorrelation function; (b) Interference cross-correlation function.
As shown in Table 1, the proposed MISNet algorithm demonstrates significant advantages in single interference suppression. In terms of interference cross-correlation peak suppression, MISNet improves by 10.12 dB compared to ICEL and by 1.20 dB compared to MPSL. In terms of autocorrelation peak sidelobe suppression, MISNet improves by 7.83 dB compared to ICEL and by 1.91 dB compared to MPSL. This result proves the effectiveness of complex neural networks in handling radar waveform optimization problems, achieving both effective interference signal suppression and good autocorrelation sidelobe control.

Table 1.
Performance Comparison of Different Algorithms under Single Interference Source.
4.4. Robustness Verification in Multi-Interference Environment
To further verify the robustness of the proposed method in complex multi-interference environments, we select three dual-interference combinations: , , and , and compare them with CNN, PSO, and ANN algorithms. The evaluation metrics include Autocorrelation Peak Sidelobe Level (APSL) and Peak of Interference Cross-correlation Level (PICL) for both interference sources.
From Figure 5, it can be observed that in multi-interference environments, the MISNet algorithm maintains good sidelobe suppression characteristics near the main peak of the autocorrelation function while achieving the lowest correlation levels in the cross-correlation functions of both interference sources. In contrast, other algorithms show obvious performance degradation when handling multiple interferences.
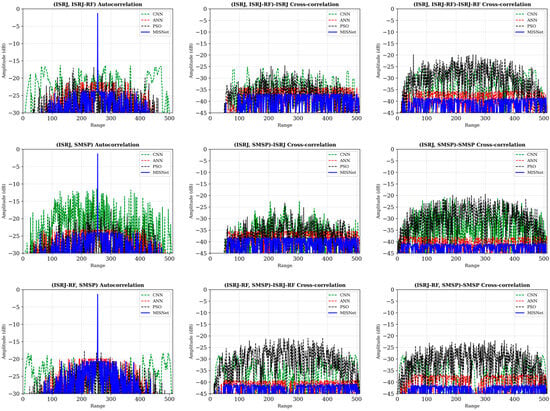
Figure 5.
Correlation function comparison of different algorithms under multi-interference sources. First row: autocorrelation function, ISRJ cross-correlation function, and ISRJ-RF cross-correlation function for combination; Second row: correlation functions for combination; Third row: correlation functions for combination.
As shown in Table 2, in all multi-interference scenarios, the proposed MISNet algorithm demonstrates optimal performance. For different interference type combinations, MISNet exhibits good adaptability. The ANN algorithm, as the second-best solution, approaches MISNet’s performance in some cases, while CNN and PSO algorithms perform significantly poorly in multi-interference environments. This validates the superiority and robustness of complex neural networks combined with gating mechanisms in handling complex interference scenarios. Due to the relatively small autocorrelation weight, the autocorrelation performance decreases compared to the single interference scenario in Figure 4, but the interference suppression performance is significantly improved.

Table 2.
Performance Comparison of Different Algorithms under Multi-Interference Sources (PICL1 and PICL2 represent the interference cross-correlation peak suppression levels corresponding to the first and second interference matrices, respectively).
Additionally, to verify the impact of the peak parameter on algorithm performance, we conduct experiments using the interference combination under different values. The pulse compression peak constraint parameter reflects the system’s degrees of freedom, with smaller values indicating more relaxed constraint conditions, thereby providing higher design flexibility.
From Figure 6, it can be observed that as the value decreases, the sidelobe level of the autocorrelation function gradually decreases, and the cross-correlation levels of both interferences also decrease accordingly. When , the algorithm demonstrates optimal performance in all three subplots, with smoother and lower correlation function curves.
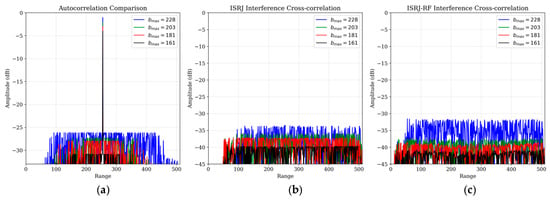
Figure 6.
Correlation function comparison under different values. (a) Autocorrelation function; (b) ISRJ interference cross-correlation function; (c) ISRJ-RF interference cross-correlation function.
As shown in Table 3, as the value decreases, the system constraints become more relaxed, and the optimization algorithm obtains higher design degrees of freedom, thereby achieving better sidelobe suppression and interference suppression performance. When decreases from 228 to 161, the APSL improves from −26.14 dB to −30.83 dB, the suppression of ISRJ interference improves from −33.49 dB to −39.66 dB, and the suppression of ISRJ-RF interference improves from −31.54 dB to −40.67 dB. Therefore, the experimental results validate the correctness of the theoretical analysis.

Table 3.
Performance Comparison under Different Values for (PICL1 and PICL2 represent the interference cross-correlation peak suppression levels corresponding to the first and second interference matrices, respectively).
4.5. Hyperparameter Sensitivity Analysis
To validate the rationality of the weighting parameters selection and analyze the algorithm’s sensitivity to hyperparameter variations, we conduct systematic single-parameter sensitivity experiments (Table 4, Table 5 and Table 6). The experiments employ a controlled variable approach, fixing two parameters while varying the third parameter within a reasonable range. All experiments are performed under the ISRJ+ISRJ-RF multi-interference scenario to evaluate the impact on APSL, PICL1, and PICL2 performance metrics.

Table 4.
Performance under different values (, ).

Table 5.
Performance under different values (, ).

Table 6.
Performance under different values (, ).
The sensitivity analysis reveals several key insights: First, each weighting parameter exhibits distinct and relatively independent control functions. Parameter primarily governs the autocorrelation peak sidelobe level, with increasing values improving APSL from −21.85 dB to −25.32 dB while slightly affecting interference suppression performance. Parameters and specifically control the suppression of their corresponding interference sources, with higher weights yielding approximately 5 dB and 4 dB improvements in PICL1 and PICL2, respectively. Second, the algorithm demonstrates good robustness to hyperparameter variations, with performance changes remaining moderate within reasonable parameter ranges. Finally, the selected parameter combination , , achieves an optimal balance among multiple optimization objectives, maximizing the overall system performance.
5. Conclusions
In this paper, we have proposed the Multi-Interference Suppression Network (MISNet) for joint waveform and filter design to suppress multiple interference signals simultaneously. The design criterion is formulated by minimizing the APSL of the transmit waveform and receive filter, and the PICL and ELCF of multiple interference signals with the receive filter. To solve this non-smooth and non-convex optimization problem, we introduce complex neural networks with gating mechanisms that transform the optimization into a differentiable problem through end-to-end training. Numerical simulation results demonstrate that the proposed MISNet approach significantly outperforms traditional iterative algorithms and other neural network methods in multi-interference suppression. In single interference environments, MISNet effectively reduces interference cross-correlation peaks and autocorrelation sidelobes compared to existing methods. In multi-interference scenarios, MISNet exhibits excellent robustness across different interference combinations, significantly outperforming CNN, PSO, and ANN approaches. The proposed method enhances radar interference suppression capability and target detection performance in complex multi-interference environments. Future research may focus on extending the approach to handle interference with varying Doppler frequency shifts and more complex adaptive interference patterns.
Author Contributions
R.C. contributed the central idea, analyzed most of the data, and wrote the initial draft of the paper. C.S. and W.D. contributed the idea of simulation experiment and provided constructive suggestion. M.B. contributed to revise the paper and polish the language. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
Author Rui Cai is employed by AVIC Xi’an Aircraft Industry Group Company Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Sparrow, M.J.; Cikalo, J. ECM Techniques to Counter Pulse Compression Radar. U.S. Patent Application 7,081,846, 25 July 2006. [Google Scholar]
- Li, N.; Zhang, Y. A survey of radar ECM and ECCM. IEEE Trans. Aerosp. Electron. Syst. 1995, 31, 1110–1120. [Google Scholar] [CrossRef]
- Heagney, C.P. Digital radio frequency memory synthetic instrument enhancing US navy automated test equipment mission. IEEE Instrum. Meas. Mag. 2018, 21, 41–63. [Google Scholar] [CrossRef]
- Berger, S.D. Digital radio frequency memory linear range gate stealer spectrum. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 725–735. [Google Scholar] [CrossRef]
- Chen, J.; Wu, W.; Xu, S.; Chen, Z.; Zou, J. Band pass filter design against interrupted-sampling repeater jamming based on time-frequency analysis. IET Radar Sonar Navig. 2019, 13, 1646–1654. [Google Scholar] [CrossRef]
- Wang, X.; Chen, H.; Zhu, Y.; Ni, M.; Shen, W.; Zhou, Y.; Hou, M. SMSP interference suppression method based on time-domain interference matching. IET Conf. Proc. 2023, 2023, 991–997. [Google Scholar] [CrossRef]
- Jiu, B.; Liu, H.; Wang, X.; Zhang, L.; Wang, Y.; Chen, B. Knowledge-based spatial-temporal hierarchical MIMO radar waveform design method for target detection in heterogeneous clutter zone. IEEE Trans. Signal Process. 2014, 63, 543–554. [Google Scholar] [CrossRef]
- Zhou, K.; Li, D.; Su, Y.; Liu, T. Joint design of transmit waveform and mismatch filter in the presence of interrupted sampling repeater jamming. IEEE Signal Process. Lett. 2020, 27, 1610–1614. [Google Scholar] [CrossRef]
- Xie, L.; He, Z.; Tong, J.; Li, J.; Li, H. Transmitter polarization optimization for space-time adaptive processing with diversely polarized antenna array. Signal Process. 2020, 169, 107401. [Google Scholar] [CrossRef]
- Song, J.; Babu, P.; Palomar, D.P. Sequence design to minimize the weighted integrated and peak sidelobe levels. IEEE Trans. Signal Process. 2015, 64, 2051–2064. [Google Scholar] [CrossRef]
- Imani, S.; Nayebi, M.M.; Ghorashi, S.A. Colocated MIMO radar SINR maximization under ISL and PSL constraints. IEEE Signal Process. Lett. 2018, 25, 422–426. [Google Scholar] [CrossRef]
- Ge, M.; Yu, X.; Yan, Z.; Cui, G.; Kong, L. Joint cognitive optimization of transmit waveform and receive filter against deceptive interference. Signal Process. 2021, 185, 108084. [Google Scholar] [CrossRef]
- Zhang, Y.; Ding, K. Research on SMSP jamming suppression based on matched filtering in FrFT domain. In Proceedings of the 7th International Conference on Computer Information Science and Application Technology (CISAT), Hangzhou, China, 12–14 July 2024; pp. 963–966. [Google Scholar]
- Zuo, L.; Lan, Z.; Lu, X.; Gao, Y.; Mao, L. Joint transmit-receive filter design with lower APSL and ICPL to suppress interference. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 3673–3687. [Google Scholar] [CrossRef]
- Oyedare, T.; Shah, V.K.; Jakubisin, D.J.; Reed, J.H. Interference suppression using deep learning: Current approaches and open challenges. IEEE Access 2022, 10, 58507–58531. [Google Scholar] [CrossRef]
- Jiang, Y.; Yang, Y.; Zhang, W.; Guo, L. Deep learning-based active jamming suppression for radar main lobe. IET Signal Process. 2024, 2024, 3179667. [Google Scholar] [CrossRef]
- Cho, H.-W.; Choi, S.; Cho, Y.-R.; Kim, J. Complex-valued channel attention and application in ego-velocity estimation with automotive radar. IEEE Access 2021, 9, 28847–28858. [Google Scholar] [CrossRef]
- Li, X.; Liu, Z.; Huang, Z. Attention-based radar PRI modulation recognition with recurrent neural networks. IEEE Access 2020, 8, 57426–57439. [Google Scholar] [CrossRef]
- Xia, M.; Gong, W.; Yang, L. A novel waveform optimization method for orthogonal-frequency multiple-input multiple-output radar based on dual-channel neural networks. Sensors 2024, 24, 5471. [Google Scholar] [CrossRef]
- Metwaly, K.; Kweon, J.; Alhujaili, K.; Gini, F.; Greco, M.S.; Rangaswamy, M.; Monga, V. MIMO radar beampattern design via algorithm unrolling. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 9204–9220. [Google Scholar] [CrossRef]
- Lan, Z.; Zuo, L.; Liao, B.; Yang, T. Joint waveform and filter design for interference suppression in moving target environments. IEEE Trans. Aerosp. Electron. Syst. 2025, 1–15. [Google Scholar] [CrossRef]
- Benaya, A.M.; Hassan, M.S.; Ismail, M.H.; Landolsi, T. Aerial ISAC: A HAPS-Assisted Integrated Sensing, Communications and Computing Framework for Enhanced Coverage and Security. IEEE Trans. Green Commun. Netw. 2025. early access. [Google Scholar] [CrossRef]
- Wang, S.; Wang, W.; Zheng, Y. Dual-Functional Quasi-Uniform Beam-Scanning Antenna Array with Endfire Radiation Capability for Integrated Sensing and Communication Applications. IEEE Trans. Veh. Technol. 2025, 1–11. [Google Scholar] [CrossRef]
- Cheng, Z.; He, Z.; Zhang, S.; Li, J. Constant modulus waveform design for MIMO radar transmit beampattern. IEEE Trans. Signal Process. 2017, 65, 4912–4923. [Google Scholar] [CrossRef]
- Cui, G.; Li, H.; Rangaswamy, M. MIMO radar waveform design with constant modulus and similarity constraints. IEEE Trans. Signal Process. 2013, 62, 343–353. [Google Scholar] [CrossRef]
- Friedel, E. Convolutional Neural Network (CNN) for Digital Radio Frequency Memory (DRFM). Ph.D. Thesis, Johns Hopkins University, Baltimore, MD, USA, 2023. [Google Scholar]
- Wallin, E. Detecting Jamming and Interference in Airborne Radar Using Convolutional Neural Networks. Ph.D. Thesis, Chalmers University Technology, Gothenburg, Sweden, 2019. [Google Scholar]
- Moon, J.W. Radar Interference Mitigation Using Deep Learning with Neural Architecture Search. Ph.D. Thesis, Seoul National University, Seoul, Republic of Korea, 2023. [Google Scholar]
- Vaidyanathan, P.P. Multirate Systems and Filter Banks; Prentice Hall: Hoboken, NJ, USA, 1993. [Google Scholar]
- Hirose, A. Complex-Valued Neural Networks: Theories and Applications; World Scientific: Singapore, 2003. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).