Spatiotemporal Forecasting of Regional Electric Vehicles Charging Load: A Multi-Channel Attentional Graph Network Integrating Dynamic Electricity Price and Weather

Abstract

Accurate spatiotemporal forecasting of electric vehicle (EV) charging load is essential for smart grid management and efficient charging service operation. This paper introduced a novel spatiotemporal graph convolutional network with cross-attention (STGCN-Attention) for multi-factor charging load prediction. The model demonstrated a strong capability to capture cross-scale spatiotemporal correlations by adaptively integrating historical charging load, charging pile occupancy, dynamic electricity prices, and meteorological data. Evaluations in real-world charging scenarios showed that the proposed model achieved superior performance in hour forecasting, reducing Mean Absolute Error (MAE) by 9% and 16% compared to traditional STGCN and LSTM models, respectively. It also attained approximately 30% higher accuracy than 24 h prediction. Furthermore, the study identified an optimal 1-2-1 multi-scale temporal window strategy (hour–day–week) and revealed key driver factors. The combined input of load, occupancy, and electricity price yielded the best results (RMSE = 37.21, MAE = 27.34), while introducing temperature and precipitation raised errors by 2–8%, highlighting challenges in fine-grained weather integration. These findings provided actionable insights for real-time and intraday charging scheduling.

1. Introduction

The large-scale adoption of electric vehicles (EVs) is creating complex, spatiotemporally dynamic charging loads that challenge urban power distribution networks [1,2,3,4]. Accurate prediction of these loads is, therefore, crucial for infrastructure planning and grid operations, such as peak shaving and renewable energy integration.

Under the influence of traffic patterns [5], environmental conditions, electricity prices, charging approaches [6], and meteorological factors, regional EV charging loads form a highly dynamic, nonlinear spatiotemporal correlation network [7]. Existing prediction methods are primarily divided into simulation-based and data-driven approaches. Simulation methods model travel-charging behaviors to estimate load [8], offering interpretability but often lacking accuracy in real-world systems due to reliance on assumptions. For instance, Guo et al. employed Monte Carlo algorithms to establish probability distribution functions for EV user travel habits, enabling correlation modeling of EV charging loads [9]. Gao et al. [10] construct a charging behavior model based on dynamic travel chains using key nonlinear modeling within a stochastic utility framework for spatiotemporal demand estimation. In contrast, machine learning techniques, particularly deep learning models like CNNs [11], RNNs [12,13], and GCNs [14,15], learn directly from monitoring data and demonstrated stronger predictive performance by capturing intrinsic spatiotemporal features [16,17]. Tian et al. [18] introduced a pyramid split attention module to process multi-scale data, incorporating a graph attention mechanism module to explore spatial heterogeneity. Wang et al. [19] proposed a hybrid prediction model STDR with LSTM. Recognizing the association of EV charging loads with factors like charging pile and electricity prices, Md Fazla et al. [20] conducted short-term load forecasting experiments based on time-series network models, concluding that incorporating external features enhances prediction accuracy.

Among these, graph convolutional networks (GCNs) and spatiotemporal attention mechanisms have demonstrated superior performance over CNNs and traditional time-series models (e.g., ARIMA). Recent studies, such as the physics-informed graph learning approach by Qu et al. [14] and the spatiotemporal multi-graph convolutional network (STMGCN) by Shi et al. [21], consistently confirm that models incorporating these techniques achieve higher predictive accuracy than benchmarks like ARIMA, LSTM, and CNN-LSTM. The integration of GCN and spatiotemporal attention mechanisms enables the simultaneous handling of temporal and spatial dependencies, thereby effectively capturing the coupling relationships.

However, a significant challenge remains in effectively integrating multiple factors (e.g., electricity price, weather, traffic) that dynamically influence spatial relationships between charging nodes over time [22,23]. Guo et al. [24] proposed an attention-based spatial–temporal graph convolutional network that integrated multi-scale temporal modeling, spatiotemporal graph convolution, and spatiotemporal attention. This framework earned widespread recognition for its ability to effectively capture dynamic patterns and deliver superior performance in traffic flow forecasting. Liu et al. [25] proposed an attention-based spatial–temporal graph convolutional recurrent network (ASTGCRN) for traffic forecasting. Its core module, the graph convolutional recurrent network (GCRN), integrates gated recurrent units with adaptive graph convolutional networks to dynamically learn graph structures while capturing spatial and local temporal dependencies. However, limitations remained when applied to prediction problems involving multiple factor inputs, primarily due to the difficulty in disentangling the dynamic key relationships between factors.

To overcome these limitations, this study proposes a multi-scale charging load prediction method with multi-factor fusion input via a spatiotemporal graph convolutional network with cross-attention (STGCN-Attention). The core objective is to achieve accurate regional EV charging load prediction by integrating information such as electricity prices and weather across different temporal scales. The key contributions and innovations are as follows.

(1) Model Innovation: A novel architecture integrating multi-scale (hourly, daily, weekly) temporal feature extraction with a spatiotemporal graph convolution module. This enables simultaneous modeling of multi-factor temporal characteristics and spatial topological correlations. Furthermore, an embedded cross-attention module dynamically enhances the weights of critical features from various factors, adaptively capturing key influences at different temporal scales.

(2) Application Innovation: A comprehensive multi-factor forecasting framework that incorporates charging load, occupancy, weather, and electricity price data is developed. This framework is designed not only to improve prediction accuracy but also to reveal the varying impact of factors like price and weather across temporal scales.

Finally, the proposed method is applied to conduct spatiotemporal prediction experiments on a real-world dataset. Concurrently, the sensitivity of these relevant factors on prediction is explored, aiming to reveal the impact of factors such as electricity prices and weather on charging load prediction. This work will provide theoretical tools and technical support for the dynamic optimization of smart grids.

2. Proposed Approach

Regional EV charging load prediction constitutes a spatiotemporal sequence forecasting challenge influenced by multi-source dynamic factors. Considering the complexity and dynamics of regional charging loads, the proposed approach integrates spatiotemporal feature learning and multi-factor feature learning. As illustrated in Figure 1, the proposed STGCN-Attention model consists of two modules, namely (a) a multi-scale temporal feature extraction (MSTFE) module, which extracts temporal feature inputs of different factors from hour, day, and week scales; (b) a spatiotemporal graph convolution integrating cross-attention (STGCN-A) module, which combines graph convolution, convolution, and cross-attention layers to process dynamic spatiotemporal correlation features under multiple factors. The input factors include historical charging load, charging pile occupancy, electricity prices, and weather. By setting two prediction mechanisms for the next hour (hour prediction) and the next 24 h with an interval of 24 h (24 h prediction), hourly and daily predictions can be achieved. Another critical input to the STGCN-A module is the adjacency matrix. This matrix represents the inter-node relationships within the regional graph structure. In this study, the adjacency matrix is computed by taking the reciprocal of the distance between nodes. In the following sections, the prediction problem will be defined, and then, the details of each module will be described.

2.1. Data Pre-Processing

The dataset of this study comprises hourly data on charging load volume, charging pile occupancy, electricity prices, and weather. The charging load volume is the electricity consumption collected per hour, and the charging pile occupancy is calculated as the ratio of busy piles to all piles. Before being fed into the model, the collected multi-source data underwent systematic preprocessing, which included data alignment, data cleaning, and data normalization. Data alignment is performed primarily to ensure temporal consistency across all datasets. Using timestamp and charging station ID as key fields, all data (load volume, electricity price, weather) were aligned to a unified hourly time granularity, constructing a comprehensive dataset. The data cleaning involved handling missing values and outliers. As missing values resulting from communication interruptions are usually short-lived, linear interpolation was applied to maintain the short-term smoothness of the time series. Given the maximum power rating (<50,000 kW) and the physical impossibility of a negative load, the valid data range is set to [0, 50,000] kW for outlier detection. Data points exceeding this threshold are identified as invalid and removed, followed by imputation using interpolation.

Given that different features (e.g., load volume, electricity price, weather) possess varying units and numerical ranges, Min–Max normalization is adopted to rescale the values to the [0, 1] interval. This prevents any single feature from disproportionately dominating the model training process. After model prediction, the output results underwent a reverse normalization process to revert them to their original units for evaluation.

2.2. STGCN-Attention Model

2.2.1. Problem Definition

This study models the regional EV charging load as an undirected graph G = (V, E, A), where |V| = N represents the set of spatial nodes, with N denoting the number of spatial nodes. E is the set of edges, indicating the connectivity between nodes, and A is the adjacency matrix of graph G, which captures the topological relationships and represents the correlations between nodes.

In graph G, each node records data with f-dimensional features at each time step $f\in \{1,\dots ,F\}$, where F is the total number of features. The f-th feature on the i-th node at time t is defined as $x_{t,i,f}\in R$. ${\mathrm{x}}_t\in R^{N\times F}$ represents the feature values of all nodes at time t. The input data is represented as a three-dimensional tensor with dimensions corresponding to time, space, and feature.

Given the three-dimensional spatiotemporal tensor representing all feature dimensions across all spatial nodes within the historical time series $T_{\mathrm{a}}$ and the graph structure G, a learning model is employed to predict the EV charging load $Y_p=({\mathrm{y}}_1,{\mathrm{y}}_2,\dots ,{\mathrm{y}}_{T_p})\in R^{T_p\times N}$ for all nodes over the future time period $T_p$.

Dynamic input factors include charging load, charging occupancy, electricity price, and weather at multiple timescales (hourly, daily, weekly, etc.) from the past.

Prediction target: Future charging load at timestamp t.

2.2.2. Multi-Scale Temporal Feature Extraction (MSTFE) Module

This module primarily handles the extraction of temporal features from the input data X. For the input data comprising multiple factors, temporal segments at three distinct scales (hourly, daily, and weekly) are extracted [24]. These segments are concatenated to form a multi-scale tensor and are subsequently fed into the following STGCN module. The lengths of the extracted hourly, daily, and weekly temporal segments are $T_r,T_d,T_w$, respectively. The representations of these three temporal segments are given as follows:

$$x_{\mathrm{r}}=(x_{t_0-T_p\times r},x_{t_0-T_p\times r+1},\dots ,x_{t_0-T_p\times (r-1)},\dots ,x_{t_0-T_p},\dots ,x_{t_0})\in R^{T_{\mathrm{r}}\times N\times F}$$

(1)

$$x_d=(x_{t_0-q\times d-T_p},x_{t_0-q\times d-T_p+1},\dots ,x_{t_0-q\times d},x_{t_0-q\times (d-1)-T_p},\dots ,x_{t_0-q\times (d-1)},x_{t_0-q-T_p},\dots ,x_{t_0-q})\in R^{T_d\times N\times F}$$

(2)

$$x_{\mathrm{w}}=(x_{t_0-7\times q\times \mathrm{w}-T_p},x_{t_0-7\times q\times \mathrm{w}-T_p+1},\dots ,x_{t_0-7\times q\times \mathrm{w}},x_{t_0-7\times q\times (\mathrm{w}-1)-T_p},\dots ,x_{t_0-7\times q\times (\mathrm{w}-1)},x_{t_0-7\times q-T_p},\dots ,x_{t_0-7\times q})\in R^{T_{\mathrm{w}}\times N\times F}$$

(3)

Taking the hour prediction as an example, assume the model input factors are historical charging load, occupancy, electricity price, and weather. With the extraction window sizes of 1-1-1 for the hourly, daily, and weekly scales, $x_{\mathrm{r}}$, $x_{\mathrm{r}}$, $x_{\mathrm{r}}$ represent the historical data of these four factors from the previous hour, the same hour of the previous day, and the same hour of the previous week, respectively. These three components are combined into a spatiotemporal tensor $x_{t,i,f}\in R$, where t denotes the time step, i represents the spatial node index, and f indexes the feature values (encompassing the four factors). Ultimately, the synthesized input array takes the form of a time-feature matrix. The multi-scale temporal feature extraction model involves reorganizing input–output data pairs from multi-source data, which incurs substantial computational overhead.

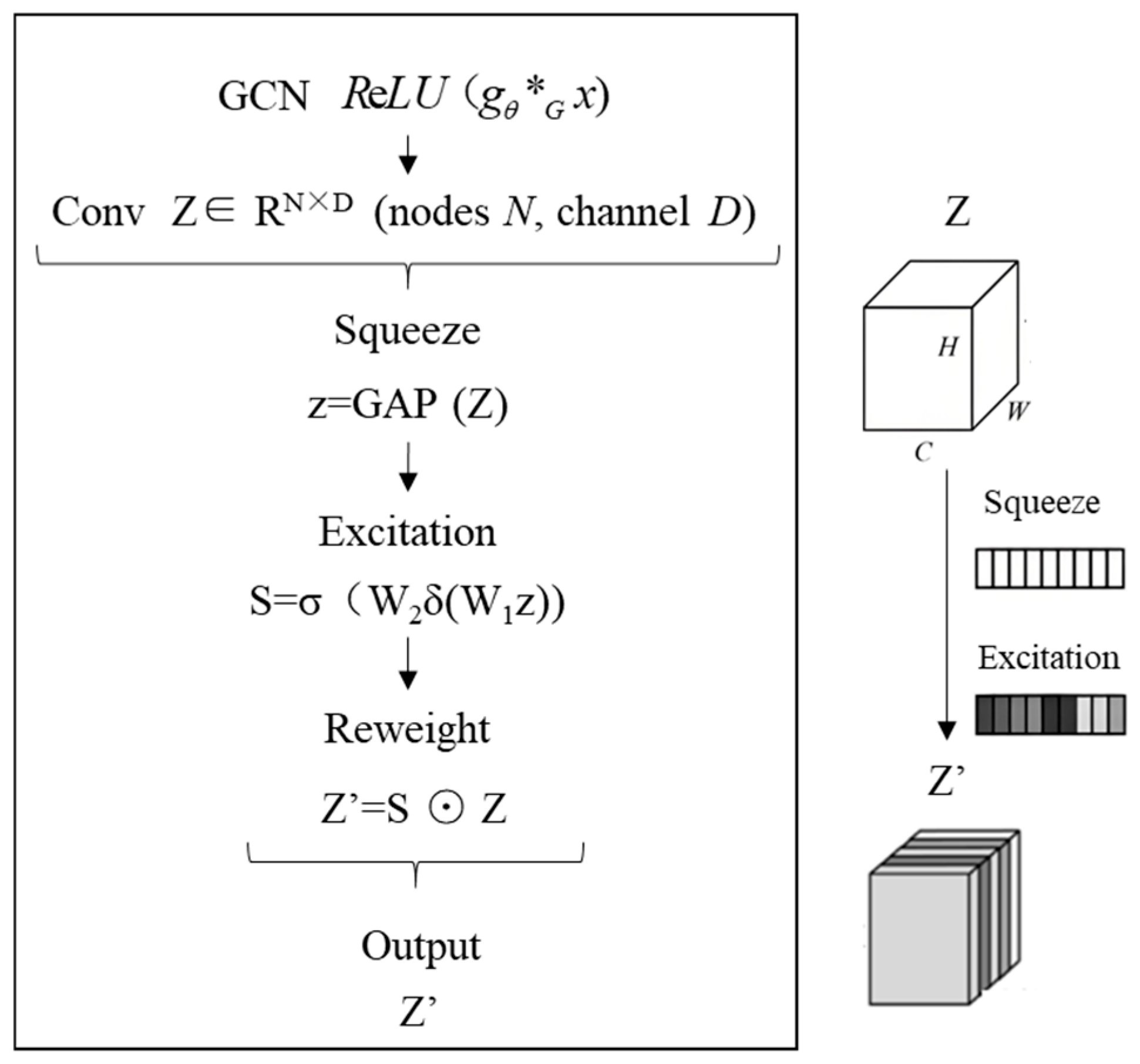
2.2.3. STGCN-A Module

This module employs a stacked architecture of graph convolution and cross-attention layers to perform spatiotemporal feature learning on the spatiotemporal tensor. The spatiotemporal tensor is entered into the GCN layer [26]. The output from the GCN layer is then passed through another convolution (Conv) layer before entering the cross-attention layer.

Conv Layer: The Conv layer is intended to further aggregate the extracted features and generate a more global representation.

Cross-attention Layer: The incorporation of the cross-attention layer effectively captures interdependencies between multiple factors and adaptively reweights the importance of features across different channels.

The GCN layer employs graph convolution with a Chebyshev polynomial-based kernel to capture the spatial dependencies between neighboring nodes [27]. The Laplacian matrix corresponding to the graph structure is defined as follows:

$$L=I_N-D^{-{\displaystyle \frac{1}{2}}}A{D}^{-{\displaystyle \frac{1}{2}}}\in R^{N\times N}$$

(4)

where A is the weighted adjacency matrix of the graph, $I_N$ is the identity matrix; $D\in R^{N\times N}$ is the diagonal degree matrix of the network nodes $D_{ii}={\displaystyle {\sum }_j{A}_{ij}}$. Leveraging the Chebyshev polynomial approximation, the graph convolution operator is defined as follows:

$$g_{\theta }{*}_{G}x=g_{\theta }(L)x={\displaystyle \sum _{k=0}^{K-1}{\theta }_k{T}_k(}\tilde{L})x$$

(5)

where $\theta \in R^K$ is the vector of Chebyshev coefficients, $L={\displaystyle \frac{2}{{\lambda }_{\max }}}L-I_N$, ${\lambda }_{\max }$ is the largest eigenvalue of the Laplacian matrix, and $x$ is the input from the temporal segment tensor. The Chebyshev polynomial is expanded to extract the spatial dependencies of each node from its 0-th to (K − 1)-th order neighboring nodes via graph convolution. Finally, this graph convolution module employs the ReLU function as the activation function to produce the output $R\mathrm{e}LU(g_{\theta }{*}_{G}x)$.

The cross-attention layer is a multi-channel attention layer comprising three components: Squeeze, Excitation, and Reweight (Figure 2). In the Squeeze part, Global Average Pooling (GAP) reduces spatial information to generate a channel descriptor vector. The Excitation part learns inter-channel dependencies through two fully connected layers, outputting a weight vector. The Reweight part performs channel-wise weighting on the original features.

2.3. Algorithm of Prediction

The hour prediction utilizes the sequence from the recent past hour as its input. Conversely, for the 24 h prediction, the input is derived from the corresponding historical sequence observed at the same hour of the previous day. For the hour prediction, the modeling and prediction process can be described in five steps.

Step 1: Sample data preprocessing—Prepare an hourly historical dataset containing elements such as charging load volume, occupancy, electricity price, weather, time, and spatial location.

Step 2: Multi-scale temporal feature extraction: Determine the window sizes for extracting temporal segments at the hourly, daily, and weekly scales in the MSTFE module. From the sample data, extract the sequence according to the specified window sizes. For instance, with a three-scale window configuration of 1-2-1, use the data from the preceding hour, the preceding two days, and the previous week as the temporal segment input. The charging load on the subsequent hour is used as the output target. Prepare corresponding input–output data pairs.

Step 3: Adjacency matrix preparation—Compute the adjacency matrix by taking the inverse of the distance between any two nodes in network G. This matrix characterizes the spatial correlation between nodes and serves as another input to the model.

Step 4: Model training—First, initialize the model parameters. Then, partition the input–output data pairs into training, validation, and test sets, and proceed with model training. During training, the forward pass proceeds sequentially through the following layers: GCN layer, Conv layer, and cross-attention layer. Finally, compute the optimal model parameters based on the performance evaluated using both the training and validation sets.

Step 5: Predictive testing: Using the optimal model, conduct test evaluation on the test set to perform next-hour forecasting using the preceding one-hour sequence.

For the 24 h prediction, the process likewise consists of the abovementioned five steps. However, the preparation of input–output data pairs in Step 2 differs. Specifically, the sequence data from the corresponding hour on the preceding day is extracted as the input to predict the same hour on the subsequent day. For instance, with a three-scale window configuration of 1-2-1, the temporal segments used as input would be the corresponding hour from the previous two days and the corresponding hour from the previous week. The charging load at the same hour on the subsequent day serves as the output target, forming the input–output data pair. In other words, this approach entails predicting 00:00 using data from 00:00 on the previous day, predicting 01:00 using data from 01:00 on the previous day, and so forth for each hour.

The training algorithm for the prediction model (detailed in Algorithm 1) uses a shared adjacency matrix across both prediction horizons while processing distinct input feature sets for short-term (next-hour) and long-term (24 h) forecasts. For each prediction mechanism and each specific prediction time step, the model training is customized using different observed samples. Through iterative training, the optimal parameterized model is obtained and subsequently deployed for regional spatiotemporal charging load forecasting at both hourly and 24 h horizons.

Algorithm 1: Training Procedure of the STGCN-Attention Model

Input: Xf: Historical sequences included charging load, occupancy, price, weather       {Xf_hour, Xf_day, Xf_week}      A: Adjacency matrix      Y: Future charging load      K: Order of Chebyshev polynomials    Epochs_max: Maximum training epochs

Output: Trained STGCN-Attention model parameters $\theta$

Begin: 1.   Initialize model parameters $\theta$ randomly. 2.   for epoch=1 to epochs_max do 3.      #1. Multi-scale temporal feature extraction 4.     Z_hour←Temporal(Xf _hour); Z_day←Temporal(Xf _day); Z_week←Temporal(Xf _week) 5.      # 2. Spatial-Temporal Graph Convolution 6.     H_hour←GCN(Z_hour, A, K); H_day←GCN(Z_day, A, K); H_week←GCN(Z_week, A, K) 7.      # 3. Cross-Attention Fusion 8.     H_fused←[ ] 9.     for H in {H_hour, H_day, H_week} do 10.   $\alpha$←Softmax(Attention_Network(H, U)) 11.   H_attended←$\alpha$* H 12.   H_fused.append(H_attended) 13.   end for 14.   H_final←Concatenate(H_fused) 15.    # 4. Output & Loss Calculation 16.   Y_hat←Output_Layer(H_final) 17.   L←Mean_Squared_Error(Y, Y_hat) 18.    # 5. Backward Propagation 19.   $\theta$ ← Adam_Optimizer(∇_$\theta$ L, $\theta$) 20.   # Early Stopping Check 21.   if validation_loss does not decrease for p epochs, then 22.   break 23.   end if 24. end for 25. return $\theta$ 26. end

3. Case Study

3.1. Data

This study conducts a case study using a dataset collected in Shenzhen, China [28]. The real-world dataset comprises hourly charging load data from 1681 public charging stations spanning 1 September 2022 to 31 August 2023, with their spatial distribution illustrated in Figure 3. The dataset includes time-point parameters such as charging load volume (defined as the total electricity consumption in kWh across all chargers within a station), charger occupancy, real-time electricity price, and total charger count per station. Corresponding weather data were obtained from the China Meteorological Administration (CMA), including hourly precipitation and surface air temperature in Shenzhen. From a temporal perspective, the data with a total of 8760 timestamps is divided into training, validation, and test sets with a ratio of 6:2:2. Moreover, each method is configured to run separately to predict the charging demand in two different prediction mechanisms, hour prediction and 24 h prediction.

3.2. Spatiotemporal Characteristics of EV Charging Load

Before conducting forecasting experiments, it was essential to identify the spatiotemporal characteristics of regional charging loads to establish an intuitive understanding and discern patterns. This study analyzed the charging load characteristics in the Shenzhen case. As shown in Figure 4, the charging loads across all 1681 public charging stations were plotted to reveal trend distributions at hourly, daily, weekly, and monthly scales. The average hourly charging load ranged from 60 to 140 kWh. A distinct 24 h cyclical pattern was observed, with peak loads occurring during nighttime hours (0 a.m. to 8 a.m.) and a minor surge in the afternoon. Weekly variations indicated significantly higher charging loads on Saturdays compared to other days. Monthly analysis revealed significantly elevated charging loads during autumn and winter months (September–December) compared to spring/summer periods. This seasonal pattern has been confirmed by the existing literature and is primarily attributable to diminished lithium-ion battery charging efficiency under low-temperature conditions [29].

As presented in Figure 3, the spatial analysis revealed that most charging stations exhibited hourly loads below 200 kWh, with noticeable clustering in urban core areas. A small but prominent subset of stations demonstrated exceptionally high loads exceeding 2000 kWh per hour, though these “super stations” constituted a low overall proportion.

In summary, charging loads exhibited significant spatial correlations (where charging behaviors in adjacent areas influenced each other) and temporal dependencies (where historical loads affected future loads). These findings provided critical theoretical guidance for constructing graph-based forecasting models in subsequent research.

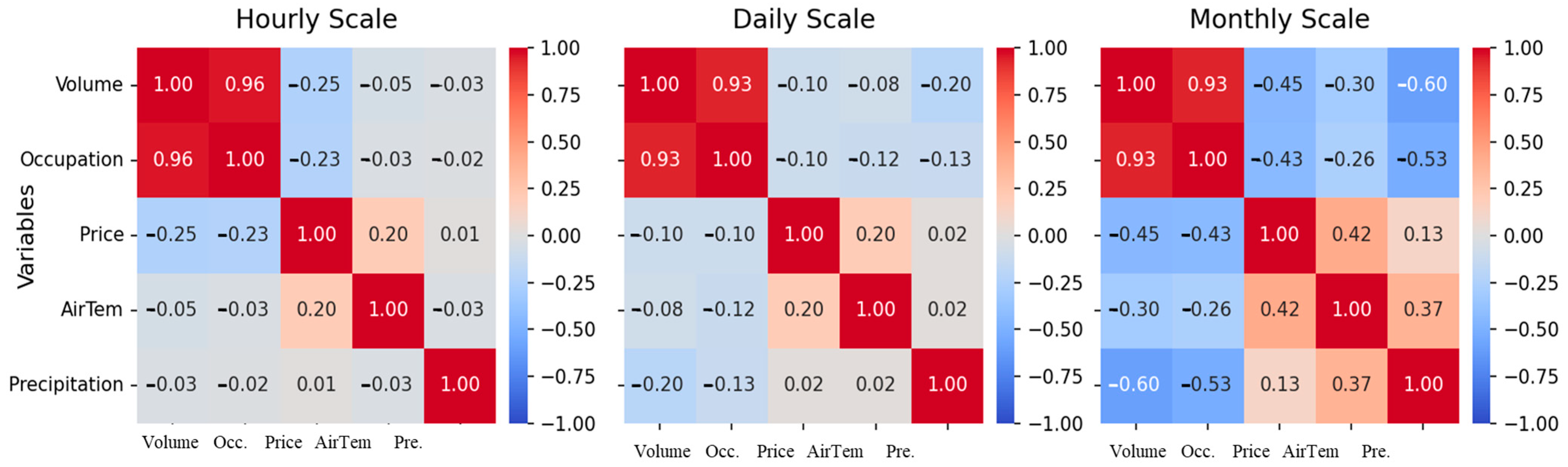
3.3. Correlation Between Charging Load and Multiple Factors

Correlations between charging loads and factors including occupancy, electricity prices, air temperature, and precipitation were revealed. Through association analysis, key factors influencing the spatiotemporal distribution of charging loads were identified preliminarily, providing direction for subsequent predictive model development. Given the distinct scale effects of these factors on charging loads, Pearson correlation coefficients (PC) were calculated at hourly, daily, and monthly timescales, as illustrated in Figure 5. Two significant patterns emerged. First, across all timescales, charging loads exhibited stronger correlations with occupancy and electricity prices (PC ≈ 0.93 and −0.45, respectively), whereas correlations with weather factors (temperature and precipitation) remained weak (PC ≈ −0.03~−0.6). Second, the relationships between charging loads and different factors demonstrated scale-dependent dynamics. The PC between charging loads and electricity prices/weather factors increased with larger temporal scales, peaking at the monthly level. For example, the PC between volume and precipitation was −0.03 at the hourly scale, −0.2 at the daily scale, and increased to −0.6 at the monthly scale. This scaling effect implied that integrating multi-factor inputs could potentially introduce higher prediction errors on the hourly scale.

3.4. Prediction Evaluation

3.4.1. The Model Setting and Evaluation

For the hour prediction, the window length was fixed at 1 h. For the 24 h prediction, a window of length 24 was used to produce predictions across 24 timestamps. The key hyperparameters of the model include the architecture parameters, training strategy parameters, regularization, and convergence control parameters. The hyperparameters were selected through a combination of empirical guidelines from the related literature and iterative tuning on a held-out validation set to achieve optimal performance. This involved several deliberate choices that also define the current limitations of our approach.

The architecture utilized a single-stacked spatiotemporal block with a Chebyshev polynomial order of K = 2 in the spatial graph convolution. The choice of a single block was made to balance model complexity and computational efficiency, as preliminary experiments indicated that deeper architectures did not yield significant performance gains on our dataset but increased the risk of overfitting. Referring to Qu et al., [14] the value of K = 2 was chosen as it effectively captures the immediate and secondary neighbor influences (i.e., 1st- and 2nd-order proximities) in the graph structure, which was sufficient for modeling local spatial dependencies without introducing excessive computational overhead. While effective for capturing immediate spatial neighborhoods, this choice represents a simplification, as it may not fully capture longer-range, higher-order spatial dependencies that could exist in the urban network. The reduction ratio in the cross-attention layer was set to 4, a standard value that effectively models channel-wise dependencies while preserving a compact intermediate representation.

For the training procedure, the model was optimized using the Adam optimizer due to its adaptive learning rate capabilities. A relatively small learning rate of 0.001 was chosen to ensure stable convergence, coupled with a weight decay coefficient of 1 × 10⁻⁴ to regularize the weights and prevent overfitting. The Mean Squared Error (MSE) was adopted as the loss function, aligning with the regression nature of the load forecasting task. A batch size of 32 was found to provide a good trade-off between training stability and memory usage. To further enhance generalization, a dropout rate of 0.2 was applied to both graph convolutional and cross-attention layers. This rate was determined via grid search over {0.1, 0.2, 0.3, 0.5}, with 0.2 yielding the best validation performance. An early stopping mechanism with a patience of 50 epochs was implemented to halt training when the validation loss ceased to improve, thus preventing overfitting. The training process demonstrated stable convergence, with both training and validation losses decreasing steadily and stabilizing after approximately 20 epochs, indicating that the chosen parameters were appropriate for the task.

However, the use of a fixed dropout rate across is a pragmatic simplification, as different layers might benefit from varying degrees of regularization. The early stopping mechanism, while preventing overfitting, inherently limits the exploration of longer, potentially beneficial training trajectories that might emerge with a different patience strategy. In summary, the parameter set represents a balanced and functional configuration. These choices involve approximations and trade-offs between model capacity, generalization, and computational cost, which point to avenues for further refinement in future work.

To facilitate comparative model analysis and validate the effectiveness of the proposed approach, Root Mean Square Error (RMSE), Mean Absolute Error (MAE), and Mean Absolute Percentage Error (MAPE) were adopted as evaluation criteria. All reported results represent the averaged values across all grid nodes at each prediction time step.

3.4.2. Compared Methods

LSTM and a modified Spatiotemporal Graph Convolutional Network (STGCN), excluding the multi-channel attention layer, were adopted as baseline models to evaluate the effectiveness of the proposed STGCN-Attention framework. Since LSTM specializes in modeling temporal dependencies and STGCN captures spatiotemporal graph structures, we selected them as benchmarks to compare predictive performance under these distinct mechanisms. Crucially, the LSTM model was not equipped with the multi-scale temporal feature extraction module, while both the STGCN and STGCN-Attention models retained this module. To ensure fair comparison, all model configurations followed recommendations from the relevant literature authors, and identical training settings, including window size, early stopping mechanism, batch size, loss function, and optimizer, were deployed consistently across all experiments [30].

3.4.3. Evaluation Results

Model performance was evaluated from three perspectives: (1) prediction errors were compared against baseline models to demonstrate the model’s effectiveness under both hourly and 24 h prediction mechanism; (2) sensitivity of window sizes for hourly/daily/weekly temporal feature extraction was examined to validate the predictive efficacy of the multi-scale sequence feature extraction module; (3) sensitivities of occupancy, electricity prices, and weather factors (temperature and precipitation) were analyzed to substantiate the forecasting performance under multi-factor fusion.

As shown in

Table 1. Performance comparison of the three models in different prediction mechanisms.

	RMSE		MAE		MAPE
	Hour	24 h	Hour	24 h	Hour	24 h
LSTM	42.64	61.26	32.72	48.02	0.27	0.37
STGCN	40.85	58.72	30.12	45.80	0.29	0.39
STGCN-Attention	37.32	54.13	27.34	43.12	0.25	0.36

, a comparative analysis of the STGCN-Attention model against two baseline methods confirms its superior predictive accuracy. The proposed model achieved the lowest error rates across all metrics and forecasting horizons. Specifically, for hour prediction, it attained values of RMSE = 37.32, MAE = 27.34, and MAPE = 0.25. For 24 h prediction, it maintained robust performance with RMSE = 54.13, MAE = 43.12, and MAPE = 0.36. Compared to the STGCN model, these values represented approximate reductions of 8% in RMSE, 9% in MAE, and 14% in MAPE, while relative to the LSTM model, the reductions reached 12% (RMSE), 16% (MAE), and 7% (MAPE). Overall, hourly prediction demonstrated significantly superior performance to 24 h prediction, with a predicted MAE reduction of about 30%.

Examination of the results from a representative charging station (Figure 6 and Figure 7) reveals two key patterns. In the hour prediction (Figure 6), all models exhibited minor underfitting at peak loads, although the STGCN-Attention model’s predictions aligned most closely with the observed values. For instance, the predictions were lower than the observed values around 05:00 on August 4 and August 6. In contrast, the 24 h prediction (Figure 7) displayed greater discrepancies, as seen in the larger deviation around 05:00 on August 4th. This increased error volatility can be attributed to the strong influence of the previous day’s values at the same hour, which amplifies deviations from the actual load.

3.5. Sensitivity Analysis

3.5.1. Sensitivity of Multi-Scale Temporal Feature Extraction (MSTFE) Module

To investigate the influence of incorporating hourly, daily, and weekly scales within the multi-scale temporal feature extraction module on prediction performance, we designed sensitivity experiments examining varying window sizes for sequence extraction. Excluding other relevant factors, historical charging loads served as the sole input. Predictive performance was evaluated using diverse combinations of temporal segment windows, where configurations such as Hour1, Day2, and Week1 denoted extracting (1) the immediate past 1 h segment, (2) corresponding segments from the past two consecutive days, and (3) the corresponding segment from exactly one week prior. The prediction sensitivity of window sizes ranging from 1 to 6 was visualized in Figure 8, based on model performance across these configurations. To ensure testing realism, when evaluating hour-scale sensitivity, the day and week scales were disabled. During day-scale testing, the hour scale was fixed at 1 with the week scale disabled. For week-scale assessment, both hour and day scales were set to 1.

Figure 8 presents the variation in the MAE of model predictions as the sequence extraction window increases from 1 to 6 across the hour scale, day scale, and week scale. An overall increasing trend was observed. The smallest MAE was achieved on the day scale, but local inflection points were also present. For example, on the day scale, the MAE with 27 reached its minimum when the window size was 2. These characteristics suggested that the introduction of the day scale factor significantly reduced the prediction error. This was likely attributable to the distinct daily periodicity of EV charging loads, which enhanced the model’s accuracy upon integration. In contrast, the incorporation of the week scale factor led to escalating errors with larger windows, and the overall error was consistently higher compared to the hour scale and day scale. Nonetheless, on the week scale, when the extraction window was set to 1, the MAE was approximately 28. Compared to the results from larger windows on the hour scale and day scale, this MAE was relatively small. In other words, incorporating the factor with a week-scale extraction window of 1 yielded favorable results for the model predictions.

In summary, for the MSTFE module, the optimal combination of the three temporal extraction windows was 1-2-1 (Hour1, Day2, Week1). Any suboptimal configuration was found to increase the prediction error.

3.5.2. Sensitivity of Different Input Factors

To quantify the impact of charging load, occupancy, weather, and electricity price-related factors on EV charging load forecasting, the forward selection method was used to conduct hourly and 24 h forecasting sensitivity experiments.

Multiple factor combinations were configured as model inputs: historical charging load volume (Volume), charging pile occupancy (Occupation), real-time electricity prices, air temperature (AirTem), and precipitation. These factors were integrated to form a T×N×F tensor input. The MSTFE module with setting 1-2-1 was employed throughout this sensitivity analysis, with all reported results representing averages from multiple experimental trials. Comparative prediction outcomes across different factor combinations are presented in

Table 2. Sensitivity of different input factors in the STGCN-Attention model.

Input Factor	RMSE		MAE		MAPE
	Hour	24 h	Hour	24 h	Hour	24 h
Volume	38.94	59.23	30.10	47.45	0.26	0.37
Volume + Occupation	37.67	57.31	28.97	46.34	0.26	0.39
Volume + Price	37.01	59.02	27.63	46.78	0.25	0.37
Volume + AirTem	39.35	61.03	31.10	48.90	0.31	0.40
Volume + Precipitation	40.94	60.29	32.98	48.01	0.33	0.42
Volume + Occupation + Price	37.32	58.72	27.34	45.80	0.25	0.36
Volume + Occupation + Price + AirTem	38.75	59.23	29.29	46.56	0.27	0.38
Volume + Occupation + Price + Precipitation	38.04	58.98	29.03	46.26	0.27	0.36

.

As presented in Table 2, the hour prediction outperformed the 24 h prediction across all factor combinations. For example, the MAE for the hour prediction ranged from approximately 27.34 to 32.98, while that for the 24 h prediction ranged from approximately 45.80 to 48.90. The hourly predictions were about 30% lower in MAE than the 24 h predictions. Meanwhile, the model achieved optimal performance when integrating volume, occupancy, and electricity prices. For the input combination of Volume + Occupation + Price, the RMSE, MAE, and MAPE for the hour prediction were 37.32, 27.34, and 0.25, respectively. This configuration yielded approximate reductions of 4% in RMSE, 9% in MAE, and 4% in MAPE, compared to using the input factor of volume alone. This phenomenon most likely stems from the strong correlation between charger occupancy and load demand and underscores the substantial governing effect of electricity prices on charging behavior. Conversely, incorporating air temperature (AirTem) and precipitation degraded predictive performance relative to the optimal feature set. For the input combination of Volume + Occupation + Price + Precipitation, the RMSE, MAE, and MAPE for the hour prediction were 38.04, 29.03, and 0.27, respectively. Compared to the configuration with input factor Volume + Occupation + Price, the RMSE, MAE, and MAPE increased by 2%, 7%, and 8%, respectively. This limitation likely stemmed from scarce precipitation events within the dataset timeframe and the weak hourly scale correlation between weather factors and charging loads. These findings highlighted the need for more refined integration strategies when incorporating meteorological factors in spatiotemporal charging load forecasting.

Accompanying the preceding analysis, which indicated that weather factors exhibited stronger correlations at the monthly scale, directly incorporating weather factors into hourly scale forecasting proved suboptimal. One approach employed feature engineering to extract weather information across different temporal scales, thereby constructing multi-scale feature factors that encompassed seasonal, monthly, daily, and hourly characteristics. Alternatively, considering that user behavior dominated at the hourly scale while the influence of weather factors diminished, another strategy decomposed the charging load sequence into long-term trend, seasonal trend, and residual components [31]. This adopted a decomposed sequence modeling approach with carefully designed input factors for each sub-sequence, which also constituted a superior alternative.

4. Conclusions

Spatiotemporal forecasting of electric vehicle (EV) charging loads plays a pivotal role in enhancing intelligent dispatching for urban power grids and smart transportation systems. For instance, it enables dynamic power allocation based on predicted charging demand and guides EV owners to stations with lower real-time utilization, thereby improving user experience. To address the spatiotemporal prediction challenges of regional EV charging loads, this study proposes a spatiotemporal graph convolutional network with multi-scale temporal features extraction and cross-attention (STGCN-Attention). By integrating multi-source data, including charging loads, charging pile occupancy, real-time electricity prices, and weather factors, the model successfully captured spatiotemporal correlations across multiple factors. Validation experiments were conducted for both 1 h and 24 h prediction mechanisms using real-world data encompassing historical charging patterns, occupancy, pricing, and weather conditions.

Empirical findings demonstrated that the synergistic integration of spatiotemporal graph convolution and attention mechanisms significantly enhanced prediction accuracy, reducing MAE by about 9% and 16% compared to conventional STGCN and LSTM models, respectively. Short-term forecasting (1 h) exhibited particularly superior performance, achieving approximately 30% higher accuracy than 24 h prediction reliant on historical same-period data, revealing the critical dominance of dynamic temporal correlations in short-term load fluctuations. Notably, sensitivity analysis of multi-scale temporal windows identified the optimal segment combination as 1-2-1 (Hour1, Day2, Week1). Furthermore, multiple factors sensitivity analysis confirmed that fusing historical loads, occupancy, and electricity prices yielded optimal results (RMSE = 37.21, MAE = 27.34 for hour prediction), whereas incorporating air temperature and precipitation increased errors by 2–8%, highlighting limitations of coarse-grained meteorological data integration. These discoveries offer dual practical implications: first, high-precision short-term forecasting enables minute-level dynamic pricing adjustments (e.g., 15 min peak-load response) and intelligent charging station allocation to reduce user wait times; second, weather factor integration requires refined strategies incorporating monthly/seasonal multi-scale features. For future research, the utilization of feature engineering to construct multi-scale weather features encompassing seasonal, monthly, daily, and hourly characteristics would be proposed for integration into the forecasting model. From another perspective, due to distinct influence effects across different scales, decomposition modeling of the charging load sequence was also planned to enhance predictive performance for relevant factors at their respective scales.

The STGCN-Attention model proposed in this study provided an effective solution for short-term electric vehicle charging load forecasting. However, it must be noted that the model’s validity was verified within the scope of the static graph structure and specific dataset used in this work, and its performance might be constrained by data quality, regional characteristics, and dynamic external factors. The model performed excellently in short-term (hourly and 24 h) forecasting, but its accuracy naturally decreased as the forecasting horizon extended to longer terms (such as weekly or monthly). It was primarily suitable for operational-level scheduling rather than strategic long-term planning. Future work would involve further validation of the model’s generalization capability across cities with different characteristics. Its application in regions with less available or lower-quality data would present significant challenges and could necessitate the use of data augmentation or transfer learning techniques to maintain performance. Addressing these limitations represents a key direction for our future research.