KG-FLoc: Knowledge Graph-Enhanced Fault Localization in Secondary Circuits via Relation-Aware Graph Neural Networks
Abstract
1. Introduction
- (1)
- Our work establishes a principled integration of knowledge graph technology with secondary circuit fault localization. Secondary components such as circuit breakers, disconnectors, and measuring devices are abstracted as nodes in the graph, while various relationships such as electrical connections, control logic, and information flow channels are used as edges between nodes.
- (2)
- When graph neural networks process circuit data, accurately capturing local and global features is of great significance. To this end, the method designs a relation-aware gated unit (RGU) module, which finely regulates information flow through the gating mechanisms of forget gates, input gates, and output gates.
- (3)
- The message-passing mechanism has a significant impact on the performance of GNNs in circuit fault detection. This method adopts an N-layer GIN neural network structure to design the message-passing mechanism, which can more efficiently capture graph structure information and make more comprehensive use of graph prompt information during training and inference.
2. Related Work
2.1. The Limitations of Traditional Fault Detection Methods
- (1)
- Single information dimension: Reliance on single fault features (such as temperature, alarm sequences, or network connectivity) leads to weak integration capabilities for multi-source and multi-dimensional fault information.
- (2)
- Manual modeling dependency: Formal models (fault trees, Petri nets, enumeration methods, etc.) require significant manual intervention, resulting in high maintenance costs and difficulty in quickly adapting to topological changes.
- (3)
- Limited generalization ability: Statistical or rule-based methods have poor generalization to new faults and data-scarce scenarios and struggle to handle concurrent multi-point faults.
2.2. Research Progress of Graph Neural Networks in Secondary Circuit Detection
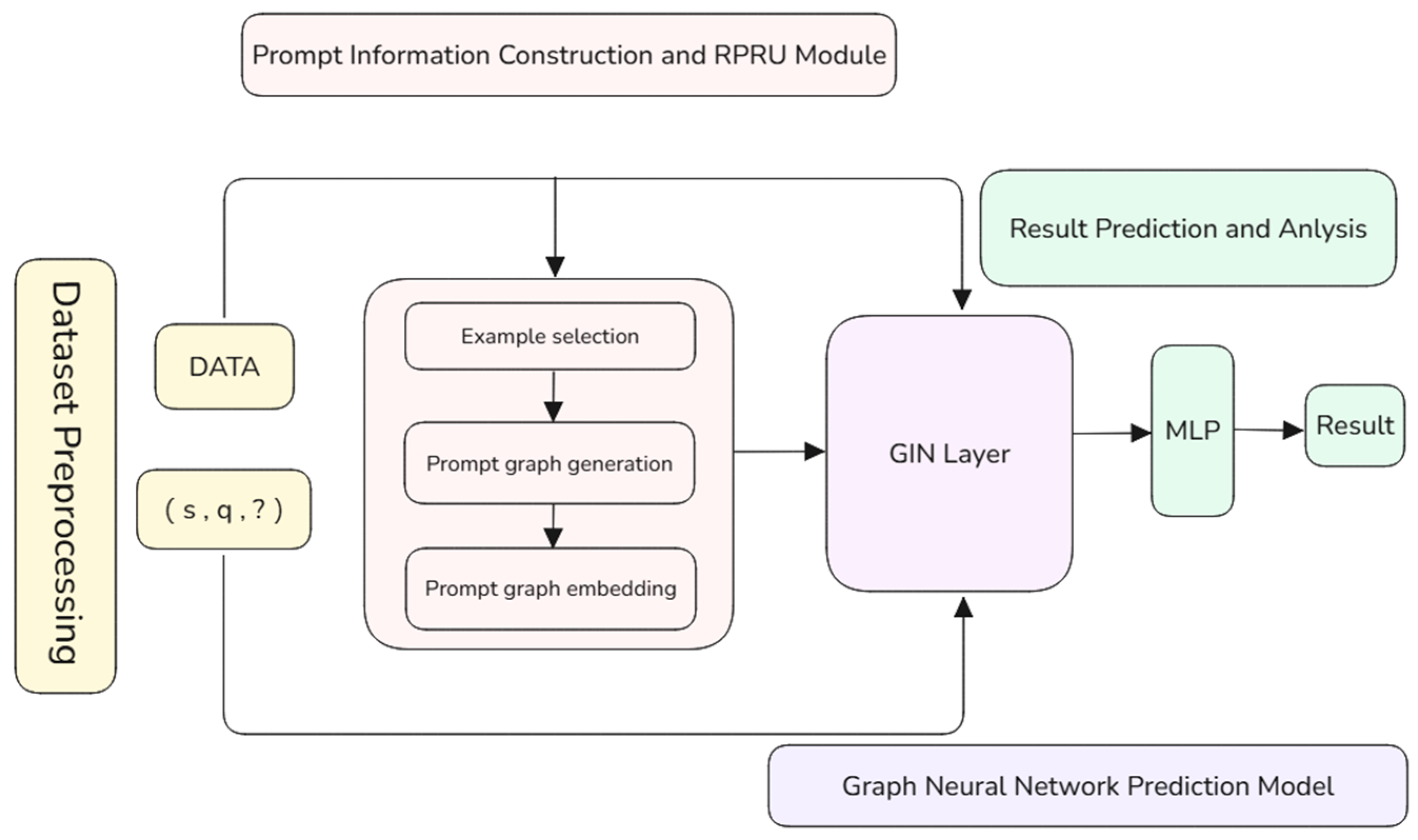
3. Proposed Methodology
- (1)
- Dataset preprocessing, where raw telemetry, remote control, and remote signaling data are integrated into a unified graph structure;
- (2)
- Prompt information construction, which selects context-aware examples (e.g., historical fault patterns) and generates prompt graphs to guide model reasoning;
- (3)
- Graph neural network development, featuring an N-layer GIN with RGU modules to capture local-global dependencies;
- (4)
- Result prediction, where fault probabilities are computed via inner-product scoring between node embeddings and a learnable weight matrix.
3.1. Dataset Preprocessing
3.2. Prompt Information Construction and RPRU Module
3.2.1. Example Selection
3.2.2. Prompt Graph Generation
3.2.3. Prompt Graph Embedding
3.3. Graph Neural Network Prediction Model
3.4. Result Prediction and Analysis
4. Experiments
4.1. Dataset and Experimental Setup
4.1.1. Graph Construction from SCD Files
4.1.2. Fault Sampling and Dataset Composition
4.2. Competing Models
4.3. Performance Analysis
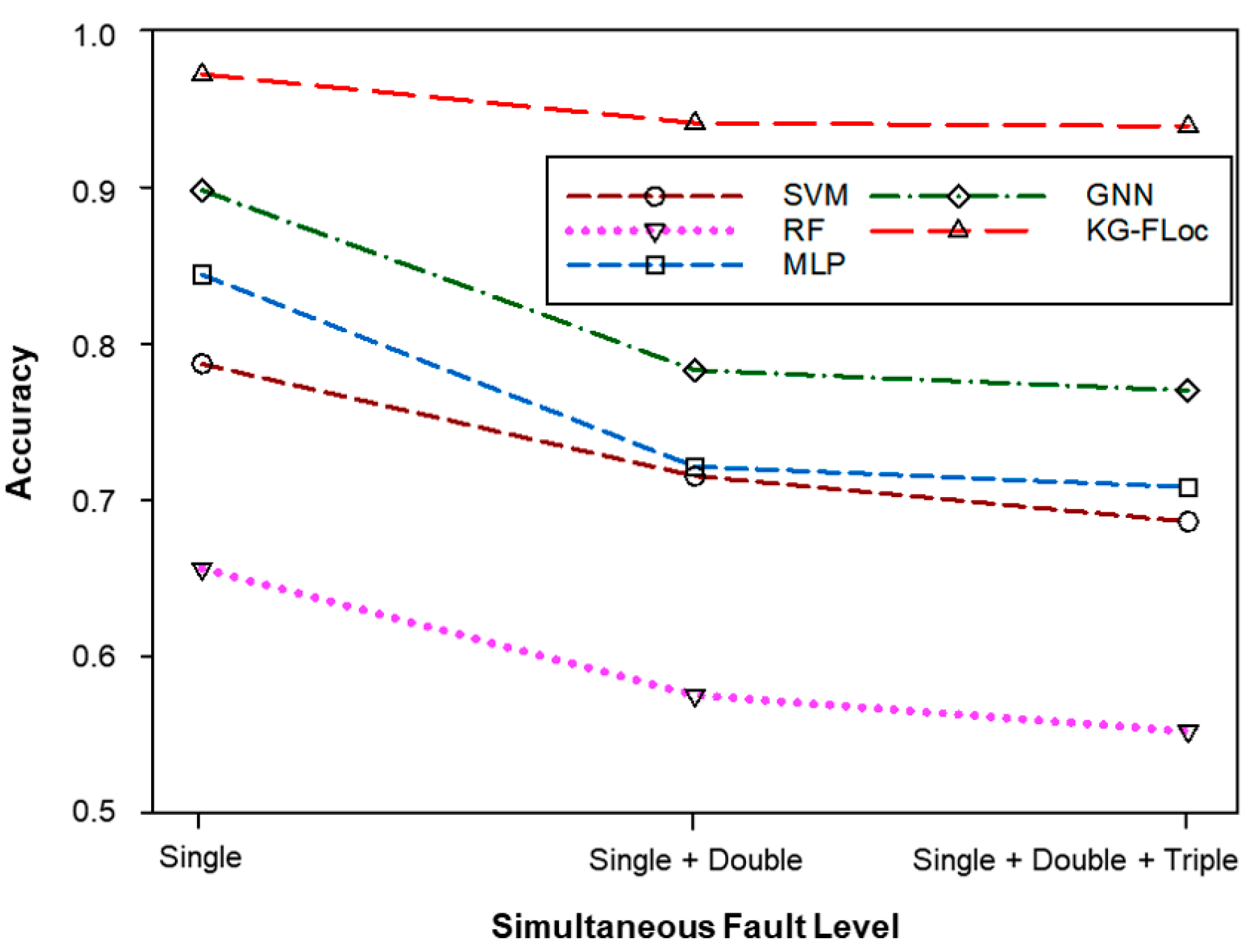
- For single-fault datasets, the complexity of the involved nodes is limited, allowing general models to handle fault location tasks effectively under such scenarios.
- When the double simultaneous fault dataset is introduced, multiple faults involve a greater number of nodes and significantly increase the inter-node correlation complexity. This results in higher confusion among different classes and a corresponding decrease in classification accuracy.
- The relationships among nodes are primarily captured in the double simultaneous fault dataset; even with the introduction of a triple simultaneous fault dataset, the performance does not degrade significantly.
4.4. Ablation Study
5. Conclusions
- (1)
- Online Adaptation: Developing incremental learning algorithms to handle dynamic topology changes in secondary circuits without retraining.
- (2)
- Knowledge-Large Model Synergy: Integrating pre-trained language models (e.g., GPT-4) to enhance contextual reasoning for rare fault patterns.
- (3)
- Edge Deployment: Optimizing KG-FLoc into a lightweight version deployable on substation edge devices, targeting latency < 10 ms per inference.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| ID | Fault Type | Description |
|---|---|---|
| 1 | Transformer Fault | Faults occurring within the transformer, such as winding short circuits, insulation failures, or internal component damage that disrupt the transformer’s function. |
| 2 | Circuit Breaker Fault | Faults in the breaker mechanism, such as mechanical failure, improper operation, or electrical faults leading to arcing or improper isolation. |
| 3 | Busbar Fault | Faults within the busbar, which may include grounding issues or short circuits between busbar sections, causing disruptions in power flow. |
| 4 | Disconnector Fault | Faults within the disconnector (or isolator) that prevent proper isolation of sections during maintenance or failure to disconnect during operation. |
| 5 | Protection Relay Fault | Malfunction or failure of protection relays, leading to incorrect detection or response to faults in the system. |
| 6 | Current Transformer (CT) Fault | Failure of the current transformer, resulting from short circuits, saturation, or mechanical issues, affecting current measurement and protection functionality. |
| 7 | Voltage Transformer (VT) Fault | Faults in voltage transformers, including insulation failure, open circuits, or incorrect voltage scaling that disrupt system measurements. |
| 8 | Fiber Optic Port Failure | Failure in the fiber optic communication ports, either from internal device faults or connection issues, affecting data transmission between devices. |
| 9 | Fiber Optic Cable Fault | Physical damage or misconnection in the fiber optic cables, leading to loss of communication or improper data transfer between devices. |
| 10 | Board Fault (Control Panel) | Faults in control panels or boards, including issues like component burnout, incorrect wiring, or malfunctioning digital or analog circuits affecting system control. |
| 11 | Switchgear Fault | Faults within switchgear, such as incorrect switching or failure in isolation between electrical sections, often due to mechanical wear or electrical malfunction. |
| 12 | Power Capacitor Fault | Internal issues within power capacitors, such as short circuits or dielectric failure, affecting reactive power compensation and voltage stability. |
| 13 | Overvoltage Protection Relay Fault | Fault in the relay designed to protect against overvoltage conditions, potentially leading to false tripping or non-response during actual overvoltage conditions. |
| 14 | Undervoltage Protection Relay Fault | Failure of the undervoltage protection relay, which may not operate correctly under low voltage conditions, leading to potential system instability. |
| 15 | Insulation Failure | Breakdown of insulation materials in electrical components, leading to short circuits or leakage currents, posing a risk of further equipment damage. |
| 16 | Overcurrent Fault | Fault caused by a current exceeding the rated capacity, often resulting in equipment damage due to excessive thermal or mechanical stress. |
| 17 | Grounding Fault | Faults due to improper grounding or loss of ground connection, leading to unsafe voltage levels and potential electrical shock hazards. |
| 18 | Arc Flash | A type of fault resulting in an electric arc flash, which can cause severe damage to electrical components and pose significant safety risks to personnel. |
| 19 | Short Circuit between Busbars | A direct short circuit between two busbars, often leading to high fault currents and potential damage to circuit breakers and transformers. |
| 20 | Transformer Oil Leak | Leaks or spills of insulating oil in transformers, which can result in system contamination, overheating, and fire hazards. |
| 21 | Switchgear Contact Fault | Faults related to the contacts in switchgear, leading to improper closure or opening of circuits, affecting the overall reliability of the system. |
| 22 | Misconnection between Substations | Fault caused by incorrect wiring or configuration between substations, leading to unexpected behavior or failure of the system’s operation. |
| 23 | Overheating of Equipment | Occurs when electrical components such as transformers, cables, or circuit breakers exceed their rated operating temperature, resulting in thermal damage. |
| 24 | Mechanical Fault in Generator | Faults in the mechanical components of a generator, such as rotor imbalance or mechanical wear, leading to operational failures or inefficiency. |
| 25 | Loss of Synchronization | Occurs when generators or electrical machines fail to remain synchronized, causing disruptions in power flow or potential damage to generators. |
References
- Xiang, X.M.; Dong, X.C.; He, J.Q.; Zheng, Y.K.; Li, X.Y. A study on the fault location of secondary equipment in smart substation based on the graph attention network. Sensors 2023, 23, 9384. [Google Scholar] [CrossRef]
- Peng, Z.; Chen, G.; Zhang, J.; Liu, J.; Chen, J.; Wang, J. Method for locating secondary circuit faults in substations based on graph neural networks. Heliyon 2024, 10, e40042. [Google Scholar] [CrossRef] [PubMed]
- Chen, F.; Luo, J.; Wang, R.; Shi, Q.; Yang, J.; Wu, T. Research on fault diagnosis method of substation relay protection secondary circuit based on improved DS evidence theory. Measurement 2025, 256, 118232. [Google Scholar] [CrossRef]
- Kuang, H.; Yi, P.; Luo, Y.; Tan, J.; Yin, H.; Wei, S.; Wang, R. Research on Fault Diagnosis Method of Secondary Equipment in Intelligent Substation. J. Phys. Conf. Ser. 2022, 2260, 012020. [Google Scholar] [CrossRef]
- Shiping, E.; Zhang, H.; Liu, D.; Wang, Z.; Zhang, K.; Zhao, S.; Li, H. Fault Diagnosis of Secondary Equipment Based on Big Data of Smart Substation. In Proceedings of the 2022 4th Asia Energy and Electrical Engineering Symposium (AEEES), Chengdu, China, 25–27 March 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 869–873. [Google Scholar]
- Wang, L.; Zheng, J.; Zhou, H.; Pei, Y.; Chang, Z.; Fan, C.; Lv, L. Research on Fault Diagnosis Methods for Secondary Circuits in Smart Substations. In Proceedings of the International Joint Conference on Energy, Electrical and Power Engineering, Singapore, 22–24 November 2024; Springer Nature Singapore: Singapore, 2024; pp. 494–502. [Google Scholar]
- Wang, J.; Jing, S.; Yao, Y.; Wang, K.; Li, B. A state evaluation and fault diagnosis strategy for substation relay protection system integrating multiple intelligent algorithms. J. Eng. 2024, 2024, e70013. [Google Scholar] [CrossRef]
- Tanaka, T.; Uezono, T.; Suenaga, K.; Hashimoto, M. In-Situ Hardware Error Detection Using Specification-Derived Petri Net Models and Behavior-Derived State Sequences. arXiv 2025, arXiv:2505.04108. [Google Scholar]
- Yan, Z.; Xu, F.; Tan, J.; Liu, H.; Liang, B. Reinforcement learning-based integrated active fault diagnosis and tracking control. ISA Trans. 2023, 132, 364–376. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Wang, B. A knowledge graph method towards power system fault diagnosis and classification. Electronics 2023, 12, 4808. [Google Scholar] [CrossRef]
- Ma, M.; Zhu, J. Interpretable Recurrent Variational State-Space Model for Fault Detection of Complex Systems Based on Multisensory Signals. Appl. Sci. 2024, 14, 3772. [Google Scholar] [CrossRef]
- Shen, J.; Yang, S.; Zhao, C.; Ren, X.; Zhao, P.; Yang, Y.; Han, Q.; Wu, S. FedLED: Label-free equipment fault diagnosis with vertical federated transfer learning. IEEE Trans. Instrum. Meas. 2024, 73, 1–10. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, Z.; Zhang, X.; Du, M.; Zhang, H.; Liu, B. Power system fault diagnosis method based on deep reinforcement learning. Energies 2022, 15, 7639. [Google Scholar] [CrossRef]
- Cui, Y.; Sun, Z.; Hu, W. A prompt-based knowledge graph foundation model for universal in-context reasoning. Adv. Neural Inf. Process. Syst. 2024, 37, 7095–7124. [Google Scholar]
- Zhou, H.; Huang, J.; Zhang, C. Petri net based fault diagnosis for GOOSE circuits of smart substation. South. Power Syst. Technol. 2017, 11, 49–56. [Google Scholar]
- Volkanovski, A.; Čepin, M.; Mavko, B. Application of the fault tree analysis for assessment of power system reliability. Reliab. Eng. Syst. Saf. 2009, 94, 1116–1127. [Google Scholar] [CrossRef]
- Fan, G.F.; Wei, X.; Li, Y.T.; Hong, W.C. Fault detection in switching process of a substation using the SARIMA–SPC model. Sci. Rep. 2020, 10, 11417. [Google Scholar] [CrossRef] [PubMed]
- Ullah, I.; Yang, F.; Khan, R.; Liu, L.; Yang, H.; Gao, B.; Sun, K. Predictive maintenance of power substation equipment by infrared thermography using a machine-learning approach. Energies 2017, 10, 1987. [Google Scholar] [CrossRef]
- Hong, J.; Kim, Y.H.; Nhung-Nguyen, H.; Kwon, J.; Lee, H. Deep-learning based fault events analysis in power systems. Energies 2022, 15, 5539. [Google Scholar] [CrossRef]
- Qiu, X.; Du, X. Fault Diagnosis of TE Process Using LSTM-RNN Neural Network and BP Model. In Proceedings of the 2021 IEEE 3rd International Conference on Civil Aviation Safety and Information Technology (ICCASIT), Weihai, China, 15–17 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 670–673. [Google Scholar]
- Nguyen, B.L.; Vu, T.V.; Nguyen, T.T.; Panwar, M.; Hovsapian, R. Spatial-temporal recurrent graph neural networks for fault diagnostics in power distribution systems. IEEE Access 2023, 11, 46039–46050. [Google Scholar] [CrossRef]
- Xu, K.; Hu, W.; Leskovec, J.; Jegelka, S. How Powerful Are Graph Neural Networks? arXiv 2018, arXiv:1810.00826. [Google Scholar]
- Brusamarello, B.; Da Silva, J.C.C.; de Morais Sousa, K.; Guarneri, G.A. Bearing fault detection in three-phase induction motors using support vector machine and fiber Bragg grating. IEEE Sens. J. 2022, 23, 4413–4421. [Google Scholar] [CrossRef]
- Fezai, R.; Dhibi, K.; Mansouri, M.; Trabelsi, M.; Hajji, M.; Bouzrara, K.; Nounou, H.; Nounou, M. Effective random forest-based fault detection and diagnosis for wind energy conversion systems. IEEE Sens. J. 2020, 21, 6914–6921. [Google Scholar] [CrossRef]
- Tang, W.; Huang, G.; Li, G.; Yang, G.; Geng, X.X. Measurement Performance Improvement Method for Optically Pumped Magnetometer based on Multilayer Perceptron. IEEE Sens. J. 2024, 24, 38851–38860. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Z.; Li, M.; Dai, X.; Wang, R.; Shi, L. A Gearbox Fault Diagnosis Method Based on Graph Neural Networks and Markov Transform Fields. IEEE Sens. J. 2024, 24, 25186–25196. [Google Scholar] [CrossRef]
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A next-generation hyperparameter optimization framework. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; ACM: New York, NY, USA, 2019; pp. 2623–2631. [Google Scholar]



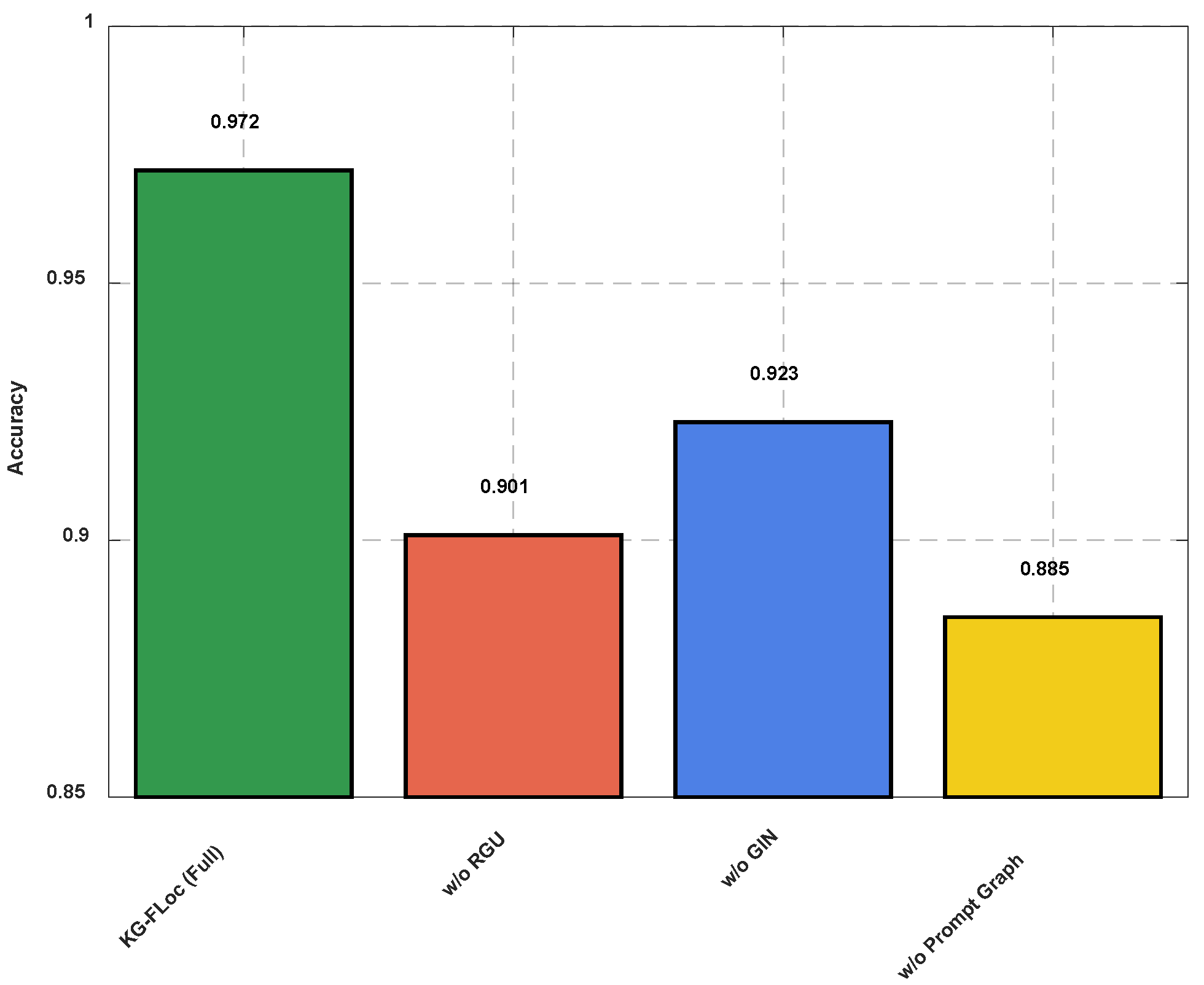
| Simultaneous | #Graphs | #Fault Classes | #Average Node Count | #Average Edges |
|---|---|---|---|---|
| Single | 1250 | 25 | 3.91 | 3.28 |
| Single + Double | 2150 | 25 | 6.14 | 5.77 |
| Single + Double + Triple | 2950 | 25 | 7.78 | 7.45 |
| Model | Level of Simultaneous Faults | ||
|---|---|---|---|
| Single | Single + Double | Single + Double + Triple | |
| SVM | 0.787 (±0.008) | 0.715 (±0.011) | 0.686 (±0.015) |
| RF | 0.656 (±0.032) | 0.575 (±0.044) | 0.552 (±0.048) |
| MLP | 0.844 (±0.025) | 0.721 (±0.052) | 0.708 (±0.065) |
| GNN | 0.898 (±0.024) | 0.783 (±0.055) | 0.770 (±0.076) |
| KG-FLoc | 0.972 (±0.007) | 0.941 (±0.011) | 0.939 (±0.014) |
| Model | Macro-Average F1-Score |
|---|---|
| SVM | 0.761 |
| RF | 0.632 |
| MLP | 0.821 |
| GNN | 0.894 |
| KG-FLoc | 0.965 |
| Model Variant | Accuracy |
|---|---|
| KG-FLoc (Full Model) | 97.2% |
| w/o RGU (Replaced with concatenation) | 90.1% |
| w/o GIN (Replaced with GCN) | 92.3% |
| w/o Prompt Graph (Random initialization) | 88.5% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, X.; Chen, C.; Yan, X.; Song, J.; Qi, H.; Xue, W.; Wang, S. KG-FLoc: Knowledge Graph-Enhanced Fault Localization in Secondary Circuits via Relation-Aware Graph Neural Networks. Electronics 2025, 14, 4006. https://doi.org/10.3390/electronics14204006
Song X, Chen C, Yan X, Song J, Qi H, Xue W, Wang S. KG-FLoc: Knowledge Graph-Enhanced Fault Localization in Secondary Circuits via Relation-Aware Graph Neural Networks. Electronics. 2025; 14(20):4006. https://doi.org/10.3390/electronics14204006
Chicago/Turabian StyleSong, Xiaofan, Chen Chen, Xiangyang Yan, Jingbo Song, Huanruo Qi, Wenjie Xue, and Shunran Wang. 2025. "KG-FLoc: Knowledge Graph-Enhanced Fault Localization in Secondary Circuits via Relation-Aware Graph Neural Networks" Electronics 14, no. 20: 4006. https://doi.org/10.3390/electronics14204006
APA StyleSong, X., Chen, C., Yan, X., Song, J., Qi, H., Xue, W., & Wang, S. (2025). KG-FLoc: Knowledge Graph-Enhanced Fault Localization in Secondary Circuits via Relation-Aware Graph Neural Networks. Electronics, 14(20), 4006. https://doi.org/10.3390/electronics14204006






