Abstract
This paper details the design and fabrication of a triode–anode magnetron injection gun (MIG) for a 170 GHz gyrotron for use in magnetic confinement thermonuclear fusion. To solve the mismatch problem of electric and magnetic fields in the electron emission area caused by geometric deformation under the thermal field, the temperature of the MIG was tested to accurately describe the thermal field distribution, and geometric dimension variables under the operating temperature were simulated. By analyzing the electric and magnetic fields under the thermal field, the design scheme of the MIG was optimized to achieve the goals of reducing the spread of electron beam velocity in the interaction region and improving the interaction efficiency.
1. Introduction
Physical experimental research on electron cyclotron resonance heating in Tokamak experimental devices and the commercial application of fusion energy are gradually improving the expected megawatt-level performance of gyrotrons [1,2,3,4,5,6,7,8,9]. The International Thermonuclear Experimental Reactor (ITER) and China Fusion Engineering Test Reactor (CFETR), both in progress, have put forward the application requirements for high-frequency megawatt-level gyrotrons. A 170 GHz gyrotron has been under development at the Beijing Vacuum Electronic Research Institute (BVERI) for several years.
In 2017, the first version of a 170 GHz gyrotron was designed in BVERI, which employed the TE25,10 as the operating mode. Its operating voltage was 80 kV and the current was 40 A, while the operating magnetic field intensity was 6.72 T. The theoretical calculation of the output power of the high-frequency cavity was about 1.1 MW (without considering the effect of velocity scattering). The transmission system, including the mode converter and window, had an efficiency of about 96%. The 170 GHz verification sample tube of the TE25,10 mode output was completed in 2021. The power of this gyrotron achieved 200 kW at the 61 kV, 30 A operating point, and 300 kW at the 75 kV, 40 A operating point [10].
On the basis of the 2021 research, contributing to the components of ceramic optimized, the resistance of the cathode and anode was increased to withstand 80 kV accelerating voltage. In 2022, a Gaussian quasi-optics mode transformation was employed to transverse the output mode from the TE25,10 to the Gaussian beam, and a single depressed collector was designed and applied to the upgraded gyrotron. In addition, in the process of designing MIG, it was necessary to pay close attention to matching of electric and magnetic fields, as well as the electrode deformation under the thermal field, since the cathode operates at high temperature. In this paper, the electric field (E-field), the magnetic field (M-field) and the thermal field(T-field) are comprehensively considered to analyze the influence of thermal field on the beam performance of MIG.
2. Design of MIG Without Thermal Field
To generate high-power microwave energy at high frequency, gyrotrons employ a resonator that couples the cyclotron electron beam and high-order mode to convert the electron kinetic energy into microwave energy. As shown in Figure 1, the cyclotron electron beam (black circle) is designed at the peak of the E-field (red area) to maximize the interaction efficiency. Simultaneously, the interaction needs three parameters, namely guidance center radius, pitch factor, and velocity spread, to satisfy the requirements.
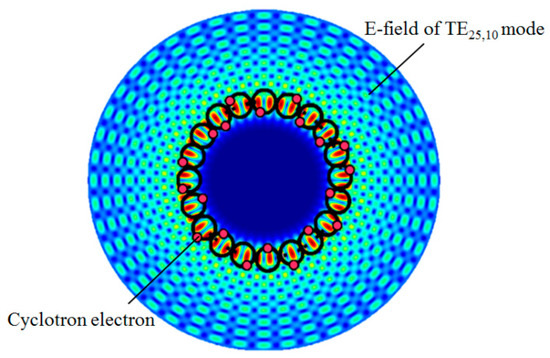
Figure 1.
Schematic diagram of cyclotron electron beam and high-order mode interaction.
We designed a triode MIG to provide a cyclotron electron beam for a 170 GHz gyrotron. As shown in Figure 2, the MIG had a gun region, transition region, and drifting region.
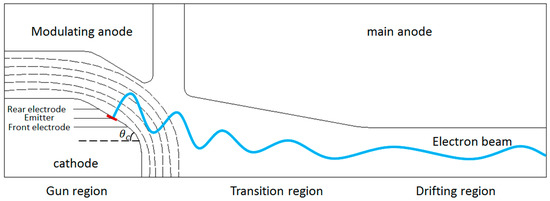
Figure 2.
Principle schematic diagram of diode–anode MIG. The blue curve represents an electronic beam emitted from a cathode, and injected into the resonance of the gyrotron.
In the gun region, the emitter potential was identical for the rear electrode and front electrode, and the potential difference between the cathode and modulating anode caused a strong E-field to exist on the cathode surface. The E-field on the cathode surface was exactly perpendicular to the emitter and could be decomposed into and by refined optimization, resulting in the velocity of electrons emitted from the cathode being decomposed into and .
To guide the electrons following the desired trajectory, it was necessary to arrange the gradually varied M-field in the axial direction in these three regions ). In the transition region, the electron cyclotron frequency increases with the M-field, and the electron transverse velocity increases under the adiabatic compression effect.
As the E-field approaches zero, an equipotential space forms in the drifting region. Along the M-field field line, the intensity of the M-field increases and the change rate of the M-field decreases as the M-field at the exit of the MIG approaches a constant maximum value, in which the helical velocity reaches the designed maximum and the guiding center radius tends to be stable. The formula of the M-field compression ratio can be expressed as
It is convenient to calculate the correlation between the guiding center radius of electron and the M-field intensity along the axial, where and are the M-field intensity and guiding center radius at the position of resonator, and and are the M-field intensity and guiding center radius at the position of the emitter. Therefore, according to the guiding center radius of the electron beam in the interaction resonator and the M-field distribution of superconducting magnet, the radius of emitter can be determined.
The essence of the interaction between the electron beam and the microwave is to convert the angular (transverse) kinetic energy of electron into RF microwave energy. It should be noted that the transverse kinetic energy will be much greater than the longitudinal energy if the employed M-field is stronger than the matched E-field; therefore, the emitted electron may be trapped by the magnetic mirror in the reverse direction and accelerated by the E-field in the forward direction. The trapped electron increases the ionization probability, and the ionized particles [11]. The pitch factor is defined to estimate the ratio of average transverse velocity to average longitudinal velocity as follows:
The transverse velocity of the electron at the interaction region can be estimated as follows [12,13]:
Here, is the relativistic factor and is the electron emitted angle, which depends on the cathode angle. and are the E-field and M-field at the cathode, respectively. So and the match between the E-field and the M-field are the significant factors for the pitch factor under the determined accelerating voltage and operating magnetic field intensity.
Transverse velocity spread and longitudinal velocity spread can be estimated as follows:
There are three types of influencing factors of velocity spread in the experiment, which involves E-field and M-field mismatch , surface roughness , and thermal emission spread , and where the total transverse spread can be estimated as follows [14]:
In the above formula, is mostly affected by the surface roughness of the cathode, and is mostly affected by the cathode material and its operating temperature. This paper focuses on the velocity spread caused by the matching E-field and M-field. In general, the magnetic line of force is perpendicular to the electric field line on the cathode surface, which benefits from the increase in the initial uniformity of the electron beam emitted from cathode. By optimizing the above, a triode–anode MIG was designed, for which parameters are shown in Table 1. Under 80 kV of accelerating voltage, 45 A of operating current, and 6.72 T of interacting magnetic field for the fundamental 170 GHz/ TE25,10 mode gyrotron, the simulated average pitch factor was 1.27, which satisfied the interaction requirement, while the transverse velocity spread was 2.72% and the longitudinal velocity spread was 4.87%. As shown in Figure 3, the M-field of the emitter ring was 0.29 T and the . At the interaction area, the guiding center of beam was 7.41 mm and the thickness of the beam was 0.45 mm.

Table 1.
Design parameters of triode MIG for 170 GHz gyrotron.
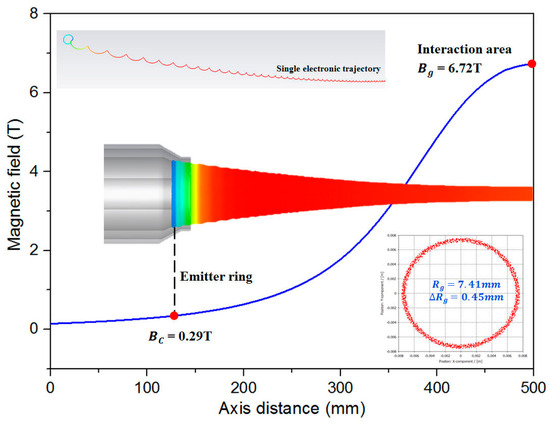
Figure 3.
Schematic of MIG for 170 GHz gyrotron. Emitter ring and interaction area are marked as the initial and target location of electron beam. The single cycling electronic trajectory is shown at the top of figure.
3. Analysis of MIG with Thermal Field
Under operating conditions, a high temperature was distributed in the electrode since the gyrotron employed a thermal cathode operating at approximately 1000 °C normally [15], therefore it was critical to analyze the thermal field of the operating MIG and control the effect of electrode thermal deformation. A thermal experiment of MIG was designed to observe the temperature distribution in different areas of the MIG and obtain the correlation coefficient of the filament power and electrode temperature. By using the design scheme of the triode–anode MIG for a 170 GHz gyrotron described in Section 2, a MIG component containing a modulation anode was fabricated, and employed a quartz disk window welding at the MIG output to maintain component at a low vacuum leakage rate, combining with an ion pump to maintain the vacuum degree at better than Pa, to ensure a normal operating state of the filament and identical operating state with the gyrotron.
The temperature of the cathode, front electrode, and rear electrode were accurately measured from a quartz disk window by an infrared camera. As shown in Figure 4, the color of the cathode surface was bright yellow under high operating temperature conditions, and an orange color could be observed at the surface of the front electrode and rear electrode, which had a lower temperature.

Figure 4.
Photo of thermal experiment. The area of bright yellow color (approximately 1000 °C) is the emitter ring.
In the experiment, we changed the filament power in the range of 90 W–450 W by adjusting the filament supply voltage and current, and observed and recorded corresponding electrode temperature data shown in Table 2.

Table 2.
Thermal experiment data of MIG for 170 GHz gyrotron.
Based on the cathode thermal experiment, a calculation model was built and simulated using Annsys 16.1 software, with filament power set as the input parameter, to monitor the temperature of electrode as the judgment of calculation accuracy. To uniformize calculation and experiment results, the thermal emissivity coefficients and thermal conduction coefficients between various materials were modified. Typically, the thermal emissivity of molybdenum electrode was set to 0.15 at 600 °C and the surface of the cathode was set to 0.16 at approximately 930 °C; thus, reliable geometry deformation variables with measured temperature distribution under MIG operating conditions were obtained. The correlation of the relationship between the cathode surface temperature and heater power are shown in Figure 5, which describes the temperature of the simulation comparable with the experiment.
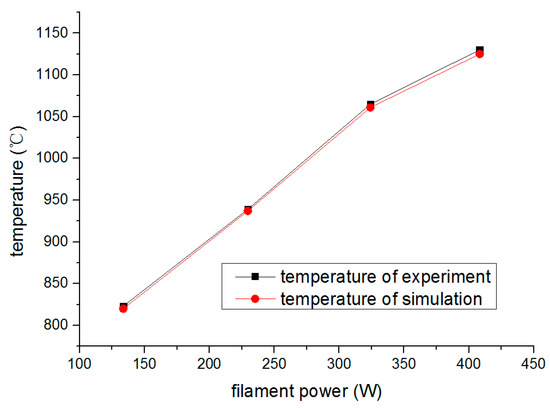
Figure 5.
Correlation between filament power and temperature of emitter ring.
Figure 6 displays the temperature distribution of the MIG front view under a filament power of 220 W, where the temperature of the cathode surface is 937 °C (red ring). Because we employed a structure with superior thermal insulation capability, the temperature of the adjoining electrode showed obvious distinction, while the temperature of the front electrode was 655.9 °C and the temperature of the rear electrode was 608 °C. In practice, electron emission may cause the cathode surface temperature to decrease by approximately 3 °C per A/cm2 of emission current density, meaning the cathode surface temperature in the operating gyrotron will be approximately 12 °C lower than the simulated value. This gap was ignored in the thermal deformation simulation as it is a subtle effect.
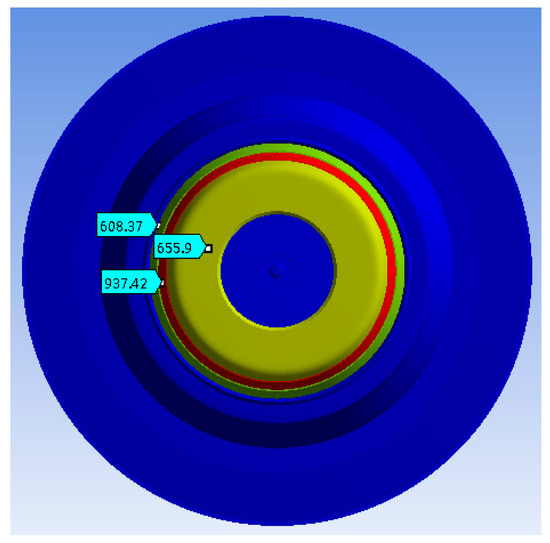
Figure 6.
Temperature of MIG by simulation.
Based on the above model and results, the electrode geometric deformation of a 170 GHz gyrotron MIG under the described operating conditions was simulated. The power of the gyrotron filament was set at 220 W while the accelerating voltage was 80 kV and the operating current was 40 A in the experiment; three electrode geometric deformations are shown in Figure 7. Under the influence of the thermal field, the cathode radius increased by 0.19 mm, equivalent to 0.53% of the original geometric dimensions, and the radial expansion dimensions of the front electrode and rear electrode were 0.11 mm and 0.12 mm due to their lower temperature under the operating state. At the same time, because the MIG component was welded to the tube body, these three electrodes expanded approximately 0.548 mm in the axial direction towards the cavity. The temperature of the modulating anode rose less than 10 °C and the geometric deformation caused by the thermal field was less than 0.01 mm. The simulated values of the electrodes’ deformation are listed in Table 3.

Figure 7.
Radial and axial geometric deformation of MIG electrodes under the operating state.

Table 3.
The simulated geometric deformation variable values of MIG electrodes under the operating state.
4. Experimental Research
To analyze the effect of thermal deformation caused by the thermal field on the electron beam characters of a MIG for a 170 GHz gyrotron, the deformation of electrodes simulated in Section 3 were corrected in the initial design model, and the MIG models with/without thermal field are shown in Figure 8. The peak electrode field strength along the cathode surface increased from 8.0 × 106 V/m to 1.09 × 107 V/m, because the distance between the cathode and anode was reduced in the operating state. The red line in Figure 8, which represents the operating state, spiked at the front electrode, and the compatibility between the E-field and the M-field in the cathode region was seriously damaged, which may cause an increase of initial electronic velocity, with the emitted angle changing and velocity consistency reducing. The main parameters comparing the electron beam performance with and without the thermal field are shown in Table 4. Under the operating conditions, pitch factor increased by approximately 25%, and the transverse velocity spread and perpendicular velocity spread were more than doubled, exceeding the design baseline of 5%, which had a significant effect on beam–wave interaction.
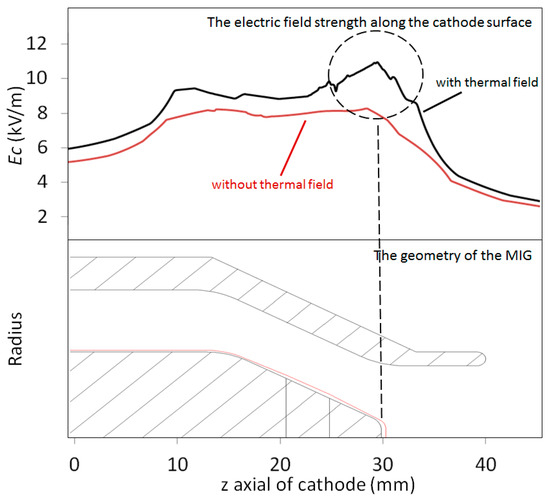
Figure 8.
The lower part shows the MIG electrode outline operating with (red line)/without (black line) the thermal field, and the upper part shows the magnetic field distribution along the cathode surface in the corresponding area.

Table 4.
Simulation results of primary MIG without/with thermal field and optimized structure with thermal field.
To eliminate the influence of geometric deformation on the performance of the electron beam under the thermal field, practicability must be considered. Therefore, an optimized scheme of a triode–anode MIG was designed. The E-field distribution between the cathode and anode was adjusted by changing the configuration of three anodes, while decreasing the voltage of the modulating anode to suppress the peak E-field of the front electrode. The E-field and M-field of the cathode surface were analyzed and are shown in Figure 9, in which the abscissa is the cathode position along the z-axis, the blue curve represents the E-field intensity on the cathode surface, and the red one represents the M-field strength at the axis of the MIG. At the emitter area, where the longitudinal length was 5 mm, the gradient of the E-field and the gradient of the M-field , an electromagnetic field match was perfectly achieved.
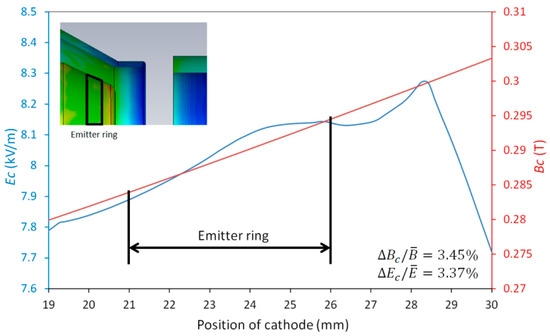
Figure 9.
E-field and M-field distribution curve at the cathode area.
The optimized MIG, which considered both electromagnetic and thermal fields, is shown in the Table 4. The results indicate that the pitch factor was reduced from 1.59 to 1.29, the transverse velocity spread was reduced from 5.91% to 3.27%, and the longitudinal velocity spread was reduced from 17.06% to 5. 82%, close to the initial simulation results of the MIG without the thermal field.
Using the initial MIG design scheme, Gyrotron-II was fabricated in 2022, with 80 kV of accelerating voltage, 40 A of operating current, and a 6.72 T magnetic field, and a Gaussian microwave beam was measured which achieved 10% efficiency at a frequency of 169.3 GHz. Based on the modified structure which eliminated the influence of geometric deformation with the thermal field, Gyrotron-III was fabricated in 2023 and achieved 19.7% efficiency under the same operating conditions, nearly doubling the beam-wave interaction efficiency.
5. Conclusions
To reduce the influence of thermal deformation of the electron beam under a cathode temperature of approximately 1000 °C, a MIG based on an initial design was fabricated and the temperature of each electrode was measured as the power of the filament reached the operating value. Based on the temperature distribution, the geometric deformation was simulated, which showed the cathode increased by 0.55 mm along the axial direction and 0.19 mm along the radial direction. To solve the problem of the increase and spike of the E-field on the cathode surface, a new MIG was designed which considered thermal deformation, so that the E-field and M-field of the emitter were well matched. In the simulation, the pitch factor was 1.29 and velocity spread was 3.27% under the operating conditions, which were close to the expect design values. Using the new MIG, a 170 GHz gyrotron was fabricated for which the measured output power reached 0.71 MW. The improved interaction efficiency of the electron beam after optimizing the MIG under the operating conditions based on the cathode thermal experiment was verified.
Author Contributions
Conceptualization, Y.Z.; validation, W.H., B.L. and K.L.; formal analysis, Y.Z.; software, D.G.; investigation, J.F.; resources, J.F.; data curation, Y.Z.; writing—original draft preparation, Y.Z.; writing—review and editing, J.F.; visualization, W.H.; supervision, X.Z.; project administration, X.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received Stable Support Scientific Project K2410259 funding acquisition.
Data Availability Statement
All data included in this study are available upon request by contacting with the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Thumm, M. State-of-the-art of high power gyro-devices and free electron masers, update 2009. J. Infrared Millim. Terahertz Waves 2020, 41, 1–140. [Google Scholar] [CrossRef]
- Gantenbein, G.; Erckmann, V.; Illy, S.; Kern, S.; Kasparek, W.; Lechte, C.; Leonhardt, W.; Liévin, W.; Samartsev, A.; Schlaich, A.; et al. 140 GHz, 1 MW CW Gyrotron Development for Fusion Applications-Progress and Recent Results. Infrared Milli Terahertz Waves 2011, 32, 320–328. [Google Scholar] [CrossRef]
- Thumm, M. Progress on gyrotrons for ITER and Future Thermonuclear Fusion Reactors. IEEE Trans. Plasma Sci. 2011, 39, 971–979. [Google Scholar] [CrossRef]
- Henderson, M.A.; Saibene, G. Critical interface issues associated with the ITER EC system. Nucl. Fusion 2008, 48, 054017. [Google Scholar] [CrossRef]
- Sakamoto, K.; Kasugai, A.; Kajiwara, K.; Takahashi, K.; Oda, Y.; Hayashi, K.; Kobayashi, N. Progress of high power 170 GHz gyrotron in JAEA. Nucl. Fusion 2009, 49, 095019. [Google Scholar] [CrossRef]
- Denisov, G.G.; Kuftin, A.N.; Malygin, V.I.; Venediktov, N.P.; Vinogradov, D.V.; Zapevalov, V.E. 110 GHz gyrotron with a built-in high-efficiency converter. Int. J. Electron. 1992, 72, 1079–1091. [Google Scholar] [CrossRef]
- Blank, M.; Kreischer, K.; Temkin, R.J. Theoretical and Experimental Investigation of a Quasi-Optical Mode Converter for a 110-GHz Gyrotron. IEEE Trans. Plasma Sci. 1996, 24, 1058–1066. [Google Scholar] [CrossRef]
- Illy, S.; Beringer, M.H.; Kern, S.; Thumm, M. collector design studies for a 1 MW cylindrical-cavity and a 4 MW coaxial-cavity gyrotron. In Proceedings of the 35th International Conference on Infrared, Millimeter, and Terahertz Waves, Rome, Italy, 5–10 September 2010. [Google Scholar]
- Parth, C.; Kalaria, M.V.; Thumm, M. Design of 170 GHz, 1.5-MW Conventional Cavity Gyrotron for Plasma Heating. IEEE Trans. Plasma Sci. 2014, 42, 1522–1528. [Google Scholar]
- Zhang, Y.; Zeng, X.; Bai, M.; Jin, M.; Hao, W.; Gao, D.; Liu, Q.; Feng, J. The development of 170 GHz Mega-watts Gyrotron for Fusion Application. Electronics 2022, 11, 1279. [Google Scholar] [CrossRef]
- Jiang, W.; Liu, Y.; Lu, C.; Dai, B.; Wang, J.; Pu, Y. Design and Analysis of a Diode Magnetron Injection Gun for a G-Band Gyro-TWT. IEEE Trans. Electron Devices 2022, 69, 1429–1434. [Google Scholar] [CrossRef]
- Baird, J.M.; Lawson, W. Magnetron injection gun (MIG) design for gyrotron applications. Int. J. Electron. 1986, 61, 953–967. [Google Scholar] [CrossRef]
- CYuan, P.; Chang, T.H.; Chen, N.C.; Yeh, Y.S. Magnetron injection gun for a broadband gyrotron backward-wave oscillator. Phys. Plasmas 2009, 16, 073109. [Google Scholar] [CrossRef]
- Ma, G. Theory and Experimental Study for 140 GHz Gyrotron; Institute of Applied Electronics, China Academy of Engineering Physics: Chengdu, China, 2019. [Google Scholar]
- Lun, L.Z.; Wang, X.J. Cathode Electronics; National Defense Industry Press: Beijing, China, 2013. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).