Numerical Simulation Study of Electromagnetic Pulse in Low-Altitude Nuclear Explosion Source Regions

Abstract

A nuclear electromagnetic pulse (NEMP) is the fourth effect of a nuclear explosion, characterized by a strong electromagnetic field that can instantly damage electronic devices. To investigate the spatial field value distribution characteristics of the source region of low-altitude NEMPs, this study employed a finite-difference time-domain (FDTD) method based on a rotating ellipsoidal hyperbolic coordinate system. Due to intense field variations near the explosion center, non-uniform grids were employed for both spatial and temporal steps, and an OpenMP parallel algorithm was utilized to enhance computational efficiency. Analysis focused on the following two scenarios: varying angles at a constant distance and varying distances at a constant angle, considering both transverse magnetic (TM) and transverse electric (TE) waves. The results indicate that the spatial field value distribution characteristics differ between the two wave types. For TM waves, the electric and magnetic fields share the same polarity, but their waveform polarities are opposite above and below the explosion center. A TE wave is exactly the opposite. Compared with a TM wave, a TE wave has stronger peak electromagnetic fields but narrower pulse widths and lower overall energy. This research provides significant support for the development of nuclear explosion detection technology and offers theoretical foundations for the protection of surrounding environmental facilities.

1. Introduction

Nuclear explosions produce not only shockwaves, thermal radiation, and radioactive contaminations but also a significant destructive effect known as the nuclear electromagnetic pulse (NEMP) [1,2]. A NEMP is a strong electromagnetic wave released at the moment of a nuclear explosion, posing a severe threat to various electronic devices and systems [3,4,5,6]. To fully understand the information contained within NEMPs, it is essential to have a clear understanding of the source region. Compared to high-altitude nuclear explosions, due to the relatively high air density in a low-altitude environment, the average free path of gamma rays is shorter, so low-altitude nuclear detonations have a smaller source region; however, the energy is concentrated in a smaller area, resulting in greater destructive power in nearby regions. Therefore, in-depth research on the electromagnetic field distribution characteristics of NEMPs from low-altitude nuclear explosions is crucial in enhancing nuclear explosion detection technology and improving systems’ resistance to nuclear radiation.

Gilinsky Victor et al. [7] proposed a dipole model for low-altitude NEMPs. Longley H Jerry et al. [8] employed a two-dimensional time-domain finite-difference method based on a spherical–cylindrical coordinate system to calculate the source region fields of near-surface nuclear explosions. The Northwest Nuclear Technology Research Institute was the first to develop a two-dimensional differential calculation program for simulating low-altitude NEMPs [9]. Wang Taichun et al. [10] derived approximate analytical formulas for the current and electric field generated by instantaneous gamma photons in the source region under the conditions of a low-altitude nuclear explosion. Liang Rui et al. [11] conducted numerical calculations of the electromagnetic pulse signals from low-altitude nuclear explosions propagating into space using the finite-difference time-domain (FDTD) method. Cui Zhitong et al. [12] analyzed the amplitude and frequency domain characteristics of far-field electric field signals from low-altitude nuclear explosions. Chen Jiannan et al. [13] considered the scattering effects of the Earth and air on radiation and the capture effects on neutrons, using the MCNP program to simulate the radiation environment near the ground during a nuclear explosion at low altitudes. The authors discussed the impact of the ground on the source region fields of low-altitude NEMPs and performed parallel acceleration for source region simulations [14,15].

Overall, previous research on low-altitude NEMPs is limited, especially regarding comparative analyses of field characteristics at different monitoring points within the source region; this area requires thorough and detailed work.

The FDTD method is widely used in various fields of electromagnetic field simulation due to its simplicity [16,17,18,19]. This study employed the FDTD method based on a rotating ellipsoidal–hyperbolic orthogonal coordinate system. Considering the intense field variations near ground zero, both spatial and temporal steps were set non-uniformly; spatial grids were defined as exponential functions while time steps were determined by Courant–Friedrichs–Lewy (CFL) conditions. OpenMP parallel algorithms were utilized to enhance computational efficiency. First, we determined the coverage area of the source region (considering explosion yield and altitude), then investigated field value distribution characteristics at monitoring points at equal distances but different angles from ground zero as well as at equal angles but different distances. The study provides a theoretical foundation for further research on nuclear explosion detection and offers scientific support for formulating relevant protective measures.

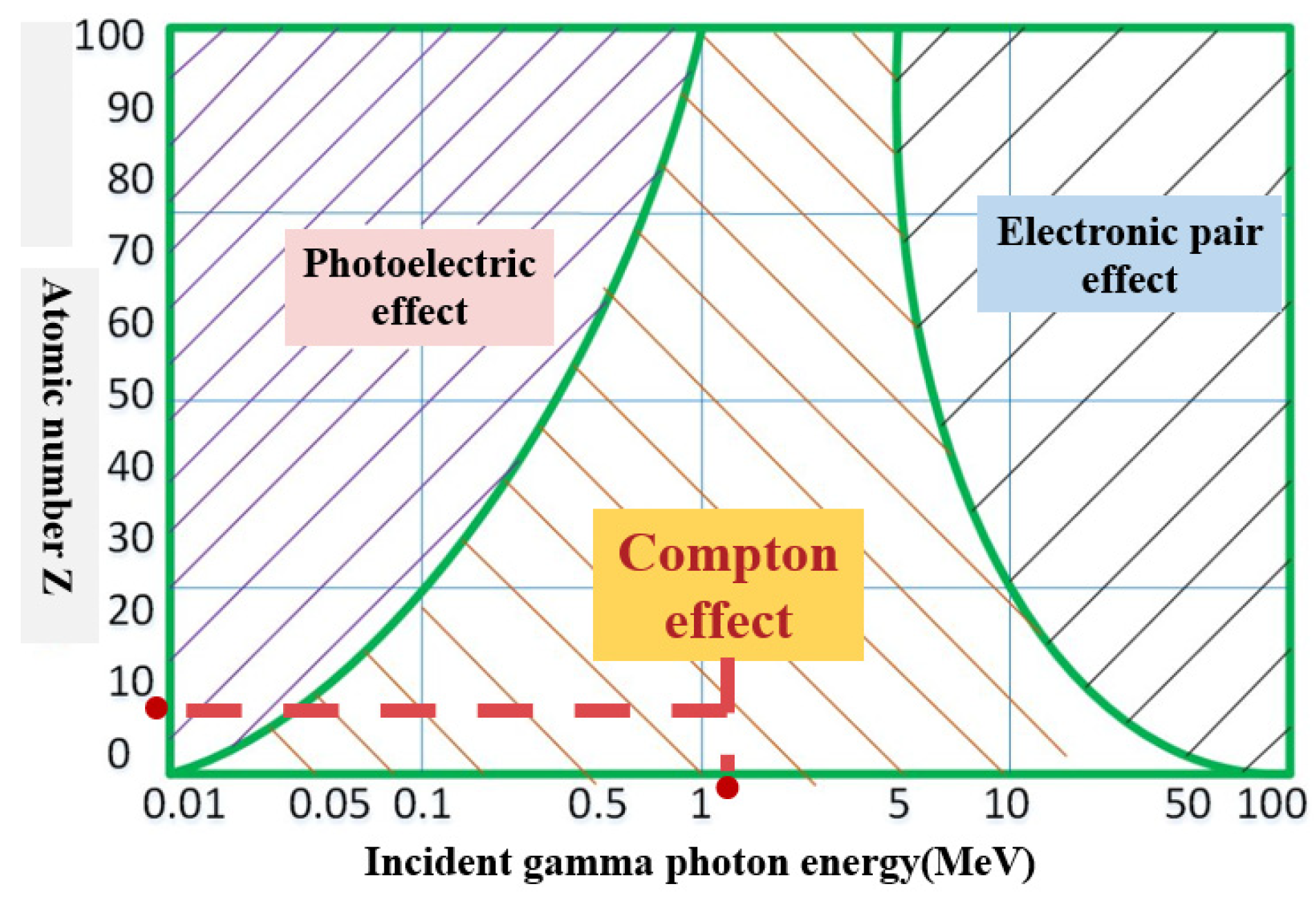
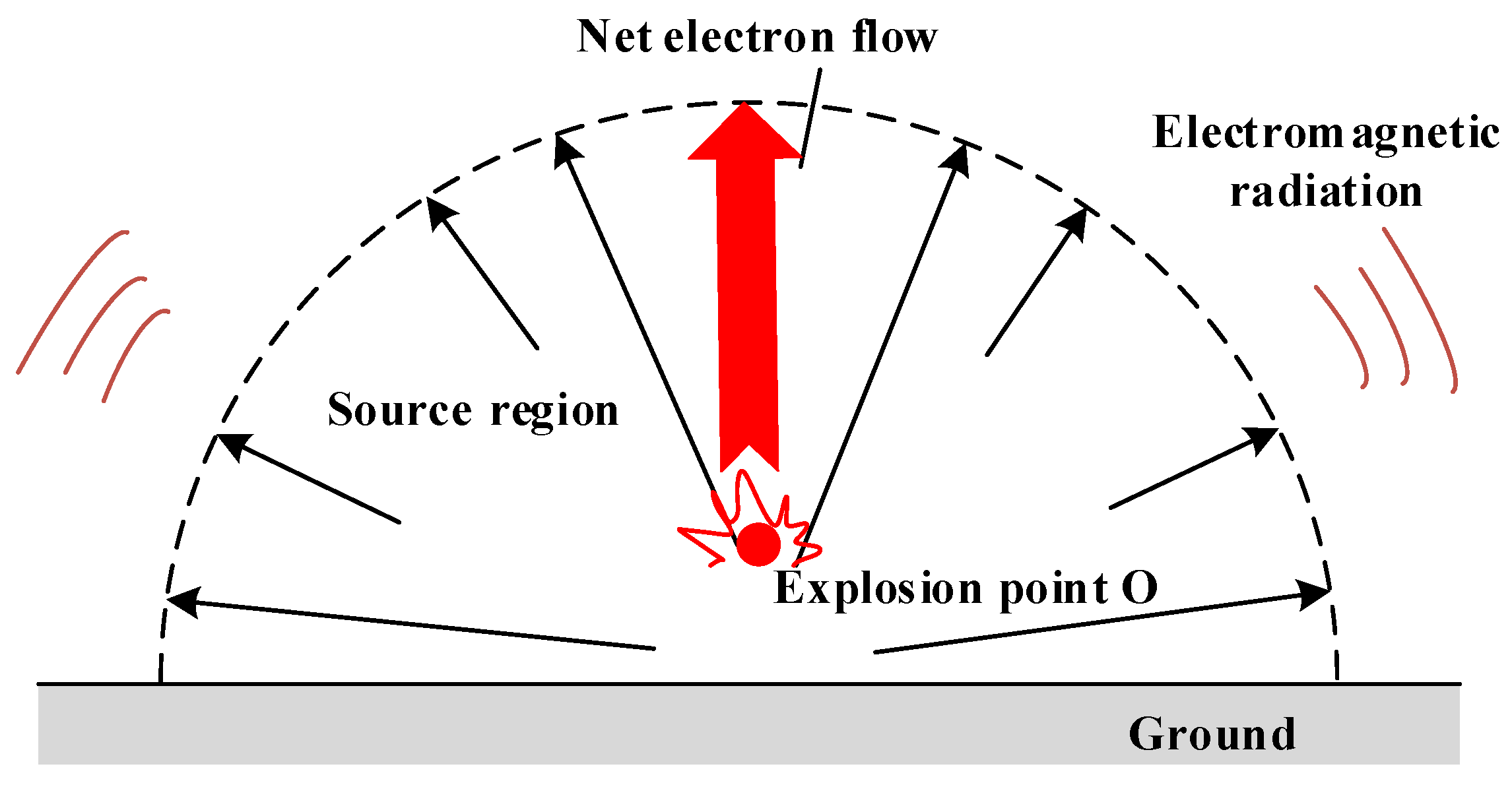
2. Mechanism of Generation

A NEMP is a strong electromagnetic wave generated instantaneously during a nuclear explosion. The large amount of gamma rays released by the explosion interacts with the surrounding atmosphere, primarily involving the electron–positron pair production, photoelectric effect, and Compton scattering. The average energy of the photons (1.5 MeV) and the atomic numbers of the atmospheric constituents (such as nitrogen and oxygen) determine that the Compton effect is the primary mechanism exciting the NEMP, as illustrated in Figure 1. This paper mainly considers the physical process whereby radiation interacts with surrounding air molecules to produce Compton currents, thereby exciting electromagnetic pulses [20].

When a nuclear weapon detonates in a low-altitude environment, the photons radiated downward are absorbed by the upper layers of the ground’s geological medium. In contrast, radiation emitted outward and upward ionizes the air, causing charge separation and resulting in the generation of a significant number of Compton electrons. These electrons move outward, creating a Compton current, which manifests as a net vertical flow of electrons directed upward. Consequently, the source region is excited and radiates electromagnetic energy outward. The electromagnetic pulse generated by low-altitude nuclear explosion is shown in Figure 2.

3. Introduction to Numerical Simulation Methods

A NEMP primarily originates from the Compton currents generated by the interaction of prompt gamma rays produced by explosions with air (or ground media). The ionization of air results in changes in conductivity. Therefore, the calculation of the source region field requires a coupled solution of Maxwell’s equations and the air ionization equations [20].

The Maxwell’s equations under the CGS-G (centimeter-gram-second-gauss) unit system are as follows:

$$\{\begin{array}{l}{\displaystyle \frac{1}{c}}{\displaystyle \frac{\partial \mathit{B}}{\partial t}}=-\nabla \times \mathit{E}\\ {\displaystyle \frac{\mu \epsilon }{c}}{\displaystyle \frac{\partial \mathit{E}}{\partial t}}+4\pi \mu \left(\sigma \mathit{E}+\mathit{J}\right)=\nabla \times \mathit{B}\end{array}$$

(1)

Here, $c$ represents the speed of light in a vacuum, $\mathit{E}$ represents the electric field strength, $\mathit{B}$ represents the magnetic flux density, $\mathit{J}$ is the current density, $\sigma$ is the electrical conductivity of the medium, $\epsilon$ and $\mu$ mean the permittivity and permeability, respectively.

The study employs a rotating ellipsoidal hyperbolic orthogonal coordinate system ($\xi ,\zeta ,\phi$), as illustrated in Figure 3. The explosion point is located at one of the foci of the rotating ellipsoid, while the ground is situated on the perpendicular plane of the major axis of the rotating ellipsoid. The advantages of the rotating ellipsoidal–hyperbolic orthogonal coordinate system are that the ground serves as one of the surfaces of $\xi =0$, facilitating the handling of ground connection conditions. Furthermore, the explosion point is located at one of the foci of the rotating ellipsoidal–hyperbolic orthogonal coordinate system. The sphere centered at this focus is a significant auxiliary surface, which can be easily represented using the $(\xi ,\zeta )$ spatial straight line.

The simulation of electromagnetic fields in the source region employs an OpenMP parallel FDTD. A nuclear explosion can be considered as originating from a single point and radiating gamma rays outward. Consequently, parameters such as current and conductivity near the explosion point change drastically, while the far explosion point changes slowly. Therefore, non-uniform grids are used for spatial sampling, as shown in (2), $a$ represents the explosion height, $I_0,I_1,I_{\max },J_{\max }$ represents the number of grid cells, and the time grid step size can be obtained from the CFL condition. This method improved the computational efficiency.

$$\begin{array}{l}{\xi }_I=\{\begin{array}{c}1+\left[1-100\times \left({1.01}^I-1\right)\right]\times 0.0025,\\ \left(1-{1.02}^{I-I_1}\right)\times 0.6385,\end{array}\begin{array}{cc}& \begin{array}{c}1\le I\le I_0,\\ I_1\le I\le I_{\max },\end{array}\end{array}\\ {\zeta }_J=a\ast \left\{1+\left[50\times \left({1.02}^J-1\right)-1\right]\times 0.06\right\}\begin{array}{cc}& 1\le J\le J_{\max },\end{array}\end{array}$$

(2)

Assuming the quantities possess axial symmetry, meaning that the partial derivative with respect to the $\varphi$ direction is zero, the two curl equations in Maxwell’s equations can be decomposed into two sets of independent equations, corresponding to the transverse magnetic (TM) wave and transverse electric (TE) wave equations.

The equation for the TM wave is as follows:

$$\{\begin{array}{l}{\displaystyle \frac{\partial E_{\xi }}{\partial \tau }}+{\displaystyle \frac{4\pi \sigma }{\epsilon }}{E}_{\xi }=-{\displaystyle \frac{4\pi }{\epsilon }}{J}_{\xi }+{\displaystyle \frac{1}{\epsilon }}{\displaystyle \frac{\partial B_{\varphi }}{\partial \zeta }}-{\displaystyle \frac{1}{\epsilon }}{\displaystyle \frac{\partial B_{\varphi }}{\partial \tau }}\\ {\displaystyle \frac{\partial E_{\zeta }}{\partial \tau }}+{\displaystyle \frac{4\pi \sigma }{\epsilon }}{E}_{\zeta }=-{\displaystyle \frac{4\pi }{\epsilon }}{J}_{\zeta }-{\displaystyle \frac{1}{\epsilon a}}{\displaystyle \frac{\partial B_{\varphi }}{\partial \xi }}-{\displaystyle \frac{1}{\epsilon }}{\displaystyle \frac{\partial B_{\varphi }}{\partial \tau }}\\ {\displaystyle \frac{\partial B_{\varphi }}{\partial \tau }}=-{\psi }_{\xi }\left({\displaystyle \frac{1}{a}}{\displaystyle \frac{\partial E_{\zeta }}{\partial \xi }}+{\displaystyle \frac{\partial E_{\zeta }}{\partial \tau }}\right)+{\psi }_{\zeta }\left({\displaystyle \frac{\partial E_{\xi }}{\partial \varsigma }}-{\displaystyle \frac{\partial E_{\xi }}{\partial \tau }}\right)\end{array}$$

(3)

The equation for the TE wave is as follows:

$$\{\begin{array}{l}{\displaystyle \frac{\partial B_{\xi }}{\partial \tau }}=-{\displaystyle \frac{\partial E_{\varphi }}{\partial \zeta }}+{\displaystyle \frac{\partial E_{\varphi }}{\partial \tau }}\\ {\displaystyle \frac{\partial B_{\zeta }}{\partial \tau }}={\displaystyle \frac{1}{a}}{\displaystyle \frac{\partial E_{\varphi }}{\partial \xi }}+{\displaystyle \frac{\partial E_{\varphi }}{\partial \tau }}\\ {\displaystyle \frac{\partial E_{\varphi }}{\partial \tau }}+{\displaystyle \frac{4\pi \sigma }{\epsilon }}{E}_{\varphi }=-{\displaystyle \frac{4\pi }{\epsilon }}{J}_{\varphi }+{\displaystyle \frac{{\psi }_{\xi }}{\epsilon }}\left({\displaystyle \frac{1}{a}}{\displaystyle \frac{\partial B_{\zeta }}{\partial \xi }}+{\displaystyle \frac{\partial B_{\zeta }}{\partial \tau }}\right)-{\displaystyle \frac{{\psi }_{\zeta }}{\epsilon }}\left({\displaystyle \frac{\partial B_{\xi }}{\partial \varsigma }}-{\displaystyle \frac{\partial B_{\xi }}{\partial \tau }}\right)\end{array}$$

(4)

In Equations (3) and (4), $J_{\xi }$, $J_{\varsigma }$ and $J_{\varphi }$ are the three components of the Compton current in the rotating ellipsoidal hyperbolic orthogonal coordinate system.

The Compton current is obtained as the product of charge, electron velocity, and electron density, as shown in (5).

$$\mathit{J}=-g(\mathrm{r}){\displaystyle \frac{e_q}{c}}{\displaystyle {\int }_0^{R_e/\beta }\overrightarrow{V}({\tau }^{\prime })}f\left(\tau -{\tau }^{\prime }+{\displaystyle \frac{\kappa ({\tau }^{\prime })}{c}}\right)d{\tau }^{\prime }$$

(5)

Here, $g(r)$ means the coefficient, $e_q$ is the absolute value of the electronic charge, $R_e$ means the average range of Compton electrons in air, and $\beta$ is deduced to $V_0/c$, $\tau$ represents the delayed time.

The three components of the Compton current in spherical coordinates are as shown in (6), and $f_r$ represents the gamma dose rate at position $r$.

$$\{\begin{array}{l}{J}_r(r,\theta ,\varphi ,\tau )=-{\displaystyle \frac{e_q}{c}}g(r){\displaystyle {\int }_0^{R_e/\beta }{f}_r(\tau -\chi ({\tau }^{\prime }}))({\sin }^2\theta \cdot \cos \omega {\tau }^{\prime }+{\cos }^2\theta )d{\tau }^{\prime }\\ J_{\theta }(r,\theta ,\varphi ,\tau )=-{\displaystyle \frac{e_q}{c}}g(r){\displaystyle {\int }_0^{R_e/\beta }{f}_r(\tau -\chi ({\tau }^{\prime }}))\sin \theta \cdot \cos \theta (\cos \omega {\tau }^{\prime }-1)d{\tau }^{\prime }\\ J_{\varphi }^{\prime }(r,\theta ,\varphi ,\tau )=-{\displaystyle \frac{e_q}{c}}g(r){\displaystyle {\int }_0^{R_e/\beta }{f}_r(\tau -\chi ({\tau }^{\prime }}))\sin \theta \cdot \sin \omega {\tau }^{\prime }d{\tau }^{\prime }\end{array}$$

(6)

In practical calculations, convert $J_r$, $J_{\theta }$, and $J_{\varphi }^{\prime }$ to the rotated ellipsoidal hyperbolic orthogonal coordinate system, as shown in (7).

$$\{\begin{array}{c}{J}_{\xi }=-a(1-{\xi }^2)J_r-\sqrt{(1-{\xi }^2)({\zeta }^2-a^2)}{J}_{\theta }\\ J_{\zeta }={\displaystyle \frac{{\zeta }^2-a^2}{a}}{J}_r-\sqrt{(1-{\xi }^2)({\zeta }^2-a^2)}{J}_{\theta }\\ J_{\varphi }=\sqrt{(1-{\xi }^2)({\zeta }^2-a^2)}{J}_{\varphi }^{\prime }\end{array}$$

(7)

The Compton electrons continuously ionize and recombine with the air medium during their motion. There are two types of recombination: one involves the recombination of free electrons with positive ions, and the other involves electrons attaching to neutral atoms to form negative ions, which then recombine with positive ions. The above processes can be summarized in the following ionization-recombination equations:

$$\begin{array}{l}c{\displaystyle \frac{d{N}_e}{d\tau }}+[{\alpha }_e+\beta (N_e+N_{-})]N_e=S(\tau )\\ c{\displaystyle \frac{d{N}_{-}}{d\tau }}+{\beta }_i(N_e+N_{-})N_{-}={\alpha }_e{N}_e\end{array}$$

(8)

In Equation (8), ${\alpha }_e$ is the attachment coefficient of oxygen, $\beta$ is the recombination coefficient of electrons and positive ions, ${\beta }_i$ means the recombination coefficient of positive and negative ions, $N_e$ means the electron density, $N_{-}$ represents the negative ion density, and $S(\tau )$ represents the number of electrons per unit time and volume.

The difference solution of the above ionization-recombination equations are as follows:

$$\{\begin{array}{l}{N}_e^{n+1}=e^{-x_1}{N}_e^n+(1-e^{-x_1}){({\displaystyle \frac{B_1}{A_1}})}^{n+1/2}\\ N_{-}^{n+1}=e^{-x_2}{N}_{-}^n+(1-e^{-x_2}){({\displaystyle \frac{B_2}{A_2}})}^{n+1/2}\end{array}$$

(9)

Among them:

$$\{\begin{array}{l}{x}_1=A_1^{n+1/2}\Delta \tau \\ A_1=({\alpha }_e+\beta (N_e^n+N_{-}^n))/c\\ B_1=S(t)\\ x_2=A_2^{n+1/2}\Delta \tau \\ A_2=({\beta }_i(N_e^n+N_{-}^n)N_{-}^n)/c\\ B_2=({\alpha }_{\mathrm{e}}{N}_e)/c\end{array}$$

(10)

The conductivity can be obtained from (9), as shown in (11). The electronic conductivity is ${\mathsf{\mu }}_{\mathrm{e}}$, and ${\mathsf{\mu }}_{\mathrm{i}}$ represents the ionic conductivity.

$$\sigma ={\displaystyle \frac{e_q}{c}}\left[N_e{\mu }_e+\left(2N_{-}+N_e\right){\mu }_i\right]$$

(11)

4. Algorithm Verification and Results Analysis

The gamma waveform used in the low-altitude NEMP was a double-pulse waveform, where the two pulses represented the primary and secondary nuclear reactions of the nuclear device, respectively. The time interval between these two pulses corresponded to the action time interval between the primary and secondary stages of a thermonuclear bomb. The two pulses reached their peak values at 0.1 $\mathsf{\mu }\mathrm{s}$ and 1.6 $\mathsf{\mu }\mathrm{s}$, with a peak ratio of 33.5:1.

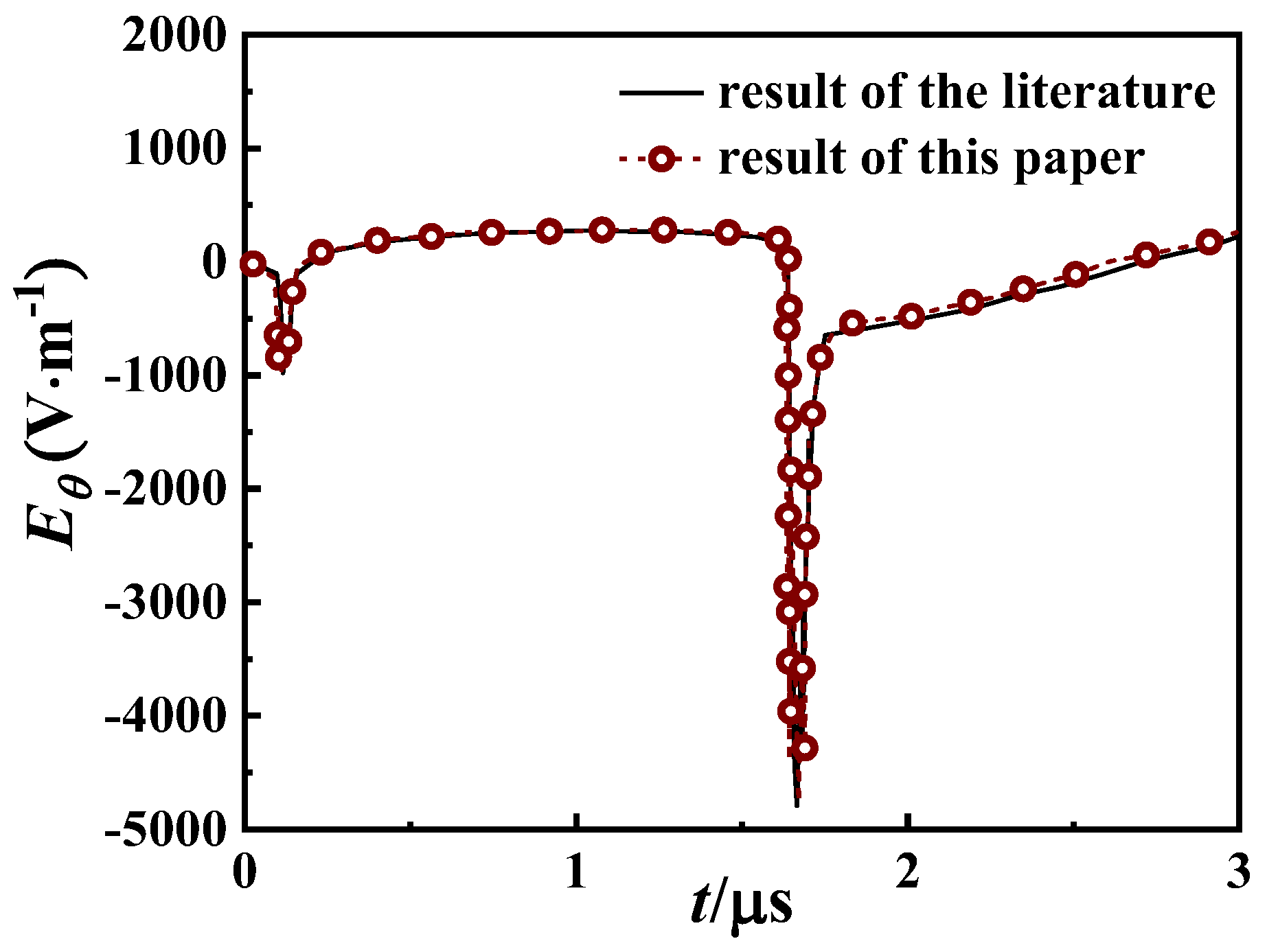
4.1. Algorithm Verification

To verify the correctness of the algorithm presented in this paper, we set the input parameters, such as ground parameters, explosion height, and explosive yield, to be consistent with those in the literature [21]. We selected an explosive yield of 100 kilotons and an explosion height of 10 km, and simulated $E_{\theta }$ time-domain waveforms at the monitoring point r = 11.3 km, $\mathsf{\theta }=49.9°$. The results were then compared with those from the literature.

As shown in Figure 4, the scatter points and the line represent the computed results of this study and those from the literature, respectively. It can be observed that the results of both are in good agreement.

Using single-thread calculation, the time step consisted of 7200 steps, and a single calculation took 208 min. However, when OpenMP parallel computing was employed with 6 threads, only requiring 45 min, the acceleration ratio reached 4.62 times, significantly improving computational efficiency.

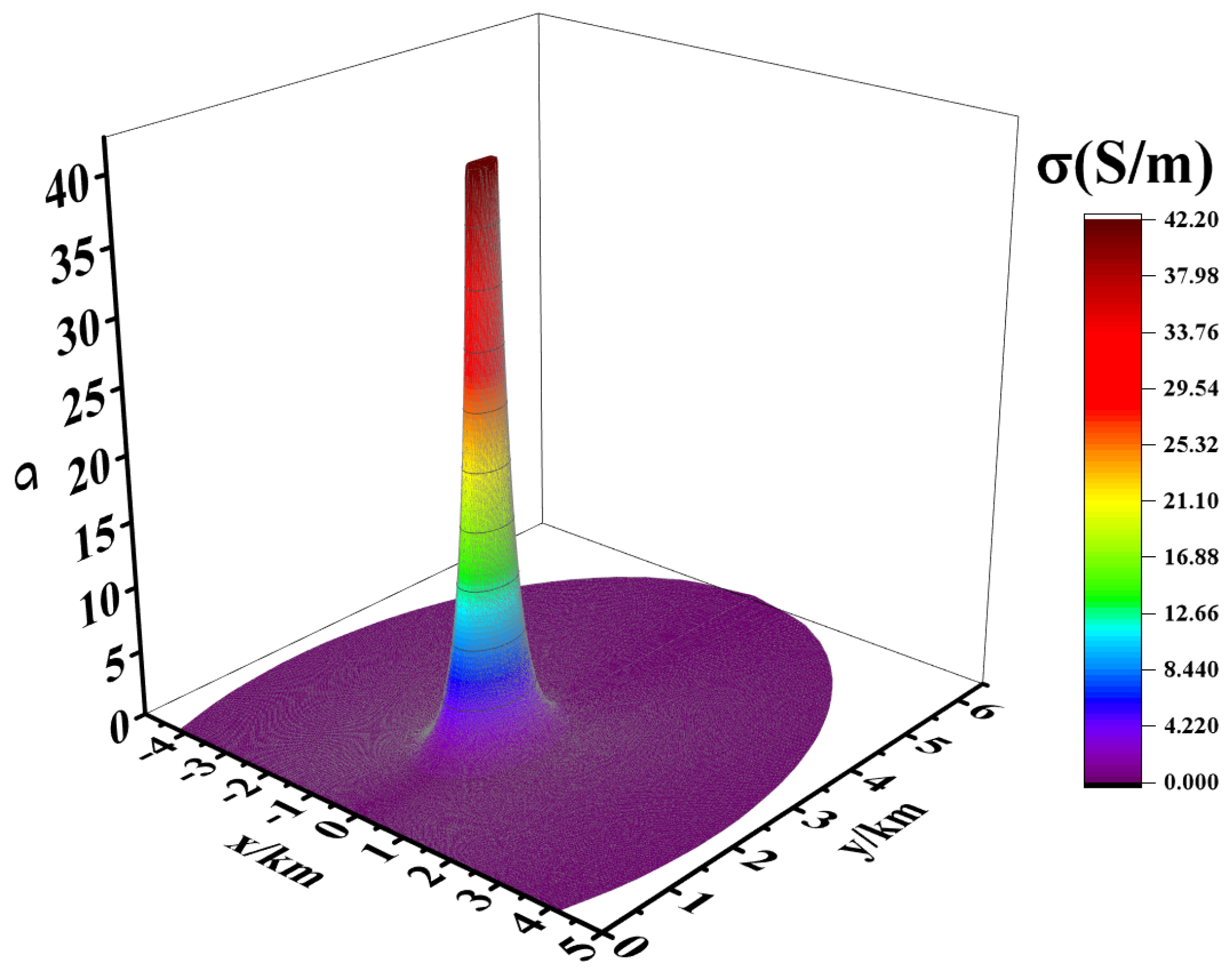
4.2. Coverage Area of the Source Region

A low-altitude NEMP source region formed by gamma radiation is a function of the yield and detonation altitude, lacking a clear boundary. Its radius can be estimated based on the air conductivity being greater than a certain threshold, denoted as ${10}^{-7}$ S/m [19]. In this study, we considered a yield of 10 kilotons and a detonation altitude of 2 km, with the soil’s relative permittivity represented by ${\epsilon }_r=10$ and conductivity represented by $\sigma =1\times {10}^{-3}$ S/m (in electromagnetic calculations, constant conductivity is generally assumed). During a low-altitude nuclear explosion, gamma photons deposit energy in the ground, altering its electrical properties. However, due to the high density of soil, gamma-ray energy deposition is typically limited to the surface, leading to the common assumption that subsurface conductivity remains constant in electromagnetic environment calculations [20]). The distribution map of the surface source region is illustrated in Figure 5, with the negative and positive values on the x-axis representing the left and right sides of the explosion point above the ground, respectively, and the positive values on the y-axis indicating positions above the ground. This paper selected an explosion height of 2 km, at which point the conductivity reached its maximum near y = 2 km. The area below the y-axis represents locations beneath the ground. Given that this paper primarily investigated the spatial electromagnetic pulse above ground, the figure only displays the conductivity distribution above the ground.

From Figure 5, it can be observed that the source region radius is within 6 km under the aforementioned conditions. Therefore, in analyzing the spatial electromagnetic field distribution characteristics of low-altitude nuclear explosion electromagnetic pulses, this study focused on monitoring points located within 6 km of the explosion center. The following simulation analyzed the comparison results of time-domain waveforms under two scenarios: one with varying angles at the same distance and another with varying distances at the same angle.

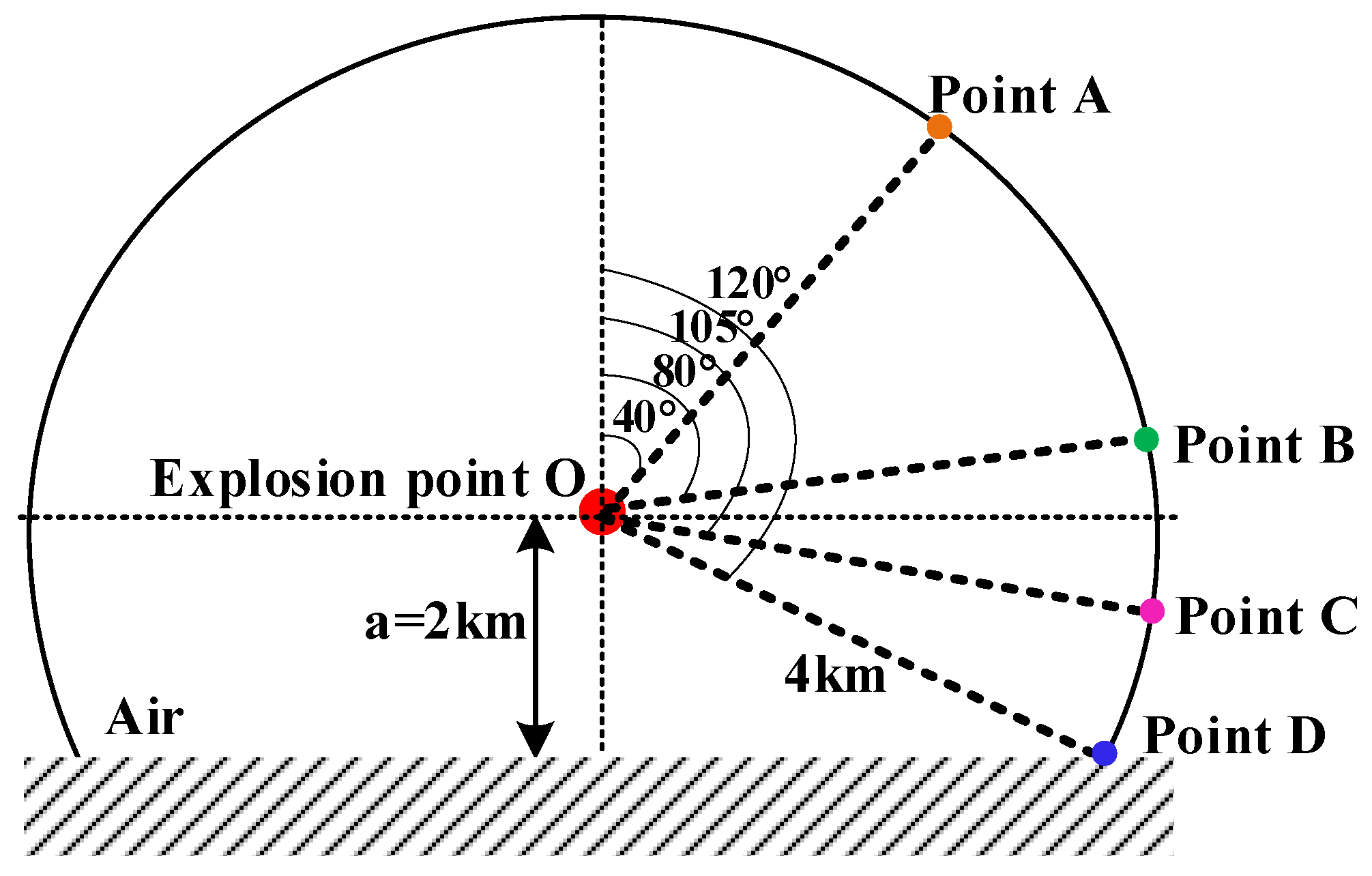
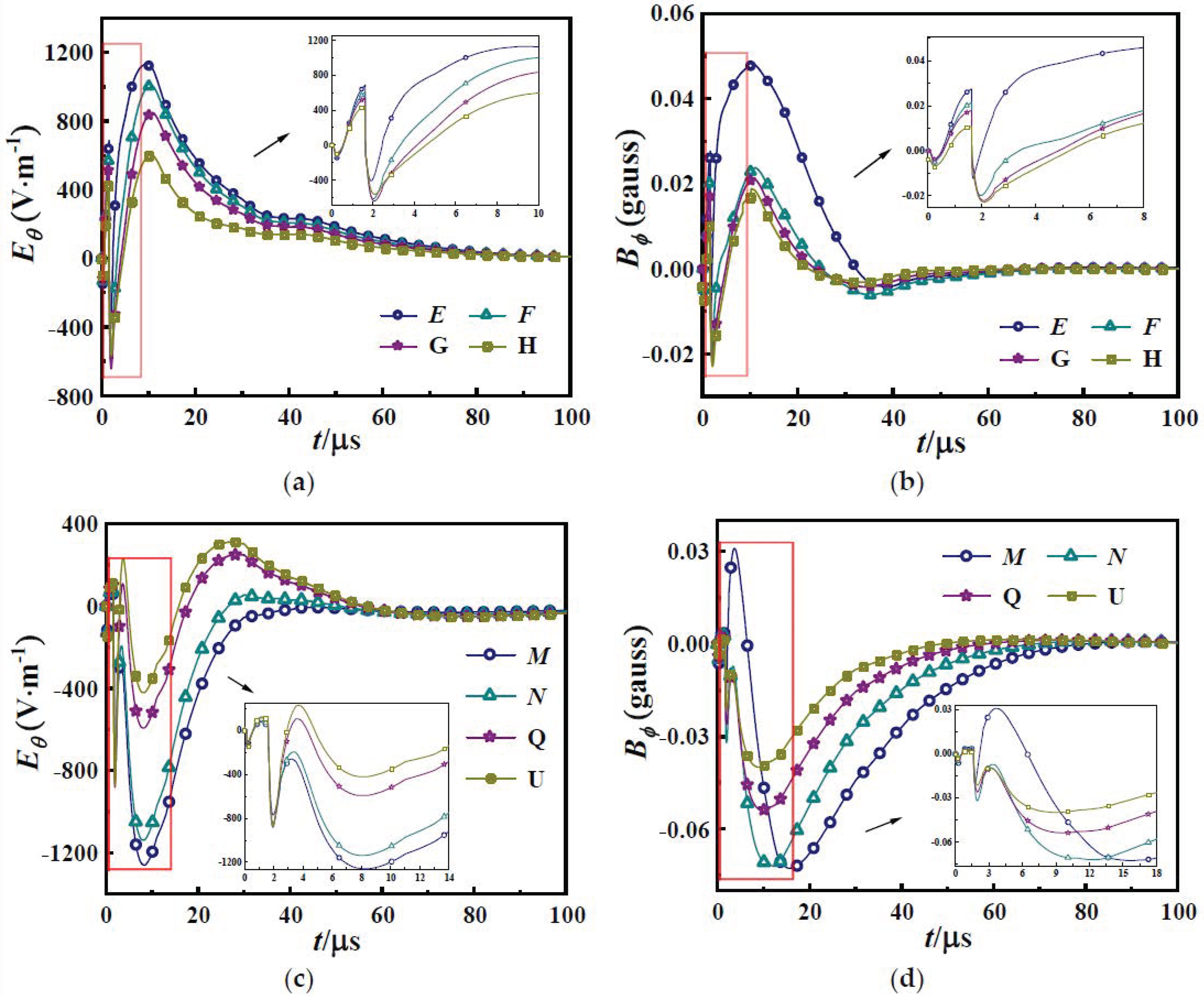
4.3. Analysis of Field Values at Different Angles from the Same Distance to the Explosion Center

The analysis was conducted using monitoring points that were equidistant from the explosion’s epicenter but positioned at different angles. Points A and B were located above the epicenter, while points C and D were situated below it, all at a distance of 4 km from the epicenter. The spatial relationship between the monitoring points and the explosion site is illustrated in Figure 6.

4.3.1. Comparison of Time-Domain Waveforms of TM Wave

The TM wave field components were $E_r,E_{\theta },B_{\phi }$. Energy in the radial direction can propagate outward, while energy in the $\theta$ and $\varphi$ directions does not radiate outward. Therefore, we primarily analyzed the energy in the radial direction. When the radial electric or magnetic field is multiplied by other components, it only generates energy in the $\theta$ and $\varphi$ directions, so this paper focused on $E_{\theta }$ and $B_{\phi }$. The time-domain waveform comparisons at four observation points are shown in Figure 7. Figure 7a,b represent the time-domain waveforms of the electric field and magnetic field at four monitoring points, respectively. To facilitate analysis, local enlarged views are provided in the figures.

From Figure 7, it can be observed that:

(1)

The waveform characteristics of the TM wave exhibit a narrow pulse at the beginning that adequately reflects the instantaneous gamma characteristics, followed by a slowly varying wide pulse. Here, $J_r$ serves as the primary current source exciting the TM wave (as derived from Equations (3) and (7), where the TM wave is stimulated by $J_r$ and $J_{\theta }$. For low-altitude nuclear explosions, the average forward range of Compton electrons is only a few meters, which is significantly smaller than their Larmor radius in the geomagnetic field. The value of $J_{\theta }$ is much smaller than that of $J_r$, therefore, $J_r$ is the main excitation source for the TM wave). Due to the varying distances from different points in the source region to the monitoring point, there is a time difference in arrival at the monitoring point, leading to a phenomenon known as time delay, which results in a broader pulse width for the TM wave.

(2)

In TM wave, $E_{\theta }$ and $B_{\varphi }$ have the same polarity; the waveform above and below the explosion center exhibits opposite polarities. When $\theta <90°$, both are positive polarity, while $\theta >90°$, both are negative polarity. For points equidistant from the explosion center, the field characteristics of the TM wave differ above and below the explosion center. The field in the source region below the explosion center is characterized by low impedance, with magnetic induction intensity $B_{\varphi }$ being significantly stronger than $E_{\theta }$; conversely, the source region above the explosion center exhibits characteristics of a high impedance field, with magnetic induction intensity $B_{\varphi }$ being much weaker than $E_{\theta }$. Overall, the strong electromagnetic field in the source region poses a considerable threat to electronic systems operating within that area.

4.3.2. Comparison of Time-Domain Waveforms of TE Wave

The TE wave field components were $B_r,B_{\theta },E_{\phi }$. Since the $B_r$ field does not radiate outward, this paper focused on $E_{\phi }$ and $B_{\theta }$, and the time-domain waveform comparisons at four observation points are shown in Figure 8.

From Figure 8, it can be observed that:

(1)

The pulse width of TE wave is narrower compared to TM wave. This is attributed to the fact that $J_{\varphi }^{\prime }$ serves as the primary current source for exciting TE wave (as derived from Equations (4) and (7), which indicate that TM wave are excited by $J_{\varphi }^{\prime }$). Since gamma rays propagate forward at the speed of light $c$, the resulting Compton electrons also travel slightly below the speed of light. From the monitoring point’s perspective, the contributions of the current sources along the line connecting the explosion center to the monitoring point to the NEMP are nearly simultaneous, leading to a narrower pulse width for TE wave.

(2)

In the TE wave, $E_{\varphi }$ and $B_{\theta }$ opposite polarities. The waveform above the explosion center shares the same polarity as that below it, with $E_{\varphi }$ being negatively polarized and $B_{\theta }$ positively polarized. For points equidistant from the explosion center, maximum electromagnetic field strength at $\theta =80°$. This is explained by Equation (6), where the exciting current $J_{\varphi }^{\prime }$ includes a $\sin \theta$ factor, thus indicating that the maximum value should occur at $\theta =90°$. The peak values at the four monitoring points are arranged in descending order based on their angles, designated as $80°,105°,120°,40°$.

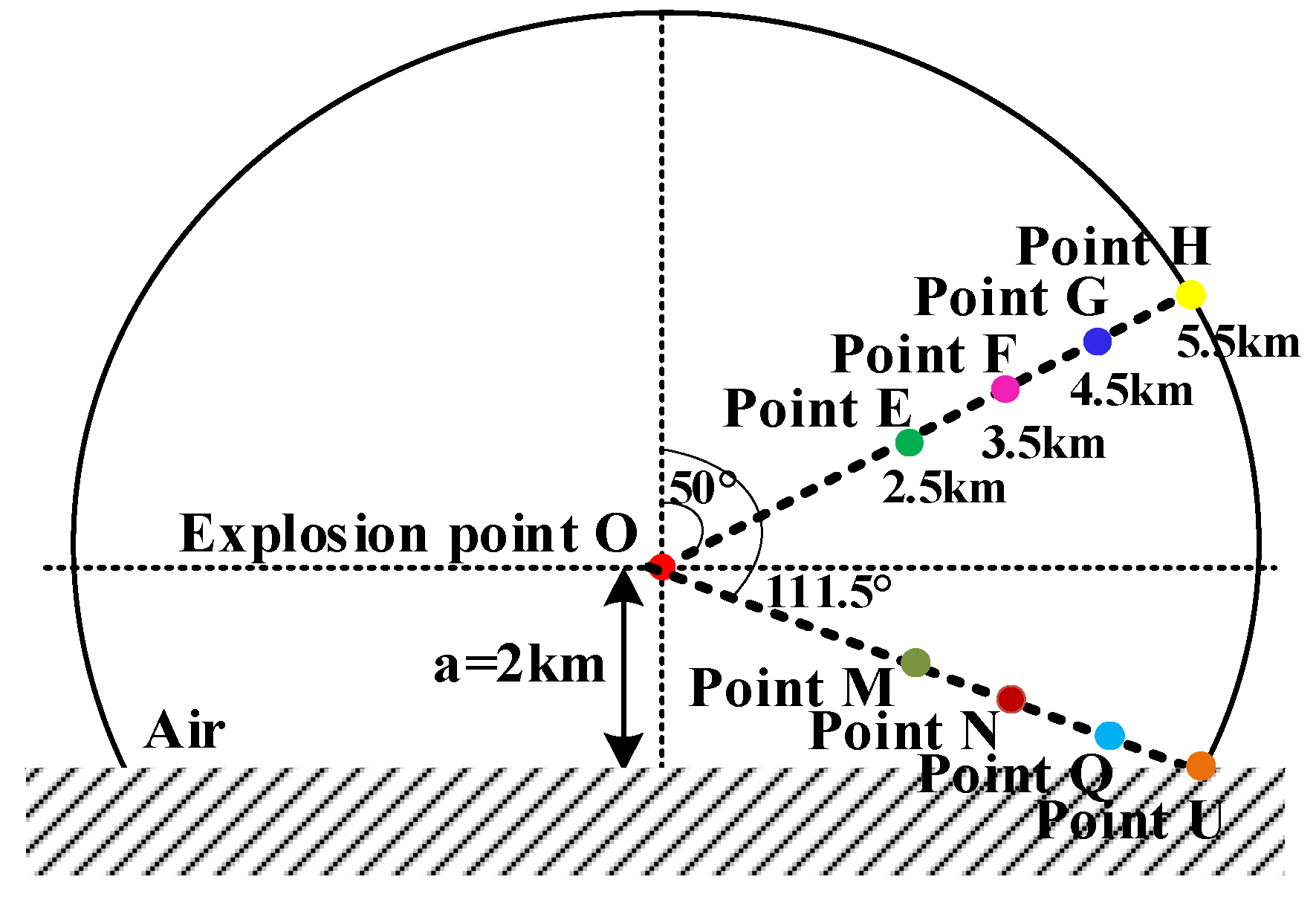
4.4. Analysis of Field Values at Different Distances from the Same Angle to the Explosion Center

The analysis was conducted using monitoring points selected at the same angle from the explosion center but at different distances. Points E, F, and G were located above the explosion center, forming an angle $50°$ with it, while points M, N, and Q were situated below the explosion center, forming an angle $110°$ with it. The positional relationship between the monitoring points and the explosion site is illustrated in Figure 9.

4.4.1. Comparison of Time-Domain Waveforms of TM Wave

The comparison of time-domain waveforms at six observation points are shown in Figure 10. Figure 10a,b represent the time-domain waveforms of the electric field and magnetic field at four monitoring points (E, F, G, H) above the explosion center. Figure 10c,d represent the time-domain waveforms of the electric field and magnetic field at four monitoring points (M, N, Q, U) below the explosion center, respectively. To facilitate analysis, local enlarged views are provided in the figures.

From Figure 10, it can be observed that:

(1)

In the vicinity of the explosion center, both the electric field strength and the magnetic induction intensity of TM wave gradually decrease with increasing distance. This phenomenon occurs because, as the distance from the explosion center increases, the atmosphere absorbs more gamma rays, resulting in a lower photon density of $\gamma$ rays interacting with the atmosphere. Consequently, this leads to a reduction in Compton electrons, which in turn decreases the Compton current and ultimately results in a lower peak value of the electromagnetic pulse.

(2)

Above the epicenter, compared to the magnetic field, the variation in electric field value is relatively small. The peak electric field values at 5.5 km, 4.5 km, and 3.5 km are approximately 0.5, 0.7, and 0.9 times that at r = 2.5 km, respectively, while the peak magnetic field at 5.5 km, 4.5 km, and 3.5 km is about half of that at 2.5 km. Conversely, below the epicenter, the magnetic field values show less variation compared to the electric field, with the peak magnetic field at 5.5 km and 4.5 km being approximately 0.5 and 0.7 times that at 2.5 km and 3.5 km, while the peak electric field at 5.5 km and 4.5 km is about half of its value at the other two distances.

4.4.2. Comparison of Time-Domain Waveforms of TE Wave

The waveforms above and below the explosion center exhibited the same polarity, therefore, only one analysis was necessary. Taking points M, N, and Q above the explosion center as examples, the comparison of the time-domain waveforms at these three observation points are illustrated in Figure 11.

From Figure 11, it can be observed that:

(1)

The electric field strength and magnetic induction intensity of the TE wave gradually decrease with increasing distance. At distances of 5.5 km, 4.5 km, and 3.5 km, the peak values of the electric and magnetic fields are approximately 0.5, 0.6, and 0.8 times that at r = 2.5 km, respectively.

(2)

Within the source area, the types of damage caused by TM and TE waves to equipment and systems differ. The peak electric and magnetic field strengths of the TE wave are stronger than those of the TM wave, resulting in a rapid release of energy during propagation, which can lead to instantaneous failures or interference in electronic devices or communication systems. Additionally, the high-frequency components of the TE wave are significantly more abundant than those of the TM wave, making it more suitable for detecting NEMPs. In contrast, the TM wave has a longer pulse duration and overall energy that is much higher than that of the TE wave, with its effects on facilities manifesting more as thermal effects and long-term damage issues. Therefore, the choice between these two types should be based on specific requirements to minimize potential harm to surrounding environments and equipment.

5. Conclusions

This study investigated the generation mechanism and spatial distribution characteristics of electromagnetic pulses produced by low-altitude nuclear explosions through numerical simulations. The analysis compared time-domain waveform simulations under different angles and distances, as well as contrasting TM wave with TE wave. The main conclusions are as follows.

(1)

In a TM wave, $E_{\theta }$ and $B_{\varphi }$ exhibit the same polarity, while the waveforms above and below the explosion center have opposite polarities. When $\theta <90°$, both are positive polarity, whereas $\theta >90°$, both are negative polarity. The field above the explosion center demonstrates high impedance characteristics, while the field below exhibits low impedance.

(2)

In a TE wave, $E_{\varphi }$ and $B_{\theta }$ show opposite polarities, with the waveforms above and below the explosion center sharing the same polarity. $E_{\varphi }$ is negative polarity, while $B_{\theta }$ is positive polarity.

(3)

The amplitudes of electric field strength and magnetic induction intensity for both TM and TE waves gradually decrease with increasing distance from the source.

(4)

Compared to TE waves, TM waves exhibit weaker peak electromagnetic fields but have broader pulse widths and overall higher energy levels.

This research provides a significant reference for nuclear explosion detection technology and aids in a deeper understanding of the spatial field characteristics of nuclear explosion source areas. By analyzing the distribution and variation patterns of the electromagnetic field following a nuclear detonation, we can obtain detailed information regarding the range and intensity of the nuclear explosion’s effects. These findings not only support the theoretical development of nuclear explosion detection technologies but also promote the refinement and optimization of relevant theoretical models. Furthermore, they lay a solid theoretical foundation for advancing anti-nuclear radiation protection measures and fortification efforts. Additionally, these research outcomes contribute to enhancing safety capabilities in related fields, enabling more effective protective measures against potential nuclear threats, thereby safeguarding personnel and facilities.