Author Contributions
Conceptualization, J.L. and M.X.; methodology, J.L. and M.X.; software, J.L.; validation, M.X.; formal analysis, J.L., M.X. and H.Y.; writing—original draft preparation, J.L.; writing—review and editing, J.L., Z.Q. and H.L.; visualization, J.L. and H.Y.; supervision, Z.Q., W.G., Y.T. and B.W.; project administration, W.G., Y.T., B.W. and H.L.; funding acquisition, H.L. All authors have read and agreed to the published version of the manuscript.
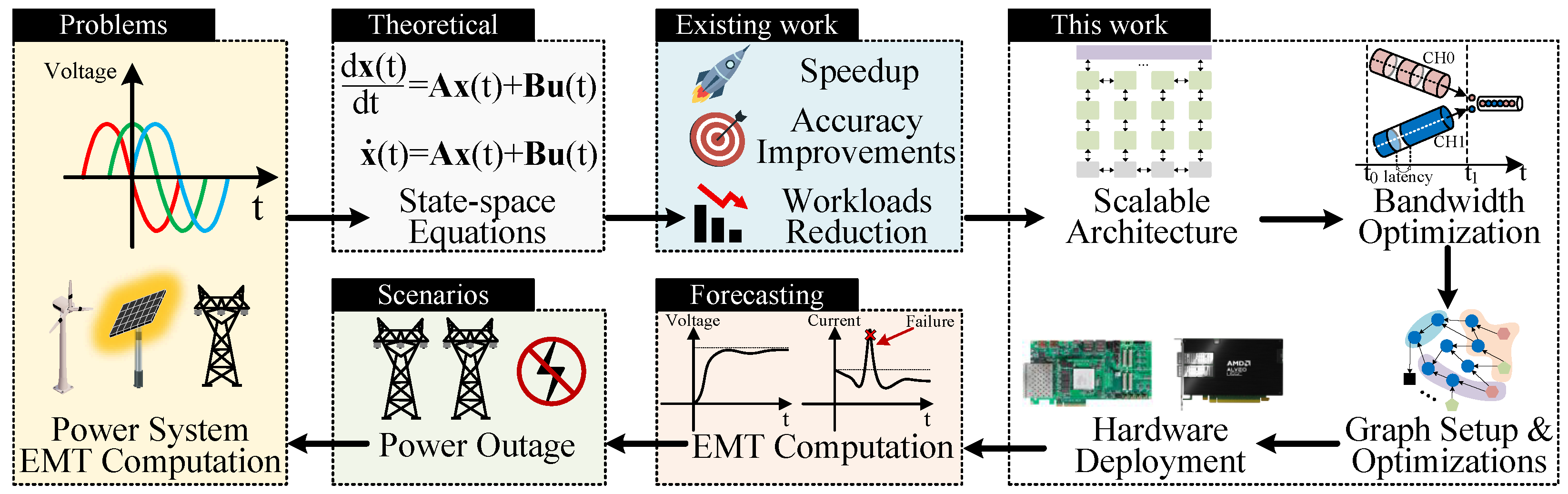
Figure 1.
The overview of FPGA-accelerated EMT computation. This article focuses on accelerating large-scale EMT computation through systematic exploration of scalable hardware architecture and design optimization methods, particularly targeting state-space equations derived from power grid EMT models under power outage scenarios.
Figure 1.
The overview of FPGA-accelerated EMT computation. This article focuses on accelerating large-scale EMT computation through systematic exploration of scalable hardware architecture and design optimization methods, particularly targeting state-space equations derived from power grid EMT models under power outage scenarios.
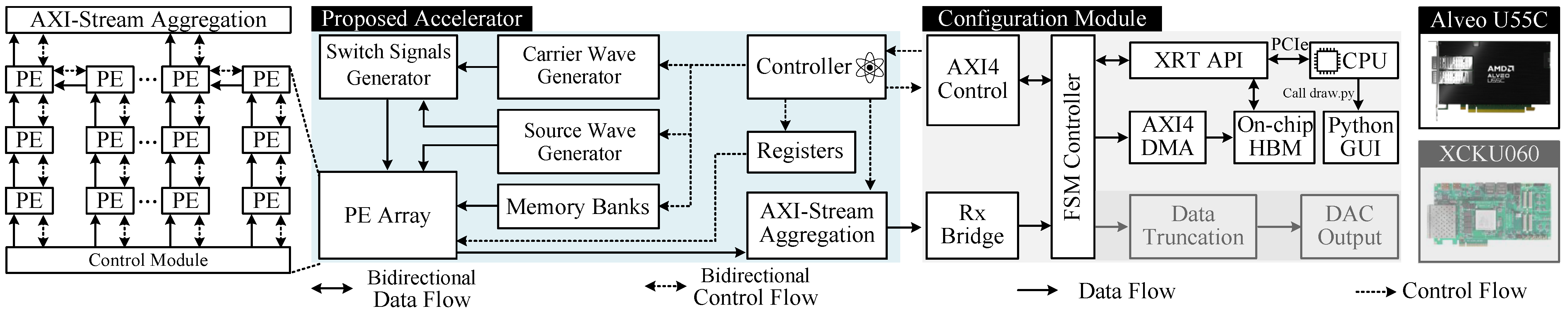
Figure 2.
The overview of proposed hardware architecture. Our design can support traditional FPGAs with hardware in loop and advanced FPGAs with accelerator card framework.
Figure 2.
The overview of proposed hardware architecture. Our design can support traditional FPGAs with hardware in loop and advanced FPGAs with accelerator card framework.
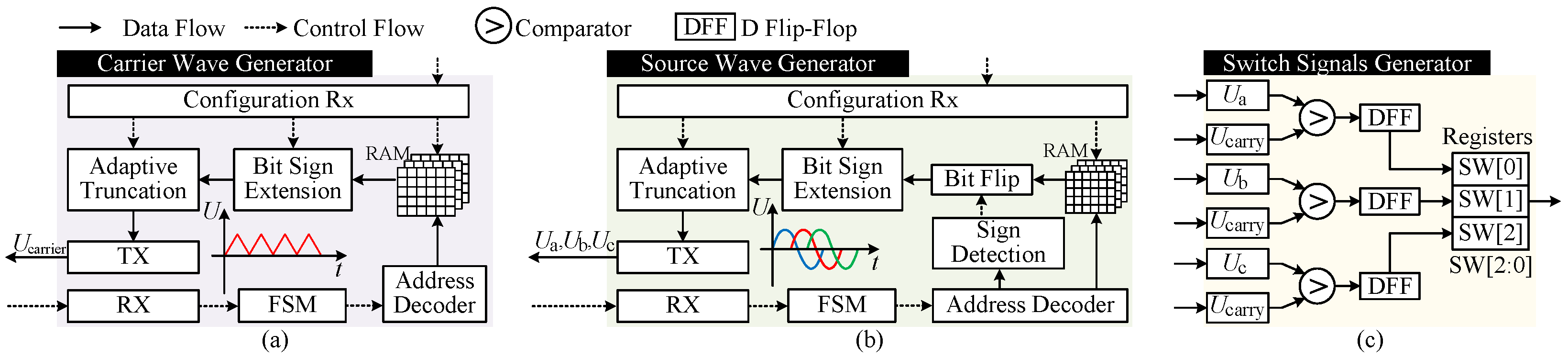
Figure 3.
Customized components for EMT computation of multi-converter systems. (a) Carrier wave generator. (b) Source wave generator. (c) Switch Signals generator.
Figure 3.
Customized components for EMT computation of multi-converter systems. (a) Carrier wave generator. (b) Source wave generator. (c) Switch Signals generator.
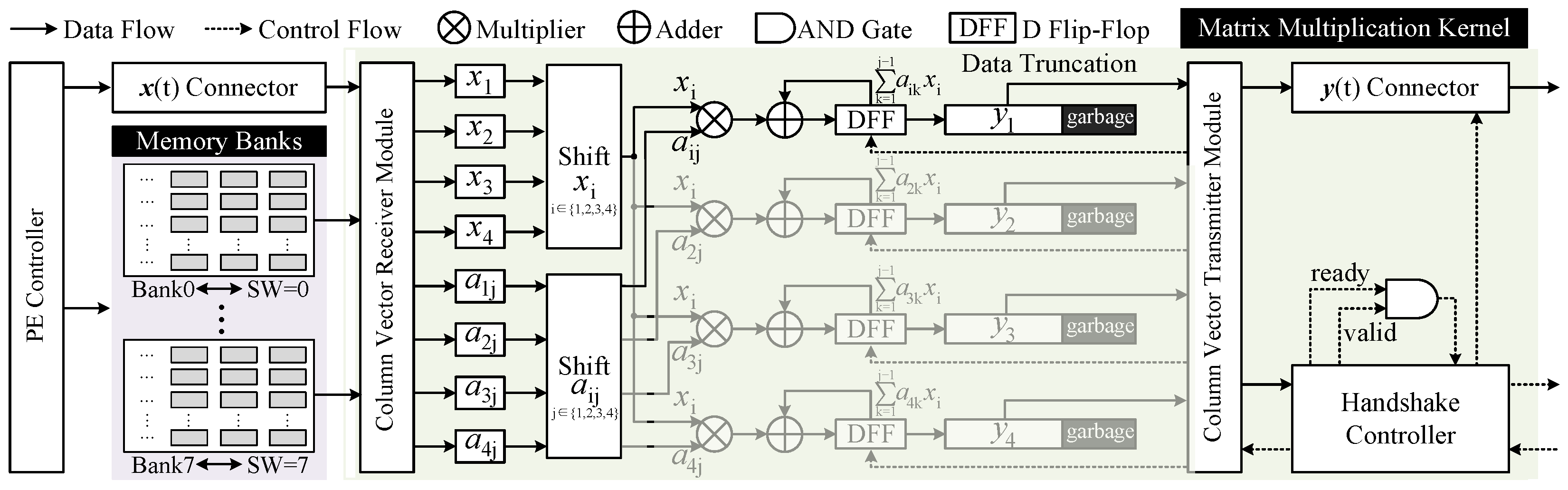
Figure 4.
The workflow of memory mapping and matrix multiplication.
Figure 4.
The workflow of memory mapping and matrix multiplication.
Figure 5.
Example of memory mapping distribution and the computation workflow with different mode, where ADDR represent the start address in BRAM, SW denotes the 3-bit switch signal, and data[3:0] is responsible for stored column vector of coefficient matrices in the memory. The denotes the state vector at the t-th clock.
Figure 5.
Example of memory mapping distribution and the computation workflow with different mode, where ADDR represent the start address in BRAM, SW denotes the 3-bit switch signal, and data[3:0] is responsible for stored column vector of coefficient matrices in the memory. The denotes the state vector at the t-th clock.
Figure 6.
Example of matrix multiplication kernel (MMK) module when and .
Figure 6.
Example of matrix multiplication kernel (MMK) module when and .
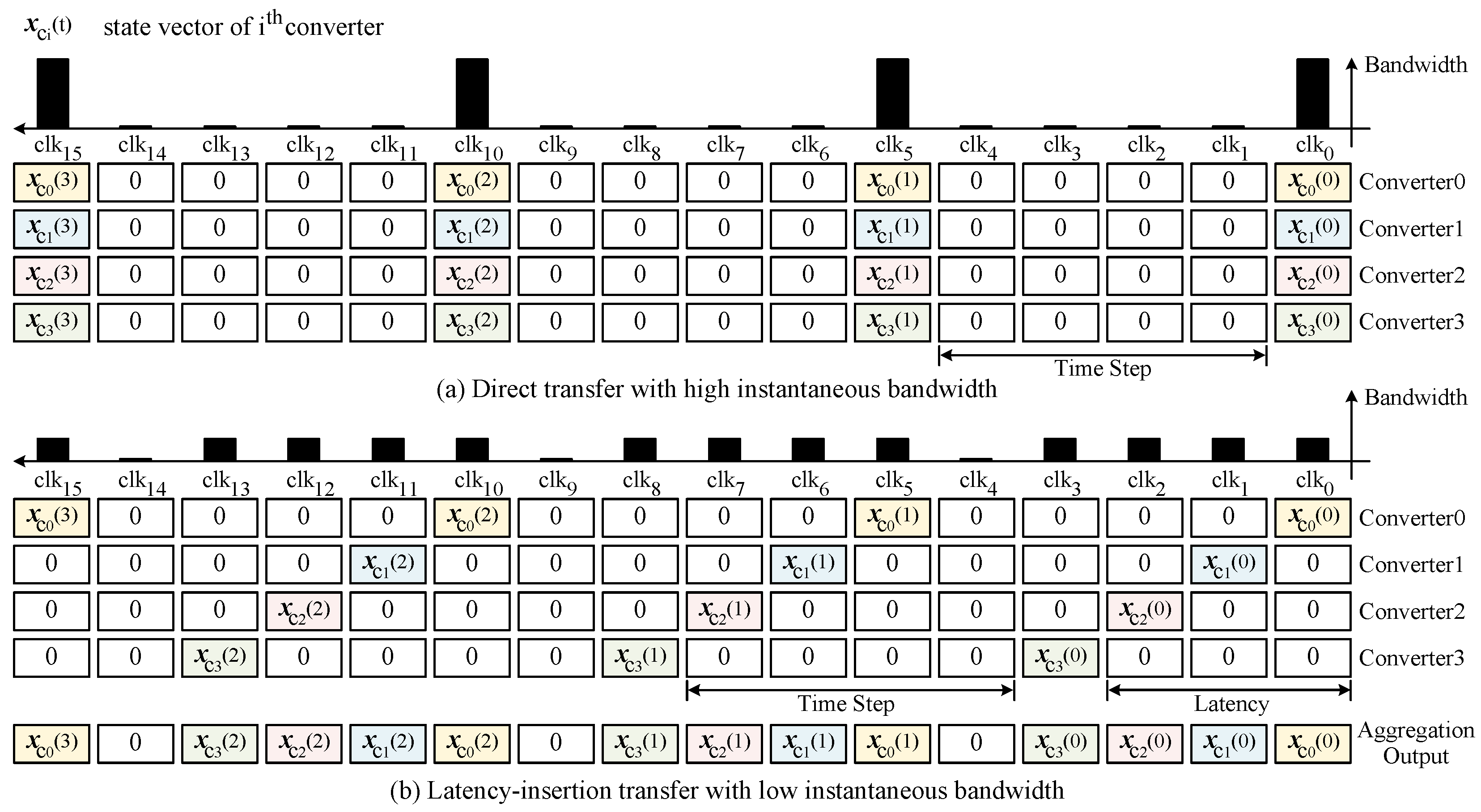
Figure 7.
Example of different transfers, where represents the state vector of ith converter. (a) Direct transfer with high instantaneous bandwidth has large waste. (b) Latency-insertion transfer with low instantaneous bandwidth spreads the instantaneous bandwidth evenly across each clock.
Figure 7.
Example of different transfers, where represents the state vector of ith converter. (a) Direct transfer with high instantaneous bandwidth has large waste. (b) Latency-insertion transfer with low instantaneous bandwidth spreads the instantaneous bandwidth evenly across each clock.
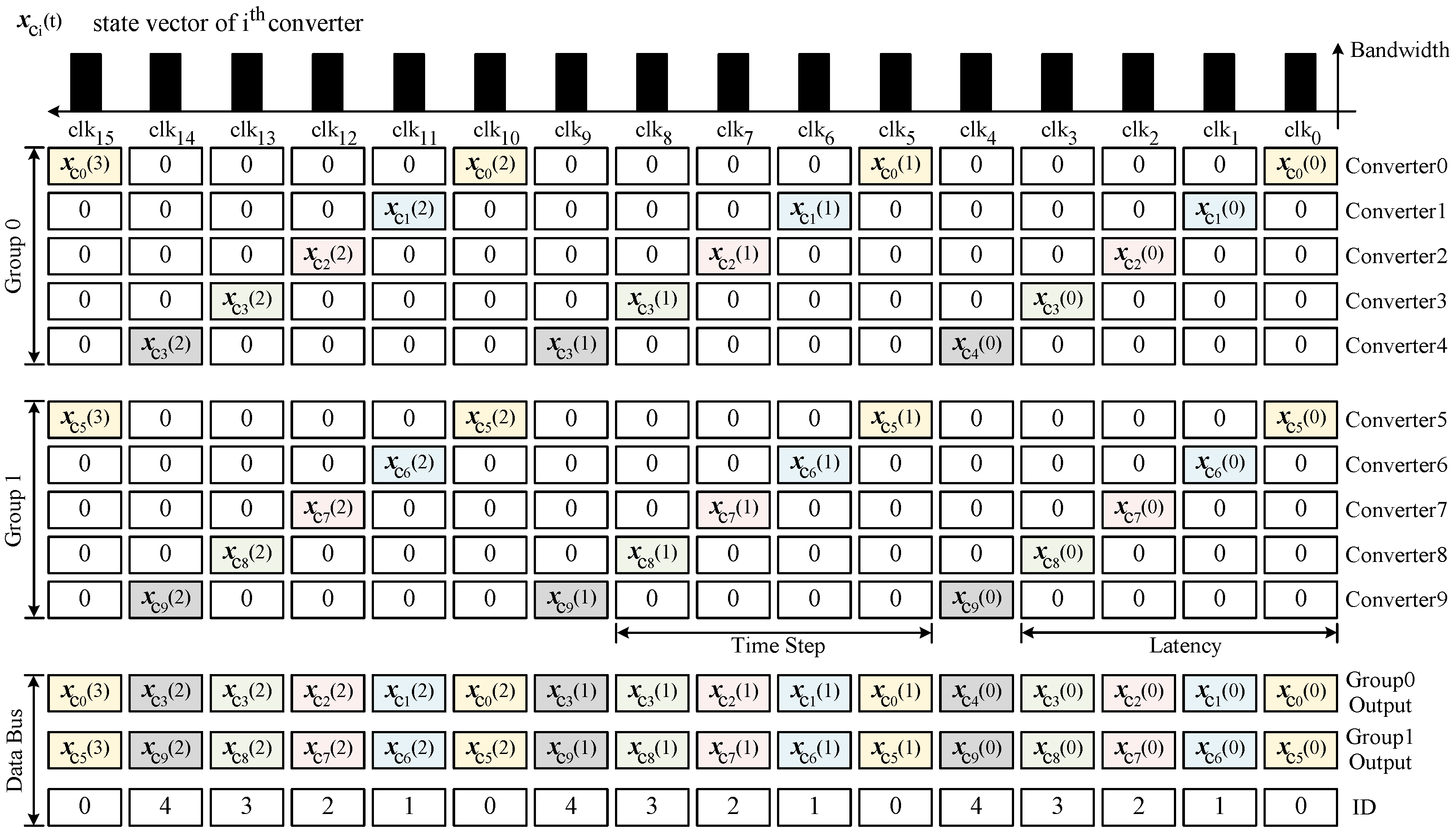
Figure 8.
Example of final bandwidth optimizations with , where represents the state vector of i-th converter, .
Figure 8.
Example of final bandwidth optimizations with , where represents the state vector of i-th converter, .
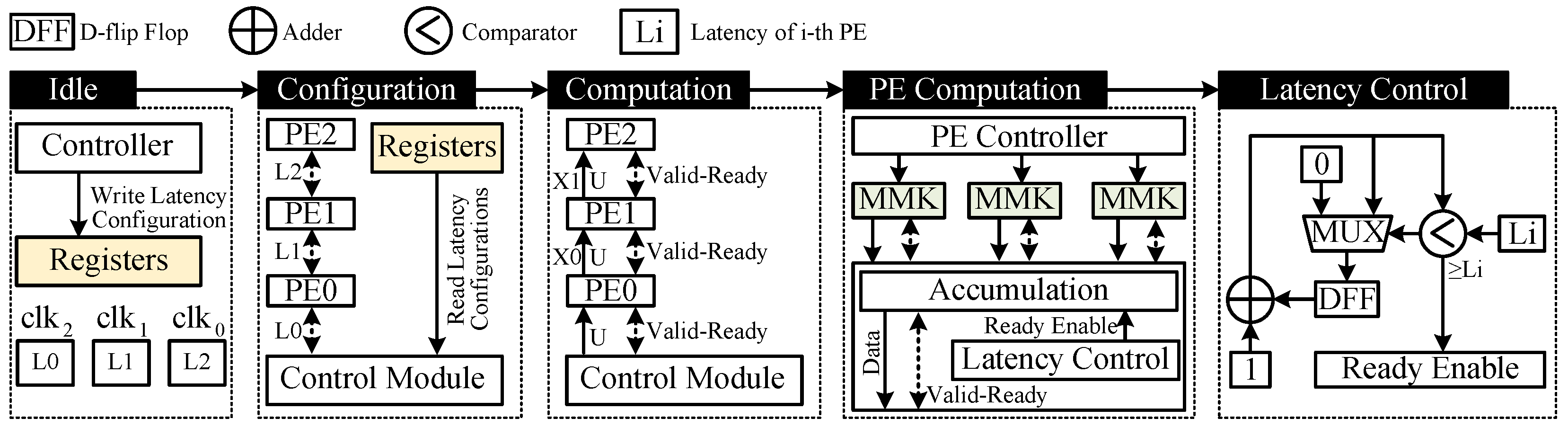
Figure 9.
The workflow of latency insertion including idle state for writing registers, configuration state for writing latency values to each PE and computation state. During PE computation, if the latency control module monitors count value more than , then it enables next calculation. Otherwise, the ready signal maintains low to stop all the calculation.
Figure 9.
The workflow of latency insertion including idle state for writing registers, configuration state for writing latency values to each PE and computation state. During PE computation, if the latency control module monitors count value more than , then it enables next calculation. Otherwise, the ready signal maintains low to stop all the calculation.
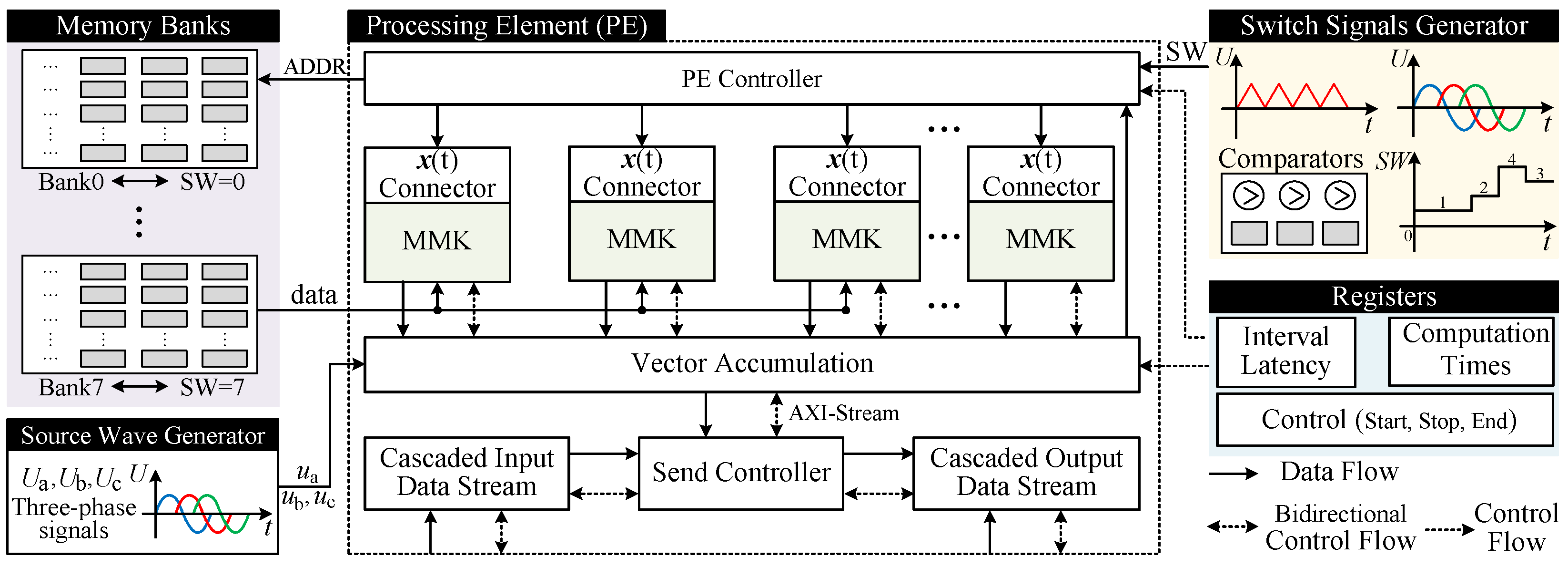
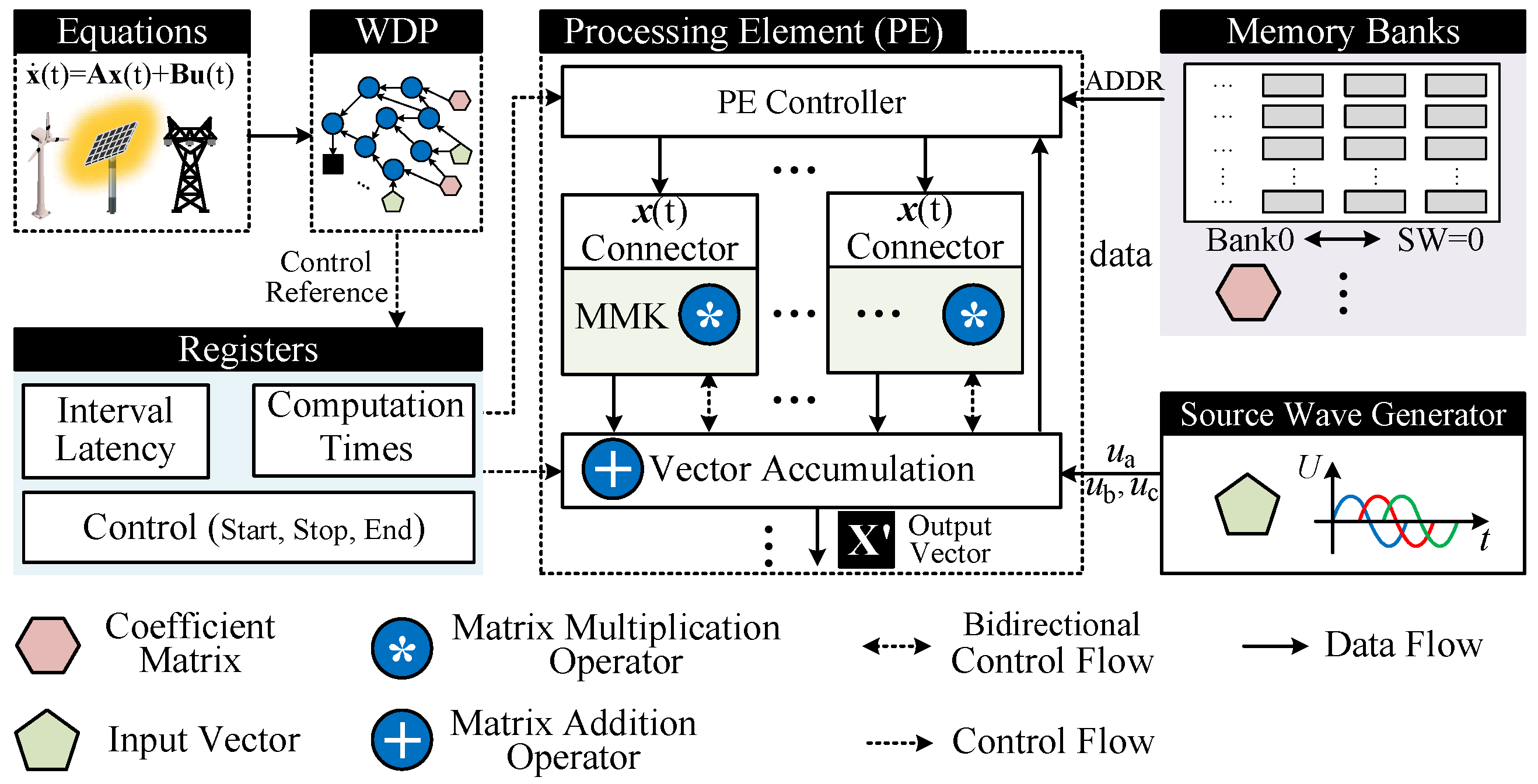
Figure 10.
Design of processing element (PE) module.
Figure 10.
Design of processing element (PE) module.
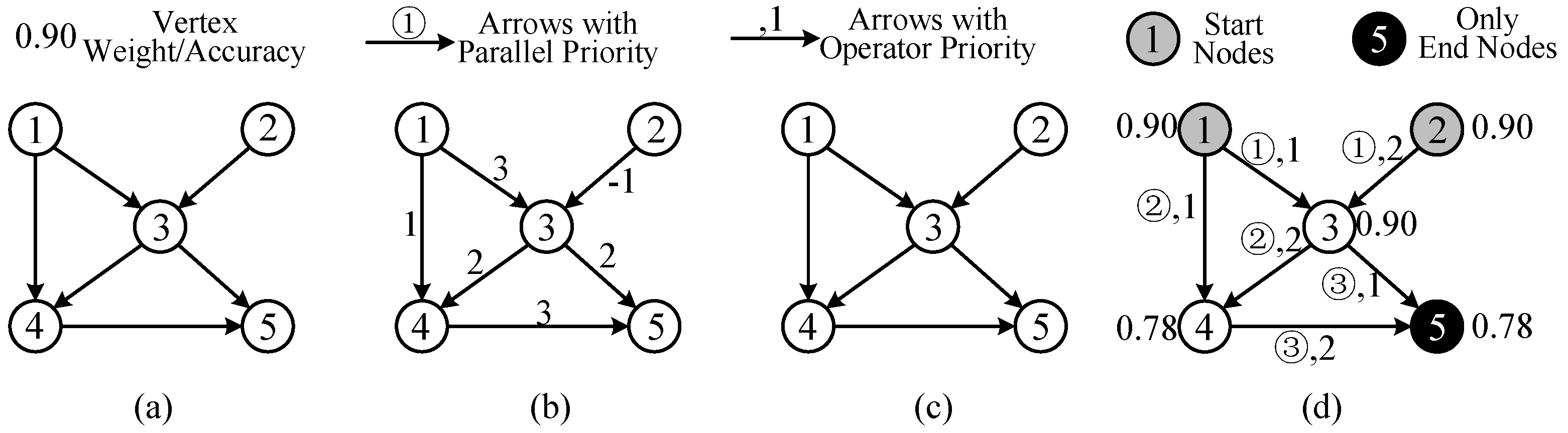
Figure 11.
Topologies of graph (a), weighted graph (b), digraph (c), and (d) weighted diagraph with priority (WDP).
Figure 11.
Topologies of graph (a), weighted graph (b), digraph (c), and (d) weighted diagraph with priority (WDP).
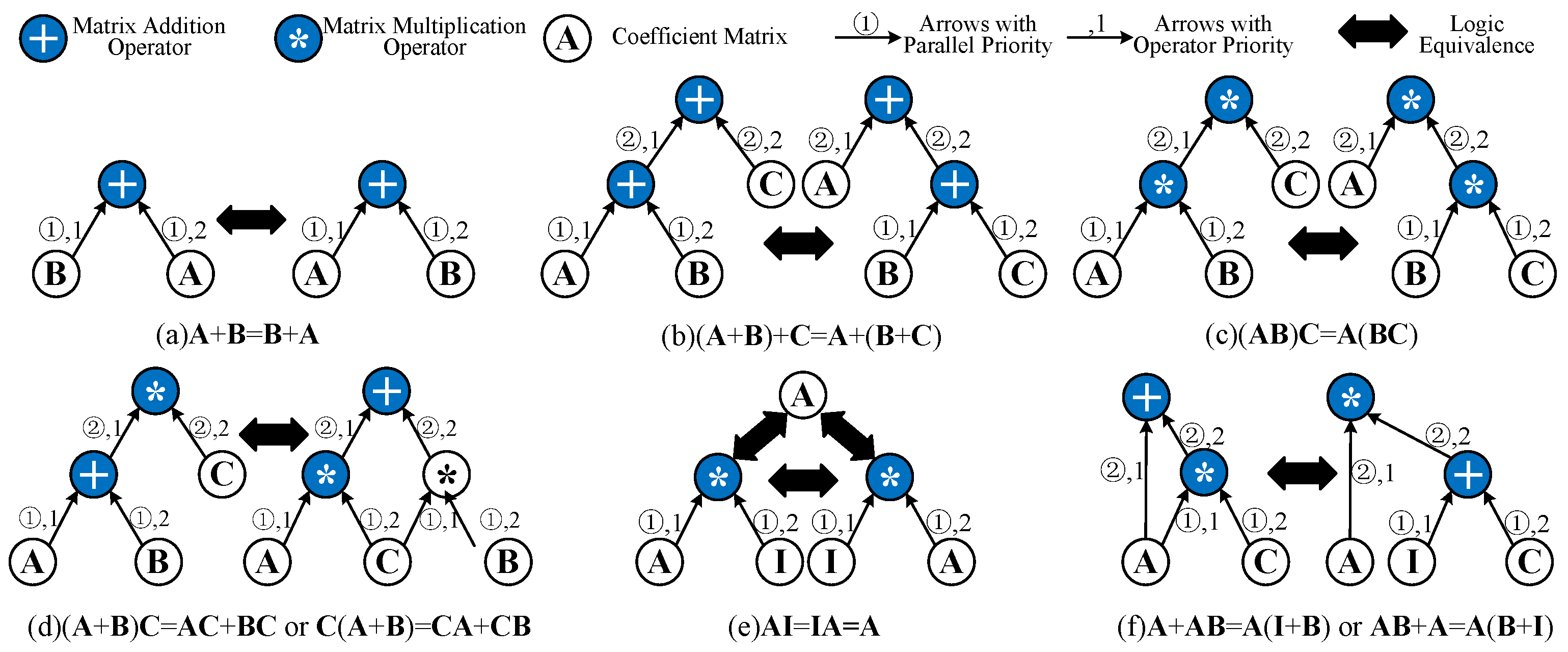
Figure 12.
The logic equivalence rules based on the fundamental operation laws of matrices. (a) The commutative law of addition. (b) The associative law of addition. (c) The associative law of multiplication. (d) The distributive law of multiplication. (e) The elimination of the identity matrix. (f) The introduction of the identity matrix.
Figure 12.
The logic equivalence rules based on the fundamental operation laws of matrices. (a) The commutative law of addition. (b) The associative law of addition. (c) The associative law of multiplication. (d) The distributive law of multiplication. (e) The elimination of the identity matrix. (f) The introduction of the identity matrix.
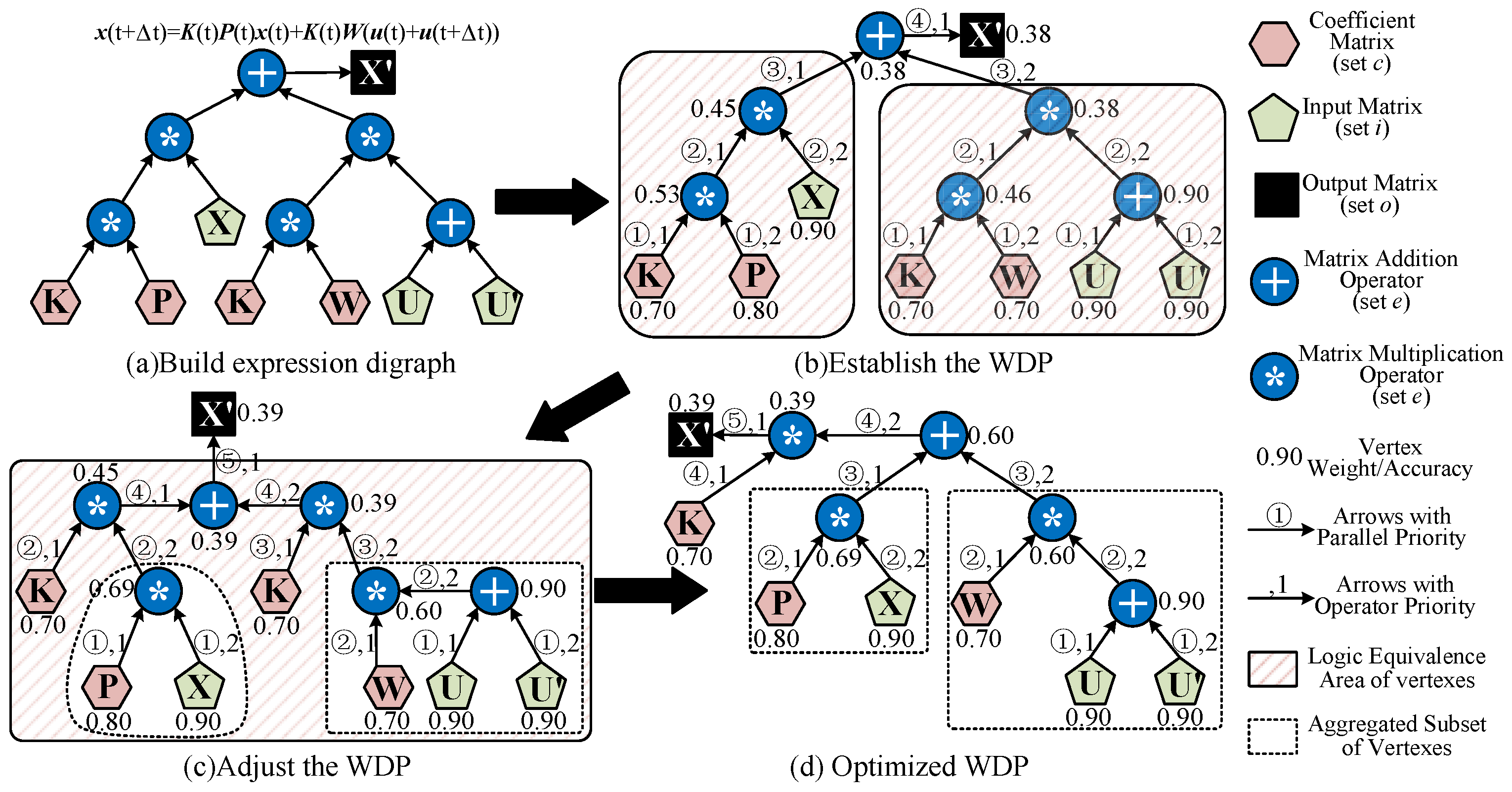
Figure 13.
The setup and optimization of a WDP for Equation (
6), where each vertex is assigned an exemplary weight. (
a) Build expression digraph. (
b) Append the priority and allocate weight for each edge to establish the WDP. (
c) Adjust the WDP by following logic equivalence. (
d) Optimized WDP.
Figure 13.
The setup and optimization of a WDP for Equation (
6), where each vertex is assigned an exemplary weight. (
a) Build expression digraph. (
b) Append the priority and allocate weight for each edge to establish the WDP. (
c) Adjust the WDP by following logic equivalence. (
d) Optimized WDP.
Figure 14.
The instance of mapping from a WDP to the PE module.
Figure 14.
The instance of mapping from a WDP to the PE module.
Figure 15.
Real machine operation for real-time computation based on FPGAs. (a) FPGA-CPU heterogeneous system equipped with AMD Alveo U55C accelerator cards is used to deploy large-scale EMT computation. (b) U55C FPGAs are connected to CPU server by PCIe interface. (c) The high-performance XCKU060-implemented computation system with 125 MHz DAC.
Figure 15.
Real machine operation for real-time computation based on FPGAs. (a) FPGA-CPU heterogeneous system equipped with AMD Alveo U55C accelerator cards is used to deploy large-scale EMT computation. (b) U55C FPGAs are connected to CPU server by PCIe interface. (c) The high-performance XCKU060-implemented computation system with 125 MHz DAC.
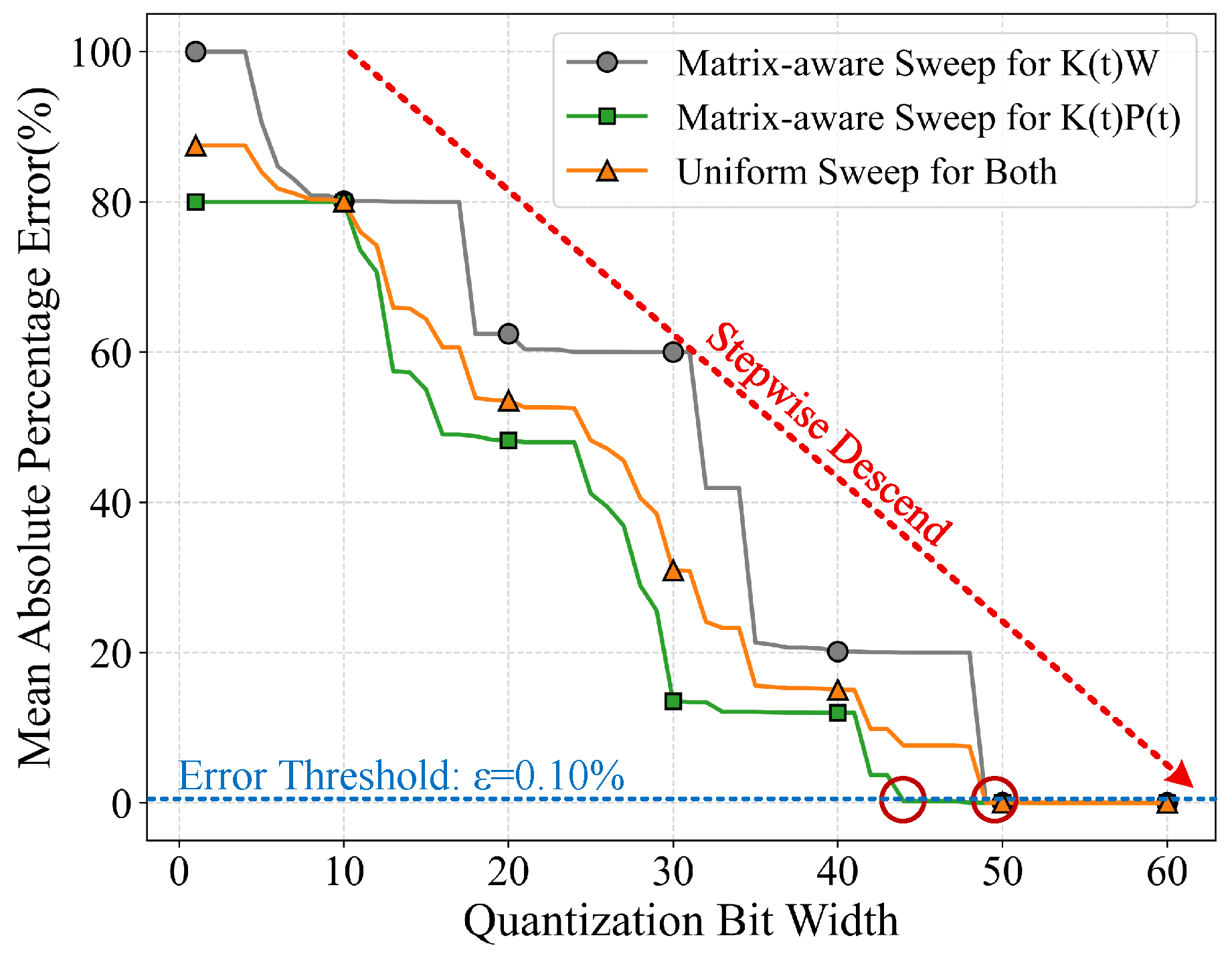
Figure 16.
Proposed matrix-aware fixed-point quantization bit width search method and uniform bit-width sweep method for coefficient matrices.
Figure 16.
Proposed matrix-aware fixed-point quantization bit width search method and uniform bit-width sweep method for coefficient matrices.
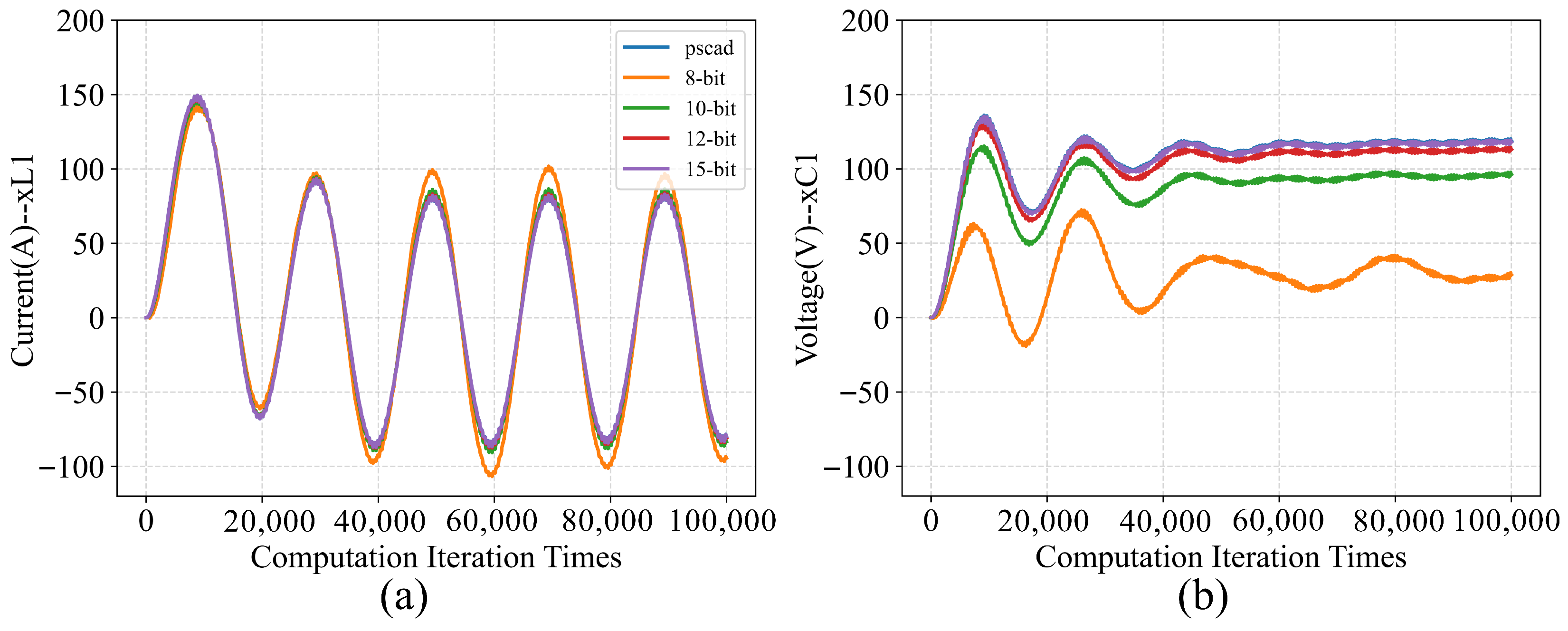
Figure 17.
Quantization verification for state variables by MATLAB with various quantization widths. (a) The transient response of the state . (b) The transient response of the state .
Figure 17.
Quantization verification for state variables by MATLAB with various quantization widths. (a) The transient response of the state . (b) The transient response of the state .
Figure 18.
Quantization error for state variables by MATLAB with various quantization widths. (a) The relationship between the mean squared error (MSE) and the quantization bit width. (b) The relationship between the relative error (RE) and the quantization bit width.
Figure 18.
Quantization error for state variables by MATLAB with various quantization widths. (a) The relationship between the mean squared error (MSE) and the quantization bit width. (b) The relationship between the relative error (RE) and the quantization bit width.
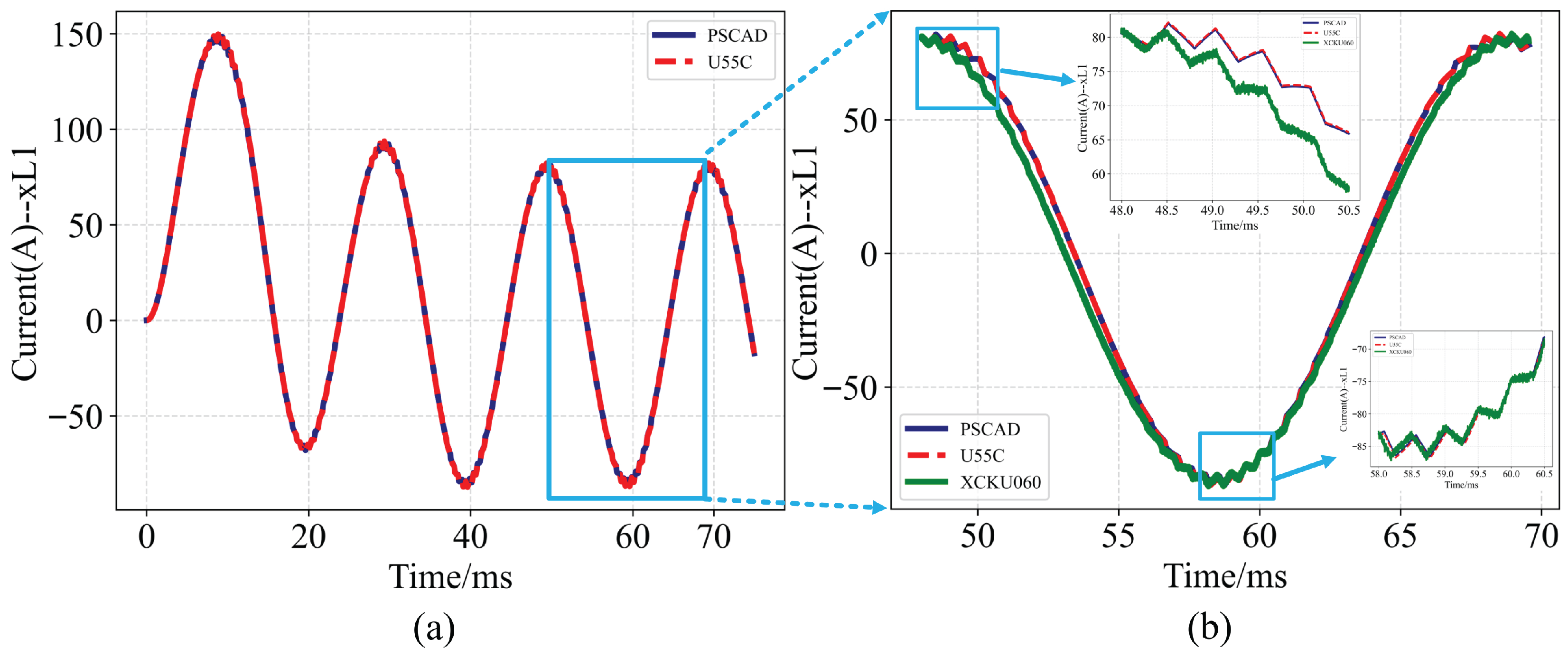
Figure 19.
Waveform results of real-time power system computation. (a) A-phase current of the VSC. (b) Enlargement of A-phase current waveform near 60 ms in (a), including PSCAD results, U55C transferring data by PCIe, and KU060 outputting physical waveform by 14-bit DAC.
Figure 19.
Waveform results of real-time power system computation. (a) A-phase current of the VSC. (b) Enlargement of A-phase current waveform near 60 ms in (a), including PSCAD results, U55C transferring data by PCIe, and KU060 outputting physical waveform by 14-bit DAC.
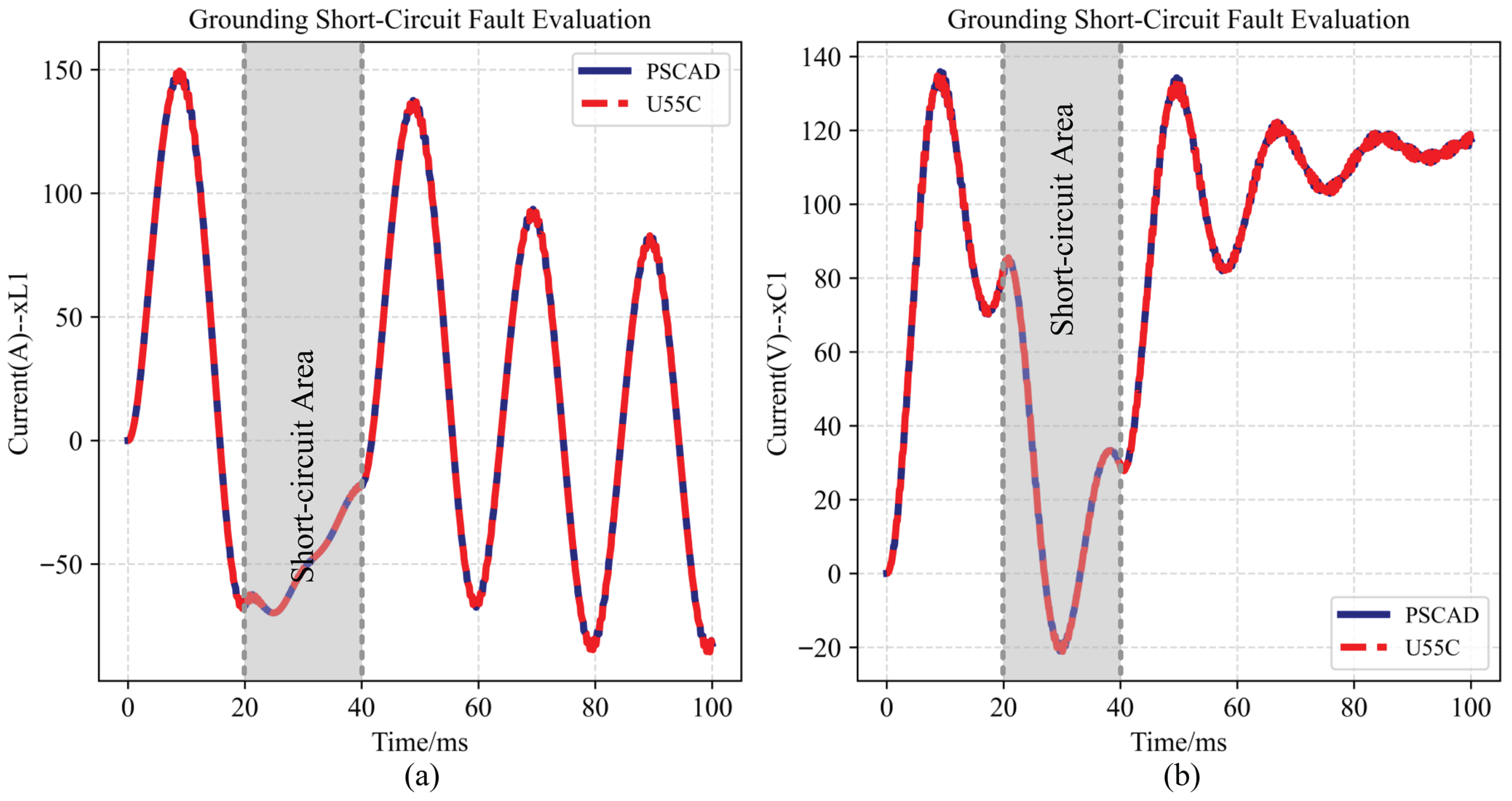
Figure 20.
Grounding short-circuit fault evaluation. (a) The transient response of the state . (b) The transient response of the state .
Figure 20.
Grounding short-circuit fault evaluation. (a) The transient response of the state . (b) The transient response of the state .
Figure 21.
Relationship between resource consumption and computation scale. (a) FPGA-accelerated implementation obtains 53 ns ultra low latency and maintains 95 converters with 570 switches. (b) FPGA-accelerated implementation obtains 373 ns latency and maintains 150 converters with 900 switches.
Figure 21.
Relationship between resource consumption and computation scale. (a) FPGA-accelerated implementation obtains 53 ns ultra low latency and maintains 95 converters with 570 switches. (b) FPGA-accelerated implementation obtains 373 ns latency and maintains 150 converters with 900 switches.
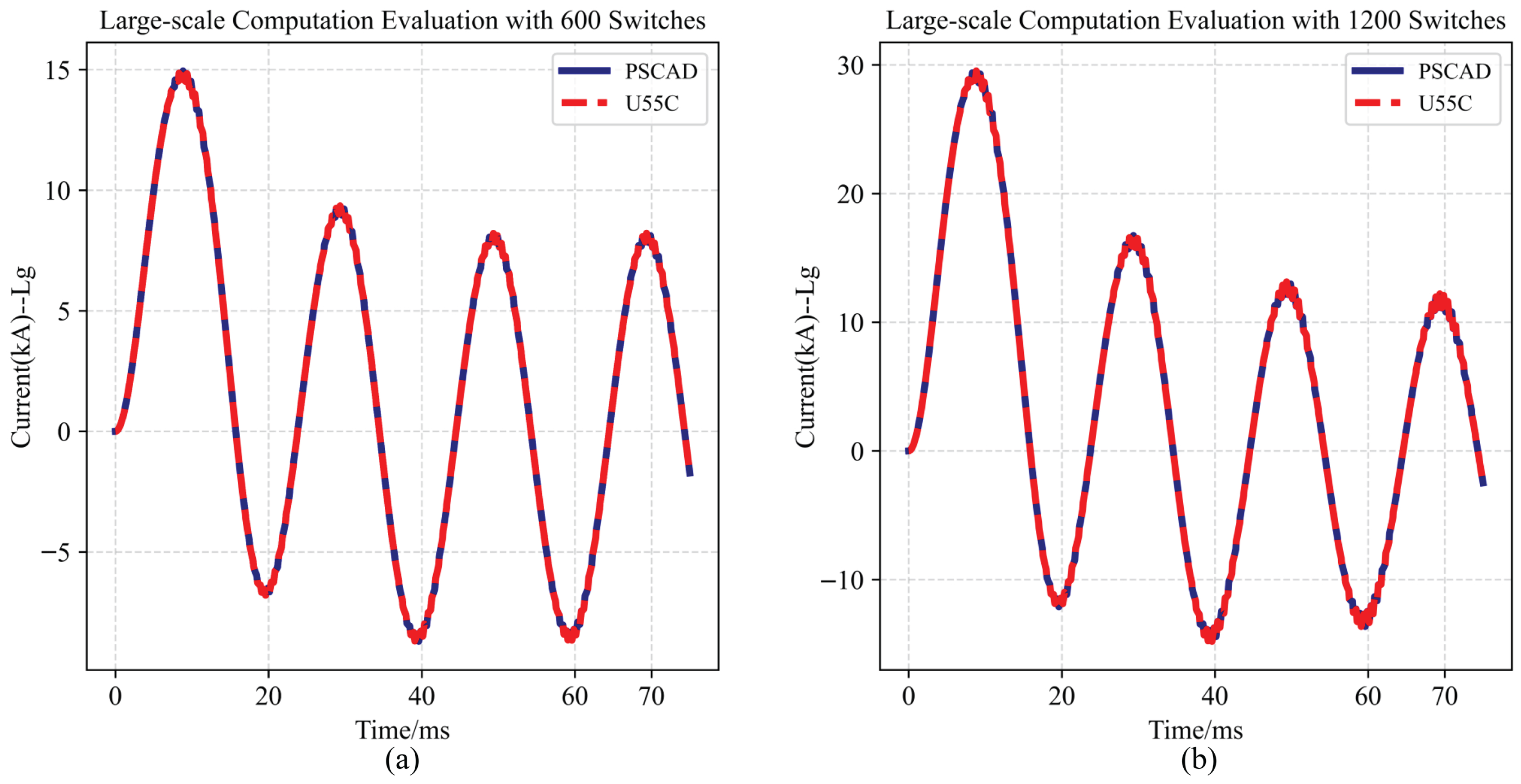
Figure 22.
Evaluation of the relative errors for different switch scales. (a) Multi-converter system testing with 600 switches scale. (b) Multi-converter system testing with 1200 switches scale.
Figure 22.
Evaluation of the relative errors for different switch scales. (a) Multi-converter system testing with 600 switches scale. (b) Multi-converter system testing with 1200 switches scale.
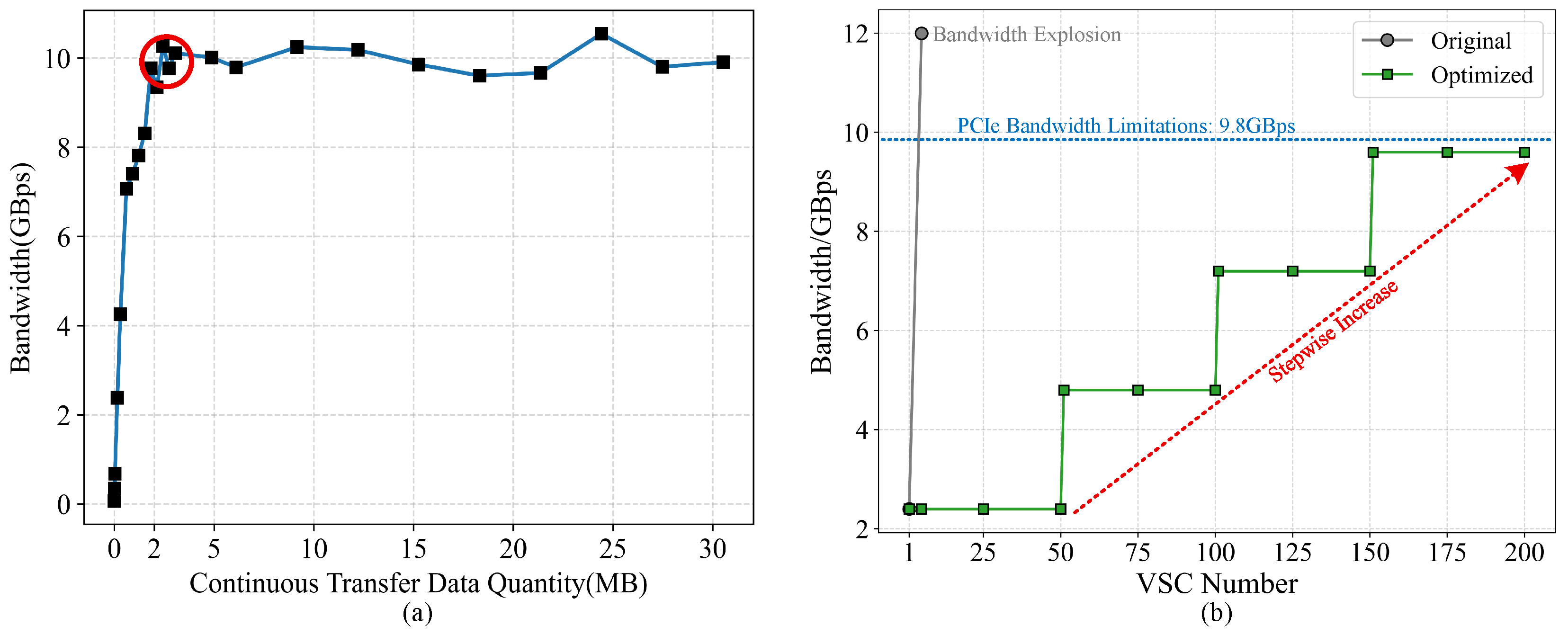
Figure 23.
Bandwidth limitations. (a) The relationship between PCIe bandwidth and data transfer volume in U55C. (b) The relationship between bandwidth and the number of VSCs.
Figure 23.
Bandwidth limitations. (a) The relationship between PCIe bandwidth and data transfer volume in U55C. (b) The relationship between bandwidth and the number of VSCs.
Table 1.
Key variables for the proposed design (parameters listed in this table are collected directly by Xu et al.’s model [
17]).
Table 1.
Key variables for the proposed design (parameters listed in this table are collected directly by Xu et al.’s model [
17]).
| Symbol | Description | Symbol | Description |
|---|
| G, , , etc. | Topological graph | | Global error threshold |
| V, , , etc. | Vertices set | | Element-wise tolerance |
| E, , , etc. | Edges set | , etc. | Inductance state variables |
| State matrices | , etc. | Capacitance state variables |
| Input matrix | | Switches on-resistance |
| Identity matrix | | Switches off-resistance |
| , , etc. | Matrices | | Load resistance |
| Time step | | Capacitance |
| Sub-graphs set | | Inductance |
| , , etc. | Sub-graph of G | | Three-phase voltage with 400 V magnitude |
| Receptive fields | | Maximum amplitude voltage 326 V |
| Quantization operator | | Source resistor |
| Smallest quantization width | | Line load resistance |
| MAPE quantization error | | Line load inductance |
Table 2.
Comparison of runtime for various platforms.
Table 2.
Comparison of runtime for various platforms.
| Platform | Frequency | Time 1 | Time (with WDP) 1 |
|---|
| U55C-FPGA | 150.00 MHz | 1.58 s | 0.05 s |
| EPYC-9554 | 3.76 GHz | 38.77 s | 33.32 s |
| i9-14900K | 6.00 GHz | 22.77 s | 19.60 s |
| i9-14900K + RTX4090 | 6.00 GHz | 121.07 s | 70.35 s |
Table 3.
Comparison of resource utilization and latency.
Table 3.
Comparison of resource utilization and latency.
| | Without WDP | With WDP |
|---|
| Platform | XCKU060 | XCU55C | XCKU060 | XCU55C |
| LUTs | 1316 | 1602 | 1073 | 1463 |
| FFs | 1653 | 2671 | 1032 | 1727 |
| BRAMs | 35.5 | 35.5 | 35.5 | 35.5 |
| DSPs | 21 | 21 | 12 | 12 |
| Latency (ns) | 500 | 500 | 373 | 373 |
Table 4.
Comparisons of FPGA resource utilization and latency for single converter.
Table 4.
Comparisons of FPGA resource utilization and latency for single converter.
| Benchmark | G-ADC [21] | SNP [13] | ADC [31] | EP-ON [33] | Zhao et al. [32] | IEC [29] | IEM [30] | Xu et al. [17] | Ours | Ours |
|---|
| Year | 2018 | 2019 | 2020 | 2022 | 2023 | 2024 | 2024 | 2025 | 2025 | 2025 |
| Platform | XC7K410T | XC7VX485T | XC7K325T | XCKU060 | XC7VX485T | XC7K325T | XC7K325T | XCKU060 | XCKU060 | XCU55 |
| Frequency | NA | 175 MHz | NA | 142.8 MHz | NA | 50 MHz | 100 MHz | 100 MHz | 150 MHz | 150 MHz |
| LUTs | 50,734 | 134,110 | 13,439 | 59,702 | 16,988 | 24,456 | 23,731 | 2593 | 1599 | 2102 |
| FFs | 53,350 | 129,734 | 11,699 | 79,603 | 16,024 | 15,896 | 15,753 | 2052 | 1328 | 2020 |
| BRAMs | 91.0 | 206.0 | NA | 129.5 | NA | 31.5 | 31.0 | 35.5 | 35.5 | 35.5 |
| DSPs | 211 | 325 | 337 | 1490 | 468 | 127 | 128 | 70 | 34 | 35 |
| Latency (ns) | 475 | 800 | 100 | 455 | 100 | 500 | 500 | 80 | 53 | 53 |
| Related Errors (%) | >5.00 | >5.00 | 0.60 | 1.51 | 1.00 | NA | NA | 0.86 | 0.17 | 0.17 |
Table 5.
Resource consumption with 373 ns latency for radial topology on U55C FPGA.
Table 5.
Resource consumption with 373 ns latency for radial topology on U55C FPGA.
| Converters | 1 | 10 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 |
|---|
| Switches | 6 | 60 | 120 | 240 | 360 | 480 | 600 | 720 | 840 | 960 | 1080 | 1200 |
| LUTs | 1406 | 8289 | 14,813 | 28,883 | 43,087 | 57,088 | 71,162 | 85,192 | 99,365 | 113,432 | 127,405 | 141,467 |
| FFs | 1737 | 9761 | 18,731 | 36,671 | 54,618 | 72,556 | 90,499 | 108,440 | 126,382 | 144,320 | 162,264 | 180,204 |
| BRAMs | 35.5 | 94 | 159 | 289 | 419 | 549 | 679 | 809 | 939 | 1069 | 1199 | 1329 |
| DSPs | 12 | 120 | 240 | 480 | 720 | 960 | 1200 | 1440 | 1680 | 1920 | 2160 | 2400 |
Table 6.
Resource consumption of proposed accelerator for trunk topology on U55C FPGA.
Table 6.
Resource consumption of proposed accelerator for trunk topology on U55C FPGA.
| Converters | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 |
|---|
| Switches | 30 | 60 | 90 | 120 | 150 | 180 | 210 | 240 | 270 | 300 | 330 |
| LUTs | 32,253 | 64,696 | 97,578 | 129,848 | 161,430 | 195,259 | 227,809 | 261,073 | 293,339 | 326,163 | 376,949 |
| FFs | 25,122 | 49,753 | 74,381 | 98,942 | 123,535 | 148,227 | 172,856 | 197,500 | 222,060 | 246,699 | 271,346 |
| BRAMs | 14 | 26 | 37.5 | 49 | 61 | 72.5 | 84 | 96 | 107.5 | 119 | 131 |
| DSPs | 828 | 1653 | 2478 | 3303 | 4128 | 4953 | 5778 | 6603 | 7428 | 8253 | 9002 |
Table 7.
Reported EMT solver for converter systems.
Table 7.
Reported EMT solver for converter systems.
| Existing Solvers | Work Year | High Accuracy 4 | Low Latency 5 | Scalable Design | Computation Switches 6 |
|---|
| SSN [42] | 2010 | - | ✘ | ✔ | - |
| L/C-ADC [21] 1,2 | 2018 | ✘ | ✔ | ✘ | 6 |
| G-ADC [21] 1,2 | 2018 | ✘ | ✔ | ✘ | 6 |
| SNP [13] 1,2 | 2019 | - | ✘ | ✔ | 36 |
| LB-LMC [38] 1,2 | 2019 | ✔ | ✔ | ✔ | 38 |
| ADC [31] 1,2 | 2020 | ✔ | ✔ | ✘ | 6 |
| EMT [43] | 2020 | ✔ | ✘ | ✔ | 60 |
| DMM [44] 1,2 | 2021 | ✔ | ✔ | ✘ | 8 |
| EP-ON [33] 1,2 | 2022 | ✘ | ✔ | ✘ | 6 |
| SPL [10] 1,2 | 2023 | ✘ | ✔ | ✘ | 120 |
| RTDM [45] 1,2 | 2023 | ✔ | ✔ | ✘ | 8 |
| TA-MP [11] 1,2 | 2023 | ✔ | ✔ | ✘ | 224 |
| IEC [29] 1,2 | 2024 | - | ✔ | ✘ | 6 |
| IEM [30] 1,2 | 2024 | - | ✔ | ✘ | 6 |
| MDM [46] | 2024 | - | ✘ | ✔ | 120 |
| eHS [47] 1,3 | 2024 | - | ✔ | ✔ | 128 |
| Xu et al. [17] 1,2 | 2025 | ✔ | ✔ | ✔ | 780 |
| Ours 1,3 | 2025 | ✔ | ✔ | ✔ | 1200 |