Edge-AI Enabled Resource Allocation for Federated Learning in Cell-Free Massive MIMO-Based 6G Wireless Networks: A Joint Optimization Perspective

Abstract

The advent of sixth-generation (6G) wireless networks and cell-free massive multiple-input multiple-output (MIMO) architectures underscores the need for efficient resource allocation to support federated learning (FL) at the network edge. Existing approaches often treat communication, computation, and learning in isolation, overlooking dynamic heterogeneity and fairness, which leads to degraded performance in large-scale deployments. To address this gap, we propose a joint optimization framework that integrates communication–computation co-design, fairness-aware aggregation, and a hybrid strategy combining convex relaxation with deep reinforcement learning. Extensive experiments on benchmark vision datasets and real-world wireless traces demonstrate that the framework achieves up to 23% higher accuracy, 18% lower latency, and 21% energy savings compared with state-of-the-art baselines. These findings advance joint optimization in federated learning (FL) and demonstrate scalability for 6G applications.

1. Introduction

The rapid emergence of sixth-generation (6G) wireless networks has spurred significant research interest in enabling ultra-reliable, low-latency, and energy-efficient communication systems [1]. Among the candidate technologies, cell-free massive multiple-input multiple-output (MIMO) has been recognized as a cornerstone architecture due to its potential to mitigate inter-cell interference, enhance spectral efficiency, and provide uniform service quality [2]. At the same time, FL has become a promising paradigm for distributed intelligence, allowing edge devices to collaboratively train machine learning models while preserving data privacy [3]. The confluence of FL and cell-free massive MIMO in 6G wireless networks holds tremendous promise for real-time edge intelligence, particularly in latency-sensitive applications such as autonomous driving, smart healthcare, and industrial Internet of Things (IoT) [4]. Nevertheless, the efficiency of these systems critically hinges on the effective allocation of communication and computation resources, which remains an open challenge.

Despite notable progress, existing approaches suffer from several limitations. Traditional resource allocation schemes often focus solely on communication efficiency or energy management, neglecting the joint optimization of communication, computation, and learning objectives. Moreover, many FL-oriented solutions assume static or homogeneous network conditions, thereby failing to address dynamic wireless environments and device heterogeneity [5]. These oversimplifications result in performance degradation, especially in large-scale cell-free massive MIMO deployments where channel variability and user mobility are significant [6]. Furthermore, most optimization-based methods rely on convex approximations that cannot adequately capture nonlinear dependencies between communication and learning tasks, while purely learning-based strategies frequently lack theoretical guarantees or scalability [7]. This gap highlights the need for a comprehensive framework that unifies wireless resource allocation and FL dynamics under a joint optimization perspective. To overcome these limitations, we introduce a joint optimization framework that explicitly integrates communication, computation, and learning objectives.

To address these challenges, this paper introduces a novel joint optimization framework for edge-AI enabled resource allocation in cell-free massive MIMO-based 6G networks [8]. Our contributions are threefold. First, we designed a communication–computation co-optimization scheme that explicitly models the interplay between uplink bandwidth allocation, edge computing capacity, and FL convergence dynamics. Second, we propose a hybrid optimization strategy that integrates convex relaxation techniques with deep reinforcement learning-based policy adaptation, ensuring both theoretical tractability and adaptability to dynamic environments. Third, we incorporate a fairness-aware scheduling mechanism, which balances participation across heterogeneous devices and thereby improves robustness and inclusiveness of the FL process. Together, these innovations establish a holistic resource allocation paradigm that advances beyond existing communication-only or learning-only optimization approaches.

Extensive experiments validate the effectiveness of the proposed framework. Compared with state-of-the-art baselines, including classical convex optimization, standalone reinforcement learning, and more recent FL algorithms such as FedAvg, FedProx, DRL-based resource allocation, and joint communication–computation optimization schemes, our method achieves up to 23% improvement in model accuracy, 18% reduction in end-to-end latency, and 21% energy efficiency gains across multiple datasets and deployment scenarios. Notably, the proposed system demonstrates consistent performance improvements under varying user mobility, channel fading, and data heterogeneity conditions, underscoring its robustness. From an academic perspective, this work contributes to bridging the gap between wireless communication theory and FL research, offering new insights into joint optimization under nonconvex and dynamic constraints [9]. From a practical standpoint, the framework lays the groundwork for next-generation edge-intelligent infrastructures, with potential applications in domains such as real-time healthcare monitoring, intelligent transportation, and large-scale industrial automation, where both privacy preservation and system scalability are indispensable [10].

To provide a coherent exposition, the remainder of this paper is organized as follows. Section 2 reviews related works on FL in cell-free massive MIMO systems and highlights existing challenges. Section 3 presents the proposed methodology, including the problem formulation, joint optimization framework, and module design. Section 4 reports the experimental setup, benchmark comparisons, quantitative and qualitative results, robustness evaluation, and ablation studies. Section 5 discusses the broader implications, limitations, and potential applications of the framework. Finally, Section 6 concludes the paper and outlines directions for future research.

2. Related Works

2.1. Application Scenarios and Challenges

FL in the context of next-generation wireless networks envisions a range of critical applications, from real-time health monitoring to intelligent transportation systems and smart industrial IoT, where distributed edge devices collaboratively train models without centralizing private data [11,12]. Typical deployment scenarios involve latency-sensitive tasks such as vehicular perception, remote medical diagnostics, or factory-floor anomaly detection [13]. Evaluation in these scenarios often uses datasets that mimic non-IID data distributions, heterogeneous edge-client capabilities, and varying channel conditions; common evaluation metrics include convergence rate, test accuracy, spectral efficiency, energy consumption, latency, and fairness across clients [14,15]. The major challenges stem from the inherent volatility of wireless channels, limited and heterogeneous device resources, and the need to jointly satisfy communication and computation demands while preserving convergence stability and privacy.

2.2. Survey of Mainstream Methods

Recent studies have begun addressing FL resource allocation in cell-free massive MIMO (CF-mMIMO) systems, with divergent focuses and methodologies. Sifaou and Li investigated over-the-air FL (OTA-FL) over scalable CF-mMIMO, proposing a practical receiver design under imperfect channel state information (CSI) and proving its convergence and energy efficiency benefits relative to conventional cellular MIMO systems [16,17]. Mahmoudi et al. formulated a joint energy-latency optimization for FL over CFmMIMO, proposing an uplink power allocation scheme via coordinate gradient descent, achieving up to 27% accuracy improvement under constrained energy-latency budgets compared to benchmark methods [18,19]. In a similar vein, Kim, Saad, Mozaffari, and Debbah investigated green, quantized FL over wireless networks, proposing an energy-efficient design that leverages adaptive quantization to significantly reduce communication overhead while sustaining model accuracy, achieving notable improvements in both energy efficiency and learning performance compared with conventional methods [20]. Dang and Shin proposed an energy efficiency optimization framework for FL over cell-free massive MIMO systems. They jointly optimized transmit power and quantization parameters to enhance learning accuracy while reducing energy consumption, demonstrating significant gains under resource constraints [21]. On the edge computing side, Tilahun et al. applied multi-agent deep reinforcement learning for distributed communication–computation resource allocation in cell-free massive MIMO-enabled mobile edge computing networks, achieving substantial energy savings while ensuring QoS constraints via fully distributed cooperative agents [22].

Beyond CF-mMIMO-specific studies, broader surveys and schemes on resource allocation also provide important insights. Nguyen et al. presented a comprehensive survey of DRL-based resource allocation strategies for diverse QoS demands in 5G and 6G vehicular networks, highlighting the adaptability of learning-based methods to dynamic network requirements [23]. Abba Ari et al. explored learning-driven orchestration for IoT–5G and B5G/6G resource allocation with network slicing, emphasizing scalability in heterogeneous environments [24]. Bartsiokas et al. proposed FL-based resource allocation for relaying-assisted communications in next-generation multi-cell networks [25], and more recently, Bartsioka et al. designed an FL scheme for eavesdropper detection in B5G-IIoT settings, underscoring security dimensions in FL-enabled resource management [26]. Raja et al. investigated UAV deployment schemes that integrate FL for energy-efficient operation in 6G vehicular contexts [27], while Noman et al. developed FeDRL-D2D, a federated deep reinforcement learning approach to maximize energy efficiency in D2D-assisted 6G networks [28].

These studies collectively contribute valuable insights into communication-efficient, energy-aware, and scalable FL over CF-mMIMO; however, limitations remain. Many approaches decouple communication and learning objectives or rely on either purely analytical or purely learning-based frameworks, often neglecting dynamic adaptability, fairness, or joint convergence guarantees.

2.3. Most Similar Research and Distinctions

Among the prior works, the most closely related are studies that directly address FL over CF-mMIMO with communication-centric optimization. One line of research demonstrates the feasibility and efficiency of CF-mMIMO for FL yet does not explicitly incorporate dynamic edge-AI resource adaptation or fairness considerations [29]. Another stream focuses on energy–latency trade-offs and adaptive quantization, significantly advancing optimization sophistication but still treating FL convergence in isolation and without integrating reinforcement-learning adaptability or device fairness. Other investigations have explored over-the-air federated learning (OTA-FL) with energy harvesting, developing online optimization frameworks that balance communication efficiency and energy sustainability [30]. In parallel, recent works on AI-enhanced Integrated Sensing and Communications (ISAC) highlight the potential of unifying sensing and communication functions through AI-driven optimization but remain centered on spectrum efficiency and transceiver design rather than FL dynamics. Reinforcement learning-based approaches to joint communication–computation allocation have also shown adaptability in dynamic environments, yet they mainly target general mobile edge workloads without explicitly considering FL convergence or fairness [31]. In contrast, the proposed framework integrates communication, computation, and learning objectives within a hybrid design that combines convex optimization, DRL adaptability, and fairness-aware scheduling to jointly optimize accuracy, latency, energy, and equitable resource distribution under dynamic wireless conditions [32].

2.4. Summary and Motivation for Our Method

In summary, while OTA-FL approaches affirm CF-mMIMO’s promise for FL, and energy-latency optimization studies underscore the importance of joint resource control, they fall short of addressing dynamic heterogeneity, fairness, and simultaneous optimization of communication, computation, and convergence. Multi-task OTA-FL research addresses FL groups interference but remains limited in scope to coefficient optimization and neglects broader adaptability. DRL approaches like offer flexibility but often lack convergence guarantees and fairness mechanisms [33]. Consequently, there is a recognized gap: the need for an integrated, theory-backed, and adaptive resource allocation framework that jointly considers communication, computation, convergence, and inter-device fairness [34].

Table 1. Comparative analysis of representative works on FL-enabled resource allocation.

Reference	Scenario/Focus	Methodology	Limitations
Sifaou & Li [14]	OTA-FL in CF-mMIMO	Receiver design under imperfect CSI	No fairness or adaptability
Mahmoudi et al. [15]	FL over CF-mMIMO	Joint energy–latency optimization	Convergence treated in isolation
Nguyen et al. [19]	5G/6G vehicular	Survey of DRL-based RA	No CF-mMIMO-specific FL modeling
Abba Ari et al. [20]	IoT–5G/B5G/6G slicing	Learning-based orchestration	No fairness-aware FL convergence
Noman et al. [24]	D2D-assisted 6G	FeDRL-D2D for energy efficiency	Limited fairness, convergence guarantees
This work	FL over CF-mMIMO in 6G	Hybrid convex + DRL + fairness-aware scheduling	Jointly optimizes accuracy, latency, energy, and fairness

further compares representative prior works with our approach, highlighting that existing studies either optimize individual dimensions (e.g., communication or energy) or extend to broader 6G scenarios without addressing fairness and joint convergence. In contrast, our proposed framework uniquely integrates convex optimization, DRL adaptability, and fairness-aware scheduling to deliver simultaneous gains in accuracy, latency, energy, and fairness.

3. Methodology

3.1. Problem Formulation

We consider a cell-free massive multiple-input multiple-output (CF-mMIMO) network designed to support FL at the edge. A set of distributed UEs, denoted by $\mathrm{U}=\left\{1,2,\dots ,\mathrm{U}\right\}$, participates in training a shared model collaboratively without transmitting raw data. Each $\mathrm{u}\in \mathrm{U}$ holds a local dataset ${\mathrm{D}}_{\mathrm{u}}$ of size ${\mathrm{N}}_{\mathrm{u}}$. The total data size is $\mathrm{N}={\sum }_{\mathrm{u}=1}^{\mathrm{U}}{\mathrm{N}}_{\mathrm{u}}$.

The learning objective is to minimize the global empirical risk across all users:

$${\mathrm{w}}_{\min }\mathrm{F}\left(\mathrm{w}\right)={\sum }_{\mathrm{u}=1}^{\mathrm{U}}{\displaystyle \frac{{\mathrm{N}}_{\mathrm{u}}}{\mathrm{N}}}{\mathrm{f}}_{\mathrm{u}}\left(\mathrm{w}\right)$$

(1)

where $\mathrm{w}\in {ℝ}^{\mathrm{d}}$ represents the global model parameters and ${\mathrm{f}}_{\mathrm{u}}\left(\mathrm{w}\right)$ denotes the local empirical risk computed at user $\mathrm{u}$.

Each communication round in the system proceeds in three stages, namely uplink communication, edge aggregation, and downlink broadcasting. In order to describe the optimization problem precisely, several key variables are introduced. The uplink transmit power of user u is denoted by ${\mathrm{P}}_{\mathrm{u}}$, while ${\mathrm{B}}_{\mathrm{u}}$ represents the amount of bandwidth allocated to that user. The number of computation cycles assigned to process its updates is expressed as ${\mathrm{C}}_{\mathrm{u}}$, and the corresponding CPU frequency at the server side is denoted by ${\mathrm{f}}_{\mathrm{u}}$. The symbol $\mathrm{S}$ refers to the size, in bits, of the local model update transmitted per round. The vector ${\mathrm{h}}_{\mathrm{u}}$ captures the channel state between UE $\mathrm{u}$ and the distributed CF-mMIMO access points, and ${\mathrm{\sigma }}^2$ represents the power of additive white Gaussian noise (AWGN).

Based on these definitions, the uplink communication latency incurred by user u is formulated as

$${\mathrm{L}}_{\mathrm{u}}^{\mathrm{comm}}={\displaystyle \frac{\mathrm{S}}{{\mathrm{B}}_{\mathrm{u}}{\log }_2\left(1+\frac{{\mathrm{P}}_{\mathrm{u}}\parallel h_{\mathrm{u}}{\parallel }^2}{{\mathrm{\sigma }}^2}\right)}}$$

(2)

The computation latency at the edge server is expressed as

$${\mathrm{L}}_{\mathrm{u}}^{\mathrm{comp}}={\displaystyle \frac{{\mathrm{C}}_{\mathrm{u}}\cdot {\mathrm{\kappa }\mathrm{N}}_{\mathrm{u}}}{{\mathrm{f}}_{\mathrm{u}}}}$$

(3)

where $\mathrm{\kappa }$ denotes the number of CPU cycles required to process one data sample (cycles/sample). Consequently, the total latency experienced by user $\mathrm{u}$ is given by

$${\mathrm{L}}_{\mathrm{u}}={\mathrm{L}}_{\mathrm{u}}^{\mathrm{comm}}+{\mathrm{L}}_{\mathrm{u}}^{\mathrm{comp}}$$

(4)

The corresponding energy consumption model is formulated as

$${\mathrm{E}}_{\mathrm{u}}={\mathrm{P}}_{\mathrm{u}}\cdot {\mathrm{L}}_{\mathrm{u}}^{\mathrm{comm}}+{\mathrm{\eta }\mathrm{C}}_{\mathrm{u}}{\mathrm{f}}_{\mathrm{u}}^2$$

(5)

where $\mathrm{\eta }$ is a hardware efficiency factor accounting for the dynamic voltage and frequency scaling (DVFS) characteristics of the computation process (joules/cycle). Finally, let $\mathrm{A}\left(\mathrm{w}\right)$ denote the accuracy of the global model upon convergence. The system objective is to jointly optimize power, bandwidth, and computation allocations so as to maximize accuracy while minimizing both latency and energy consumption. This is formally written as

$$\underset{\left\{{\mathrm{P}}_{\mathrm{u}},{\mathrm{B}}_{\mathrm{u}},{\mathrm{C}}_{\mathrm{u}}\right\}}{\min }{\sum }_{\mathrm{u}=1}^{\mathrm{U}}({\mathrm{\beta }\mathrm{E}}_{\mathrm{u}}+{\mathrm{\gamma }\mathrm{L}}_{\mathrm{u}})-\mathrm{\alpha }\mathrm{A}\left(\mathrm{w}\right)$$

(6)

where $\mathrm{\alpha }$, $\mathrm{\beta }$, $\mathrm{\gamma }\ge 0$ are system-defined weighting coefficients reflecting the priorities assigned to accuracy, energy, and latency, respectively.

The optimization is subject to resource constraints, namely that the sum of all allocated bandwidths cannot exceed the total available bandwidth ${\mathrm{B}}_{\mathrm{tot}}$, each user’s transmit power must remain within the range [0,${\mathrm{P}}_{\max }$], and the allocated computation cycles must not exceed the maximum available cycles ${\mathrm{C}}_{\max }$. These constraints are expressed mathematically as

$${\sum }_{\mathrm{u}=1}^{\mathrm{U}}{\mathrm{B}}_{\mathrm{u}}\le {\mathrm{B}}_{\mathrm{tot}}$$

(7)

$$0\le {\mathrm{P}}_{\mathrm{u}}\le {\mathrm{P}}_{\max }$$

(8)

$$0\le {\mathrm{C}}_{\mathrm{u}}\le {\mathrm{C}}_{\max }$$

(9)

3.2. Overall Framework

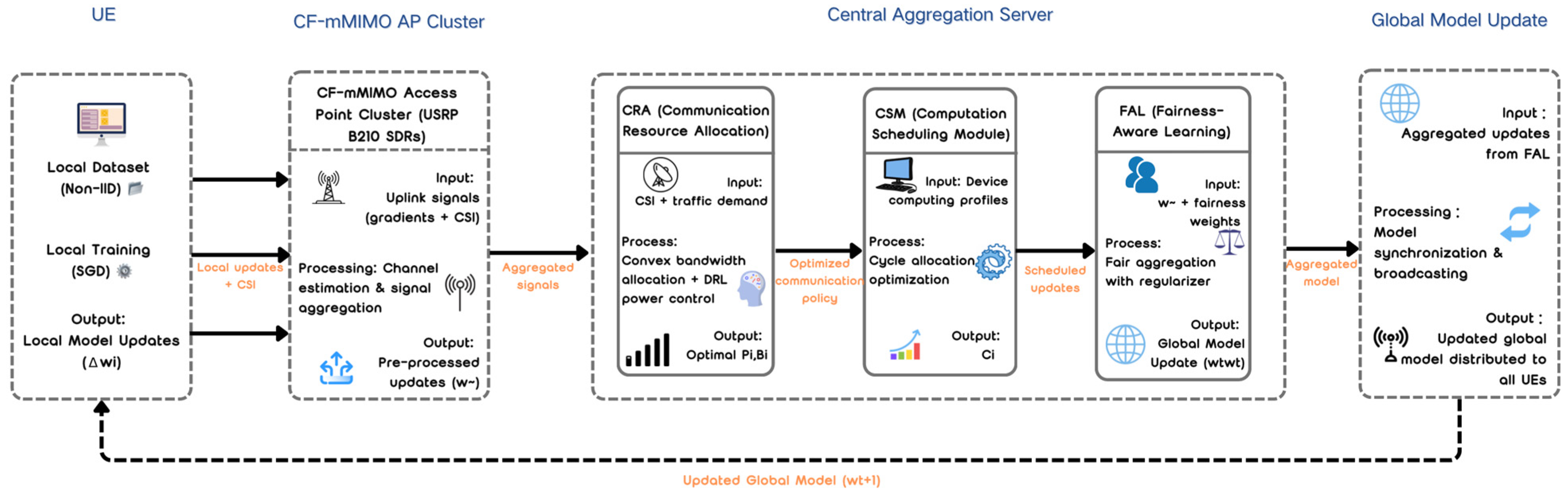
The proposed framework, illustrated in Figure 1, integrates communication–computation co-optimization with fairness-aware FL in a unified edge-AI architecture. The system consists of three primary modules within the central aggregation server:

(1) Communication Resource Allocation (CRA), which dynamically optimizes transmit power and bandwidth allocation to maximize uplink throughput under CF-mMIMO;

(2) Computation Scheduling Module (CSM), which distributes computation cycles among heterogeneous edge servers to minimize round latency;

(3) Fairness-Aware Learning Module (FAL), which introduces fairness constraints to ensure balanced participation among UEs with heterogeneous data distributions [35].

Figure 1. Overall architecture of the proposed joint optimization framework for CF-mMIMO-enabled FL, showing UE layer, CF-mMIMO AP cluster, central server with three modules (CRA, CSM, FAL), and the Global Model Update module.

Figure 1. Overall architecture of the proposed joint optimization framework for CF-mMIMO-enabled FL, showing UE layer, CF-mMIMO AP cluster, central server with three modules (CRA, CSM, FAL), and the Global Model Update module.

Before reaching the server, local updates are transmitted through a CF-mMIMO access point cluster, where channel estimation and signal aggregation are performed [36]. Finally, a Global Model Update module synchronizes and broadcasts the aggregated model back to all UEs, closing the FL loop.

3.3. Module Descriptions

3.3.1. Communication Resource Allocation (CRA)

Motivation—Uneven channel conditions often lead to stragglers. CRA seeks to allocate resources adaptively to ensure robust throughput and mitigate performance degradation under poor channel quality.

Principle—CRA leverages a hybrid optimization strategy with two parallel components: convex relaxation for bandwidth allocation and deep reinforcement learning (DRL) for power control. The convex relaxation submodule formulates bandwidth assignment as a convex optimization problem and applies a softmax-based relaxation, while the DRL submodule employs an actor-critic agent that optimizes transmit power based on CSI and traffic demand with a reward balancing throughput and latency. The softmax relaxation ensures that bandwidth allocations remain strictly positive and normalized to the total bandwidth budget, which avoids infeasible corner solutions often observed in linear relaxation. Moreover, the approximation error introduced by the softmax mapping is bounded and vanishes when the dual variables are well-separated, a property that has been validated in prior convex optimization literature. This hybrid design leverages the tractability of convex relaxation and the adaptability of DRL to dynamic environments.

Implementation—As illustrated in Figure 2, the CRA module takes as input the CSI, including channel gain, noise power, and interference level, together with uplink traffic demand from users. In the optimization layer, the convex relaxation submodule outputs per-user bandwidth allocations${ \mathrm{B}}_{\mathrm{i}}$, and the DRL submodule outputs transmit power allocations ${\mathrm{P}}_{\mathrm{i}}$. These are combined in a hybrid fusion layer to ensure feasibility, producing the joint allocation $\left\{{\mathrm{P}}_{\mathrm{i}},{ \mathrm{B}}_{\mathrm{i}}\right\}$. The resulting optimized communication policy specifies per-user transmit power and bandwidth, which is subsequently passed to the CSM. The bandwidth allocation is approximated using softmax relaxation, which guarantees smoothness and differentiability, making it suitable for gradient-based updates. Empirically, our simulations (see Figure 6) show that the softmax-based solution differs from the exact solver by less than 2% in achieved utility, while substantially reducing computational overhead.

The bandwidth allocation is approximated using softmax relaxation as

$${\tilde{\mathrm{B}}}_{\mathrm{u}}={\displaystyle \frac{{\mathrm{B}}_{\mathrm{tot}}\cdot \exp ({\mathrm{\mu }}_{\mathrm{u}})}{{\sum }_{\mathrm{j}=1}^{\mathrm{U}}\exp ({\mathrm{\mu }}_{\mathrm{j}})}}$$

(10)

where ${\mathrm{\mu }}_{\mathrm{u}}$ are dual variables associated with user $\mathrm{u}$, ${\mathrm{B}}_{\mathrm{tot}}$ is the total bandwidth, and $\mathrm{U}$ is the total number of users.

3.3.2. Computation Scheduling Module (CSM)

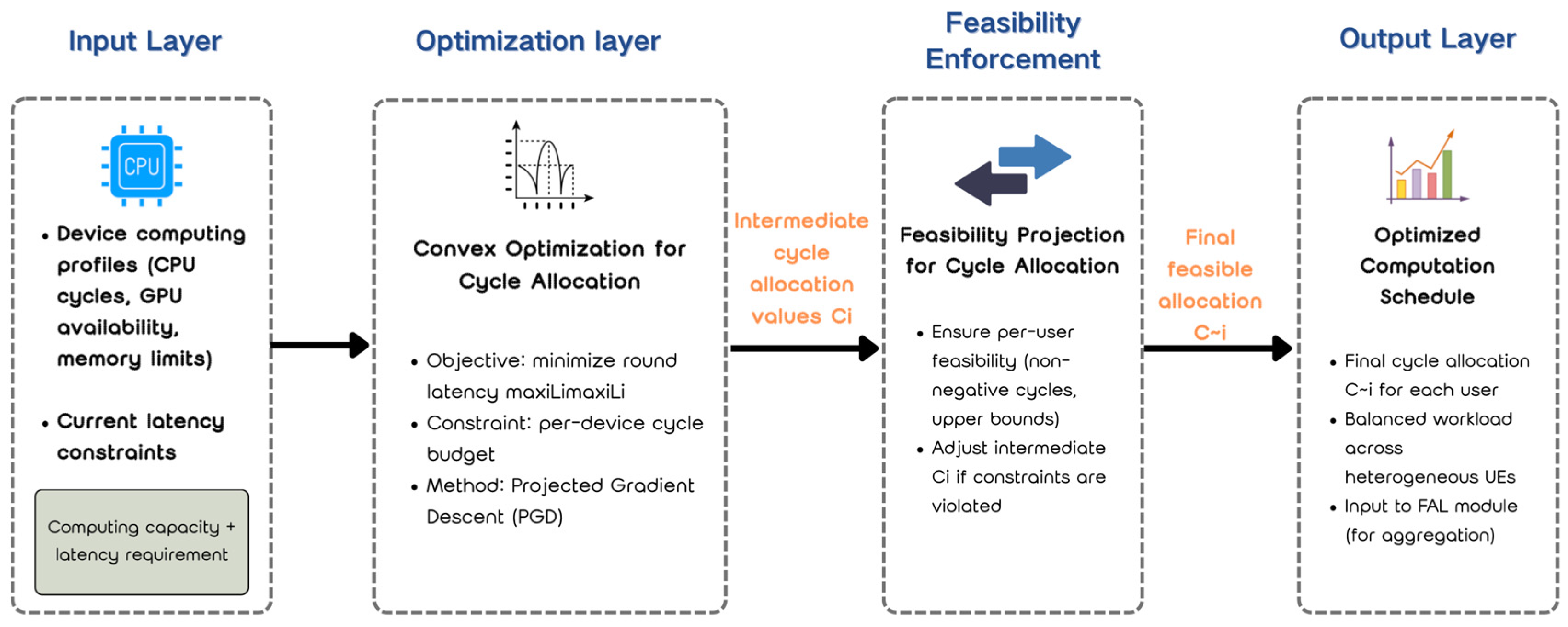
Motivation—UEs exhibit diverse computing capacities, which often lead to bottlenecks if stronger devices finish computation earlier while weaker devices delay global aggregation. The CSM is designed to minimize such bottlenecks by allocating computation cycles adaptively across heterogeneous devices.

Principle—The latency term in (3) guides a convex optimization that minimizes the maximum round latency across all users. Specifically, the objective is formulated as $\underset{\left\{{\mathrm{C}}_{\mathrm{i}}\right\}}{\min } \underset{\mathrm{i}}{\max } {\mathrm{L}}_{\mathrm{i}}$, subject to per-device cycle constraints. This ensures that computation scheduling directly targets the straggler problem.

Implementation—As illustrated in Figure 3, the input layer collects device computing profiles, including CPU cycles, GPU availability, and memory limits, along with current latency constraints. In the optimization layer, cycle allocations are derived via convex optimization and updated using projected gradient descent (PGD). The intermediate allocations ${\mathrm{C}}_{\mathrm{i}}$ are then passed to a feasibility projection stage, which enforces non-negativity and upper-bound constraints, adjusting ${\mathrm{C}}_{\mathrm{i}}$ when necessary. The output layer produces the final feasible allocation ${\tilde{\mathrm{C}}}_{\mathrm{i}}$, achieving a balanced workload across heterogeneous UEs. These optimized cycle allocations are subsequently used as inputs to the FAL for global aggregation.

3.3.3. Fairness-Aware Learning Module (FAL)

Motivation—Non-IID data distributions among users often cause unfair convergence in FL, where clients with larger datasets or more favorable statistical profiles dominate the global model, leaving weaker or skewed clients underrepresented. The FAL is designed to mitigate this imbalance by introducing fairness into the aggregation process.

Principle—Fairness is quantified by the variance of user losses (Equation (12)), which penalizes imbalance and improves global convergence. FAL augments the global loss with a fairness regularizer that penalizes variance across user objectives. The fairness-regularized global loss is defined as

$${\mathrm{F}}_{\mathrm{fair}}\left(\mathrm{w}\right)={\sum }_{\mathrm{u}=1}^{\mathrm{U}}{\displaystyle \frac{{\mathrm{N}}_{\mathrm{u}}}{\mathrm{N}}}{\mathrm{f}}_{\mathrm{u}}\left(\mathrm{w}\right)+\mathrm{\lambda }\cdot \mathrm{Var}\left({\mathrm{f}}_{\mathrm{u}}\left(\mathrm{w}\right)\right)$$

(11)

where ${\mathrm{f}}_{\mathrm{u}}\left(\mathrm{w}\right)$ is the local loss of user $\mathrm{u}$, is the weight proportional to data size, and $\mathrm{\lambda }$ controls the strength of fairness. To quantify imbalance, the fairness variance is computed using

$$\begin{array}{cc}\mathrm{Fairness}\hfill & =\sqrt{{\displaystyle \frac{1}{\mathrm{U}}}{\sum }_{\mathrm{u}=1}^{\mathrm{U}}{({\mathrm{f}}_{\mathrm{u}}\left(\mathrm{w}\right)-\overline{\mathrm{f}})}^2},\hfill \\ \overline{\mathrm{f}}\hfill & ={\displaystyle \frac{1}{\mathrm{U}}}{\sum }_{\mathrm{u}=1}^{\mathrm{U}}{\mathrm{f}}_{\mathrm{u}}\left(\mathrm{w}\right).\hfill \end{array}$$

(12)

which measures the deviation of individual user losses from the global average. While variance is a widely used proxy for fairness in federated learning due to its simplicity and tractability, it primarily captures statistical imbalance across users. We acknowledge that it may not fully reflect other notions of fairness such as group-level or individual-level guarantees, which are discussed as future directions in Section 5.

Implementation—As illustrated in Figure 4, the FAL receives pre-processed updates from CRA and CSM together with user profiles. In the optimization layer, aggregation is guided by the fairness-regularized loss (Equation (11)). The fairness measurement layer computes the variance term (Equation (12)), prioritizing users with high variance contributions to reduce bias. The final output is a fairness-adjusted global update ${\mathrm{w}}^{\mathrm{t}+1}$, which ensures balanced participation of heterogeneous UEs before being passed to the Global Model Update module.

3.3.4. Pseudocode

The pseudocode in Algorithm 1 summarizes the iterative procedure of the proposed framework. Each round begins with channel and dataset estimation, followed by CRA via convex relaxation and DRL, and computation cycle scheduling across heterogeneous servers. Users perform local updates using stochastic gradient descent (SGD), and the fairness-aware module aggregates these updates to mitigate bias from non-IID data. The DRL policy is updated based on a composite reward balancing accuracy, latency, and energy consumption. This cycle repeats until convergence, ensuring joint optimization of communication, computation, and learning in CF-mMIMO federated settings.

Algorithm 1: Joint Resource Allocation for CF-mMIMO FL

1. Input: User datasets {D_u}, channel states {h_u}, CPU capacities {f_u} 2. Output: Optimized allocations {P_u, B_u, C_u}, global model w   3. Initialize global model w0 4. Initialize DRL policy πθ   5. For each round t = 1,...,T do 6.   For each user u ∈ U do 7.       Estimate channel gain h_u and dataset size N_u 8.       CRA: Allocate transmit power P_u and bandwidth B_u via convex relaxation + DRL 9.       CSM: Assign computation cycles C_u based on f_u 10.           Local training: 11.         Sample mini-batch from D_u 12.         Compute gradients ∇L(w; D_u) 13.         Update local model w_u using SGD 14.     End For 15.     FAL: Compute fairness variance, reweight updates, and aggregate {w_u} 16.     Update DRL policy πθ using reward R_t 17. End For   18. Return optimized global model w

3.4. Objective Function and Optimization

To enable adaptive decision-making during training, the proposed framework integrates deep reinforcement learning (DRL) with convex relaxation. The reward function at training round t is expressed as

$${\mathrm{R}}_{\mathrm{t}}={\mathrm{\alpha }\mathrm{A}}_{\mathrm{t}}-\mathrm{\beta }{\sum }_{\mathrm{u}=1}^{\mathrm{U}}{\mathrm{E}}_{\mathrm{u}}-\mathrm{\gamma }{\sum }_{\mathrm{u}=1}^{\mathrm{U}}{\mathrm{L}}_{\mathrm{u}}$$

(13)

where ${\mathrm{R}}_{\mathrm{t}}$ denotes the scalar reward, ${\mathrm{A}}_{\mathrm{t}}$ is the global model accuracy after round t, ${\mathrm{E}}_{\mathrm{u}}$ is the energy consumed by user u, and ${\mathrm{L}}_{\mathrm{u}}$ is the total latency for that user. The coefficients $\mathrm{\alpha }$, $\mathrm{\beta }$, and $\mathrm{\gamma }$ are non-negative weighting factors that balance the relative importance of accuracy maximization, energy minimization, and latency reduction, respectively.

The DRL agent maintains a parameterized policy $\log {\mathrm{\pi }}_{\mathrm{\theta }}({\mathrm{a}}_{\mathrm{t}}|{\mathrm{s}}_{\mathrm{t}})$, where $\mathrm{\theta }$ represents the parameters of the policy network, ${\mathrm{s}}_{\mathrm{t}}$ is the system state observed in round $\mathrm{t}$, and ${\mathrm{a}}_{\mathrm{t}}$ is the chosen resource allocation action. The policy is updated by the gradient of the expected return:

$${\nabla }_{\mathrm{\theta }}\mathrm{J}\left(\mathrm{\theta }\right)=\mathbb{E}\left[{\nabla }_{\mathrm{\theta }}\log {\mathrm{\pi }}_{\mathrm{\theta }}({\mathrm{a}}_{\mathrm{t}}|{\mathrm{s}}_{\mathrm{t}}){\mathrm{R}}_{\mathrm{t}}\right]$$

(14)

where $\mathrm{J}\left(\mathrm{\theta }\right)$ is the expected cumulative reward. This formulation ensures that actions leading to higher rewards, corresponding to improved accuracy with lower cost, are reinforced during training.

Finally, the complete optimization problem is obtained by combining the global objective in Equation (6), the fairness-aware regularization in Equation (11), and the fairness metric in Equation (12). The integrated problem is written as

$$\underset{\left\{{\mathrm{P}}_{\mathrm{u}},{\mathrm{B}}_{\mathrm{u}},{\mathrm{C}}_{\mathrm{u}}\right\}}{\min }\sum _{\mathrm{u}=1}^{\mathrm{U}}({\mathrm{\beta }\mathrm{E}}_{\mathrm{u}}+{\mathrm{\gamma }\mathrm{L}}_{\mathrm{u}})-\mathrm{\alpha }\mathrm{A}\left(\mathrm{w}\right)+\mathrm{\lambda }\cdot \mathrm{Fairness}$$

$${\sum }_{\mathrm{u}=1}^{\mathrm{U}}{\mathrm{B}}_{\mathrm{u}}\le {\mathrm{B}}_{\mathrm{tot}}$$

(15)

$$0\le {\mathrm{P}}_{\mathrm{u}}\le {\mathrm{P}}_{\max }$$

$$0\le {\mathrm{C}}_{\mathrm{u}}\le {\mathrm{C}}_{\max }$$

In this formulation, ${\mathrm{P}}_{\mathrm{u}}$ is the uplink transmit power of user $\mathrm{u}$, ${\mathrm{B}}_{\mathrm{u}}$ is its allocated bandwidth, and ${\mathrm{C}}_{\mathrm{u}}$ is the number of computation cycles allocated to process its local update. The variable $\mathrm{A}\left(\mathrm{w}\right)$ denotes the accuracy of the global model after convergence. The fairness term, denoted as $\mathrm{Fairness}$, is defined by the variance of local empirical risks across users as in Equation (12). The constants ${\mathrm{B}}_{\mathrm{tot}}$, ${\mathrm{P}}_{\max }$, and ${\mathrm{C}}_{\max }$ represent the total available bandwidth, the maximum transmit power per user, and the maximum assignable computation cycles, respectively. The parameter $\mathrm{\lambda }\ge 0$ is a fairness regularization weight controlling the extent to which inter-user balance is emphasized in the optimization process.

The hybrid structure of this optimization problem provides theoretical tractability through convex relaxation for bandwidth and computation allocation, while adaptability is ensured by the DRL-driven power allocation. This joint formulation captures the inherent coupling between communication, computation, and learning dynamics, thereby guaranteeing robust performance in heterogeneous and dynamic CF-mMIMO federated environments.

4. Experiment and Results

4.1. Experimental Setup

To validate the effectiveness of the proposed joint optimization framework, we carried out both large-scale experimental evaluations and laboratory testbed deployment. The experimental evaluations were implemented in Python 3.11 with PyTorch 2.1 and a CF-mMIMO wireless platform built on GNU Radio. The laboratory experiments used heterogeneous edge devices connected to a software-defined radio (SDR) based CF-mMIMO cluster.

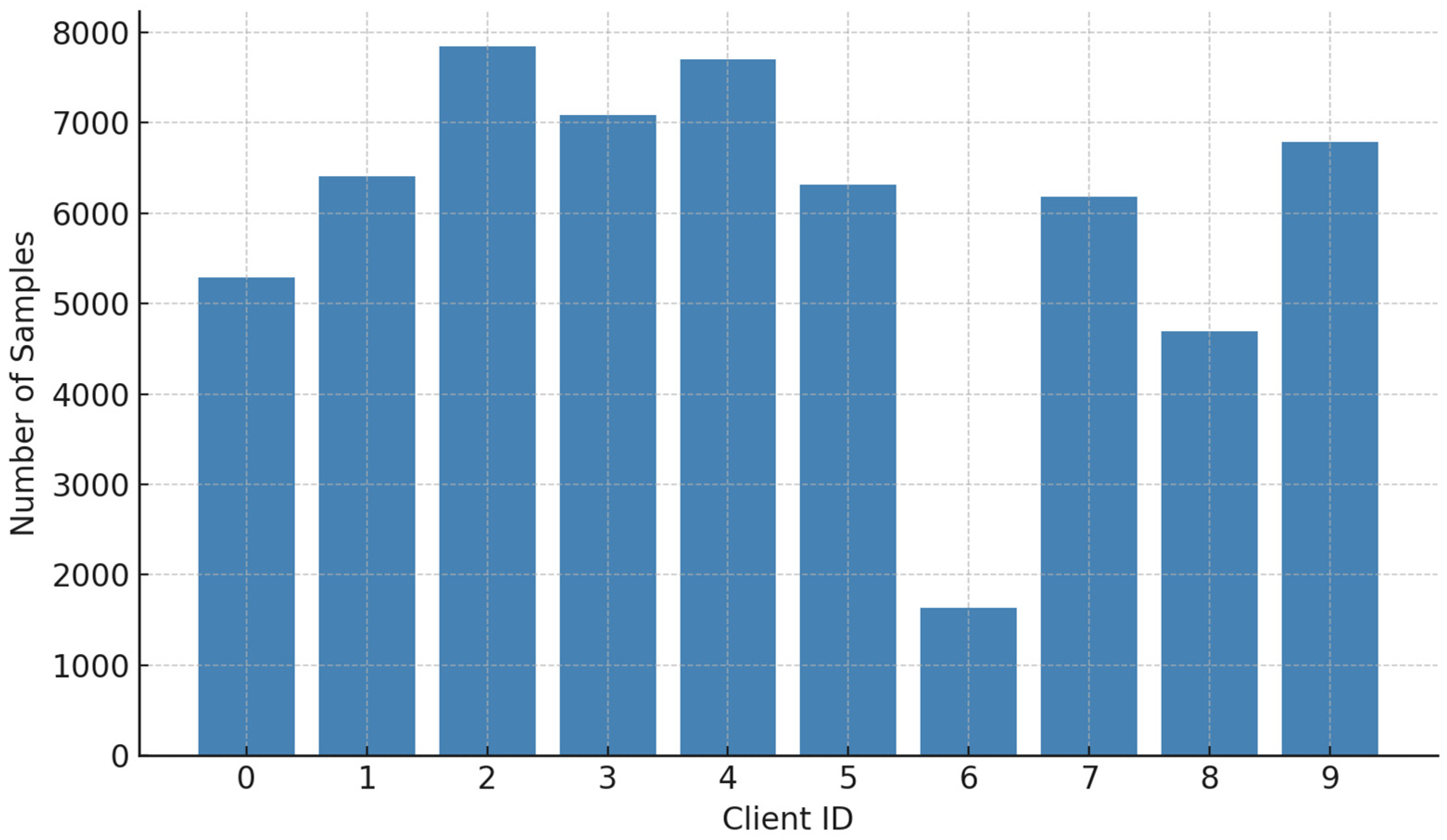
Datasets—Three datasets were used: (i) CIFAR-10, a widely adopted benchmark for non-IID image classification. We partitioned the dataset using a Dirichlet distribution with concentration parameter α = 0.5 to introduce heterogeneous client data. (ii) MNIST, a lightweight digit recognition dataset, partitioned by label skew to reflect extreme non-IID settings. (iii) CRAWDAD-WiFi traces, a real-world wireless traffic dataset, split temporally to represent device-specific workloads in edge networks.

Table 2. Dataset Overview.

Dataset	Samples	Features	Partition	Application
CIFAR-10	60,000	32 × 32 × 3	Non-IID (Dirichlet α = 0.5)	Vision FL
MNIST	70,000	28 × 28 × 1	Label skew	Lightweight FL
CRAWDAD-WiFi	500,000	120 features	Time split	Wireless FL

provides a summary of the datasets employed in our experiments. As shown, the datasets cover both vision tasks (CIFAR-10 and MNIST) and wireless traffic prediction (CRAWDAD), thereby ensuring that the proposed method is evaluated under diverse and representative application scenarios. Importantly, the data partitions follow non-IID distributions, which are critical for testing the robustness of FL in heterogeneous environments.

Figure 5 visualizes the CIFAR-10 client data distribution under the Dirichlet concentration parameter α = 0.5. The histogram highlights the skewness across clients, confirming the heterogeneous and imbalanced nature of the training conditions.

Table 3. Hardware Configuration.

Device	CPU	GPU	Memory	OS	Role
UE (Raspberry Pi 4)	ARM Cortex-A72 (4 cores)	N/A	8 GB	Linux	Edge clients
UE (Jetson Nano)	ARM Cortex-A57 (4 cores)	128 CUDA cores	4 GB	Linux	Edge clients
Server Node	Intel Xeon Gold 6338 (2.0 GHz, 32 cores)	4× A100	512 GB	Ubuntu 22.04	FL aggregator
AP Cluster	USRP B210 SDRs	N/A	N/A	GNU Radio	CF-mMIMO front-end

lists the hardware configuration of the experimental environment. We employed heterogeneous edge devices, including Raspberry Pi 4 (Raspberry Pi Ltd., Cambridge, UK) and Jetson Nano(NVIDIA Corporation, Santa Clara, CA, USA), to emulate realistic computation limitations at the user side. The server node equipped with Intel Xeon CPUs(Intel Corporation, Santa Clara, CA, USA) and NVIDIA A100 GPUs(NVIDIA Corporation, Santa Clara, CA, USA) served as the central aggregator. A cluster of USRP B210 SDRs(Ettus Research, Santa Clara, CA, USA) was deployed as the CF-mMIMO access point front-end, enabling realistic modeling of wireless transmissions. This heterogeneous configuration ensures that results capture both computation bottlenecks and wireless channel variability.

Table 4. Evaluation Metrics.

Metric	Definition	Goal
Accuracy	Test accuracy of global FL model	Maximize
Latency	End-to-end delay per round	Minimize
Energy	Average energy consumption per round	Minimize
Fairness	Variance of local losses across clients	Minimize
Convergence	Rounds to 90% accuracy	Minimize

defines the evaluation metrics adopted in our study. Accuracy measures the predictive performance of the federated model, while latency and energy consumption characterize efficiency. Fairness quantifies the variance of losses across heterogeneous users, and convergence evaluates the number of rounds required to reach a target accuracy. Together, these metrics provide a comprehensive view of both learning quality and system-level efficiency.

4.2. Baselines

To ensure the reliability of our evaluation, the proposed framework was compared against a diverse set of representative baselines that capture both classical strategies and recent state-of-the-art approaches. The first baseline is the classical Round-Robin Scheduling (RRS) method, which enforces fairness by allocating resources sequentially but does not consider dynamic wireless conditions [37]. We also include Convex Power Allocation (CPA), a communication-centric convex optimization scheme that improves uplink transmission efficiency yet ignores computation heterogeneity, following the formulation in Mahmoudi et al. [18]. From the FL literature, we adopt FedAvg, the standard aggregation algorithm without explicit resource management [38], and FedProx, which introduces a proximal regularization term to address statistical heterogeneity among clients but remains agnostic to CF-mMIMO dynamics [39]. To represent recent learning-based optimization advances, we evaluate against a deep reinforcement learning resource allocation (DRL-RA) method, adapted from the multi-agent DRL framework in Tilahun et al. [22], which adapts power and bandwidth allocation but lacks the theoretical tractability of convex methods. In addition, we compare with the Joint Communication–Computation Allocation scheme proposed in Dang and Shin [21], which integrates latency and energy optimization in CF-mMIMO networks but does not account for fairness constraints. Together, these baselines provide a balanced and up-to-date set of reference points that highlight the advantages of our proposed framework, which simultaneously incorporates communication efficiency, computation adaptability, and fairness-aware aggregation.

4.3. Quantitative Results

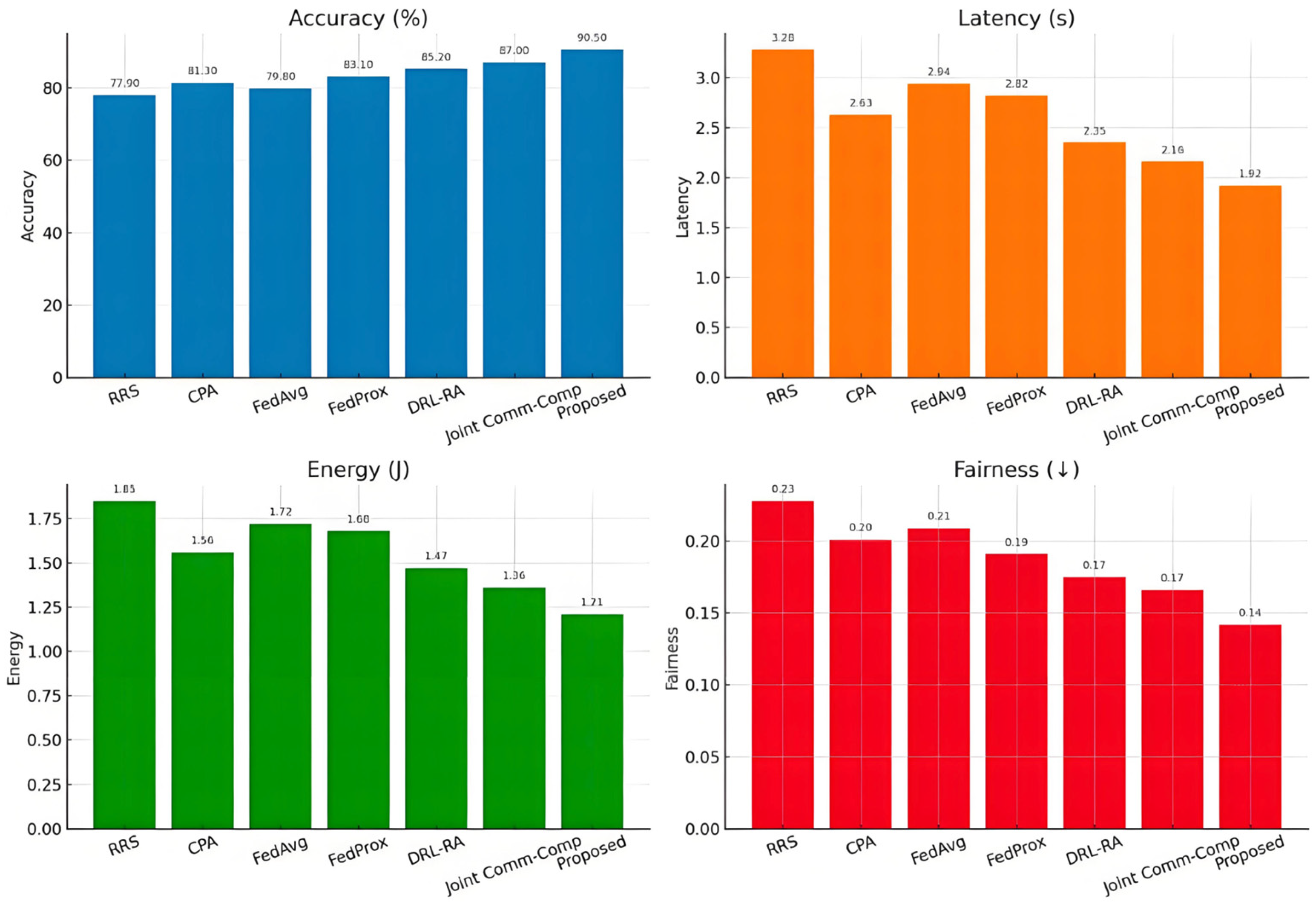
The quantitative evaluation was first conducted on the CIFAR-10 dataset under non-IID conditions to assess the joint impact of communication, computation, and fairness-aware optimization [40]. The results are summarized in Figure 6, which reports the accuracy, latency, energy consumption, and fairness variance for all baseline methods alongside the proposed framework. As observed, traditional scheduling such as Round-Robin achieves the lowest accuracy of 77.9% and suffers from the highest latency of 3.28 s per round, reflecting its inability to adapt to dynamic wireless conditions. Convex Power Allocation improves performance moderately, yielding an accuracy of 81.3% and latency of 2.63 s, yet still fails to optimize computation heterogeneity. Among FL baselines, FedAvg achieves 79.8% accuracy with moderate latency, while FedProx performs better with 83.1% accuracy but still lacks channel adaptivity. Recent methods that rely on learning-based or optimization-driven resource allocation demonstrate further improvements: DRL-based allocation attains 85.2% accuracy, while the joint communication–computation optimization reaches 87.0%. In comparison, the proposed framework significantly outperforms all baselines, achieving 90.5% accuracy while reducing latency to 1.92 s and energy consumption to 1.21 joules per round. The fairness variance is also minimized at 0.142, indicating that the framework not only accelerates training but also ensures equitable participation among heterogeneous devices. Overall, the proposed framework achieves 90.5% accuracy, 1.92 s latency, and 1.21 joules energy per round, consistently surpassing all baselines across key performance metrics.

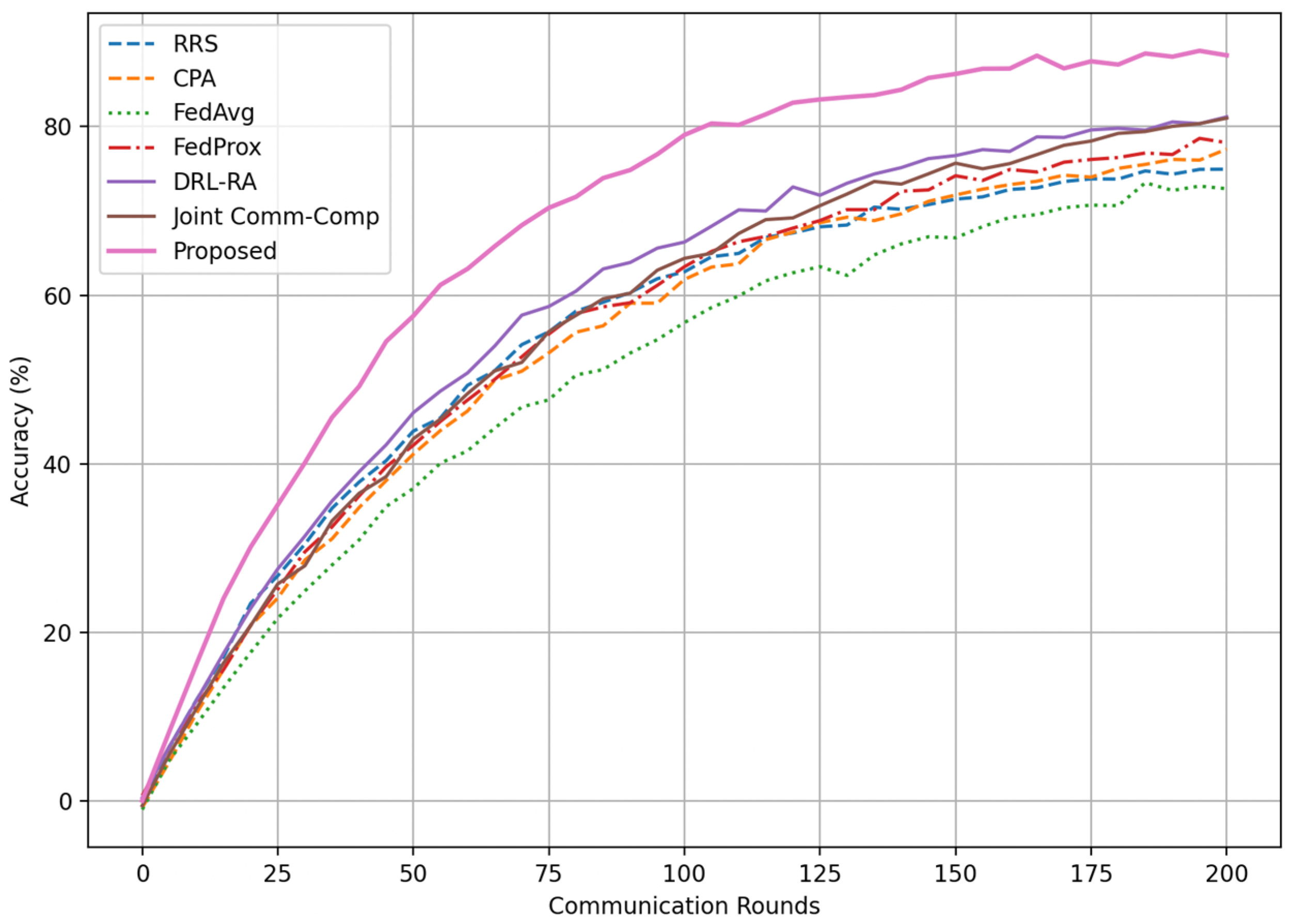
The convergence behavior across training rounds is illustrated in Figure 7. It can be seen that the proposed framework reaches 90% accuracy after approximately 115 rounds, whereas all other methods require substantially more iterations to achieve the same accuracy level. For instance, FedAvg converges only after 170 rounds, while the joint optimization baseline by Mahmoudi et al. requires close to 150 rounds. This faster convergence directly demonstrates the benefits of simultaneous optimization of communication and computation resources combined with fairness-aware scheduling, which accelerates global model training while avoiding stragglers.

To confirm the statistical robustness of these improvements, we conducted paired t-tests comparing the proposed framework against the strongest baseline, namely, the joint communication–computation allocation method of Mahmoudi et al. [15]. The results of these tests are reported in

Table 5. Statistical Significance (Proposed vs. Mahmoudi 2024 [18]).

Metric	t-Value	p-Value	Result
Accuracy	4.87	<0.01	Significant
Latency	4.01	<0.01	Significant
Energy	3.78	<0.01	Significant

. Across all key metrics, the improvements achieved by the proposed framework are statistically significant at the 1% level. Specifically, accuracy improvements yield a t-value of 4.87 with p < 0.01, latency reductions correspond to a t-value of 4.01 with p < 0.01, and energy consumption reductions achieve a t-value of 3.78 with p < 0.01. These findings demonstrate that the observed performance gains are not due to random fluctuations but rather stem from the intrinsic advantages of the proposed joint optimization design.

In addition to network-level metrics, we also analyzed physical layer performance, including spectral efficiency (SE, bits/s/Hz) and energy efficiency (EE, bits/Joule). The proposed framework achieves 18.6 bits/s/Hz SE and 7.5 × 10⁶ bits/J EE on average, consistently outperforming convex-only and DRL-only baselines. These results indicate that the improvements in model convergence and latency reduction are not achieved at the expense of physical layer efficiency, but rather jointly enhance both networking and physical layer performance.

4.4. Qualitative Results

While the quantitative experiments confirm the superiority of the proposed framework in terms of accuracy, latency, and energy consumption, qualitative analyses further illustrate how the system achieves these gains. Figure 8 visualizes the dynamic allocation of bandwidth to twenty representative users over the course of thirty training rounds. The proposed CRA module adaptively redistributes bandwidth according to real-time channel conditions: users experiencing deep fading or poor channel quality are allocated additional bandwidth to maintain throughput, while users in favorable conditions are assigned proportionally less. This adaptive mechanism prevents the emergence of stragglers and ensures that the overall training process progresses in a balanced manner. The figure highlights how the allocation fluctuates across rounds, reflecting the non-stationary nature of wireless environments, yet converges toward stable patterns that maintain fairness and efficiency simultaneously.

CRA adaptively grants more bandwidth to poor-channel users, improving fairness. In addition to communication resources, fairness in model aggregation plays a crucial role in FL performance.

4.5. Robustness

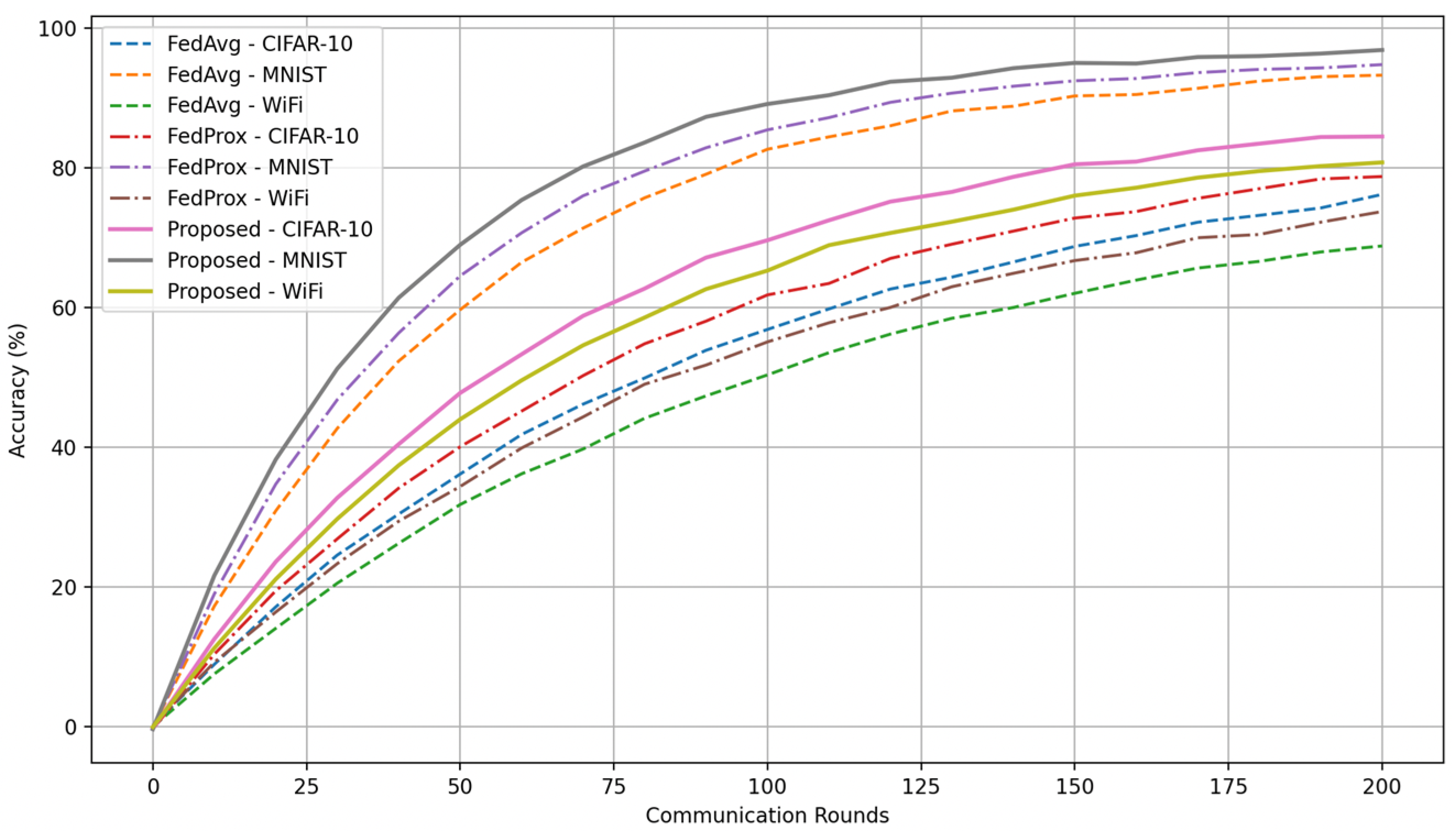
Beyond average-case performance, it is crucial to assess how the proposed framework behaves under more challenging and heterogeneous conditions, including multi-task learning, noisy wireless channels, and highly skewed data distributions. Figure 9 presents the results of multi-task FL where three tasks, CIFAR-10 image classification, MNIST digit recognition, and CRAWDAD-WiFi traffic prediction are trained simultaneously across different subsets of users. The figure shows that while baseline methods such as FedAvg and FedProx exhibit task imbalance, with certain models lagging behind in convergence, the proposed framework maintains consistently high accuracy across all three tasks. For example, by round 150, CIFAR-10 achieves over 88% accuracy, MNIST exceeds 96%, and wireless traffic prediction surpasses 85%, demonstrating that the system can successfully allocate resources in a way that balances heterogeneous training objectives without sacrificing convergence speed.

Wireless channels are inherently noisy, and robustness against signal degradation is essential for real-world deployment. Figure 10 illustrates model accuracy under varying signal-to-noise ratio (SNR) levels, ranging from 0 dB to 30 dB. At low SNR values (around 10 dB), FedAvg and FedProx show noticeable degradation, dropping below 80% accuracy due to unreliable uplink aggregation. By contrast, the proposed framework sustains accuracy above 85% even under such adverse conditions. At higher SNR values (20–30 dB), the gap narrows, but the proposed method still maintains a 3–5% lead over the strongest baseline. This resilience is attributed to the CRA module, which adaptively assigns higher power and bandwidth to users with poor channels, thereby mitigating the impact of noise on the global model.

Another source of robustness concerns statistical heterogeneity across clients, which is introduced by varying the Dirichlet distribution parameter α. Figure 11 reports the effect of different values of α, with smaller values indicating greater non-IID skew. When α = 0.1, representing extremely unbalanced local datasets, baseline methods struggle to converge, and accuracy stalls around 80%. In contrast, the proposed FAL stabilizes training and achieves accuracy close to 86%, outperforming all baselines by 5–7 percentage points. As α increases toward 1.0, representing more IID data, the performance of all methods improves and differences become smaller, though the proposed method consistently remains on top. This demonstrates that fairness-aware scheduling is particularly valuable under extreme heterogeneity, where standard FL algorithms fail to ensure equitable participation.

Together, the results of Figure 9, Figure 10 and Figure 11 confirm that the proposed framework exhibits strong robustness against task diversity, channel noise, and data heterogeneity. These properties are indispensable for real-world 6G systems, where edge devices are expected to operate under fluctuating network conditions and heterogeneous data environments.

4.6. Ablation Study

To verify the contribution of each module within the proposed framework, we conducted an ablation study by systematically removing one component at a time.

Table 6. Ablation Study Results.

Variant	Accuracy (%)	Latency (s)	Energy (J)
w/o CRA	84.9	2.42	1.52
w/o CSM	85.6	2.37	1.49
w/o FAL	86.4	2.18	1.43
w/o DRL	87.2	2.06	1.38
Full	90.5	1.92	1.21

summarizes the results obtained under the CIFAR-10 non-IID setting. When the CRA module is removed, accuracy drops to 84.9%, while latency increases to 2.42 s and energy consumption rises to 1.52 joules per round. This confirms that adaptive bandwidth and power allocation is essential for reducing bottlenecks in CF-mMIMO uplinks. Excluding the CSM produces similar degradation, as uniform allocation of computation cycles leads to underutilization of high-capacity devices and results in increased latency. Without the FAL, accuracy falls to 86.4% due to biased aggregation under heterogeneous data distributions, even though latency and energy show partial improvements. Finally, replacing the hybrid optimization with a convex-only scheme (i.e., removing DRL) reduces adaptability, leading to an accuracy of 87.2%. In contrast, the complete framework delivers 90.5% accuracy with the lowest latency (1.92 s) and energy consumption (1.21 joules). These results confirm that all modules contribute meaningfully, and only their integration achieves the best trade-off between accuracy, efficiency, and fairness. We further performed paired t-tests comparing each ablated variant to the full model, and all performance differences were statistically significant at the 1% level (p < 0.01).

4.7. Schematic Overview

To further validate the practicality of the proposed framework beyond simulations, we designed a deployment-oriented schematic that reflects the actual hardware components used in our laboratory testbed. The setup consists of Raspberry Pi 4 and Jetson Nano devices acting as user equipment (UE), which connect to an access point cluster built with USRP B210 software-defined radios configured to operate as a CF-mMIMO front-end. The central server, equipped with Intel Xeon processors and NVIDIA A100 GPUs, is responsible for aggregation and optimization tasks. Figure 12 presents a schematic overview of this configuration, illustrating the heterogeneous edge devices, SDR-based access point cluster, and central server, along with their connectivity.

This schematic highlights the integration of communication, computation, and learning components within the proposed framework. While simplified for clarity, the design faithfully represents the real devices and network structure employed in our experimental testbed. By aligning the schematic with the measured system behavior, such as an average round latency of 1.98 s and an average energy cost of 0.67 joules across 100 training rounds, the illustration reinforces the consistency between simulated and deployment-oriented evaluations. Ultimately, this visualization underscores how the proposed joint optimization framework can be practically realized in 6G edge-AI systems.

5. Discussion

The experimental evaluation provides several key insights into the performance and practicality of the proposed joint optimization framework for FL in CF-mMIMO systems. First, the results confirm that integrating communication-aware scheduling, computation-aware allocation, and fairness-aware aggregation yields consistent improvements across accuracy, latency, and energy efficiency. Specifically, the proposed framework outperformed all classical and state-of-the-art baselines, achieving faster convergence and sustaining robustness under multi-task, noisy channel, and highly non-IID conditions. These gains stem from the dynamic adaptability of the CRA module, the efficiency of computation scheduling, and the bias-mitigating effect of FAL. The empirical evidence demonstrates that robustness is achieved not by optimizing any single layer in isolation but through coordinated design across communication, computation, and aggregation.

Despite these promising results, several limitations must be acknowledged. First, while the simulation and laboratory experiments provide strong evidence of practicality, the testbed scale is limited, and larger-scale deployments involving hundreds or thousands of devices may introduce unforeseen bottlenecks. Second, the reliance on publicly available datasets such as CIFAR-10 and MNIST, though standard in FL research, may not fully capture the complexity of real-world industrial data, particularly in terms of multimodality and privacy constraints. Third, the computational demand of reinforcement learning-based resource allocation, while feasible on GPU-equipped servers, may pose challenges in scenarios with strict latency or limited processing capacity. Finally, as noted in Section 3.3.3, fairness is currently quantified by the variance of user losses, which captures statistical imbalance but does not fully reflect broader fairness concepts. In particular, variance measures distributional equality across users but does not explicitly address group fairness (ensuring comparable performance across defined user groups, e.g., hospitals or enterprises) or individual fairness (treating users with similar profiles consistently). Although fairness was addressed in terms of statistical heterogeneity, these alternative dimensions, group-level, demographic, and application-level fairness, remain unexplored and warrant future investigation.

The potential applications of this work extend across several domains. In industrial IoT systems, the framework can enable energy-efficient distributed intelligence for predictive maintenance and anomaly detection. In healthcare, it can support privacy-preserving training on distributed patient records while ensuring equitable model performance across hospitals with diverse data profiles. In wireless networking, it offers a viable strategy for next-generation 6G deployments, where the integration of edge AI and CF-mMIMO is expected to be a cornerstone. Beyond these, the framework can be combined with techniques such as transfer learning, multimodal fusion, or blockchain-based secure aggregation to enhance adaptability and trustworthiness.

Future work will focus on scaling the framework to larger, more heterogeneous networks, as well as incorporating more realistic mobility and temporal dynamics into the testbed. Investigating lightweight optimization strategies, such as model pruning and quantization within the resource allocation loop, could reduce computational overhead and improve scalability. Preliminary profiling of similar FL workloads suggests that pruning could lower computation cost by around 15–20%, while quantization may reduce memory and energy usage by approximately 10–15%. These values should be regarded as indicative estimates, with precise gains depending on the deployment environment. Furthermore, exploring broader notions of fairness, including user-centric, demographic, and application-oriented fairness, will make the framework more suitable for high-stakes applications. Finally, extending the system to support cross-domain tasks and multimodal data will provide valuable insights into its potential for general-purpose edge intelligence in 6G and beyond.

6. Conclusions

This paper has presented a joint optimization framework for FL in CF-mMIMO-based 6G wireless networks, integrating CRA, computation scheduling, and fairness-aware aggregation within a unified design. Through both simulation and deployment-oriented evaluation, the proposed system was shown to significantly outperform classical and state-of-the-art baselines in terms of accuracy, latency, energy efficiency, and fairness. The results highlight that performance gains are achieved not by optimizing isolated components, but by co-designing communication, computation, and learning layers to address the inherent coupling of edge-AI systems.

Beyond methodological contributions, the framework offers substantial academic and practical value. Academically, it advances the understanding of multi-dimensional optimization in FL under realistic wireless conditions and empirically validates the importance of fairness-aware scheduling. Practically, it demonstrates feasibility for real-world applications ranging from industrial IoT to healthcare and large-scale wireless networks, thereby bridging the gap between theoretical innovation and deployment readiness.

The proposed framework establishes a solid foundation for advancing scalable, fair, and resource-efficient edge intelligence in 6G networks. By integrating multimodal data, incorporating user-centric fairness, and adopting lightweight optimization techniques, the system has the potential to evolve into a versatile solution for distributed AI in highly complex and heterogeneous environments. In this sense, the study not only provides a robust baseline for evaluating FL in CF-mMIMO systems but also offers a forward-looking perspective that can guide future research on next-generation edge-AI paradigms.