TimeWeaver: Orchestrating Narrative Order via Temporal Mixture-of-Experts Integrated Event–Order Bidirectional Pretraining and Multi-Granular Reward Reinforcement Learning
Abstract
1. Introduction
- We present a novel narrative-order-aware framework, TimeWeaver, for story generation, which proposes an event–order bidirectional pretrained model integrated with temporal mixture-of-experts to enhance the understanding of event temporal order and mitigate the imbalanced narrative order distribution bias.
- In TimeWeaver, an event sequence narrative-order-aware model is pretrained with bidirectional reasoning between event and order to encode event temporal orders and event correlations, where the temporal mixture-of-experts routes events with various narrative orders to corresponding experts, facilitating each type of expert grasping distinct orders of narrative generation.
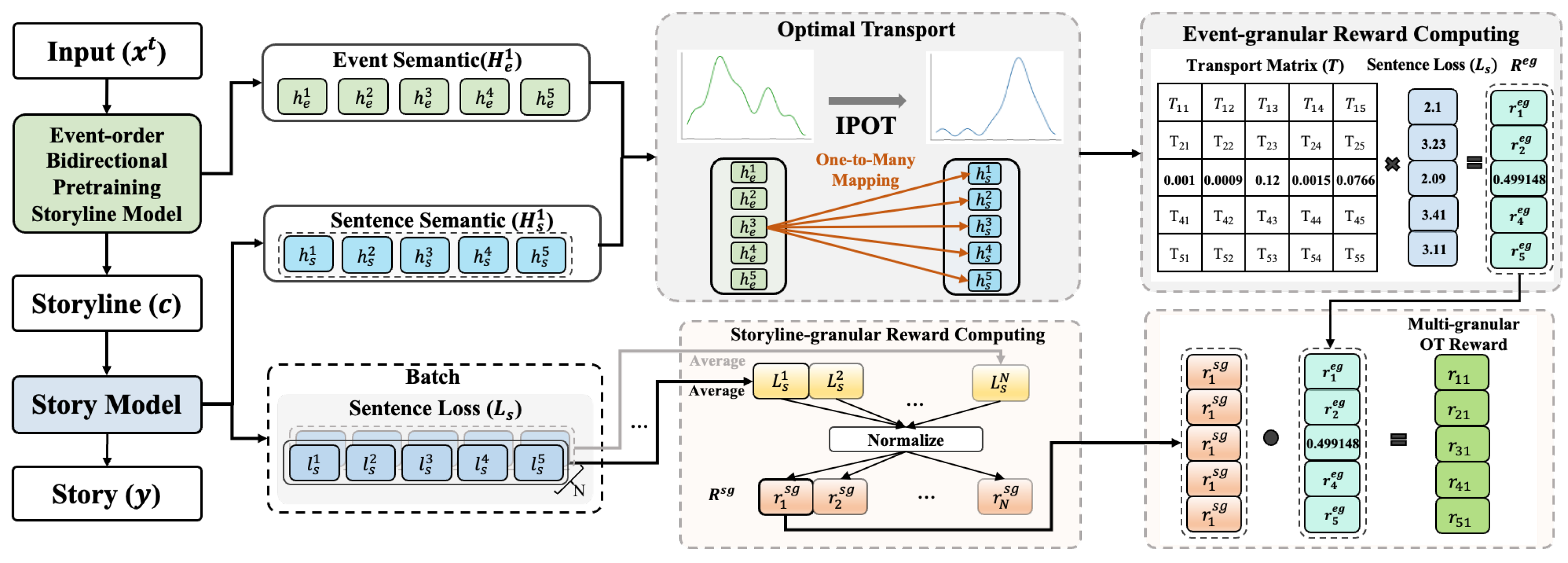
- We design a reinforcement learning algorithm with the innovative multi-granular OT reward to further improve the generated event quality at the fine-tuning stage. The multi-granular reward effectively measures the quality of generated events based on the mappings captured by OT.
- Extensive automatic and manual experiments validate the effectiveness of our framework in orchestrating diverse narrative orders during story generation.
2. Related Work
2.1. Story Generation
2.2. Optimal Transport
2.3. Event-Centric Pretraining
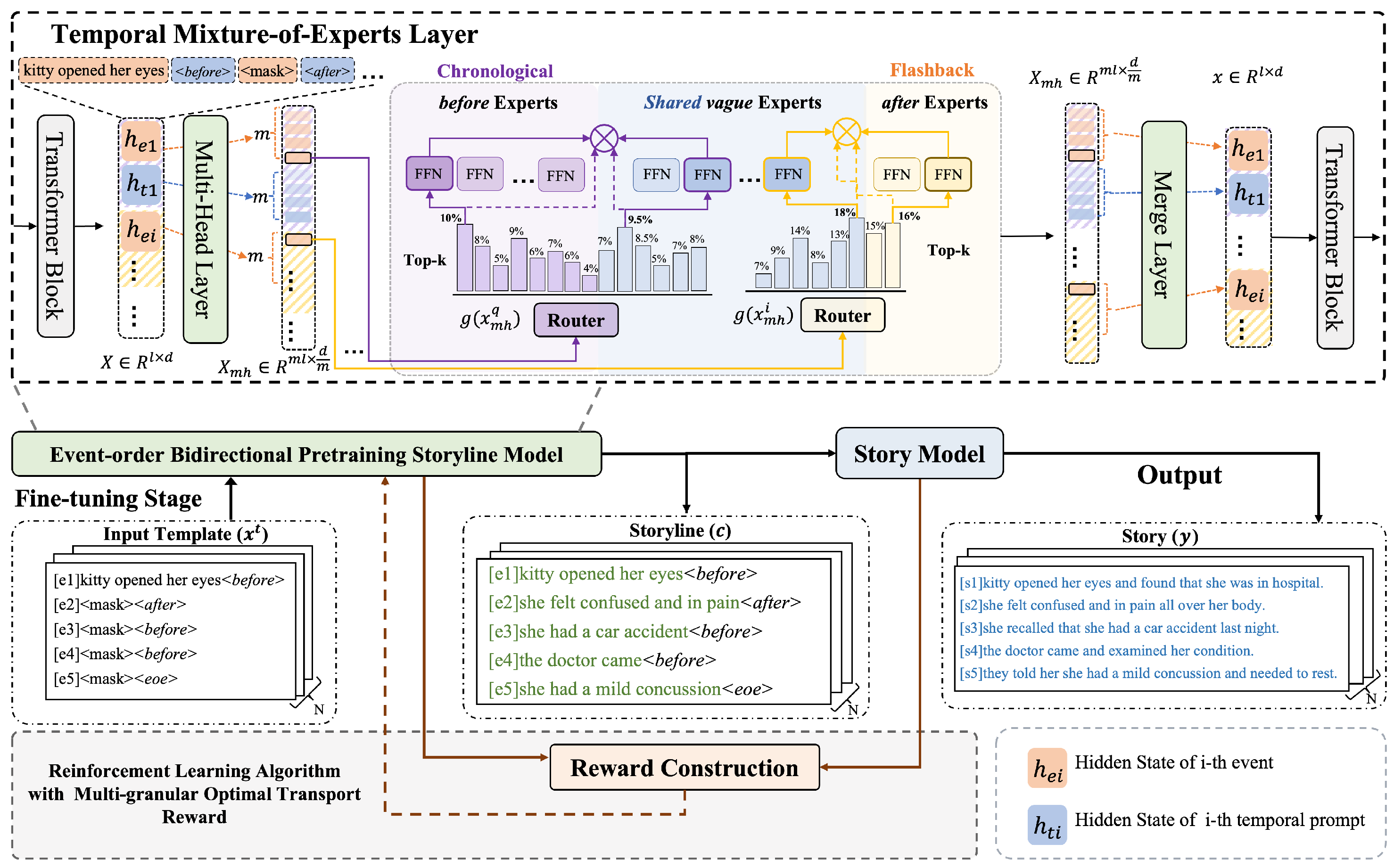
3. Method
3.1. Overview and Storyline Design
3.2. Temporal Mixture-of-Experts
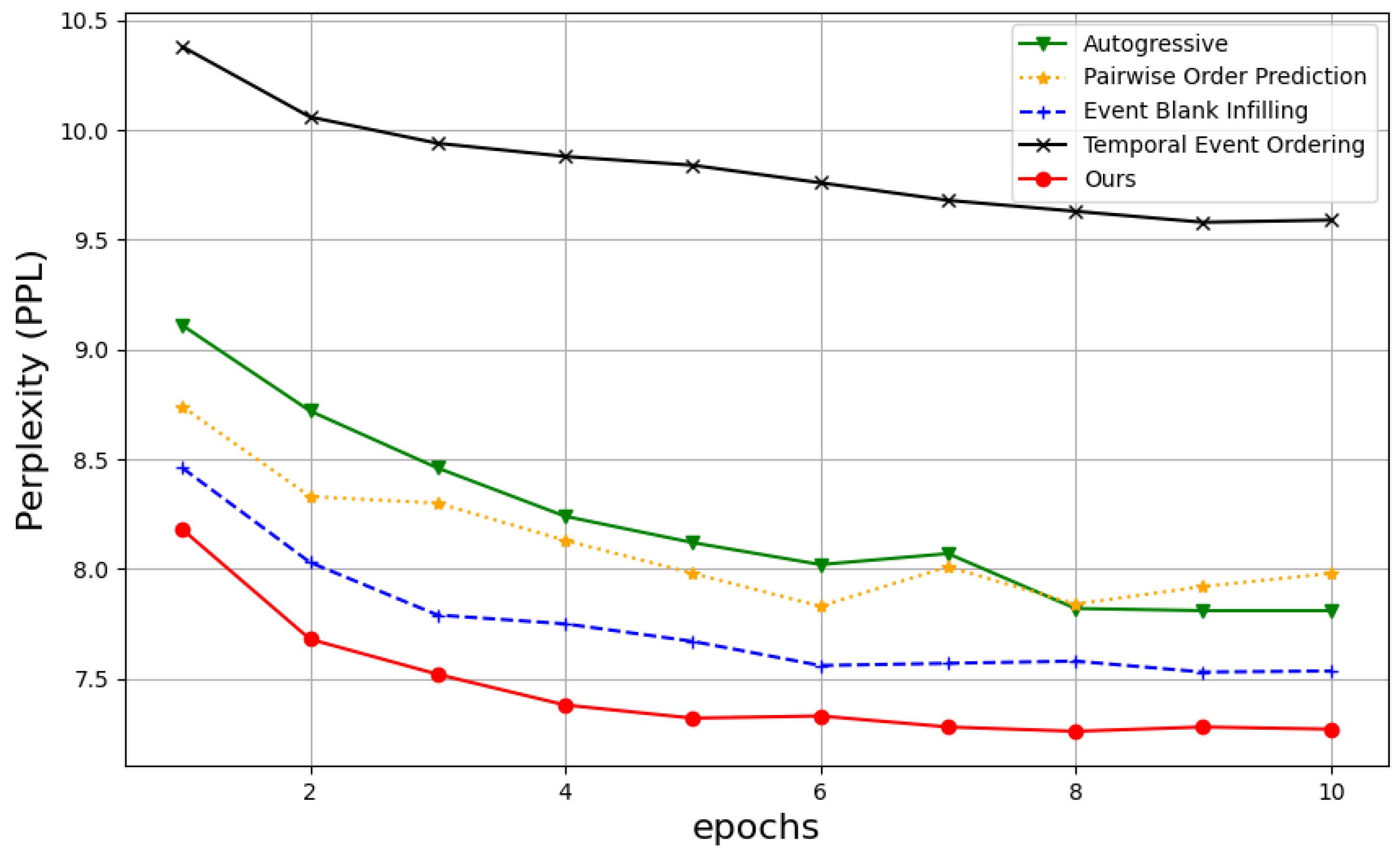
3.3. Event–Order Bidirectional Pretraining
3.4. Reinforcement Learning Algorithm with Multi-Granular Optimal Transport Reward
| Algorithm 1: Pseudo-code For training and optimization |
 |
4. Experiments
4.1. Datasets
4.2. Baseline Models
- BART [30]: It receives the input template and directly generates the story without the intermediate storyline generation and temporal prompt.
- BART-PLANNING-E [30]: It regards the event as a mask unit in the structured storyline design. The rest remains unchanged with the baseline BART-PLANNING-A.
- FLASHBACK-VANILLA [5]: Based on the baseline BART-PLANNING-A, it introduces the temporal prompt in the structured storyline design.
- BPOT-VANILLA [42]: Based on the baseline BART-PLANNING-E, it introduces the temporal prompt in the structured storyline design.
- TEMPORALBART [8]: It adopts the temporal event pretraining to mine the event temporal knowledge. We utilize the pretrained weights to initialize the storyline model of baseline BPOT-VANILLA.
- CONTENT-PLANNING [39]: Based on the baseline BART-PLANNING-A, it additionally trains some classifiers to refine the storyline on the WritingPrompts.
- FLASHBACK [5]: Based on the baseline BPOT-VANILLA, it adopts the autoregressive mask strategy [40] to pretrain the storyline model with the large-scale Book corpus [43], which includes 74 million sentences of 10k books. It also adopts the reinforcement learning algorithm to realize the joint optimization of the storyline and story model.
- ONE-SHOT-LLMs [44]: LLMs have shown powerful capability in natural language generation. We select the mainstream open-source LLMs (i.e., Qwen2.5-7b [44], Llama3-8b [45]) to generate the story under the one-shot settings. The specific prompt design for LLMs is shown in Table 1. The generated stories are utilized in manual evaluation and case studies.
4.3. Evaluation Metrics
Implementation Details
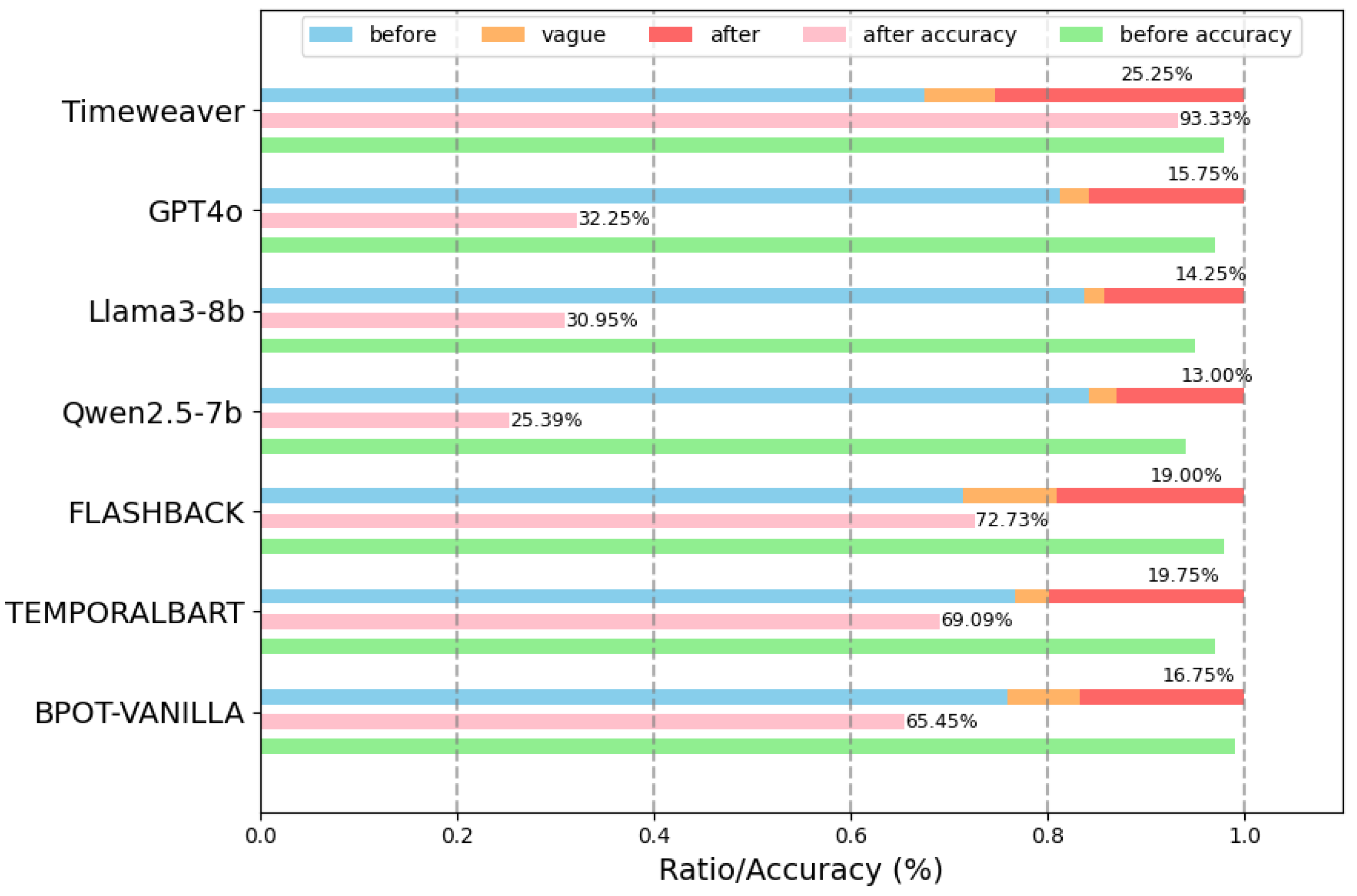
4.4. Experimental Results
4.5. Ablation Study
4.6. Case Study
5. Conclusions and Future Works
6. Limitations
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AIGC | Artificial Intelligence-Generated Content |
| NLP | Natural Language Processing |
| OT | Optimal Transport |
| PLMs | Pretrained Language Models |
| SRL | Semantic Role Labeling |
| MoE | Mixture-of-Experts |
| FFN | Feed-Forward Neural |
| NOD | Narrative Order Diversity |
| NOA | Narrative Order Accuracy |
| EGNR | Event-Granular Naive Reward |
| EGOTR | Event-Granular Optimal Transport Reward |
| SGR | Storyline-Granular Reward |
References
- Martin, L.J.; Ammanabrolu, P.; Wang, X.; Hancock, W.; Singh, S.; Harrison, B.; Riedl, M.O. Event Representations for Automated Story Generation with Deep Neural Nets; Association for the Advancement of Artificial Intelligence (AAAI): Menlo Park, CA, USA, 2018; Volume 32. [Google Scholar]
- Xu, J.; Ren, X.; Zhang, Y.; Zeng, Q.; Cai, X.; Sun, X. A Skeleton-Based Model for Promoting Coherence Among Sentences in Narrative Story Generation. In Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing, Brussels, Belgium, 31 October–4 November 2018; pp. 4306–4315. [Google Scholar] [CrossRef]
- Yao, L.; Peng, N.; Weischedel, R.; Knight, K.; Zhao, D.; Yan, R. Plan-and-Write: Towards Better Automatic Storytelling. Proc. AAAI Conf. Artif. Intell. 2019, 33, 7378–7385. [Google Scholar] [CrossRef]
- Xu, P.; Patwary, M.; Shoeybi, M.; Puri, R.; Fung, P.; Anandkumar, A.; Catanzaro, B. MEGATRON-CNTRL: Controllable Story Generation with External Knowledge Using Large-Scale Language Models. In Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing (EMNLP), Online, 16–20 November 2020; pp. 2831–2845. [Google Scholar] [CrossRef]
- Han, R.; Chen, H.; Tian, Y.; Peng, N. Go Back in Time: Generating Flashbacks in Stories with Event Temporal Prompts. In Proceedings of the 2022 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Seattle, WA, USA, 10–15 July 2022; pp. 1450–1470. [Google Scholar] [CrossRef]
- Mostafazadeh, N.; Chambers, N.; He, X.; Parikh, D.; Batra, D.; Vanderwende, L.; Kohli, P.; Allen, J. A Corpus and Cloze Evaluation for Deeper Understanding of Commonsense Stories. In Proceedings of the 2016 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, San Diego, CA, USA, 12–17 June 2016; pp. 839–849. [Google Scholar] [CrossRef]
- Han, R.; Ren, X.; Peng, N. ECONET: Effective Continual Pretraining of Language Models for Event Temporal Reasoning. In Proceedings of the 2021 Conference on Empirical Methods in Natural Language Processing, Online and Punta Cana, Dominican Republic, 7–11 November 2021; pp. 5367–5380. [Google Scholar] [CrossRef]
- Lin, S.T.; Chambers, N.; Durrett, G. Conditional Generation of Temporally-ordered Event Sequences. In Proceedings of the 59th Annual Meeting of the Association for Computational Linguistics and the 11th International Joint Conference on Natural Language Processing (Volume 1: Long Papers); Zong, C., Xia, F., Li, W., Navigli, R., Eds.; Association for Computational Linguistics: Stroudsburg, PA, USA, 2021; pp. 7142–7157. [Google Scholar] [CrossRef]
- Zhou, B.; Chen, Y.; Liu, K.; Zhao, J.; Xu, J.; Jiang, X.; Li, Q. Generating Temporally-ordered Event Sequences via Event Optimal Transport. In Proceedings of the 29th International Conference on Computational Linguistics, Gyeongju, Republic of Korea, 12–17 October 2022; pp. 1875–1884. [Google Scholar]
- Yuan, C.; Xie, Q.; Ananiadou, S. Temporal relation extraction with contrastive prototypical sampling. Knowl.-Based Syst. 2024, 286, 111410. [Google Scholar] [CrossRef]
- Han, P.; Zhou, S.; Yu, J.; Xu, Z.; Chen, L.; Shang, S. Personalized Re-ranking for Recommendation with Mask Pretraining. Data Sci. Eng. 2023, 8, 357–367. [Google Scholar] [CrossRef]
- Babhulgaonkar, A.R.; Bharad, S.V. Statistical machine translation. In Proceedings of the 2017 1st International Conference on Intelligent Systems and Information Management (ICISIM), Aurangabad, India, 5–6 October 2017; pp. 62–67. [Google Scholar] [CrossRef]
- Fan, A.; Lewis, M.; Dauphin, Y. Hierarchical Neural Story Generation. In Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers); Gurevych, I., Miyao, Y., Eds.; Association for Computational Linguistics: Stroudsburg, PA, USA, 2018; pp. 889–898. [Google Scholar] [CrossRef]
- Fan, A.; Lewis, M.; Dauphin, Y. Strategies for Structuring Story Generation. In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, Florence, Italy, 28 July–2 August 2019; pp. 2650–2660. [Google Scholar] [CrossRef]
- Chen, G.; Liu, Y.; Luan, H.; Zhang, M.; Liu, Q.; Sun, M. Learning to Generate Explainable Plots for Neural Story Generation. IEEE/ACM Trans. Audio Speech Lang. Proc. 2020, 29, 585–593. [Google Scholar] [CrossRef]
- Tan, B.; Yang, Z.; Al-Shedivat, M.; Xing, E.; Hu, Z. Progressive Generation of Long Text with Pretrained Language Models. In Proceedings of the 2021 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Online, 6–11 June 2021; pp. 4313–4324. [Google Scholar] [CrossRef]
- Kong, X.; Huang, J.; Tung, Z.; Guan, J.; Huang, M. Stylized Story Generation with Style-Guided Planning. In Proceedings of the Findings of the Association for Computational Linguistics: ACL-IJCNLP 2021, Online, 1–6 August 2021; pp. 2430–2436. [Google Scholar] [CrossRef]
- Xie, Y.; Hu, Y.; Li, Y.; Bi, G.; Xing, L.; Peng, W. Psychology-guided Controllable Story Generation. In Proceedings of the 29th International Conference on Computational Linguistics, Gyeongju, Republic of Korea, 12–17 October 2022; pp. 6480–6492. [Google Scholar]
- Feng, Y.; Song, M.; Wang, J.; Chen, Z.; Bi, G.; Huang, M.; Jing, L.; Yu, J. SS-GEN: A Social Story Generation Framework with Large Language Models. Proc. AAAI Conf. Artif. Intell. 2025, 39, 1300–1308. [Google Scholar] [CrossRef]
- Yuan, A.; Coenen, A.; Reif, E.; Ippolito, D. Wordcraft: Story Writing with Large Language Models. In Proceedings of the 27th International Conference on Intelligent User Interfaces, New York, NY, USA, 22–25 March 2022; pp. 841–852. [Google Scholar] [CrossRef]
- Wang, X.; Chen, Z.; Wang, H.; U, L.H.; Li, Z.; Guo, W. Large Language Model Enhanced Knowledge Representation Learning: A Survey. arXiv 2024, arXiv:2407.00936. [Google Scholar] [CrossRef]
- Kantorovich, L. On a problem of Monge. J. Math. Sci. 2004, 133, 15–16. [Google Scholar] [CrossRef]
- Cuturi, M. Sinkhorn Distances: Lightspeed Computation of Optimal Transport. In Proceedings of the Advances in Neural Information Processing Systems 26: 27th Annual Conference on Neural Information Processing Systems 2013, Lake Tahoe, NV, USA, 5–8 December 2013; pp. 2292–2300. [Google Scholar]
- Xie, Y.; Wang, X.; Wang, R.; Zha, H. A Fast Proximal Point Method for Computing Exact Wasserstein Distance. In Proceedings of the 35th Uncertainty in Artificial Intelligence Conference, Tel Aviv, Israel, 22–25 July 2019; Volume 115, pp. 433–453. [Google Scholar]
- Lee, S.; Lee, D.; Jang, S.; Yu, H. Toward Interpretable Semantic Textual Similarity via Optimal Transport-based Contrastive Sentence Learning. In Proceedings of the 60th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers); Muresan, S., Nakov, P., Villavicencio, A., Eds.; Association for Computational Linguistics: Stroudsburg, PA, USA, 2022; pp. 5969–5979. [Google Scholar] [CrossRef]
- Guerreiro, N.M.; Colombo, P.; Piantanida, P.; Martins, A. Optimal Transport for Unsupervised Hallucination Detection in Neural Machine Translation. In Proceedings of the 61st Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers); Rogers, A., Boyd-Graber, J., Okazaki, N., Eds.; Association for Computational Linguistics: Stroudsburg, PA, USA, 2023; pp. 13766–13784. [Google Scholar] [CrossRef]
- Radford, A.; Narasimhan, K. Improving Language Understanding by Generative Pre-Training. OpenAI Blog 2018. Available online: https://api.semanticscholar.org/CorpusID:49313245 (accessed on 19 September 2025).
- Zhou, Y.; Geng, X.; Shen, T.; Long, G.; Jiang, D. EventBERT: A Pre-Trained Model for Event Correlation Reasoning. In Proceedings of the ACM Web Conference 2022, New York, NY, USA, 25–29 April 2022; pp. 850–859. [Google Scholar] [CrossRef]
- Gardner, M.; Grus, J.; Neumann, M.; Tafjord, O.; Dasigi, P.; Liu, N.F.; Peters, M.; Schmitz, M.; Zettlemoyer, L. AllenNLP: A Deep Semantic Natural Language Processing Platform. In Proceedings of the Workshop for NLP Open Source Software (NLP-OSS), Melbourne, Australia, 20 July 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Lewis, M.; Liu, Y.; Goyal, N.; Ghazvininejad, M.; Mohamed, A.; Levy, O.; Stoyanov, V.; Zettlemoyer, L. BART: Denoising Sequence-to-Sequence Pre-training for Natural Language Generation, Translation, and Comprehension. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, Online, 5–10 July 2020; pp. 7871–7880. [Google Scholar] [CrossRef]
- Ye, H.; Xu, D. TaskExpert: Dynamically Assembling Multi-Task Representations with Memorial Mixture-of-Experts. In Proceedings of the IEEE/CVF International Conference on Computer Vision, ICCV 2023, Paris, France, 1–6 October 2023; pp. 21771–21780. [Google Scholar] [CrossRef]
- Chen, T.; Chen, X.; Du, X.; Rashwan, A.; Yang, F.; Chen, H.; Wang, Z.; Li, Y. AdaMV-MoE: Adaptive Multi-Task Vision Mixture-of-Experts. In Proceedings of the IEEE/CVF International Conference on Computer Vision, ICCV 2023, Paris, France, 1–6 October 2023; pp. 17300–17311. [Google Scholar] [CrossRef]
- Ma, J.; Zhao, Z.; Yi, X.; Chen, J.; Hong, L.; Chi, E.H. Modeling Task Relationships in Multi-task Learning with Multi-gate Mixture-of-Experts. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, KDD 2018, London, UK, 19–23 August 2018; pp. 1930–1939. [Google Scholar] [CrossRef]
- Chen, C.; Cai, F.; Chen, W.; Zheng, J.; Zhang, X.; Luo, A. BP-MoE: Behavior Pattern-aware Mixture-of-Experts for Temporal Graph Representation Learning. Knowl. Based Syst. 2024, 299, 112056. [Google Scholar] [CrossRef]
- Wu, X.; Huang, S.; Wang, W.; Ma, S.; Dong, L.; Wei, F. Multi-Head Mixture-of-Experts. In Proceedings of the Advances in Neural Information Processing Systems 38: Annual Conference on Neural Information Processing Systems 2024, NeurIPS 2024, Vancouver, BC, Canada, 10–15 December 2024. [Google Scholar]
- Lepikhin, D.; Lee, H.; Xu, Y.; Chen, D.; Firat, O.; Huang, Y.; Krikun, M.; Shazeer, N.; Chen, Z. GShard: Scaling Giant Models with Conditional Computation and Automatic Sharding. arXiv 2020, arXiv:2006.16668. [Google Scholar] [CrossRef]
- Sutton, R.S.; McAllester, D.A.; Singh, S.; Mansour, Y. Policy Gradient Methods for Reinforcement Learning with Function Approximation. In Proceedings of the Advances in Neural Information Processing Systems 12, Denver, CO, USA, 29 November–4 December 1999; pp. 1057–1063. [Google Scholar]
- Yao, W.; Huang, R. Temporal Event Knowledge Acquisition via Identifying Narratives. In Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers); Gurevych, I., Miyao, Y., Eds.; Association for Computational Linguistics: Stroudsburg, PA, USA, 2018; pp. 537–547. [Google Scholar] [CrossRef]
- Goldfarb-Tarrant, S.; Chakrabarty, T.; Weischedel, R.; Peng, N. Content Planning for Neural Story Generation with Aristotelian Rescoring. In Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing (EMNLP), Online, 16–20 November 2020; pp. 4319–4338. [Google Scholar] [CrossRef]
- Radford, A.; Wu, J.; Child, R.; Luan, D.; Amodei, D.; Sutskever, I. Language Models are Unsupervised Multitask Learners. OpenAI Blog 2019, 1, 9. [Google Scholar]
- Zhou, X.; Sun, Z.; Li, G. DB-GPT: Large Language Model Meets Database. Data Sci. Eng. 2024, 9, 102–111. [Google Scholar] [CrossRef]
- Lu, Z.; Jin, L.; Xu, G.; Hu, L.; Liu, N.; Li, X.; Sun, X.; Zhang, Z.; Wei, K. Narrative Order Aware Story Generation via Bidirectional Pretraining Model with Optimal Transport Reward. In Findings of the Association for Computational Linguistics: EMNLP 2023; Bouamor, H., Pino, J., Bali, K., Eds.; Association for Computational Linguistics: Singapore, 2023; pp. 6274–6287. [Google Scholar] [CrossRef]
- Zhu, Y.; Kiros, R.; Zemel, R.; Salakhutdinov, R.; Urtasun, R.; Torralba, A.; Fidler, S. Aligning Books and Movies: Towards Story-Like Visual Explanations by Watching Movies and Reading Books. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 19–27. [Google Scholar] [CrossRef]
- Yang, A.; Yang, B.; Zhang, B.; Hui, B.; Zheng, B.; Yu, B.; Li, C.; Liu, D.; Huang, F.; Wei, H.; et al. Qwen2.5 Technical Report. arXiv 2024, arXiv:2412.15115. [Google Scholar] [CrossRef]
- Dubey, A.; Jauhri, A.; Pandey, A.; Kadian, A.; Al-Dahle, A.; Letman, A.; Mathur, A.; Schelten, A.; Yang, A.; Fan, A.; et al. The Llama 3 Herd of Models. arXiv 2024, arXiv:2407.21783. [Google Scholar] [CrossRef]
- Papineni, K.; Roukos, S.; Ward, T.; Zhu, W.J. BLEU: A method for automatic evaluation of machine translation. In Proceedings of the 40th Annual Meeting on Association for Computational Linguistics, Philadelphia, PA, USA, 7–12 July 2002; pp. 311–318. [Google Scholar] [CrossRef]
- Lin, C.Y. ROUGE: A Package for Automatic Evaluation of Summaries. In Proceedings of the Text Summarization Branches Out, Barcelona, Spain, 25–26 July 2004; pp. 74–81. [Google Scholar]
- Shao, Z.; Huang, M.; Wen, J.; Xu, W.; Zhu, X. Long and Diverse Text Generation with Planning-based Hierarchical Variational Model. In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP); Inui, K., Jiang, J., Ng, V., Wan, X., Eds.; Association for Computational Linguistics: Hong Kong, China, 2019; pp. 3257–3268. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.U.; Polosukhin, I. Attention is All you Need. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2017; Volume 30. [Google Scholar]
- Ning, Q.; Wu, H.; Peng, H.; Roth, D. Improving Temporal Relation Extraction with a Globally Acquired Statistical Resource. In Proceedings of the 2018 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, NAACL-HLT 2018, Volume 1 (Long Papers), New Orleans, LA, USA, 1–6 June 2018; Walker, M.A., Ji, H., Stent, A., Eds.; Association for Computational Linguistics: Stroudsburg, PA, USA, 2018; pp. 841–851. [Google Scholar] [CrossRef]





| Instruction | You are a proficient storyteller and able to orchestrate diverse narrative orders (chronological and flashback) for crafting compelling stories. |
| Task definition | The different narrative orders of story are hinted at by pairwise event temporal orders. The types of event temporal order include <before>, <after>, and <vague>. Concretely, “sentence1 <before> sentence2” indicates the event in sentence1 occurs earlier than the event in sentences, which expresses the chronological narrative order. Likewise, “sentence1 <after> sentence2” indicates the event in sentence1 occurs later than the event in sentence2, which expresses the flashback narrative order. Last,“sentence1 <vague> sentence2” indicates the event temporal order between the event in sentence1 and the event in sentence2 is arbitrary, which can be both <before> and <after>. Taking sentence1 “the police were trying to catch a neighborhood thief” and sentence2 “the thief had stolen a car” as examples, “sentence1 <after> sentence2” and “sentence2 <before> sentence1” are both reasonable, because the event “trying to catch a neighborhood” in sentence1 occurs earlier than the event “had stolen a car” in sentence2. Next, we will provide the start sentence and the specific event temporal order between pairwise sentences to hint at the narrative order, your task is to come up with a five-sentence (including the start sentence) short story no more than 48 words, which is logically coherent and conforms to the narrative order. |
| Input/Output | Input: start sentence = “nina needed blood tests done”, specific event temporal order of the story = “start sentence <before> sentence1 <after> sentence2 <before> sentence3 <before> sentence4” Output: nina needed blood tests done. she had been feeling unwell for weeks. the docter ordered it to determine the cause. when it was over, relief washed over her. the blood results came back perfectly! Input: start sentence = “a friend of mine just broke up”, specific event temporal order of the story = “start sentence <after> sentence1 <before> sentence2 <after> sentence3 <before> sentence4” Output: … |
| Models | ROCStories | WritingPrompts | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PPL↓ | B-3↑ | R-L↑ | R-2↓ | Dis↑ | PPL↓ | B-3↑ | R-L↑ | R-2↓ | Dis↑ | Tks↑ | ||
| BART [30] | 20.24 | 4.98 | 19.11 | 47.78 | 62.44 | 31.15 | 0.57 | 9.28 | 20.92 | 59.37 | 148.6 | |
| MEGATRON * [4] | - | 2.57 | 19.29 | 60.75 | 85.42 | - | - | - | - | - | - | |
| BART-PLANNING-A [30] | 26.93 | 5.02 | 19.14 | 49.98 | 60.65 | 31.04 | 0.67 | 9.43 | 23.40 | 60.27 | 160.2 | |
| BART-PLANNING-E [30] | 27.30 | 5.13 | 19.29 | 49.77 | 61.80 | 30.65 | 1.76 | 9.41 | 23.70 | 57.31 | 218.7 | |
| FLASHBACK-VANILLA [5] | 22.85 | 5.07 | 19.39 | 46.11 | 63.42 | 30.77 | 1.44 | 10.95 | 23.70 | 59.83 | 208.6 | |
| BPOT-VANILLA [42] | 25.51 | 5.08 | 19.40 | 47.68 | 62.55 | 30.71 | 1.97 | 11.34 | 25.20 | 57.89 | 248.9 | |
| TemporalBART [8] | 24.65 | 5.01 | 19.12 | 50.62 | 62.13 | 30.69 | 1.38 | 10.89 | 25.60 | 60.13 | 210.7 | |
| FLASHBACK [5] | 15.45 | 5.20 | 19.49 | 50.05 | 64.76 | 30.73 | 1.64 | 11.03 | 24.20 | 58.86 | 222.4 | |
| TimeWeaver (Ours) | 13.42 | 5.42 | 19.82 | 46.73 | 66.95 | 28.37 | 2.19 | 11.57 | 23.30 | 62.74 | 256.3 | |
| CONTENT-PLANNING [39] | - | - | - | - | - | - | 3.46 | 14.40 | - | 78.16 | 252.3 | |
| TimeWeaver-Large (Ours) | 9.72 | 5.61 | 19.97 | 45.26 | 67.73 | 26.81 | 3.41 | 13.51 | - | 64.81 | 326.3 | |
| Method | NOD↑ | NOA↑ | Coherence↑ | Overall↓ |
|---|---|---|---|---|
| BPOT-VANILLA | 0.654 | 0.903 | 2.408 | 6.35 |
| TEMPORALBART | 0.714 | 0.905 | 2.536 | 5.99 |
| FLASHBACK | 0.709 | 0.915 | 2.922 | 4.65 |
| Qwen2.5-7b | 0.549 | 0.788 | 4.182 | 3.05 |
| Llama3-8b | 0.588 | 0.748 | 4.386 | 2.73 |
| GPT4o | 0.627 | 0.803 | 4.512 | 2.30 |
| TimeWeaver | 0.819 | 0.970 | 4.242 | 2.91 |
| Method | PPL↓ | B-3↑ | R-L↑ | R-2↓ | Dis↑ |
|---|---|---|---|---|---|
| Vanilla | 25.51 | 5.08 | 19.40 | 47.68 | 62.55 |
| +MRRL | 14.52 | 5.31 | 19.67 | 48.06 | 65.21 |
| +TMoE | 13.86 | 5.36 | 19.75 | 47.23 | 66.18 |
| +EOBP | 13.42 | 5.42 | 19.82 | 46.73 | 66.95 |
| Method | NOD↑ | NOA↑ | Coherence↑ |
|---|---|---|---|
| Vanilla | 0.654 | 0.903 | 2.408 |
| +MRRL | 0.707 | 0.938 | 3.528 |
| +TMoE | 0.783 | 0.950 | 3.962 |
| +EOBP | 0.819 | 0.970 | 4.242 |
| Method | PPL↓ | B-3↑ | R-L↑ | R-2↓ | Dis↑ |
|---|---|---|---|---|---|
| EGNR | 14.26 | 5.24 | 19.56 | 47.38 | 65.28 |
| EGOTR | 13.78 | 5.38 | 19.72 | 46.92 | 66.56 |
| SGR | 13.98 | 5.32 | 19.68 | 46.86 | 66.34 |
| Ours | 13.42 | 5.42 | 19.82 | 46.73 | 66.95 |
| Input | [s1] terry was in bed sleeping. |
| prompt | <before><before><after><before> |
| Flashback | [s2] suddenly, he heard a loud crash. [s3] he jumped out of bed to see what it was. [s4] it was a car accident. [s5] terry rushed to the hospital. |
| Qwen2.5-7b | [s2] his alarm clock had just stopped ringing. [s3] he finally managed to fall asleep. [s4] when he woke up, he realized he had overslept. [s5] the day ahead seemed long and tiring. |
| GPT4o | [s2] the moonlight cast shadows on the wall. [s3] suddenly, a loud crash woke him up. [s4] he rushed downstairs to find the window shattered. [s5] realizing it was just the wind, he returned to bed. |
| TimeWeaver | [s2] suddenly, he heard a loud noise. [s3] he jumped out of bed to see what it was. [s4] it was a burglar trying to break into his house. [s5] terry called the police and reported the burglar. |
| Input | [s1] a friend of mine just broke up. |
| prompt | <after><before><after><before> |
| Flashback | [s2] she had a boyfriend who was cheating on her. [s3] i tried to talk to him, but he wouldn’t talk to me. [s4] i asked him why he cheated on me. [s5] he told me that he didn’t want to be friends with me. |
| Qwen2.5-7b | [s2] she had been noticing the distance for some time. [s3] one day, she finally told him it was over. [s4] later, I comforted her. [s5] her friends planned a night out to cheer her up. |
| GPT4o | [s2] they had been dating him for two years. [s3] They met at a concert, sparks flying instantly. [s4] Now, she finds solace in music, healing slowly. [s5] Her heart will mend. |
| Timewaver | [s2] they had been dating for a year. [s3] i asked her why. [s4] she told me that he cheated on her with another woman. [s5] i felt bad for her. |
| Input | [s1] kim had a burning sensation in her bladder. |
| prompt | <before><after><vague><before> |
| Flashback | [s2] she went to the bathroom to find out what it was. [s3] she realized she had flushed the toilet. [s4] she called the plumber. [s5] he came and fixed the toilet for her. |
| Qwen2.5-7b | [s2] she decided to see a doctor right away. [s3] the nurse took her medical history first. [s4] then, she was given a urine test to confirm the issue. [s5] relief followed when the test came back negative. |
| GPT4o | [s2] she remembered drinking too much coffee the day before. [s3] the doctor diagnosed her with a mild infection. [s4] after taking prescribed medication, she felt better. [s5] grateful for the quick recovery, she vowed to drink more water. |
| Timewaver | [s2] she went to the bathroom to see what was wrong. [s3] she realized that she had a clogged bladder. [s4] kim had to go to the emergency room. [s5] the doctor treated her and gave her some medication. |
| Input | [s1] tom was depressed. |
| prompt | <after><before><vague><before> |
| Flashback | [s2] he didn’t have much money. [s3] he decided to buy a lottery ticket. [s4] he spent a lot of money. [s5] tom won the jackpot. |
| Qwen2.5-7b | [s2] he decided to talk to a therapist. [s3] during their session, they discussed his feelings. [s4] afterwards, he felt a bit lighter. [s5] finally, he started to see small improvements in his mood. |
| GPT4o | [s2] he remembered happier times with friends. [s3] they had drifted apart over the years. [s4] seeking solace, he visited the old park bench where they once laughed. [s5] as he sat there, a sense of peace slowly returned. |
| Timewaver | [s2] he didn’t have anything to cheer him up. [s3] he decided to go to a bar. [s4] he drank a lot of beer. [s5] tom felt much better. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Z.; Jia, W.; Tian, C.; Jin, L.; Bai, Y.; Xu, G. TimeWeaver: Orchestrating Narrative Order via Temporal Mixture-of-Experts Integrated Event–Order Bidirectional Pretraining and Multi-Granular Reward Reinforcement Learning. Electronics 2025, 14, 3880. https://doi.org/10.3390/electronics14193880
Lu Z, Jia W, Tian C, Jin L, Bai Y, Xu G. TimeWeaver: Orchestrating Narrative Order via Temporal Mixture-of-Experts Integrated Event–Order Bidirectional Pretraining and Multi-Granular Reward Reinforcement Learning. Electronics. 2025; 14(19):3880. https://doi.org/10.3390/electronics14193880
Chicago/Turabian StyleLu, Zhicong, Wei Jia, Changyuan Tian, Li Jin, Yang Bai, and Guangluan Xu. 2025. "TimeWeaver: Orchestrating Narrative Order via Temporal Mixture-of-Experts Integrated Event–Order Bidirectional Pretraining and Multi-Granular Reward Reinforcement Learning" Electronics 14, no. 19: 3880. https://doi.org/10.3390/electronics14193880
APA StyleLu, Z., Jia, W., Tian, C., Jin, L., Bai, Y., & Xu, G. (2025). TimeWeaver: Orchestrating Narrative Order via Temporal Mixture-of-Experts Integrated Event–Order Bidirectional Pretraining and Multi-Granular Reward Reinforcement Learning. Electronics, 14(19), 3880. https://doi.org/10.3390/electronics14193880






