Abstract
With the widespread deployment of deep neural networks in real-world physical environments, assessing their robustness against adversarial attacks has become a central issue in AI safety. However, the existing two-dimensional adversarial methods often lack robustness in the physical world, while three-dimensional adversarial camouflage generation typically relies on high-fidelity 3D models, limiting practicality. To address these limitations, we propose CAM3D, a cross-domain 3D adversarial camouflage generation framework based on single-view image input. The framework establishes an inverse graphics network based on the Mamba architecture, integrating a hybrid non-causal state-space-duality module and a wavelet-enhanced dual-branch local perception module. This design preserves global dependency modeling while strengthening high-frequency detail representation, enabling high-precision recovery of 3D geometry and texture from a single image and providing a high-quality structural prior for subsequent adversarial camouflage optimization. On this basis, CAM3D employs a progressive three-stage optimization strategy that sequentially performs multi-view pseudo-supervised reconstruction, real-image detail refinement, and cross-domain adversarial camouflage generation, thereby systematically improving the attack effectiveness of adversarial camouflage in both the digital and physical domains. The experimental results demonstrate that CAM3D substantially reduces the detection performance of mainstream object detectors, and comparative as well as ablation studies further confirm its advantages in geometric consistency, texture fidelity, and physical transferability. Overall, CAM3D offers an effective paradigm for adversarial attack research in real-world physical settings, characterized by low data dependency and strong physical generalization.
1. Introduction
In recent years, deep neural networks have achieved remarkable success in the field of computer vision. Technologies represented by deep neural networks have been integrated into various areas of daily life, providing notable benefits to both industrial production and everyday activities [1]. However, recent research has shown that deep neural networks are susceptible to adversarial examples [2,3]. By introducing subtle and deliberately constructed perturbations into the original input, the model’s output can be significantly altered, which presents serious challenges for applications that demand strict security protection [4]. Therefore, it is of great academic importance to carry out research related to adversarial attacks [5,6].
Adversarial attacks can be classified into two-dimensional and three-dimensional domains according to the target of application. Those in the two-dimensional domain focus on images, adding carefully designed small perturbations in pixel space to produce adversarial examples that mislead the model’s inference and final decision [7,8]. Such approaches have shown remarkable success in digital-domain tasks such as image classification and object detection. However, 2D-domain adversarial attacks face inherent limitations when deployed in practical applications. The adversarial examples generated in 2D space often lack robustness under real-world conditions, where factors such as illumination variation, changes in viewpoint, and sensor noise can significantly diminish their effectiveness [9]. Moreover, the insufficient decoupling between 3D representations and 2D supervision signals often results in a notable discrepancy between optimization outcomes in the digital domain and actual physical observations. This gap severely restricts the efficacy of 2D-based attacks in real-world 3D perception systems, such as those found in autonomous driving or UAV navigation [10]. These challenges highlight the inadequacy of relying solely on 2D-level perturbations to meet the increasingly complex demands of practical applications.
To overcome this dimensional limitation, 3D-domain adversarial attacks have been proposed. These methods operate directly on 3D data by perturbing geometric structures or surface properties of target objects to interfere with model predictions, and they have demonstrated promising results in physical settings [11,12]. Nevertheless, the existing approaches in this domain often rely on high-precision 3D models to construct geometric constraints, which significantly raises the cost and complexity of data acquisition [13]. Given these constraints, it becomes especially valuable to investigate cross-domain adversarial attack methods that can generate 3D adversarial textures from 2D images. To this end, we introduce CAM3D, a cross-domain adversarial attack framework under single-view supervision. By leveraging a wavelet-enhanced Mamba network, which we call DWT-Mamba, the framework explicitly models the generation process from 2D images to 3D attributes, thereby enabling accurate perturbation of 3D object textures. This cross-domain attack not only improves the effectiveness of adversarial interference in real-world 3D perception models but also provides theoretical and methodological support for generating robust 3D perturbations from 2D visual data.
Specifically, the main contributions of this study are as follows:
- We present a cross-domain three-dimensional adversarial texture framework, CAM3D. Using only one target image, the framework restores object geometry and texture through view augmentation and inverse graphics modeling, then adopts this structured representation to optimize adversarial textures across domains. The pipeline therefore moves from two-dimensional input to physical deployment, extending adversarial attacks to low-supervision and cross-domain settings.
- We build a state-space inverse graphics network, which we call DWT-Mamba. Centered on an efficient linear Mamba decoder, it integrates a hybrid non-causal state-space block and a wavelet-enhanced dual-branch local perception unit. This design improves modeling of global structure and local high-frequency detail, providing a high-fidelity three-dimensional basis for later adversarial texture generation.
- We devise a progressive three-stage learning and adversarial optimization scheme that alleviates the inherent ambiguity of single-view reconstruction, improves cross-domain generalization, and markedly raises the transfer and robustness of the adversarial texture in both the digital domain and real physical scenes. Experiments confirm the practical deployability of the method.
The rest of this paper is organized as follows. Section 2 reviews the key methodologies and representative works in the field of adversarial attacks and discusses the development status of the Mamba architecture in vision tasks. Section 3 defines the adversarial attack problem based on single-view image input and introduces the novel three-stage cross-domain texture generation framework CAM3D, detailing the implementation of its core inverse network DWT-Mamba and its internal hybrid non-causal state-space-duality (HNC-SSD) and WD-LPM modules. Section 4 combines quantitative results and visual analysis to validate the effectiveness and physical robustness of the CAM3D framework in the digital and physical domains. Section 5 discusses the experimental results, further exploring CAM3D’s potential applications and limitations in low-data-dependency scenarios, physical robustness, and cross-domain attacks. Finally, Section 6 summarizes the paper’s main contributions and outlines directions for future work.
2. Related Work
2.1. Adversarial Attacks
In recent years, research on adversarial attacks targeting deep neural networks has gained increasing attention, gradually expanding from conventional 2D image domains to 3D data scenarios. Adversarial attacks in the 2D domain have been relatively well developed. Representative methods include the FGSM proposed by Goodfellow et al. [2], which utilizes gradient information of the model’s loss function to rapidly generate adversarial examples, revealing the vulnerability of deep models at the pixel level. Building on this, Madry et al. [14] introduced PGD, which improves attack success rates through iterative optimization of perturbations. Carlini and Wagner [15] further proposed the C&W attack, which formulates the adversarial objective as an optimization problem with carefully designed constraints and loss terms, leading to more stealthy and effective attacks. Most of these approaches rely on imperceptible perturbations applied directly in the digital domain. However, due to the lack of physical-world modeling, the effectiveness of 2D adversarial attacks is often significantly degraded under real-world conditions, where environmental noise, viewpoint variation, and sensor artifacts can easily interfere with attack performance [16,17]. To address these limitations, various strategies have been proposed to enhance the physical robustness of adversarial perturbations. One such approach is EOT, which simulates realistic environmental variations during optimization to improve attack transferability [18]. Despite these efforts, adversarial attacks in the 2D domain still face substantial challenges in generalizing across domains, particularly when confronted with more complex 3D visual tasks.
In response to the limitations of 2D adversarial methods in 3D perception tasks, adversarial attacks in the 3D domain have emerged as a growing area of research [19]. Athayle et al. [18] were among the first to demonstrate the feasibility of constructing 3D adversarial examples, which has since led to a surge of interest in attacks targeting either the geometric structures or surface textures of 3D models. Most existing 3D-domain adversarial approaches are based on mesh or point cloud representations, and they aim to directly optimize object geometry or surface texture in high-dimensional 3D space. Xiang et al. [20] proposed the first attack strategy specifically for 3D point clouds by introducing adversarial perturbations to the geometric structure. Subsequent studies have further explored this direction. For instance, Tsai et al. [21] developed a method that perturbs critical points to enhance attack efficiency, while Zeng et al. [22] proposed a strategy for mesh-based models that manipulates surface geometry to mislead the target model. More recently, full-coverage texture attacks have gained attention as a promising direction in 3D adversarial research. Representative methods such as FCA [23] and RAUCA [24] optimize global texture patterns across object surfaces to improve both the robustness and generalization of adversarial perturbations. Although these methods have demonstrated considerable success, most of them depend heavily on access to high-precision 3D models, making data acquisition costly and hindering practical deployment.
To address the limitations of the existing methods, cross-domain adversarial attacks from 2D images to 3D textures have attracted increasing attention. Huang et al. [25] proposed TT3D, which constructs 3D textured meshes from multiple 2D images and employs joint optimization in both the NeRF and mesh domains to generate adversarial examples with enhanced cross-view transferability and physical robustness. In addition, Li et al. [26] introduced Adv3D, which embeds adversarial signals into NeRF to generate consistent 3D perturbations for autonomous driving scenarios. Although both approaches perform well under multi-view and pose supervision, their effectiveness decreases significantly in single-view or low-supervision settings. Chen et al. [7] utilized diffusion priors to generate highly realistic and transferable 2D adversarial examples. However, the lack of explicit 3D geometry or physical rendering constraints results in limited robustness and consistency across views. Motivated by these challenges, this paper introduces CAM3D, a cross-domain 3D adversarial attack framework under single-view supervision. By integrating a DWT-Mamba network enhanced via discrete wavelet transform, the proposed method effectively fuses spatial- and frequency-domain information into the 3D feature extraction process. This approach provides a high-fidelity 3D foundation for subsequent adversarial texture generation and 3D attackoptimization, thereby not only ensures the naturalness and efficiency of the generated adversarial examples but also significantly improves generalization across models and viewpoints.
2.2. State-Space Models
Recent advances in state-space models (SSMs) have attracted increasing attention as alternatives to transformer architectures for sequence modeling due to their linear computational complexity and ability to capture long-range dependencies [27,28]. Models such as S4 first demonstrated the effectiveness of the HiPPO framework in efficiently modeling sequences [29]. Building upon these foundations, the Mamba method introduced selective scan mechanisms and hardware-aware optimizations, enabling SSMs to achieve transformer-level performance with significantly reduced inference cost [30]. Recently, Mamba2 further improved accuracy and efficiency through state-space duality (SSD) [31]. However, mainstream SSMs, including the Mamba series, typically impose causal constraints and favor low-frequency features, which limits their performance on two-dimensional image data requiring high-frequency detail modeling [32,33,34]. To address these issues, we propose integrating frequency-domain representations into a non-causal SSM framework to enhance high-frequency modeling, thereby enabling effective decoupling of 3D attributes from single-view images.
3. Methods
3.1. Problem Definition
The main problem investigated in this paper is how, given only a single-view image, to generate three-dimensional adversarial texture samples that possess robustness across domains so that they can effectively induce target detection models to output incorrect predictions in both the digital and physical domains. Let the input be a single-view RGB image representing the visible facet of the target object from a specific viewpoint. First, an inverse graphics network , working together with a differentiable renderer, reconstructs the target’s three-dimensional geometry and texture attributes from the input image, thereby providing a structured optimization bridge that can be deployed in physical settings for the subsequent introduction of adversarial perturbations; this process can be expressed as
where denotes the vertex set, denotes the face indices, and denotes the initial texture map.
Therefore, while keeping the geometric structure unchanged, we further optimize the texture map to obtain an adversarial texture . By applying this texture to the surface of the target’s three-dimensional geometry and performing the corresponding rendering, we generate an adversarial image sample . Given a target detection model , the adversarial image sample is fed into the model to produce an output . Assuming that the model correctly recognizes the target category on a clean image , the adversarial attack is regarded as successful if the following condition is satisfied:
3.2. Discrete Wavelet-Enhanced State-Space Inverse Graphics Architecture
3.2.1. Overall Architecture
To enhance the accuracy and reliability of 3D attribute recovery under single-view image input conditions, we propose a novel inverse graphics network architecture termed DWT-Mamba, which is augmented with wavelet transforms. This architecture adopts a typical four-stage pyramid design. The input image is first processed by an initial convolutional stem to extract shallow features, followed by four progressively downsampled stages to capture deep semantic representations. Each stage comprises a stack of DWT-Mamba blocks, with the number of blocks per stage set to [2, 4, 8, 4] and output channel dimensions of [64, 128, 256, 512], respectively. For effective multiscale feature modeling, the number of attention heads in each stage is configured as [2, 4, 8, 16], in proportion to the channel width. Overlapping convolutional layers with a stride of 2 are used for downsampling between stages to maintain spatial continuity and support efficient multiscale semantic feature extraction. The structure of the network is illustrated in Figure 1.
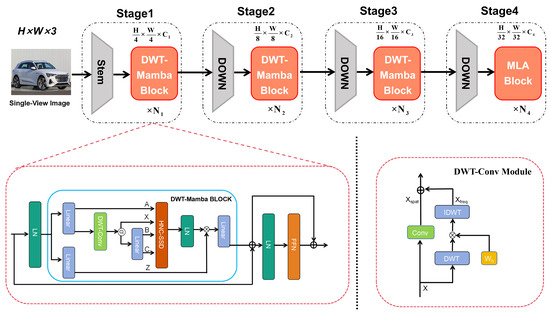
Figure 1.
Overall architecture of the proposed DWT-Mamba inverse graphics network. Given a single-view image as input, the network outputs the target object’s 3D attributes (mesh, texture, and lighting). A four-stage pyramid backbone stacks DWT-Mamba blocks for hierarchical feature representation, while the terminal MLA block enhances global semantic modeling. Insets detail the internal WD-LPM and HNC-SSD backbone of each DWT-Mamba block, as well as the fusion of frequency-domain and spatial-domain features performed in the DWT-Conv sub-module.
In the first three stages, the DWT-Mamba block serves as the core component and is repeatedly stacked. Based on the linear decoding advantages of state-space models, this block introduces a non-causal modeling mechanism to eliminate information flow constraints and implements an HNC-SSD. This design enables the joint modeling of local structures and long-range dependencies, effectively overcoming the inherent causal limitations of conventional state-space formulations. Furthermore, to address the intrinsic suppression of high-frequency texture details by the Mamba architecture, a wavelet-enhanced dual-branch local perception module (WD-LPM) is incorporated at the front end of the network. This module models high-frequency information through parallel pathways in both the frequency and spatial domains and employs a high-frequency gating mechanism for adaptive fusion, thereby improving the modeling capacity for boundary contours and fine-grained structures.
In addition, prior studies have shown that self-attention mechanisms are beneficial for modeling high-level semantic relationships [35]. Unlike the uniform distribution strategy adopted by Mamba2 [31], our architecture strategically replaces the final DWT-Mamba block with a Multi-Head Latent Attention (MLA) module. By introducing a small number of learnable latent tokens, this module enables efficient global semantic interaction while significantly reducing computational complexity compared to standard multi-head self-attention. This not only enhances the modeling of high-order feature dependencies but also complements the earlier wavelet-enhanced modules focused on local detail refinement.
Overall, the proposed DWT-Mamba network integrates the efficiency of state-space modeling with the multiscale frequency-aware capabilities of wavelet enhancement while incorporating lightweight attention mechanisms. This combination facilitates unified modeling from local structural detail to global semantic abstraction. The specific design and implementation of the HNC-SSD and WD-LPM modules are detailed in the following sections.
3.2.2. Hybrid Non-Causal State-Space Duality
To improve context modeling and local structure expression of state-space models in non-causal vision tasks, this study introduces an HNC-SSD. The module combines global non-causal modeling with local window perception and employs a hierarchical aggregation scheme for unified multiscale feature representation. It mitigates the restricted information flow and limited fine granularity found in conventional state-space models when used in non-causal vision applications.
In a conventional SSM, the state update equation can be expressed as [29]
where denotes the hidden state, denotes the input vector at time t, denotes the output, together with represent the state transition matrix and the input mapping matrix, respectively, while denotes the output mapping matrix.
From the equation, it is clear that the conventional update rule is causal, meaning that the current state must rely on the previous hidden state , which creates a strict one-direction propagation path. This sequential dependence limits information flow in both directions within the sequence and leads to insufficient use of information when processing images or other non-temporal data, presenting evident constraints in vision tasks that demand long-range dependence and global context.
To overcome the above limitation, the HNC-SSD block adopts the idea of state-space duality [31]. The state transition matrix is reduced to a scalar on each channel, and a non-recursive structure converts the state update into a prefix sum accumulation that can be executed in parallel, thus enabling non-causal global information aggregation. The corresponding state update equation is provided by
where denotes the scalar form of the simplified state transition matrix and regulates the contribution of the current token to the hidden state. For brevity, denote . Unrolling Equation (4) provides a prefix-weighted sum
This reformulation eliminates the dependence on the previous hidden state, enabling parallel computation while preserving the non-causal aggregation property.
This structure is essentially equivalent to a prefix-weighted sum and permits information from all positions in the sequence to be accumulated in a non-recursive parallel manner. Each token’s contribution no longer depends on the hidden state of the preceding token; instead, it is directly weighted by . In this way, every token becomes self-referenced, enabling information to flow in both directions within the sequence and thus eliminating the causal constraint.
Further, a two-direction scan strategy integrates the forward and backward pass results to model information in both directions, thus producing a global hidden state. To capture bidirectional context, we define the forward and backward prefix accumulations at position i:
Therefore, for each token i, its hidden state is expressed as
Here, L denotes the sequence length, i.e., the total number of tokens after flattening the spatial dimensions of the input feature map . The index j enumerates over this flattened sequence.
By omitting the bias term and simplifying, we obtain
The above expression indicates that the model at every position can access the full input feature structure. All tokens share a single global hidden state, which realizes non-causal information aggregation.
Although global non-causal modeling improves context awareness, its lack of local perception with high-resolution images can limit the capture of fine detail [36]. The HNC-SSD block therefore adopts a hierarchical aggregation scheme. In the early layers, a local window mechanism models spatial neighborhoods, a spatial decay kernel strengthens fine feature extraction, and the layered fusion keeps both local and global information while retaining non-causality. Let a local window function denote the neighborhood of token i at distance r; the local hidden state is then provided by
Here, is a learnable Gaussian kernel, and the normalization factor keeps the local weight distribution stable by ensuring it sums to one even when the window size varies.
This design lets each position aggregate only its neighborhood information, preserves the non-causal property, reduces computation, and improves sensitivity to local edges and textures. In deeper layers, the global aggregation of Equation (8) is restored, gathering features from all positions to produce the global hidden state . To combine local and global cues, HNC-SSD introduces a gated fusion coefficient and performs dynamic weighted fusion of the two hidden states, expressed as
where is a tunable factor that balances the contributions of local and global information. The layered aggregation ensures effective integration across levels, widening modeling scope while refining detail representation.
3.2.3. Wavelet-Enhanced Dual-Branch Local Perception Module
To mitigate the suppression of high-frequency information observed in Mamba-based vision tasks, this study proposes a wavelet-enhanced dual-branch local perception module, denoted as WD-LPM. By means of an explicit frequency-domain and spatial-domain two-branch design, WD-LPM preserves computational efficiency while markedly improving the model’s ability to capture high-frequency detail, thereby correcting the inherent low-frequency bias of the Mamba architecture.
Given an input image , the frequency-domain branch first applies a two-dimensional discrete wavelet transform (DWT) in the horizontal and vertical directions, decomposing X into one low-frequency subband and three high-frequency subbands . The transform adopts the classical two-dimensional orthogonal Haar basis, whose filter bank is obtained by taking the Kronecker product of a low-pass filter and a high-pass filter [37]. To ensure perfect reconstruction and strict consistency between decomposition and synthesis, both the DWT and its inverse (lDWT) adopt the same set of orthogonal Haar filters and use mirror padding at the boundaries throughout the frequency-domain pathway.
To highlight key high-frequency cues, a scheme of dynamic modulation of weights is introduced. Low-frequency semantic information is used to adjust the response strength of the high-frequency subbands. Specifically, Global Average Pooling (GAP) is applied to the low-frequency subband, and the high-frequency modulation weights are defined by
Here, denotes the Sigmoid activation function. The resulting weights are split into three channel groups and applied to the three high-frequency subbands through per-channel multiplication implemented as
where ⊙ denotes multiplication applied to each channel, and C denotes the channel count. The mechanism enables the network to enhance high-frequency representations adaptively according to low-frequency global semantics, thereby supplying dynamic compensation for high-frequency information.
Next an inverse discrete wavelet transform (IDWT) rebuilds the frequency domain from the modulated subbands, producing the enhanced frequency feature . On the spatial branch, a lightweight asymmetric depth-separable convolution extracts local spatial cues and generates an efficient spatial representation .
Finally, to balance the contributions of frequency and spatial features, a dynamic gating mechanism driven by high-frequency energy is introduced. The proportion of low-frequency energy to the total high-frequency energy is mapped to a fusion coefficient , which adaptively weights and merges the frequency and spatial paths. The procedure is formulated as
where denotes the L1 norm of the feature map and denotes a small constant that keeps the computation stable. When low-frequency energy is dominant, the mechanism preserves more spatial structural cues, whereas a pronounced high-frequency component strengthens frequency domain detail, leading to smooth fusion of the two branches.
With the explicit cooperation of wavelet domain decomposition and spatial convolution, the method compensates for the Mamba architecture’s limited attention to high-frequency detail without notable extra computation and markedly improves both high-frequency feature modeling and overall performance.
To further enhance the transparency and reproducibility of our method, we provide a unified pseudocode implementation that systematically summarizes the entire forward process of a single DWT-Mamba block. Building on the modular decomposition in Section 3.2.2 and Section 3.2.3, the pseudocode explicitly integrates the WD-LPM and HNC-SSD modules, following the exact order of frequency-domain feature modulation, energy-gated fusion, and non-causal global–local aggregation. This formal description not only bridges the theoretical derivations above with the practical realization shown in Figure 1 but also facilitates precise reproduction of the block’s computation pipeline in both research and application scenarios. The detailed procedure is presented in Algorithm 1.
| Algorithm 1: DWT-Mamba Block (Forward) | |
| 1: | Input: feature map ; orthogonal Haar filters ; ; linear map |
| ; gating scalar ; learnable positive scalars ; radii | |
| ; kernel MLP | |
| 2: | Output: non-causal representation |
| WD-LPM | |
| 3: | |
| 4: | |
| 5: | |
| 6: | |
| 7: | |
| 8: | |
| 9: | |
| HNC-SSD | |
| 10: | |
| 11: | |
| 12: | for to L do |
| 13: | |
| 14: | end for |
| 15: | |
| 16: | for to L do |
| 17: | |
| 18: | |
| 19: | |
| 20: | |
| 21: | |
| 22: | |
| 23: | end for |
| 24: | |
| 25: | return H |
3.3. Cross-Domain 3D Adversarial Texture Generation Framework
To address adversarial texture generation for three-dimensional objects in real-world target detection, this study presents a three-stage framework supervised by a single-view two-dimensional image. Using the image as guidance, the pipeline performs geometric modeling, texture refinement, and adversarial optimization in sequence, gradually producing a three-dimensional texture with strong adversarial effect and physical robustness. The workflow of the first two training stages is shown in Figure 2.
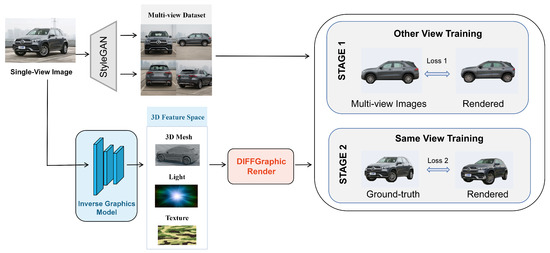
Figure 2.
Two-stage training pipeline of CAM3D from a single-view image. In stage 1, multi-view images synthesized by StyleGAN provide pseudo-supervision, jointly with differentiable rendering, to guide the inverse graphics network in recovering 3D mesh, lighting, and texture. Stage 2 uses real images under the same view as high-fidelity supervision, incorporating color consistency and visual smoothness losses to further refine texture quality and perceptual fidelity.
Stage 1. Training stage for 3D attribute recovery with multi-view pseudo-supervision. Earlier work shows that differentiable renderers can train neural networks for three-dimensional inference, but they usually require multi-view images, camera parameters, and object silhouettes to reach high accuracy [38,39,40], and collecting such data is costly. To overcome the scarcity of real three-dimensional data, this stage adopts a synthetic multi-view supervision scheme. The aim is to train the proposed inverse graphics model, the DWT-Mamba block, to predict the target object’s mesh, texture, and lighting. A StyleGAN generator [41] supplies latent three-dimensional structure encoded in its hidden space, allowing a single-view target image to be expanded into a large set of multi-view images of the same object. The inverse graphics model is updated with these multi-view signals; it decouples the input view from a randomly sampled target view and exploits geometric constraints between views to guide the learning of latent three-dimensional representations.
The overall stage 1 training pipeline (multi-view pseudo-supervision for 3D attribute recovery) is illustrated in Algorithm 2. During training, the network receives a single-view image . The DWT-Mamba block predicts the target’s three-dimensional attributes, which a differentiable renderer converts into images from other views . These renderings are compared with the new views produced by StyleGAN, and the resulting difference defines the loss to be minimized. This strategy prevents the network from fitting only one viewpoint.
| Algorithm 2: CAM3D Stage 1: Multi-View Pseudo-Supervised Reconstruction | |
| 1: | Input: single-view image x; StyleGAN generator G; inverse-graphics network F (DWT- |
| Mamba, params ); differentiable renderer R; feature extractor ; viewpoint set V; | |
| edge set E; loss weights ; learning rate ; maximum iteration | |
| 2: | Output: updated |
| 3: | Initialize: |
| 4: | for to do |
| 5: | |
| 6: | |
| 7: | |
| 8: | |
| 9: | |
| 10: | |
| 11: | |
| 12: | |
| 13: | end for |
| 14: | return |
We first define an image perceptual reconstruction loss. A pretrained feature extractor chosen as ResNet 50 computes at several feature levels m the masked difference between the synthesized target-view image and the rendered image , written as
To secure geometric accuracy, we introduce a geometric consistency loss
where and denote the predicted and true mask regions at view , respectively. A Laplacian smoothness loss further constrains the difference between unit normals of adjacent mesh vertices, expressed as
where denotes the unit normal of the i-th vertex and denotes the mesh edge set. These losses, combined with fixed weights, form the stage 1 training objective
At this stage, because the synthetic data contain view inconsistencies, the goal is to obtain reliable three-dimensional mesh predictions and a plausible texture estimate rather than a finely detailed texture. The multi-view supervision scheme limits single-view overfitting; random viewpoint shifts help the model to remain stable under unstructured noise. Although local representation errors exist across views, the random sampling makes these errors mutually uncorrelated, so statistical consistency steers the network toward an optimal geometric solution. Mathematically, this process is equivalent to a maximum-likelihood multi-hypothesis ensemble learning method.
Stage 2. Training stage for high-fidelity texture refinement from real single-view real image. After the first stage, the inverse graphics model attains stable preliminary predictions of three-dimensional attributes. Because the pseudo-supervision used earlier lacks certain details, the initial texture is coarse and shows color shift and edge noise. The objective now shifts from enforcing consistency across multiple views to fine-tuning texture detail under the real single view. The input remains the original single-view image , the network outputs the three-dimensional feature triple , and the differentiable renderer produces a rendered image from the same view. In contrast with stage one, the real input image itself serves as the high-fidelity supervision signal, thereby enhancing the detail quality of the generated texture. The stage 2 fine-tuning procedure for high-fidelity texture refinement from a real single view is illustrated in Algorithm 3.
| Algorithm 3: CAM3D Stage 2: Real-Image Detail Refinement | |
| 1: | Input: real image x at view ; trained ; renderer R; texture-domain pixel set ; |
| neighbor index set ; loss weights ; learning rate ; | |
| maximum iteration | |
| 2: | Output: updated parameters |
| 3: | Initialize: set train mode of F and load |
| 4: | for to do |
| 5: | |
| 6: | |
| 7: | |
| 8: | |
| 9: | |
| 10: | |
| 11: | |
| 12: | end for |
| 13: | return |
This stage maintains the losses from stage one and adds a color consistency loss and a visual smoothness loss to raise texture quality.
The color consistency loss ensures that the predicted texture matches the real texture in color space and is defined by
where denotes the set of all pixel indices; and are the predicted and real color values at pixel n. Optimizing this term improves color fidelity and lowers the visual gap between predicted and real textures.
The visual smoothness loss is provided by
where lists all pixel neighborhood pairs in the texture map. Minimizing this loss discourages abrupt color changes and yields a smoother texture appearance.
The overall objective for stage two is
With real-image supervision and the joint perceptual, color, and smooth constraints, the inverse graphics network preserves sound geometry and lighting while achieving finer texture detail through more accurate view alignment.
Stage 3. Adversarial texture generation stage. After completing three-dimensional reconstruction and texture recovery, this phase aims to create physically robust adversarial textures able to mislead mainstream detectors such as YOLOv5, DETR, CenterNet, and YOLOX across diverse viewpoints, lighting conditions, and paint application errors. Accordingly, this phase establishes an end-to-end differentiable optimization process built upon the pretrained inverse graphics network and the neural renderer. This stage’s pipeline is summarized in Figure 3, and the optimization steps are detailed in Algorithm 4.
| Algorithm 4: CAM3D Stage 3: Cross-Domain Adversarial Texture Optimization | |
| 1: | Input: target image x; trained network ; renderer R; detector set ; viewpoint |
| set V; lighting set ; perturbation model ; reference view ; reference | |
| light ; weights ; learning rate ; label y; box b; | |
| maximum iteration | |
| 2: | Output: physically robust adversarial texture |
| 3: | Initialize: |
| 4: | for to do |
| 5: | |
| 6: | for do |
| 7: | for do |
| 8: | |
| 9: | |
| 10: | |
| 11: | end for |
| 12: | end for |
| 13: | |
| 14: | |
| 15: | |
| 16: | |
| 17: | |
| 18: | |
| 19: | end for |
| 20: | return |
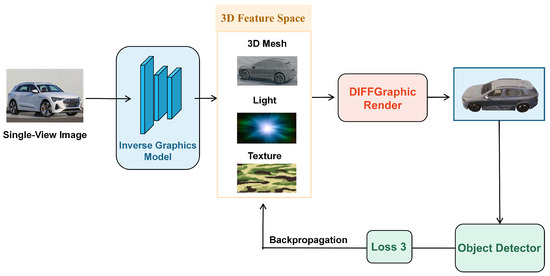
Figure 3.
End-to-end adversarial texture generation and optimization pipeline of CAM3D (stage 3). The pretrained inverse graphics model recovers the 3D mesh, lighting, and texture from a single-view image. These attributes are forwarded to a differentiable renderer to synthesize augmented views, which are evaluated by the target detector. The overall adversarial loss is computed based on detection results and back-propagated to jointly optimize texture and lighting, producing robust adversarial camouflage.
First, the inverse-graphics model takes a single-view image of the target and automatically reconstructs its 3D mesh, texture maps, and illumination parameters. A differentiable renderer then synthesizes 2D renderings under varied viewpoints, lighting, and simulated physical conditions, thereby emulating the diverse camouflage scenarios expected in practice. These renderings are fed to mainstream object detectors to evaluate the deception effect, and a joint adversarial loss is computed from their outputs. Finally, back-propagation simultaneously optimizes the texture, illumination, and related parameters, strengthening the adversarial texture against changes in viewpoint, complex lighting, and a spectrum of real-world disturbances, including color deviations from imperfect printing or spraying.
Specifically, the joint loss in this stage comprises four components, namely a basic adversarial loss, a multi-view robustness loss, an illumination robustness loss, and a paint-error constraint. We first define the basic adversarial loss , which combines the detector classification error and the bounding-box localization error to quantify how effectively the current texture deceives the detection model:
where denotes the cross-entropy loss between the predicted class and the true class y, and denotes the localization error between the predicted box and the ground-truth box b, usually measured with IoU.
At the same time, to simulate robustness degradation arising from viewpoint changes in real deployments, we introduce the multi-view robustness loss . With the current optimized three-dimensional attributes, a set of predefined viewing angles V is specified, and a differentiable renderer produces two-dimensional renderings at each angle. Every rendering is fed to the object detector, the basic adversarial loss is computed, and their mean value is adopted as the optimization target for viewpoint invariance:
This loss encourages the optimized adversarial texture to mislead the detector over diverse viewpoints, thereby strengthening the generalization of the attack.
To further accommodate illumination variations encountered in physical environments and to ensure that the generated adversarial texture preserves a consistent attack capability under different light intensities, we introduce the illumination robustness loss . With the texture and three-dimensional mesh features held fixed, the environmental illumination vector L is varied, images are rendered under diverse lighting conditions, and the mean detection loss serves as the constraint
In real-world deployment, adversarial textures undergo color shifts from painting and printing. To model these physical perturbations during training, we introduce a paint-error loss . Given the current texture , we render both the original and a color-perturbed version with controllable bounded deviations and minimize the average adversarial loss over the two renders:
The total loss for this stage combines all terms with fixed weights
By optimizing this joint objective, the proposed three-stage method yields three-dimensional adversarial textures that stay effective and robust under multiple perturbations in real environments. The approach is applicable to a wide range of targets, such as cars, aircraft, and ships, and offers promising practical value.
In order to provide a solid empirical foundation for the aforementioned methodological innovations, it is particularly critical to construct a comprehensive experimental framework that is tightly aligned with the theoretical design. Accordingly, the subsequent experimental section is organized to be highly consistent with the overall design philosophy of CAM3D, systematically covering both quantitative and qualitative validation for each key module. Specifically, to rigorously assess the improvements in geometric reconstruction accuracy and texture fidelity brought by the DWT-Mamba backbone—including its hybrid state-space modeling and wavelet enhancement modules—we first design and conduct systematic single-view 3D reconstruction experiments across diverse object categories. Building upon this, to quantitatively evaluate the cross-domain robustness and transferability of adversarial textures generated by the three-stage optimization, we further devise adversarial attack experiments that encompass both digital simulation and real-world physical scenarios, thus thoroughly reflecting the challenges encountered by the model under multi-view and diverse weather conditions in practical deployment. Finally, in order to dissect the independent contributions of each structural module and clarify the computational advantages of the state-space design, we perform targeted ablation studies and efficiency analyses. Meanwhile, we also systematically investigate the effects and synergistic contributions of different training stages and loss function combinations on the overall adversarial and reconstruction performance. Through this progressive and purpose-driven experimental design, we ensure that each methodological innovation is rigorously and scientifically mapped to empirical evidence, thereby laying a solid foundation for the subsequent analysis and theoretical discussion of experimental results.
4. Experiment
4.1. Datasets
To obtain the multi-view supervision required for training the inverse graphics model and the differentiable renderer, we train StyleGAN2 models corresponding to cars, airplanes, sofas, and ships, thus covering representative targets in both transportation and furniture domains. For cars, we directly employ the official publicly released StyleGAN2 model, pretrained on approximately 5.7 million real images from the LSUN Car dataset, which spans a wide range of vehicle types and viewpoints and can generate stable high-quality image sequences. For airplanes and sofas, we construct dedicated training sets from the LSUN Airplane and LSUN Sofa raw data, each containing a large and diverse collection of real-world images. To ensure data quality and manage the training scale, we apply a combination of automated filtering and manual inspection to perform initial data cleaning, selecting 120,000 high-quality images for each category, and then train category-specific StyleGAN2 models following the same procedure as for cars. For ships, we assemble a multi-source dataset comprising approximately 32,000 images, combining our self-built high-resolution ShipVis set with the publicly available ABOShips and Visible Ship datasets. The ship data encompass six major surface categories: engineering vessel, passenger ship, speed boat, cargo ship, ferry, and warship. With each trained StyleGAN2 model, we annotate camera parameters only once for the single-view image corresponding to each latent code, and then synthesize viewpoint-aligned image sequences by rotating a virtual camera. One set of annotations requires about one minute, following the procedure of Zhang et al. [42]. The resulting large-scale synthetic multi-view supervision supports stage 1 training of the inverse graphics network and optimization of the renderer.
4.2. Experimental Settings
To ensure the reproducibility and efficiency of the experiments, all evaluations were conducted on a computing platform equipped with an Intel® Xeon® Platinum 8488C processor (Intel Corporation, Santa Clara, CA, USA) and an NVIDIA® Tesla A100 GPU (NVIDIA Corporation, Santa Clara, CA, USA). The software environment was configured using Python 3.7, with PyTorch 1.12.0 installed via PyPI. This setup provided a stable foundation for executing all model training, inference, and evaluation procedures under high-performance computing conditions.
Meanwhile, all experiments in this work are conducted using the Adam optimizer, with a learning rate of , a batch size of 4, and a total of 100 training epochs. The loss weights are set as follows: , , and (stage 1); , , and (stage 2); , , , and (stage 3).
4.3. Evaluation Metrics
To evaluate the proposed cross-domain three-dimensional adversarial texture method with single-view input on target detection, this study adopts AP@0.5 (average precision at IoU = 0.5), attack success rate (ASR), and confidence decline rate (CDR) as the main metrics. AP@0.5 measures overall detection accuracy, ASR quantifies the rate at which originally correct detections become failures after perturbation, and CDR describes the decline rate of the detector’s average confidence under CAM3D’s attack.
AP@0.5 is a standard evaluation metric in object detection, designed to measure the average precision of predicted bounding boxes under the condition that their Intersection over Union (IoU) with the ground-truth boxes exceeds 0.5.
Specifically, for a given detector , the predicted results are evaluated by computing the precision at different recall levels , and the final score is obtained by integrating the corresponding precision–recall curve as follows:
Here, the AP@0.5 metric reflects the extent to which adversarial perturbations degrade the overall performance of the detector, serving as a key quantitative indicator for measuring the global reduction in detection accuracy across both the digital and physical domains.
The ASR is used to measure whether targets that are initially correctly identified by the detector can be successfully misled under the influence of adversarial perturbations. Consider the set of samples in the test set for which the model can correctly predict the category on clean images , with correct predictions satisfying
Here, for each sample in the set , if its corresponding adversarial image fails to be correctly detected, it is counted as a successful attack. The final attack success rate is defined as
where denotes the indicator function, which takes the value 1 if the condition inside the parentheses holds and 0 otherwise. This metric excludes samples that the model fails to detect even without perturbation, thereby accurately reflecting the extent to which adversarial textures compromise detection robustness.
The CDR is used to quantify confidence-level degradation on the same set of targets that are correctly detected on clean images. For each , let denote the detector confidence for the clean image and denote the corresponding confidence for the adversarial image. If the target is not detected in the adversarial image, set . The confidence decline rate is defined as
This formulation measures how much the average confidence under CAM3D drops relative to the corresponding clean detections. The confidence values are taken from detections matched to the ground-truth objects using the same matching protocol as in AP computation so that AP, ASR, and CDR are evaluated on a consistent basis.
4.4. Cross-Domain Attack Results
4.4.1. Comparative Analysis of 3D Reconstruction from a Single-View Image
To comprehensively evaluate the single-view 3D reconstruction performance of CAM3D and mainstream baseline methods, we employ CD, PSNR, and LPIPS as evaluation metrics, covering both geometric accuracy and texture fidelity.
Firstly, Figure 4 illustrates the three-dimensional reconstruction results achieved by the proposed CAM3D framework after the two-stage training process. To systematically evaluate the reconstruction quality, the experiment deliberately selects input samples with varying object categories and viewpoints. These include two vehicle images featuring distinct car models captured from diferent viewpoints, two ship images with markedly different structural characteristics, and additional images of one airplane model and one sofa model. For each sample, three outputs are shown: the input image, the rendered result from the same viewpoint, and the rendered result from a novel viewpoint. The same-view rendering is used to assess the model’s fidelity in recovering geometric and texture details under the input view, while the novel-view rendering evaluates the model’s capacity for inferring and generalizing the shape and texture of unseen regions.

Figure 4.
Recovery of target 3D attributes by CAM3D from a single-view image. For each sample, input image, same-view rendering, and novel-view rendering are shown. The results confirm high-fidelity recovery of geometry, texture, and lighting, as well as strong generalization to unseen viewpoints across car, watercraft, aircraft, and sofa categories.
As shown in Figure 4, the proposed model achieves high-quality 3D reconstruction on samples of vehicles, ships, aircraft, and sofas. For vehicle samples, the same-view rendering demonstrates that the model can accurately reconstruct the 3D geometry and high-frequency texture details of the input image. Clear local structures and continuous texture patterns are visible in regions such as the headlight contours, window edges, and reflective surfaces on the car body, which together enhance the realism of adversarial textures in real-world deployment. In the novel-view rendering, the reconstructed vehicles maintain strong geometric consistency, with smooth and natural transitions in previously unseen areas such as the rooftop and rear, highlighting the robustness and generalization ability of the model under viewpoint changes. For ship samples, including both large watercrafts and small speedboats, the model successfully recovers the primary structural outlines and key high-frequency texture features in the same-view rendering, including well-preserved deck hierarchies, hull-side line patterns, and illumination cues. In addition, we further conduct single-view 3D reconstruction experiments on aircraft and sofa categories, as shown in the figure. The CAM3D model achieves impressive results on targets in both transportation and sofa domains, further demonstrating the diversity and general applicability of the proposed framework.
Likewise, in novel-view renderings, the model is able to plausibly infer and reconstruct previously occluded side and frontal structures, preserving both geometric and textural coherence across the full-view field. Overall, the CAM3D framework achieves high-quality 3D reconstruction across vehicles, ships, airplanes, and sofas, thereby validating its feasibility and effectiveness as a foundation for cross-domain adversarial texture generation.
To further validate the capability of the proposed method in predicting 3D attributes from a single-view image, a qualitative comparison is conducted on selected vehicle samples between CAM3D and two advanced single-view 3D reconstruction approaches, SPAR3D [43] and LRM [44], as illustrated in Figure 5. The vehicle category is chosen as a comparison benchmark due to its extensive availability of multi-view training samples in public datasets, which ensures that the baseline methods are well-optimized for this class. In addition, vehicle surfaces are characterized by abundant high-frequency textures, reflective lighting patterns, and intricate local geometries—properties that make them particularly suitable for revealing differences in texture reconstruction quality and geometric consistency across different methods.
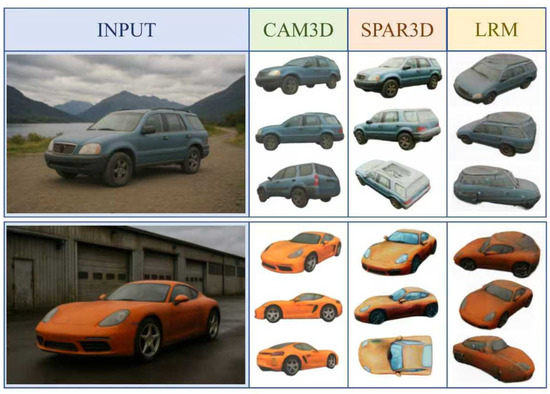
Figure 5.
Qualitative comparison of single-view 3D reconstruction methods for cars. Results show 3D attribute recovery of CAM3D, SPAR3D, and LRM under both same and novel viewpoints. CAM3D preserves geometric consistency and texture fidelity; SPAR3D exhibits view-dependent color shifts, while LRM suffers from over-smoothing and structural distortions.
The comparison shows that CAM3D attains higher geometric consistency and texture fidelity in both the reference view and novel views. It faithfully restores vehicle details and overall structure and keeps textures continuous when the viewpoint changes, a property that is essential for cross-domain adversarial texture generation. SPAR3D also reproduces the input appearance well in the reference view and yields clear and detailed body textures. However, it relies on a sparse point cloud as the intermediate representation and does not explicitly separate lighting from texture. Under novel views, it therefore fails to distinguish surface texture from view-related reflection, producing noticeable color differences and distortion between the roof and the body. The sparsity and discontinuity of the point cloud also hinder inference of geometry and texture in hidden regions when the viewpoint varies widely, leading to missing structures and broken textures. The unclosed area on the roof in Figure 5 illustrates the limited generalization of this method to unseen views.
LRM combines a transformer with an implicit neural field (NeRF) for end-to-end reconstruction and tends to output probabilistic averages for geometry and texture. This causes noticeable blur and overly smooth textures in the original view, and it fails to maintain the high-frequency features and color details of the input. In novel views, the lack of sufficient geometric constraints and texture inference for occluded regions leads to incomplete structures, degraded textures, and dim colors, which greatly reduces both view generalization and reconstruction quality.
It should also be noted that SPAR3D and LRM, while performing reasonably in general three-dimensional reconstruction, do not address consistency across views, separation of lighting, or physical deployability. By contrast, CAM3D, through stage-wise training and optimization across domains, keeps high-fidelity texture and clear geometry in the original view and maintains strong robustness and consistency in novel views, offering reliable support for adversarial textures in both the digital and physical domains.
Meanwhile, Table 1 provides a quantitative comparison of different methods on the ShapeNet dataset in terms of CD, PSNR, and LPIPS. It can be observed that CAM3D achieves the lowest CD value of 0.146, indicating the highest geometric reconstruction accuracy. At the same time, it attains the highest texture fidelity with a PSNR of 26.9 and the best perceptual similarity with an LPIPS of 0.074. These results comprehensively demonstrate the significant advantages of CAM3D over mainstream baselines in both geometric and visual quality. The experimental findings further substantiate the original design rationale of the DWT-Mamba architecture presented in the Section 3. Specifically, the HNC-SSD module, by introducing a non-causal long-range dependency mechanism, effectively suppresses the global structural relaxation and excessive texture smoothing frequently observed in baseline methods when reconstructing complex objects—a benefit directly reflected in the significant reduction in CD and the improvement of reconstruction accuracy. Meanwhile, the WD-LPM module, leveraging multiscale feature enhancement in the wavelet domain, substantially augments the network’s ability to model local high-frequency details such as edges and abrupt texture transitions, which translates into optimal performance on perceptual metrics like PSNR and LPIPS. The joint optimization of these two modules not only overcomes the traditional trade-off between detail recovery and structural consistency but also enables CAM3D to consistently deliver geometrically accurate and finely detailed 3D models across diverse categories and multi-view conditions.

Table 1.
Comparison of geometry and texture metrics across methods. Geometry metric: CD (lower is better). Texture metrics: PSNR (higher is better) and LPIPS (lower is better).
4.4.2. Comparative Evaluation of Adversarial Attack in the Digital Domain
To systematically evaluate CAM3D’s adversarial attack capability in digital simulation environments across multi-viewpoint, multi-weather, and multi-distance scenarios, this subsection adopts average precision at IoU 0.5 (AP@0.5) and attack success rate (ASR) as evaluation metrics and conducts quantitative and qualitative analyses of the attack effectiveness and robustness of the generated adversarial samples on mainstream detectors.
In the digital domain experiment, ships are chosen as the target class to test whether CAM3D can generalize to large and complex objects that lack high-precision public three-dimensional models. The trained inverse graphics network and the differentiable renderer first predict the three-dimensional geometry and texture of a ship from one view image and generate three texture sets: the original texture, which we refer to as NORMAL; a randomly perturbed texture, which we denote RANDOM; and the optimized adversarial texture, generated by CAM3D. Each texture is mapped to the ship mesh and rendered on a sea scene in the Town10HD map of the UE4 Carla simulator. Data are collected at four distances, eight weather combinations, and azimuth angles from zero to three-hundred-sixty degrees in steps of two-point-five degrees. For every texture, four-thousand-six-hundred-eight RGB images are recorded, providing a comprehensive simulation of typical deployment conditions.
Table 2 provides the detection performance (AP@0.5 and ASR) of the ship model under three texture settings, where the performance is tested on five detectors. These five detectors are divided into two categories of target detectors: anchor-based target detectors include YOLOv5, DETR, and Faster RCNN, and anchor-free target detectors include CenterNet and YOLOX. Under NORMAL, all detectors obtain AP@0.5 values between 0.78 and 0.93, showing that, without perturbation, they recognize complex ships with stable accuracy. After RANDOM, the AP@0.5 of each detector decreases only slightly, the mean drop is below 0.1, and the ASR of most of them does not exceed 0.15, except for the oldest CenterNet; random noise therefore has little impact, and the detectors remain robust to unstructured texture change. By contrast, the adversarial texture generated by CAM3D produces a marked decline: AP@0.5 falls to 0.256, 0.229, 0.319, 0.036, and 0.263 for the five detectors, almost a seventy percent reduction relative to the NORMAL case, and every ASR exceeds 0.6, far above the random-texture level. CenterNet reaches the highest ASR of 0.946, meaning that in most samples it fails to detect the ship. These results indicate that the CAM3D texture can attack mainstream detection models with considerable generality.

Table 2.
Comparison of AP and ASR for five mainstream object detectors in a digital-simulation setting, evaluated on a ship model rendered with NORMAL, RANDOM, and CAM3D textures.
Meanwhile, the above experimental results further demonstrate that the adversarial textures generated by CAM3D consistently maintain significant attack efficacy across different simulated viewpoints, illumination intensities, and environmental conditions. This phenomenon fully reflects the central role of the stage-wise optimization strategy in enhancing model generalization and stability. Specifically, the multi-view consistency loss effectively constrains the geometric alignment of adversarial textures under varying camera poses, thereby ensuring the stable transmission of key attack signals across multi-view re-renderings. The illumination robustness term, on the other hand, reinforces the persistence of perturbation features under changes in exposure, shadow, and other lighting scenarios, enabling the model to reliably interfere with detection processes even in complex simulated environments. Thanks to these mechanism designs, CAM3D exhibits not only outstanding robustness under conventional simulation variations but also consistent adversarial transferability across mainstream detection frameworks, fully validating its generality and effectiveness in practical deployment.
Figure 6 shows typical YOLOv5 ship-detection outputs under three texture conditions. With NORMAL and RANDOM, the detector still locates the ship with high confidence and places accurate bounding boxes, and neither category scores nor box positions vary noticeably. After CAM3D adversarial texture is applied, the predictions deteriorate markedly. In the first image, the ship is mistaken for the class “kite”, and the predicted box no longer aligns with the target. In the second image, two boxes appear and are misclassified as “kite” and “person”. These results demonstrate that CAM3D produces a robust three-dimensional adversarial coating that deceives mainstream detectors across complex targets and diverse environmental settings, providing a solid basis for subsequent cross-domain physical attacks.

Figure 6.
Representative ship detection results under three texture conditions in the digital domain using YOLOv5. The original texture (NORMAL) and the randomly perturbed texture (RANDOM) are both correctly classified as “ship”, while the CAM3D adversarial texture results in misclassification and bounding-box drift, demonstrating the strong adversarial effect of CAM3D.
4.4.3. Comparative Evaluation of Adversarial Attack in the Physical Domain
To further evaluate the generalization performance of the adversarial textures generated by CAM3D in real-world physical environments, this section presents physical-domain adversarial attack experiments targeting ship objects. Specifically, a scaled-down 3D-printed ship model is fabricated, and the adversarial texture generated by the CAM3D framework is printed and precisely applied to the surface of the model, completing the physical deployment. The evaluation is conducted by capturing images of the textured ship model under various real-world conditions—including different shooting distances, illumination settings, and camera parameters—and assessing detection robustness on multiple mainstream detectors (e.g., YOLOv5 and DETR) using metrics such as AP@0.5, ASR, and Confidence Drop Rate (CDR).
To enhance the diversity and representativeness of the experimental conditions, data collection is conducted in both natural and artificial water environments. During image acquisition, the camera parameters are strictly controlled as follows: image sensor (1/2-inch CMOS), resolution (12.0 megapixels, 4000 × 3000), lens (field of view: 84°, equivalent focal length: 24 mm, aperture: f/2.8, and focus range: 1 m to infinity), and ISO range (100–3200, auto mode). The camera maintains a fixed direction, while its distance from the ship model is adjustable; multi-view data is acquired by rotating the ship model in place. Specifically, an image set is captured every 15° of the model’s rotation, with 2–10 images included in each set. Each set covers shooting distances ranging from approximately 20 cm to 3 m and shooting angles from 0° (parallel to the water surface) to a 75° downward viewing angle. After that, the experiment spans three controlled weather and illumination conditions to simulate realistic deployment scenarios:
- -
- Sunny: 100,000–130,000 lux (midday and clear sky).
- -
- Cloudy: 10,000–20,000 lux (overcast and diffuse light).
- -
- Rainy: 500–2000 lux (low light and rain clouds).
To ensure experimental robustness, several artificial interference factors—including plant occlusion, covering occlusion, and camera defocus—are also introduced under each weather condition. In total, 1080 RGB images are collected for each of the NORMAL and CAM3D textures, with 432 images captured under Sunny conditions, 216 under Cloudy, and 432 under Rainy conditions for each texture.
Table 3 presents adversarial performance in the physical domain, evaluated with AP@0.5, ASR, and CDR. CDR denotes the mean drop in predicted confidence relative to the NORMAL texture. The evaluation spans three environmental conditions and five detectors. Under NORMAL, all detectors maintain high AP across weather variations, indicating robustness to natural scene changes.

Table 3.
Comparison of the ship model in the physical domain across three environments (Cloudy/Sunny/Rainy) under NORMAL vs. CAM3D textures.
With the CAM3D texture applied, degradation appears across all architectures, although the pattern differs by family. The two-stage anchor-based Faster R-CNN retains comparatively higher AP and shows lower ASR, indicating greater stability under attack, although CAM3D still induces a marked confidence decline and nontrivial ASR. Anchor-free models exhibit higher vulnerability. CenterNet, a classic anchor-free design, shows the most pronounced degradation, with ASR up to 0.909 and CDR above 92% across settings, reflecting limited adaptation to physical perturbations. YOLOX, introduced in 2021 as a newer anchor-free detector, achieves higher AP@0.5 than CenterNet under benign conditions and demonstrates stronger robustness to CAM3D. An interesting observation is that, under attack, YOLOX exhibits robustness broadly comparable to YOLOv5, whereas in clean settings it attains higher AP. This pattern reflects YOLOX’s role as a successor to YOLOv5 and suggests shared feature-extraction principles between the two.
DETR, representing the transformer-based paradigm, achieves the highest AP@0.5 without attack across all weather scenarios, highlighting the representational capacity of attention mechanisms. Under adversarial conditions, its performance declines markedly, with ASR reaching 0.737 in Sunny and CDR reaching 90.1%. These findings indicate that transformer-based detectors excel in clean environments yet remain sensitive to tailored physical perturbations.
Overall, the CAM3D adversarial texture proves effective across diverse detector architectures and environmental conditions, with particularly strong effects on anchor-free and transformer-based models, demonstrating broad generalization in realistic deployments.
Figure 7 presents typical detection outcomes. Taking the cloudy scenario as an example, under NORMAL, YOLOv5 delivers clear bounding boxes and accurate class labels. After CAM3D is applied, the detection quality of the physical samples declines markedly. In the first two images, the ship is misclassified as the categories “kite” and “bird”, respectively, while in the last sample the detector fails to recognize the ship at all and instead identifies a blurry truck that happens to appear in the background. Similarly, similar results are also observed under sunny and rainy conditions. These experimental results closely align with the findings from the digital domain, further demonstrating that CAM3D can maintain a high adversarial attack success rate under diverse weather and camera conditions in real-world environments. This stable performance is primarily attributed to the introduction of the spray error loss function during the third-stage optimization. This mechanism specifically models the attenuation of attack effectiveness caused by physical factors such as texture spraying errors and color fluctuations in practical applications. By imposing robustness constraints during the optimization phase, various degradations encountered in the physical environment are proactively addressed. As a result, the generated adversarial textures are able to effectively preserve key perturbation signals even after real-world capture and under different environmental interferences. This ensures that the physical samples can consistently reproduce the performance observed in the digital domain across a wide range of real scenarios, further highlighting the generalization capability and engineering applicability of the proposed method for practical deployment.

Figure 7.
Representative physical-world detections of ship models under NORMAL and CAM3D textures using YOLOv5 across three weather conditions. While the NORMAL texture enables accurate detection, the CAM3D adversarial texture leads to misclassification and missed detections across multiple viewpoints, demonstrating the strong adversarial effect and physical robustness of CAM3D.
In summary, the CAM3D framework establishes an end-to-end cross-domain adversarial pipeline from single-view image input to physical-world texture deployment. It substantially reduces dependence on high-precision 3D modeling data and demonstrates strong adversarial robustness and transferability in both the digital and physical domains. This provides an efficient, reliable, and low-cost technical solution for implementing adversarial attacks in the real world.
4.5. Ablation Studies
To quantitatively evaluate the contribution of each key component within the CAM3D framework, we conduct a comprehensive ablation study focusing on both the network architecture and the loss function design.
4.5.1. Ablation Study on DWT-Mamba Network Architecture
Within the CAM3D framework, we design a new Mamba network based on an SSD structure, named DWT-Mamba. To evaluate how each key module contributes to cross-domain three-dimensional reconstruction and adversarial texture generation, we conduct a detailed ablation study. The car, watercraft, aircraft, and sofa classes in the ShapeNet dataset, rich in structure and texture detail, are used for testing. Computational complexity is measured with #Param and FLOPs, structural accuracy is measured with Chamfer Distance (↓) and F-score at 0.1 (↑), while texture quality is measured with PSNR (↑) and LPIPS (↓). Each metric is averaged over many models in the class and their multi-view renderings, so the results reflect generalization across samples and viewpoints.
Table 4 summarizes the performance comparison across different ablation settings. Bold text indicates the best performance for a given metric, while underlined values denote the second-best results. Compared to the SPAR3D baseline, our method demonstrates clear advantages across all four evaluation metrics. Specifically, PSNR and LPIPS are improved by 4.7% and 12.9%, respectively, while F-score@0.1 and Chamfer Distance (CD) remain comparable. These results indicate that the proposed DWT-Mamba architecture achieves a more favorable trade-off between geometric consistency and texture fidelity. To further assess the contribution of individual components, we ablate the WD-LPM and HNC-SSD modules, replacing them with conventional structures. When WD-LPM is removed, the model exhibits notable degradation in PSNR and LPIPS, suggesting that this module significantly enhances the preservation of fine texture details. In contrast, replacing HNC-SSD with a standard Mamba-based SSM leads to marked drops in F-score@0.1 and CD, indicating that the HNC-SSD module plays a critical role in capturing complex structural details, highlighting the necessity of structure-aware feature extraction.

Table 4.
Ablation results for DWT-Mamba on the ShapeNet car, watercraft, aircraft, and sofa categories. Computational complexity metrics include parameter count #Param and FLOPs, geometry metrics include F-score@0.1 ↑ and CD ↓, while texture metrics include PSNR ↑ and LPIPS ↓. Bold values mark the best performance for each metric and underlined values the second best.
To further verify the advantage of DWT-Mamba over other classic feature extractors, we compare it with EffNet-B4 [45], Swin-T [46], MLLA-T [47], and two CAM3D model variants: one in which WD-LPM is replaced by a standard convolutional block and another in which HNC-SSD is replaced by a standard SSM. These five baselines cover convolution, self-attention, linear attention, and a conventional state-space model with similar parameter counts and computation cost. CAM3D and its variants exhibit similar parameter counts and FLOPs, maintaining moderate computational complexity relative to convolutional and attention-based baselines. Importantly, these efficiency benefits are rooted in the architectural design of DWT-Mamba rather than resource scaling. The HNC-SSD module utilizes state-space duality to realize long-range global context modeling with computational cost that grows approximately linearly with feature map size, thus substantially reducing the overhead compared to conventional quadratic-complexity self-attention mechanisms. Simultaneously, the WD-LPM module employs orthogonal wavelet-domain multiscale enhancement and lightweight dynamic gating to capture fine-grained texture details without incurring significant parameter or memory increase, as typically seen in large-kernel convolutions or dense attention layers. As demonstrated in Table 4, CAM3D achieves superior geometric and texture performance (lower CD, higher PSNR, and lower LPIPS) compared to other baselines with similar or even higher parameter and FLOP budgets. This indicates that the observed advantages are not the result of simply increasing computational resources but rather arise from more efficient and expressive feature representations enabled by the proposed modules. These findings further validate the favorable trade-off between accuracy and efficiency provided by our method, reinforcing its scalability and practical value for cross-domain adversarial texture optimization.
4.5.2. Ablation Study on Loss Components
The effectiveness of the adversarial texture is not only dependent on the quality of the 3D reconstruction but also critically hinges on the design of the loss function during the stage 3 optimization. To dissect the contribution of each loss term towards the final adversarial strength, we conduct an ablation study on the loss components. We evaluate the attack success rates (ASRs) of the adversarial textures—generated under different loss configurations—against five object detectors (YOLOv5, DETR, Faster R-CNN, CenterNet, and YOLOX) under the comprehensive digital-domain simulation settings described in Section 4.4.2, encompassing varied viewpoints, distances, and weather conditions to rigorously test robustness.
Table 5 summarizes the ablation study on the contribution of different loss components within the stage 3 adversarial optimization pipeline. The attack success rate (ASR) is reported across five mainstream object detectors. The baseline configuration using only the basic adversarial loss establishes a foundation for attack, with ASR ranging from 0.492 (YOLOv5) to 0.824 (CenterNet). Progressively incorporating the multi-view robustness loss and the illumination robustness loss leads to consistent and substantial improvements in ASR across all detectors, with gains of over 10 percentage points for several model combinations. In contrast, the spray loss contributes limited improvement to the digital-domain ASR, which aligns with its original design purpose as a physical-domain robustness regularizer. It simulates spray perturbations to improve the stability of adversarial textures in the physical world. The joint optimization with multiple regularizers () further enhances the overall ASR, highlighting the complementarity and synergistic gains among the different loss terms. This trend is consistently verified across different detectors, demonstrating the scientific and systematic nature of the loss design.

Table 5.
Ablation results on loss-component combinations for CAM3D adversarial texture optimization. The table reports ASR ↑ across five detectors (YOLOv5, DETR, Faster R-CNN, CenterNet, and YOLOX).
The results clearly demonstrate that each proposed loss term contributes uniquely to the overall adversarial strength. The multi-view loss provides the most significant boost in the digital domain, particularly for detectors like YOLOv5 and YOLOX, highlighting its crucial role in enforcing viewpoint invariance. The illumination loss shows a strong effect, especially on DETR, aligning with the expectation regarding transformer. The specialized design of is reflected in its results. Its primary objective is to improve transferability to the physical domain by building resilience against painting errors, which explains its smaller impact within the purely digital simulation. The ablation confirms that the proposed joint optimization with multiple regularizers, as configured in this paper, is essential for achieving high and robust attack success rates.
4.5.3. Ablation Study on Training Stage Combinations
To validate the effectiveness of the multi-stage training strategy in CAM3D, we conducted an ablation study on different stage combinations. As presented in Table 6, using only the first-stage multi-view pseudo-supervision (stage 1) allows for a certain degree of 3D geometry and texture recovery, but the texture fidelity remains limited, with a PSNR of 22.1 and an LPIPS of 0.136. Incorporating the real-image supervision before the pseudo-supervision (stage 2 + stage 1) improves the texture metrics, achieving a PSNR of 25.3 and reducing LPIPS to 0.093. However, the geometric consistency metrics do not show significant improvement, with an FS@0.1 of 0.732 and a CD of 0.156, indicating the critical influence of stage ordering on reconstruction quality. In contrast, the strategy adopted in this paper, which employs multi-view pretraining followed by single-view refinement (stage 1 + stage 2), achieves the best performance across all four metrics. It elevates the FS@0.1 to 0.749, reduces the CD to 0.146, increases the PSNR to 26.9, and further lowers the LPIPS to 0.074. These results demonstrate that multi-view supervision provides the model with a more robust geometric prior, facilitating subsequent high-fidelity texture recovery under the guidance of real images, thereby validating the effectiveness of the proposed collaborative multi-stage strategy.

Table 6.
Ablation on stage combinations. Geometry metrics: FS@0.1 (higher is better) and CD (lower is better); texture metrics: PSNR (higher is better) and LPIPS (lower is better).
4.5.4. Multi-Level Feature Fusion Analysis
To further elucidate the practical contributions of the WD-LPM and HNC-SSD modules in the CAM3D framework, we conducted additional quantitative analyses on deep features across different model stages. Specifically, we introduced two complementary metrics to comprehensively evaluate the abilities of feature representations in detail preservation and structural alignment. Among them, Edge-F1 measures the consistency of edge structures between the input image and the features at each stage, where a higher value indicates better edge alignment. The high-frequency ratio reflects the extent to which structural details are retained during feature transformations, with higher values representing better preservation of fine-grained information.
Table 7 and Table 8 demonstrate that the introduction of the HNC-SSD module significantly improves the Edge-F1-scores at the intermediate stages, indicating its effectiveness in enhancing edge alignment of the network. The addition of the WD-LPM module further strengthens multi-level feature fusion at deeper stages, resulting in an overall upward trend for both Edge-F1 and across the network hierarchy. When both modules are applied together, the model achieves higher Edge-F1 and values at all levels compared to the baseline and other ablated variants, clearly confirming that the proposed approach enables effective fusion of fine-grained information across different network layers and thus supports the theoretical motivation underlying the model design.

Table 7.
Comparative results of edge-structure consistency (Edge-F1, %) across different stages, evaluating the contribution of WD-LPM and HNC-SSD modules to multi-level feature alignment.

Table 8.
Comparative results of high-frequency detail preservation (, %) across different stages, evaluating the contribution of WD-LPM and HNC-SSD modules to fine-grained structural fidelity.
These experiments provide direct quantitative evidence supporting the effectiveness of multi-layer feature fusion and further demonstrate the importance of the WD-LPM and HNC-SSD modules in enhancing feature discriminability and detail preservation. This lays a solid theoretical foundation for the superior performance of the CAM3D framework.
5. Discussion and Future Work
5.1. Discussion on Experiments
This study addresses how to produce three-dimensional physically robust adversarial perturbations from a single-view image without high-precision three-dimensional models. A multi-level experimental system across domains is designed. In the experiment on three-dimensional attribute extraction and prediction with a single-view image, CAM3D shows clear geometric consistency and detail fidelity in both the reference and unseen views. Although it does not rely on dense meshes, it still yields a geometry and texture base of high fidelity that supports later adversarial texture generation. By contrast, the sparse point cloud in SPAR3D leads to missing local geometry, and the LRM method yields smooth textures with limited detail. The evident improvement of CAM3D in detail expression and spatial consistency confirms the value of the two-stage training that joins synthetic multi-view pseudo-supervision with single-view refinement. In digital- and physical-domain attack tests, CAM3D reaches an attack success rate above sixty percent on mainstream detectors and maintains stable performance under different lighting, viewpoints, and distances. This shows that the loss design and optimization strategy in the three-stage framework are key to robustness and transfer. These findings support the idea that single-view input can enable cross-domain three-dimensional adversarial attacks, offer a feasible path with low data demand and strong physical robustness, and provide useful insight for future defense and security research.
5.2. Discussion on CAM3D
In the existing research on physical-domain adversarial attacks, most methods rely on high-precision three-dimensional models of the object itself to ensure the effectiveness and consistency of adversarial perturbations under different viewpoints and physical conditions. However, this dependence not only incurs significant data collection costs but also limits generalizability and applicability in low-resource environments. To address this limitation, this study proposes a hypothesis: if a framework with spatial consistency modeling and high-frequency feature expression capabilities can be built from a single-view image, three-dimensional adversarial texture generation with physical transferability and robustness can still be achieved. Based on this hypothesis, the CAM3D framework is designed with an end-to-end inverse graphics modeling and multi-stage optimization mechanism. It innovatively positions the process of extracting and predicting three-dimensional attributes as an intermediate representation from a single-view image to adversarial texture optimization, providing a stable and controllable three-dimensional geometry and texture foundation for perturbation generation. The core inverse graphics network in CAM3D, DWT-Mamba, is built on the Mamba state-space model, inheriting its advantages in efficient long-sequence modeling and spatial dependency capture. It extends the expression capability of high-frequency texture features through WD-LPM, providing rich and controllable detail priors for adversarial perturbations. The HNC-SSD module, with its hybrid non-causal aggregation strategy, further overcomes the limitations of traditional state-space methods in locality and recursion, significantly enhancing the global consistency and cross-view generalization of the three-dimensional attributes. The ablation study results also validate the collaborative effects of the components, showing that different feature extraction structures have significant differences in texture and geometry expression, directly affecting the quality of adversarial texture generation and physical transferability. Additionally, it is noteworthy that the three-stage training strategy of CAM3D is not a simple linear step-by-step process but a multi-stage collaborative optimization deeply coupled with the model’s mechanisms. The first stage uses synthetic multi-view pseudo-supervision to reduce reliance on real three-dimensional data and enhance spatial representation. The second stage strengthens texture alignment and structural consistency in a single view. The third stage focuses on improving adversarial robustness across multiple environmental conditions. Overall, the multi-structure and multi-stage collaborative fusion in the CAM3D framework is not merely a stacking of modules but a theoretically driven innovation. Its end-to-end design and deep collaboration promote a new paradigm for cross-domain three-dimensional adversarial sample generation with low data dependence and physical robustness.
5.3. Limitations
Although the CAM3D framework enables low-data-dependence single-view-based cross-domain adversarial texture generation and exhibits strong robustness in both digital and physical tests, several notable limitations remain. Firstly, the initial stage of the framework depends on independently pretrained StyleGAN2 models for each target category to synthesize multi-view pseudo-supervision signals, which subsequently support the disentanglement and optimization of 3D attributes. However, when a category lacks sufficiently high-quality generative priors, or when its real-world distribution differs significantly from the pretraining data, the consistency and fidelity of the synthesized views are reduced. This results in the accumulation and propagation of geometric errors and texture artifacts throughout the inverse graphics reconstruction and texture generation stages, thereby diminishing the model’s reconstruction accuracy and adversarial robustness for unseen or few-shot categories. In practical tests, we found that the pretrained StyleGAN model performs notably better for the vehicle category, which is closely related to its large training set of approximately 5.7 million real vehicle images. By contrast, for the ship category, despite manual filtering and fine-tuning of a self-built dataset with around 32,000 samples, the generative results are still significantly inferior to those for vehicles. This further illustrates the constraints imposed by data scale and distribution differences on the generalization performance of the method, especially under unseen categories and extreme few-shot conditions.
Secondly, the CAM3D framework also incurs substantial engineering costs in parameter tuning. The three-stage optimization process involves adjusting multiple loss weights, and, especially in the third stage of adversarial optimization, different hyperparameter settings have a significant impact on the visual quality and attack effectiveness of the final texture. In the current implementation, a complete adversarial optimization process is typically time-consuming, and finding the optimal combination of parameters often requires multiple rounds of experimental comparisons, considerably increasing the tuning burden in practical deployment.
Finally, although various structural and regularization constraints have been introduced into the texture generation and optimization processes to improve robustness under diverse imaging conditions and physical deployment scenarios, some generated textures still exhibit pronounced high-frequency noise and color artifacts in complex backgrounds or under extreme illumination. Similar phenomena have been reported in the recent literature (such as FCA [23], DTA [48], and NGC-LGPD [49]). Excessive high-frequency components and unbalanced color distributions not only affect the visual quality of the textures but may also increase the risk of detection or recognition when high stealth is required. Therefore, further enhancing constraints on texture quality and improving robustness across different environmental conditions remain key challenges for the reliable application of this method.
5.4. Future Works
Future research will focus on addressing the current limitations of the model and meeting practical application requirements through systematic optimization. To mitigate the strong dependency on category-specific priors and enhance cross-domain applicability while improving texture stealth, we plan to employ general conditional generators such as diffusion models. This approach will reduce prior dependency and broaden cross-domain capabilities. Simultaneously, we will introduce perceptual similarity losses (e.g., SSIM and LPIPS) and frequency-domain masking mechanisms into the adversarial optimization process, combined with region-wise layered perturbation strategies. These measures aim to reduce the visual salience of textures while maintaining adversarial robustness, thereby enhancing practical security in complex real-world environments. Secondly, to address the demand for maintaining texture consistency and stable adversarial effects in dynamic systems where target motion may cause coherence loss, we will attempt to constrain smooth transitions of texture parameters between adjacent frames through temporal regularization terms. This will involve constructing a hybrid optimization paradigm of “offline pretraining of a temporal generator–online incremental update”. Combined with optical flow-guided projection consistency loss, we can ensure visual coherence during target translation, rotation, or non-rigid deformation. Additionally, we will introduce new attack stability metrics within a time window to quantify the persistence of adversarial effects in dynamic scenes. Furthermore, to address the limitations of high computational complexity in real-time deployment and the need for improved physical realizability, we consider leveraging the structural advantages of Voronoi diagrams. Through Lloyd’s algorithm to optimize seed point distribution, we can replace the traditional per-pixel high-dimensional texture representation with a patch-level partitioned representation [50], reducing the optimization variables from millions of pixels to a small set of seed points to significantly lower computational complexity. Meanwhile, the clear vector edge structure of Voronoi diagrams supports digital cutting and printing, balancing real-time deployment efficiency and physical realizability. Finally, to overcome the weak generalization of single visible-light modality and the difficulty in dealing with multi-sensor monitoring scenarios, we envision constructing an RGB-Infrared (IR) dual-spectrum joint optimization framework. By incorporating material thermal radiation parameters into the differentiable rendering process and balancing the attack effects in both domains through multi-modal losses, we can ensure that the generated textures stably mislead detection models in multi-sensor environments, further enhancing generalization capabilities.
6. Conclusions
To address the limited robustness of digital-domain adversarial attacks in real-world applications and the reliance of physical-domain methods on high-precision 3D models, this paper introduces CAM3D, a cross-domain adversarial framework driven by single-view input. The framework is designed to generate physically transferable adversarial texture perturbations under limited supervision, facilitating the transition from digital to physical domains without requiring dense 3D data. CAM3D integrates inverse 3D attribute reconstruction and adversarial texture optimization within a unified pipeline, supported by differentiable rendering, allowing for joint modeling of detailed geometric and texture representations. This integration significantly reduces the need for high-precision 3D meshes or extensive multi-view supervision. To improve the expressiveness and transferability of adversarial textures, the framework incorporates the DWT-Mamba network, which combines the sequential modeling capacity of state-space architectures with the multiscale feature decomposition capabilities of wavelet transforms. This design enables the generation of structure-aware texture-rich 3D intermediate representations from single-view inputs. Within the network, the HNC-SSD module strengthens spatial consistency across views, while the WD-LPM module compensates for the Mamba backbone’s limitations in capturing high-frequency visual details, together enhancing the fidelity and robustness of the adversarial texture basis. The training process adopts a progressive co-optimization strategy that encompasses pseudo-supervised multi-view construction, adaptive refinement of geometric and textural attributes under single-view supervision, and robustness-oriented optimization across diverse environmental conditions. This cohesive mechanism strengthens the coupling between geometric understanding and adversarial robustness, improving the generalization of the generated textures under varying real-world scenarios.
At the experimental level, CAM3D shows strong performance in both the digital domain and real physical settings. This study uses ships as the target class. In a digital simulation, the adversarial textures drive the mean AP@0.5 of mainstream detectors such as YOLOv5 and DETR down by 74.9 percent, with an attack success rate of 75.1 percent. In physical-world experiments on a printed model, we take the sunny environment—where the attack effect is the best—as an example: the detection accuracy of detectors drops by 71.1 percent, the attack success rate reaches 72.3 percent, and the average CDR is 82.2 percent, showing strong cross-domain transfer and promising real-world applicability. Ablation studies also confirm the effectiveness of the DWT-Mamba structure and its modules, providing about 4.7% gain in PSNR and 12.9% gain in LPIPS over the baseline for three-dimensional reconstruction quality. These results support the advantages of the method in geometric consistency and texture detail, and they strengthen the transfer adaptability and physical robustness of the subsequent adversarial textures.
Overall, this study introduces in theory a unified cross-domain attack framework that joins three-dimensional modeling, differentiable rendering, and adversarial perturbation generation. Methodologically, it builds an end-to-end system that uses a refined structure, multiscale cooperation, and enhanced robustness, and the experiments confirm both its cross-domain attack capacity and potential for practical deployment. In practice, our CAM3D framework holds significant promise for a wide range of real-world applications. In autonomous driving, it could be utilized to evaluate and enhance the robustness of perceptual systems against adversarial camouflage on vehicles. In the domain of surveillance security, it offers a potential tool for designing privacy-preserving techniques that protect individuals from being automatically identified by intelligent cameras. Future work will explore class-agnostic camera-controllable generative priors to broaden cross-category adaptability. Meanwhile, we will also explore introducing actionable imperceptibility constraints during the optimization process. Specifically, we propose shifting perceptual consistency evaluation from rendered images to the UV (texture) space, directly comparing the generated texture and its reference under unified coordinates to avoid the effects of multi-view misalignment and background noise. In addition, soft radial frequency-domain masking can be selectively applied only to the incremental component above the base texture, thereby suppressing excessive high-frequency components and reducing visible artifacts. By combining alternating optimization and the late-stage introduction of regularization weights, we aim to enhance stealthiness while maximally preserving adversarial robustness. These directions are expected to further strengthen the practical value and safety of CAM3D in complex real-world environments.
Author Contributions
Methodology, Z.L. and W.L.; software, Z.L. and S.G.; validation, Z.L. and W.L.; data curation, Z.L., J.Z., and Z.W.; writing—original draft, Z.L. and S.G.; writing—review and editing, Z.W. and J.Z.; visualization, Z.L. and J.Z.; funding acquisition, W.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by The National Natural Science Foundation of China, Ye Qisun Science Foundation: U2341228.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The datasets analyzed in this study are publicly available. These include the LSUN Car dataset (https://www.tensorflow.org/datasets/catalog/lsun; Accessed on 24 September 2025), the ABOships dataset (https://research.abo.fi/en/datasets/aboships-plus-2; Accessed on 24 September 2025), and the Visible Ship Dataset (https://github.com/Qunfunction/Visible-ship-dataset; Accessed on 24 September 2025).
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| HNC-SSD | Hybrid Non-Causal State-Space Duality |
| WD-LPM | Wavelet-Enhanced Dual-Branch Local Perception Module |
| SSM | State-Space Model |
| SSD | State-Space Duality |
| MLA | Multi-Head Latent Attention |
| DWT | Discrete Wavelet Transform |
| GAP | Global Average Pooling |
| IDWT | Inverse Discrete Wavelet Transform |
| AP@0.5 | Average Precision at IoU = 0.5 |
| ASR | Attack Success Rate |
| IoU | Intersection over Union |
| NeRF | Implicit Neural Radiance Field |
| CD | Chamfer Distance |
References
- Chib, P.S.; Singh, P. Recent Advancements in End-to-End Autonomous Driving Using Deep Learning: A Survey. IEEE Trans. Intell. Veh. 2024, 9, 103–118. [Google Scholar] [CrossRef]
- Goodfellow, I.J.; Shlens, J.; Szegedy, C. Explaining and Harnessing Adversarial Examples. In Proceedings of the International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Mahmood, K.; Mahmood, R.; van Dijk, M. On the Robustness of Vision Transformers to Adversarial Examples. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 11–17 October 2021; pp. 7818–7827. [Google Scholar] [CrossRef]
- Bortsova, G.; González-Gonzalo, C.; Wetstein, S.C.; Dubost, F.; Katramados, I.; Hogeweg, L.; Liefers, B.; van Ginneken, B.; Pluim, J.P.W.; Veta, M.; et al. Adversarial Attack Vulnerability of Medical Image Analysis Systems: Unexplored Factors. Med. Image Anal. 2021, 73, 102141. [Google Scholar] [CrossRef] [PubMed]
- Ding, K.; Liu, X.; Niu, W.; Zhang, X.; Wang, Y.; Lu, J. A Low-Query Black-Box Adversarial Attack Based on Transferability. Knowl.-Based Syst. 2021, 226, 107102. [Google Scholar] [CrossRef]
- Liu, X.; Hu, T.; Ding, K.; Bai, Y.; Niu, W.; Lu, J. A Black-Box Attack on Neural Networks Based on Swarm Evolutionary Algorithm. In Information Security and Privacy; Liu, J., Cui, H., Eds.; Springer: Cham, Switzerland, 2020; pp. 247–267. [Google Scholar] [CrossRef]
- Chen, J.; Chen, H.; Chen, K.; Zhang, Y.; Zou, Z.; Shi, Z. Diffusion Models for Imperceptible and Transferable Adversarial Attack. IEEE Trans. Pattern Anal. Mach. Intell. 2025, 47, 961–977. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Liu, H.; Wang, P.; Wu, Y.; Li, K. DIPA: Adversarial Attack on DNNs by Dropping Information and Pixel-Level Attack on Attention. Information 2024, 15, 391. [Google Scholar] [CrossRef]
- Du, A.; Yang, X.; Qi, L.; Li, G.; Zhou, T.; Zhao, J.; Zhang, W.; Wu, Y. Physical Adversarial Attacks on an Aerial Imagery Object Detector. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 4–9 January 2022; pp. 3798–3808. [Google Scholar] [CrossRef]
- Cheng, Z.; Liang, J.; Choi, H.; Tao, G.; Cao, Z.; Liu, D.; Zhang, X. Physical Attack on Monocular Depth Estimation with Optimal Adversarial Patches. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; pp. 514–532. [Google Scholar] [CrossRef]
- Tu, J.; Zhu, H.; Yang, Y.; Zhang, R.; Zhang, B.; Ouyang, Y.; Wang, L.; Hu, X. Physically Realisable Adversarial Examples for LiDAR Object Detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 13713–13722. [Google Scholar] [CrossRef]
- Dimitriu, A.; Michaletzky, T.V.; Remeli, V. Improving Transferability of Physical Adversarial Attacks on Object Detectors Through Multi-Model Optimization. Appl. Sci. 2024, 14, 11423. [Google Scholar] [CrossRef]
- Hu, Z.; Huang, S.; Zhu, X.; Sun, F.; Zhang, B.; Hu, X. Adversarial Texture for Fooling Person Detectors in the Physical World. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 13307–13316. [Google Scholar]
- Madry, A.; Makelov, A.; Schmidt, L.; Tsipras, D.; Vladu, A. Towards Deep Learning Models Resistant to Adversarial Attacks. In Proceedings of the 6th International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Carlini, N.; Wagner, D. Towards Evaluating the Robustness of Neural Networks. In Proceedings of the 2017 IEEE Symposium on Security and Privacy, San Jose, CA, USA, 22–24 May 2017; pp. 39–57. [Google Scholar] [CrossRef]
- Eykholt, K.; Evtimov, I.; Fernandes, E.; Li, B.; Rahmati, A.; Xiao, C.; Prakash, A.; Kohno, T.; Song, D. Robust Physical-World Attacks on Deep Learning Visual Classification. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 1625–1634. Available online: https://openaccess.thecvf.com/content_cvpr_2018/papers/Eykholt_Robust_Physical-World_Attacks_CVPR_2018_paper.pdf (accessed on 24 September 2025).
- Brown, T.B.; Mané, D.; Roy, A.; Abadi, M.; Gilmer, J. Adversarial Patch. arXiv 2017, arXiv:1712.09665. [Google Scholar]
- Athalye, A.; Engstrom, L.; Ilyas, A.; Kwok, K. Synthesizing Robust Adversarial Examples. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 284–293. Available online: https://proceedings.mlr.press/v80/athalye18b.html (accessed on 24 September 2025).
- Cai, M.; Wang, X.; Sohel, F.; Lei, H. Unsupervised Anomaly Detection for Improving Adversarial Robustness of 3D Object Detection Models. Electronics 2025, 14, 236. [Google Scholar] [CrossRef]
- Xiang, C.; Qi, C.R.; Li, B. Generating 3D Adversarial Point Clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 9136–9144. [Google Scholar]
- Tsai, T.; Yang, K.; Ho, T.-Y.; Jin, Y. Robust Adversarial Objects against Deep Learning Models. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; pp. 954–962. Available online: https://cdn.aaai.org/ojs/5443/5443-13-8668-1-10-20200511.pdf (accessed on 24 September 2025).
- Zeng, X.; Liu, C.; Wang, Y.-S.; Qiu, W.; Xie, L.; Tai, Y.-W.; Tang, C.-K.; Yuille, A.L. Adversarial Attacks Beyond the Image Space. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 4302–4311. [Google Scholar]
- Wang, D.; Jiang, T.; Sun, J.; Zhou, W.; Zhang, X.; Gong, Z.; Yao, W.; Chen, X. FCA: Learning a 3D Full-Coverage Vehicle Camouflage for Multi-View Physical Adversarial Attack. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 22–23 February 2022; pp. 2414–2421. [Google Scholar]
- Zhou, J.; Lyu, L.; He, D.; Li, Y. RAUCA: A Novel Physical Adversarial Attack on Vehicle Detectors via Robust and Accurate Camouflage Generation. In Proceedings of the 41st International Conference on Machine Learning, Vienna, Austria, 21–27 July 2024; pp. 62076–62087. [Google Scholar]
- Huang, Y.; Dong, Y.; Ruan, S.; Yang, X.; Su, H.; Wei, X. Towards Transferable Targeted 3D Adversarial Attack in the Physical World. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 16–20 June 2024; pp. 24512–24522. Available online: https://openaccess.thecvf.com/content/CVPR2024/papers/Huang_Towards_Transferable_Targeted_3D_Adversarial_Attack_in_the_Physical_World_CVPR_2024_paper.pdf (accessed on 24 September 2025).
- Li, L.; Lian, Q.; Chen, Y.C. Adv3D: Generating 3D Adversarial Examples for 3D Object Detection in Driving Scenarios with NeRF. In Proceedings of the 2024 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Abu Dhabi, United Arab Emirates, 14–18 October 2024; pp. 10813–10820. [Google Scholar]
- Xiao, C.; Li, M.; Zhang, Z.; Meng, D.; Zhang, L. Spatial-Mamba: Effective Visual State Space Models via Structure-Aware State Fusion. In Proceedings of the International Conference on Learning Representations (ICLR 2025), Singapore, Singapore, 24–28 April 2025; Available online: https://proceedings.iclr.cc/paper_files/paper/2025/file/b7216f4a324864e1f592c18de4d83d10-Paper-Conference.pdf (accessed on 24 September 2025).
- Zhu, L.; Liao, B.; Zhang, Q.; Wang, X.; Liu, W.; Wang, X. Vision Mamba: Efficient Visual Representation Learning with Bidirectional State Space Model. In Proceedings of the Forty-First International Conference on Machine Learning, Vienna, Austria, 21–27 July 2024; pp. 62429–62442. Available online: https://openreview.net/pdf?id=YbHCqn4qF4 (accessed on 24 September 2025).
- Gu, A.; Goel, K.; Ré, C. Efficiently Modeling Long Sequences with Structured State Spaces. In Proceedings of the 10th International Conference on Learning Representations, Virtual, 25–29 April 2022; Available online: https://openreview.net/pdf?id=uYLFoz1vlAC (accessed on 24 September 2025).
- Gu, A.; Dao, T. Mamba: Linear-Time Sequence Modeling with Selective State Spaces. In Proceedings of the Conference on Language Modeling, Philadelphia, PA, USA, 12–14 September 2023. [Google Scholar]
- Dao, T.; Gu, A. Transformers are SSMs: Generalized Models and Efficient Algorithms Through Structured State Space Duality. In Proceedings of the 41st International Conference on Machine Learning, Vienna, Austria, 21–27 July 2024; pp. 10041–10071. Available online: https://proceedings.mlr.press/v235/dao24a.html (accessed on 24 September 2025).
- Guo, H.; Li, J.; Dai, T.; Ouyang, Z.; Ren, X.; Xia, S.-T. MambaIR: A Simple Baseline for Image Restoration with State-Space Model. In Proceedings of the European Conference on Computer Vision, Milan, Italy, 29 September–4 October 2024; pp. 222–241. [Google Scholar]
- Liu, Y.; Tian, Y.; Zhao, Y.; Yu, H.; Xie, L.; Wang, Y.; Ye, Q.; Liu, Y. VMamba: Visual State Space Model. In Proceedings of the 38th Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 10–15 December 2024; pp. 103031–103063. [Google Scholar]
- Li, D.; Liu, Y.; Fu, X.; Huang, J.; Xu, S.; Zhu, Q.; Zha, Z.-J. FourierMamba: Fourier Learning Integration with State Space Models for Image Deraining. In Proceedings of the 42nd International Conference on Machine Learning, Vancouver, BC, Canada, 13–19 July 2025; Available online: https://icml.cc/virtual/2025/poster/43723 (accessed on 24 September 2025).
- Hatamizadeh, A.; Kautz, J. MambaVision: A Hybrid Mamba-Transformer Vision Backbone. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 15–20 June 2025; pp. 25261–25270. Available online: https://openaccess.thecvf.com/content/CVPR2025/papers/Hatamizadeh_MambaVision_A_Hybrid_Mamba-Transformer_Vision_Backbone_CVPR_2025_paper.pdf (accessed on 24 September 2025).
- Shi, Y.; Dong, M.; Li, M.; Xu, C. VSSD: Vision Mamba with Non-Causal State Space Duality. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Honolulu, HI, USA, 19–23 October 2025; Available online: https://iccv.thecvf.com/virtual/2025/poster/1477 (accessed on 24 September 2025).
- Finder, S.E.; Amoyal, R.; Treister, E.; Freifeld, O. Wavelet Convolutions for Large Receptive Fields. In Proceedings of the European Conference on Computer Vision, Milan, Italy, 29 September–4 October 2024; pp. 363–380. [Google Scholar] [CrossRef]
- Chen, W.; Ling, H.; Gao, J.; Smith, E.; Lehtinen, J.; Jacobson, A.; Fidler, S. Learning to Predict 3D Objects with an Interpolation-Based Differentiable Renderer. In Proceedings of the 33rd Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; pp. 9609–9619. Available online: https://papers.neurips.cc/paper_files/paper/2019/file/f5ac21cd0ef1b88e9848571aeb53551a-Paper.pdf (accessed on 24 September 2025).
- Monnier, T.; Fisher, M.; Efros, A.A.; Aubry, M. Share with Thy Neighbors: Single-View Reconstruction by Cross-Instance Consistency. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; pp. 285–303. Available online: https://www.ecva.net/papers/eccv_2022/papers_ECCV/papers/136610282.pdf (accessed on 24 September 2025).
- Dundar, A.; Gao, J.; Tao, A.; Catanzaro, B. Progressive Learning of 3D Reconstruction Network from 2D GAN Data. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 793–804. [Google Scholar] [CrossRef] [PubMed]
- Karras, T.; Laine, S.; Aittala, M.; Hellsten, J.; Lehtinen, J.; Aila, T. Analyzing and Improving the Image Quality of StyleGAN. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 8110–8119. Available online: https://openaccess.thecvf.com/content_CVPR_2020/papers/Karras_Analyzing_and_Improving_the_Image_Quality_of_StyleGAN_CVPR_2020_paper.pdf (accessed on 24 September 2025).
- Zhang, Y.; Chen, W.; Ling, H.; Gao, J.; Zhang, Y.; Torralba, A.; Fidler, S. Image GANs Meet Differentiable Rendering for Inverse Graphics and Interpretable 3D Neural Rendering. In Proceedings of the International Conference on Learning Representations (ICLR), Virtual, 3–7 May 2021. [Google Scholar]
- Huang, Z.; Boss, M.; Vasishta, A.; Rehg, J.M.; Jampani, V. SPAR3D: Stable Point-Aware Reconstruction of 3D Objects from Single Images. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 15–20 June 2025; pp. 16860–16870. Available online: https://openaccess.thecvf.com/content/CVPR2025/papers/Huang_SPAR3D_Stable_Point-Aware_Reconstruction_of_3D_Objects_from_Single_Images_CVPR_2025_paper.pdf (accessed on 24 September 2025).
- Hong, Y.; Zhang, K.; Gu, J.; Bi, S.; Zhou, Y.; Liu, D.; Liu, F.; Sunkavalli, K.; Bui, T.; Tan, H. LRM: Large Reconstruction Model for Single Image to 3D. In Proceedings of the 12th International Conference on Learning Representations (ICLR 2024), Messe Wien Exhibition & Congress Center, Vienna, Austria, 7–11 May 2024. [Google Scholar]
- Tan, M.; Le, Q.V. EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA; 2019; pp. 6105–6114. Available online: https://proceedings.mlr.press/v97/tan19a.html (accessed on 24 September 2025).
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin Transformer: Hierarchical Vision Transformer Using Shifted Windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 11–17 October 2021; pp. 10012–10022. Available online: https://openaccess.thecvf.com/content/ICCV2021/papers/Liu_Swin_Transformer_Hierarchical_Vision_Transformer_Using_Shifted_Windows_ICCV_2021_paper.pdf (accessed on 24 September 2025).
- Han, D.; Wang, Z.; Xia, Z.; Han, Y.; Pu, Y.; Ge, C.; Song, J.; Song, S.; Zheng, B.; Huang, G. Demystify Mamba in Vision: A Linear Attention Perspective. In Proceedings of the 38th Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 10–15 December 2024. [Google Scholar] [CrossRef]
- Wang, Z.; Li, J.; Chen, X.; Zhang, D.; Yang, X. Differentiable Transformation Attack (DTA) for Physical Camouflage. IEEE Trans. Intell. Transp. Syst. 2022, 23, 21456–21467. [Google Scholar]
- Liang, J.W.; Liang, S.Y.; Huang, J.J.; Si, C.X.; Zhang, M.; Cao, X.C. Physical Adversarial Camouflage through Gradient Calibration and Regularization. arXiv 2025, arXiv:2508.05414. [Google Scholar] [CrossRef]
- Hu, Z.; Chu, W.; Zhu, X.P.; Zhang, H.; Zhang, B.; Hu, X. Physically Realizable Natural-Looking Clothing Textures Evade Person Detectors via 3D Modeling. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 18–22 June 2023; pp. 16975–16984. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).