Robust UAV Path Planning Using RSS in GPS-Denied and Dense Environments Based on Deep Reinforcement Learning
Abstract
1. Introduction
- A novel collision avoidance method is proposed under the GPS-denied condition. Unlike existing works that require GPS signals, the proposed method is developed to avoid collision using the strongest RSS measured from surrounding UAVs. In the proposed framework, an EKF is applied to mitigate noise and interference, which are related to RSS fluctuations. By filtering out the fluctuations in RSS, the accuracy of distance estimation and the reliability of collision avoidance can be enhanced.
- To simultaneously achieve a smooth and efficient trajectory by considering the dynamic multiple unknown UAVs, a novel strategy is proposed that utilizes the DRL method. Instead of the grid-based action, the proposed method enables relatively smooth path planning and collision avoidance by applying the UAV’s attitude.
- Unlike previous methods that assume a no-fly zone, the simulation is performed considering a 3D dense environment where numerous unknown UAVs exist in the environment. Specifically, two scenarios are considered for comprehensive performance evaluation: single- and multi-target scenarios. The simulation results demonstrate that the proposed method is practically applicable even in challenging environments.
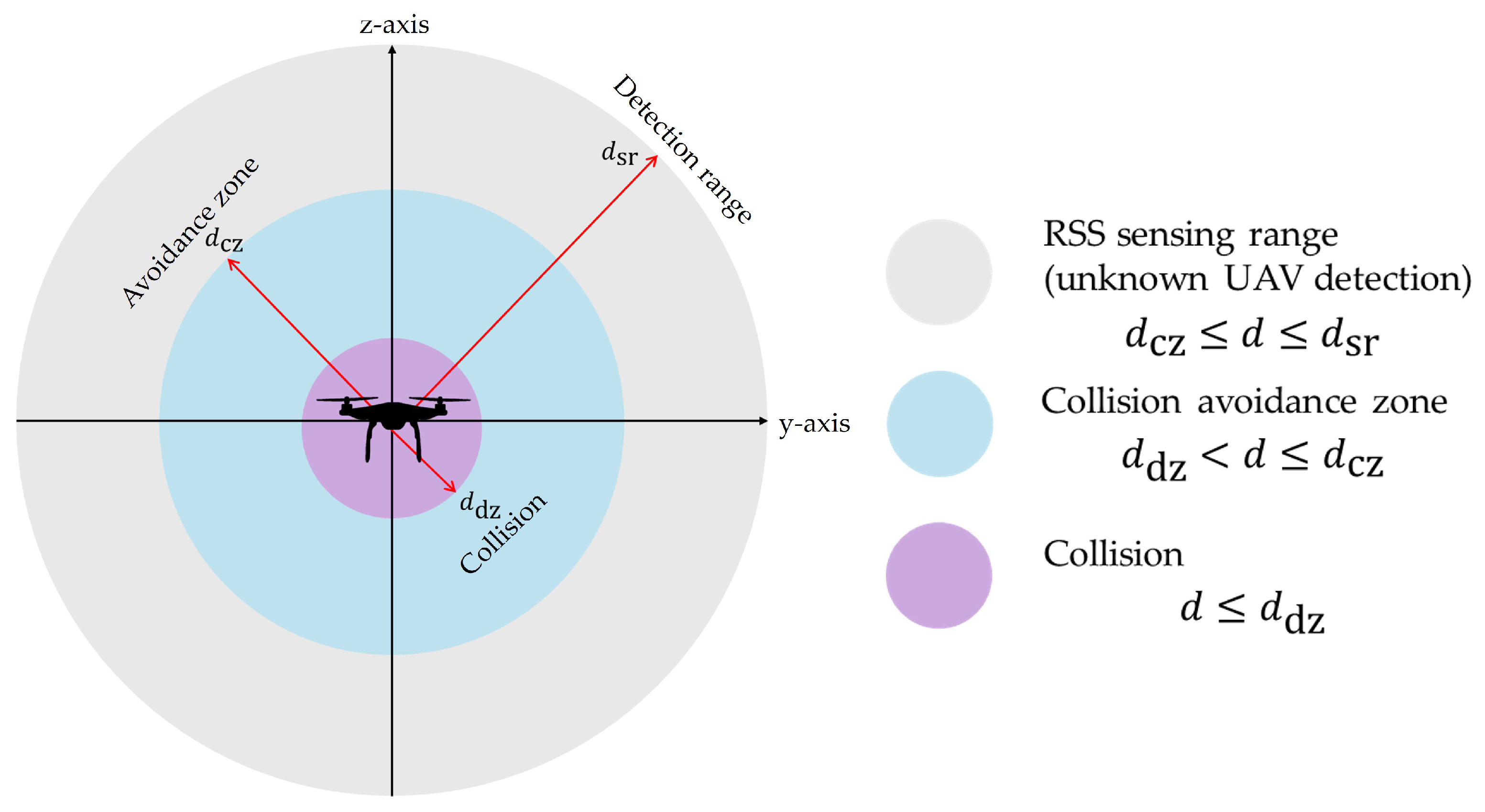
2. System Model
2.1. Path Loss Model
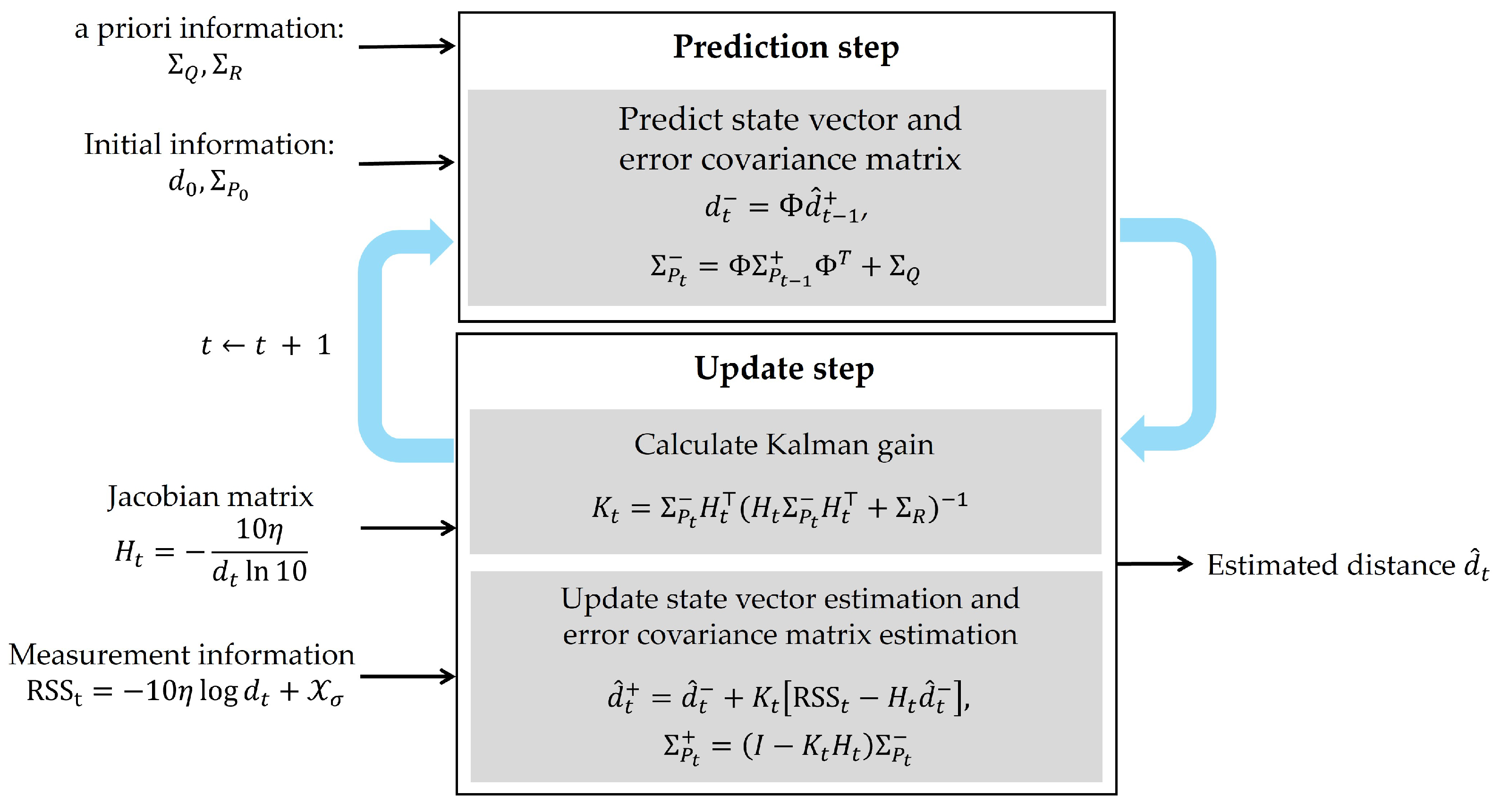
2.2. RSS-Based Distance Estimation Algorithm
3. UAV Kinematic and Positioning Model
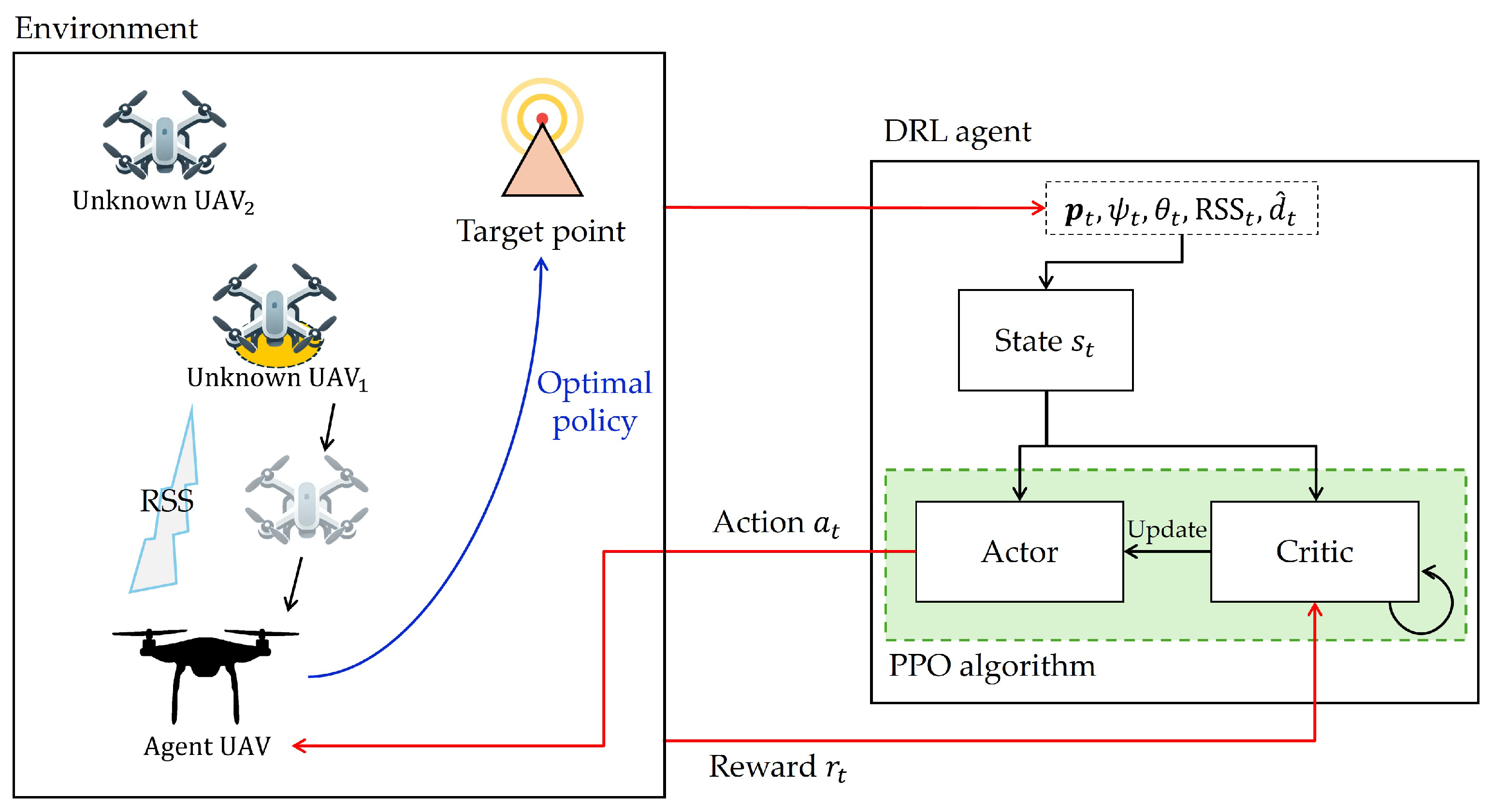
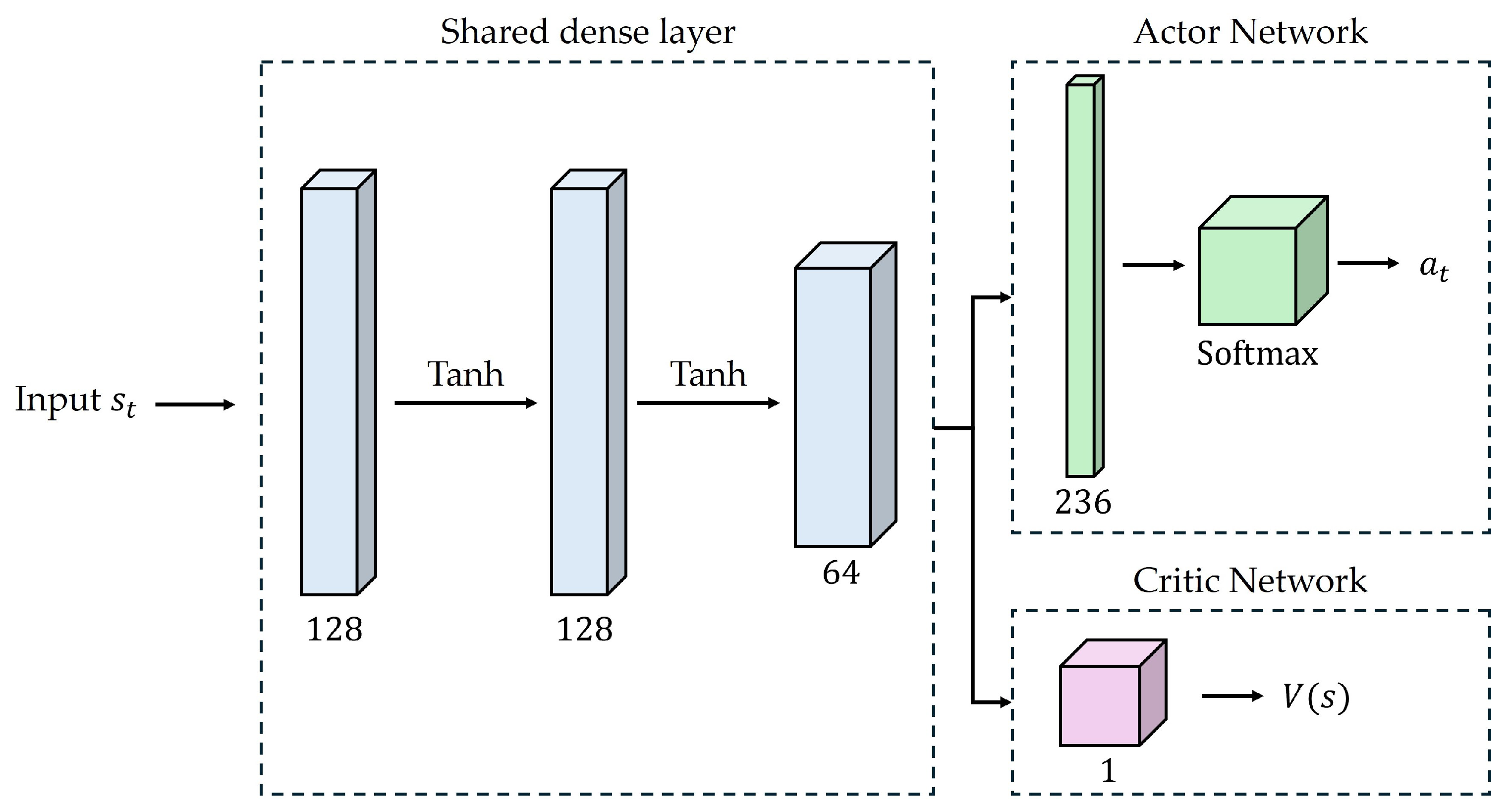
4. DRL-Based Path Planning and Collision Avoidance
4.1. State and Action Spaces
4.2. Reward Function
4.3. Proximal Policy Optimization (PPO) Algorithm
5. Simulation Results
5.1. Simulation Setup
5.2. Simulation Results
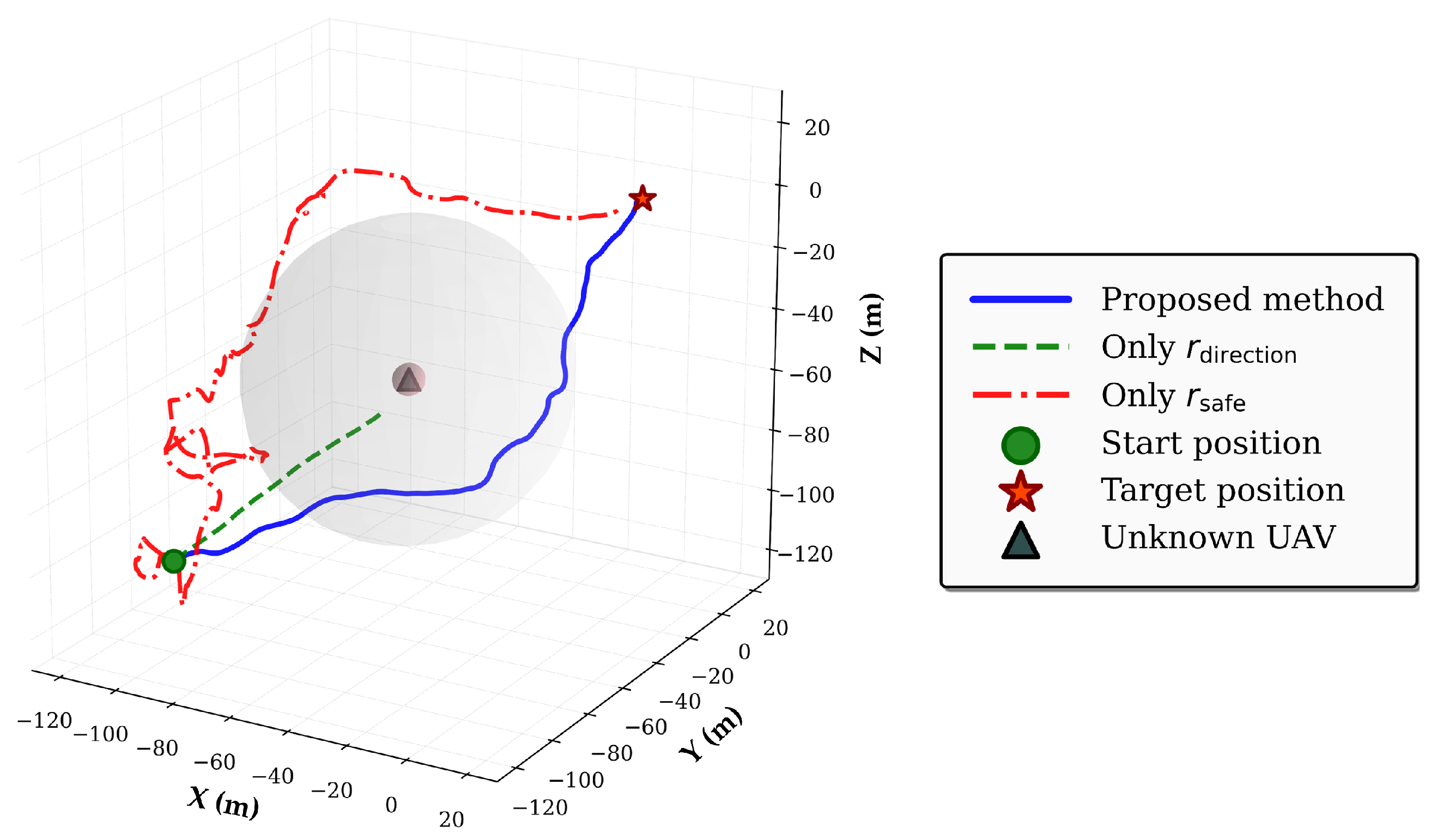
5.2.1. Analysis of Reward Function Component
5.2.2. Collision Avoidance Performance
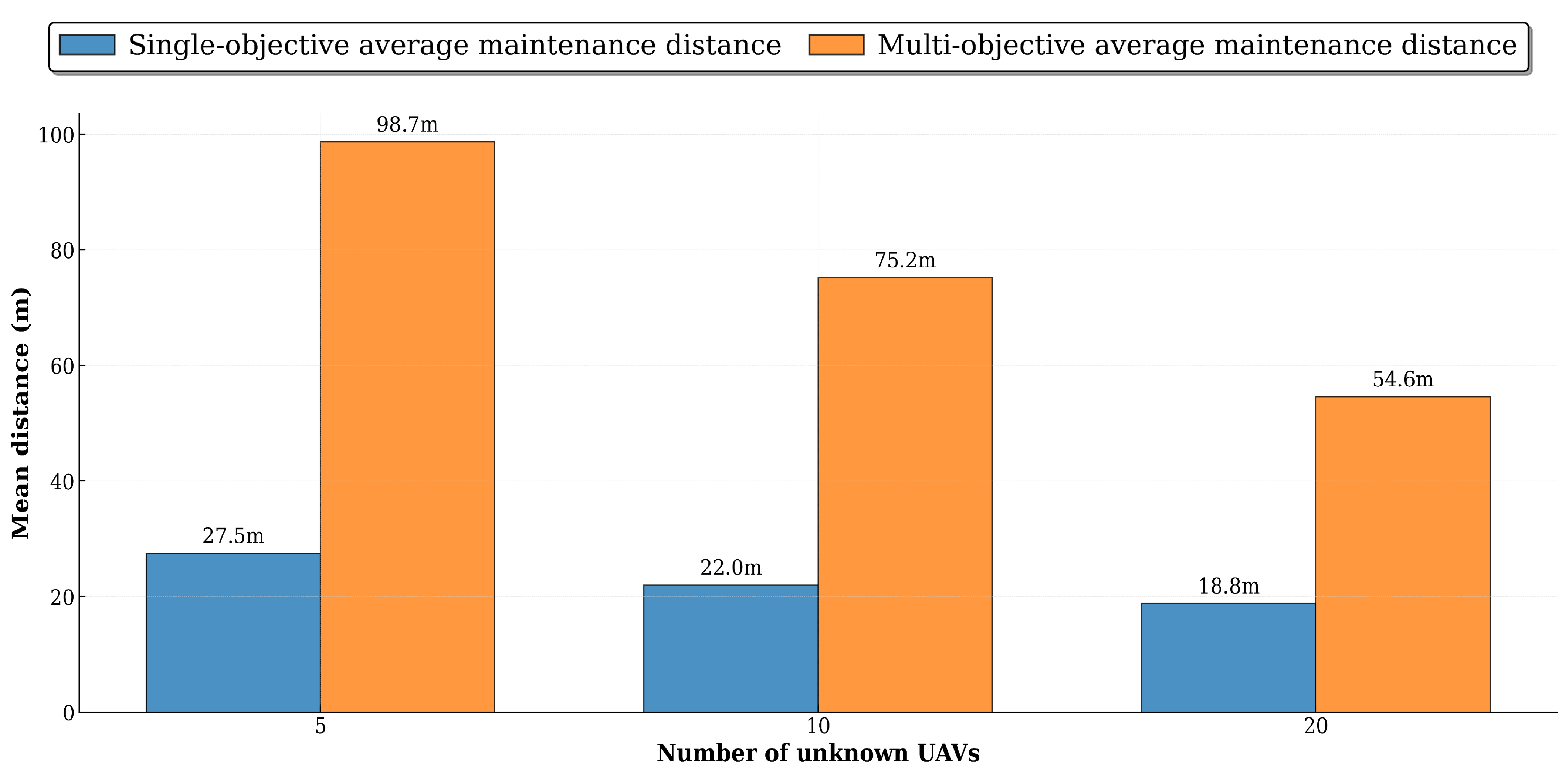
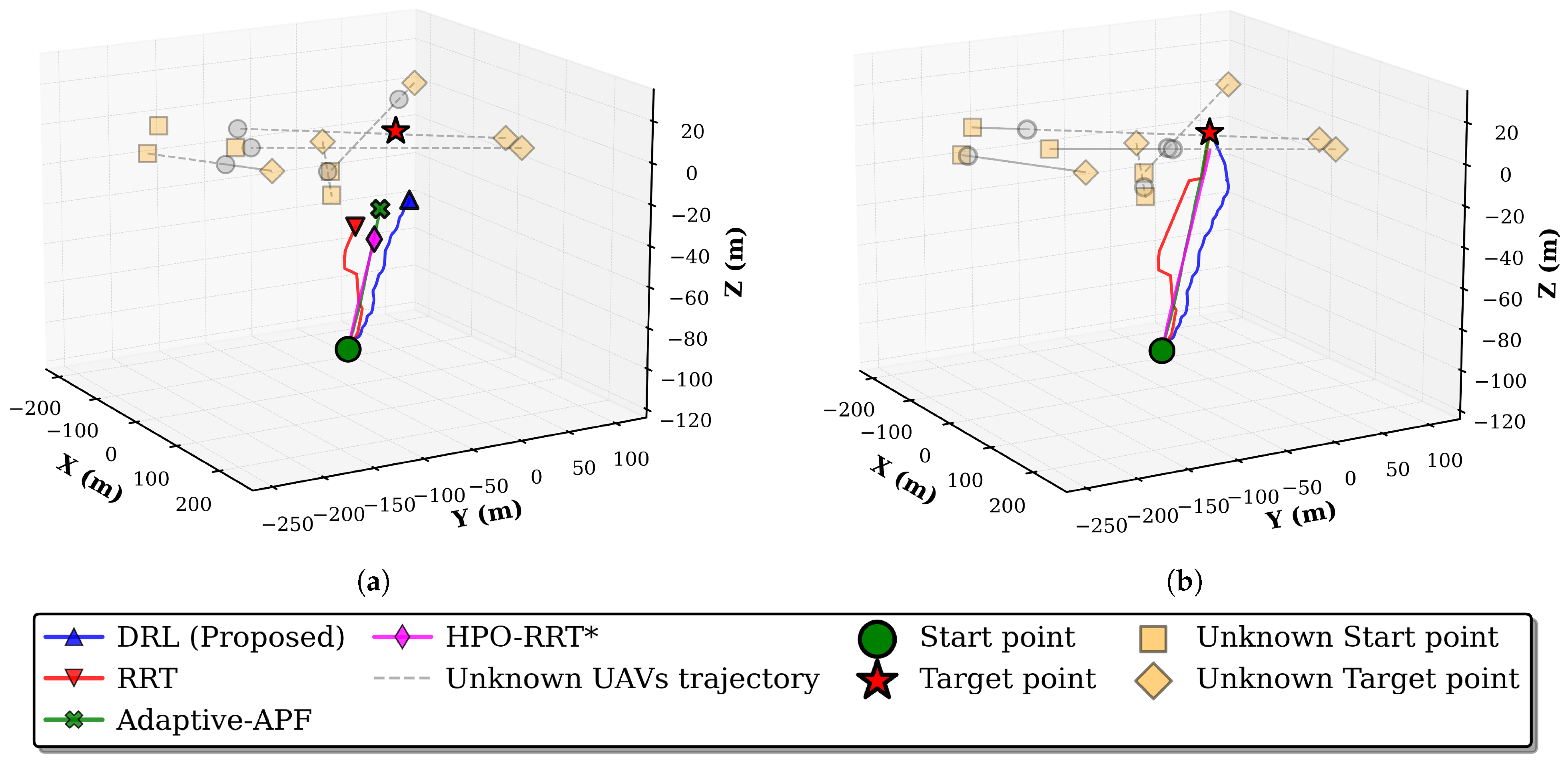
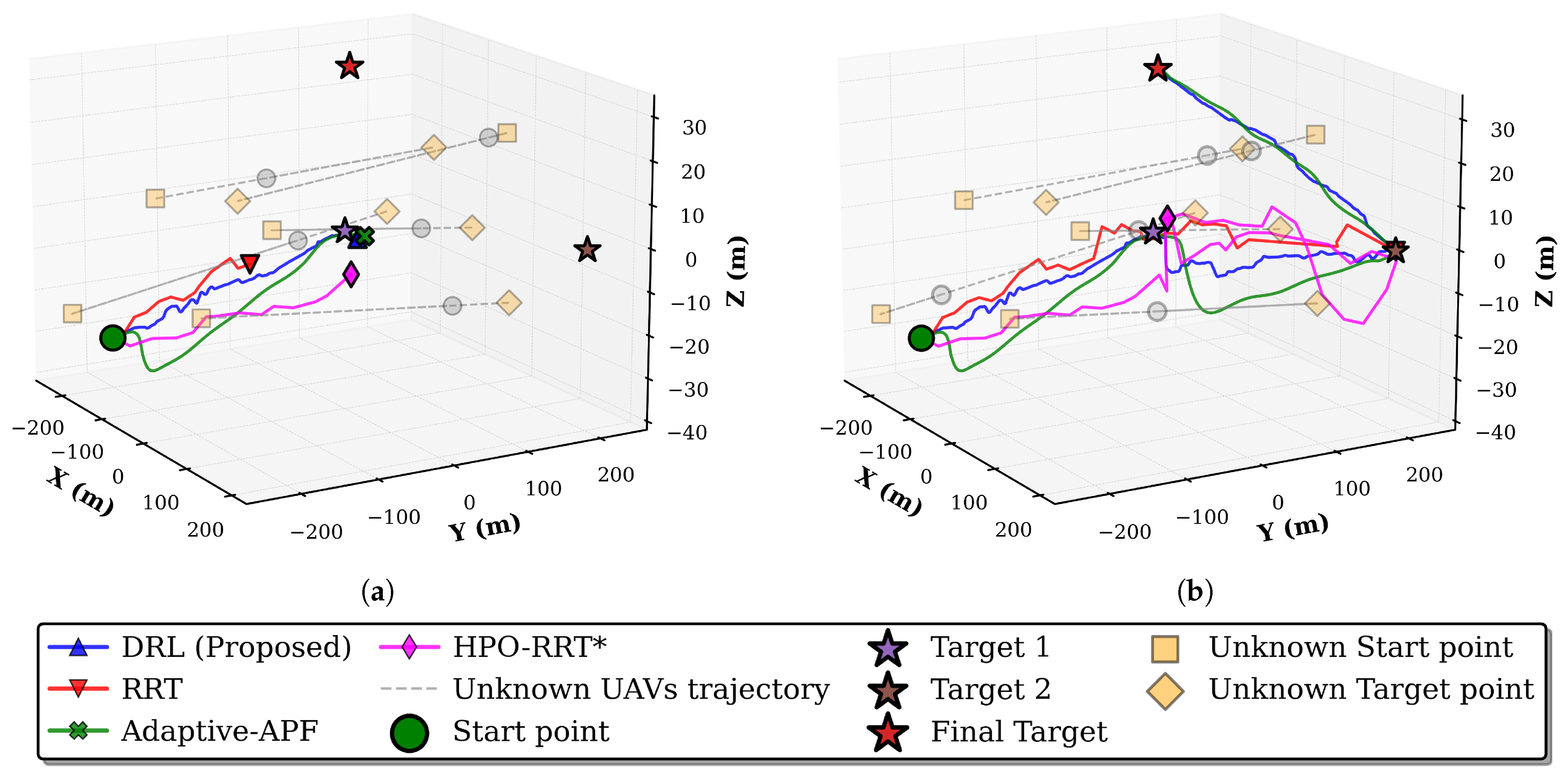
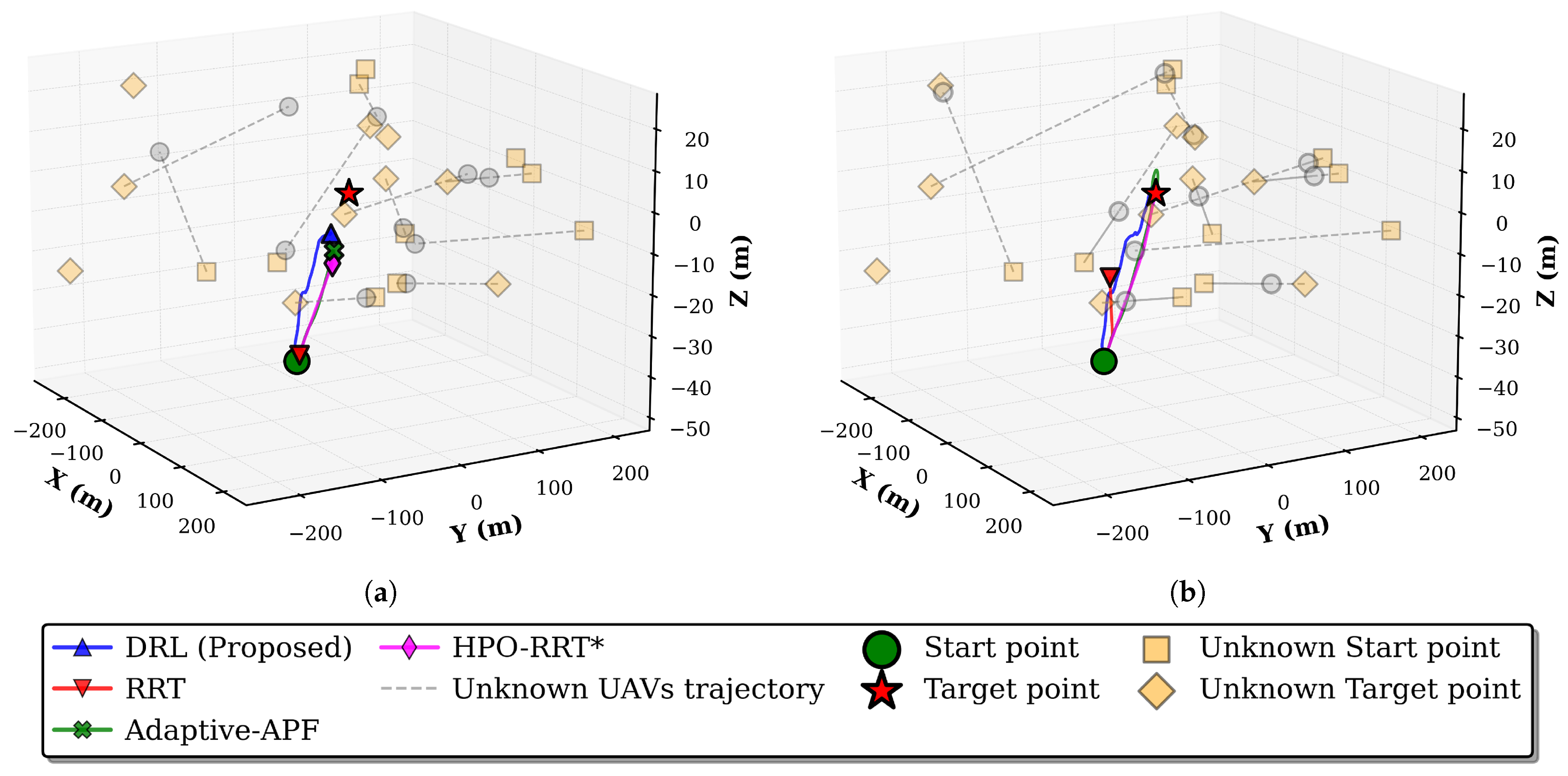
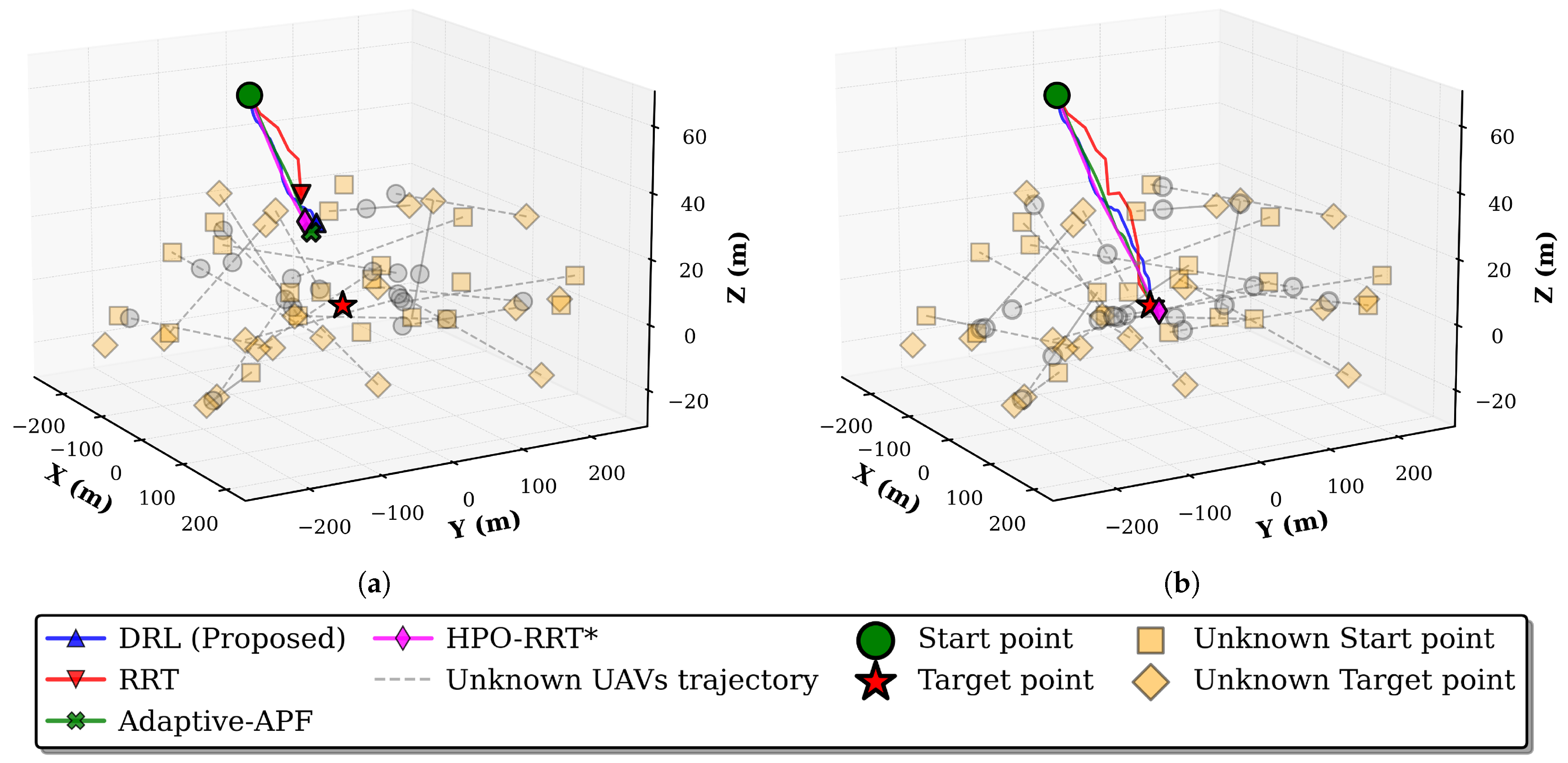
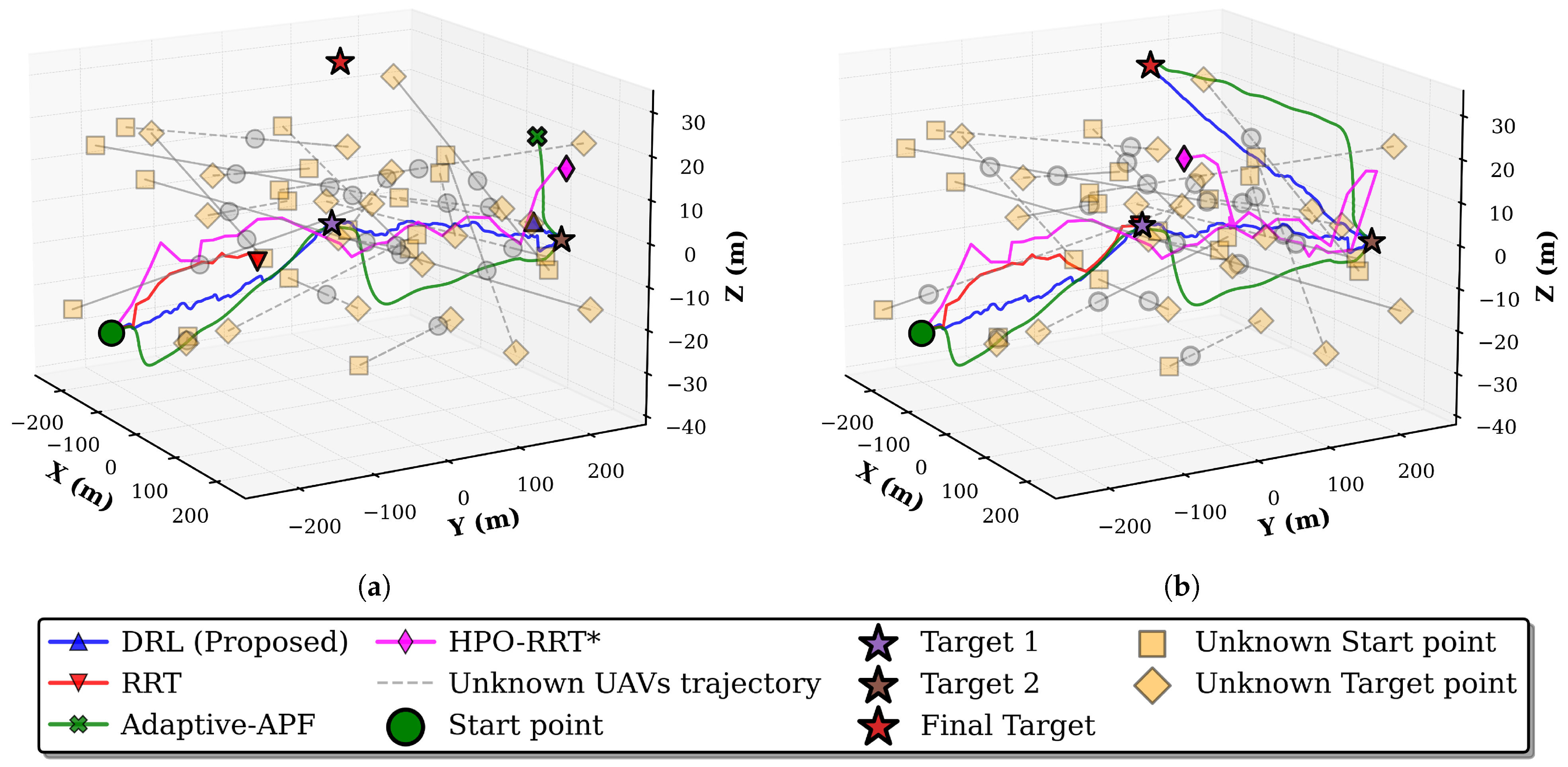
5.2.3. Performance Evaluation and Discussions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Debnath, D.; Vanegas, F.; Sandino, J.; Hawary, A.F.; Gonzalez, F. A Review of UAV Path-Planning Algorithms and Obstacle Avoidance Methods for Remote Sensing Applications. Remote Sens. 2024, 16, 4019. [Google Scholar] [CrossRef]
- Mcfadyen, A.; Mejias, L. A Survey of Autonomous Vision-Based See and Avoid for Unmanned Aircraft Systems. Prog. Aeosp. Sci. 2016, 80, 1–17. [Google Scholar] [CrossRef]
- Hossein Motlagh, N.; Taleb, T.; Arouk, O. Low-Altitude Unmanned Aerial Vehicles-Based Internet of Things Services: Comprehensive Survey and Future Perspectives. IEEE Internet Things J. 2016, 3, 899–922. [Google Scholar] [CrossRef]
- Wang, H.; Mao, W.; Eriksson, L. A Three-Dimensional Dijkstra’s Algorithm for Multi-Objective Ship Voyage Optimization. Ocean Eng. 2019, 186, 106131. [Google Scholar] [CrossRef]
- Huang, X.; Dong, X.; Ma, J.; Liu, K.; Ahmed, S.; Lin, J.; Qiu, B. The Improved A* Obstacle Avoidance Algorithm for the Plant Protection UAV with Millimeter Wave Radar and Monocular Camera Data Fusion. Remote Sens. 2021, 13, 3364. [Google Scholar] [CrossRef]
- LaValle, S.M. Rapidly-Exploring Random Trees: A New Tool for Path Planning. Annu. Res. Rep. 1998. Technical Report. Available online: https://api.semanticscholar.org/CorpusID:14744621 (accessed on 25 September 2025).
- Zhang, J.; An, Y.; Cao, J.; Ouyang, S.; Wang, L. UAV Trajectory Planning for Complex Open Storage Environments Based on an Improved RRT Algorithm. IEEE Access 2023, 11, 23189–23204. [Google Scholar] [CrossRef]
- Guo, Y.; Liu, X.; Jia, Q.; Liu, X.; Zhang, W. HPO-RRT*: A Sampling-Based Algorithm for UAV Real-Time Path Planning in a Dynamic Environment. Complex Intell. Syst. 2023, 9, 7133–7153. [Google Scholar] [CrossRef]
- Khatib, O. Real-Time Obstacle Avoidance for Manipulators and Mobile Robots. In Proceedings of the 1985 IEEE International Conference on Robotics and Automation, St. Louis, MO, USA, 25–28 March 1985; Volume 2, pp. 500–505. [Google Scholar] [CrossRef]
- Zhang, H.Y.; Lin, W.M.; Chen, A.X. Path Planning for the Mobile Robot: A Review. Symmetry 2018, 10, 450. [Google Scholar] [CrossRef]
- Mao, J.; Jia, Z.; Gu, H.; Shi, C.; Shi, H.; He, L.; Wu, Q. Robust UAV Path Planning with Obstacle Avoidance for Emergency Rescue. In Proceedings of the 2025 IEEE Wireless Communications and Networking Conference (WCNC), Milan, Italy, 24–27 March 2025; pp. 1–6. [Google Scholar] [CrossRef]
- Chen, Z.; Zhou, H.; Du, S.; Liu, J.; Zhang, L.; Liu, Q. Reinforcement Learning-Based Resource Allocation and Energy Efficiency Optimization for a Space-Air-Ground-Integrated Network. Electronics 2024, 13, 1792. [Google Scholar] [CrossRef]
- Mai, X.; Dong, N.; Liu, S.; Chen, H. UAV Path Planning Based on a Dual-Strategy Ant Colony Optimization Algorithm. Intell. Robot. 2023, 3, 666–684. [Google Scholar] [CrossRef]
- Zhang, M.; Han, Y.; Chen, S.; Liu, M.; He, Z.; Pan, N. A Multi-Strategy Improved Differential Evolution algorithm for UAV 3D trajectory planning in complex mountainous environments. Eng. Appl. Artif. Intell. 2023, 125, 106672. [Google Scholar] [CrossRef]
- Wu, J.; Sun, Y.; Bi, J.; Chen, C.; Xie, Y. A Novel Hybrid Enhanced Particle Swarm Optimization for UAV Path Planning. IEEE Trans. Veh. Technol. 2025, 74, 11806–11819. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, S.; Ma, T.; Xiao, Y.; Chen, M.Z.; Wang, L. Swarm intelligence: A survey of model classification and applications. Chin. J. Aeronaut. 2025, 38, 102982. [Google Scholar] [CrossRef]
- Wang, X.; Wang, S.; Liang, X.; Zhao, D.; Huang, J.; Xu, X.; Dai, B.; Miao, Q. Deep Reinforcement Learning: A Survey. IEEE Trans. Neural Netw. Learn. Syst. 2024, 35, 5064–5078. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, W.; Wang, J.; Yuan, Y. Recent Progress, Challenges and Future Prospects of Applied Deep Reinforcement Learning: A Practical Perspective in Path Planning. Neurocomputing 2024, 608, 128423. [Google Scholar] [CrossRef]
- Lei, X.; Zhang, Z.; Dong, P. Dynamic Path Planning of Unknown Environment Based on Deep Reinforcement Learning. J. Robot. 2018, 2018, 5781591. [Google Scholar] [CrossRef]
- Alibabaei, K.; Gaspar, P.D.; Assunção, E.; Alirezazadeh, S.; Lima, T.M.; Soares, V.N.G.J.; Caldeira, J.M.L.P. Comparison of On-Policy Deep Reinforcement Learning A2C with Off-Policy DQN in Irrigation Optimization: A Case Study at a Site in Portugal. Computers 2022, 11, 104. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, Z.; Qu, J.; Chen, X. APPA-3D: An Autonomous 3D Path Planning Algorithm for UAVs in Unknown Complex Environments. Sci. Rep. 2024, 14, 1231. [Google Scholar] [CrossRef]
- Arafat, M.Y.; Alam, M.M.; Moh, S. Vision-Based Navigation Techniques for Unmanned Aerial Vehicles: Review and Challenges. Drones 2023, 7, 89. [Google Scholar] [CrossRef]
- Ouyang, X.; Zeng, F.; Lv, D.; Dong, T.; Wang, H. Cooperative Navigation of UAVs in GNSS-Denied Area With Colored RSSI Measurements. IEEE Sens. J. 2021, 21, 2194–2210. [Google Scholar] [CrossRef]
- Gu, S.; Yang, L.; Du, Y.; Chen, G.; Walter, F.; Wang, J.; Knoll, A. A Review of Safe Reinforcement Learning: Methods, Theories, and Applications. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 11216–11235. [Google Scholar] [CrossRef]
- Ebrahimi, D.; Sharafeddine, S.; Ho, P.H.; Assi, C. Autonomous UAV Trajectory for Localizing Ground Objects: A Reinforcement Learning Approach. IEEE. Trans. Mob. Comput. 2021, 20, 1312–1324. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, Z. Location, Localization, and Localizability: Location-Awareness Technology for Wireless Networks; Springer: New York, NY, USA, 2011. [Google Scholar] [CrossRef]
- Singh, N.; Choe, S.; Punmiya, R. Machine Learning Based Indoor Localization Using Wi-Fi RSSI Fingerprints: An Overview. IEEE Access 2021, 9, 127150–127174. [Google Scholar] [CrossRef]
- Zafari, F.; Gkelias, A.; Leung, K.K. A Survey of Indoor Localization Systems and Technologies. IEEE Commun. Surv. Tutor. 2019, 21, 2568–2599. [Google Scholar] [CrossRef]
- Zekavat, R.; Buehrer, R.M. The Kalman Filter and Its Applications in GNSS and INS; Wiley-IEEE Press: Hoboken, NJ, USA, 2012; pp. 709–751. [Google Scholar] [CrossRef]
- Luo, C.; McClean, S.I.; Parr, G.; Teacy, L.; De Nardi, R. UAV Position Estimation and Collision Avoidance Using the Extended Kalman Filter. IEEE Trans. Veh. Technol. 2013, 62, 2749–2762. [Google Scholar] [CrossRef]
- Xiang, B.; Yan, F.; Zhu, Y.; Wu, T.; Xia, W.; Pang, J.; Liu, W.; Heng, G.; Shen, L. UAV Assisted Localization Scheme of WSNs Using RSSI and CSI Information. In Proceedings of the 2020 IEEE 6th International Conference on Computer and Communications (ICCC), Chengdu, China, 11–14 December 2020; pp. 718–722. [Google Scholar] [CrossRef]
- Kabiri, M.; Cimarelli, C.; Bavle, H.; Sanchez-Lopez, J.L.; Voos, H. A Review of Radio Frequency Based Localisation for Aerial and Ground Robots with 5G Future Perspectives. Sensors 2023, 23, 188. [Google Scholar] [CrossRef] [PubMed]
- Beard, R.W.; McLain, T.W. Small Unmanned Aircraft: Theory and Practice; Princeton University Press: Princeton, NJ, USA, 2012. [Google Scholar]
- Lee, T.; Leok, M.; McClamroch, N.H. Geometric Tracking Control of a Quadrotor UAV on SE(3). In Proceedings of the 49th IEEE Conference on Decision and Control (CDC), Atlanta, GA, USA, 15–17 December 2010; pp. 5420–5425. [Google Scholar] [CrossRef]
- Coates, E.M.; Fossen, T.I. Geometric Reduced-Attitude Control of Fixed-Wing UAVs. Appl. Sci. 2021, 11, 3147. [Google Scholar] [CrossRef]
- Yuan, X.; Xu, J.; Li, S. Design and Simulation Verification of Model Predictive Attitude Control Based on Feedback Linearization for Quadrotor UAV. Appl. Sci. 2025, 15, 5218. [Google Scholar] [CrossRef]
- Li, Y.; Tan, G. Attitude Control of Quadrotor UAV Using Improved Active Disturbance Rejection Control. Front. Comput. Intell. Syst. 2023, 5, 90–95. [Google Scholar] [CrossRef]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal Policy Optimization Algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar] [CrossRef]
- Chang, Z.; Deng, H.; You, L.; Min, G.; Garg, S.; Kaddoum, G. Trajectory Design and Resource Allocation for Multi-UAV Networks: Deep Reinforcement Learning Approaches. IEEE Trans. Netw. Sci. Eng. 2023, 10, 2940–2951. [Google Scholar] [CrossRef]
- Qi, C.; Wu, C.; Lei, L.; Li, X.; Cong, P. UAV Path Planning Based on the Improved PPO Algorithm. In Proceedings of the 2022 Asia Conference on Advanced Robotics, Automation, and Control Engineering (ARACE), Qingdao, China, 26–28 August 2022; pp. 193–199. [Google Scholar] [CrossRef]
- Andrychowicz, M.; Raichuk, A.; Stańczyk, P.; Orsini, M.; Girgin, S.; Marinier, R.; Hussenot, L.; Geist, M.; Pietquin, O.; Michalski, M.; et al. What Matters In On-Policy Reinforcement Learning? A Large-Scale Empirical Study. In Proceedings of the 9th International Conference on Learning Representations (ICLR), Vienna, Austria, 3–7 May 2021. [Google Scholar]
- Moro, S.; Teeda, V.; Scazzoli, D.; Reggiani, L.; Magarini, M. Experimental UAV-Aided RSSI Localization of a Ground RF Emitter in 865 MHz and 2.4 GHz Bands. In Proceedings of the 2022 IEEE 95th Vehicular Technology Conference: (VTC2022-Spring), Helsinki, Finland, 19–22 June 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Li, H.; Duan, X.L. Research on Adaptive Artificial Potential Field Obstacle Avoidance Technology for Unmanned Aerial Vehicles in Complex Environments. Int. J. Wirel. Mob. Comput. 2025, 29, 10072641. [Google Scholar] [CrossRef]

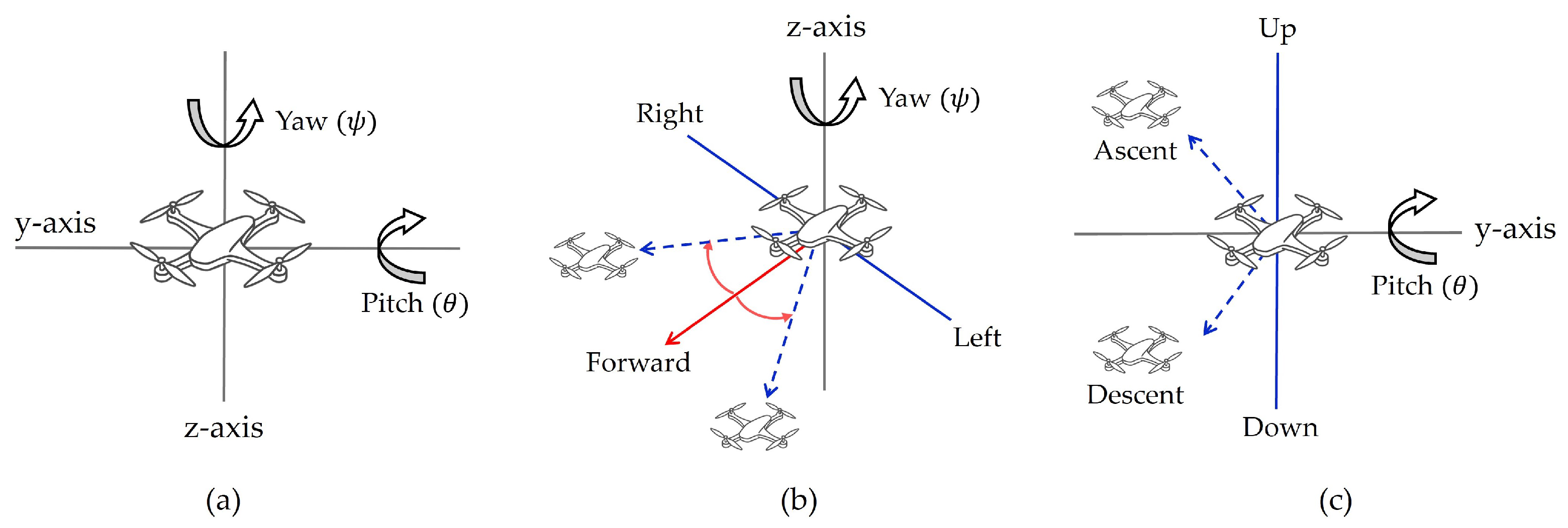
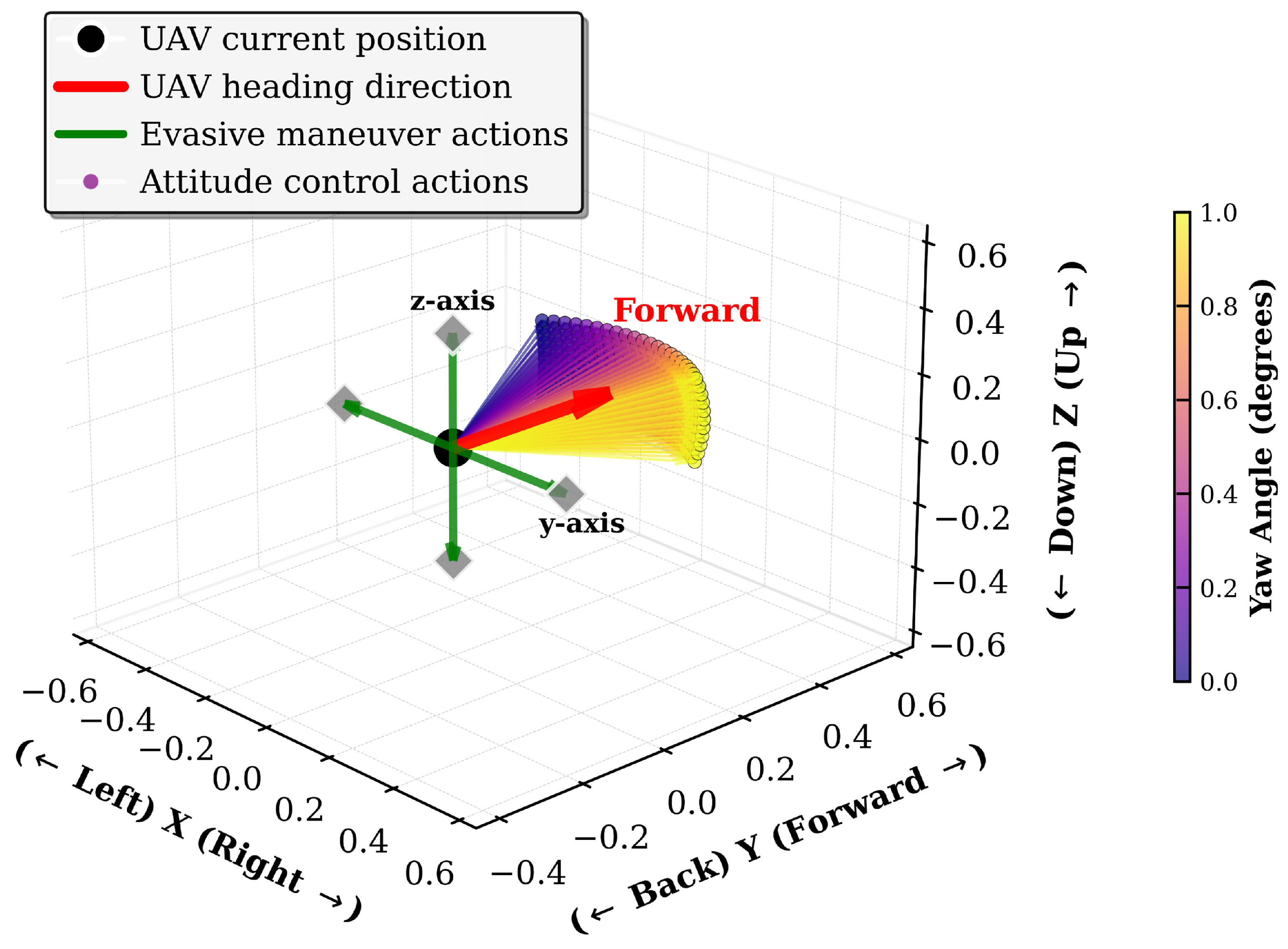


| Actions | Yaw / | Pitch / | Description |
|---|---|---|---|
| Stop | Set velocity v to 0. | ||
| Forward | Maintain direction. | ||
| Yaw right | Horizontal right turn. | ||
| Yaw left | Horizontal left turn. | ||
| Pitch up | Altitude ascent. | ||
| Pitch down | Altitude descent. | ||
| Attitude control | Direction changed by . |
| Parameter | Value |
|---|---|
| UAV agent’s velocity v | 1.0 (m/s) |
| RSS sensing range | 100.0 (m) |
| Collision avoidance range | 50.0 (m) |
| Collision threshold | 5.0 (m) |
| Number of unknown UAV | [5, 10, 20] |
| Unknown UAV’s velocity | 2.0–10.0 (m/s) |
| Path loss exponent | 2.2–4.0 |
| weight | 0.7 |
| weight | 1.3 |
| Clip factor | 0.2 |
| Actor learning rate | |
| Critic learning rate |
| Methodology | Single-Target Scenario (m) | Multi-Target Scenario (m) |
|---|---|---|
| Baseline (Optimal path) | 164.54 | 932.51 |
| Proposed | 172.37 (+7.83) | 971.38 (+38.87) |
| Adaptive-APF | 193.41 (+28.87) | 1092.13 (+159.62) |
| HPO-RRT* | 176.70 (+12.16) | 1046.44 (+113.93) |
| RRT | 171.13 (+6.59) | No path found |
| GEPSO | 217.43 (+52.89) | 1277.83 (+345.32) |
| Methodology | Single-Target Scenario (%) | Multi-Target Scenario (%) |
|---|---|---|
| Proposed | 98.27 | 99.40 |
| Adaptive-APF | 89.07 | 89.43 |
| HPO-RRT* | 43.18 | 0.4 |
| RRT | 3.8 | Not applicable |
| GEPSO | 97.41 | 87.83 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, K.; Seon, J.; Kim, J.; Kim, J.; Sun, Y.; Lee, S.; Kim, S.; Hwang, B.; Lee, M.; Kim, J. Robust UAV Path Planning Using RSS in GPS-Denied and Dense Environments Based on Deep Reinforcement Learning. Electronics 2025, 14, 3844. https://doi.org/10.3390/electronics14193844
Kim K, Seon J, Kim J, Kim J, Sun Y, Lee S, Kim S, Hwang B, Lee M, Kim J. Robust UAV Path Planning Using RSS in GPS-Denied and Dense Environments Based on Deep Reinforcement Learning. Electronics. 2025; 14(19):3844. https://doi.org/10.3390/electronics14193844
Chicago/Turabian StyleKim, Kyounghun, Joonho Seon, Jinwook Kim, Jeongho Kim, Youngghyu Sun, Seongwoo Lee, Soohyun Kim, Byungsun Hwang, Mingyu Lee, and Jinyoung Kim. 2025. "Robust UAV Path Planning Using RSS in GPS-Denied and Dense Environments Based on Deep Reinforcement Learning" Electronics 14, no. 19: 3844. https://doi.org/10.3390/electronics14193844
APA StyleKim, K., Seon, J., Kim, J., Kim, J., Sun, Y., Lee, S., Kim, S., Hwang, B., Lee, M., & Kim, J. (2025). Robust UAV Path Planning Using RSS in GPS-Denied and Dense Environments Based on Deep Reinforcement Learning. Electronics, 14(19), 3844. https://doi.org/10.3390/electronics14193844









