A Simple Burst-Mode Multiple-Entropy TRNG Based on Standard Logic Primitives
Abstract
1. Introduction
1.1. Modern Solutions for TRNGs
1.2. TRNG Core Concept
2. Materials and Methods
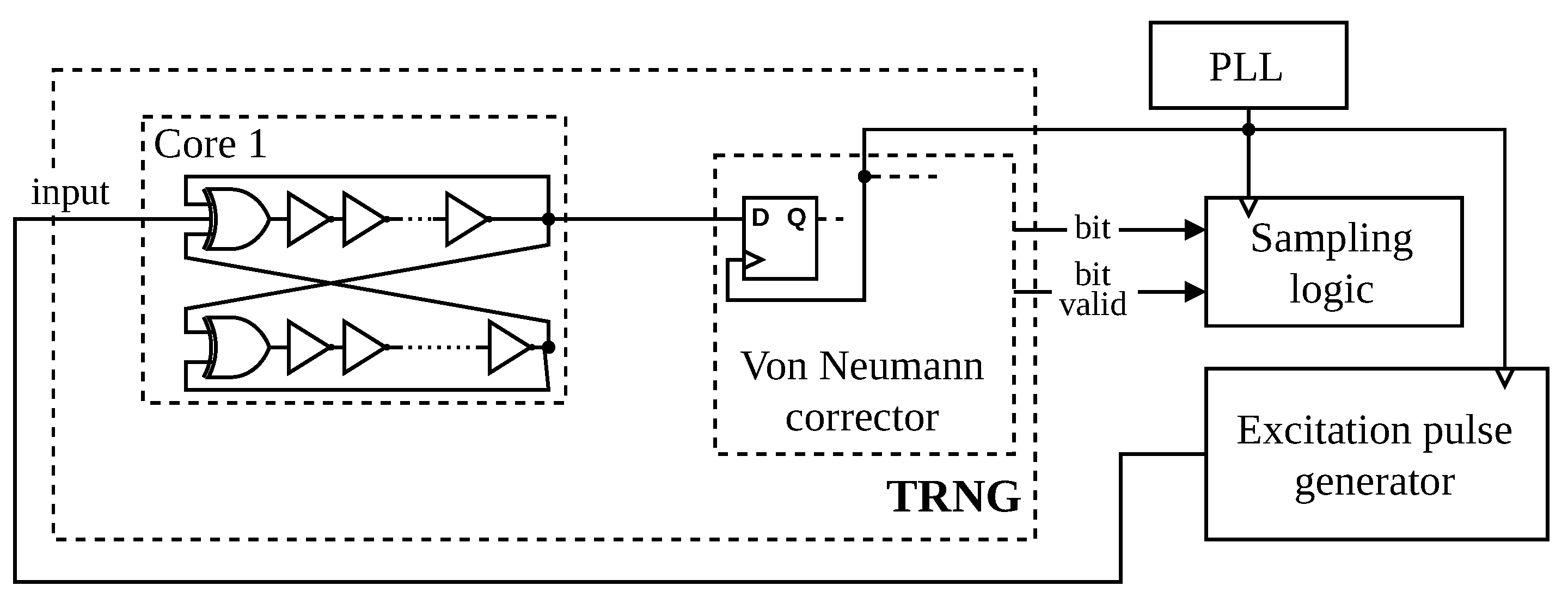
2.1. Macromodel of the TRNG Core
2.2. TRNG Implementation in CPLD
2.3. Data Acquisition Method
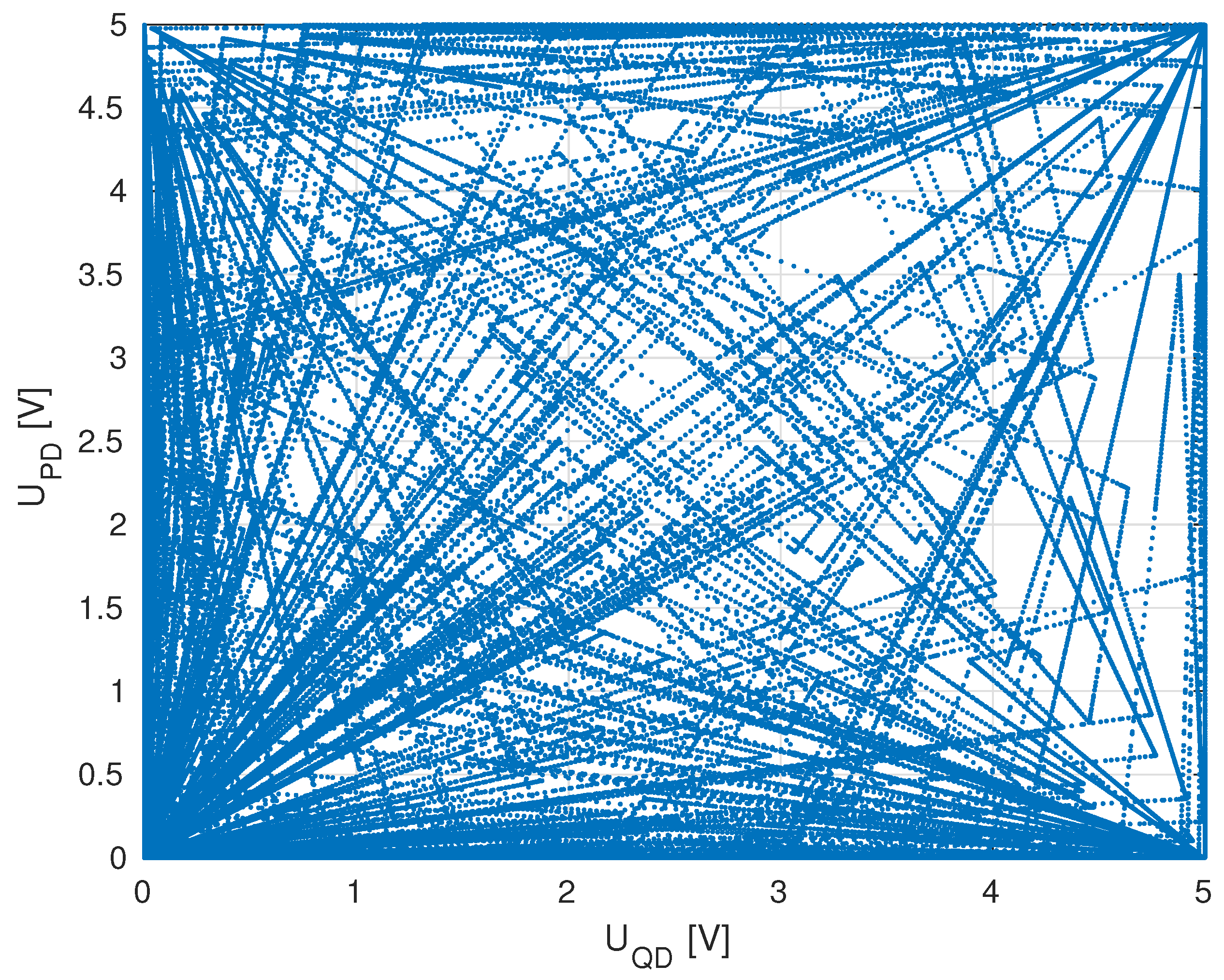
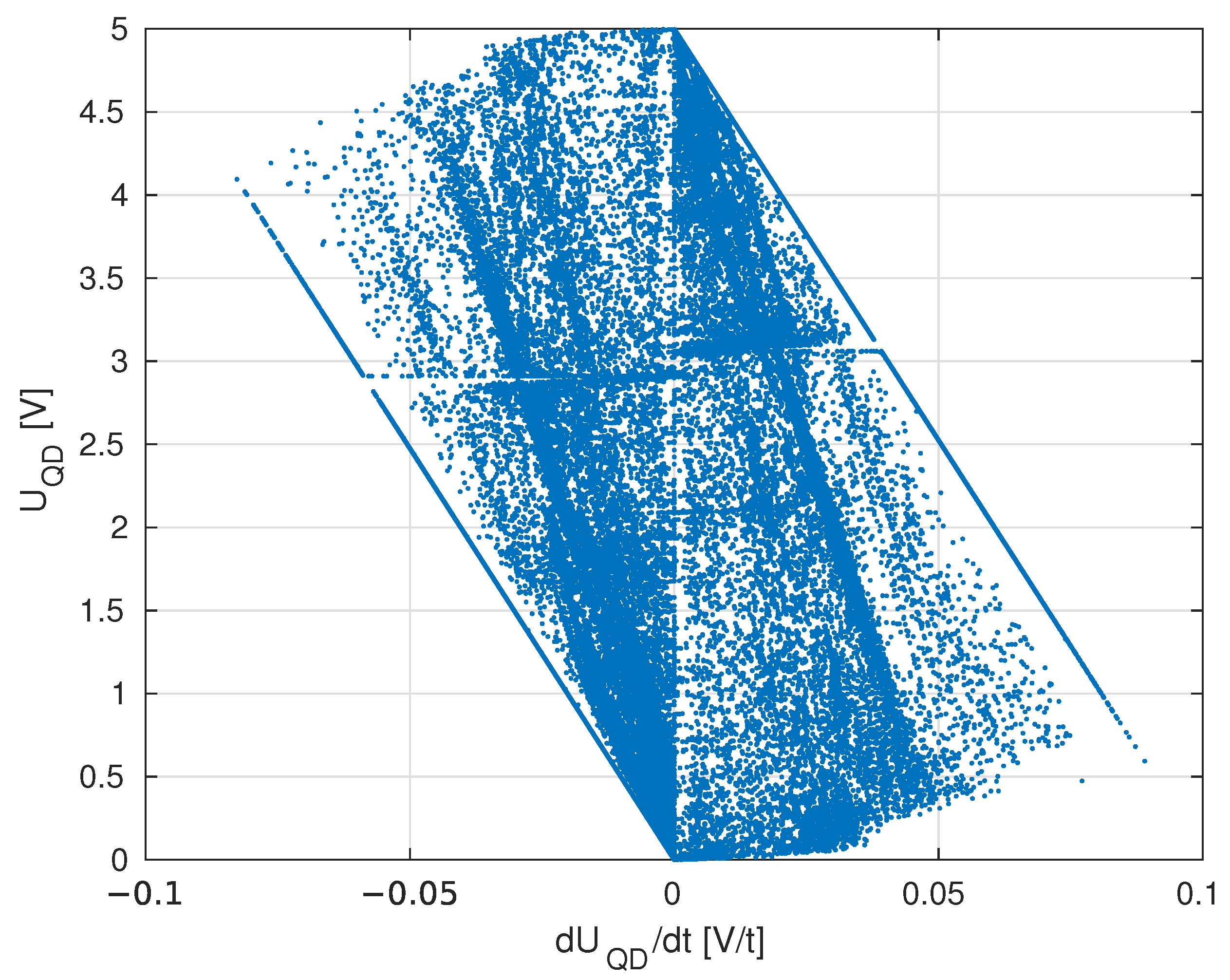
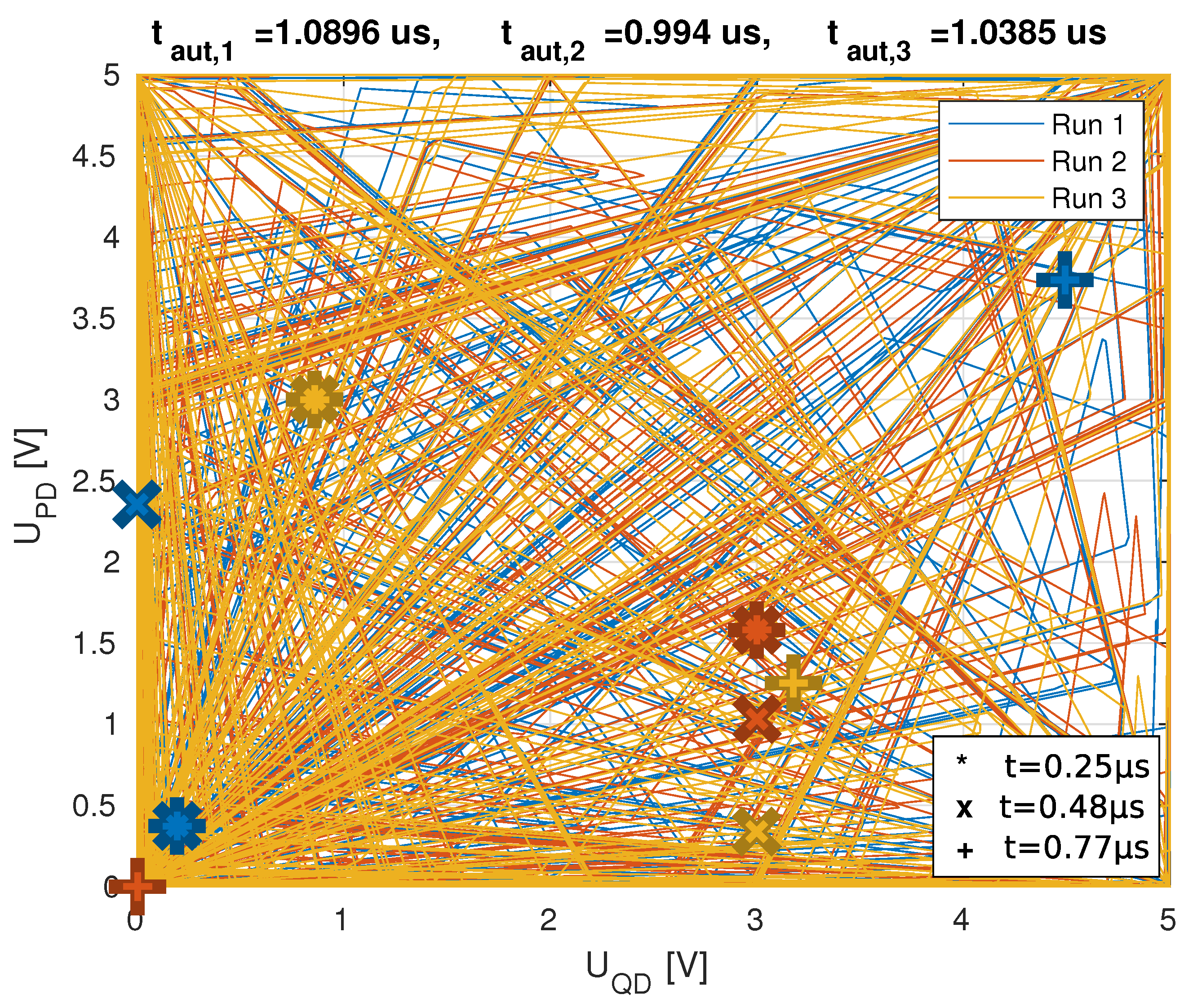
3. Results
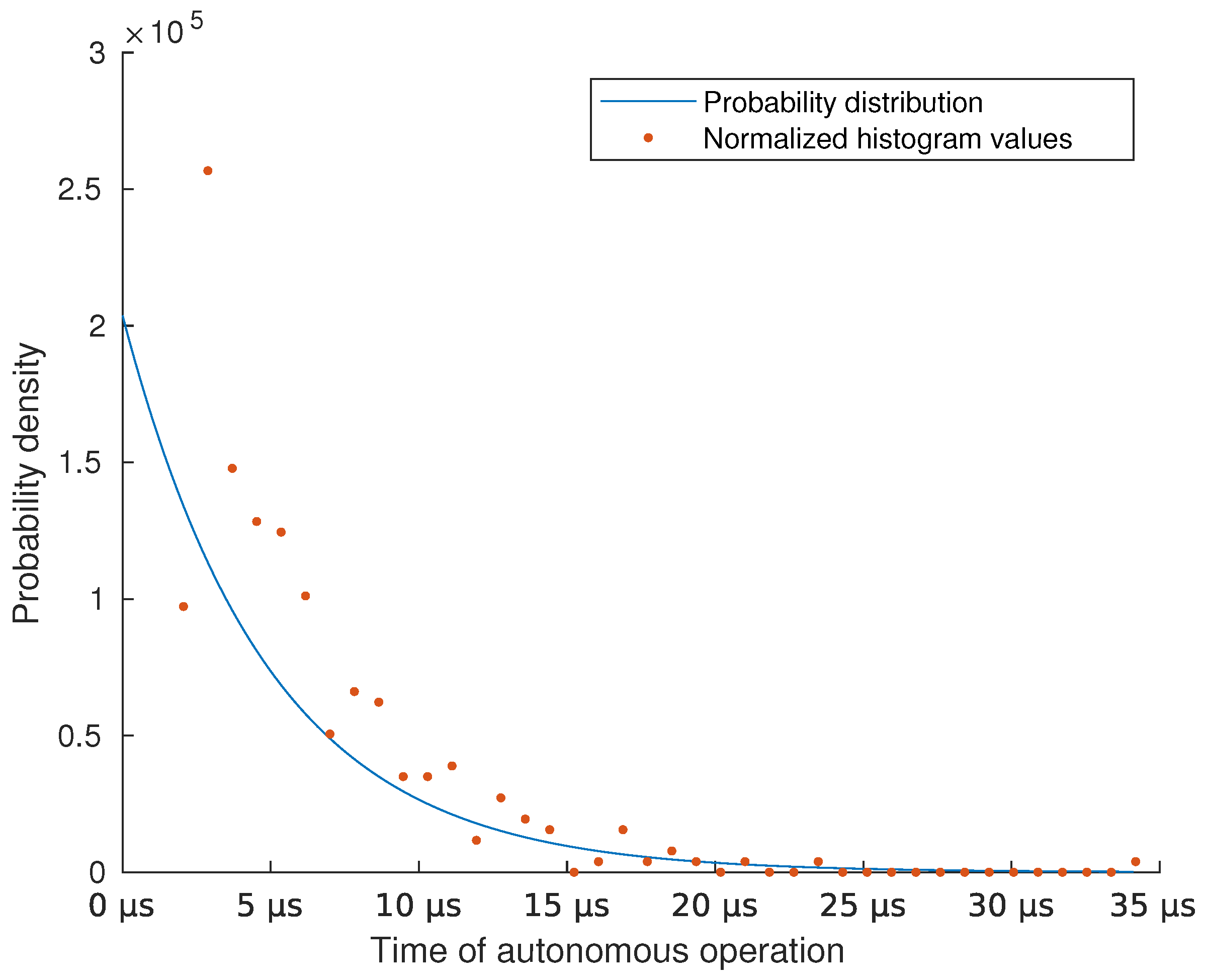
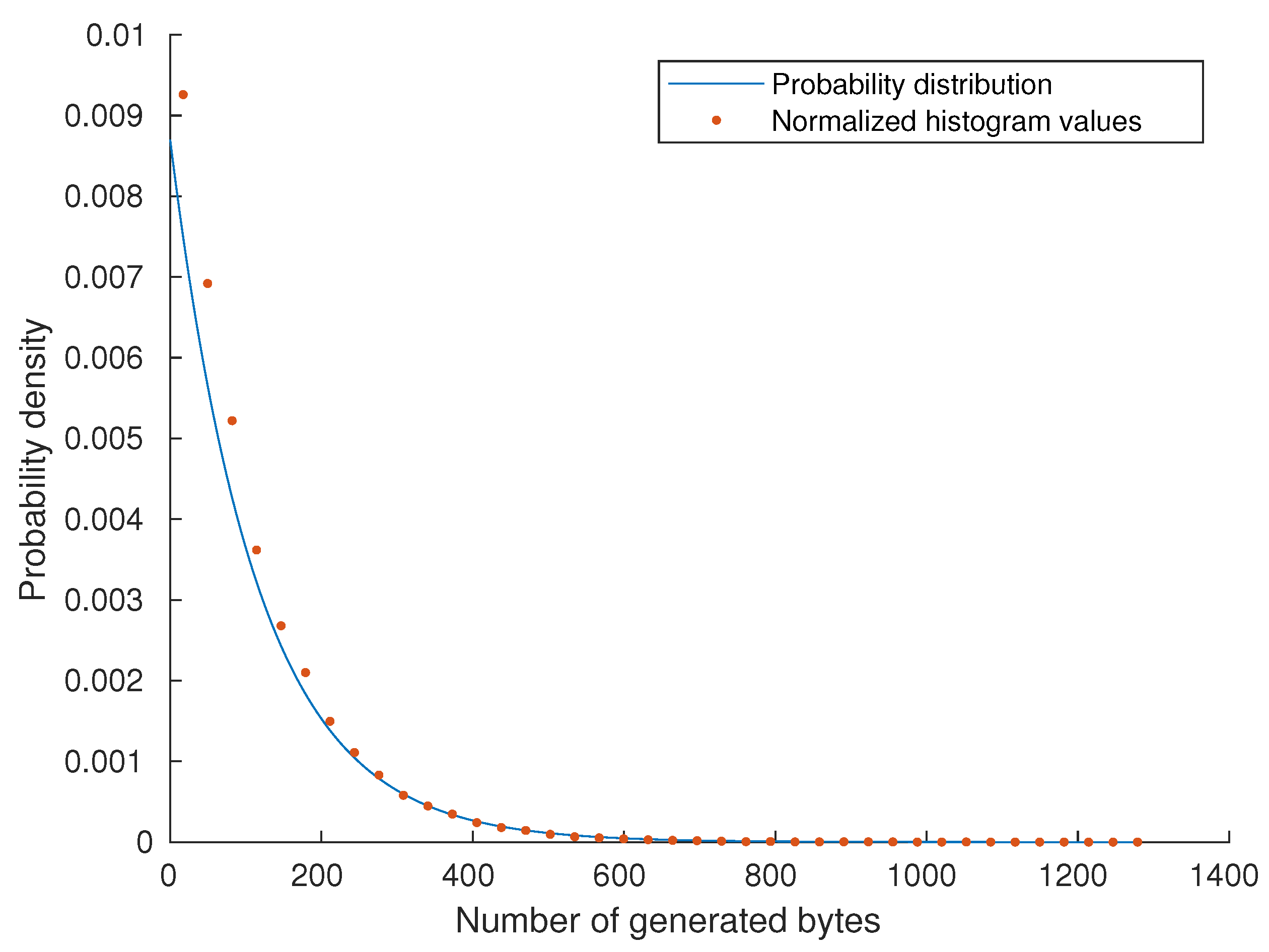
3.1. Numerical Analysis
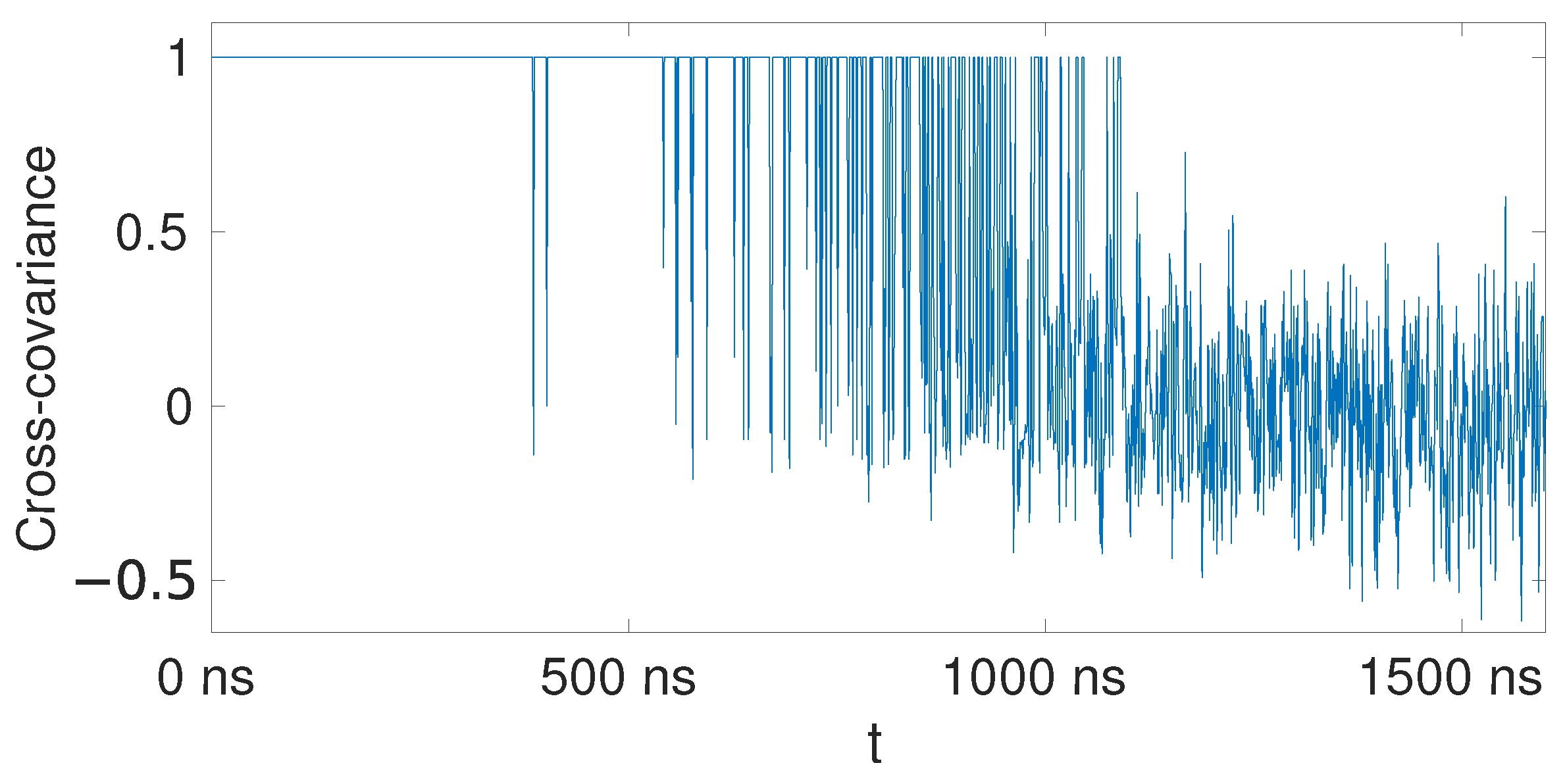
3.2. Empirical Verification
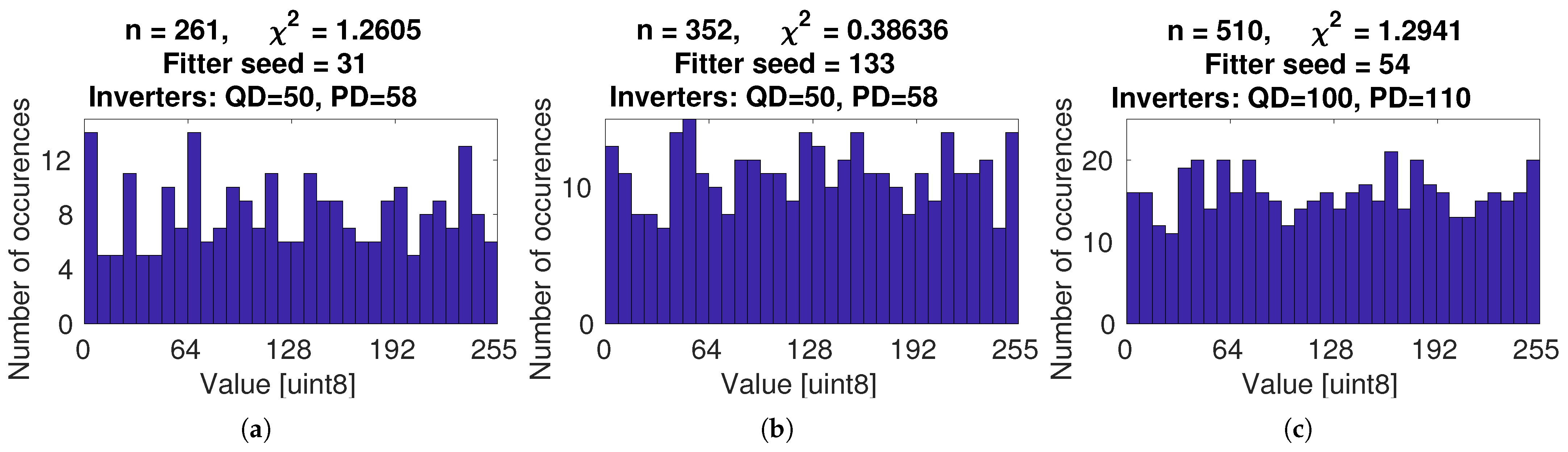
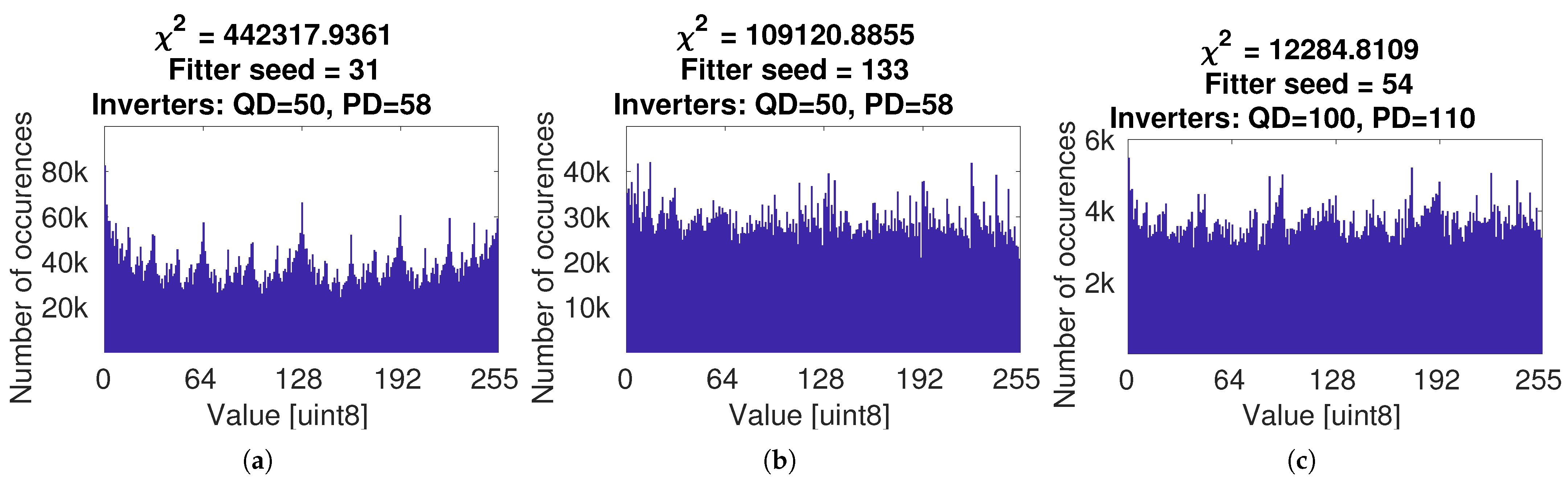
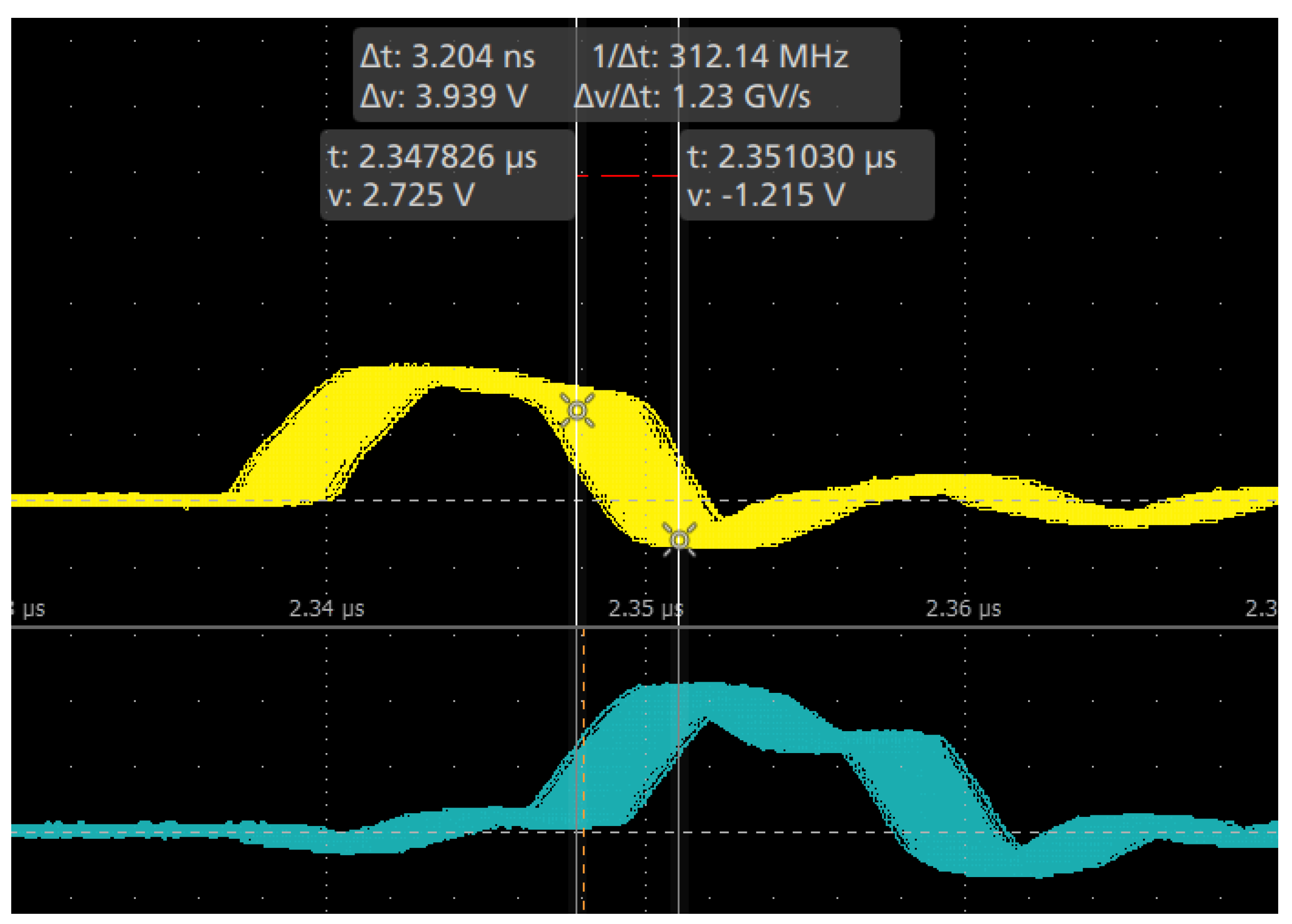
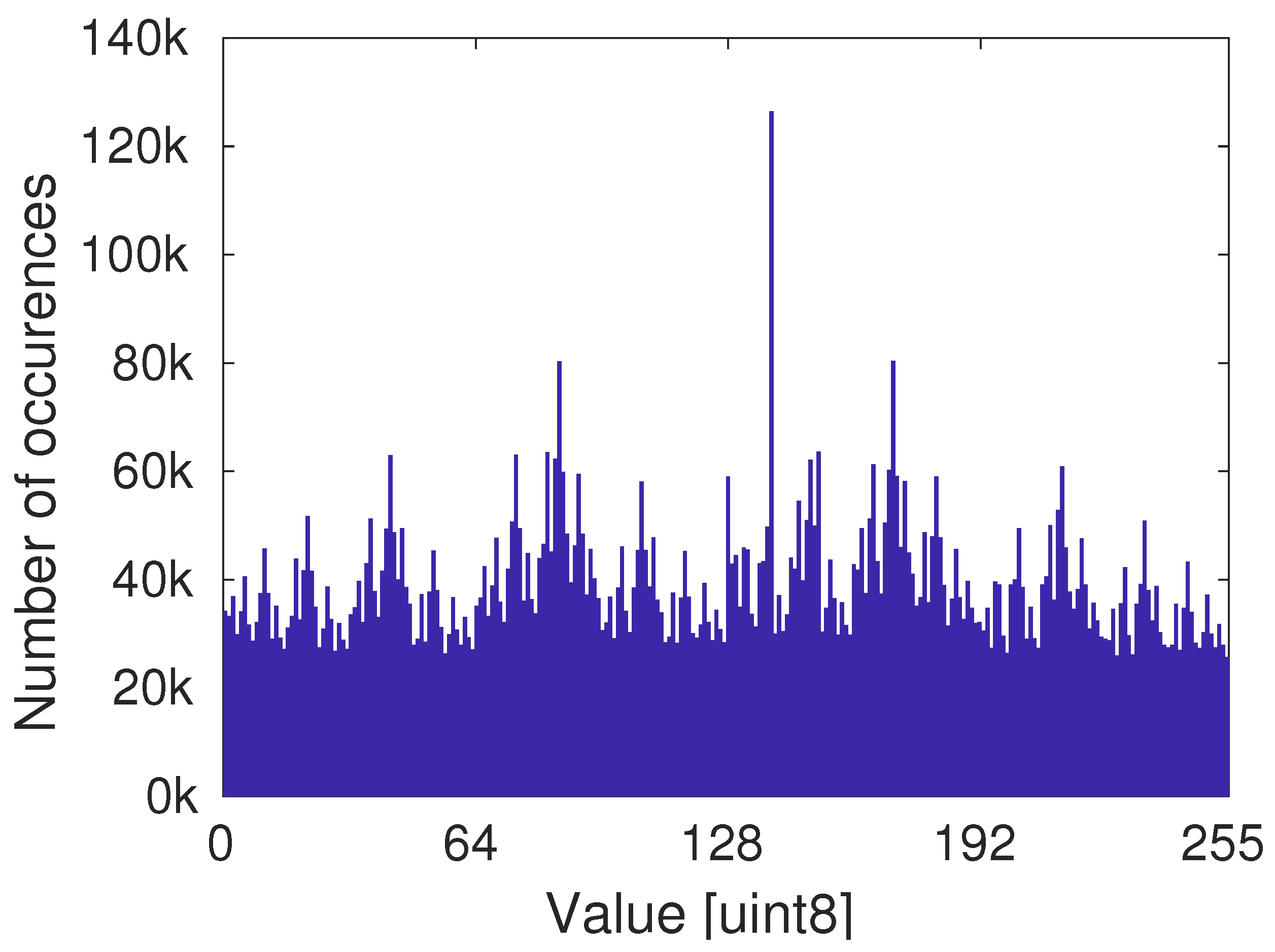
3.2.1. Single Core Performance
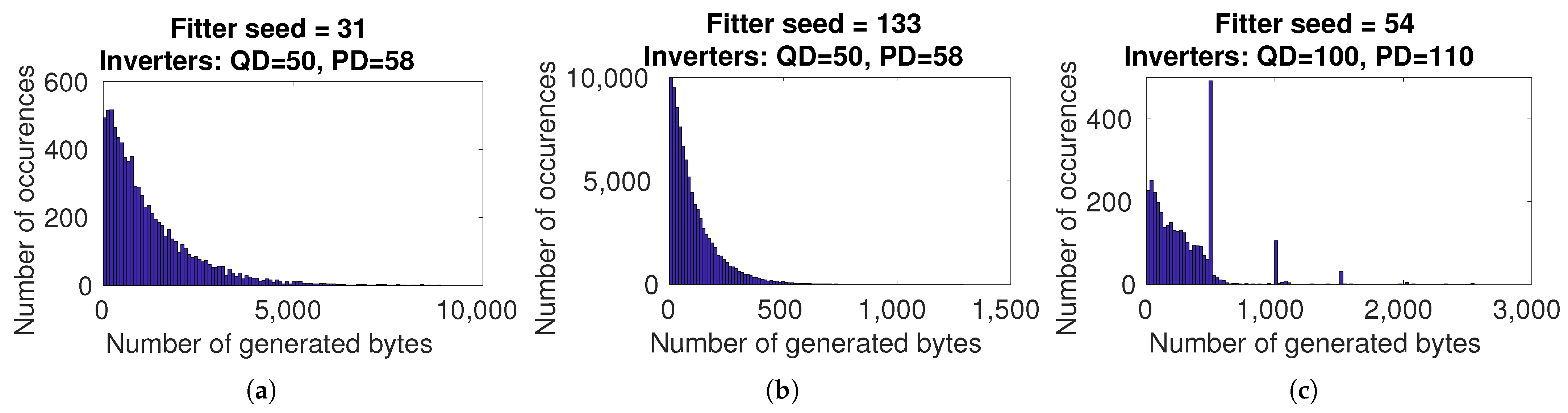
3.2.2. Dual Core Performance
- It is important to note that the majority of LUTs are consumed for delay paths, and the circuit was not optimized in terms of resources used. We focused on properly operating designs according to the macromodel.
- Throughput had to be reduced due to limitations of the platform. Sampling speed had to be slow enough to allow the sampler and transmitter logic to work. The VN corrector itself reduces the transmission rate by at least half. Up to a certain point, there is an interchangeability between sampling speed and number of cores; however, the limitation is burst length—more intense decimation results in lower burst lengths (measured in number of output bits).
- Our design can work on most low-resource platforms—no specialized hardware resources are necessary.
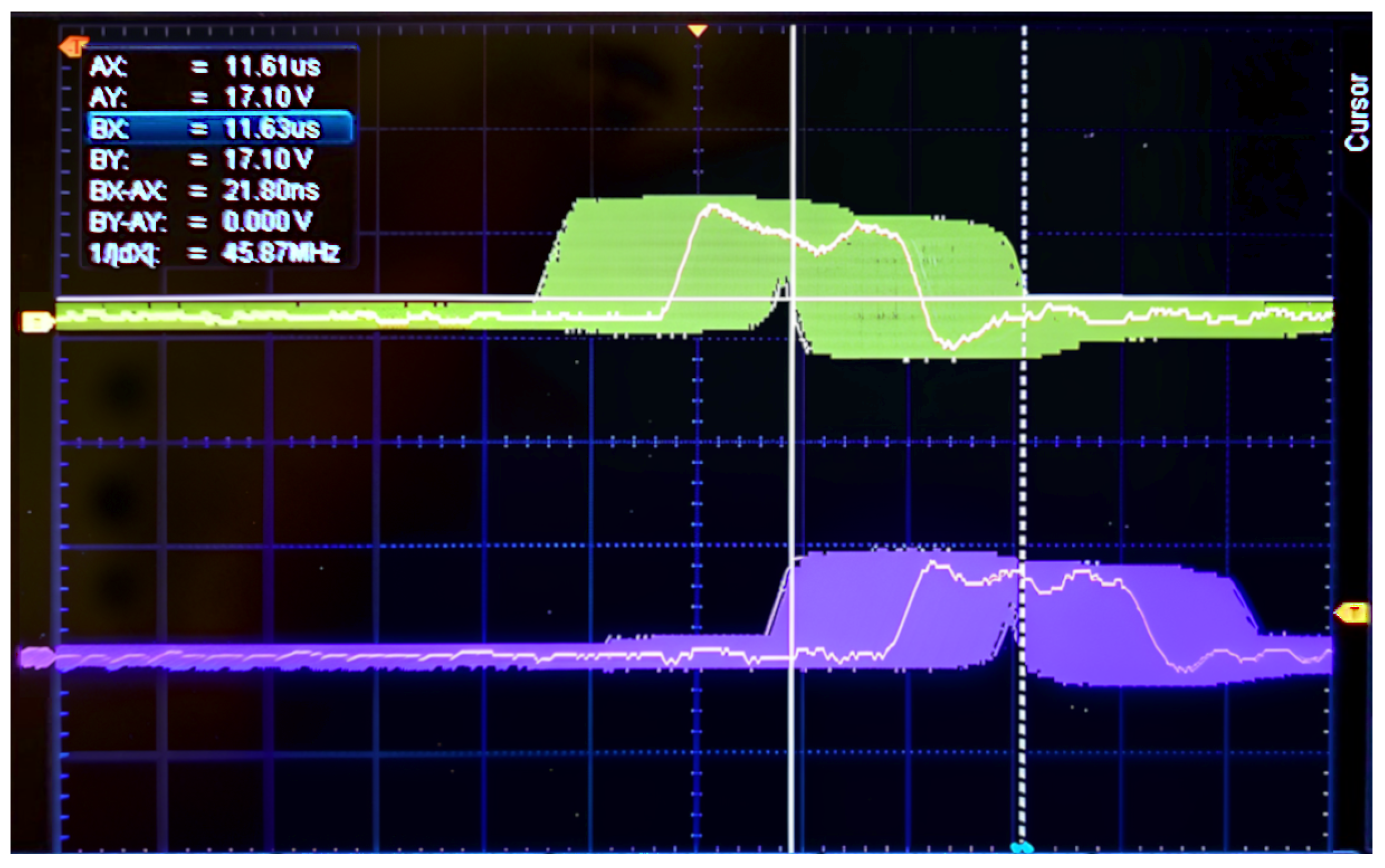
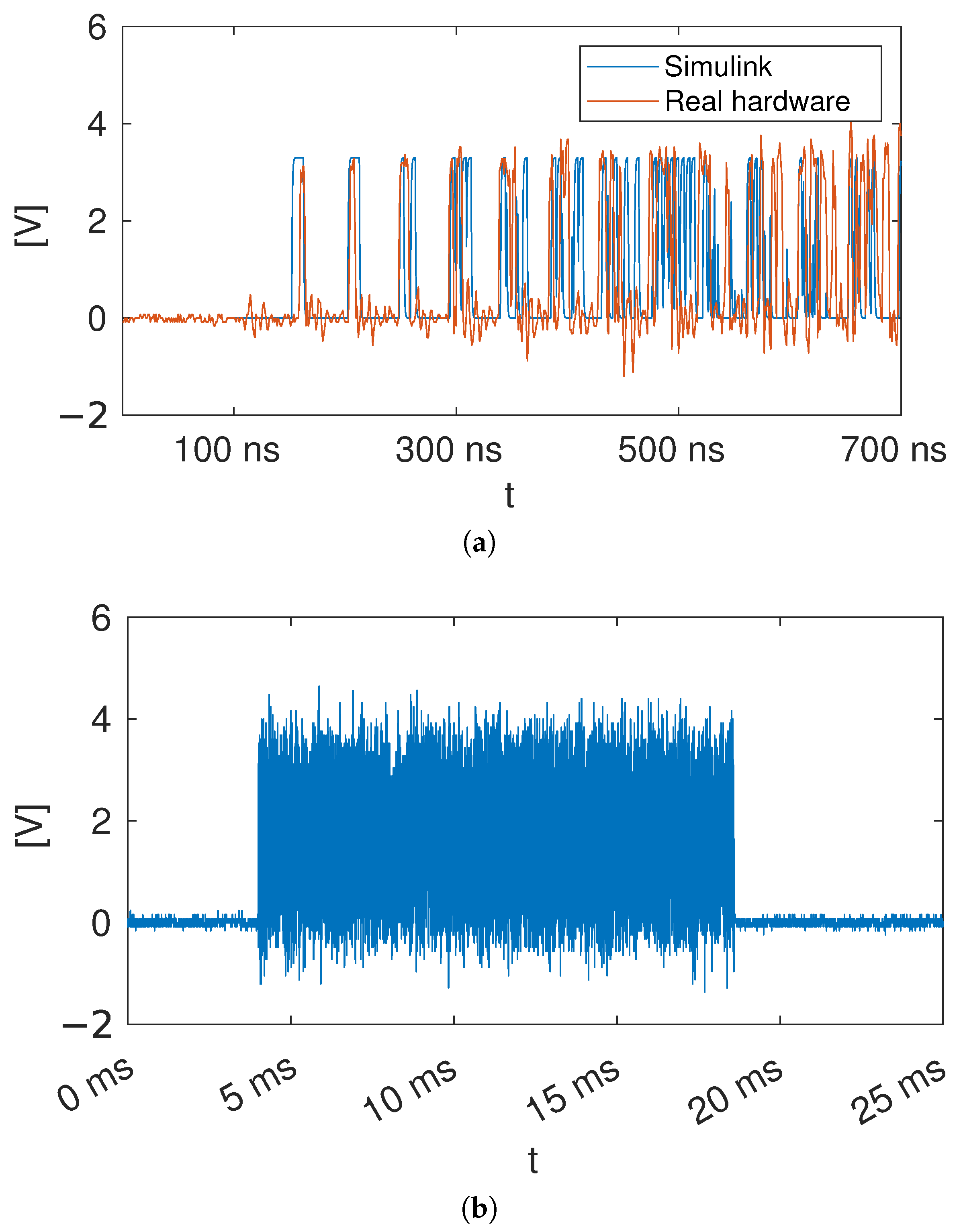
3.2.3. Concept Validation with an FPGA
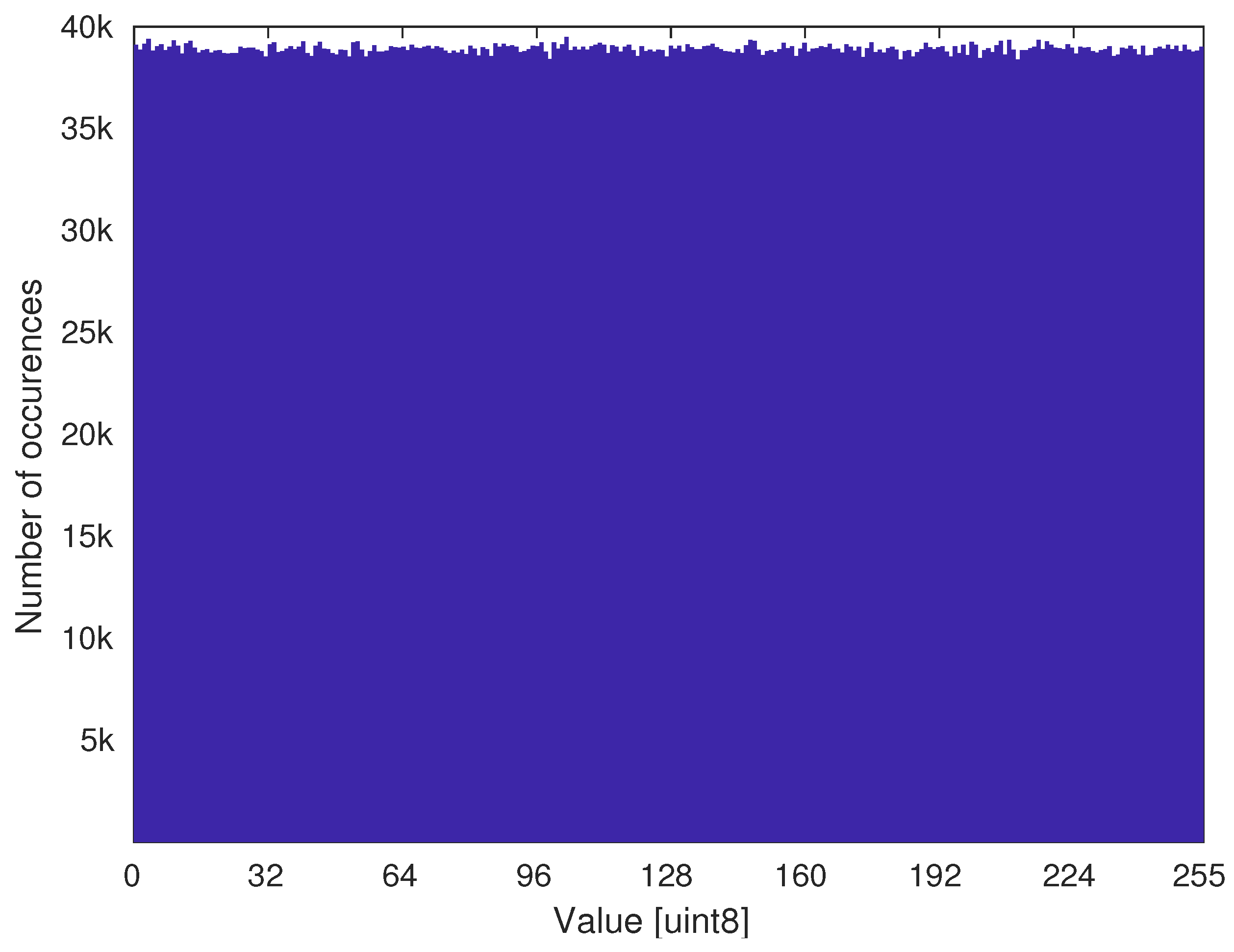
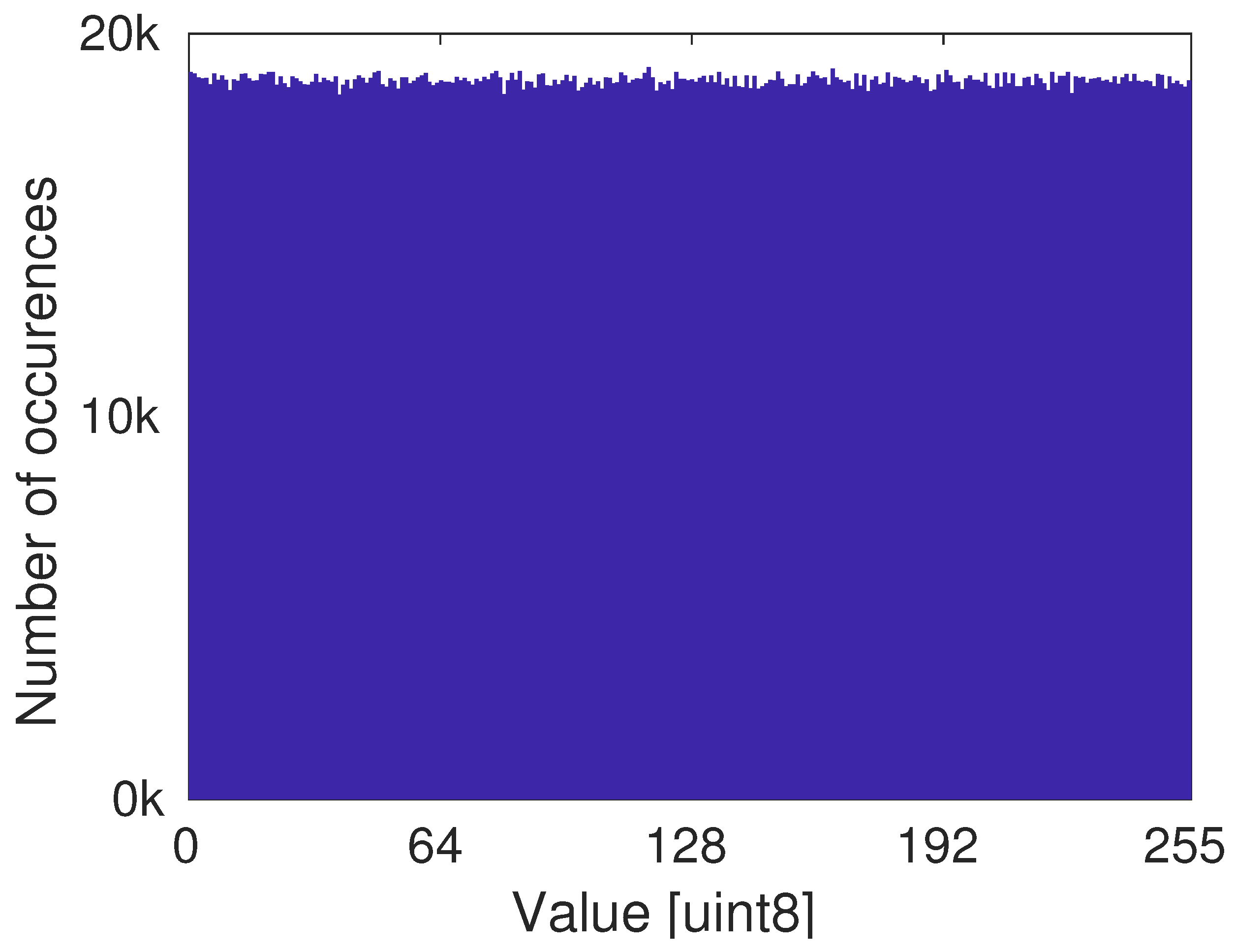
3.3. Statistical Tests
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Goldberg, I.; Wagner, D. Randomness and the netscape browser. Dr. Dobb’s J. 1996. [Google Scholar]
- Peterson, I. Lava Lamp Randomness. Available online: https://www.sciencenews.org/article/lava-lamp-randomness (accessed on 1 September 2025).
- Hofemeier, G.H. What is Intel® Secure Key Technology? Available online: https://www.intel.com/content/www/us/en/developer/articles/technical/what-is-secure-key-technology.html (accessed on 1 September 2025).
- Taylor, G.; Cox, G. Behind Intel’s new random-number generator. IEEE Spectrum, 2 December 2021; pp. 1–9. [Google Scholar]
- Bassham, L.E.; Rukhin, A.L.; Soto, J.; Nechvatal, J.R.; Smid, M.E.; Barker, E.B.; Leigh, S.D.; Levenson, M.; Vangel, M.; Banks, D.L.; et al. SP 800-22 Rev. 1a. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications; Technical Report; National Institute of Standards & Technology: Gaithersburg, MD, USA, 2010. [Google Scholar]
- Safi, M.; Simpson, B.; Clark, E.; Idriss, H.; Idriss, T. Lightweight Random Obfuscation Protocol: A PUF-based Mutual Authentication Protocol for IoT Devices. In Proceedings of the 2023 IEEE International Conference on Artificial Intelligence, Blockchain, and Internet of Things (AIBThings), Mount Pleasant, MI, USA, 16–17 September 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Kok, C.L.; Ho, C.K.; Lee, T.K.; Loo, Z.Y.; Koh, Y.Y.; Chai, J.P. A Novel and Low-Cost Cloud-Enabled IoT Integration for Sustainable Remote Intravenous Therapy Management. Electronics 2024, 13, 1801. [Google Scholar] [CrossRef]
- Cui, J.; Yi, M.; Cao, D.; Yao, L.; Wang, X.; Liang, H.; Huang, Z.; Qi, H.; Ni, T.; Lu, Y. Design of True Random Number Generator Based on Multi-Stage Feedback Ring Oscillator. IEEE Trans. Circuits Syst. II Express Briefs 2022, 69, 1752–1756. [Google Scholar] [CrossRef]
- Bharat Meitei, H.; Kumar, M. Design and Implementation of Multiple Ring Oscillator-Based TRNG Architecture by Using ADPLL. IEEE Access 2025, 13, 9252–9264. [Google Scholar] [CrossRef]
- Della Sala, R.; Bellizia, D.; Scotti, G. Unveiling the True Power of the Latched Ring Oscillator for a Unified PUF and TRNG Architecture. IEEE Trans. Very Large Scale Integr. (VLSI) Systems 2024, 32, 2403–2407. [Google Scholar] [CrossRef]
- Ahmed, H.O.; Kim, D.; Buchanan, W.J. A True Random Number Generator Based on Race Hazard and Jitter of Braided and Cross-Coupled Logic Gates Using FPGA. IEEE Access 2024, 12, 182943–182955. [Google Scholar] [CrossRef]
- Wang, X.; Liang, H.; Wang, Y.; Yao, L.; Guo, Y.; Yi, M.; Huang, Z.; Qi, H.; Lu, Y. High-Throughput Portable True Random Number Generator Based on Jitter-Latch Structure. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 741–750. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, Y.; Chen, B.; Sang, P.; Wu, J.; Wei, X.; Zhan, X.; Chen, J. High-Speed True Random Number Generator with Multiple Entropy Sources: Ring Oscillator Jitter and Random Telegraph Noise. IEEE Embed. Syst. Lett. 2025, 1. [Google Scholar] [CrossRef]
- Rajski, J.; Trawka, M.; Tyszer, J.; Włodarczak, B. A Lightweight True Random Number Generator for Root of Trust Applications. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2023, 42, 2815–2825. [Google Scholar] [CrossRef]
- Della Sala, R.; Bellizia, D.; Scotti, G. High-Throughput FPGA-Compatible TRNG Architecture Exploiting Multistimuli Metastable Cells. IEEE Trans. Circuits Syst. I Regul. Pap. 2022, 69, 4886–4897. [Google Scholar] [CrossRef]
- Chen, C.; Li, S.; Song, C. A 200 kb/s 36 µw True Random Number Generator Based on Dual Oscillators for IOT Security Application. Electronics 2023, 12, 2332. [Google Scholar] [CrossRef]
- Mahalingam, H.; Rethinam, S.; Janakiraman, S.; Rengarajan, A. Non-Identical Inverter Rings as an Entropy Source: NIST-90B-Verified TRNG Architecture on FPGAs for IoT Device Integrity. Mathematics 2023, 11, 1049. [Google Scholar] [CrossRef]
- Matuszewski, Ł.; Jessa, M. A Low-Complexity Start–Stop True Random Number Generator for FPGAs. Appl. Sci. 2024, 14, 5642. [Google Scholar] [CrossRef]
- Frustaci, F.; Spagnolo, F.; Corsonello, P.; Perri, S. A High-Speed and Low-Power DSP-Based TRNG for FPGA Implementations. IEEE Trans. Circuits Syst. II Express Briefs 2024, 71, 4964–4968. [Google Scholar] [CrossRef]
- Cao, Y.; Liu, W.; Zheng, Y.; Chen, S.; Ye, J.; Qian, L.; Chang, C.H. A New Reconfigurable True Random Number Generator and Physical Unclonable Function Unified Chip with On-Chip Auto-Calibration. IEEE Trans. Circuits Syst. I Regul. Pap. 2023, 70, 4900–4913. [Google Scholar] [CrossRef]
- Ni, T.; Peng, Q.; Bian, J.; Yao, L.; Huang, Z.; Yan, A.; Wang, S.; Wen, X. Design of True Random Number Generator Based on Multi-Ring Convergence Oscillator Using Short Pulse Enhanced Randomness. IEEE Trans. Circuits Syst. I Regul. Pap. 2023, 70, 5074–5085. [Google Scholar] [CrossRef]
- Guan, Z.; Liu, M.; Xu, J.; Lin, C. A hybrid entropy source scheme for true random number generator. Integration 2025, 104, 102473. [Google Scholar] [CrossRef]
- Grujić, M.; Verbauwhede, I. TROT: A Three-Edge Ring Oscillator Based True Random Number Generator with Time-to-Digital Conversion. IEEE Trans. Circuits Syst. I Regul. Pap. 2022, 69, 2435–2448. [Google Scholar] [CrossRef]
- Wang, J.; Huang, Z.; Chen, Y.; Liu, J.; Zhou, L.; Jiang, X.; Zhou, J.; Wang, Q. An Ultrahigh-Throughput and FPGA-Compatible TRNG Based on Dynamic Hybrid Metastability and Jitter Entropy Cells. IEEE Trans. Circuits Syst. I Regul. Pap. 2025, 72, 2202–2215. [Google Scholar] [CrossRef]
- Frustaci, F.; Spagnolo, F.; Perri, S.; Corsonello, P. A High-Speed FPGA-Based True Random Number Generator Using Metastability With Clock Managers. IEEE Trans. Circuits Syst. II Express Briefs 2023, 70, 756–760. [Google Scholar] [CrossRef]
- Yang, S.; Liang, H.; Hu, R.; Yao, L.; Huang, Z.; Yi, M.; Lu, Y. Lightweight Hybrid Entropy Source True Random Number Generator Based on Jitter and Metastability. IEEE Trans. Circuits Syst. II Express Briefs 2024, 71, 3513–3517. [Google Scholar] [CrossRef]
- Gołofit, K.; Wieczorek, P.Z.; Pilarz, M. A chaos-metastability TRNG for natively flexible IGZO circuits. AEU Int. J. Electron. Commun. 2023, 170, 154835. [Google Scholar] [CrossRef]
- Lu, Y.; Cao, C.; Liu, Y.; Liang, H.; Yao, L.; Ma, L. High throughput true random number generator based on dynamically superimposed hybrid entropy sources. Integration 2025, 102, 102380. [Google Scholar] [CrossRef]
- Liao, T.L.; Wan, P.Y.; Yan, J.J. Design and Synchronization of Chaos-Based True Random Number Generators and Its FPGA Implementation. IEEE Access 2022, 10, 8279–8286. [Google Scholar] [CrossRef]
- Vaidyanathan, S.; Sambas, A.; Abd-El-Atty, B.; El-Latif, A.A.A.; Tlelo-Cuautle, E.; Guillén-Fernández, O.; Mamat, M.; Mohamed, M.A.; Alçin, M.; Tuna, M.; et al. A 5-D Multi-Stable Hyperchaotic Two-Disk Dynamo System With No Equilibrium Point: Circuit Design, FPGA Realization and Applications to TRNGs and Image Encryption. IEEE Access 2021, 9, 81352–81369. [Google Scholar] [CrossRef]
- Yuan, F.; Li, S.; Deng, Y.; Li, Y.; Chen, G. Cu-Doped TiO2-x Nanoscale Memristive Applications in Chaotic Circuit and True Random Number Generator. IEEE Trans. Ind. Electron. 2023, 70, 4120–4127. [Google Scholar] [CrossRef]
- Paul, P.S.; Sadia, M.; Hossain, M.R.; Muldrey, B.; Hasan, M.S. Cascading CMOS-Based Chaotic Maps for Improved Performance and Its Application in Efficient RNG Design. IEEE Access 2022, 10, 33758–33770. [Google Scholar] [CrossRef]
- Wu, H.; Yin, Z.; Xie, J.; Ding, P.; Liu, P.; Song, H.; Chen, X.; Xu, S.; Liu, W.; Zhang, Y. Design and implementation of true random number generators based on semiconductor superlattice chaos. Microelectron. J. 2021, 114, 105119. [Google Scholar] [CrossRef]
- Magfirawaty, M.; Lestari, A.A.; Nurwa, A.R.A.; MT, S.; Ramli, K. A Novel Discrete-Time Chaos-Function-Based Random-Number Generator: Design and Variability Analysis. Symmetry 2022, 14, 2122. [Google Scholar] [CrossRef]
- Koyuncu, I.; Ozcerit, A.T.; Pehlivan, I. Implementation of FPGA-based real time novel chaotic oscillator. Nonlinear Dyn. 2014, 77, 49–59. [Google Scholar] [CrossRef]
- Taki, T. Approximation of junction field-effect transistor characteristics by a hyperbolic function. IEEE J. Solid-State Circuits 1978, 13, 724–726. [Google Scholar] [CrossRef]
- Wieczorek, P.Z.; Opalski, L.J. Non-linear modelling of resolve time in D-latch circuits. In Proceedings of the 18th International Conference Mixed Design of Integrated Circuits and Systems—MIXDES 2011, Gliwice, Poland, 16–18 June 2011; pp. 456–459. [Google Scholar]
- Wieczorek, P.Z.; Gołofit, K. True Random Number Generator Based on Flip-Flop Resolve Time Instability Boosted by Random Chaotic Source. IEEE Trans. Circuits Syst. I Regul. Pap. 2018, 65, 1279–1292. [Google Scholar] [CrossRef]
- Naccache, D. von Neumann Correction. In Encyclopedia of Cryptography, Security and Privacy; Jajodia, S., Samarati, P., Yung, M., Eds.; Springer Nature: Cham, Switzerland, 2025; p. 2742. [Google Scholar] [CrossRef]
- Spartan-7 FPGAs Data Sheet: DC and AC Switching Characteristics; Release Date: 18 October 2024; AMD/Xilinx: Santa Clara, CA, USA, 2024; Data Sheet DS189, Revision 1.11.
- Wieczorek, P.Z.; Gołofit, K. Dual-Metastability Time-Competitive True Random Number Generator. IEEE Trans. Circuits Syst. I Regul. Pap. 2014, 61, 134–145. [Google Scholar] [CrossRef]
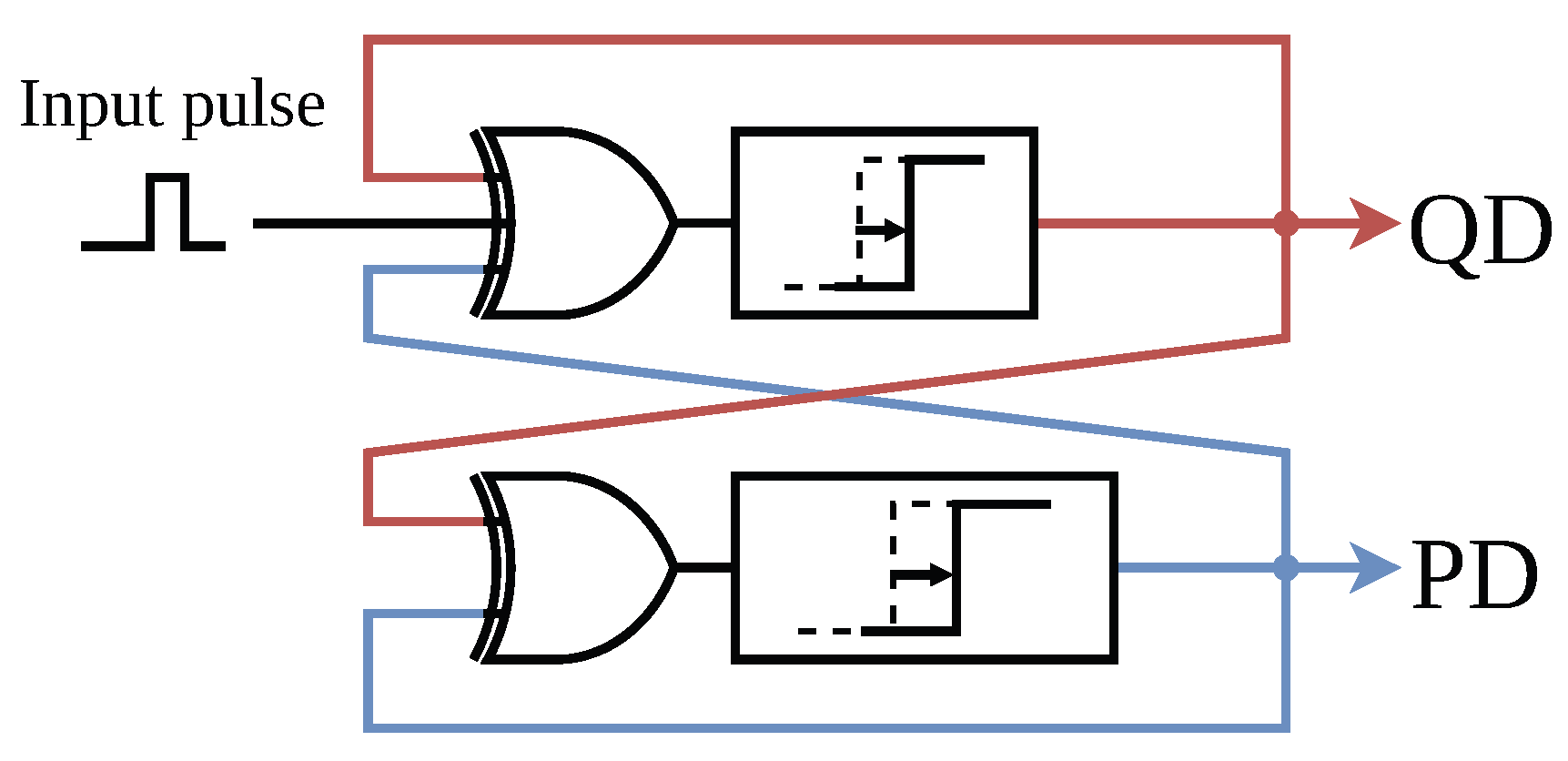
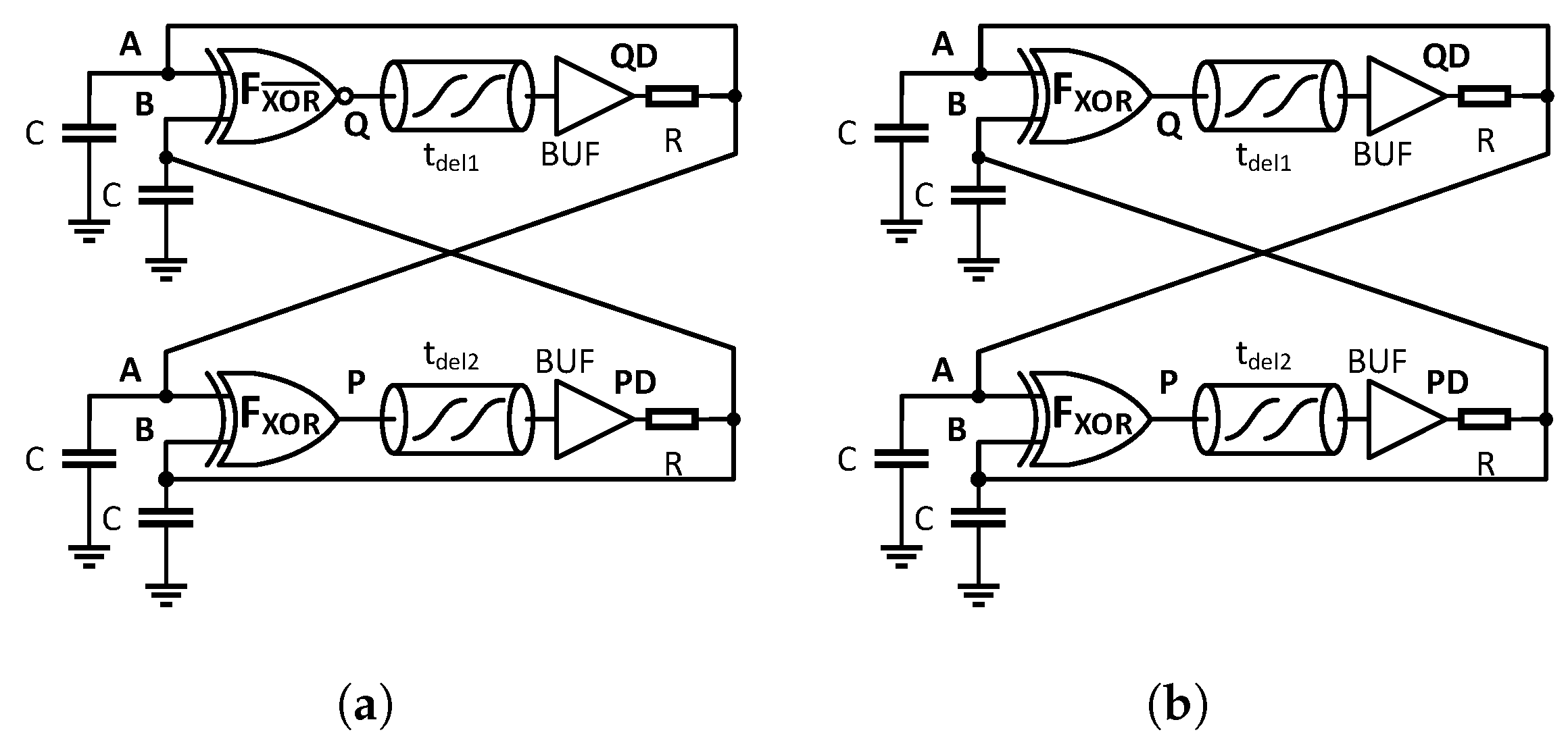
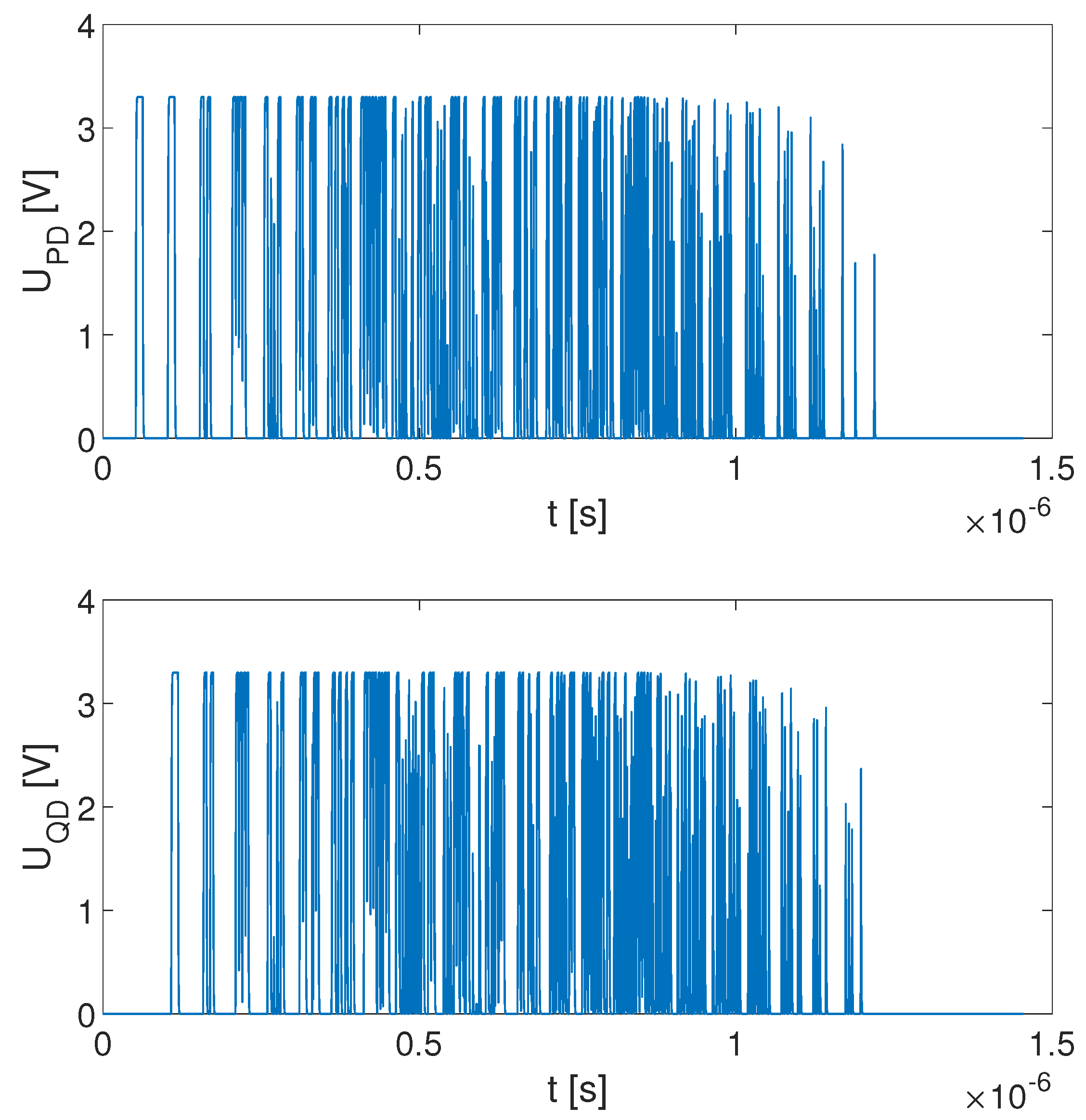
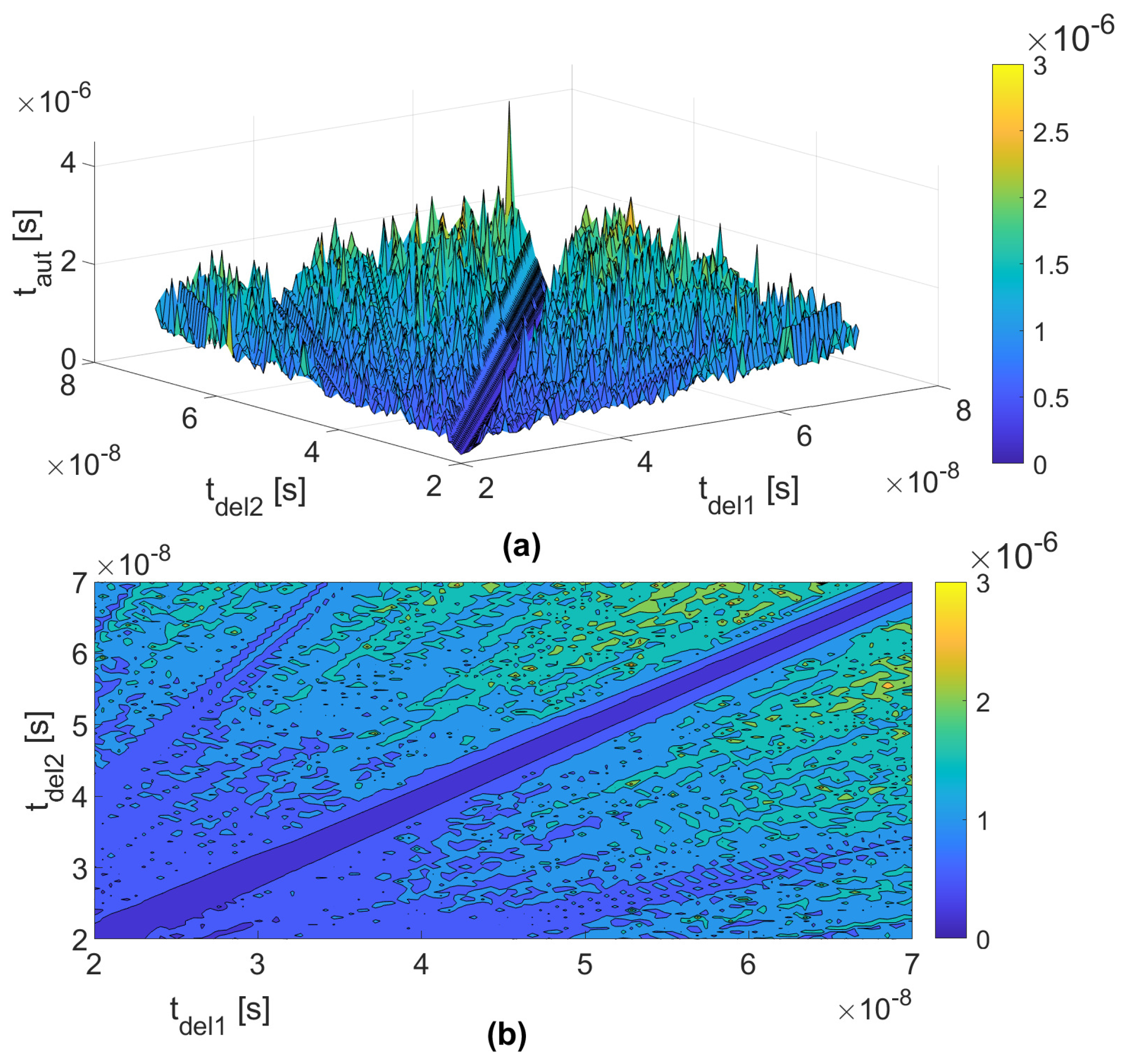
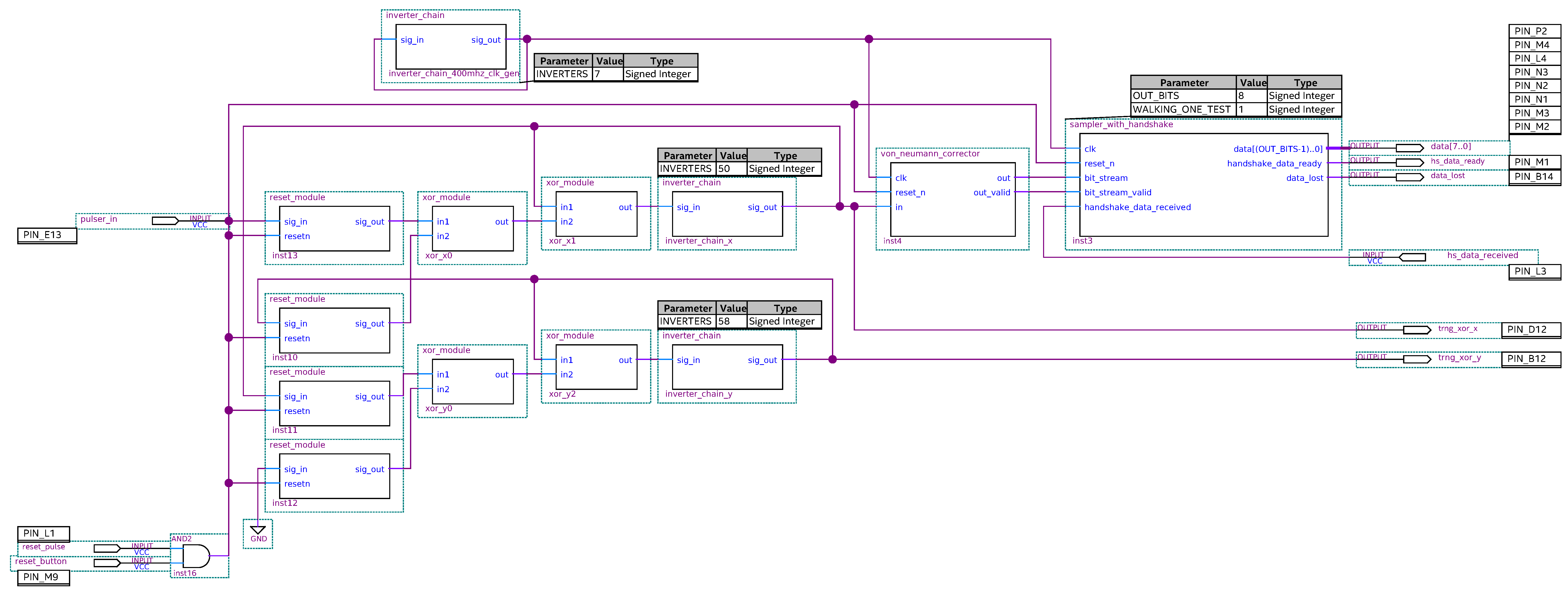
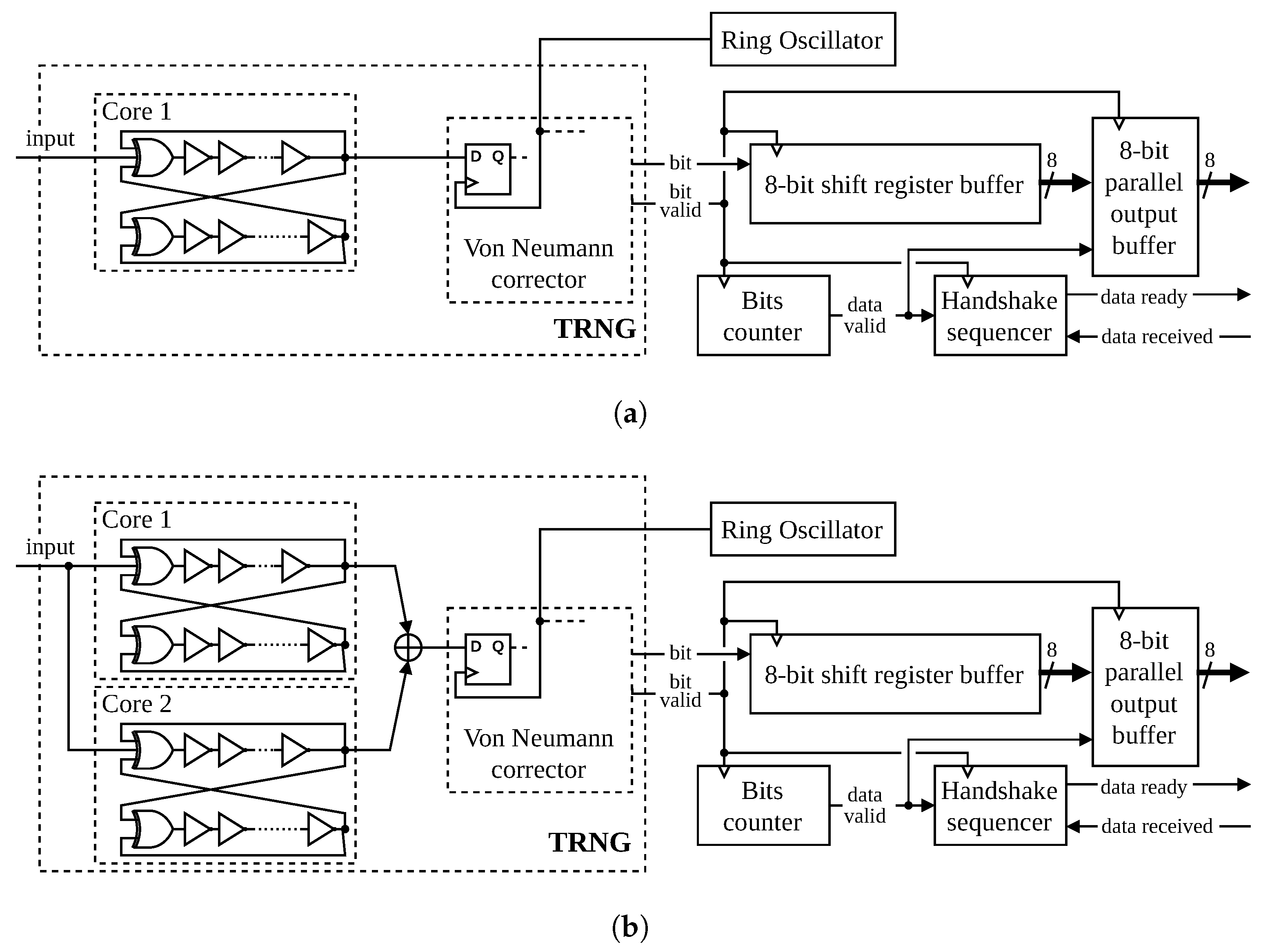
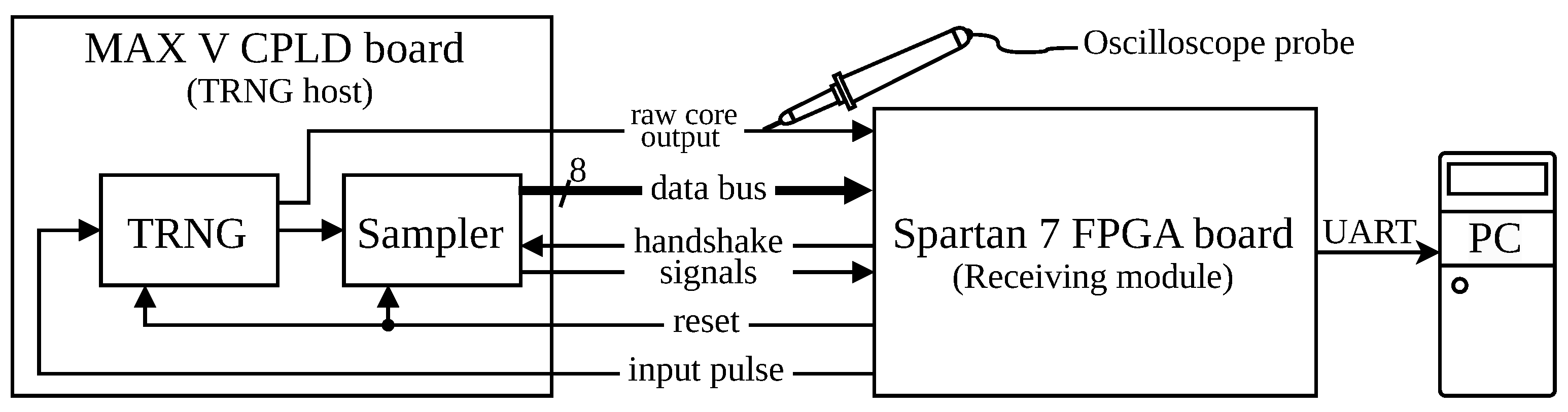
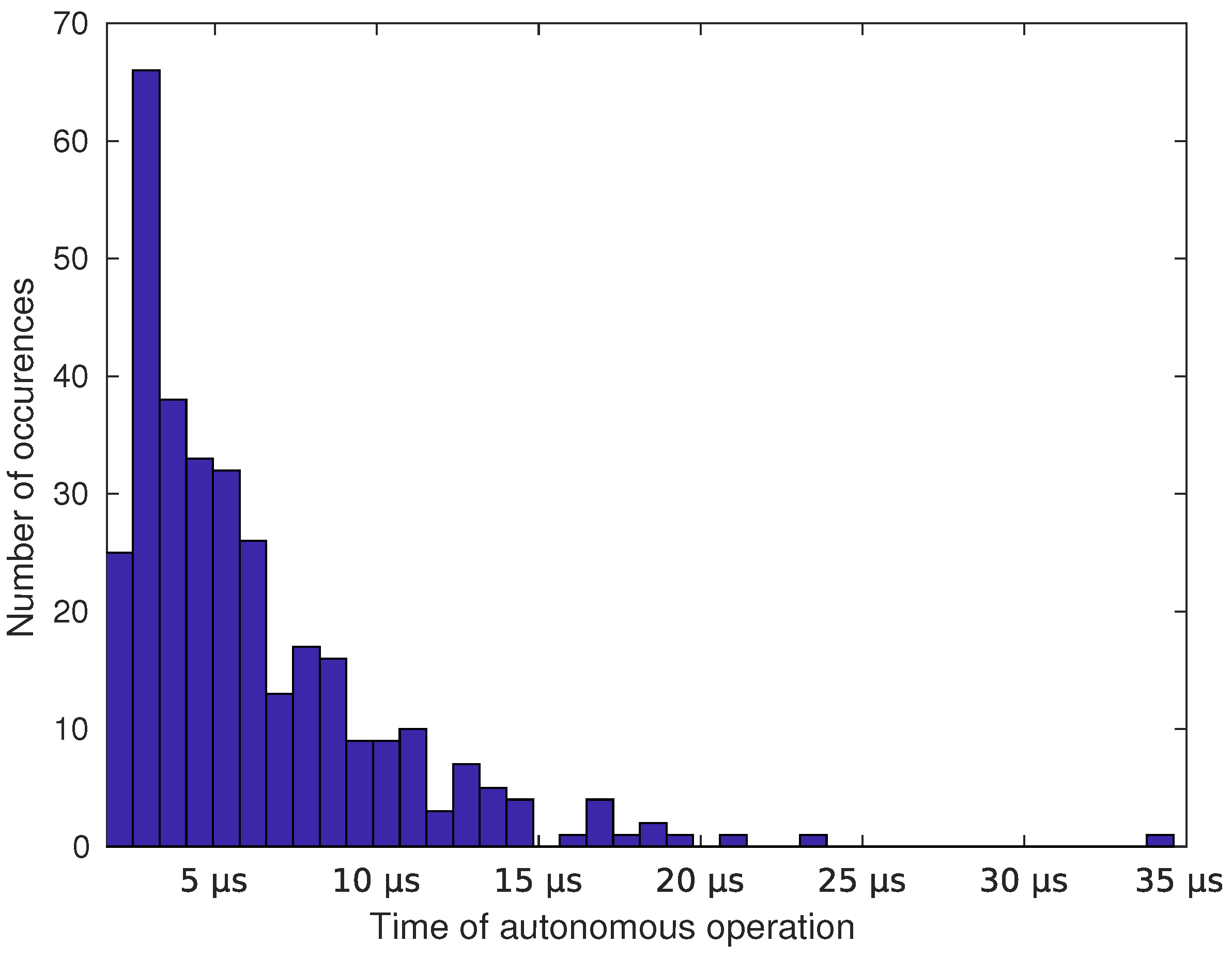



| Cores | XOR Gates | Delay Path QD | Delay Path PD | VN Corrector | Total |
|---|---|---|---|---|---|
| Single | 4 LUT | 51 LUT | 59 LUT | 3 LUT, 4 FF | 117 LUT, 4 FF |
| Dual | 9 LUT | 102 LUT | 118 LUT | 3 LUT, 4 FF | 232 LUT, 4 FF |
| Ref. | Platforms | Entropy Sources | Resources Utilization | Specialized Resources or Procedures | Throughput [Mb/s] | Power [mW] |
|---|---|---|---|---|---|---|
| [24] | Artix-7, Kintex-7, Virtex-6 | Jitter, Metastability | 15 LUT, 8 FF, 8 MUX, 6 slices | Requires specifying origin slice coordinates | 525–550 | 95–111 |
| [25] | Zynq-7000 | Mestastability, Race condition | 38 LUT, 121 FF, 38 slices | DCM, carry-chain | 300 | 119 |
| [26] | Artix-7, Kintex-7 | Jitter, Metastability | 12 LUT, 10 FF, 38 slices | None | 150–200 | – |
| [11] | Cyclone-V GT | Jitter, Race hazard | 23 LUT, 3 FF | None | 300 | 4.31 |
| [8] | Spartan-6, Virtex-6 | Jitter | 23 LUT, 3 FF | None | 150–290 | 3703 |
| [30] | Virtex-7 | Chaos, Jitter | 31 708 LUT, 30 3600 FF, 25 342 LUT-FF Pairs | None | 416 | – |
| [29] | Zynq-7000 | Chaos | 12 383 LUT, 13 483 FF, 131 LUTRAM, 145 DSP | DSP slices | 4.895 | – |
| [17] | Cyclone IV | Jitter | 15 LUT, 13 FF | None | 3.5 | 41.26 |
| [15] | Spartan-6 | Jitter, Metastability | 32 LUT, 8 slices | Placement and routing constraints | 12.5 | – |
| This work | MAX V CPLD | Jitter, Mestastability, Chaos | 232 LUT, 4 FF (out of which 220 LUTs were delay paths) | None | 43.7I | 57.51 |
| Test Name | p-Value | Passrate |
|---|---|---|
| Frequency | 0.1562 | 0.9936 |
| BlockFrequency | 0.1125 | 0.9872 |
| CumulativeSums (ALL) 1 | 0.1442, 0.7681 | 0.9936 |
| Runs | 0.7681 | 0.9872 |
| LongestRun | 0.1976 | 0.9808 |
| Rank | 0.8217 | 0.9936 |
| FFT | 0.3062 | 1.0000 |
| NonOverlappingTemplate (ALL) | 0.0043 ( test) | 0.9908 |
| OverlappingTemplate | 0.4506 | 0.9679 |
| Universal | 0.7399 | 0.9872 |
| ApproximateEntropy | 0.7681 | 0.9808 |
| RandomExcursions (ALL) | 0.0170 ( test) | 0.9858 |
| RandomExcursionsVariant (ALL) | 0.3458 ( test) | 0.9913 |
| Serial (ALL) 1 | 0.3505, 0.5926 | 0.9968 |
| LinearComplexity | 0.3986 | 0.9744 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szkoda, B.M.; Wieczorek, P.Z. A Simple Burst-Mode Multiple-Entropy TRNG Based on Standard Logic Primitives. Electronics 2025, 14, 3803. https://doi.org/10.3390/electronics14193803
Szkoda BM, Wieczorek PZ. A Simple Burst-Mode Multiple-Entropy TRNG Based on Standard Logic Primitives. Electronics. 2025; 14(19):3803. https://doi.org/10.3390/electronics14193803
Chicago/Turabian StyleSzkoda, Bartosz Mikołaj, and Piotr Zbigniew Wieczorek. 2025. "A Simple Burst-Mode Multiple-Entropy TRNG Based on Standard Logic Primitives" Electronics 14, no. 19: 3803. https://doi.org/10.3390/electronics14193803
APA StyleSzkoda, B. M., & Wieczorek, P. Z. (2025). A Simple Burst-Mode Multiple-Entropy TRNG Based on Standard Logic Primitives. Electronics, 14(19), 3803. https://doi.org/10.3390/electronics14193803







