Flux-Weakening Control Methods for Permanent Magnet Synchronous Machines in Electric Vehicles at High Speed
Abstract
1. Introduction
- (a)
- Appropriate machine weight and space.
- (b)
- The entire cost of production and materials.
- (c)
- Defined standards for dependability.
- (d)
- The overload capability of the drive.
- (e)
- The characteristic of speed versus torque.
- (f)
- The overall efficiency of the operation.
- High efficiency through magnet steels and appropriate copper alloys reduces copper and iron losses.
- Cost reduction through contemporary configurations that maintain the same flux density and straightforward cooling system while relying on inexpensive non-rare-earth magnet material.
- Motor design needs to be improved to facilitate recycling and separation.
- High power density thanks to a high-performance cooling system that increases power capabilities and speed range.
- Control speed and torque using the right power electronics design to maximize the electric machine’s efficiency.
- The machine’s inductance value, the flux distribution, saturation of the magnetic materials, and reluctance of the machine are nonlinearly altered, which leads to achieving the high saturation level required for both PMSMs and SyRMs to achieve optimal performance at high-speed ranges.
- The drivetrain experiences losses due to the current total harmonic distortion control produced by the inverter or torque ripple.
- Automatic algorithms that take into account the flux-weakening (FW) regulation and automatically adjust the parameters of the low-level controllers for electric machines.
- A thorough overview of flux-weakening control strategies (voltage-based, current-based, feedforward, feedback, and hybrid methods), including their theoretical foundations and practical implementation considerations.
- New comparative evaluations of these FW methods, with summary tables providing qualitative and quantitative comparisons of performance, efficiency, and stability across different approaches.
- A comparative analysis of FW control in different machine types—specifically contrasting SPMSM, IPMSM, and SynRM—to highlight how machine characteristics influence flux-weakening capability and control strategy selection.
- Critical analysis and practical guidance for selecting appropriate FW control methods in EV applications, as well as the identification of current challenges and future research directions in this field.
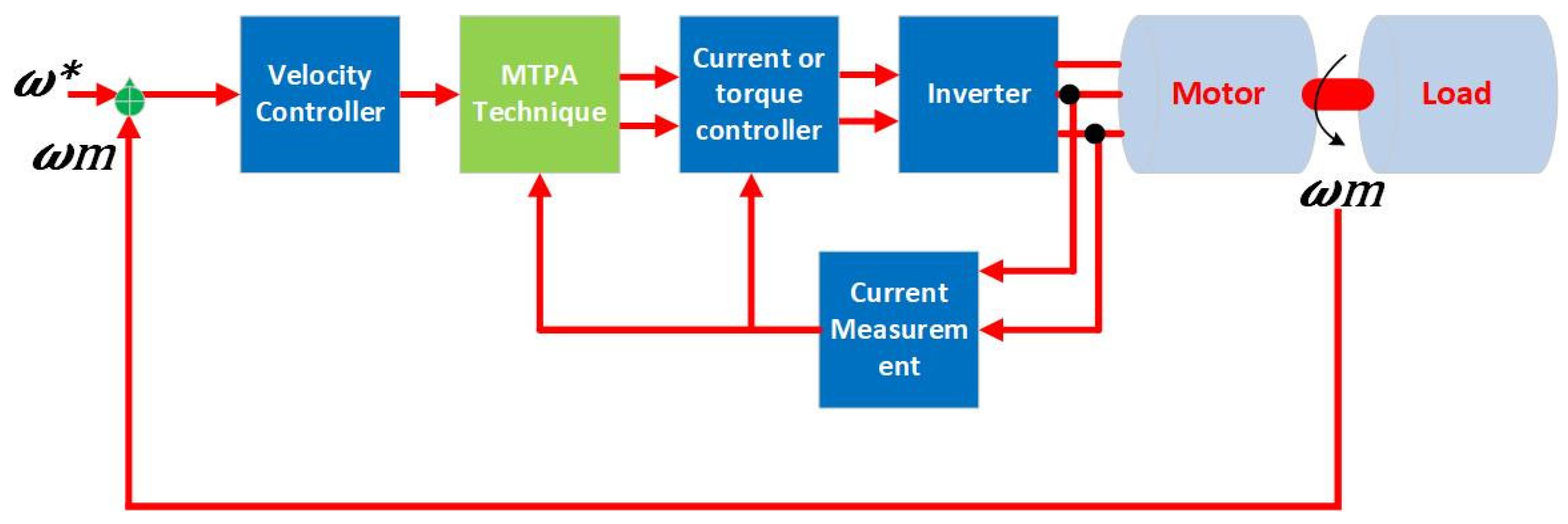
2. Different Techniques for Controlling PMSM
2.1. Field-Oriented Control
2.2. Direct Flux Vector Control
2.3. Direct Torque Control
2.4. Direct Voltage Control
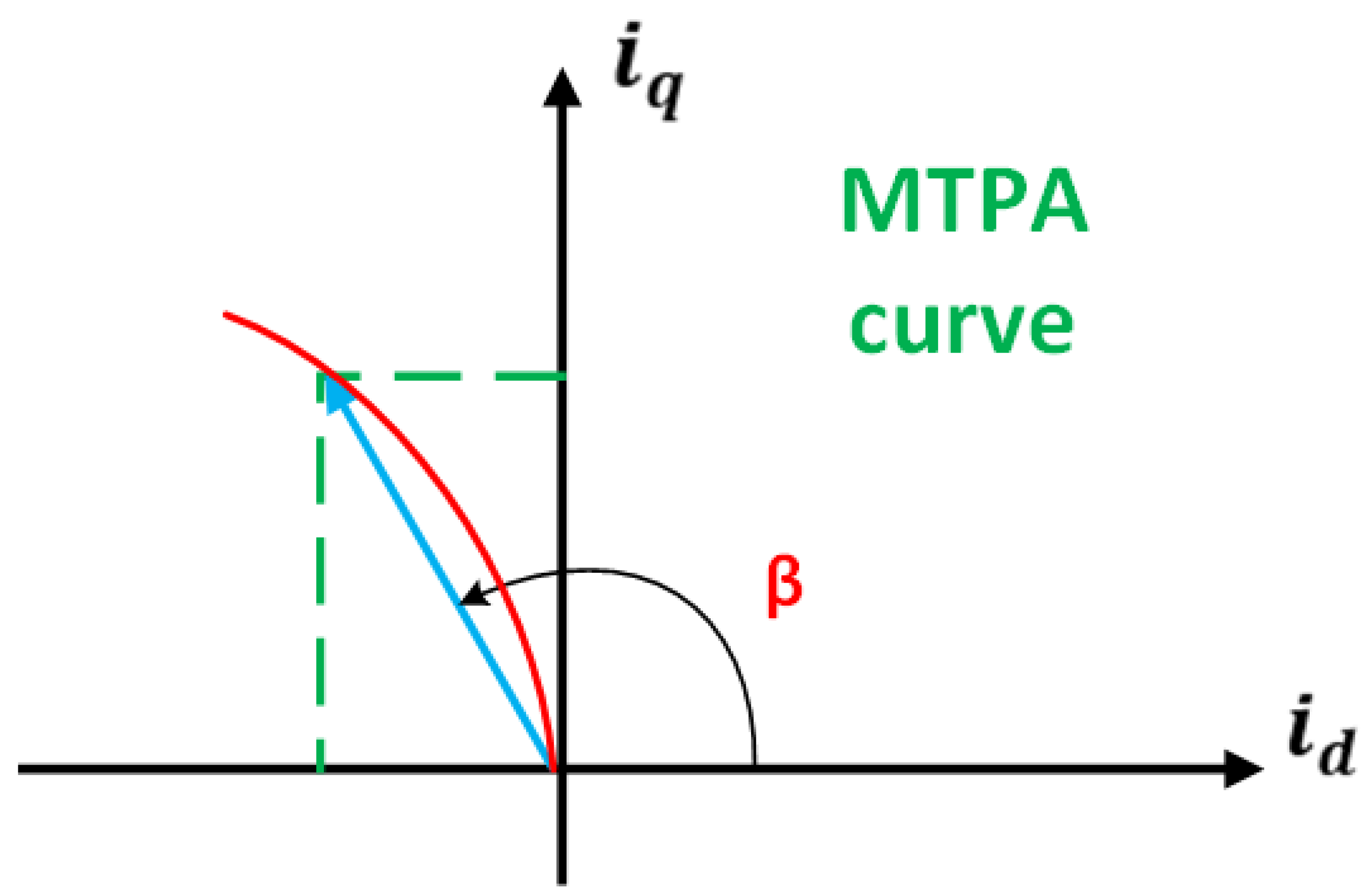
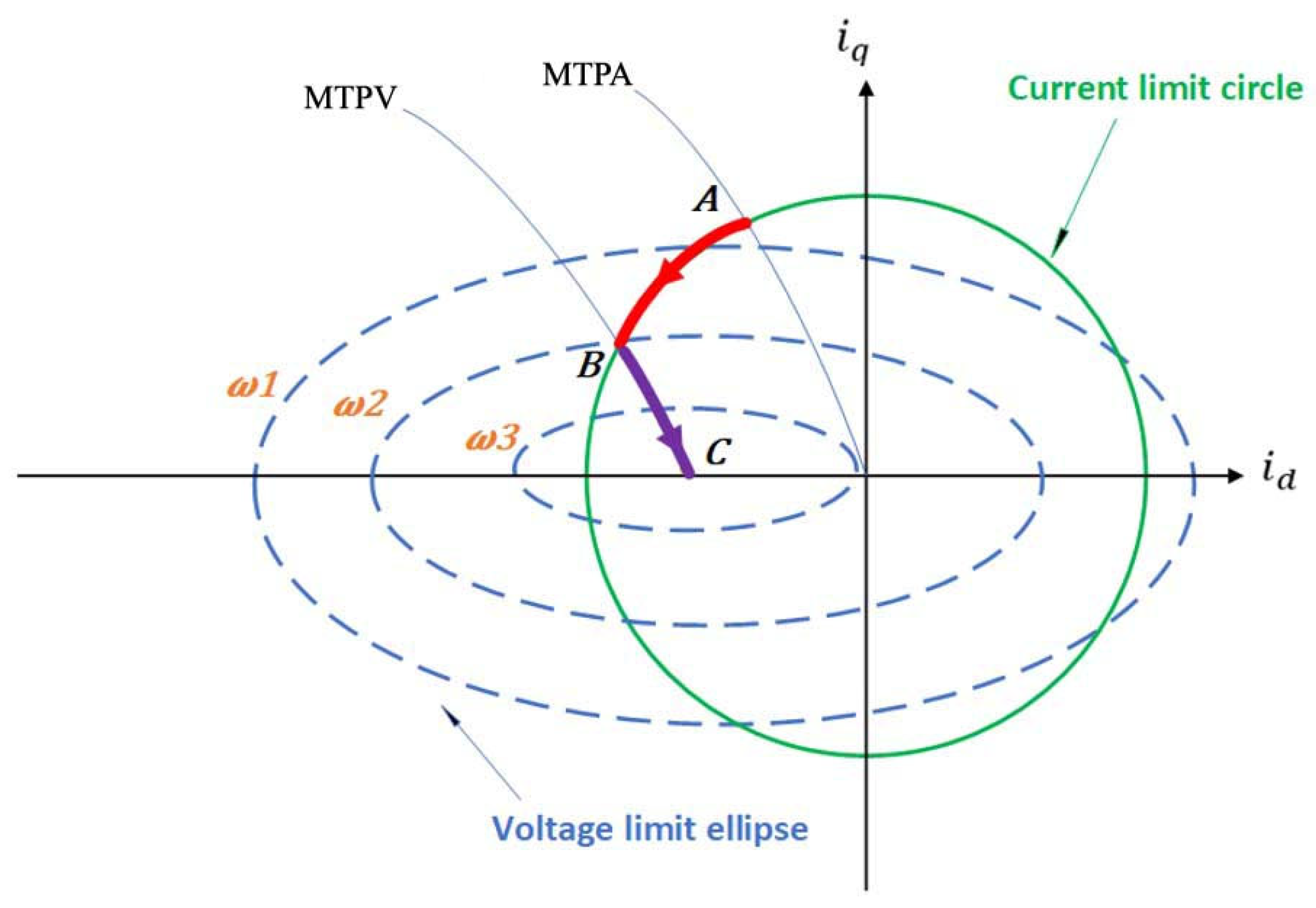
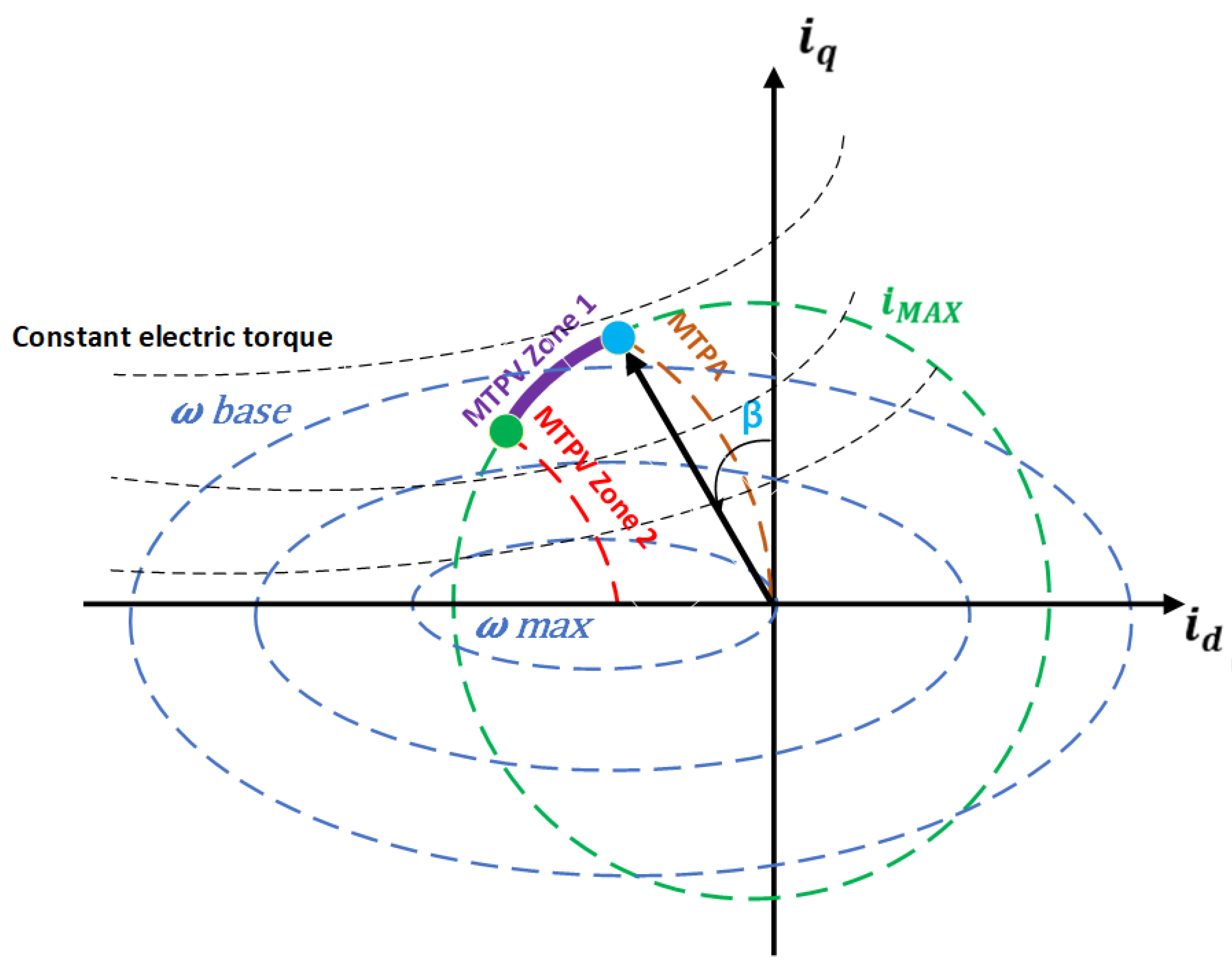
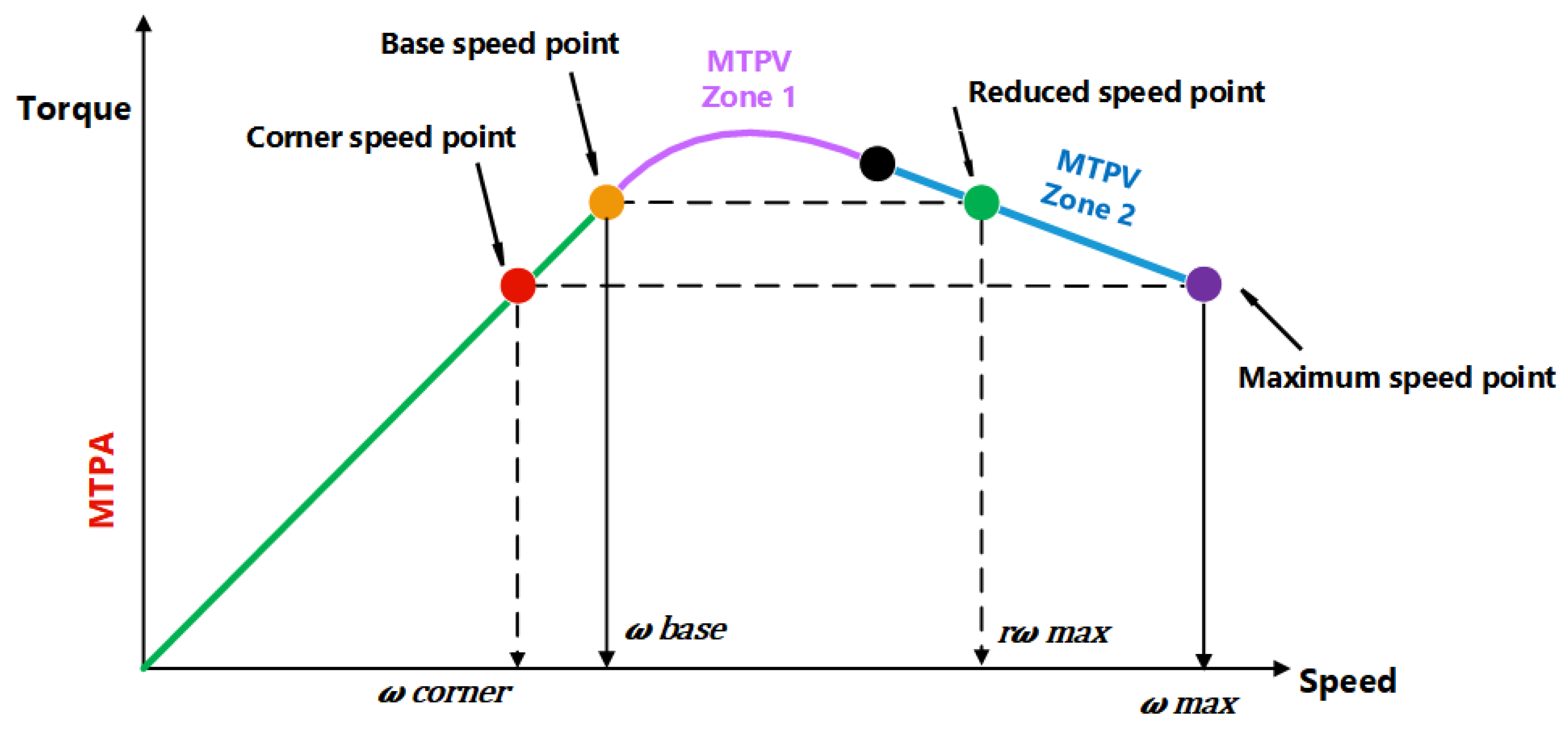
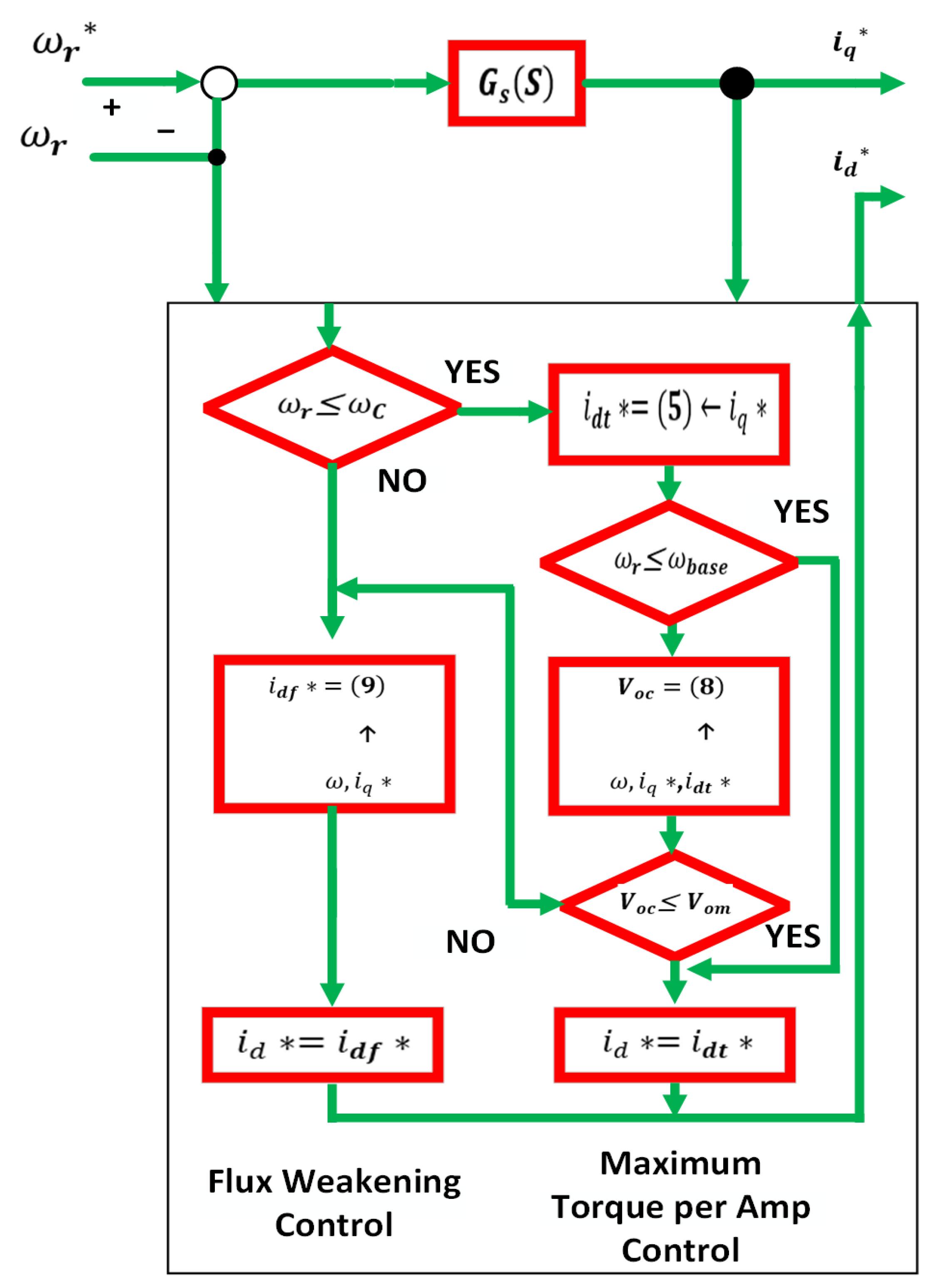
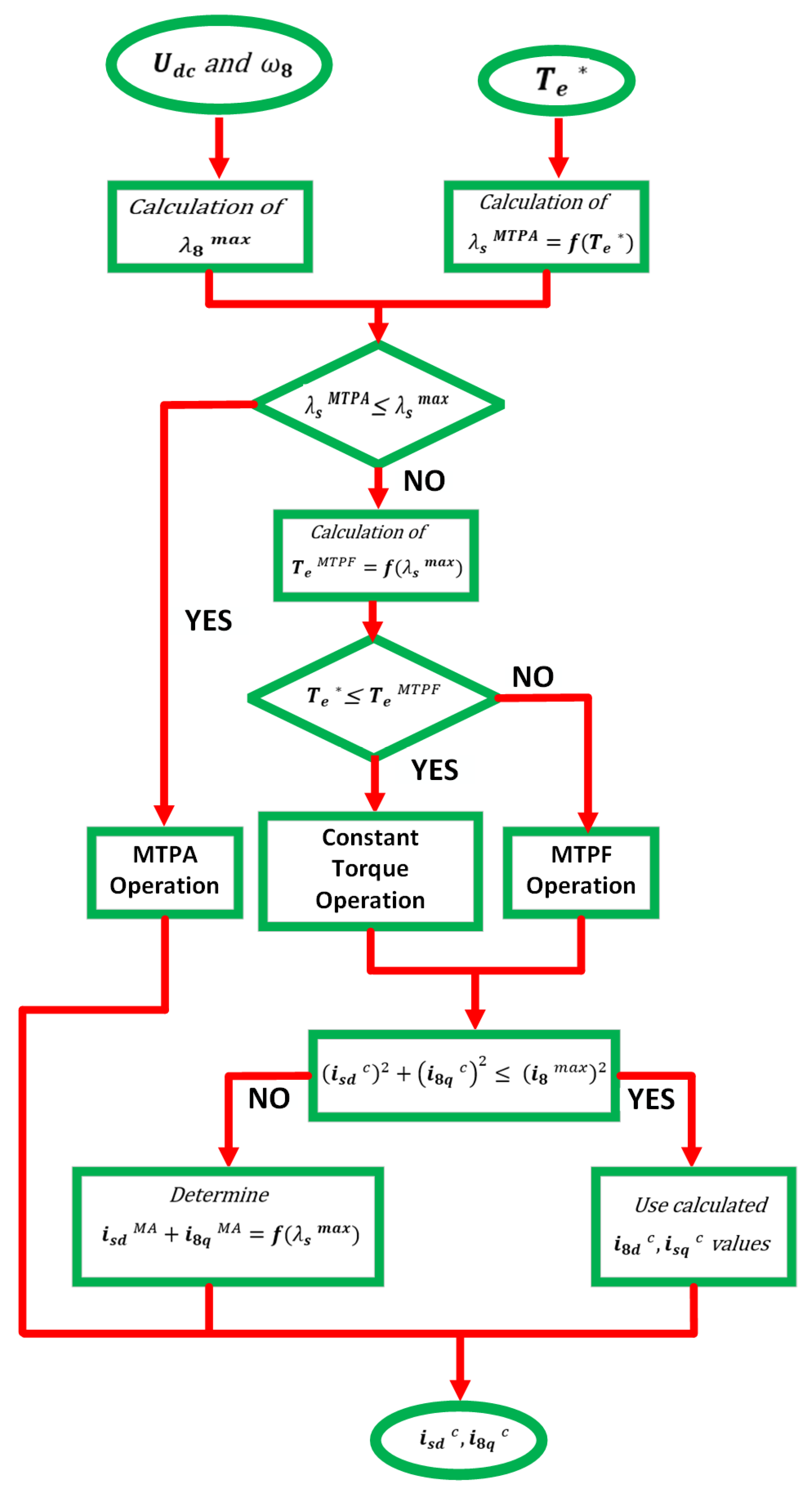
3. Maximum Torque per Ampere MTPA Region
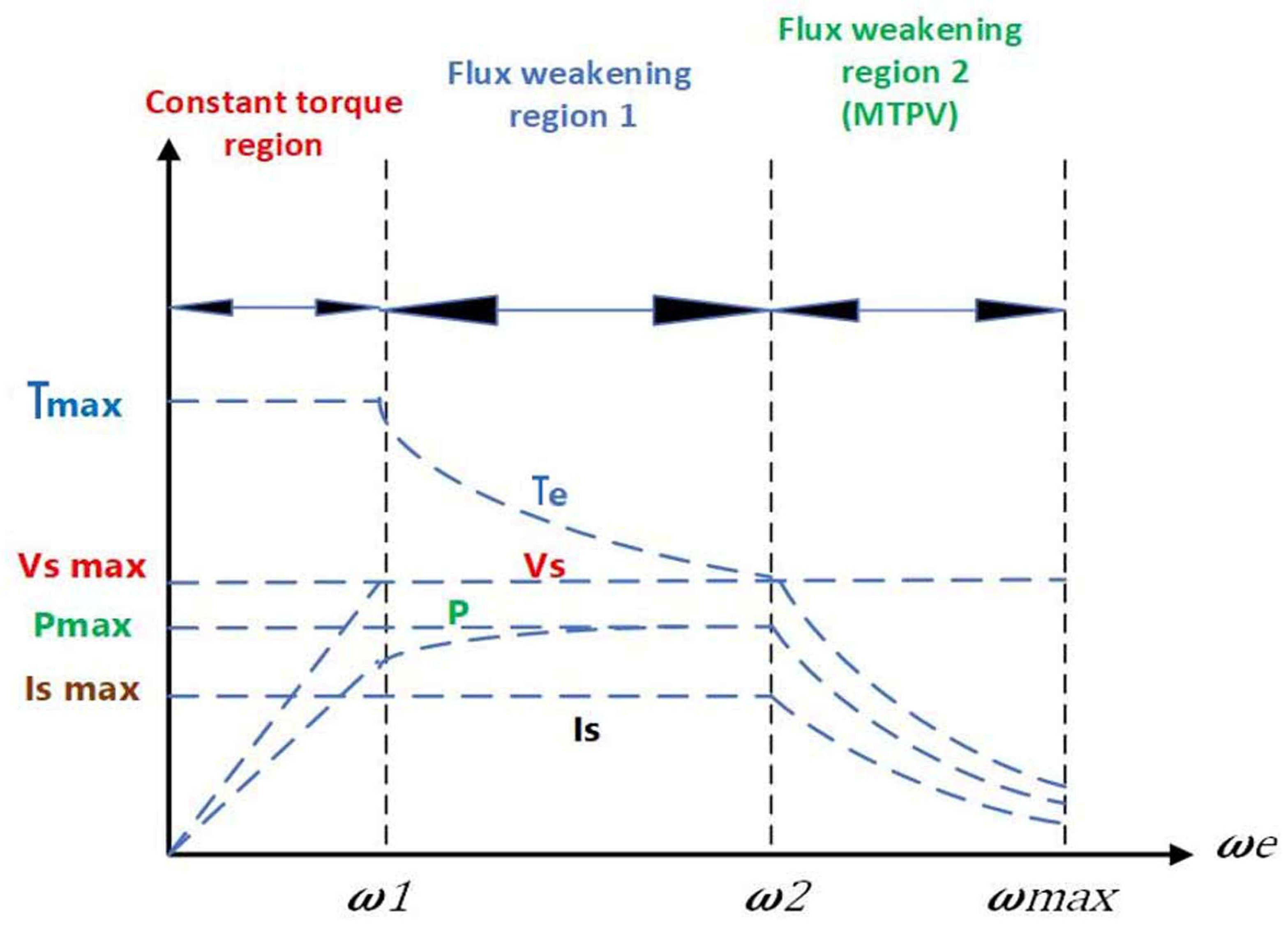
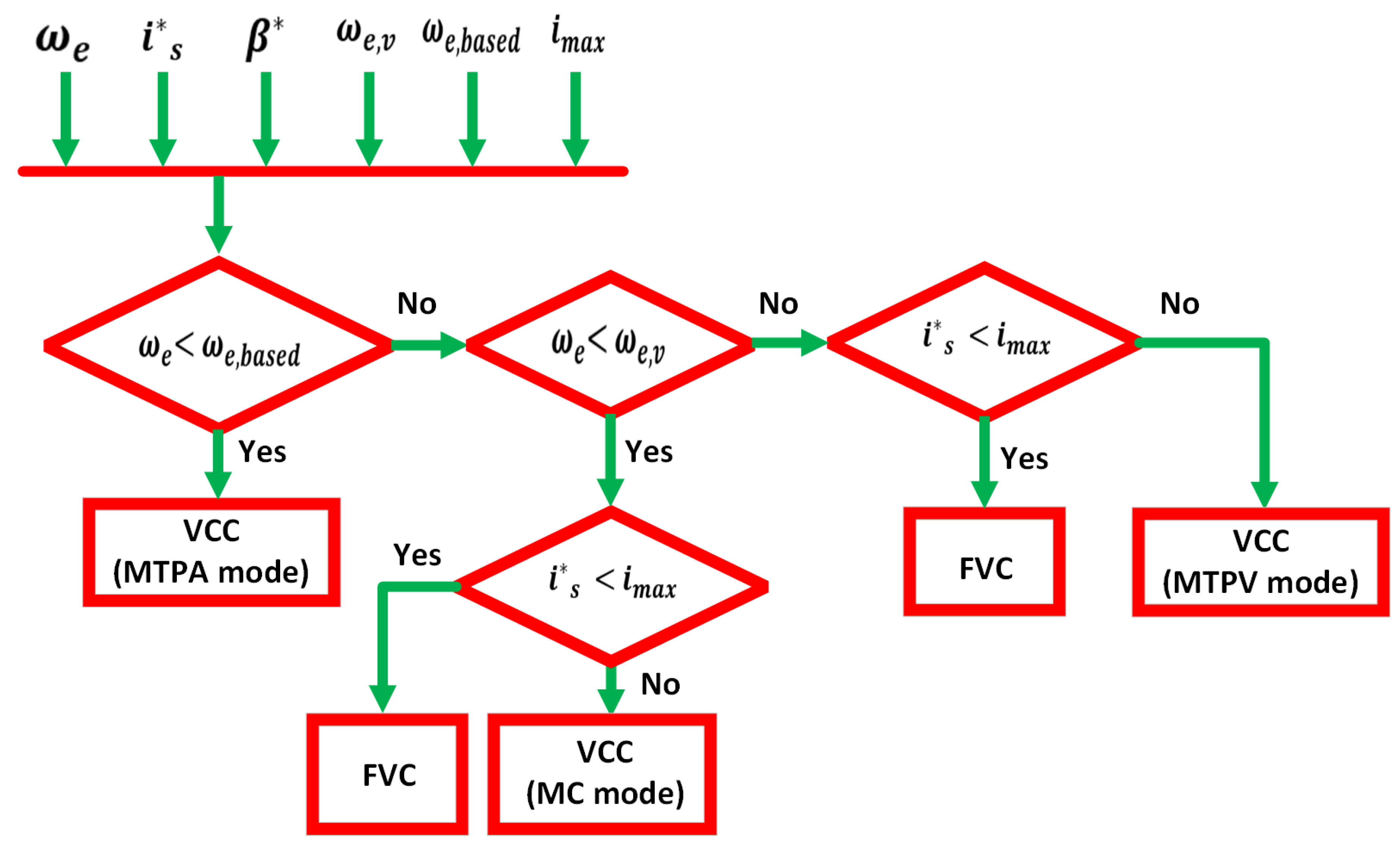
4. PMSMs and Flux Weakening (FW)
4.1. Operation Limits
4.2. PMSM Back Electromotive Force (BEMF)
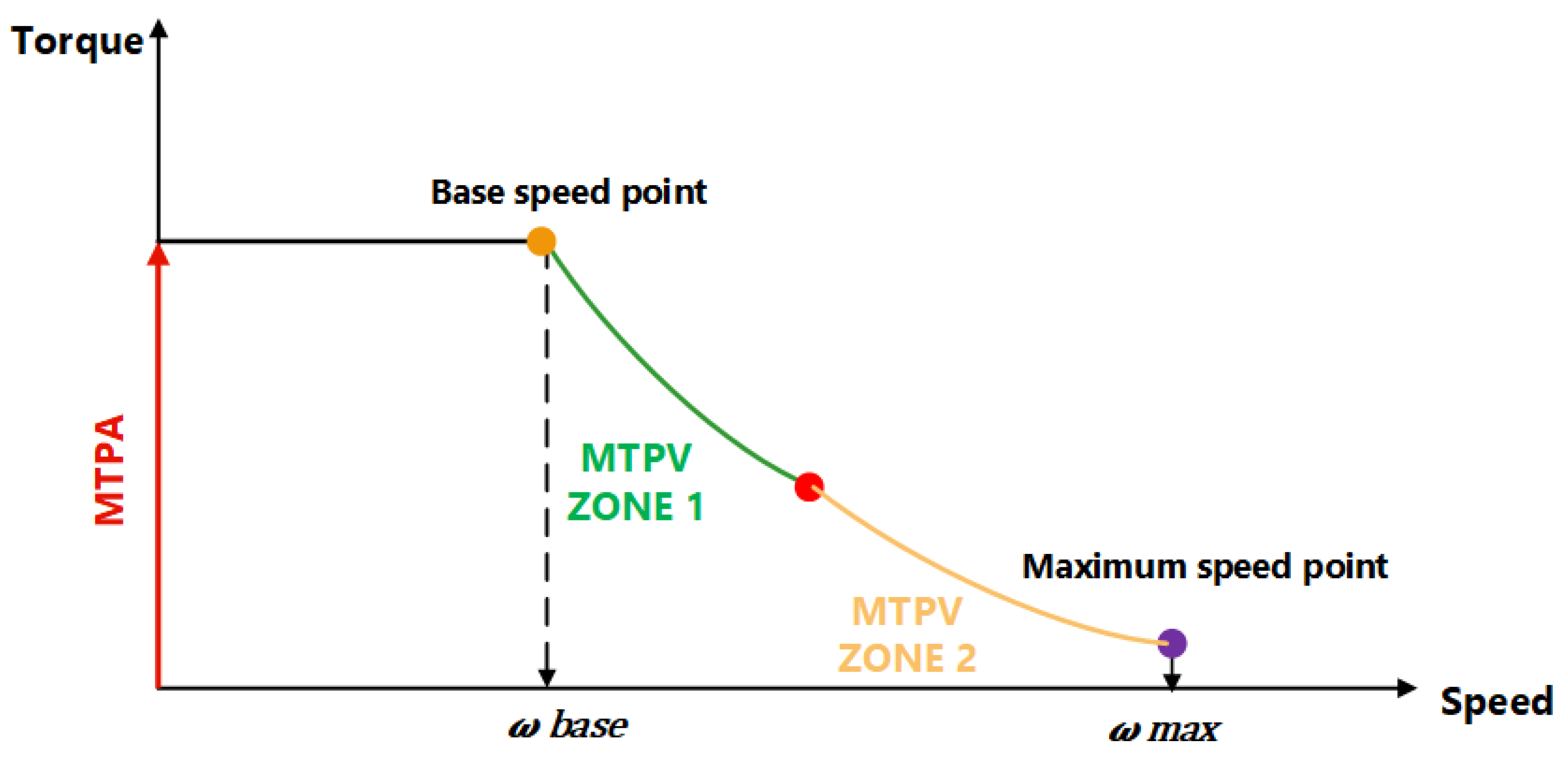
4.3. Maximum Torque per Voltage (MTPV) Region
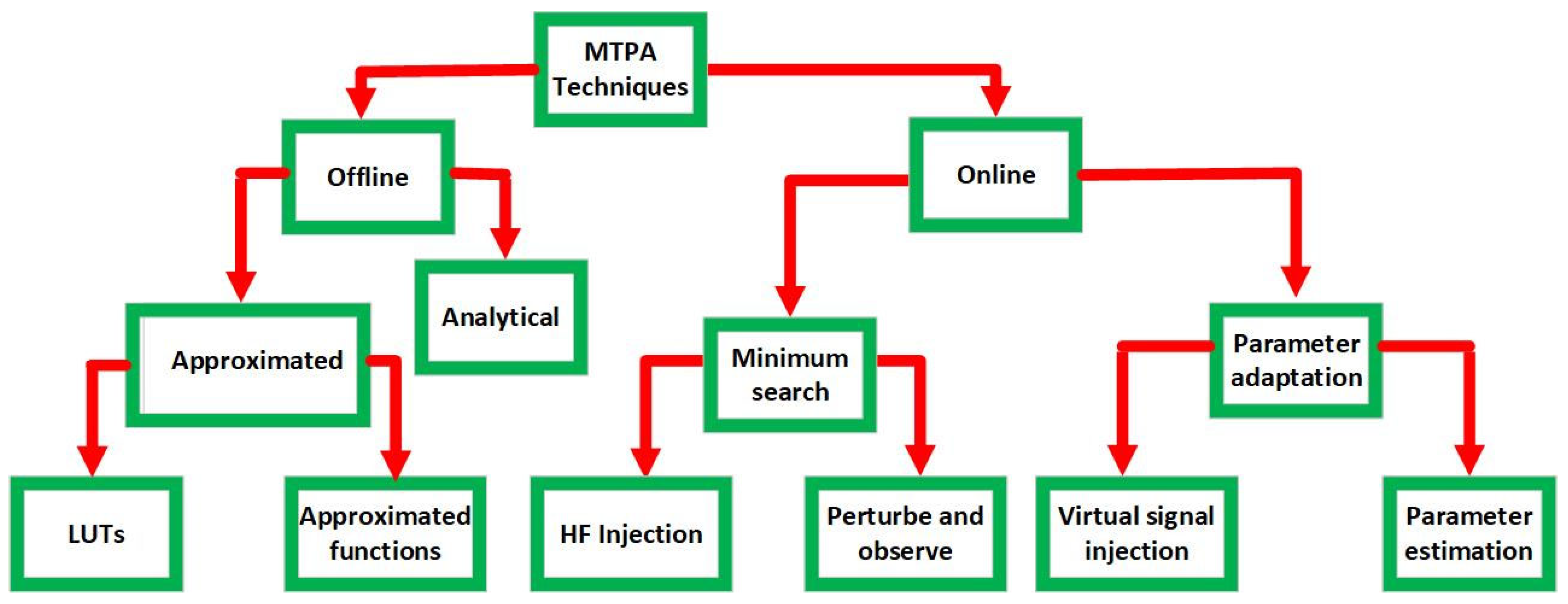
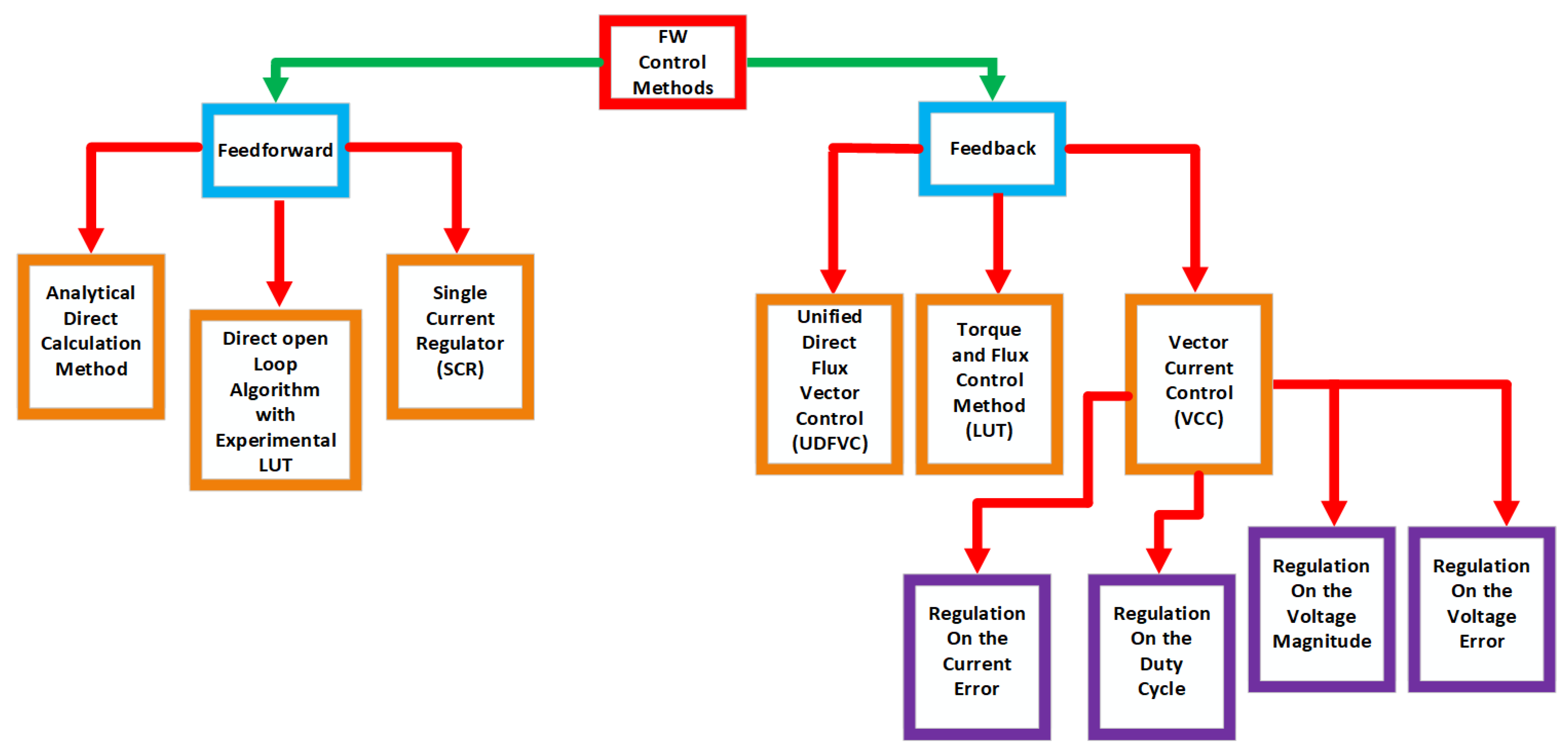
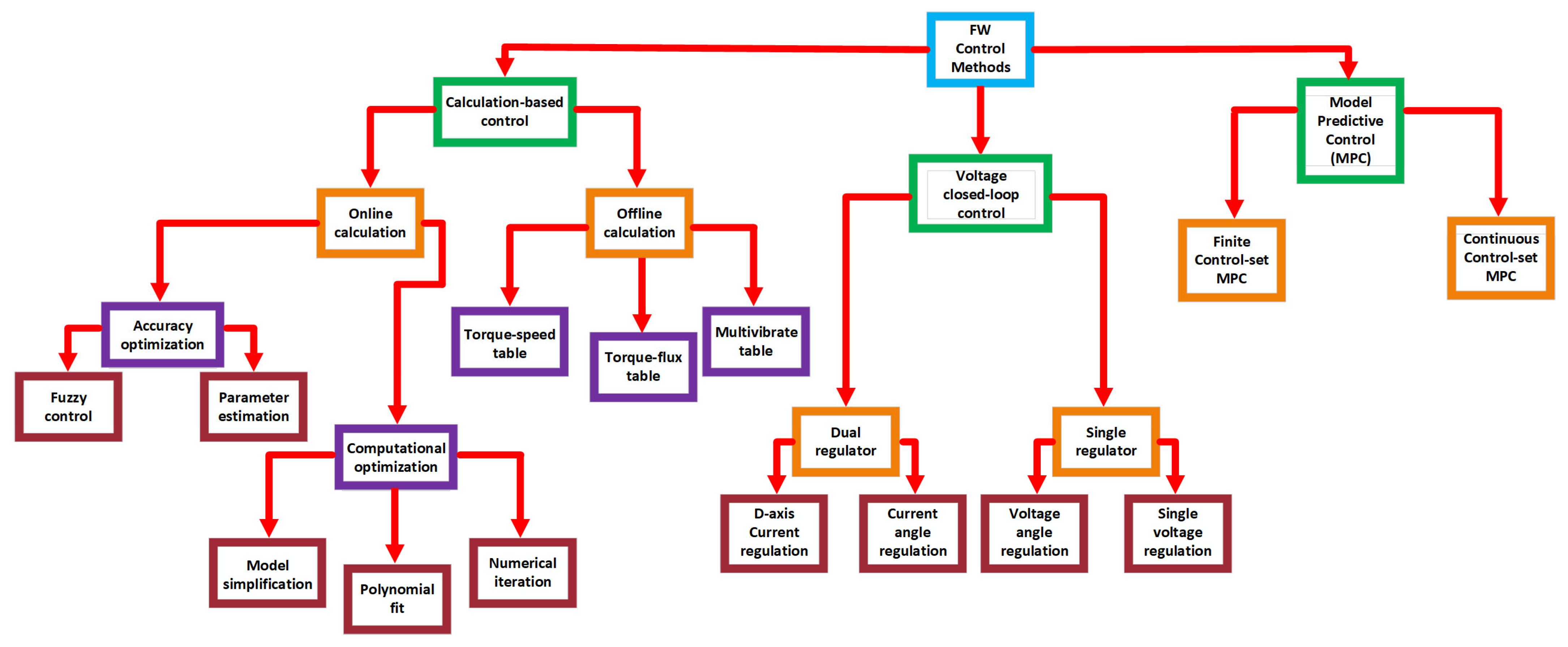
5. Flux-Weakening Control Methods
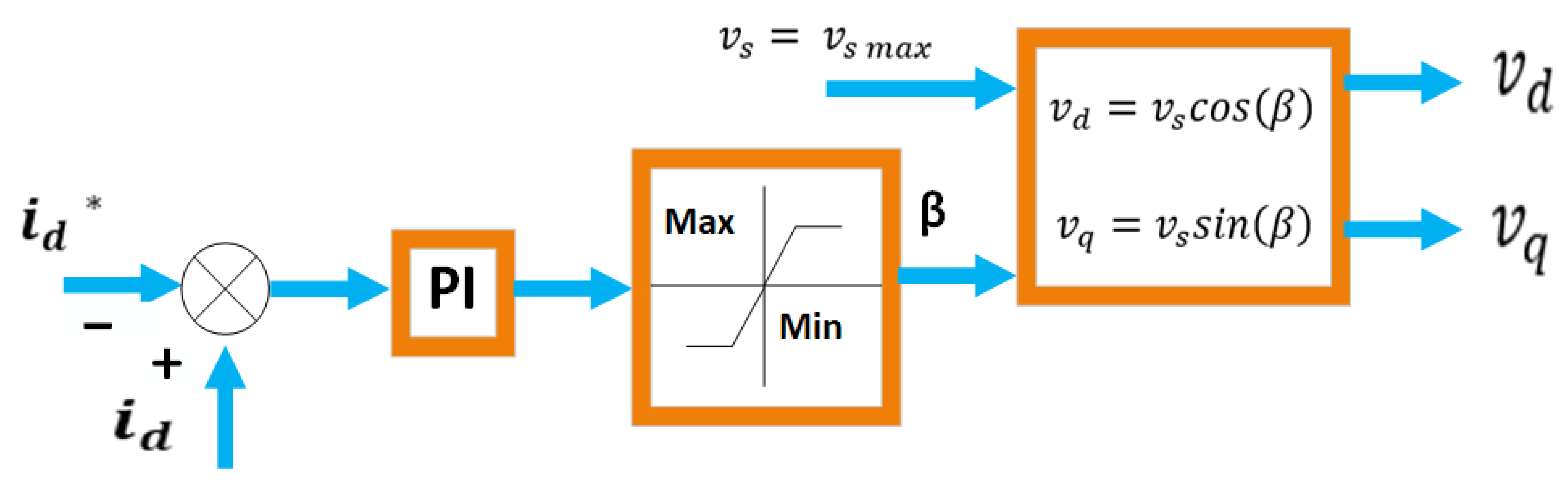
5.1. Analytical Direct Calculation Method
5.2. Direct Open-Loop Algorithm with Experimental LUT
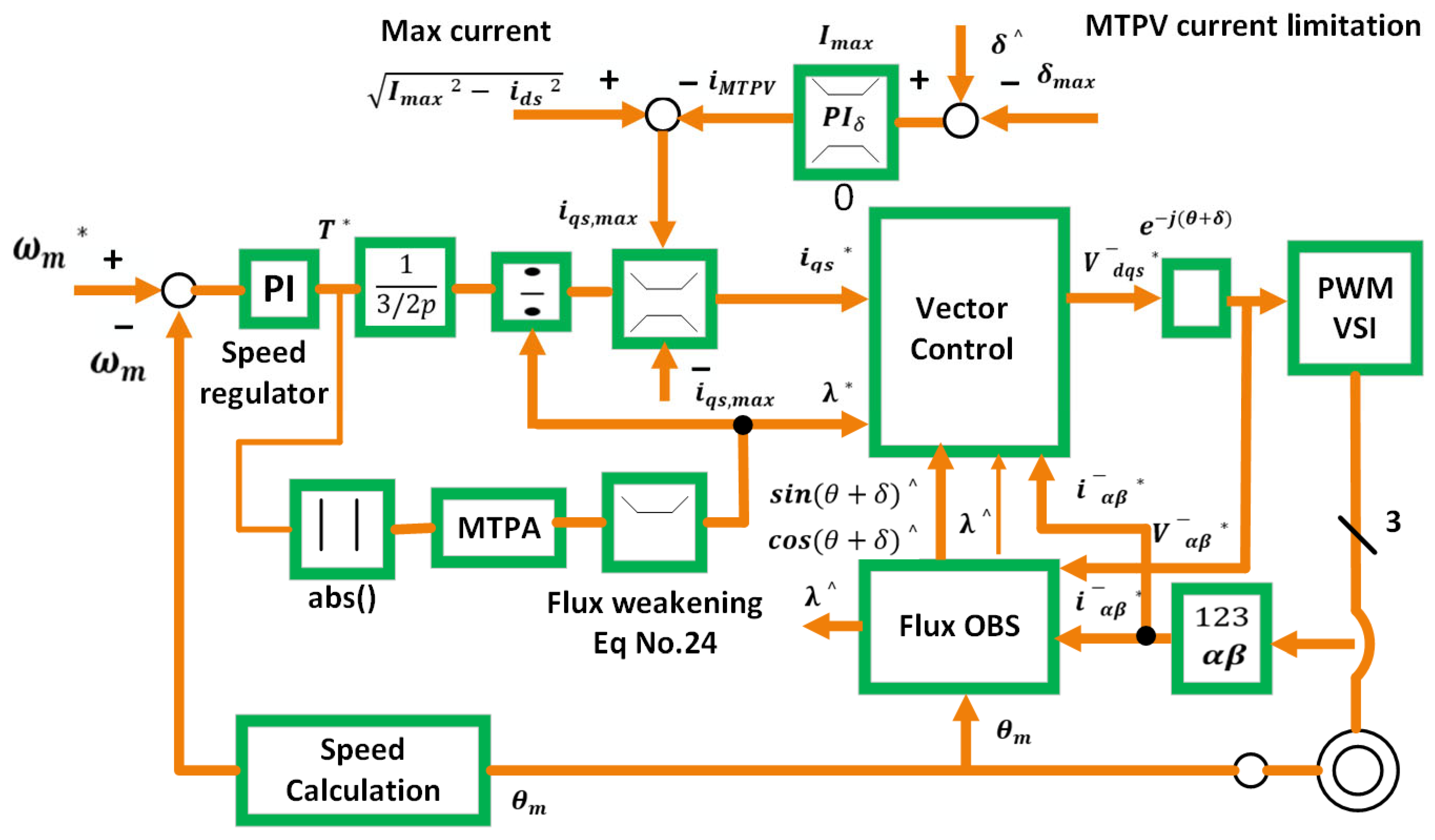
5.3. Single Current Regulator
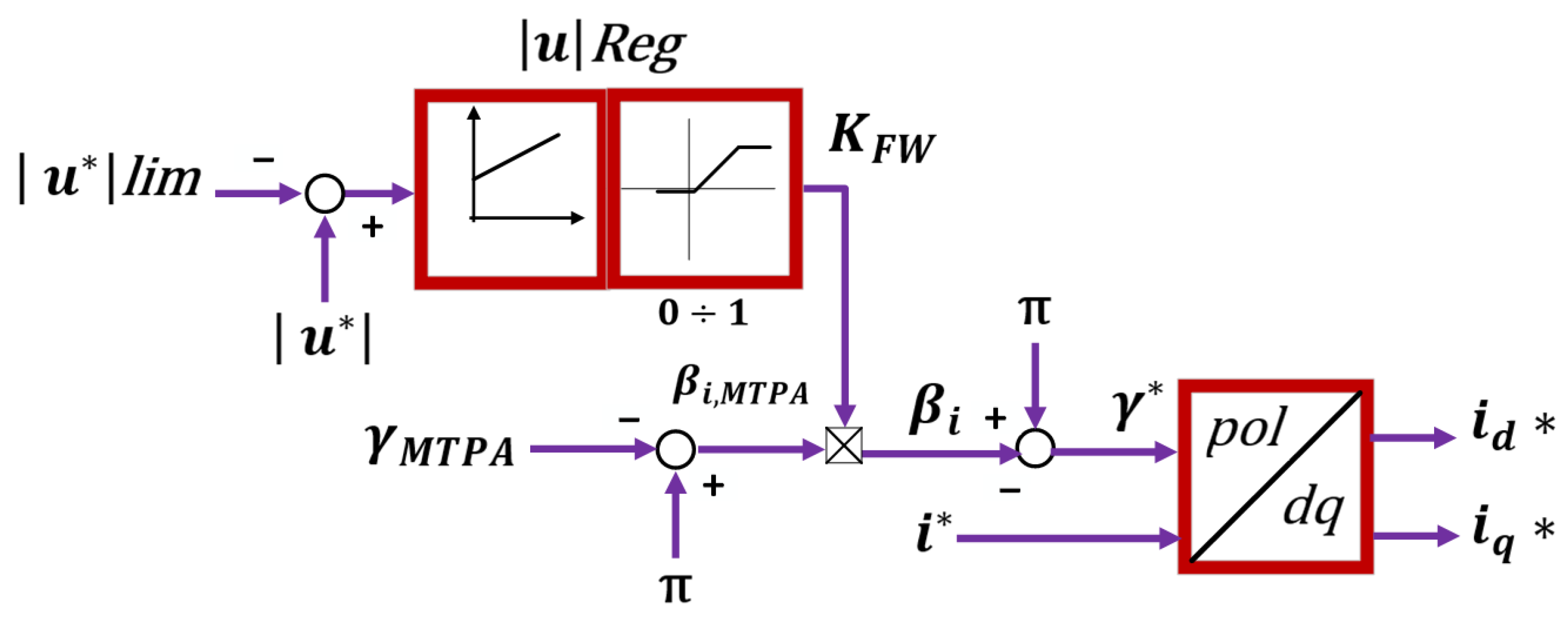
5.4. Unified Direct Flux Vector Control (UDFVC)
- q-axis current;
- flux linkage magnitude;
- load angle limit at high-speed ranges.
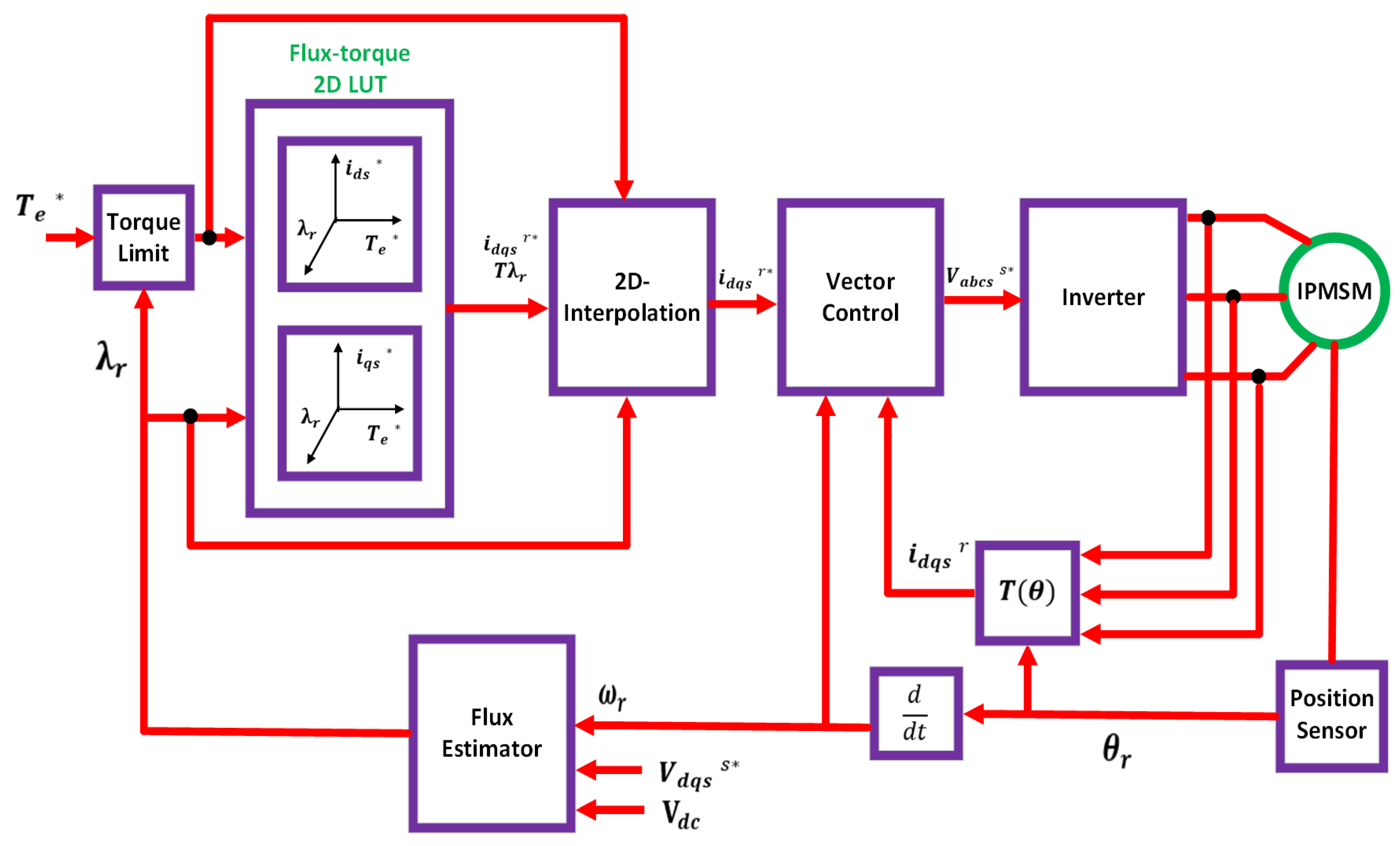
5.5. Torque and Flux Control Method with (LUTs)
- Dynamic torque control;
- Seamless transition between FW and Six-Step operation;
- Current harmonics because of the Six-Step which generated the current ripple for the inverter’s DC link capacitor and reduced its lifetime.
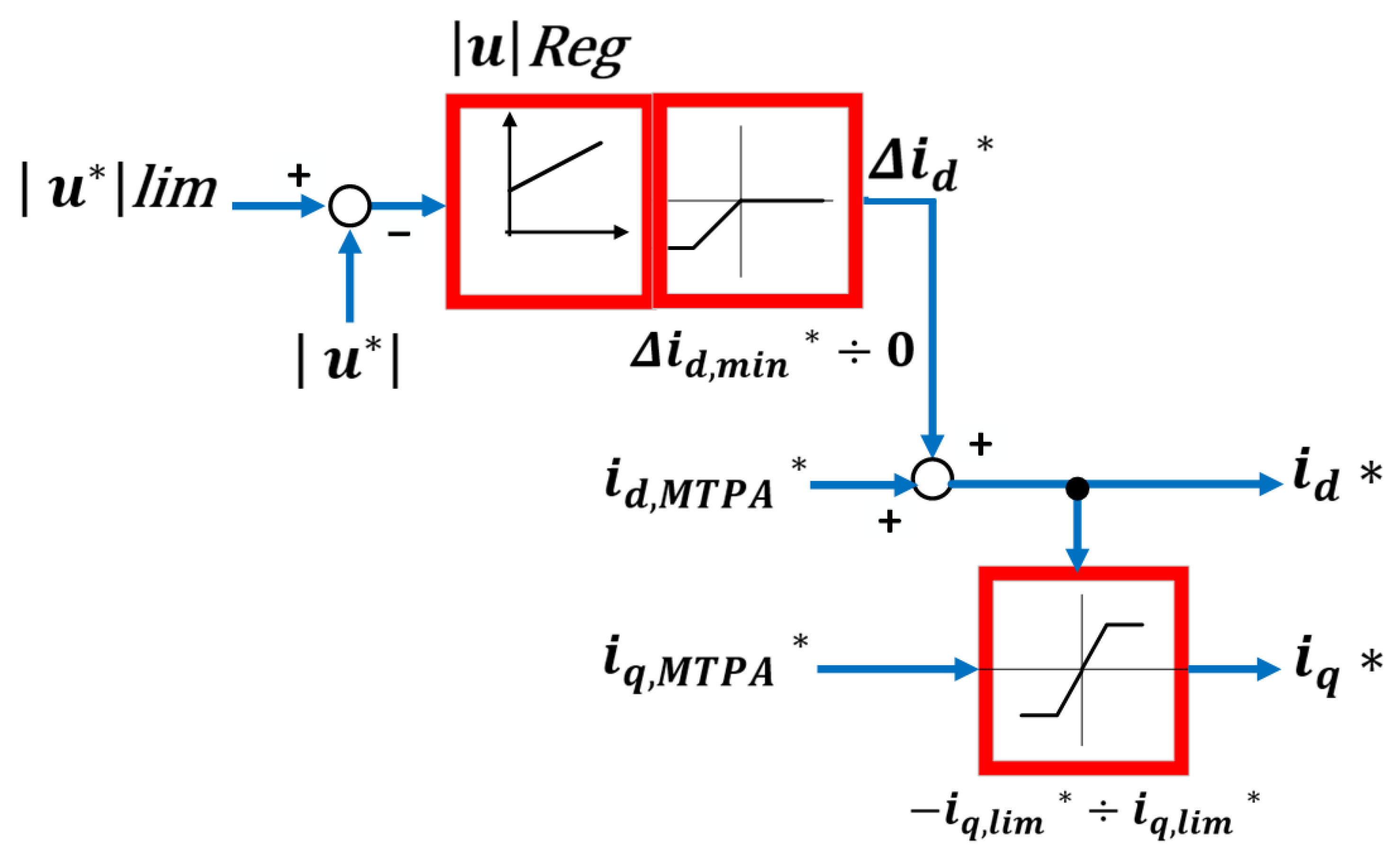
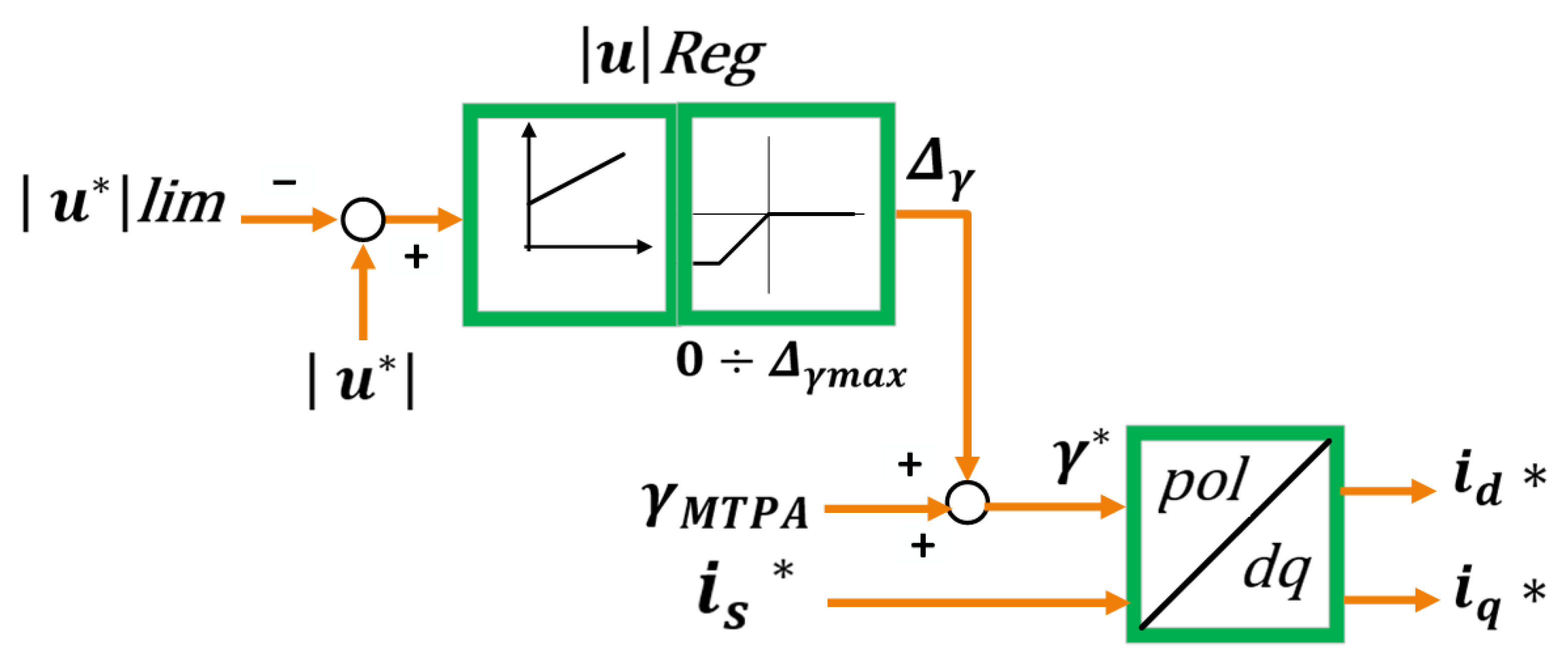
5.6. Vector Current Control (VCC)
6. Discussion
- Light weight and compact size.
- Low maintenance requirements.
- Unique rotor structure that contributes to extra torque generation.
- High torque and power density
- Low torque ripple combined with high efficiency.
- Precise speed control capability.
- Effective performance at high-speed ranges.
- Flux-weakening capability enabling extended constant-power operation.
| Control Method | Approach and Key Principle | Speed Range Extension |
|---|---|---|
| Analytical Direct Calculation (solving equations FW) | Solves simplified motor equations for id, iq setpoints (often neglecting saturation) to satisfy the voltage limit | Moderate—achieves FW by design, but accuracy depends on the model |
| Open-Loop Voltage Angle Control (Voltage-based FW) | Controls the inverter voltage angle (d-axis voltage component) to weaken flux above base speed directly. Essentially, a feed-forward voltage control using the margin to the voltage limit | Moderate extending speed by utilizing available voltage headroom |
| Single Current Regulator (SCR) (single-loop FW) | Uses one current regulator in the FW region instead of separate d/q regulators. At base speed, control switches from standard dual-loop (MTPA) to single-loop (FW) mode that directly controls d-axis current (with q-axis voltage held at limit) | High—designed for deep FW operation, pushing to inverter voltage limit while maintaining stability |
| Unified Direct Flux Vector Control (UDFVC) | Directly controls stator flux linkage via d-axis voltage and torque via q-axis current in the stator reference frame; manages load angle to stay within stability margin | High capability of spanning full speed range, including deep FW, by adjusting flux and torque in coordination |
| Torque and Flux Control with LUT (Feed-forward and feedback) | Combines a conventional closed-loop torque control (PI regulator for torque or speed) with feed-forward look-up tables that provide optimal id and iq setpoints for each operating condition (obtained via offline characterization) | Very high achievement near optimal FW (approaches MTPV limit) as LUT can be populated with points that maximize speed for given torque |
| Vector Current Control (VCC) (Enhanced FOC for FW) | Real-time adjusts the current vector (magnitude and angle) to meet torque demand while respecting the inverter voltage limit. Often implemented as an extension of FOC that gradually shifts the current angle as speed increases (includes variants like adaptive or voltage-angle-limited FOC) | High—many automotive drives use this to transition into FW smoothly; fully utilizes DC bus in steady-state FW, though may not push as close to limits as LUT methods |
| References | Control Method | Pros | Cons |
|---|---|---|---|
| [83,89,90,91,92,93] | Analytical Direct Calculation Method |
|
|
| [98,99] | Direct Open-loop Algorithm with Experimental LUT |
|
|
| [92,93,100,101,102] | Single Current Regulator (SCR) |
|
|
| [53,93,103] | Unified Direct Flux Vector Control (UDFVC) |
|
|
| [104,105,106,107,108,109,110,111,112,113,114,115] | Torque and Flux Control (TFC) Method with (LUTs) |
|
|
| [84,87,90,92,117,118,119,120,121,122,123] | Vector Current Control (VCC) (Voltage magnitude) |
|
|
| |||
| [136,137,159] | Vector Current Control (VCC) (Duty cycle error) |
|
|
| [139,140,141] | Vector Current Control (VCC) (Voltage error) |
|
|
| Machine Type | Reference Signal | Reference System | Coordinate System | MTPV Implementation | Voltage Controller Output | Transition to FW | References |
|---|---|---|---|---|---|---|---|
| IPMSM | Speed | Real | Cartesian | ✓ | d-axis current | Continuous | [120] |
| IPMSM | Torque | Real | Cartesian | ✓ | d-axis current | Continuous | [93] |
| SyRM | Speed | Per-unit | Polar | ✓ | Current angle | Continuous | [134] |
| IPMSM | Speed | Real | Cartesian | ✕ | d-axis current | Continuous | [131] |
| IPMSM | Speed | Real | Cartesian | ✓ | d-axis current | Switched | [121] |
| IPMSM | Torque | Real | Polar | ✕ | Current angle | Continuous | [125] |
| SPMSM | Speed | Real | Cartesian | ✓ | dq-axis current | Switched | [123] |
| Approach | VCC | DCC | DFVC | LUT |
|---|---|---|---|---|
| Implementation | Easy to implement | Easy to implement | Easy to implement | Complex |
| Stability in the FW region | Performance varies across different operating regions due to controller parameter influence | Maintains stable operation | Maintains stable operation | Ensures stability even under strong magnetic saturation effects |
| Acceleration State | Automatically manages transitions between MTPA and FW control | Transitioning between MTPA and FW is challenging when the operating point is always outside the current limit circle | Transitioning between MTPA and FW is challenging when the operating point is always outside the current limit circle | Roaming is very convenient based on the lookup table |
| Method | Feature | Execution | Drawback | References |
|---|---|---|---|---|
| LUT Methods (Torque Speed) | Straightforward and simple table creation | Direct look-up table (LUT) | Fixed voltage boundaries | [160,161,162,163,164,165,166] |
| LUT Methods (Torque-Flux) | Extends the voltage limits without requiring new tables | Calculation of flux and LUT | Requires indirect flux vector measurements | [109,167,168] |
| LUT Methods (Multivariate) | Offers precise results across varying motor parameters | Multivariate LUT calculations | Complex and difficult table generation | [169,170,171,172] |
| Online Calculation (Model Simplification) | Produces exact solutions with minimal feedback information | Direct calculation of voltages from reference values | Complex numerical operations | [173,174,175,176,177,178] |
| Online Calculation (Polynomial Fit) | Provides approximate solutions based on offline data | Computes FOC reference currents using polynomial fit iterative | Relies on offline solution data as the currents of FW | [179] |
| Online Calculation (Numerical Iteration) | Delivers approximate solutions using an initial value | Iterative computation of FOC reference currents | Dependent on iteration cycles and convergence | [97,180,181,182,183,184,185,186,187] |
| Online Calculation (Parameter Estimation) | Enhances model precision | Estimates flux, resistance, and inductance online | Requires precalculated offline parameter tables or signal injection | [188,189,190,191,192,193,194] |
| Online Calculation (Fuzzy Control) | Improves system resilience against mismatches | Dynamically adjusts for model mismatch and errors | Depends on defined fuzzy logic rules | [147,195,196] |
| Dual Regulator (D-axis current regulation) | Dynamic adjustment of voltage boundaries | Feedback based current reference adjustments | Dependent on motor characteristics | [131,197,198,199] |
| Dual Regulator (Anti-saturation Control) | Prevents excessive voltage during FW control | Corrects pre-limited voltages | Limited by saturation adjustments | [139,151,200,201,202,203,204,205] |
| Dual Regulator (Time Domain Optimization) | Optimized control using response times | Adjusts FW current based on time domain parameters | Possible overshoots during current regulation | [151,197,201,204,206,207] |
| Dual Regulator (Tuning Frequency Domain) | Fine tuning for adaptive performance | Regulates control bandwidth for dynamic response | Slower response to time-based changes | [117,202,203,208] |
| Dual Regulator (Current Angle Regulation) | Boosts voltage gain by adaptive control | Adjusts voltage gain | Limited by the adaptability of voltage gain | [209] |
| Dual Regulator (Frequency Feedback Control) | Guarantees system stability using feedback based on frequency | Feedback tuning based on frequency domain analysis | Difficult implementation | [87,209] |
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sivkov, O.; Novak, J. Flux weakening control of permanent magnet synchronous motor with losses reduction. In Proceedings of the 2021 XVIII International Scientific Technical Conference Alternating Current Electric Drives (ACED), Ekaterinburg, Russia, 24–27 May 2021. [Google Scholar] [CrossRef]
- Alwaqfi, S.M.N. Direct Voltage Control of an Interior Permanent Magnet Synchronous Motor in Overspeed Conditions. Master’s Thesis, Texas Tech University, Lubbock, TX, USA, 2024. [Google Scholar]
- Bilgin, B.; Magne, P.; Malysz, P.; Yang, Y.; Pantelic, V.; Preindl, M.; Korobkine, A.; Jiang, W.; Lawford, M.; Emadi, A. Making the case for electrified transportation. IEEE Trans. Transp. Electrif. 2015, 1, 4–17. [Google Scholar] [CrossRef]
- Finken, T.; Felden, M.; Hameyer, K. Comparison and design of different electrical machine types regarding their applicability in hybrid electrical vehicles. In Proceedings of the 2008 18th International Conference on Electrical Machines, Vilamoura, Portugal, 6–9 September 2008. [Google Scholar] [CrossRef]
- Karki, A.; Phuyal, S.; Tuladhar, D.; Basnet, S.; Shrestha, B.P. Status of Pure Electric Vehicle Power Train Technology and future prospects. Appl. Syst. Innov. 2020, 3, 35. [Google Scholar] [CrossRef]
- Abd Elhafez, A.A.; Aldalbehia, M.A.; Aldalbehia, N.F.; Alotaibi, F.R.; Alotaibia, N.A.; Alotaibi, R.S. Comparative Study for Machine Candidates for High Speed Traction Applications. Int. J. Electr. Eng. 2017, 10, 71–84. [Google Scholar]
- Cao, W.; Mecrow, B.C.; Atkinson, G.J.; Bennett, J.W.; Atkinson, D.J. Overview of Electric Motor Technologies Used for More Electric Aircraft (MEA). IEEE Trans. Ind. Electron. 2012, 59, 3523–3531. [Google Scholar] [CrossRef]
- Zeraoulia, M.; Benbouzid, M.E.H.; Diallo, D. Electric motor drive selection issues for hev propulsion systems: A comparative study. IEEE Trans. Veh. Technol. 2006, 55, 1756–1764. [Google Scholar] [CrossRef]
- Dorrel, D.; Knight, A.; Popescu, M.; Evans, L.; Staton, D. Comparison of different motor design drives for hybrid electric vehicles. In Proceedings of the 2010 IEEE Energy Conversion Congress and Exposition, Atlanta, GA, USA, 12–16 September 2010; pp. 3352–3359. [Google Scholar]
- Yang, Z.; Shang, F.; Brown, I.; Krishnamurthy, M. Comparative study of interior permanent magnet, induction, and switched reluctance motor drives for ev and hev applications. IEEE Trans. Transp. Electrif. 2015, 1, 245–254. [Google Scholar] [CrossRef]
- Zheng, P.; Wu, F.; Lei, Y.; Sui, Y.; Yu, B. Investigation of a novel 24-slot/14-pole sixphase fault-tolerant modular permanent-magnet in-wheel motor for electric vehicles. Energies 2013, 6, 4980–5002. [Google Scholar] [CrossRef]
- Wang, J.; Yuan, X.; Atallah, K. Design optimization of a surface-mounted permanentmagnet motor with concentrated windings for electric vehicle applications. IEEE Trans. Veh. Technol. 2013, 62, 1053–1064. [Google Scholar] [CrossRef]
- Fodorean, D.; Idoumghar, L.; Brevilliers, M.; Minciunescu, P.; Irima, C. Hybrid differential evolution algorithm employed for the optimum design of a high-speed PMSM used for ev propulsion. IEEE Trans. Ind. Electron. 2017, 64, 9824–9833. [Google Scholar] [CrossRef]
- Fodorean, D. Study of a high-speed motorization with improved performances dedicated for an electric vehicle. IEEE Trans. Magn. 2014, 50, 921–924. [Google Scholar] [CrossRef]
- Öksüztepe, E. In-Wheel Switched Reluctance Motor Design for Electric Vehicles by Using a Pareto-Based Multiobjective Differential Evolution Algorithm. IEEE Trans. Veh. Technol. 2017, 66, 4706–4715. [Google Scholar] [CrossRef]
- Bazzi, A.M. Electric machines and Energy Storage Technologies in evs and hevs for over a century. In Proceedings of the 2013 International Electric Machines & Drives Conference, Chicago, IL, USA, 12–15 May 2013. [Google Scholar] [CrossRef]
- Zhu, Z.Q.; Chu, W.Q.; Guan, Y. Quantitative comparison of electromagnetic performance of electrical machines for hevs/evs. CES Trans. Electr. Mach. Syst. 2017, 1, 37–47. [Google Scholar] [CrossRef]
- Riba, J.-R.; López-Torres, C.; Romeral, L.; Garcia, A. Rare-earth-free propulsion motors for Electric Vehicles: A technology review. Renew. Sustain. Energy Rev. 2016, 57, 367–379. [Google Scholar] [CrossRef]
- Finken, T.; Hombitzer, M.; Hameyer, K. Study and comparison of several permanent-magnet excited rotor types regarding their applicability in electric vehicles. In Proceedings of the 2010 Emobility—Electrical Power Train, Leipzig, Germany, 8–9 November 2010. [Google Scholar] [CrossRef]
- Boldea, I.; Tutelea, L.N.; Parsa, L.; Dorrell, D. Automotive electric propulsion systems with reduced or no permanent magnets: An overview. IEEE Trans. Ind. Electron. 2014, 61, 5696–5711. [Google Scholar] [CrossRef]
- Burwell, M.; Goss, J.; Popescu, M. Performance/cost comparison of induction-motor & permanent-magnet-motor in a hybrid electric car. Int. Copp. Assoc. 2013. [Google Scholar]
- Soderžnik, M.; Rožman, K.Ž.; Kobe, S.; McGuiness, P. The grain-boundary diffusion process in Nd–Fe–B sintered magnets based on the electrophoretic deposition of DYF3. Intermetallics 2012, 23, 158–162. [Google Scholar] [CrossRef]
- Thomson, M.M.; Nietfeld, J.L. Knowledge, monitoring, and beliefs: A comparative analysis among preservice teachers from three different stem-focused programs. J. Interdiscip. Teach. Leadersh. 2017, 1, 19–27. [Google Scholar] [CrossRef]
- Jahns, T. Getting rare-earth magnets out of EV traction machines: A review of the many approaches being pursued to minimize or eliminate rare-earth magnets from future EV drivetrains. IEEE Electrif. Mag. 2017, 5, 6–18. [Google Scholar] [CrossRef]
- Guan, Y.; Zhu, Z.Q.; Afinowi, I.A.A.; Mipo, J.C.; Farah, P. Difference in maximum torque-speed characteristics of induction machine between motor and Generator Operation Modes for Electric Vehicle Application. Electr. Power Syst. Res. 2016, 136, 406–414. [Google Scholar] [CrossRef]
- Sira-Ramirez, H.; Gonzalez-Montanez, F.; Cortes-Romero, J.A.; Luviano-Juarez, A. A robust linear field-oriented voltage control for the induction motor: Experimental results. IEEE Trans. Ind. Electron. 2013, 60, 3025–3033. [Google Scholar] [CrossRef]
- Bozhko, S.; Dymko, S.; Kovbasa, S.; Peresada, S.M. Maximum torque-per-AMP control for traction IM drives: Theory and experimental results. IEEE Trans. Ind. Appl. 2017, 53, 181–193. [Google Scholar] [CrossRef]
- Chau, K.T.; Li, W. Overview of electric machines for electric and hybrid vehicles. Int. J. Veh. Des. 2014, 64, 46. [Google Scholar] [CrossRef]
- Chinmaya, K.A.; Singh, G.K. Integrated onboard single-stage battery charger for pevs incorporating asymmetrical six-phase Induction Machine. IET Electr. Syst. Transp. 2019, 9, 8–15. [Google Scholar] [CrossRef]
- Morimoto, S.; Ooi, S.; Inoue, Y.; Sanada, M. Experimental evaluation of a rare-earth-free pmasynrm with ferrite magnets for automotive applications. IEEE Trans. Ind. Electron. 2014, 61, 5749–5756. [Google Scholar] [CrossRef]
- Bianchi, N.; Mahmoud, H. An analytical approach to design the PM IN PMAREL motors robust toward the demagnetization. IEEE Trans. Energy Convers. 2016, 31, 800–809. [Google Scholar] [CrossRef]
- Bianchi, N.; Bolognani, S.; Carraro, E.; Castiello, M.; Fornasiero, E. Electric vehicle traction based on synchronous reluctance motors. IEEE Trans. Ind. Appl. 2016, 52, 4762–4769. [Google Scholar] [CrossRef]
- Reddy, P.B.; Grace, K.; El-Refaie, A. Conceptual design of sleeve rotor synchronous reluctance motor for traction applications. IET Electr. Power Appl. 2016, 10, 368–374. [Google Scholar] [CrossRef]
- Trancho, E.; Ibarra, E.; Arias, A.; Kortabarria, I.; Prieto, P.; de Alegría, I.M.; Andreu, J.; López, I. Sensorless Control Strategy for light-duty EVS and efficiency loss evaluation of high frequency injection under standardized urban driving cycles. Appl. Energy 2018, 224, 647–658. [Google Scholar] [CrossRef]
- Ding, W.; Yang, S.; Hu, Y.; Li, S.; Wang, T.; Yin, Z. Design consideration and evaluation of a 12/8 high-torque modular-stator hybrid excitation switched reluctance machine for EV applications. IEEE Trans. Ind. Electron. 2017, 64, 9221–9232. [Google Scholar] [CrossRef]
- Afjei, E.; Toliyat, H.A. A novel multilayer switched reluctance motor. IEEE Power Eng. Rev. 2002, 22, 73. [Google Scholar] [CrossRef]
- Desai, P.C.; Krishnamurthy, M.; Schofield, N.; Emadi, A. Novel switched reluctance machine configuration with higher number of rotor poles than stator poles: Concept to implementation. IEEE Trans. Ind. Electron. 2010, 57, 649–659. [Google Scholar] [CrossRef]
- Cheewoo, L.; Krishnan, R. New designs of a two-phase e-core switched reluctance machine by optimizing the magnetic structure for a specific application: Concept, design, and analysis. IEEE Trans. Ind. Appl. 2009, 45, 1804–1814. [Google Scholar] [CrossRef]
- Nguyen, D.-M.; Bahri, I.; Krebs, G.; Berthelot, E.; Marchand, C.; Ralev, I.; Burkhart, B.; De Doncker, R.W. Efficiency improvement by the intermittent control for switched reluctance machine in automotive application. IEEE Trans. Ind. Appl. 2019, 55, 4167–4182. [Google Scholar] [CrossRef]
- Ooi, S.; Morimoto, S.; Sanada, M.; Inoue, Y. Performance Evaluation of a High-Power-Density PMASynRM With Ferrite Magnets. IEEE Trans. Ind. Appl. 2013, 49, 1308–1315. [Google Scholar] [CrossRef]
- Vagati, A.; Boazzo, B.; Guglielmi, P.; Pellegrino, G. Ferrite assisted synchronous reluctance machines: A general approach. In Proceedings of the 2012 20th International Conference on Electrical Machines, Marseille, France, 2–5 September 2012; pp. 1315–1321. [Google Scholar] [CrossRef]
- Krishnan, R. Permanent Magnet Synchronous and Brushless DC Motor Drives; CRC Press: Boca Raton, FL, USA, 2010; pp. 34–42. [Google Scholar]
- Idoko, H.C.; Akuru, U.B.; Wang, R.; Popoola, O. Potentials of Brushless Stator-Mounted Machines in Electric Vehicle Drives—A Literature Review. World Electr. Veh. J. 2022, 13, 93. [Google Scholar] [CrossRef]
- Hedon, M. Modeling and Simulation of a Hybrid Powertrain. Master’s Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2018; pp. 29–34. Available online: https://kth.diva-portal.org/smash/get/diva2:1249494/FULLTEXT01.pdf (accessed on 3 June 2023).
- Fresneau, D. Increasing the Range of EV with the Same Battery—Part II—More Efficiency with Better Software, Silicon Mobility. 2019. Available online: https://www.silicon-mobility.com/increasing-the-range-of-ev-with-the-same-battery-part-ii-more-efficiency-with-better-software/ (accessed on 4 June 2023).
- Park, J.-H.; Jo, W.; Jeon, E.-T.; Kim, S.-H.; Lee, C.-H.; Lee, J.-H.; Lee, J.-H.; Yi, J.; Won, C.-Y. Variable Switching Frequency Control-Based Six-Step Operation Method of a Traction Inverter for Driving an Interior Permanent Magnet Synchronous Motor for a Railroad Car. IEEE Access 2022, 10, 33829–33843. [Google Scholar] [CrossRef]
- Gerada, D.; Mebarki, A.; Brown, N.L.; Gerada, C.; Cavagnino, A.; Boglietti, A. High-Speed Electrical Machines: Technologies, Trends, and Developments. IEEE Trans. Ind. Electron. 2014, 61, 2946–2959. [Google Scholar] [CrossRef]
- Chedot, L.; Friedrich, G. A cross saturation model for interior permanent magnet synchronous machine. Application to a starter-generator. In Proceedings of the Conference Record of the 2004 IEEE Industry Applications Conference, 2004. 39th IAS Annual Meeting, Seattle, WA, USA, 3–7 October 2004; p. 70. [Google Scholar] [CrossRef]
- Tan, L.N.; Pham, T.C. Optimal Tracking Control for PMSM With Partially Unknown Dynamics, Saturation Voltages, Torque, and Voltage Disturbances. IEEE Trans. Ind. Electron. 2022, 69, 3481–3491. [Google Scholar] [CrossRef]
- Bose, B.K. Variable Frequency Permanent Magnet AC Machine Drives. In Power Electronics and Variable Frequency Drives: Technology and Applications; IEEE: Piscataway, NJ, USA, 1997; pp. 277–331. [Google Scholar] [CrossRef]
- Taghavi, S.M.; Jain, M.; Williamson, S.S. A comparative study of sensorless control techniques of interior permanent magnet synchronous motor drives for electric vehicles. In Proceedings of the 2011 IEEE Vehicle Power and Propulsion Conference, Chicago, IL, USA, 6–9 September 2011; pp. 1–7. [Google Scholar] [CrossRef]
- Pellegrino, G.; Armando, E.; Guglielmi, P. Direct Flux Field-Oriented Control of IPM Drives with Variable DC Link in the Field-Weakening Region. IEEE Trans. Ind. Appl. 2009, 45, 1619–1627. [Google Scholar] [CrossRef]
- Pellegrino, G.; Bojoi, R.I.; Guglielmi, P. Unified Direct-Flux Vector Control for AC Motor Drives. IEEE Trans. Ind. Appl. 2011, 47, 2093–2102. [Google Scholar] [CrossRef]
- Jung, S.-Y.; Hong, J.; Nam, K. Current Minimizing Torque Control of the IPMSM Using Ferrari’s Method. IEEE Trans. Power Electron. 2013, 28, 5603–5617. [Google Scholar] [CrossRef]
- Ohnuma, T. Current control of PMSM based on maximum torque control reference frame. In Proceedings of the AIP Conference Proceedings, Penang, Malaysia, 27–29 January 2016. [Google Scholar] [CrossRef]
- Nakashima, S.; Inagaki, Y.; Miki, I. Sensorless initial rotor position estimation of surface permanent-magnet synchronous motor. IEEE Trans. Ind. Appl. 2000, 36, 1598–1603. [Google Scholar] [CrossRef]
- Field-Weakening Control (with MTPA) of PMSM (No Date) Field-Weakening Control (with MTPA) of PMSM—MATLAB & Simulink Example. Available online: https://www.mathworks.com/help/mcb/gs/field-weakening-control-mtpa-pmsm.html#d124e5944 (accessed on 11 June 2023).
- Alzayed, M.; Chaoui, H. Efficient Simplified Current Sensorless Dynamic Direct Voltage MTPA of Interior PMSM for Electric Vehicles Operation. IEEE Trans. Veh. Technol. 2022, 71, 12701–12710. [Google Scholar] [CrossRef]
- Shakib, S.M.S.I.; Xiao, D.; Dutta, R.; Alam, K.S.; Osman, I.; Rahman, M.F.; Akter, P. An Analytical Approach to Direct Torque and Flux Control of Interior Permanent Magnet Synchronous Machine for Deep Field Weakening Without Using Pre-calculated Lookup Tables. In Proceedings of the 2019 10th International Conference on Power Electronics and ECCE Asia (ICPE 2019—ECCE Asia), Busan, Republic of Korea, 27–30 May 2019; pp. 3196–3202. [Google Scholar] [CrossRef]
- Meyer, M.; Grote, T.; Bocker, J. Direct torque control for interior permanent magnet synchronous motors with respect to optimal efficiency. In Proceedings of the 2007 European Conference on Power Electronics and Applications, Aalborg, Denmark, 2–5 September 2007; pp. 1–9. [Google Scholar] [CrossRef]
- Inoue, Y.; Morimoto, S.; Sanada, M. Comparative Study of PMSM Drive Systems Based on Current Control and Direct Torque Control in Flux-Weakening Control Region. IEEE Trans. Ind. Appl. 2012, 48, 2382–2389. [Google Scholar] [CrossRef]
- Dwivedi, S.; Singh, B. Vector Control vs Direct Torque Control comparative evaluation for PMSM drive. In Proceedings of the 2010 Joint International Conference on Power Electronics, Drives and Energy Systems & 2010 Power India, New Delhi, India, 20–23 December 2010; pp. 1–8. [Google Scholar] [CrossRef]
- Montalvo-Ortiz, E.E.; Foster, S.N.; Cintron-Rivera, J.G.; Strangas, E.G. Comparison between a spoke-type PMSM and a PMASynRM using ferrite magnets. In Proceedings of the 2013 International Electric Machines & Drives Conference, Chicago, IL, USA, 12–15 May 2013; pp. 1080–1087. [Google Scholar] [CrossRef]
- Tinazzi, F.; Sandulescu, P.; Peretti, L.; Zigliotto, M. On the true maximum efficiency operations of synchronous motor drives. In Proceedings of the 2017 IEEE 12th International Conference on Power Electronics and Drive Systems (PEDS), Honolulu, HI, USA, 12–15 December 2017; pp. 1043–1048. [Google Scholar] [CrossRef]
- Hackl, C.M.; Kullick, J.; Eldeeb, H.; Horlbeck, L. Analytical computation of the optimal reference currents for MTPC/MTPA, MTPV and MTPF operation of anisotropic synchronous machines considering stator resistance and mutual inductance. In Proceedings of the 2017 19th European Conference on Power Electronics and Applications (EPE’17 ECCE Europe), Warsaw, Poland, 11–14 September 2017; pp. P.1–P.10. [Google Scholar] [CrossRef]
- Rahman, M.A.; Zhou, P. Analysis of brushless permanent magnet synchronous motors. IEEE Trans. Ind. Electron. 1996, 43, 256–267. [Google Scholar] [CrossRef]
- Jahns, T.M.; Kliman, G.B.; Neumann, T.W. Interior Permanent-magnet synchronous motors for adjustable-speed drives. IEEE Trans. Ind. Appl. 1986, IA-22, 738–747. [Google Scholar] [CrossRef]
- Pillay, P.; Krishnan, R. Application characteristics of permanent magnet synchronous and brushless DC motors for servo drives. IEEE Trans. Ind. Appl. 1991, 27, 986–996. [Google Scholar] [CrossRef]
- Chaoui, H.; Khayamy, M.; Okoye, O. MTPA based Operation Point Speed tracking for PMSM drives without explicit current regulation. Electr. Power Syst. Res. 2017, 151, 125–135. [Google Scholar] [CrossRef]
- Samala, Naga Santhoshi. Cogging Torque and Torque Ripple Analysis on Permanent Magnet Synchronous Machines. 2019. Available online: https://www.politesi.polimi.it/handle/10589/148988 (accessed on 14 October 2024).
- Pellegrino, G.; Armando, E.; Guglielmi, P. Direct-Flux Vector Control of IPM Motor Drives in the Maximum Torque Per Voltage Speed Range. IEEE Trans. Ind. Electron. 2012, 59, 3780–3788. [Google Scholar] [CrossRef]
- Kim, S.-H.; Sul, S.-K. Voltage control strategy for maximum torque operation of an induction machine in the field-weakening region. IEEE Trans. Ind. Electron. 1997, 44, 512–518. [Google Scholar] [CrossRef]
- Bae, B.-H.; Patel, N.; Schulz, S.; Sul, S.-K. New field weakening technique for high saliency interior permanent magnet motor. In Proceedings of the 38th IAS Annual Meeting on Conference Record of the Industry Applications Conference, 2003, Salt Lake City, UT, USA, 12–16 October 2003; Volume 2, pp. 898–905. [Google Scholar] [CrossRef]
- Lubin, T.; Razik, H.; Rezzoug, A. Magnetic saturation effects on the control of a synchronous reluctance machine. IEEE Trans. Energy Convers. 2002, 17, 356–362. [Google Scholar] [CrossRef]
- Guha, S.; Kar, N.C. A New Method of Modeling Magnetic Saturation in Electrical Machines. In Proceedings of the 2006 Canadian Conference on Electrical and Computer Engineering, Ottawa, ON, Canada, 7–10 May 2006; pp. 1094–1097. [Google Scholar] [CrossRef]
- Chen, H.; Chen, Y.; Huang, S.-R.; Zhang, F. Calculation of inductance of permanent magnet synchronous motor considering permanent magnet flux linkage variation of load conditions. In Proceedings of the 2014 IEEE Conference and Expo Transportation Electrification Asia-Pacific (ITEC Asia-Pacific), Beijing, China, 31 August–3 September 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Aoyama, M.; Noguchi, T. Flux Intensifying PM-Motor with Variable Leakage Magnetic Flux Technique. In Proceedings of the 2018 International Power Electronics Conference (IPEC-Niigata 2018-ECCE Asia), Niigata, Japan, 20–24 May 2018; pp. 718–725. [Google Scholar] [CrossRef]
- Soong, W.L. Design and Modelling of Axially Laminated Interior Permanent Magnet Motor Drives for Field-Weakening Applications. Ph.D. Thesis, University of Glasgow, Scotland, UK, 1993. [Google Scholar]
- Morimoto, S.; Takeda, Y.; Hirasa, T.; Taniguchi, K. Expansion of operating limits for permanent magnet motor by current vector control considering inverter capacity. IEEE Trans. Ind. Appl. 1990, 26, 866–871. [Google Scholar] [CrossRef]
- Song, T.; Zhang, Z.; Liu, H.; Hu, W. Multi-objective optimisation design and performance comparison of permanent magnet synchronous motor for EVS based on FEA. IET Electr. Power Appl. 2019, 13, 1157–1166. [Google Scholar] [CrossRef]
- Jia, L.; Qin, Y.; Liang, J.; Liu, Z.; Diao, L.; An, M. (Eds.) Proceedings of the 5th International Conference on Electrical Engineering and Information Technologies for Rail Transportation (EITRT) 2021; Lecture Notes in Electrical Engineering; Springer Nature: London, UK, 2022. [Google Scholar] [CrossRef]
- Lu, D.; Kar, N.C. A review of flux-weakening control in permanent magnet synchronous machines. In Proceedings of the 2010 IEEE Vehicle Power and Propulsion Conference, Lille, France, 1–3 September 2010; pp. 1–6. [Google Scholar] [CrossRef]
- Morimoto, S.; Sanada, M.; Takeda, Y. Wide-speed operation of interior permanent magnet synchronous motors with high-performance current regulator. IEEE Trans. Ind. Appl. 1994, 30, 920–926. [Google Scholar] [CrossRef]
- Kim, J.-M.; Sul, S.-K. Speed control of interior permanent magnet synchronous motor drive for the flux weakening operation. IEEE Trans. Ind. Appl. 1997, 33, 43–48. [Google Scholar] [CrossRef]
- Miguel-Espinar, C.; Heredero-Peris, D.; Gross, G. Llonch-Masachs and D. Montesinos-Miracle. Maximum Torque per Voltage Flux-Weakening Strategy with Speed Limiter for PMSM Drives. IEEE Trans. Ind. Electron. 2021, 68, 9254–9264. [Google Scholar] [CrossRef]
- Command Modes (No Date) FluxMotor Doc. Available online: https://fluxmotordoc.altair.com/helponlines/helponline/292 (accessed on 13 July 2023).
- Bolognani, S.; Calligaro, S.; Petrella, R. Adaptive Flux-Weakening Controller for Interior Permanent Magnet Synchronous Motor Drives. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 236–248. [Google Scholar] [CrossRef]
- Wang, J.; Wu, J.; Gan, C.; Sun, Q. Comparative study of flux-weakening control methods for PMSM drive over wide speed range. In Proceedings of the 2016 19th International Conference on Electrical Machines and Systems (ICEMS), Chiba, Japan, 13–16 November 2016; pp. 1–6. [Google Scholar]
- Tursini, M.; Chiricozzi, E.; Petrella, R. Feedforward Flux-Weakening Control of Surface-Mounted Permanent-Magnet Synchronous Motors Accounting for Resistive Voltage Drop. IEEE Trans. Ind. Electron. 2010, 57, 440–448. [Google Scholar] [CrossRef]
- Sepulchre, L.; Fadel, M.; Pietrzak-David, M.; Porte, G. Flux-weakening strategy for high speed PMSM for vehicle application. In Proceedings of the 2016 International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles & International Transportation Electrification Conference (ESARS-ITEC), Toulouse, France, 2–4 November 2016; pp. 1–7. [Google Scholar] [CrossRef]
- Fangyang, Z.; Feng, R.; Jianjun, L.; Peng, H. Study on Flux-Weakening Control for PMSM. In Proceedings of the 2011 Fourth International Symposium on Knowledge Acquisition and Modeling, Sanya, China, 8–9 October 2011; pp. 192–195. [Google Scholar] [CrossRef]
- Gao, F.; Bozhko, S.; Shen, Y.S.; Asher, G. Control design for PMM starter-generator operated in flux-weakening mode. In Proceedings of the 2013 48th International Universities’ Power Engineering Conference (UPEC), Dublin, Ireland, 2–5 September 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Sepulchre, L.; Fadel, M.; Pietrzak-David, M.; Porte, G. MTPV Flux-Weakening Strategy for PMSM High Speed Drive. IEEE Trans. Ind. Appl. 2018, 54, 6081–6089. [Google Scholar] [CrossRef]
- Sanz, A.; Oyarbide, E.; Gálvez, R.; Bernal, C.; Molina, P.; Vicente, I.S. Analytical maximum torque per volt control strategy of an interior permanent magnet synchronous motor with very low battery voltage. IET Electr. Power Appl. 2019, 13, 1042–1050. [Google Scholar] [CrossRef]
- Shi, Y.F.; Zhu, Z.Q.; Chen, Y.S.; Howe, D. Influence of winding resistance on flux-weakening performance of a permanent magnet brushless AC drive. In Proceedings of the 2002 International Conference on Power Electronics, Machines and Drives (Conf. Publ. No. 487), Sante Fe, NM, USA, 16–18 April 2002; pp. 392–397. [Google Scholar] [CrossRef]
- Olarescu, N.V.; Weinmann, M.; Zeh, S.; Musuroi, S. Novel flux weakening control algorithm for PMSMS. In Proceedings of the 2009 International Conference on Power Engineering, Energy and Electrical Drives, Lisbon, Portugal, 18–20 March 2009; pp. 123–127. [Google Scholar] [CrossRef]
- Wang, S.; Kang, J.; Degano, M.; Galassini, A.; Gerada, C. An Accurate Wide-Speed Range Control Method of IPMSM Considering Resistive Voltage Drop and Magnetic Saturation. IEEE Trans. Ind. Electron. 2020, 67, 2630–2641. [Google Scholar] [CrossRef]
- Meyer, M.; Bocker, J. Optimum Control for Interior Permanent Magnet Synchronous Motors (IPMSM) in Constant Torque and Flux Weakening Range. In Proceedings of the 2006 12th International Power Electronics and Motion Control Conference, Portoroz, Slovenia, 30 August–1 September 2006; pp. 282–286. [Google Scholar] [CrossRef]
- Kunter, M.S.; Schoenen, T.; Hoffmann, W.; De Doncker, R.W. IPMSM control regime for a hybrid-electric vehicle application. In Proceedings of the 2010 Emobility—Electrical Power Train, Leipzig, Germany, 8–9 November 2010; pp. 1–5. [Google Scholar] [CrossRef]
- Xu, L.; Zhang, Y.; Guven, M.K. A new method to optimize q-axis voltage for deep flux weakening control of IPM machines based on single current regulator. In Proceedings of the 2008 International Conference on Electrical Machines and Systems, Wuhan, China, 17–20 October 2008; pp. 2750–2754. [Google Scholar]
- Zhang, Y.; Güven, M.K.; Guven, M.K.; Chi, S.; Illindala, M. Experimental Verification of Deep Field Weakening Operation of a 50-kW IPM Machine by Using Single Current Regulator. IEEE Trans. Ind. Appl. 2011, 47, 128–133. [Google Scholar] [CrossRef]
- Zhu, L.; Xue, S.; Wen, X.; Li, Y.; Kong, L. A new deep field-weakening strategy of IPM machines based on single current regulator and voltage angle control. In Proceedings of the 2010 IEEE Energy Conversion Congress and Exposition, Atlanta, GA, USA, 12–16 September 2010; pp. 1144–1149. [Google Scholar] [CrossRef]
- Boldea, I.; Paicu, M.C.; Andreescu, G.-D. Active Flux Concept for Motion-Sensorless Unified AC Drives. IEEE Trans. Power Electron. 2008, 23, 2612–2618. [Google Scholar] [CrossRef]
- Ekanayake, S.; Dutta, R.; Rahman, F.; Xuan, B.M. Position Sensorless Control of an Interior Permanent Magnet Synchronous Machine (IPMSM) in Deep Flux-weakening Region. In Proceedings of the 2018 IEEE 9th International Symposium on Sensorless Control for Electrical Drives (SLED), Helsinki, Finland, 13–14 September 2018; pp. 114–119. [Google Scholar] [CrossRef]
- Peters, W.; Huber, T.; Böcker, J. Control Realization for an Interior Permanent Magnet Synchronous Motor (IPMSM) in Automotive Drive Trains. In Proceedings of the International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management (PCIM Europe), Nuremberg, Germany, 17–19 May 2011. [Google Scholar]
- Huber, T.; Peters, W.; Bocker, J. Voltage controller for flux weakening operation of interior permanent magnet synchronous motor in automotive traction applications. In Proceedings of the 2015 IEEE International Electric Machines & Drives Conference (IEMDC), Coeur d’Alene, ID, USA, 10–13 May 2015; pp. 1078–1083. [Google Scholar] [CrossRef]
- Bae, B.H.; Sul, S.K.; Kwon, J.H.; Byeon, J.S. Implementation of sensorless vector control for super-high-speed PMSM of turbo-compressor. IEEE Trans. Ind. Appl. 2003, 39, 811–818. [Google Scholar] [CrossRef]
- Choi, G.-Y.; Kwak, M.-S.; Kwon, T.-S.; Sul, S.-K. Novel Flux-Weakening Control of an IPMSM for Quasi Six-Step Operation. In Proceedings of the 2007 IEEE Industry Applications Annual Meeting, New Orleans, LA, USA, 23–27 September 2007; pp. 1315–1321. [Google Scholar] [CrossRef]
- Kwon, T.-S.; Choi, G.-Y.; Kwak, M.-S.; Sul, S.-K. Novel Flux-Weakening Control of an IPMSM for Quasi-Six-Step Operation. IEEE Trans. Ind. Appl. 2008, 44, 1722–1731. [Google Scholar] [CrossRef]
- Huang, L.; Zhao, G.; Huang, P. An approach to improve the torque performance of IPMSM by considering cross saturation applied for hybrid electric vehicle. In Proceedings of the 2010 International Conference on Electrical Machines and Systems, Incheon, Republic of Korea, 10–13 October 2010; pp. 1378–1381. [Google Scholar]
- Chen, Y.Z.; Fang, Y.T.; Huang, X.Y.; Zhang, J. Torque and Flux Weakening Control with MTPV for Interior Permanent Magnet Synchronous Motor. In Proceedings of the 2016 IEEE Vehicle Power and Propulsion Conference (VPPC), Hangzhou, China, 17–20 October 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Ekanayake, S.; Dutta, R.; Rahman, M.F.; Xiao, D.; Fletcher, J. Operation along the maximum torque per voltage trajectory in a direct torque and flux controlled interior permanent magnet synchronous motor. In Proceedings of the 8th IET International Conference on Power Electronics, Machines and Drives (PEMD 2016), Glasgow, UK, 19–21 April 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Ekanayake, S.; Dutta, R.; Xiao, D.; Rahman, M.F. Direct torque and flux control of a fractional-slot concentrated-winding IPMSM in deep flux-weakening region. In Proceedings of the 2017 20th International Conference on Electrical Machines and Systems (ICEMS), Sydney, Australia, 11–14 August 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Ekanayake, S.; Dutta, R.; Rahman, M.F.; Xiao, D. Direct torque and flux control of interior permanent magnet synchronous machine in deep flux-weakening region. IET Electr. Power Appl. 2017, 12, 98–105. [Google Scholar] [CrossRef]
- Ekanayake, S.; Dutta, R.; Rahman, M.F.; Bui, M.X. Performances of a Fractional-Slot Concentrated-Winding Permanent Magnet Synchronous Machine Under Position Sensorless Control in Deep Flux-Weakening Region. IEEE Trans. Ind. Appl. 2019, 55, 5938–5946. [Google Scholar] [CrossRef]
- Kim, D.-Y.; Lee, J.-H. Compensation of Interpolation Error for Look-Up Table-Based PMSM Control Method in Maximum Power Control. Energies 2021, 14, 5526. [Google Scholar] [CrossRef]
- Bozhko, S.; Rashed, M.; Hill, C.I.; Yeoh, S.S.; Yang, T. Flux-Weakening Control of Electric Starter–Generator Based on Permanent-Magnet Machine. IEEE Trans. Transp. Electrif. 2017, 3, 864–877. [Google Scholar] [CrossRef]
- Bolognani, S.; Calligaro, S.; Petrella, R. Optimal voltage feed-back flux-weakening control of IPMSM. In Proceedings of the IECON 2011—37th Annual Conference of the IEEE Industrial Electronics Society, Melbourne, Australia, 7–10 November 2011; pp. 4170–4175. [Google Scholar] [CrossRef]
- Fadel, M.; Sepulchre, L.; Pietrzak-David, M. Deep flux-weakening strategy with MTPV for high-speed IPMSM for vehicle application. IFAC-PapersOnLine 2018, 51, 616–621. [Google Scholar] [CrossRef]
- Li, J.; Ekanayake, S.; Rahman, M.F.; Dutta, R.; Huang, X.; Ma, J.; Fang, Y. Deep flux weakening control with six-step overmodulation for a segmented interior permanent magnet synchronous motor. In Proceedings of the 2017 20th International Conference on Electrical Machines and Systems (ICEMS), Sydney, Australia, 11–14 August 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, W.; Sun, D. Comparative research of two flux-weakening method of PMSMs in high speed range. In Proceedings of the 2017 20th International Conference on Electrical Machines and Systems (ICEMS), Sydney, Australia, 11–14 August 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Miguel-Espinar, C.; Heredero-Peris, D.; Subirats-Rillo, O.; Escaler, X.; Montesinos-Miracle, D. Novel Flux-Weakening Strategy Considering the Saturation Effects for Electric Vehicles. In Proceedings of the PCIM Europe Digital Days 2021; International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Online, 3–7 May 2021; pp. 1–8. [Google Scholar]
- Hu, D.; Zhu, L.; Xu, L. Maximum Torque per Volt operation and stability improvement of PMSM in deep flux-weakening Region. In Proceedings of the 2012 IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, 15–20 September 2012; pp. 1233–1237. [Google Scholar] [CrossRef]
- Bianchi, N.; Bolognani, S.; Zigliotto, M. High-performance PM synchronous motor drive for an electrical scooter. IEEE Trans. Ind. Appl. 2001, 37, 1348–1355. [Google Scholar] [CrossRef]
- Wai, J.; Jahns, T.M. A new control technique for achieving wide constant power speed operation with an interior PM alternator machine. In Proceedings of the Conference Record of the 2001 IEEE Industry Applications Conference. 36th IAS Annual Meeting (Cat. No.01CH37248), Chicago, IL, USA, 30 September–4 October 2001; Volume 2, pp. 807–814. [Google Scholar] [CrossRef]
- Bianchini, C.; Franceschini, G.; Torreggiani, A. Improvement on flux weakening control strategy for Electric Vehicle Applications. Appl. Sci. 2021, 11, 2422. [Google Scholar] [CrossRef]
- Manzolini, V.; Da Rù, D.; Bolognani, S. An effective voltage control loop for a deep flux-weakening in IPM synchronous motor drives. In Proceedings of the 2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 1–5 October 2017; pp. 3979–3985. [Google Scholar] [CrossRef]
- Manzolini, V.; Da Rù, D.; Bolognani, S. A new control strategy for high efficiency wide speed range synchronous reluctance motor drives. In Proceedings of the 2017 IEEE International Electric Machines and Drives Conference (IEMDC), Miami, FL, USA, 21–24 May 2017; pp. 1–7. [Google Scholar] [CrossRef]
- Sepulchre, L.; Fadel, M.; Ptetrzak-David, M. MTPV for Continuous Flux-Weakening Strategy Control Law for IPMSM. In Proceedings of the 2018 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Amalfi, Italy, 20–22 June 2018; pp. 1221–1226. [Google Scholar] [CrossRef]
- Khanh, P.Q.; Huy Anh, H.P. Advanced Deep Flux Weakening Operation Control Strategies for IPMSM. Int. J. Electr. Comput. Eng. (IJECE) 2021, 11, 3798. [Google Scholar] [CrossRef]
- Ding, D.; Wang, G.; Zhao, N.; Zhang, G.; Xu, D. Enhanced Flux-Weakening Control Method for Reduced DC-Link Capacitance IPMSM Drives. IEEE Trans. Power Electron. 2019, 34, 7788–7799. [Google Scholar] [CrossRef]
- Deng, T.; Su, Z.; Li, J.; Tang, P.; Chen, X.; Liu, P. Advanced Angle Field Weakening Control Strategy of Permanent Magnet Synchronous Motor. IEEE Trans. Veh. Technol. 2019, 68, 3424–3435. [Google Scholar] [CrossRef]
- Vaclavek, P.; Blaha, P. Interior permanent magnet synchronous machine field weakening control strategy—The analytical solution. In Proceedings of the 2008 SICE Annual Conference, Chofu, Japan, 20–22 August 2008; pp. 753–757. [Google Scholar] [CrossRef]
- Manzolini, V.; Da Rù, D.; Bolognani, S. An Effective Flux Weakening Control of a SyRM Drive Including MTPV Operation. IEEE Trans. Ind. Appl. 2019, 55, 2700–2709. [Google Scholar] [CrossRef]
- Sepulchre, L.; Fadel, M.; Pietrzak-David, M.; Porte, G. New high speed PMSM flux-weakening strategy. In Proceedings of the 2016 19th International Conference on Electrical Machines and Systems (ICEMS), Chiba, Japan, 13–16 November 2016; pp. 1–6. [Google Scholar]
- Jun; Wang, Q.-R.; Yu, J.; Xiong, J. Field-weakening Control Algorithm for Interior Permanent Magnet Synchronous Motor Based on Space-Vector Modulation Technique. J. Converg. Inf. Technol. 2013, 8, 167–175. [Google Scholar]
- Lin, P.-Y.; Lai, Y.-S. Voltage Control Technique for the Extension of DC-Link Voltage Utilization of Finite-Speed SPMSM Drives. IEEE Trans. Ind. Electron. 2012, 59, 3392–3402. [Google Scholar] [CrossRef]
- Lin, P.-Y.; Lee, W.-T.; Chen, S.-W.; Hwang, J.-C.; Lai, Y.-S. Infinite speed drives control with MTPA and MTPV for interior permanent magnet synchronous motor. In Proceedings of the IECON 2014—40th Annual Conference of the IEEE Industrial Electronics Society, Dallas, TX, USA, 29 October–1 November 2014; pp. 668–674. [Google Scholar] [CrossRef]
- Liu, H.; Zhu, Z.Q.; Mohamed, E.; Fu, Y.; Qi, X. Flux-Weakening Control of Nonsalient Pole PMSM Having Large Winding Inductance, Accounting for Resistive Voltage Drop and Inverter Nonlinearities. IEEE Trans. Power Electron. 2012, 27, 942–952. [Google Scholar] [CrossRef]
- Pothi, N. Improvement of flux-weakening control of surface mounted permanent magnet synchronous machine considering inverter nonlinearity. In Proceedings of the 2017 International Electrical Engineering Congress (iEECON), Pattaya, Thailand, 8–10 March 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Kim, M.; Yim, J.-S.; Sul, S.-K.; Lim, S.-I. Implementation of super high-speed permanent magnet synchronous machine drive. In Proceedings of the 2009 IEEE Energy Conversion Congress and Exposition, San Jose, CA, USA, 20–24 September 2009; pp. 1700–1704. [Google Scholar] [CrossRef]
- Lee, H.-J.; Shon, J.-G. Improved voltage flux-weakening strategy of permanent magnet synchronous motor in high-speed operation. Energies 2021, 14, 7464. [Google Scholar] [CrossRef]
- Jing, R.; Wang, G.; Zhang, G.; Xu, D. Review of Field Weakening Control Strategies of Permanent Magnet Synchronous Motors. CES Trans. Electr. Mach. Syst. 2024, 8, 319–331. [Google Scholar] [CrossRef]
- Krishnan, R. Control and operation of PM synchronous motor drives in the field-weakening region. In Proceedings of the International Conference on Industrial Electronics, Control, and Instrumentation, Maui, HI, USA, 15–18 November 1993; Volume 2, pp. 745–750. [Google Scholar]
- Verl, A.; Bodson, M. Torque maximization for permanent magnet synchronous motors. IEEE Trans. Control Syst. Technol. 1998, 6, 740–745. [Google Scholar] [CrossRef]
- Bech, M.M.; Frederiksen, T.S.; Sandholdt, P. Accurate torque control of saturated interior permanent magnet synchronous motors in the field-weakening region. In Proceedings of the 2005 Industry Applications Conference, Hong Kong, China, 2–6 October 2005; Volume 4, pp. 2526–2532. [Google Scholar]
- Uddin, M.N.; Rahman, M.A. High-speed control of IPMSM drives using improved fuzzy logic algorithyms. IEEE Trans. Ind. Electron. 2007, 54, 190–199. [Google Scholar] [CrossRef]
- Macminn, S.R.; Jahns, T.M. Control techniques for improved highspeed performance of interior PM synchronous motor drives. IEEE Trans. Ind. Appl. 1991, 27, 997–1004. [Google Scholar] [CrossRef]
- Song, H.; Kim, J.M.; Sul, S.K. A new robust SPMSM control to parameter variations in flux weakening region. In Proceedings of the IEEE Industrial Electronics Society Annual Conference 1996, Orlando, FL, USA, 10–15 November 1996; pp. 1193–1198. [Google Scholar]
- Doleček, R.; Šimánek, J.; Novák, J.; Černý, O. Dynamics of a feedback optimal-current-vector flux-weakening strategy for traction permanent-magnet synchronous motors. In Proceedings of the 2009 ELECTROMOTION, Lille, France, 1–3 July 2009; pp. 1–6. [Google Scholar]
- Kwon, T.; Sul, S. Novel antiwindup of a current regulator of a surface-mounted permanent-magnet motor for flux-weakening control. IEEE Trans. Ind. Appl. 2006, 42, 1293–1300. [Google Scholar] [CrossRef]
- Sue, S.; Pan, C. Voltage-constraint-tracking-based field-weakening control of IPM synchronous motor drives. IEEE Trans. Ind. Electron. 2008, 55, 340–347. [Google Scholar] [CrossRef]
- Zhu, Z.Q.; Chen, Y.S.; Howe, D. Online optimal flux-weakening control of permanent-magnet brushless AC drives. IEEE Trans. Ind. Appl. 2000, 36, 1661–1668. [Google Scholar]
- Chen, J.J.; Chin, K.P. Minimum copper loss flux-weakening control of surface mounted permanent magnet synchronous motors. IEEE Trans.Power Electron. 2003, 18, 929–936. [Google Scholar] [CrossRef]
- Gallegos-López, G.; Gunawan, F.S.; Walters, J.E. Optimum torque control of permanent-magnet AC machines in the field-weakened region. IEEE Trans. Ind. Appl. 2005, 41, 1020–1028. [Google Scholar] [CrossRef]
- Kwon, T.; Sul, S.; Alberti, L.; Bianchi, N. Design and control of an axial-flux machine for a wide flux-weakening operation region. IEEE Trans. Ind. Appl. 2009, 45, 1258–1266. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, C.; Zhou, M.; You, X. Flux-Weakening in PMSM Drives: Analysis of Voltage Angle Control and the Single Current Controller Design. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 437–445. [Google Scholar] [CrossRef]
- Bolognani, S.; Calligaro, S.; Petrella, R.; Pogni, F. Flux-weakening in IPM motor drives: Comparison of state-of-art algorithms and a novel proposal for controller design. In Proceedings of the 2011 14th European Conference on Power Electronics and Applications, Birmingham, UK, 30 August–1 September 2011. [Google Scholar]
- Sudhoff, S.D.; Corzine, K.A.; Hegner, H.J. A flux-weakening strategy for current-regulated surface-mounted permanent-magnet machine drives. IEEE Trans. Energy Convers. 1995, 10, 431–437. [Google Scholar] [CrossRef]
- Ogasawara, S.; Nishimura, M.; Akagi, H.; Nabae, A.; Nakanishi, Y. A High Performance AC Servo System with Permanent Magnet Synchronous Motors. IEEE Trans. Ind. Electron. 1986, IE-33, 87–91. [Google Scholar] [CrossRef]
- Kim, S.; Seok, J.-K. Maximum Voltage Utilization of IPMSMs Using Modulating Voltage Scalability for Automotive Applications. IEEE Trans. Power Electron. 2013, 28, 5639–5646. [Google Scholar] [CrossRef]
- Ge, H.; Miao, Y.; Bilgin, B.; Nahid-Mobarakeh, B.; Emadi, A. Speed Range Extended Maximum Torque per Ampere Control for PM Drives Considering Inverter and Motor Nonlinearities. IEEE Trans. Power Electron. 2017, 32, 7151–7159. [Google Scholar] [CrossRef]
- Wu, J.H.; Wang, J.; Gan, C.; Sun, Q.; Kong, W. Efficiency Optimization of PMSM Drives Using Field-circuit Coupled FEM for EV/HEV Applications. IEEE Access 2018, 6, 15192–15201. [Google Scholar] [CrossRef]
- Watthewaduge, G.; Toulabi, M.S.; Filizadeh, S.; Gole, A.M. Performance Analysis and Operating Limits of a Dual-Inverter Open-Winding IPMSM Drive. IEEE Trans. Energy Convers. 2019, 34, 1655–1666. [Google Scholar] [CrossRef]
- Nair, S.V.; Harikrishnan, P.; Hatua, K. Six-step Operation of a Symmetric Dual Three-phase PMSM with Minimal Circulating Currents for Extended Speed Range in Electric Vehicles. IEEE Trans. Ind. Electron. 2022, 69, 7651–7662. [Google Scholar] [CrossRef]
- Sierra-Gonzalez, A.; Pescetto, P.; Alvarez-Gonzalez, F.; Heriz, B.; Trancho, E.; Lacher, H.; Ibarra, E.; Pellegrino, G. Full-speed Range Control of a Symmetrical Six-phase Automotive IPMSM Drive with a Cascaded DC-link Configuration. IEEE Trans. Ind. Appl. 2023, 59, 3413–3424. [Google Scholar] [CrossRef]
- Chen, Y.Z.; Huang, X.Y.; Wang, J.; Niu, F.; Zhang, J.; Fang, Y.; Wu, L. Improved Flux-weakening Control of IPMSMs Based on Torque Feedforward Technique. IEEE Trans. Power Electron. 2018, 33, 10970–10978. [Google Scholar] [CrossRef]
- Yoo, J.; Lee, J.; Sul, S.-K. Analysis of Instability in Torque Control of Sensorless PMSM Drives in Flux Weakening Region. IEEE Trans. Power Electron. 2021, 36, 10815–10826. [Google Scholar] [CrossRef]
- Liu, T.-H.; Liu, C.-H. A Multiprocessor-based Fully Digital Control Architecture for Permanent Magnet Synchronous Motor Drives. IEEE Trans. Power Electron. 1990, 5, 413–423. [Google Scholar] [CrossRef]
- Nalepa, R.; Orlowska-Kowalska, T. Optimum Trajectory Control of the Current Vector of a Nonsalient-pole PMSM in the Field-weakening Region. IEEE Trans. Ind. Electron. 2012, 59, 2867–2876. [Google Scholar] [CrossRef]
- Lee, H.; Woldesemayat, M.L.; Nam, K. Zero Torque Control for EV Coasting Considering Cross-coupling Inductance. IEEE Trans. Ind. Electron. 2017, 64, 6096–6104. [Google Scholar] [CrossRef]
- Huang, Z.R.; Lin, C.; Xing, J.L. A Parameter-independent Optimal Field-weakening Control Strategy of IPMSM for Electric Vehicles Over Full Speed Range. IEEE Trans. Power Electron. 2021, 36, 4659–4671. [Google Scholar] [CrossRef]
- Chen, J.-J.; Chin, K.-P. Automatic Flux-weakening Control of Permanent Magnet Synchronous Motors Using a Reduced-order Controller. IEEE Trans. Power Electron. 2000, 15, 881–890. [Google Scholar] [CrossRef]
- Consoli, A.; Scelba, G.; Scarcella, G.; Cacciato, M. An Effective Energy-saving Scalar Control for Industrial IPMSM Drives. IEEE Trans. Ind. Electron. 2013, 60, 3658–3669. [Google Scholar] [CrossRef]
- Sun, T.F.; Wang, J.B. Extension of Virtual-signal-injection-based MTPA Control for Interior Permanent-magnet Synchronous Machine Drives Into the Field-weakening Region. IEEE Trans. Ind. Electron. 2015, 62, 6809–6817. [Google Scholar] [CrossRef]
- Sun, T.F.; Wang, J.B.; Koc, M. Self-learning Direct Flux Vector Control of Interior Permanent-magnet Machine Drives. IEEE Trans. Power Electron. 2017, 32, 4652–4662. [Google Scholar] [CrossRef]
- Alzayed, M.; Chaoui, H. Direct Voltage MTPA Speed Control of IPMSM-Based Electric Vehicles. IEEE Access 2023, 11, 33858–33871. [Google Scholar] [CrossRef]
- Alzayed, M.; Chaoui, H.; Farajpour, Y. Dynamic Direct Voltage MTPA Current Sensorless Drives for Interior PMSM-Based Electric Vehicles. IEEE Trans. Veh. Technol. 2023, 72, 3175–3185. [Google Scholar] [CrossRef]
- Pan, C.-T.; Sue, S.-M. A Linear Maximum Torque per Ampere Control for IPMSM Drives Over Full-speed Range. IEEE Trans. Energy Convers. 2005, 20, 359–366. [Google Scholar] [CrossRef]
- Lemmens, J.; Vanassche, P.; Driesen, J. PMSM Drive Current and Voltage Limiting as a Constraint Optimal Control Problem. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 326–338. [Google Scholar] [CrossRef]
- Choi, K.; Kim, Y.; Kim, K.-S.; Kim, S.-K. Real-time Optimal Torque Control of Interior Permanent Magnet Synchronous Motors based on a Numerical Optimization Technique. IEEE Trans. Control Syst. Technol. 2021, 29, 1815–1822. [Google Scholar] [CrossRef]
- Xu, Q.S.; Cai, L.L. Developing an Approach in Calculating Reference Currents for Field-weakening Control. IEEE Trans. Transp. Electrif. 2023, 9, 60–74. [Google Scholar] [CrossRef]
- Zuo, K.K.; Wang, F.X.; Li, Z.; Ke, D.; Kennel, R.; Heldwein, M.L. A Robust Unified Strategy for Maximum Torque per Ampere and Field Weakening in Permanent Magnet Synchronous Motor. IEEE Trans. Power Electron. 2024, 39, 5286–5297. [Google Scholar] [CrossRef]
- Xia, Z.K.; Filho, S.R.; Xiao, D.X.; Fang, G.; Sun, Y.; Wiseman, J.; Emadi, A. Computation-efficient Online Optimal Tracking Method for Permanent Magnet Synchronous Machine Drives for MTPA and Flux-weakening Operations. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 5341–5353. [Google Scholar] [CrossRef]
- Liu, S.Y.; Liu, C.H.; Zhao, H.; Liu, Y.; Dong, Z. Improved Flux Weakening Control Strategy for Five-phase PMSM Considering Harmonic Voltage Vectors. IEEE Trans. Power Electron. 2022, 37, 10967–10980. [Google Scholar] [CrossRef]
- Liu, S.Y.; Song, Z.X.; Liu, Y.X.; Chen, Y.; Liu, C. Flux-weakening Controller Design of Dual Three-phase PMSM Drive System with Copper Loss Minimization. IEEE Trans. Power Electron. 2023, 38, 2351–2363. [Google Scholar] [CrossRef]
- Dong, W.Z.; Li, S.H.; Gao, Y.X.; Balasubramanian, B.; Hong, Y.-K.; Sun, Y.; Cheng, B. Neural Network with Cloud-based Training for MTPA, Flux-weakening, and MTPV Control of IPM Motors and Drives. IEEE Trans. Transp. Electrif. 2024, 10, 1012–1030. [Google Scholar] [CrossRef]
- Kim, H.-S.; Sul, S.-K. Real-time Torque Control of IPMSM under Flux Variations. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 3345–3356. [Google Scholar] [CrossRef]
- Mubarok, M.S.; Liu, T.-H. An Adjustable Wide-range Speed-control Method for Sensorless IPMSM Drive Systems. IEEE Access 2022, 10, 42727–42738. [Google Scholar] [CrossRef]
- Schoonhoven, G.; Uddin, M.N. MTPA- and FW-based Robust Nonlinear Speed Control of IPMSM Drive Using Lyapunov Stability Criterion. IEEE Trans. Ind. Appl. 2016, 52, 4365–4374. [Google Scholar] [CrossRef]
- Uddin, M.N.; Chy, M.M.I. Online Parameter-estimation-based Speed Control of PM AC Motor Drive in Flux-weakening Region. IEEE Trans. Ind. Appl. 2008, 44, 1486–1494. [Google Scholar] [CrossRef]
- Morimoto, S.; Sanada, M.; Takeda, Y. Effects and Compensation of Magnetic Saturation in Flux-weakening Controlled Permanent Magnet Synchronous Motor Drives. IEEE Trans. Ind. Appl. 1994, 30, 1632. [Google Scholar] [CrossRef]
- Hoang, K.D.; Aorith, H.K.A. Online Control of IPMSM Drives for Traction Applications Considering Machine Parameter and Inverter Nonlinearities. IEEE Trans. Transp. Electrif. 2015, 1, 312–325. [Google Scholar] [CrossRef]
- Alzayed, M.; Chaoui, H. Energy Efficiency Improvement Using Simplified Dynamic Direct Voltage Maximum Torque Per Ampere Control for Interior PMSMs. IEEE/ASME Trans. Mechatron. 2023, 28, 3143–3154. [Google Scholar] [CrossRef]
- Uddin, M.N.; Chy, M.M.I. A Novel Fuzzy-logic-controller-based Torque and Flux Controls of IPM Synchronous Motor. IEEE Trans. Ind. Appl. 2010, 46, 1220–1229. [Google Scholar] [CrossRef]
- Elhaj, A.; Alzayed, M.; Chaoui, H. MTPA Speed Control for IPMSM Drives Without Current Sensing. IEEE Access 2024, 12, 11411–11422. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, B.; Yu, Y.; Zhang, J.; Xu, D. Torque Adaptive Hexagon Voltage Extension Method For PMSM Flux-weakening Control based on Dual PI Cascade Structure. IEEE Trans. Power Electron. 2023, 38, 332–345. [Google Scholar] [CrossRef]
- Wang, B.; Wang, L.Z.; Yu, Y.; Xu, D. Adaptive Overmodulation Strategy for PMSM Field-weakening Control based on Working Quadrant. IEEE Trans. Ind. Electron. 2023, 70, 9959–9970. [Google Scholar] [CrossRef]
- Wang, L.Z.; Yu, Y.; Wang, B.; Xu, D. Power-model-based Adaptive Overmodulation Scheme for Field-weakening Control of PMSM. IEEE Trans. Ind. Electron. 2024, 71, 11898–11909. [Google Scholar] [CrossRef]
- Pan, D.; Liang, F.; Wang, Y.; Lipo, T.A. Extension of the Operating Region of an IPM Motor Utilizing Series Compensation. IEEE Trans. Ind. Appl. 2014, 50, 539–548. [Google Scholar] [CrossRef]
- Xu, W.; Ismail, M.M.; Liu, Y.; Islam, R. Parameter Optimization of Adaptive Flux-weakening Strategy for Permanent-magnet Synchronous Motor Drives based on Particle Swarm Algorithm. IEEE Trans. Power Electron. 2019, 34, 12128–12140. [Google Scholar] [CrossRef]
- Wang, C.; Zhu, Z.Q.; Zhan, H.L. Adaptive Voltage Feedback Controllers on Nonsalient Permanent Magnet Synchronous Machine. IEEE Trans. Ind. Appl. 2020, 56, 1529–1542. [Google Scholar] [CrossRef]
- Kshirsagar, P.; Burgos, R.P.; Jang, J.; Lidozzi, A.; Wang, F.; Boroyevich, D.; Sul, S.-K. Implementation and Sensorless Vector-control Design and Tuning Strategy for SMPM Machines in Fan-type Applications. IEEE Trans. Ind. Appl. 2012, 48, 2402–2413. [Google Scholar] [CrossRef]
- Ismail, M.M.; Xu, W.; Wang, X.G.; Junejo, A.K.; Liu, Y.; Dong, M. Analysis and Optimization of Torque Ripple Reduction Strategy of Surface-mounted Permanent-magnet Motors in Flux-weakening Region based on Genetic Algorithm. IEEE Trans. Ind. Appl. 2021, 57, 4091–4106. [Google Scholar] [CrossRef]
- Kwon, Y.-C.; Kim, S.; Sul, S.-K. Voltage Feedback Current Control Scheme for Improved Transient Performance of Permanent Magnet Synchronous Machine Drives. IEEE Trans. Ind. Electron. 2012, 59, 3373–3382. [Google Scholar] [CrossRef]
- Bolognani, S.; Tubiana, L.; Zigliotto, M. EKF-based Sensorless IPM Synchronous Motor Drive for Flux-weakening Applications. IEEE Trans. Ind. Appl. 2003, 39, 768–775. [Google Scholar] [CrossRef]
- SalomÄki, J.; Hinkkanen, M.; Luomi, J. Influence of Inverter Output Filter on Maximum Torque and Speed of PMSM Drives. IEEE Trans. Ind. Appl. 2008, 44, 153–160. [Google Scholar] [CrossRef]
- Bedetti, N.; Calligaro, S.; Petrella, R. Analytical Design and Autotuning of Adaptive Flux-weakening Voltage Regulation Loop in IPMSM Drives with Accurate Torque Regulation. IEEE Trans. Ind. Appl. 2020, 56, 301–313. [Google Scholar] [CrossRef]
- Zhang, Z.S.; Dhale, S.; Nahid-Mobarakeh, B.; Emadi, A. Adaptive Voltage Controller for Permanent Magnet Synchronous Motor in Six-step Operation. IEEE Trans. Ind. Appl. 2023, 59, 2483–2490. [Google Scholar] [CrossRef]
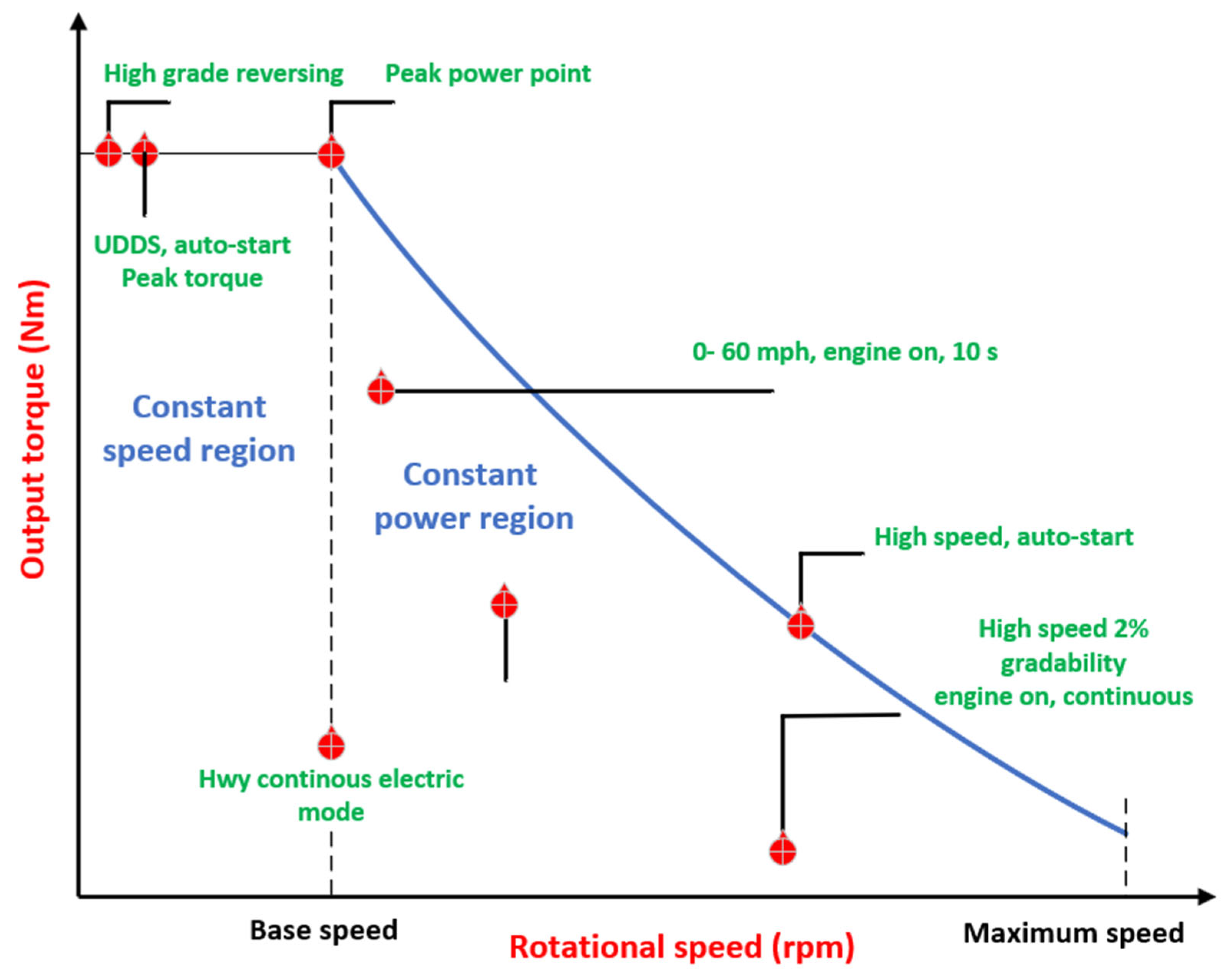
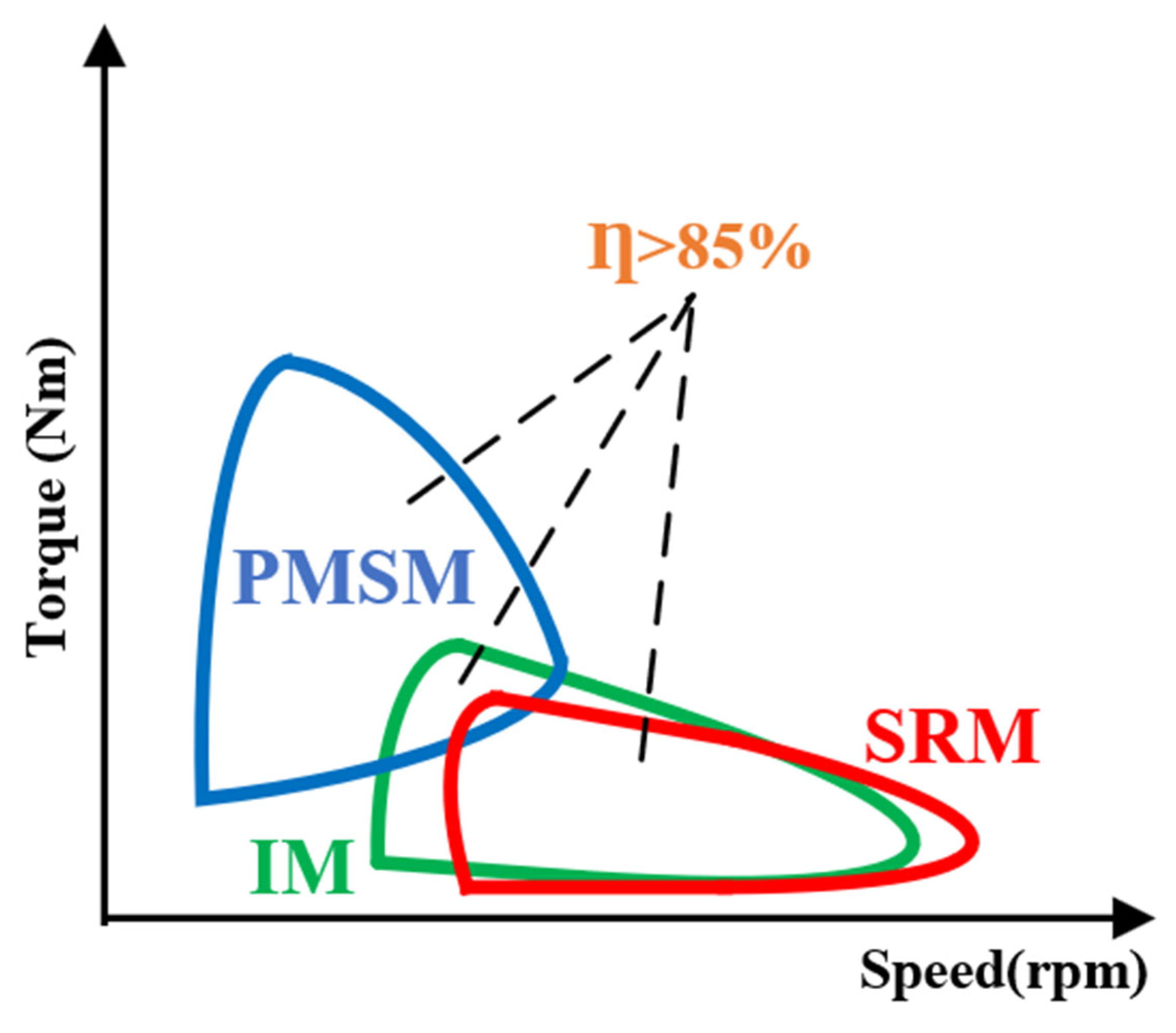
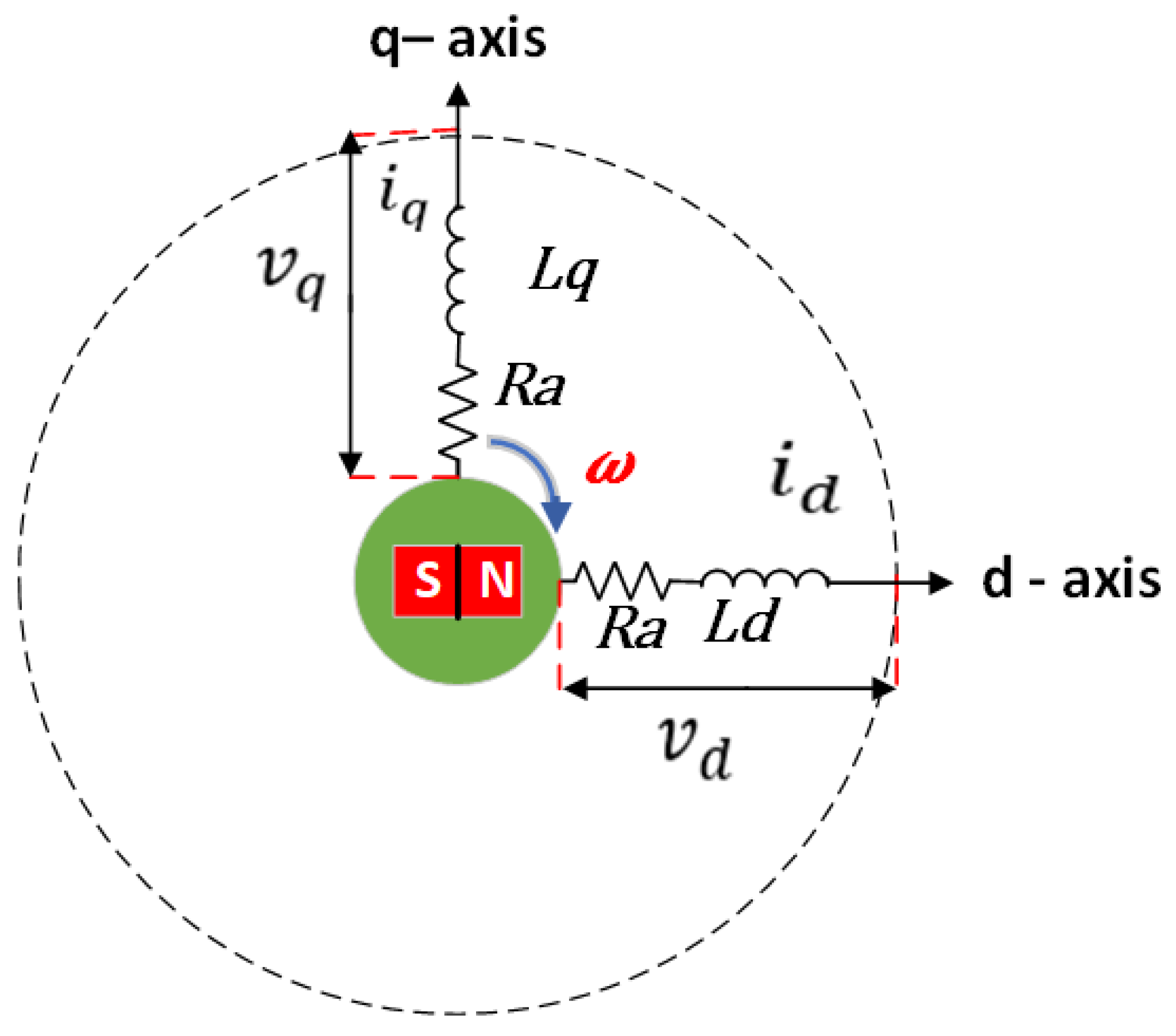
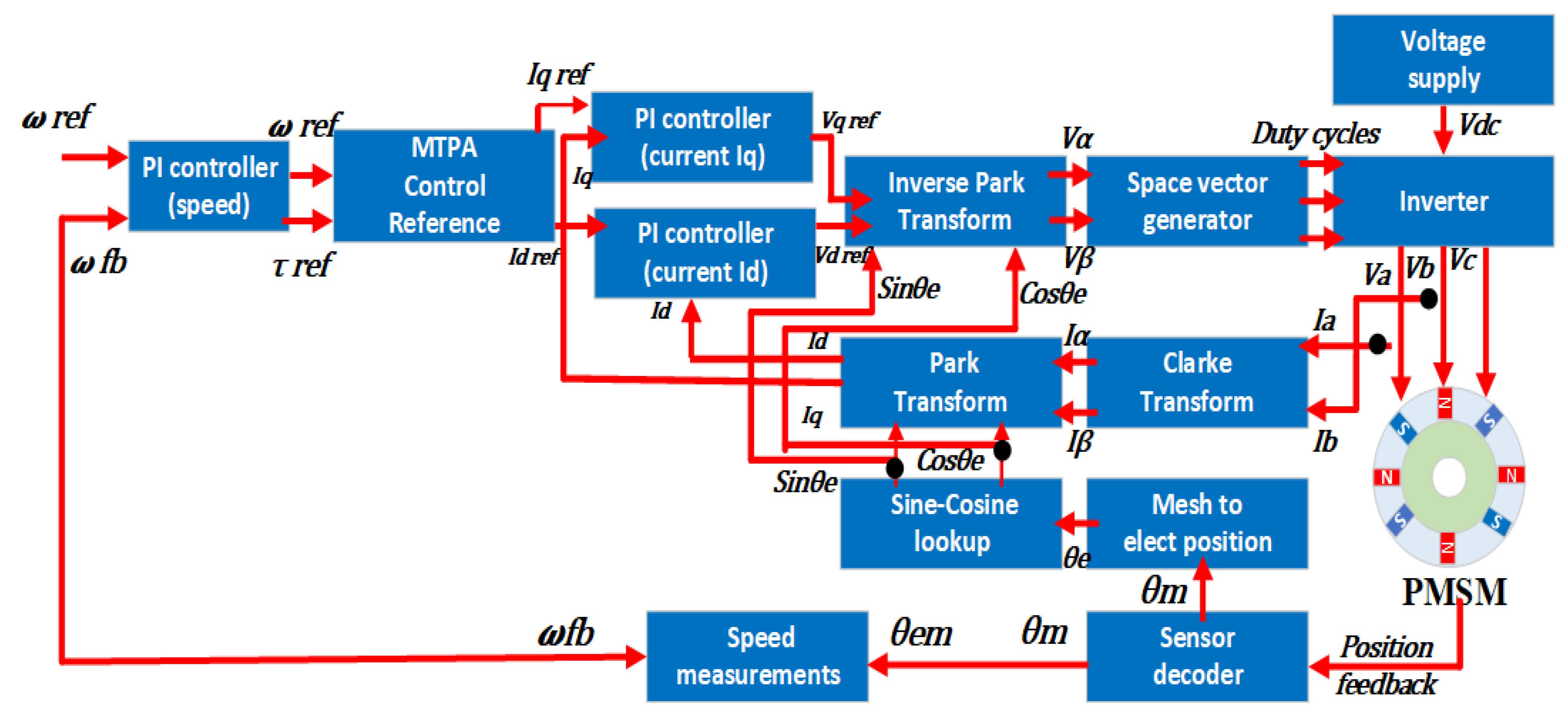
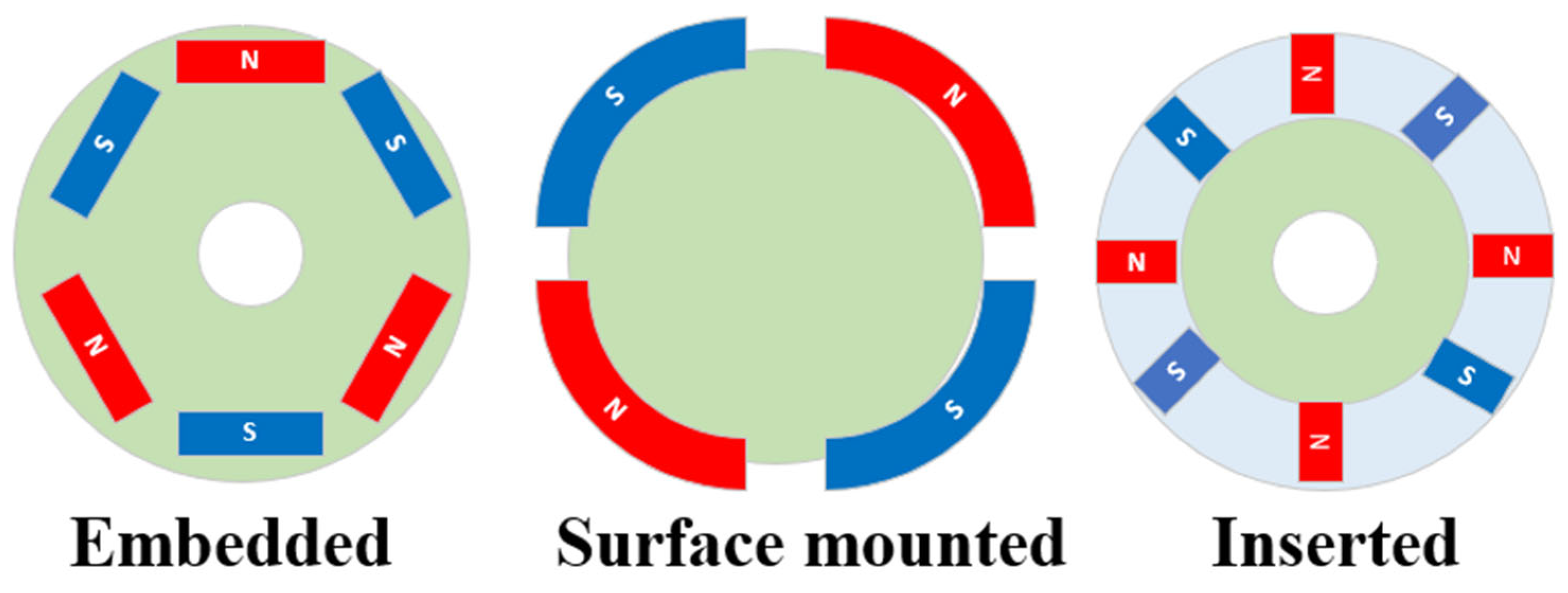
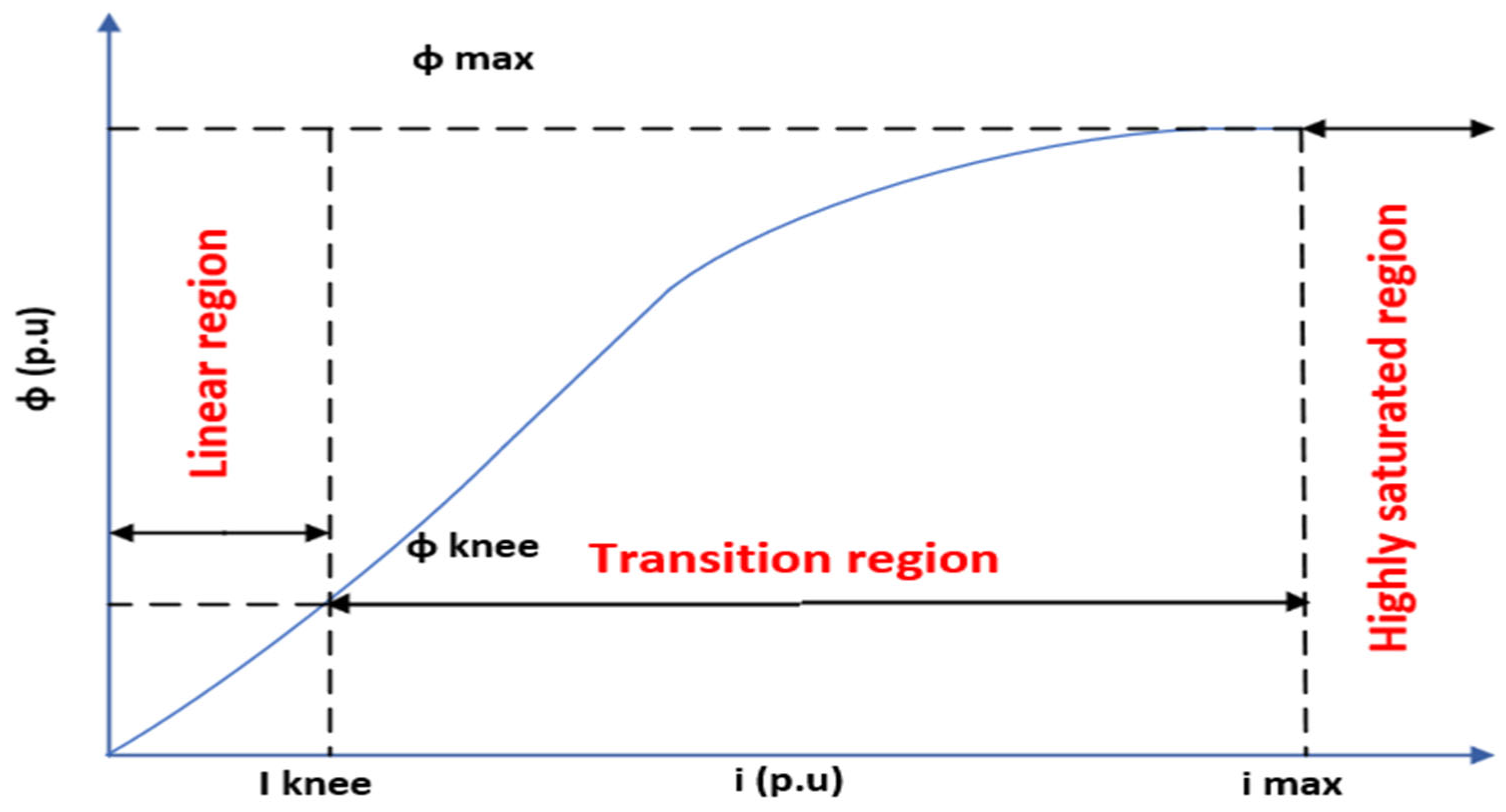
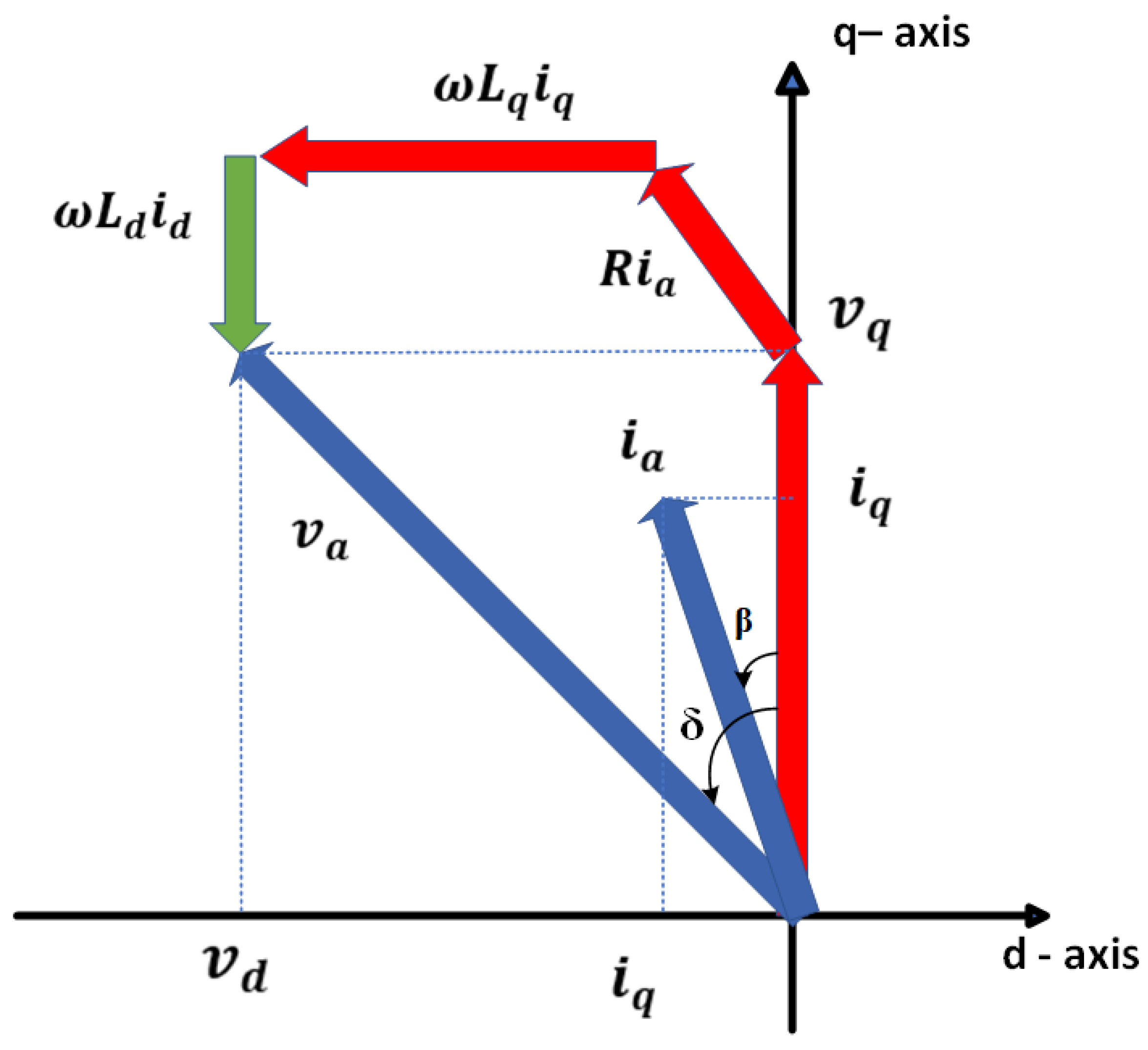
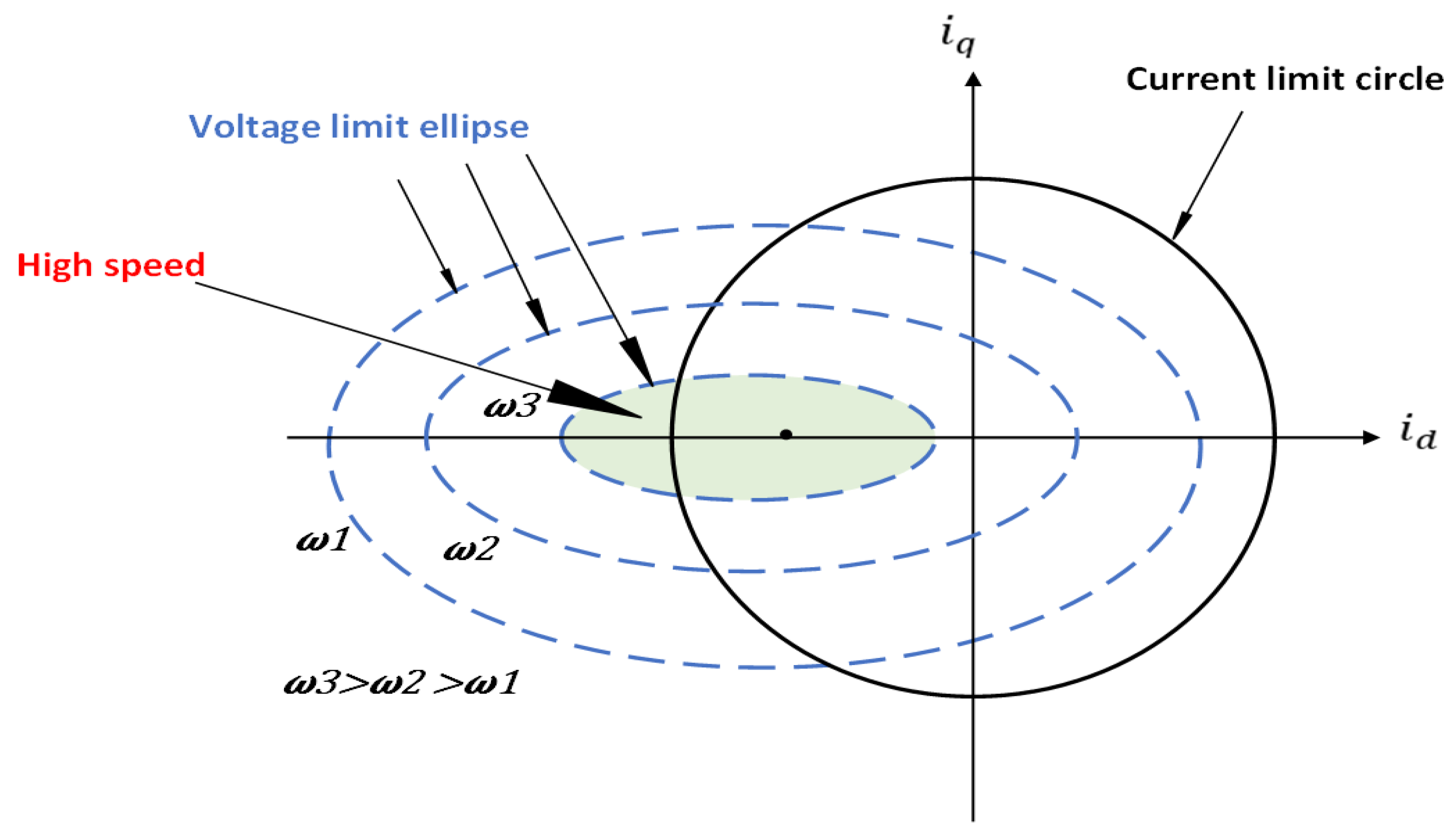
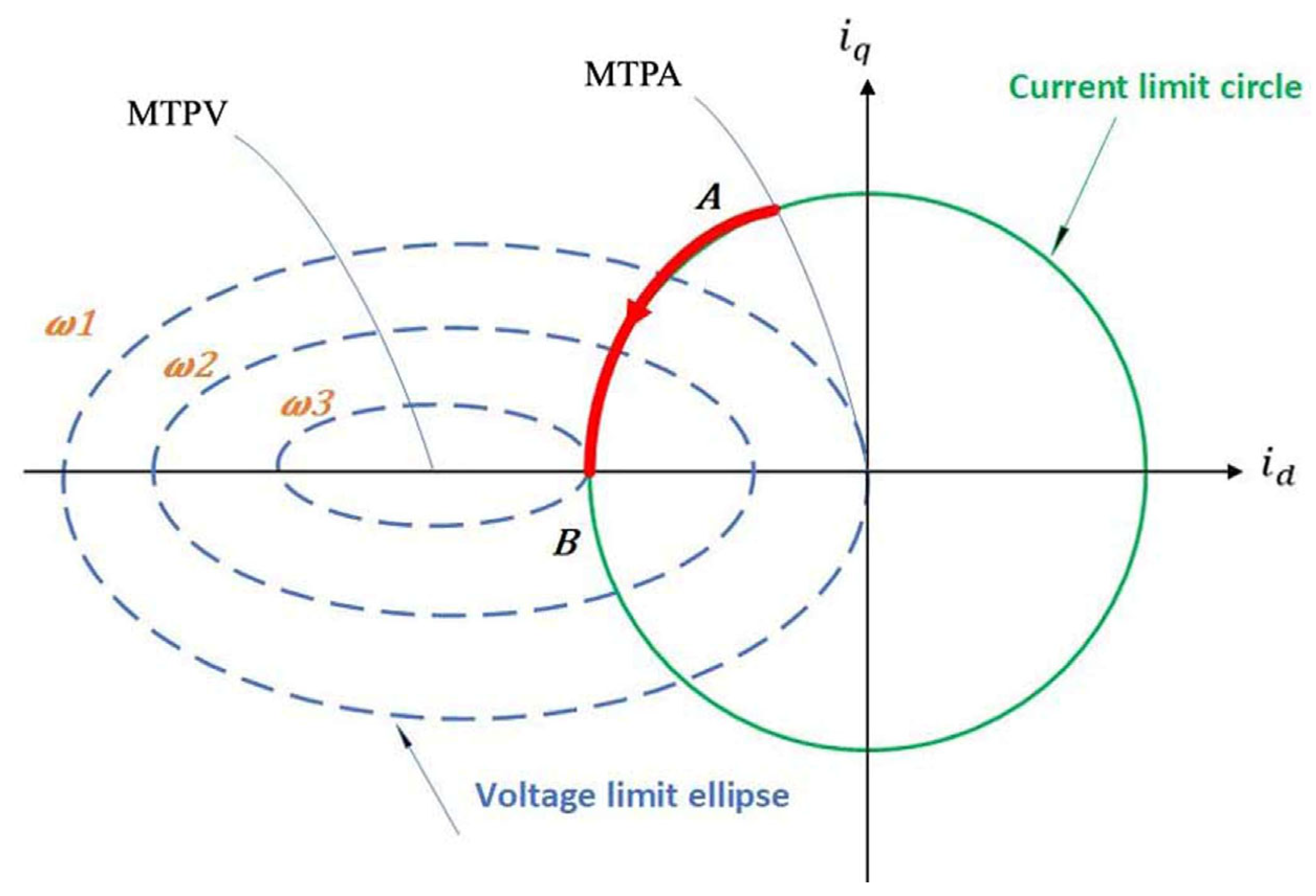
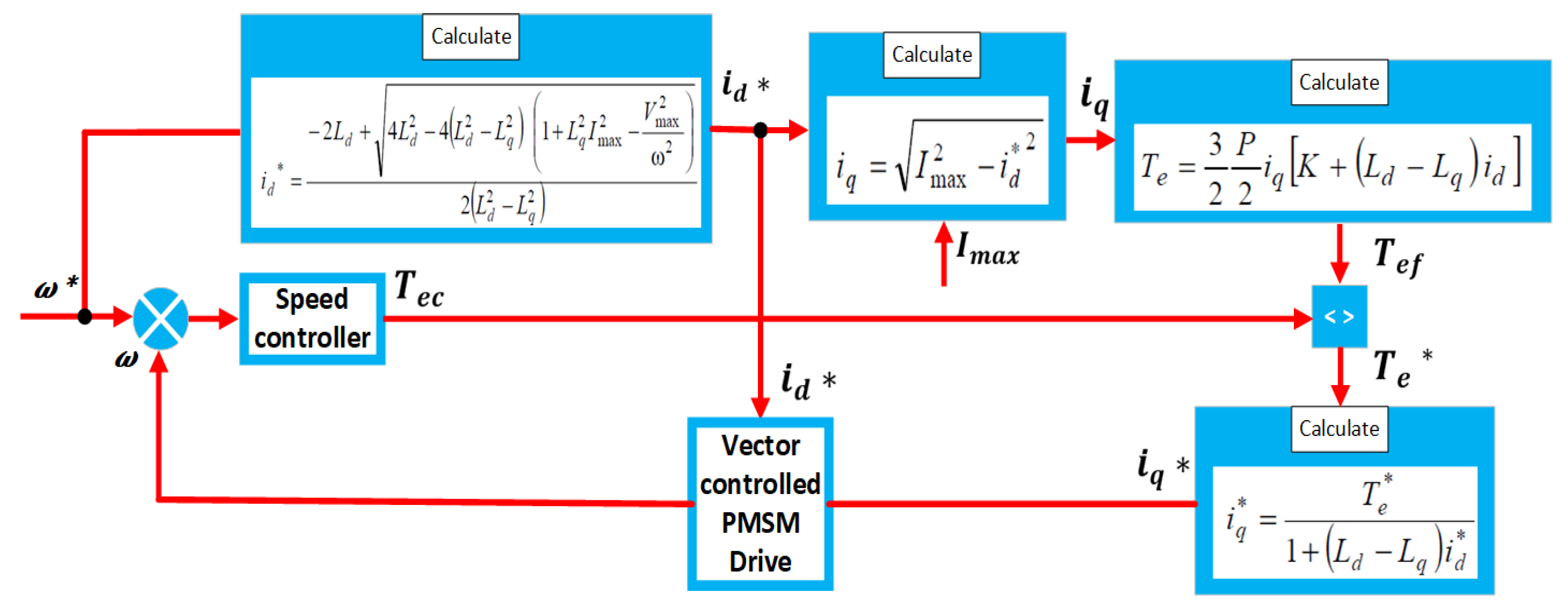
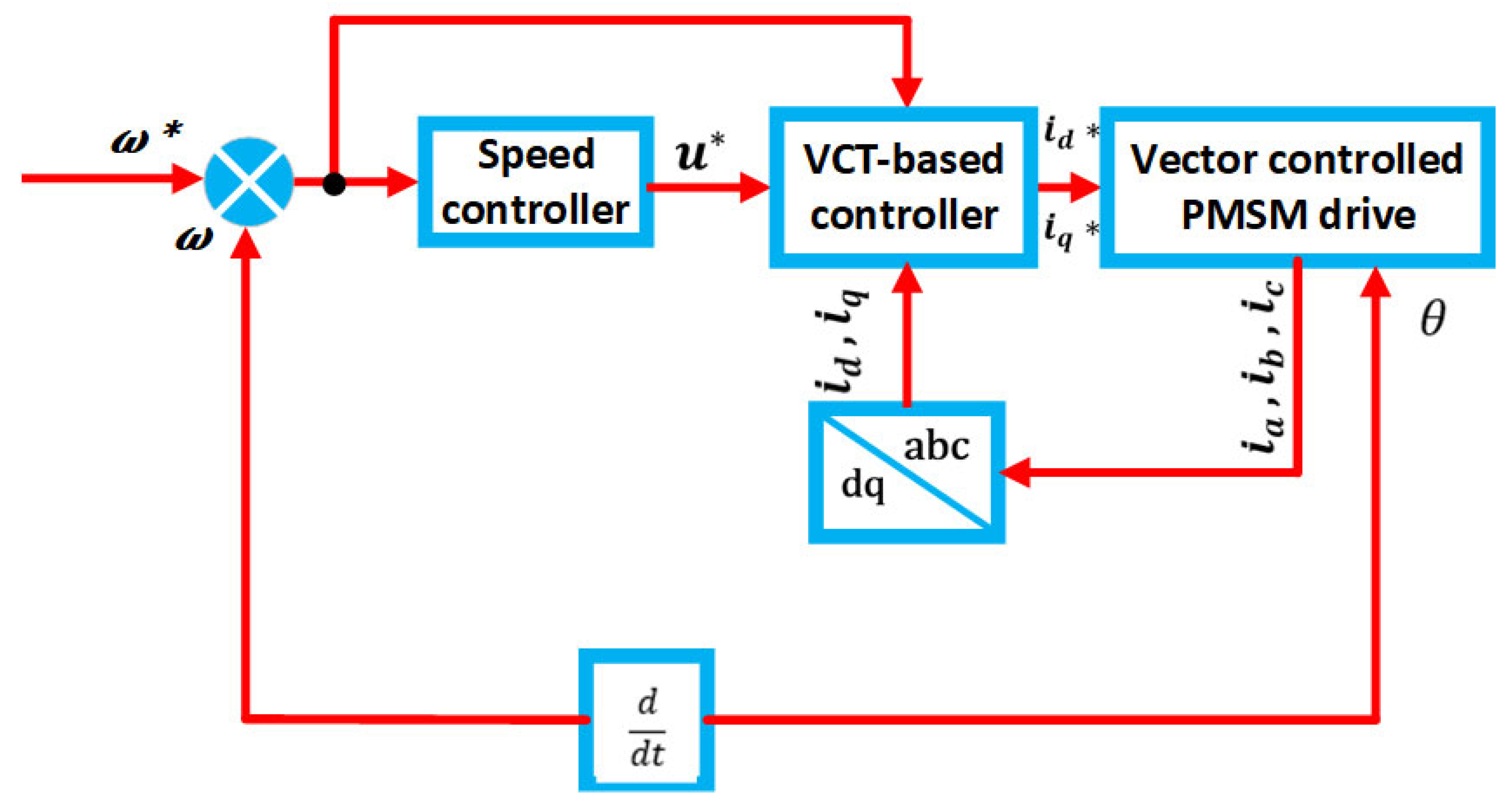
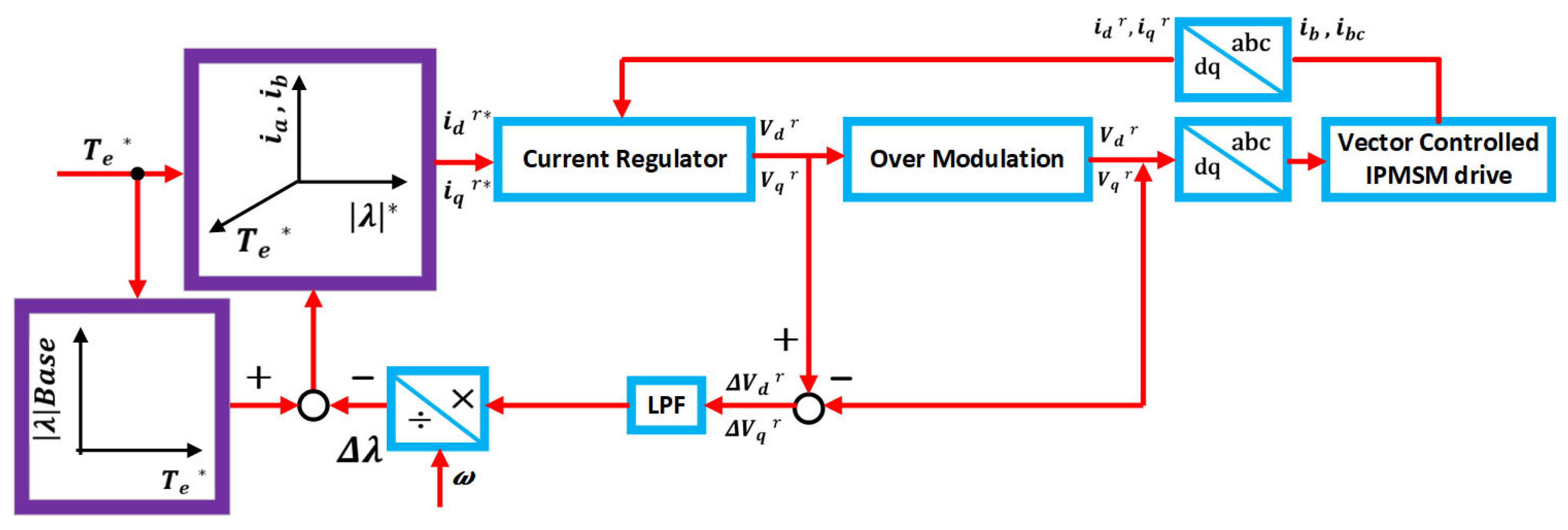
| Features | IM | PMSM | SRM | PM-Assisted SynRM |
|---|---|---|---|---|
| Torque ripple | Low | Low | Very high | Low |
| Wide speed range | No | Yes | Yes | Yes |
| Fault tolerance | No | Yes | Yes | Yes |
| Close loop control simplicity | Yes | Yes | Yes | Yes |
| Preferred torque control method | FOC, DTC | FOC, DTC | DITC, ADITC, IDITC | FOC, DTC |
| Reliability | High | Moderate | Moderate | Moderate |
| Flux-weakening capability | Yes | Yes | Yes | Yes |
| Power density/Current | 2.5 KW/I | 3.3–10.2 KW/I | 2.6–4.5 KW/I | 6.8 KW/I |
| Efficiency at constant torque | 79–86% | 91.3–95.8% | 85.1–89% | 87–93% |
| Cost | Medium | High | Low | Medium |
| Control Method | Pros | Cons | Key References |
|---|---|---|---|
| Analytical Direct Calculation Method | Good choice for high-power motors with small stator resistance; Nice transient response; Stable transition between LBEMF and FW | Not effective in MTPV region (though potentially extendable to it); Susceptible to machine parameter variations; Requires additional computation time for d–q current calculation; Neglects magnetic saturation effects | [89,90,91,83] |
| Direct Open-loop Algorithm with Experimental LUT | No need for complex mathematical equations or real-time computation | Depends on accurate inductance characterization (cross-magnetization and saturation effects); Inverter follows the torque reference without considering magnetic saturation; Requires large experimental setup and significant LUT memory; Time-consuming and risky experimental tuning process | [92,93,100,101,102] |
| Single Current Regulator (SCR) | No conflict between d- and q-axis current regulators in FW mode (single regulator simplifies control) | Easily drives the inverter into voltage saturation (since the single current controller operates near the maximum voltage limit); Possible instability due to interaction of two current components in deep FW; Non-smooth switching between LBEMF (MTPA) and FW modes; Stability is very sensitive to the current limit setting and controller parameter values | [53,93,103] |
| Unified Direct Flux Vector Control (UDFVC) | Appropriate for many types of AC machines; Direct flux control through a single regulation channel for torque setpoints; Experimentally validated as a reliable method to find maximum load torque | Requires a flux observer which depends on accurate machine parameters; Does not operate in the MTPV region (limited high-speed capability) | [105,106,107,108,109,110,111,112,113,114,104,115] |
| Torque and Flux Control (TFC) with LUTs | Decreases flux and torque ripple compared to classic DTC; Considers magnetic saturation effects in control | Requires large memory to store extensive 2D- and 1D- LUTs; Potential control conflicts if multiple controllers operate simultaneously in FW; Many offline measurements needed to populate the LUTs | [87,90,92,84,117,118,119,120,121,122,123] |
| Machine Type | Reference Signal | Reference System | Coordinate System | Control Implementation | Transition to FW | Reference |
|---|---|---|---|---|---|---|
| IPMSM | Speed | Real | Cartesian | d-axis current | Continuous | [120] |
| IPMSM | Torque | Real | Cartesian | d-axis current | Continuous | [93] |
| SyRM | Speed | Per-unit | Polar | Current angle | Continuous | [134] |
| IPMSM | Speed | Real | Cartesian | d-axis current | Continuous | [131] |
| IPMSM | Speed | Real | Cartesian | d-axis current | Switched | [121] |
| IPMSM | Torque | Real | Polar | Current angle | Continuous | [125] |
| SPMSM | Speed | Real | Cartesian | d–q axis currents | Switched | [123] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alwaqfi, S.; Alzayed, M.; Chaoui, H. Flux-Weakening Control Methods for Permanent Magnet Synchronous Machines in Electric Vehicles at High Speed. Electronics 2025, 14, 3779. https://doi.org/10.3390/electronics14193779
Alwaqfi S, Alzayed M, Chaoui H. Flux-Weakening Control Methods for Permanent Magnet Synchronous Machines in Electric Vehicles at High Speed. Electronics. 2025; 14(19):3779. https://doi.org/10.3390/electronics14193779
Chicago/Turabian StyleAlwaqfi, Samer, Mohamad Alzayed, and Hicham Chaoui. 2025. "Flux-Weakening Control Methods for Permanent Magnet Synchronous Machines in Electric Vehicles at High Speed" Electronics 14, no. 19: 3779. https://doi.org/10.3390/electronics14193779
APA StyleAlwaqfi, S., Alzayed, M., & Chaoui, H. (2025). Flux-Weakening Control Methods for Permanent Magnet Synchronous Machines in Electric Vehicles at High Speed. Electronics, 14(19), 3779. https://doi.org/10.3390/electronics14193779








