Radiation Pattern Recovery from Tilted Orbital Sampling Measurements via Sparse Spherical Harmonic Expansion

Abstract

This paper proposes a reconstruction framework for estimating the far-field (FF) radiation patterns of large, heavy, or non-rotatable wireless-enabled systems. The method combines a tilted orbital sampling (ToS) strategy with sparse spherical harmonic (SH) expansion, compressed sensing (CS), and convex optimization (CO), thereby linking a mechanically constrained acquisition scheme with a mathematically efficient recovery process. The purpose of this integration is not only to reduce the number of measurements but also to retrieve the radiation information most relevant to Internet of Things (IoT) devices and bulky equipment that cannot be easily rotated within anechoic chambers. The framework is validated on two representative cases: a canonical half-wave dipole and a commercial Wi-Fi-enabled device. In the latter and more challenging case, accurate reconstruction is achieved with fewer than 30 SH coefficients and using less than 20% of the measurements required by a conventional full-sphere scan, with the normalized root-mean-square error remaining below 5%. Although inaccessible angular regions may be partially uncharacterized, such directions are of minor relevance for the intended operational coverage. The resulting SH-based representation can be seamlessly integrated into ray-tracing propagation simulators and electromagnetic optimization workflows, enabling efficient and application-oriented OTA characterization under realistic chamber constraints.

1. Introduction

Short-range wireless communication technologies such as Wi-Fi, Zigbee, and Bluetooth have become increasingly ubiquitous in modern electronic systems. Accurate and efficient characterization of EM radiation patterns is essential for validating and optimizing these devices, particularly for large-scale IoT systems. However, conventional anechoic chamber methodologies based on full-sphere scanning or dense near-field sampling present significant challenges when applied to bulky, heavy, or fixed devices. Factors such as irregular geometry, excessive weight, or integration into larger infrastructures often prevent the complete mechanical rotation required for exhaustive measurements.

In this context, Rahola [1] introduced a representation of the vector far field based on scalar spherical harmonics with vector coefficients, which facilitates pattern rotation and interpolation and allows least-squares fitting even under incomplete angular coverage. Building on this basis, Fuchs et al. [2] demonstrated fast far-field characterization via sparse SH expansions and ℓ1-minimization, proposing low-redundancy sampling schemes that substantially reduce the number of measurements. Likewise, Schmitz et al. [3] validated SH modeling of measured antenna patterns and efficiently integrated this representation into ray-tracing simulation frameworks. On the theoretical side, Candès and Tao [4] and Donoho [5] established the foundations of CS for the stable recovery of sparse signals from incomplete measurements using CO (basis pursuit). Specifically for the spherical domain, Rauhut and Ward [6] proved recovery guarantees for sparse SH expansions from a reduced number of samples by means of a preconditioning that enables verification of restricted isometry properties.

In the last decade, several works have specifically addressed the measurement of complex or large devices under reduced sampling conditions. Valdez et al. achieved accurate multi-frequency antenna characterization using less than 25% of conventional samples with errors below −40 dB [7]. Bangun and Culotta-López proposed optimized sensing matrices for spherical near-field setups, outperforming classical spiral and “Igloo” grids in reconstruction efficiency [8]. Cornelius et al. demonstrated that CS-based near-field to far-field transformations can recover the essential SH spectrum with substantially fewer measurements [9]. In the context of IoT and over-the-air (OTA) scenarios, Sun et al. reported up to 40% reduction in measurement time using CS-based schemes [10], and Behjoo et al. showed efficient sparse recovery for bulky devices without compromising angular fidelity [11].

Despite these advances, most existing methods presume near-complete spherical accessibility to the EUT. This leaves a gap for scenarios where only partial angular coverage is physically possible, as frequently encountered when characterizing large IoT devices embedded in real installations.

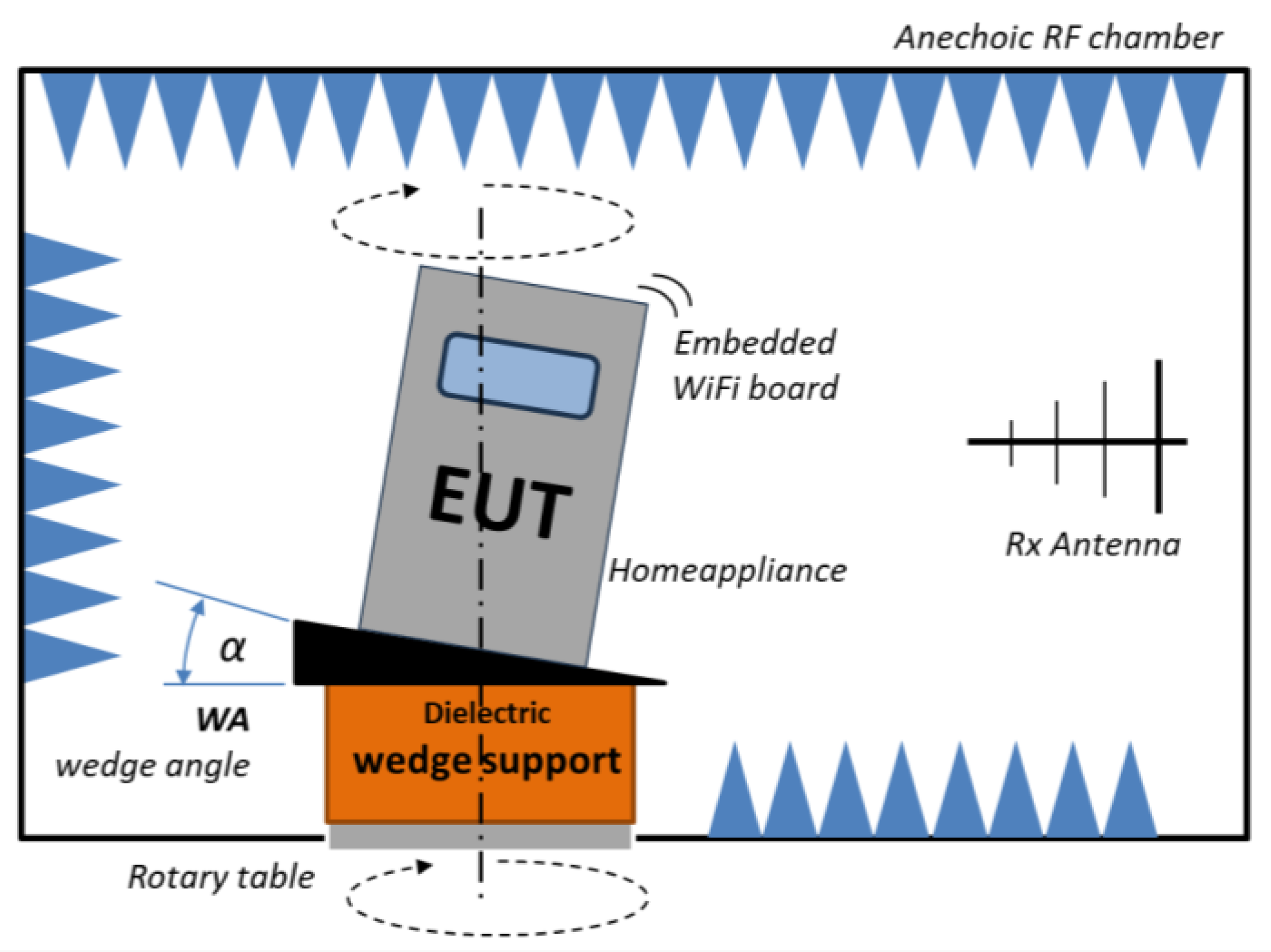
To address this gap, this paper proposes a reconstruction framework combining a ToS strategy—implemented with a mechanical wedge tool (WT) to acquire inclined orbits around the EUT (Figure 1)—with sparse SH expansion and CS/CO.

The novelty of the proposed framework lies in applying this integration to recover the radiation pattern regions most relevant to the operational use of bulky, heavy, or non-rotatable IoT devices under realistic testing constraints, using significantly fewer measurements. The approach is explicitly application-oriented, prioritizing the angular sectors that are relevant to the application and physically accessible without full inversion or complex handling of the EUT. As a result, radiation details in hard-to-access directions may remain partially uncharacterized; however, such regions typically contribute less to the device’s intended coverage and are of lower impact for application-driven performance assessment.

The methodology is validated through two representative cases: a canonical half-wave dipole and a real commercial Wi-Fi-enabled device. In the last and practical case, results demonstrate accurate “enough” reconstruction using no more than 30 SH coefficients and less than 20% of the measurements required for a full-sphere scan, with a defined root-mean-square (RMS)-based error value below 14%. This highlights the method’s potential as a resource-efficient alternative for OTA characterization under realistic chamber constraints while bridging practical measurement limitations with advanced sparse recovery theory.

The novelty of the proposed framework lies in explicitly targeting the recovery of radiation pattern regions most relevant to the operational use of bulky, heavy, or non-rotatable IoT devices under realistic testing constraints, thereby achieving accurate and application-oriented characterization with significantly fewer measurements.

2. Materials and Methods

2.1. Overview of the Proposed Framework

Accurate characterization of EM radiation patterns in anechoic chambers critically depends on the adopted angular sampling strategy. The distribution and density of measurement points determine both the quality of the reconstructed FF pattern and the efficiency of the acquisition process. For conventional setups, precise pattern recovery typically requires either complete three-axis rotation of the EUT for full-sphere scanning, or dense near-field measurements combined with computational near-to-far-field transformations. While effective, both approaches become impractical for large, heavy, or fixed installations due to mechanical constraints and the high number of measurements required. Over the last decades, several sampling methodologies have been developed to optimize the trade-off between angular coverage, sampling density, and reconstruction fidelity:

• Classical Equiangular Sampling

Measurements are acquired on a regular grid with constant azimuthal ($\varphi$) and elevation ($\theta$) steps, where $\varphi$ and $\theta$ are the standard angular coordinates in the spherical system. This straightforward approach aligns well with traditional SH expansion algorithms [12,13] but leads to oversampling near the poles, increasing measurement effort without proportional improvements in accuracy [14].

• Solid-Angle Uniform Sampling (“Igloo”)

To mitigate polar oversampling, constant-area schemes distribute measurement points such that each covers approximately the same solid angle. This reduces the total number of samples while preserving reconstruction fidelity and remains compatible with SH-based and sparse reconstruction techniques [1,3].

• Spherical Spiral Sampling

Continuous spiral trajectories provide homogeneous angular coverage and avoid discontinuities inherent in rectangular grids. Fuchs et al. demonstrated that spiral sampling is particularly suitable for sparse recovery frameworks due to its continuity and compatibility with interpolation algorithms [2].

• Compressed Sensing (CS)-Based Sampling

More recently, the CS framework has been applied to radiation pattern measurement, leveraging the fact that many patterns are sparse or compressible in the SH domain [13,15]. By exploiting sparsity and using CO, accurate reconstructions can be obtained from a reduced subset of measurements, significantly decreasing acquisition time.

• Proposed Methodology

The approach presented in this paper belongs to the latter category and is specifically designed for characterizing large, heavy, or non-rotatable devices under realistic anechoic chamber constraints. The goal is to reconstruct the full-sphere EM radiation pattern from a limited set of partial measurements while minimizing mechanical and infrastructural requirements. To achieve this, the proposed framework integrates two key components:

• Tilted Orbital Sampling

ToS is a mechanically constrained acquisition technique that generates partial angular measurements along inclined circular orbits around the EUT using a WT device. This setup avoids full 3D rotation and allows access to complementary regions of the radiation sphere even for bulky or fixed devices (Figure 1).

2.

Sparse Spherical Harmonic Reconstruction

A post-processing pipeline that exploits the compressibility of the radiation pattern in the SH basis and applies ${\mathcal{l}}_1$-regularized CS/CO to recover the complete pattern from undersampled data.

By combining ToS acquisition with sparse SH reconstruction by means of CS/CO, the methodology enables efficient and application relevant full-sphere pattern estimation with significantly fewer measurements. This resource-efficient alternative extends CS concepts to OTA testing of large IoT systems and addresses practical limitations of traditional full-sphere scanning techniques.

2.2. Spherical Harmonic Representation of the Radiation Pattern

In this work, the FF radiation pattern is represented in terms of a real, positive scalar function proportional to the power flux density received in the anechoic chamber, such as the typical Directivity $D(\theta ,\varphi )$, or Gain $G(\theta ,\varphi )$, function expressed in standard spherical coordinates. This choice follows standard OTA measurement practice, where the voltage detected at the probe antenna is proportional to the radiated power density and is used to compute normalized power-based quantities rather than the complex electric field ([16], pp. 810–814). The function $D(\theta ,\varphi )$ (or $G(\theta ,\varphi )$) is approximated by a truncated expansion in real or complex SH functions:

$$D\left(\theta ,\varphi \right)\approx {\sum }_{l=0}^{L \mathrm{m}\mathrm{a}\mathrm{x}}{\sum }_{m=-l}^{+l}{c}_l^m{Y}_l^m(\theta ,\varphi )$$

(1)

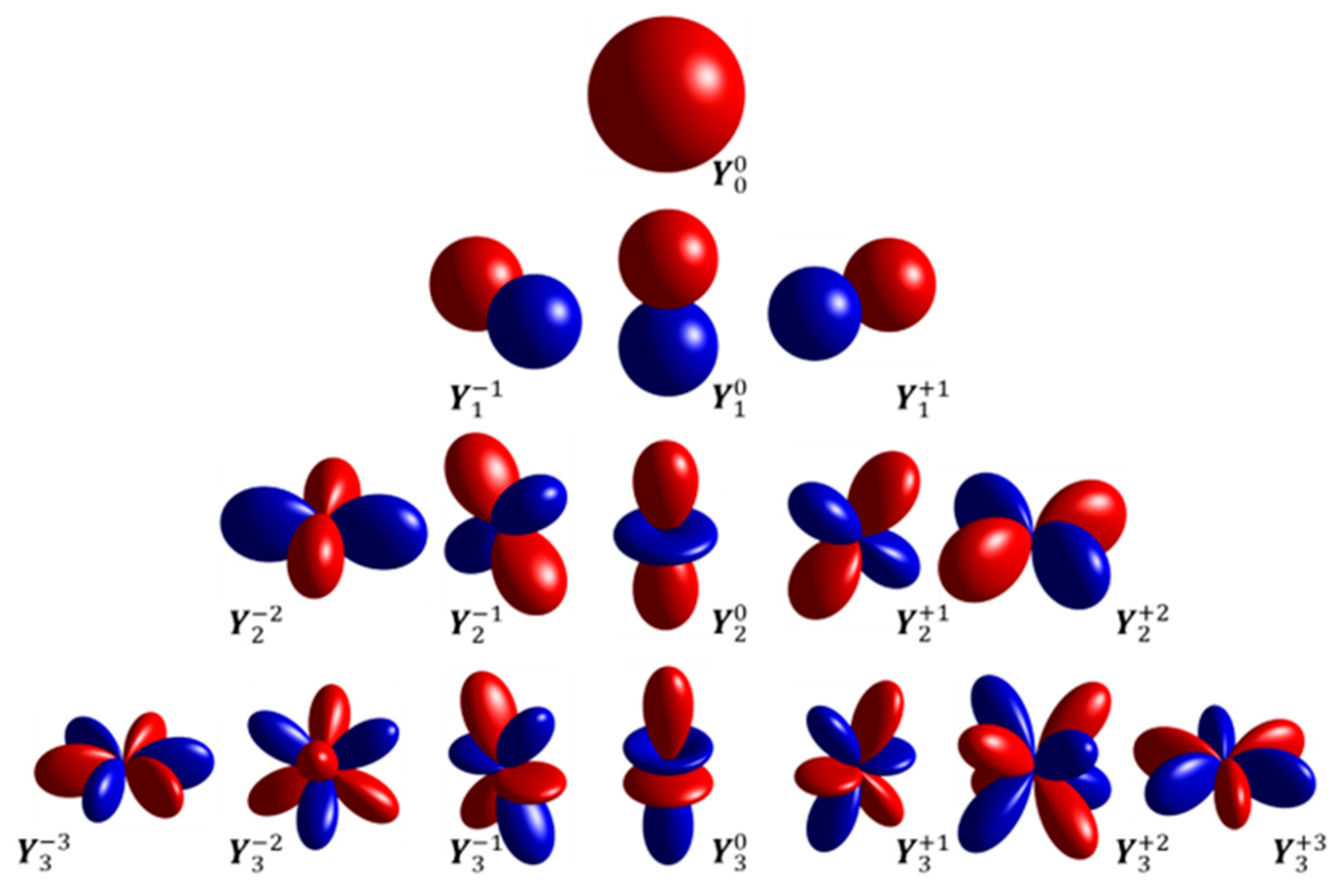
where $Y_l^m\left(\theta ,\varphi \right)=\sqrt{{\displaystyle \frac{\left(2\mathcal{l}+1\right)}{4\pi }}{\displaystyle \frac{\left(\mathcal{l}-m\right)!}{\left(\mathcal{l}+m\right)!}}} P_l^m\left(cos\theta \right) e^{im\varphi }$ are the normalized SH basis functions (see Figure 2), $c_l^m$ are the expansion coefficients, $l \in {\mathbb{N}}_0$ denotes the “degree”, $m\in \{-l,\dots ,+l \}$ is the “order”, and $L_{max}$ denotes the chosen maximum degree of expansion, as in many practical applications this truncated representation provides an efficient approximation with a finite number of coefficients [1,2].

For sufficiently smooth patterns, the SH representation additionally exhibits compressibility, meaning that the coefficients decay rapidly and most of the energy is captured by a reduced subset of terms [5,17]. This property enables accurate reconstruction with significantly fewer than the total ${{(L}_{max}+1)}^2$ coefficients. The choice of $L_{max}$ would follow standard criteria, combining:

• an estimate based on the small-enough electrical size of the radiator and the expected angular variation of $D(\theta ,\varphi )$,
• a sampling-density constraint ${{(L}_{max}+1)}^2\lesssim \mathrm{K}$, where $K$ is the number of independent measurements acquired, and
• a convergence check of the reconstructed pattern.

By adopting a power-based quantity such as Directivity, or Gain, as the target function, the SH expansion is directly compatible with the type of data typically captured in practical anechoic measurements, where the instrumentation delivers values proportional to radiated power density rather than the complex field. This definition ensures consistency between the mathematical formulation and the experimental results presented in Section 3.1 and Section 3.2, both expressed in terms of normalized power patterns.

2.3. Tilted Orbital Sampling Acquisition Strategy

The ToS method acquires measurement data along circular orbits whose tilt angle with respect to the horizontal plane is directly defined by the inclination of a mechanical WT while the chamber’s azimuthal positioner performs the orbital sweep. The maximum WT angle is limited to values compatible with the mechanical and structural constraints of the EUT, as in the case of large or heavy objects, where the tilt must remain within a safe range to avoid compromising the integrity of the setup or the device under test (Figure 1).

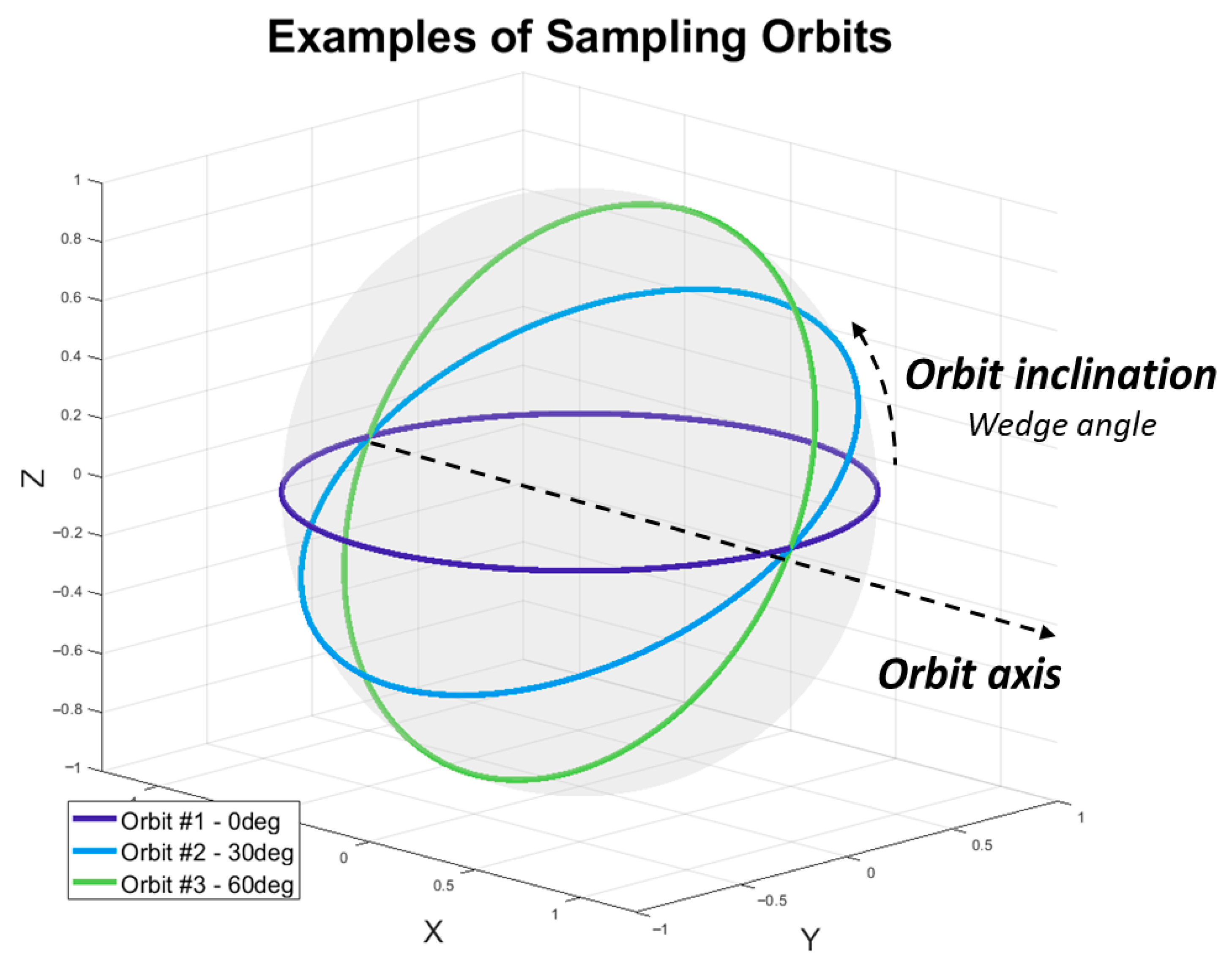
Each tilted orbit provides a set of measurement points $({\theta }_k,{\mathsf{\varphi }}_k)$ covering complementary slices of the unit sphere (Figure 3). By combining several tilted orbits with different WT angles and orbit axis directions, it is possible to capture a significant portion of the angular spectrum without requiring full three-axis mechanical rotation of the EUT.

2.4. Measurement Model and Gaussian Observation Reduction

Let $x_K ϵ {\mathbb{R}}^{Kx1}$ be the column vector of measurements acquired from all ToS trajectories. Each entry $x_i$ corresponds to a specific angular direction $({\theta }_i,{\varphi }_i)$ on the sphere and is initially represented in the canonical Dirac Delta function basis ${\delta }_i({\theta }_i,{\varphi }_i)$. Therefore, the measurement space is $K$-dimensional, with as many independent components as angular samples. The relationship between the measurements and the unknown SH coefficients is given by the linear model:

$$x_K=A_{K \times Q} q_Q$$

(2)

where

• $A_{K\times Q}$ is the measurement matrix constructed by evaluating the SH basis functions at the sampled directions $({\theta }_i,{\varphi }_i)$,
• $q_Q ϵ {\mathbb{R}}^{Q\times 1}$ is the vector of unknown SH coefficients,
• $Q={(L_{max}+1)}^2$ is the number of basis functions for a maximum degree $L_{max}$.

In typical ToS configurations, the number of measurements $K$ is greater than the number of SH coefficients $Q$, i.e., $K > Q$. Nevertheless, to exploit sparsity and cast the recovery problem as an underdetermined system suitable for CO, a randomized dimensionality reduction is performed. Specifically, the full measurement vector $x_K$ is projected onto a lower-dimensional subspace using a Gaussian sensing matrix $G\in {\mathbb{R}}^{M \times K}$ with $M<K$ to obtain the compressed vector $y_M \in {\mathbb{R}}^{M \times 1}$:

$$y_M=G_{M \times K}\hspace{0.17em}{x}_K$$

(3)

The entries of $G_{M\times K}$ are independent and identically distributed (i.i.d.) Gaussian random variables with zero mean and variance ${\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$M$}\right.}$, i.e.,

$$G_{ij}\sim N(0,{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$M$}\right.})$$

(4)

This projection preserves the information content required for accurate reconstruction due to the Restricted Isometry Property (RIP) and the high incoherence of Gaussian matrices with respect to most representation bases, including spherical harmonics. Combining the above with the SH acquisition model leads to the compressed system:

$$y_M={\mathrm{G}}_{M \times K}{\mathrm{x}}_K=\left(G_{M \times K}\hspace{0.17em}{A}_{K \times Q}\right)q_Q={\Psi }_{M \times Q}{q}_Q,$$

(5)

where $\Psi ϵ {\mathbb{R}}^{M \times Q}$ is the effective reduced sensing matrix.

• Theoretical Basis for Dimensionality Reduction

According to the theoretical results of Candès, Donoho, and others, a signal that is $s$-sparse in a given basis of dimension $Q$ (i.e., with only $s\ll Q$ non-zero coefficients) can be accurately recovered from a significantly smaller number of linear measurements than traditionally required. If the sensing matrix satisfies RIP and is incoherent with the representation basis, the minimum number of measurements $M$ required satisfies:

$$M\gtrsim C s\log Q$$

(6)

where

• $s$ is the sparsity level of $\left\{q_i\right\}$,
• $Q$ is the ambient dimensionality of the SH basis,
• $C$ is a constant dependent on the reconstruction guarantee and noise level.

This result establishes the fundamental limit for compressed sampling and justifies the use of Gaussian matrices for reducing the system size in sparse reconstruction problems [5,17]. In the proposed methodology, this principle enables projecting a high-dimensional measurement vector $x\in {\mathbb{R}}^K$ into a compressed domain $y\in {\mathbb{R}}^M$ using ${\mathrm{G}}_{M \times K}$, while retaining the relevant information to estimate the $s$-sparse set of SH coefficients $q_Q$. The resulting system is then solved using ${\mathcal{l}}_1$-regularized CO, allowing efficient recovery of the radiation pattern from significantly fewer measurements.

2.5. Sparse Recovery via Convex Optimization

Exploiting the sparsity and compressibility of the SH representation, the estimation of $q_Q$ is formulated as an ${\mathcal{l}}_1$-minimization problem [4,6]:

$$\min {\left|\right|q_Q\left|\right|}_1\mathrm{subjetc} \mathrm{to} {\left|\right|y_M-\left(GA\right) q_Q\left|\right|}_2\le \epsilon ,$$

(7)

where $ϵ$ is a tolerance parameter accounting for measurement noise and model mismatch. This formulation leverages the dimensional-reduced Gaussian observations to recover a sparse set of coefficients and, consequently, to reconstruct efficiently the SH expansion of the radiation pattern.

For computational implementation, the CVX package in MATLAB [18] was used in this study, providing a declarative environment for convex programming [19] and supporting efficient ${\mathcal{l}}_1$-regularized solvers.

2.6. Coefficient Reduction

To improve spectral clarity and promote a more compact representation of the radiation pattern in the SH domain, a post-processing step referred to as coefficient reduction is applied to the recovered SH expansion.

• Linear-Scale Formulation

Let $\left\{q_i\right\}$ be the set of SH coefficients obtained from the reconstruction, and let

$$Q_{max}=\mathrm{m}\mathrm{a}\mathrm{x}\left|q_i\right|$$

(8)

denote the maximum absolute value among them. The reduction is performed by applying a relative threshold T on a linear scale: any coefficient whose magnitude falls below a fractionof $Q_{max}$ is set exactly to zero, i.e.,

$$\mid qi\mid <T\hspace{0.17em}{Q}_{max}⟹q_i=0\forall i$$

(9)

Here, $T\in \left(\mathrm{0,1}\right)$ is a user-defined parameter that controls the level of sparsification. This rule preserves only the coefficients that contribute significantly to the reconstructed pattern, reducing model complexity while maintaining accuracy.

• Logarithmic Implementation in This Work

In the numerical experiments presented in this paper, the same criterion has been implemented in the logarithmic domain, expressing the coefficients in dB:

$$q_i\left[dB\right]=10{log}_{10}\mid q_i\mid$$

(10)

and applying a threshold relative to the maximum value $Q_{max}$:

$$q_i\left[\mathrm{d}\mathrm{B}\right]<(Q_{max} [dB]-T_{dB} [dB\left]\right)⟹q_i=0.$$

(11)

In this case, the threshold $T_{dB}$ is also defined in dB, and coefficients below this relative level are discarded. This logarithmic version is equivalent to using the previous multiplicative threshold in linear scale and is convenient for visualizing and tuning the reduction parameter. The new reduced coefficient vector is denoted as the Reduced SH Coefficient Vector, $q_Q^r$.

Further studies are required to determine the optimal value of the threshold as a function of the application and the characteristics of the measured radiation patterns.

2.7. Pattern Reconstruction and Error Rate Calculation

To quantify the accuracy of the reconstruction of the original function $D(\theta ,\varphi )$, an error metric is defined ($Error$) based on the root mean square (RMS) of the differences between the measured values at the sampling points and the values reconstructed from the SH expansion $q_Q^r$ at the same angular positions. Formally,

$$Error=\sqrt{{\displaystyle \frac{1}{K}} {\sum }_{i=1}^K{(x_i-{\sum }_{j=1}^Q{A}_{ij} q_j^r )}^2}$$

(12)

This RMS-based error metric provides a normalized measure of the reconstruction fidelity and is robust against measurement noise, ensuring a balanced evaluation of the solution quality, allowing the entire process to be iterative in pursuit of convergence towards a minimum error.

2.8. Summary of the Reconstruction Workflow

The overall procedure of the proposed method can be summarized in seven steps:

• Step 1. ToS Data Acquisition

Perform ToS using the WT to obtain $K$ partial angular measurements around the EUT, forming the raw observation vector $x_K$.

• Step 2. Measurement Matrix

Construct the measurement matrix $A_{K \times Q}$ by evaluating the SH basis functions at the sampled angles so that $x_K=A_{K \times Q} q_Q$. At this stage, the maximum degree $L_{max}$ of the SH expansion must be selected according to the expected electrical size of the radiator, the angular smoothness of the pattern, and the number of available measurements, as it determines the total number of coefficients ${{Q=(L}_{max}+1)}^2$ to be processed.

• Step 3. Gaussian Observations Reduction

Project the raw measurements onto a lower-dimensional subspace using a Gaussian random matrix $G$, producing the reduced observation vector $y_M=G_{M \times K} x_K$ and the compressed sensing model $y_M=(G_{M \times K} A_{K \times Q}) q_Q$. This step preserves the essential information while converting the initially overdetermined system into an underdetermined one suitable for sparse recovery.

• Step 4. Sparse Recovery

Solve the resulting underdetermined inverse problem via convex ${\mathcal{l}}_1$-minimization to estimate the sparse set of SH coefficients $q_Q$ by means of CS/CO.

• Step 5. Coefficient Reduction

Apply a post-processing thresholding step to the recovered SH coefficients $q_Q$ to enhance spectral clarity and obtain a more compact representation $q_Q^r$. Coefficients below a relative “threshold” parameter, either in linear or logarithmic scale, with respect to the maximum, are set to zero, thereby reducing model complexity while maintaining sufficient pattern fidelity.

• Step 6. Pattern Reconstruction and RMS Error Rate Evaluation

Substitute the reduced coefficients vector $q_Q^r$ into the truncated SH expansion to reconstruct the full-sphere far-field radiation pattern. Quantify the reconstruction accuracy using an RMS-based error metric comparing the reconstructed and reference values at the sampling points. This provides an objective measure of pattern fidelity and supports the evaluation of different acquisition and reconstruction configurations in an eventual iterative process towards a minimum error.

2.9. Parameter Selection and Tuning

As several parameters are heuristic and empirically tuned, the target systems are devices with embedded wireless connectivity rather than purpose-built telecom devices. Their radiation behavior and accuracy requirements are moderate, so a pragmatic approach is appropriate, and we propose a feedback loop method: start from conservative defaults, evaluate reconstruction (normalized RMS error, lobe preservation, stability), and adjust iteratively until balancing fidelity and cost (orbits, samples, computation). This promotes reproducibility and accumulation of practice-driven knowledge across device classes.

• Parameter C: Gaussian observation reduction

Let $\mathsf{\Psi }≔GA\in R^{M\times Q}$ denote the sensing operator with measurements $y=\Psi \hspace{0.17em}q+\eta$, where $q$ is the SH coefficient vector, $M$ is the number of observations, and $\eta$ is the perturbations (thermal noise, ADC quantization, chamber reflections, probe misalignment, calibration errors). This motivates a residual-bounded formulation in convex recovery: $|\Psi q - y| \le \epsilon$.

The problem is underdetermined when $M < Q$; the constant $C$ scales $M$ and thus controls underdetermination:

• Smaller $C$: Fewer equations, larger feasible set, possible support ambiguity, spurious coefficients, lobe artifacts, higher error, and instability.
• Larger $C$: More equations, better conditioning, more reliable support, improved accuracy, and noise robustness, at the cost of more samples and time. Beyond a point, gains diminish.

Guidance: Adopt default $C = 1$. For devices with rich spectra, increase $C$ slightly to avoid artifacts. For simpler patterns, $C = 1$ suffices. Apply the recommended short feedback loop.

• Parameter $\epsilon$: Convex optimization tolerance

We recover $q$ by solving

$$min\left|\right|q|{|}_1 s.t.|\Psi q-y|\le \epsilon .$$

(13)

The tolerance $\epsilon$ controls fidelity to measurements versus robustness. Too small $\epsilon$ forces overfitting to noise; too large $\epsilon$ allows excessive deviation.

Guidance: Set $\epsilon$ proportional to estimated noise level (from chamber calibration, receiver SNR, or probe uncertainties). Validate with reconstruction error on a subset. Adjust $\epsilon$ upward if artifacts appear due to mis-modeling; lower if patterns lose detail. Empirically, setting ε between 1% and 5% of the measurement power yields stable results.

• Parameter $s$: Sparsity level

The sparsity $s$ defines the maximum number of SH coefficients retained. Too low $s$ removes relevant features; too high $s$ admits noise and increases computation.

Guidance: Estimate angular complexity from device size: electrically large devices typically need higher $s$. Start with $s$ proportional to $ka$ (wavenumber × radius). Validate by RMS error and lobe preservation. Increase $s$ until improvements plateau. Record optimal values for reuse.

• Sampling parameters (number of orbits, samples per orbit)

Sampling affects both identifiability and cost. Too few samples limit reconstruction quality; too many increases effort without benefit.

• Number of orbits: increasing orbits improves angular coverage.
• Samples per orbit: adopt the standard sampling configuration of the available measurement chamber.

Guidance: Start with 4–6 orbits at different tilts and expand only if reconstructions exhibit artifacts and always validate visually and by RMS error.

• General recommendations

• Estimate expected sparsity and angular complexity from device form factor and use case.
• Initialize parameters with conservative defaults suited to electrically large DUTs; prioritize stability.
• Use a small validation subset to quantify error and visually check features; adjust parameters accordingly.
• Prefer slightly higher measurement cost over unstable reconstructions.
• Record settings and outcomes to build guidelines for similar devices.
• Future improvements should include systematic calibration of $\epsilon$ using noise models and adaptive selection of $C$ and $s$ based on device geometry. This will progressively narrow recommended ranges for device classes and enhance reproducibility.

3. Results

This section presents the application of the proposed methodology for the reconstruction of the radiation pattern in two representative scenarios:

• “Theoretical case”: An ideal half-wavelength electric dipole.
• “Experimental case”: A real commercial device with Wi-Fi connectivity.

In both cases, data acquisition is performed using a reduced number of ToS paths, with the aim of assessing the validity and robustness of the proposed approach.

The estimated radiation pattern is represented, in both examples, in terms of the directivity function $D\left(\theta ,Ф\right)$—a real, positive scalar function that does not include phase or complex field information—of the radiating system expressed in dimensionless linear units, in accordance with standard practices in experimental environments such as anechoic chambers where the received signals are proportional to the power flux density and are used to compute $D\left(\theta ,Ф\right)$ ([16], pp. 810–814).

3.1. Theoretical Case: Ideal Half-Wavelength Electric Dipole

The structure of a resonant half-wavelength electric dipole represents one of the simplest and most extensively studied radiators in antenna theory, with a well-known analytical radiation pattern. By applying the reconstruction method proposed in this work, it is possible to compare the resulting representation with the corresponding theoretical reference solution.

This comparison enables an objective evaluation of the method’s ability to accurately capture the characteristics of the radiated electromagnetic field, even when starting from a highly reduced set of measurements.

3.1.1. Theoretical Step 1: ToS Data Acquisition

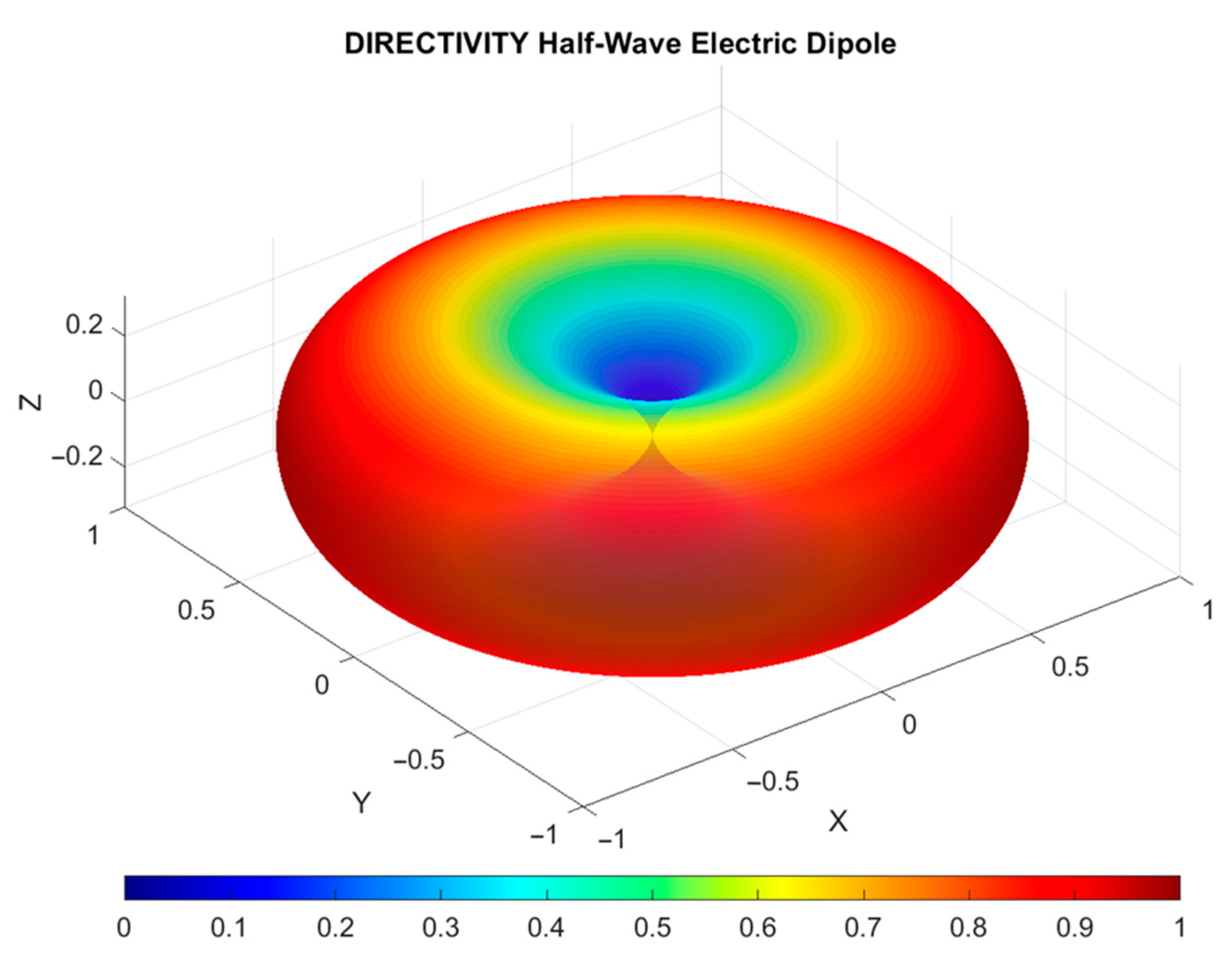
In this basic theoretical validation example, the function $D\left(\theta ,Ф\right)$ is defined as the “directivity” pattern of a canonical half-wave dipole antenna. This quantity represents the angular distribution of the FF radiated power density normalized to its maximum value:

$$D\left(\theta ,\mathrm{Ф}\right)={\displaystyle \frac{4\pi U(\theta ,\mathrm{Ф})}{P_{rad}}},$$

(14)

where $U(\theta ,Ф)$ is the time-average radiation intensity, and $P_{rad}$ is the total radiated power. For the resonant half-wave dipole, the analytical reference directivity is accurately approximated by the classical closed-form expression ([16], pp. 182–184):

$$D\left(\theta ,Ф\right)=D_0{\left({\displaystyle \frac{\mathit{cos}\left(\frac{pi}{2}\right)\mathit{cos}\left(\theta \right)}{\mathit{sin}\left(\theta \right)}}\right)}^2\approx D_0{(\sin \theta )}^3$$

(15)

where $D_0\approx 1.64$ (2.15 dBi) is the maximum directivity. This real-valued pattern, independent of angle variable $Ф$ due to the rotational symmetry of the radiator, serves as the ground truth for evaluating the sparse SH reconstruction. This functional form has been widely used as a reference model in studies applying SH expansions for antenna modeling. For instance, in [3], this approximation serves as the basis for integrating measured patterns into ray-tracing simulations. The corresponding theoretical pattern is shown in Figure 4.

A small number of five orbits are defined to assess the validity of the proposed method. Each orbit is characterized by the azimuthal direction of its inclination axis and by its WT angle with respect to the horizontal $XY$-plane. Along each orbit, measurements are taken at uniformly spaced azimuthal angles $\varphi$ along the trajectory. The geometric configuration of these orbits is illustrated in Figure 5.

Based on these five orbits, with regularly spaced 36 samples/orbit, a column vector $x_K=x_{180}$ ($K=5 orbits \times 36 samples/orbit = 180 samples$) of samples is constructed representing the original function on the Dirac Delta basis.

3.1.2. Theoretical Step 2: Measurement Matrix

A different basis from the Dirac Delta function sampling one is used to represent the directivity function $D(\theta ,Ф)$: a series of SH functions $Y_l^m$.

Assuming that $D$ is sufficiently smooth, due to the small electrical size of the source $(ka ={\displaystyle \raisebox{1ex}{$2\pi $}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.}\ast {\displaystyle \raisebox{1ex}{$\lambda $}\!\left/ \!\raisebox{-1ex}{$4$}\right.} ={\displaystyle \raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$2$}\right.})$, the SH series can be truncated with a maximum degree $L_{max}=6$ (to be verified a posteriori), from which the corresponding order of the basis functions is derived, and the number of coefficients becomes

$$Q={(L_{max}+1)}^2={(6+1)}^2=49,$$

(16)

leading to the specific matrix formulation:

$$x_{180}= A_{180 \times 49} q_{49}$$

(17)

where $q_{49}$ is the coefficient vector in the truncated SH representation basis, and $A_{180 \times 49}$ is the transformation matrix from the Dirac delta sampling basis to the SH representation basis.

3.1.3. Theoretical Step 3: Gaussian Observations Reduction

It is estimated that the directivity function $D$ is sparse in SH representation function basis and that no more than $s=10$ relevant coefficients out of 49 total coefficients would be required for an accurate reconstruction of $x_{180}$ in the SH domain (this assumption is to be verified a posteriori). Under these assumptions, the theoretical expression described in Section 2.4 is applied to determine the minimum number of observations required for a reliable reconstruction of the radiation pattern:

$$M\gtrsim C s\log Q=1\ast 10\ast \log \left(49\right)=16.90 observations$$

(18)

$$M=20 observations$$

(19)

If the reconstruction proves insufficient, the constant $C$ could be increased to demand a higher number of measurements. The following equation illustrates a random Gaussian matrix $G_{20 \times 180}$, which enables dimensionality reduction to a linear system with only twenty equations.

$$G_{20\times 180}(\mu =0,{\sigma }^2={\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$20$}\right.})=\left[\begin{array}{ccc}{G}_{\mathrm{1,1}}(0,{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$20$}\right.})& \dots & G_{\mathrm{1,180}}(0,{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$20$}\right.})\\ \dots & \dots & \dots \\ G_{\mathrm{20,1}}(0,{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$20$}\right.})& \dots & G_{\mathrm{20,180}}(0,{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$20$}\right.})\end{array}\right]$$

(20)

This results in an underdetermined linear system with 20 equations and 49 unknowns, to be solved via CO:

$$y_{20}={\mathrm{G}}_{20 \times 180}{x}_{180}={\mathrm{G}}_{20 \times 180}(A_{180 \times 49}{q}_{49} )$$

(21)

$$y_{20}={\Psi }_{20\times 49}{q}_{49}$$

(22)

where ${\Psi }_{20\times 49}={\mathrm{G}}_{20\times 180}{A}_{180\times 49}$ is the effective measurement matrix.

3.1.4. Theoretical Step 4: Sparse Recovery

As previously discussed, the “CVX” package in MATLAB is used in this work due to its ability to formulate convex problems using clear and concise syntax. We aim to solve the linear system given by:

$$y_{20}={\Psi }_{20\times 49}{q}_{49}$$

(23)

A tolerance parameter $\epsilon$ (epsilon) is introduced to allow a bound error in the solution:

$${\left|\left|y_{20}-{\Psi }_{20\times 49} q_{49}\right|\right|}_2\le \epsilon$$

(24)

Tolerance parameter was discretionally set to $\epsilon =0.90$. As it was already said, further studies are required to determine the optimal value of $\epsilon$ depending on the specific characteristics of each application case.

The application of CVX to the proposed system yields a solution vector $q_{49}$ containing the SH coefficients.

3.1.5. Theoretical Step 5: Coefficient Reduction

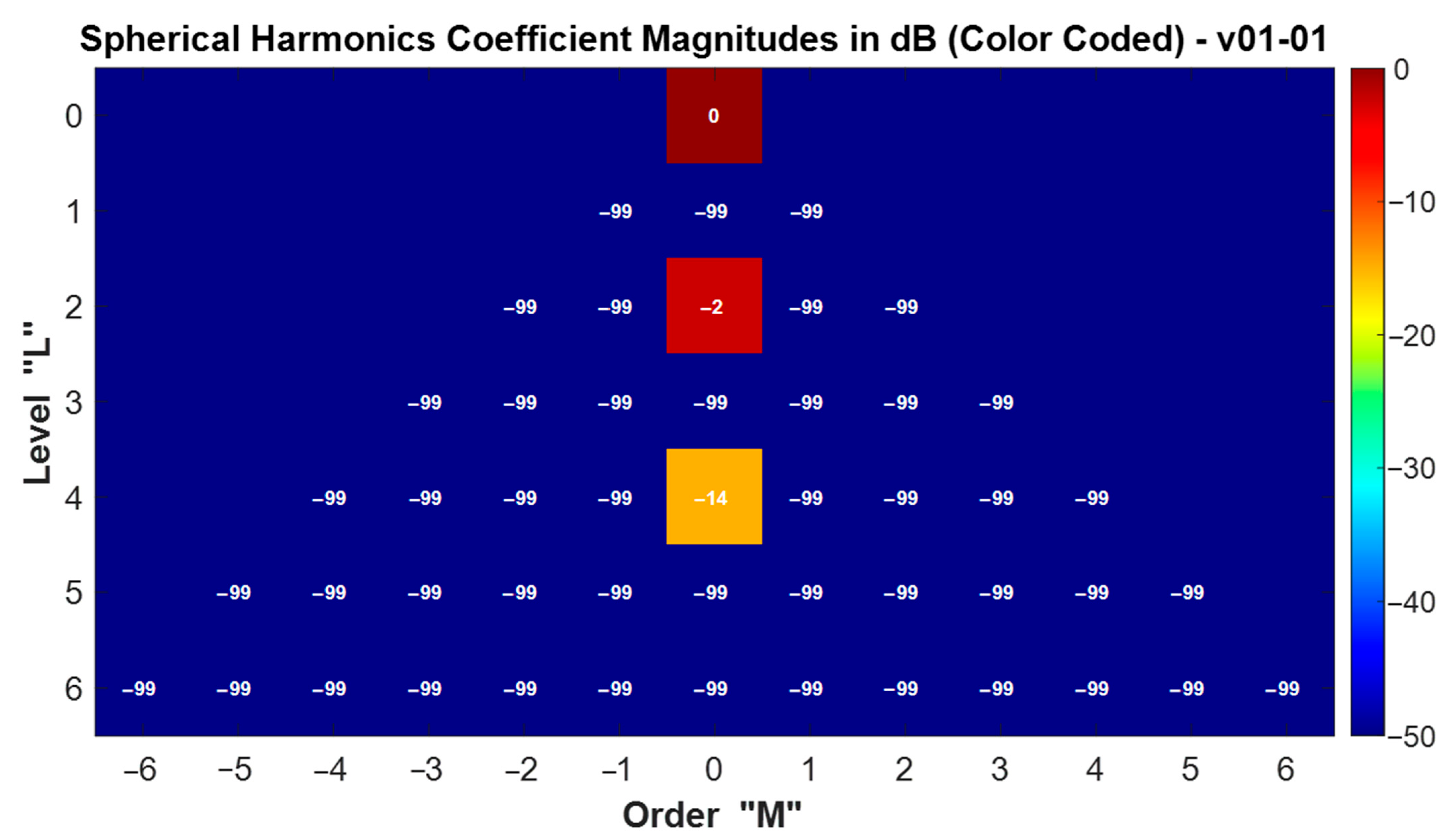
In this example, the value for coefficient reduction was discretionally set to $T_{dB}=15 \mathrm{d}\mathrm{B}$. The resulting solution is represented graphically using a triangular map of SH coefficients arranged in two dimensions according to their degree $L$ and order $M$. The modulus of each coefficient $q_i$ is plotted in logarithmic scale (dB), with a minimum display level of −99 dB. The most significant coefficients are highlighted using a color-coded scheme (Figure 6).

It can be observed in the solution vector $q_{49}$ that the signal is indeed sparse on the SH representation basis, and that only three spherical harmonics—$Y_0^0$ $Y_2^0$ $Y_4^0$—are required. Notably, just 3 SH components out of the total 69 are accurate enough for practical purposes (see SH radiation patterns on Figure 3).

3.1.6. Theoretical Step 6: Pattern Reconstruction and Error Rate Calculation

The RMS-based error rate was computed as defined in Equation (12), using the original data and the reconstructed values, both at the sampling directions $({\theta }_k,{\varphi }_k)$.

Finally, a comparative graphical representation is provided, showing both the original theoretical function and the reconstruction obtained via SH expansion. The calculated error rate is also reported ($Error=0.027208$), enabling a direct visual assessment of the approximation quality (Figure 7).

The results demonstrate that it is possible to reconstruct the original function $D$ with relevant high accuracy using only 180 samples distributed over five orbits with a maximum WT angle of 30°.

3.1.7. Theoretical Summary of the Reconstruction

The reconstruction can be summarized as follows:

• Only 180 samples were acquired, and they were distributed across five orbits with 36 samples per orbit at a maximum WT angle of 30°.
• The SH expansion was successfully truncated at order $L_{max}=6$, as the highest solved order coefficient corresponds to order $l=4$.
• The original function $x_K=D$(${\theta }_K,{\varphi }_K$) is finally sparse on the truncated SH series basis and can be robustly reconstructed using only 3 coefficients out of 49 total(initial estimates suggested fewer than 10 coefficients would be needed).
• The resulting defined error rate is considered lower than 3%.
• The visual comparison between the original and reconstructed functions is highly favorable.

These excellent results can be attributed to the inherently smooth and sparse nature of the directivity function of an ideal half-wave dipole in the SH representation basis, as well as the effectiveness of the proposed method in recovering the relevant information from a very limited number of measurements.

3.2. Experimental Case: Real Commercial Device with Wi-Fi Connectivity

The experimental case addresses the reconstruction of the radiation pattern of a real commercial device equipped with embedded Wi-Fi connectivity. The EUT is a bulky, non-rotatable system intended for non-telecommunications use with maximum external dimensions of approximately 600 mm × 400 mm × 100 mm. The DUT was mounted on a purpose-built dielectric wedge fixture [20] and operated in continuous-wave mode inside a fully anechoic chamber. A motorized turntable was employed to perform the ToS method proposed in this work. Due to confidentiality constraints concerning both the facility and the DUT, no further details or photographs can be provided. However, it should be emphasized that all measurements were carried out using the following instrumentation:

• Rohde & Schwarz FSH20 Spectrum Analyzer (9 kHz–20 GHz); Rohde & Schwarz GmbH & Co. KG, Munich, Germany.
• Rohde & Schwarz ZNL6 Vector Network Analyzer (5 kHz–6 GHz); Rohde & Schwarz GmbH & Co. KG, Munich, Germany.
• Rohde & Schwarz HL562E Ultralog Antenna; Rohde & Schwarz GmbH & Co. KG, Munich, Germany.
• Agilent EMC E7402 Spectrum Analyzer (9 kHz–3 GHz); Agilent Technologies Inc., Santa Clara, CA, USA.
• Agilent 11955A Biconical Antenna; Agilent Technologies Inc., Santa Clara, CA, USA.

The tests were conducted at an operating frequency within the 2.4 GHz ISM band used by the device’s Wi-Fi interface. This combination of frequency and physical size corresponds to an electrically moderate-to-large object (ka ≈ 30), ensuring sufficient angular field variability to challenge the smooth and sparse SH reconstruction process. As is typical in practical OTA characterization of such devices, the available radiation pattern data are necessarily partial and limited.

3.2.1. Experimental Step 1: ToS Data Acquisition

The radiation pattern of the EUT was characterized by means of uniform azimuthal sweeps $Ф$, performed along only five orbits with a maximum WT angle of 30°. In this real-world case, only a limited number of ToS orbits were defined. Each orbit is characterized by an independent azimuthal direction of its inclination axis and its WT angle with respect to the horizontal $XY$-plane (

Table 1. Geometric configuration of the five tilted sampling orbits used for radiation pattern acquisition, showing the uniform azimuthal direction and the corresponding inclination WT angles up to a maximum of 30°.

ORBIT #	Axis Direction	Wedge Angle
#1	0°	0°
#2	0°	30°
#3	0°	−30°
#4	90°	30°
#5	90°	−30°

).

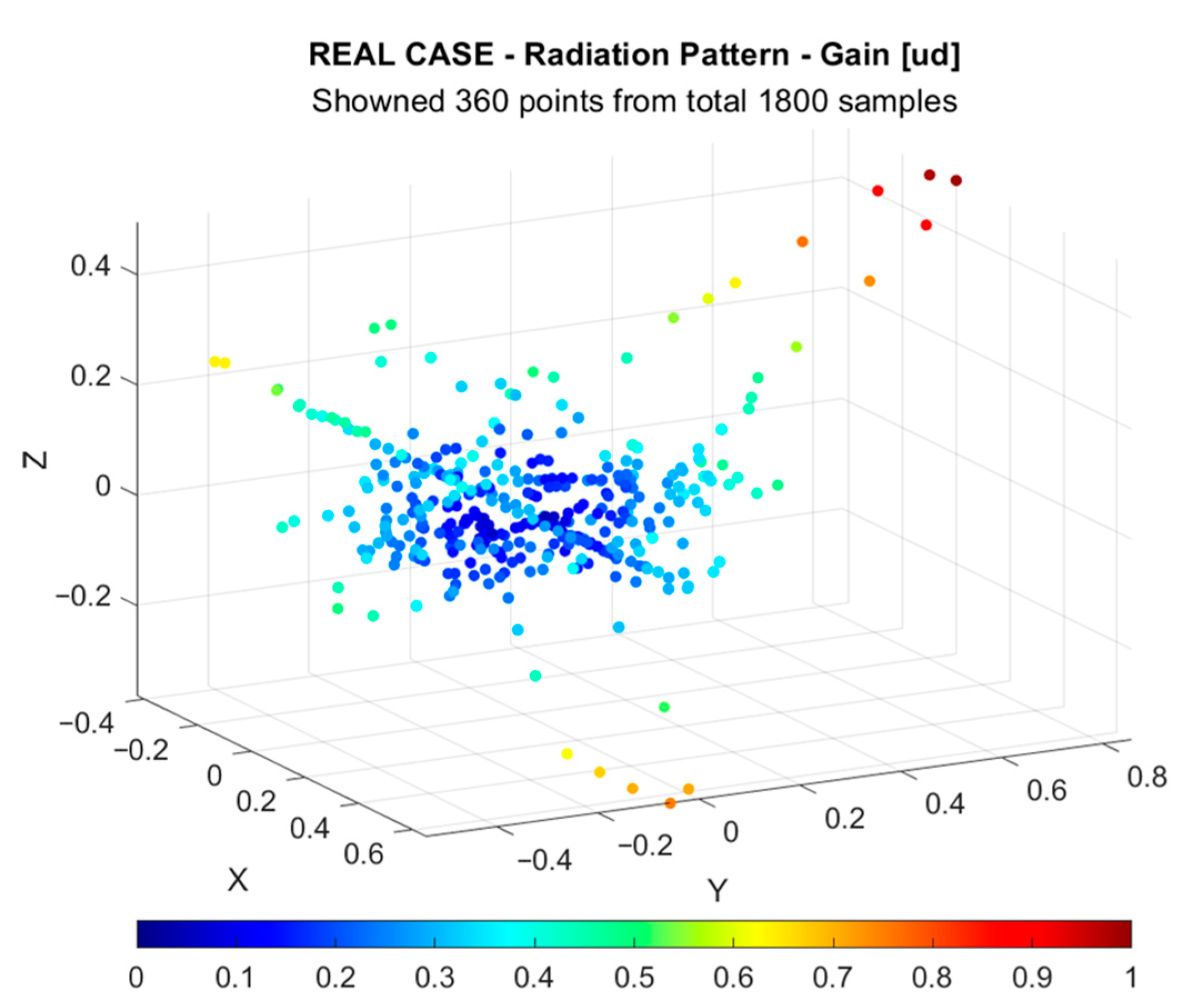
As an illustration, Figure 8 shows a representative subset of cloud points corresponding to the recorded measurements. Due to the nature of this acquisition strategy, the resulting sampling of the complete radiation pattern is inherently sparse and limited, with most of the measurements concentrated at very low elevation angles $\theta$.

A column vector $x_K=x_{1800}$ ($K=5 orbits \times 360 samples/orbit = 1800 samples$) is constructed representing the original function on the canonical Dirac Delta basis.

3.2.2. Experimental Step 2: Measurement Matrix

Again, a different basis from the initial Dirac Delta sampling one is used to represent the directivity function $D(\theta ,Ф)$: a truncated series of SH functions $Y_l^m$. Assuming that $D$ is sufficiently smooth $(ka \approx 30)$, the SH series can be truncated with a maximum degree $L_{max}=12$ (to be verified a posteriori), from which the corresponding order of the basis functions is derived, and the number of coefficients becomes

$$Q={(L_{max}+1)}^2={(12+1)}^2=169,$$

(25)

leading to the specific matrix formulation

$$x_{1800}=A_{1800\times 169} q_{169},$$

(26)

where $q_{169}$ is the coefficient vector in the truncated SH representation basis, and $A_{1800 \times 169}$ is the transformation matrix from the Dirac Delta sampling basis to the SH representation basis.

3.2.3. Experimental Step 3: Gaussian Observations Reduction

It is also estimated that the original directivity function $D$ is sparse in the truncated SH function series basis and that no more than $s=20$ relevant coefficients out of the total 169 would be required for an accurate reconstruction of $x_{1800}$ in the SH domain—this assumption is to be verified a posteriori. Under this hypothesis, the theoretical expression from Section 2.4 is applied to determine the minimum number of observations required for an accurate reconstruction:

$$M\gtrsim C s\log Q=1\ast 20\ast \log \left(169\right)=44.55 observations$$

(27)

$$M=50 observations$$

(28)

If the reconstruction proves to be insufficient, the coefficient $C$ may be increased to demand a greater number of measurements $M$. To reduce the dimensionality to a linear system with 50 equations, a Gaussian random matrix $G_{50 \times 1800}$ is generated, leading to:

$$y_{50}={\mathrm{G}}_{50\times 1800} x_{1800}={\mathrm{G}}_{50\times 1800}(A_{1800\times 169} q_{169})$$

(29)

$$y_{50}={\Psi }_{50\times 169} q_{169}$$

(30)

where ${\Psi }_{50\times 169}={\mathrm{G}}_{50\times 1800}{A}_{1800\times 169}$ is the effective measurement matrix.

3.2.4. Experimental Step 4: Sparse Recovery

As in the previous case, the CVX package in MATLAB is used to formulate and solve the underdetermined system of linear equations:

$$y_{50}={\Psi }_{50\times 169} q_{169}$$

(31)

A tolerance parameter $\epsilon$ (epsilon) is included in the solution process to allow for a controlled level of approximation error:

$${\left|\left|y_{50}-A_{50\times 169} q_{169}\right|\right|}_2\le \epsilon$$

(32)

Tolerance was discretionally set to $\epsilon =0.90$. As before, further research is required to determine the optimal value of this parameter depending on the specific characteristics of each application scenario. Solving the system yields a solution vector $q_{169}$ containing the SH coefficients.

3.2.5. Experimental Step 5: Coefficient Reduction

In this example, the value for coefficient reduction was again discretionally set to $T_{dB}=15 \mathrm{d}\mathrm{B}$. The resulting solution is represented graphically using a triangular map of SH coefficients arranged in two dimensions according to their degree $L$ and order $M$. The modulus of each coefficient $q_i$ is plotted in logarithmic scale (dB), with a minimum display level of −99 dB. The most significant coefficients are highlighted using a color-coded scheme (Figure 9).

It can be observed in the solution vector $q_{169}$ that the signal really exhibits sparsity when represented in the SH basis. Notably, 30 SH components out of initial 169 are accurate enough for practical purposes (see SH radiation patterns on Figure 3).

3.2.6. Experimental Step 6: Pattern Reconstruction and Error Rate Calculation

The error rate was computed as defined in Equation (12) using the original and reconstructed values at the sampling nodes.

Finally, a comparative graphical representation is provided, showing both the original theoretical function and the reconstruction obtained via spherical harmonic expansion. The calculated error rate, evaluated at the original sampling nodes, is also reported ($Error = 0.13293 \approx 14\%$), enabling a direct visual assessment of the approximation quality (Figure 10). This observed error level warrants further discussion regarding its practical acceptability and relation to typical measurement uncertainties. In the practical case, the reconstruction error reached an average value of 14%. Although this figure may appear relatively high, it remains acceptable within an application-driven characterization framework. First, it is of the same order of magnitude as typical measurement uncertainties in anechoic chambers (≈5–10%), which depend on probe calibration, system stability, and noise levels. Second, most of this error is concentrated in angular sectors that are mechanically inaccessible, with negligible contribution to the device’s effective wireless coverage. In the operationally relevant directions, the error remains well below the global average. Finally, for bulky and non-rotatable devices, the primary objective is not to achieve a full-sphere reconstruction but to provide reliable information in the regions of interest, enabling seamless integration of the SH-based representation into propagation simulators and electromagnetic optimization workflows. The results demonstrate that the original function can be recovered with sufficient accuracy using only 1800 samples distributed over five orbits with a maximum WT angle of 60°.

3.2.7. Experimental Summary of the Reconstruction

The reconstruction of the experimental case can be summarized as follows:

• Only 1800 samples were acquired, distributed across five orbits with 360 samples per orbit at a maximum WT angle of 60°.
• An SH expansion up to order $L_{max}=12$ was employed, and only 4 coefficients out of 30 corresponded to that highest order.
• The original function $x_K=D$(${\theta }_K,{\varphi }_K$) is sparse on the truncated SH series basis and can be effectively reconstructed using just 30 coefficients out of the 169 available (initial estimates suggested around 20 coefficients would be required and, because of that, the number of reduced observations $M$ could be adjusted in a second computation within an iterative process).
• The resulting defined error rate is lower than 14%.
• As in the theoretical case, in this case as well the visual comparison between the original and reconstructed functions is highly favorable.

This case has proven challenging due to the limited number of sampling orbits (only five orbits) and their restricted inclination (up to 60° above the horizontal plane), in the context of modeling a complex radiation pattern not associated with a dedicated antenna design, but rather with the uncontrolled emission of a non-communication electronic device equipped with a Wi-Fi channel. Nevertheless, a simple and useful model of the system has been obtained using a relatively small number of coefficients.

4. Discussion

The results obtained in both the theoretical dipole case and the experimental real Wi-Fi device case demonstrate the feasibility of combining the proposed ToS method with sparse SH reconstruction for efficient characterization of EM radiation patterns. The canonical dipole provided a controlled scenario for validating the pipeline under idealized conditions, confirming that a reduced number of SH coefficients can accurately represent smooth FF pattern distributions. The experimental case, on the other hand, highlighted the method’s applicability to realistic IoT devices with mechanical and geometrical constraints in anechoic chamber setups.

A key outcome is that the integration of physically constrained acquisition with CS principles enables accurate reconstruction from significantly fewer measurements than required by traditional full-sphere scanning. The use of Gaussian dimensionality reduction further optimizes the acquisition-to-reconstruction pipeline, transforming a dense observation set into a compressed representation without noticeable loss of information and allowing the use of ${\mathcal{l}}_1$-regularized CO for coefficient recovery.

The coefficient reduction stage introduced as post-processing proved effective in promoting compact representations by discarding low-energy components without degrading pattern fidelity. Additionally, the RMS-based error rate provided a robust and quantitative metric for evaluating reconstruction accuracy under both simulated and experimental conditions, allowing the entire process to be iterative in pursuit of convergence towards a minimum error.

While the validation on a half-wave dipole and a single commercial Wi-Fi device establishes a proof-of-concept, the scope of this work is primarily methodological. The intention is to present a resource-efficient alternative for radiation pattern measurement in scenarios where mechanical rotation or full-sphere sampling are impractical, rather than to exhaustively cover all possible electromagnetic environments. Extending the evaluation to devices with more complex radiation characteristics, such as large arrays or strongly directive systems, constitutes a natural direction for future work.

In summary, the proposed methodology bridges practical measurement constraints and advanced sparse recovery techniques, providing a flexible framework for over-the-air testing of bulky, heavy, or fixed IoT devices. By reducing acquisition requirements while maintaining reconstruction fidelity, it contributes to the development of efficient electromagnetic characterization strategies suited for modern wireless systems.

5. Future Work

While the proposed methodology has demonstrated promising results in both theoretical and real-world scenarios, several avenues remain open for further development and optimization.

First, future studies should aim to refine the spatial configuration of the TOS. This includes optimizing the number of orbits, their inclination angles, and the azimuthal orientation of their rotational axes, all while preserving the main practical advantage of the method: a reduced-cost measurement process. Balancing angular coverage and sampling efficiency against infrastructure limitations (e.g., chamber size, mechanical rotation constraints, and acquisition time) will be key to expanding the method’s applicability.

Second, the selection of the constant $C$ in the theoretical estimation of the minimum number of required observations in Gaussian observations reduction should be systematically investigated. Its influence on reconstruction accuracy and robustness in undersampled regimes is of particular interest.

Third, further work is needed to identify the optimal truncation level of the SH’s basis. Choosing an appropriate expansion order $L_{max}$ is critical to ensuring a compact yet accurate representation of the radiation pattern.

Fourth, improvements can be pursued in the configuration of the CO solver used during reconstruction. This includes analyzing the effect of the number of equations, the tolerated error rate level, and the tuning of the parameter $\epsilon$. Alternative convex or non-convex optimization algorithms should also be explored to potentially enhance performance or reduce computational costs.

Fifth, the inclusion of measurement noise in the model should be explicitly addressed. The impact of noise on reconstruction fidelity may justify the introduction of regularization techniques such as Tikhonov regularization or other noise-aware formulations.

Sixth, both theoretical and experimental validation should be conducted to assess the suitability of establishing a threshold value in the reduction of SH coefficients.

Seventh, future theoretical research will extend the proposed ToS and sparse SH reconstruction framework to more complex scenarios, including electrically large radiators and planar dipole arrays. These cases will allow assessing the method’s performance under highly oscillatory radiation patterns and denser angular spectra, complementing the canonical validation presented in this work.

Lastly, the methodology should be tested on a broad range of practical devices. Applying the ToS strategy to various real-world EUTs will allow a more comprehensive validation of its effectiveness and identify potential domain-specific adjustments.

It should be noted that the use of ToS inherently implies discarding certain radiation directions or accepting a higher reconstruction error in directions that are vertical to the horizontal plane of the EUT, as these are generally less relevant for the device’s intended use.

By addressing these points, the proposed framework may evolve into a robust and general-purpose tool for efficient EM radiation characterization under realistic constraints.