Transform Domain Based GAN with Deep Multi-Scale Features Fusion for Medical Image Super-Resolution
Abstract
1. Introduction
- We designed two types of multi-scale feature extraction blocks (the MSID block and the GMS block). The MSID block can exploit the potential features from medical images by adaptively detecting the long- and short-path features at different scales, and the GMS block can achieve greater multi-scale feature extraction capabilities with less computing load at the granular level by expanding the range of receptive fields for each network layer.
- We conducted experiments on our medical image dataset, which demonstrates that our method can achieve higher PSNR/SSIM values and preserve global topological structure and local texture detail more effectively than existing state-of-the-art methods.
2. Related Work
2.1. CNN-Based SR
2.2. GAN-Based SR
2.3. Medical Image SR
3. Proposed Method
3.1. Overview
3.2. Multi-Scale Features Fusion Generative Adversarial Network (MSFF-GAN) Structure
3.2.1. MSID Block for MSFE
3.2.2. GMS Block for MSFE
3.3. Loss Function
3.4. Non-Subsampled Shearlet Transform (NSST) Prediction
4. Experimental Results and Analysis
4.1. Medical Image Datasets
4.2. Implementation Details
4.3. Evaluation Protocols
4.4. Comparison with State-of-the-Art Methods
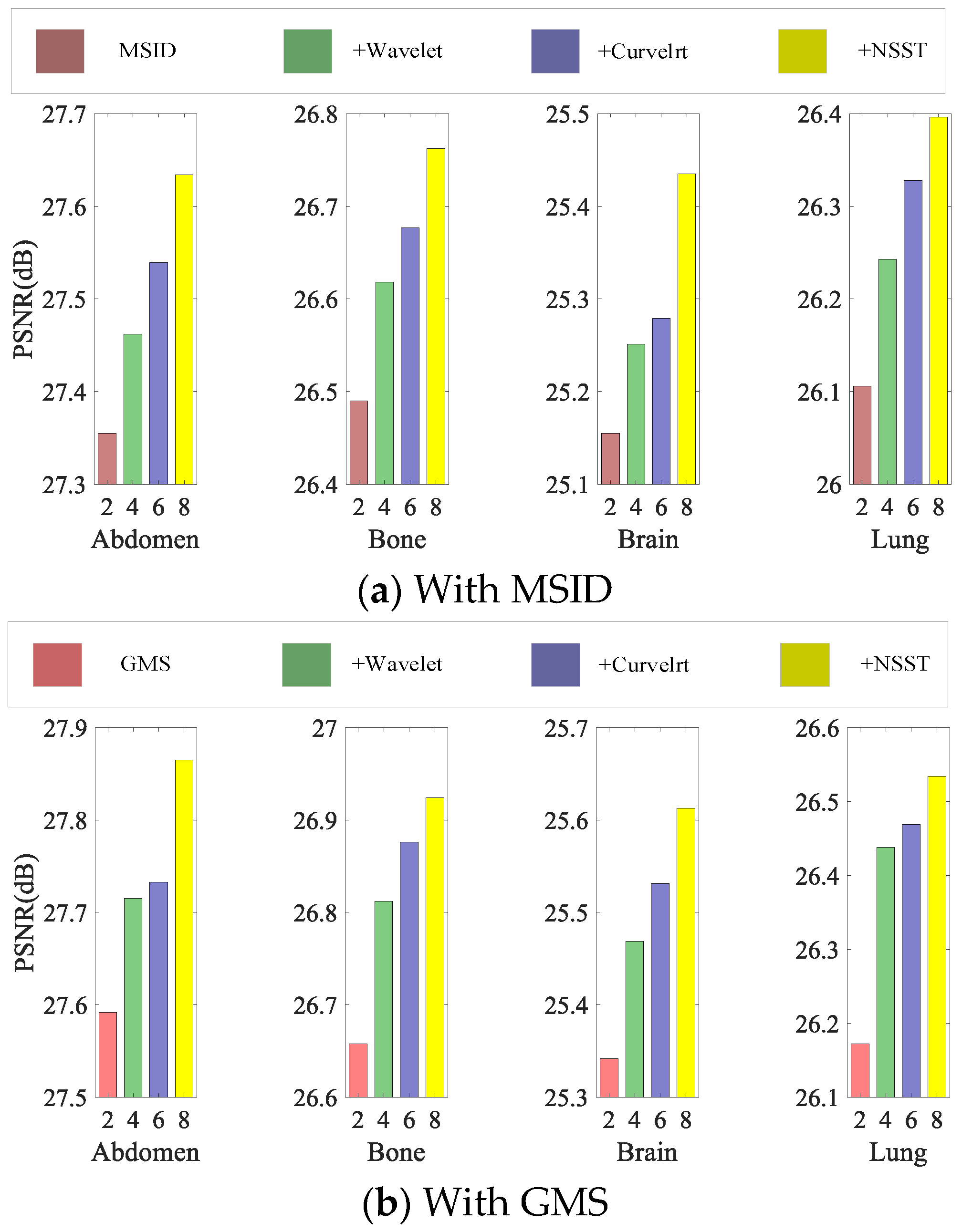
4.5. Ablation Study
4.5.1. Effectiveness of MSID Block
4.5.2. Effectiveness of GMS Block
4.5.3. Effectiveness of NSST
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviation | Full Form | First Appearance |
| HR | High-Resolution | Abstract |
| CT | Computed Tomography | Abstract |
| MSFF-GAN | Multi-Scale Features Fusion Generative Adversarial Network | Abstract |
| SR | Super-Resolution | Abstract |
| GANs | Generative Adversarial Networks | Abstract |
| CNNs | Convolutional Neural Networks | Abstract |
| MSID | Multi-Scale Information Distillation | Abstract |
| GMS | Granular Multi-Scale | Abstract |
| NSST | Non-Subsampled Shearlet Transform | Abstract |
| SSIM | Structural Similarity Index | Abstract |
| PSNR | Peak Signal-to-Noise Ratio | Abstract |
| MRI | Magnetic Resonance Imaging | Introduction |
| LR | Low-Resolution | Introduction |
| SNR | Signal-to-Noise Ratio | Introduction |
| DL | Deep Learning | Introduction |
| SRCNN | Super-Resolution Convolutional Neural Network | Section 2.1 |
| VDSR | Very Deep Super-Resolution | Section 2.1 |
| RCAN | Residual Channel Attention Network | Section 2.1 |
| SRDenseNet | Super-Resolution Dense Network | Section 2.1 |
| MemNet | Memory Network | Section 2.1 |
| RDN | Residual Dense Network | Section 2.1 |
| IDN | Information Distillation Network | Section 2.1 |
| MSRN | Multi-Scale Residual Network | Section 2.1 |
| AMRSR | Attention-based Multi-Reference Super-Resolution | Section 2.1 |
| AdderSR | Adder-based Super-Resolution | Section 2.1 |
| MARP | Multi-scale Attention and Residual Pooling | Section 2.1 |
| SRGAN | Super-Resolution Generative Adversarial Network | Section 2.2 |
| ESRGAN | Enhanced Super-Resolution GAN | Section 2.2 |
| RankSRGAN | Ranker-guided SRGAN | Section 2.2 |
| CGAN | Conditional Generative Adversarial Network | Section 2.2 |
| EventSR | Event-based Super-Resolution | Section 2.2 |
| LIWT | Local Implicit Wavelet Transformer | Section 2.2 |
| DMSN | Deep Multi-Scale Network | Section 2.3 |
| MAPANet | Multi-scale Attention-guided Progressive Aggregation Network | Section 2.3 |
| SFE | Shallow Feature Extraction | Section 3.2 |
| DFE | Deep Feature Extraction | Section 3.2 |
| MSFE | Multi-Scale Feature Extraction | Section 3.2 |
| NSLPF | Non-Subsampled Laplacian Pyramid Filters | Section 3.4 |
| TCIA | The Cancer Imaging Archive | Section 4.1 |
| MOS | Mean Opinion Score | Section 4.3 |
| WT | Wavelet Transform | Section 3.4 |
| DCT | Discrete Cosine Transform | Section 2.1 |
| LP | Laplacian Pyramid | Section 3.4 |
| DFB | Directional Filter Bank | Section 3.4 |
| NSCT | Non-Subsampled Contourlet Transform | Section 3.4 |
| ST | Shearlet Transform | Section 3.4 |
| TV | Total Variation | Section 3.3 |
Notation and Symbols
| Symbol | Description | Shape and Notes |
| Low-resolution (LR) input image | ||
| High-resolution (HR) ground-truth image | ||
| Generator output (predicted HR) | Same shape as y | |
| Generator network with parameters | / | |
| Discriminator network with parameters | Outputs real/fake score | |
| Trainable parameters of G and D | Vectors/tensors | |
| Upscaling factor | ||
| Ideal/implicit upsampling operator by factor r | Conceptual; not necessarily implemented as naive interpolation | |
| Downsampling operator by factor r | / | |
| Training set of LR–HR pairs | N samples | |
| Number of training samples | / | |
| Mini-batch size | / | |
| True data distribution of HR images | Used in adversarial objective | |
| Model distribution induced by G | / |
References
- Chaudhari, S.; Fang, Z.; Kogan, F.; Wood, J.; Stevens, K.J.; Gibbons, E.K. Super-resolution musculoskeletal MRI using deep learning. Magn. Reson. Med. 2018, 80, 2139–2154. [Google Scholar] [CrossRef]
- Umehara, K.; Ota, J.; Ishida, T. Application of super-resolution convolutional neural network for enhancing image resolution in chest CT. J. Digit. Imaging 2018, 31, 441–450. [Google Scholar] [CrossRef]
- Zhu, J.; Yang, G.; Lio, P. How Can We Make Gan Perform Better in Single Medical Image Super-Resolution? A Lesion Focused Multi-Scale Approach. In Proceedings of the 16th IEEE International Symposium on Biomedical Imaging, Venice, Italy, 8–11 April 2019; pp. 1669–1673. [Google Scholar]
- Dharejo, F.A.; Zawish, M.; Zhou, Y.C.; Dev, K.; Khowaja, S.A.; Qureshi, N.M.F. Multimodal-boost: Multimodal medical image super-resolution using multi-attention network with wavelet transform. IEEE/ACM Trans. Comput. Biol. Bioinform. 2023, 20, 2420–2433. [Google Scholar] [CrossRef] [PubMed]
- Aly, H.; Dubois, E. Regularized image up-sampling using a new observation model and the level set method. In Proceedings of the International Conference on Image Processing, Barcelona, Spain, 14–17 September 2003; pp. III–665. [Google Scholar]
- Aly, H.A.; Dubois, E. Image up-sampling using total-variation regularization with a new observation model. IEEE Trans. Image Process. 2005, 14, 1647–1659. [Google Scholar] [CrossRef] [PubMed]
- Su, C.Y.; Zhuang, Y.T.; Li, H.; Wu, F. Steerable pyramid-based face hallucination. Pattern Recognit. 2025, 38, 813–824. [Google Scholar] [CrossRef]
- Yang, J.C.; Wright, J.; Huang, T.; Ma, Y. Image super-resolution as sparse representation of raw image patches. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Anchorage, AK, USA, 23–28 June 2008; pp. 1–8. [Google Scholar]
- Chan, T.M.; Zhang, J.; Pu, J. Neighbor embedding based super-resolution algorithm through edge detection and feature selection. Pattern Recognit. Lett. 2009, 30, 494–502. [Google Scholar] [CrossRef]
- Yang, J.; Wright, J.; Huang, T.S.; Ma, Y. Image Super-Resolution Via Sparse Representation. IEEE Trans. Image Process. 2010, 19, 2861–2873. [Google Scholar] [CrossRef]
- Zhang, K.; Gao, X.; Tao, D.; Li, X. Single image super-resolution with non-local means and steering kernel regression. IEEE Trans. Image Process 2012, 21, 4544–4556. [Google Scholar] [CrossRef]
- Khizar, H. Multimedia super-resolution via deep learning: A survey. Digit. Signal Process. 2018, 81, 198–217. [Google Scholar] [CrossRef]
- Cheng, B.; Xiao, R.; Wang, J.; Huang, T.; Zhang, L. High frequency residual learning for multi-scale image classification. In Proceedings of the British Machine Vision Conference (BMVC), Cardiff, UK, 9–12 September 2019. [Google Scholar]
- Borji, A.; Cheng, M.-M.; Hou, Q.; Jiang, H.; Li, J. Salient object detection: A survey. Comput. Vis. Media 2019, 5, 117–150. [Google Scholar] [CrossRef]
- Yang, W.; Zhang, X.; Tian, Y.; Wang, W.; Xue, J.-H.; Liao, Q. Deep Learning for Single Image Super-Resolution: A Brief Review. IEEE Trans. Multimed. 2019, 21, 3106–3121. [Google Scholar] [CrossRef]
- Anwar, S.; Khan, S.; Barnes, N. A deep journey into super-resolution: A survey. ACM Comput. Surv. 2021, 53, 1–34. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, J.; Hoi, S.C.H. Deep Learning for Image Super-Resolution: A Survey. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 3365–3387. [Google Scholar] [CrossRef] [PubMed]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Learning a Deep Convolutional Network for Image Super-Resolution. In European Conference on Computer Vision; Springer International Publishing: Cham, Switzerland, 6–12 September 2014; Volume 8692. [Google Scholar]
- Kim, J.; Lee, J.K.; Lee, K.M. Accurate Image Super-Resolution Using Very Deep Convolutional Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1646–1654. [Google Scholar]
- Tai, Y.; Yang, J.; Liu, X.; Xu, C. MemNet: A Persistent Memory Network for Image Restoration. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 4549–4557. [Google Scholar]
- Zhang, Y.; Li, K.; Li, K.; Wang, L.; Zhong, B.; Fu, Y. Image Super-Resolution Using Very Deep Residual Channel Attention Networks. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018; Volume 11211. [Google Scholar]
- Zhang, Y.; Tian, Y.; Kong, Y.; Zhong, B.; Fu, Y. Residual Dense Network for Image Super-Resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 2472–2481. [Google Scholar]
- Hui, Z.; Wang, X.; Gao, X. Fast and Accurate Single Image Super-Resolution via Information Distillation Network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 723–731. [Google Scholar]
- Li, J.C.; Fang, F.M.; Mei, K.F.; Zhang, G.X. Multi-scale residual network for image super-resolution. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 527–542. [Google Scholar]
- Shu, Z.; Cheng, M.; Yang, B.; Su, Z.; He, X. Residual Magnifier: A Dense Information Flow Network for Super Resolution. In Proceedings of the IEEE International Conference on Multimedia and Expo (ICME), Shanghai, China, 8–12 July 2019; pp. 646–651. [Google Scholar]
- Li, Z.; Yang, J.; Liu, Z.; Yang, X.; Jeon, G.; Wu, W. Feedback Network for Image Super-Resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–21 June 2019; pp. 3862–3871. [Google Scholar]
- Du, J.; Wang, M.; Wang, X.; Yang, Z.; Li, X.; Wu, X. Reference-based image super-resolution with attention extraction and pooling of residuals. J. Supercomput. 2024, 81, 240. [Google Scholar] [CrossRef]
- Xie, C.; Zhang, X.; Li, L.; Fu, Y.; Gong, B.; Li, T.; Zhang, K. MAT: Multi-Range Attention Transformer for Efficient Image Super-Resolution. IEEE Trans. Circuits Syst. Video Technol. 2025. [Google Scholar] [CrossRef]
- Pesavento, M.; Volino, M.; Hilton, A. Attention-based Multi-Reference Learning for Image Super-Resolution. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 11–17 October 2021; pp. 14677–14686. [Google Scholar]
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.P.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 105–114. [Google Scholar]
- Wang, X.T.; Yu, K.; Wu, S.; Gu, J.; Liu, Y.; Dong, C.; Qiao, Y.; Loy, C.C. ESRGAN: Enhanced super-resolution generative adversarial networks. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 63–79. [Google Scholar]
- Dou, H.; Chen, C.; Hu, X.; Xuan, Z.; Hu, Z.; Peng, S. PCA-SRGAN: Incremental Orthogonal Projection Discrimination for Face Super-Resolution. In Proceedings of the 28th ACM International Conference on Multimedia (MM), Seattle, WA, USA, 12–16 October 2020; pp. 1891–1899. [Google Scholar]
- Zhang, W.; Liu, Y.; Dong, C.; Qiao, Y. RankSRGAN: Generative Adversarial Networks with Ranker for Image Super-Resolution. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–3 November 2019; pp. 3096–3105. [Google Scholar]
- Maeda, S. Unpaired Image Super-Resolution Using Pseudo-Supervision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; pp. 288–297. [Google Scholar]
- Wang, L.; Kim, T.-K.; Yoon, K.-J. EventSR: From Asynchronous Events to Image Reconstruction, Restoration, and Super-Resolution via End-to-End Adversarial Learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; pp. 8312–8322. [Google Scholar]
- Zhang, K.; Liang, J.; Van Gool, L.; Timofte, R. Designing a Practical Degradation Model for Deep Blind Image Super-Resolution. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 11–17 October 2021; pp. 4771–4780. [Google Scholar]
- Gao, S.; Zhuang, X. Bayesian Image Super-Resolution with Deep Modeling of Image Statistics. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 1405–1423. [Google Scholar] [CrossRef]
- Liu, H.; Li, Z.; Shang, F.; Liu, Y.; Wan, L.; Feng, W.; Timofte, R. Arbitrary-scale Super-resolution via Deep Learning: A Comprehensive Survey. Inf. Fusion 2024, 102, 102015. [Google Scholar] [CrossRef]
- Chen, Y.; Li, J.; Xiao, H.; Jin, X.; Yan, S.; Feng, J. Dual path networks. In Proceedings of the 31st International Conference on Neural Information Processing Systems (NIPS’17), Red Hook, NY, USA, 4–9 December 2017; pp. 4470–4478. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely Connected Convolutional Networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 June 2017; pp. 2261–2269. [Google Scholar]
- Wang, C.; Wang, S.; Ma, B.; Li, J.; Dong, X.; Xia, Z. Transform Domain Based Medical Image Super-resolution via Deep Multi-scale Network. In Proceedings of the ICASSP 2019—2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 2387–2391. [Google Scholar]
- Liu, Y.T.; Guo, Y.C.; Zhang, S.H. Enhancing multi-scale implicit learning in image super-resolution with integrated positional encoding. arXiv 2021, arXiv:2112.05756. [Google Scholar]
- Wang, Y.; Li, Y.; Wang, G.; Liu, X. Multi-scale attention network for single image super-resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 17–21 June 2024; pp. 5950–5960. [Google Scholar]
- Gao, S.-H.; Cheng, M.-M.; Zhao, K.; Zhang, X.-Y.; Yang, M.-H.; Torr, P. Res2Net: A New Multi-Scale Backbone Architecture. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 652–662. [Google Scholar] [CrossRef]
- Guo, T.; Mousavi, H.S.; Vu, T.H.; Monga, V. Deep Wavelet Prediction for Image Super-Resolution. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Honolulu, HI, USA, 22–25 July 2017; pp. 1100–1109. [Google Scholar]
- Li, W.; Guo, H.; Liu, X.; Liang, K.; Hu, J.; Ma, Z.; Guo, J. Efficient Face Super-Resolution via Wavelet-based Feature Enhancement Network. In Proceedings of the 32nd ACM International Conference on Multimedia (MM ’24), New York, NY, USA, 28 October–1 November 2024; pp. 4515–4523. [Google Scholar]
- Angarano, S.; Salvetti, F.; Martini, M.; Chiaberge, M. Generative Adversarial Super-Resolution at the edge with knowledge distillation. Eng. Appl. Artif. Intell. 2023, 123, 106407. [Google Scholar] [CrossRef]
- Xiao, H.; Wang, X.; Wang, J.; Cai, J.-Y.; Deng, J.-H.; Yan, J.-K.; Tang, Y.-D. Single image super-resolution with denoising diffusion GANS. Sci. Rep. 2024, 14, 4272. [Google Scholar] [CrossRef]
- Aloisi, L.; Sigillo, L.; Uncini, A.; Comminiello, D. A wavelet diffusion GAN for image super-resolution. arXiv 2024, arXiv:2410.17966. [Google Scholar] [CrossRef]
- Park, S.H.; Moon, Y.S.; Cho, N.I. Perception-Oriented Single Image Super-Resolution using Optimal Objective Estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 18–22 June 2023; pp. 1725–1735. [Google Scholar]
- Duan, M.; Qu, L.; Liu, S.; Wang, M. Local Implicit Wavelet Transformer for Arbitrary-Scale Super-Resolution. arXiv 2024, arXiv:2411.06442. [Google Scholar] [CrossRef]
- Shrisha, H.S.; Anupama, V. NVS-GAN: Benefit of Generative Adversarial Network on Novel View Synthesis. Int. J. Intell. Netw. 2024, 5, 184–195. [Google Scholar] [CrossRef]
- Huang, Y.; Shao, L.; Frangi, A.F. DOTE: Dual cOnvolutional filTer lEarning for Super-Resolution and Cross-Modality Synthesis in MRI. In Medical Image Computing and Computer Assisted Intervention—MICCAI; 2017 Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2017; pp. 89–98. [Google Scholar]
- Huang, Y.; Shao, L.; Frangi, A.F. Simultaneous Super-Resolution and Cross-Modality Synthesis of 3D Medical Images Using Weakly-Supervised Joint Convolutional Sparse Coding. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 5787–5796. [Google Scholar]
- Iwamoto, Y.; Takeda, K.; Li, Y.; Shiino, A.; Chen, Y.-W. Unsupervised MRI Super Resolution Using Deep External Learning and Guided Residual Dense Network with Multimodal Image Priors. IEEE Trans. Emerg. Top. Comput. Intell. 2023, 7, 426–435. [Google Scholar] [CrossRef]
- Pan, B.; Du, Y.; Guo, X. Super-Resolution Reconstruction of Cell Images Based on Generative Adversarial Networks. IEEE Access 2024, 12, 72252–72263. [Google Scholar] [CrossRef]
- Nimitha, U.; Ameer, P.M. MRI super-resolution using similarity distance and multi-scale receptive field based feature fusion GAN and pre-trained slice interpolation network. Magn. Reson. Imaging 2024, 110, 195–209. [Google Scholar]
- Liu, L.; Liu, T.; Zhou, W.; Wang, Y.; Liu, M. MAPANet: A Multi-Scale Attention-Guided Progressive Aggregation Network for Multi-Contrast MRI Super-Resolution. IEEE Trans. Comput. Imaging 2024, 10, 928–940. [Google Scholar] [CrossRef]
- Wei, J.; Yang, G.; Wang, Z.; Liu, Y.; Liu, A.; Chen, X. Misalignment-Resistant Deep Unfolding Network for multi-modal MRI super-resolution and reconstruction. Knowl.-Based Syst. 2024, 296, 111866. [Google Scholar] [CrossRef]
- Ji, Z.; Zou, B.; Kui, X.; Vera, P.; Ruan, S. Deform-Mamba Network for MRI Super-Resolution. In Medical Image Computing and Computer Assisted Intervention–MICCAI; Springer Nature: Cham, Switzerland, 6–10 October 2024; pp. 242–252. [Google Scholar]
- Shi, W.; Caballero, J.; Huszár, F.; Totz, J.; Aitken, A.P.; Bishop, R.; Rueckert, D.; Wang, Z. Real-Time Single Image and Video Super-Resolution Using an Efficient Sub-Pixel Convolutional Neural Network. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1874–1883. [Google Scholar]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Proceedings of the 28th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; Volume 2, pp. 2672–2680. [Google Scholar]
- Glorot, X.; Bordes, A.; Bengio, Y. Deep sparse rectifier neural networks. In Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics, Fort Lauderdale, FL, USA, 11–13 April 2011; pp. 315–323. [Google Scholar]
- Johnson, J.; Alahi, A.; Li, F. Perceptual losses for real-time style transfer and super-resolution. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; Springer International Publishing: Cham, Switzerland, 2016; pp. 694–711. [Google Scholar]
- Karen, S.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Lee, K.M. Enhanced Deep Residual Networks for Single Image Super-Resolution. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Honolulu, HI, USA, 22–25 July 2017; pp. 1132–1140. [Google Scholar]
- Mallat, S. A Wavelet Tour of Signal Processing. In The Sparse Way, 3rd ed.; Academic Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Candès, E.J.; Donoho, D.L. New tight frames of curvelets and optimal representations of objects with piecewise C2 singularities. Commun. Pure Appl. Math. 2004, 57, 219–266. [Google Scholar] [CrossRef]
- Do, M.N.; Vetterli, M. The contourlet transform: An efficient directional multiresolution image representation. IEEE Trans. Image Process. 2005, 14, 2091–2106. [Google Scholar] [CrossRef] [PubMed]
- Da Cunha, A.L.; Zhou, J.; Do, M.N. The Nonsubsampled Contourlet Transform: Theory, Design, and Applications. IEEE Trans. Image Process. 2006, 15, 3089–3101. [Google Scholar] [CrossRef] [PubMed]
- Labate, D.; Lim, W.Q.; Kutyniok, G.; Weiss, G. Sparse multidimensional representation using shearlets. In Optics and Photonics; SPIE: San Diego, CA, USA, 2005; pp. 254–262. [Google Scholar]
- Hou, B.; Zhang, X.; Bu, X.; Feng, H. SAR Image Despeckling Based on Nonsubsampled Shearlet Transform. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 809–823. [Google Scholar] [CrossRef]
- Zhang, K.; Van Gool, L.; Timofte, R. Deep Unfolding Network for Image Super-Resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; pp. 3214–3223. [Google Scholar]
- Horé, A.; Ziou, D. Image Quality Metrics: PSNR vs. SSIM. In Proceedings of the 20th International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; pp. 2366–2369. [Google Scholar]
- Zhang, J.; Long, C.; Wang, Y.; Piao, H.; Mei, H.; Yang, X.; Yin, B. A Two-Stage Attentive Network for Single Image Super-Resolution. IEEE Trans. Circuits Syst. Video Technol. 2022, 32, 1020–1033. [Google Scholar] [CrossRef]








| Datasets | Scale | Bicubic | DWSR [45] | IDN [23] | MSRN [24] | RCAN [21] | DMSN [41] | USRNET [73] | TSAN [75] | Diff-GAN [48] | MapaNet [58] | MAT [28] | Ours (with MSID) | Ours (with GMS) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Abdomen | 4 | 27.902 | 29.934 | 30.341 | 30.407 | 30.673 | 30.523 | 30.696 | 30.913 | 30.927 | 31.051 | 31.338 | 31.654 | 32.186 |
| 8 | 24.694 | 26.095 | 26.199 | 26.325 | 26.900 | 26.591 | 26.964 | 27.217 | 27.436 | 27.514 | 27.911 | 28.134 | 28.625 | |
| Bone | 4 | 26.414 | 28.451 | 28.555 | 28.631 | 28.822 | 28.685 | 28.863 | 28.995 | 29.073 | 29.231 | 29.352 | 29.877 | 30.175 |
| 8 | 24.478 | 25.759 | 25.790 | 25.956 | 26.165 | 26.031 | 26.204 | 26.297 | 26.220 | 26.319 | 26.431 | 26.962 | 27.224 | |
| Brain | 4 | 26.517 | 28.268 | 28.454 | 28.841 | 29.374 | 28.964 | 29.443 | 29.570 | 29.773 | 29.816 | 30.029 | 30.582 | 30.838 |
| 8 | 22.338 | 23.926 | 24.184 | 24.317 | 24.952 | 24.733 | 24.957 | 25.016 | 24.958 | 25.326 | 25.634 | 25.851 | 26.413 | |
| Lung | 4 | 27.338 | 29.196 | 29.323 | 29.455 | 30.356 | 29.958 | 30.506 | 30.693 | 30.718 | 30.936 | 30.942 | 31.314 | 31.793 |
| 8 | 23.795 | 25.027 | 25.231 | 25.402 | 25.744 | 25.685 | 25.831 | 25.948 | 25.943 | 26.164 | 26.232 | 26.696 | 27.088 |
| Datasets | Scale | Bicubic | DWSR [45] | IDN [23] | MSRN [24] | RCAN [21] | DMSN [41] | USRNET [73] | TSAN [75] | Diff-GAN [48] | MapaNet [58] | MAT [28] | Ours (with MSID) | Ours (with GMS) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Abdomen | 4 | 0.796 | 0.852 | 0.856 | 0.857 | 0.860 | 0.858 | 0.861 | 0.863 | 0.863 | 0.865 | 0.867 | 0.870 | 0.875 |
| 8 | 0.673 | 0.717 | 0.722 | 0.728 | 0.740 | 0.730 | 0.741 | 0.743 | 0.745 | 0.746 | 0.749 | 0.751 | 0.757 | |
| Bone | 4 | 0.427 | 0.644 | 0.649 | 0.662 | 0.666 | 0.661 | 0.669 | 0.670 | 0.671 | 0.673 | 0.674 | 0.678 | 0.681 |
| 8 | 0.342 | 0.368 | 0.372 | 0.377 | 0.381 | 0.380 | 0.382 | 0.384 | 0.383 | 0.384 | 0.385 | 0.389 | 0.392 | |
| Brain | 4 | 0.831 | 0.865 | 0.868 | 0.872 | 0.880 | 0.875 | 0.883 | 0.884 | 0.886 | 0.886 | 0.889 | 0.894 | 0.896 |
| 8 | 0.704 | 0.755 | 0.759 | 0.763 | 0.776 | 0.764 | 0.780 | 0.785 | 0.784 | 0.788 | 0.790 | 0.792 | 0.798 | |
| Lung | 4 | 0.895 | 0.869 | 0.871 | 0.874 | 0.881 | 0.879 | 0.884 | 0.888 | 0.889 | 0.891 | 0.891 | 0.895 | 0.899 |
| 8 | 0.739 | 0.779 | 0.783 | 0.786 | 0.795 | 0.791 | 0.798 | 0.802 | 0.802 | 0.804 | 0.805 | 0.810 | 0.814 |
| Methods | Number of Evaluation Images (120 in Total) | MOS (Mean and Standard Deviation) | |||
|---|---|---|---|---|---|
| 1 (Poor) | 2 (Fair) | 3 (Good) | 4 (Very Good) | ||
| Bicubic | 94 | 26 | 0 | 0 | 1.22 ± 0.5932 |
| DWSR [45] | 16 | 42 | 58 | 4 | 2.42 ± 0.8457 |
| MSRN [24] | 9 | 34 | 70 | 7 | 2.63 ± 0.8514 |
| RCAN [21] | 9 | 31 | 73 | 7 | 2.65 ± 0.8433 |
| TSAN [75] | 7 | 30 | 75 | 8 | 3.70 ± 0.8526 |
| MAT [28] | 4 | 20 | 88 | 8 | 2.83 ± 0.7656 |
| Ours (with MSID) | 1 | 14 | 93 | 12 | 2.97 ± 0.7430 |
| Ours (with GMS) | 1 | 4 | 101 | 14 | 3.07 ± 0.7146 |
| Number of MSID Blocks | 2 | 4 | 6 | 8 | 10 | 12 |
|---|---|---|---|---|---|---|
| Average PSNR value | 26.983 | 27.136 | 27.351 | 27.465 | 27.568 | 27.583 |
| High-Frequency Level of NSST Decomposition | Body Part | |||
|---|---|---|---|---|
| Abdomen | Bone | Brain | Lung | |
| (The number of decomposition directions is 2 and 4, respectively) 2 levels | 27.284 | 26.751 | 25.419 | 26.273 |
| (The number of decomposition directions is 4 and 8, respectively) 3 levels | 27.634 | 26.762 | 25.435 | 26.296 |
| (The number of decomposition directions are 2, 4, and 8, respectively) 4 levels | 27.288 | 26.764 | 25.438 | 26.297 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Wei, Q.; Sang, Y. Transform Domain Based GAN with Deep Multi-Scale Features Fusion for Medical Image Super-Resolution. Electronics 2025, 14, 3726. https://doi.org/10.3390/electronics14183726
Yang H, Wei Q, Sang Y. Transform Domain Based GAN with Deep Multi-Scale Features Fusion for Medical Image Super-Resolution. Electronics. 2025; 14(18):3726. https://doi.org/10.3390/electronics14183726
Chicago/Turabian StyleYang, Huayong, Qingsong Wei, and Yu Sang. 2025. "Transform Domain Based GAN with Deep Multi-Scale Features Fusion for Medical Image Super-Resolution" Electronics 14, no. 18: 3726. https://doi.org/10.3390/electronics14183726
APA StyleYang, H., Wei, Q., & Sang, Y. (2025). Transform Domain Based GAN with Deep Multi-Scale Features Fusion for Medical Image Super-Resolution. Electronics, 14(18), 3726. https://doi.org/10.3390/electronics14183726





