State-Space Modelling of Schottky Diode Rectifiers Including Parasitic and Coupling Effects up to the Terahertz Band
Abstract
1. Introduction
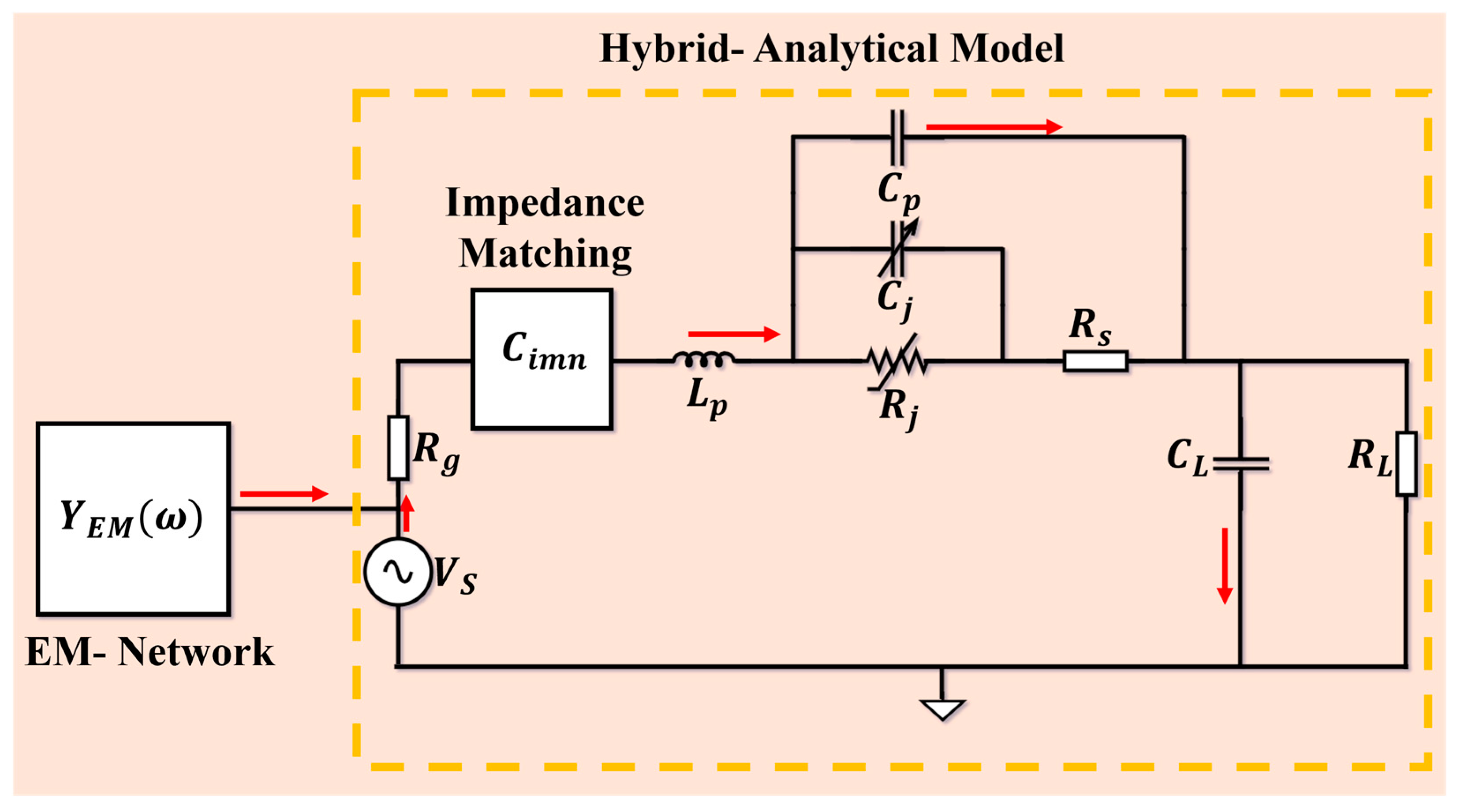
2. Hybrid Analytical-Electromagnetic Modelling of Schottky Rectifiers
2.1. Assumption and Diode Modelling
- PEC surfaces: Neglecting conductor losses may slightly overestimate RF–DC conversion efficiency; however, high-conductivity metals and the 5.8 GHz operating frequency ensure minimal error.
- Frequency-independent material properties: Ignoring dispersion and dielectric loss variation introduces minor deviations at high frequencies; within the tested narrowband range, the impact on predictive accuracy is negligible.
- Neglect of spatial thermal gradients: At the low-input power considered (−10 dBm), self-heating is minimal, so assuming uniform junction temperature is reasonable.
- Ideal filters and resistive load: These assumptions simplify the analysis and limit the model to narrowband operation; practical design implications are discussed in the validation section.
- Linearization for sensitivity analysis: Applied only for stability and does not affect primary transient or steady-state predictions.
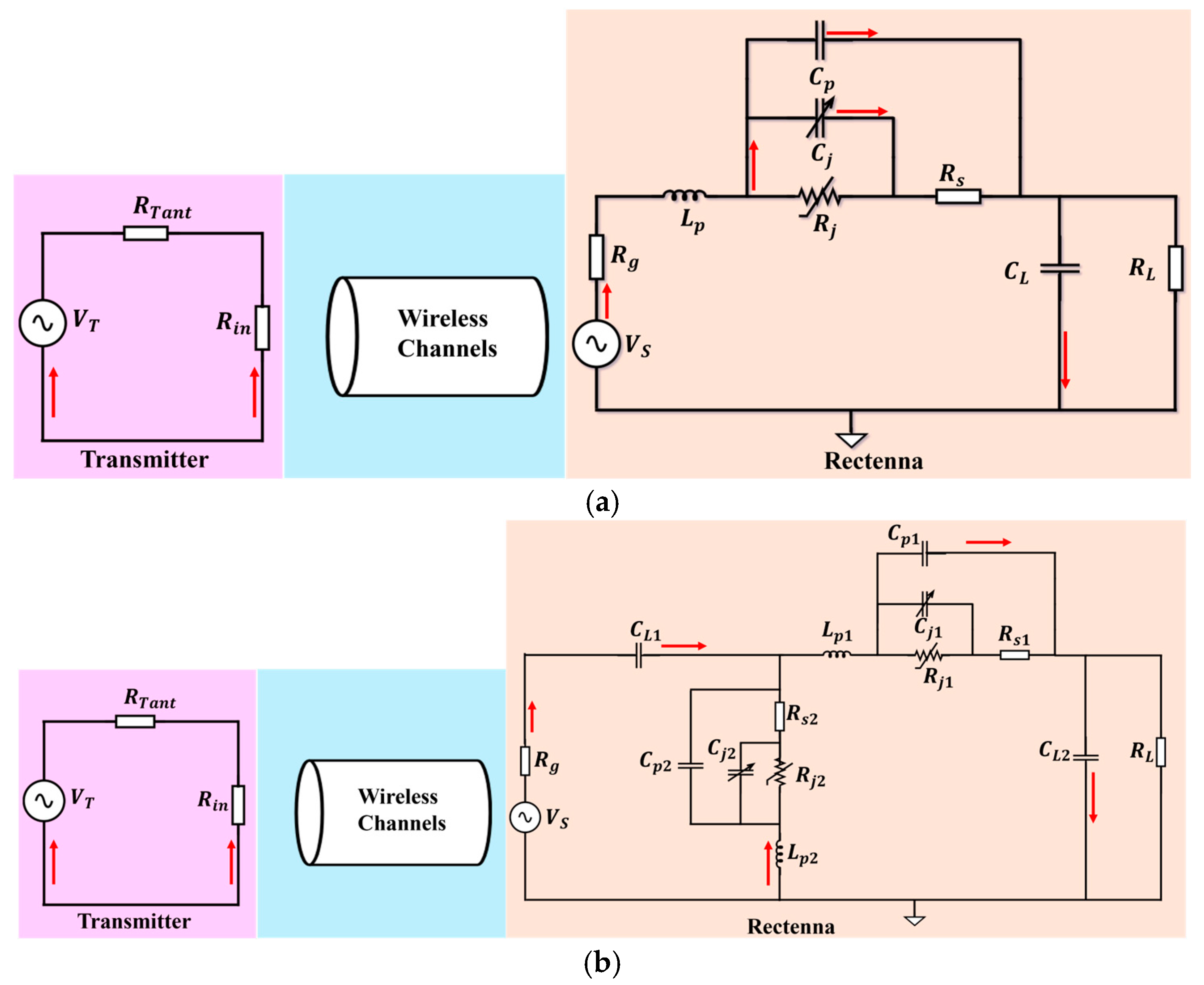
2.2. Half-Wave Rectifier: Nonlinear Circuit with Electromagnetic Embedding
2.3. Electromagnetic Coupling and Port Reduction
2.4. Derivation of the Coupling Operators
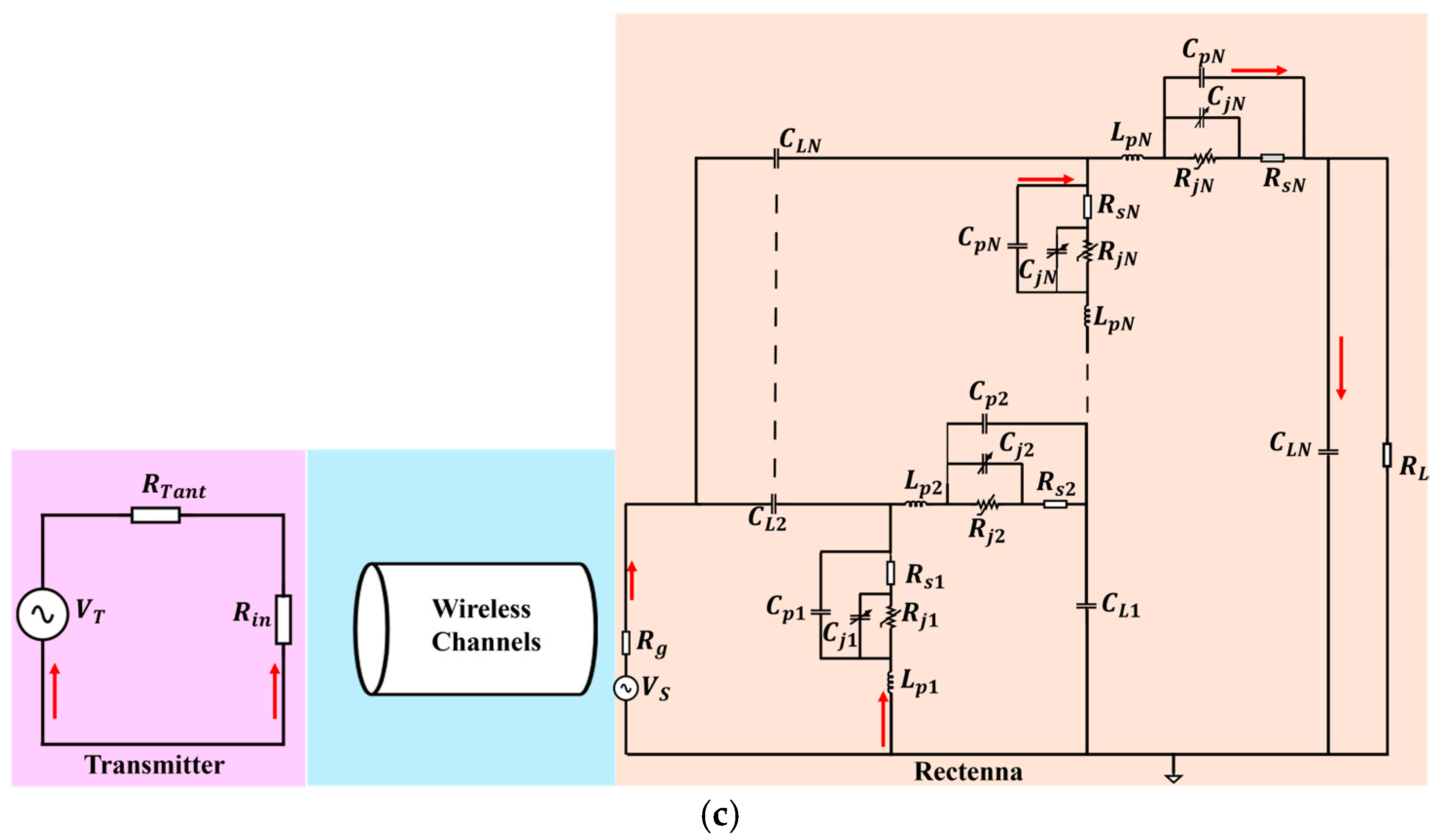
2.5. Voltage Doubler and n-Stage Multipliers
2.6. Hybrid PDE–ODE State-Space Form
2.7. Transient Stability and Settling Time
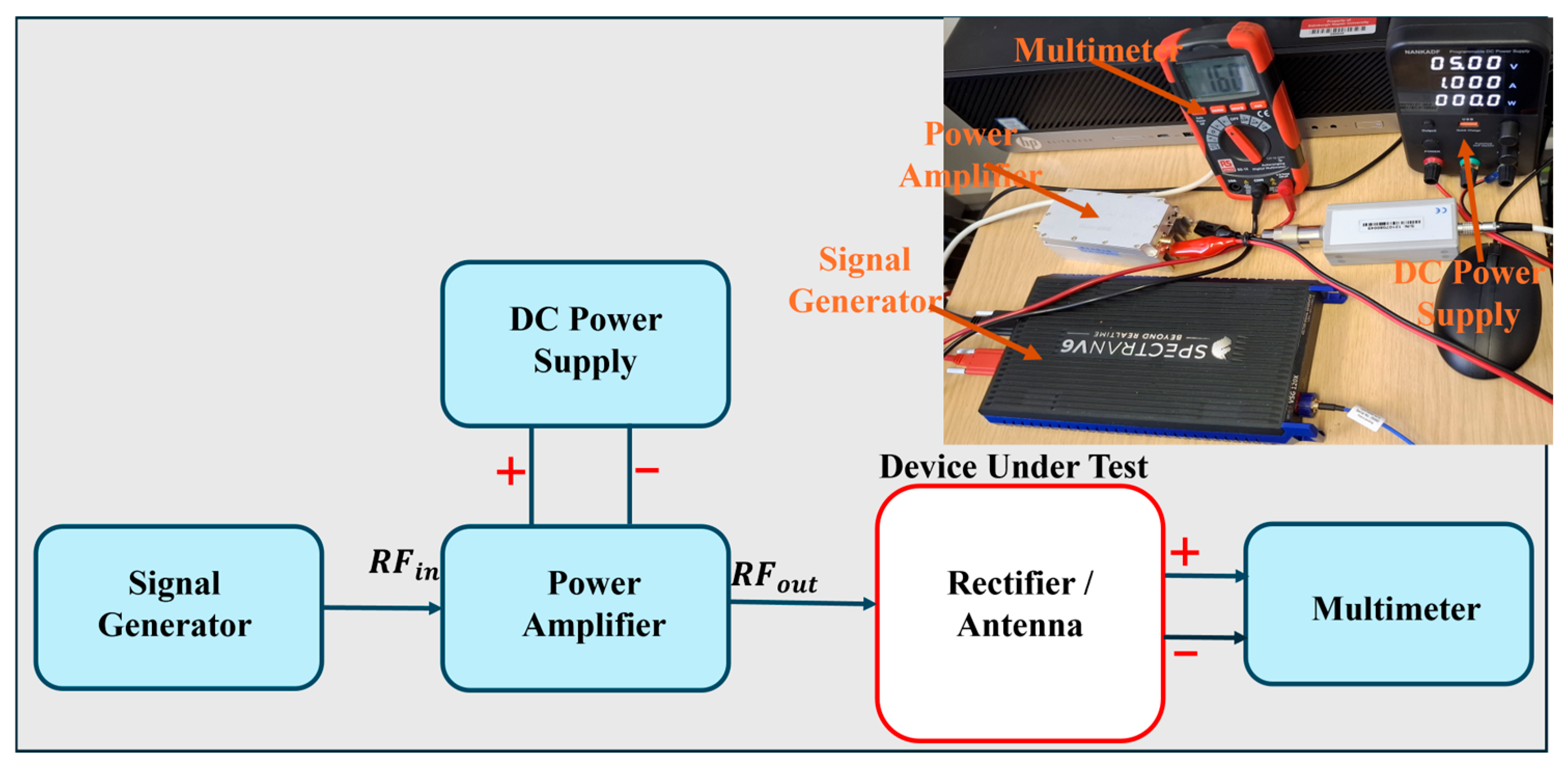
3. Experimental and Computational Validation
3.1. Comparison with Existing Models and Fabrication of 5.8 GHz Schottky Rectifier
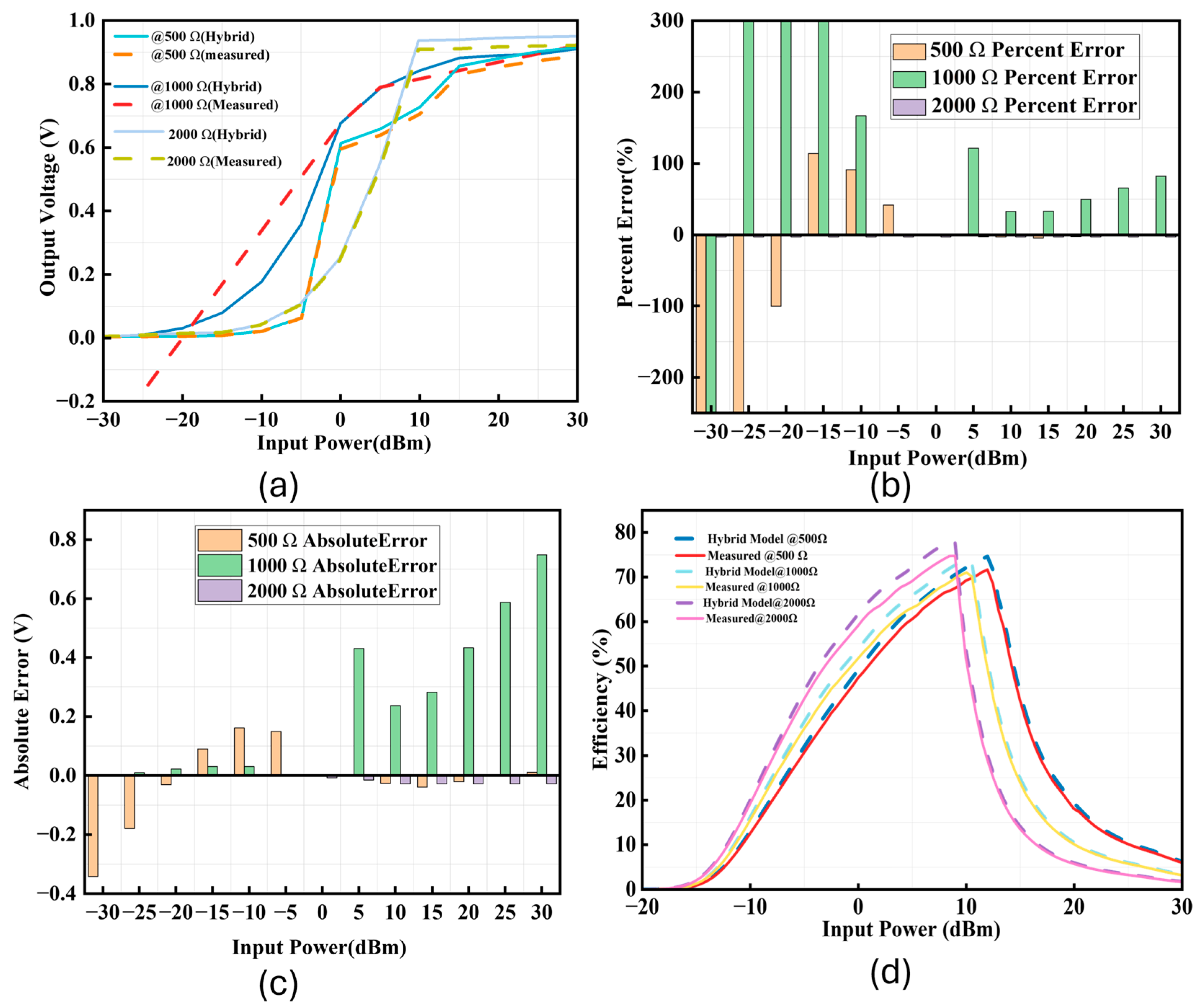
3.2. Model to Measurement Validation
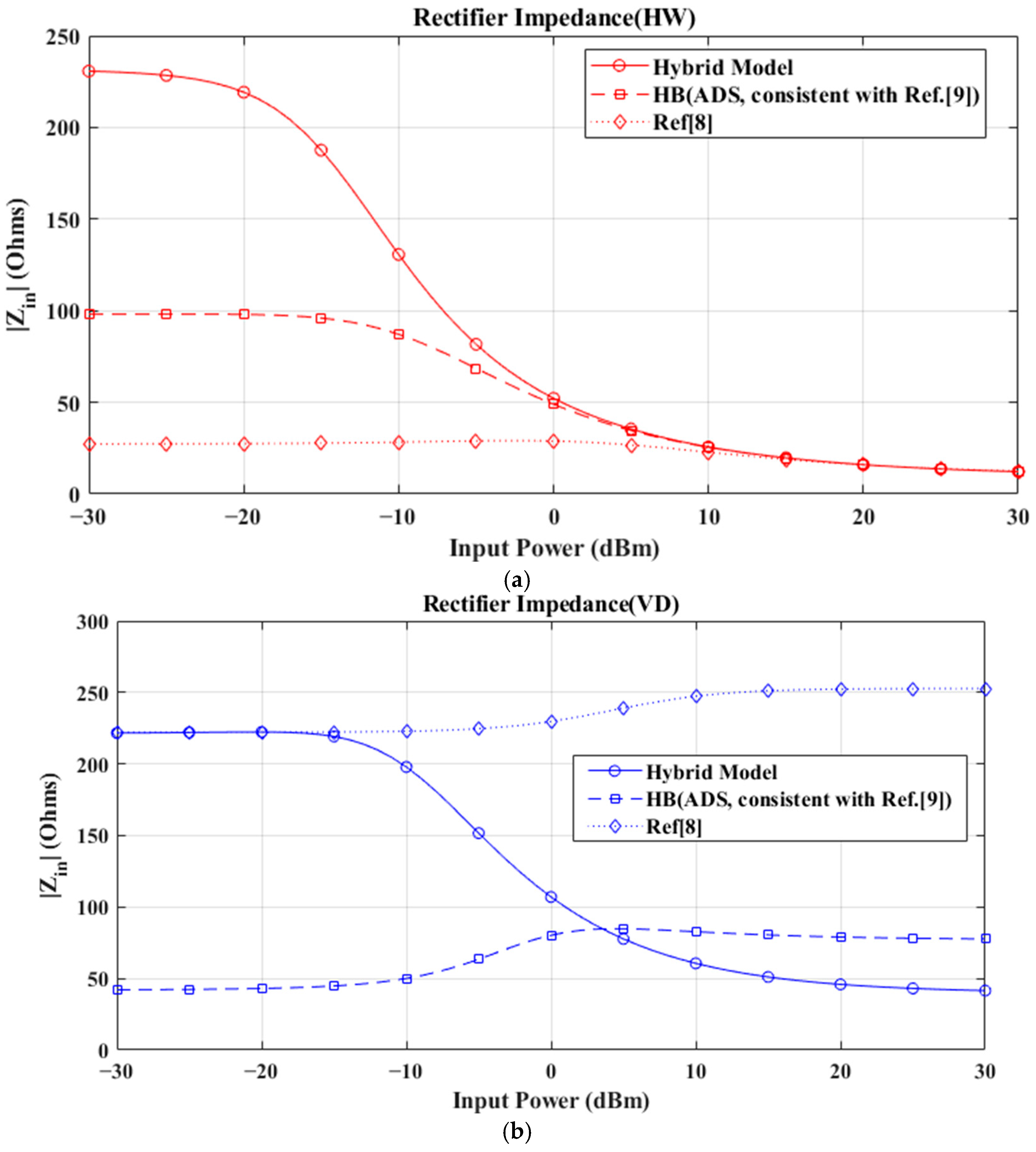
3.3. Benchmarking Against ADS and Harmonic Balance
3.4. Computational Cost and Convergence
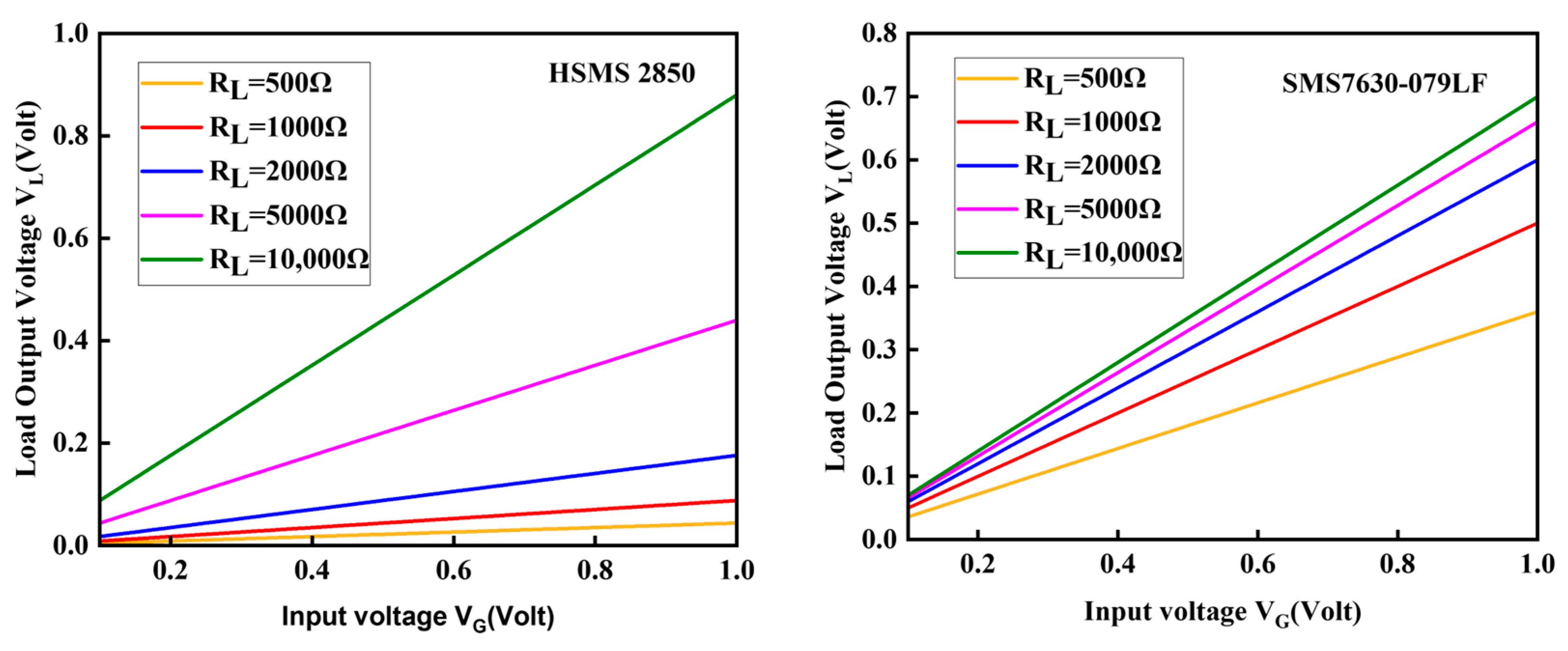
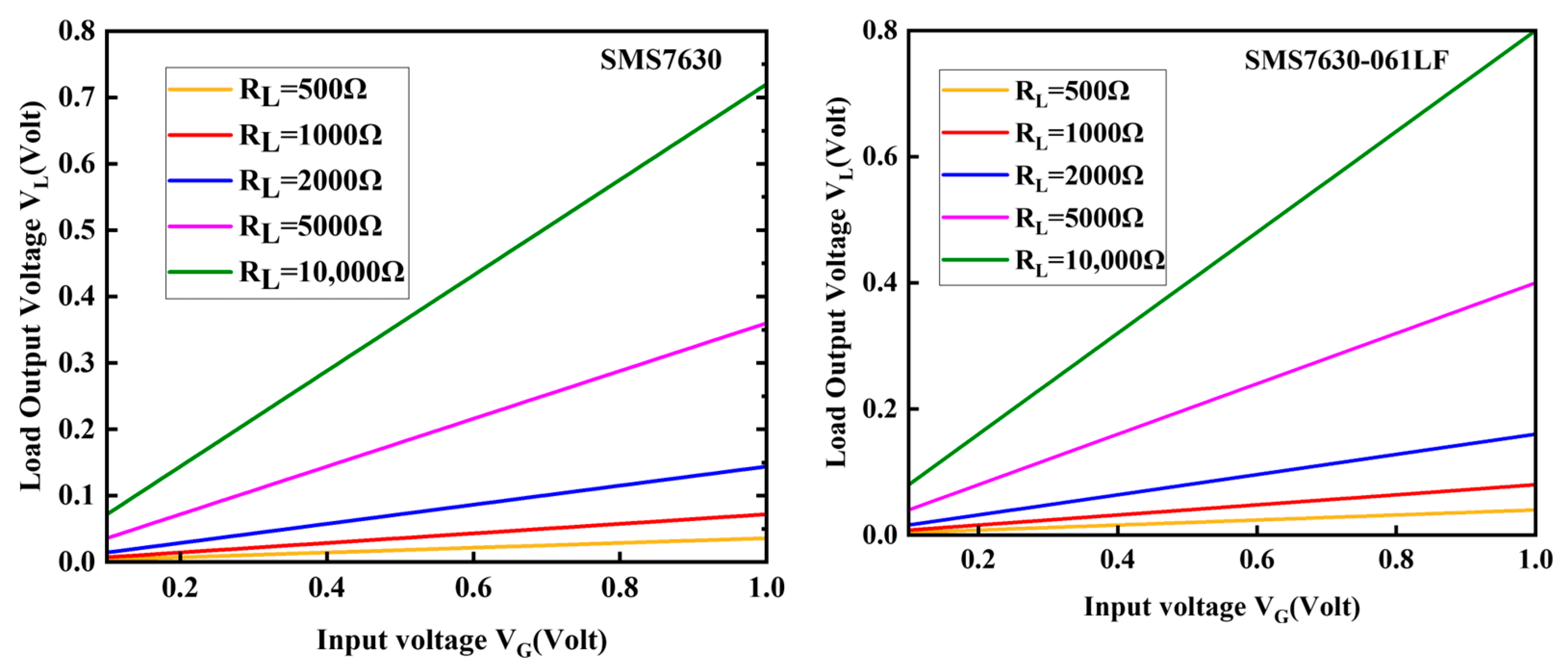
3.5. Frequency, Load, and Diode Scaling
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, X.; Guan, J. PI Parameters Tuning for Frequency Tracking Control of Wireless Power Transfer System Based on Improved Whale Optimization Algorithm. IEEE Access 2024, 12, 13055–13069. [Google Scholar] [CrossRef]
- Cheng, F.; Wang, H.-Y.; Ni, W.; Chen, X.; Yang, Y.; Huang, K. Single-Layer Rectenna Array with Integrated Matching Circuit for Wireless Power Transfer. IEEE Trans. Antennas Propag. 2025, 73, 4466–4475. [Google Scholar] [CrossRef]
- Odiamenhi, M.; Basherlou, H.J.; See, C.H.; Parchin, N.O.; Goh, K.; Yu, H. Advancements and Challenges in Antenna Design and Rectifying Circuits for Radio Frequency Energy Harvesting. Sensors 2024, 24, 6804. [Google Scholar] [CrossRef]
- Almoneef, T.S. Design of a Rectenna Array without a Matching Network. IEEE Access 2020, 8, 109071–109079. [Google Scholar] [CrossRef]
- He, Z.; Lan, J.; Liu, C. Compact Rectifiers with Ultra-wide Input Power Range Based on Nonlinear Impedance Characteristics of Schottky Diodes. IEEE Trans. Power Electron. 2021, 36, 7407–7411. [Google Scholar] [CrossRef]
- Li, Q.-X.; Li, Y.; Liu, T.; Huang, R.-P.; Zhu, X.; Liu, P.-B.; Wang, X.; Chen, Z.-W.; You, J.; Liu, Z.-C.; et al. Design and Fabrication of Milliwatt and Microwatt Microwave Rectifiers Based on Low Turn-On GaN Schottky Barrier Diodes. IEEE Microw. Wirel. Technol. Lett. 2025, 35, 444–447. [Google Scholar] [CrossRef]
- Ou, J.-H.; Zheng, S.Y.; Andrenko, A.S.; Li, Y.; Tan, H.-Z. Novel Time-Domain Schottky Diode Modeling for Microwave Rectifier Designs. IEEE Trans. Circuits Syst. I Regul. Pap. 2018, 65, 1234–1244. [Google Scholar] [CrossRef]
- Yao, L.; Dolmans, G.; Romme, J. Accurate and Efficient Time-Domain Model for Generic Wireless Power Rectennas. IEEE Sens. J. 2025, 25, 17384–17394. [Google Scholar] [CrossRef]
- Zbitou, J.; Latrach, M.; Toutain, S. Hybrid rectenna and monolithic integrated zero-bias microwave rectifier. IEEE Trans. Microw. Theory Tech. 2006, 54, 147–152. [Google Scholar] [CrossRef]
- Reddaf, A.; Boudjerda, M.; Bouchachi, I.; Babes, B.; Elrashidi, A.; AboRas, K.M.; Ali, E.; Ghoneim, S.S.; Elsisi, M. Modeling of Schottky diode and optimal matching circuit design for low power RF energy harvesting. Heliyon 2024, 10, e27792. [Google Scholar] [CrossRef] [PubMed]
- Hansen, J.; Chang, K. Diode modeling for rectenna design. In Proceedings of the 2011 IEEE International Symposium on Antennas and Propagation (APSURSI), Spokane, WA, USA, 3–8 July 2011; IEEE Access: Piscataway, NJ, USA, 2011; pp. 1077–1080. [Google Scholar] [CrossRef]
- Takhedmit, H.; Cirio, L.; Picon, O.; Luk, J.D.L.S. An accurate linear electrical model applied to a series and parallel 2.45 GHz dual-diode rectenna array. In Proceedings of the 2012 6th European Conference on Antennas and Propagation (EUCAP), Prague, Czech Republic, 26–30 March 2012; IEEE Access: Piscataway, NJ, USA, 2012; pp. 2510–2513. [Google Scholar] [CrossRef]
- Pan, Y.; Wang, K.; Pan, C.; Zhu, H.; Wang, J. Self-Sustainable Reconfigurable Intelligent Surface Aided Simultaneous Terahertz Information and Power Transfer (STIPT). IEEE Trans. Wirel. Commun. 2022, 21, 5420–5434. [Google Scholar] [CrossRef]
- Pauu, K.T.; Wu, J.; Bashir, A.K. TeraPRI: Homomorphic Terahertz-Empowered Joint Wireless Power and Information Transfer with Privacy-Preserving for 6G-Autonomous Vehicles. IEEE Trans. Consum. Electron. 2025, 71, 6201–6214. [Google Scholar] [CrossRef]
- Yee, K. Numerical solution of initial boundary value problems involving maxwell’s equations in isotropic media. IEEE Trans. Antennas Propag. 1966, 14, 302–307. [Google Scholar] [CrossRef]
- Johnson, S.G.; Ibanescu, M.; Skorobogatiy, M.A.; Weisberg, O.; Joannopoulos, J.D.; Fink, Y. Perturbation theory for Maxwell’s equations with shifting material boundaries. Phys. Rev. E 2002, 65, 066611. [Google Scholar] [CrossRef] [PubMed]
- Marti, J. Accurate Modelling of Frequency-Dependent Transmission Lines in Electromagnetic Transient Simulations. IEEE Trans. Power Appar. Syst. 1982, PAS-101, 147–157. [Google Scholar] [CrossRef]
- Ni, X.; Luan, H.; Kim, J.-T.; Rogge, S.I.; Bai, Y.; Kwak, J.W.; Liu, S.; Yang, D.S.; Li, S.; Li, S.; et al. Soft shape-programmable surfaces by fast electromagnetic actuation of liquid metal networks. Nat. Commun. 2022, 13, 5576. [Google Scholar] [CrossRef]
- García-Luque, A.; Mata-Contreras, F.J.; Martín-Guerrero, T.M. Analysis, Formulation, and Implementation of a Nonlinear Equivalent Circuit for High-Frequency Semiconductor Diodes. IEEE Microw. Mag. 2025, 26, 25–41. [Google Scholar] [CrossRef]
- Fan, L.; Knott, A.; Jorgensen, I.H.H. Nonlinear Parasitic Capacitance Modelling of High Voltage Power MOSFETs in Partial SOI Process. Elektron. Elektrotech. 2016, 22, 37–43. [Google Scholar] [CrossRef]
- Perez-Moreno, C.G.; Grajal, J. Physical Electro-Thermal Model for the Design of Schottky Diode-Based Circuits. IEEE Trans. Terahertz Sci. Technol. 2014, 4, 597–604. [Google Scholar] [CrossRef]




| Model | Key Assumption | (dBm) | Freq (GHz) | Diode/Topology | PCE (%) | Difference zvs Hybrid (%) | R |
|---|---|---|---|---|---|---|---|
| Time Domain | Ignores reverse current and packaging effect | 8.4 | 5.8 | BAT15-03W/shunt | 69.4 | –7.4 | [7] |
| Time Domain | Neglects reverse current and EM–VI coupling | 10 | 2.45 | HSMS2860/series | 35 | +27 | [8] |
| Frequency Domain | No reverse current; EM–VI coupling; no packaging effect | 10 | 2.45 | HSMS2820/voltage doubler | 62 | 0 | [9] |
| Frequency Domain | No reverse current; EM–VI coupling; no packaging effect | 12 | 2.45 | HSMS2850/series | 48 | +14 | [10] |
| Hybrid State Space | Includes reverse current, packaging effects, and EM–VI coupling | −10 | 5.8 | SMS7630/series | 62 | 0 | This work |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Odiamenhi, M.A.; Basherlou, H.J.; See, C.H.; Parchin, N.O.; Goh, K.; Yu, H. State-Space Modelling of Schottky Diode Rectifiers Including Parasitic and Coupling Effects up to the Terahertz Band. Electronics 2025, 14, 3718. https://doi.org/10.3390/electronics14183718
Odiamenhi MA, Basherlou HJ, See CH, Parchin NO, Goh K, Yu H. State-Space Modelling of Schottky Diode Rectifiers Including Parasitic and Coupling Effects up to the Terahertz Band. Electronics. 2025; 14(18):3718. https://doi.org/10.3390/electronics14183718
Chicago/Turabian StyleOdiamenhi, Martins Aizanabor, Haleh Jahanbakhsh Basherlou, Chan Hwang See, Naser Ojaroudi Parchin, Keng Goh, and Hongnian Yu. 2025. "State-Space Modelling of Schottky Diode Rectifiers Including Parasitic and Coupling Effects up to the Terahertz Band" Electronics 14, no. 18: 3718. https://doi.org/10.3390/electronics14183718
APA StyleOdiamenhi, M. A., Basherlou, H. J., See, C. H., Parchin, N. O., Goh, K., & Yu, H. (2025). State-Space Modelling of Schottky Diode Rectifiers Including Parasitic and Coupling Effects up to the Terahertz Band. Electronics, 14(18), 3718. https://doi.org/10.3390/electronics14183718










