A Novel Optimised Feature Selection Method for In-Session Dropout Prediction Using Hybrid Meta-Heuristics and Multi-Level Stacked Ensemble Learning
Abstract
1. Introduction
1.1. The Contribution
- ▪
- Accuracy improvement: feature selection optimisation ensures that only the most optimal features are used, leading to more accurate dropout predictions.
- ▪
- Data Imbalance Reduction: GA-CFS feature selection helps to address class imbalance and ensuring that the model performs well even when dropout rates are unevenly distributed.
- ▪
- Improved interpretability: Feature optimisation simplifies the model by reducing the number of input variables, making it more predictive when applied to different learning scenarios.
1.2. Paper Organisation
2. Literature Review
- ▪
- Feature Selection Optimisation: The GA with CFS is able to find the most related and non-redundant subset of features from the dataset. By reducing noise and redundancy, this phase ensures that the predictive models are trained on useful, high-quality data.
- ▪
- Multi-Level Stacked Ensemble Learning: the use of base learners such as AdaBoost, RF, XGBoost, and GBC techniques able to build an efficient stacked ensemble model. The results output from the base learners is passed to MLP acting as the meta-learner. Predictive accuracy and generalisation are improved by this hierarchical method, especially in datasets that are balanced.
3. Problem Identification
- ▪
- Objective 1. Avoid class Imbalance and Complexity
- ▪
- Objective 2. Optimising Feature Selection
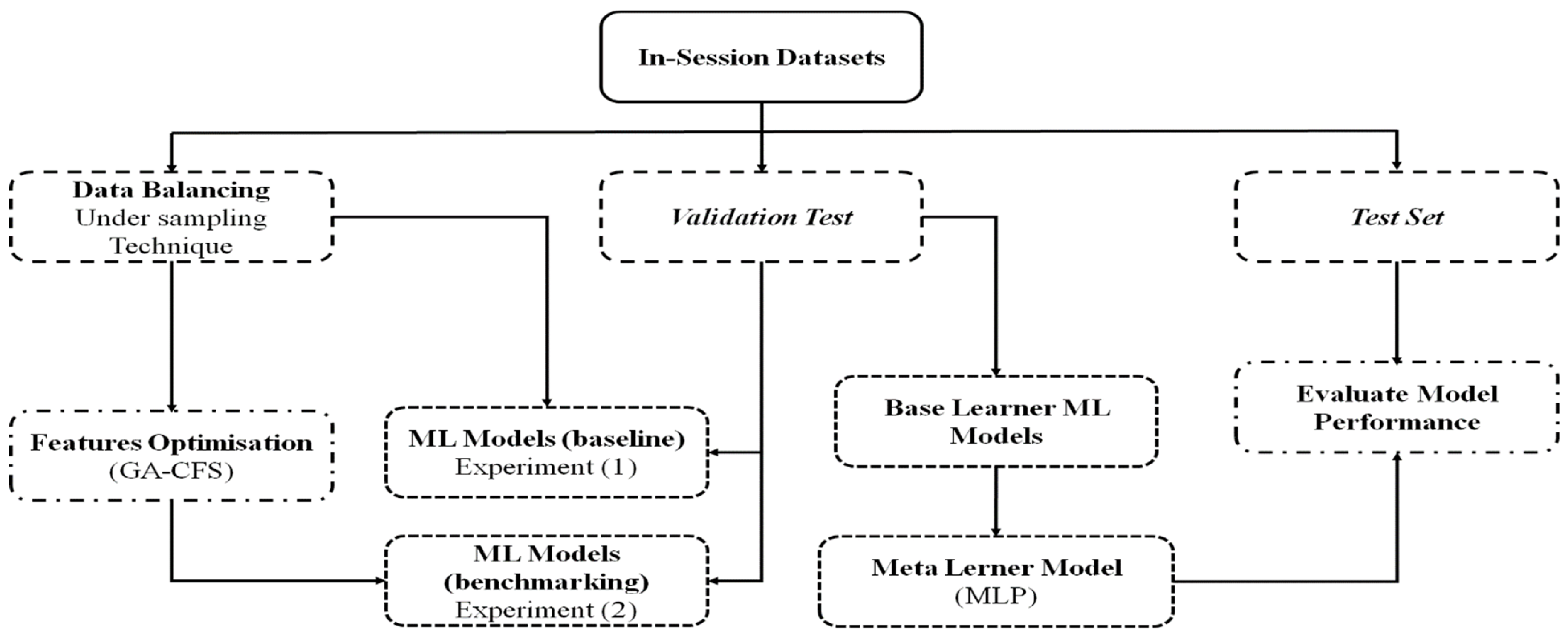
4. The Methodology
- ▪
- HP 1: Optimised feature selection increases the dropout prediction accuracy.
- ▪
- HP 2: ML Models as base learners
- ▪
- HP 3: Stacked Ensemble models will increase the prediction accuracy compared to individual models.
4.1. Data Collection
4.2. Feature Engineering and Preprocessing
4.2.1. Numerical Features
4.2.2. Binary Features
- ▪
- Identify features strongly correlate with dropout behaviour.
- ▪
- Address class imbalance by using the RUS method.
- ▪
- Perform feature selection to retain only the most informative features.
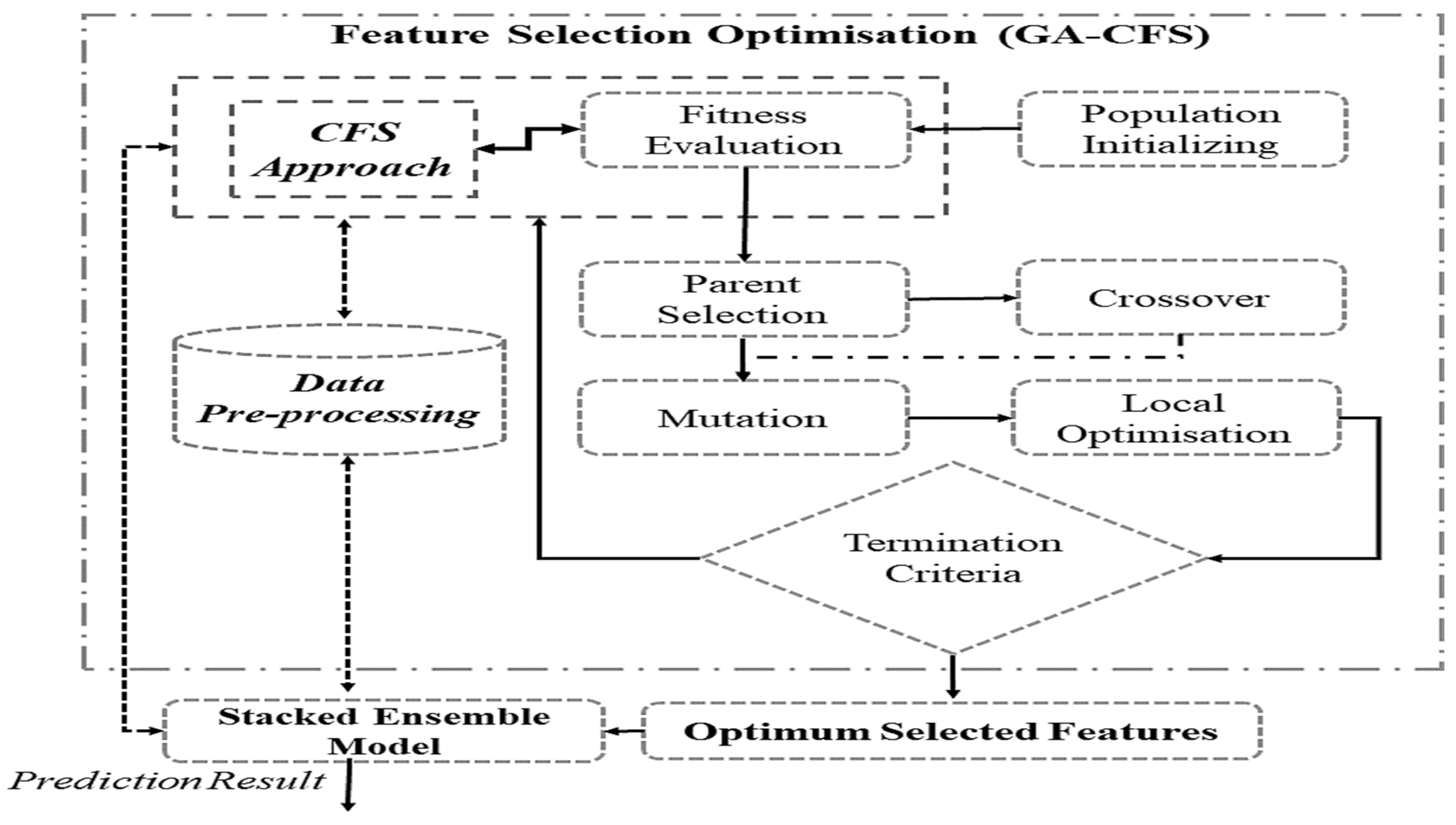
4.3. Feature Selection Optimisation
| Algorithm 1. Feature Selection Optimisation by Hybrid GA-CFS Approach |
| Input: In-session Dataset ), target variable y, GA parameters: population size , individual solution (), max generations , crossover probability (), mutation probability (), crossover threshold () Output: Optimised feature subset ()
|
4.4. Multi-Level Stacked Ensemble Model
5. Experimental Results and Discussion
- ▪
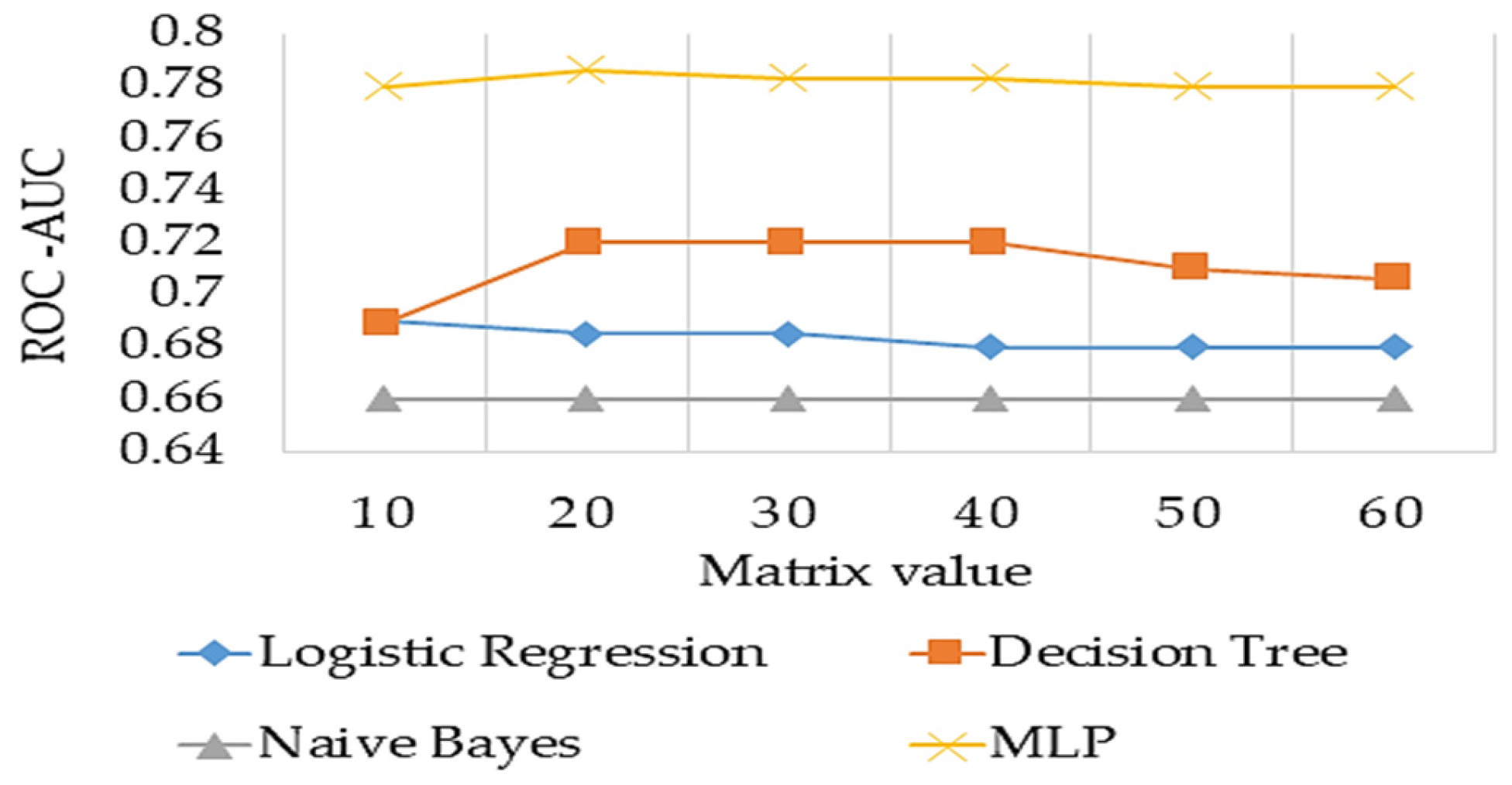
- Evaluates the meta-learner models to identify the most effective configuration for predicting student dropout behaviour. The results show which meta-learner model is outperformed.
- ▪
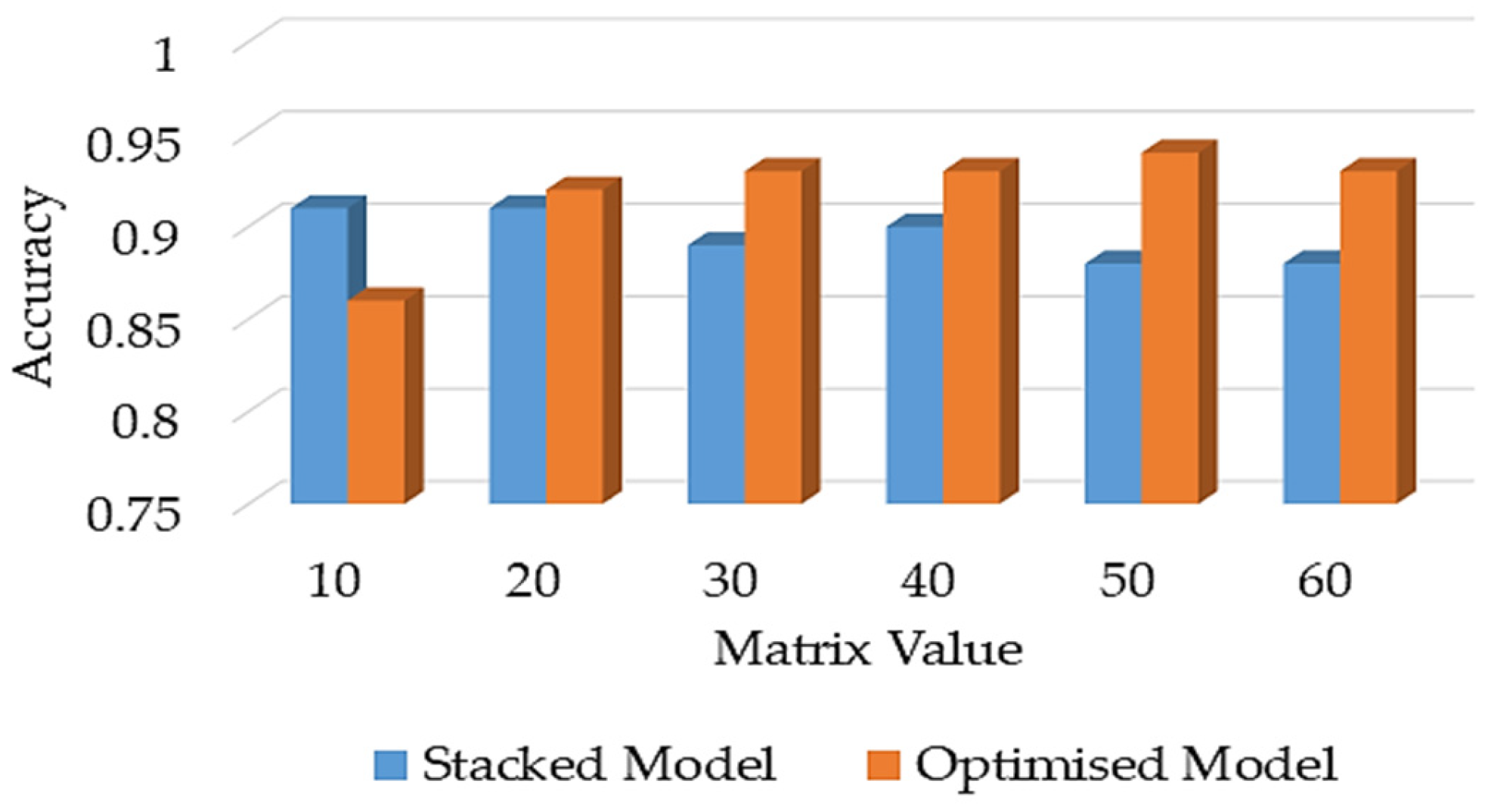
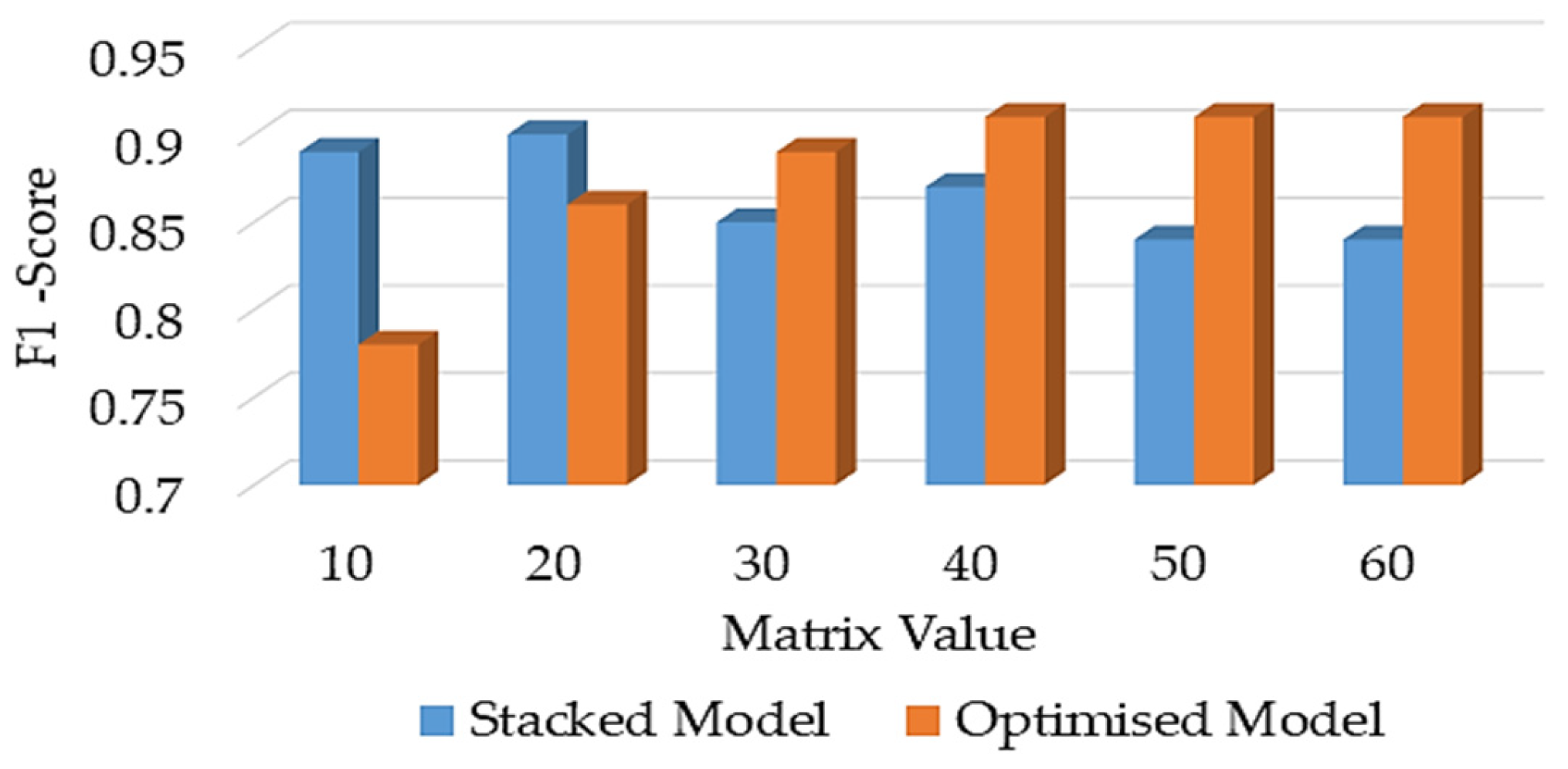
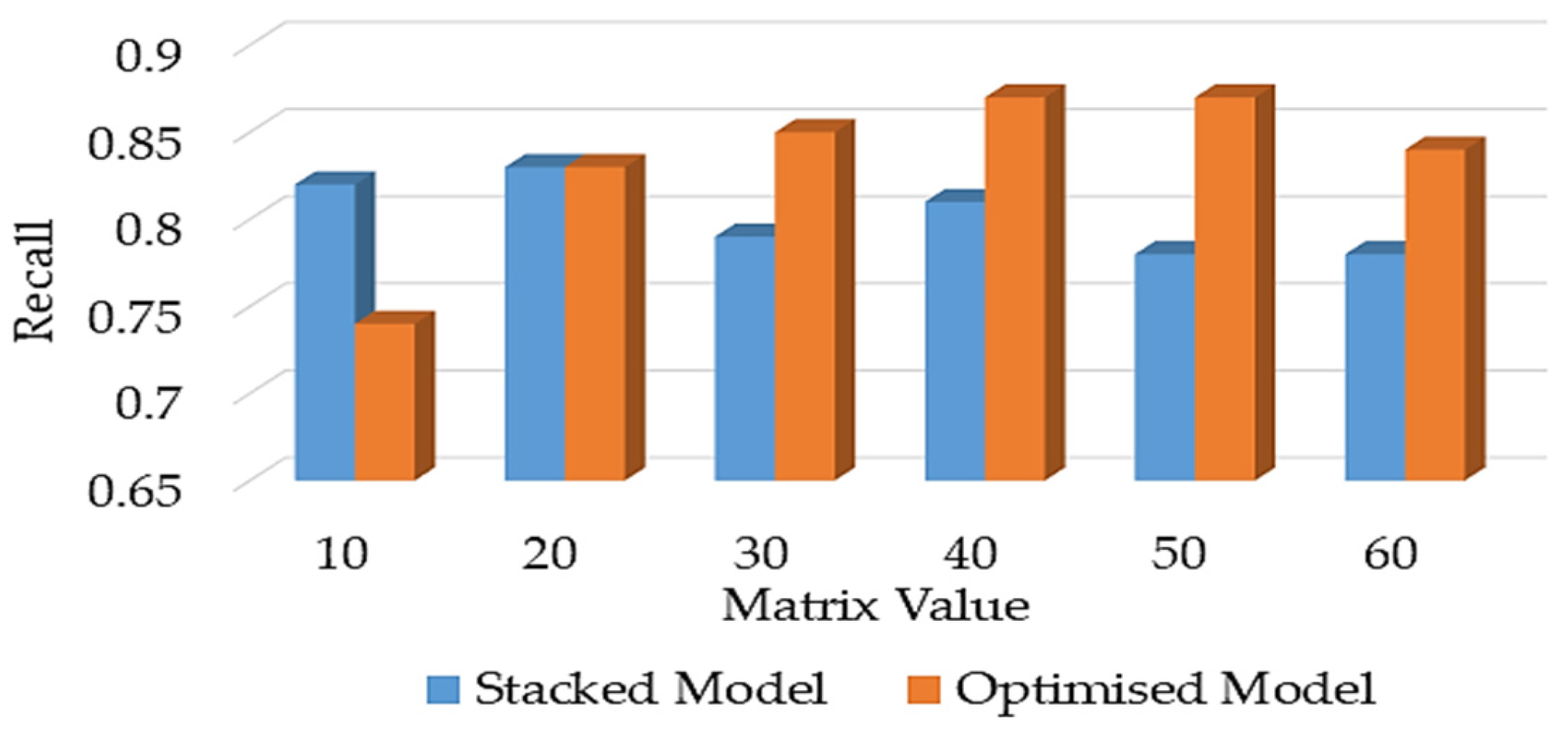
- Evaluates the stacked ensemble model before and after the proposed feature selection optimisation to evaluate its performance to improve the accuracy.
- ▪
- The final evaluation highlights the performance of the proposed framework against the Benchmarking Models used in the baseline study.
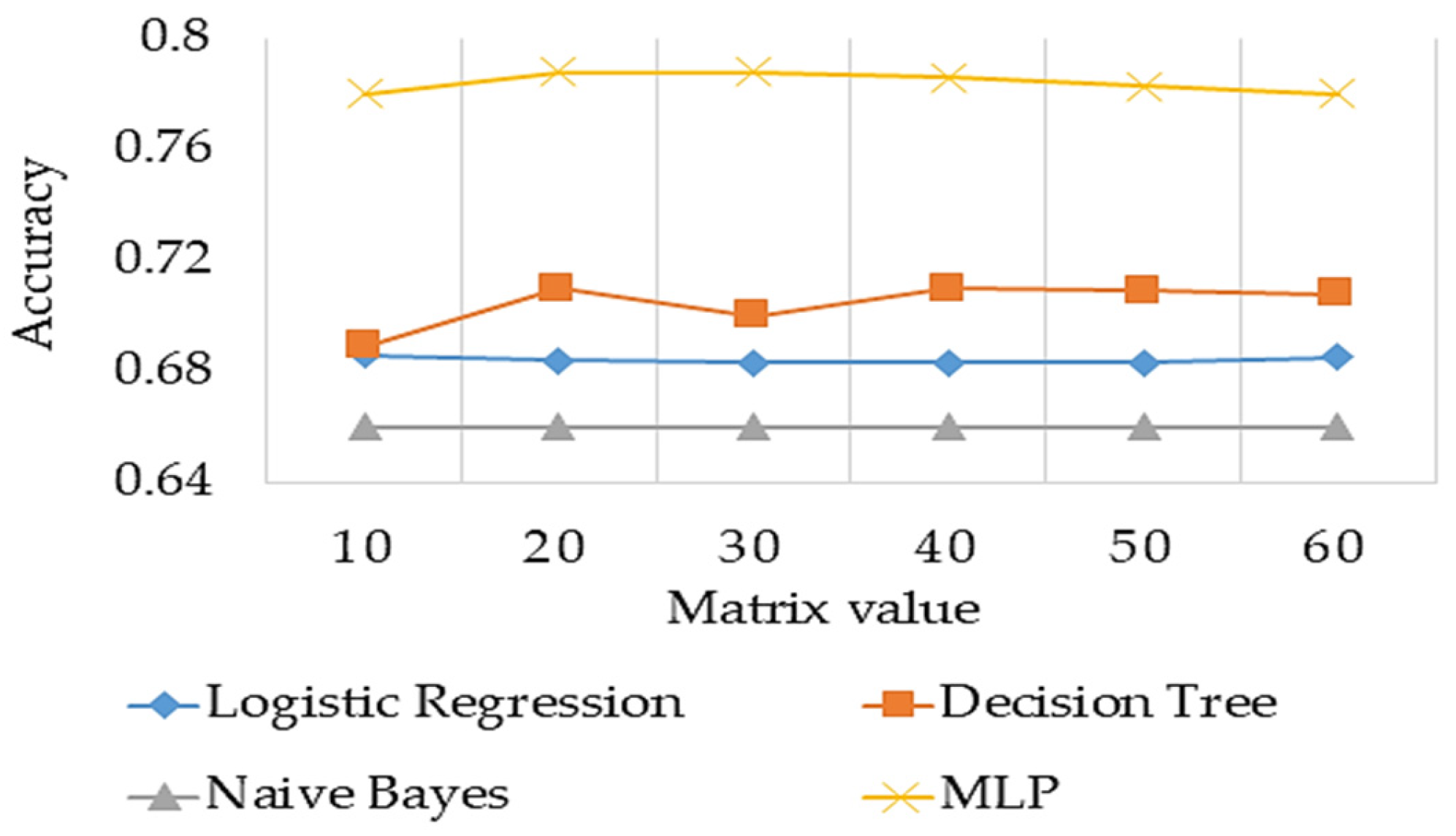
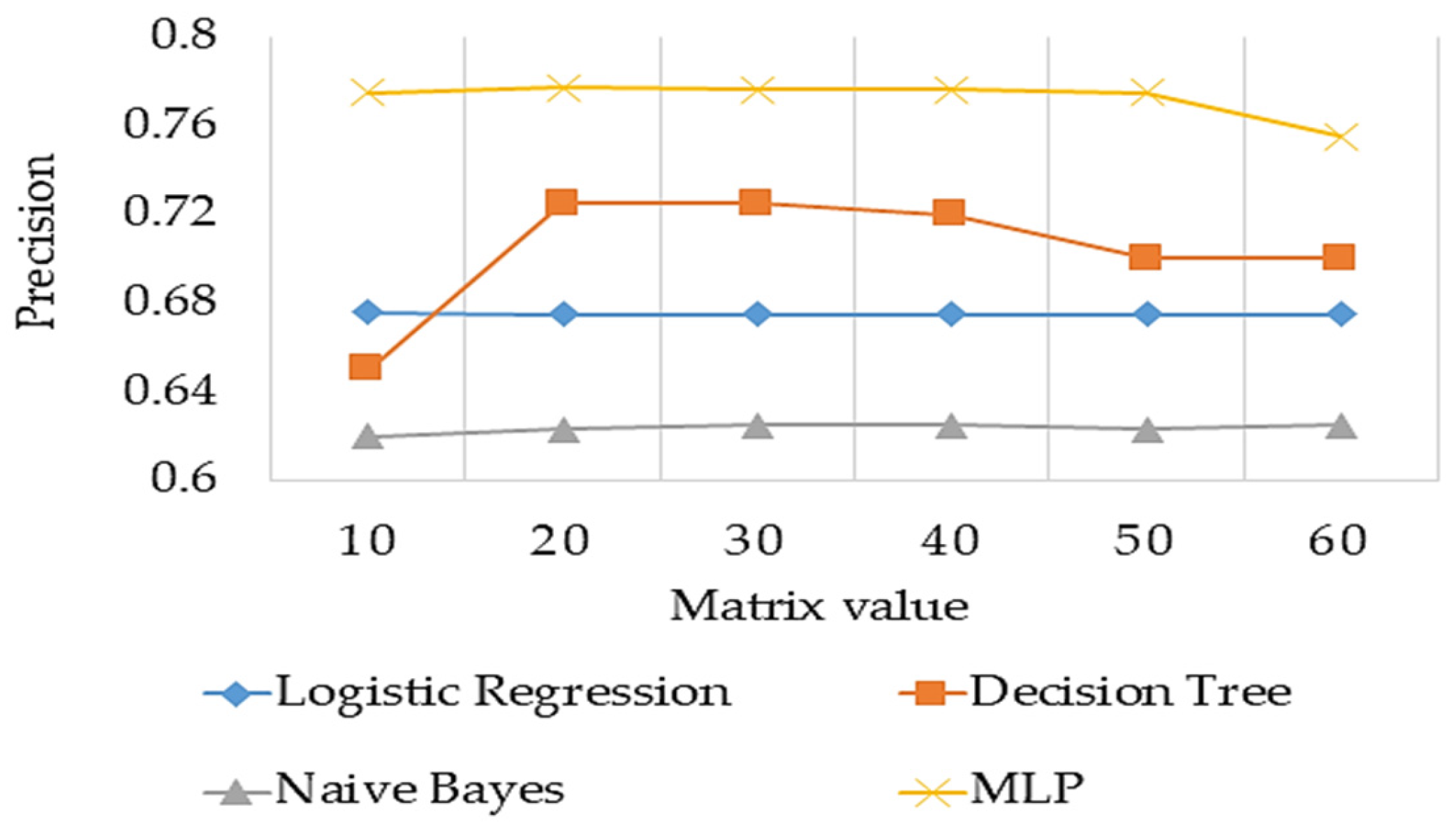
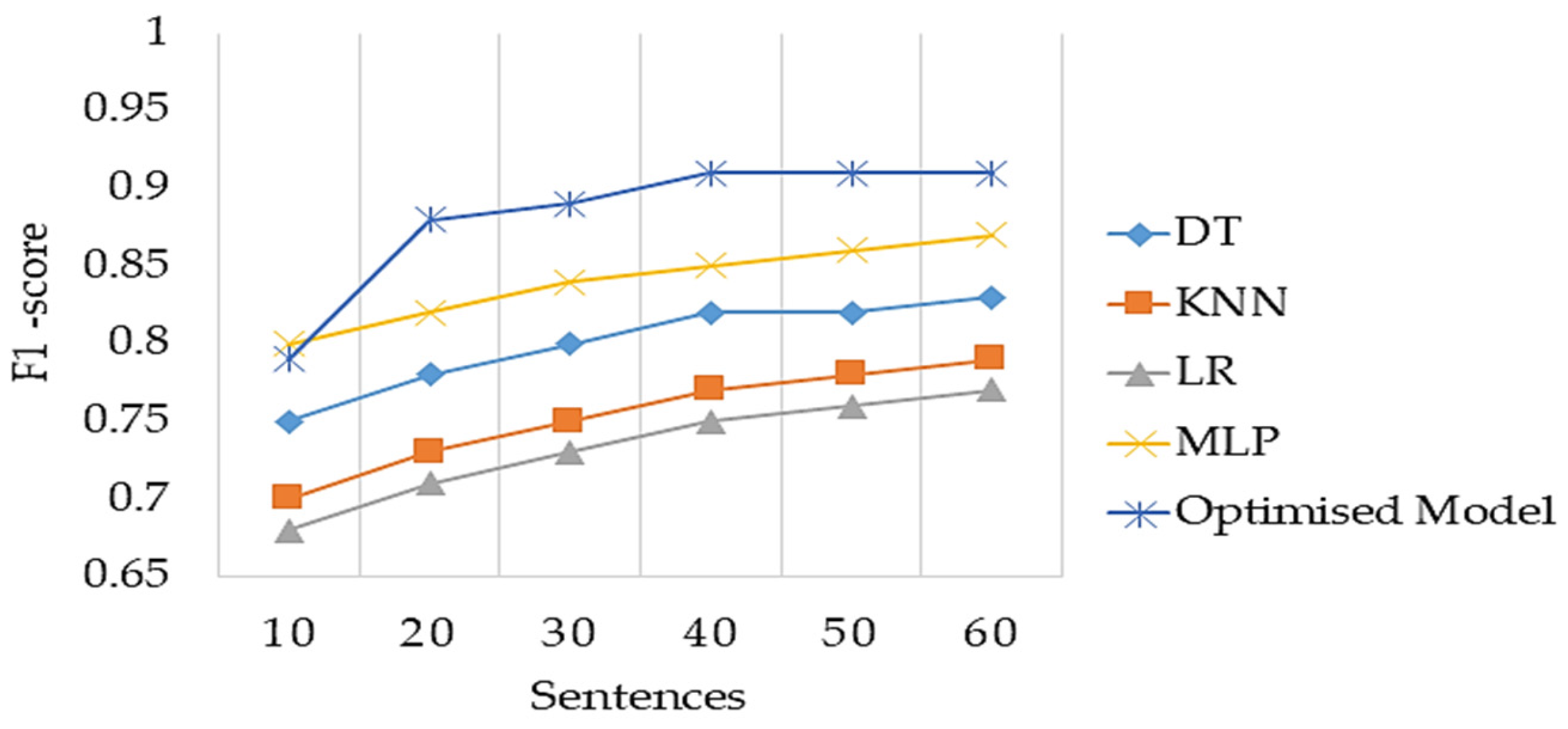
5.1. Meta Learner Model Performance
5.2. Optimised Stacked Ensemble Model Performance
5.3. Comparison with Benchmarking Models
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
References
- Smirani, L.K.; Yamani, H.A.; Menzli, L.J.; Boulahia, J.A.; Huang, C. Using Ensemble Learning Algorithms to Predict Student Failure and Enabling Customised Educational Paths. Sci. Program. 2022, 2022, 3805235. [Google Scholar] [CrossRef]
- Zhou, Y.; Xu, Z. Multi-Model Stacking Ensemble Learning for Dropout Prediction in MOOCs. J. Phys. Conf. Ser. 2020, 1607, 012004. [Google Scholar] [CrossRef]
- Cho, C.H.; Yu, Y.W.; Kim, H.G. A Study on Dropout Prediction for University Students Using Machine Learning. Appl. Sci. 2023, 13, 12004. [Google Scholar] [CrossRef]
- Nithya, S.; Umarani, S. MOOC Dropout Prediction using FIAR-ANN Model based on Learner Behavioural Features. Int. J. Adv. Comput. Sci. Appl. (IJACSA) 2022, 13, 607–617. [Google Scholar] [CrossRef]
- Marcolino, M.R.; Porto, T.R.; Primo, T.T.; Targino, R.; Ramos, V.; Queiroga, E.M.; Munoz, R.; Cechinel, C. Student dropout prediction through machine learning optimization: Insights from moodle log data. Sci. Rep. 2025, 15, 9840. [Google Scholar] [CrossRef]
- Talamás-Carvajal, J.A.; Ceballos, H.G. A stacking ensemble machine learning method for early identification of students at risk of dropout. Educ. Inf. Technol. 2023, 28, 12169–12189. [Google Scholar] [CrossRef]
- Putra, M.R.P.; Utami, E. A Blending Ensemble Approach to Predicting Student Dropout in Massive Open Online Courses (MOOCs). JUITA J. Inform. 2025, 13, 11–18. [Google Scholar] [CrossRef]
- Malik, S.; Patro, S.G.K.; Mahanty, C.; Hegde, R.; Naveed, Q.N.; Lasisi, A.; Buradi, A.; Emma, A.F.; Kraiem, N. Advancing educational data mining for enhanced student performance prediction: A fusion of feature selection algorithms and classification techniques with dynamic feature ensemble evolution. Sci. Rep. 2025, 15, 8738. [Google Scholar] [CrossRef]
- Rabelo, A.M.; Zárate, L.E. A model for predicting dropout of higher education students. Data Sci. Manag. 2025, 8, 72–85. [Google Scholar] [CrossRef]
- Putra, M.R.P.; Utami, E. Comparative Analysis of Hybrid Model Performance Using Stacking and Blending Techniques for Student Drop Out Prediction In MOOC. J. RESTI (Rekayasa Sist. Dan Teknol. Inf.) 2024, 8, 346–354. [Google Scholar] [CrossRef]
- Niyogisubizo, J.; Liao, L.; Nziyumva, E.; Murwanashyaka, E.; Nshimyumukiza, P.C. Predicting student’s dropout in university classes using two-layer ensemble machine learning approach: A novel stacked generalization. Comput. Educ. Artif. Intell. 2022, 3, 100066. [Google Scholar] [CrossRef]
- Kumar, G.; Singh, A.; Sharma, A. Ensemble Deep Learning Network Model for Dropout Prediction in MOOCs. Int. J. Electr. Comput. Eng. Syst. 2023, 14, 187–196. [Google Scholar] [CrossRef]
- Rzepka, N.; Simbeck, K.; Müller, H.-G.; Pinkwart, N. Keep It Up: In-Session Dropout Prediction to Support Blended Classroom Scenarios. In Proceedings of the 14th International Conference on Computer Supported Education, Online, 22–24 April 2022; Volume 2, pp. 131–138. [Google Scholar] [CrossRef]
- Alghamdi, S.; Soh, B.; Li, A. ISELDP: An Enhanced Dropout Prediction Model Using a Stacked Ensemble Approach for In-Session Learning Platforms. Electronics 2025, 14, 2568. [Google Scholar] [CrossRef]
- Faucon, L.; Olsen, J.K.; Haklev, S.; Dillenbourg, P. Real-Time Prediction of Students’ Activity Progress and Completion Rates. J. Learn. Anal. 2020, 7, 18–44. [Google Scholar] [CrossRef]
- Mbunge, E.; Batani, J.; Mafumbate, R.; Gurajena, C.; Fashoto, S.; Rugube, T.; Akinnuwesi, B.; Metfula, A. Predicting Student Dropout in Massive Open Online Courses Using Deep Learning Models—A Systematic Review. In Cybernetics Perspectives in Systems; Silhavy, R., Ed.; CSOC 2022. Lecture Notes in Networks and Systems; Springer: Cham, Switzerland, 2022; Volume 503. [Google Scholar] [CrossRef]
- Psathas, G.; Chatzidaki, T.K.; Demetriadis, S.N. Predictive Modeling of Student Dropout in MOOCs and Self-Regulated Learning. Computers 2023, 12, 194. [Google Scholar] [CrossRef]
- Bujang, S.D.A.; Selamat, A.; Krejcar, O.; Mohamed, F.; Cheng, L.K.; Chiu, P.C.; Fujita, H. Imbalanced Classification Methods for Student Grade Prediction: A Systematic Literature Review. IEEE Access 2023, 11, 1970–1989. [Google Scholar] [CrossRef]
- Hassan, M.A.; Muse, A.H.; Nadarajah, S. Predicting Student Dropout Rates Using Supervised Machine Learning: Insights from the 2022 National Education Accessibility Survey in Somaliland. Appl. Sci. 2024, 14, 7593. [Google Scholar] [CrossRef]
- Bohrer, J.d.S.; Dorn, M. Enhancing classification with hybrid feature selection: A multi-objective genetic algorithm for high-dimensional data. Expert Syst. Appl. 2024, 255, 124518. [Google Scholar] [CrossRef]
- Feng, G. Feature selection algorithm based on optimized genetic algorithm and the application in high-dimensional data processing. PLoS ONE 2024, 19, e0303088. [Google Scholar] [CrossRef]
- Al-Alawi, L.; Al Shaqsi, J.; Tarhini, A.; Al-Busaidi, A.S. Using machine learning to predict factors affecting academic performance: The case of college students on academic probation. Educ. Inf. Technol. 2023, 28, 12407–12432. [Google Scholar] [CrossRef]
- Jin, C. MOOC student dropout prediction model based on learning behaviour features and parameter optimization. Interact. Learn. Environ. 2020, 31, 714–732. [Google Scholar] [CrossRef]
- Hussain, M.M.; Akbar, S.; Hassan, S.A.; Aziz, M.W.; Urooj, F. Prediction of Student’s Academic Performance through Data Mining Approach. J. Inform. Web Eng. 2024, 3, 241–251. [Google Scholar] [CrossRef]
- Namoun, A.; Alshanqiti, A. Predicting Student Performance Using Data Mining and Learning Analytics Techniques: A Systematic Literature Review. Appl. Sci. 2021, 11, 237. [Google Scholar] [CrossRef]
- Roy, K.; Farid, D.M. An Adaptive Feature Selection Algorithm for Student Performance Prediction. IEEE Access 2024, 12, 75577–75598. [Google Scholar] [CrossRef]
- Mumuni, A.; Mumuni, F. Automated data processing and feature engineering for deep learning and big data applications: A survey. J. Inf. Intell. 2024, 3, 113–153. [Google Scholar] [CrossRef]
- Setiadi, H.; Larasati, I.P.; Suryani, E.; Wardani, D.W.; Wardani, H.D.C.; Wijayanto, A. Comparing Correlation-Based Feature Selection and Symmetrical Uncertainty for Student Dropout Prediction. J. RESTI (Rekayasa Sist. Dan Teknol. Inf.) 2024, 8, 542–554. [Google Scholar] [CrossRef]
- Hao, J.; Gan, J.; Zhu, L. MOOC performance prediction and personal performance improvement via Bayesian network. Educ. Inf. Technol. 2022, 27, 7303–7326. [Google Scholar] [CrossRef]
- Li, J.L.; Xie, S.T.; Wang, J.N.; Lin, Y.Q.; Chen, Q. Prediction and Learning Analysis Using Ensemble Classifier Based on GA in SPOC Experiments. In Data Mining and Big Data; Tan, Y., Shi, Y., Tang, Q., Eds.; DMBD 2018. Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2018; Volume 10943. [Google Scholar] [CrossRef]
- Albreiki, B.; Zaki, N.; Alashwal, H. A Systematic Literature Review of Student’ Performance Prediction Using Machine Learning Techniques. Educ. Sci. 2021, 11, 552. [Google Scholar] [CrossRef]
- Sun, L.; Qin, H.; Przystupa, K.; Cui, Y.; Kochan, O.; Skowron, M.; Su, J. A Hybrid Feature Selection Framework Using Improved Sine Cosine Algorithm with Metaheuristic Techniques. Energies 2022, 15, 3485. [Google Scholar] [CrossRef]
- Dey, R.; Mathur, R. Ensemble Learning Method Using Stacking with Base Learner, A Comparison. In Proceedings of International Conference on Data Analytics and Insights; Chaki, N., Roy, N.D., Debnath, P., Saeed, K., Eds.; Lecture Notes in Networks and Systems; Springer: Singapore, 2023; Volume 727. [Google Scholar] [CrossRef]
- Tong, T.; Li, Z.; Akbar, S. Predicting learning achievement using ensemble learning with result explanation. PLoS ONE 2025, 20, e0312124. [Google Scholar] [CrossRef]
- Sultan, S.Q.; Javaid, N.; Alrajeh, N.; Aslam, M. Machine Learning-Based Stacking Ensemble Model for Prediction of Heart Disease with Explainable AI and K-Fold Cross-Validation: A Symmetric Approach. Symmetry 2025, 17, 185. [Google Scholar] [CrossRef]
- Chi, Z.; Zhang, S.; Shi, L. Analysis and Prediction of MOOC Learners’ Dropout Behavior. Appl. Sci. 2023, 13, 1068. [Google Scholar] [CrossRef]
- Ismail, W.N.; Alsalamah, H.A.; Mohamed, E. GA-Stacking: A New Stacking-Based Ensemble Learning Method to Forecast the COVID-19 Outbreak. Computers. Mater. Contin. 2023, 74, 3945–3976. [Google Scholar] [CrossRef]
- Nafea, A.A.; Mishlish, M.; Shaban, A.M.S.; Al-Ani, M.M.; Alheeti, K.M.A.; Mohammed, H.J. Enhancing Student’s Performance Classification Using Ensemble Modeling. Iraqi J. Comput. Sci. Math. 2023, 4, 204–214. [Google Scholar] [CrossRef]
- Cam, H.N.T.; Sarlan, A.; Arshad, N.I. A hybrid model integrating recurrent neural networks and the semi-supervised support vector machine for identification of early student dropout risk. PeerJ Comput. Sci. 2024, 10, e2572. [Google Scholar] [CrossRef]




| Abbreviations | Description |
|---|---|
| AdaBoost | Adaptive Boosting Learning |
| CFS | Correlation-Based Feature Selection |
| CNN | Convolutional Neural Network |
| CNT | Complex Non-Linear Transformation |
| CMA | Correlation Matrix Analysis |
| DT | Decision Tree |
| FCBF | Fast Correlation-Based Filter |
| GBC | Gradient Boosting Classifier |
| GA | Genetic Algorithm |
| KNN | K-Nearest Neighbours |
| LightGBM | Light Gradient Boosting Decision Tree Implementation |
| LSTM | Long Short-Term Memory Network |
| MLP | Multilayer Perceptron |
| MMSE | Minimum Mean Square Error |
| NB | Naïve Bayes |
| PCA | Principal Component Analysis |
| PCC | Pearson’s Correlation Coefficient |
| RF | Random Forest |
| SVM | Support Vector Machine |
| SGD | Stochastic Gradient Descent |
| XGBoost | Extreme Gradient Boosting |
| Citations | Contribution | Model Algorithms | Feature Selection Method | Highlights |
|---|---|---|---|---|
| [7] | Developed a blending ensemble learning for online dropout prediction | DT, NB, and XGBoost | feature importance based on RF | High accuracy approx. to 90% |
| [8] | Evaluates Enhanced Feature Selection approaches for predicting student performance | DT, RF, SVM, NN, NB | CMA, information gain, and Chi-square | Gives high accuracy of 94% with correlation matrix analysis |
| [9] | Improves the prediction performance for student activity during online classes | LR, DT, NN | Fully, Stepwise, and Lasso | Moderate accuracy approx. to 89% |
| [10] | Evaluates different ML approaches using stacking and blending models to predict the dropout rate of students | KNN, DT, and NB | CNT-based NB function | Moderate accuracy approx. to 83% |
| [11] | Evaluates different feature selection approaches with ML-based ensembling methods | SVM, KNN, DT, NB, LR, and stacked Voting | Chi-square, FCBF, Relief method, and PCC | Higher accuracy by 93% with relief method and stacked voting |
| [12] | Novel stacking ensemble based on a hybrid ML model to predict students’ dropout in university classes | NN, RF, GBC, XGBoost | CNT | Higher precision and recall |
| [13] | MLP-based model using stepwise session data for adapted dropout prediction on in-session platforms. | DT, KNN, LR, MLP | temporal/session-based modelling | accuracy with 87% |
| Category | Features | Description |
|---|---|---|
| Numerical features | First solution | The time or correctness of the first solution |
| distracted | If the user was distracted during the session | |
| Success | The success rate of answers | |
| difficulty | The difficulty level of tasks or questions | |
| School hours | The number of school hours associated with user activity | |
| Multiple false | The number of incorrect attempts made by the user | |
| Matrix | Current sentence number or matrix value in the dataset | |
| mistakes | The total number of mistakes during the session | |
| Class level | The user’s academic level or grade | |
| Years registered | The years have been registered in the system by users. | |
| Pending tasks count | Count of pending or incomplete tasks | |
| Steps | The number of steps or interactions during a task | |
| Binary features | School hours | Binary indicator for whether school hours participated in the session |
| Previous break | If there were a break before the current session | |
| User attribute | A specific attribute of the user | |
| Type capitalisation | Errors related to capitalisation in user input | |
| Type grammar | Grammar-related errors in user input | |
| Type hyphenation | Hyphenation-related errors in user input | |
| Type comma formation | Comma-related errors in user input | |
| Type the sound letters | Errors related to sounds or letters in user input | |
| homework | If the session was related to homework | |
| Voluntary work | Voluntary work performed by the user | |
| Post-test | Participation in a post-test | |
| Pre-test | Participation in a pre-test | |
| Interim test | Participation in an interim test | |
| Gender male | Binary indicator for male gender | |
| Gender female/male | Binary indicator for female gender | |
| Test-position check | If the user is in a test position | |
| Test-position training | If the user is in a training position | |
| Test-position version | The version of the test position (categorical/binary). |
| Models | Parameters | Values |
|---|---|---|
| RF | Max Number of estimators | 150 |
| Max learning rate | 0.2 | |
| Max depth | 10 | |
| AdaBoost | Number of estimators | 150 |
| Max learning rate | 1 | |
| GBC | Number of estimators | 150 |
| Max learning rate | 0.2 | |
| Max depth | 7 | |
| XGBoost | Number of estimators | 150 |
| Max learning rate | 0.3 | |
| Max depth | 7 | |
| MLP | Hidden layer sizes | 35 |
| Max iterations | 100 |
| Scenarios | Accuracy | F1-Score | Precision | Recall | ROC-AUC |
|---|---|---|---|---|---|
| Baseline Stacked Model | 0.88 | 0.84 | 0.99 | 0.78 | 0.88 |
| Optimised Model | 0.91 | 0.88 | 1.00 | 0.85 | 0.92 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alghamdi, S.; Soh, B.; Li, A. A Novel Optimised Feature Selection Method for In-Session Dropout Prediction Using Hybrid Meta-Heuristics and Multi-Level Stacked Ensemble Learning. Electronics 2025, 14, 3703. https://doi.org/10.3390/electronics14183703
Alghamdi S, Soh B, Li A. A Novel Optimised Feature Selection Method for In-Session Dropout Prediction Using Hybrid Meta-Heuristics and Multi-Level Stacked Ensemble Learning. Electronics. 2025; 14(18):3703. https://doi.org/10.3390/electronics14183703
Chicago/Turabian StyleAlghamdi, Saad, Ben Soh, and Alice Li. 2025. "A Novel Optimised Feature Selection Method for In-Session Dropout Prediction Using Hybrid Meta-Heuristics and Multi-Level Stacked Ensemble Learning" Electronics 14, no. 18: 3703. https://doi.org/10.3390/electronics14183703
APA StyleAlghamdi, S., Soh, B., & Li, A. (2025). A Novel Optimised Feature Selection Method for In-Session Dropout Prediction Using Hybrid Meta-Heuristics and Multi-Level Stacked Ensemble Learning. Electronics, 14(18), 3703. https://doi.org/10.3390/electronics14183703







