A Security-Enhanced Scheme for ModBus TCP Protocol Based on Lightweight Cryptographic Algorithm

Abstract

In modern industrial control systems (ICSs), communication protocols such as Modbus TCP remain widely used due to their simplicity, interoperability, and real-time performance. However, these communication protocols (e.g., Modbus TCP) were originally designed without security considerations, lacking essential features such as encryption, integrity protection, and authentication. This exposes ICS deployments to severe security threats, including eavesdropping, command injection, and replay attacks, especially when operating over unsecured networks. To address these critical vulnerabilities while preserving the lightweight nature of the protocol, we propose a Modbus TCP security enhancement scheme that integrates ASCON, an NIST-standardized authenticated encryption algorithm, with the CBOR Object Signing and Encryption (COSE) framework. Our design embeds COSE_Encrypt0 structures into Modbus application data, enabling end-to-end confidentiality, integrity, and replay protection without altering the protocol’s semantics or timing behavior. We implement the proposed scheme in C and evaluate it in a simulated embedded environment representative of typical ICS devices. Experimental results show that the solution incurs minimal computational and memory overhead, while providing robust cryptographic guarantees. This work demonstrates a practical pathway for retrofitting legacy ICS protocols with modern lightweight cryptography, enhancing system resilience without compromising compatibility or performance.

1. Introduction

Industrial control systems (ICSs) and supervisory control and data acquisition (SCADA) networks rely heavily on communication protocols such as Modbus [1], Distributed Network Protocol 3 (DNP3) [2], EtherNet/IP [3], and Powerlink [4] to connect programmable logic controllers (PLCs), sensors, and Human–Machine Interfaces (HMIs). Although widely adopted in critical infrastructure and industrial automation systems, these industrial communication protocols were originally designed to meet the demands of reliability and real-time responsiveness, with little or no consideration for security. As a result, they commonly suffer from inherent security weaknesses such as the lack of authentication, encryption, and integrity checks.

Modbus TCP [5], the most prevalent variant of Modbus used in Ethernet-based industrial environments, transmits all payloads in plaintext and lacks identity verification mechanisms. This makes it susceptible to a wide range of attacks including eavesdropping, unauthorized command injection, replay attacks, and data manipulation.

To address these shortcomings, several security extensions have been proposed, such as wrapping industrial protocols within VPN tunnels, applying Transport Layer Security (TLS), or embedding cryptographic primitives like AES-GCM or SM4 [6,7,8]. However, these solutions often introduce significant overhead in terms of computational complexity, memory usage, or latency, and may require hardware or system stack modifications that hinder deployment on embedded devices or legacy field equipment.

To reconcile the tension between security and real-time constraints in industrial protocols, this paper presents a lightweight security enhancement scheme for Modbus TCP, one of the most widely used and representative protocols in industrial control systems. Our approach is based on two emerging standards: (1) ASCON, a NIST-standardized lightweight authenticated encryption algorithm optimized for constrained devices [9], and (2) COSE_Encrypt0, a concise and structured cryptographic message format specified by the IETF for securing CBOR-encoded payloads [10].

Unlike traditional approaches that rely on heavyweight frameworks like TLS, our scheme integrates security mechanisms directly at the Modbus application layer using COSE_Encrypt0. By encapsulating Modbus function codes and parameters into COSE structures, we achieve end-to-end confidentiality, integrity, and replay protection without breaking compatibility with the existing Modbus message format or requiring changes to lower protocol layers.

To validate our design, we implement the protocol in a simulated embedded environment for performance evaluation and conduct comprehensive experiments to measure its performance overhead and memory footprint. We also compare our approach with six state-of-the-art schemes, which demonstrate the efficiency and advantages of our lightweight approach. The contributions of this paper are as follows:

• We propose a novel secure Modbus TCP protocol that integrates the lightweight cipher ASCON-128 with the standardized COSE_Encrypt0 format. The scheme provides mutual authentication, identity binding, and forward secrecy while maintaining Modbus compatibility.
• We perform a detailed security analysis of the proposed protocol, demonstrating resistance to key threats such as message manipulation, eavesdropping, and replay attacks.
• We implement and evaluate the scheme on an embedded platform and perform performance comparisons with state-of-the-art baselines including SM3/SM4-based designs. Experimental results show that our solution offers strong security with minimal computational and bandwidth overhead, especially excelling in server-side decryption performance.

2. Related Work

As a legacy protocol widely adopted in industrial control systems (ICSs), Modbus was originally designed without any built-in security mechanisms, such as authentication, encryption, or replay protection. This inherent vulnerability has made Modbus a frequent target of cyberattacks in critical infrastructure environments. A wide range of efforts have been made to retrofit security into Modbus communications.

Early cryptographic solutions primarily focused on integrating classical cryptographic primitives. Fovino et al. [11] proposed a scheme combining SHA-2 for data integrity, Rivest–Shamir–Adleman (RSA) for authentication, and timestamps for non-repudiation and replay protection. However, the use of RSA introduced significant computational overhead, limiting its practicality in resource-constrained industrial devices. Hayes et al. [12] introduced Modbus-Sec, which leveraged Stream Control Transmission Protocol (SCTP) and message authentication codes (MACs) to resist denial-of-service and man-in-the-middle attacks. Despite these strengths, the scheme relied on a single symmetric key, rendering it susceptible to unauthorized command injection and replay attacks. To further strengthen the security of Modbus, Shahzad et al. [6] proposed a hybrid encryption framework that incorporated additional security fields into Modbus packets. Their approach used Advanced Encryption Standard (AES) for data encryption and RSA for signing and encrypting the AES key. While this dual-layer design enhanced confidentiality and authenticity, it was computationally intensive due to RSA, making it ill-suited for embedded environments.

Some researchers turned to structural-level protections to mitigate performance concerns. Shang et al. [13] proposed a Modbus-aware industrial firewall utilizing a whitelist mechanism to block unauthorized traffic. Pricop et al. [14] explored embedding authentication data into the TCP header options of Modbus TCP, but did not provide a concrete authentication protocol. Xuan et al. [7] introduced the Modbus-S framework to improve identity authentication and data confidentiality, but it lacked detailed cryptographic implementation. Chochutoula et al. [15] proposed a solution based on elliptic curve cryptography (ECC), offering strong authentication and confidentiality while maintaining moderate performance costs.

Yi et al. [16] combined SM4 and SM3 to provide confidentiality and integrity with pre-shared keys and timestamp-based replay protection. However, transmitting timestamps and nonces in plaintext weakened the replay resistance of their solution. Lin et al. [17] employed AES and SHA-256 to enhance data protection, but did not address authentication. Other studies incorporated SM2, SM3, and SM4 in combination, but relied on certificate infrastructures and large key sizes, which are impractical for lightweight deployment. Liu et al. [8] presented a comprehensive SM-based security framework for Modbus, covering identity authentication, key agreement, and data protection, achieving compliance with national standards while addressing several practical constraints. Katulic et al. [18] proposed a novel Modbus TCP authentication scheme based on lightweight MACs, designed specifically for industrial control systems. Similarly, Zhang et al. [19] developed a ZUC- and SM3-based security mechanism for Modbus/TCP, enabling ultra-low-latency cryptographic protection for constrained devices, covering authentication, integrity, confidentiality, and anti-replay functionality.

In summary, existing security enhancement schemes often rely on heavyweight cryptographic primitives and complex protocol interactions, leading to considerable computational and management overhead, especially in resource-constrained environments. Additionally, most approaches lack flexibility, preventing users from tailoring security properties such as integrity, confidentiality, and authentication based on application requirements. To address these limitations, our work proposes a lightweight, modular, and message-level secure solution based on ASCON and the COSE framework, offering customizable security while maintaining compatibility with both Modbus TCP and serial variants.

3. Background

3.1. Modbus TCP Protocol

Modbus [1] is a serial communication protocol originally introduced by Modicon in 1979 for use with programmable logic controllers (PLCs). Its simplicity, openness, and ease of implementation have made it one of the most widely adopted communication protocols in industrial control systems (ICSs) and supervisory control and data acquisition (SCADA) environments. Over time, the protocol has been extended from its original serial-based formats to Ethernet-based Modbus TCP to support modern network infrastructures [5].

As shown in Figure 1, the Modbus TCP message structure consists of two main parts: the Modbus Application Protocol (MBAP) header and the Protocol Data Unit (PDU). Together, these constitute the Application Data Unit (ADU). The MBAP header is 7 bytes long and contains the following fields: (1) The Transaction Identifier used to match responses with requests and prevent message confusion during concurrent transactions. (2) The Protocol Identifier set to “0x0000” for Modbus TCP, identifying the protocol type. (3) The Length field specifies the length of the remaining bytes in the message, including the Unit Identifier, Function Code, and Data. (4) The Unit Identifier is used to address a specific remote server or a serially connected Modbus device in bridging scenarios. The PDU includes the following: (1) The Function Code indicates the type of operation requested by the client, and there are eight common types of function codes used for read and write operations on secondary device data. (2) The Data field contains the parameters associated with the function code, such as register addresses or values to be written.

This modular message structure enables Modbus to be easily parsed and extended, but also exposes a fundamental vulnerability: all fields, including the function code and data payload, are transmitted in plaintext, with no native mechanisms for authentication, encryption, or message integrity. As a result, Modbus TCP is inherently vulnerable to a wide range of attacks, including message spoofing, tampering, replay, and eavesdropping. These limitations highlight the pressing need for efficient and backward-compatible security enhancements that can integrate with existing Modbus message structures while introducing robust cryptographic protections.

3.2. ASCON Algorithm

ASCON is a family of lightweight authenticated encryption and hashing algorithms designed to offer strong security and high efficiency in resource-constrained environments [9]. It was selected as the finalist and the official standard of the NIST Lightweight Cryptography (LWC) competition, making it a leading choice for embedded systems, IoT devices, and industrial control systems (ICSs), where performance, energy consumption, and code size are key considerations. The ASCON suite includes authenticated encryption with associated data (AEAD) and hashing functions. Among them, ASCON-128 (AEAD) and ASCON-Hash are officially recommended for general-purpose use. Both share a common permutation-based sponge construction with a 320-bit internal state, offering consistency and compactness in implementation. The complete round-based descriptions, padding strategies, and permutation formulas of ASCON-128 and ASCON-Hash are provided in Appendix A. In our protocol, we adopt ASCON-MAC for message authentication, which is built upon the ASCON-Hash function using a sponge-based construction. Specifically, ASCON-MAC behaves similarly to HMAC but is optimized for lightweight environments by leveraging the same underlying permutation as ASCON-128 and ASCON-Hash. ASCON-MAC uses a keyed variant of ASCON-Hash, where the pre-shared key is injected into the initial state and then absorbed together with the message. This design ensures message integrity and authenticity with significantly reduced implementation overhead compared to traditional HMAC-SHA2, while offering comparable security guarantees.

3.2.1. ASCON-128

ASCON-128 follows an Encrypt-then-MAC paradigm and supports both confidentiality and integrity. The algorithm consists of four stages:

• Initialization: The internal state is initialized using the secret key, nonce, and a predefined constant.
• Associated Data Processing: Metadata (e.g., headers) is absorbed into the state for integrity protection.
• Plaintext Processing: The message is encrypted block-by-block, and ciphertext is generated along with an authentication tag.
• Finalization: A 128-bit authentication tag is computed from the final state and appended to the ciphertext.

ASCON-128 achieves authentication using its permutation structure rather than a separate MAC construction. This integrated approach differs from traditional HMAC, which uses Merkle–Damgard-based hash functions like SHA-2. ASCON’s sponge-based design ensures resistance to forgery and side-channel attacks while being efficient on constrained platforms.

3.2.2. ASCON-Hash

ASCON-Hash is a standalone hash function in the ASCON suite that uses the same internal structure as ASCON-128. It supports variable-length output and provides resistance to collision and preimage attacks. ASCON-Hash is used in our protocol for session key derivation, ensuring domain separation and consistency with the encryption scheme.

3.3. CBOR Object Signing and Encryption

The CBOR Object Signing and Encryption (COSE) framework [20] defines a compact cryptographic message format for protecting CBOR-encoded data [21]. COSE is particularly well-suited for constrained environments such as industrial control systems, embedded devices, and IoT networks due to its compactness, flexibility, and support for modern cryptographic algorithms. For example, unlike JSON-based JOSE (used in web environments), CBOR encoding reduces transmission size and avoids the need for complex string parsing, enabling faster encoding/decoding and lower RAM usage. Empirical evaluations [22] show that COSE outperforms JOSE in terms of average overhead and scalability with a more stable performance as payload size increases. In addition, COSE is being adopted by emerging IoT and IIoT standards (e.g., IETF SUIT [23], FIDO IoT [24]) due to its strong support for modern cryptographic primitives and its compatibility with constrained network protocols like CoAP or DTLS. These features collectively ensure compatibility with existing and future lightweight industrial communication stacks, supporting both security and interoperability requirements.

Among the different types of COSE message, COSE_Encrypt0 provides authenticated encryption with a single recipient using a symmetric key. A COSE_Encrypt0 structure is a CBOR array of three elements:

• Protected header (bstr): A CBOR-encoded map containing integrity-protected parameters, such as the algorithm identifier (e.g., ASCON).
• Unprotected header (map): Parameters not covered by the authentication tag, such as nonce (IV), sequence number, or issuer.
• Ciphertext (bstr): The encrypted payload, including the authentication tag produced by the AEAD encryption algorithm.

In our work, we adopt the COSE_Encrypt0 structure to encapsulate and protect Modbus messages at the application layer. This structure provides confidentiality through authenticated encryption, ensures integrity and authenticity by cryptographically binding both headers and payload in a single AEAD operation, and maintains low communication and processing overhead due to the compactness of the CBOR-based encoding format, which avoids the verbosity of JSON or XML.

4. Design of the Security-Enhanced Modbus Scheme

In this section, we present the design of the lightweight enhancement scheme for Modbus TCP communications. We begin with an overview of the protocol architecture, followed by detailed descriptions of each phase, including initialization and secure communication. We give the notation appearing in this paper in

Table 1. Summary of notations.

Notation	Description
$I{D}_c$	Identity of the client
$I{D}_s$	Identity of the server
$SK$	Session key shared between client and server
$N_c$	Nonce generated by client
$N_s$	Nonce generated by server
$seq$	Monotonically increasing sequence number
$iv$	Initialization vector used in AEAD encryption
M	Plaintext Modbus payload
$M_{enc}$	Encrypted Modbus payload
$tag$	Authentication tag generated by AEAD
$\mathit{Mac}$	Message authentication code
$AAD$	Associated authenticated data
ASCON_Encrypt	Authenticated encryption using ASCON-128
ASCON_Decrypt	Authenticated decryption using ASCON-128

.

Figure 2 presents the overall architecture of our protocol. The design consists of two primary phases:

• Initialization Phase: The client and server perform mutual authentication and derive a fresh session key using a pre-shared identity key and independently generated nonces. This process ensures forward secrecy and does not rely on certificate-based infrastructure. In real-world deployments, the secure distribution and management of the pre-shared key remains a significant challenge. For instance, in industrial control systems, common solutions include manual key injection during device commissioning, using secure bootstrap protocols such as IETF BRSKI [25], or leveraging trusted third-party provisioning servers with physical access constraints. While our model assumes that $K_{psk}$ is securely pre-established and kept secret, we note that our protocol can be integrated with existing secure key distribution frameworks (e.g., TPM-based hardware roots of trust or practices) without requiring major modifications.
• Secure Communication Phase: Modbus messages are encrypted and authenticated using the ASCON algorithm, and encapsulated within a COSE_Encrypt0 structure. The receiver verifies the message authenticity and decrypts the payload using the established session key before processing the Modbus PDU.

4.1. Initialization Phase

This phase establishes a secure session context between the client and the server using a pre-shared identity key $K_{psk}$ that is securely provisioned out of band and ephemeral random nonces. Each party has a unique identity: the client is denoted by ${\mathit{ID}}_c$ and the server is denoted by ${\mathit{ID}}_s$. The specific steps of authentication and key negotiation are described as follows:

(1) 

Client Authentication Request

The client generates a 128-bit cryptographically secure nonce $N_c$ and constructs a message authentication code ${\mathit{Mac}}_c$ over its identity $I{D}_c$ and the nonce using the ASCON-MAC algorithm, which is built on top of the sponge-based ASCON-Hash function:

$${\mathit{Mac}}_c=\mathit{ASCON}\_{\mathit{MAC}}_{K_{psk}}(I{D}_c\parallel N_c)$$

The authentication request message is formed as

$$M_1=[N_c,I{D}_c,{\mathit{Mac}}_c]$$

This message ensures freshness and integrity, and proves knowledge of the pre-shared key.

(2) 

Server Challenge and Response

Upon receiving $M_1$, the server verifies ${\mathit{Mac}}_c$ using the shared key $K_{psk}$. If successful, the server generates its own nonce $N_s$, and computes

$${\mathit{Mac}}_s=\mathit{ASCON}\_{\mathit{MAC}}_{K_{psk}}(I{D}_c\parallel N_c\parallel I{D}_s\parallel N_s)$$

It then sends the response message:

$$M_2=[I{D}_s,N_s,MA{C}_s]$$

This step confirms possession of the shared key and binds both nonces to the session.

(3) 

Client Verification and Key Derivation The client verifies ${\mathit{Mac}}_s$ using $K_{psk}$. Upon successful verification, both parties derive a 128-bit session key $\mathit{SK}$ using the ASCON-Hash function:

$$\mathit{SK}={\mathit{Truncate}}_{128}(\mathit{ASCON}\_\mathit{Hash}(K_{psk}\parallel N_c\parallel N_s\left)\right)$$

This key is then used to encrypt and authenticate subsequent Modbus messages.

4.2. Secure Communication Phase

After session establishment, each Modbus message is encrypted using ASCON-128 and encoded in a COSE_Encrypt0 structure, ensuring message confidentiality, integrity, and replay protection.

4.2.1. Message Structure

As shown in Figure 3, a secure Modbus packet consists of the original Modbus MBAP header and a COSE_Encrypt0 object that encapsulates the protected Modbus PDU. The COSE_Encrypt0 structure is a CBOR array containing three elements:

• Protected Header (bstr): A CBOR-encoded map containing cryptographic parameters such as the encryption algorithm identifier (e.g., “alg”: “ASCON-128”). This field is integrity-protected and included in the AEAD computation.
• Unprotected Header (map): A plaintext map including session metadata such as the initialization vector $iv$, issuer identifier $iss$, and a sequence number $seq$. Although not encrypted, these fields are authenticated as associated data.
• Ciphertext (bstr): The encrypted Modbus PDU concatenated with a 128-bit authentication tag produced by the ASCON-128 AEAD function.

The entire COSE_Encrypt0 array is appended to the standard Modbus MBAP header, maintaining compatibility with existing Modbus parsers.

4.2.2. Communication Phase

After establishing a shared session key $K_{\mathrm{session}}$ during the initialization phase, the Modbus client and the Modbus server proceed with secure communication using authenticated encryption with associated data. Each Modbus message is encrypted using the ASCON-128 algorithm and encapsulated in the COSE_Encrypt0 structure.

(1) 

Client-Side Message Construction

To construct a secure Modbus message, the client first prepares the plaintext Modbus PDU, denoted as M. It then generates a 128-bit cryptographically secure random nonce $iv$, an issuer identifier $iss$, and a monotonically increasing sequence number $seq$ to ensure freshness and ordering.

The protected header is constructed as a $\mathit{CBOR}$-encoded map containing cryptographic parameters:

$$\mathit{Protected}=\mathit{CBOR}\left(\right\{“\mathit{alg}”:“\mathit{ASCON}128”\left\}\right)$$

The unprotected header is a plaintext map that includes metadata required for session identification:

$$\mathit{Unprotected}=\{“\mathrm{iv}”:iv,“\mathrm{iss}”:iss,“\mathrm{seq}”:seq\}$$

The associated data for the AEAD operation is formed by concatenating the protected and unprotected headers:

$$\mathit{AAD}=\mathit{Protected}\parallel \mathit{Unprotected}$$

Using the established session key $\mathit{SK}$, the client encrypts the message and generates the authentication tag using ASCON-128 AEAD:

$$(M_{\mathit{enc}},\mathit{tag})=\mathit{ASCON}\_\mathit{Encrypt}(\mathit{SK},iv,M,AAD)$$

The ciphertext field is constructed by appending the tag to the encrypted payload:

$$\mathit{ciphertext}=M_{\mathit{enc}}\parallel \mathit{tag}$$

Finally, the complete Modbus message is assembled by combining the original $\mathit{MBAP}$ header and the $\mathit{COSE}\_\mathit{Encrypt}\mathit{0}$ structure:

$$\mathit{Packet}=H_{\mathit{MBAP}}\parallel COSE\_Encrypt0$$

where the $\mathit{COSE}\_\mathit{Encrypt}\mathit{0}$ object is composed of

$$\mathit{COSE}\_\mathit{Encrypt}\mathit{0}=(\mathit{Protected},\mathit{Unprotected},\mathit{Ciphertext})$$

(2) 

Server-Side Message Verification

Upon receiving a secure Modbus packet, the server begins by parsing the standard MBAP header $H_{\mathit{MBAP}}$ and extracting the COSE_Encrypt0 structure. The structure consists of the protected header $\mathit{Protected}$, unprotected header $\mathit{Unprotected}$, and the ciphertext field $\mathit{ciphertext}$.

From the unprotected header, the server retrieves the session-related metadata, including the issuer identifier $iss$, the initialization vector $iv$, and the sequence number $seq$. The protected header is CBOR-decoded and verified to ensure that the correct algorithm (e.g., ASCON-128) is specified.

The associated data for decryption is then reconstructed by combining the protected and unprotected headers:

$$\mathit{AAD}=\mathit{Protected}\parallel \mathit{Unprotected}$$

The $\mathit{ciphertext}$ field is split into the encrypted payload and the authentication $\mathit{tag}$:

$$\mathit{ciphertext}=M_{\mathit{enc}}\parallel \mathit{tag}$$

The server retrieves the session key $\mathit{SK}$ corresponding to the session identifier $iss$, and performs decryption and authentication using the ASCON-128 AEAD algorithm:

$$M=\mathit{ASCON}\_\mathit{Decrypt}(\mathit{SK},iv,M_{\mathit{enc}},\mathit{tag},AAD)$$

If the authentication tag is valid, the message is accepted and the decrypted Modbus PDU M is processed. If the tag verification fails, the message is discarded to prevent unauthorized access or tampering.

5. Security Analysis

In this section, we present a comprehensive security and privacy analysis of the proposed authenticated and encrypted Modbus protocol. We formally define the adversarial capabilities under the Dolev–Yao threat model and provide cryptographic proofs for key security properties. Additionally, we validate the correctness of our security claims through formal verification using ProVerif (Version 2.05) [26].

5.1. Security Assumptions

We adopt the Dolev–Yao adversarial model to formalize the threat environment under which the proposed protocol operates. In this model, the adversary $\mathcal{A}$ is considered a probabilistic polynomial-time (PPT) entity with the following capabilities, grouped into three main categories relevant to cryptographic protocol analysis:

• Network control capabilities: The adversary has full control over the communication channel between the Modbus client and the server. $\mathcal{A}$ can intercept, block, replay, reorder, delay, or modify any transmitted messages. This grants $\mathcal{A}$ the ability to mount man-in-the-middle (MITM) attacks and message tampering.
• Active protocol interaction: The adversary may impersonate a client or server without access to their long-term secrets. $\mathcal{A}$ can initiate concurrent sessions, interleave or reflect messages between sessions, and craft arbitrary protocol-compliant or malformed messages in an attempt to deceive the other party. However, $\mathcal{A}$ cannot forge authentication tags or decrypt ciphertexts without access to the appropriate keys.
• Passive cryptographic analysis:$\mathcal{A}$ can observe all public parameters, exchanged ciphertexts, nonces, and identifiers. Nevertheless, the adversary cannot break the underlying cryptographic primitives, such as HMAC or authenticated encryption with associated data (AEAD), which are assumed to be secure under standard assumptions. That is, cryptographic primitives behave ideally (e.g., HMAC is UF-CMA-secure, encryption schemes provide IND-CCA security), and no side-channel leakage occurs.

Despite these capabilities, the adversary is assumed to be computationally bounded and therefore cannot break cryptographic primitives. Specifically, $\mathcal{A}$ cannot recover the pre-shared key $K_{\mathit{psk}}$ or the derived session key $\mathit{SK}$ unless it is explicitly leaked, such as key compromise through side-channel attacks, weak storage protections, or inadvertent transmission via unsecured channels. While our protocol assumes secure key provisioning prior to deployment, we acknowledge that, in practice, key leakage is a real threat. To address this, the scheme supports periodic rekeying and session key regeneration through fresh nonces during each session establishment. Additionally, the damage of long-term key exposure is limited by the use of ephemeral session keys, which are never reused and are not stored persistently. It is also assumed that $\mathcal{A}$ cannot forge valid MACs or authentication tags without the corresponding secret keys. The cryptographic algorithms used—namely ASCON-128 for encryption and ASCON-Hash for key derivation—are assumed to be secure, providing resistance against cryptanalytic attacks such as forgery, collision, and differential analysis. Notably, ASCON-128 was selected by the NIST Lightweight Cryptography standardization process, and has been shown to offer strong security with low computational overhead in constrained environments such as embedded systems and industrial control networks [27,28,29,30]. This makes it particularly suitable for Modbus-based IIoT applications. Additionally, all nonces used in the protocol, including $N_C$ and $N_S$, are assumed to be generated using a cryptographically secure pseudorandom number generator and are unpredictable to the adversary.

The security goals of the adversary include compromising the confidentiality of Modbus payloads, forging or modifying protocol messages without detection, impersonating legitimate clients or servers, replaying previously captured valid messages, and attempting to recover long-term or session-specific keys. Under these assumptions, we demonstrate in the subsequent analysis that our protocol achieves mutual authentication, confidentiality, integrity, and replay protection even in the presence of an active adversary with full network control.

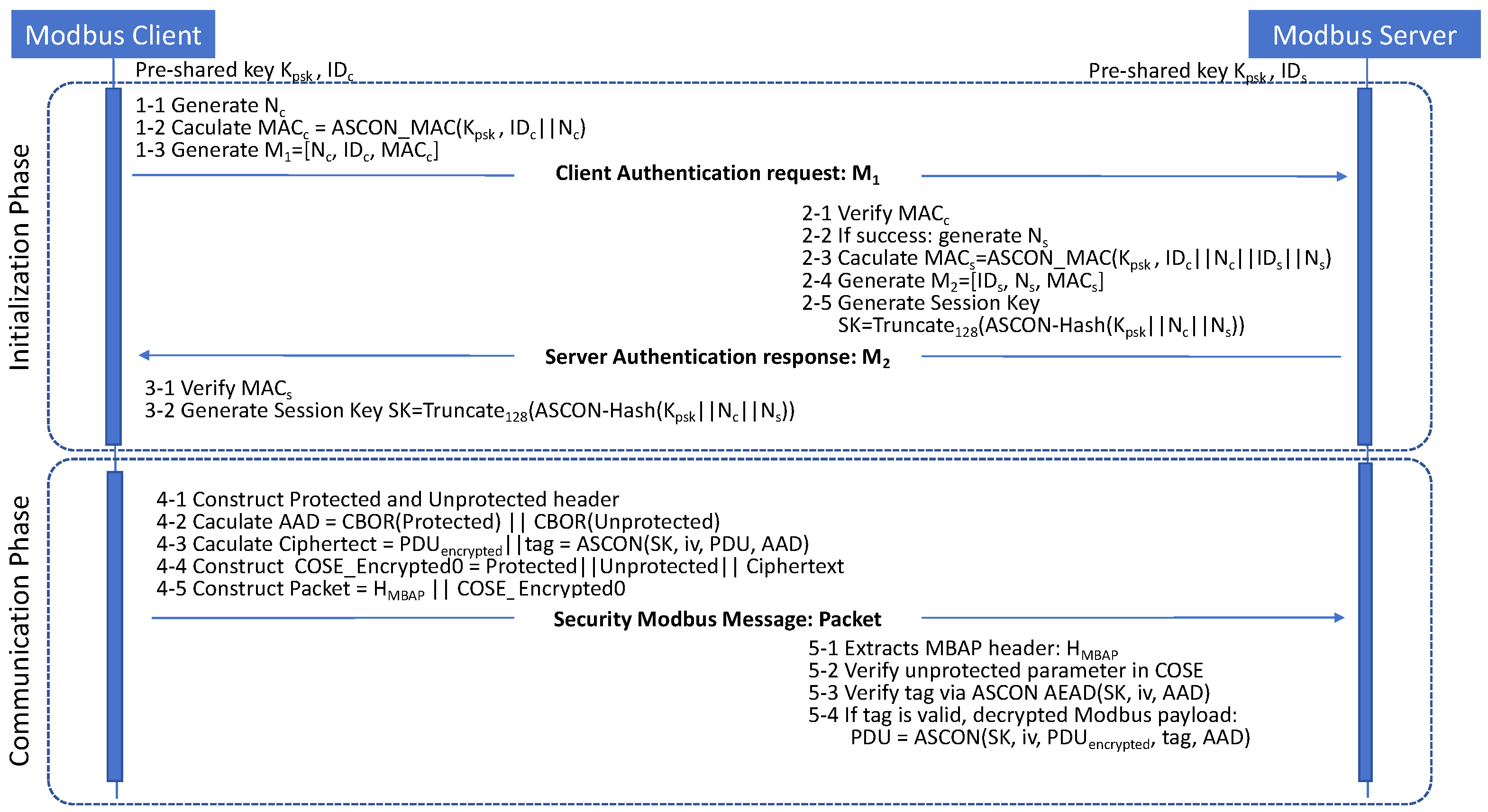
5.2. Initialization Phase Security Analysis

Theorem 1.

Mutual Authentication:   Under the assumption that HMAC is existentially unforgeable under chosen-message attacks (UF-CMA), and the nonces $N_C$ and $N_S$ are chosen uniformly at random and never reused, the mutual authentication protocol ensures the following:

(i) 

A Modbus server can verify that it is communicating with the legitimate Modbus client who knows the pre-shared key $K_{\mathit{psk}}$.

(ii) 

A Modbus client can verify that it is communicating with the legitimate Modbus server who knows $K_{\mathit{psk}}$.

Proof. 

We prove mutual authentication from both directions.

(i)

Server authenticates client: Given that the pre-shared key $K_{\mathit{psk}}$ is only known to legitimate participants, and assuming the HMAC construction based on ASCON_MAC is secure against existential forgery under chosen-message attacks (UF-CMA), an adversary cannot forge a valid MAC on a fresh pair $(I{D}_c,N_c)$. Additionally, since the nonce $N_c$ is randomly generated per session and never reused, the server can reject any replayed or pre-computed ${\mathit{Mac}}_s$. Upon receiving a valid ${\mathit{Mac}}_c$, the server is assured that the request originated from a party who knows $K_{\mathit{psk}}$, thus authenticating the client.

(ii)

Client authenticates server: Upon receiving $M_2$, the client verifies the ${\mathit{Mac}}_S$ using the pre-shared key. As before, if $K_{\mathit{psk}}$ is unknown to the adversary, then constructing a valid ${\mathit{Mac}}_S$ is computationally infeasible under UF-CMA. Moreover, because the MAC binds $N_S$ to the original client-generated $N_C$, the client can confirm that the server has received and processed its request, thereby preventing reflection or de-synchronization attacks. The freshness of $N_S$ also ensures replay resistance.

□

Conclusion. Since both authentication steps rely on cryptographically secure HMACs over unique session nonces and secret key material, and these ${\mathit{Mac}}_s$ cannot be forged or reused by an adversary under the stated assumptions, the protocol guarantees mutual authentication between the client and server. Therefore, an adversary controlling the communication channel cannot impersonate either party or interfere undetectably in the handshake process.

Formal Verification Result: We encoded the mutual authentication logic using ProVerif by defining the events client_authenticated and server_authenticated. As illustrated in Figure 4, all related security queries were successfully verified as true. These results provide formal assurance that the protocol achieves mutual authentication, even in the presence of a Dolev–Yao adversary.

Theorem 2.

Session Key Secrecy:   Assuming the hash function used in the session key derivation function is modeled as a random oracle, and that the pre-shared key $K_{\mathit{psk}}$ is kept secret, the session key SK is indistinguishable from a random value to any probabilistic polynomial-time (PPT) adversary who does not possess $K_{\mathit{psk}}$, even with full control over the network.

Proof. 

We prove that the session key established between the Modbus client and server remains secret from any adversary $\mathcal{A}$ under the standard Dolev–Yao threat model, augmented with the assumption that the hash function behaves as a random oracle.

The session key is derived from the shared key $K_{\mathit{psk}}$ and two freshly generated, uniformly random nonces $N_C$ and $N_S$. These nonces are included in the plaintext authentication messages exchanged during the initialization phase.

An adversary who does not know $K_{\mathit{psk}}$ cannot forge valid ${\mathit{Mac}}_S$ or predict future nonces, and thus cannot insert itself into the key derivation process. Moreover, since the nonces are never reused, each session produces a unique key, even if the same $K_{\mathit{psk}}$ is reused.

The key derivation function is modeled in the random oracle setting, meaning that unless $K_{\mathit{psk}}$ is known, the input to the hash function is computationally hidden from the adversary. Consequently, the adversary cannot distinguish the resulting $\mathit{SK}$ from a uniformly random 128-bit string.

Suppose by contradiction that an adversary $\mathcal{A}$ can distinguish $\mathit{SK}$ from a random string with non-negligible advantage. Then, $\mathcal{A}$ must have queried the random oracle on the correct tuple $(K_{\mathit{psk}},N_C,N_S)$, which requires knowledge of $K_{\mathit{psk}}$. However, without forging a valid MAC (which is infeasible under the UF-CMA assumption of HMAC), $\mathcal{A}$ cannot learn whether a guessed key is correct. Thus, we reach a contradiction.    □

Conclusion: Under the assumptions that the hash function used in session key derivation is modeled as a random oracle, the HMAC construction is existentially unforgeable under chosen-message attacks (UF-CMA), the nonces $N_C$ and $N_S$ are freshly generated and never reused, and the pre-shared key $K_{\mathit{psk}}$ remains secret and known only to the legitimate client and server, we conclude that no probabilistic polynomial-time (PPT) adversary can compute or distinguish the derived session key $\mathit{SK}$ from a random value. Consequently, the session key secrecy property is preserved against active and passive adversaries under the Dolev–Yao model.

Formal Verification Result: We modeled the secrecy of the session key SK in ProVerif using the query query attacker(SK). ProVerif returned false, indicating that the adversary cannot derive or guess the session key. This formally confirms that the session key secrecy property is preserved under the Dolev–Yao adversary model, as illustrated in Figure 5.

5.3. Secure Communication Phase Security Analysis

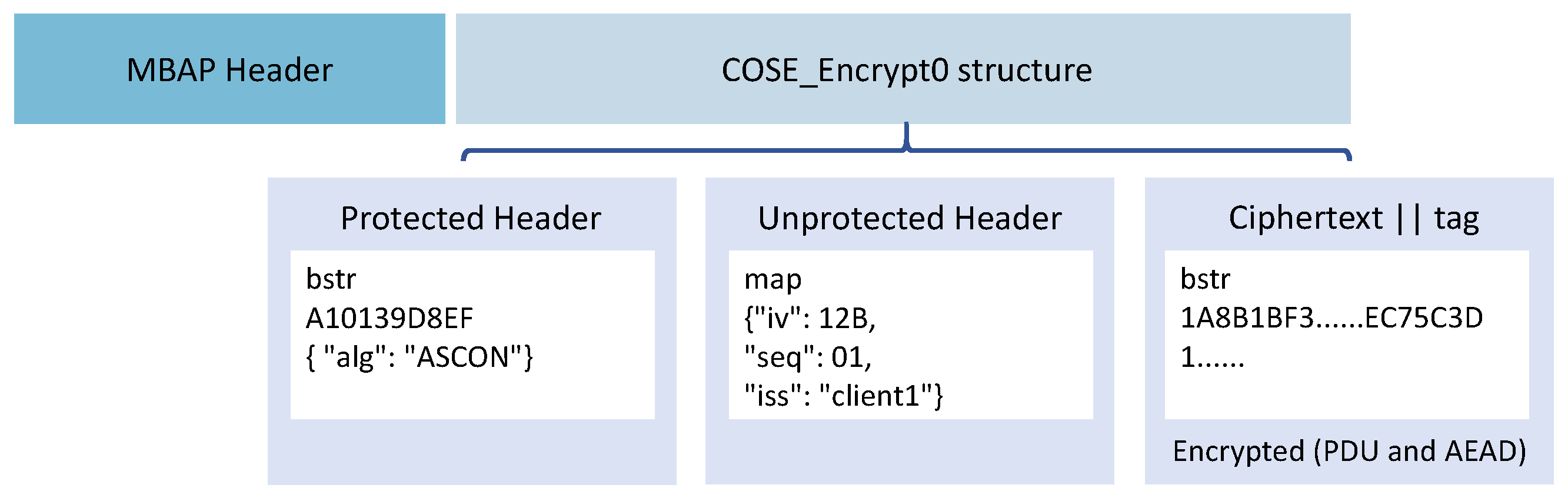
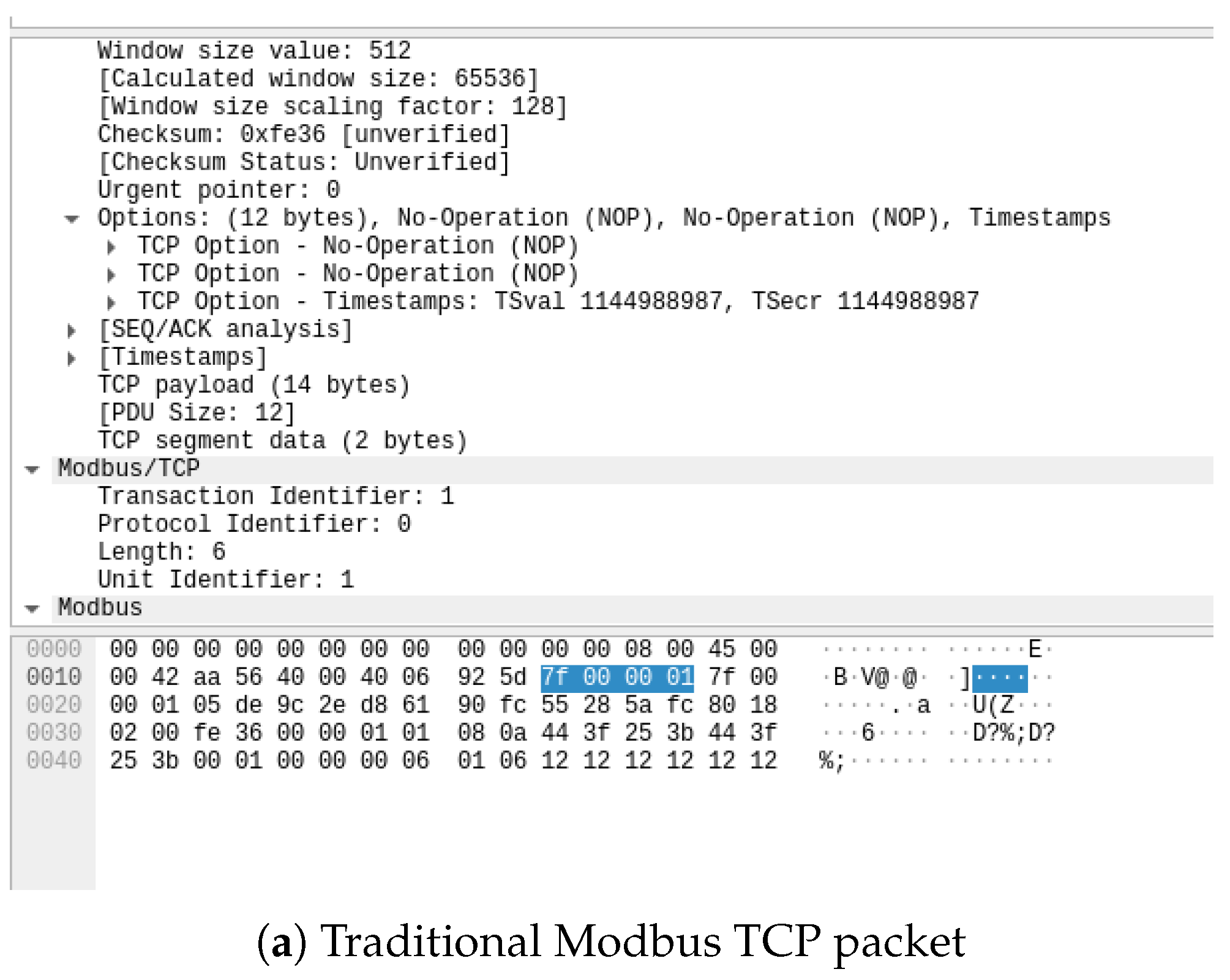
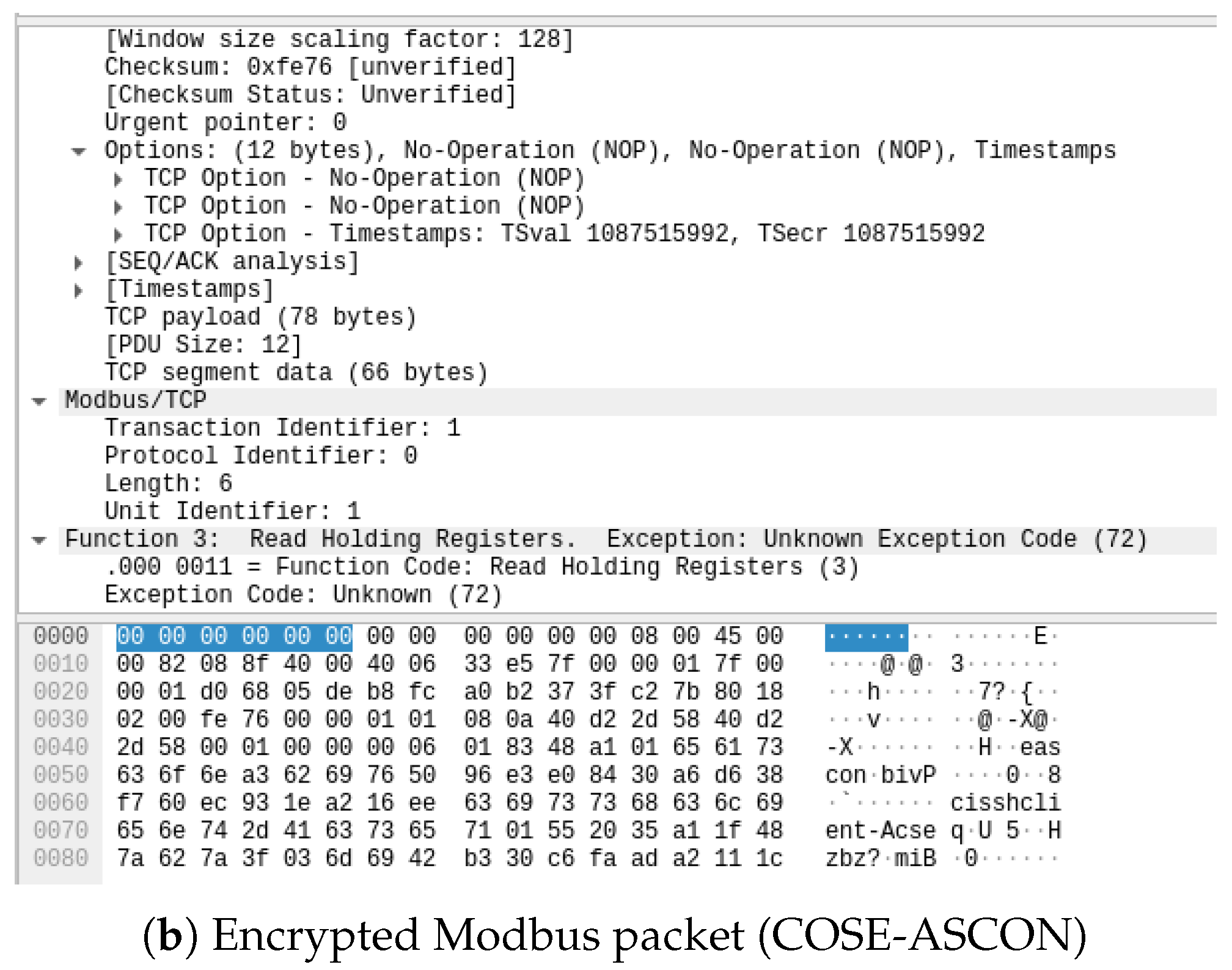
Once the session key $\mathit{SK}$ has been securely established, the Modbus client begins transmitting encrypted application-layer messages using the authenticated encryption algorithm ASCON-128, encapsulated within a COSE_Encrypt0 structure. In this section, we analyze the confidentiality, integrity, and authenticity guarantees of this message transmission stage.

Theorem 3.

Message Confidentiality:   Under the assumption that the ASCON-128 authenticated encryption scheme is IND-CCA-secure, and the session key SK remains secret, the secure Modbus transmission phase guarantees the confidentiality of the Modbus payload against any PPT adversary.

Proof. 

We assume a Dolev–Yao adversary who has full control over the communication channel: they can intercept, replay, modify, inject, or block any message exchanged between the client and server. However, the adversary does not know the session key $\mathit{SK}$, which is derived securely during the initialization phase as proven previously.

In the secure transmission phase, the Modbus client encrypts the plaintext payload M using the ASCON-128 authenticated encryption algorithm. The encryption input includes the plaintext message M, the session key $\mathit{SK}$, and optional associated data such as the protected header and unprotected header. The ASCON scheme outputs the encrypted message $M_{enc}$ and an authentication tag $tag$, which are combined and encoded into the ciphertext field of the COSE_Encrypt0 structure.

Given that ASCON-128 is IND-CCA-secure, any adversary who does not possess the correct session key cannot distinguish between the encryption of two chosen messages nor decrypt any message encrypted under that key. Moreover, attempts to tamper with the ciphertext will be detected due to the built-in authentication tag, and the message will be rejected upon decryption.    □

Conclusion: Under the assumptions that ASCON-128 provides IND-CCA security, and that the session key $\mathit{SK}$ is known only to the legitimate Modbus client and server, it follows that the ciphertext exchanged during the secure transmission phase leaks no information about the underlying Modbus payload to any PPT adversary. Therefore, the confidentiality of the Modbus message is preserved. Formal Verification Result: ProVerif confirmed the correspondence between the encrypted message output by the client and the ciphertext accepted by the server. Specifically, the query returned true, indicating that only ciphertexts generated by an authenticated sender are successfully verified and accepted by the receiver. This formally confirms the integrity and authenticity of message delivery under an active adversary, as shown in Figure 6.

Theorem 4.

Message Integrity and Authenticity:   Under the assumption that ASCON-128 is an authenticated encryption scheme with integrity of ciphertexts (INT-CTXT), and the session key $\mathit{SK}$ is known only to the legitimate participants, any modification of the ciphertext or forgery of a valid message by an adversary will be detected and rejected with overwhelming probability.

Proof. 

We consider a Dolev–Yao adversary $\mathcal{A}$ who has full access to the communication channel and can intercept, inject, replay, or modify messages. However, the adversary does not know the session key $\mathit{SK}$, which was securely established during the initialization phase and proven to remain secret.

In the secure communication phase, the Modbus client encrypts each payload using the ASCON-128 authenticated encryption scheme. Upon receiving a message, the Modbus server uses the shared session key and corresponding nonce to attempt decryption. The decryption function verifies the tag internally. If any part of the ciphertext or associated data has been altered, or if the ciphertext was not generated by someone possessing $\mathit{SK}$, the decryption will fail and the message will be rejected.

The INT-CTXT property of ASCON-128 ensures that it is computationally infeasible for any PPT adversary to generate a valid ciphertext–tag pair without knowing $\mathit{SK}$. This directly provides strong guarantees for message integrity. In addition, since only the legitimate sender can compute a valid tag over the message and associated context, successful verification at the receiver implies that the message originated from the party who shares $\mathit{SK}$—thereby establishing authenticity.

Moreover, because the tag computation includes associated data (such as protected headers), even tampering with protocol metadata or session context will result in decryption failure, ensuring contextual integrity as well.    □

Conclusion: Given that ASCON-128 is INT-CTXT-secure, and that $\mathit{SK}$ is known only to the legitimate parties, we conclude that the integrity and authenticity of the transmitted messages are guaranteed. Any attempt by an adversary to modify or forge messages will result in authentication failure and message rejection.

Formal Verification Result: The same correspondence assertion between message sent and message accepted also ensures message authenticity and integrity. ProVerif confirmed that no forged ciphertext can be accepted unless it was sent by an authenticated party.

Theorem 5.

Replay Protection:   Under the assumption that iv and sequence numbers are never reused within the same session and are strictly monotonic across messages for each sender identity, the protocol guarantees replay protection in the secure transmission phase.

Proof. 

In each session, the Modbus client includes a unique iv $\mathit{iv}$ and a strictly increasing sequence number $\mathit{seq}$ in the unprotected header of each COSE_Encrypt0 message. The issuer identifier $\mathit{iss}$ specifies the identity of the message originator, allowing the server to isolate and track sequence numbers on a per-client basis.

On the server side, for each known $\mathit{iss}$, a per-client state is maintained, recording the latest accepted sequence number or a sliding replay window. Upon receiving a new message, the server performs the following checks: (i) whether the $\mathit{seq}$ value for the given $\mathit{iss}$ has already been processed, or (ii) whether it is smaller than the expected next sequence number. If either case holds, the message is rejected as a replay.

Furthermore, because the $\mathit{iv}$, $\mathit{seq}$, and $\mathit{iss}$ are bound to the authenticated ciphertext via the authenticated encryption scheme ASCON-128 (typically as associated data), any alteration or reuse results in authentication tag failure. This ensures that replayed ciphertext, even if bit-wise-identical, is detected based on prior sequence use or contextual mismatch during tag verification. An adversary operating under the Dolev–Yao model, capable of intercepting and resending prior messages, cannot bypass these defenses without also forging a valid tag under a new context. Given the security of ASCON-128 under the INT-CTXT and nonce-respecting assumptions, such forgeries are computationally infeasible.    □

Conclusion: By embedding unique nonces and strictly increasing sequence numbers tied to the sender identity, and by enforcing per-sender replay validation and authenticated decryption, the protocol achieves strong replay protection. This guarantee holds against any PPT adversary in the Dolev–Yao model, provided that nonces and sequence numbers are used correctly and without reuse. Our current design assumes strictly increasing sequence numbers to protect against replay attacks. However, in practical environments, devices may experience unexpected reboots or desynchronization due to power loss, and networks may exhibit delays or packet reordering. To address these issues, sequence number windows (e.g., sliding window protocols) can be employed to tolerate minor reordering, and devices can securely persist their counters across reboots using non-volatile memory or secure elements. Alternatively, incorporating lightweight challenge–response mechanisms or timestamps can enhance robustness against such threats in unstable network conditions.

6. Experiments and Evaluation

In this section, we evaluate the performance and security effectiveness of the proposed secure Modbus protocol. The evaluation aims to answer the following key questions: RQ1. Does the proposed protocol introduce acceptable computational and communication overhead under constrained industrial device settings? RQ2. How does our design compare with existing lightweight secure Modbus enhancements in terms of efficiency and security guarantees?

6.1. Implementation and Experimental Setup

We implemented the proposed secure Modbus protocol entirely in C, using the ASCON-128 authenticated encryption algorithm and a lightweight CBOR encoder to support the COSE_Encrypt0 message structure. The cryptographic core is based on the official reference implementation of ASCON, released by its original designers. (https://github.com/ascon/ascon-c, accessed on 11 September 2025). The library provides both a portable reference version and optimized implementations for different architectures such as ARM, AVR, and x86. In our work, we selected the reference implementation to ensure platform independence and correctness.

The experimental platform is a bare-metal embedded system based on an ARM Cortex-M4 microcontroller running at 120 MHz with 256 KB of RAM. All code was compiled using GCC 10.3. To obtain accurate performance data, we used the processor’s built-in Data Watchpoint and Trace (DWT) cycle counter, which enables fine-grained timing measurements without additional instrumentation.

We also performed packet-level trace analysis using Wireshark to visually inspect the difference between traditional Modbus TCP communication and our secure COSE-ASCON scheme.

6.2. Wireshark Packet-Level Trace

To complement our implementation, we performed packet-level inspection using Wireshark to visually demonstrate the security benefits of the proposed Modbus+ASCON scheme, as shown in Figure 7.

Figure 7a illustrates a traditional Modbus TCP message captured during a typical operation of the 0x03 function code. The entire message is transmitted in plaintext. As a result, passive adversaries can easily infer the control logic and operational details from intercepted packets. Moreover, without any cryptographic protection, such packets are vulnerable to tampering and replay attacks by active adversaries.

In contrast, Figure 7b shows a packet protected using our COSE-ASCON scheme. The Modbus payload is fully encrypted and encapsulated in a COSE_Encrypt0 structure. The protected header contains the algorithm identifier, while the unprotected header includes the sequence number, issuer ID (iss), and initialization vector (iv). These fields are authenticated as associated data during encryption. The actual ciphertext, comprising the encrypted Modbus message and a 128-bit authentication tag, is indistinguishable from random bytes and prevents any leakage of protocol semantics.

6.3. Security Feature Comparison

6.3.1. Comparison with Existing Secure Modbus Schemes

To demonstrate the effectiveness of our proposed scheme, we compare it with representative Modbus TCP security enhancement approaches, as shown in

Table 2. Comparison of security features across secure Modbus enhancements.

Scheme	Conf.	Int./Replay	ID Binding	Std. Format	TLS-Free	Key Update
Modbus + SHA-2/AES	✓	✓	✗	✗	✓	✗
Modbus + MD5/RSA	✓	✓	✗	✗	✓	✗
Modbus over TLS	✓	✓	✓	✓	✗	✓
Modbus + SHA256/AES	✓	✓	✗	✗	✓	✗
Modbus + SM3/SM4	✓	✓	✗	✗	✓	✗
Modbus + SM enhanced	✓	✓	✗	✗	✗	✓
Our Scheme	✓	✓	✓	✓	✓	✓

Conf.: confidentiality; Int./Replay: integrity and replay protection; ID Binding: binding of device identity in authentication; Std. Format: use of standardized data format (e.g., COSE); TLS-Free: does not rely on TLS/PKI infrastructure; Key Update: support for per-message or session key derivation.

.

Schemes such as [6,7] adopt AES for data confidentiality and RSA-based digital signatures for identity authentication. While these designs achieve basic security goals, their reliance on heavyweight public key operations and the absence of structured replay protection mechanisms limit their applicability in constrained environments. For instance, ref. [7] introduces synchronization identifiers to resist replay attacks, but such mechanisms remain vulnerable to manipulation due to lack of cryptographic binding.

The approach in [31] employs TLS directly atop Modbus TCP. Although this delivers robust end-to-end security through well-established cryptographic protocols, it incurs significant complexity in certificate management and demands a full TLS stack, which is often infeasible for lightweight industrial devices.

Schemes like [17] introduce timestamps to detect replays, but transmit them in plaintext, leaving them susceptible to tampering. Similarly, ref. [16] relies on the SM3 hash function to provide data integrity and identity verification, but lacks strong replay protection. The design in [8] enhances this by incorporating random nonces and timestamps to improve freshness and authenticity, but again transmits these elements unencrypted, which weakens their effectiveness in adversarial environments.

In contrast, our scheme integrates authenticated encryption using the ASCON-128 algorithm within the COSE_Encrypt0 structure. Critical metadata such as sequence numbers, nonces (iv), and issuer identifiers (iss) are included as associated data, ensuring that they are cryptographically bound to the message and verified during decryption. This design not only guarantees message confidentiality and integrity, but also enforces strong identity binding and robust replay protection.

Furthermore, our scheme supports lightweight key update capabilities across sessions without requiring certificate-based infrastructures or TLS stack dependencies. Using a standardized COSE-based format and lightweight authenticated encryption, our solution offers a well-balanced combination of strong security, minimal overhead, and high interoperability, making it particularly well suited for deployment in resource-constrained industrial Modbus environments.

6.3.2. Comparison with Industrial Security Standards

Several standardization efforts have been developed to enhance the security of industrial communication protocols, notably IEC 62351 [32] and DNP3-SA [33]. As shown in

Table 3. Comparison with existing industrial security standards.

Aspect	IEC 62351	DNP3-SA	Our Scheme
Scope	Power system comm.	DNP3-based SCADA	Modbus IIoT systems
Protocol Layer	Transport	Application	Application
Cryptographic Features	TLS/IPsec	MAC-only	AEAD
Handshake Complexity	High (certs, DH)	Low	Low (no certs)
Resource Overhead	High	Low	Low
Encryption Algorithm	AES/TLS suite	None (MAC only)	ASCON-128
Suitable for Constrained Devices	✗	✓	✓

, these standards offer valuable security guarantees but may not be optimized for highly constrained industrial environments, particularly in legacy or resource-limited deployments such as those using Modbus. IEC 62351 is a comprehensive security framework designed for power system protocols, including IEC 60870-5-104 [34] and IEC 61850 [35]. It integrates existing transport-layer security protocols such as TLS and IPsec to provide encryption, authentication, and secure key exchange. While it ensures strong security properties, its dependence on X.509 certificate infrastructures, public key cryptography (e.g., Diffie–Hellman key exchange), and full TLS/IPsec stacks introduces considerable complexity, computational burden, and memory footprint. As a result, IEC 62351 is often impractical for deployment on microcontroller-class Modbus devices with strict resource and latency constraints.

DNP3-SA is a lightweight security extension for the Distributed Network Protocol version 3 (DNP3), widely used in SCADA systems [36]. It employs symmetric key cryptography with message authentication codes (MACs) and sequence numbers to ensure message authenticity and freshness. However, DNP3-SA does not provide confidentiality, leaving sensitive data vulnerable to eavesdropping or manipulation over untrusted networks.

In contrast, our scheme is specifically tailored for lightweight industrial protocols like Modbus that lack native security features. It incorporates authenticated encryption using the NIST-standardized ASCON algorithm and employs COSE/CBOR encapsulation to ensure structured, compact, and interoperable message formats. Unlike DNP3-SA, our scheme provides full message confidentiality in addition to integrity and replay protection. Compared to IEC 62351, it achieves significantly lower overhead by avoiding certificate management and heavy transport-layer protocols. These characteristics make our solution especially suitable for resource-constrained IIoT devices that require minimal memory, fast processing, and compatibility with legacy fieldbus architectures.

6.4. Performance Evaluation

6.4.1. Latency and Runtime Overhead

We selected the Modbus security enhancement based on SM3 and SM4 [8] as a baseline for comparison, as it currently represents one of the most efficient lightweight solutions in terms of runtime performance among TLS-free secure Modbus implementations. Its use of domestic cryptographic primitives and minimal protocol overhead makes it particularly suitable for deployment in industrial control systems with strict resource constraints and real-time requirements.

Table 4. Performance comparison between our scheme and SM3/SM4-based baseline.

Operation	Our Scheme ($\mathsf{\mu }$s)	SM3/SM4 Baseline ($\mathsf{\mu }$s)
Client Key Exchange	769.00	491.46
Client Encrypt	66.44	54.86
Server Key Exchange	274.67	436.48
Server Decrypt	4.80	368.90
Modbus PDU Size	31 bytes	28 bytes

presents a detailed comparison of runtime performance between our proposed scheme and the scheme that utilizes SM3 for hashing and SM4 for symmetric encryption. The metrics include the time cost of key exchange and payload encryption/decryption on both the client and server sides, as well as the final Modbus PDU size.

From the client-side perspective, our scheme incurs a higher computational overhead. Specifically, the key exchange takes approximately 769 $\mathsf{\mu }$s in our design, compared to 491 $\mathsf{\mu }$s for the SM-based baseline. The encryption operation shows a more significant difference: 66.44 $\mathsf{\mu }$s for COSE-ASCON versus only 55 $\mathsf{\mu }$s for SM3/SM4. This increase is primarily due to the additional COSE structure, and the overhead of AEAD computation in software. Despite this, the overhead remains within acceptable bounds for Modbus applications, which typically operate with low message frequency and real-time margins in milliseconds.

On the server side, our scheme demonstrates a clear advantage. Key exchange is faster (274 $\mathsf{\mu }$s vs. 436 $\mathsf{\mu }$s), and decryption performance is dramatically better (4.8 $\mathsf{\mu }$s vs. 369 $\mathsf{\mu }$s). This confirms the efficiency of ASCON for authenticated decryption in software environments and shows that the proposed scheme is especially suitable for server-side deployment in resource-constrained industrial nodes.

In terms of message size, the final Modbus PDU size increases slightly from 28 bytes to 31 bytes due to the inclusion of COSE headers and authentication tags. The 3-byte overhead is minimal and does not significantly impact network bandwidth in typical Modbus deployments.

To further validate the lightweight nature of our scheme, we estimate the memory and energy efficiency based on our implementation results, as shown in

Table 5. Memory usage comparison between SM3/SM4 and ASCON schemes.

Scheme	RAM (Bytes)	ROM (KB)
SM3/SM4	480	5.2
Our Scheme	376	2.3

. We conducted our evaluation using the official ASCON reference implementation [37] and the GmSSL cryptographic library [38], both compiled and executed in a simulated Linux environment. The results show that the ASCON-based implementation requires approximately 276 bytes of RAM and 2.5 KB of ROM, significantly outperforming the SM3/SM4 combination, which occupies a larger memory footprint due to internal buffers and S-box lookup tables. These findings confirm that our COSE+ASCON design is highly suitable for constrained IIoT environments with strict memory and code size limitations.

6.4.2. Cryptographic Computation Analysis

We further abstract the computation complexity of each scheme in terms of cryptographic operations in

Table 6. Comparison of computation overhead with related schemes.

Schemes	Sender	Receiver
Modbus with SHA-2/AES [6]	$H+AE{S}_E+RS{A}_S$	$H+AE{S}_D+RS{A}_V$
Mpdbus with MD5/RSA [7]	$2H+AE{S}_E+RS{A}_S$	$2H+AE{S}_D+RS{A}_V$
Modbus over TLS [31]	TLS	TLS
Modbus with SM3 [16]	$2H+SM{4}_E$	$2H+SM{4}_D$
Modbus with SHA256/AES [17]	$H+AE{S}_E$	$H+AE{S}_D$
Modbus with SM3/SM4 [8]	$4H+2SM{4}_E+SM{4}_D$	$4H+SM{4}_E+2SM{4}_D$
Our Scheme	$2H+ASCO{N}_E$	$2H+ASCO{N}_D$

H denotes a cryptographic hash function (e.g., SHA-256 or SM3); $AE{S}_E$/$AE{S}_D$ denote AES encryption and decryption; $SM{4}_E$/$SM{4}_D$ denote SM4 encryption and decryption; $RS{A}_S$/$RS{A}_V$ denote RSA signing and verification; $ASCO{N}_E$/$ASCO{N}_D$ denote ASCON authenticated encryption and decryption, respectively.

. Our design uses two hash invocations (ASCON-Hash) and a single ASCON-128 per message, while others may require additional MACs or separate encryption and hashing stages. RSA-based designs incur significant costs due to key size and signing overhead, and TLS encapsulates multiple layers of handshake and cipher negotiation.

Our scheme introduces two hash operations (one for HMAC in handshake; one for session key derivation) and a single invocation of the ASCON AEAD function per message. Compared with the SM3/SM4-based design, which requires multiple symmetric operations per message, our scheme reduces the number of cipher operations while retaining equivalent or stronger security properties.

In particular, although ASCON is a lightweight cipher, it combines both encryption and authentication in one pass, simplifying the design and reducing state management overhead. From the receiver’s perspective, the decryption side benefits from ASCON’s efficiency, resulting in faster processing as observed in our implementation.

Moreover, schemes relying on RSA incur significantly higher computational overhead due to expensive public key operations, which are unsuitable for constrained devices. TLS-based solutions, while secure and mature, bundle multiple layers of cryptographic operations, leading to opaque and relatively heavy computation.

The computation model confirms that our ASCON-based approach strikes a practical balance between performance and security. It reduces the number of cryptographic operations compared to some existing SM4-based designs, while offering modern authenticated encryption semantics and compatibility with lightweight industrial deployments.

7. Conclusions

In this paper, we present a lightweight security enhancement scheme for the Modbus TCP protocol that combines the ASCON-128 authenticated encryption algorithm with the standardized COSE_Encrypt0 message format. Our protocol provides mutual authentication, nonce-based session key derivation, and robust replay protection without altering Modbus semantics or relying on TLS. Experimental results on both embedded and Linux testbeds demonstrate that, despite modest additional overhead from CBOR encoding and AEAD processing, our scheme outperforms SM3/SM4-based approaches in server-side decryption efficiency and delivers stronger guarantees of identity binding and integrity. The modular, standards-compliant design makes it practical for deployment in resource-constrained industrial environments. Future work will focus on hardware acceleration and formal verification to further enhance performance and assurance.