1. Introduction
Atmospheric aerosols, increasingly influenced by anthropogenic activities, play critical roles in Earth’s climate system and significantly affect air quality and human health [
1,
2,
3]. Visibility, a crucial indicator of atmospheric clarity and aerosol loading, has shown a continuous decreasing trend globally due to increased anthropogenic particulate matter emissions in these years [
4,
5,
6]. The significantly deteriorated visibility level harms human health and increases risks in daily mortality, raising an urgent need for constructing a diurnal cycle of visibility level monitoring. The appearance of visibility degradation is due to the presence of particulate matter that scatters light rays, which forms the basis of visibility monitoring.
Standards instrumentation for visibility monitoring includes electro-optical sensors such as nephelometers, measuring the light scattering coefficient, and transmissometers, determining the light extinction coefficients [
7]; these measurements are converted to meteorological optical range, often termed reference visibility, using Koschmieder’s equation [
8]. While these approaches serve as ideal tools and established benchmarks, the high cost of these instruments restricts their deployment, and hence, they are scarce. Aside from these cost-prohibitive approaches, remotely sensed images are increasingly being used as the data source for monitoring visibility, including nighttime applications [
9,
10]. These studies typically relate satellite aerosol optical depth or radiance reductions over light sources to visibility values, providing accurate visibility estimates for large coverage. However, satellite-based approaches are inherently constrained by factors including cloud contamination, the presence of missing values, and relatively low update frequency (revisit frequency), making it difficult to produce a real-time and complete observation record in space and time.
Limitations of traditional visibility monitoring approaches—namely the cost and sparsity of ground stations and the temporal constraints of satellite data—have motivated exploration of alternative methods, particularly those utilizing camera imagery. For instance, the existing highway cameras or vehicle headlamps have been attempted to estimate the atmospheric visibility value [
11,
12,
13]; webcam images are explored as an alternative way to measure visibility levels with a series of image processing techniques. Methods employing such digital photographs generally capture embedded visual features (e.g., color contrasts, texture contrasts, and saturation density) that reflect scattering effects and then construct mapping functions between these visual features and visibility measurements. In addition to these fixed camera sensors, several reports have also suggested a new paradigm for monitoring that utilizes portable and low-cost sensors to provide data in near real-time [
14,
15], with the smartphone acting as an accessible and ubiquitous sensor. Consequently, smartphone photographs have been discussed as being a potentially promising atmospheric sensor in a crowdsensing way [
16,
17,
18,
19]. These methods, however, are primarily limited to daytime conditions; low light, poor quality, and impaired scenes present challenges for visibility monitoring after dark [
20].
An earlier study by Narasimhan and Nayar [
21,
22] demonstrated that glow effects observed around light sources (e.g., streetlamps and car lights) at night are prominent manifestations of multiple scattering by particulate matter. They established that the spatial distribution of this scattering light intensity, as captured by a camera, represents the atmospheric point spread function (APSF) for that light source. The APSF describes how the intensities around light sources are spread along with the angular, and how the shape of the glow is varied by weather conditions. With the APSF, two key weather parameters (i.e., optical thickness and forward scattering parameter) can be approximated, enabling visibility estimation. This foundation work provides a physics-based framework for analyzing nighttime imagery and advances the understanding of nighttime light scattering by atmospheric particles [
21,
23]. However, their proposed approach requires known reference information (e.g., distance to light sources) and involves computationally intensive optimization (tens of minutes per image) to retrieve APSF parameters, precluding real-time applications. Subsequent research has thus focused on improving efficiency. For example, inspired by the successful application of the standard haze model [
24,
25], several studies incorporated the glow effect into image formation models, often using APSF parameters to improve nighttime image dehazing [
26,
27]. Although these methods efficiently model or mitigate glow effects for visual enhancement, they were primarily designed to generate visually clear images and typically do not yield highly accurate and consistent measurements of nighttime visibility. Hence, a significant need persists for a novel algorithm capable of accurate, real-time nighttime visibility estimation from single images.
In this paper, we propose a novel algorithm for deriving two weather indices, namely optical thickness index and forward scattering index, from smartphone photographs to estimate nighttime visibility. Glow effects around light sources (glow layer) are first separated from the input smartphone image, and thus APSF can be estimated from the separated glow layer. The optical thickness index and forward scattering index are subsequently derived by fitting the estimated APSF profile with an asymmetric generalized Gaussian distribution (AGGD) model. Finally, we estimate visibility using these two derived parameters. The algorithm’s performance in estimating the nighttime visibility is validated through a national-scale case study using smartphone images crowdsourced from the Internet.
This paper is structured as follows:
Section 2 reviews the physics of multiple light scattering under various weather conditions, which is the cause of glow effects around light sources.
Section 3 details the methodology for extracting atmospheric parameters from smartphone images, including APSF estimation and AGGD model fitting, and presents the model developed for final visibility estimation.
Section 4 presents the evaluation of the model-fitting performances and the results of visibility estimation. The discussion is presented in
Section 5, and perspectives and conclusions are also included.
2. Nighttime Multiple Light Scattering Under Weather Conditions
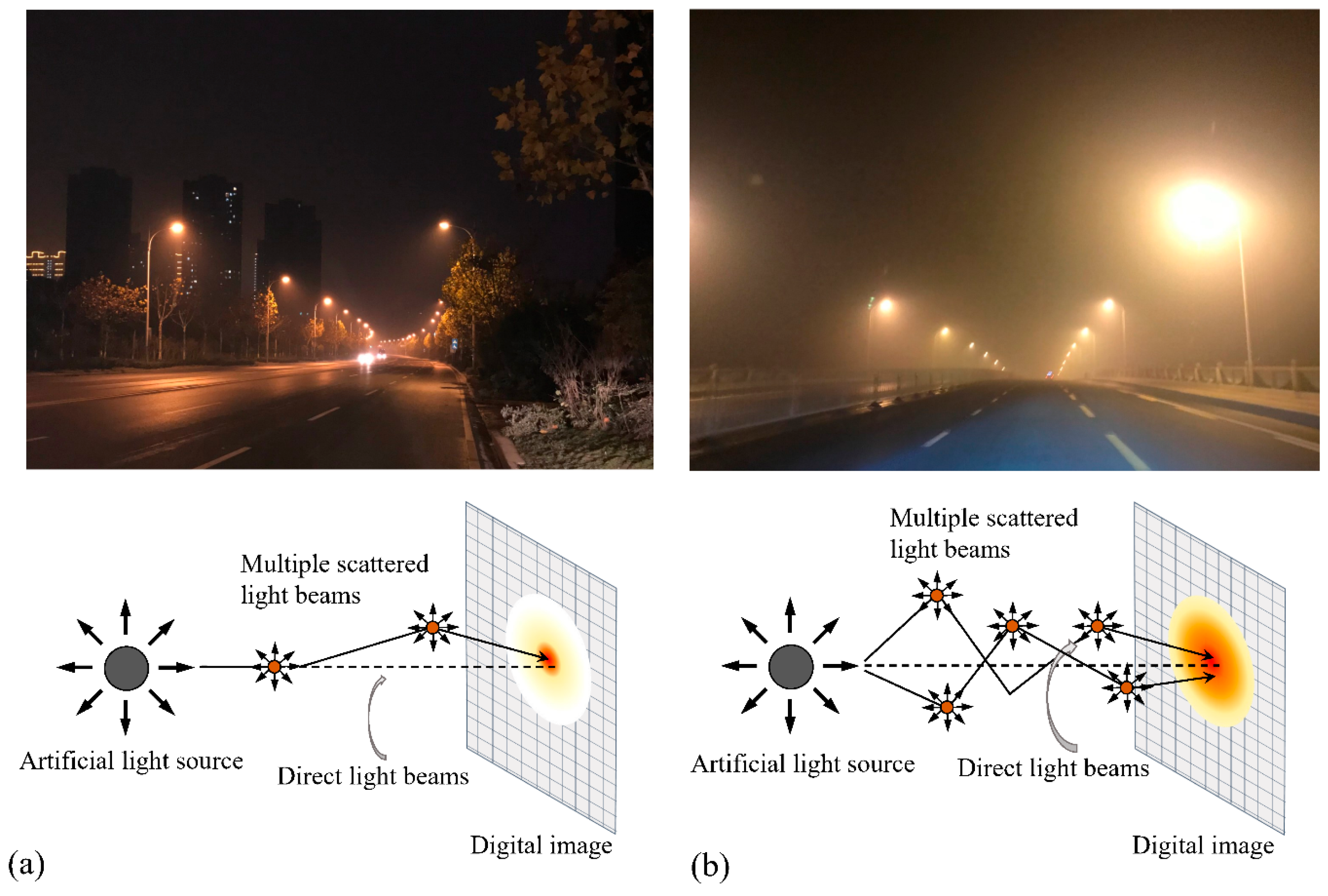
Atmospheric aerosols participate in light scattering and hence result in blurred vision. This reduction in clarity provides visual cues related to the intensity of scattering, which, in turn, can be used to infer atmospheric conditions, particularly aerosol loading. Virtually all methods for retrieving scattering properties rely on the assumption of single scattering dominance, which may be broken at nighttime when multiple scattering is prevalent. Multiple scattering refers to the light being scattered multiple times in various directions and is the dominant cause of the prominent glows around artificial light sources. On a clear night, relatively few aerosols participate in the multiple scattering process, resulting in small and concentrated glow effects around light sources (
Figure 1a). Conversely, on a heavily hazy night, a large number of aerosols are engaged in the multiple scattering process, leading to the formation of prominent, intense, and widely dispersed glow effects (
Figure 1b).
The prominent glow around artificial light sources at night arises mainly from two causes: one is the direct transmission of light, and the other one is the multiple light scattering, i.e., light becomes scattered several times in different propagation directions. Typically, the multiple scattered light is measured by the change in light flux through an infinitesimal volume by the Radiative Transfer Equation (RTE) [
28,
29], which is expressed as follows:
In Equation (1),
denotes the light intensity of a point source, which is determined by the cosine of the scattering angle
and the general phase function
. The scattering angle
is the angle between the scattered direction (
) and the incident direction (
).
is the optical thickness of the atmosphere, denoting the light attenuation in the medium, and is determined by distance
and extinction coefficient
. When taking various weather conditions into account, the general phase function in Equation (1) is usually modeled by the Henyey–Greenstein phase function [
30], which is expressed as follows:
where
is the forward scattering parameter, which varies under different weather conditions (e.g., clear air, mist, fog, or rain). The larger the particle size, the greater the forward scattering parameter. When
approaches 0, the scattering tends to be isotropic; when
approaches 1, the scattering tends to be anisotropic with the scattered direction to be
. An approximate value of the forward scattering parameter
under various weather conditions is listed in
Table 1 [
31]. From Equations (1) and (2), we can infer that the multiple light scattering depends on three factors: the optical forward scattering parameter [
], the optical thickness [
], and the scattered angle [
]. Suggested in [
21], this angle-dependent anisotropic model can be loosened to an angle-free model. The modified angle-free model constitutes the atmospheric point spread function (APSF).
As discussed above, the glow is the addition of direct transmission and multiple scattering of light in the night environment. The direct transmitted light is determined by the intensity of each artificial light source; the multiple scattered light is intimately influenced by the weather conditions (i.e., optical thickness and forward scattering parameter ), forming various shapes of the glow that can be measured or computed by the APSF. These provide the basis for discriminating against various atmospheric conditions.
3. Nighttime Visibility Estimation
As the glow present in the night image (i.e., two-dimensional glow) is a projection of the real-world APSF onto the image plane, the key factors (optical thickness and forward scattering index) for measuring the nighttime visibility level are unable to be retrieved directly. Nevertheless, the nighttime visibility can still be estimated in an indirect way by deriving the weather indices, optical thickness index (OTI), and forward scattering index (FSI) from smartphone photos.
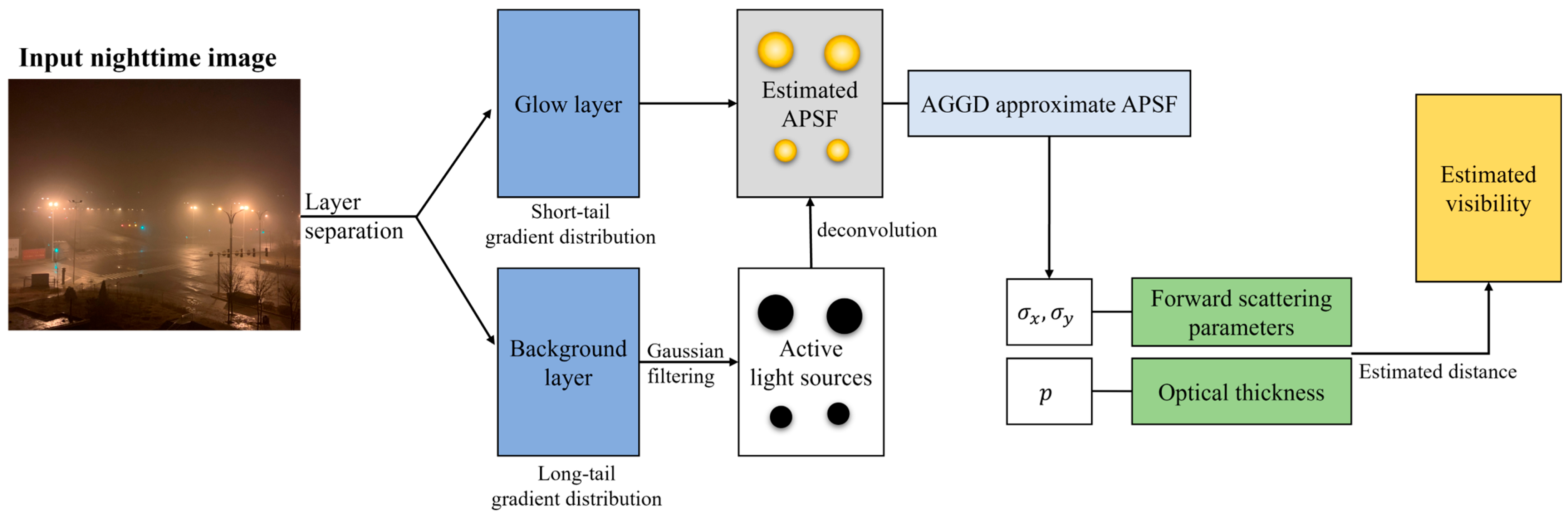
To derive a weather index from a smartphone photo, we were inspired by the common-sense observation that the naked human eye can easily distinguish an ambient environment at night using visual properties (e.g., size and shape of the glow) without additional knowledge. A schematic overview of the proposed algorithm is shown in
Figure 2. Given a smartphone photo, we first separate the layer from photographs that only contain the glow effects, i.e., the glow layer, by assuming the photographs with haze are a linear combination of multiple layers (see
Section 3.1). APSF presents how the intensity around the light source propagates and diminishes, estimated from the area where the artificial light source is detected (see
Section 3.2). The APSF is then fitted by an asymmetric generalized Gaussian distribution (AGGD) filter [
23,
32]; two weather indices, that is, the optical thickness index and the forward scattering index, can be calculated from the AGGD parameter [
23] (see
Section 3.3). Using weather indices, the visibility distance can then be estimated using the proposed model (see
Section 3.4).
3.1. Nighttime Haze Model with Glow Layer Separation
As shown in
Figure 1, particulate matter participates in the scattering and plays a significant role in booming the glow that is observed around light sources. The impaired nighttime scene is often characterized via the standard nighttime haze model [
27]:
where
is the intensity of the hazy image is observed and is the result of a linear combination of three components (i.e., direct attenuation, local air light, and the glow). The first two components constitute the nighttime image in a clear view, while the last component characterizes the glow effects when haze is presence.
, the direct attenuation, describes the scene radiance and its decay in the atmosphere; the former,
, is the scene radiance when no haze is observed; and the latter,
, represents the transmission map that denotes the light attenuation process from farthest to the observer.
describes the local airlight, resulting from the localized environmental illumination and
is the local atmospheric light.
is a glow layer, characterizing the glow effect around light sources. Thus, the nighttime hazy image can be regarded as the addition of two image layers (the clear layer and the glow layer).
In accordance with Li et al. [
27], the glow layer and clear layer of the nighttime image show distinct disparity in their texture gradient histograms, because the hazy weather imposes the dominant smoothing effect around the light sources, making the gradient histogram of the glow layer close to a short-tailed distribution, while giving the gradient histogram of the clear layers a long-tailed distribution. We exploit this feature and employ the layer separation method, in which two layers that hold significant differences in texture gradient histograms can be separated by approximating the probabilities [
33]. As discussed above,
forms the clear night view, namely de-glow layer, while
, the glow layer, presents the glow effect. Following [
33], two layers can be decomposed by constructing a probability distribution on each gradient histogram:
where
represents short-tailed Gaussian distribution with
is the gradient value of the glow layer.
is a very small value, making the Gaussian narrow and quickly fall off.
is a long-tailed distribution;
is also a small value, controlling the shape of the Gaussian.
is a normalization factor;
is a sparse penalty term that prevents
from quickly dropping to zero. The optimal solutions can be solved by standard optimization methods. Examples of separated glow layers and de-glowed layers of different nighttime photographs under various weather conditions are shown in
Figure 3.
3.2. APSF Estimation
The glow effects around light sources arise from direct transmission and multiple scattering, which are governed by the joint effect of light-source intensity and multiple scattered lights. APSF that presents at nighttime photographs can be obtained by analyzing the approximately ideal isolated light sources.
where
is the glow layer and
denotes a convolution operator.
is the locally active light source image that can be estimated through high-pass filtering or a standard moving window detection.
3.3. Weather Indices Retrieval by AGGD Filter for APSF
As shown in
Section 2, the shape of APSF varies under different weather conditions. In addition, the projection of the APSF onto the image plane manifests as a two-dimensional glow. This glow often appears as an asymmetric, radially decaying intensity pattern centered around the light source (
Figure 4B), whose characteristics are dictated by atmospheric conditions. Ideally, a solution of APSF (optical thickness and forward scattering parameter) can be obtained by numerical simulations [
21,
22]. However, solving APSF with numerical methods may not converge in all situations (all levels of hazy conditions) [
23,
27]. Alternatively, one possible approach is to use Gaussian distribution to fit the profile of APSF, which is an analog to the standard solution for point spread function (PSF) in the astronomical and satellite image deblurring literature (see, for example, [
34,
35]) and assumes that PSFs can be treated as symmetric objects with a known precise shape. In practice, however, the assumption of symmetric light scattering and a known shape of light sources is always unreasonable for smartphone photographs because of the various shooting angles and the unknown relative positions and distances to light sources.
To model the shape of the APSF, we employ the asymmetric generalized Gaussian distribution (AGGD) filter [
36], a flexible function capable of representing a wide range of distribution shapes and thus accommodating the majority of real-world conditions. The AGGD is defined as follows:
where
is the coordinate of a point of a glow region.
is the shape parameter, which controls the distribution’s kurtosis and reflects the extent of multiple scattering;
are scale parameters representing the spread in the horizontal and vertical directions, and
and
represent their mean values, respectively.
is the gamma function,
.
is a scale function. A nonlinear least-squares fit computes the AGGD approximation to an APSF as follows:
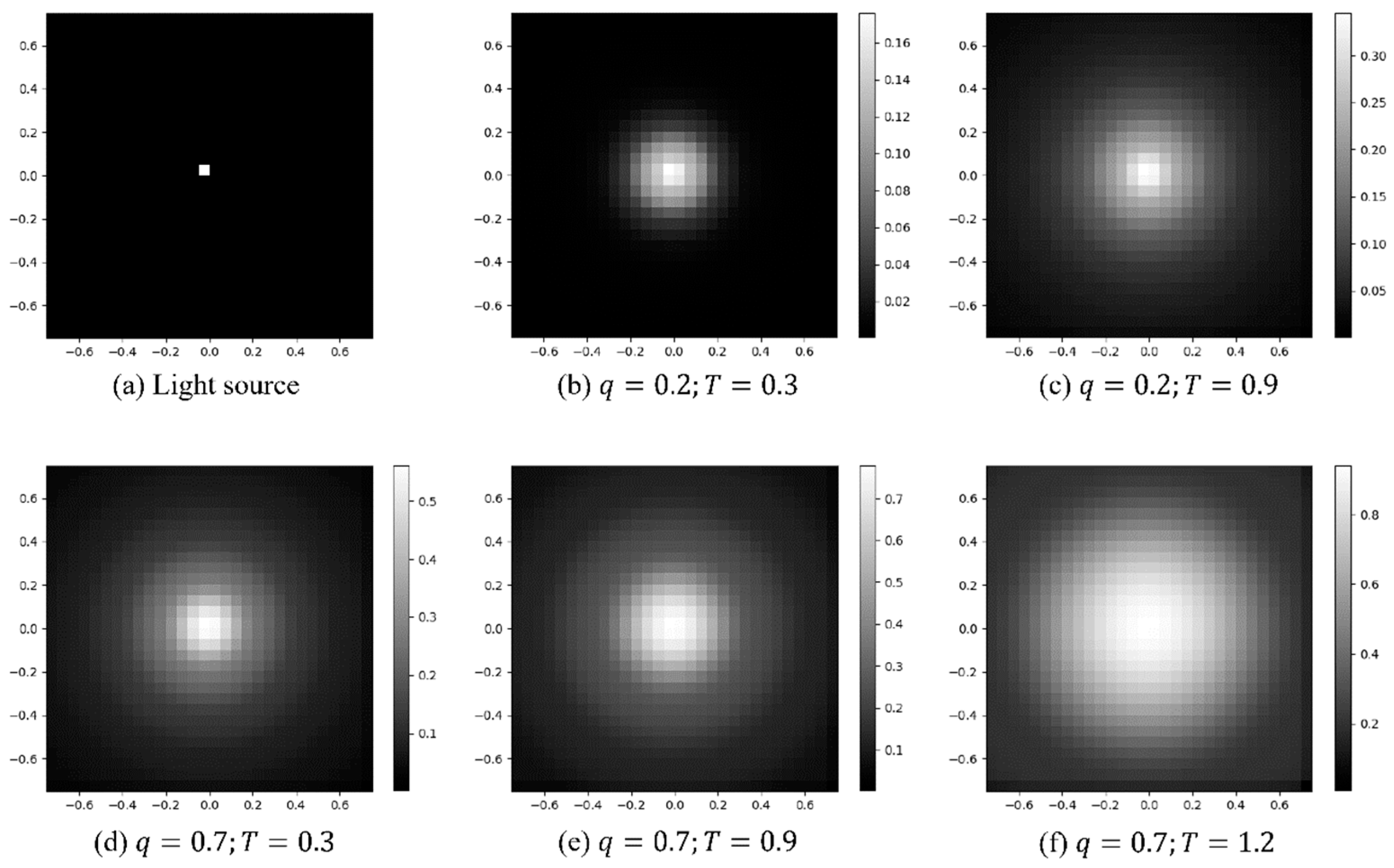
This minimization can be obtained with any standard optimization program. We note that, in practice, solutions for AGGD may sometimes not be unique. An average operation for AGGD parameters after having an anomalous detection of solutions (including abnormal variances and high costs) is generally sufficient to derive reasonable results. Examples of APSFs on the glow layers and the fitted AGGD are presented in
Figure 4.
Because the APSF extracted from a glow layer is often non-unique due to the presence of multiple light sources. Putting the single glow layer as a unity to directly estimate AGGDs for multiple APSFs may take several minutes and is indeed unnecessary to do, given the uninformative nature of the outer regions of the APSF profile. A subtraction operation, therefore, can be applied to effectively reduce the computational time used for distribution approximation. To do this, we first chop up the glow layer into non-overlapping sub-windows; each sub-window contains only an APSF, and the size of the sub-window is determined by a hard threshold, turning off all pixels whose ratio of the light intensity to the local maximum (intensity of the brightest center) is under 80%. We then discard the outer regions of each sub-window, leaving essentially an APSF contour not contaminated by the background, and compose the final results from the APSF of each inner sub-window.
The AGGD (Equation (7)) enables simulating APSF under various atmospheric conditions by adjusting its parameter (
), thus serving as a proxy for quantifying multiple scattering effects. This is consistent with observations (
Figure 4C)—as atmospheric particulate matter becomes denser, the extent of the glow increases, typically reflected by increasing the shape parameters. Suggested by previous research [
23,
26], AGGD parameters (
,
p) and weather parameters can be linked by a linear mapping. We follow the proof presented in [
23]; two weather indices, optical thickness index (OTI) and forward scattering index (FSI), can be estimated from AGGD parameters as follows:
where
is a fitting parameter. We note that
and
should be close, although values of them are naturally different.
Figure 4 shows plots of the fitted AGGD from APSF and the corresponding glow layer under three distinct weather conditions.
3.4. Visibility Estimation Model
The forward scattering index (
) and optical thickness (
) are coherently related with visibility [
37]. In this study, we only consider the nighttime photographs with haze; it is natural to assume that the forward scattering parameter should be close (as shown in
Table 1). As shown in
Section 2, the optical thickness parameter
, which refers to the ratio of intensity loss of incident light due to the scattering process in the atmosphere, is related to the visibility value:
where
is the atmospheric extinction coefficient;
is the visibility range; and
is the distance from the observed light sources to the observer. The relative distance can be measured by any object detection-based distance estimation technique [
38], assuming that the real object size is approximately the same (see
Supplementary Information S3). As suggested in [
39], a simple linear regression can be employed to model the relationship between visibility and the weather parameters. By combining Equation (8) with Equations (11) and (12), the nighttime visibility model based on the estimated optical thickness index (OTI) is given as follows:
where
is the fitting parameter. Equation (12) indicates, once the distance
is given, that the index
can be calculated; therefore, the visibility can be estimated through a linear regression model.
5. Discussion
In this paper, we have proposed an algorithm using only a single photograph to estimate nighttime visibility. This algorithm first extracts the essential feature that is influenced by multiple scattering at night, i.e., glow effects, from the separated glow layer of the photograph, and thus approximates two weather indices (i.e., optical thickness index
and forward scattering index
) from the glow by means of the AGGD filter, and then the visibility can be estimated from the weather indices. We conducted experimental validations on a nationwide dataset and evaluated the predictive power of this algorithm using the estimated visibility against ground-truth visibility. The results (
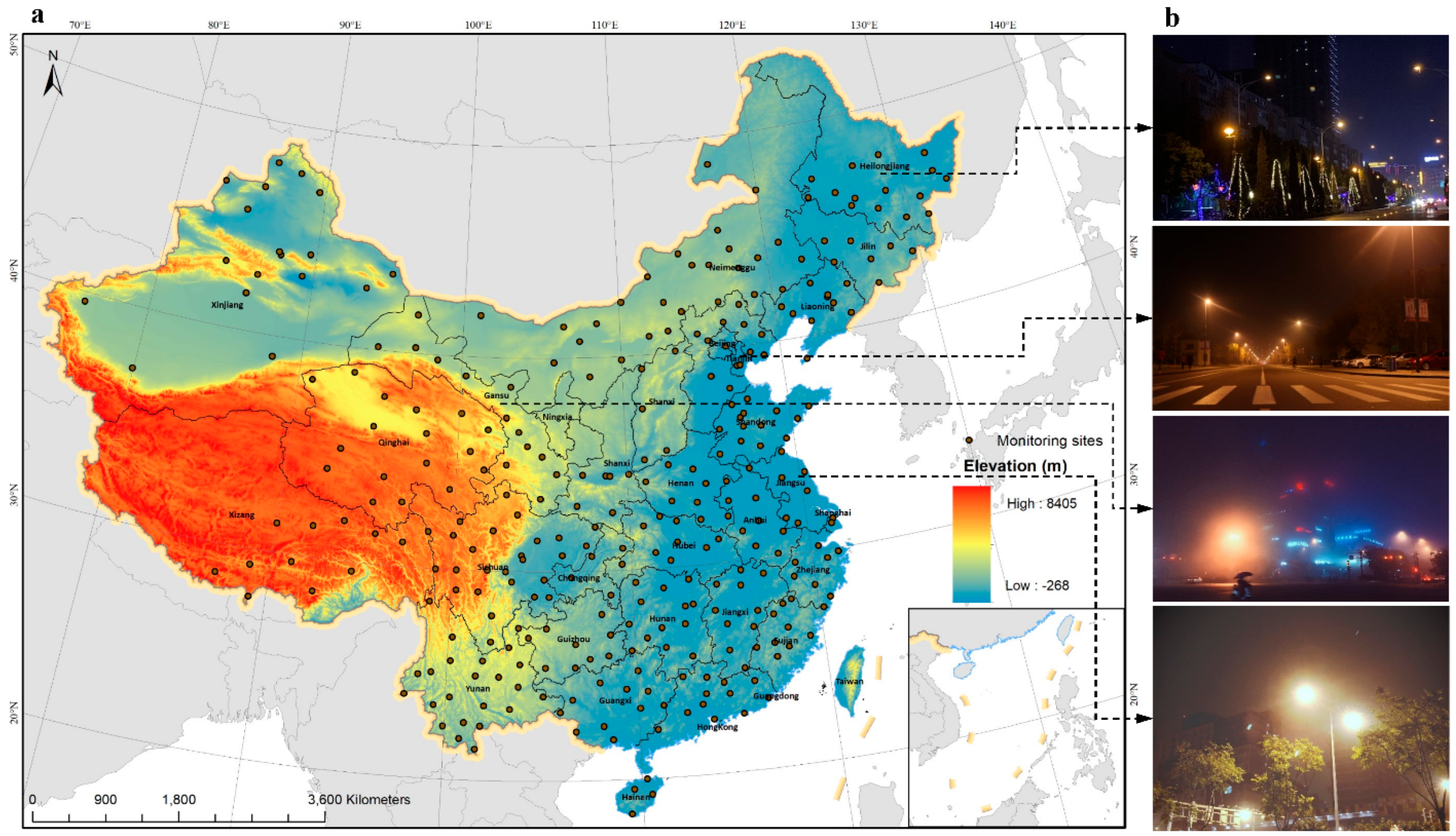
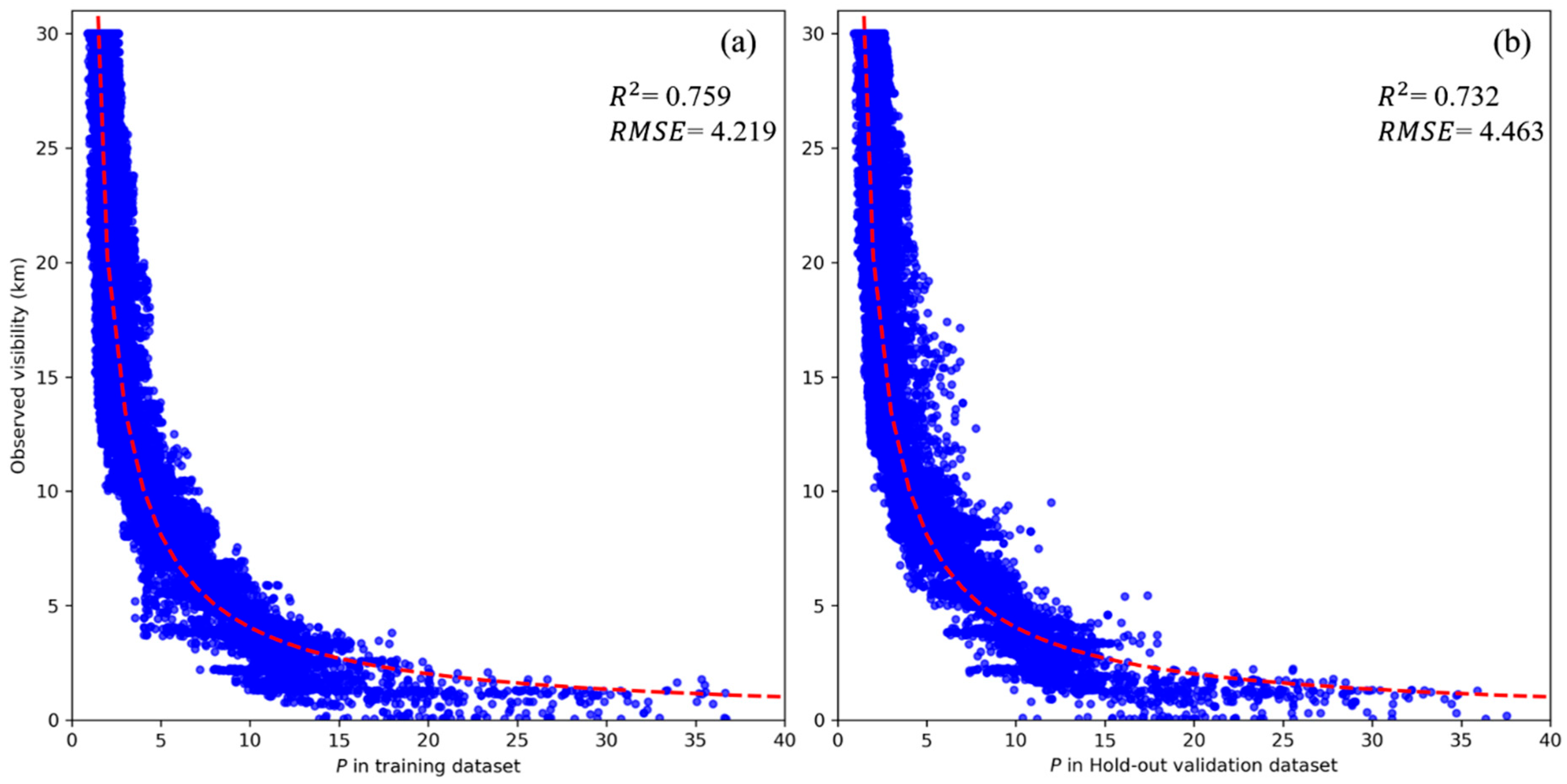
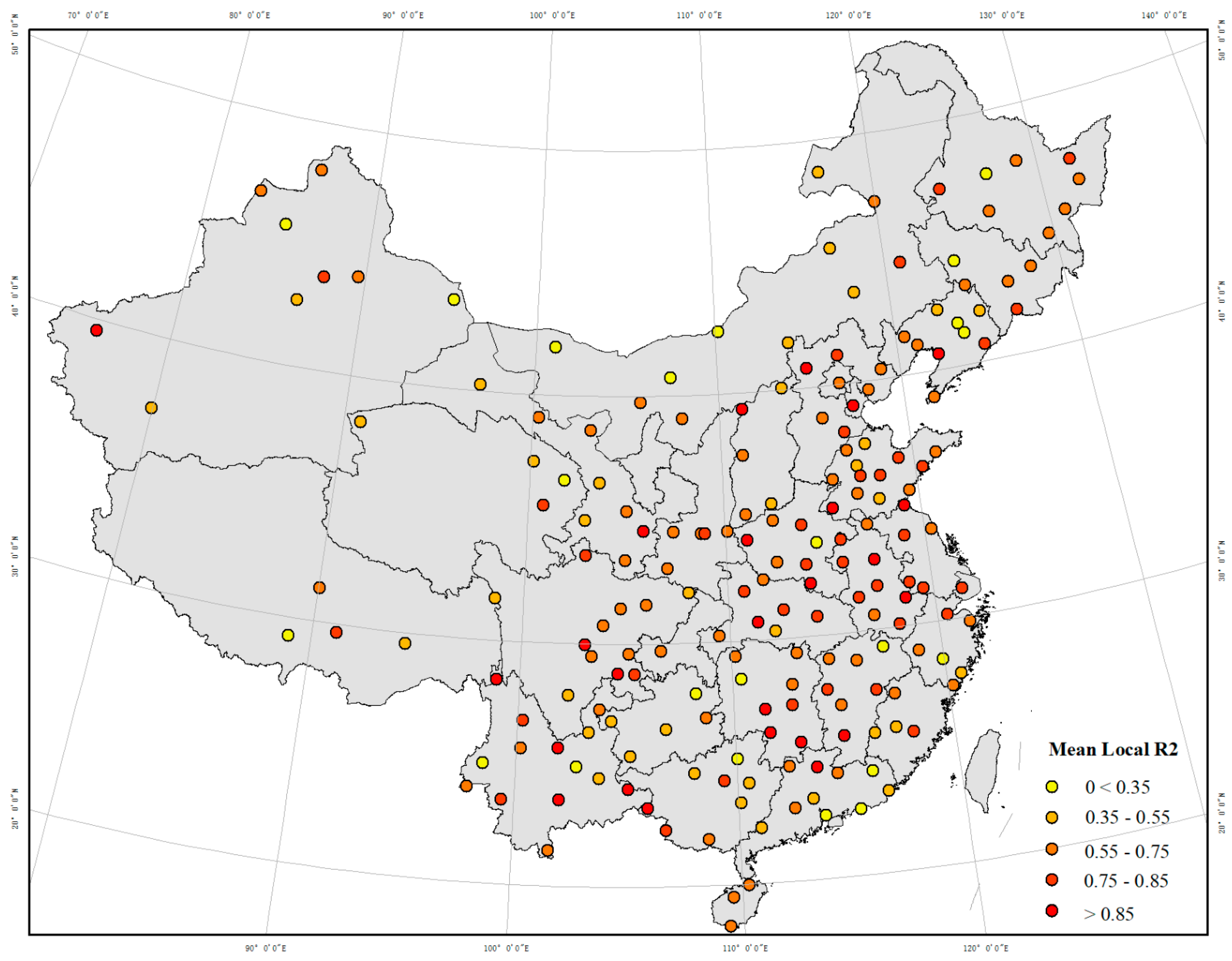
Figure 10) demonstrate that the proposed method reliably estimates nighttime visibility levels and reveals spatiotemporal heterogeneity. We also found that the local meteorological conditions and geographical patterns play key roles in visibility variability. Specifically, nighttime visibility tended to be higher (clearer) in the summer and lower (more impaired) in the winter in southern China. In contrast, the opposite pattern was observed in northern China.
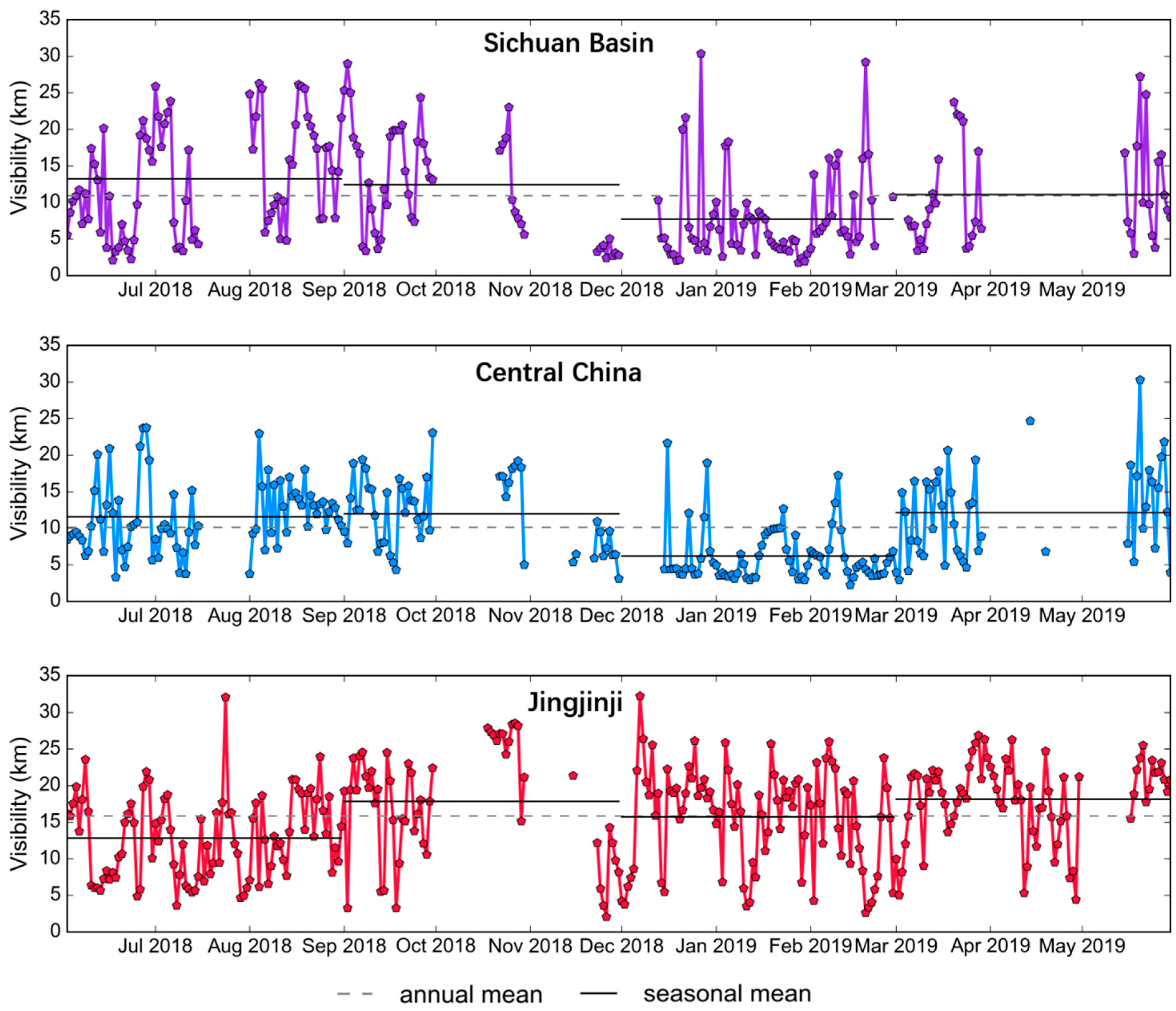
By considering the sensitivity of visibility with respect to the diverse conditions in the local regions, we further extended our study on three heavily polluted regions: Sichuan Basin, central China, and Jingjinji Metropolitan Region; presented the time series trends (from June 2018 to May 2019) of nighttime visibility estimated from crowdsourced data (
Figure 11); and analyzed the corresponding temporal variations. This regional analysis demonstrates that the visibility estimation model maintained strong prediction accuracy and proved robust for measuring visibility across areas with distinct meteorological conditions. The proposed algorithm offers a reliable nighttime visibility estimation, as reflected by the plausible long-term series trends derived (
Figure 11). This capability suggests applicability for various meteorological sensing tasks using smartphone photographs, such as complementing sparse official monitoring networks or assessing localized visibility conditions. These findings reveal that the proposed image processing-based nighttime visibility approach is feasible, holds great potential in predicting nighttime visibility trends, and therefore provides fine-scale spatiotemporal variations.
In addition, our algorithm estimates nighttime estimation relies on only a single smartphone photograph, without any auxiliary information (e.g., pre-defined reference images and pre-known visibility index), which goes beyond the methods used in previous research studies [
12]. By relaxing the restrictions on reference data, our algorithm has shown the ability and possibility of single nighttime photographs being used for real-world meteorological monitoring. Furthermore, previous studies have held negative views about applying nighttime photographs in the atmospheric perception, owing to the limitations such as low illuminance, poor quality, or impaired scenes [
58] (In contrast to these discussions, the experiments presented in this study provide evidence for the capability of using photographs in monitoring the visibility at night, broaden the potential applications with nighttime images, and highlight potential advantages to the use of mobile phones as an inexpensive and real-time meteorological sensing platform. In addition, the presented algorithm maps the spatio-temporal variations in nighttime visibility distribution, highlights the potential usage of crowd-sensed data to fill in the gap of sparsely distributed meteorological monitoring stations, and provides more portable ways to measure the visibility and sense the personal-level visibility.
Beyond the capability of the proposed algorithm, this paper shows a possible aspect of crowdsourced data to provide a new avenue for meteorological sensing. Crowdsourced data are now widely available and are considered as a potential addition to traditional observations [
15]. With the crowdsourced data, the proposed visibility estimation algorithm would be an economical approach compared to these deployed monitoring sites. As we have shown, current photographs crawled from the Internet could be used to provide real-time visibility estimates, such as long-term and large spatial coverage for monitoring. Additionally, because of the enormous amount of potential data available on the web (e.g., social media platforms like the Sina Weibo platform, Twitter, or Facebook), crowdsourcing approaches could be very effective to provide data on a small spatial scale and time granularity. Nevertheless, crowdsourced data and presented results in our study are limited to the city level because of the privacy issue; this is a problem that is relevant to many crowdsourcing endeavors, where crowdsourced observations are intended to discover potential information that may not align with the commercial intent and privacy protections of these social media platforms. Although data availability is a major concern, it does not preclude the use of such data in many studies. For example, to perform a large-coverage and fine-scale meteorological monitoring, smartphone applications or crowdsourced platforms could be deployed coupled with the proposed algorithm.
Although the proposed algorithm provides a potential avenue for monitoring the surrounding atmosphere in a crowdsourced way, it is still perhaps best viewed as an approach to supplement rather than replace the ground-based measures in the context of some limitations and assumptions. First, the proposed algorithm assumes relatively steady atmospheric conditions (e.g., clear air, haze, or fog), where pixel luminance can be modeled as the aggregate effect of scattering by numerous small particles. This assumption does not hold under precipitation (rain, ice, and snow), where scattering is dominated by large, non-spherical particles. Raindrops are individually detectable and often introduce motion streaks, while snow produces even more complex scattering due to its irregular grain shapes. These dynamic effects cannot be adequately captured by standard haze or nighttime haze models. Future work may address these conditions by integrating stereo imagery or auxiliary meteorological data. Second, the geotagged information of crowdsourced data are scarce (only city-level data are available) owing to the data availability and privacy issue. The potential heterogeneities within the city for characterizing the changes on a finer scale might not be presented. If crowdsourced data with precise geotagged information become available in the future, we will be able to make fine-grained observations in space and time. Nevertheless, this study is geared toward providing an alternative method for measuring the visibility in a low-cost manner in near real-time, and its effectiveness proves the validity of this algorithm in providing accurate nighttime visibility estimates. Third, in this work, edge intelligence refers to the use of citizen smartphones as distributed sensors, where images captured and shared online provide real-time atmospheric data from the network edge. Our focus is algorithmic, and while on-device deployment was not tested here, it remains an important direction for future work.