Ultra-Short-Term Photovoltaic Cluster Power Prediction Based on Photovoltaic Cluster Dynamic Clustering and Spatiotemporal Heterogeneous Dynamic Graph Modeling
Abstract
1. Introduction
- (1)
- We introduce a function to measure PV power convergence volatility and propose a dynamic clustering method based on volatility smoothing to extract the most predictable component of the PV cluster power.
- (2)
- We construct three heterogeneous graphs—volatility similarity, trend correlation, and amplitude matching—among sub-clusters to represent the system’s multi-layer relational structure, and we develop a spatiotemporal heterogeneous dynamic graph convolutional network to mine multiple relational patterns during system evolution and model dynamic sub-cluster nodes for effective forecasting of PV cluster power.
- (3)
- We embed a bidirectional temporal convolutional neural network that accounts for bidirectional temporal dependencies to capture node-level sequential relationships and obtain high-precision predicted PV cluster power.
2. Methodology
2.1. Dynamic Clustering of PV Stations via Aggregation-Smoothing Distance
2.2. Spatiotemporal Heterogeneous Dynamic Graph Convolutional Neural Network
3. Case Study
3.1. Comparison of Prediction Scenarios and Baseline Model
- (1)
- We apply the traditional holistic approach, cumulative method, statistical upscaling, and cluster static division strategies to forecast PV cluster power and evaluate their prediction performance and accuracy.
- (2)
- We compare the conventional dynamic cluster division schemes that rely on correlation or volatility metrics with the proposed clustering method based on the volatility-smoothing function under identical model backbones.
- (3)
- We benchmark the predictive accuracy of (i) conventional static/dynamic graph convolutional networks (SGCN/DGCN), (ii) spatiotemporal heterogeneous static/dynamic graph convolutional networks (STHSGCN/STHDGCN), and (iii) the proposed STHSGCN/STHDGCN coupled with a BITCN (STHSGCN-BITCN/STHDGCN-BITCN) across alternative division schemes.
3.2. Case Study of Traditional Cluster Power Prediction Methods
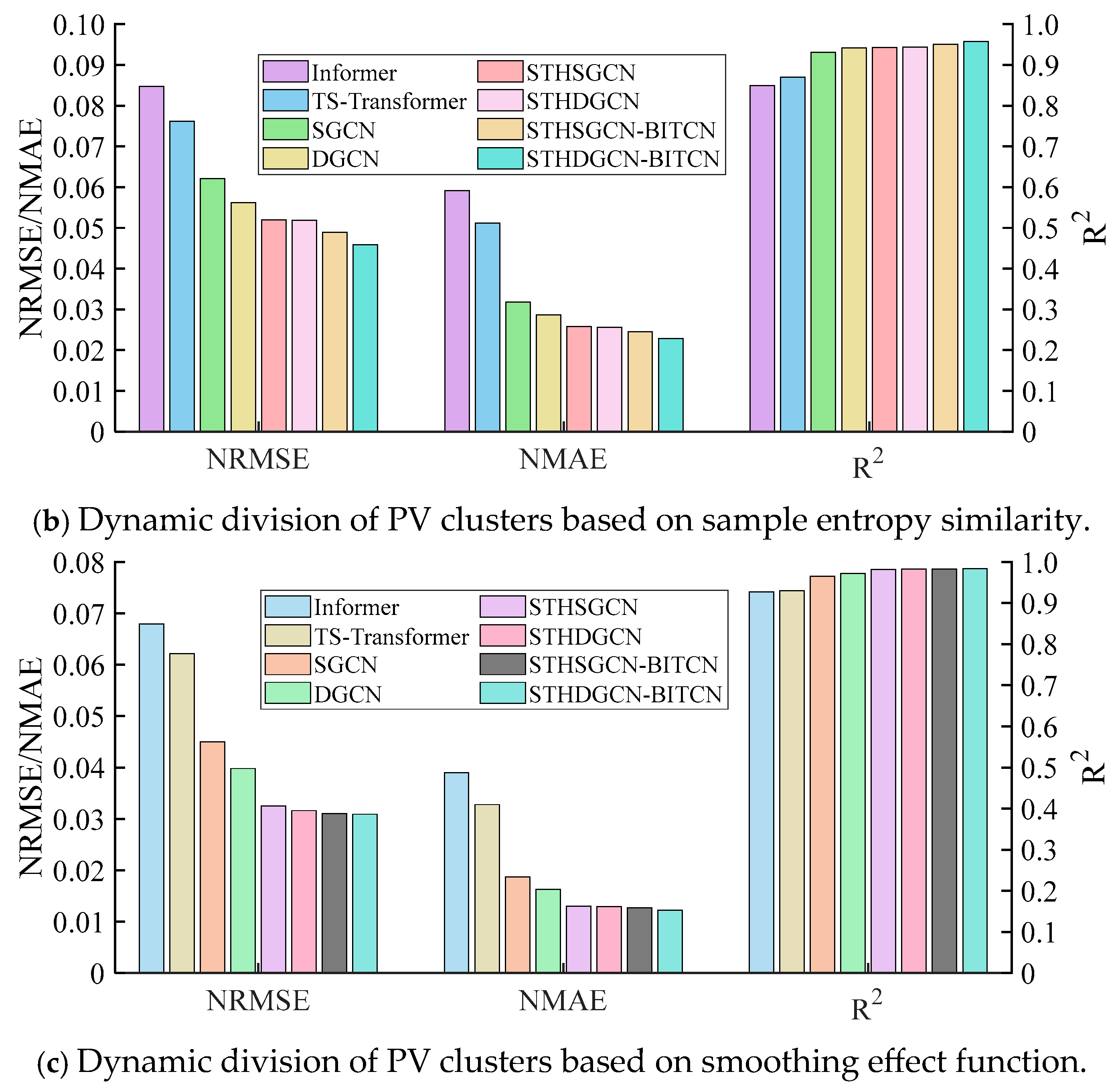
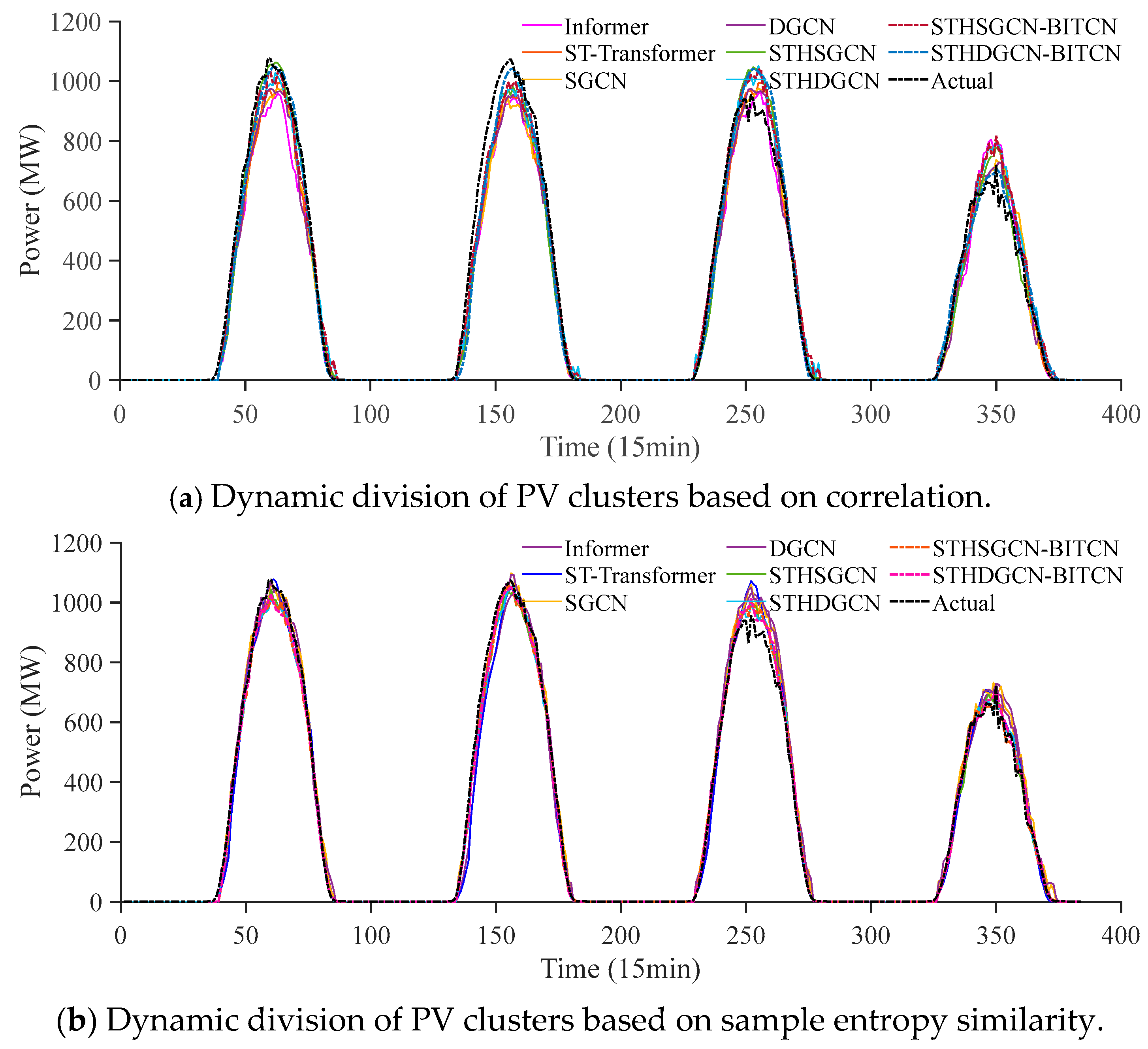
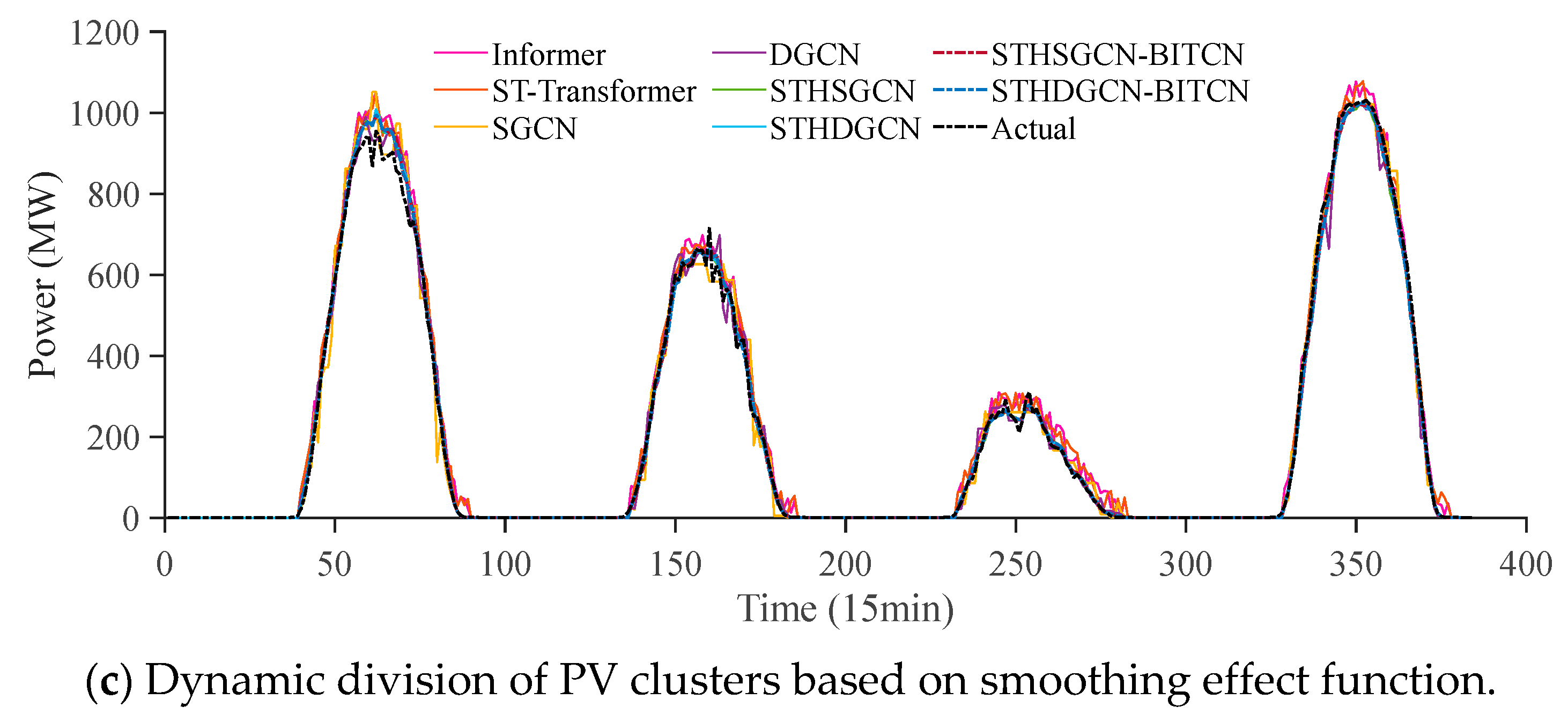
3.3. Comparative Analysis of Predictive Performance Across Different Dynamic Clustering Methods
3.4. Performance Comparison of the STHDGCN-BITCN Combined Model Across Different Clustering Methods
4. Discussion and Analysis
4.1. Modeling Cost Analysis
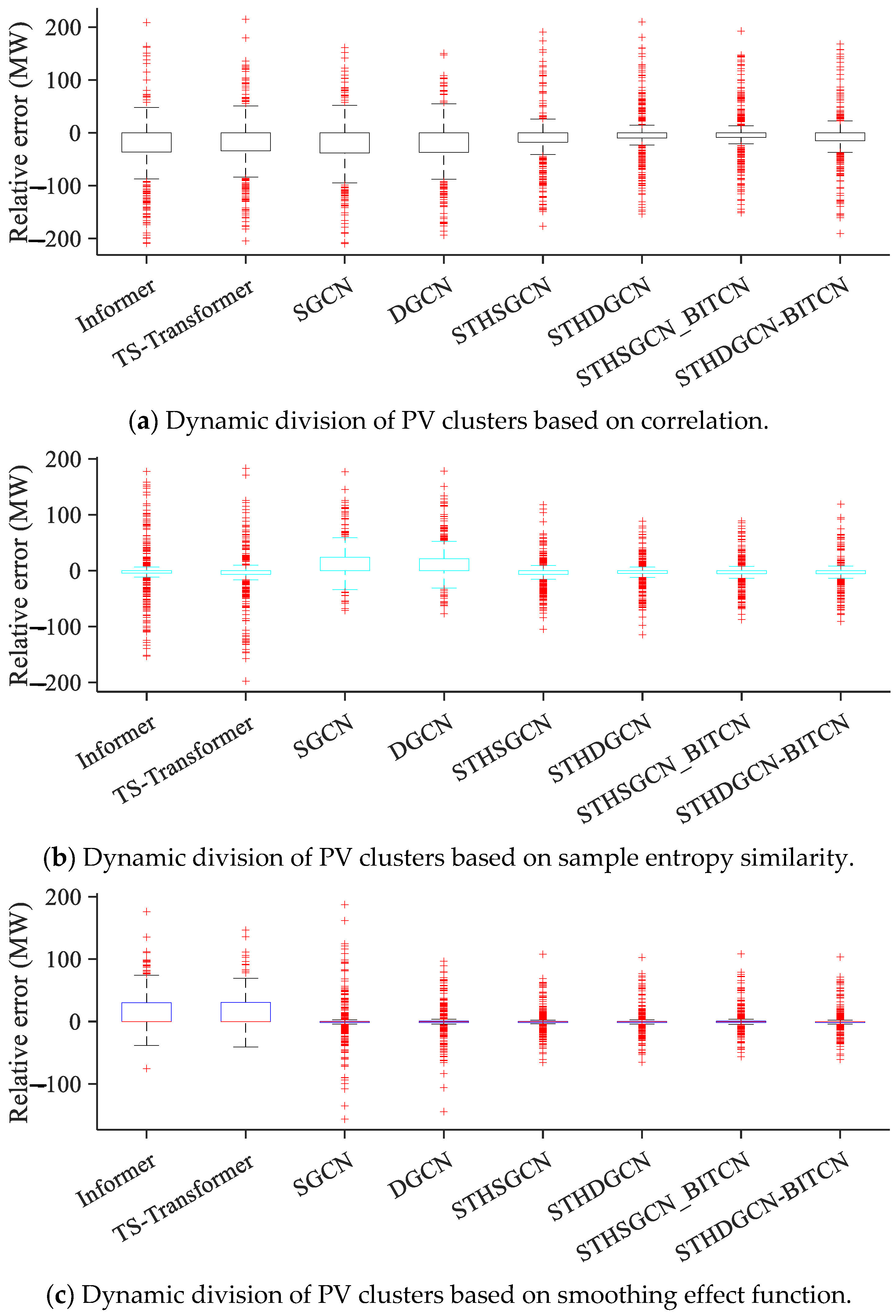
4.2. Error Behavior Under Extreme Conditions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PV | Photovoltaic |
| PCPP | Photovoltaic cluster power prediction |
| NWP | Numerical Weather Prediction |
| Pe | Permutation entropy |
| R2 | Coefficient of determination |
| NRMSE | Normalized root mean square error |
| NMAE | Normalized mean absolute error |
| k-means | k-mean clustering |
| BP | Back propagation neural network |
| RF | Random forests |
| MLR | Multiple linear regression |
| TCN | Temporal convolutional neural network |
| GRU | Gate recurrent unit neural network |
| BITCN | Bidirectional temporal convolutional neural network |
| GNN | Graph neural network |
| SGCN | Static graph convolutional network |
| DGCN | Dynamic graph convolutional network |
| STHSGCN | Spatiotemporal heterogeneous static graph convolutional network |
| STHDGCN | Spatiotemporal heterogeneous dynamic graph convolutional neural network |
| Transformer | Transformer neural network |
| Informer | Informer neural network |
| ST-Transformer | Spatiotemporal Transformer neural network |
| STHSGCN-BITCN | STHSGCN combined with BITCN |
| STHDGCN-BITCN | STHDGCN combined with BITCN |
References
- Dong, Y.; Li, W.; Zhang, J.; Luo, W.; Fu, H.; Xin, X.; Hu, P.; Dong, Y.; Tan, J. High-speed PGC demodulation model and method with subnanometer displacement resolution in a fiber-optic micro-probe laser interferometer. Photonics Res. 2024, 12, 921–931. [Google Scholar] [CrossRef]
- Zhang, C.; Dong, Y.; Hu, P.; Fu, H.; Yang, H.; Yang, R.; Dong, Y.; Zou, L.; Tan, J. Large-range displacement measurement in narrow space scenarios: Fiber microprobe sensor with subnanometer accuracy. Photonics Res. 2024, 12, 1877–1889. [Google Scholar] [CrossRef]
- Zhang, N.; Yan, J.; Hu, C.; Sun, Q.; Yang, L.; Gao, D. Price-matching-based regional energy market with hierarchical reinforcement learning algorithm. IEEE Trans. Ind. Inform. 2024, 20, 11103–11114. [Google Scholar] [CrossRef]
- Soares, A.; Gomes, Á.; Antunes, C.H.; Oliveira, C. A customized evolutionary algorithm for multiobjective management of residential energy resources. IEEE Trans. Ind. Inform. 2016, 13, 492–501. [Google Scholar] [CrossRef]
- Zhang, B.; Talihati, B.; Fan, H.; Sun, Y.; Wang, Y. A dynamic carbon flow traceability framework for integrated energy systems. J. Clean. Prod. 2025, 518, 145878. [Google Scholar] [CrossRef]
- Meng, Q.; He, Y.; Li, S.; Hussain, S.; Lu, J.; You, G.; Guerrero, J. Adaptive two-step power prediction and improved perturbation method for accelerated MPPT with reduced oscillations in photovoltaic systems. Energy Rep. 2025, 13, 5328–5338. [Google Scholar] [CrossRef]
- Gao, J.; Tian, S.; Yuan, C.; Ma, Z.; Gao, C.; Yan, G. Design and optimization of a novel double-layer Helmholtz coil for wirelessly powering a capsule robot. IEEE Trans. Power Electron. 2023, 39, 1826–1839. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, C.; Chen, Z.; Hu, W.; Lu, K.; Ge, L. ACR-Net: Learning high-accuracy optical flow via adaptive-aware correlation recurrent network. IEEE Trans. Circuits Syst. Video Technol. 2024, 34, 9064–9077. [Google Scholar] [CrossRef]
- Wang, Q.; Luo, R.; Wang, Y.; Fang, W.; Jiang, L.; Liu, Y.; Wang, R.; Dai, L.; Zhao, J.; Bai, J.; et al. Set/Reset bilaterally controllable resistance switching Ga-doped Ge2Sb2Te5 long-term electronic synapses for neuromorphic computing. Adv. Funct. Mater. 2023, 33, 2213296. [Google Scholar] [CrossRef]
- Yang, Z.; Huo, S.; Zhang, Z.; Meng, F.; Liu, B.; Wang, Y.; Ma, Y.; Wang, Z.; Xu, J.; Tian, Q.; et al. High—Precision Multibit Opto—Electronic Synapses Based on ReS2/h-BN/Graphene Heterostructure for Energy-Efficient and High-Accuracy Neuromorphic Computing. Adv. Funct. Mater. 2025, 2509119, Early View. [Google Scholar] [CrossRef]
- AlKandari, M.; Ahmad, I. Solar power generation forecasting using ensemble approach based on deep learning and statistical methods. Appl. Comput. Inform. 2024, 20, 231–250. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Zheng, B.; Cui, H.; Qi, H. Statistical analysis for estimating the optimized battery capacity for roof-top PV energy system. Renew. Energy 2025, 242, 122491. [Google Scholar] [CrossRef]
- Mayer, M.J.; Gróf, G. Extensive comparison of physical models for photovoltaic power forecasting. Appl. Energy 2021, 283, 116239. [Google Scholar] [CrossRef]
- Yang, M.; Jiang, Y.; Zhang, W.; Li, Y.; Su, X. Short-term Interval Prediction Strategy of Photovoltaic Power Based on Meteorological Reconstruction with Spatiotemporal Correlation and Multi-factor Interval Constraints. Renew. Energy 2024, 237, 121834. [Google Scholar] [CrossRef]
- Yang, M.; Jiang, Y.; Guo, Y.; Li, Y.; Huang, T. Ultra-short-term Prediction of Photovoltaic Cluster Power Based on Spatiotemporal Convergence Effect and Spatiotemporal Dynamic Graph Attention Network. Renew. Energy 2025, 255, 123843. [Google Scholar] [CrossRef]
- Yuqi, J.; An, A.; Lu, Z.; He, P.; Liu, X. Short-term load forecasting based on temporal importance analysis and feature extraction. Electr. Power Syst. Res. 2025, 244, 111551. [Google Scholar] [CrossRef]
- Yang, M.; Zhao, M.; Huang, D.; Su, X. A composite framework for photovoltaic day-ahead power prediction based on dual clustering of dynamic time warping distance and deep autoencoder. Renew. Energy 2022, 194, 659–673. [Google Scholar] [CrossRef]
- Yang, M.; Guo, Y.; Fan, F.; Huang, T. Two-stage correction prediction of wind power based on numerical weather prediction wind speed superposition correction and improved clustering. Energy 2024, 302, 131797. [Google Scholar] [CrossRef]
- Mayer, M.J.; Yang, D.; Markovics, D. The complexity and dimensionality of making deterministic photovoltaic power forecasts from ensemble numerical weather prediction. Energy Convers. Manag. 2025, 344, 120303. [Google Scholar] [CrossRef]
- Zjavka, L. Power Quality 24 h Verification in Smart Load Scheduling Based on Differentiate, Deep, and Assembly Statistics in NWP Processing. Int. Trans. Electr. Energy Syst. 2025, 2025, 8703225. [Google Scholar] [CrossRef]
- Yang, M.; Guo, Y.; Huang, T.; Fan, F.; Ma, C.; Fang, G. Wind farm cluster power prediction based on graph deviation attention network with learnable graph structure and dynamic error correction during load peak and valley periods. Energy 2024, 312, 133645. [Google Scholar] [CrossRef]
- Yang, M.; Guo, Y.; Wang, B.; Wang, Z.; Chai, R. A day-ahead wind speed correction method: Enhancing wind speed forecasting accuracy using a strategy combining dynamic feature weighting with multi-source information and dynamic matching with improved similarity function. Expert Syst. Appl. 2025, 263, 125724. [Google Scholar] [CrossRef]
- Yang, M.; Guo, Y.; Huang, T.; Zhang, W. Power prediction considering NWP wind speed error tolerability: A strategy to improve the accuracy of short-term wind power prediction under wind speed offset scenarios. Appl. Energy 2025, 377, 124720. [Google Scholar]
- Yang, M.; Guo, Y.; Huang, Y. Wind power ultra-short-term prediction method based on NWP wind speed correction and double clustering division of transitional weather process. Energy 2023, 282, 128947. [Google Scholar] [CrossRef]
- Jackson, N.D.; Gunda, T. Evaluation of extreme weather impacts on utility-scale photovoltaic plant performance in the United States. Appl. Energy 2021, 302, 117508. [Google Scholar] [CrossRef]
- Zhai, C.; He, X.; Cao, Z.; Tankari, M.; Wang, Y.; Zhang, M. Photovoltaic power forecasting based on VMD-SSA-Transformer: Multidimensional analysis of dataset length, weather mutation and forecast accuracy. Energy 2025, 324, 135971. [Google Scholar] [CrossRef]
- Sánchez-Pozo, N.N.; Vanem, E.; Bloomfield, H.; Aizpurua, J. A probabilistic risk assessment framework for the impact assessment of extreme events on renewable power plant components. Renew. Energy 2025, 240, 122168. [Google Scholar] [CrossRef]
- Markovics, D.; Mayer, M.J. Comparison of machine learning methods for photovoltaic power forecasting based on numerical weather prediction. Renew. Sustain. Energy Rev. 2022, 161, 112364. [Google Scholar] [CrossRef]
- Yang, M.; Zhao, M.; Liu, D.; Ma, M.; Su, X. Improved Random Forest Method for Ultra-short-term Prediction of the Output Power of a Photovoltaic Cluster. Front. Energy Res. 2021, 9, 749367. [Google Scholar] [CrossRef]
- Pulipaka, S.; Kumar, R. Power prediction of soiled PV module with neural networks using hybrid data clustering and division techniques. Sol. Energy 2016, 133, 485–500. [Google Scholar] [CrossRef]
- Pang, S.; Zheng, Z.; Luo, F.; Xaio, X.; Xu, L. Hybrid forecasting methodology for wind power-photovoltaic-concentrating solar power generation clustered renewable energy systems. Sustainability 2021, 13, 6681. [Google Scholar] [CrossRef]
- Jin, J.; Ye, L.; Li, J.; Zhao, Y.; Lu, P.; Wang, W. Wind and photovoltaic power time series data aggregation method based on an ensemble clustering and Markov chain. CSEE J. Power Energy Syst. 2021, 8, 757–768. [Google Scholar] [CrossRef]
- Pierro, M.; De Felice, M.; Maggioni, E.; Moser, D.; Perotto, A.; Spada, F.; Cornaro, C. Data-driven upscaling methods for regional photovoltaic power estimation and forecast using satellite and numerical weather prediction data. Sol. Energy 2017, 158, 1026–1038. [Google Scholar] [CrossRef]
- Qiu, L.; Ma, W.; Feng, X.; Dai, J.; Dong, Y.; Duan, J.; Chen, B. A hybrid PV cluster power prediction model using BLS with GMCC and error correction via RVM considering an improved statistical upscaling technique. Appl. Energy 2024, 359, 122719. [Google Scholar] [CrossRef]
- Saint-Drenan, Y.M.; Good, G.H.; Braun, M.; Freisinger, T. Analysis of the uncertainty in the estimates of regional PV power generation evaluated with the upscaling method. Sol. Energy 2016, 135, 536–550. [Google Scholar] [CrossRef]
- Lai, W.; Zhen, Z.; Wang, F.; Fu, W.; Wang, J.; Zhang, X.; Ren, H. Sub-region division based short-term regional distributed PV power forecasting method considering spatio-temporal correlations. Energy 2024, 288, 129716. [Google Scholar] [CrossRef]
- Zhang, Z.; Lv, Q.; Zhang, J. Research on the combined power forecasting of regional wind and photovoltaic power based on statistical upscaling. In Proceedings of the 2nd International Conference on Mechanical, Electronics, and Electrical and Automation Control (METMS 2022), Guilin, China, 7–9 January 2022; SPIE: Bellingham, WA, USA; Volume 12244, pp. 1141–1147. [Google Scholar]
- Fu, L.; Yang, Y.; Yao, X.; Jiao, X.; Zhu, T. A regional photovoltaic output prediction method based on hierarchical clustering and the mRMR criterion. Energies 2019, 12, 3817. [Google Scholar] [CrossRef]
- Ziane, A.; Necaibia, A.; Sahouane, N.; Dabou, R.; Mostefaoui, M.; Bouraiou, A.; Khelifi, S.; Rouabhia, A.; Blal, M. Photovoltaic output power performance assessment and forecasting: Impact of meteorological variables. Sol. Energy 2021, 220, 745–757. [Google Scholar] [CrossRef]
- Meng, X.; Shi, X.; Wang, W.; Zhang, Y.; Gao, F. An upscaling minute-level regional photovoltaic power forecasting scheme. Int. J. Electr. Power Energy Syst. 2024, 155, 109609. [Google Scholar] [CrossRef]
- Wang, H.; Lu, Z.; Wojtasiak, A.; Owyong, S.; Sun, B.; Fang, Y.; Vassigh, S.; Lin, A. Biomimetic self-shading walls via 3D-printing for reduced heat gain: Multiscale learning using graph neural networks to predict solar radiation absorption. Build. Environ. 2025, 279, 113048. [Google Scholar] [CrossRef]
- Wang, S.; Xiang, X.; Zhang, J.; Liang, Z.; Li, S.; Zhong, P.; Zeng, J.; Wang, C. A multi-task spatiotemporal graph neural network for transient stability and state prediction in power systems. Energies 2025, 18, 1531. [Google Scholar] [CrossRef]
- Hassan, A.U.; Güleryüz, C.; El Azab, I.H.; Elnaggar, A.; Mahmoud, M. A graph neural network assisted reverse polymers engineering to design low bandgap benzothiophene polymers for light harvesting applications. Mater. Chem. Phys. 2025, 339, 130747. [Google Scholar] [CrossRef]
- Sun, D.; Cao, X.; Liang, Z.; Xia, J.; Wang, Y. Distributed Photovoltaic Power Prediction Technology Based on Spatio-Temporal Graph Neural Networks. Energy Eng. 2025, 122, 3329–3346. [Google Scholar] [CrossRef]
- Zhang, M.; Zhen, Z.; Liu, N.; Zhao, H.; Sun, Y.; Feng, C. Optimal graph structure based short-term solar PV power forecasting method considering surrounding spatio-temporal correlations. IEEE Trans. Ind. Appl. 2022, 59, 345–357. [Google Scholar] [CrossRef]
- Simeunović, J.; Schubnel, B.; Alet, P.; Carrillo, R.; Frossard, R. Interpretable temporal-spatial graph attention network for multi-site PV power forecasting. Appl. Energy 2022, 327, 120127. [Google Scholar] [CrossRef]
- Zhao, C.; Li, X.; Cai, Y. A power grid topology detection method based on edge graph attention neural network. Electr. Power Syst. Res. 2025, 239, 111219. [Google Scholar] [CrossRef]
- He, Y.; Ali, A.B.M.; Aminian, S.A.; Sharma, K.; Dixit, S.; Sobti, S.; Ali, R.; Ahemedei, M.; Rajab, H.; Mazinan, M. Enhancing Intelligent HVAC optimization with graph attention networks and stacking ensemble learning, a recommender system approach in Shenzhen Qianhai Smart Community. Sci. Rep. 2025, 15, 5119. [Google Scholar] [CrossRef]
- Abdelkader, D.; Fouzi, H.; Belkacem, K.; Ying, S. Graph neural networks-based spatiotemporal prediction of photovoltaic power: A comparative study. Neural Comput. Appl. 2025, 37, 4769–4795. [Google Scholar] [CrossRef]
- Simeunović, J.; Schubnel, B.; Alet, P.J.; Carrillo, R. Spatio-temporal graph neural networks for multi-site PV power forecasting. IEEE Trans. Sustain. Energy 2021, 13, 1210–1220. [Google Scholar] [CrossRef]
- Jiao, X.; Li, X.; Lin, D.; Xiao, W. A graph neural network based deep learning predictor for spatio-temporal group solar irradiance forecasting. IEEE Trans. Ind. Inform. 2021, 18, 6142–6149. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, Y.; Zhang, Y.; Shu, S.; Zheng, J. DEST-GNN: A double-explored spatio-temporal graph neural network for multi-site intra-hour PV power forecasting. Appl. Energy 2025, 378, 124744. [Google Scholar] [CrossRef]
- Jing, S.; Xi, X.; Su, D.; Han, Z.; Wang, D. Spatio-Temporal Photovoltaic Power Prediction with Fourier Graph Neural Network. Electronics 2024, 13, 4988. [Google Scholar] [CrossRef]
- Zhang, X.; Gao, R.; Zhu, C.; Liu, C.; Mei, S. Ultra-short-term prediction of regional photovoltaic power based on dynamic graph convolutional neural network. Electr. Power Syst. Res. 2024, 226, 109965. [Google Scholar] [CrossRef]
- Li, Z.; Ye, L.; Song, X.; Luo, Y.; Pei, M.; Wang, K. Heterogeneous spatiotemporal graph convolution network for multi-modal wind-PV power collaborative prediction. IEEE Trans. Power Syst. 2023, 39, 5591–5608. [Google Scholar] [CrossRef]
- Hasnat, M.A.; Asadi, S.; Alemazkoor, N. A graph attention network framework for generalized-horizon multi-plant solar power generation forecasting using heterogeneous data. Renew. Energy 2025, 243, 122520. [Google Scholar] [CrossRef]
- Gao, Y.; Liang, L.; Su, T.; Pan, M. An embedded spatiotemporal hybrid model integrating multi-graphs and attention-driven fusion for single-and multi-site photovoltaic power forecasting. Energy Convers. Manag. 2025, 336, 119897. [Google Scholar] [CrossRef]
- Theiler, R.; Fink, O. Heterogeneous Graph Neural Networks for Short-term State Forecasting in Power Systems across Domains and Time Scales: A Hydroelectric Power Plant Case Study. arXiv 2025, arXiv:2507.06694. [Google Scholar] [CrossRef]
- Yang, K.; Cai, Y.; Cheng, J. A deep learning model based on multi-attention mechanism and gated recurrent unit network for photovoltaic power forecasting. Comput. Electr. Eng. 2025, 123, 110250. [Google Scholar] [CrossRef]
- Li, Z.; Ma, J.; Wang, Q.; Wang, M.; Jiang, F. Enhancing urban solar irradiation prediction with shadow-attention graph neural networks: Implications for net-zero energy buildings in New York City. Sustain. Cities Soc. 2025, 120, 106133. [Google Scholar] [CrossRef]
- Lin, H.; Gao, L.; Cui, M.; LIu, H.; Li, C.; Yu, M. Short-term distributed photovoltaic power prediction based on temporal self-attention mechanism and advanced signal decomposition techniques with feature fusion. Energy 2025, 315, 134395. [Google Scholar] [CrossRef]
- Zhang, C.; Song, D.; Huang, C.; Swami, A.; Chawla, N. Heterogeneous graph neural network. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 793–803. [Google Scholar]
- Bing, R.; Yuan, G.; Zhu, M.; Meng, F.; Ma, H.; Qiao, S. Heterogeneous graph neural networks analysis: A survey of techniques, evaluations and applications. Artif. Intell. Rev. 2023, 56, 8003–8042. [Google Scholar] [CrossRef]
- Jing, Y.; Yang, Y.; Wang, X.; Song, M.; Tao, D. Amalgamating knowledge from heterogeneous graph neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 15709–15718. [Google Scholar]
- Li, B.; Li, X.; Cai, Y.; Han, Q. A load forecasting method based on heterogeneous network for integrated electricity and heat systems. Electr. Power Syst. Res. 2025, 246, 111725. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, M. Ultra-Short-Term Photovoltaic Power Prediction Based on Predictable Component Reconstruction and Spatiotemporal Heterogeneous Graph Neural Networks. Energies 2025, 18, 4192. [Google Scholar] [CrossRef]
- Xu, J.; Li, Y.; Lu, W.; Wu, S.; Li, Y. A heterogeneous traffic spatio-temporal graph convolution model for traffic prediction. Phys. A Stat. Mech. Its Appl. 2024, 641, 129746. [Google Scholar] [CrossRef]
- Liu, X.; Miao, C.; Fiumara, G.; Meo, P. Information propagation prediction based on spatial–temporal attention and heterogeneous graph convolutional networks. IEEE Trans. Comput. Soc. Syst. 2023, 11, 945–958. [Google Scholar] [CrossRef]
- Cai, S.; Zhao, Y.; Hu, Y.; Wu, J.; Wu, J.; Zhang, G.; Zhao, C.; Sosu, R. CD-BTMSE: A concept drift detection model based on bidirectional temporal convolutional network and multi-stacking ensemble learning. Knowl. Based Syst. 2024, 294, 111681. [Google Scholar] [CrossRef]
- Yang, M.; Ju, C.; Huang, Y.; Guo, Y.; Jia, M. Short-term power forecasting of wind farm cluster based on global information adaptive perceptual graph convolution network. IEEE Trans. Sustain. Energy 2024, 15, 2063–2076. [Google Scholar] [CrossRef]
- Gan, J.; Lin, X.; Chen, T.; Fan, C.; Wei, P.; Li, Z.; Huo, Y.; Zhang, F.; Liu, J.; He, T. Improving short-term photovoltaic power generation forecasting with a bidirectional temporal convolutional network enhanced by temporal bottlenecks and Attention Mechanisms. Electronics 2025, 14, 214. [Google Scholar] [CrossRef]
- Feng, Y.; Zhu, J.; Qiu, P.; Zhang, X.; Shuang, C. Short-term power load forecasting based on TCN-BiLSTM-attention and multi-feature fusion. Arab. J. Sci. Eng. 2025, 50, 5475–5486. [Google Scholar] [CrossRef]
- Zhu, H.; Wang, Y.; Wu, J.; Zhang, X. A regional distributed photovoltaic power generation forecasting method based on grid division and TCN-Bilstm. Renew. Energy 2026, 256, 123935. [Google Scholar] [CrossRef]
- Yang, M.; Guo, Y. Wind power cluster ultra-short-term prediction error correction method based on the load peak and valley characteristics. CSEE J. Power Energy Syst. 2023, 1–12. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, Z.; Ning, L.; Zhang, X. Belief-based fuzzy and imprecise clustering for arbitrary data distributions. IEEE Trans. Fuzzy Syst. 2025, 33, 2755–2767. [Google Scholar] [CrossRef]
- Zhang, Y.; Feng, S.; Wang, P.; Tan, Z.; Luo, X.; Ji, Y. Learning self-growth maps for fast and accurate imbalanced streaming data clustering. IEEE Trans. Neural Netw. Learn. Syst. 2025, 36, 16049–16061. [Google Scholar] [CrossRef] [PubMed]
- Zhou, C.; Zhang, F.; Gu, S.; Zhao, Z. A short-term power prediction method based on the transformation of multi-source spatiotemporal feature for photovoltaic cluster. Int. J. Green Energy 2025, 22, 2663–2679. [Google Scholar] [CrossRef]
- Yu, W.; Dai, Y.; Ren, T.; Leng, M. Short-time Photovoltaic Power Forecasting Based on Informer Model Integrating Attention Mechanism. Appl. Soft Comput. 2025, 178, 113345. [Google Scholar] [CrossRef]
- Tang, P.; Su, Y.; Zhao, W.; Wang, Q.; Zou, L.; Song, J. A Hybrid Framework for Photovoltaic Power Forecasting Using Shifted Windows Transformer-Based Spatiotemporal Feature Extraction. Energies 2025, 18, 3193. [Google Scholar] [CrossRef]
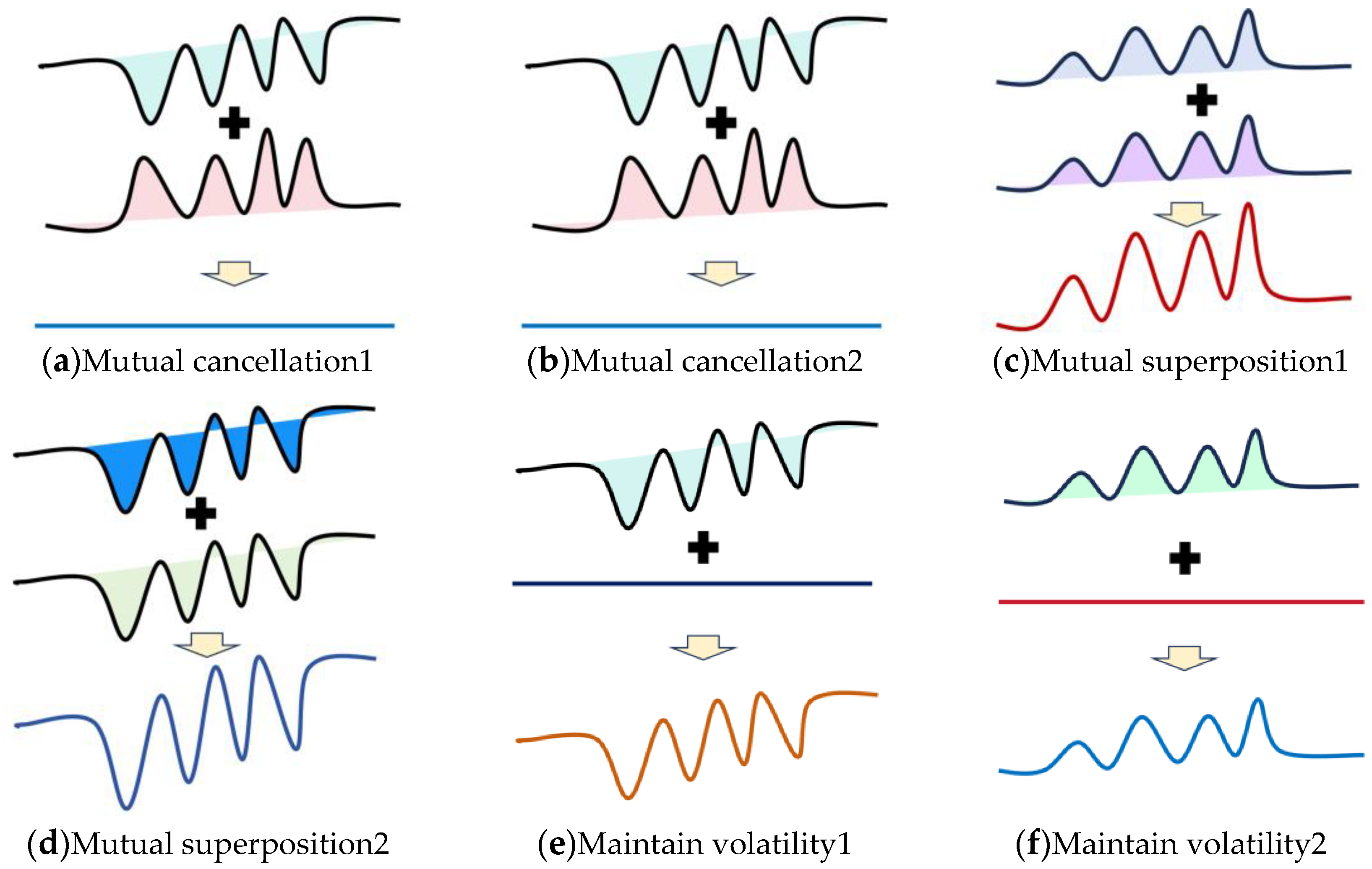
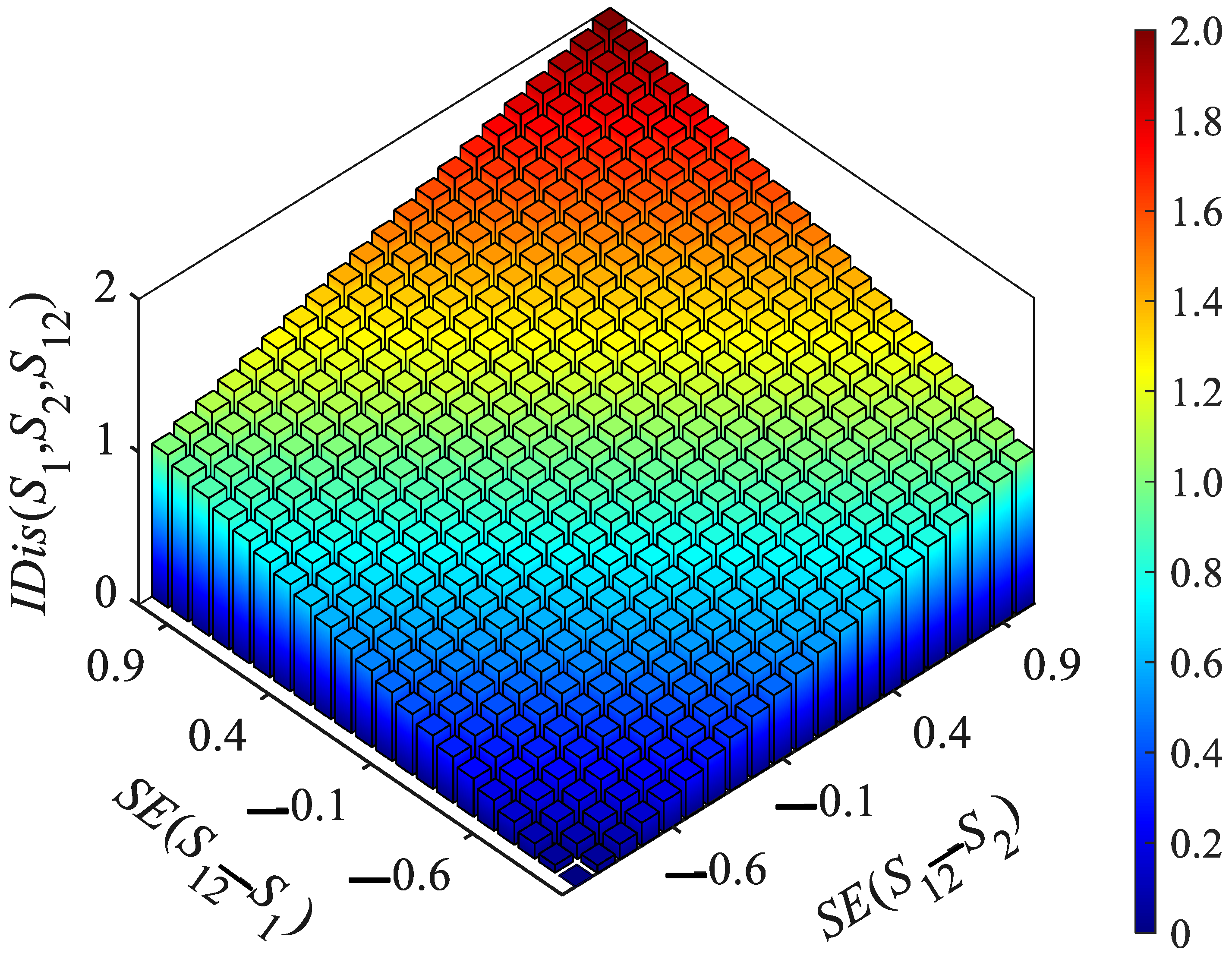
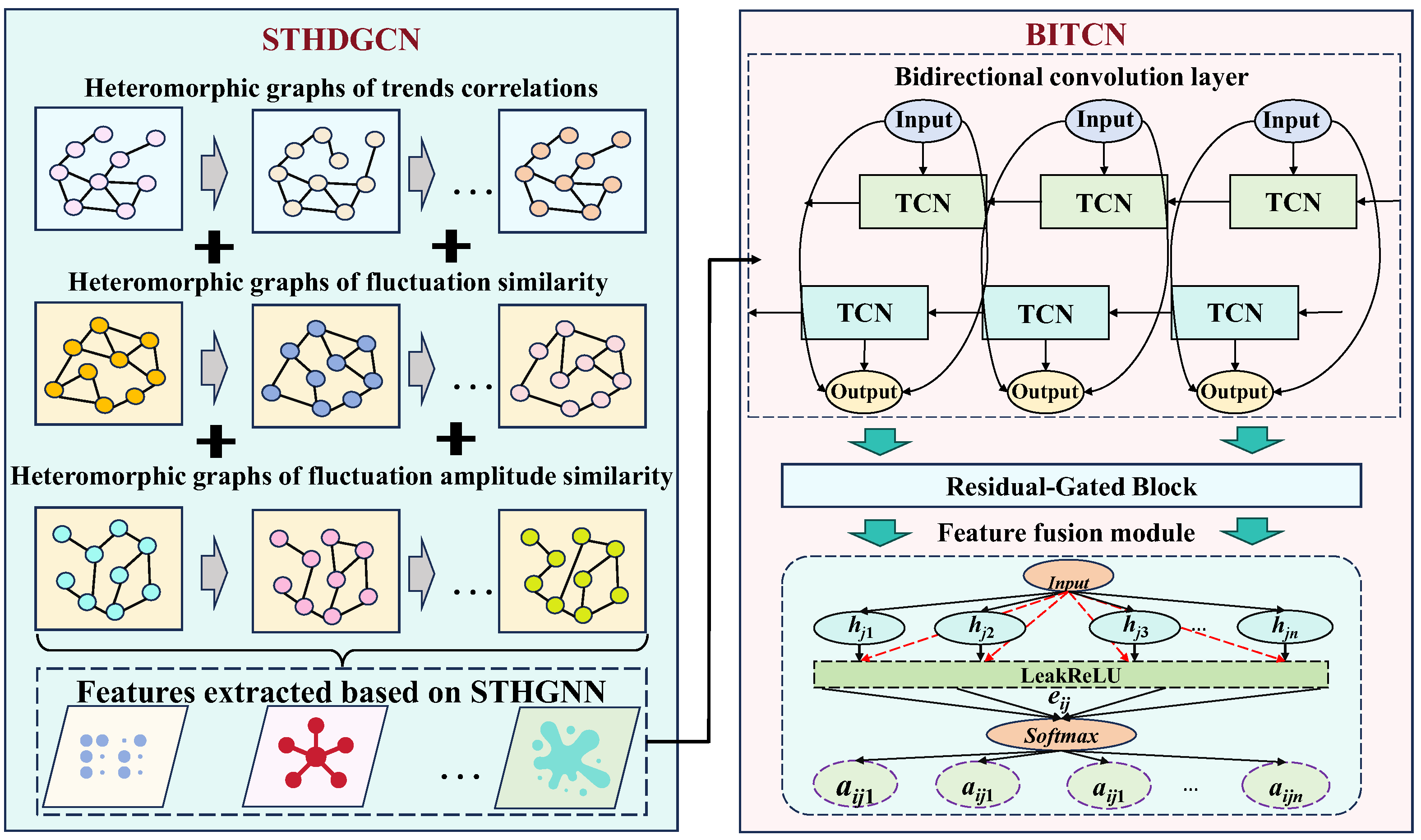
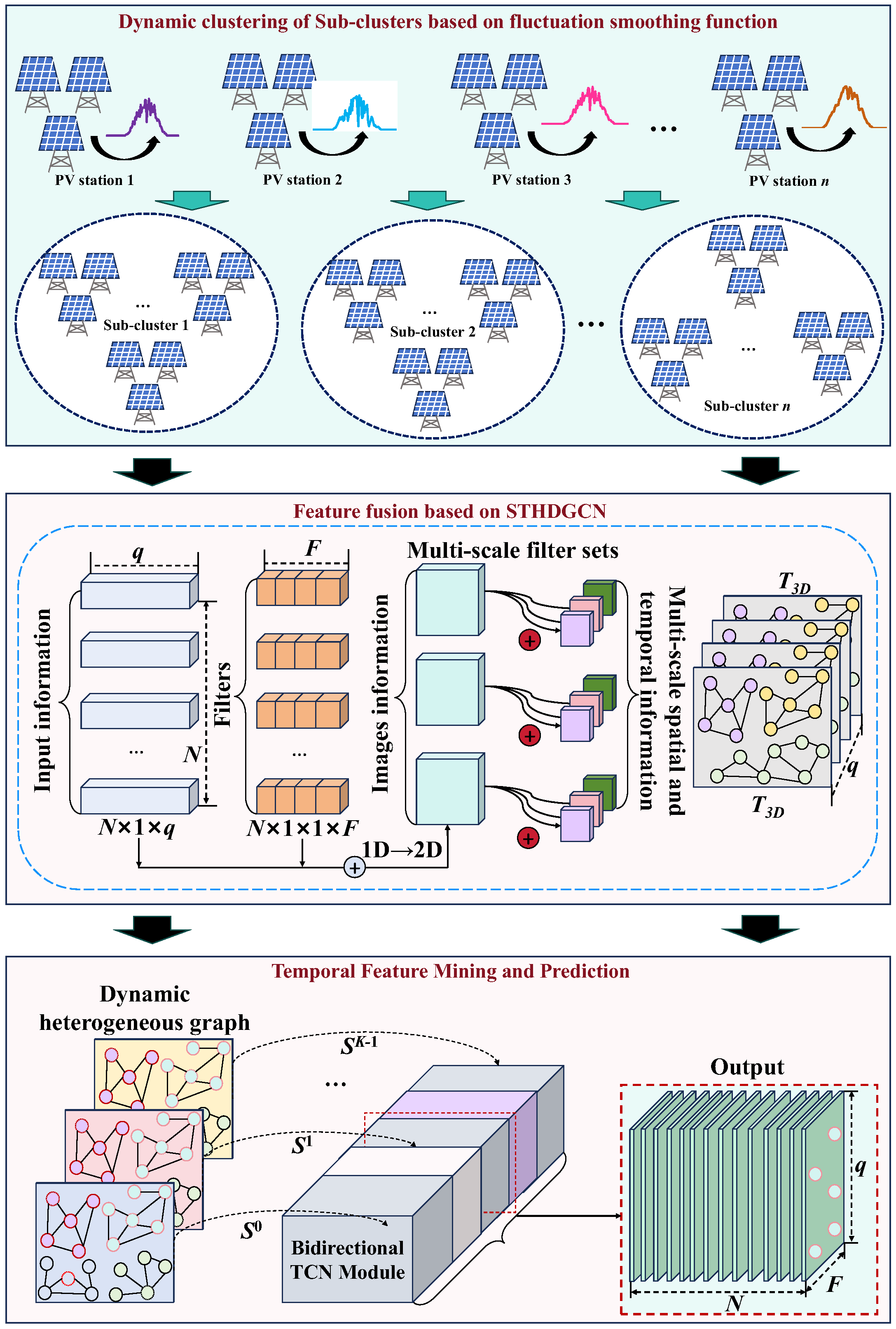

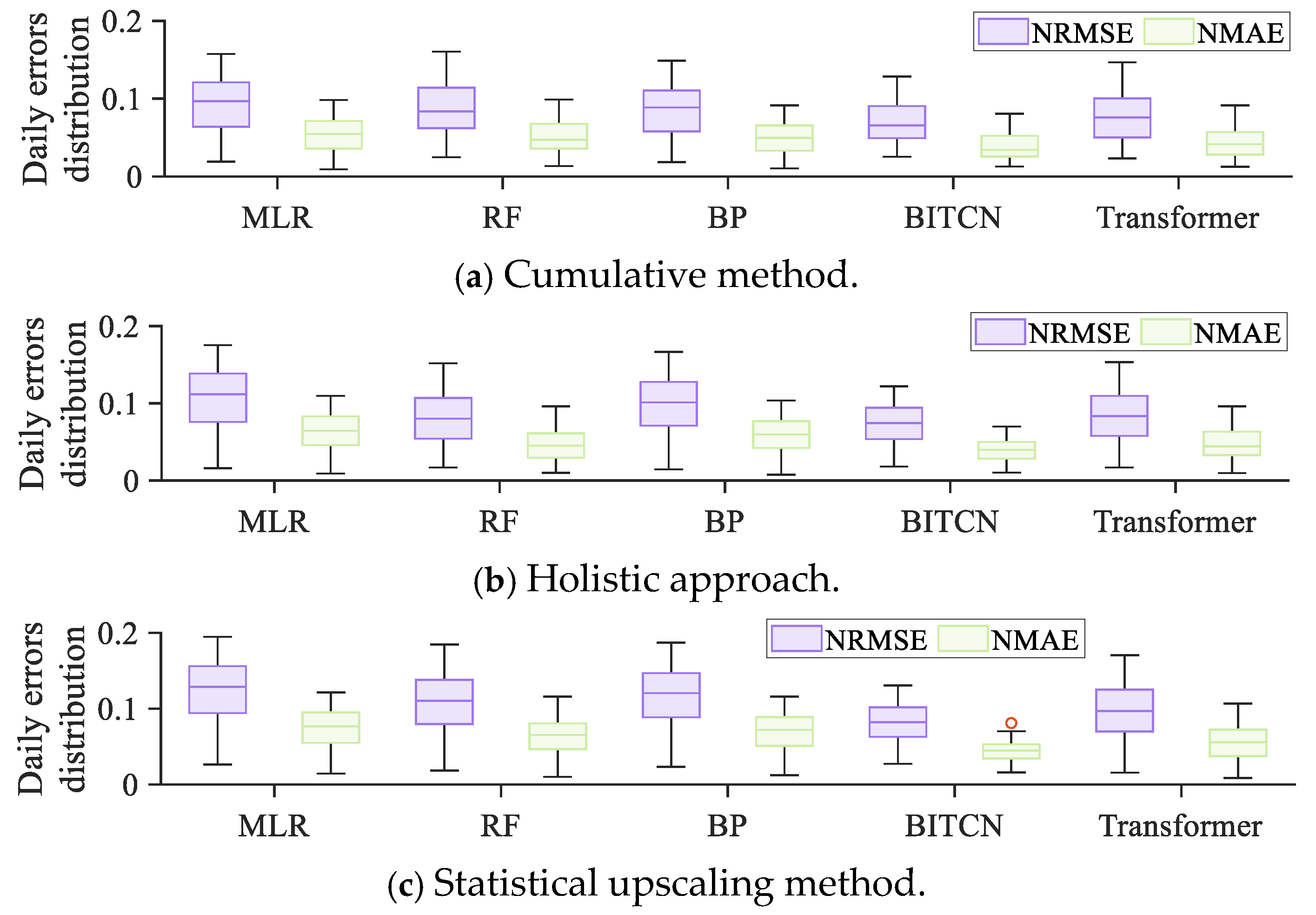
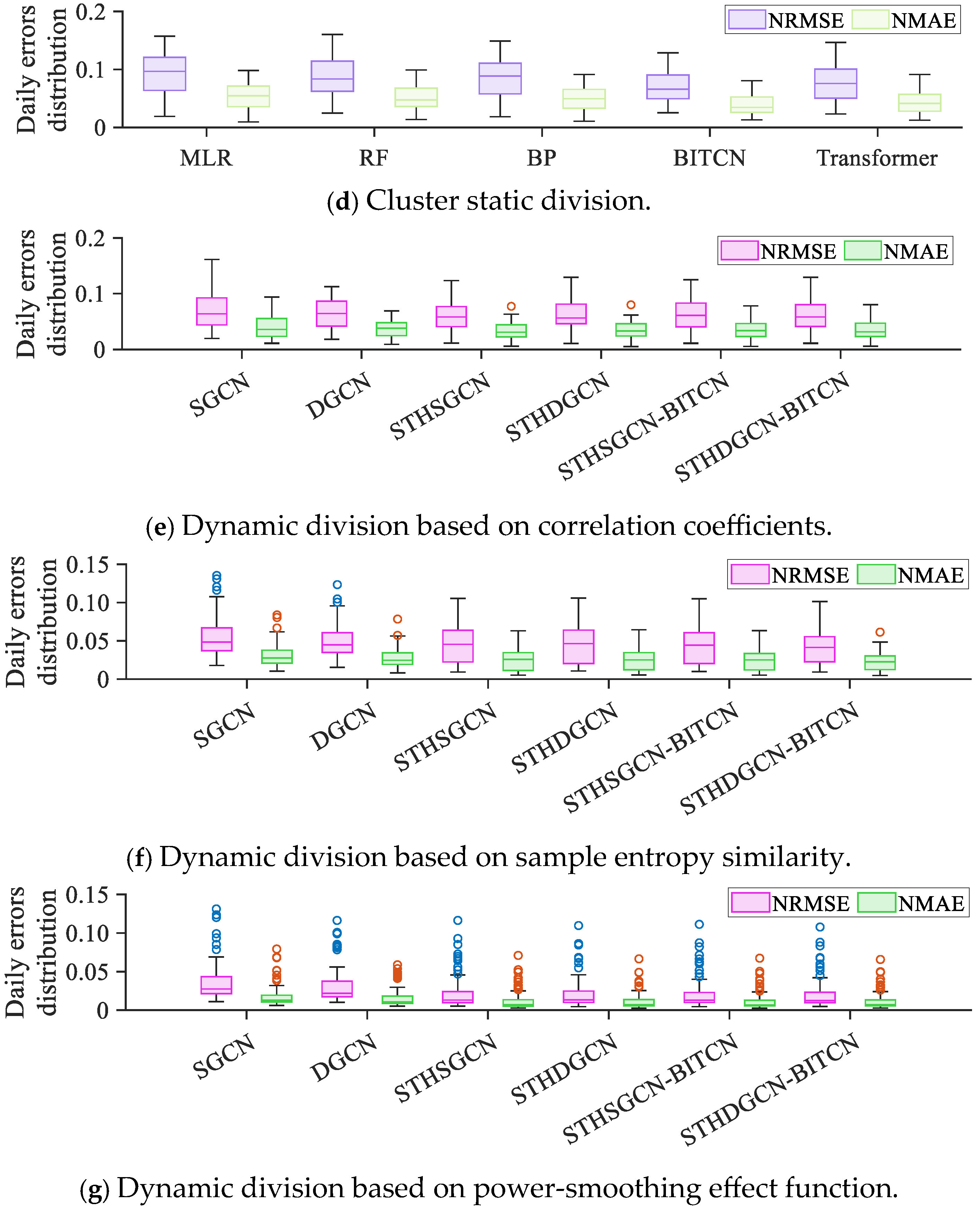
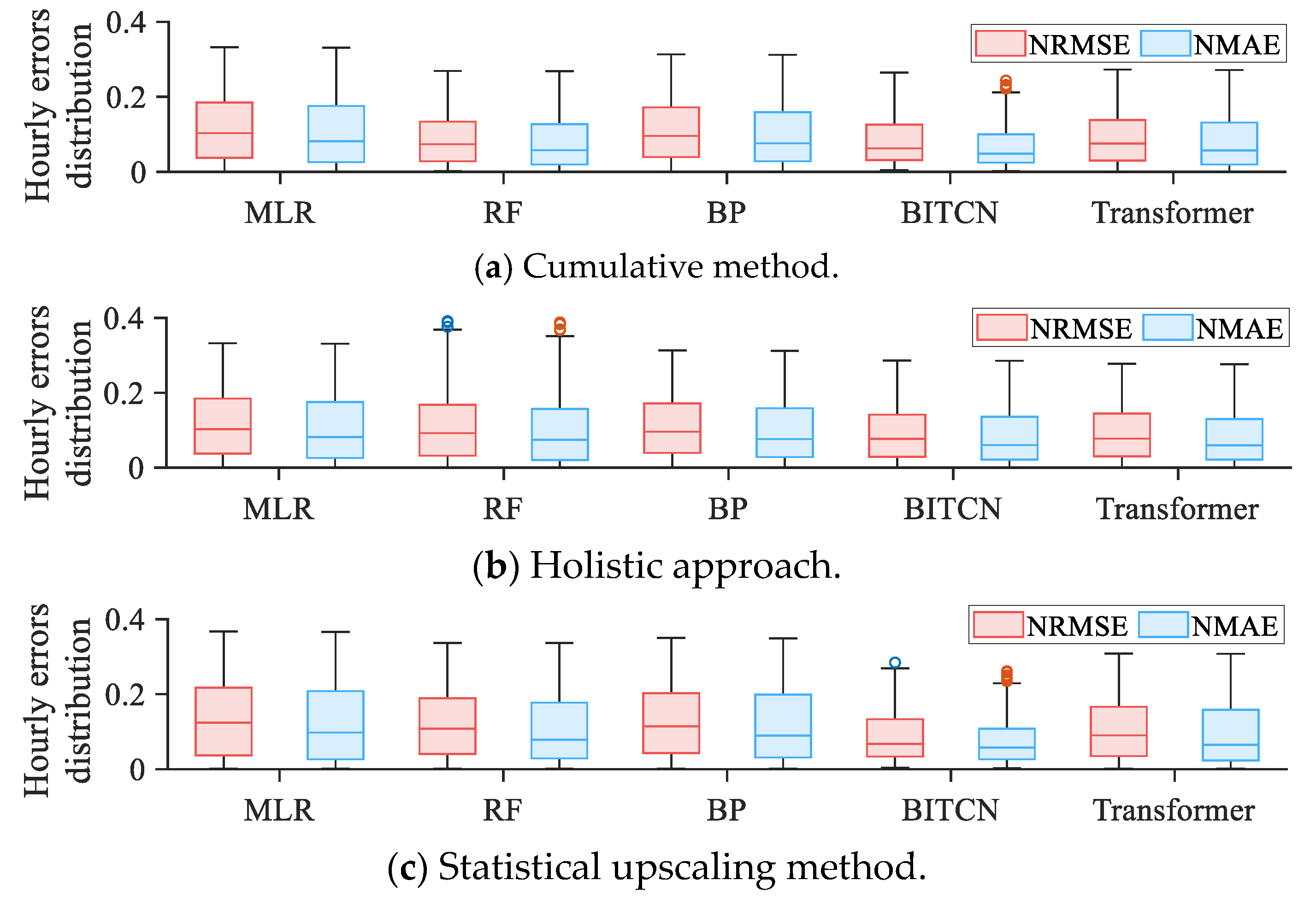
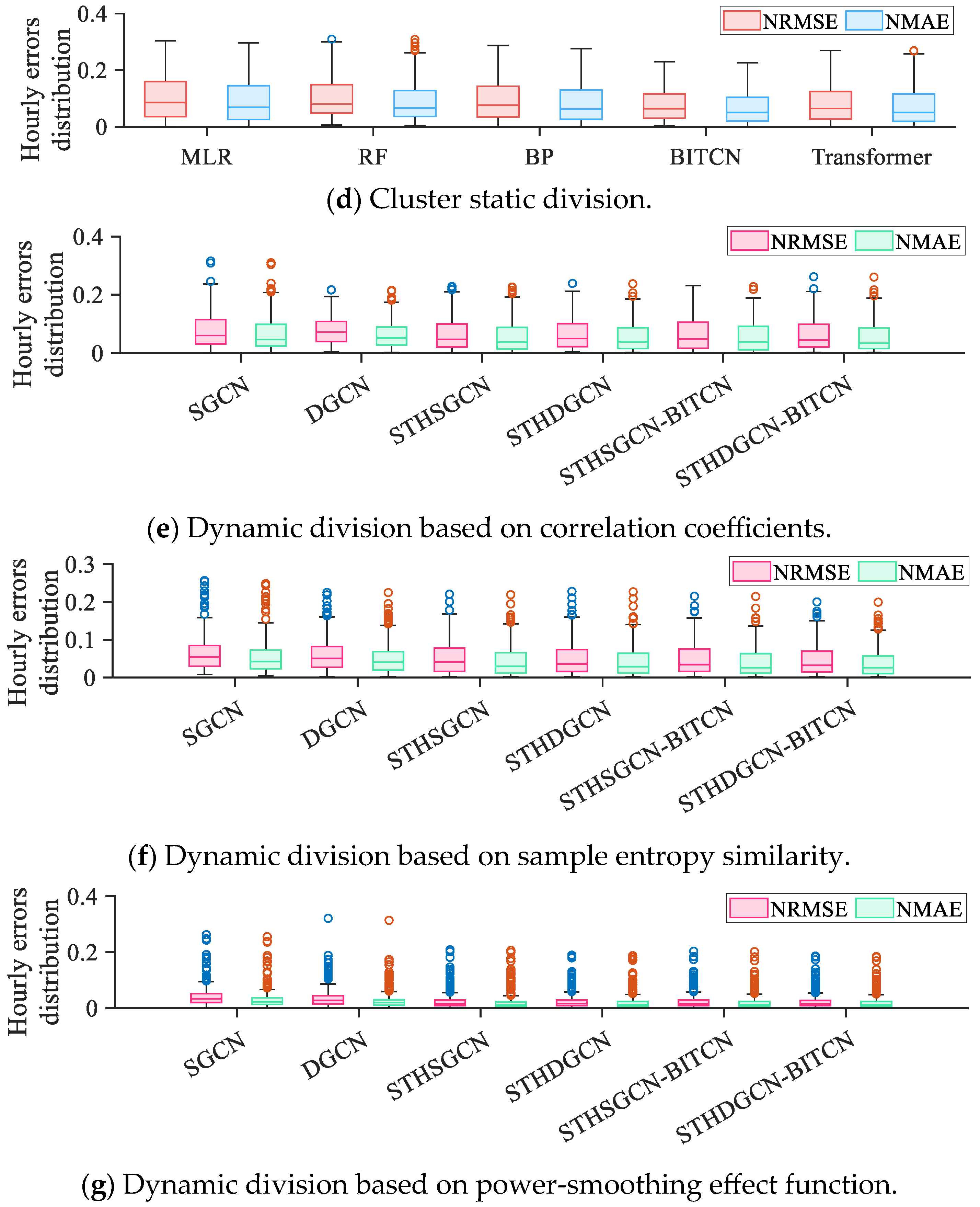
| Information Items | Value |
|---|---|
| Longitude interval | [E 96°10′~E 102°12′] |
| Latitude interval | [N 37°28′~N 40°52′] |
| Number of PV stations | 30 |
| Rated capacity | 1500 MW |
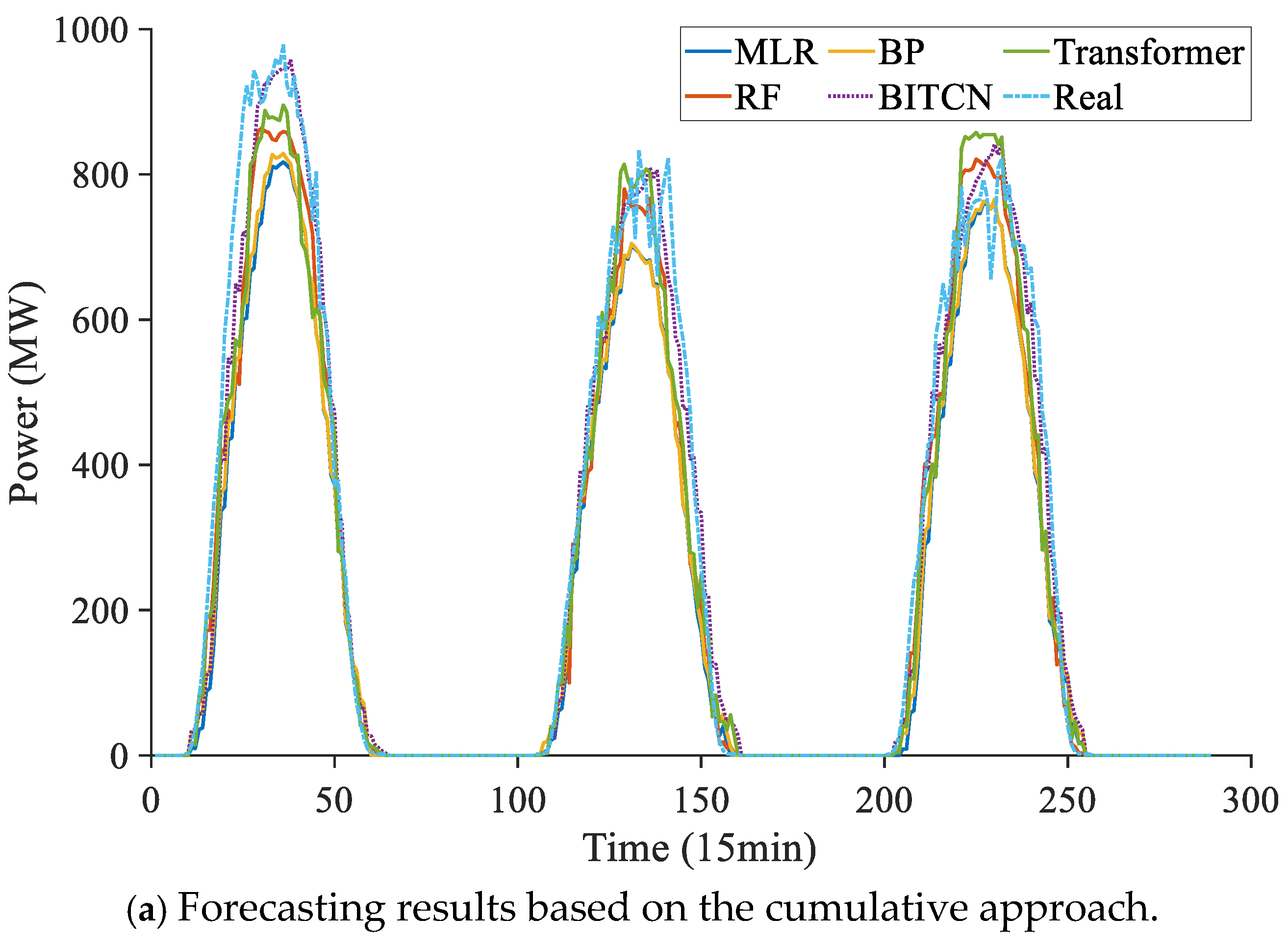
| Modeling Methods | Index | MLR | RF | BP | BITCN | Transformer |
|---|---|---|---|---|---|---|
| Cumulative method | NRMSE | 0.1158 | 0.1119 | 0.1074 | 0.0923 | 0.0922 |
| NMAE | 0.0633 | 0.0587 | 0.0588 | 0.0490 | 0.0491 | |
| R2 | 0.4609 | 0.5821 | 0.5678 | 0.7313 | 0.7402 | |
| Holistic approach | NRMSE | 0.1132 | 0.0866 | 0.1074 | 0.0783 | 0.0895 |
| NMAE | 0.0603 | 0.0461 | 0.0588 | 0.0405 | 0.0473 | |
| R2 | 0.5809 | 0.7765 | 0.5678 | 0.8728 | 0.7570 | |
| Statistical upscaling | NRMSE | 0.1322 | 0.1145 | 0.1244 | 0.0855 | 0.1035 |
| NMAE | 0.0730 | 0.0628 | 0.0687 | 0.0443 | 0.0556 | |
| R2 | 0.1335 | 0.4600 | 0.2843 | 0.8211 | 0.6159 | |
| Cluster static division | NRMSE | 0.1005 | 0.0958 | 0.0917 | 0.0747 | 0.0823 |
| NMAE | 0.0542 | 0.0521 | 0.0497 | 0.0391 | 0.0426 | |
| R2 | 0.6645 | 0.7666 | 0.7399 | 0.8594 | 0.8121 |
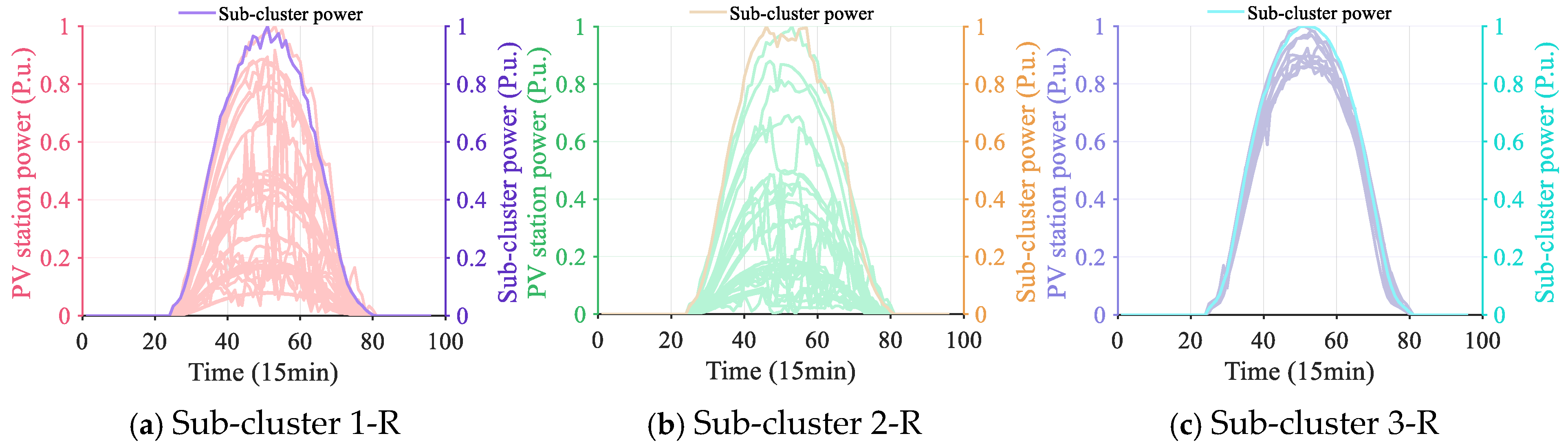
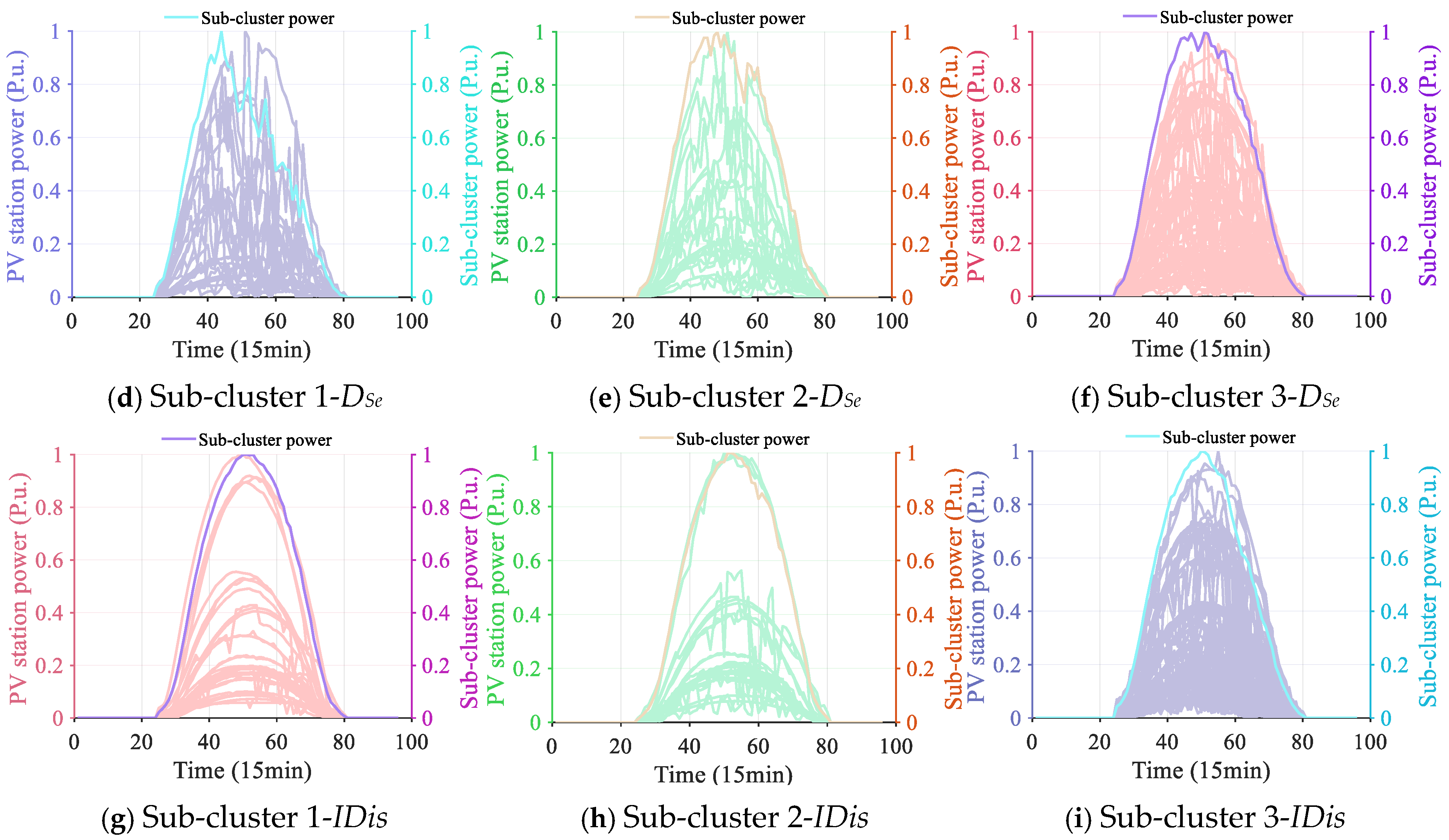
| Clustering Model | Clustering Distance | Sub-Cluster-I | Sub-Cluster-II | Sub-Cluster-III |
|---|---|---|---|---|
| DAEGC [77] | Kullback–Leibler divergence | 0.3659 | 0.7864 | 0.8841 |
| Spectral clustering | Correlation coefficient | 0.4562 | 0.6394 | 0.8772 |
| Sample entropy | 0.3522 | 0.7882 | 0.8589 | |
| IDis | 0.3721 | 0.3844 | 0.3921 | |
| k-means | Correlation coefficient | 0.4514 | 0.6454 | 0.8769 |
| Sample entropy | 0.3534 | 0.7878 | 0.8596 | |
| IDis | 0.3704 | 0.3854 | 0.3901 |
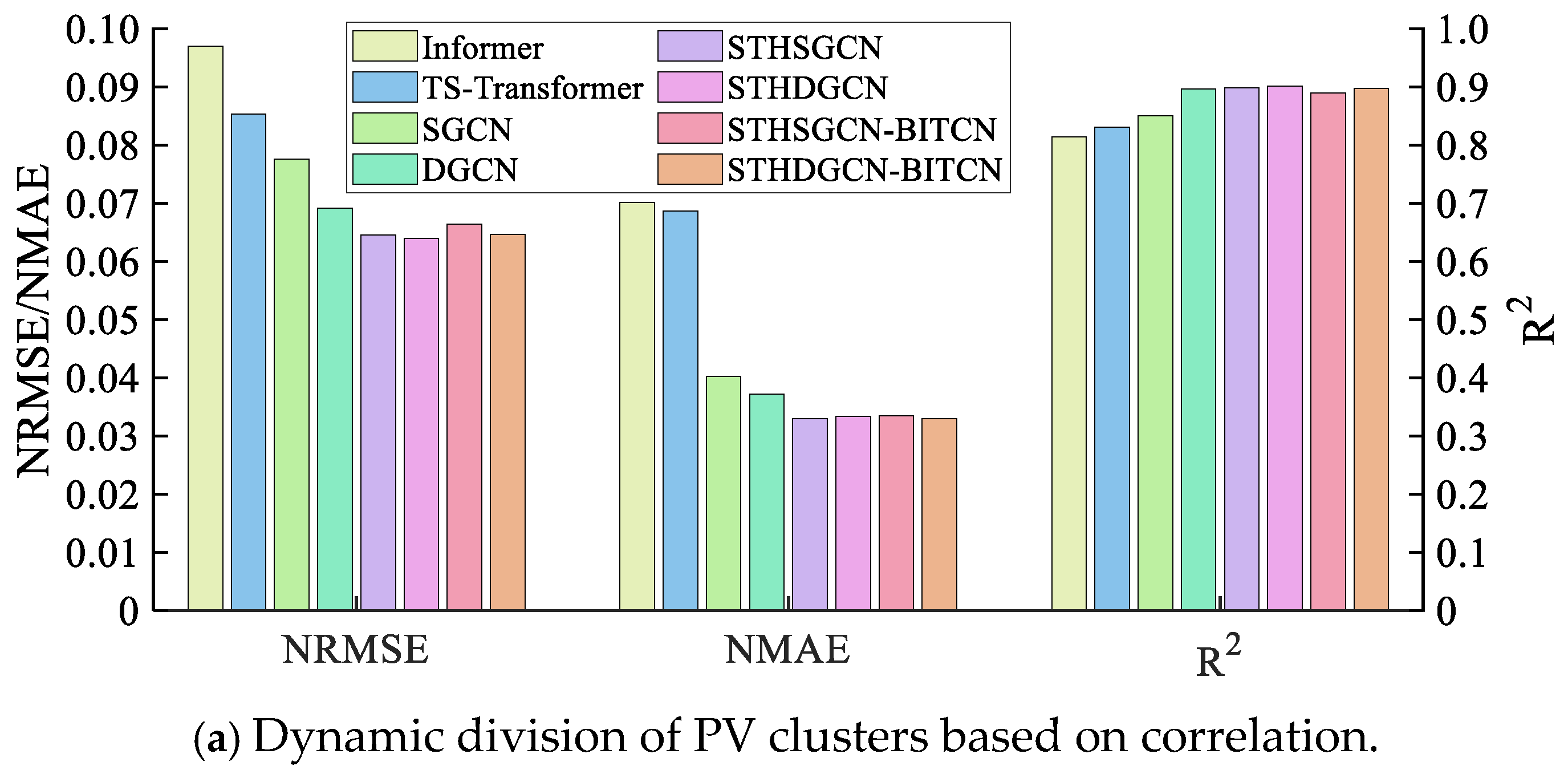
| Cluster Division Methods | Index | MLR | RF | BP | BITCN | Transformer |
|---|---|---|---|---|---|---|
| Correlation coefficient | NRMSE | 0.1140 | 0.1025 | 0.1104 | 0.0828 | 0.0842 |
| NMAE | 0.0521 | 0.0383 | 0.0492 | 0.0461 | 0.0470 | |
| R2 | 0.6660 | 0.8342 | 0.7141 | 0.7844 | 0.7736 | |
| Sample entropy similarity | NRMSE | 0.1085 | 0.1109 | 0.1070 | 0.0754 | 0.0768 |
| NMAE | 0.0474 | 0.0476 | 0.0462 | 0.0418 | 0.0427 | |
| R2 | 0.7457 | 0.8371 | 0.7743 | 0.8345 | 0.8255 | |
| Smoothing effect function | NRMSE | 0.0723 | 0.0860 | 0.0886 | 0.0665 | 0.0671 |
| NMAE | 0.0378 | 0.0430 | 0.0475 | 0.0374 | 0.0378 | |
| R2 | 0.8338 | 0.8662 | 0.7949 | 0.8801 | 0.8774 |
| Modeling Session | Cumulative Method (s) | Holistic Approach (s) | Statistical Upscaling (s) | Cluster Static Division (s) | Proposed (s) |
|---|---|---|---|---|---|
| Cluster division | # | # | # | 6.7451 | 279.9040 |
| Looking for nominal PV stations | # | # | 30.2451 | # | # |
| Constructed graph structure | # | # | # | # | 21.0461 |
| Training models | 36,045.2377 | 123.4501 | 123.6553 | 740.7201 | 302.4566 |
| Prediction | 70.6380 | 2.0545 | 10.1503 | 14.1276 | 6.5741 |
| Total | 36,115.8757 | 125.5046 | 164.0507 | 761.5928 | 609.9808 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Yang, M. Ultra-Short-Term Photovoltaic Cluster Power Prediction Based on Photovoltaic Cluster Dynamic Clustering and Spatiotemporal Heterogeneous Dynamic Graph Modeling. Electronics 2025, 14, 3641. https://doi.org/10.3390/electronics14183641
Liu Y, Yang M. Ultra-Short-Term Photovoltaic Cluster Power Prediction Based on Photovoltaic Cluster Dynamic Clustering and Spatiotemporal Heterogeneous Dynamic Graph Modeling. Electronics. 2025; 14(18):3641. https://doi.org/10.3390/electronics14183641
Chicago/Turabian StyleLiu, Yingjie, and Mao Yang. 2025. "Ultra-Short-Term Photovoltaic Cluster Power Prediction Based on Photovoltaic Cluster Dynamic Clustering and Spatiotemporal Heterogeneous Dynamic Graph Modeling" Electronics 14, no. 18: 3641. https://doi.org/10.3390/electronics14183641
APA StyleLiu, Y., & Yang, M. (2025). Ultra-Short-Term Photovoltaic Cluster Power Prediction Based on Photovoltaic Cluster Dynamic Clustering and Spatiotemporal Heterogeneous Dynamic Graph Modeling. Electronics, 14(18), 3641. https://doi.org/10.3390/electronics14183641





