Parallelization of the Koopman Operator Based on CUDA and Its Application in Multidimensional Flight Trajectory Prediction
Abstract
1. Introduction
- We propose a GPU-based parallel optimization method for computing Koopman operators, addressing the computational bottlenecks associated with high-dimensional state spaces.
- We implement a general-purpose module interface that supports multiple Koopman solving strategies, providing good scalability.
- We verify the acceleration performance and prediction stability of the proposed method on the MFTP task. The experimental results demonstrate significant improvements in training efficiency.
2. Preliminaries
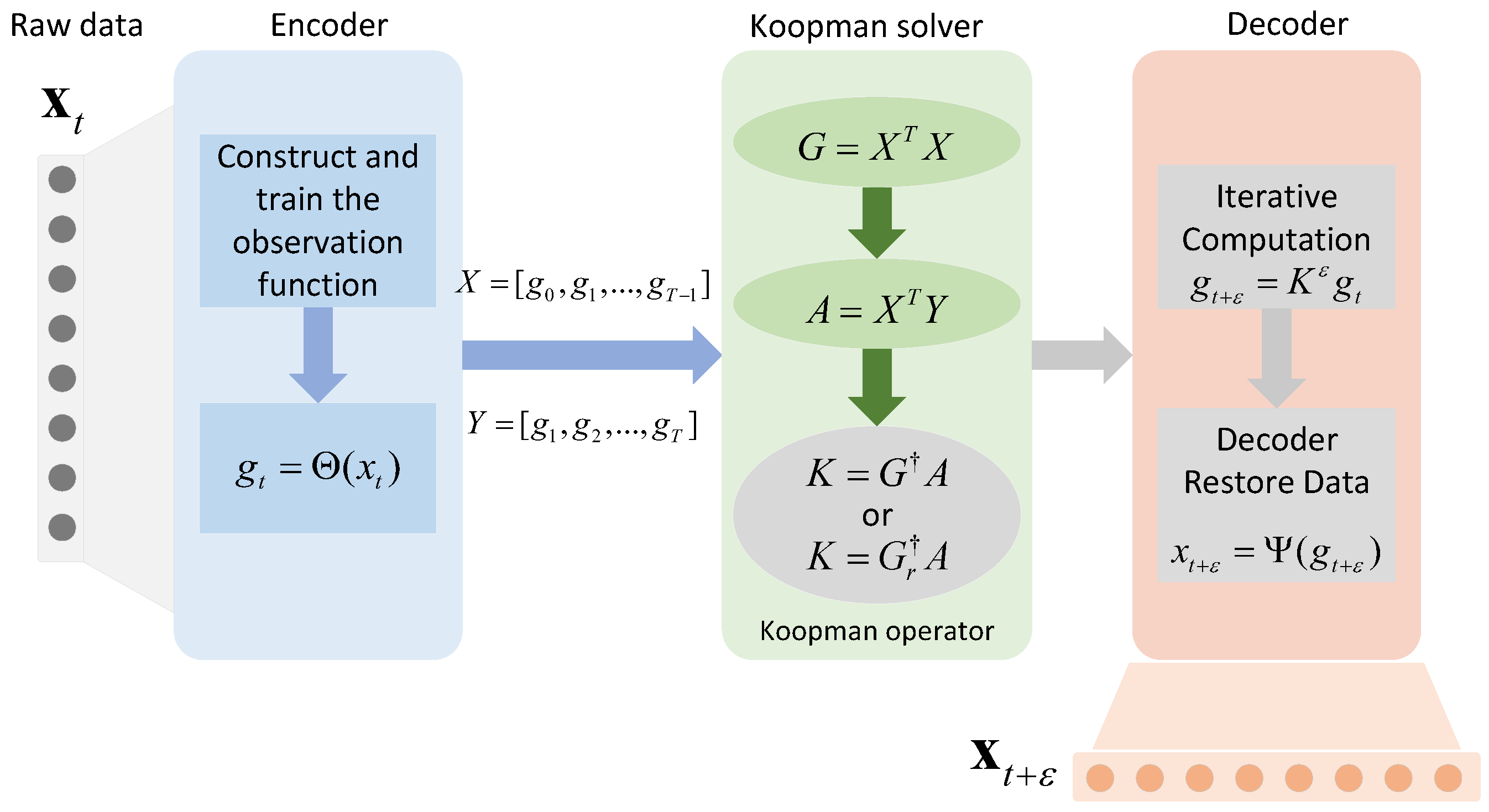
2.1. Koopman Operator
2.2. Koopman Training
- The full pseudo-inverse, which is computed using the full singular value decomposition (SVD) when solving for the pseudo-inverse of G.
- The truncated SVD, retaining only the top r singularities of G to improve the stability and control of the model’scapability. That is,
3. Algorithm Design
3.1. Computational Complexity Analysis and Optimization Motivation
3.1.1. Identification of Computation-Intensive Regions and Complexity Modeling
3.1.2. Operator Dependency DAG Modeling
3.2. Design of Parallel Algorithms for the Koopman Operator
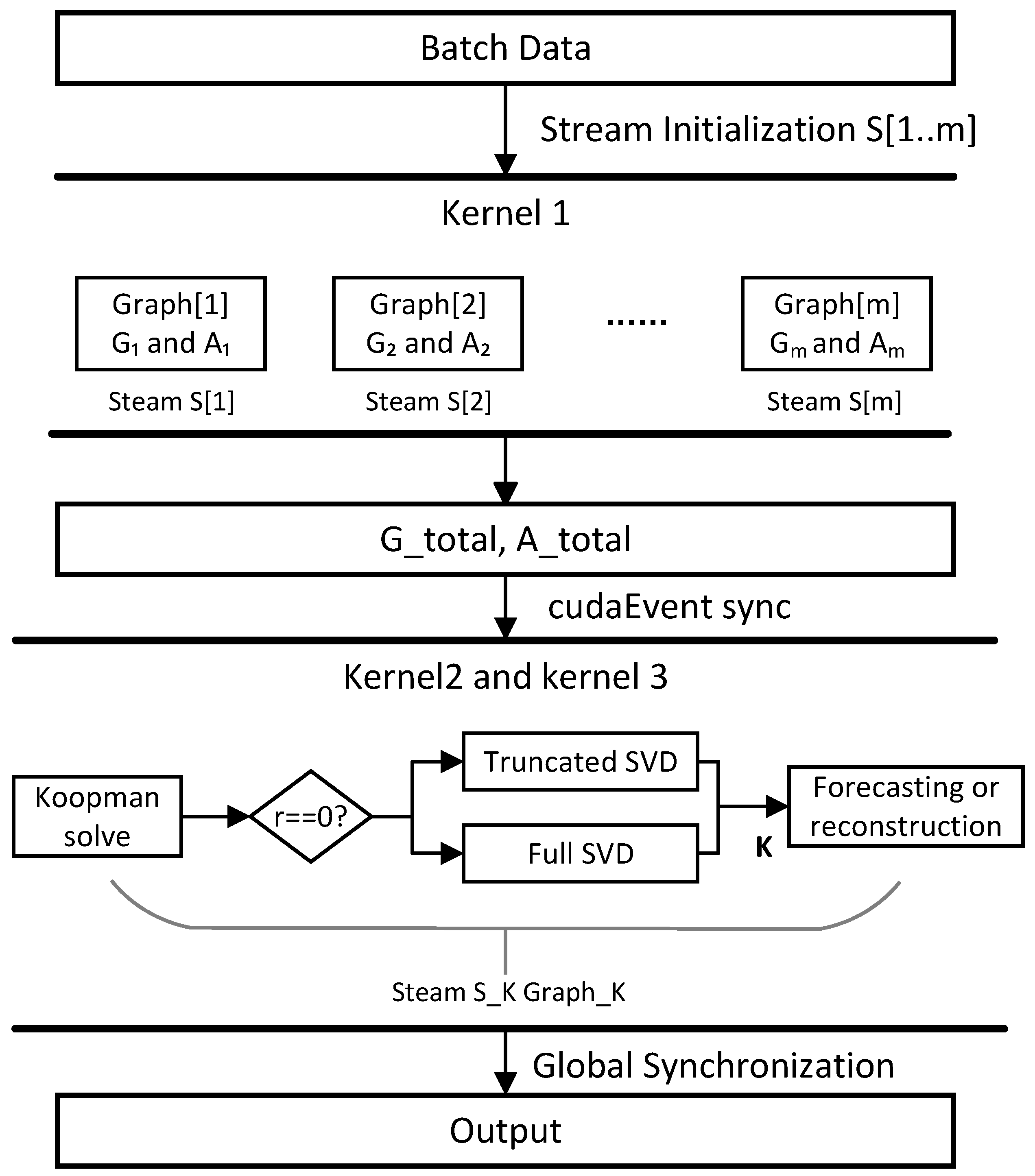
3.2.1. Multi-Granularity Parallel Task Decomposition
| Algorithm 1 KPA Framework |
|
- Kernel 1: This computes the covariance matrices for multiple batches of input data and performs normalization of matrices G and A.
- Kernel 2: The cuSOLVER library is employed to perform SVD and compute the pseudo-inverse of G, which is used to solve the Koopman operator K. Within this kernel function, KPA defines a unified solver interface that supports both full and truncated SVD strategies. If , a full pseudo-inverse is computed by retaining all singular values. If , a truncated SVD is applied, in which only the top r dominant singular values and their corresponding singular vectors are preserved. The algorithm incorporates a lightweight branching mechanism to determine the execution path—full or truncated—based on the value of r. This design avoids redundant memory accesses and the unnecessary duplication of intermediate results, thereby improving overall computational efficiency.
- Kernel 3: This applies the estimated Koopman operator K to the input data to generate prediction or reconstruction results.
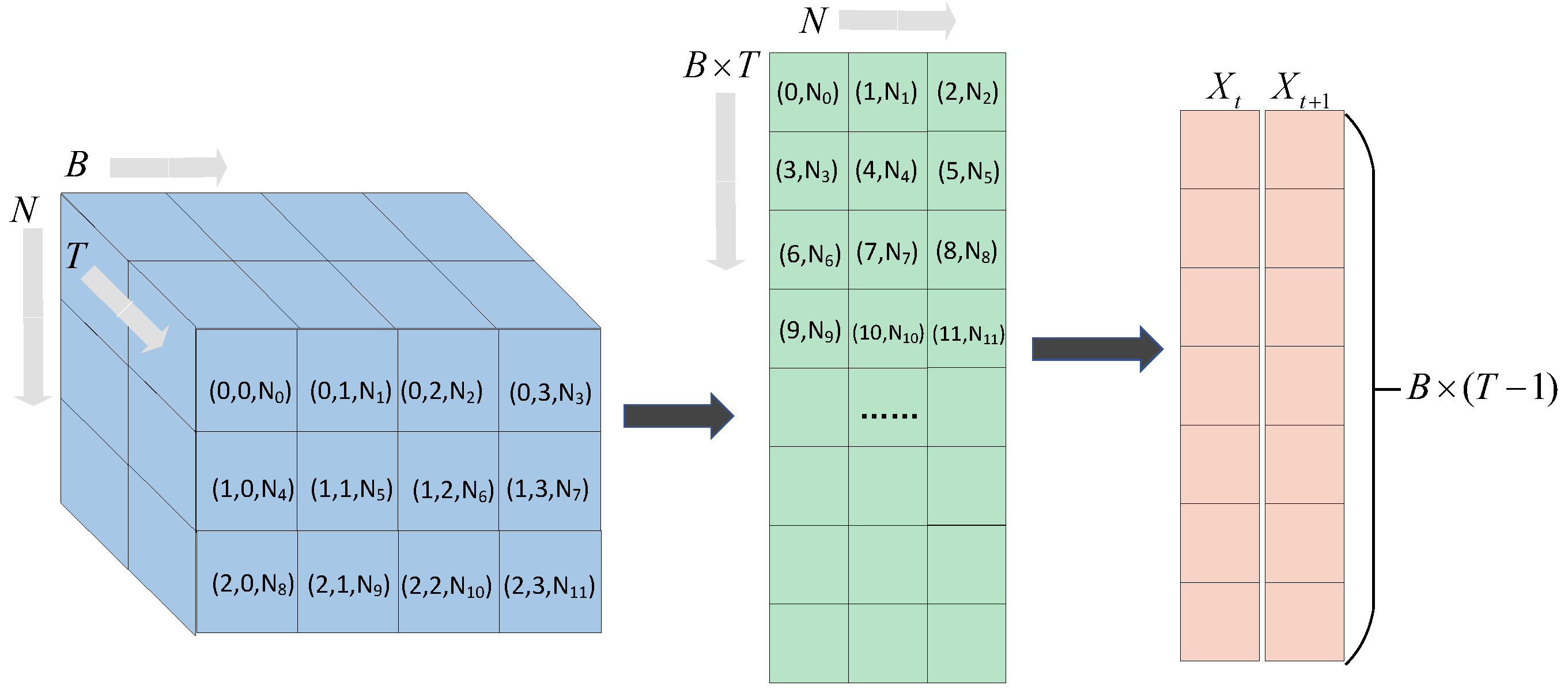
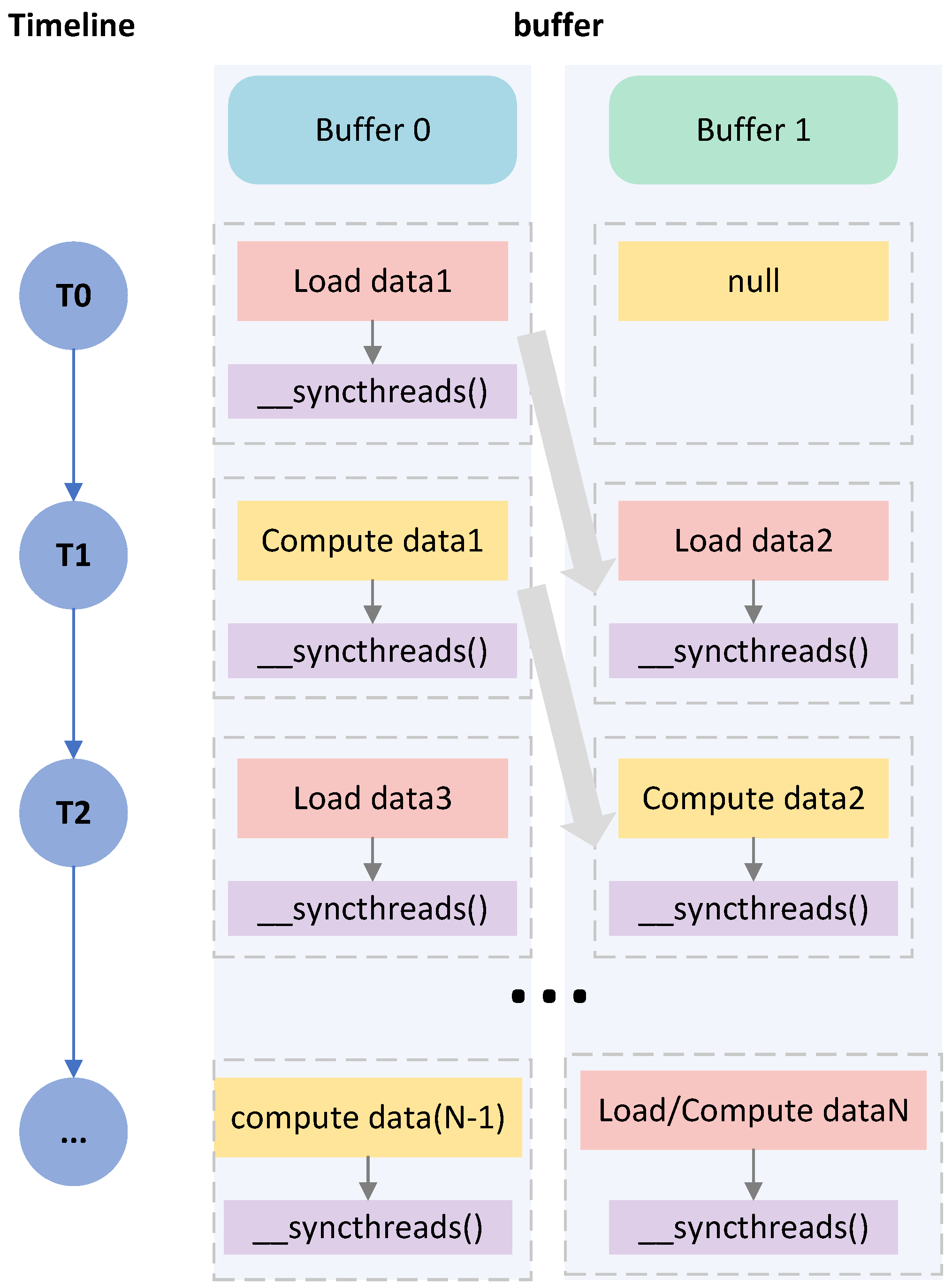
3.2.2. Memory Partitioning and Access Optimization
| Algorithm 2 KPA—Parallel Computation of G and A with Sliding Window and Double Buffer. |
|
4. Experiment and Analysis of the Results
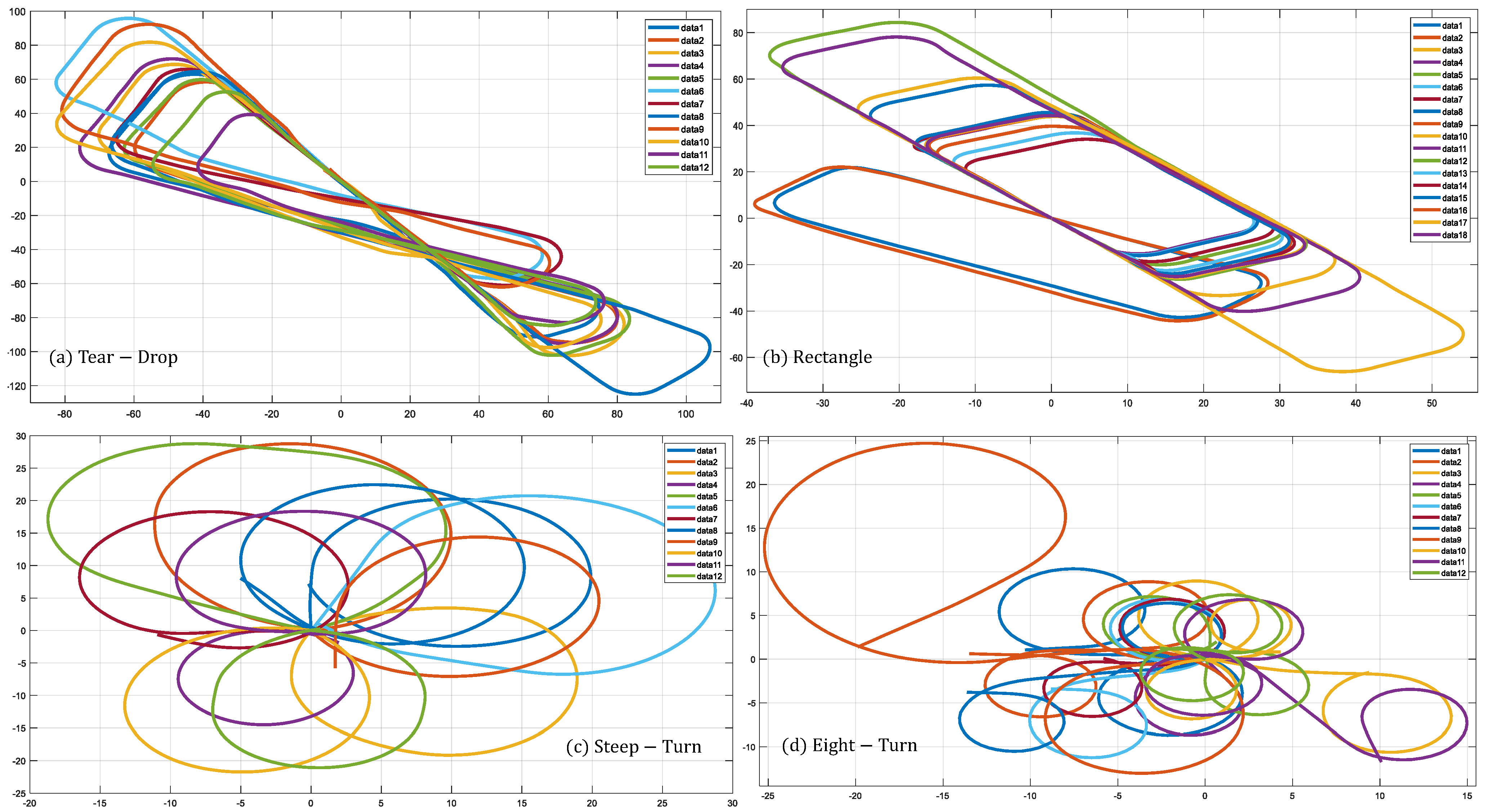
4.1. Dataset and Experimental Environment
4.2. Evaluation Metrics
4.3. Experimental Design
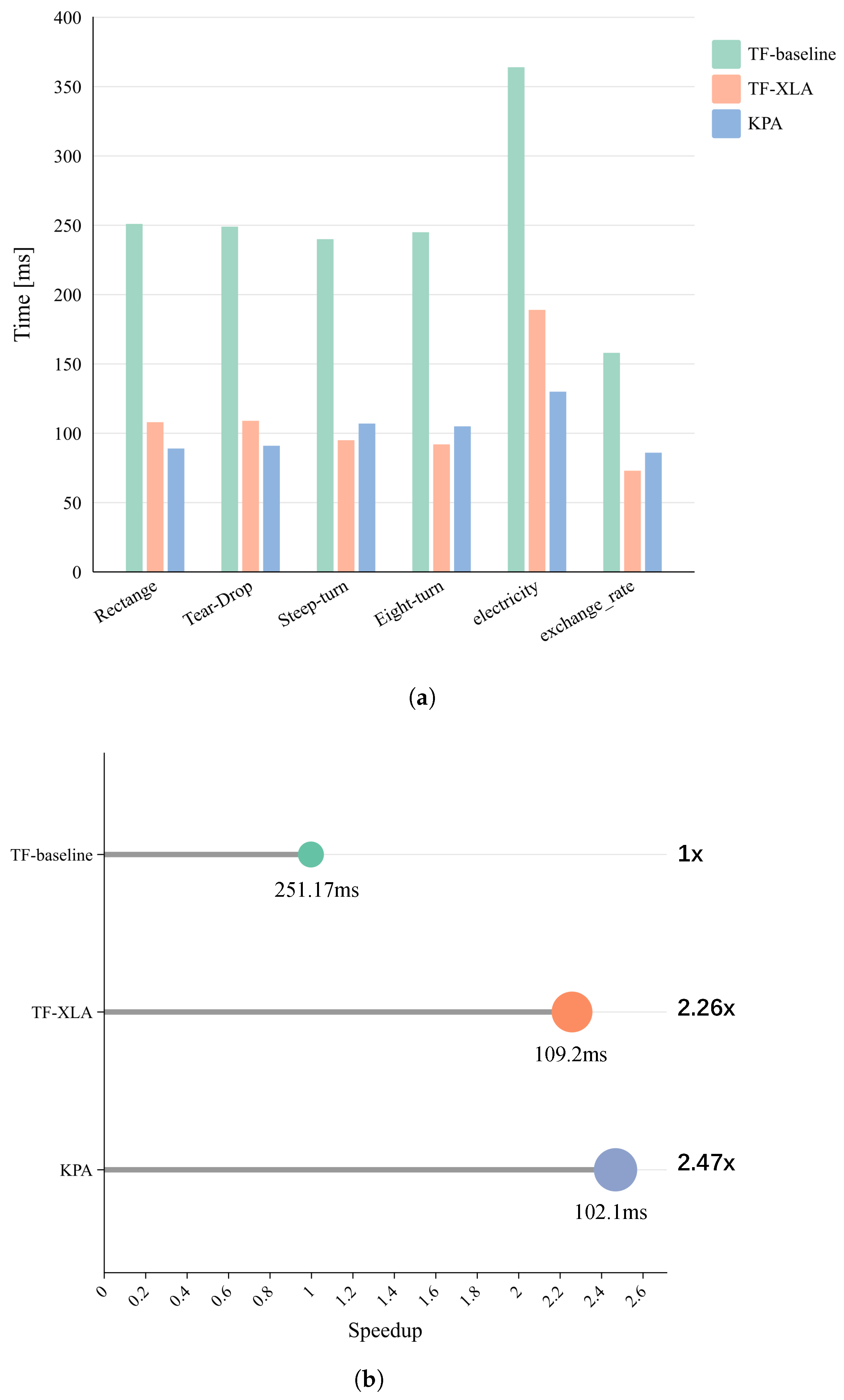
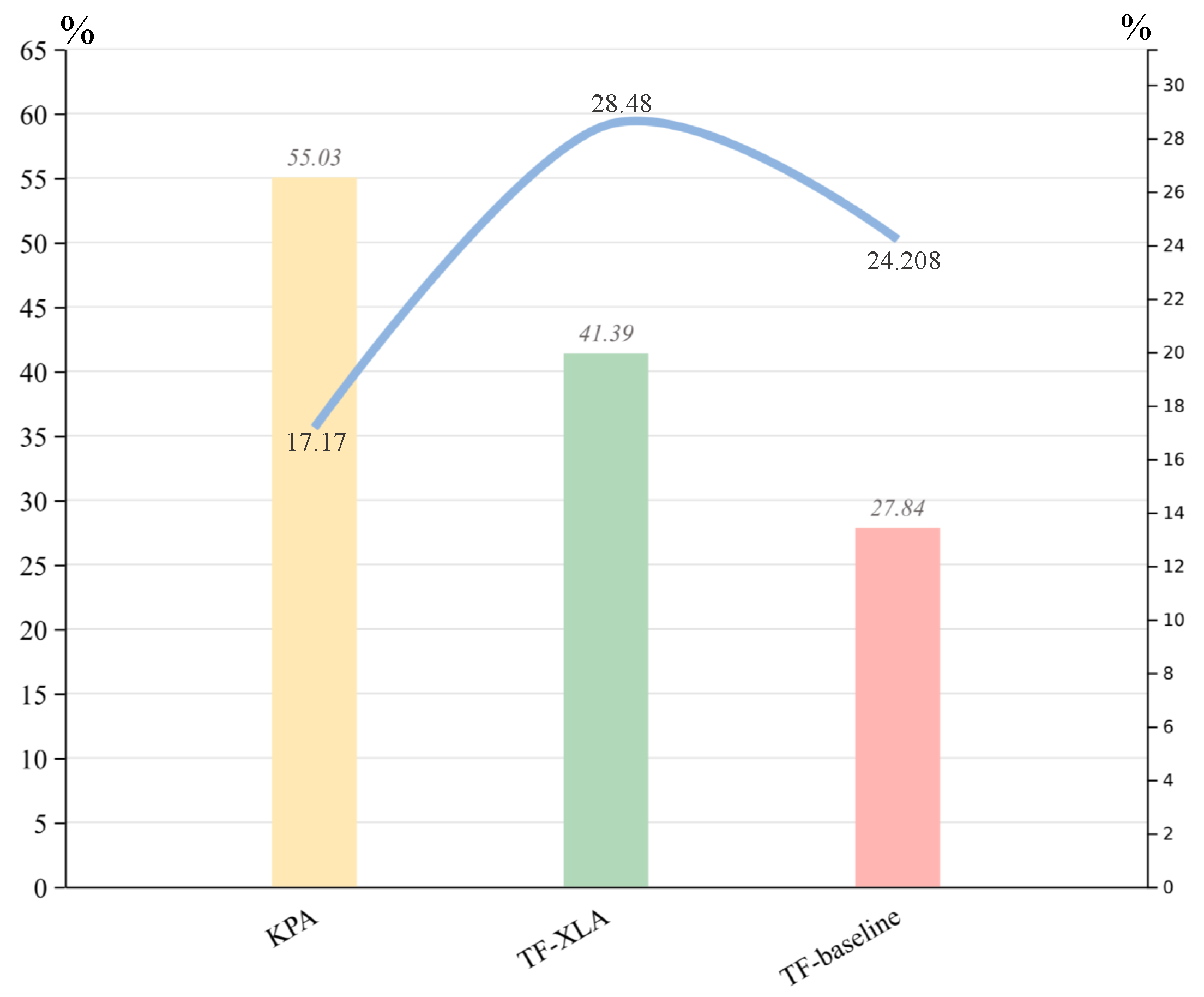
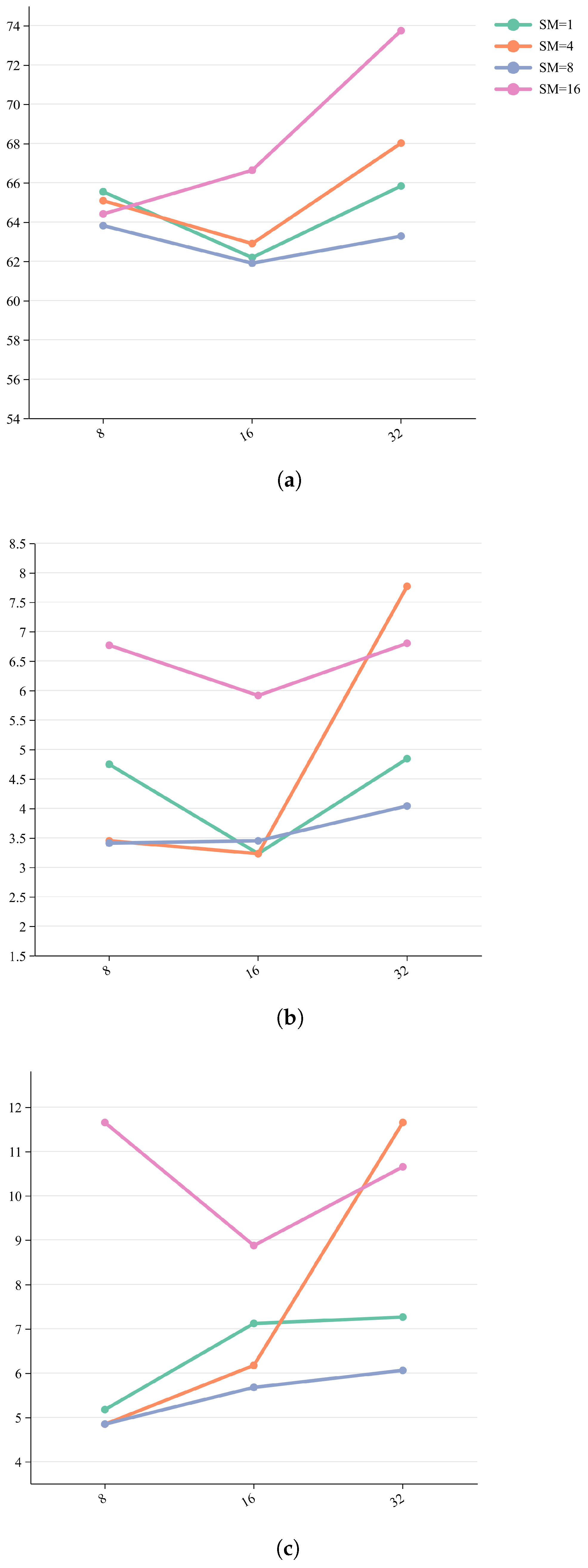
4.3.1. Benchmark Testing
4.3.2. Ablation Study
5. Conclusions
- (1)
- Optimizing pseudo-inverse computation. As shown in Figure 9, pseudo-inverse calculation remains the dominant cost in the KPA pipeline, even after kernel-level optimizations. Future work could explore randomized SVD, low-rank approximations, or hybrid GPU-CPU solvers to further reduce this bottleneck.
- (2)
- Adaptive kernel and memory tuning. Current block-size configuration is static, optimized for a specific feature dimension and GPU architecture. A promising direction is to design auto-tuning frameworks that dynamically adjust thread/block configurations and memory partitioning based on runtime profiling and problem size.
- (3)
- Currently, the KPA is an external operator. Later studies can consider integrating KPAs into differentiable pipelines and interacting with automatic graph optimizers such as XLA to further improve overall performance and scalability.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Koopman, B.O. Hamiltonian systems and transformation in Hilbert space. Proc. Natl. Acad. Sci. USA 1931, 17, 315–318. [Google Scholar] [CrossRef] [PubMed]
- Bevanda, P.; Sosnowski, S.; Hirche, S. Koopman operator dynamical models: Learning, analysis and control. Annu. Rev. Control 2021, 52, 197–212. [Google Scholar] [CrossRef]
- Brunton, S.L.; Budišić, M.; Kaiser, E.; Kutz, J.N. Modern Koopman theory for dynamical systems. arXiv 2021, arXiv:2102.12086. [Google Scholar] [CrossRef]
- Kutz, J.N.; Brunton, S.L.; Brunton, B.W.; Proctor, J.L. Dynamic Mode Decomposition: Data-Driven Modeling of Complex Systems; SIAM: Philadelphia, PA, USA, 2016. [Google Scholar]
- Schmid, P.J. Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 2010, 656, 5–28. [Google Scholar] [CrossRef]
- Haseli, M.; Cortés, J. Parallel learning of Koopman eigenfunctions and invariant subspaces for accurate long-term prediction. IEEE Trans. Control Netw. Syst. 2021, 8, 1833–1845. [Google Scholar] [CrossRef]
- Lusch, B.; Kutz, J.N.; Brunton, S.L. Deep learning for universal linear embeddings of nonlinear dynamics. Nat. Commun. 2018, 9, 4950. [Google Scholar] [CrossRef]
- Otto, S.E.; Rowley, C.W. Linearly recurrent autoencoder networks for learning dynamics. SIAM J. Appl. Dyn. Syst. 2019, 18, 558–593. [Google Scholar] [CrossRef]
- Brissette, C.; Hawkins, W.; M. Slota, G. GNN Node Classification Using Koopman Operator Theory on GPU. In Proceedings of the International Conference on Complex Networks and Their Applications, Istanbul, Türkiye, 10–12 December 2024; Springer: Cham, Switzerland, 2024; pp. 62–73. [Google Scholar]
- NVIDIA Corporation. cuSOLVER Library Documentation. 2025. Available online: https://docs.nvidia.com/cuda/cusolver/index.html (accessed on 31 August 2025).
- NVIDIA Corporation. Accelerating Linear Algebra with cuBLAS. 2025. Available online: https://docs.nvidia.com/cuda/cublas/index.html (accessed on 31 August 2025).
- Lu, J.; Jiang, J.; Bai, Y.; Dai, W.; Zhang, W. FlightKoopman: Deep Koopman for Multi-Dimensional Flight Trajectory Prediction. Int. J. Comput. Intell. Appl. 2025, 24, 2450038. [Google Scholar] [CrossRef]
- Pouria Talebi, S.; Kanna, S.; Xia, Y.; Mandic, D.P. A distributed quaternion Kalman filter with applications to fly-by-wire systems. In Proceedings of the 2016 IEEE International Conference on Digital Signal Processing (DSP), Beijing, China, 16–18 October 2016; pp. 30–34. [Google Scholar] [CrossRef]
- Liu, C.; Wang, J.; Zhang, W.; Yang, X.D.; Guo, X.; Liu, T.; Su, X. Synchronization of broadband energy harvesting and vibration mitigation via 1:2 internal resonance. Int. J. Mech. Sci. 2025, 301, 110503. [Google Scholar] [CrossRef]
- Shi, H.; Meng, M.Q.H. Deep Koopman operator with control for nonlinear systems. IEEE Robot. Autom. Lett. 2022, 7, 7700–7707. [Google Scholar] [CrossRef]
- Xiong, W.; Huang, X.; Zhang, Z.; Deng, R.; Sun, P.; Tian, Y. Koopman neural operator as a mesh-free solver of non-linear partial differential equations. J. Comput. Phys. 2024, 513, 113194. [Google Scholar] [CrossRef]
- Yeung, E.; Kundu, S.; Hodas, N. Learning deep neural network representations for Koopman operators of nonlinear dynamical systems. In Proceedings of the 2019 American Control Conference (ACC), Philadelphia, PA, USA, 10–12 July 2019; pp. 4832–4839. [Google Scholar]
- Boehm, M.; Reinwald, B.; Hutchison, D.; Evfimievski, A.V.; Sen, P. On optimizing operator fusion plans for large-scale machine learning in systemml. arXiv 2018, arXiv:1801.00829. [Google Scholar] [CrossRef]
- Chen, Y.; Brock, B.; Porumbescu, S.; Buluç, A.; Yelick, K.; Owens, J.D. Atos: A task-parallel GPU dynamic scheduling framework for dynamic irregular computations. arXiv 2021, arXiv:2112.00132. [Google Scholar] [CrossRef]
- Ekelund, J.; Markidis, S.; Peng, I. Boosting Performance of Iterative Applications on GPUs: Kernel Batching with CUDA Graphs. arXiv 2025, arXiv:2501.09398. [Google Scholar]
- Veneva, M.; Imamura, T. ML-Based Optimum Number of CUDA Streams for the GPU Implementation of the Tridiagonal Partition Method. arXiv 2025, arXiv:2501.05938. [Google Scholar] [CrossRef]
- Balagafshe, R.G.; Akoushideh, A.; Shahbahrami, A. Matrix-matrix multiplication on graphics processing unit platform using tiling technique. Indones. J. Electr. Eng. Comput. Sci. 2022, 28, 1012–1019. [Google Scholar] [CrossRef]
- Volkov, V.; Demmel, J.W. Benchmarking GPUs to tune dense linear algebra. In Proceedings of the SC’08: Proceedings of the 2008 ACM/IEEE Conference on Supercomputing, Austin, TX, USA, 15–21 November 2008; pp. 1–11. [Google Scholar]
- Adámek, K.; Dimoudi, S.; Giles, M.; Armour, W. GPU fast convolution via the overlap-and-save method in shared memory. ACM Trans. Archit. Code Optim. (TACO) 2020, 17, 18. [Google Scholar] [CrossRef]
- Abdelfattah, A.; Keyes, D.; Ltaief, H. Kblas: An optimized library for dense matrix-vector multiplication on gpu accelerators. ACM Trans. Math. Softw. (TOMS) 2016, 42, 18. [Google Scholar] [CrossRef]
- Sitchinava, N.; Weichert, V. Bank Conflict Free Comparison-based Sorting On GPUs. arXiv 2013, arXiv:1306.5076. [Google Scholar]
- Daga, T.; Bhanpato, J.; Behere, A.; Mavris, D. Aircraft Takeoff Weight Estimation for Real-World Flight Trajectory Data Using CNN-LSTM. In Proceedings of the AIAA Aviation Forum and ASCEND 2024, Las Vegas, NV, USA, 29 July–2 August 2024; p. 4291. [Google Scholar]
- Lu, J.; Chai, H.; Jia, R. A general framework for flight maneuvers automatic recognition. Mathematics 2022, 10, 1196. [Google Scholar] [CrossRef]
- Lai, G.; Chang, W.C.; Yang, Y.; Liu, H. Modeling long- and short-term temporal patterns with deep neural networks. In Proceedings of the The 41st International ACM SIGIR Conference on Research & Development in Information Retrieval, Ann Arbor, MI, USA, 8–12 July 2018; pp. 95–104. [Google Scholar]
- Wu, H.; Xu, J.; Wang, J.; Long, M. Autoformer: Decomposition transformers with auto-correlation for long-term series forecasting. Adv. Neural Inf. Process. Syst. 2021, 34, 22419–22430. [Google Scholar]
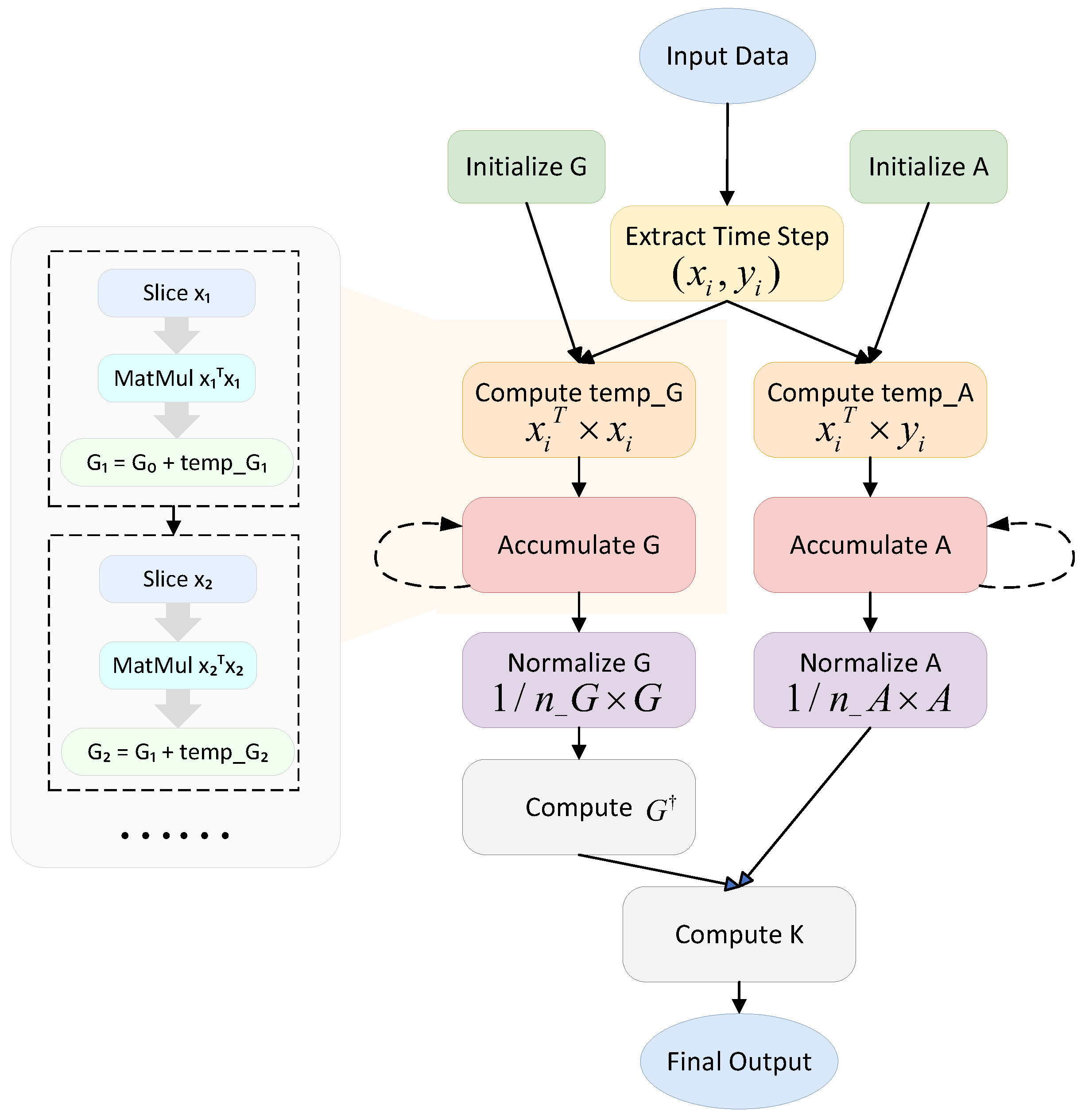

| Name | Type | Input Dependencies | Output Usage |
|---|---|---|---|
| Slice Slice | Slice | inputs_array | temp_A and temp_G at each sampling index |
| matmul(, ) matmul(, ) | MatMul | , | temp_G, temp_A |
| Accumulate G Accumulate A | Add | temp_G and G temp_A and A | G and A for the next iteration |
| ScalarMul | The accumulation of G and A | Input for | |
| matmul(pinv(G), A) | MatMul | G, A | |
| matmul(inputs, k) | MatMul | inputs, k | Model Output |
| Metric Category | Metric Name | Definition |
|---|---|---|
| Time Performance | Iteration Time | The time required to complete one Koopman operator computation. |
| Speed up Ratio | The ratio of execution times between different implementation methods. | |
| Resource Efficiency | Computational Throughput | The ratio of kernel computational performance to the theoretical peak performance of the GPU. |
| Memory Throughput | The efficiency of memory access during kernel execution. | |
| Accuracy Evaluation | Absolute Error | The degree of difference between the optimized method and the original method. |
| Notion | Description |
|---|---|
| TF-baseline | Native Koopman Operator Based on TensorFlow |
| TF-XLA | TF-Baseline with XLA for Faster and More Efficient Execution |
| KPA | Customized Koopman Operator Based on CUDA C++ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, J.; Wang, L.; Shang, Z. Parallelization of the Koopman Operator Based on CUDA and Its Application in Multidimensional Flight Trajectory Prediction. Electronics 2025, 14, 3609. https://doi.org/10.3390/electronics14183609
Lu J, Wang L, Shang Z. Parallelization of the Koopman Operator Based on CUDA and Its Application in Multidimensional Flight Trajectory Prediction. Electronics. 2025; 14(18):3609. https://doi.org/10.3390/electronics14183609
Chicago/Turabian StyleLu, Jing, Lulu Wang, and Zeyi Shang. 2025. "Parallelization of the Koopman Operator Based on CUDA and Its Application in Multidimensional Flight Trajectory Prediction" Electronics 14, no. 18: 3609. https://doi.org/10.3390/electronics14183609
APA StyleLu, J., Wang, L., & Shang, Z. (2025). Parallelization of the Koopman Operator Based on CUDA and Its Application in Multidimensional Flight Trajectory Prediction. Electronics, 14(18), 3609. https://doi.org/10.3390/electronics14183609






