Efficiency Analysis of Bridgeless Three-Level PFC Circuits Based on Modal Segment Integration Method

Abstract

Traditional methods for evaluating power electronic converter efficiency heavily rely on simulations and often lack theoretical support, which can lead to inaccuracies and limit effective design optimization. To address these shortcomings, this paper proposes a modal segment integration method based on a device loss model. The analysis begins with the operating principles of the proposed circuit topology. A detailed power loss model is then established and applied to representative operating modes. Using the modal segment integration method, the total loss over a full operating cycle is calculated. Theoretical analysis estimates the system efficiency exceeds 98%. To validate the proposed method, a 1 kW experimental prototype with a 400 V DC output is built. The results show that the maximum error between the theoretical and experimental efficiency is less than 0.4%. This method offers a reliable theoretical basis for efficiency evaluation of three-level converter topologies and supports the structural design and performance optimization of power electronic systems.

1. Introduction

With the constant development of power electronics technology, rectifier devices have been widely used in new energy vehicles, LED drives, and industrial automation. Among them, high-efficiency multilevel rectifiers have become the focus of research [1,2,3,4,5,6]. To meet international standards such as IEEE 519 [7] and IEC 61000−3−2 [8], rectifiers must have a high power factor, high current sinusoidality, and low total harmonic distortion (THD). Currently, power factor correction (PFC) is the most commonly used technical solution. Among them, the bridgeless three-level PFC rectifier demonstrates superior performance in reducing switching voltage stress and achieving high efficiency [9,10,11,12,13,14,15,16], and has received continuous attention from scholars worldwide.

Currently, high efficiency and high power density are key objectives in rectifier design, and they are crucial for system efficiency analysis and evaluation. Scholars worldwide have conducted extensive research on the efficiency improvement and loss optimization of three-level PFC rectifiers [17,18,19,20]. In [17], a bridgeless three-level PFC rectifier topology was proposed based on neutral-point capacitor voltage division. By reducing device voltage stress and optimizing current paths, the system efficiency was improved. In [18], a single-stage full-bridge boost PFC converter incorporating a passive snubber with a coupled inductor was proposed. The snubber effectively suppressed voltage spikes across the switches, reduced voltage stress and switching losses, and improved overall conversion efficiency. In [19], a single-stage current-fed boost PFC converter suitable for high-voltage applications was proposed. By forming a resonant tank with the transformer’s leakage inductance and the parasitic capacitance of the rectifier diodes, zero-current switching (ZCS) was achieved, which effectively reduced switching losses and improved the power factor. In [20], a current-controlled variable inductor was introduced into a single stage PFC boost rectifier to reduce system losses. Although the above literature has made positive progress in topology optimization, modulation strategies and loss control, the existing efficiency analysis methods mostly focus on simulation or experimental verification. These methods lack systematic, theoretical analysis, which means we cannot quickly assess the efficiency characteristics of the topology scheme at the design stage. Therefore, further improvement is needed.

In this paper, a modal segment integration method based on device loss model is proposed to analyze the system efficiency of the new bridgeless three-level PFC rectifier. Compared with traditional methods that rely on simulation or experiment, the proposed method is more systematic and has a stronger theoretical basis. It can quickly and accurately evaluate the efficiency of the topology during the design stage, helping to improve design efficiency. Firstly, the operating principle of the circuit topology is analyzed, including its operating modes, key waveform, and voltage stresses. Then, the power device loss model is established, which is combined with the typical operating modes. The modal segment integration method is used to calculate the average power loss of the whole cycle, and derive the system efficiency. Finally, an experimental prototype with an input voltage of 220 V/20 kHz, rated power of 1 kW, and DC output voltage of 400 V is built based on this proposed bridgeless three-level PFC circuit topology. This prototype is used to verify the proposed method and assess the accuracy and feasibility of its theoretical analysis.

2. Analysis of Topology and Its Working Process

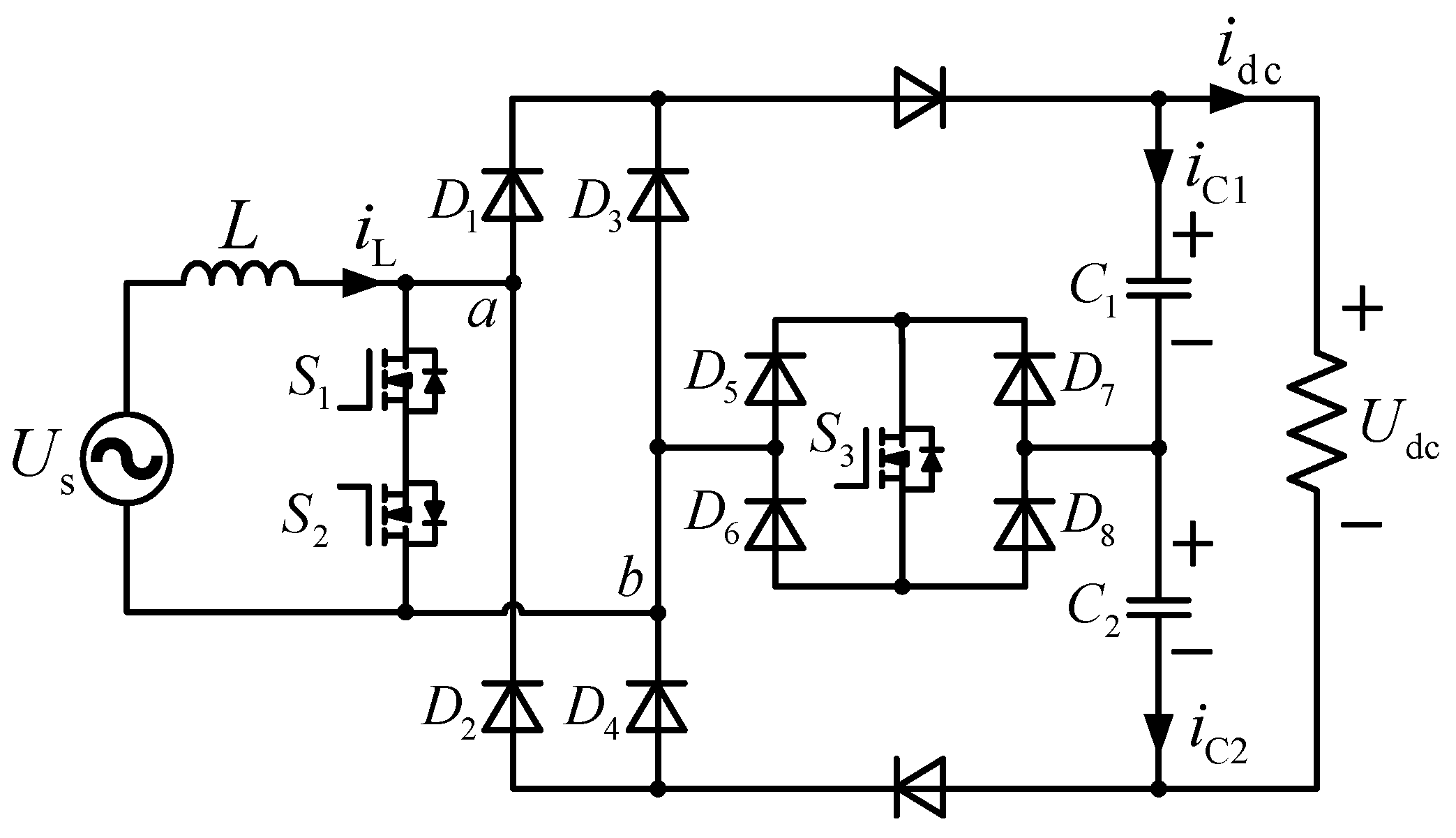
2.1. Circuit Topology

This paper proposes a bridgeless three-level power factor correction (PFC) rectifier topology, as shown in Figure 1. The circuit includes the switches S₁–S₃, the diodes D₁–D₈, the DC-link capacitors C₁ and C₂, and input inductor L. During the positive half-cycle of the grid voltage, diodes D₁ and D₄ conduct, while diodes D₂ and D₃ conduct during the negative half-cycle. The switching tubes (S₁–S₃) are used to achieve three-level voltage conversion between the two bridge legs.

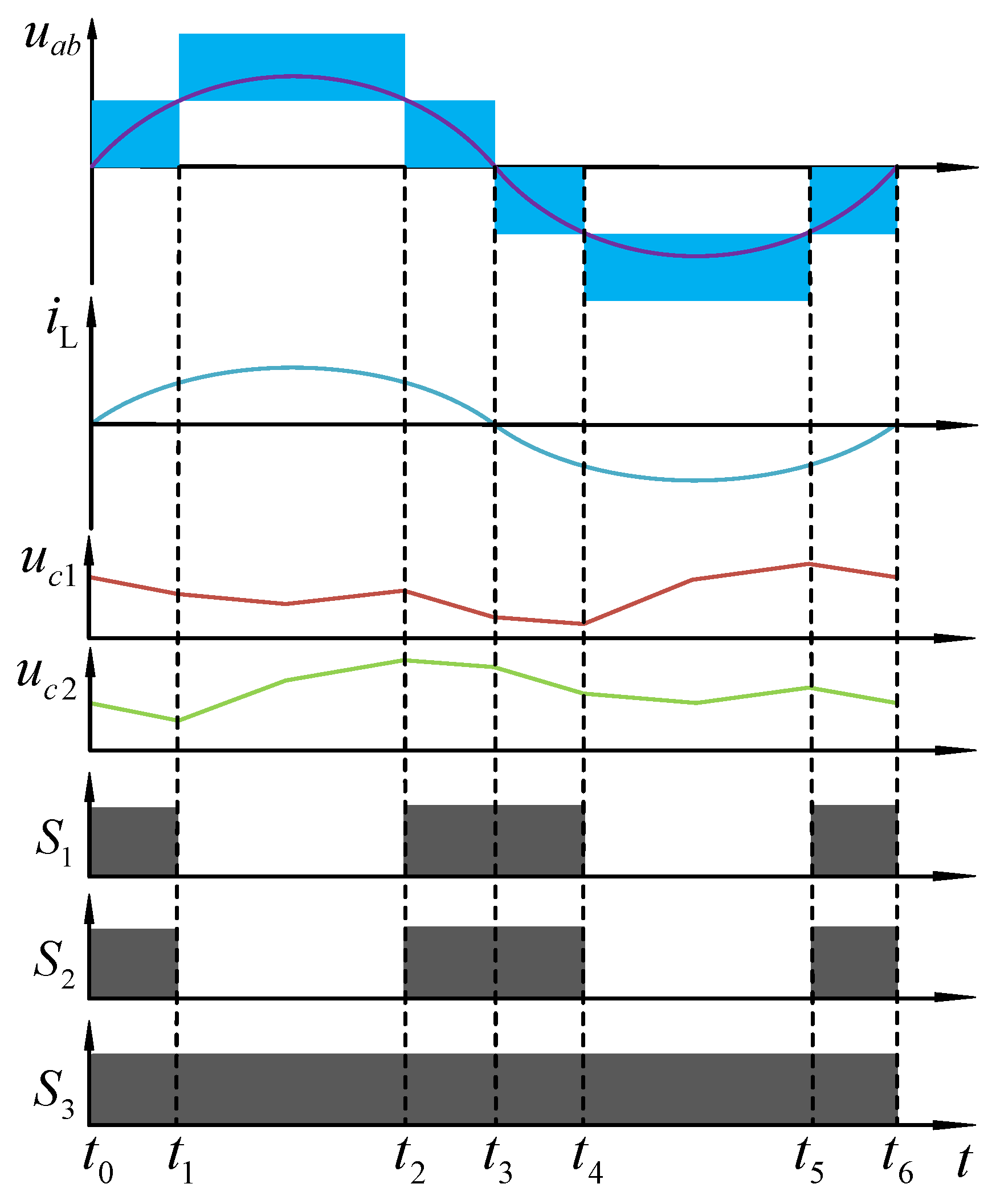
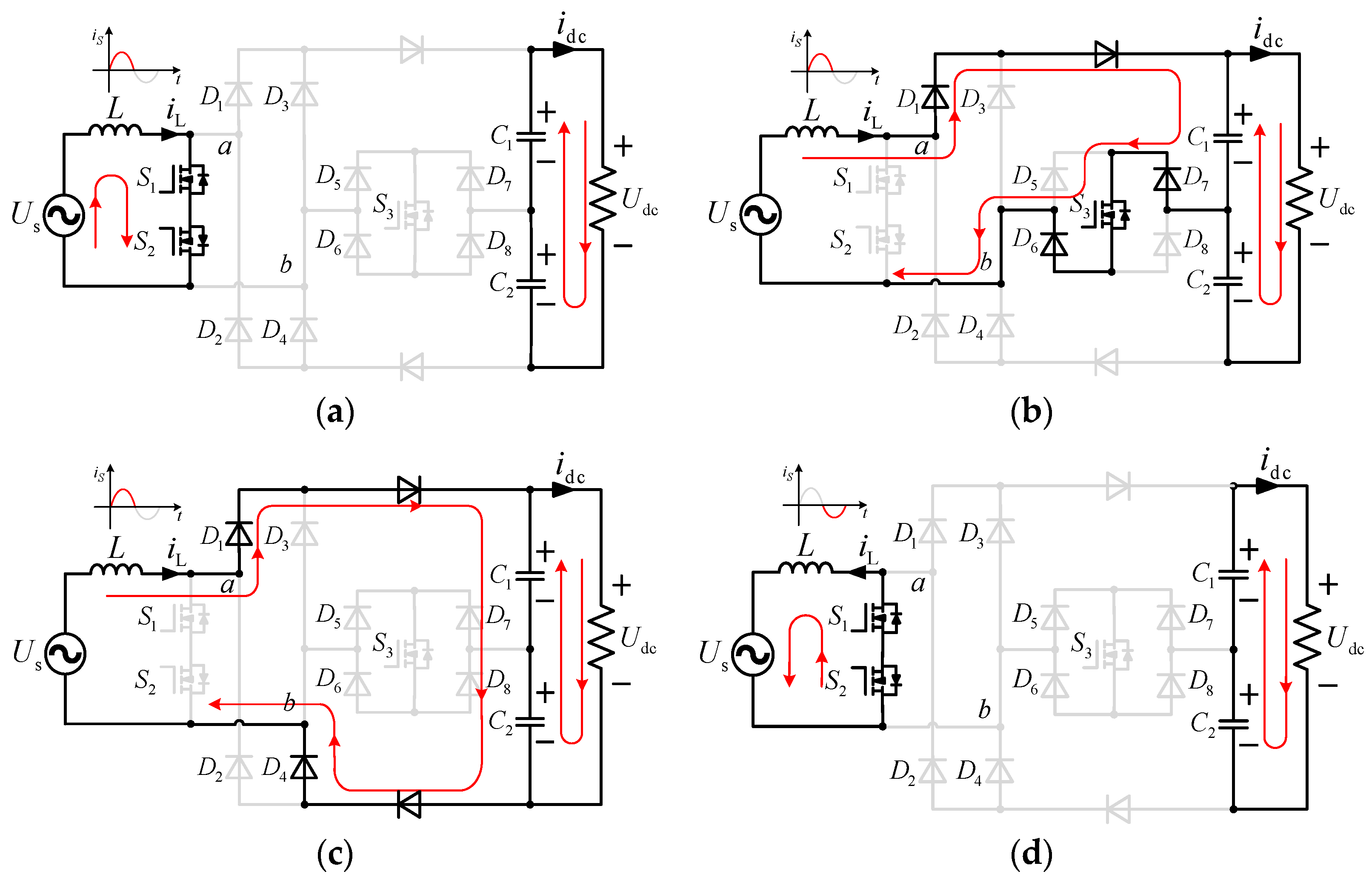
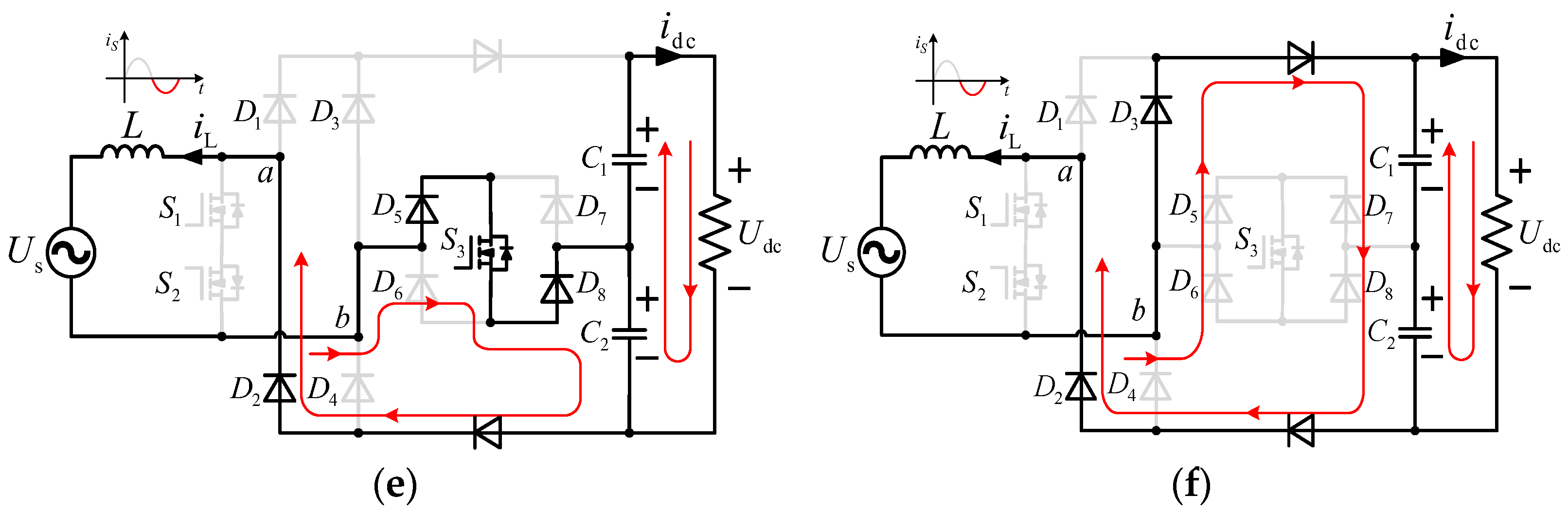
2.2. Analysis of Work Processes

To verify the circuit’s effectiveness, the topology shown in Figure 1 is analyzed. As shown in Figure 2, the key waveforms over one power-line cycle are presented, and the circuit operates symmetrically during the positive and negative half cycles. To help readers understand, Figure 3 shows the current path diagrams of the six operating modes. Figure 3a–c show the three operating states of the circuit during the positive half-cycle and Figure 3d–f show the three operating states during the negative half-cycle.

Mode 1: As shown in Figure 3a, during the positive half-cycle of the grid voltage, S₃ turns off, and S₁ and S₂ turn on. In this state, the power source charges the inductor L through S₁ and S₂. The inductor stores energy, and the current i_L increases. Meanwhile, capacitors C₁ and C₂ discharge and supply power to the load R_L. The bridge leg voltage U_ab = 0.

Mode 2: As shown in Figure 3b, during the positive half-cycle of the grid voltage, S₁ and S₂ turn off and S₃ turns on. In this state, inductor L discharges and charges capacitor C₁. The current then flows through diode D₁, capacitor C₁, diode D₇, switch S₃, and diode D₆. At this point, the bridge leg voltage U_ab = U_dc/2.

Mode 3: As shown in Figure 3c, the circuit operates during the positive half-cycle of the grid voltage and the switches S₁, S₂, and S₃ are off. The power source delivers energy to capacitors C₁, C₂, and load R_L through inductor L. The inductor current i_L decreases. The bridge leg voltage U_ab = U_dc.

Mode 4: As shown in Figure 3d, during the negative half-cycle of the grid voltage, S₃ turns off and S₂ turns on. In this state, the power source charges the inductor L through S₁ and S₂. The inductor stores energy, and the current i_L rises. In the meantime, capacitors C₁ and C₂ discharge and supply power to the load R_L. The bridge leg voltage U_ab = 0.

Mode 5: As shown in Figure 3e, the circuit works during the negative half-cycle of the grid voltage. S₁ and S₂ are off, while S₃ is on. In this process, the inductor L releases energy and charges capacitor C₂, and current flows through diode D₅, switch S₃, diode D₈, capacitor C₂, and diode D₂. At this point, the bridge leg voltage U_ab = U_dc/2.

Mode 6: As shown in Figure 3f, the circuit operates during the negative half-cycle of the grid voltage and S₁, S₂, and S₃ turn off. During this process, the power source supplies energy to capacitors C₁ and C₂, as well as to the load R_L, through inductor L. The inductor current i_L decreases during this time. At this time, the bridge leg voltage U_ab = U_dc.

The voltage stress characteristics of each MOSFET and diode in the proposed bridgeless three-level PFC circuit can be determined based on the above modal analysis.

Table 1. Voltage stress on switching devices.

Switching Device	Voltage Stress
S1	Udc
S2	Udc
S3	Udc/2
D1–D4	Udc
D5, D6	Udc/2
D7, D8	Udc/2

shows the maximum voltage stress across each switching device.

3. Loss Analysis and Efficiency Estimation

This section analyzes the power devices losses in the bridgeless three-level circuit. Most of the losses are attributed to the diodes and MOSFETs. The loss calculation formulas are derived according to the method in [21].

3.1. Diode Loss Analysis

The three main loss components of the fast recovery diode include turn-on loss, conduction loss, and turn-off loss:

$$P_{D\text{-}ON}={\displaystyle \frac{1}{2}}{f}_C{I}_F(V_{FR}-V_F)t_{\mathrm{fr}}$$

(1)

where $P_{D\text{-}ON}$ is the turn-on loss, $f_C$ is the switching frequency at 5 kHz, $I_F$ is the diode forward current, and $V_{FR}$ is the maximum diode forward recovery voltage. $V_F$ is the diode forward voltage drop, and $t_{\mathrm{fr}}$ is the diode forward recovery time.

$$P_{D\text{-}CON}=V_F{I}_{D(AV)}+r_D{I}_{D(RMS)}^2$$

(2)

where $P_{D\text{-}CON}$ is the conduction loss, $I_{D(AV)}$ is the average value of the diode current, $I_{D(RMS)}$ is the real-valued mean of the diode current, and $r_D$ is the diode conduction internal resistance.

$$P_{D\text{-}OFF}={\displaystyle \frac{1}{4}}{f}_C{I}_{D(RM)}{K}_f{V}_R{t}_{\mathrm{rr}}$$

(3)

where $P_{D\text{-}OFF}$ is the turn-off loss, $I_{D(RM)}$ is the maximum value of reverse recovery current, $K_f$ is the temperature coefficient, $V_R$ is the reverse voltage, and $t_{\mathrm{rr}}$ is the reverse recovery time.

The total loss of the fast recovery diode is

$$P_D=P_{D\text{-}ON}+P_{D\text{-}CON}+P_{D\text{-}OFF}$$

(4)

3.2. Loss Analysis of Power Switching Devices

The turn-on loss of the MOSFET device is mainly due to the energy discharged from its output capacitance $C_g$. This loss is expressed as follows:

$$P_{\mathrm{Q}\text{-}\mathrm{ON}}={\displaystyle \frac{1}{2}}{f}_C\cdot C_g\cdot U_{\mathrm{o}}^2$$

(5)

where $f_c$ is the switching frequency, ${\mathrm{C}}_g$ is the MOSFET’s equivalent output capacitance, and $U_0$ is the instantaneous turn-on voltage.

The equation used to calculate the conduction loss of the MOSFET device is

$$P_{\mathrm{Q}\text{-}\mathrm{CON}}=I_{Q(RMS)}^2\cdot R_{\mathrm{Q}}$$

(6)

where $P_{\mathrm{Q}\text{-}\mathrm{CON}}$ is the conduction loss and $I_{Q(RMS)}$ is the root mean square value of the MOSFET current.

The turn-off loss is computed as follows:

$$P_{\mathrm{Q}\text{-}\mathrm{OFF}}={\displaystyle \frac{1}{2}}{f}_c\cdot U_o\cdot I_L\cdot t_{\mathrm{fr}}$$

(7)

where $P_{\mathrm{Q}\text{-}\mathrm{OFF}}$ is the turn-off loss and $t_{\mathrm{fr}}$ is the switch-on rise time.

Equations (3)–(14) give the MOSFET turn-on loss caused by the equivalent output capacitance. Since the output capacitance $C_g$ varies nonlinearly with the drain-source voltage, it is corrected to the datasheet value $C_{oss}$, leading to the form of Equation (8). On this basis, the reverse-recovery related loss of the diode, the conduction loss, and the turn-off loss are further included to form the total loss model of the MOSFET. The total loss of the MOSFET switches is as follows:

$$P_Q={\displaystyle \frac{2}{3}}{f}_C\cdot C_{oss}\cdot U_o^2+{\displaystyle \frac{1}{4}}{f}_c\cdot I_{D(RM)}\cdot K_f\cdot V_R\cdot t_{rr}+P_{Q-CON}+P_{Q-OFF}$$

(8)

where $P_Q$ is the total loss of the MOSFET switches, $f_c$ is the switching frequency, $C_{oss}$ is the specific output capacitance value taken from the MOSFET datasheet, $I_{D(RM)}$ is the maximum value of reverse recovery current, $K_f$ is the temperature coefficient, $V_R$ is the reverse voltage, and $t_{\mathrm{rr}}$ is the reverse recovery time.

Equations (4)–(8) can be used to calculate the losses for a power-line cycle. However, the circuit topology parameters, such as the switching frequency $f_c$, the average diode current $I_{D(AV)}$, the rms diode current $I_{D(RMS)}$, the rms switching tube current $I_{Q(RMS)}$, and the turn-on instantaneous voltage $U_0$, have not been determined. These parameters will be solved in the following section.

When switch S₁ is turned on, the inductor voltage is $v_L=v_g-V_{\mathrm{dc}}$, and when S₁ is turned off, it becomes $v_L=v_g-{\displaystyle \frac{V_{\mathrm{dc}}}{2}}$. According to the principle of inductor volt-second balance, it can be derived that

$$D_n(v_g-V_{\mathrm{dc}})+(1-D_n)\left(v_g-{\displaystyle \frac{V_{\mathrm{dc}}}{2}}\right)=0$$

(9)

where $D_n$ is the ratio of the on-time of switch S₁ within one switching period to the total switching period.

After simplification, it is derived as $D_n={\displaystyle \frac{2v_g}{V_{\mathrm{dc}}}}-1$.

However, to make the inductor current track the AC input voltage and present a sinusoidal waveform, it is necessary to increase the duty cycle under stable load conditions. According to the inductor characteristics, the increased $\mathsf{\Delta }{i}_g$ can be expressed as follows:

$$D_f(v_g-V_{\mathrm{dc}})+(1-D_f)\left(v_g-{\displaystyle \frac{V_{\mathrm{dc}}}{2}}\right)=L_f{\displaystyle \frac{\mathsf{\Delta }{i}_g}{T_s}}$$

(10)

After simplification, the result is

$$D_f=\left({\displaystyle \frac{2v_g}{V_{\mathrm{dc}}}}-1\right)-{\displaystyle \frac{2L_f\mathsf{\Delta }{i}_g}{V_{\mathrm{dc}}{T}_s}}$$

(11)

If $\mathsf{\Delta }D$ be expressed as $-{\displaystyle \frac{2L_f\mathsf{\Delta }{i}_g}{V_{\mathrm{dc}}{T}_s}}$, then it is given by $D_f=D_n+\mathsf{\Delta }D$. Therefore, the final duty cycle of the controller consists of the steady-state duty cycle $D_n$ and the dynamic duty cycle $\mathsf{\Delta }D$. $D_n$ can be designed as a feed-forward voltage compensator, while $\mathsf{\Delta }D$ tracks the reference AC input current ${i_g}^{*}$.

The expression for the instantaneous value of the duty cycle is given in differential form:

$$D_t=({\displaystyle \frac{2v_g}{V_{dc}}}-1)-{\displaystyle \frac{2L_f}{V_{dc}{T}_s}}d{i}_g/dt$$

(12)

To calculate the average duty cycle for each modal time period, integrate Equation (11). The average duty cycle ${\overline{\mathit{D}}}_{\mathit{t}}$ from interval ${\theta }_i~{\theta }_j$ can then be expressed as follows:

$${\overline{\mathit{D}}}_{\mathit{t}}={\displaystyle \frac{1}{{\theta }_j-{\theta }_i}}{\displaystyle {\int }_{{\theta }_i}^{{\theta }_j}{D}_t}(\theta )d\theta$$

(13)

Substituting into Equation (4), the following can be obtained:

$${\overline{\mathit{D}}}_{\mathit{t}}={\displaystyle \frac{1}{{\theta }_j-{\theta }_i}}{\displaystyle {\int }_{{\theta }_i}^{{\theta }_j}((\frac{2v_g}{V_{dc}}-1)-\frac{2L_f}{V_{dc}{T}_s}\frac{d{i}_g}{dt})}d\theta$$

(14)

Furthermore, since

$${\mathit{v}}_{\mathit{g}}={\mathit{v}}_{\mathit{g}\mathit{m}\mathit{a}\mathit{x}}\mathit{s}\mathit{i}\mathit{n}\mathit{\theta }$$

(15)

the average duty cycle can be further obtained:

$${\overline{\mathit{D}}}_{\mathit{t}}={\displaystyle \frac{1}{{\theta }_j-{\theta }_i}}\left[{\displaystyle \frac{2v_{g, \max }}{V_{dc}}}(\cos ({\theta }_i)-\cos ({\theta }_j))-({\theta }_j-{\theta }_i)-{\displaystyle \frac{2L_f}{V_{dc}{T}_s}}(i_g({\theta }_j)-i_g({\theta }_i))\right]$$

(16)

The RMS expression for the switching device’s current in the ${\theta }_i~{\theta }_j$ interval is

$$I_{rms}=\sqrt{{\displaystyle \frac{1}{{\theta }_j-{\theta }_i}}{\displaystyle {\int }_{{\theta }_i}^{{\theta }_j}i}{(\theta )}^{2}d\theta }$$

(17)

In the interval ${\theta }_i~{\theta }_j$, the average current of the switching device is $\mathit{i}{(\mathit{\theta })}_{avg}=\mathit{k}\times {\mathit{i}}_{avg}$, and the rms value of the switching device current is $\mathit{i}{(\mathit{\theta })}_{rms}=\mathit{k}\times {\mathit{i}}_{rms}$, where $k$ = 0, 1, or ${\overline{\mathit{D}}}_{\mathit{t}}$.

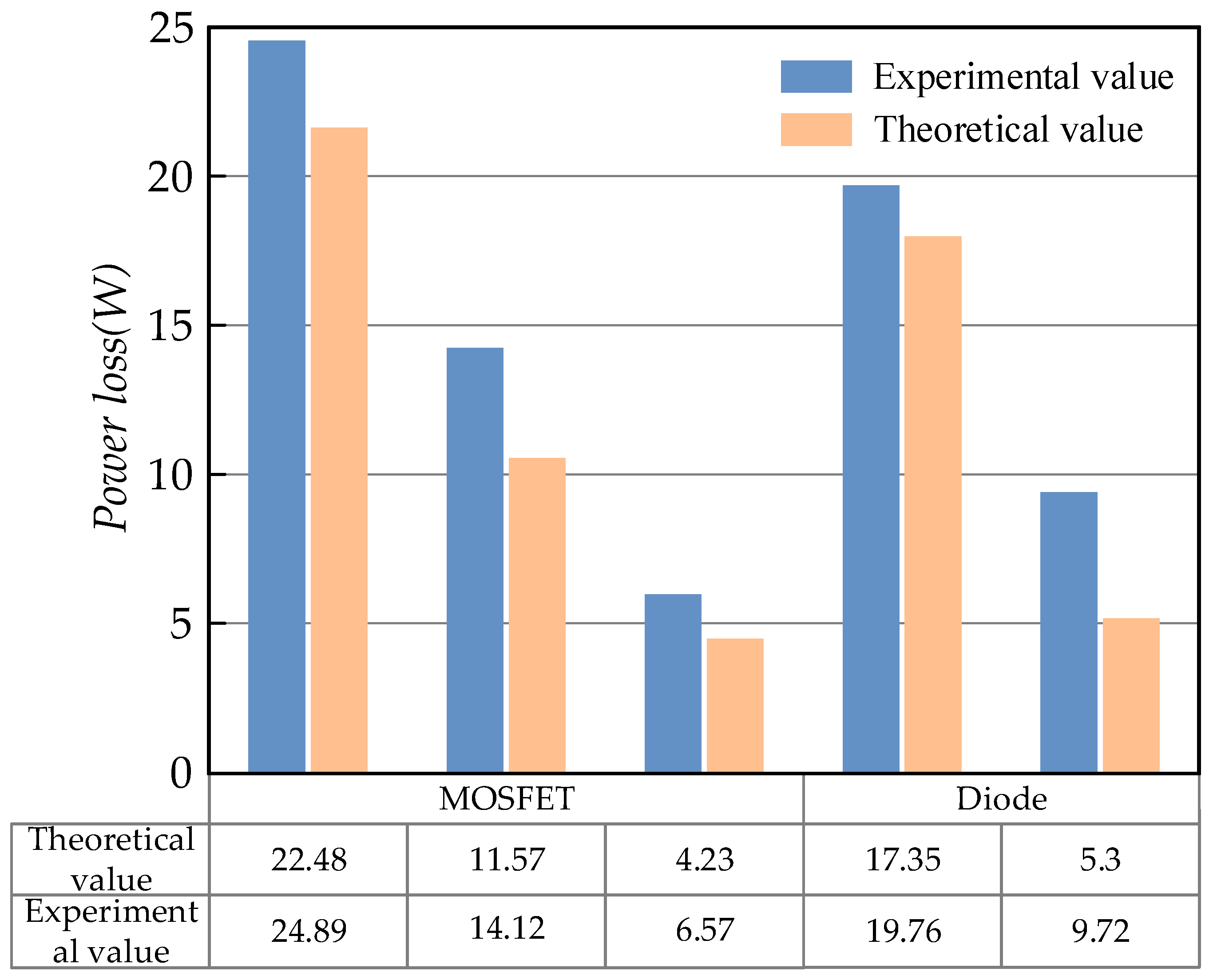
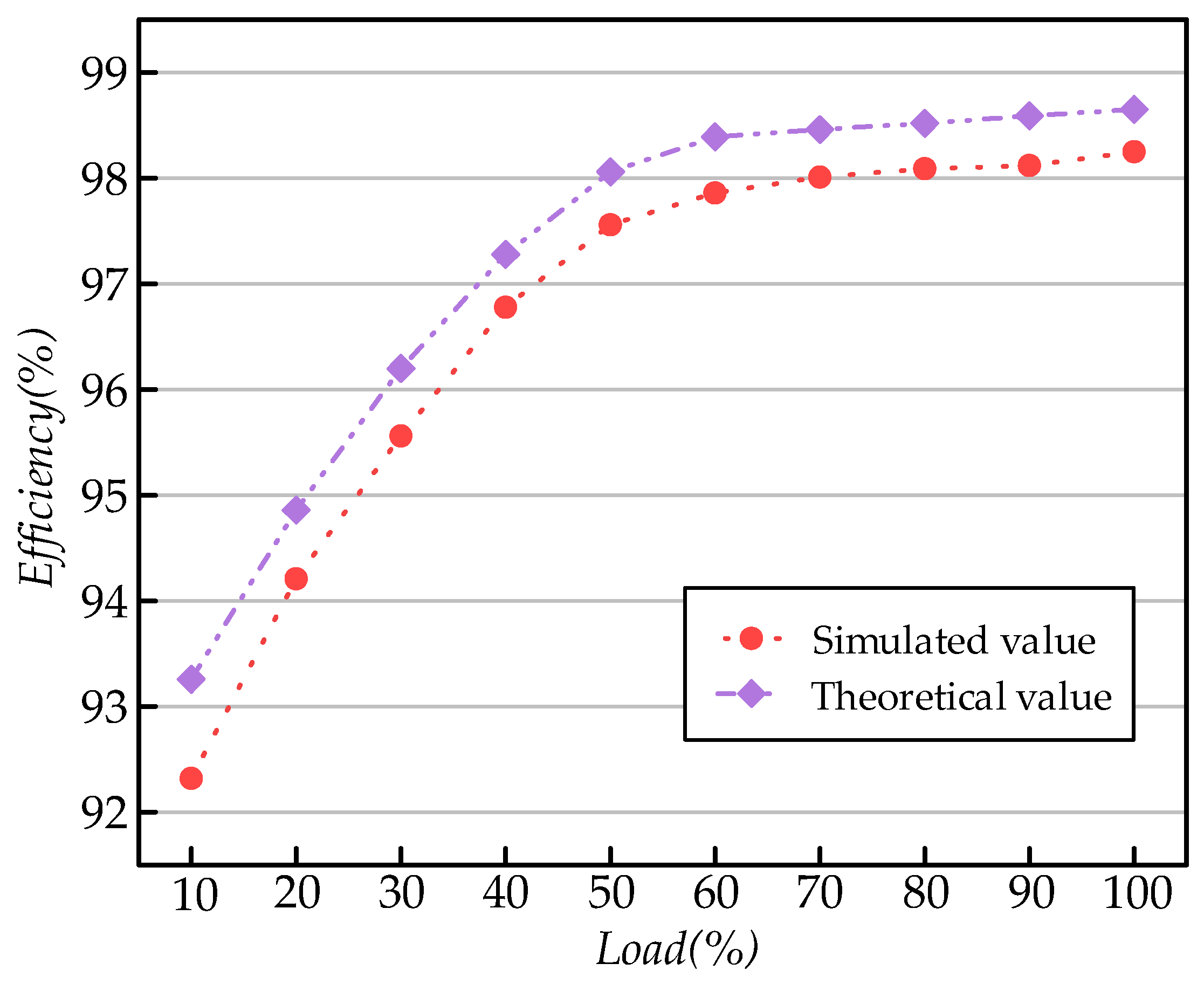
3.3. Estimation of Efficiency

In this paper, regarding the switching devices, the model STW26NM60N is selected for S₁ and S₂, and STP40NF20 is selected for S₃, and the diode is STTH30RQ06. According to their datasheet, the main parameters are as follows: For STW26NM60N, ${\mathrm{t}}_{fr}$ = 25 ns, ${\mathrm{t}}_{rr}$ = 50 ns, and $R_Q$ = 0.135 Ω. For STP40NF20, ${\mathrm{t}}_{fr}$ = 20 ns, ${\mathrm{t}}_{rr}$ = 45 ns, and $R_Q$ = 0.045 Ω. For STTH30RQ06, $V_{RRM}$ = 600 V, $I_{FAVM}$ = 30 A, $V_{FR}$ = 16 V, $V_F$ = 1.6 V, $t_{fr}$ = 150 ns, ${\mathrm{t}}_{rr}$ = 35 ns, $r_D$ = 7.1 mΩ, and $I_{D(RM)}$ = 18 A.

To accurately assess the total switching loss of the three-level PFC circuit over a power-line cycle, this paper uses a modal segment integration method to model and analyze the energy loss of the power devices based on the established device loss model. The cycle period $[0,2\pi ]$ is divided into six operating modes, namely $[0,{\theta }_1]$, $[{\theta }_1,{\theta }_2]$, $[{\theta }_2,\pi ]$, $[\pi ,{\theta }_3]$, $[{\theta }_3,{\theta }_4]$, and $[{\theta }_4,2\pi ]$. Each mode corresponds to an angular range, $[{\theta }_{m-1},{\theta }_m]$, where m = 1, 2, 3, 4, 5, or 6. The operating states of the MOSFET and diode are explicit in each mode. The corresponding on-state currents, voltage stresses, and turn-on and turn-off behaviors can be determined for each mode, so the average power loss of the devices can be calculated independently.

The total loss of the MOSFET in the m-th interval is $P_{Q_k,m}$, and the cycle-averaged loss of the MOSFET is expressed as follows:

$$P_{\mathrm{Q}}^{\mathrm{total} }={\displaystyle \frac{1}{2\pi }}{\displaystyle \sum _{m=1}^6\left[\left({\displaystyle \sum _{k=\{S1,S2,S3,S4\}}{P}_{Q_k,m}}\right)\cdot \left({\theta }_m-{\theta }_{m-1}\right)\right]}$$

(18)

The total loss of the diode in the m-th interval is $P_{D_j,m}$, and the cycle-averaged loss of the diode device is expressed as follows:

$$P_{\mathrm{D}}^{\mathrm{total} }={\displaystyle \frac{1}{2\pi }}{\displaystyle \sum _{m=1}^6\left[\left({\displaystyle \sum _{j=\{D1,D2,D3,D4\}}{P}_{D_j,m}}\right)\cdot \left({\theta }_m-{\theta }_{m-1}\right)\right]}$$

(19)

The total switching losses are

$$P_{\mathrm{total} }={\displaystyle \frac{1}{2\pi }}{\displaystyle \sum _{m=1}^6\left[\left({\displaystyle \sum _k{P}_{Q_k,m}}+{\displaystyle \sum _j{P}_{D_j,m}}\right)\cdot \left({\theta }_m-{\theta }_{m-1}\right)\right]}$$

(20)

In the modulation strategy of the three-level rectifier, the amplitude-normalized sine wave is chosen as $v_{\mathrm{ref}}(\theta )=\widehat{m}\cdot \sin (\theta )$. When $\widehat{m}=1$, the intersection of the reference waveform and the intermediate zero-level carrier occurs at $\theta =\arcsin (\pm 0.5)=\pm {\displaystyle \frac{\pi }{6}}$. To further simplify the derivation of modal integrals for device losses, this paper sets the following: ${\theta }_0=0$, ${\theta }_1=\pi /6$, ${\theta }_2=5\pi /6$, ${\theta }_3=\pi$, ${\theta }_4=7\pi /6$, ${\theta }_5=11\pi /6$, and ${\theta }_6=2\pi$. The rectifier’s efficiency at different operating conditions is calculated and simulated by substituting specific device parameters into established power loss models. The devices selected for the calculations are the STW26NM60N model (for S₁, S₂,) and STTH30RQ06 model (for S₃), and the STTH30RQ06 fast recovery diode (for D₁–D₈). The relevant device parameters, such as on-resistance, reverse recovery time, and output capacitance, are all from the device datasheet. The power-line cycle $[0,2\pi ]$ is divided, and the effective and average values are substituted into the aforementioned loss expression. With the switching frequency $f_s=20 \mathrm{kHz}$, the loss value of each power device in different modal intervals can be obtained. According to this, the average loss power of the whole cycle can be obtained. The specific loss distribution, calculated from Equations (1)–(20), is shown in Figure 4.

As shown in Figure 4, the diode’s main loss is conduction loss, while the MOSFET’s main loss is turn-on loss. At rated power, the total loss is 19.36 W, and the efficiency is 98.03%.

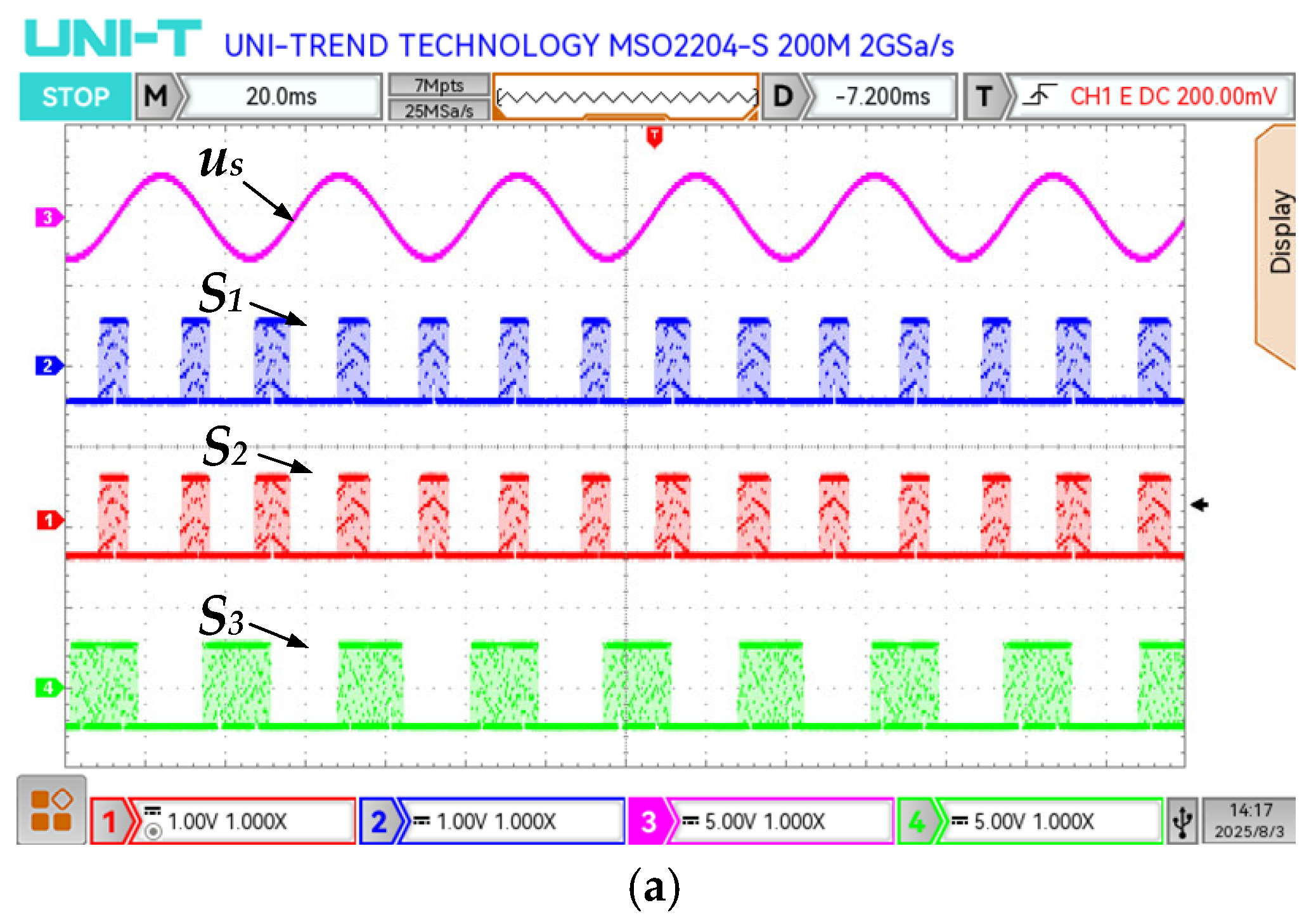
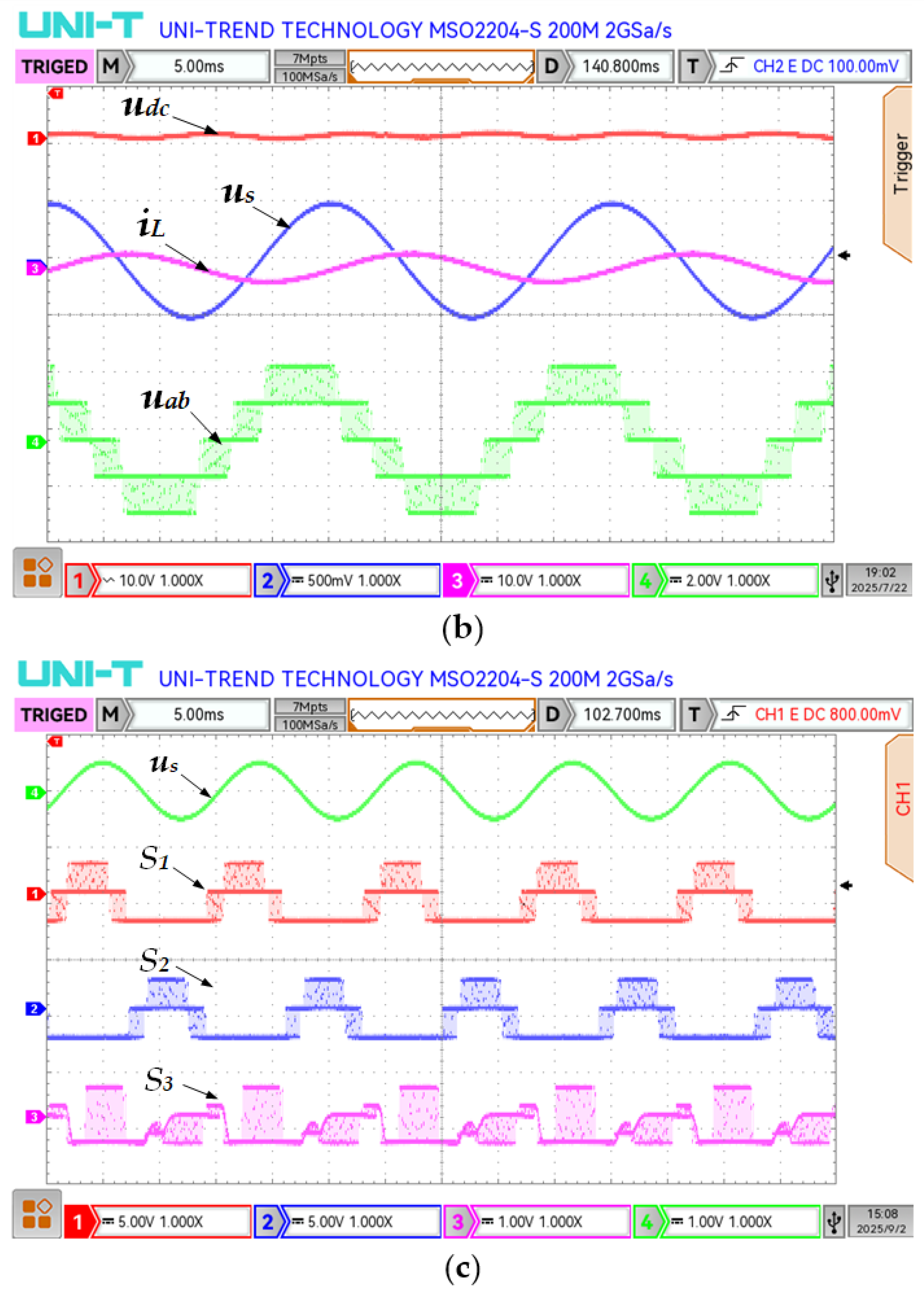
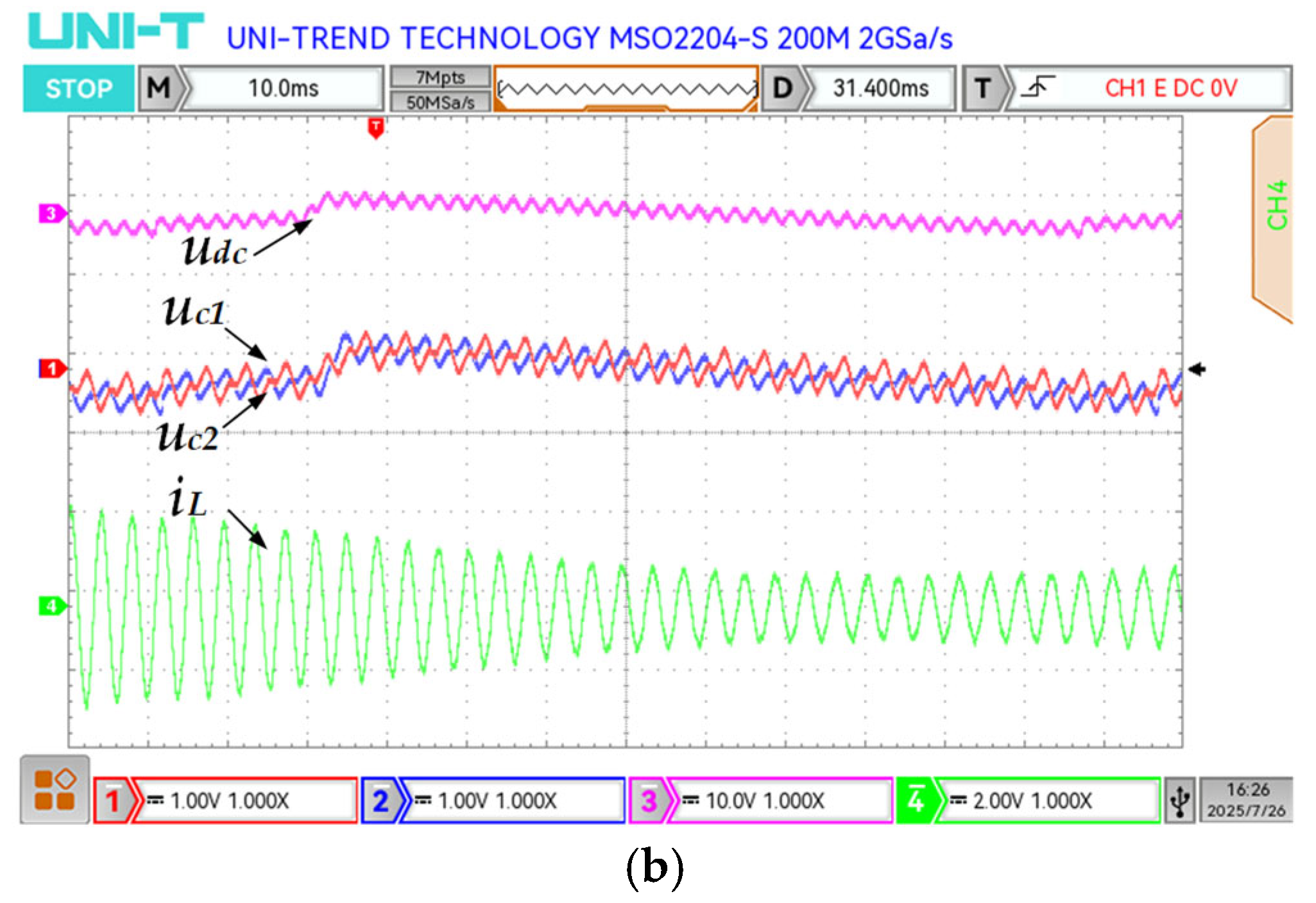
4. Experimental Simulation and Verification

In order to verify the effectiveness of the proposed topology and modal segment integration method, a 1 kW bridgeless three-level PFC experimental prototype is constructed. Figure 5 shows the experimental prototype, and the related parameters are listed in

Table 2. Experimental parameters.

Parameters	Value
Input AC voltage	220 V
Output DC voltage	400 V
Rated output power	1 kW
Switching frequency	20 kHz
Input inductor	2.5 mH
Split DC-link capacitor	2000 μF

. The input inductor is selected to ensure that the input current can follow the input voltage during power factor correction and achieve good dynamic response. Based on the system power level and control strategy, the inductance is chosen as 2.5 mH. Capacitors C₁ and C₂ are used as split DC-link capacitors to form the three-level voltage and keep the output voltage stable. According to the circuit requirements and experimental results, each capacitor is selected as 2000 μF.

The steady-state experimental results of the proposed topology are shown in Figure 6. In this figure, u_dc and i_L denote the voltage and current on the grid side, respectively. u_dc represents the output voltage on the DC side, while u_ab stands for the bridge-arm voltage. Additionally, u_c1 and u_c2 indicate the voltages across capacitors C₁ and C₂, respectively.

Figure 6a shows the switching pulse distribution waveforms for switches S₁, S₂, and S₃. From the figure, within a single operating cycle, the operational duration of S₁ and S₂ constitutes a relatively small proportion.

Figure 6b, the input voltage u_ab has three-level voltages as follows: 0, ±u_dc/2, and ±u_dc. The proposed topology is confirmed to be a three-level circuit. And the waveform of input voltage u_dc is in phase with the waveform of input current i_L, meeting the unity power factor. The output DC voltage u_dc is stable at 400 V.

Figure 6c shows the voltage waveforms of switches S₁, S₂, and S₃. The voltages of S₁ and S₂ range from 0 to 400 V, while S₃ varies between 0 and 200 V. The waveform of S₃ appears irregular due to dead time and diode conduction during current commutation, which cause small dips and distortions at the switching transitions.

The experimental results of the proposed topology operating in dynamic state are shown in Figure 7, which illustrates the transition between uncontrolled and controlled modes.

Figure 7a,b show that when the load changes, the proposed topology can still achieve power factor correction, and there are only small fluctuations in the DC side voltage. These experimental results demonstrate that the proposed system exhibits good overall performance.

Figure 8 compares the theoretical loss values calculated using the proposed method with the experimental results obtained from the experimental prototype at a rated output of 1 kW. The experimental values are slightly higher than the theoretical values, but the loss trends remain consistent. This difference arises because the theoretical results are obtained from a simplified analytical model that considers only conduction losses and idealized switching losses, in order to keep the derivation concise and highlight the methodological framework. Consequently, parasitic parameters and other non-ideal effects are excluded. In contrast, the experimental models incorporate more realistic device characteristics, which lead to slightly higher calculated switching losses. These deviations are expected and fall within a reasonable range, and they also highlight the gap between idealized models and practical conditions. Overall, the results confirm the feasibility and accuracy of the proposed modal segment integration method for efficiency estimation.

The efficiency of the experimental prototype at different load factors is obtained by adjusting the load ratio. Figure 9 shows the comparison between theoretical efficiency values of the proposed method and simulated efficiency values of the experimental prototype at different load factors.

As shown in Figure 9, the theoretical and simulated values are highly consistent, with a maximum error below 0.4%. The theoretical values are generally higher than the simulated values, which is consistent with the loss comparison in Figure 8, since parasitic effects are not included in the theoretical analysis. Overall, the proposed efficiency analysis method based on the modal segment integration method is highly accurate.

5. Conclusions

To improve upon the traditional efficiency analysis method of bridgeless three-level PFC rectifiers, which relies heavily on simulations and lacks sufficient theory, this paper proposes a modal segment integration method based on a device loss model. First, the operating principle of the proposed topology is analyzed. Then, a power device loss model is constructed and the system efficiency is estimated through modal segment integration method. Finally, the method is verified by using a 1 kW/20 kHz experimental prototype, and the conclusions are as follows:

• A modal segment integration method based on the device loss model is proposed to estimate the theoretical efficiency of bridgeless three-level PFC rectifier over a complete cycle. This method improves the theoretical basis of the efficiency analysis method and enhances its applicability during the design stage.
• Simulations and experiments demonstrate that the proposed efficiency estimation method is highly accurate. The error between the theoretical and experimental data is less than 0.4%, which verifies the method’s reliability.
• The experimental prototype was tested under both steady-state and dynamic operating conditions, and the results confirmed that the proposed topology exhibits excellent power factor correction capability and stable operational performance.
• In the future, this method can be expanded to the efficiency analysis of multilevel topologies and multiport power conversion systems. The analytical model can also be extended to include parasitic parameters, which would further improve the accuracy of theoretical prediction. In addition, it can be combined with dynamic modeling and intelligent algorithm optimization under complex operating conditions to achieve intelligent and generalized efficiency evaluation.