Voltage Control for Active Distribution Networks Considering Coordination of EV Charging Stations
Abstract
1. Introduction
- (1)
- (2)
- Compared to the temporal RC evaluation model in [12,16], which neglects uncertain EV departure behavior, the proposed RC evaluation method integrates an RVM-based probabilistic model to capture these uncertainties. By leveraging real-time EV state features and external factors such as holiday schedules, it provides confidence-bounded RC estimates, delivering a more reliable evaluation of EVCS flexibility.
- (3)
- Compared with the centralized power allocation methods in [18,19], which require high-quality communication infrastructure, a broadcast control scheme is adopted to allocate power adjustment signals among charging piles and the ESS within each EVCS, reducing operational costs and enhancing allocation efficiency through decentralized dispatch.
2. System Model
3. Proposed Control Strategy
3.1. Overview
- (1)
- Stage I: RC estimation of EVCS: the RC of EVCSs is estimated in real time by using an MLP-trained model. To incorporate the uncertain impact of unscheduled EV departures, an RVM model refines the MLP-predicted RC, yielding confidence-bounded adjustment limits for subsequent dispatch optimization.
- (2)
- Stage II: Dispatch signal calculation of EVCSs for voltage regulation: based on the final RC estimated in Stage I, the distribution system operator (DSO) formulates a voltage regulation problem to calculate the optimal power adjustment signals for EVCSs, where the control problem is relaxed as a convex program by employing the SOCP technique.
- (3)
- Stage III: Power adjustment allocation within EVCS: after receiving the optimal dispatch signal obtained in Stage II, a broadcast control scheme is employed within each EVCS to allocate the dispatch signal across individual charging piles and the ESS, minimizing control costs while adhering to internal power adjustment constraints.
3.2. Stage I: RC Estimation of EVCSs
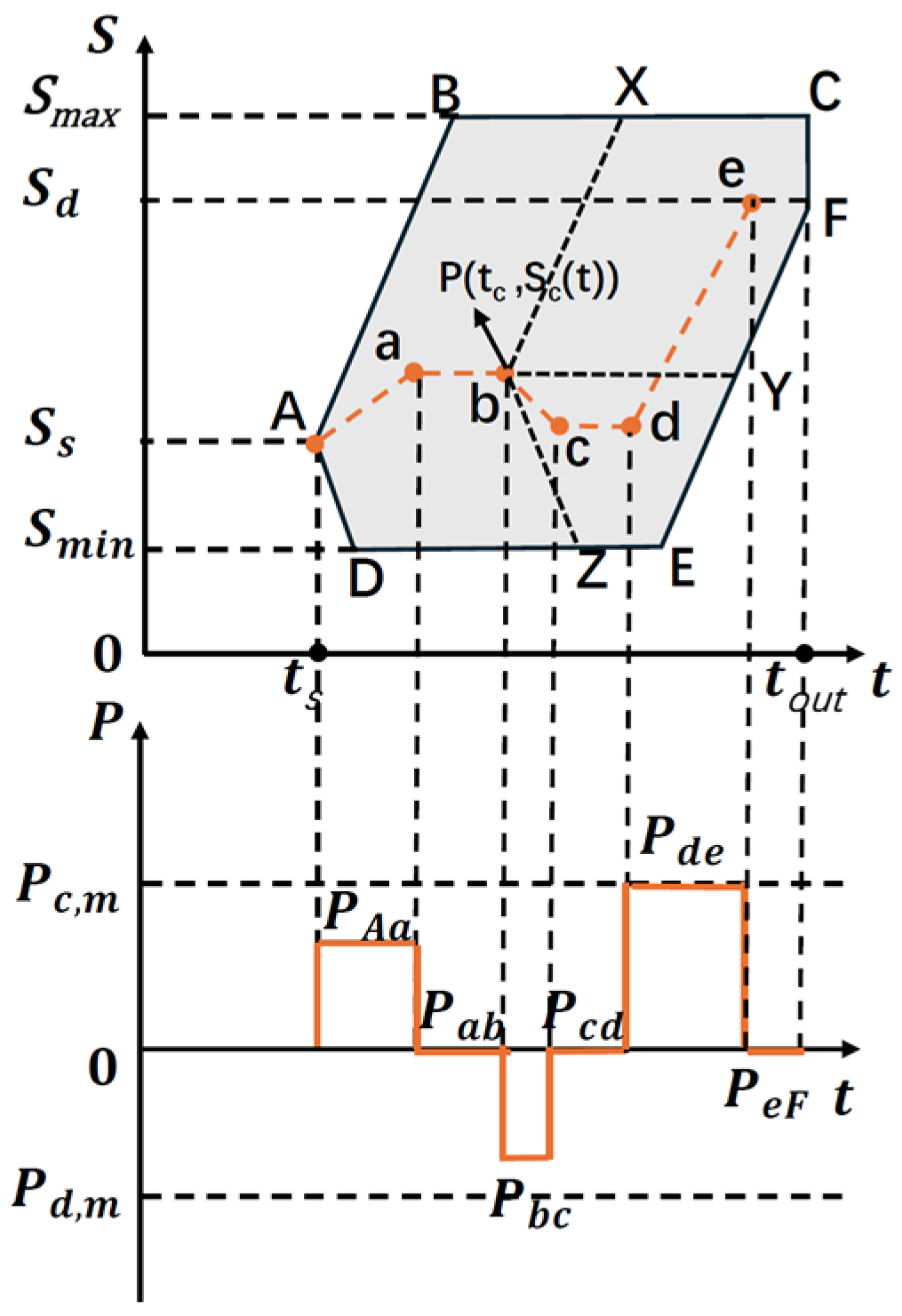
3.2.1. Controllable Region of a Single EV
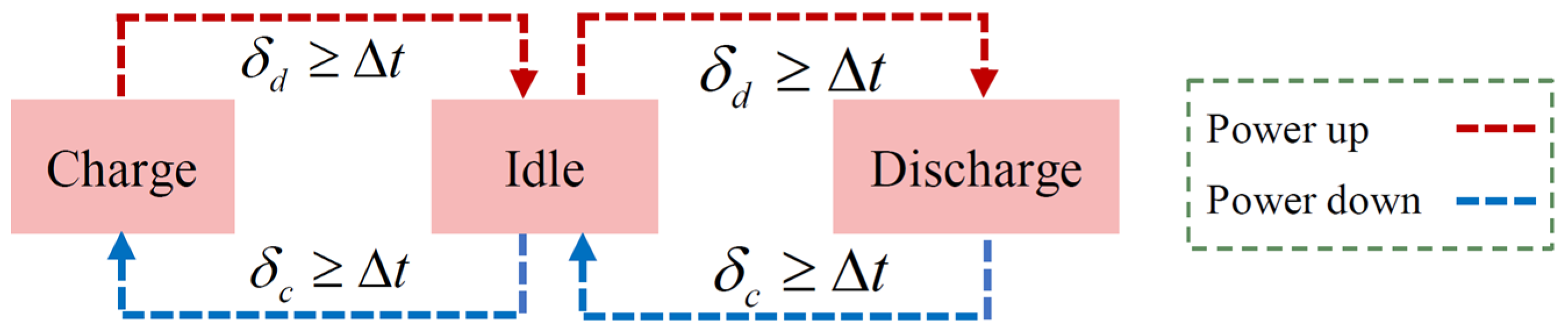
3.2.2. State-Driven Charging and Discharging Margin Estimation
3.2.3. MLP-Based RC Prediction
3.2.4. Evaluation of RC of EVCSs
3.2.5. RVM Uncertainty Modeling
3.3. Stage II: Dispatch Signal Calculation of EVCSs for Voltage Regulation
3.4. Stage III: Power Adjustment Allocation Within EVCSs
3.4.1. Optimization Problem Formulation
3.4.2. Broadcast Control Architecture
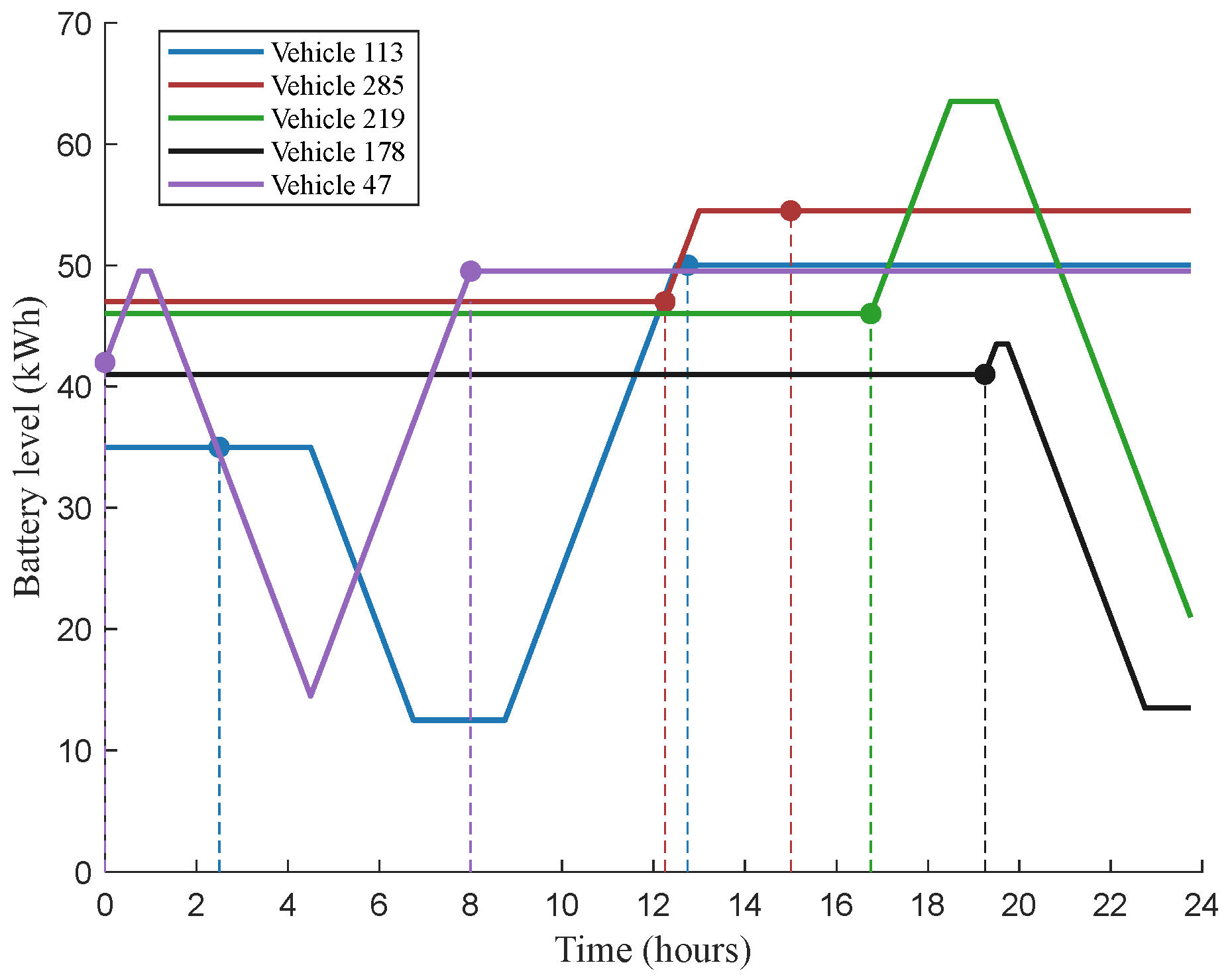
4. Case Study
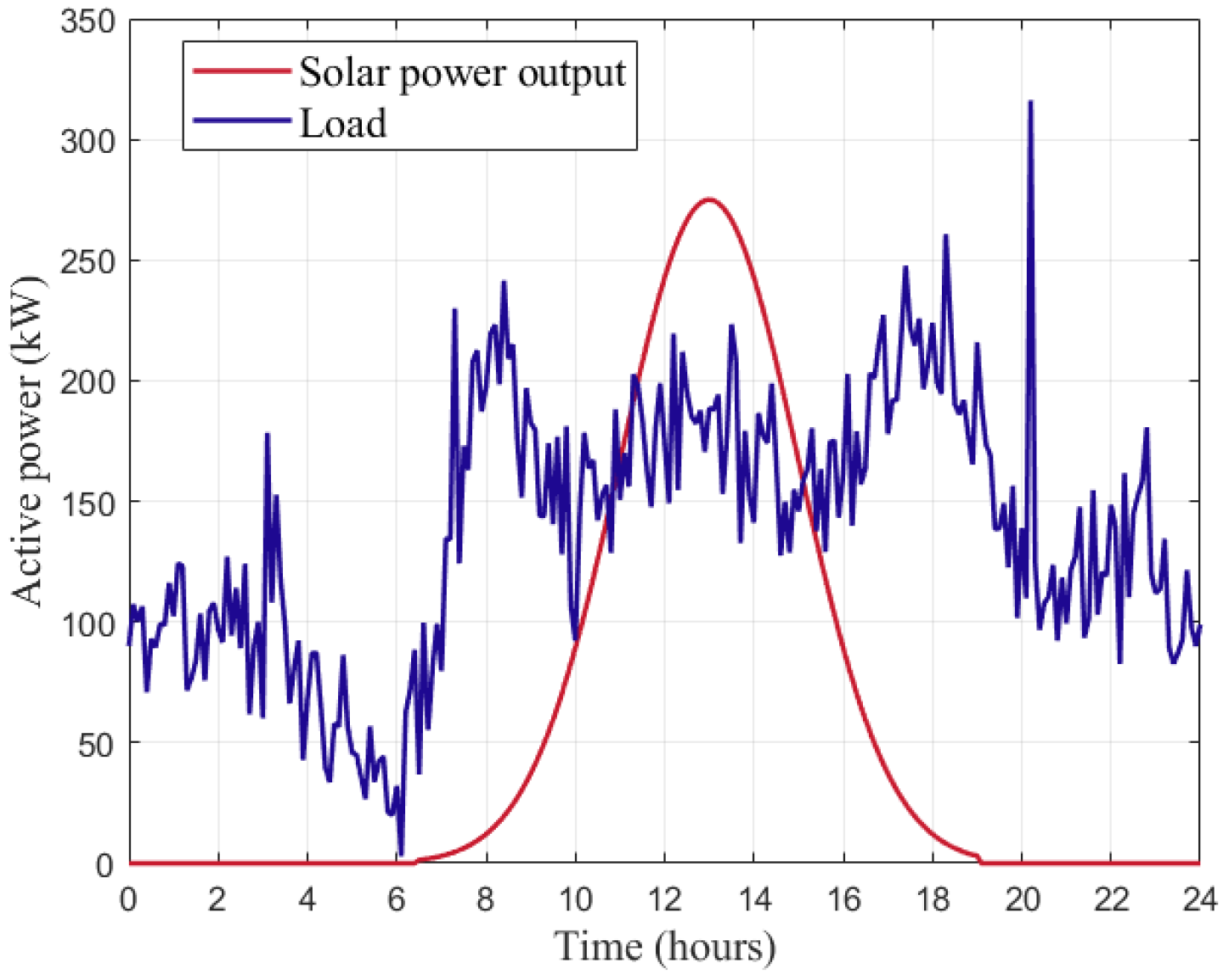
4.1. Test System and Parameter Settings
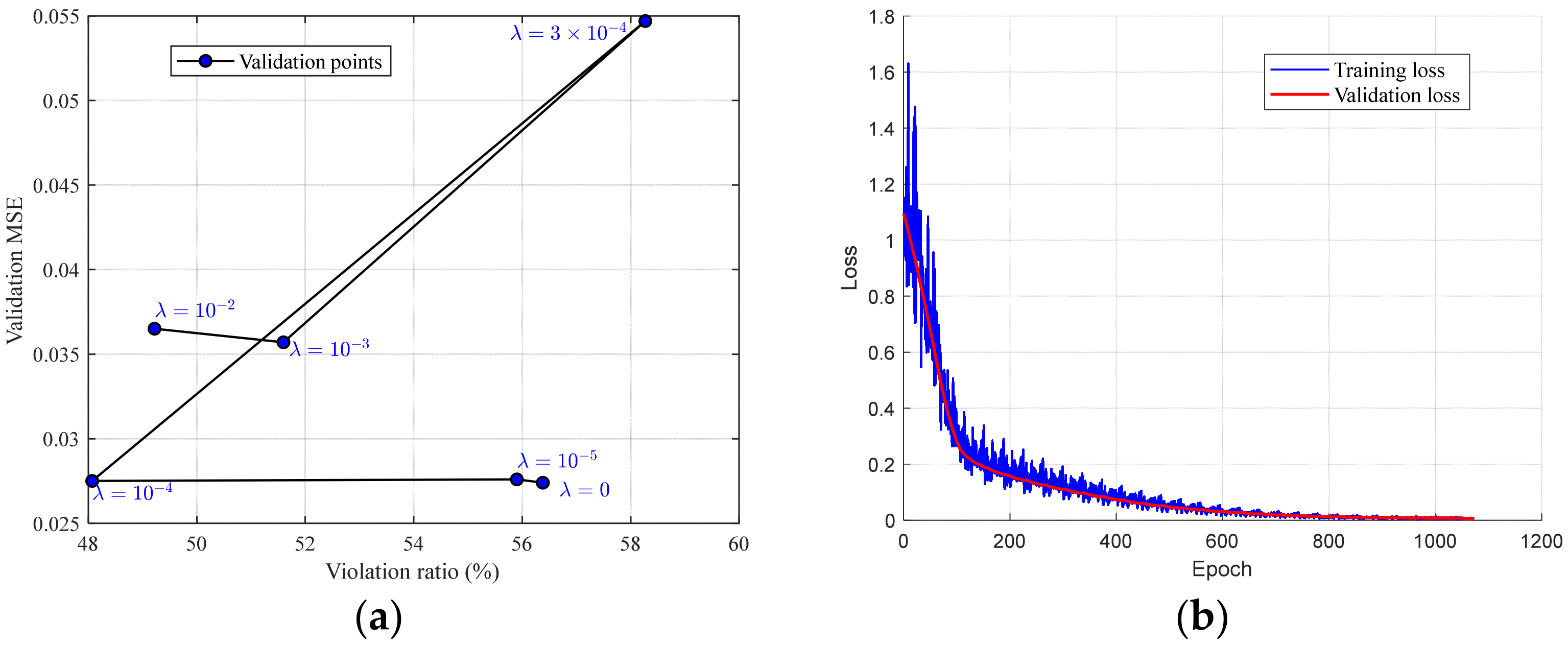
4.2. Simulation Results
- (1)
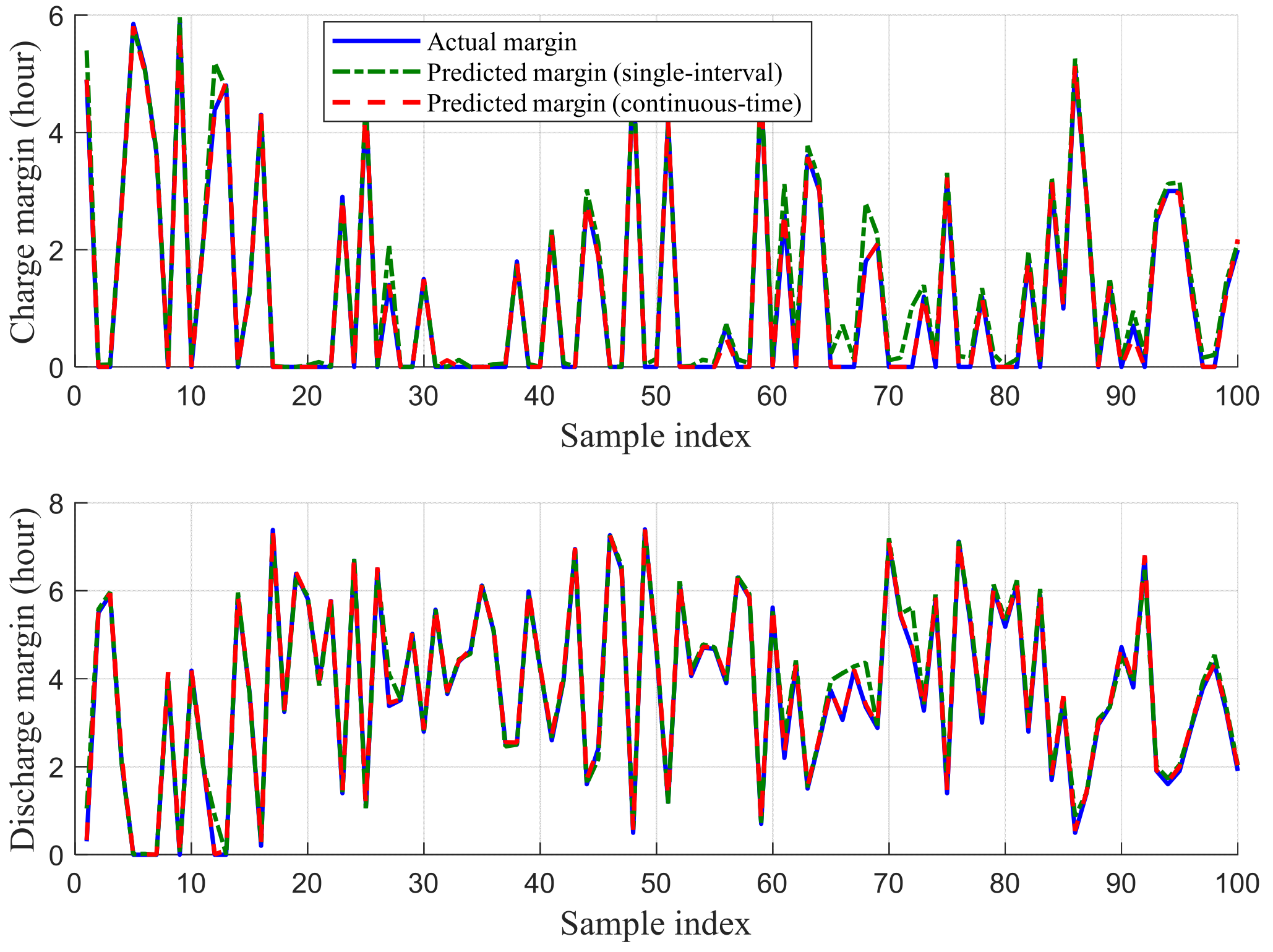
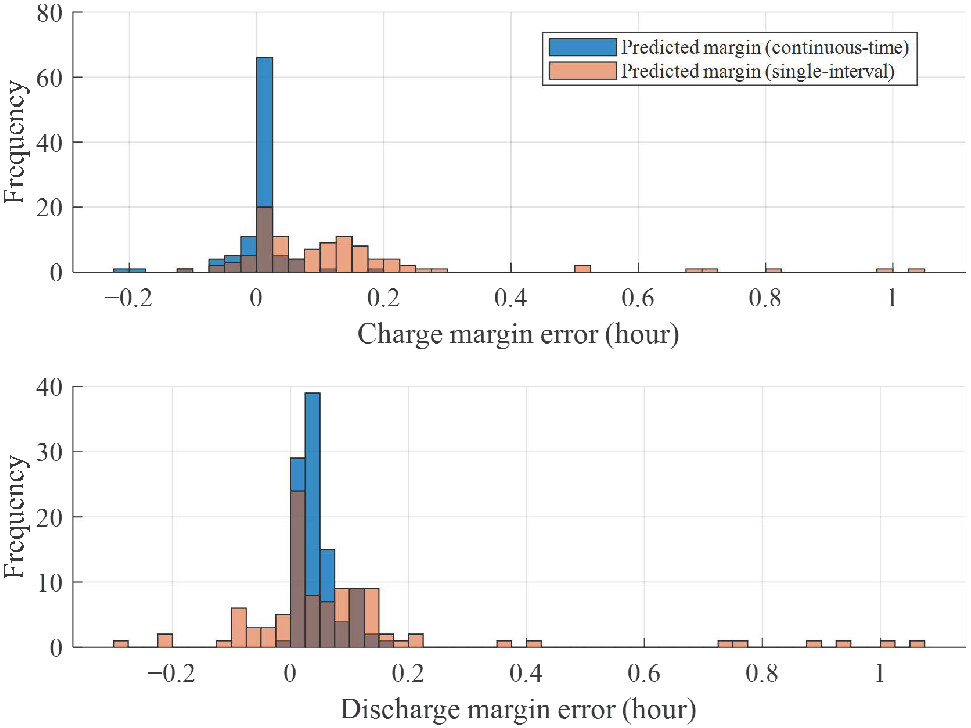
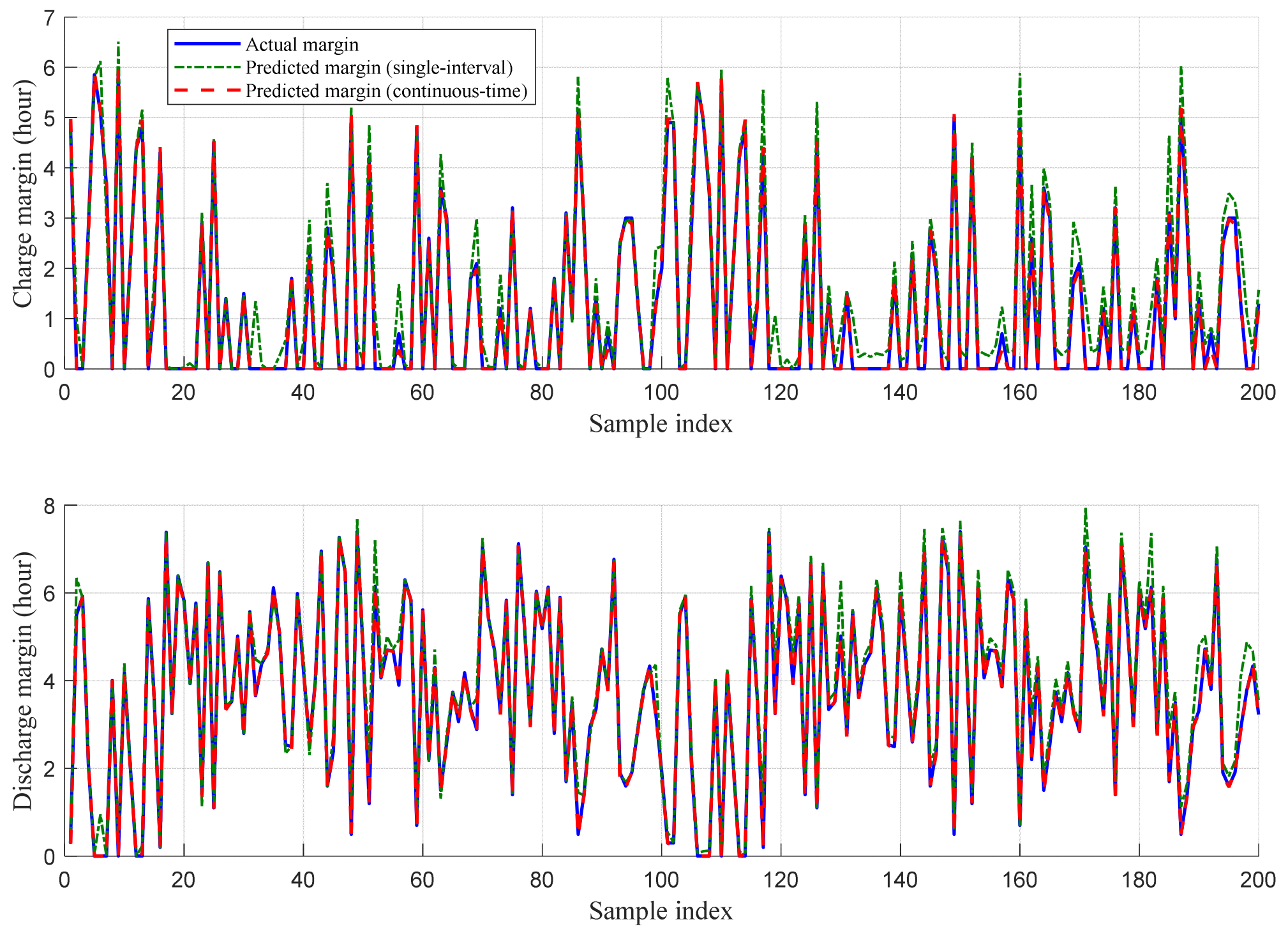
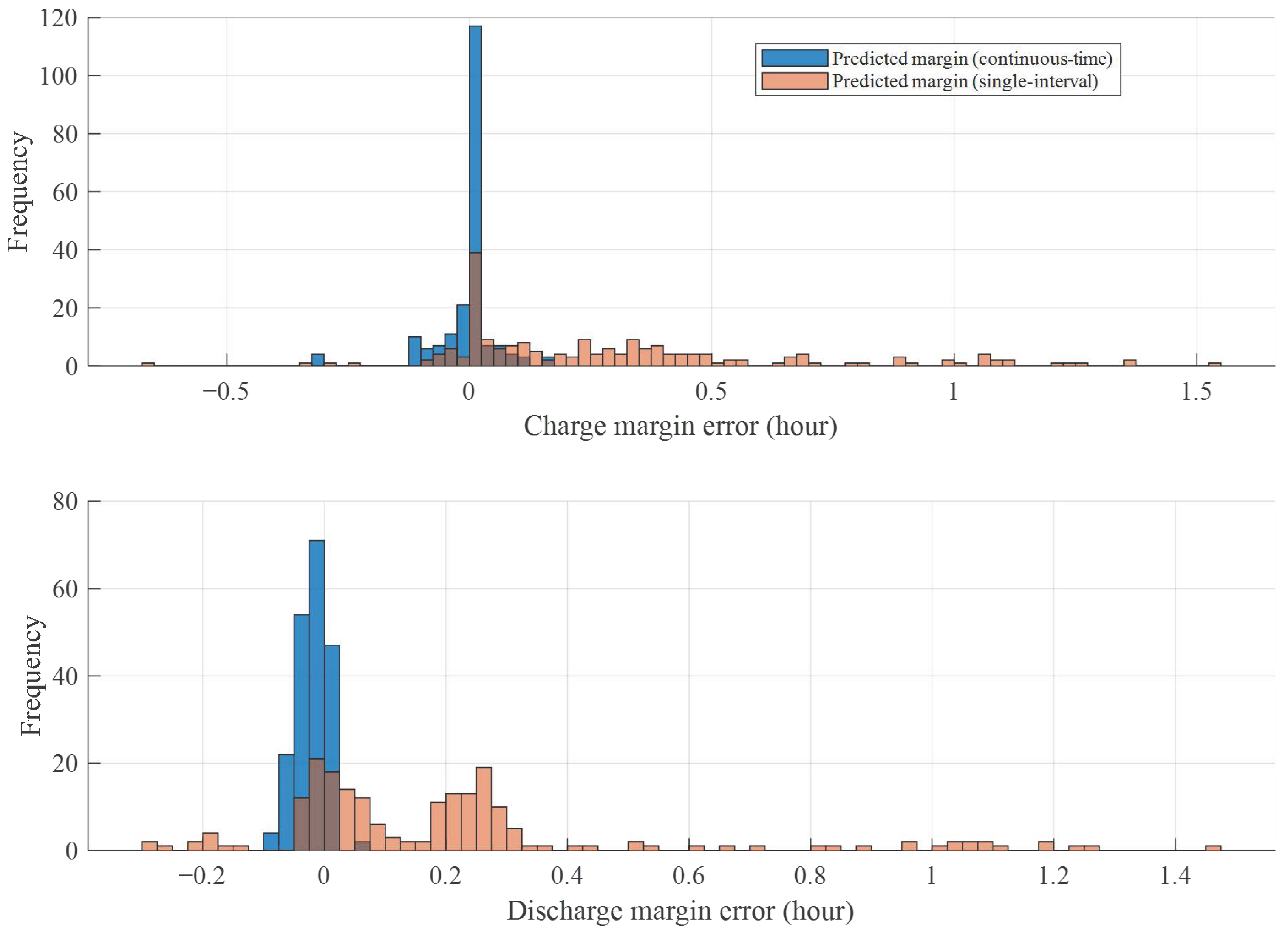
- Scenario 1—MLP model accuracy test
- (2)
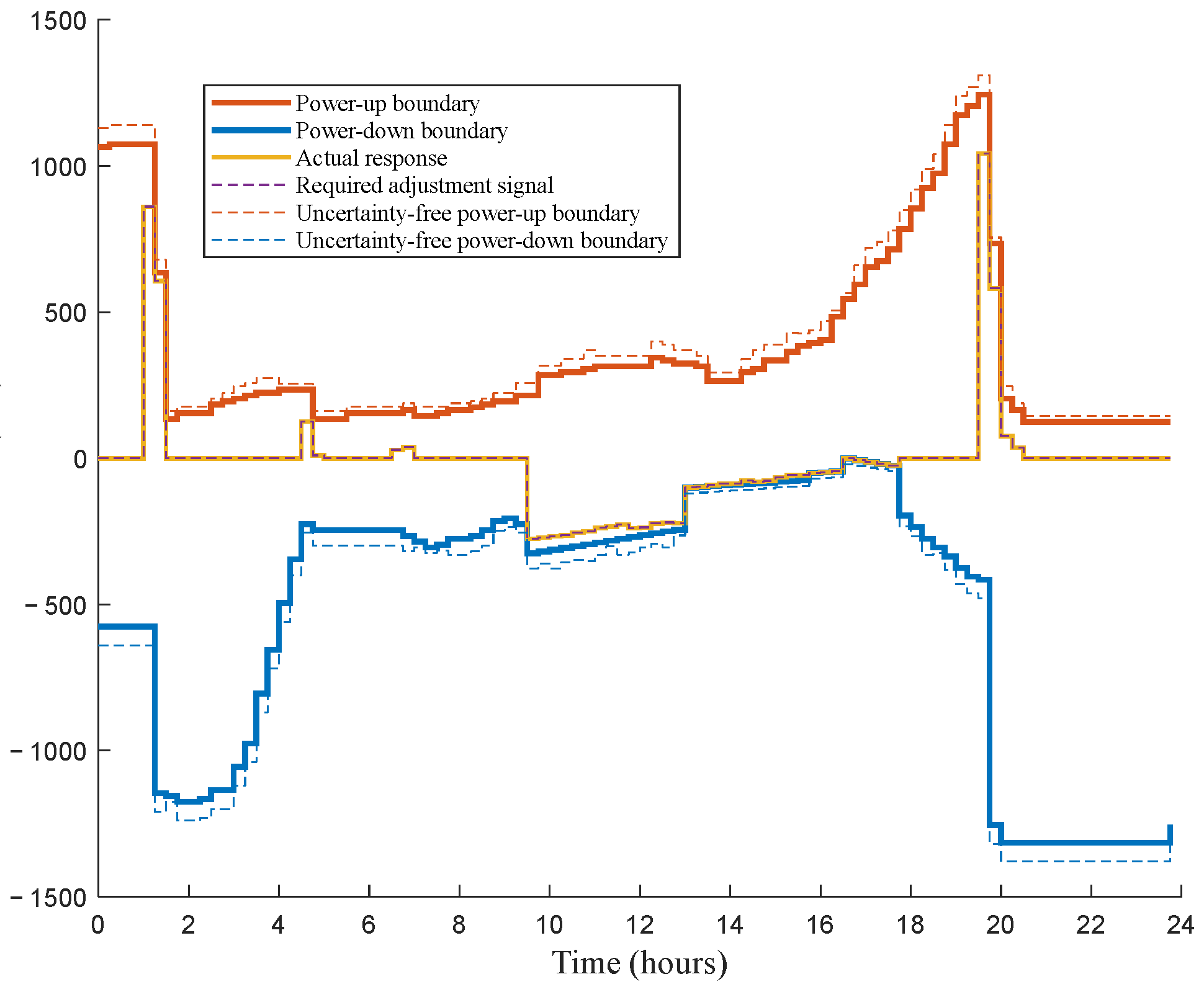
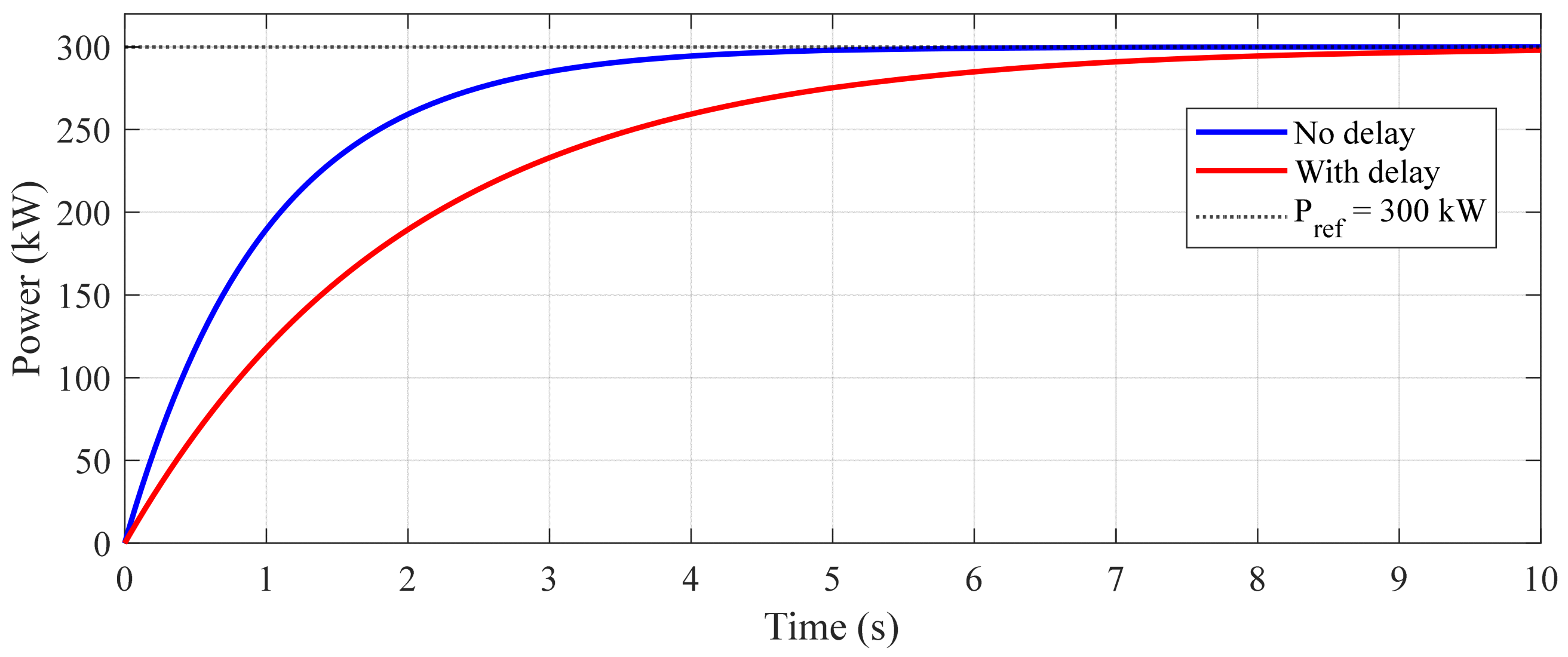
- Scenario 2—Power adjustment-response effect test
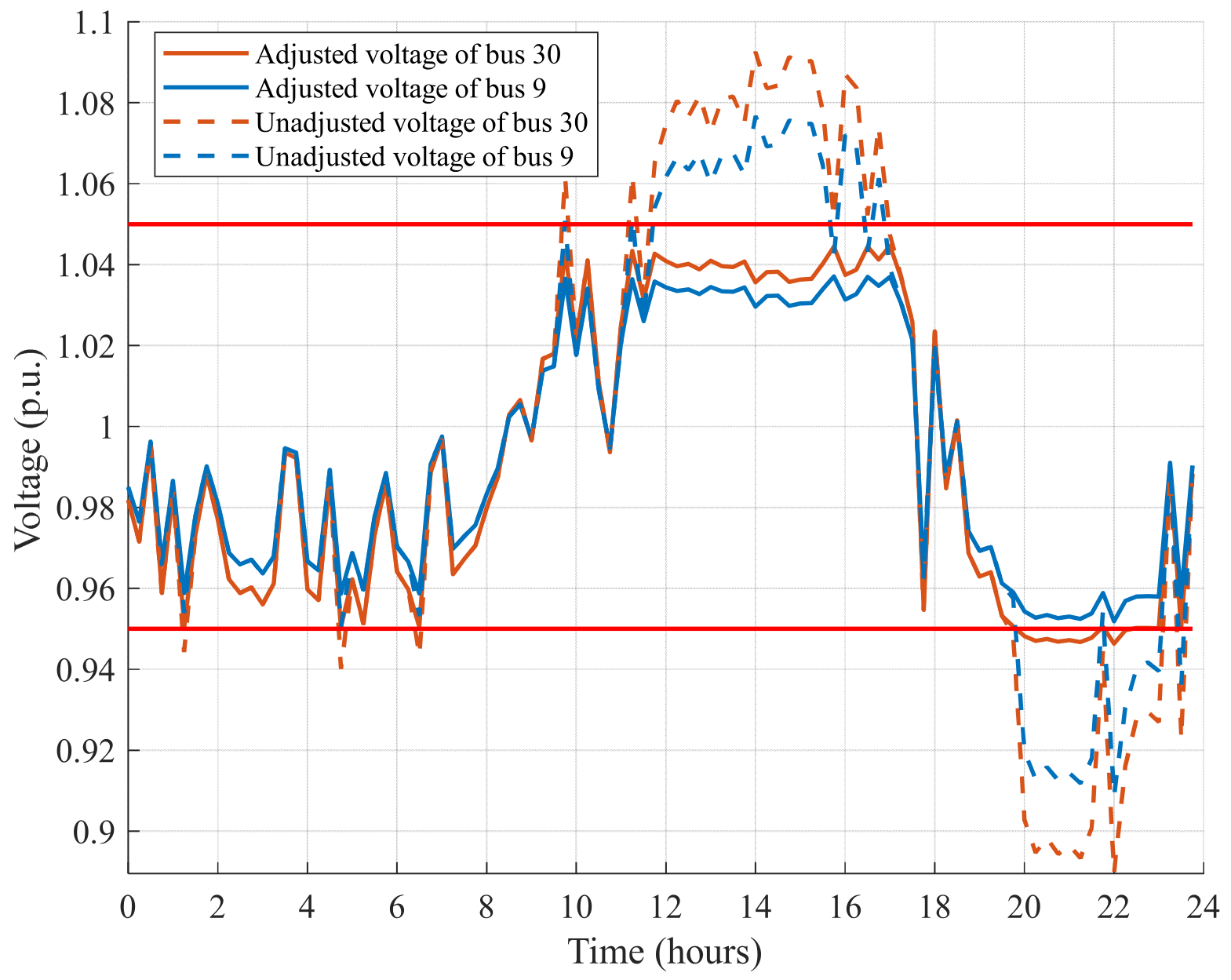
- (3)
- Scenario 3—Voltage control effectiveness test
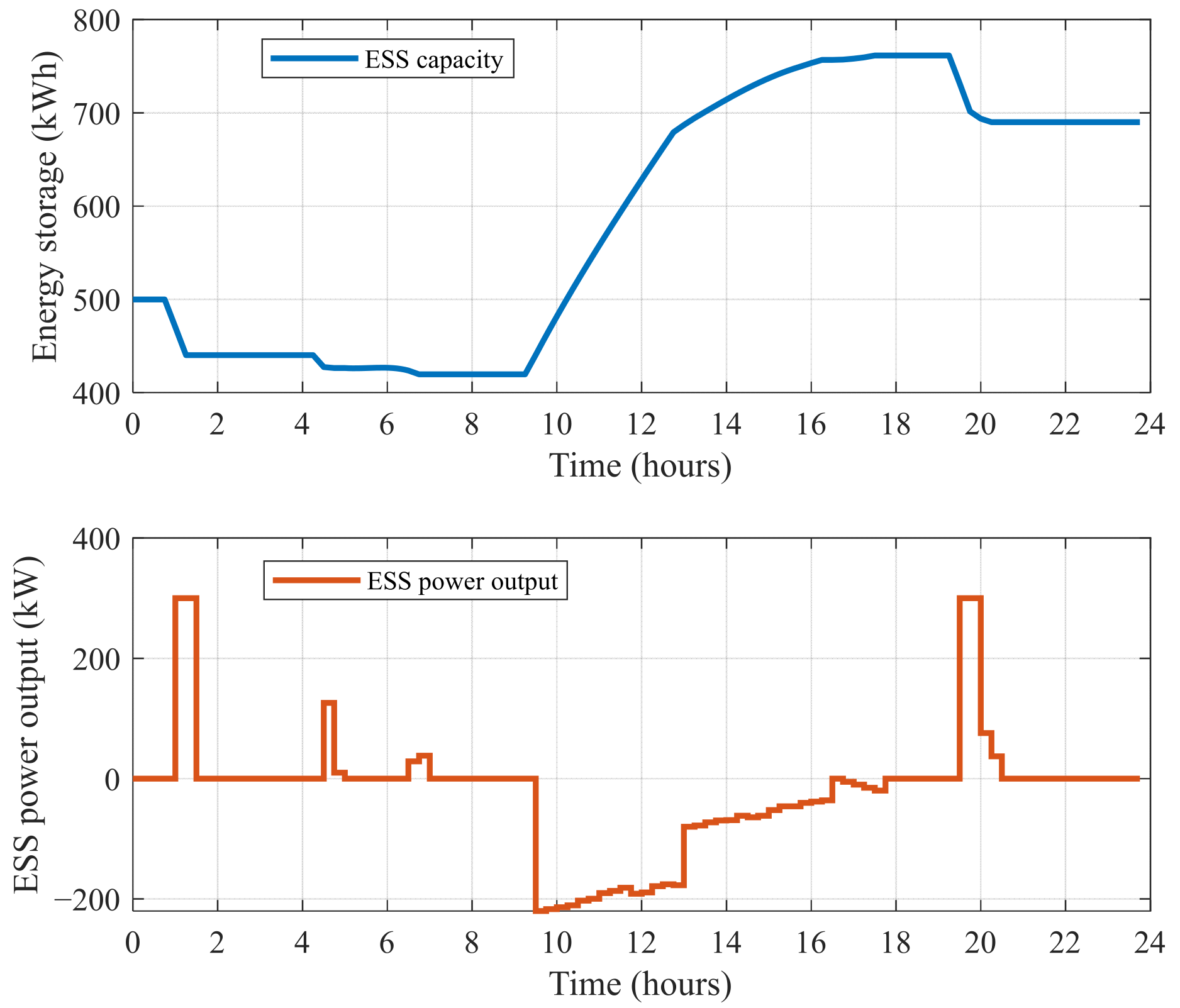
- (4)
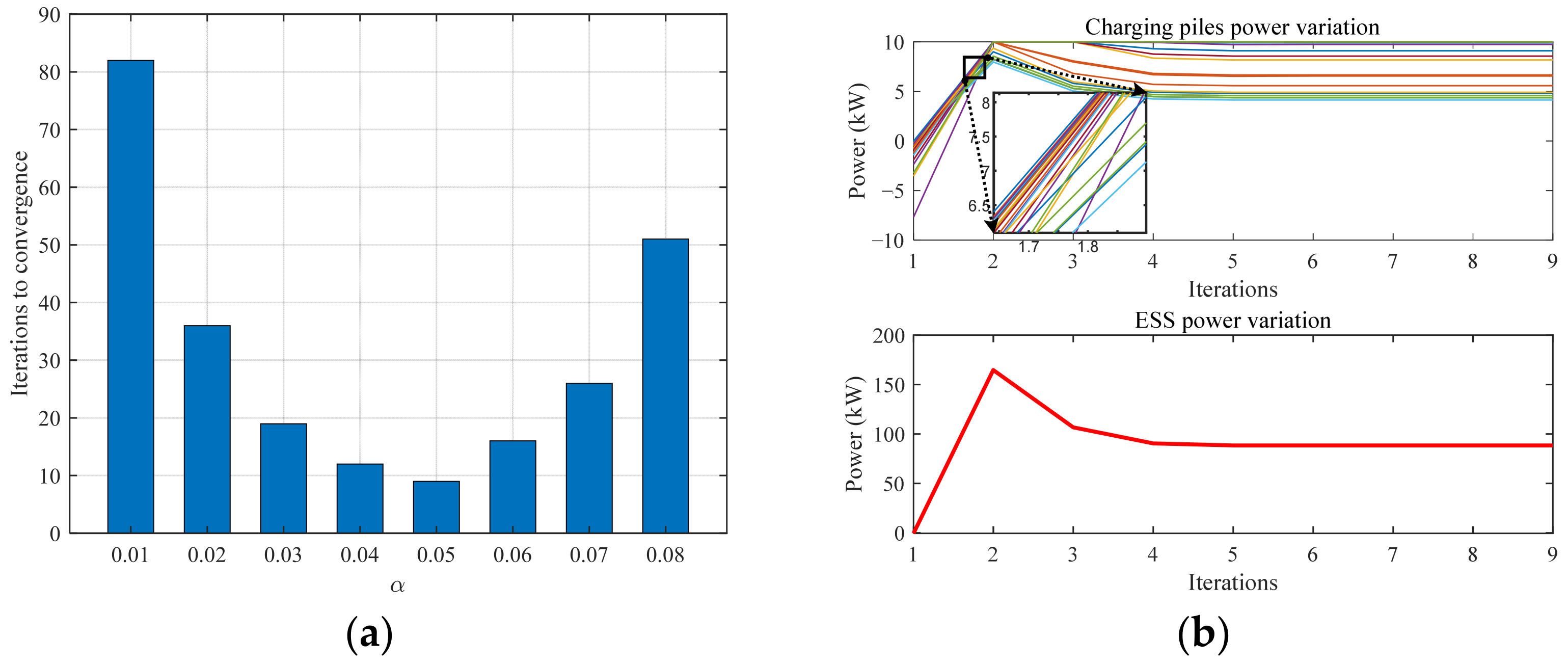
- Scenario 4—Power allocation efficiency test
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, S.; Bi, S.; Zhang, Y.J.A.; Huang, J. Electrical vehicle charging station profit maximization: Admission, pricing, and online scheduling. IEEE Trans. Sustain. Energy 2018, 9, 1722–1731. [Google Scholar] [CrossRef]
- Rahman, M.M.; Al-Ammar, E.A.; Das, H.S.; Ko, W. Comprehensive impact analysis of electric vehicle charging scheduling on load-duration curve. Comput. Electr. Eng. 2020, 85, 106673. [Google Scholar] [CrossRef]
- Chaudhari, K.; Ukil, A.; Kumar, K.N.; Manandhar, U.; Kollimalla, S.K. Hybrid optimization for economic deployment of ESS in PV-integrated EV charging stations. IEEE Trans. Ind. Inform. 2017, 14, 106–116. [Google Scholar] [CrossRef]
- Bletterie, B.; Kadam, S.; Bolgaryn, R.; Zegers, A. Voltage control with PV inverters in low voltage networks—In depth analysis of different concepts and parameterization criteria. IEEE Trans. Power Syst. 2016, 32, 177–185. [Google Scholar] [CrossRef]
- Un-Noor, F.; Padmanaban, S.; Mihet-Popa, L.; Mollah, M.N.; Hossain, E. A comprehensive study of key electric vehicle (EV) components, technologies, challenges, impacts, and future direction of development. Energies 2017, 10, 1217. [Google Scholar] [CrossRef]
- Huang, Z.; Fang, B.; Deng, J. Multi-objective optimization strategy for distribution network considering V2G-enabled electric vehicles in building integrated energy system. Prot. Control Mod. Power Syst. 2020, 5, 7. [Google Scholar] [CrossRef]
- Mojumder, M.R.H.; Ahmed Antara, F.; Hasanuzzaman, M.; Alamri, B.; Alsharef, M. Electric vehicle-to-grid (V2G) technologies: Impact on the power grid and battery. Sustainability 2022, 14, 13856. [Google Scholar] [CrossRef]
- Wu, J.; Xue, Y.; Xie, D.; Yue, D.; Wen, F.; Zhao, J. Evaluation and simulation analysis of reserve capability for electric vehicles. Autom. Electr. Power Syst. 2018, 42, 101–107. [Google Scholar]
- Zhang, H.; Hu, Z.; Xu, Z.; Song, Y. Evaluation of achievable vehicle-to-grid capacity using aggregate PEV model. IEEE Trans. Power Syst. 2016, 32, 784–794. [Google Scholar] [CrossRef]
- Wang, M.; Mu, Y.; Jia, H.; Wu, J.; Yu, X.; Qi, Y. Active power regulation for large-scale wind farms through an efficient power plant model of electric vehicles. Appl. Energy 2017, 185, 1673–1683. [Google Scholar] [CrossRef]
- Verma, A.; Asadi, A.; Yang, K.; Tyagi, S. A data-driven approach to identify households with plug-in electrical vehicles (PEVs). Appl. Energy 2015, 160, 71–79. [Google Scholar] [CrossRef]
- Xu, X.; Li, K.; Wang, F.; Mi, Z.; Jia, Y.; Wei, W.; Jing, Y. Evaluating multitimescale response capability of EV aggregator considering users’ willingness. IEEE Trans. Ind. Appl. 2021, 57, 3366–3376. [Google Scholar] [CrossRef]
- Liu, H.; Lian, H.; Ge, S. Timing response capability model of electric vehicle battery swapping station and strategy formulation of charging plan. Autom. Electron. Power Syst. 2017, 41, 91–97. [Google Scholar]
- Xu, X.; Mi, Z.; Zhan, Z.; Ji, L. Response capability evaluation model of electric vehicle aggregator based on evolutionary game and response anticipation. Front. Energy Res. 2023, 11, 1225327. [Google Scholar]
- Thran, J.; Marecek, J.; Shorten, R.N.; Green, T.C. Reserve Provision from Electric Vehicles: Aggregate Boundaries and Stochastic Model Predictive Control. IEEE Trans. Power Syst. 2025, 40, 4081–4092. [Google Scholar] [CrossRef]
- Zhang, Y.; Mu, Y.; Jia, H.; Wang, M.; Zhou, Y.; Xu, Z. Response capability evaluation model with multiple time scales for electric vehicle virtual power plant. Autom. Electr. Power Syst. 2019, 43, 94–103. [Google Scholar]
- Zhang, K.; Xu, Y.; Sun, H. Joint chance-constrained program based electric vehicles optimal dispatching strategy considering drivers’ response uncertainty. Appl. Energy 2024, 356, 122313. [Google Scholar] [CrossRef]
- González-Garrido, A.; González-Pérez, M.; Asensio, F.J.; Cortes-Borray, A.F.; Santos-Mugica, M.; Vicente-Figueirido, I. Hierarchical control for collaborative electric vehicle charging to alleviate network congestion and enhance EV hosting in constrained distribution networks. Renew. Energy 2024, 230, 120823. [Google Scholar] [CrossRef]
- Alaee, P.; Shao, J.; Bemš, J.; Guerrero, J.M. Coordinated routing optimization and charging scheduling in a multiple-charging station system: A strategic bilevel multi-objective programming. Sustain. Energy Grids Netw. 2025, 42, 101659. [Google Scholar] [CrossRef]
- Baran, M.; Wu, F.F. Optimal sizing of capacitors placed on a radial distribution system. IEEE Trans. Power Deliv. 2002, 4, 735–743. [Google Scholar] [CrossRef]
- Li, T.; Tao, S.; He, K.; Lu, M.; Xie, B.; Yang, B.; Sun, Y. V2G multi-objective dispatching optimization strategy based on user behavior model. Front. Energy Res. 2021, 9, 739527. [Google Scholar] [CrossRef]
- Wang, M.; Mu, Y.; Jiang, T.; Jia, H.; Li, X.; Hou, K.; Wang, T. Load curve smoothing strategy based on unified state model of different demand side resources. J. Mod. Power Syst. Clean Energy 2018, 6, 540–554. [Google Scholar] [CrossRef]
- Dörfler, F.; Grammatico, S. Gather-and-broadcast frequency control in power systems. Automatica 2017, 79, 296–305. [Google Scholar] [CrossRef]
- Chen, L.; Li, N.; Low, S.H.; Doyle, J.C. Two market models for demand response in power networks. In Proceedings of the 2010 First IEEE International Conference on Smart Grid Communications, Gaithersburg, MD, USA, 4–6 October 2010; IEEE: Piscataway, NJ, USA, 2010. [Google Scholar]
- Sun, B.; Huang, Z.; Tan, X.; Tsang, D.H. Optimal scheduling for electric vehicle charging with discrete charging levels in distribution grid. IEEE Trans. Smart Grid 2016, 9, 624–634. [Google Scholar] [CrossRef]
- Bahramirad, S.; Reder, W.; Khodaei, A. Reliability-constrained optimal sizing of energy storage system in a microgrid. IEEE Trans. Smart Grid 2012, 3, 2056–2062. [Google Scholar] [CrossRef]
- IEEE PES Distribution Test Feeder. IEEE PES Distribution System Analysis Subcommittee Resources. 2017. Available online: https://cmte.ieee.org/pes-testfeeders/resources/ (accessed on 8 May 2025).


| Quantity | Value | Comment | |
|---|---|---|---|
| 300 | kW | Rated power of PV | |
| 1000 | kWh | Rated capacity of ESS | |
| 275 | kW | Maximum charging/discharging power of ESS | |
| 0.95/0.95 | - | Charging/discharging efficiency of ESS | |
| [, ] | [30%, 80%] | - | SOC limitation of ESS |
| 10 | kW | Maximum charging/discharging power of EVs | |
| 0.92/0.92 | - | Charging/discharging efficiency of EVs | |
| 0.2 | - | Minimum capacity of EVs | |
| 0.05 | - | The step length controlling the Lagrange-multiplier update rate | |
| 0.01 | - | Initial value of Lagrange multiplier | |
| 15 or 5 | minute | Sampling period |
| Bus | Violation Duration Before Optimization (hours) | Violation Duration After Optimization (hours) | Voltage Peak Reduction (p.u.) |
|---|---|---|---|
| 9 | 8.5 | 0 | 0.0397 |
| 30 | 10.25 | 2.25 | 0.0480 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Xu, K.; Xu, W.; Shao, F.; He, X.; Tang, Z. Voltage Control for Active Distribution Networks Considering Coordination of EV Charging Stations. Electronics 2025, 14, 3591. https://doi.org/10.3390/electronics14183591
Liu C, Xu K, Xu W, Shao F, He X, Tang Z. Voltage Control for Active Distribution Networks Considering Coordination of EV Charging Stations. Electronics. 2025; 14(18):3591. https://doi.org/10.3390/electronics14183591
Chicago/Turabian StyleLiu, Chang, Ke Xu, Weiting Xu, Fan Shao, Xingqi He, and Zhiyuan Tang. 2025. "Voltage Control for Active Distribution Networks Considering Coordination of EV Charging Stations" Electronics 14, no. 18: 3591. https://doi.org/10.3390/electronics14183591
APA StyleLiu, C., Xu, K., Xu, W., Shao, F., He, X., & Tang, Z. (2025). Voltage Control for Active Distribution Networks Considering Coordination of EV Charging Stations. Electronics, 14(18), 3591. https://doi.org/10.3390/electronics14183591






