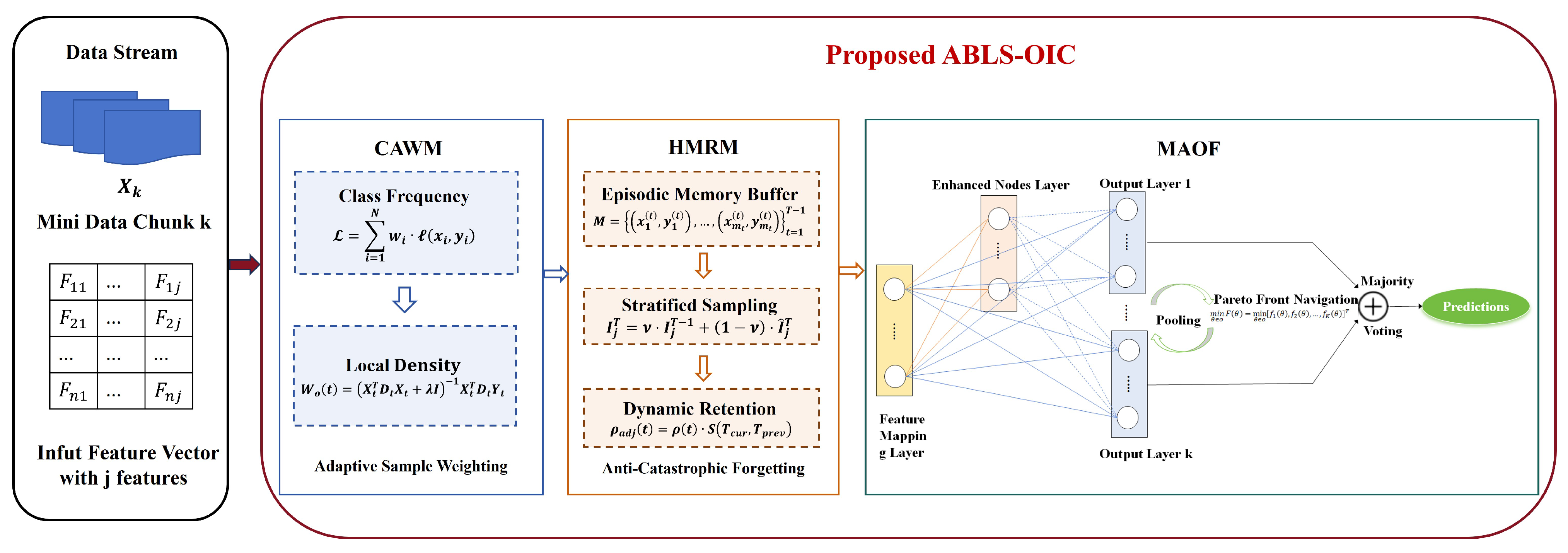
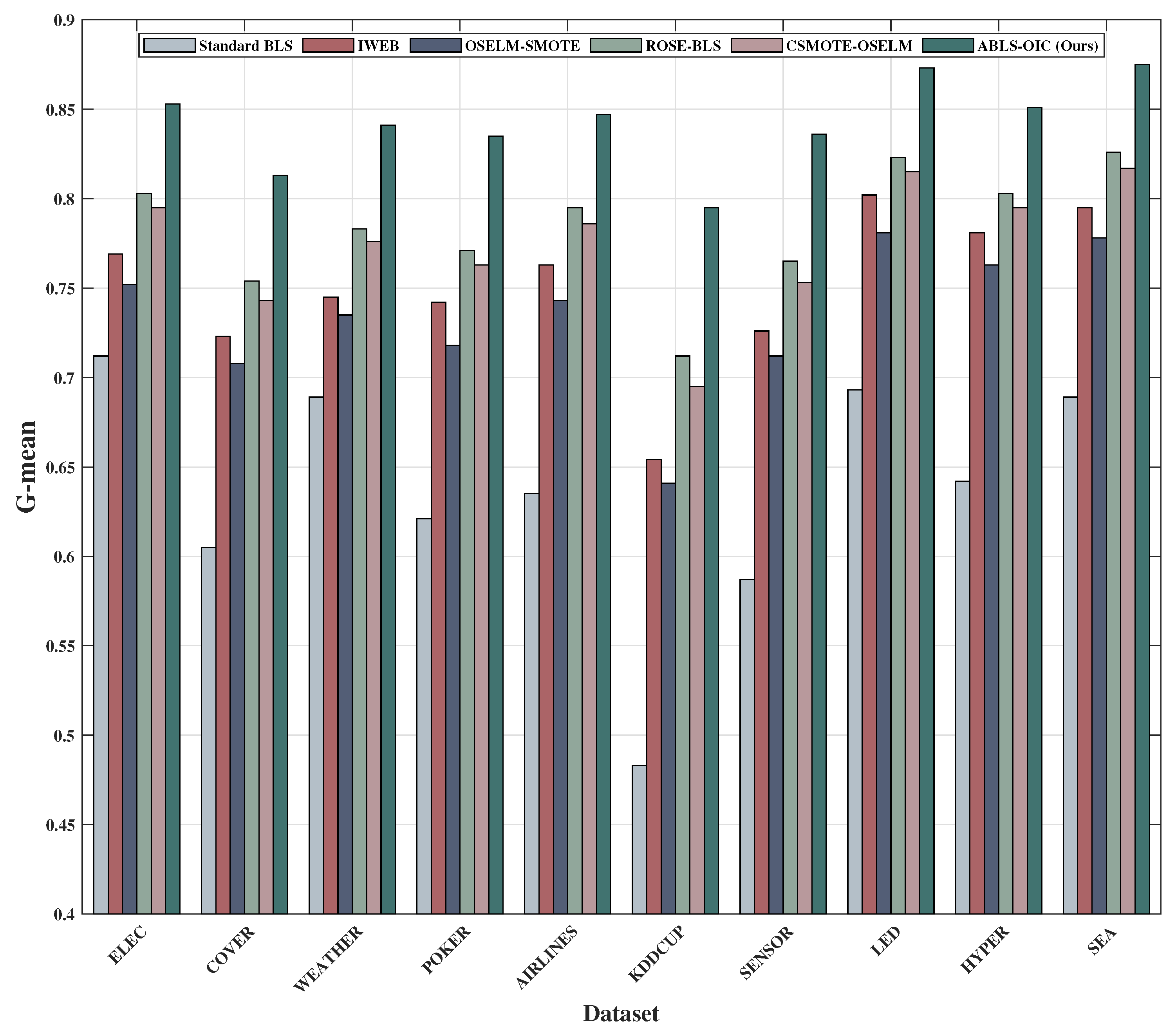
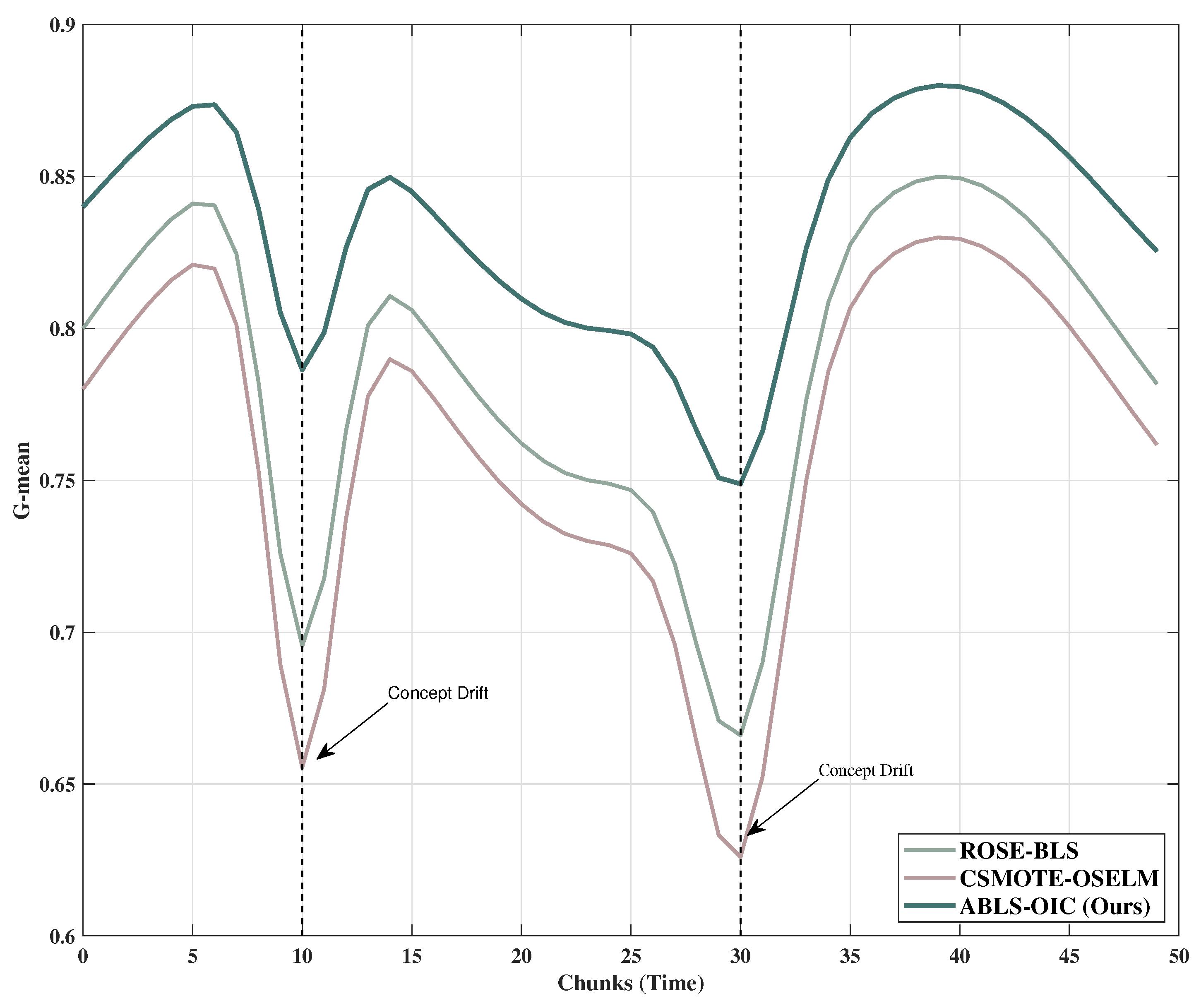
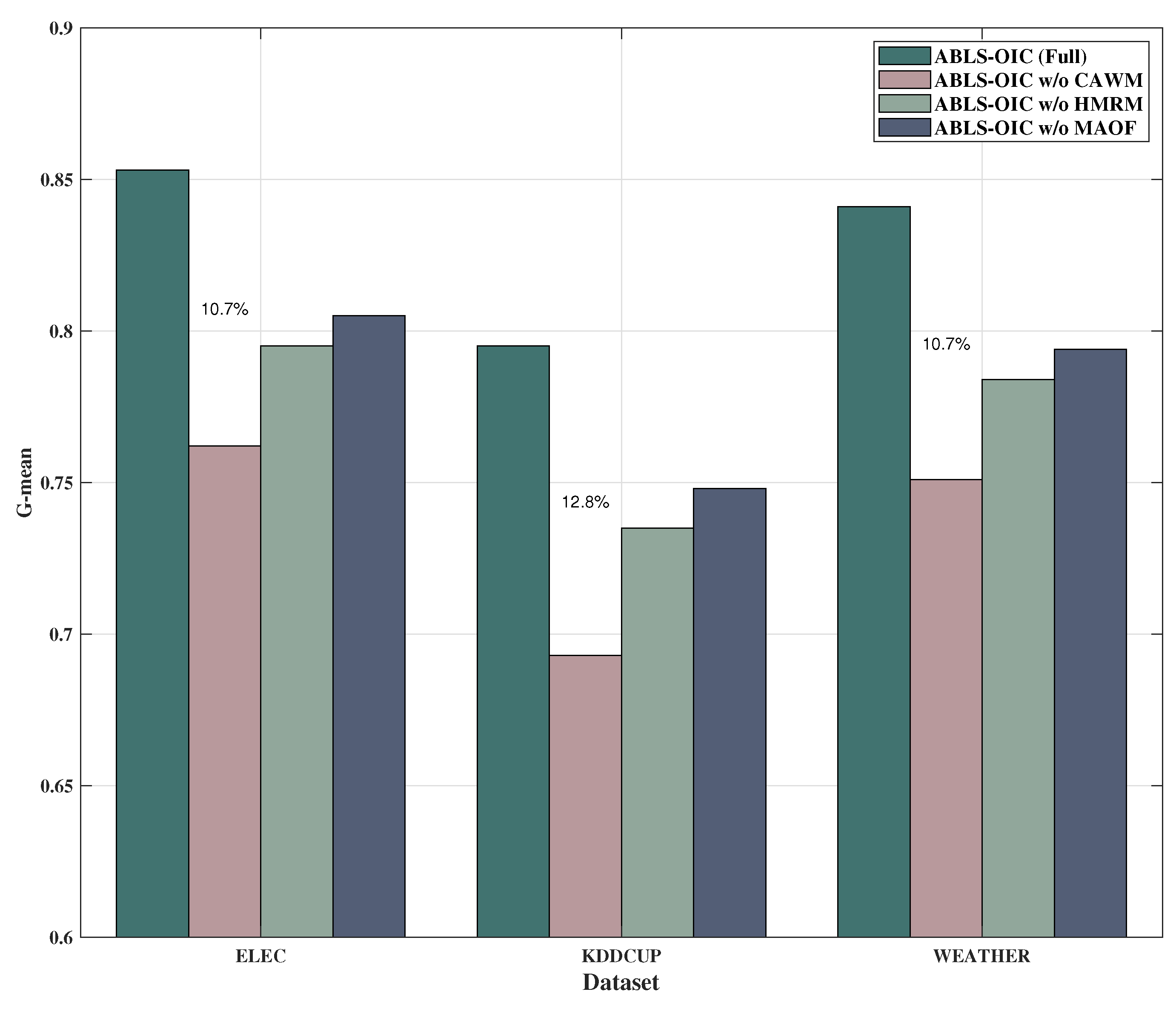This section presents the Class-Adaptive Weighted Broad Learning System with Hybrid Memory Retention for Online Imbalanced Classification (ABLS-OIC). This framework integrates three principal innovations: a Class-Adaptive Weight Matrix (CAWM) that dynamically modifies the significance of each sample, a Hybrid Memory Retention Mechanism (HMRM) that judiciously retains the most representative samples, and a Multi-Objective Adaptive Optimization Framework (MAOF) that proficiently equilibrates multiple learning objectives in real time.
3.2. Class-Adaptive Weighting Mechanism (CAWM)
The CAWM extends the BLS framework to effectively address challenges such as class imbalance and varying sample importance in classification tasks. By dynamically assigning weights to individual samples during training, CAWM ensures that minority class instances and critical samples exert a proportionally greater influence on the learning process. This mechanism is especially valuable in scenarios where certain classes are underrepresented or sample quality is inconsistent. CAWM achieves this aim by assigning a weight
to each sample
i based on three key factors: the frequency of its class, the model’s performance on that class, and the local data density around the sample. These adaptive weights directly impact the model update by modifying the loss function or optimization objective, thereby enhancing sensitivity to minority classes and difficult instances. The weighted ridge regression for a data batch is formulated as
where
is the combined feature-enhancement matrix,
is the diagonal weight matrix containing the sample weights,
is the label matrix, and
is a regularization hyperparameter. The weights
are computed adaptively for each sample.
The weight
for a sample
i belonging to class
is defined as
where
is the recent frequency of class
,
is the performance score of class
,
is the local density around sample
i,
is a small constant to avoid division by zero, and
are hyperparameters that control the influence of frequency, performance, and density, respectively. The frequency
is computed as the proportion of samples in the training set that belong to class
. The performance score
is derived from the current model’s accuracy or precision on class
, reflecting how well the model distinguishes samples from that class. The local density
is calculated using a k-nearest neighbors (k-NN) approach, where
is inversely proportional to the average distance between sample
i and its k-nearest neighbors.
By integrating these factors, CAWM ensures that samples from minority classes are assigned higher weights, effectively compensating for their underrepresentation in the dataset. Likewise, samples belonging to classes with lower model performance are emphasized, enhancing the model’s ability to correctly classify these challenging categories. The inclusion of the local density term further prioritizes samples in dense regions—those more likely to reflect the core characteristics of their respective classes—while naturally reducing the influence of outliers. This comprehensive weighting strategy enables CAWM to deliver more balanced and robust classification performance, particularly in imbalanced or complex data scenarios.
Lemma 1. Gradient Scaling. The gradient of the weighted loss function is scaled by , ensuring that samples with higher weights have a proportionally larger influence on the model update. The weighted loss function iswhere is the loss for sample i. Proof. The gradient of the weighted loss function with respect to the model parameters
is
Using the linearity of differentiation, this becomes
This expression shows that the gradient contribution of each sample is scaled by its weight , emphasizing the importance of samples with higher weights. □
Lemma 2. Regularization Effect. The use of weighted ridge regression ensures stability during optimization. The closed-form solution for the output weights iswhere is the diagonal weight matrix. Proof. The optimization objective for weighted ridge regression is
The first term minimizes the weighted loss, while the second term penalizes large values in
. The closed-form solution is derived by setting the gradient of
with respect to
to zero:
Rearranging terms and solving for
gives
The regularization term ensures that large values in are penalized, reducing the likelihood of overfitting and ensuring stability during optimization. □
3.3. Hybrid Memory Retention Mechanism (HMRM)
The HMRM is designed to address the critical challenge of catastrophic forgetting in continual learning scenarios. When neural networks are trained on sequential tasks, they often overwrite previously learned knowledge, leading to substantial performance degradation on earlier tasks. HMRM offers a principled solution to this issue by integrating multiple complementary strategies within a unified framework. By selectively retaining and replaying representative samples from past data, HMRM helps preserve important information from earlier tasks, thereby maintaining model performance and stability over time.
The episodic memory buffer
M stores representative samples from previously encountered tasks:
Here,
represents the
i-th sample from task
t, where
is the number of stored samples from task
t, and
T is the current task index. The memory buffer employs a stratified sampling strategy to ensure balanced representation:
In this equation, represents the importance weight assigned to task t, while denotes the number of classes in task t. The term refers to the number of samples from class j in task t, and identifies the specific class of sample i in task t. This sampling approach ensures proportional representation across tasks and classes.
The parameter importance matrix
quantifies the contribution of each parameter
to the performance on previous tasks:
This formulation incorporates
as the loss for sample
under parameters
, with
representing the parameter change during task
t. The temporal decay factor
gradually reduces the influence of older tasks, where
controls the rate of this decay. The importance is updated incrementally after each task:
Here, functions as a momentum coefficient while represents the importance estimated specifically on the current task, providing a balance between historical and recent parameter significance.
The dynamic retention rate
controls the balance between stability (memory retention) and plasticity (new task learning):
This equation incorporates
as the minimum retention rate and
as the maximum retention rate. The parameters
and
represent the starting time step and decay time constant, respectively, controlling how quickly the retention rate declines over time. The retention rate is further modulated by task similarity:
Here,
measures the cosine similarity between feature representations of current and previous tasks:
This similarity-based adjustment ensures that the retention mechanism adapts to the relationship between sequential tasks.
The composite loss function integrates current task learning with memory retention:
This expression balances multiple components:
represents the loss on the current task, while
captures the loss on memory samples. The parameter
controls the balance between current and memory learning. The regularization strength is determined by
, which scales the importance-weighted parameter deviation from reference values
established after learning previous tasks. Additionally,
serves as a general regularization coefficient scaling
, which typically implements standard regularization like L2 norm. The memory loss is further defined as
In this formulation, ℓ represents the task-specific loss function (such as cross-entropy), and implements a task recency weight. The hyperparameter controls the recency bias, allowing the model to adjust the relative importance of tasks based on their temporal proximity.
HMRM consolidates knowledge through a dual-pathway approach. The first pathway, the Explicit Memory Pathway, implements a direct replay of stored samples with the loss:
where
represents the memory batch size. The second pathway, the Implicit Regularization Pathway, implements parameter-space regularization with
This dual approach ensures comprehensive knowledge retention through both data rehearsal and parameter constraint mechanisms. The memory buffer is updated using a reservoir sampling algorithm with importance weighting. For a new sample
from task
t, the process begins by computing the sample importance as
. This is then normalized to obtain
. The replacement probability is calculated as
. If the current memory size
is less than the target size
, the sample is directly added to
. Otherwise, a randomly selected sample is replaced with probability
. This strategy ensures that more informative samples are preferentially retained in memory. The weight between the current task and memory is dynamically adjusted according to
In this equation, represents the initial weight, while defines the maximum possible change in weight over time. The parameter specifies the midpoint of the sigmoid function, marking the time at which the weight reaches the midpoint of its trajectory. The parameter controls the steepness of the transition, determining how abruptly the weight changes near the midpoint. This adaptive weighting allows the system to smoothly transition its focus between retaining old knowledge and acquiring new information as learning progresses.
HMRM employs gradient modulation to protect important parameters:
where
is a scaling factor controlling the strength of modulation. This approach ensures that gradients are selectively dampened for parameters that are crucial for previous tasks.
3.4. Multi-Objective Adaptive Optimization Framework (MAOF)
The MAOF addresses the fundamental challenge of simultaneously optimizing multiple, often competing, objectives in machine learning systems. Traditional optimization methods typically collapse these objectives into a single aggregate function with fixed weights, which can obscure the inherent trade-offs and limit system flexibility. In contrast, MAOF explicitly models the Pareto front of optimal trade-offs, allowing for dynamic and context-aware navigation of the solution space according to evolving requirements. This approach is particularly valuable in settings where stakeholder priorities differ, requirements change over time, or the relative importance of objectives cannot be predefined. By treating multi-objective optimization as a central concern, MAOF empowers machine learning systems to achieve a nuanced, adaptive, and transparent balance among competing demands, such as accuracy versus fairness, precision versus recall, or performance versus computational efficiency.
The multi-objective optimization problem is formally defined as simultaneously minimizing a vector of objective functions:
where
represents the model parameters within the feasible parameter space
, and
for
represents the
K different objective functions to be minimized. Each objective function quantifies a distinct aspect of model performance, such as prediction error, computational complexity, or fairness violations. The framework accommodates both differentiable and non-differentiable objectives, enabling the integration of diverse performance metrics. These objectives typically conflict with each other, meaning that improving one objective often comes at the expense of others. For instance, increasing model complexity may reduce training error but increase inference time and risk of overfitting. The goal is to identify the set of Pareto optimal solutions where no objective can be improved without degrading at least one other objective.
The concept of Pareto optimality defines the set of non-dominated solutions:
where
indicates that
for all
. A solution
is Pareto optimal if no other solution can improve all objectives simultaneously. The image of the Pareto optimal set in the objective space forms the Pareto front:
This front represents the fundamental trade-offs inherent in the problem. The framework employs several metrics to characterize the Pareto front, including the hypervolume indicator:
where
is a set of solutions in objective space,
is a reference point dominated by all points in
, and
is the Lebesgue measure. The hypervolume provides a scalar measure of the quality of a set of solutions, capturing both convergence to the true Pareto front and diversity along this front.
MOOF incorporates preference information through a variety of mechanisms to guide the search toward the most relevant regions of the Pareto front. The preference function
maps objective vectors to scalar values based on preference parameters
:
The function includes both weighted transformations of individual objectives
and interaction terms
that capture the joint effects of pairs of objectives. Common transformation functions include linear scaling, logarithmic compression, or sigmoid normalization to handle objectives with different scales or distributions. The preference parameters
can be specified directly by domain experts or learned from demonstrated preferences through inverse optimization:
where
is a set of preference examples indicating that solution
is preferred over
, and
is a ranking loss function such as the hinge loss
with margin parameter
.
To navigate the Pareto front during optimization, MOOF employs dynamic scalarization methods that transform the multi-objective problem into a sequence of single-objective problems. The general form of the scalarization function is
where
are scalarization parameters,
is a reference point, and
is an aggregation function. Several scalarization methods are supported:
where
and
for the Weighted Sum method.
where
is an ideal reference point for the Weighted Tchebycheff method.
with
as an augmentation coefficient for the Augmented Weighted Tchebycheff method.
where
are penalty coefficients for the Chebyshev–Penalty method. The scalarization parameters
are systematically varied during optimization to explore different regions of the Pareto front according to the adaptive strategy:
where
is the optimal solution for the current scalarization,
is a step size, and
is a projection onto the feasible set of scalarization parameters.