Robust Observer Design for the Longitudinal Dynamics of a Fixed-Wing Aircraft
Abstract
1. Introduction
- A novel Control-Based Observer (CbO) framework is proposed for simultaneous estimation of aircraft states and disturbance signals. By formulating the observer design as a control problem, the framework integrates disturbance estimation in a straightforward fashion within the observer structure and minimizes the output error between the plant and its model.
- A Robust observer design is developed within the CbO framework, which explicitly accounts for nonlinearities and variations in operating points by optimizing over multiple neighboring operating conditions to ensure reliable performance under worst-case scenarios.
- A comprehensive comparative analysis is conducted between the proposed CbO approaches (both nominal and robust ) and a conventional linear observer, demonstrating the superiority of the proposed methods in terms of accuracy and robustness in estimating states and disturbances of a fixed-wing aircraft.
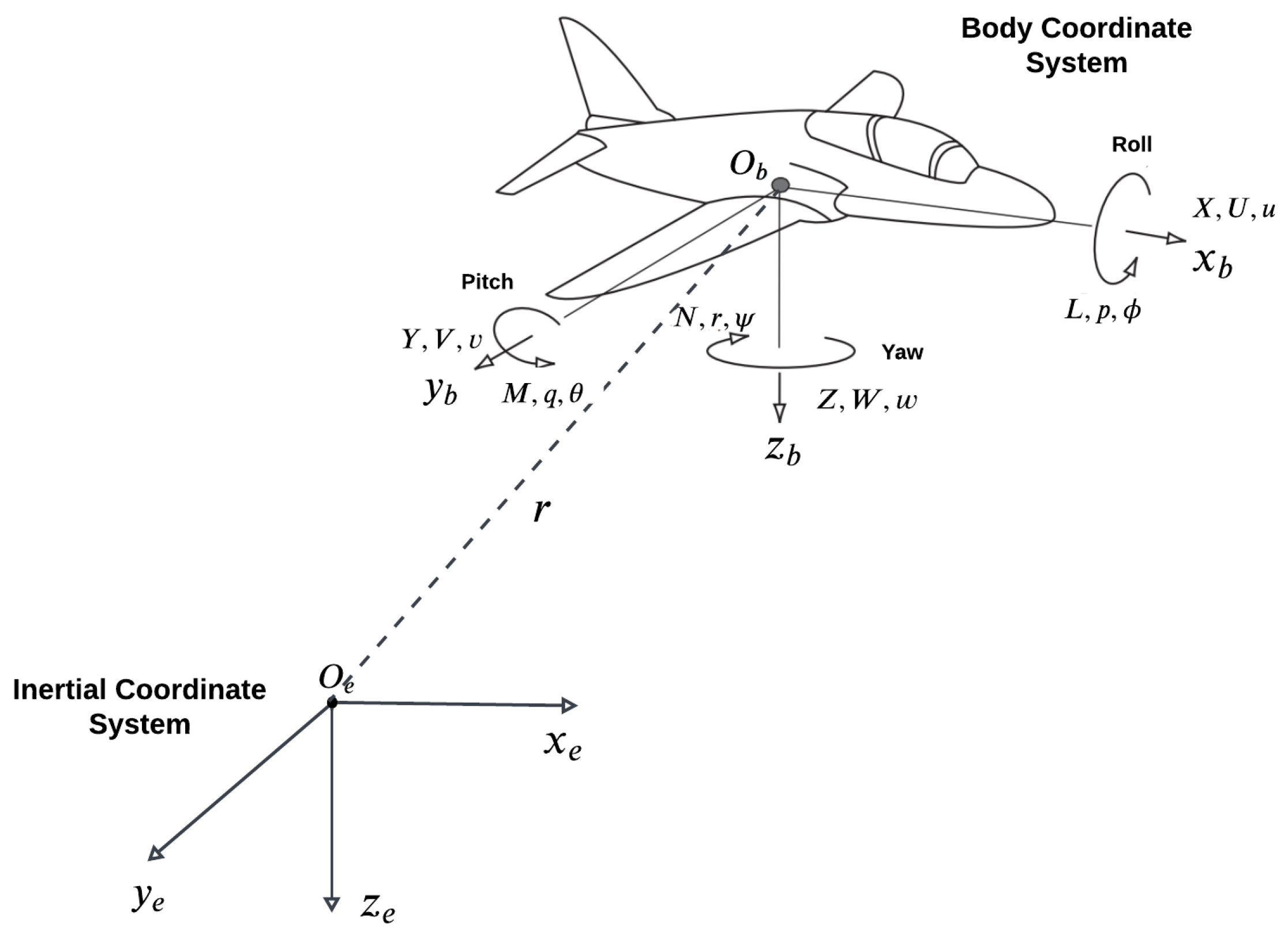
2. System Modeling
- The aircraft is treated as a rigid body, assuming that a piece of mass on it does not move relative to another piece of mass.
- The rotational speed of the Earth is considered negligible.
- The mass loss due to fuel consumption is ignored.
- The force equations describe the translational motion of the aircraft and are derived from Newton’s Second Law of Motion.
- The moment equations govern the rotational dynamics of the aircraft and are based on Euler’s equations of motion. These equations describe the effects of aerodynamic and control surface-induced torques on the aircraft’s angular motion.
- The kinematic equations establish the relationship between the aircraft’s angular velocities and its orientation, typically expressed using Euler angles or quaternions to facilitate attitude representation [28].
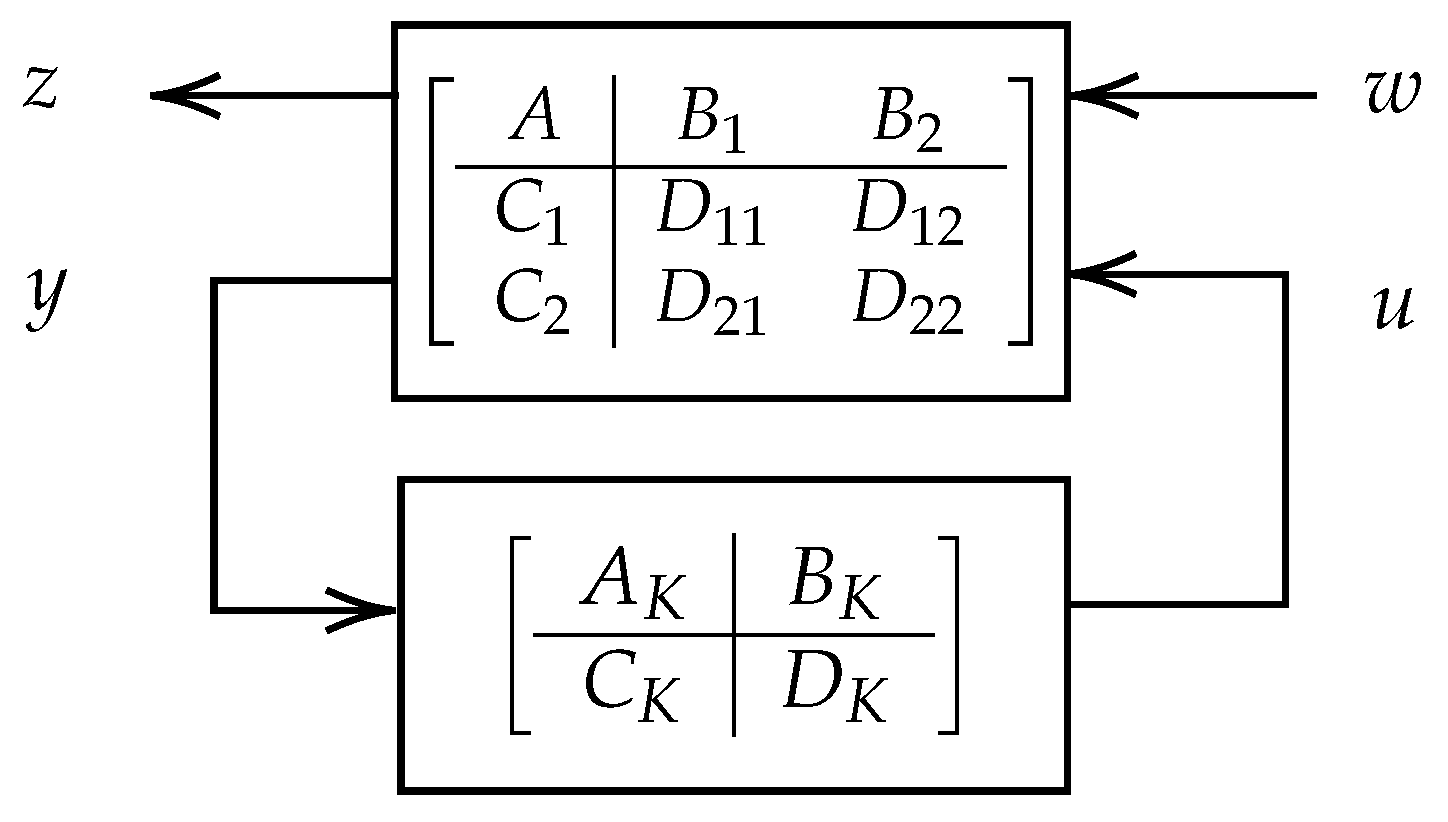
3. Control Problem and Controller Synthesis
3.1. Control Problem
3.2. Controller Design
3.3. Output Feedback Controller Design via LMI Formulation
3.4. Robust Controller Design
- The nonlinear system is linearized around a set of points (all of which are close to the one primary point the system is expected to operate at);
- For each system, the system is obtained;
- The following optimization problem is considered:
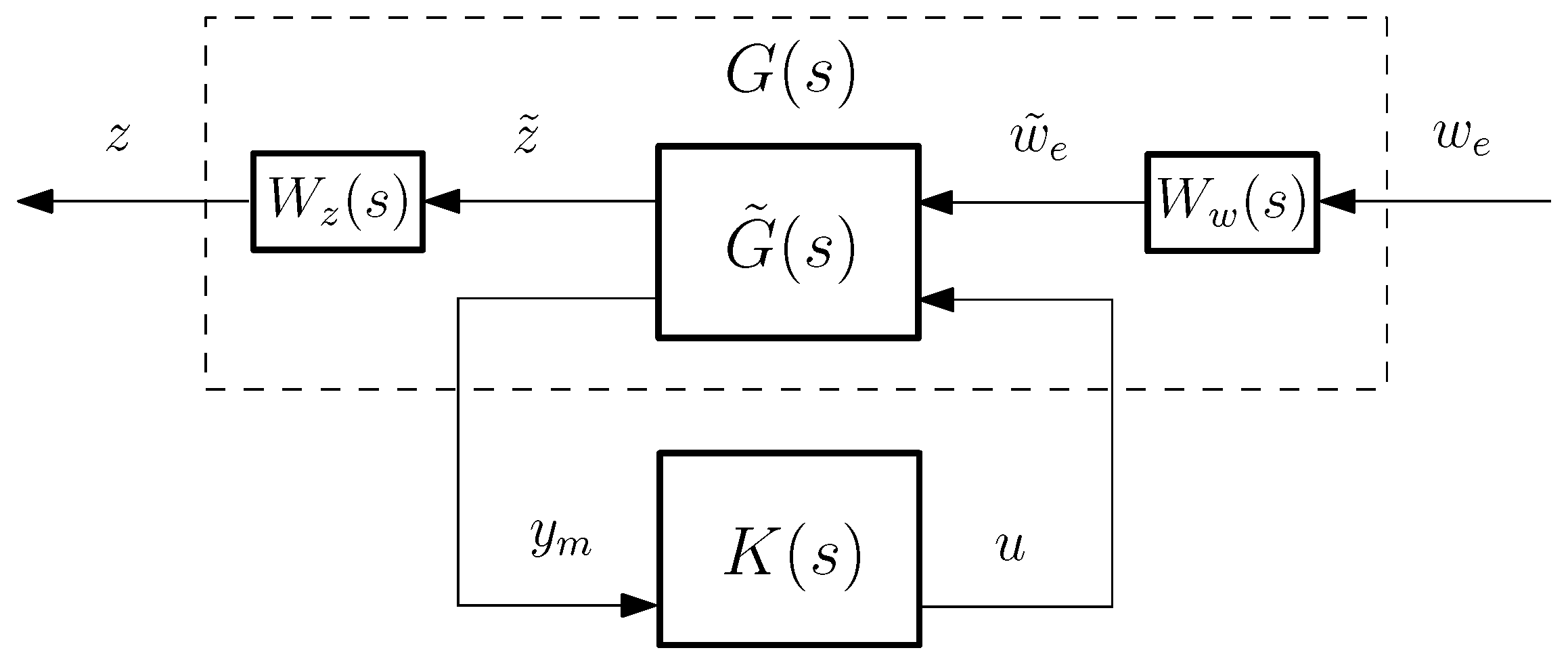
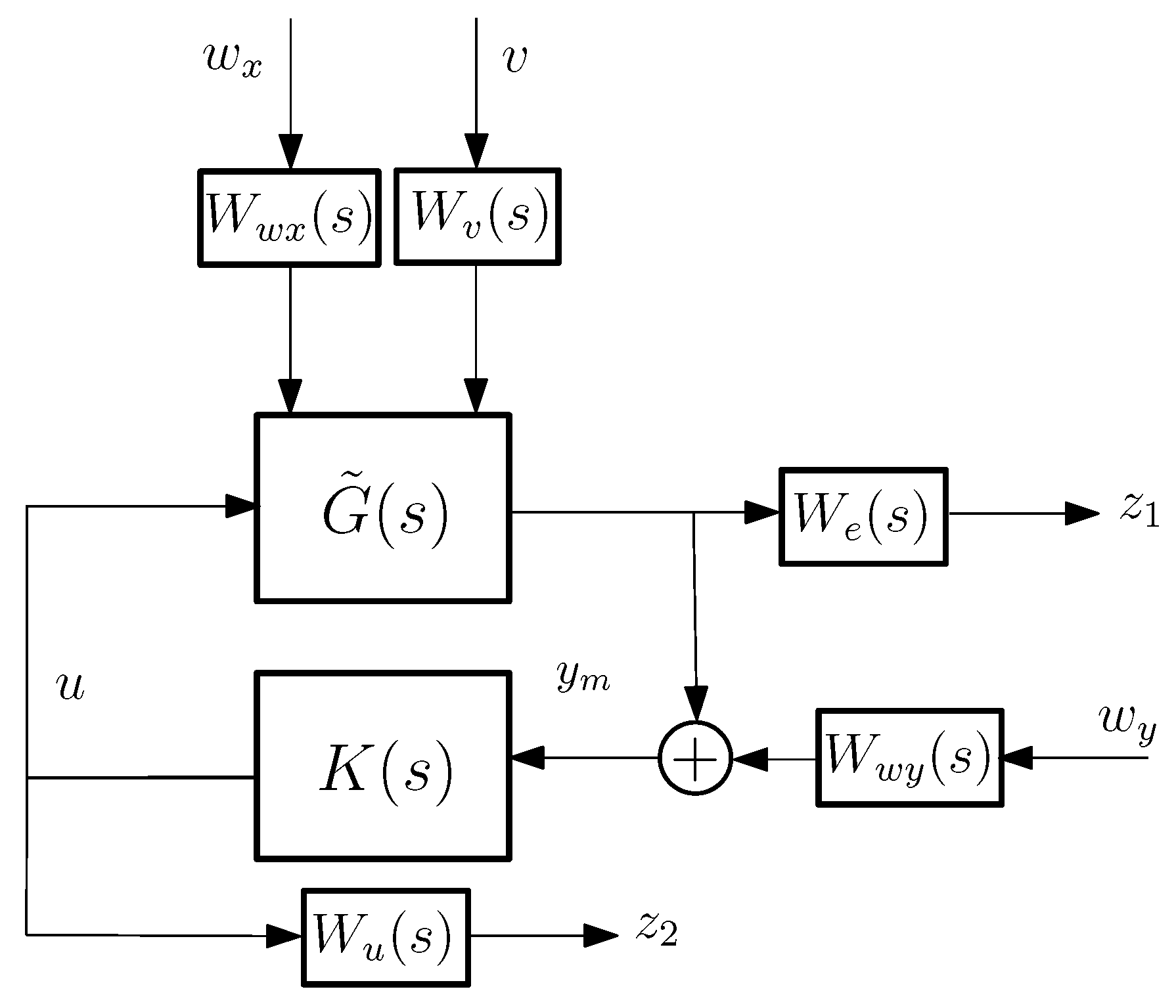
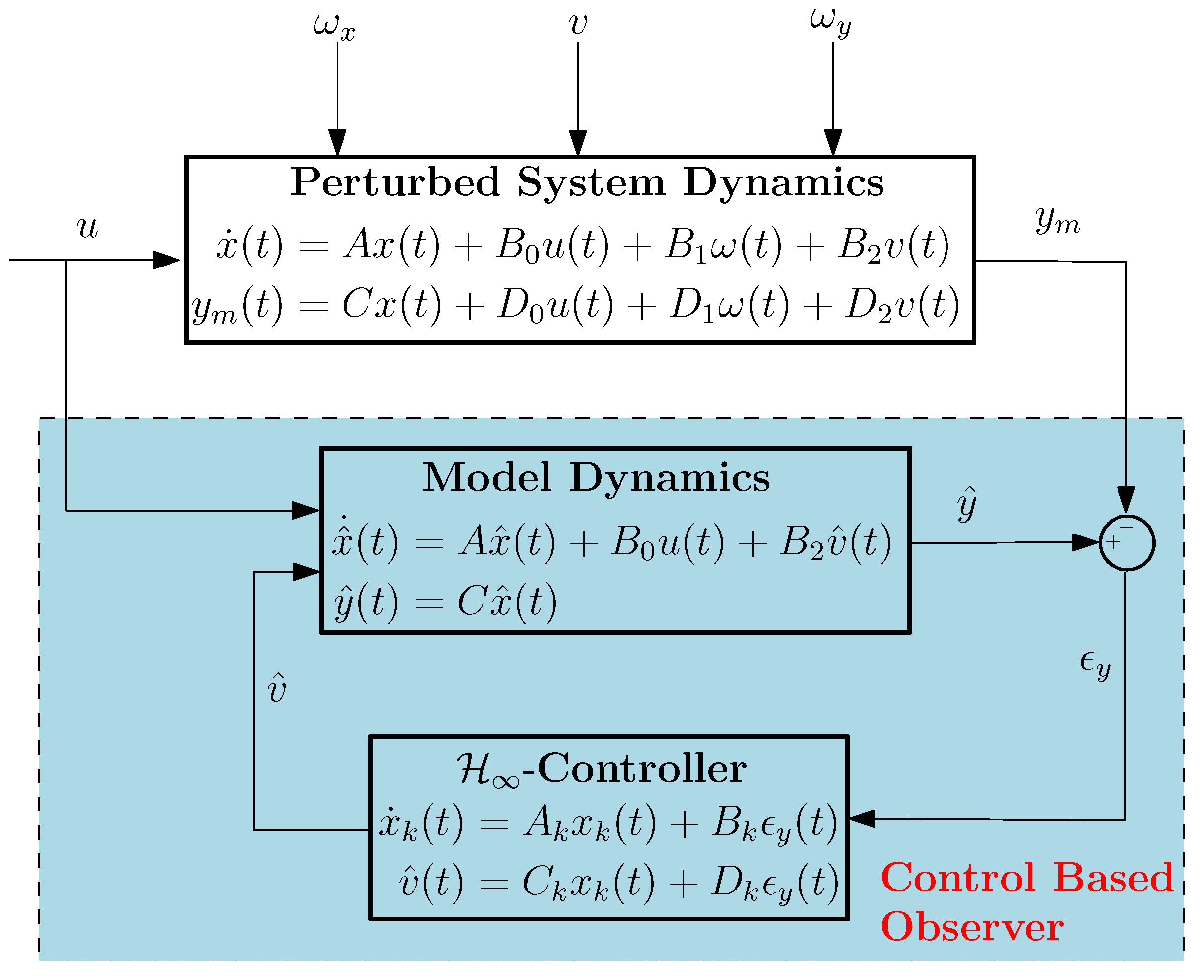
4. Control-Based Observer Design Using Controller
4.1. Observer Design Concept
- is observable
- is controllable
4.2. System Linearization
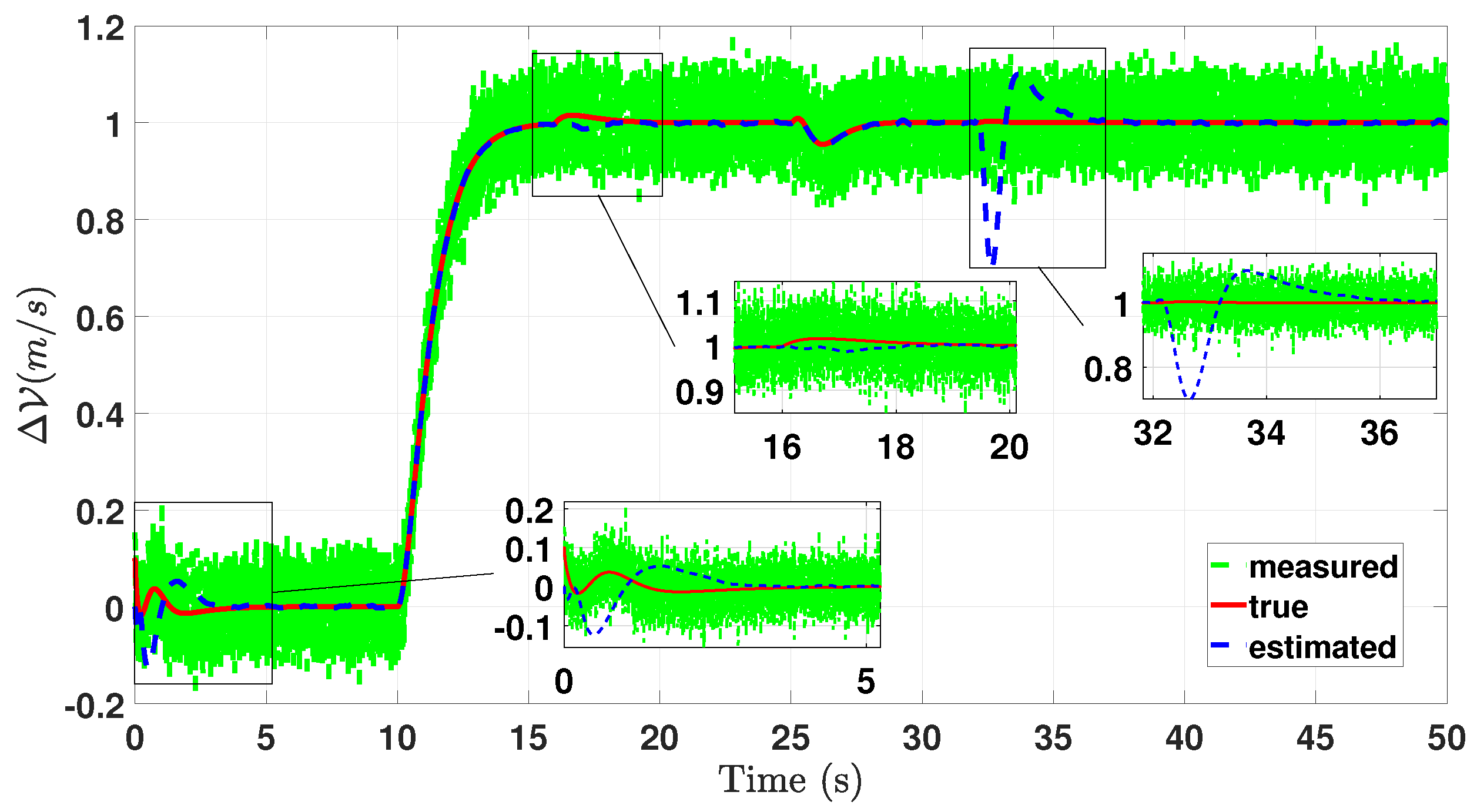
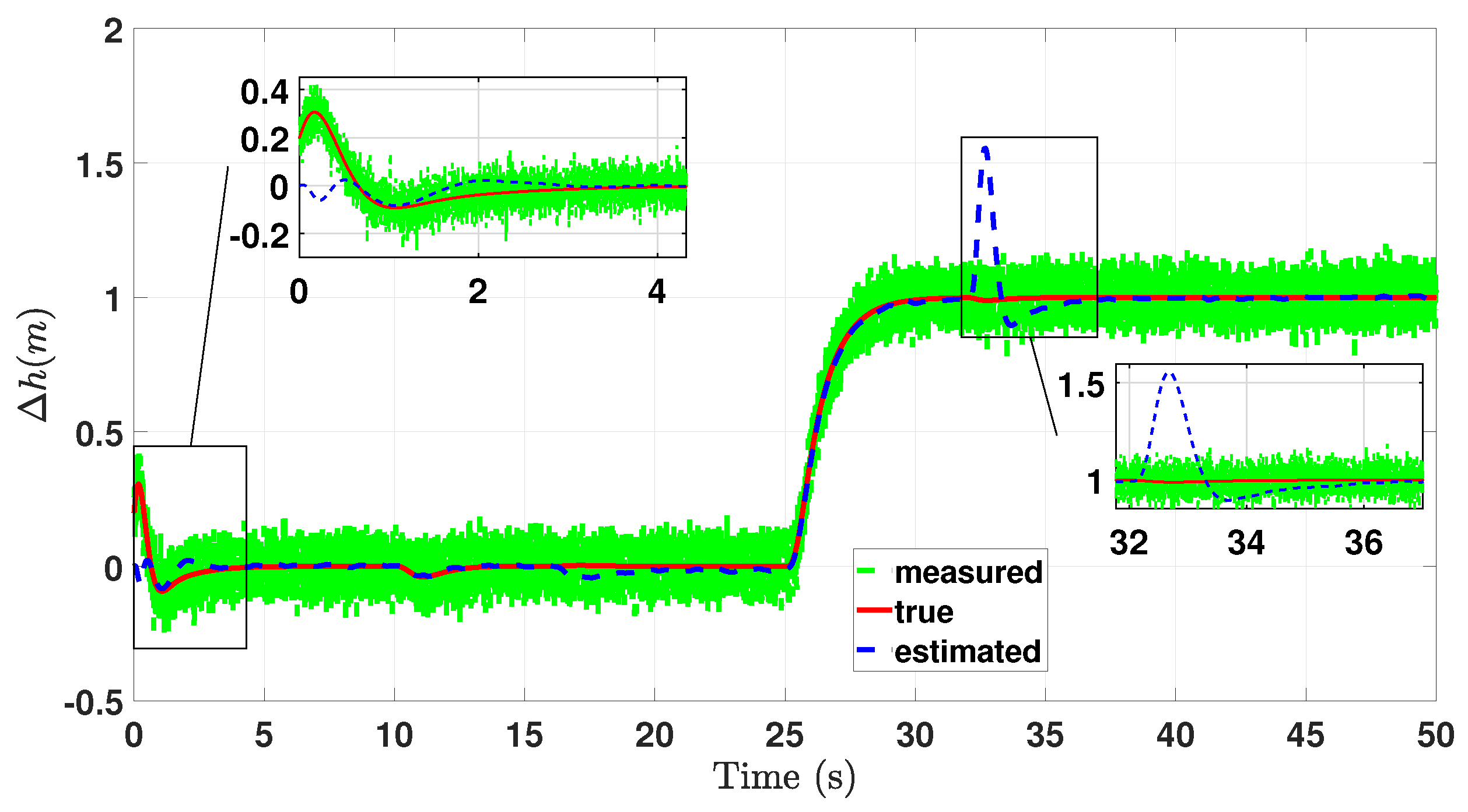
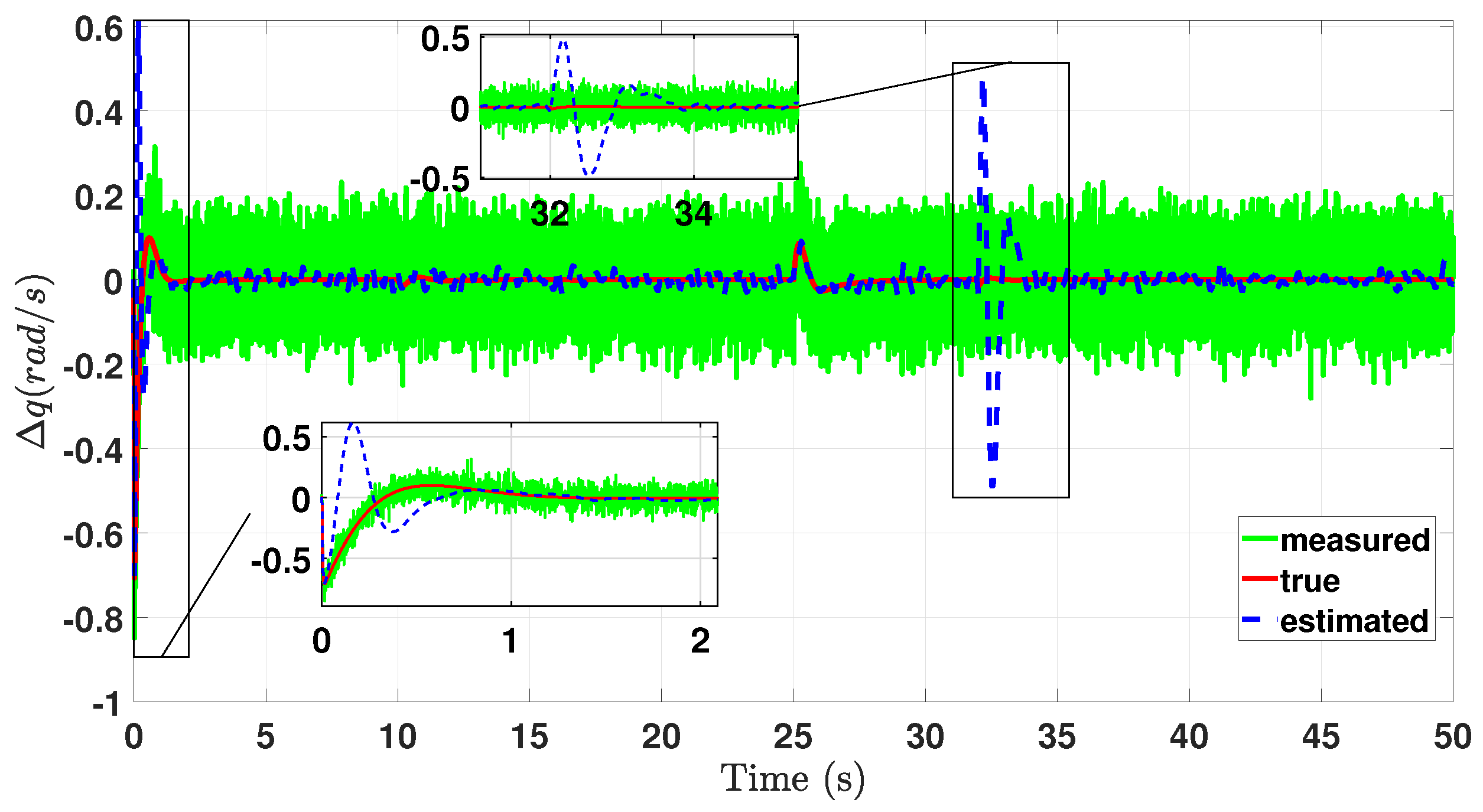
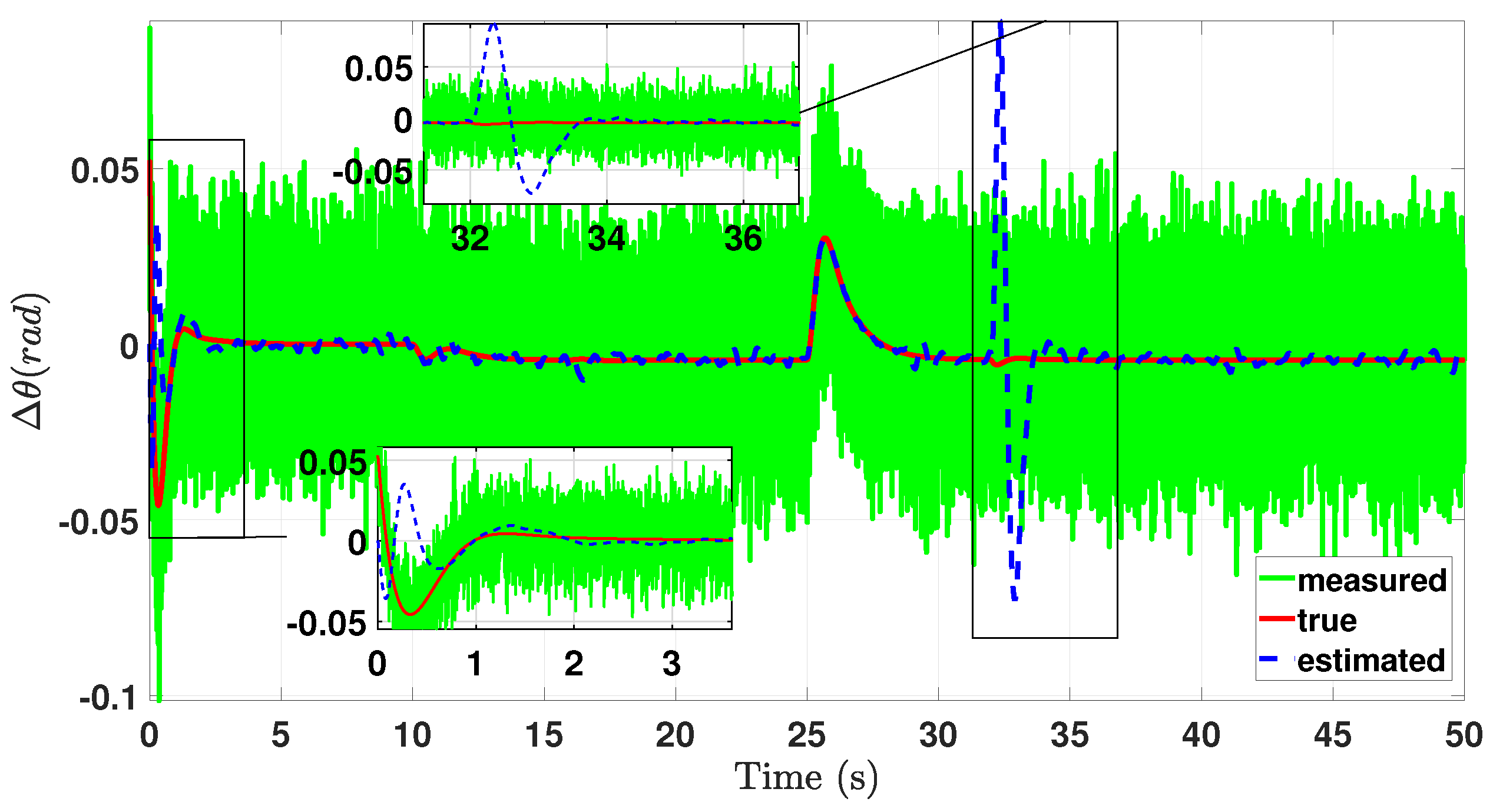
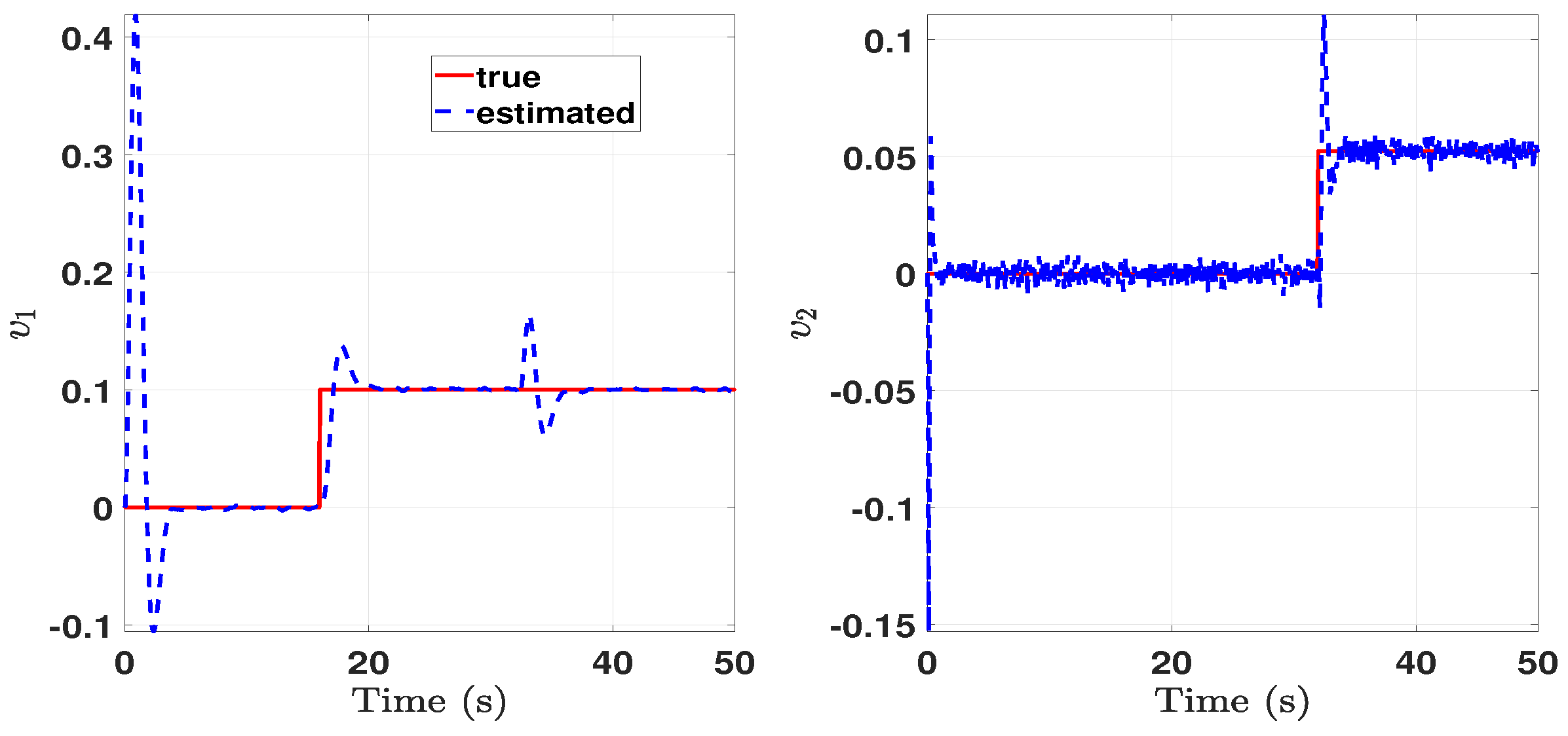
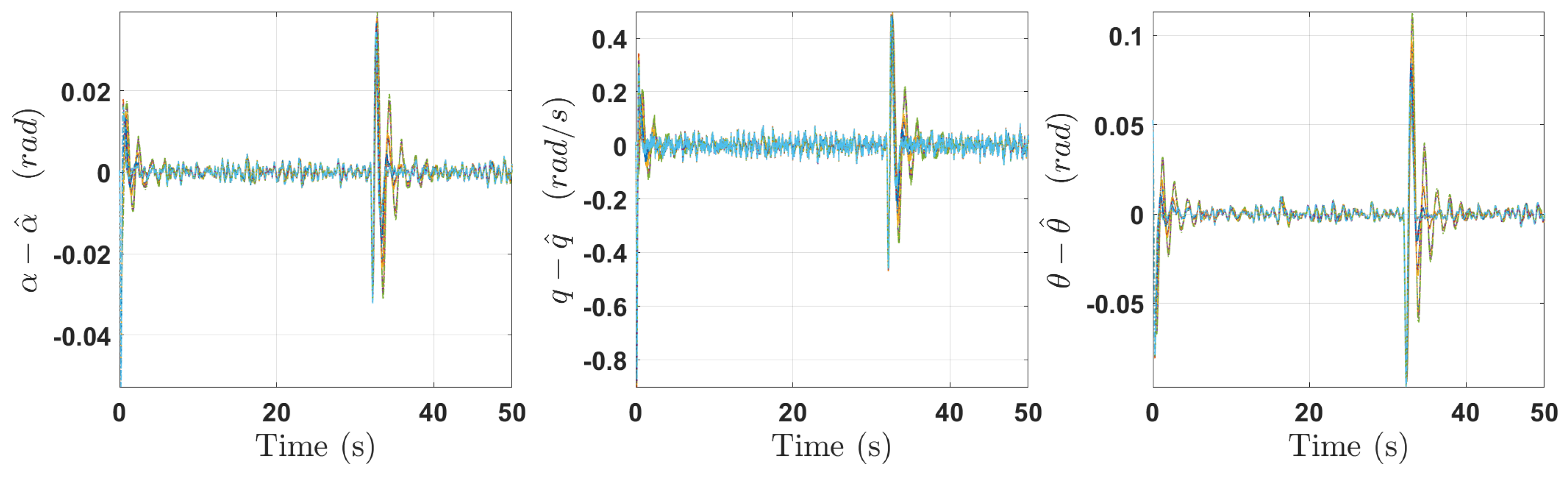
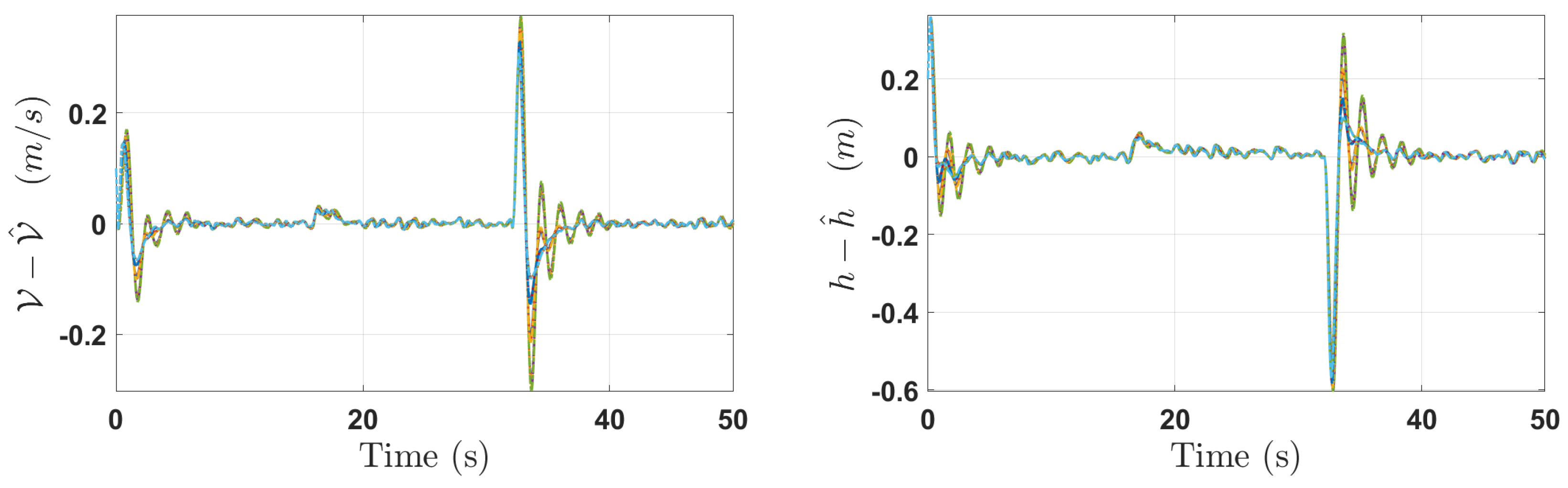
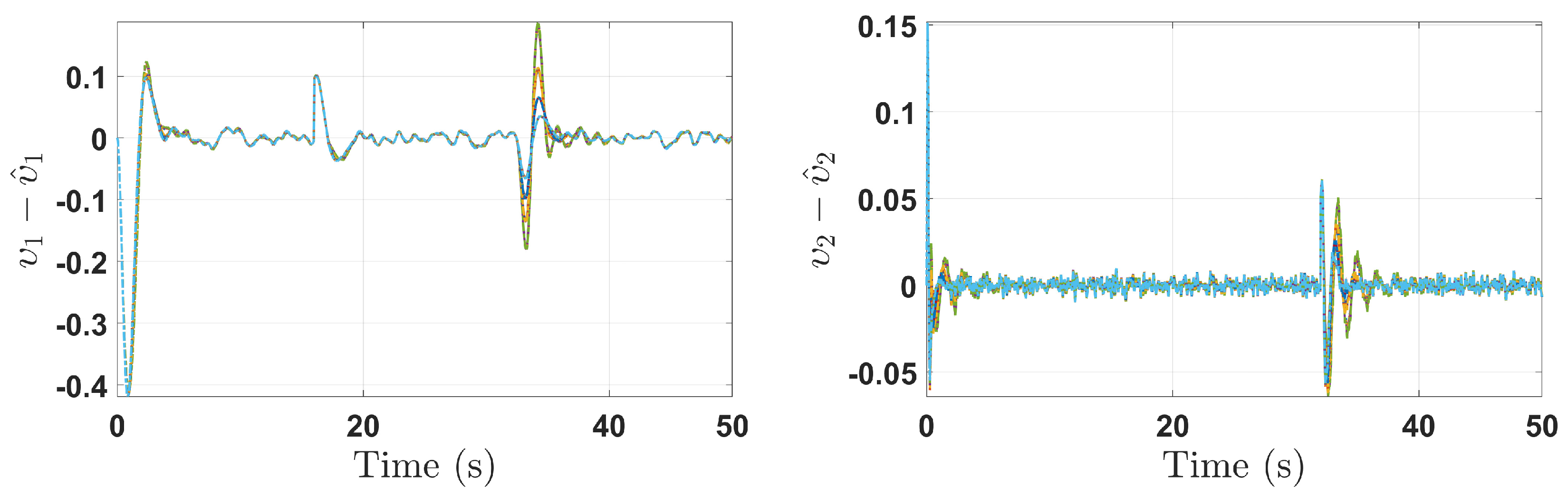
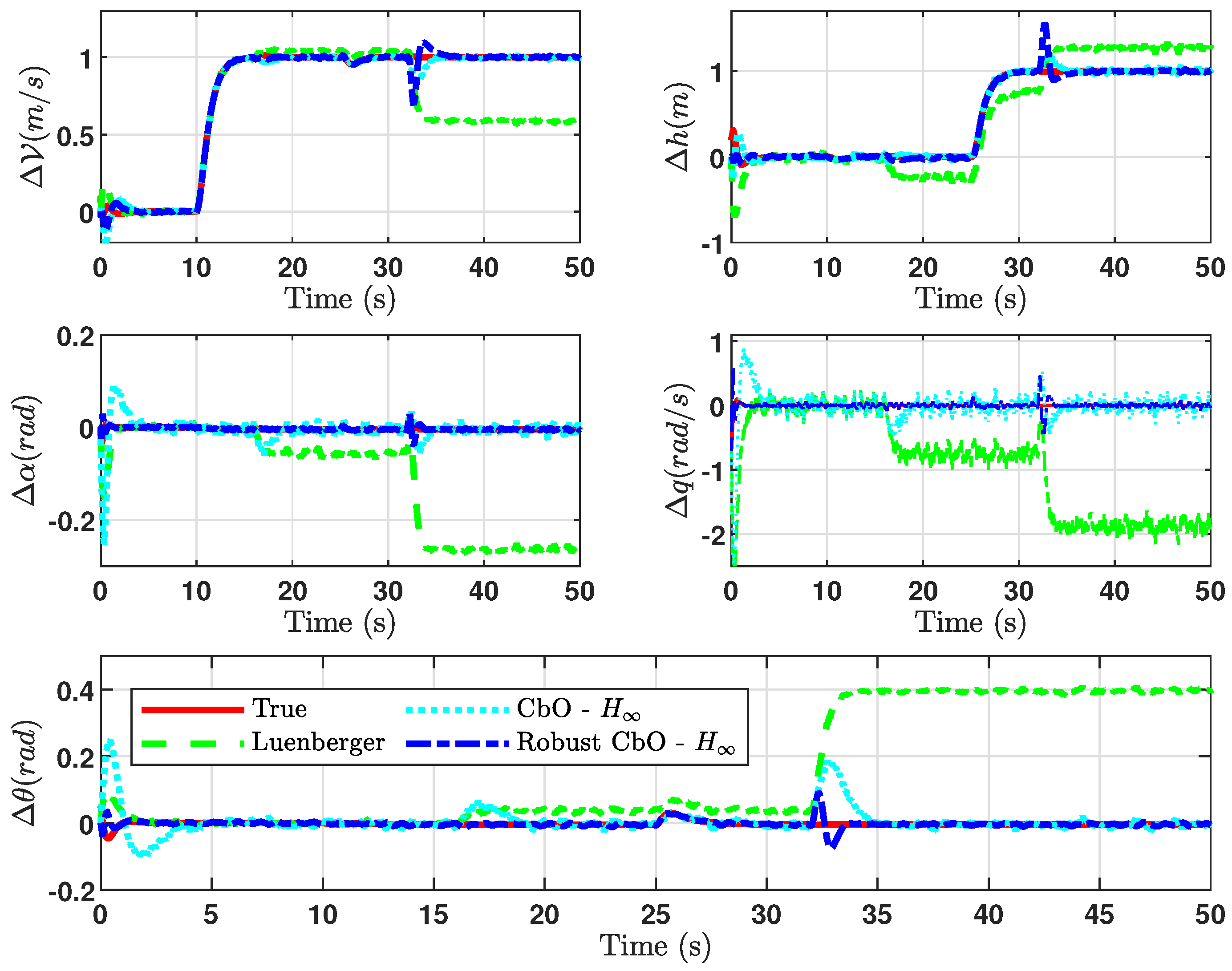
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gunes, U.; Sel, A.; Kasnakoglu, C. Stabilizer Autopilot Design For Fixed Wing UAV Using ODSMC. In Proceedings of the International Conference on System Theory, Control and Computing, Sinaia, Romania, 10–12 October 2018; pp. 740–746. [Google Scholar] [CrossRef]
- Sel, A.; Gunes, U.; Kasnakoglu, C. Output Feedback Discrete SMC Design For Quadratic Buck DC-DC Converter. In Proceedings of the 2018 22nd International Conference on System Theory, Control and Computing, Sinaia, Romania, 10–12 October 2018; pp. 728–733. [Google Scholar] [CrossRef]
- Sel, A.; Sel, B.; Coskun, U.; Kasnakoglu, C. SOS–Based Nonlinear Observer Design for Simultaneous State and Disturbance Estimation Designed for a PMSM Model. Sustainability 2022, 14, 10650. [Google Scholar] [CrossRef]
- Popescu, A.; Besancon, G.; Voda, A. A new robust observer approach for unknown input and state estimation. In Proceedings of the IEEE 2018 European Control Conference (ECC), Limassol, Cyprus, 12–15 June 2018; pp. 1607–1612. [Google Scholar]
- Besançon, G.; Munteanu, I. Control strategy for state and input observer design. Syst. Control Lett. 2015, 85, 118–122. [Google Scholar] [CrossRef]
- Kim, H.J.; Kim, J.Y.; Kim, J.W.; Kim, S.K.; Na, W.S. Unmanned Aerial Vehicle-Based Automated Path Generation of Rollers for Smart Construction. Electronics 2023, 13, 138. [Google Scholar] [CrossRef]
- Feng, J.; Sun, C.; Zhang, J.; Du, Y.; Liu, Z.; Ding, Y. A UAV Path Planning Method in Three-Dimensional Space Based on a Hybrid Gray Wolf Optimization Algorithm. Electronics 2023, 13, 68. [Google Scholar] [CrossRef]
- Peng, H.; Liang, M.; Yuan, C.; Ma, Y. EDF-YOLOv5: An Improved Algorithm for Power Transmission Line Defect Detection Based on YOLOv5. Electronics 2023, 13, 148. [Google Scholar] [CrossRef]
- Imran, I.H.; Wood, K.; Montazeri, A. Adaptive Control of Unmanned Aerial Vehicles with Varying Payload and Full Parametric Uncertainties. Electronics 2024, 13, 347. [Google Scholar] [CrossRef]
- Guerra, T.; Márquez, R.; Kruszewski, A.; Bernal, M. H∞ LMI-Based Observer Design for Nonlinear Systems via Takagi–Sugeno Models with Unmeasured Premise Variables. IEEE Trans. Fuzzy Syst. 2018, 26, 1498–1509. [Google Scholar] [CrossRef]
- López-Estrada, F.; de León, H.H.; Estrada-Manzo, V.; Bernal, M. LMI-based fault detection and isolation of nonlinear descriptor systems. In Proceedings of the IEEE International Conference on Fuzzy Systems, Naples, Italy, 9–12 July 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Popescu, A.; Besancon, G.; Voda, A. Comparison between different control strategies for estimation purposes using Control-based Observer paradigm. In Proceedings of the International Conference on System Theory, Control and Computing, Sinaia, Romania, 10–12 October 2018; pp. 135–140. [Google Scholar] [CrossRef]
- Robles, R.; Sala, A.; Bernal, M.; González, T. Subspace-Based Takagi–Sugeno Modeling for Improved LMI Performance. IEEE Trans. Fuzzy Syst. 2017, 25, 754–767. [Google Scholar] [CrossRef]
- Tsukamoto, H.; Chung, S.; Slotine, J. Neural Stochastic Contraction Metrics for Learning-Based Control and Estimation. IEEE Control Syst. Lett. 2021, 5, 1825–1830. [Google Scholar] [CrossRef]
- Duan, G.; Yu, H. LMIs in Control Systems; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar] [CrossRef]
- Boyd, S.; Ghaoui, L.; Feron, E.; Balakrishnan, V. Linear Matrix Inequalities in System and Control Theory; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1994. [Google Scholar] [CrossRef]
- Miklosovic, R.; Radke, A.; Gao, Z. Discrete implementation and generalization of the extended state observer. In Proceedings of the IEEE 2006 American Control Conference, Minneapolis, MN, USA, 14–16 June 2006; p. 6. [Google Scholar]
- Dong, X. Proportional Integral Observer (PIO) Design for Linear Control Systems. Master’s Thesis, University of Rhode Island, Kingston, RI, USA, 2016. [Google Scholar]
- Della Rossa, M.; Tanwani, A.; Zaccarian, L. Max–min Lyapunov functions for switched systems and related differential inclusions. Automatica 2020, 120, 109123. [Google Scholar] [CrossRef]
- Kurkcu, B.; Kasnakoglu, C.; Efe, M. Disturbance/Uncertainty Estimator Based Integral Sliding-Mode Control. IEEE Trans. Autom. Control 2018, 63, 3940–3947. [Google Scholar] [CrossRef]
- Khattar, V.; Ding, Y.; Sel, B.; Lavaei, J.; Jin, M. A CMDP-within-online framework for Meta-Safe Reinforcement Learning. In Proceedings of the International Conference on Learning Representations (ICLR) 2023, Kigali, Rwanda, 1–5 May 2023. [Google Scholar] [CrossRef]
- Madhukar, P.; Prasad, L. State Estimation using Extended Kalman Filter and Unscented Kalman Filter. In Proceedings of the IEEE 2020 International Conference on Emerging Trends in Communication, Control and Computing (ICONC3), Lakshmangarh, India, 21–22 February 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Wei, X.; Rey, W.; Liu, X. Substation Inspection Robot Location Method Based on Improved Particle Filter. In Proceedings of the IEEE 2024 7th International Conference on Intelligent Robotics and Control Engineering (IRCE), Xi’an, China, 7–9 August 2024; pp. 77–82. [Google Scholar] [CrossRef]
- Niu, H.; Ma, Z.; Huang, J.; Lin, G. Ultra-Local Model-Free Predictive Current Control for PMLSM drive systems with Moving Horizon Estimator. In Proceedings of the 2022 IEEE Transportation Electrification Conference and Expo, Asia-Pacific (ITEC Asia-Pacific), Haining, China, 28–31 October 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Coskun, U.; Sel, B.; Plaster, B. Magnetic field mapping of inaccessible regions using physics-informed neural networks. Sci. Rep. 2022, 12, 12858. [Google Scholar] [CrossRef]
- Stengel, R. Flight Dynamics; Princeton University Press: Princeton, NJ, USA, 2022. [Google Scholar] [CrossRef]
- Stevens, B.; Lewis, F.; Johnson, E. Aircraft Control and Simulation: Dynamics, Controls Design, and Autonomous Systems; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar] [CrossRef]
- Etkin, B.; Reid, L. Dynamics of Flight: Stability and Control, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 1996. [Google Scholar] [CrossRef]
- Nelson, R. Flight Stability and Automatic Control, 2nd ed.; McGraw–Hill: Columbus, OH, USA, 1998. [Google Scholar] [CrossRef]
- Cook, M. Flight Dynamics Principles: A Linear Systems Approach to Aircraft Stability and Control, 3rd ed.; Butterworth–Heinemann: Oxford, UK, 2013. [Google Scholar] [CrossRef]
- Abzug, M.; Larrabee, E. Airplane Stability and Control: A History of the Technologies that Made Aviation Possible, 2nd ed.; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar] [CrossRef]
- Phillips, W. Mechanics of Flight, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar] [CrossRef]
- Boyd, S.; Barratt, C. Linear Controller Design: Limits of Performance; Prentice Hall: Hoboken, NJ, USA, 1991. [Google Scholar] [CrossRef]
- Basar, T.; Bernhard, P. H∞-Optimal Control and Related Minimax Design Problems: A Dynamic Game Approach, 2nd ed.; Birkhäuser Boston: Cambridge, MA, USA, 2008. [Google Scholar] [CrossRef]
- Chen, B. Robust and H∞ Control; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar] [CrossRef]
- Green, M.; Limebeer, D. Linear Robust Control; Dover Publications: Garden City, NY, USA, 2013. [Google Scholar]
- Nasihati, F.; Kiani, M.; Pourtakdoust, S. Satellite pose estimation using Earth radiation modeled by artificial neural networks. Adv. Space Res. 2022, 70, 2195–2207. [Google Scholar] [CrossRef]
- Pourtakdoust, S.; Mehrjardi, M.; Hajkarim, M.; Nasihati, F. Advanced fault detection and diagnosis in spacecraft attitude control systems: Current state and challenges. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2023, 237, 2679–2699. [Google Scholar] [CrossRef]
- Nasihati, F.; Kiani, M.; Pourtakdoust, S. Autonomous temperature-based orbit estimation. Aerosp. Sci. Technol. 2019, 86, 671–682. [Google Scholar] [CrossRef]
- Nasihati, F.; Kiani, M.; Pourtakdoust, S. On-line orbit and albedo estimation using a strong tracking algorithm via satellite surface temperature data. IEEE Trans. Aerosp. Electron. Syst. 2020, 57, 1443–1454. [Google Scholar] [CrossRef]
- Zhou, K.; Doyle, J.; Glover, K. Robust and Optimal Control; Prentice Halll: Hoboken, NJ, USA, 1995. [Google Scholar]
- Tawaha, A.; Kaushik, H.; Sel, B.; Jia, R.; Jin, M. Decision-Focused Learning for Inverse Noncooperative Games: Generalization Bounds and Convergence Analysis. IFAC-PapersOnLine 2023, 56, 9336–9341. [Google Scholar] [CrossRef]
- Sel, B.; Tawaha, A.; Ding, Y.; Jia, R.; Ji, B.; Lavaei, J.; Jin, M. Learning-to-Learn to Guide Random Search: Derivative-Free Meta Blackbox Optimization on Manifold. In Proceedings of the The 5th Annual Learning for Dynamics and Control Conference, PMLR (Proceedings of Machine Learning Research), Philadelphia, PA, USA, 15–16 June 2023; Matni, N., Morari, M., Pappas, G.J., Eds.; Volume 211, pp. 38–50. [Google Scholar]
- Jin, M.; Khattar, V.; Kaushik, H.; Sel, B.; Jia, R. On Solution Functions of Optimization: Universal Approximation and Covering Number Bounds. Proc. AAAI Conf. Artif. Intell. 2023, 37, 8123–8131. [Google Scholar] [CrossRef]
- Gu, S.; Sel, B.; Ding, Y.; Wang, L.; Lin, Q.; Jin, M.; Knoll, A. Balance Reward and Safety Optimization for Safe Reinforcement Learning: A Perspective of Gradient Manipulation. Proc. AAAI Conf. Artif. Intell. 2024, 38, 21099–21106. [Google Scholar] [CrossRef]
- Gu, S.; Sel, B.; Ding, Y.; Wang, L.; Lin, Q.; Knoll, A.; Jin, M. Safe and Balanced: A Framework for Constrained Multi-Objective Reinforcement Learning. IEEE Trans. Pattern Anal. Mach. Intell. 2025, 47, 3322–3331. [Google Scholar] [CrossRef] [PubMed]
- Jin, M.; Sel, B.; Hardeep, F.; Yin, W. Democratizing Energy Management with LLM-Assisted Optimization Autoformalism. In In Proceedings of the 2024 IEEE International Conference on Communications, Control, and Computing Technologies for Smart Grids (SmartGridComm), Oslo, Norway, 17–20 September 2024; pp. 258–263. [Google Scholar] [CrossRef]
- Duan, G. Generalized Sylvester Equations; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar] [CrossRef]
- Duan, G. Analysis and Design of Descriptor Linear Systems, 2010 ed.; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar] [CrossRef]
- Khalil, H. Nonlinear Control, 1st ed.; Pearson Education: Hoboken, NJ, USA, 2015. [Google Scholar]
- Khalil, H. Control Systems: An Introduction; Michigan Publishing Services: Ann Arbor, MI, USA, 2023. [Google Scholar] [CrossRef]
- Durham, W. Aircraft Flight Dynamics and Control, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Gunes, U.; Sel, A.; Kasnakoglu, C.; Kaynak, U. Output Feedback Sliding Mode Control of a Fixed-Wing UAV Under Rudder Loss. In Proceedings of the AIAA SCITECH Forum. American Institute of Aeronautics and Astronautics, San Diego, CA, USA, 7–11 January 2019. [Google Scholar] [CrossRef]
- Gunes, U.; Sel, A.; Sel, B.; Kasnakoglu, C. Dynamic Modeling and Trajectory Tracking of a Quadcopter via Linear and Backstepping Controller. In Proceedings of the AIAA SCITECH Forum. American Institute of Aeronautics and Astronautics, National Harbor, MD, USA/Online, 23–27 January 2023. [Google Scholar] [CrossRef]
- Khalil, H. High-Gain Observers in Nonlinear Feedback Control; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2017; Volume 31. [Google Scholar] [CrossRef]
- Bayrak, A.; Kurkcu, B.; Efe, M. A New Adaptive Disturbance/Uncertainty Estimator Based Control Scheme For LTI Systems. IEEE Access 2022, 10, 106849–106858. [Google Scholar] [CrossRef]
- Zipfel, P. Modeling and Simulation of Aerospace Vehicle Dynamics, 3rd ed.; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2014. [Google Scholar]

| Parameter Set | Variable | Value |
|---|---|---|
| Geometry and Mass | [ 0.225 1.477 ] 0.332 [ 0.48 0.2109 0.1083 ] [ 0 0 0 ] 1.39 | |
| Aerodynamic Drag Derivatives | 0.031 0.13 0 0.06 0 | |
| Aerodynamic Y-Force Derivatives | 0 −0.31 −0.037 0.21 0 0.187 | |
| Aerodynamic Lift Derivatives | 0.31 5.143 3.9 0.43 0 | |
| Aerodynamic X-Moment Derivatives | 0 −0.089 −0.47 0.096 −0.178 0.0147 | |
| Aerodynamic Y-Moment Derivatives | −0.015 −0.89 −12.4 −1.28 0 | |
| Aerodynamic Z-Moment Derivatives | 0 0.065 −0.03 −0.099 −0.053 0.0657 |
| Observer Type | () | ||||
|---|---|---|---|---|---|
| Luenberger | |||||
| CbO- | |||||
| Robust CbO- |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gunes, U.; Sel, A.; Sayar, E.; Kasnakoglu, C. Robust Observer Design for the Longitudinal Dynamics of a Fixed-Wing Aircraft. Electronics 2025, 14, 3555. https://doi.org/10.3390/electronics14173555
Gunes U, Sel A, Sayar E, Kasnakoglu C. Robust Observer Design for the Longitudinal Dynamics of a Fixed-Wing Aircraft. Electronics. 2025; 14(17):3555. https://doi.org/10.3390/electronics14173555
Chicago/Turabian StyleGunes, Uygar, Artun Sel, Erdi Sayar, and Cosku Kasnakoglu. 2025. "Robust Observer Design for the Longitudinal Dynamics of a Fixed-Wing Aircraft" Electronics 14, no. 17: 3555. https://doi.org/10.3390/electronics14173555
APA StyleGunes, U., Sel, A., Sayar, E., & Kasnakoglu, C. (2025). Robust Observer Design for the Longitudinal Dynamics of a Fixed-Wing Aircraft. Electronics, 14(17), 3555. https://doi.org/10.3390/electronics14173555






