Abstract
Convolutional neural networks (CNNs) can efficiently extract image features and perform corresponding classification. Typically, the CNN architecture uses the softmax layer to map the extracted features to classification probabilities, and the cost function used for training is the cross-entropy loss. In this paper, we evaluate the influence of a number of representative composite cross-entropy loss functions on the learned feature space at the fully connected layer, when a target classification is introduced into a multi-class classification task. In addition, the accuracy and robustness of CNN models trained with different composite cross-entropy loss functions are investigated. Improved robustness is achieved by changing the loss between the input and the target classification. Preliminary experiments were conducted using ResNet-50 on the Cholec80 dataset for surgical tool recognition. Furthermore, the model trained with the proposed composite cross-entropy loss incorporating another target all-one classification demonstrates a 31% peak improvement in adversarial robustness. Adversarial training with target adversarial samples yields 80% robustness against PGD attack. This investigation shows that the careful choice of the loss function can improve the robustness of CNN models.
1. Introduction
Cross-entropy was initially employed to quantify the degree of asynchronism between two time series [1]. It was also widely adopted as a logistic loss in classification tasks [2]. Numerous variants of cross-entropy and multiscale cross-entropy methods have been introduced in the recent literature [1]. Specifically, in neural network training, the cross-entropy loss is used to compute the error between the predicted outputs and the ground truth following the softmax transformation. However, recent studies suggest that cross-entropy can lead to a poor margin rather than an optimal value, resulting in overlapping class regions and a lack of robustness to adversarial attack [3]. To improve the robustness of models trained with cross-entropy, Mao et al. [2] presented a theoretical analysis of cross-entropy-like loss functions and introduced Smooth Adversarial Comp-sum Loss for improving adversarial robustness. A Reverse Cross-entropy Loss was proposed to encourage the network to better distinguish adversarial samples [4]. Differential training uses a loss function defined based on pairs of points from each class to maximize the margin between classes [3]. Other approaches aim to improve robustness by altering the feature distribution through alternative loss functions. For instance, Gaussian Mixture Loss assumes the learned features to follow a Gaussian Mixture distribution [5]. Mustafa et al. introduced Prototype Conformity Loss to force the features to lie inside a convex polytope [6]. Additionally, Bounded Conformity Loss has been implemented to facilitate better training convergence [7].
In addition to applying adversarial training [8,9] or incorporating alternative forms of loss functions, a neural network can be trained by a series of cross-entropy loss functions. The generated gradients are homological and can be easily fine-tuned through various compositions. Related work on altering the cross-entropy loss can be found in label smoothing [10,11], where the cross-entropy loss uses a soft target instead of 0–1 hard labels. This regularization mechanism prevents the model from being over-confident and less adaptable. However, the generalization ability on adversarial attack was not evaluated. Pang et al. proposed the reverse label vector in the cross-entropy objective [4]. The true label element in the reverse label vector is zero, and other label elements are uniformly distributed. Training to minimize the loss with respect to this reverse label has to negate the final logits before softmax transformation. In this study, we introduced several other target labels, evaluated a series of cross-entropy loss combinations with these new targets, and analyzed their impact on the learned feature space and model robustness. The contributions of the proposed composite cross-entropy loss are summarized as follows:
- We introduce a second-term auxiliary cross-entropy loss for assistance in the objective loss function. For this second cross-entropy loss, a target classification is assigned instead of the ground truth . Three target classifications were tested in our experiments: the false classification label, the all-one label, and the model’s prediction. The impacts of this auxiliary loss on feature distribution and adversarial robustness were investigated.
- We provide an analysis of the influence of the auxiliary cross-entropy loss on the training process. The gradients generated by this auxiliary loss have various forms and impacts on the final solution. Some functions encourage the model to learn a more spread-out structured feature space, while others reduce the distance of features between data points with improved robustness.
- The specific target classes were also integrated in the adversarial training algorithms, and model robustness was improved by training with these target adversarial examples. The target labels used for adversary generation are as follows: the most likely incorrect label, the all-one label, a specific classification, and the model’s prediction (the cross-entropy loss refers to the negative Shannon entropy, which can be interpreted as the KL divergence between the model’s prediction and all-one class). The performances of these target adversarial trained models were evaluated and compared with a non-target adversarial trained model.
2. Method
2.1. Materials
In our experiments, convolutional neural networks were trained to recognize surgical tools, aiming to be deployed in medical applications to improve the efficiency of laparoscopic surgery procedures. The source dataset is the Cholec80 dataset [12]; it contains 80 cholecystectomy videos in which seven kinds of surgical tools are present (see Figure 1). Images containing a single type of surgical tool were extracted to create a derived dataset suitable for the softmax-based single-label classification (see Table 1). In the multi-class classification task, seven types of surgical tools were required to be recognized. Images from the first 40 videos (31,477 images) were used for training, while those from the remaining 40 videos (48,713 images) were reserved for testing. Specifically, images from videos 41 to 45 (7260 images) were designated as an evaluation set to measure the model’s adversarial robustness and feature distribution. The convolutional neural network architecture used for surgical tool recognition was ResNet-50 [13]. ResNet-50 is a popular convolutional neural network used for image classification tasks, and it has four stages of residual convolution blocks, followed by average pooling and a fully connected layer before the softmax activation [13]. Additionally, to explore the generalization and practical applicability of the proposed composite loss, another model architecture—EfficientNet [14]—was employed for an extended experiment. EfficientNet has a baseline network architecture that is finalized by a pooling layer, a fully connected layer, and a softmax layer, with the compound scale method applied to scale it up [14].
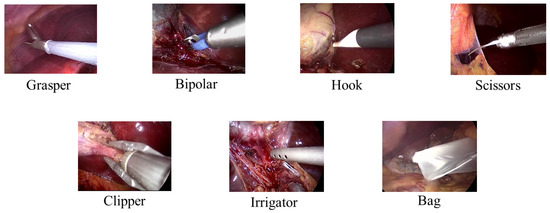
Figure 1.
Seven surgical tools present in the Cholec80 dataset [12].

Table 1.
The class index, corresponding surgical tool, and number of frames in the derived 1-class dataset [15].
2.2. Composite Cross-Entropy Loss
The training process of convolutional neural networks (CNNs) is often difficult to monitor due to their large parameter space, and their optimization process is typically treated as a black box. CNN models usually contain several hidden layers before the final output layer. Such large parameter spaces also produce large feature spaces when images proceed through different stages of the model architecture. Therefore, to simplify the observation of the training process, we focus on the logit layer (i.e., the fully connected layer in ResNet-50) and measure the optimization procedure by observing changes in this particular feature space. Normally, an input image passes through several hidden layers, undergoing a series of filtering operations and nonlinear transformations, and is ultimately represented as a feature vector (logits) after the fully connected layer. These logits are then transformed into probabilities via the softmax function. Finally, the probabilities are compared with the ground truth using the cross-entropy loss function (see Equation (1)). Assuming classes in a classification problem, is a binary vector of length (, , denoting the one-hot-encoded ground truth of class (), for the input . then represents an -valued vector with the predicted class probabilities for input .
For the model using softmax activation to map the logits, when backpropagating the cross-entropy loss through the logit layer, the error of the feature is equal to the difference between prediction and [16]. The errors are then backpropagated through the entire neural network to update the parameter space . As a result, after each training iteration, the prediction probabilities for the same input shall be closer to the ground truth, and the feature for shall have synchronized change according to the optimized parameter space.
Instead of training the neural network with the standard cross-entropy loss, a composition of multiple cross-entropy losses can be implemented as a new objective loss function. Particularly, denotes a subsequent component of composite cross-entropy loss, and an auxiliary target classification is assigned instead of the ground truth . is a vector with the same size as . A frame of this composite objective function is defined in Equation (2):
Here, denotes the weight assigned to the standard cross-entropy loss, while represents the weight associated with the additional components of the new composite loss function.
The special target classification can take various forms. In this research, three different forms of target classification and corresponding cross-entropy loss are considered:
- : At the beginning of the training process, the model misclassifies a larger proportion of the data. To encourage faster learning from these incorrectly classified samples, the target classification can incorporate the falsely classified label, thereby increasing the loss between the prediction and the misclassification. This target class label can be represented as a conditional vector (see Equation (3)), where is the one-hot-encoded label of the current model classification.Specifically, when an objective function is defined as , the aggregated gradients during backpropagation at the fully connected layer can be expressed in the general form: . When , , where is the current incorrect predicted label, in this case, . The gradient for the incorrect label element becomes +1, and that for the true label element remains −1. The element-wise difference for all other labels is 0.
- : The second special target classification is the all-one class label, where all the elements in the vector are one, denoted as , which can be interpreted as a random-directed adversarial label. Model robustness is enhanced by reducing the loss between the prediction and this all-one target. In adversarial training, the process involves first increasing the loss associated with the correct label (or decreasing the loss for an incorrect label) to generate adversaries, followed by training the model to correctly classify these adversaries by minimizing the loss with respect to the true label [8]. Reducing the loss for the all-one class simply resembles the process of target adversary generation. However, since the parameter space is optimized simultaneously by the separate components of the composite loss, the learning process from the “adversaries” must remain dominated by the standard cross-entropy. Therefore, the weight assigned to the cross-entropy with respect to the all-one class should be smaller than that of the standard cross-entropy to avoid destabilizing the training process.
- Another special target classification is the model’s prediction . The cross-entropy of the original prediction is also known as Shannon entropy [17]. Shannon entropy can be described in an alternative form, which also defines the Kullback–Leibler (KL) divergence between the prediction and the all-one classification (see Equation (4)):
2.3. Categories of Composite Cross-Entropy Loss
To simplify the analysis of the training process when using a composition of cross-entropy losses, particularly regarding its effects on the feature space and robustness to adversaries, we focus specifically on the optimization procedure at the fully connected layer. At each training iteration, the model first makes a prediction for the input, after which the loss is backpropagated to update the parameter space. The initial stage of this backpropagation occurs through the fully connected layer, followed by propagation through the shallower layers of the model architecture for further optimization.
With varying auxiliary target classifications and weight assignments, our experiments employ different loss function configurations as summarized in Table 2. In this table, is the standard cross-entropy, corresponds to the cross-entropy loss involving the false class (see Equation (3)), represents the cross-entropy loss of the all-one class, and refers to the Shannon entropy. Several different weights were assigned to the components of the composite cross-entropy. Particularly, functions 3 and 4 introduce the false label into the subsequent component, aiming to increase the loss associated with the model’s misclassification to improve accuracy. Functions 5 to 6 incorporate the all-one class target for robustness improvement. Moreover, the Shannon entropy produces a distinct type of gradient, with its impact via KL divergence on the all-one class evaluated in functions 7 and 8.

Table 2.
Composite cross-entropy objective functions and their backpropagated gradients. is standard cross-entropy, corresponds to cross-entropy loss involving the false class (see Equation (3)), represents the cross-entropy loss of the all-one class, and refers to the Shannon entropy.
2.4. Target Adversarial Training
Adversarial training typically involves incorporating adversarial examples—generated by various adversarial techniques—into the training process, enabling the model to improve robustness against these adversarial attacks. Most existing algorithms adopt non-targeted adversarial generation methods, such as Projected Gradient Descent (PGD) (see Equation (7)), which increases the loss of the input and its corresponding correct label in a multi-step form to produce a powerful adversary. However, the adversary can be generated by reducing the loss to designated target classes. For instance, the target label can be explicitly assigned as a specific class among the classes or as the most likely incorrect label; moreover, the all-one class represents a random-directed target label, and indicates the KL divergence between the model’s prediction and the all-one target. These designated classification targets were employed to generate adversaries for adversarial training. The target adversary generation process is defined in Equation (5):
Here, denotes the clean sample, represents the adversarial sample generated at the iteration, is the designated target, is the cross-entropy loss between the model prediction and the target , and is the step size at the iteration. can be a constant value during iterations, which is the same as in the Iterative Fast Gradient Sign Method (i-FGSM) [18], or adaptive to the loss among the iterations to acquire fewer perturbations—the step-adaptive Iterative Fast Gradient Sign Method (S-a-i-FGSM) [8,15].
2.5. Evaluation Metrics
To quantify changes in the feature space, we measured the variation in classification area size by computing two metrics: the mean Euclidean distance from individual image features to their respective class center , as well as the mean Euclidean distance between a class center and the centers of all other classes (see Equation (6)). In Equation (6), denotes the feature vector of an image, and and represent the feature centers of class and class , respectively. is the number of images in class , and is the number of classes.
Additionally, we aimed to assess the impact on adversarial robustness when the model was trained to produce either a sparser or more compact feature distribution on the same dataset. The model’s robustness was assessed through the widely used Projected Gradient Descent (PGD) adversarial attack method [19]. PGD is a multi-step adversary generation algorithm which can create strong adversarial attacks (see Equation (7)) [19]:
3. Results
We evaluated the influence on adversarial robustness when ResNet-50 was trained using composite cross-entropy loss functions. Table 3 presents the model’s robustness against PGD attacks, with the attack strength set to . Additionally, the class distribution in the learned feature space was analyzed using the Euclidean distance, which quantifies the spread and separation of the learned features.

Table 3.
The adversarial robustness and accuracy of ResNet-50 models trained with different cross-entropy loss functions were evaluated. The results were calculated as the mean value over 10 epochs. At the 10th epoch, the inter-class distance and intra-class distance were measured to characterize the structure of the learned feature space. Function index 0 was trained using a constant learning rate of 0.001, while the other functions were trained with an iteratively decaying learning rate schedule.
Models trained with the composite cross-entropy loss demonstrated increased robustness to adversarial attacks; however, this improvement in robustness was accompanied by a slight decrease in test set accuracy for most configurations. Training with a combination of false classification targets did not improve accuracy on the test set.
Meanwhile, training with the all-one class entropy reduced the distance between data points in the feature space while still enhancing robustness against PGD attacks. However, there are variations in robustness in the test set when the algorithm is run a second time (see Table 3), even though the robustness of the training set approximates 50% during training using functions (5) and (6). Increasing Shannon entropy (7)—equivalently, reducing the KL divergence to the all-one class—produced a comparable effect, promoting tighter clustering of features while improving adversarial robustness. A contrary effect was observed when minimizing Shannon entropy (8): as the KL divergence to the all-one class space was increased, the learned feature space became even sparser.
The same experiment was conducted using EfficientNet [14]. For comparison, we chose function (6) and function (7), which demonstrated higher robustness in the results (see Table 3), to train EfficientNet. Table 4 shows the results of EfficientNet. Similarly to the results of ResNet-50, robustness was enhanced by these two functions, while the feature distance between data points was reduced. However, the general performance of EfficientNet is worse than ResNet-50.

Table 4.
The adversarial robustness and accuracy of EfficientNet models trained with different cross-entropy loss functions were evaluated. The results were calculated as the mean value over 10 epochs. At the 10th epoch, the inter-class distance and intra-class distance were measured to characterize the structure of the learned feature space. The functions were trained with an iteratively decaying learning rate schedule.
3.1. Sparser Feature Distribution
As shown in Figure 2, a continuous increase in both intra-class and inter-class distances within the training-set feature space is observed. The learned feature spaces are noticeably sparser compared to when using standard cross-entropy with a constant learning rate. The two types of learning rate used for training—constant and iteratively decaying—led to different outcomes when applied to standard cross-entropy. In particular, the composition incorporating Shannon entropy achieved the highest intra-class and inter-class distances; this composite cross-entropy loss function encourages further optimization and promotes a more separable and structured feature distribution.
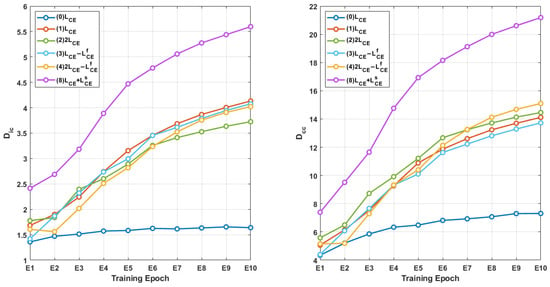
Figure 2.
The mean intra-class distance and mean inter-class distance of the training-set features show that the models trained with the Shannon entropy exhibit larger feature distances compared to those trained with standard cross-entropy.
3.2. Incorporation into Adversarial Training
We investigate the incorporation of an auxiliary loss component into adversarial training, specifically the false classification loss (see Equation (3)), to encourage the model to better distinguish adversarial examples. Additionally, the auxiliary false classification loss was also applied in the clean data training. The adversarial training algorithm used in this experiment was introduced in our previous work [8], which employed a step-adaptive i-FGSM function (S-a-i-FGSM (2)) to generate borderline adversarial examples, and this method has been proved to outperform common PGD training [8]. Table 5 presents the results of incorporating the false classification loss into the adversarial training loss functions. In this table, and denote the standard cross-entropy losses on clean data and adversarial data, respectively, while and indicate the corresponding losses using the false class target. With this additional target, the model’s robustness against PGD attack improved compared to using standard cross-entropy only (see Table 5). However, the accuracy was reduced, and the feature distribution became more compact.

Table 5.
The mean robustness and accuracy of ResNet-50 with borderline training algorithms using a step-adaptive i-FGSM function (S-a-i-FGSM (2)) ( = 2). The feature distribution was measured by inter-class distance and intra-class distance .
In the above experiments, the adversarial examples are generated by increasing the loss associated with the correct label. In the following experiments, we used the target classification for adversary generation, and the generation process was accomplished by minimizing the loss with respect to these designated target classes. In particular, the all-one class and the Shannon entropy, which are shown to be effective in enhancing model robustness, were utilized in adversarial training. The third target class employed was the label with the highest predicted probability, except for the correct label (i.e., the most likely incorrect label or the nearest misclassification label); but if the image was misclassified, the target class was set to . In addition, a specific class can be assigned as the target, guiding the generated adversary to produce features oriented toward this particular class. This approach is useful for analyzing the effect of adversarial training on feature distribution. A comparison of the efficiency of increasing adversarial loss across various adversarial generation algorithms is provided in Appendix A.
Table 6 shows the results of adversarial-trained ResNet-50 using target classification for adversary generation. denotes the nearest misclassification label, and and represent the label for class 3 and class 4, respectively. Compared to the non-target adversarial training (see Table 5), most algorithms in target adversarial training exhibit lower robustness against PGD attack, and overall accuracy also declines. Particularly, when the specific classes (e.g., and ) are used as target labels for adversary generation, the model tends to overfit to these classes; thus, both its accuracy and robustness are inferior to other algorithms. Nevertheless, the feature activations generated by these adversarial samples may encourage the model to learn a sparser feature distribution.

Table 6.
The mean robustness and accuracy of ResNet-50 with borderline training algorithms using different target misclassifications ( = 2). The feature distribution was measured by inter-class distance and intra-class distance .
4. Discussion
When training ResNet-50, although the models learned sparser feature spaces on both the training and test sets, and the softmax-transformed probabilities of some samples were closer to the ground truth, the training error on the entire training set was higher than with the standard cross-entropy loss (see Figure 3). This suggests that the new form of backpropagated gradients has altered the parameter space optimization process, influencing not only the anterior feature distribution but also the posterior probability distribution.
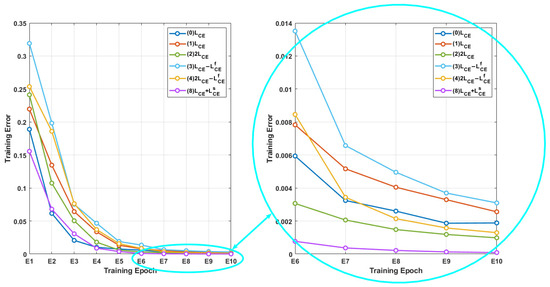
Figure 3.
The error on the entire training set at different training epochs is shown. At earlier stages of training, the models trained with composite cross-entropy have larger errors than the model trained with standard cross-entropy. The error of the model trained with becomes the smallest after the 5th epoch (right).
If we calculate the cross-entropy error for each class, the training error shows differences between classes. Figure 4 illustrates the cross-entropy error of each class when ResNet-50 is trained at the 10th epoch. From Figure 4 (left), a significant difference in cross-entropy can be observed for scissors (class 4). In general, the models exhibit larger training errors on weaker classes (e.g., scissors and bag), indicating that the training is affected by the imbalanced dataset problem. However, the correlation between different label elements in the backpropagated error remains unknown, and how they influence the parameter optimization process is difficult to monitor.
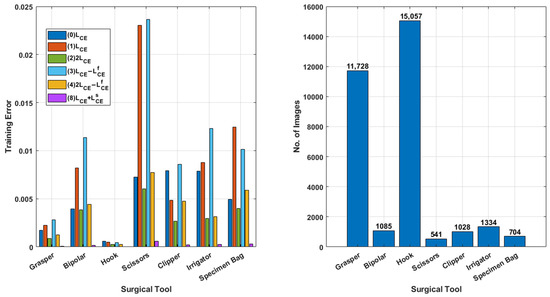
Figure 4.
The error for each class (surgical tool) in the training set at the 10th epoch (left). The number of images for each class (surgical tool) in the training set (right).
4.1. Trade-Off in Robustness and Feature Distribution
Although some composite cross-entropy losses can enhance model robustness by encouraging the model to learn a more spread-out feature distribution, others that exhibit higher robustness result in a more compact feature space. Take the all-one class loss and negative Shannon entropy as examples, which are denoted as functions (5, 6) and function (7) in Table 3; both intra-class and inter-class distances are notably smaller than other compositions. Meanwhile, the accuracy, which is typically noted as a trade-off factor with robustness, has no significant difference from the result from standard training. Figure 5 illustrates the feature distances of the entire training set across different training epochs. These distances are much smaller than the functions shown in Figure 2. In addition, intra-class distances are reduced rather than increased as training advances. The training errors are larger than those shown in Figure 3, though there are minor differences in accuracy. Particularly, unlike adversarial training, which involves training with additional features generated by adversarial examples, the composite cross-entropy only trained with the features generated by clean samples. The auxiliary term, such as the all-one class loss, introduces negative errors in the incorrect label elements in the backpropagated gradients (see Table 2), which have a significant influence on the feature evolution during training.
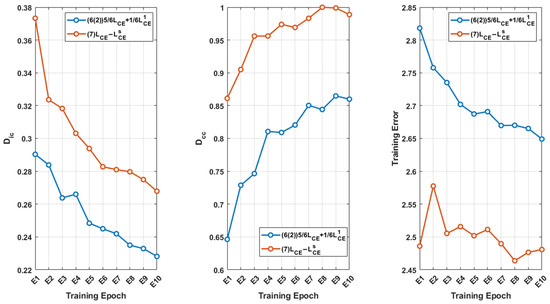
Figure 5.
The mean intra-class distance and mean inter-class distance of the training set features, and the training errors of the model trained with the all-one class and negative Shannon entropy. Compared to the standard trained model, the feature distances are smaller and the training errors are larger.
4.2. Limitations
The composition of the objective function and the weights assigned to the components have a significant impact on model performance. Specifically, they have a direct influence on the direction and size of gradients generated to optimize the model parameters. For example, if the objective function contains a component that aims to increase the loss for the all-one class entropy, even a small weight assigned to this component can crash the training process. But this phenomenon does not arise when increasing the KL divergence to the all-one class using the Shannon entropy (i.e., function (8)).
Similarly, the additional target classification can be defined using different vector representations, so that the objective function has alternative compositions. For example, the all-one class auxiliary target can be replaced by the nearest misclassification label (i.e., the label element with maximum probability with the exception of the correct label), which closer resembles adversarial training.
Overall, in Table 2, we used a limited number of weights for evaluation. Assigning different weight values could lead to different optimization dynamics and outcomes.
The training procedure using composite cross-entropy loss generally requires a longer time for optimization, as the aggregated gradients are more complicated and demand a higher computational cost.
This experiment was conducted exclusively on the Cholec80 dataset using the ResNet-50 architecture. Future experiments should be performed on other datasets and with additional model architectures to generalize the conclusions.
5. Conclusions
In this research, we introduced several auxiliary target terms into the cross-entropy cost function. Among them, Shannon entropy significantly enhances the separability of the feature space, while the other targets contribute to improved robustness against adversarial attacks. Adversarial training incorporating these auxiliary targets demonstrates a comparable effect in enhancing robustness. However, the optimization procedure using the composite cross-entropy requires further exploration in the future.
Author Contributions
Conceptualization, N.D.; methodology, N.D.; software, N.D.; validation, N.D.; formal analysis, N.D.; investigation, N.D.; resources, K.M.; data curation, N.D.; writing—original draft preparation, N.D.; writing—review and editing, N.D. and K.M.; visualization, N.D.; supervision, K.M.; project administration, K.M.; funding acquisition, K.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by the German Federal Ministry of Research and Education (BMBF) under grants CoHMed/PersonaMed A/B FKZ 13FH5I06IA, 13FH5I09IA, and DIAKat+ FKZ 13FH066KX2, the European Commission under grant DCPM #872488, and DAAD Grant AIDE-ASD FKZ 57656657.
Data Availability Statement
The database used in this study is Cholec80. The Cholec80 dataset is available from the respective publisher upon request (http://camma.u-strasbg.fr/datasets/ (accessed on 22 March 2017)).
Conflicts of Interest
The authors state no conflicts of interest.
Appendix A
Different adversary generation functions have various impacts on the efficiency of increasing adversarial loss, which is related to their effectiveness in identifying and addressing weak points during adversarial training. However, the outcome of adversarial training is also influenced by the properties of features generated by different functions. For instance, various adversarial attacks produce different kinds of adversaries, and the feature activations generated by these adversaries have different deviations from those generated by clean samples, which correspond to the adversary learning part of adversarial training. The attack strength instead affects the magnitude of adversarial loss, associated with the error distribution during adversary learning.
Figure A1 illustrates the adversarial loss for the true label when generating an adversary using target adversarial attack. A steeper slope indicates a faster increase in loss values. Particularly, for the all-one and negative Shannon entropy target classification, the loss of certain images has a drop in later iterations, indicating inconsistencies in gradient direction across iterations. Figure A2 presents the boundary adversarial loss when the images change their classifications. The boundary loss shows slight differences among various adversary generation functions.
In borderline adversarial training, the gradients generated by adversarial samples in the logit layer are given by [8]. Here, is the feature activation of adversary , is the prediction of adversary , and denotes the difference between the model prediction and ground truth .
When using a single class as the target, the adversary induces an increased backpropagated error in the corresponding target class element in (see Figure A3); also, the class-oriented feature activations have a potential influence on parameter optimization. As a result, learning from these class-specific target adversaries may result in overfitting to this particular class, which manifests as reduced model separability and increased possibility of class overlap; the model’s ability in recognizing this particular class is deteriorated, which is reflected in a lower recall metric in the test results.
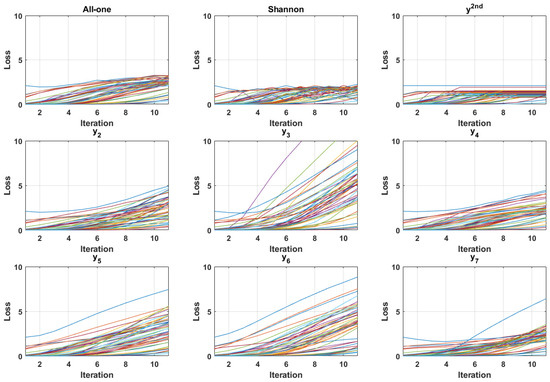
Figure A1.
Adversarial loss of 50 Grasper images (class 1) using various target adversary generation functions. Each line represents one image sample. The adversary was generated over 10 iterations with a constant step size of 0.2. The target classes for adversary generation in order are as follows: all-one, negative Shannon entropy, most likely incorrect label, and classes 2 to 7.
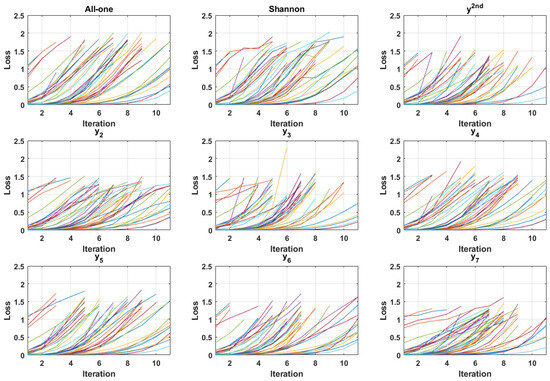
Figure A2.
Adversarial loss at the classification boundary of 50 Grasper images (Class 1) using various target adversary generation functions. Each line represents one image sample. The adversary was generated over 10 iterations with a constant step size of 0.2. The target classes for adversary generation in order are as follows: all-one, negative Shannon entropy, most likely incorrect label, and classes 2 to 7.
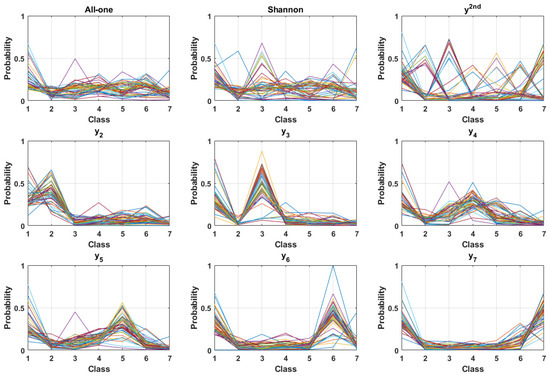
Figure A3.
Probability distribution at the classification boundary for 50 Grasper images (Class 1) using various target adversary generation functions. Each line represents one image sample. The adversary was generated over 10 iterations with a constant step size of 0.2. The target classes for adversary generation in order are as follows: all-one, negative Shannon entropy, most likely incorrect label, and classes 2 to 7.
References
- Jamin, A.; Humeau-Heurtier, A. (Multiscale) Cross-Entropy Methods: A Review. Entropy 2020, 22, 45. [Google Scholar] [CrossRef] [PubMed]
- Mao, A.; Mohri, M.; Zhong, Y. Cross-Entropy Loss Functions: Theoretical Analysis and Applications. In Proceedings of the 40th International Conference on Machine Learning, Honolulu, HI, USA, 23–29 July 2023; pp. 23803–23828. Available online: https://proceedings.mlr.press/v202/mao23b.html (accessed on 18 March 2025).
- Nar, K.; Ocal, O.; Sastry, S.S.; Ramchandran, K. Cross-Entropy Loss Leads To Poor Margins. September 2018. Available online: https://openreview.net/forum?id=ByfbnsA9Km (accessed on 25 March 2025).
- Pang, T.; Du, C.; Dong, Y.; Zhu, J. Towards Robust Detection of Adversarial Examples. arXiv 2018, arXiv:1706.00633. [Google Scholar] [CrossRef]
- Wan, W.; Zhong, Y.; Li, T.; Chen, J. Rethinking Feature Distribution for Loss Functions in Image Classification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake, UT, USA, 18 June 2018; pp. 9117–9126. Available online: https://openaccess.thecvf.com/content_cvpr_2018/html/Wan_Rethinking_Feature_Distribution_CVPR_2018_paper.html (accessed on 25 March 2025).
- Mustafa, A.; Khan, S.; Hayat, M.; Goecke, R.; Shen, J.; Shao, L. Adversarial Defense by Restricting the Hidden Space of Deep Neural Networks. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 3385–3394. Available online: https://openaccess.thecvf.com/content_ICCV_2019/html/Mustafa_Adversarial_Defense_by_Restricting_the_Hidden_Space_of_Deep_Neural_ICCV_2019_paper.html (accessed on 25 March 2025).
- Ding, N.; Arabian, H.; Möller, K. Feature space separation by conformity loss driven training of CNN. IFAC J. Syst. Control. 2024, 28, 100260. [Google Scholar] [CrossRef]
- Ding, N.; Möller, K. Adversarial training with borderline samples. J. Supercomput. 2025, 81, 1025. [Google Scholar] [CrossRef]
- Goodfellow, I.J.; Shlens, J.; Szegedy, C. Explaining and Harnessing Adversarial Examples. arXiv 2015, arXiv:1412.6572. [Google Scholar] [CrossRef]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the Inception Architecture for Computer Vision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 2818–2826. [Google Scholar] [CrossRef]
- Müller, R.; Kornblith, S.; Hinton, G.E. When Does Label Smoothing Help? arXiv 2020, arXiv:1906.02629. [Google Scholar] [CrossRef]
- Twinanda, A.P.; Shehata, S.; Mutter, D.; Marescaux, J.; de Mathelin, M.; Padoy, N. EndoNet: A Deep Architecture for Recognition Tasks on Laparoscopic Videos. IEEE Trans. Med. Imaging 2017, 36, 86–97. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. Available online: https://openaccess.thecvf.com/content_cvpr_2016/html/He_Deep_Residual_Learning_CVPR_2016_paper.html (accessed on 19 March 2025).
- Tan, M.; Le, Q. Rethinking Model Scaling for Convolutional Neural Networks. arXiv 2020, arXiv:1905.11946. [Google Scholar] [CrossRef]
- Ding, N.; Möller, K. Minimally Distorted Adversarial Images with a Step-Adaptive Iterative Fast Gradient Sign Method. AI 2024, 5, 922–937. [Google Scholar] [CrossRef]
- Derivation of the Gradient of the cross-entropy Loss. Available online: https://jmlb.github.io/ml/2017/12/26/Calculate_Gradient_Softmax/ (accessed on 19 March 2025).
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Kurakin, A.; Goodfellow, I.; Bengio, S. Adversarial Machine Learning at Scale. arXiv 2017, arXiv:1611.01236. [Google Scholar] [CrossRef]
- Madry, A.; Makelov, A.; Schmidt, L.; Tsipras, D.; Vladu, A. Towards Deep Learning Models Resistant to Adversarial Attacks. arXiv 2019, arXiv:1706.06083. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).