Impact of Grain Boundaries on Zero-Temperature Coefficient Characteristics in a 3D-Stacked Transistor
Abstract
1. Introduction
2. Device Structure and Simulation Method
3. Results and Discussion
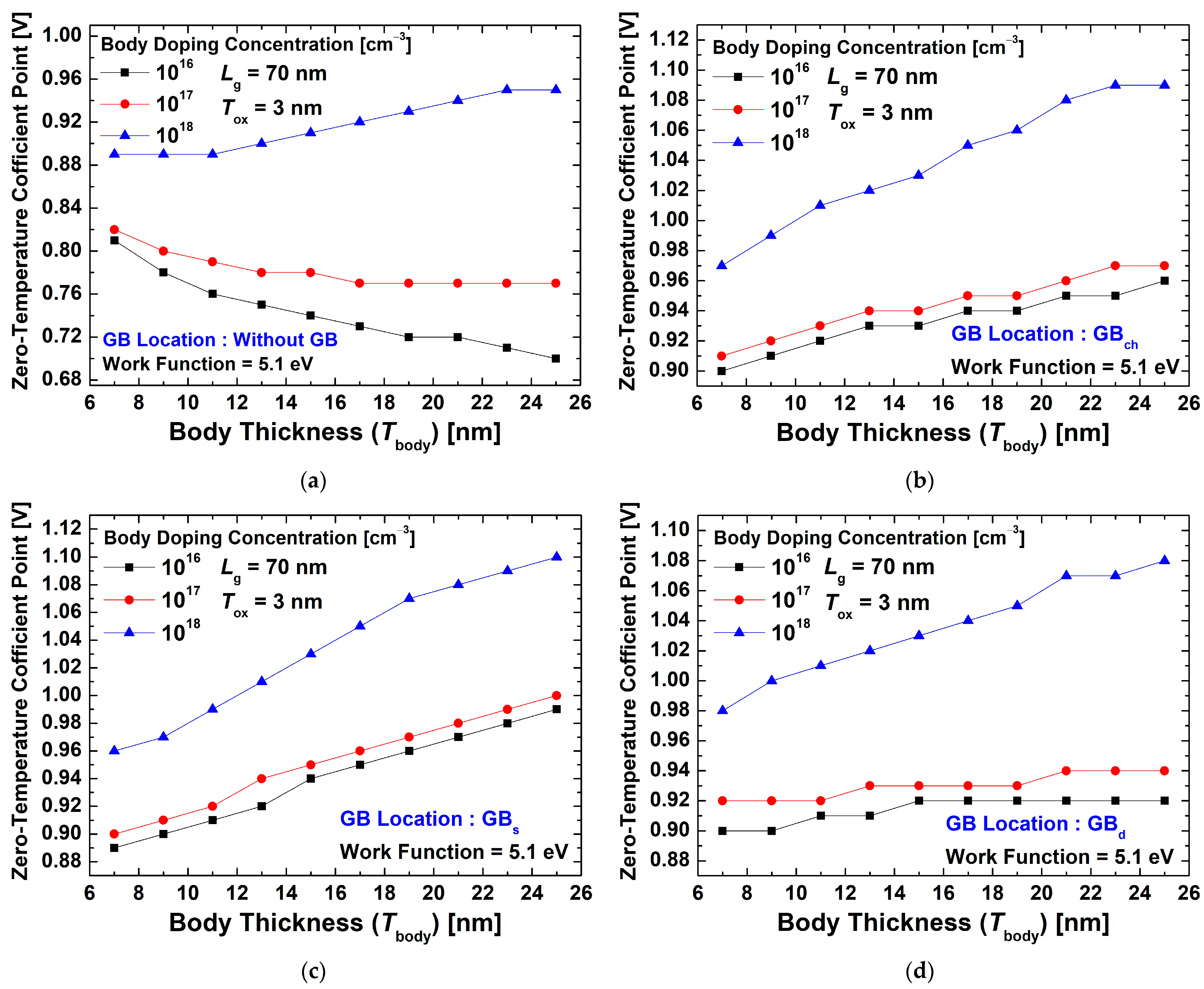
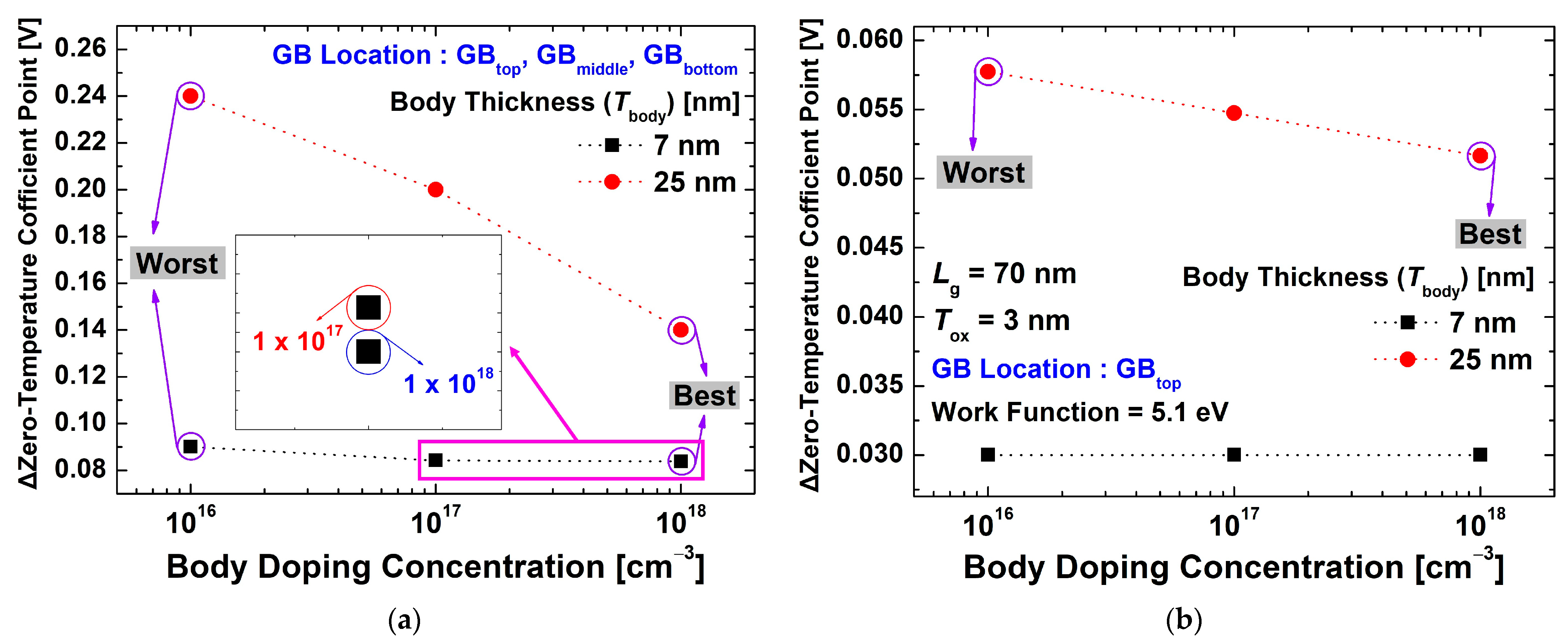
3.1. Characteristics of Single-Layer Device
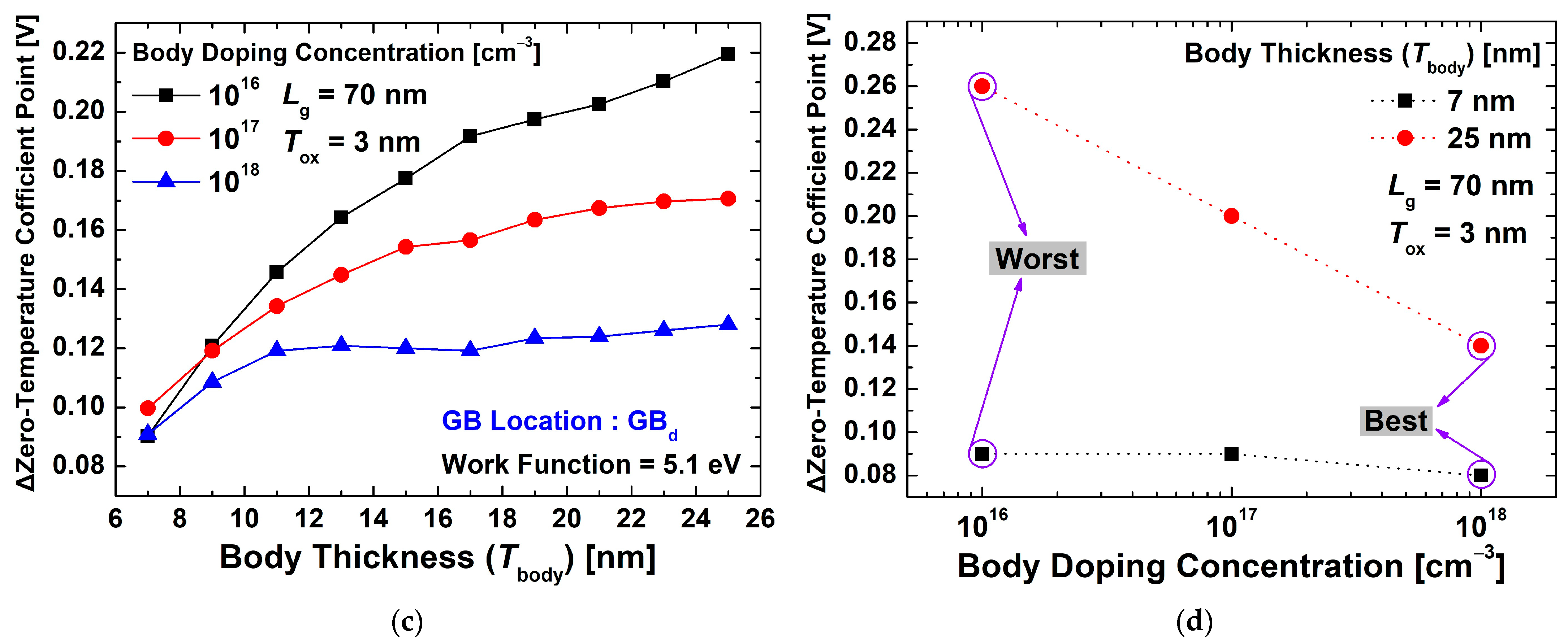
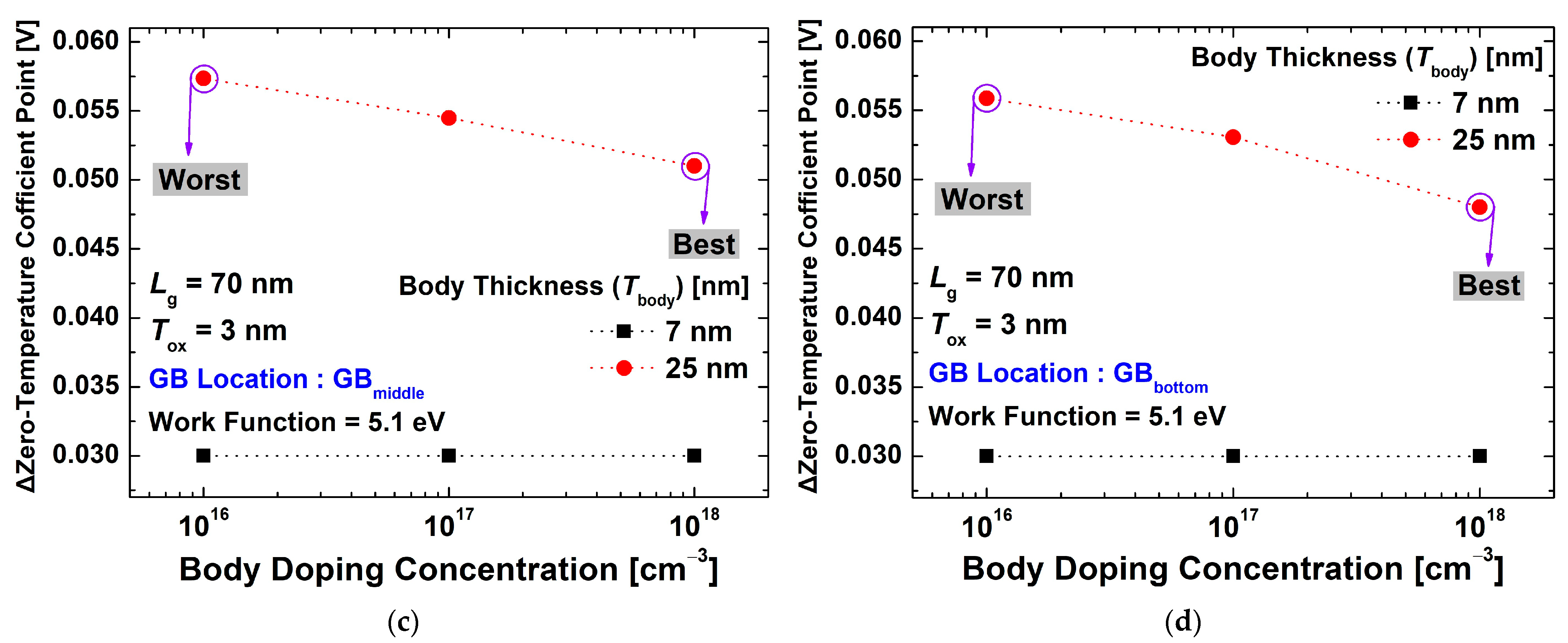
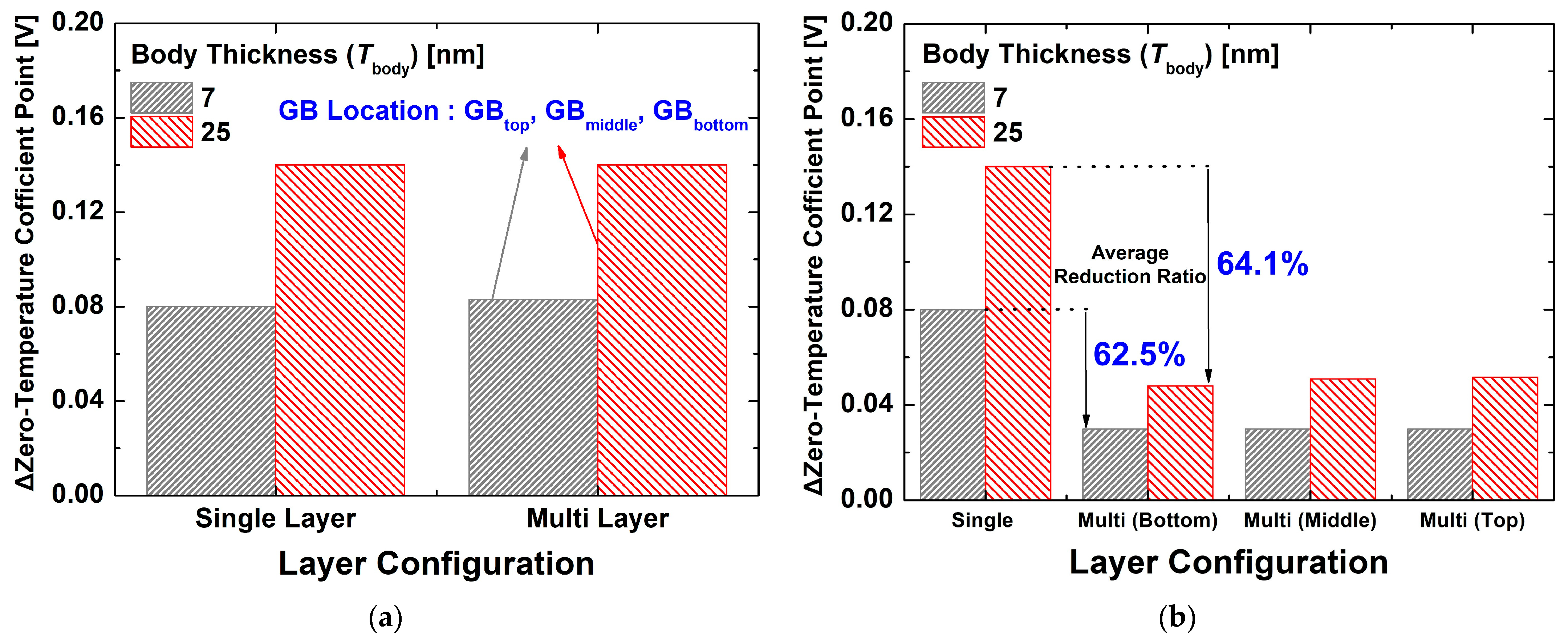
3.2. Characteristics of Multi-Layer Device
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Okhonin, S.; Nagoga, M.; Sallese, J.M.; Fazan, P. A capacitor-less 1T-DRAM cell. IEEE Electron. Device Lett. 2002, 23, 85–87. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Raychowdhury, A.; Roy, K. Accurate estimation of total leakage current in scaled CMOS logic circuits based on compact current modeling. In Proceedings of the 2003 Design Automation Conference (DAC), Anaheim, CA, USA, 2–6 June 2003; pp. 169–174. [Google Scholar] [CrossRef]
- Abbas, Z.; Olivieri, M. Impact of technology scaling on leakage power in nano-scale bulk CMOS digital standard cells. Microelectron. J. 2014, 45, 179–195. [Google Scholar] [CrossRef]
- Seo, J.H.; Yoon, Y.J.; Yu, E.; Sun, W.; Shin, H.; Kang, I.M.; Lee, J.-H.; Cho, S. Fabrication and Characterization of a Thin-Body Poly-Si 1T DRAM with Charge-Trap Effect. IEEE Electron. Device Lett. 2019, 40, 566–569. [Google Scholar] [CrossRef]
- Lee, S.H.; Yoon, Y.J.; Seo, J.H.; Cho, M.S.; Park, J.; An, H.D.; Min, S.R.; Kim, G.U.; Kang, I.M. Effect of Work-function Variation on Transfer Characteristics and Memory Performances for Gate-all-around JLFET based Capacitorless DRAM. J. Semicond. Technol. Sci. 2021, 21, 381–389. [Google Scholar] [CrossRef]
- Bae, J.-H.; Back, J.-W.; Kwon, M.-W.; Seo, J.H.; Yoo, K.; Woo, S.Y.; Park, K.; Park, B.-G.; Lee, J.-H. Characterization of a Capacitorless DRAM cell for Cryogenic Memory Applications. IEEE Electron. Device Lett. 2019, 40, 1614–1617. [Google Scholar] [CrossRef]
- Prijić, Z.D.; Dimitrijev, S.S.; Stojadinović, N.D. The determination of zero temperature coefficient point in CMOS transistors. Microelectron. Reliab. 1992, 32, 769–773. [Google Scholar] [CrossRef]
- Osman, A.A.; Osman, M.A.; Dogan, N.S.; Imam, M.A. Zero-temperature-coefficient biasing point of partially depleted SOI MOSFET’s. IEEE Trans. Electron. Devices 1995, 42, 1709–1711. [Google Scholar] [CrossRef]
- Camillo, L.M.; Martino, J.A.; Simoen, E.; Claeys, C. The temperature mobility degradation influence on the zero temperature coefficient of partially and fully depleted SOI MOSFETs. Microelectron. J. 2006, 37, 952–957. [Google Scholar] [CrossRef]
- Tan, T.H.; Goel, A.K. Zero-temperature-coefficient biasing point of a fully-depleted SOI MOSFET. Microw. Opt. Technol. Lett. 2003, 37, 366–370. [Google Scholar] [CrossRef]
- Kim, K.H.; Kim, K.M.; Kim, Y.H.; Im, J.B.; Choi, G.H.; Kang, I.M.; Yoon, Y.J. Design Optimization of Capacitor-less DRAM using zero-temperature coefficient point. J. Inst. Korean Electr. Electron. Eng. 2024, 28, 369–374. [Google Scholar] [CrossRef]
- Kim, K.H.; Kim, K.M.; Kim, Y.H.; Im, J.B.; Choi, G.H.; Kang, I.M.; Yoon, Y.J. Optimization of One-transistor (1T) DRAM using Device Parameters-dependent Zero-temperature Coefficient Point. J. Semicond. Technol. Sci. 2025, 25, 274–283. [Google Scholar] [CrossRef]
- Wenger, Y.; Meinerzhagen, B. Low-Voltage Current and Voltage Reference Design Based on the MOSFET ZTC Effect. IEEE Trans. Circuits Syst. I Regul. Pap. 2019, 66, 3445–3456. [Google Scholar] [CrossRef]
- Cho, M.S.; Mun, H.J.; Lee, S.H.; Jang, J.; Bae, J.-H.; Kang, I.M. Simulation of capacitorless dynamic random access memory based on junctionless FinFETs using grain boundary of polycrystalline silicon. Appl. Phys. A 2020, 126, 943. [Google Scholar] [CrossRef]
- Lee, S.H.; Jang, W.D.; Yoon, Y.J.; Seo, J.H.; Mun, H.J.; Cho, M.S.; Jang, J.; Bae, J.-H.; Kang, I.M. Polycrystalline-Silicon-MOSFET-Based Capacitorless DRAM with Grain Boundaries and Its Performances. IEEE Access 2021, 9, 50281–50290. [Google Scholar] [CrossRef]
- Kim, G.U.; Yoon, Y.J.; Seo, J.H.; Lee, S.H.; Park, J.; Kang, G.E.; Heo, J.H.; Jang, J.; Bae, J.-H.; Lee, S.-H.; et al. Design of a Capacitorless DRAM Based on Storage Layer Separated Using Separation Oxide and Polycrystalline Silicon. Electronics 2022, 11, 3365. [Google Scholar] [CrossRef]
- Yoo, S.; Sun, W.; Shin, H. Analysis of a Lateral Grain Boundary for Reducing Performance Variations in Poly-Si 1T-DRAM. Micromachines 2020, 11, 952. [Google Scholar] [CrossRef]
- Ho, C.-H.; Panagopoulos, G.; Roy, K. A Physical Model for Grain-Boundary-Induced Threshold Voltage Variation in Polysilicon Thin-Film Transistors. IEEE Trans. Electron. Devices 2012, 59, 2396–2402. [Google Scholar] [CrossRef]
- Kim, H.; Yoo, S.; Kang, I.-M.; Cho, S.; Sun, W.; Shin, H. Analysis of the Sensing Margin of Silicon and Poly-Si 1T-DRAM. Micromachines 2020, 11, 228. [Google Scholar] [CrossRef]
- Kimura, M.; Inoue, S.; Shimoda, T.; Sameshima, T. Device Simulation of Carrier Transport through Grain Boundaries in Lightly Doped Polysilicon Films and Dependence on Dopant Density. Jpn. J. Appl. Phys. 2001, 40, 5237–5243. [Google Scholar] [CrossRef]
- An, U.; Yoon, G.; Go, D.; Park, J.; Kim, D.; Kim, J.; Lee, J.-S. Effects of Poly-Si Grain Boundary on Retention Characteristics under Cross-Temperature Conditions in 3-D NAND Flash Memory. Micromachines 2023, 14, 2199. [Google Scholar] [CrossRef]
- Sporea, R.A.; Wheeler, L.J.; Stolojan, V.; Silva, S.R.P. Towards manufacturing high uniformity polysilicon circuits through TFT contact barrier engineering. Sci. Rep. 2018, 8, 17558. [Google Scholar] [CrossRef]
- Morimoto, Y.; Jinno, Y.; Hirai, K.; Ogata, H.; Yamada, T.; Yoneda, K. Influence of the Grain Boundaries and Intragrain Defects on the Performance of Poly-Si Thin Film Transistors. J. Electrochem. Soc. 1997, 144, 2495–2501. [Google Scholar] [CrossRef]
- Wu, T.-T.; Huang, W.-H.; Yang, C.-C.; Chen, H.-C.; Hsieh, T.-Y.; Lin, W.-S.; Kao, M.-H.; Chen, C.-H.; Yao, J.-Y.; Jian, Y.-L.; et al. High Performance and Low power Monolithic Three-Dimensional Sub-50 nm Poly Si Thin Film Transistor (TFTs) Circuits. Sci. Rep. 2017, 7, 1368. [Google Scholar] [CrossRef]
- Park, J.; Lee, S.-H.; Kang, G.-E.; Heo, J.-H.; Jeon, S.-R.; Kim, M.-S.; Bae, S.-J.; Hong, J.-W.; Jang, J.-W.; Bae, J.-H.; et al. Simulation of Capacitorless DRAM Based on the Polycrystalline Silicon Nanotube Structure with Multiple Grain Boundaries. Nanomaterials 2023, 13, 2026. [Google Scholar] [CrossRef] [PubMed]
- Mishin, Y.; Herzig, C. Grain boundary diffusion: Recent progress and future research. Mater. Sci. Eng. A 1999, 260, 55–71. [Google Scholar] [CrossRef]
- Lin, P.-J.; Chiu, Y.-Y.; Chen, F.; Shirota, R. Simulation Study of the Instability Induced by the Variation of Grain Boundary Width and Trap Density in Gate-All-Around Polysilicon Transistor. IEEE Trans. Electron. Devices 2021, 68, 1969–1974. [Google Scholar] [CrossRef]
- Wang, Z.; Zheng, L.; Lin, Z.; Zhao, J.; Tang, W.; Feng, L.; Liu, Z.; Li, X.; Guo, X.; Si, M. CMOS Logic and Capacitorless DRAM by Stacked Oxide Semiconductor and Poly-Si Transistors for Monolithic 3-D Integration. IEEE Trans. Electron. Devices 2024, 71, 4664–4669. [Google Scholar] [CrossRef]
- Baek, M.-H.; Kim, H. Polysilicon-Channel Synaptic Transistors for Implementation of Short- and Long-Term Memory Characteristics. Biomimetics 2023, 8, 368. [Google Scholar] [CrossRef]
- Lee, S.H.; Park, J.; Min, S.R.; Kim, G.U.; Jang, J.; Bae, J.-H.; Lee, S.-H.; Kang, I.M. 3-D stacked polycrystalline-silicon-MOSFET-based capacitorless DRAM with superior immunity to grain-boundary’s influence. Sci. Rep. 2022, 12, 14455. [Google Scholar] [CrossRef] [PubMed]
- Synopsys Inc. Sentaurus Device User Guide, Version P-2019.03; Synopsys Inc.: San Jose, CA, USA, 2019. [Google Scholar]
- IRDS. More Moore, 2023 International Roadmap for Devices and Systems (IRDS™) Edition. Available online: https://irds.ieee.org/editions/2023 (accessed on 20 June 2025).
- Macambira, C.N.; Itocazu, V.T.; Almeida, L.M.; Martino, J.A.; Simoen, E.; Claeys, C. Ground plane influence on Zero-Temperature-Coefficient in SOI UTBB MOSFETs with different silicon film thicknesses. In Proceedings of the 31st Symposium on Microelectronics Technology and Devices (SBMicro), Belo Horizonte, Brazil, 29 August–1 September 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Chiah, S.B.; Zhou, X.; Yuan, L. Compact Zero-Temperature Coefficient Modeling Approach for MOSFETs Based on Unified Regional Modeling of Surface Potential. IEEE Trans. Electron. Devices 2013, 60, 2164–2170. [Google Scholar] [CrossRef]
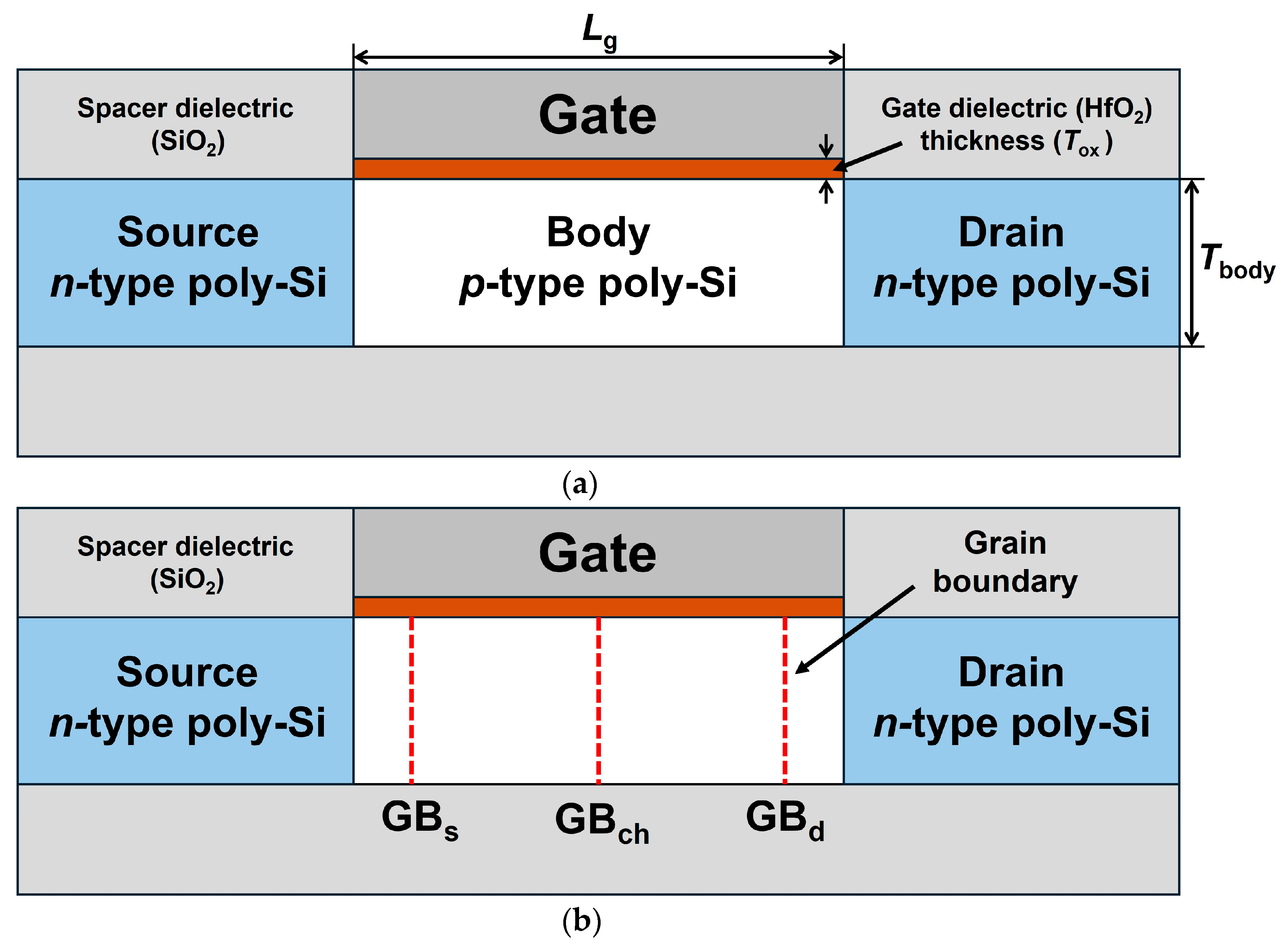
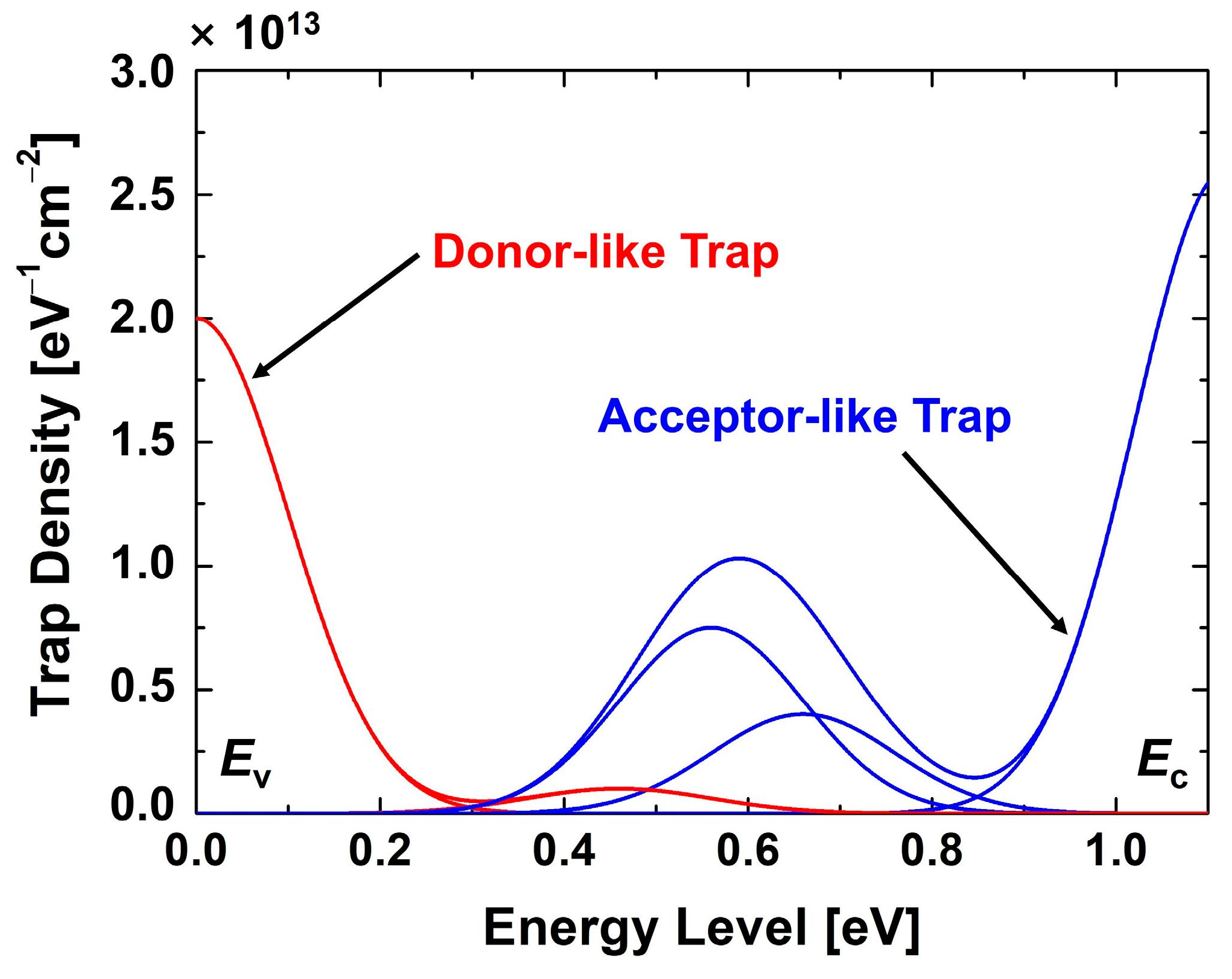



| Parameters | Values |
|---|---|
| Gate length (Lg) | 70 nm |
| Body thickness (Tbody) | 7–25 nm |
| Gate dielectric (HfO2) thickness (Tox) | 3 nm |
| Source/Drain doping concentration | n-type, 5 × 1019 cm−3 |
| Body doping concentration | p-type, 1 × 1016–1 × 1018 cm−3 |
| Gate work function | 5.1 eV |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, K.H.; Kang, I.M.; Yoon, Y.J.; Kim, K. Impact of Grain Boundaries on Zero-Temperature Coefficient Characteristics in a 3D-Stacked Transistor. Electronics 2025, 14, 3494. https://doi.org/10.3390/electronics14173494
Kim KH, Kang IM, Yoon YJ, Kim K. Impact of Grain Boundaries on Zero-Temperature Coefficient Characteristics in a 3D-Stacked Transistor. Electronics. 2025; 14(17):3494. https://doi.org/10.3390/electronics14173494
Chicago/Turabian StyleKim, Kyung Hee, In Man Kang, Young Jun Yoon, and Kibeom Kim. 2025. "Impact of Grain Boundaries on Zero-Temperature Coefficient Characteristics in a 3D-Stacked Transistor" Electronics 14, no. 17: 3494. https://doi.org/10.3390/electronics14173494
APA StyleKim, K. H., Kang, I. M., Yoon, Y. J., & Kim, K. (2025). Impact of Grain Boundaries on Zero-Temperature Coefficient Characteristics in a 3D-Stacked Transistor. Electronics, 14(17), 3494. https://doi.org/10.3390/electronics14173494






